椭圆的简单几何性质课件(2) 新人教A版选修2-1

合集下载

2.2.2椭圆的简单几何性质课件(人教A版选修2-1)

设P(x,y)为椭圆
x2 a2
y2 b2
1(a
b
0)上任一点, 则
| PO |
x2 y2
x2
b2 a2
(a2
x2 )
c2x2 a2b2 ,
a
∵-a≤x≤a,∴当x=0时,|PO|有最小值b,这时P在短轴端点处;当
x=±a时,|PO|有最大值a,这时P在长轴端点处,这一性质在
实际解题中会经常用到.如椭圆
C.有相同的焦点 D.有相等的焦距
解析:当0<k<9时,(25-k)-(9-k)=25-9=16=c2,∴c=4,而焦点一个在x轴上,一个在y轴上,∴两椭圆的焦点不同,因此,有相同的焦距,故选D.
答案:D
3.已知椭圆的长轴长是短轴长的2倍, 则椭圆的离心率等于( )
A. 1 B. 3 C. 1
1, ①
x22 y22 1, ②① ②得 43
(x1 x2 )(x1 x2 ) ( y1 y2 )( y1 y2 ) 0,
4
3
y1 y2 3 x1 x2 .又M(1,1)为AB的中点, x1 x2 4 y1 y2
x1
14e 5 0.
e 1 或e 5 (舍去).
2
4
规律技巧:求椭圆离心率的一般方法是:求出a,c的值或找出a 与c的关系式,解方程求出离心率e.(注意应用条件 a2=b2+c2).
变式训练3:椭圆的一个顶点与两个焦点构成等边三角形,则此椭圆的离心率是( )
A. 1 B. 3 C. 3
D. 1
点对称. (2)椭圆具备上述①､②､③条,因此椭圆关于､x\,y轴和坐标原
点对称.
2.椭圆性质的分类
椭圆的几何性质可分为两类:一类是与坐标系无关的本身的固有性质,如长轴长､短轴长､焦距､离心率;一类是与坐标系有关的性质,如顶点､焦点､中心坐标､x,y的范围.

高二数学人教A版选修2-1课件：2.2.2 椭圆的简单几何性质

或��2
25
+
2��02 =1.
一二三
知识精要
典题例解
迁移应用
(2)∵椭圆的长轴长是 6,cos∠OFA=23,
∴点 A 不是长轴的端点(是短轴的端点). ∴|OF|=c,|AF|=a=3.
∴��
3
=
23.∴c=2, b2= 32- 22= 5.
∴椭圆的方程是��2
目标导航
预习导引
12
轴长焦点
长轴长为 2a,短轴长为 2b
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
焦点的位置焦点在 x 轴上
焦点在 y 轴上
焦距对称性
2c 对称轴为 x 轴和 y 轴,对称中心为原点
离心率
e=c ,其中 c= a2-b2
a
目标导航
预习导引
12
求椭圆 16x2+25y2=400 的长轴长、短轴长、离心率以及焦点和顶点的坐标.
一二三
知识精要
典题例解
迁移应用
由 e= 23,得
��+2 ��+3
=
23,∴m=1.
∴椭圆的标准方程为
x2+
��2
1
=1,
4
∴a=1,b=12,c= 23. ∴椭圆的长轴和短轴的长分别为 2 和 1,两焦点坐标分别为
F1
-
3 2
,0
和 F2
3 2
,0
,四个顶点分别为
A1(-1,0),A2(1,0),B1
9
+
��2 5
=1

2016-2017年数学·人教A版选修2-1课件：2.2.2第1课时椭圆的简单几何性质

(1)椭圆的离心率 e 越大，椭圆就越“圆”．( )
(2)椭圆既是轴对称图形，又是中心对称图形．( )
(3)椭圆x92＋2y52 ＝1 的长轴长为 6.(
)
(4)两椭圆2x52＋y92＝1 与x92＋2y52 ＝1 形状完全相同，位
置不同．( )
答案：(1)× (2)√ (3)× (4)√
第九页，编辑于星期五：十七点四十七分。
第十四页，编辑于星期五：十七点四十七分。
类型 1 椭圆的简单几何性质(自主研析) [典例 1] 求椭圆 4x2＋9y 2＝36 的长轴长和短轴长、焦点坐标、顶点坐标和离心率，并用描点法画出它的图形．解：把椭圆的方程化为标准方程x92＋y42＝1.
第十五页，编辑于星期五：十七点四十七分。
可知此椭圆的焦点在 x 轴上，且长半轴长 a＝3，短半轴长 b＝2；又得半焦距 c＝ a2－b2＝ 9－4＝ 5.
第三十六页，编辑于星期五：十七点四十七分。
1．已知椭圆的方程讨论性质时，若不是标准形式，应先化成标准形式．
2．根据椭圆的几何性质，可以求椭圆的标准方程，其基本思路是“先定型，再定量”，常用的方法是待定系数法，在椭圆的基本量中，能确定类型的量有焦点、顶点，而不能确定类型的量有长轴长、短轴长、离心率 e、焦距．
第十一页，编辑于星期五：十七点四十七分。
4. 若椭圆的对称轴为坐标轴，长轴长与短轴长的和
为 18，一个焦点的坐标是(3，0)，则椭圆的标准方程为
________________．
2a＋2b＝18，
a＝5，
Байду номын сангаас
解析：由题意，得c＝3，
解得
a2＝b2＋c2，
b＝4.

人教A版高中数学选修2-1课件2.2.2椭圆的简单几何性质(2)

高中数学课件
灿若寒星整理制作
标准方程图形
x2 + y2 = 1a > b > x2 + y2 = 1a > b > 0
b2 a2 y
F2
P
O
x
F1
不同点
相同点
焦点坐标定义
a、b、c的关系
F1 -c , 0，F2 c , 0
F1 0,- c，F2 0,c
（2）解：利用椭圆的几何性质，以坐标轴为对称轴的椭圆与坐标轴的交点就是椭圆的顶点，于是焦点在x轴上，且点P、Q分别是椭圆长轴与短轴的一个端点，故a＝3，b＝2，故椭圆的标准方程为
x2 y2 1
94
x2
（3）

y2
1或
y2 x2 1
100 64
100 64
作业：P49T5
。
练：已知x轴上的一定点A（1,0），Q为椭圆上x2的动y2 1
点，求AQ中点M的轨迹方程.
4
y
解：设动点M的坐标为(x,y)，
Q M
则Q的坐标为(2x-1,2y)
-2
O A 2 x 因为Q点为椭圆上x的2 点y2 1
4
所以有 (2x 1)2 (2 y)2 1 4
即 (x 1)2 4y2 1 2
所以点M的轨迹方程是 (x 1 )2 4 y2 1 2
y
4 B2
3
2
A1
1
A2
-5 -4 -3 -2 --11 1 2 3 4 5 x
-2
-3
-4 B1
y
4
3 2
B2
A1
1
A2
-5 -4 -3 -2 --11 1 2 3 4 5 x

高二数学(人教A版)选修2-1课件2-2-2 椭圆的简单几何性质

x2 y2 (2)设椭圆的方程为 2＋ 2＝1(a>b>0)． a b 如图所示，△A1FA2 为等腰直角三角形，
OF 为斜边 A1A2 的中线(高)，且|OF|＝c，|A1A2|＝2b， ∴c＝b＝4，∴a2＝b2＋c2＝32， x2 y2 故所求椭圆的方程为32＋16＝1.
[点评]
利用椭圆的几何性质求标准方程，通常采用待定
成才之路· 数学
人教A版 ·选修2-1
路漫漫其修远兮吾将上下而求索
第二章
圆锥曲线与方程
第二章
2．2 椭圆
第二章
第 2 课时椭圆的简单几何性质
课前自主预习课堂巩固训练课堂典例讲练课后强化作业方法规律总结
课程目标解读
1．掌握椭圆的简单几何性质． 2．了解椭圆的离心率对椭圆扁平程度的影响． 3．掌握椭圆标准方程中的 a、b 以及 c、e 的几何意义，a、 b、c、e 之间的相互关系．
＝3，故椭圆的长轴和短轴的长分别为 2a＝10,2b＝8，离心率 e c 3 ＝＝，焦点坐标 F1(0，－3)，F2(0,3)，顶点坐标为 A1(0，－ a 5 5)，A2(0,5)，B1(－4，0)，B2(4,0).
ቤተ መጻሕፍቲ ባይዱ
命题方向
利用椭圆的几何性质求标准方程
[例 2]
求适合下列条件的椭圆的标准方程．
率、焦点和顶点坐标． [分析] 由题目可获取以下主要信息：①已知椭圆的方
程；②研究椭圆的几何性质．解答本题可先把方程化成标准形式然后再写出性质．
[解析]
x2 y2 把已知方程化成标准方程＋＝1， 16 9
于是 a＝4，b＝3，c＝ 16－9＝ 7， ∴椭圆的长轴长和短轴长分别是 2a＝8 和 2b＝6，离心率 c 7 e＝a＝ 4 ，两个焦点坐标分别是(－ 7，0)，( 7，0)，四个顶点坐标分别是(－4,0)，(4,0)，(0，－3)，(0,3)．

人教高中数学选修2-1：2.2.2椭圆的简单几何性质课件(共17张PPT)

例题讲解
例2：已知椭圆方程为16x2+25y2=400.
它的长轴长是： 10 .短轴长是： 8 .
焦距是 6
3
. 离心率等于 5
.
焦点坐标是： ( 3, 0 ) .顶点坐标是：(5, 0) (0, 4 )
分析：椭圆方程转化为标准方程为：
16x225y2400 x2y21 25 16
a=5 b=4 c=3
ox
y2 a2
bx22
1(ab0)
y
ox
-a≤ x≤ a, -b≤ y≤ b -b≤ x≤ b, -a≤ y≤ a
关于x轴、y轴成轴对称；关于原点成中心对称.
（±a , 0）,(0, ±b) （±b ,0）,(0,±a)
(±c,0)
(0, ±c)
长轴长＝___2_a___，短轴长＝___2_b___
(2)已知方程化为标准方程为
y2 81
x2 9
1,
故可得长轴长为18，短轴长为6，离心率为
2
2 3
,
焦点坐标为 0,6 2 ，顶点坐标（0,±9）,（±3,0）.
标准方程
图象
课范围堂对称性
顶点坐标
小焦点坐标结轴长
焦距 a,b,c关系离心率
x2 y2 1(ab0) a2 b2
y
焦距
2c
练习1：求下列椭圆的范围、焦点坐标
及其顶点坐标：
1x2y21
169
2y2x21
2516
解 1 4 ： x 4 , 3 y 3
焦点坐标： 7,0
顶点坐标：4,0,0,3
2 4 x 4 , 5 y 5
焦点坐标：0,3 顶点坐标：4,0,0,5

人教A版高中数学选修2-1课件2.1.2椭圆的简单几何性质(2).pptx

的最大值为 a+c ；则当P的
坐标为---(-a-,-0--)--时，PF1
的最小值为 a-c 。 7、椭圆 x2 16来自y2 121上一点
P
到两个焦点 F1, F2 的距
离之差为 2，试判断 F1PF2 的形状。
小结：
1、椭圆上一点P与椭圆的两个焦点所成的三角形称为焦点三角形。
例、设点
P
是
2
为。 2
2、若椭圆的两个焦点及一个短轴端点构成正三角
1
形，则其离心率为。 2
3、若椭圆的的两个焦点把长轴分成三等分，则其
离心率为。
1 3
4、若某个椭圆的长轴、短轴、焦距依次成等差数列，
3
则其离心率e=________5__
5、以椭圆的焦距为直径并过两焦点的圆，交椭圆于四个不同的点，顺次连接这四个点和两个焦点恰好组
9 16
x2 y2 B. 1.
25 16
C . x2 y2 1或 x2 y2 1.
x2 y2 D. 1
25 16
16 25
16 25
2、下列方程所表示的曲线中，关于x轴和y轴
都对称的是（）D
A、x2=4yB、x2+2xy+y=0C、x2-4y2=x D、9x2+y2=4
练习
1、若椭圆的焦距长等于它的短轴长，则其离心率
成一个正六边形，那么这个椭圆的离心率。3 1
6、点P是椭圆
x2 a2
y2 b2
1上的动点，当P的坐标为(±a,0)时，
P到原点O的最大距离为
a
；当P的坐标为(0,±b)时，
P到原点O的最小距离为------b-------；设F（1 c,0),则当P的

椭圆的简单几何性质课件

第二章圆锥曲线与方程
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
[解析] 把已知方程化成标准方程1x62 ＋y92＝1，于是 a＝4，b＝3，c＝ 16－9＝ 7， ∴椭圆的长轴长和短轴长分别是 2a＝8 和 2b＝6，离心率 e ＝ac＝ 47，两个焦点坐标分别是(－ 7，0)，( 7，0)，四个顶点坐标分别是(－4,0)，(4,0)，(0，－3)，(0,3)．
第二章圆锥曲线与方程
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
椭圆的主要几何量求椭圆 9x2＋16y2＝144 的长轴长、短轴长、离心率、焦点和顶点坐标． [分析] 由题目可获取以下主要信息：①已知椭圆的方程； ②研究椭圆的几何性质．解答本题可先把方程化成标准形式然后再写出性质．
___|x_|_≤_a_，__|y_|≤_b_____
____|x_|_≤_b_，__|y_|≤__a___
关于__x_轴__、__y_轴__和__原__点__对称
_(_±__a_,0_)_，__(_0_，__
轴
长轴长__2_a____，短轴长___2_b___
第二章圆锥曲线与方程
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
[方法规律总结] 1.由椭圆方程讨论其几何性质的步骤： (1)化椭圆方程为标准形式，确定焦点在哪个轴上． (2)由标准形式求a、b、c，写出其几何性质． 2．椭圆的几何性质与椭圆的形状、大小和位置的关系 (1)椭圆的焦点决定椭圆的位置； (2)椭圆的范围决定椭圆的大小； (3)椭圆的离心率刻画椭圆的扁平程度； (4)对称性是圆锥曲线的重要性质，椭圆的顶点是椭圆与对称轴的交点，是椭圆上的重要的特殊点，在画图时应先确定这些点．

人教A版高中数学选修2-1教案椭圆的简单几何性质(2)

科目数学课题 2.2.2椭圆的简单几何性质（二）教学班级中级班三维目标知识与技能会用椭圆的定义解决实际问题；通过例题了解椭圆的第二定义，准线及焦半径的概念，利用信息技术初步了解椭圆的第二定义．过程与方法通过椭圆的方程研究其几何性质及其应用过程，培养学生观察、分析问题的能力，利用数形结合思想解决问题的能力情感态度与价值观通过数与形的辩证统一，对学生进行辩证唯物主义教育，通过对椭圆对称美的感受，激发学生对美好事物的追求教学用具教学重点椭圆的定义解决实际问题，了解椭圆的第二定义教学难点了解椭圆的第二定义教学步骤及要点：教学过程：（一）复习：椭圆的简单几何性质1．椭圆81922=+y x 的长轴长为 18 ，短轴长为 6 ，半焦距为26，离心率为322，焦点坐标为)26,0(±，顶点坐标为)9,0(±)0,3(±，. 2．短轴长为8，离心率为53的椭圆两焦点分别为1F 、2F ，过点1F 作直线l 交椭圆于A 、B 两点，则2ABF ∆的周长为 20 .（二）新授例1．如图，一种电影放映灯的反射镜面是旋转椭圆面的一部分．对称的截口BAC 是椭圆的一部分，灯丝位于椭圆的一个焦点1F 上，片门位于另一个焦点2F 上，由椭圆一个焦点1F 发出的光线，经过旋转椭圆面反射后集中到另一个焦点2F ．已知12BC F F ⊥，1 2.8F B cm =，12 4.5F F cm =．建立适当的坐标系，求截口BAC 所在椭圆的方程．解析：建立适当的直角坐标系，设椭圆的标准方程为22221x y a b+=，算出,,a b c 的值；此题应注意两点：①注意建立直角坐标系的两个原则；②关于,,a b c 的近似值，原则上在没有注意精确度时，看题中其他量给定的有效数字来决定．引申：如图所示， “神舟七号”截人飞船发射升空，进入预定轨道开始巡天飞行，其轨道是以地球的中心2F 为一个焦点的椭圆，近地点A 距地面200km ，远地点B 距地面350km ，已知地球的半径6371R km =．建立适当的直角坐标系，求出椭圆的轨迹方程．例2．如图，设(),M x y 与定点()4,0F 的距离和它到直线l ：254x =的距离的比是常数45，求点M 的轨迹方程．分析：若设点(),M x y ，则()224MF x y =-+，到直线l ：254x =的距离254d x =-，则容易得点M 的轨迹方程．引申：若点(),M x y 与定点(),0F c 的距离和它到定直线l ：2a x c=的距离比是常数ce a=()0a c >>，则点M 的轨迹方程是椭圆．其中焦点(),0F c 相应的准线是定直线l ：2a x c =；焦点(),0F c '-，相应的准线l '：2a x c=-,由椭圆的第二定义e dMF =∴||。

3.1.2椭圆的简单几何性质课件(第2课时)-高二上学期数学人教A版(2019)选择性必修第一册

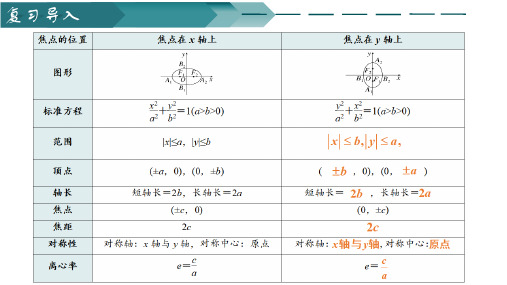
2
2
相应的准线方程分别为 = − 和 = .

|1 |
|2 |
=

，

= .
由椭圆第二定义得 2
2
+ 0
− 0
a2
l : x
c
a2
l:x
c
y
P
•
•
F1
O
|1 | = + 0 ，|2 | = − 0 .
说明：|1|, |2|称为椭圆的焦半径，此公式称为焦半径公式.
(2)当 Δ＝0，即 m＝±3 2 时，直线 l 与椭圆 C 有且只有一个公共点．
方法总结
方法总结：判断直线与椭圆的位置关系的方法
[注意]：方程组解的个数与直线与椭圆的公共点的个数之间是等价关系．
练习巩固
变式7-2: 求下列直线与椭圆的交点坐标:
2 2
2 2

+
= 1.
(1)3 + 10 − 25 = 0，
复习导入
第三章
圆锥曲线的方程
3.1.2椭圆的简单几何性质
（第2课时）
练习巩固
例5：如图，一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的
曲面)的一部分.过对称轴的截口是椭圆的一部分，灯丝位于椭圆的一个焦点1 上，
片门位于另一个焦点2 上.由椭圆一个焦点1 发出的光线，经过旋转椭圆面反射后集中
|F1 B|2 + |F1 F2 |2 = 2.82 + 4.52 .
由椭圆的性质知，|F1 B| + |F2 B| = 2a.
所以a =
1
(|F1 B|
2

《椭圆》课件1(新人教A版选修2-1)

A1(5,0), A2 (5,0), B1(0,4), B2 (0,4)
补充题：如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆.已知它的近地点A(离地面最近的点)距地面 439km,远地点B(离地面最远的点)距地面2384km, 并且F2、A、B在同一直线上,地球半径约为 6371km.求卫星运行的轨道方程(精确到1km).
心率、焦点和顶点坐标解：把已知方程化成标准方程
x2
+
y2 = 1
52
42
这里， a 5, b 4, c 25 16 3
因此，椭圆的长轴长和短轴长分别是 2a 10,2b 8
离心率 e c 3 0.6 a5
焦点坐标分别是
F1(3,0), F2 (3,0)
四个顶点坐标是
轴焦点坐标
离心率
a, 0 0, b
0, a b, 0
x 轴，y 轴，长轴长 2a, 短轴长 2b
c, 0
c a2 b2 0, c
e c 0 e 1
a
c a2 b2
例4 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离
y
又 a2 b2 c2 a 2
c 1, a 2 3,b 1 3
x
3
3
椭圆方程为： y2 x2 1
4
3
练习3：已知椭圆的中心在原点，一个顶点和一个焦点分
别是直线 x + 3y –6=0与两坐标轴的交点，求x它的标
准方程。
解：如右图所示，若A(6,0)为顶点， B(0, 2)为焦点，则b=6 , c=2, a2=b2+c2=40. 此时椭圆的标准方程为

人教A版高中数学选修2-1《2.2.2椭圆的简单几何性质(二)》课件

反思与感悟
跟踪训练 2 (1)已知直线 l 过点(3，－1)，且椭圆 C：2x52 ＋3y62 ＝1，则直线 l 与椭圆 C 的公共点的个数为答案解析
A.1
B.1或2
C.2
D.0
因为直线过定点(3，－1)且2352 ＋－3612<1，所以点(3，－1)在椭圆的内部，故直线l与椭圆有2个公共点.
(2)在平面直角坐标系 xOy 中，经过点(0， 2)且斜率为 k 的直线 l 与椭圆
x22＋y2＝1 有两个不同的交点 P 和 Q.求 k 的取值范围. 解答
由已知条件知直线 l 的方程为 y＝kx＋ 2，代入椭圆方程得x22＋(kx＋ 2)2
＝1.整理得12＋k2x2＋2 2kx＋1＝0.直线 l 与椭圆有两个不同的交点 P 和 Q
思考2
类比点与圆的位置关系的判定，你能给出点 P(x0，y0)与椭圆ax22＋by22＝1 (a>b>0)的位置关系的判定吗？答案
当 P 在椭圆外时，ax202＋by202>1；当 P 在椭圆上时，ax202＋by202＝1；当 P 在椭圆内时，ax202＋by202<1.
梳理
设 P(x0，y0)，椭圆ax22＋by22＝1(a>b>0)，则点 P 与椭圆的位置关系如下表所示：
引申探究在本例中求弦AB的长. 解答
由上例得直线AB方程为x＋2y－4＝0.
x＋2y－4＝0，

联立方程组1x62 ＋y42＝1，
消去 y 并整理，得
x(x－4)＝0，得x＝0或x＝4，
得两交点坐标A(0，2)，B(4，0)，
故|AB|＝ 0－42＋2－02＝2 5.
反思与感悟
直线与椭圆的交点问题，一般考虑直线方程与椭圆方程组成的方程组的解的问题，即判断消元后所得的一元二次方程的根的判别式Δ.解决弦长问题，一般应用弦长公式.而用弦长公式时，若能结合根与系数的关系 “设而不求”，可大大简化运算过程.

(教师参考)高中数学 2.2.2 椭圆的简单几何性质课件1 新人教A版选修2-1

e＝ac＝||FO2FB22||＝cos∠OF2B2.
(4)若椭圆的标准方程为ax22＋yb22＝1(a>b>0)，则椭圆与 x 轴的交点 A1，A2 到焦点 F2 的距离分别最大和最小，且|A1F2|＝a＋c，|A2F2| ＝a－c.
精选ppt
15
思考:已知椭圆的长轴A1A2和短轴B1B2 ，
怎样确定椭圆焦点的位置？
知椭圆的标准方程，则根据a、b的值可确定其性质．
(2)明确a，b的几何意义，a是长半轴长，b是短半轴长，不
要与长轴长、短轴长混淆，由c2＝a2－b2，可得“已知椭圆
的四个顶点，求焦点”的几何作图法，只要以短轴的端点
B1(或B2)为圆心，以a为半径作弧交长轴于两点，这两点就是焦点．
精选ppt
14
(3)如图所示椭圆中的△OF2B2 找出 a，b，c， e 对应的线段或量为 a＝|F2B2|，b＝|OB2|，c＝|OF2|，
B2
a
A1
F1 c
b
oc
a
A2
F2
因为a2=b2+c2,所以以椭圆B1 短轴端点为
圆心,a长为半径的圆与x轴的交点即为
椭圆焦点.
精选ppt
16
4 离心率
思考观察不同的图2椭 .1圆 9,我们发, 现
椭圆的扁平程 ,那度么 ,用不什一么量可以画椭圆的扁平 ? 程度呢
18
我们把椭圆的焦轴距长与 c的称长为椭：圆的离心率
用e来表示， e即 c.
a
a
因为 a >c>0,所以 e 的取值范围是:__0_<_e_<_1___
e 越接近于1,则c越接近于a,从而b就越小,因此椭圆就越扁反之,e越接近于0, c 就越接近于0,从而b 就越接近于 a,这时椭圆就越接近于圆

人教A版高中数学选修2-1课件《2.2.2椭圆的简单几何性质(第二课时)》

y M
OF
x
最大值为a＋c，最小值为a－c.
新知探究
椭圆上一点M(x0，y0)到左焦点F1(－c， 0)和右焦点F2(c，0)的距离分别是
|MF1|＝a＋ex0
y M
|MF2|＝a－ex0
F1 O
F2
x
新知探究
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径，上述结果就是椭圆的焦半径公式.
|MF1|＝a＋ex0
椭圆左准线的距离为10，求点P到椭圆右焦点的距离.
12
典型例题
例2已知椭圆的两条准线方程为
y＝±9，离心率为，1 求此椭圆的标准方
程.
3
x2 y2 1
89
典型例题
例3已知椭圆中心在原点，焦点在x轴上，点P为直线x＝3与椭圆的一个交点，若点P到椭圆两焦点的距离分别是6.5 和3.5，求椭圆的方程.
课堂小结
2.一个椭圆有两条准线，并与两个焦点相对应，两条准线在椭圆外部，且与长轴垂直，关于短轴对称.
课堂小结
3.椭圆焦半径公式的两种形式与焦点位置有关，可以记忆为“左加右减，下加上减”.
布置作业
P49习题2.2A组：
3，4，5，10.
l
M
H
F
新知探究
直的的线准准叫线线做方，x =椭程相ac圆是应2 相于应焦于点焦F1(点－xFc=2(，-c， 0a)2 0)
y
c
a2 x= -
c
a2 x=
c
F1 O F2
x
新知探究
椭圆的bx22 准 ay线22 方1程a 是 by 0
F2
y = a2 c
O
x
F1
a2 y= -

高中数学人教A版选修2-1：2.2.2-2 椭圆的简单几何性质课件(共11张PPT)教学课件

脚踏实地过好每一天，最简单的恰恰是最难的。拿梦想去拼，我怎么能输。只要学不死，就往死里学。我会努力站在万人中央成为别人的光。行为决定性格，性格决定命运。不曾扬帆，何以至远方。人生充满苦痛，我们有幸来过。如果骄傲没有被现实的大海冷冷拍下，又怎么会明白要多努力才能走到远方。所有的豪言都收起来，所有的呐喊都咽下去。十年后所有难过都是下酒菜。人生如逆旅，我亦是行人。驾驭命运的舵是奋斗，不抱有一丝幻想，不放弃一点机会，不停止一日努力。失败时郁郁寡欢，这是懦夫的表现。所有偷过的懒都会变成打脸的巴掌。越努力，越幸运。每一个不起舞的早晨，都是对生命的辜负。死鱼随波逐流，活鱼逆流而上。墙高万丈，挡的只是不来的人，要来，千军万马也是挡不住的既然选择远方，就注定风雨兼程。漫漫长路，荆棘丛生，待我用双手踏平。不要忘记最初那颗不倒的心。胸有凌云志，无高不可攀。人的才华就如海绵的水，没有外力的挤压，它是绝对流不出来的。流出来后，海绵才能吸收新的源泉。感恩生命，感谢她给予我们一个聪明的大脑。思考疑难的问题，生命的意义；赞颂真善美，批判假恶丑。记住精彩的瞬间，激动的时刻，温馨的情景，甜蜜的镜头。感恩生命赋予我们特有的灵性。善待自己，幸福无比，善待别人，快乐无比，善待生命，健康无比。一切伟大的行动和思想，都有一个微不足道的开始。在你发怒的时候，要紧闭你的嘴，免得增加你的怒气。获致幸福的不二法门是珍视你所拥有的、遗忘你所没有的。骄傲是胜利下的蛋，孵出来的却是失败。没有一个朋友比得上健康，没有一个敌人比得上病魔，与其为病痛暗自流泪，不如运动健身为生命添彩。有什么别有病，没什么别没钱，缺什么也别缺健康，健康不是一切，但是没有健康就没有一切。什么都可以不好，心情不能不好；什么都可以缺乏，自信不能缺乏；什么都可以不要，快乐不能不要；什么都可以忘掉，健身不能忘掉。选对事业可以成就一生，选对朋友可以智能一生，选对环境可以快乐一生，选对伴侣可以幸福一生，选对生活方式可以健康一生。含泪播种的人一定能含笑收获一个有信念者所开发出的力量，大于个只有兴趣者。忍耐力较诸脑力，尤胜一筹。影响我们人生的绝不仅仅是环境，其实是心态在控制个人的行动和思想。同时，心态也决定了一个人的视野、事业和成就，甚至一生。每一发奋努力的背后，必有加倍的赏赐。懒惰像生锈一样，比操劳更消耗身体。所有的胜利，与征服自己的胜利比起来，都是微不足道。所有的失败，与失去自己的失败比起来，更是微不足道挫折其实就是迈向成功所应缴的学费。在这个尘世上，虽然有不少寒冷，不少黑暗，但只要人与人之间多些信任，多些关爱，那么，就会增加许多阳光。一个能从别人的观念来看事情，能了解别人心灵活动的人，永远不必为自己的前途担心。当一个人先从自己的内心开始奋斗，他就是个有价值的人。没有人富有得可以不要别人的帮助，也没有人穷得不能在某方面给他人帮助。时间告诉你什么叫衰老，回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵，昨天的太阳，晒不干今天的衣裳。今天做别人不愿做的事，明天就能做别人做不到的事。到了一定年龄，便要学会寡言，每一句话都要有用，有重量。喜怒不形于色，大事淡然，有自己的底线。趁着年轻，不怕多吃一些苦。这些逆境与磨练，才会让你真正学会谦恭。不然，你那自以为是的聪明和藐视一切的优越感，迟早会毁了你。无论现在的你处于什么状态，是时候对自己说：不为模糊不清的未来担忧，只为清清楚楚的现在努力。世界上那些最容易的事情中，拖延时间最不费力。崇高的理想就像生长在高山上的鲜花。如果要搞下它，勤奋才能是攀登的绳索。行动是治愈恐惧的良药，而犹豫、拖延将不断滋养恐惧。海浪的品格，就是无数次被礁石击碎又无数闪地扑向礁石。人都是矛盾的，渴望被理解，又害怕被看穿。经过大海的一番磨砺，卵石才变得更加美丽光滑。生活可以是甜的，也可以是苦的，但不能是没味的。你可以胜利，也可以失败，但你不能屈服。越是看起来极简单的人，越是内心极丰盛的人。盆景秀木正因为被人溺爱，才破灭了成为栋梁之材的

人教A版高中数学选修2-1课件2.2.2椭圆的几何性质(1)

高中数学课件
灿若寒星整理制作
解析几何研究的主要问题是什么？（1）根据已知条件，求出表示曲线的方程。（2）通过方程，研究平面曲线的性质。
2.2.2 椭圆的简单几何性质（1）
观察椭圆
x2 a2

y2 b2
1
(a b 0) 的形状，
你能从图上看出它的范围吗？它具有怎样的对称性？
椭圆上哪些点比较特殊？
y B2 M
A1 F1 0 B1
F2 A2 x
1. 椭圆的范围
由
x2 a2

y2 b2
1得
x2 a2

1和
y2 b2
1
即 x a和 y b
y
说明：椭圆位于直线
x=±a和y=±b所围成的
o
x
矩形之中。
3. 椭圆的顶点
y
B2
A1
o ︱
F1
︱
F2
A2 x
B1
3. 椭圆的顶点
在
x2 a2
a5
a 10，c 6 .
b2 a2 c2 64 .

x2 y2 1 或 100 64
y2 x2 1. 100 64
例 3.
已知 F1,F2 是椭圆 C:
x2 a2

y2 b2
1（ a
b

0 ）的
左、右焦点，点 P ( 2,1) 在椭圆上，线段 PF2 与 y 轴的交点
2 x0 2
10 5x0 10
y N
10 3x1 4 y1 10.
F1 O F2
x
国庆作业
1、练习册： 1.3节+1.4节+复习与小结+2.1节+2.2.1(1)、(2)

人教A版高中数学选修2-1课件【13】椭圆的简单几何性质

1 1 B10，－2，B20，2.
11．如图所示，F1，F2 分别为椭圆的左，右焦点，椭圆上点 2 M 的横坐标等于右焦点的横坐标，其纵坐标等于短半轴长的3，求椭圆的离心率．
解：设椭圆的长半轴，短半轴，半焦距长分别为 a，b，c.则焦点为 F1(－c,0)，F2(c,0)，M 点的坐标为为直角三角形．在 Rt△MF1F2 中， |F1F2|2＋|MF2|2＝|MF1|2， 4 2 即 4c ＋9b ＝|MF1|2.
12. 2 如图，在 Rt△ABC 中，∠CAB＝90° ，AB＝2，AC＝ 2 .一曲线 E 过点 C，动点 P 在曲线 E 上运动，且保持|PA|＋|PB|的值不变． (1)建立适当的坐标系，求曲线 E 的方程； (2)试判断该方程是否为椭圆方程，若是，请写出其长轴长、焦距、离心率．
解：(1)以 AB 所在直线为 x 轴，AB 的中点 O 为原点建立平面直角坐标系，则 A(－1,0)，B(1,0)， 2 由题设可得|PA|＋|PB|＝|CA|＋|CB|＝＋ 2 由椭圆定义知动点 P 的轨迹为椭圆． x2 y2 不妨设动点 P 的轨迹方程为a2＋b2＝1(a＞b＞0)，则 a＝ 2， c＝1，b＝ a2－b2＝1， x2 2 ∴曲线 E 的方程为＋y ＝1. 2 2
b x ＋x ＝－， a c 1 1 2 解析：由题意 e＝a＝2， x1x2＝－ c， a
2 2 2 2 a － c b 2 c c 7 2 2 2 ∴ x1 ＋ x 2 ＝ (x1 ＋ x2) － 2x1x2 ＝ a2 ＋ a ＝ a2 ＋ 1 ＝ 2 － a2＝ 4
＜2. ∴点 P(x1，x2)在圆 x2＋y2＝2 内．
2 答案：3
三、解答题：每小题 15 分，共 45 分． 3 10．已知椭圆 x ＋(m＋3)y ＝m(m＞0)的离心率 e＝，求 m 2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y
a 直线 x 叫做椭圆相应于焦点 c c
2
a x c
2
a x c
F1 O F2 x
2
新知探究
x2 y 2 椭圆 2 2 1 a b 0 的准线方程是 b a 2 y a y c
F2
O
F1
x
a y c
2
y 2 x2 3 2 1 例2．椭圆 a 2 b （a>b>0）的离心率 e 2 ，
新知探究
椭圆上的点到椭圆焦点的距离的最大值和最小值分别是什么？
y
B2
M
F2
|MF2|min=|A2F2| =a-c |MF2|max=|A1F2| A2 x =a+c
A1 F
1
O B1
新知探究
点M在椭圆上运动，当点M在什么位置时，∠F1MF2为最大？
y M F1 O
点M为短轴的端点.
F2
x 此时△F1MF2的面积最大
焦点到椭圆上点的最短距离为2－ 3求椭圆的方程.
x y 例3. 设F1、F2为椭圆 2 2 1 a b 0 a b
2
2
的两焦点，若椭圆上存在点P，使
∠F1PF2＝60°，求椭圆离心率的取
值范围.
y
B
F1 O
1 e [ ,1) 2
P F2焦点，椭圆上存在点M使得MF1⊥MF2,求椭圆的离心率的范围.
y l M o d H x
F
将上式两边平方，并化简，得9 x 2 25 y 2 225,
x2 y 2 即 1 25 9
所以，点M的轨迹是长轴、短轴长分别为10、6的椭圆。
变式: 1.已知点M到定点F的距离与M到定直线l的距离的比为0.8,则动点M的轨迹是( B ) A.圆 B.椭圆 C.直线 D.无法确定
知识回顾
2.椭圆离心率的取值范围？离心率变化对椭圆的扁平程度有什么影响？ e∈(0，1). e越接近于0，椭圆越圆； e越接近于1，椭圆越扁.
新知探究
x y 对于椭圆 2 2 1 a b 0 b a y
M O x
2
2
椭圆上的点到椭圆中心的距离的最大值和最小值分别是最大值为a，最小值为b.
25 解：设d是点M到直线l : x 的距离，根据题意， 4 MF 4 点M的轨迹就是集合P M , d 5 ( x 4) y 2 4 由此得 . 25 5 x 4
例1.点M(x,y)与定点F(4,0)的距离和它到直线 4 25 l:x= 的距离的比是常数 5 ，求点M的轨 4 迹.
布置作业
1、P49习题2.2A组：
3，4，5，10.
2
c a
M
O F
H
x
椭圆上的点M(x，y)到焦点F(c，0)的距 2 a 的距离之比等于离离与它到直线 x c 心率.
a x c
2
新知探究
若点F是定直线l外一定点，动点M到点F的距离与它到直线l的距离之比等于常数e(0＜e＜1)，则点M的轨迹是椭 l 圆.
M F H
新知探究
F2(c，0)的准线，相应于焦点 a2 F1(－c，0)的准线方程是 x
2.2.2
椭圆的简单几何性质
第二课时
知识回顾
y x 2 2 2 1. 椭圆 2 2 1 a b 0, a b c a b
2
2
的范围、对称性、顶点、离心率范围：－a≤y≤a，－b≤x≤b. 对称性：关于x轴、y轴、原点对称.
顶点：(0 ，± a)，(±b ,0 ).
c 离心率： e . a
新知探究
1.对于椭圆的原始方程,
(x + c ) + y +
2
2 2
(x - c) + y = 2a
2 2
2
2
变形后得到 a - cx = a (x - c) + y , 再变形为
（x - c） y
2 2
这个方程的几何意义如何？
a2 x c
c a
.
新知探究
y
2 2
l
（x - c） y a x c
y
BM
F1 O F2 x
课堂小结
1.椭圆上的点到一个焦点的距离与它到相应准线的距离之比等于椭圆的离心率，这是椭圆的一个重要性质，通常将它称为椭圆的第二定义.
课堂小结
2.一个椭圆有两条准线，并与两个焦点相对应，两条准线在椭圆外部，且与长轴垂直，关于短轴对称.
课堂小结
3.椭圆焦半径公式的两种形式与焦点位置有关，可以记忆为“左加右减，下加上减”.