第二章 晶体结构14版
第二章 晶体结构ppt课件

空间点阵——每个阵点处原子都具有相同的环境,其种类有限 (仅有14种)。
亦即是说,每种空间点阵都可以形成无限多的晶体结构。
空间点阵概括地表明了原子、离子、原子集团、分 子等粒子在晶体结构空间中作周期分别的最基本规律。 空间点阵是把晶体中的质点抽象为阵点,用来描述和分 析晶体结构的周期性与对称性,要求各个阵点的周围环 境相同,它只能有14种类型。 晶体结构则是晶体中实际质点(原子、离子或分子) 的具体排列情况,它们能组成各种类型的排列,因此, 实际存在的晶体结构是无限的。 无论多么复杂的晶体结构都只有一个空间点阵。
二、结合力与结合能(续)
1-3 双原子结合力、结合能模型
双原子互作用力模型
双原子互作用能模型
三、原子半径(Ra)
1.计算公式 当R=R0时,两个正离子间的 中心距,称为原子直径(2Ra),亦 即R0=2Ra;
2.影响因素 ① 致密度越高,则Ra越小;
②键合力越高,则Ra越小;
③不同方向上Ra也可能不同;
四、晶体性
1.固体的分类 晶体——原子呈周期性排列; 非晶体——原子呈不规则排列; 2. 晶体的分类 单晶体——整个物质由一个晶粒组成,其中原子排列位向相同, 具有各向异性。 多晶体——有许多位向不同的小单晶体组成,具有各向同性(单 个经历的各向异性被“平均化”)。 3.晶体和非晶体相互关系 晶体和非晶体在一定的条件下可以相互转化。例如,在极大的冷 速下,可以得到非晶态金属。其原因是液态金属在冷却时来不及 转变成晶体就凝固了,非晶体实质上是一种过冷的液体结构(短 程有序)。
Material Material
大学材料科学基础第2章 材料中的晶体结构PPT课件

30.10.2020
DALIAN JIAOTONG UNIVERSITY
21
2.点阵常数
晶胞棱边长度a、b、c与原子半径r之间 的关系:
体心立方结构(a=b=c) a = 4 (√3 /3) r
面心立方结构(a=b=c) a = 2 (√2 ) r 密排六方结构(a=b c) a = 2r
30.10.2020
阵点——构成空间点阵的每一个点
晶格——将阵点用一系列相互平行的直线连接 起来形成空间格架
晶胞——构成晶格的最基本单元
30.10.2020
DALIAN JIAOTONG UNIVERSITY
2
图2-1 晶体结构 a) 晶体 b) 晶格 c) 晶胞
30.10.2020
DALIAN JIAOTONG UNIVERSITY
式中, Ni 、 Nf 、 Nr分别表示位于晶胞内部、 面心和角顶上的原子数;m为晶胞类型参数, 立方晶系的m = 8,六方晶系的m =6。 体心立方 N = 1 + 81/8 = 2 面心立方 N = 6 1/2+ 81/8 = 4 密排六方 N = 3 + 2 1/2+ 121/6 = = 6
10
晶向指数间的关系
① 一个晶向指数代表着相互平行、方向一致的所有晶向; ② 若晶体中两晶向相互平行但方向相反,则晶向指数中的数
字相同,而符号相反。 ③晶向族——晶体中原子排列情况相同但空间位向不同的一
组晶向称为,用<UVW>表示。
立方晶系:<111> =
非立方晶系: <100> [100]、[010]、[001],因为在这三个 晶向上的原子间距分别为a、b、c,其上的原子排列情况 不同,性质亦不同,所以不能属于同一晶向族。
材料科学基础第二章

y
[111]
x
[111]
例:画出晶向
[112 ]
2.立方晶系晶面指数
晶面指数的确定方法
(a)建立坐标系,结点为原点, 三棱为方向,点阵常数为单位 (原点在标定面以外,可以采 用平移法); (b)晶面在三个坐标上的截距a1 a2 a3 ; (c)计算其倒数 b1 b2 b3 ; (d)化成最小、整数比h:k:l ; 放在圆方括号(hkl),不加逗号, 负号记在上方 。
3.六方晶系晶面和晶向指数
三指数表示六方晶系晶面和晶向的缺点:晶体学上等价的 晶面和晶向不具有类似的指数。 例:
晶面指数
(11 0)
(100)
[010] [100]
从晶面指数上不能明确表示等同晶面,为了克服这一缺点, 采用a1、a2、a3及c四个晶轴, a1、a2、a3之间的夹角均 为120º ,晶面指数以(hkil)表示。 根据立体几何,在三维空间中独立的坐标轴不会超过三 个可证明 : i= - (h+k) 或 h+k+i=0
六方晶系
d hkl
h k l a b c
2 2 2
d hkl
a h2 k 2 l 2
1 l c
2
4 h 2 hk k 2 3 a2
注:以上公式是针对简单晶胞而言的,如为复杂晶胞, 例如体心、面心,在计算时应考虑晶面层数增加的影 响,如体心立方、面心立方、上下底(001)之间还有 一层同类型晶面,实际
[1 00 ]
[0 1 0]
[010]
[1 00]
y
[100]
x
[00 1]
晶体结构

事实上,采用三个点阵矢量a,b,c 来 描述晶胞是很方便的。这三个矢量不仅确 定了晶胞的形状和大小,而且完全确定了 此空间点阵。只要任选一个结点为原点, 以这三个矢量作平移(即平移的方向和单 位距离由点阵矢量所规定),就可以确定 空间点阵中任何一个结点的位置: ruvw = ua + vb + wc (2-101 ) 式中 ruvw为从原点到某一阵点的矢量, u,v,w 分别表示沿三个点阵矢量的平移 量,亦即该阵点的坐标值。
二、空间点阵(Space Lattice) 晶体中原子或原子集团排列的周期性规 律,可以用一些在空间有规律分布的几何 点来表示。并且,令沿任一方向上相邻点 之间的距离就等于晶体沿该方向的周期。 这样的几何点的集合就构成空间点阵( 这样的几何点的集合就构成空间点阵(简 称点阵), ),每个几何点称为点阵的结点或 称点阵),每个几何点称为点阵的结点或 阵点。 阵点。
2.晶胞的选取 我们在前面引出的晶胞和点阵常数的概念是不严格的, 原因是晶胞的选取不是惟一的。就是说,从同一点阵中可 以选取出大小、形状都不同的晶胞。相应的点阵常数自然 也就不同,这样就会给晶体的描述带来很大的麻烦。为了 确定起见,必须对晶胞的选取方法作一些规定。这规定就 是,所选的晶胞应尽量满足以下三个条件。 (1)能反映点阵的周期性 能反映点阵的周期性。将晶胞沿a,b,c三个晶轴 能反映点阵的周期性 方向无限重复堆积(或平移)就能得出整个点阵(既不漏 掉结点,也不产生多余的结点)。 (2)包含尽可能多的直角 包含尽可能多的直角,尽量直观地反映点阵的对称 包含尽可能多的直角 性。 (3)晶胞的体积最小 晶胞的体积最小。 晶胞的体积最小 其中,第(1)个条件是所有晶胞都要满足的必要条件。 第(2)和第(3)两个条件若不能兼顾,则至少要满足一个。
第2章 材料中的晶体结构

b. 已知两不平行晶向[u1v1w1]和[u2v2w2 ],由其决定的 晶面指数(hkl)为:
h v1 w 2 v 2 w 1 , k w 1u 2 w 2 u 1, l u 1 v 2 u 2 v1
补充
cos
2
(对于立方晶系)
两个晶面(h1k1l1)与(h2k2l2)之间的夹角φ
h h
1 2
k k
1 2
2
2
ll
1
2 2 2
(h1
k
2 1
l1 )
(h 2
k
l
2 2
)
两个晶向[u1v1w1]与[u2v2w2]之间的夹角θ
cos
2
u u
1
2
vv
1 2
2
w w
1 2
2
(u 1
v
2 1
w1)
(u 2
v
2 2
w
2 2
)
晶面(hkl)与晶向[uvw]之间的夹角ψ
晶向指数用[uvtw] 来表示。其中 t =-(u+v)
120° 120°
晶面指数的标定
1.求晶面与四个轴的截距
2.取倒数
3.再化成简单整数
4.用圆括号括起来(h k i l)
六方系六个侧面的指数分别为:
(1 1 00),(01 1 0),(10 1 0),(1 100),(0 1 10),(1 010)
(210)
(012)
(362)
注意
选坐标原点时,应使其位于待定晶面以外,防止 出现零截距。 已知截距求晶面指数,则指数是唯一的;而已知 晶面指数,画晶面时,这个晶面就不是唯一的。
第二章材料中的晶体结构
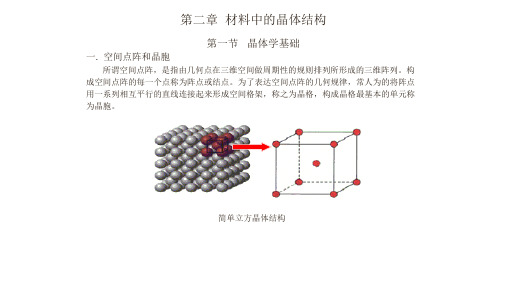
TiO2
体心四方
1个正离子 2个负离子
6
3
八面体 VO2, NbO2, MnO2, SnO2, PbO2, …
7. MgAl2O4(尖晶石)晶型
8.Al2O3(刚玉)晶型
第四节 共价晶体的结构
一、共价晶体的主要特点 1. 共价键结合,键合力通常强于离子键 2. 键的饱和性和方向性,配位数低于金属和离 子晶体 3. 高熔点、高硬度、高脆性、绝缘性
(2) 求投影.以晶格常数为单位,求待定 晶向上任一阵点的投影值。
(3) 化整数.将投影值化为一组最小整数。
(4) 加括号.[uvw]。
2.晶面指数及其确定方法
1) 晶面指数 — 晶体点阵中阵点面的 方向指数。 2) 确定已知晶面ห้องสมุดไป่ตู้指数。
(1) 建坐标.右手坐标,坐标轴为晶胞 的棱边,坐标原点不能位于待定晶面内。
cph
a=b≠c
a 2r
5. 致密度 — 晶胞中原子体积占总体积的分数
bcc
fcc
cph
3 0.68
8
2 0.74
6
2 0.74
6
6. 间隙 — 若将晶体中的原子视为球形,则相 互接触的最近邻原子间的空隙称为间隙。
间隙内能容纳的最大刚性球的半径称为
间隙半径 rB。 间隙大小常用间隙半径与原子半径 rA之
比 rB / rA 表示。
1) 面心立方结构晶体中的间隙 正八面体间隙:位于晶胞各棱边中点及体心位置.
一个晶胞中共有4个.
rB / rA 0.414
正四面体间隙:位于晶胞体对角线的四分之一处. 一个晶胞中共有8个.
rB / rA 0.225
2) 体心立方结构晶体中的间隙 扁八面体间隙:位于晶胞各棱边中点及面心处. 一个晶胞中共有6个. rB / rA 0.155
金属晶格结构

(二)
晶体中的缺陷
2 线缺陷:线缺陷主要是指各种形式的“位错”。 所谓位错是指晶体中某一列或若干列原子发生有规 律的错排现象。它引起的晶格错线为中心轴的一个 管状区域。 位错有多种。最简单直观的一种称为刃型位错。它 象一个刀刃的切入,故称刃型位错,见图2-11。 晶格中的位错多少,可用位错密度来表示。位错密 度是指单位体积内位错的错线长度,量纲为(cm-2)。 晶体中的位错首先是产生于晶体的结晶过程。 晶体材料的内部的位错在相应的条件下,可以产生 滑移,增值,交割,缠结,攀移等行为。这对金属 的强度、塑性等力学性能有重要影响。金属材料
上一页 下一页
(一)基本概念
2 晶胞:晶体中原子排列规律具有明显的周期变化。因此 在晶格中就存在一个能够代表晶格特征的最小几何单元, 称之为晶胞。图2-1c是一个简单的晶胞示意图。晶胞在空 间的重复排列就构成整个晶格。因此,晶胞的特征就可以 反映出晶格和晶体的特征。 3 晶格参数与晶格常数:在晶体学中,用来描述晶胞大小 有形状的几何参数称为晶格参数。包括晶胞的三个棱边的 长度a,,b,c和三个棱边夹角。α ,β ,γ 共六个参数。 其中决定晶胞大小的三个棱长又称为晶格常数。图2-1c
上一页 下一页
(2)负电性因素:所谓负电性是指某元素 的原子从其它元素原子夺取电子而变成负 离子的能力。在元素周期表中,两种元素 的位置距离愈远,则其负电性差也愈大。 两元素负电性愈大,则化学亲合的能力也 愈大。它们之间就易于形成化合物,而不 利于形成固溶体,即使形成固溶体其溶解 度也很小。
上一页
上一页 下一页
(二)
晶体中的缺陷
这里说的缺陷不是指晶体的宏观缺陷,而是指晶体中局 部原子排列不规则的区域。根据晶体缺陷的几何特点和 原子对排列不规则性的影响范围可分为三大类。 1.点缺陷:点缺陷是指以一个点为中心。在它的周围造成 原子排列的不规则,产生晶格的畸变和内应力的晶体缺陷。 主要有间隙原子,置换原子,晶格空位三种,见图2-10。 在晶格的间隙处出现多余的晶体缺陷称为间隙原子;在晶 格的接点处出现缺少原子的晶体称为晶体空格;在晶格的 结点处出现的原子直径不同的异类原子的晶体缺陷称为置 换原子。间隙原子和大径的置换原子会引起一个以一个点 为中心的晶格局部“撑开”现象,称之为正畸变。而晶格 空位和小直径的置换原子会引起一个点为中心的晶格局部 “靠拢”现象,称之为负畸变。 晶体中的点缺陷都是处在不断的变化和运动中,其位置随 时在变。这是金属原子扩散的一种主要方式,也是金属在 固态下“相变”和化学热处理工艺的基础。
大学材料科学基础第二章材料中的晶体结构

4.晶面间距(Interplanar crystal spacing)
两相邻近平行晶面间的垂直距离—晶面间 距,用dhkl表示,面间距计算公式见(1-6)。 通常,低指数的面间 距较大,而高指数的 晶面间距则较小 晶面间距愈大,该晶 面上的原子排列愈密 集;晶面间距愈小, 该晶面上的原子排列 愈稀疏。
晶体结构 = 空间点阵 + 结构单元
如:Cu, NaCl, CaF2有不同的晶体结构, 但都属于面心立方点阵。 思考题:空间点阵与布拉菲点阵。
三、 晶向指数与晶面指数
(Miller Indices of Crystallographic Directions and Planes) 在晶体中,由一系列原子所组成的平面称 为晶面,原子在空间排列的方向称为晶向。 晶体的许多性能都与晶体中的特定晶面和晶 向有密切关系。为区分不同的晶面和晶向, 采用晶面和晶向指数来标定。
5.晶带 (Crystal zone) 所有平行或相交于同一直线的晶面构 成一个晶带,此直线称为晶带轴。
晶带轴[u v w]与该晶带的晶面(h k l) 之间存在以下关系: hu + kv + lw = 0 凡满足此关系的晶面都属于以[u v w]为 晶带轴的晶带,律应用举例
1 晶胞中原子数 (Number of Atoms in Unit Cell)
一个晶胞内所包含的原子数目。 体心立方晶胞:2个。 面心立方晶胞:4个。 密排六方晶胞:6个。
2 原子半径 r 与点阵常数 a 的关系
严格的说,原子半径并不是一个常数,它 随外界条件(温度)、原子结合键、配位数而 变,在理论上还不能精确地计算原子半径。 定义为晶胞中原子密排方向上相邻两原子 之间平衡距离的一半,用点阵常数表示。
结晶学 第二章 晶体构造理论

25
十四种布拉菲格子
立方晶系:简单立方、面心立方、体心立方 四方晶系:简单立方、体心立方 正交晶系:简单正交、面心正交、体心正交、 底心正交 三方晶系:简单三方 单斜晶系:简单单斜、底心单斜 三斜晶系:简单三斜 六方晶系:体心六方
26
三维布拉菲格子汇总表格
简单P 立方 四方 正交 三方 六方 单斜 三斜 体心I 面心F ? ? ? ? ? ? ? 底心C ? ? ?
三方R
19
(5)单斜晶系 a≠b≠c
α=γ=90°≠β
C.P
单斜P
单斜C
20
(6)三斜晶系
a≠b≠c α≠β≠γ≠90° P
三斜P
21
(7)六方(六角)晶系 a=b≠c
α=β=90° γ=120° P(C)
六方P or C
本次课带14种布氏格子!
22
23
24
§2.2 布拉菲格子
目前格子划分方法已形成广泛的共识(三原则): ①首先,所选取单位的外形应能尽量反映点阵的对称性; (对称性高) ②之后,使所选单位各棱(边)间夹角尽可能等于直角; (多直角) ③最后,所选单位占空间最小;(空间小) 如此选择单位而确立的格子,称作布拉菲在格子的。
12
1) 所选取的平行六面体的外形应能充分反映空间点 阵的对称性;(对称性高) 2)在满足1)条件下,应使平行六面体中的各个棱间 夹角尽可能等于直角;(多直角) 3)在满足1)2)条件下,平行六面体的体积最小;
图2.2.1 平面点阵中的平行四边形
13
空间平行六面体六个参数的定义
14
七个晶系的划分
11
2.2 十四种空间点阵形式
为了比较和研究点阵形式方便,一般情况 只需研究点阵中的一个空间格子中结点的分布 方式就可以了。 由于对同一空间点阵,划分空间格子的方 式是多种多样的。为使点阵和点阵中选取的格 子之间具有一一对应的关系,人们对在点阵中 选择的单位平行六面体格子作了一些规定。 ** 三条规定
SSP第2章晶体结构几何2-110823-P

食盐(NaCl)晶体 常见外形
晶体外形上的对称性,是晶体内部结构规则性的反映。 研究晶体对称性的目的:1、研究晶体内部结构;2、研究晶 体物理性质
3
2.3 晶体结构的对称性
2.3.2 对称性操作类型
(1) 操作 晶体经过某种操作原状的过程也是晶体中各质点坐标的某种 变换。 由于操作不改变晶体中任意二点的距离,因此,数学上这种 操作是线性变换。 设有操作A,将晶格中一点 r(x,y,z) 变换到 r’(x’,y’,z’),则这 一变换表为r’=Ar
计入平移后的对称操作 4度螺旋轴和滑移反映面示意图
17
2.3 晶体结构的对称性
2.3.6 晶系,布拉菲晶胞
晶胞区别于原胞的一个重要特征:晶胞不仅反映了晶体结构 的周期性,也反映了晶体的宏观对称性。 晶胞基本特征用基矢来描述,即,基矢 a, b, c的长度及其它 们间的夹角来描述。 可以证明,晶胞基矢由长度和夹角不同的组合方式只能有7 种。 每种组合称为一个晶系。 7大晶系:立方晶系,六方晶系,四方晶系,正交晶系,单 斜晶系,三斜晶系,三方晶系,六方晶系。 考虑到格点是否在体面和体心,7个晶系共包含14种不同类 型的晶胞,称为14种布拉菲晶胞。
(2) 基本操作一:转动 设晶体绕 x1轴转过 θ 角,晶体中作一点 r(x1,x2,x3)移到 r’(x1’,x2’,x3’) 则有:
x1 ' = x1
x3
x3 ’ x3
θ
x2 ' = r cos(θ + ϕ ) = r (cos θ cos ϕ − sin θ sin ϕ ) = x2 cos θ − x3 sin ϕ x3 ' = r sin(θ + ϕ ) = r (sin θ cos ϕ + cos θ sin ϕ ) = x2 sin θ + x3 cos ϕ
02第二章-晶体结构-基础-结合力和结合能-140903

D: [211]
在四方晶系中,晶面(110)与晶棱[110]相互( C)。
A: 正交
B: 平行
C: 斜交
D: A或B
School of materials Science and engineering
2.2 晶体中质点的结合力与结合能
2.2.1 晶体中质点间的结合力
(1)晶体中键 的类型
(略讲)
范德华键(分子键):通过“分子力”而产生的键合。
葛生力(Keesen force)或定向作用力: 发生在极性分子与极性分子间;
分子力
德拜力(Debye force)或诱导作用力:发 生在极性分子与非极性分子之间;
伦敦力(London force)或分散作用力 (色散力):发性在非极性分子与 非极性分子之间。
氢键 氢原子核与极性分子 弱 有方向性和饱和性
间的库仑引力
School of materials Science and engineering
(2)晶体中离子键、共价键比例的估算
1 离子键(%)=1 exp[ 4 ( X A
X B )2 ]
式中:XA、XB为A、B元素的电负性值。如:SiO2 离子键成分约45%,有的书中说47%。
(1)选坐标轴“一般标记为X(a)轴、 Y(b)轴、Z(c)轴”。三个坐标 轴的交点应位于晶体的中心。选坐 标轴不同任意的,一般选对称轴或 平行于晶棱的直线等。对于不同的 晶系的晶体,有不同的选择结晶轴 的方法。每两个坐标轴之间的交角 称为轴角,通常α=b∧c、β= c∧a、γ=a∧b。
(2)决定坐标轴的轴单位。
School of materials Science and engineering
晶向与晶面的关系
第二章 晶体结构(3)-无机单质及化合物晶体结构

CaF2——激光基质材料,在玻璃工业中常作为助熔剂
和晶核剂,在水泥工业中常用作矿化剂;
TiO2——集成光学棱镜材料;
SiO2——光学材料和压电材料。
此外还有层状CdI2和CdCl2型结构,可作固体润滑剂。
AX2型晶体也具有按r+/r-选取结构类型的倾向。 第二章 晶体结构——2.3~4无机单质及化合物晶体结构
第二章 晶体结构——2.3~4无机单质及化合物晶体结构
纤锌矿结构中六方柱晶胞
纤锌矿结构中平行六面体晶胞
资源加工与生物工程学院
(2)纤锌矿结构与热释电性及声电效应
某些纤锌矿型结构,其结构中无对称中心存在,使得晶体具 有热释电性,可产生声电效应。
热释电性是指加热使晶体温度变化时,在与该晶体c轴平行
一、AX型结构, 二、AX2型结构, 三、A2X3型结构, 四、 ABO3型结构, 五、 AB2O4型(尖晶石)结构, 六、无机化合物结构与鲍林规则(Pauling’s rule)
第二章 晶体结构——2.3~4无机单质及化合物晶体结构
资源加工与生物工程学院
一、AX型结构
有CsCl,NaCl,ZnS,NiAs等类型结构,其中:
第二章 晶体结构——2.3~4无机单质及化合物晶体结构
资源加工与生物工程学院
r AX型化合物的结构类型与 的关系 r
结构类型 CsCl型 NaCl型
r r
1.000~0.732 0.732~0.414
实 例(右边数据为
r r 比值)
CsCl 0.91 CsBr 0.84 CsI 0.75 KF 1.00 SrO 0.96 BaO 0.96 RbF 0.89 RbCl 0.82 BaS 0.82 CaO 0.80 CsF 0.80 PbBr 0.76 BaSe 0.75 NaF 0.74 KCl 0.73 SrS 0.73 RbI 0.68 KBr 0.68 BaTe 0.68 SrSe 0.66 CaS 0.62 KI 0.61 SrTe 0.60 MgO 0.59 LiF 0.59 CaSe 0.56 NaCl 0.54 NaBr 0.50 CaTe 0.50 MgS 0.49 NaI 0.44 LiCl 0.43 MgSe 0.41 LiBr 0.40 LiF 0.35 MgTe 0.37 BeO 0.26 BeS 0.20 BeSe 0.18 BeTe 0.17
第2章晶体结构讲解

第2章晶体结构讲解第2章晶体结构为了便于对材料进⾏研究,常常将材料进⾏分类。
如果按材料的状态进⾏分类,可以将材料分成晶态材料,⾮晶材料及准晶材料。
因所有的晶态材料有其共同的规律,近代晶体学知识就是为研究这些共同规律⽽必备的基础。
同时为了研究⾮晶材料与准晶材料及准晶材料也必须以晶体学理论做为基础。
在⼀般的教材中对晶体学的基础知识已经有了不同深度的阐述,作为辅导教材,对教科书上已经有较多阐述的内容,本章中就简要的进⾏说明,⽽重点在于⽤动画形式,将在教材中难以⽤⽂字表达清楚的内容进⾏较多的阐述,加深对教材内容的理解记忆2.1晶体学基础2.1.1 空间点阵和晶胞具有代表性的基本单元(最⼩平⾏六⾯体)作为点阵的组成单元,称为晶胞。
将晶胞作三维的重复堆砌就构成了空间点阵。
为了便于分析研究晶体中质点的排列规律性,可先将实际晶体结构看成完整⽆缺的理想晶体并简化,将其中每个质点抽象为规则排列于空间的⼏何点,称之为阵点。
这些阵点在空间呈周期性规则排列并具有完全相同的周围环境,这种由它们在三维空间规则排列的阵列称为空间点阵,简称点阵。
同⼀空间点阵可因选取⽅式不同⽽得到不相同的晶胞<晶胞、晶轴和点阵⽮量>根据6个点阵参数间的相互关系,可将全部空间点阵归属于7种类型,即7个晶系。
按照"每个阵点的周围环境相同"的要求,布拉菲(Bravais A.)⽤数学⽅法推导出能够反映空间点阵全部特征的单位平⾯六⾯体只有14种,这14种空间点阵也称布拉菲点阵。
空间点阵是晶体中质点排列的⼏何学抽象。
1 空间点阵最初⼈们认为凡是具有规则外形的天然矿物均为晶体。
但现在⼈们认识到晶体的规则的⼏何外形是内部结构规律的外在反映. 近代的科学研究表明了下⾯的两个基本事实:1)如果说某⼀种材料是晶体,其基本的特征是:组成该材料的内部的微观粒⼦(原⼦,分⼦,离⼦等)在三微的空间做有规则的周期性的排列。
2)这种排列的规律决定了材料的性能。
第二章 无机盐的晶体结构

2012版
第二章-无机盐的晶体结构
12
红砷镍的晶体结构
红砷镍矿(NiAs)的晶体结构: 砷化镍属六方晶系 空间群:D6h4—P63mc 晶胞参数:a=b=3.602Å,
c=5.009 Å 轴率:c/a=1.391 分子数:Z=2 单胞体积:V=56.28Å3
2012版
第二章-无机盐的晶体结构
35
晶体的物理性质
a. 光学颜色:纯萤石为无色,含杂质离子Y、Ce、Ca 时,产生色心,常见的颜色有浅绿色至深绿色,蓝、
绿蓝、黄、酒黄、紫、紫罗兰色、灰、褐、玫瑰红、
深红等。 光泽: 玻璃光泽。
b. 透明度:透明至半透明。
c. 光性:均质体。
d. 折射率:1.438(±0.01) ,无多色性。
第二章-无机盐的晶体结构
10
表:TiO2(金红石)的类质同像体
化合物
a/Å
c/Å
V/Å3
CoF2
4.695
3.180
70.10
FeF2
4.697
3.309
73.00
MgF2
4.623
3.052
65.23
MnF2
4.873
3.310
78.60
NiF2
4.651
3.084
66.71
ZnF2
4.703
3.134
空间群:D414h P42 / mnm
晶胞参数:a=b=4.5937Å, c=2.9587 Å
轴率:a/c=1.55 分子数:Z=2
Rutile的单胞结构
单胞体积V=62.433 Å3
晶体结构之二:对称性

第二章晶体结构一、教学要求(1)内容提要:物质通常有三种聚集状态:气态、液态和固态。
而按照原子(或分子)排列的规律性又可将固态物质分为两大类,晶体和非晶体。
晶体中的原子在空间呈有规则的周期性重复排列;而非晶体的原子则是无规则排列的。
原子排列在决定固态材料的组织和性能中起着极重要的作用。
金属、陶瓷和高分子的一系列特性都和其原子的排列密切相关。
一种物质是否以晶体或以非晶体形式出现,还需视外部环境条件和加工制备方法而定,晶态与非晶态往往是可以互相转化的。
本章主要内容包括::晶体学基础;金属的晶体结构;合金相结构;离子晶体结构;共价晶体结构;聚合物的晶态结构;非晶态结构。
(2)基本要求掌握晶体的空间点阵、晶胞、晶向和晶面指数、晶体的对称性等结晶学基础知识,了解32种点群和230种空间群等;掌握三种典型的金属晶体结构、合金相结构、离子晶体结构和硅酸盐晶体结构,了解共价晶体结构和分子与高分子晶体结构。
(3)重点难点重点:结晶学基本原理及典型的金属晶体、合金相、离子晶体结构。
难点:空间点阵、非化学计量化合物和鲍林规则。
(4)主讲内容①晶体学基础;②金属的晶体结构;③合金相结构;④离子晶体结构;⑤共价晶体结构;⑥聚合物晶体结构。
《第二章晶体结构》目录——引言——晶体的结构特征与基本性质(1.0h)2.1晶体结构的周期性(4.0-6.0h)2.2.1点阵与平移群一、点阵结构与点阵(1)一维点阵结构与直线点阵;(2)二维点阵结构与平面点阵(3)三维点阵结构与空间点阵二、点阵的条件与性质(1)定义;(2)条件;(3)点阵与点阵结构的对应关系。
2.2.2点阵单位与点阵参量一、点阵单位与点阵常数(1)直线点阵单位与线段参数(2)平面点阵单位与网格参数(3)空间点阵单位与晶胞参数二、其他晶体结构参数(1)(原子)阵点坐标与原子间距;(2)晶向(直线点阵)指数(3)晶面(平面点阵)指数;(4)晶面间距与晶面夹角(5)晶带与晶带定律三、极射投影*2.2.3 倒易点阵与晶体衍射*2.2晶体结构的对称性(4.0h)2.3.1对称性的基本概念——对称及其对称元素与对称操作2.3.2宏观对称性—晶体外形(有限)表现的对称性—点对称性一、点对称操作与宏观对称元素;二、点群及其表示方法——32个点群(晶类);三、晶系与空间点阵型式——7种晶系与14种布拉菲点阵2.3.3微观称对性—晶格基元(无限)排列的对称性—体对称性一、空间对称操作与微观对称元素;二、空间群及其表示方法;三、等效点系——2.3.4点群与空间群的关系2.3.4 晶体结构符号2.3典型晶体结构分析(8.0h)2.3.1金属晶体结构2.3.2共价晶体结构2.3.3离子晶体结构2.3.4分子晶体结构2.3.5高分子(晶体)结构2.4 合金相结构2.2晶体结构的对称性——强调:对称操作与矩阵变换(点阵与矩阵)2.2.1对称性的基本概念——对称的概念(定义与划分)擅长形象思维的中国人在西汉〈韩诗外传〉就有:“凡草木花(注:有生命)多五出,雪花(注:无生命)独六出。
ssp-02-晶体结构(下)-2014

简单四方 体心四方
C4 , C4h D4 , C 4 v D4 h , S4 , D2 d
C6 , C6 h , D6 , C 3 v D6 h , C 3 h , D2 h
六角晶系
ab 1200
c a, b abc
六
角
立方晶系
abc
900
简单立方 体心立方 面心立方
例题2.1 写出并画出立方晶体<100>、<110>、 <111>所代表的各等效晶向。 解:
100 : [100]、 [100]、 [010]、 [010]、 [001]、 [001] 110 : [110]、 [110]、 [110]、 [110] [101]、 [101]、 [101]、 [101] [011]、 [011]、 [011]、 [011] 111 : [111]、 [111]、 [111]、 [111] [111]、 [111]、 [111]、 [111]
—— 对于单胞,也有类 似的晶向指数
第二讲_晶向 晶面和它们的标志 —— 晶体结构
RA 3a1 a2 a3
RA 2a1 3a2
晶向指数
[311]
晶向指数
[230]
第二讲_晶向 晶面和它们的标志 —— 晶体结构
单胞晶向指数 基矢原胞系统和轴矢单胞系统中都可以定义晶向指数。 如果不特别说明,在凝聚态和材料物理文献中出现的 晶向指数,习惯上都理解为定义在轴矢单胞系统中。 我们的课程中也这样要求。
—— 在布拉伐格子中 作一簇平行的直线, 这些平行直线可以将 所有的格点包括无遗
平行直线 —— 晶列
第二讲_晶向 晶面和它们的标志 —— 晶体结构
晶体结构2-2014
四、 晶体中质点的堆积最紧密堆积原理: 晶体中各离子间的相互结合,可以看作 是球体的堆积。
球体堆积的密度越大, 系统的势能越低,晶体越稳定。
此即球 体最紧密堆积原理。
质点堆积方式: 根据质点的大小不同,球体最紧密 堆积方式分为等径球和不等径球两种情况。
同层球堆积 (平面堆积)准密排面 CB密排面凹坑:C:尖角向上;B:尖角向下 凹坑hcpfcc面心立方最紧密堆积1 2 3 5 4 6 5 4 2 31 6A1 6 5 4 2 3B C面心立方最紧密堆积A C B A C B AABCABC……, 即每三层重复一次面心立方最紧密堆积ABC六方最紧密堆积ABABAB…… 每两层重复一次A B A B A六方晶胞——六方密堆积A A B B A A密 排 面二、体心立方结构(bcc)体心立方结构不是紧密堆积,但是一种有效的对称堆积单层的堆积面近似于密 排面,每个原子与四个 最邻近原子接触;四个 最邻近原子构成一个四 边形凹坑第二层原子填充在第一层原子形成 的四边形凹坑中,而第三层原子填 充在第二层原子形成的四边形凹坑 中,且位于第一层原子的正上方, 形成ABAB…堆积形式,从而得到体 心立方结构配位数(coupling number, CN) 一个原子周围最邻近的原子数(晶体 结构中为发生键合的质点数 ) 称为 配位 数。
在等径球体密堆积中,配位数为12最紧密堆积的空隙其他堆积方 式中的空隙简单立方空隙由于球体之间是刚性点接触堆积,最 紧密堆积中仍然有空隙存在。
从形状上 看,空隙有两种:一种是四面体空隙,由4 个球体所构成,球心连线构成一个正四面 体;另一种是八面体空隙,由6个球体构 成,球心连线形成一个正八面体。
显然,由同种球组成的四面体空隙小 于八面体空隙。
空隙分布情况:1个球的周围有8个四面体空隙 每个球体周围有多少个四面体空隙? N个球最密堆积时系统四面体空 每个球体周围有多少个八面体空隙? 隙数为nx8/4=2n1个球的周围有6个八面体空隙 N个球最密堆积时系统八面体空 隙数为nx6/6=n面心立方晶胞中四面体空隙的分布晶胞内四面体空隙数目:8面心立方晶胞中八面体空隙的分布ABC晶胞内八面体空隙数目:1+12x1/4=4 八面体空隙的位置:1/2 1/2 1/2, 0 0 1/2, 1/2 0 0, 0 1/2 0六方晶胞中的四面体空隙分布一个晶胞中有两个质点 (000)(2/3 1/3 1/2)一个晶胞中有4个四面体 空隙六方晶胞中的八面体空隙分布一个晶胞中有2个八面体空隙体心立方晶胞中的四面体空隙体心立方晶胞中的八面体空隙分布空间利用率•立方密堆和六方密堆的空间利用率为74.05%,而简单立方堆积的空间利用率仅为52%。
第二章 晶体结构2.4

2.4 晶体中的对称操作群 1晶体中的基本对称操作E 是不变操作。
n C 正当转动 (1A =) 对称操作。
由于晶体周期性的限制,转角只能是2; 1,2,3,4,6n n π=,显然1C E =,2,3,4,6n =的转轴分别称为二度、三度、四度、六度转轴。
n 只有五个取值的证明如下。
设想有转角为θ 的旋转对称操作,画出布拉伐格子中垂直转轴的晶面,在这个晶面内选取基矢a 1和a 2,晶面内所有布拉伐格点都可以表示为l 1a 1 + l 2a 2。
B '图2.5.1 转动对称操作称位于原点的格点为A ,由它画出a 1达到的格点为B ,如果绕A 转θ 角,则将使B 格点转到B’位置,由于转动不改变格子,在B’处必定原来就有一个格点,因为B 和A 完全等价,所有旋转同样可以绕B 进行,设想绕B 转-θ 角,这将使A 格点转到A’的位置,同样A’处原来也必定有一个格点。
由于ABA’B’组成等腰梯形,因此B’A’ = n AB ,即a 1 + 2a cos ()πθ-= na 1,则()θc o s 21-=n (2.4.1) 因为cos θ 必须在1到-1之间,n 必须为整数,只能取-1, 0, 1, 2, 3五个值,相应地θ = 0︒, 60︒, 90︒, 120︒, 180︒ (2.4.2) 因此晶体的宏观对称操作只能是旋转以上五种角度,其转轴分别称为1, 6, 4, 3, 2重旋转对称轴。
i 对原点的反演。
σ镜象反映。
n S 非正当转动2n π,2,3,4,6n =。
这是转动n C 和垂直于转动轴平面镜象反映的组合操作;1S σ=,2S i =。
h σ对水平面的反映。
水平面垂直于对称度最高的转轴。
v σ对垂直水面的反映。
平面通过对称轴。
d σ对于一个平分角平面的反映。
这个平面包含对称轴并平分两个垂直于对称轴的二度轴的夹角,显然,d σ是一种特殊的v σ。
2 点群如果不计入平移对称性,可以证明上面所介绍的这些对称操作可以组成32个不同的对称性群。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
An Introduction to Science for Inorganic Materials (I)
南京工业大学
材料科学与工程学院 郭露村
推荐阅读文献
Suggested Reading
M. A. Omar, Elementary Solid State Physics, 1st ed., Addison-Wesley Publishing Company, 1975 C. Kittle, Introduction to Solid State Physics, 4th ed. John Wiley & Sons, Inc., New York, 1971, (5th ed. or 6th ed. even better, if available.) G. M. Barrow, Physic Chemistry, 5th ed., McGrawHill, Inc., 1988 L. H. Van Vlack, Elements of Materials Science and Engineering, 5th ed., Addison-Wesley Publishing Company, 1985 (6th ed., 1994) W. S. Kingery, Introduction to Ceramics, 2nd ed., John Wiley & Sons, Inc., New York, 1976.
2.1.2. 晶体结构基本要素及构成
Basic elements and buildup of cystals
【晶格与格点】crystal lattice and lattice sites 从具体的晶体抽象出来的几何立体格子称晶格,简 称格子, 其中所有的原子位置(atomic sites)均被格点 (lattice sites or lattice points)取代。
Note: The bcc is not a close-packed structure!
【基】又称:基元 basis
晶体中最小的周期性重复的单元的原子(离子)或原子 团称为基。 例如:NaCl, 蛋白质晶体的基中含一万 个原子, CH4分子晶体
CH4分子晶体中 作为基元的CH4
+ CH4
fcc lattice
【对称操作要素】
【点群与点群对称】
【空间群】
【对称操作与要素】
Symmetry Operations and Elements
对称操作完成后晶格保持不变! A Symmetry operation is an operation that can be performed either physically or imaginatively that results in no change in the appearance of an object,including
自然态
【超晶格】super lattice 【超材料】super material
非自然态
【晶体】crystal
A halite crystal
An aquamarine
crystal
A quartz crystal
单晶体外貌
内部原子排列完全周期性
【多晶体】polycrystalline 陶瓷 ceramics
【旋转对称】Rot Rotation Axis
2-fold
3-fold
4-fold
6-fold
1-fold 5-fold 8-fold
a=b≠c
α=β=γ= 90º
α=β=90º,γ = 120º
13
14
Body-centered
Face-centered
立方 Cubic
a=b=c
α=β=γ= 90º
【七大晶系】The 7 crystal systems
14种Bravais lattices 抽去含格点的不同(P, I, F, C)即得到7大晶系
Crystal System 三斜 Triclinic 单斜 Monoclinic
Unit Cell axes angles α ≠ β ≠ γ≠ 90º
a≠b≠c
a≠b≠c
斜方 Orthorhombic
a≠b≠c
α=β=γ≠ 90º
四方 Tetragonal 三角 Trigonal 六方Hexagonal
【fcc面心立方 & bcc体心立方结构 】
face-centered cubic & body-centered cubic)
Interstitial sites in fcc
体心立方bcc
面心立方fcc
2 types of hole –Tetrahedral or Octahedral (larger)
Face-centered: F,
Base-centered: C
Bravais Lattice 1 2 3 4 5 6 7 8 9 10 11 12 Simple Simple Base-centered Simple Base-centered Body-centered Face-centered Simple Body-centered (Simple) (Simple) Simple
特点: 具有长程取向序, 而无平移对称 (无排列周期性)
【液晶】 liquid crystal
in a solid crystal state
in a liquid crystal state
in a liquid state
T1 液晶相温区
T2
Temperature
Within layers, the molecules can slide around each other !
Crystal = Lattice + Basis
【基矢量、格矢量】basis vectors & lattice vectors
晶格中任意格点可用格矢Rn(a1, a2, a3 )表示
Rn = n1 a1 + n2 a2 + n3a3
a1, a2, a3 为基矢
a2
a1
Rn
a1,a2 为该2元晶格的基矢(量)
面心立方的单位胞、原胞及W-S胞
面心立方:单胞、原胞、W-S胞
体心立方:单胞、原胞、W-S胞
2.2 Bavais格子及晶系
The Bravais lattices & crystal systems
晶体的微观对称
【Bravais 格子与非Bravais 格子】
Bravais lattice & non-Bravais lattice)
【 紧密堆积结构】
Close-packed structures
hcp &fcc
六方紧密堆积 hcp structure
ABABA.. packing
(hexagonally-close packed)
ABCABC.. packing
立方紧密堆积 fcc structure
(face-centered cubic, 面心立方)
Bravais格子: 所有的格点(lattice points)是等价的。它是 最基本的格子(fundamental type of lattice) 三维晶体可能存在的最多格子形式只有14种 非Bravais 格子: 看成是Bravais 格子 + 基元而成。 也可以看成是多个Bravais 格子套装而成。
液晶显微结构
Photo of the smectic C phase (using polarizing microscope) Cross-polarised light microscopy
SEM
Photo of the smectic C phase (using polarizing microscope)
W. D. 金格瑞等著[美]. 清华译. 《陶瓷导论》. 北京:建筑工 业出版社,1982 L. H. 范. 弗莱克著[美]. 夏宗宁等译. 《材料科学与工程基础》 (第四版). 机械工业出版社.1984 冯端等主编,《材料科学导论》化学工业出版社. 2002.5 关振铎等编. 《无机材料物理性能》清华大学出版社,1992 顾宜主编. 《材料科学与工程基础》 化学工业出版社. 2002 吴刚主编. 《材料结构表征及应用》 化学工业出版社. 2002 李言荣,恽正中编. 《材料物理学概论》清华大学出版社,2001 张立德等著. 《纳米材料和纳米结构》. 科学出版社,2001
对 称 性
T
Unit Cell and reciprocal cell of Hexagonal
Hexagonal cells Hexagonal representation (4axes) Rhombic representation (3 axes)
2.3. 点群与空间群
point group and space group
【 W-S单胞】Wigner-Seitz
cell(维格纳-赛茨晶胞)
【单胞】又称单位晶胞、晶胞(unit cell)
为了更加清楚地表示晶体地对称关系,常常可能选择 更大范围的六面体作为单位来表示晶胞。通常称其为 单胞。 单胞 注意: 原胞 单位晶胞的体积大于或等于原胞。 单位胞是原胞体积的整数倍(2n)。 非原胞的单胞可以用原胞来表示,但几何未必重叠。 通常的“晶胞常数”是指单包。
SiO2玻璃(浮法玻璃)
Transmitted polarised light microscopy
非晶态物质结构
玻璃体
高分子
非晶态金属
