第三章关于测定垂线偏差和大地水准面差距的基本概念2共50页文档
重力异常与垂线偏差资料

重力异常与垂线偏差重力相关资料1.相关坐标系地球上任何一个质点都同时受到地心引力和由于地球自转产生的离心力的作用,两个力的合力称为重力。
离心力与引力之比约为1:300,所以重力中起主要作用的还是地心引力。
重力的作用线称为铅垂线,重力线方向就是铅垂线方向。
1.1 水准面与大地水准面当液体处于静止状态时,其表面必处处与重力方向正交,否则液体就要流动。
这个液体静止的表面就称为水准面。
水准面是一个客观存在的、处处与铅垂线正交的面。
通过不同高度的点,都有一个水准面,所以水准面有无穷多个。
为了使测量结果有一个共同的基准面,可以选择一个十分接近地球表面又能代表地球形状和大小的水准面作为共同标准。
设想海洋处于静止平衡状态,并将它延伸到大陆内部且保持处处与铅垂线正交的水准面,来表示地球的形状是最理想的,这个面称为大地水准面。
它是一个光滑的闭合曲面,又称为地球的物理表面。
由它包围的形状是地球的真实形体,称为大地体。
地球自然表面的起伏不平、地壳内部物质密度分布不均,使得引力方向产生不规则的变化。
因而引力方向除总的变化趋势外,还会出现局部变化,这就引起铅垂线方向发生不规则的变化。
由于大地水准面处处与铅垂线正交,所以它是一个略有起伏的不规则的表面。
图1 椭球面与大地水准面1.2 参考椭球面从整体上看,大地体接近于一个具有微小扁率的旋转椭球,与大地体吻合的最好的旋转椭球称为总地球椭球,也叫总椭球或平均椭球。
要确定总椭球,必须在整个地球表面上布设连成一体的天文大地网和进行全球性的重力测量。
为了大地测量工作的实际需要,各个国家和地区只有根据局部的天文、大地和重力测量资料,研究局部大地水准面的情况,确定一个于总椭球相近的椭球,以表示地球的大小,作为处理大地测量成果的依据。
这样的椭球只能较好的接近局部地区的大地水准面,不能反映整个大地体的情况,所以叫做参考椭球面。
1.3大地坐标系与天文坐标系表1 大地坐标系与天文坐标系的对比由于大地水准面起伏,导致同一点的法线和垂线不一致,两者之间的微小夹角称为垂线偏差;导致天地高和海拔高(正高)不一致,两者之间的差距称为大地水准面差距。
地球重力场

Q0 Q
Q0
在某一位置处,质点的引力位就是将单位质点从无穷远处移动 到该点所做功。 (假设无穷远处V=0) r r fM fM A Fdr 2 dr M Q r r
F m
fM 0 V A V A r
§3.1-地球及其运动的基本概念
2、地球大气
大气厚度:2000~3000km; 大气质量:3.9×1021克 从地面由低到高可分为:对流层,平流层,中层,电离层 (热层),外层(散逸层) 对流层:海平面以上40~50km;气温随高度增加而降低; 空气对流,运动显著;湿度大;天气多变。 平流层:对流层以上50~55km,气温不受地面影响;空气 水平运动;水汽含量极少。 中 层:平流层以上80~85km,气温随高度增加而迅速下 降,空气对流。 电离层:中层顶部到800km的高空;温度随高度增加而急剧 上升,大部分空气被电离,对电磁波的传播影响较大。 外 层:电离层一上;空气十分稀薄;受地球引力小。
2、重力位的特性
gx gy gz
(1)重力位对三坐标标求偏导则得重力分量或重力加 速度分量:
W Q V x x x V W Q y y y W Q V z z z
2
算 子 Q
2Q x 2
2Q y 2
2Q z 2
2 2 0
§3.2-地球重力场的基本理论
四、重力位
1、重力位
位函数是标函数,重力是引力和离心力的合力,则 重力位就是引力位和离心力位之和: W = V+ Q
W f
dm 2 2 x y r 2
大地测量学知识点

一、水准面与大地水准面1、水准面我们把重力位相等的面称为重力等位面,也就是我们通常所说的水准面。
水准面有无数个。
1)水准面具有复杂的形状。
2)水准面相互既不能相交也不能相切。
3)每个水准面都对应着唯一的位能W=C=常数,在这个面上移动单位质量不做功,亦即所做的功等于0,即dW=-gsds,可见水准面是均衡面。
4)在水准面上,所有点的重力均与水准面正交。
于是水准面又可定义为所有点都与铅垂线正交的面。
故设想与平均海水面相重合,不受潮汐、风浪及大气压变化影响,并延伸到大陆下面处处与铅垂线相垂直的水准面称为大地水准面大地水准面作为测量外业的基准面,而与其相垂直的铅垂线则是外业的基准线。
似大地水准面与大地水准面在海洋上完全重合,而在大陆上也几乎重合,在山区只有2-4m 的差异我们选择参考椭球面作为测量内业计算的基准面,而与其相垂直的法线则是内业计算的基准线。
1.参心坐标系建立一个参心大地坐标系,必须解决以下问题:(1)确定椭球的形状和大小;(2)确定椭球中心的位置,简称定位;(3)确定椭球中心为原点的空间直角坐标系坐标轴的方向,简称定向;(4)确定大地原点。
我国几种常用参心坐标系:BJZ54、GDZ802.地心坐标系地心坐标系分为地心空间大地直角坐标系和地心大地坐标系等。
地心空间大地直角坐标系又可分为地心空间大地平面直角坐标系和空间大地舜时直角坐标系。
1)建立地心坐标系的意义:2)建立地心坐标系的最理想方法是采用空间大地测量的方法。
3)地心坐标系的表述形式(判断)1)WGS一84大地坐标系WGS-84坐标系统的全称是World Geodical System-84(世界大地坐标系-84),它是一个地心地固坐标系统。
WGS-84坐标系统由美国国防部制图局建立,于1987年取代了当时GPS所采用的坐标系统―WGS-72坐标系统而成为GPS的所使用的坐标系统。
WGS一84坐标系的几何定义是:坐标系的原点是地球的质心,Z轴指向BIHl984.0定义的协议地球极(CTP)方向,X轴指向BIHl984.0的零度子午面和CTP赤道的交点,y轴和Z、X轴构成右手坐标系。
地球重力场及地球形状的基本理论

A b
O C
a
3、球面三角形公式(单位球)
余切公式(四元素)
cot a sin c cos c cos B sin B cot A
cot a sin b cos b cos C sin C cot A
cot
A sin
C
cos C
cos b
sin
b cot
a
x y
si
1
nB
L
sinB L
1
cos
B
L
x1 y1
sinA cosc cosC sinB sinC cos B cosa sinB cosc cosC sinA sinC cos A cosb sinC cosb cos B sinA sinB cos A cosc
3 拉普拉斯方程
以测站为中心作单位半径的辅助球,ZO为法线,Z1O为垂线,μ 为 垂线偏差,η 为其在卯酉圈上(东西方向)的分量,ξ 为其在子午圈 上(南北方向)的分量。
BF
BF sin a OB BE BF sin A BD OB BD
BE
sin a sin b sin c sin A sin B sin C
单位球 sin a sin b sin c
R R R (半径为R) sin A sin B sin C
3、球面三角形公式(单位球)
cos A sin A
900-B-ξ
Q
A′
六、垂线偏差公式(天文经纬度的归算)
Z
大地测量学基础课程大纲-黄继锋

中国海洋大学本科生课程大纲课程属性:公共基础/通识教育/学科基础/专业知识/工作技能,课程性质:必修、选修一、课程介绍1.课程描述:《大地测量学基础》是测绘学科的专业核心课程,在海洋测绘与地理信息系统专业方向的课程体系中占有重要地位,是本专业学生必修的专业基础课。
本课程涵盖了整个大地测量领域的基本理论和方法,以现代大地测量学的新成就和发展为着眼点,着重阐述大地测量学的基础理论、主要技术与方法,包括坐标系的建立,地球重力场及地球形状,地球椭球的几何与物理性质,地图投影及坐标计算和核算,控制网布设等。
这些是海洋测绘与地理信息系统方向的学生必须掌握的基本知识与技能,通过该课程的学习,使学生掌握扎实的大地测量理论基础和基本技能,培养学生创新思维和灵活运用能力。
为后续专业课的学习及继续深造打下比较牢固的基础。
2.设计思路:《大地测量学基础》是所有测绘相关专业必修的专业基础课。
主要内容包含如下几个方面的内容:(1)坐标系统和时间系统;(2)地球重力场和地球形状的基本理论;(3)地球椭球及其数学投影变换的基本理论;(4)大地测量基本技术与方法。
3.课程与其他课程的关系:- 4 -本课程要求学生先修的课程有:数字地形测量学,高等数学,线性代数,普通物理学,计算机程序设计。
为后续《GPS测量与数据处理》等课程的学习打下基础。
二、课程目标通过本课程的学习,要求学生:1、掌握大地测量基本概念与基础理论:包括大地测量坐标系统、时间系统,地球重力场的基本概念、确定地形状及大小的基本原理、高程系统,地球椭球面上的大地测量计算原理与方法、地面观测值归算、投影基本理论、高斯平面直角坐标系的建立方法及其灵活运用。
2、掌握大地测量基本技术与方法:平面与高程控制网的建立,通过课间实习实践环节熟悉精密水准仪与水准尺的操作;大地测量计算,坐标变换等,提高编程计算能力。
3、了解现代大地测量学科现状和发展趋势、深空大地测量基本概念。
三、学习要求为达到最佳学习成果,学生应该在课前熟悉教学大纲,做好课前预习,课后应该认真完成课后作业和复习。
大地测量学基础

大地测量学基础:《大地测量学基础》是2010年5月1日武汉大学出版社出版的图书,作者是孔祥元。
图书简介:该书是“十一五”国家级规划教材,也是国家精品课程教材。
本教材严格按照教育部批准的“十一五”国家级规划教材立项要求和全国高等学校测绘学科教学指导委员会以及武汉大学的具体要求进行编写,是全国高等学校测绘工程专业本科教学用教材,也可供从事测绘工程专业及相关专业的科技人员、管理人员及研究生等参考。
图书目录:序第二版前言前言第1章绪论1.1 大地测量学的定义和作用1.1.1 大地测量学的定义1.1.2 大地测量学的地位和作用1.2 大地测量学的基本体系和内容1.2.1 大地测量学的基本体系1.2.2 大地测量学的基本内容1.2.3 大地测量学同其他学科的关系1.3 大地测量学的发展简史及展望1.3.1 大地测量学的发展简史1.3.2 大地测量的展望第2章坐标系统与时间系统2.1 地球的运转2.1.1 地球绕太阳公转2.1.2 地球的自转2.2 时间系统2.2.1 恒星时(ST)2.2.2 世界时(UT)2.2.3 历书时(ET)与力学时(DT)2.2.4 原子时(AT)2.2.5 协调世界时(UTC)2.2.6 卫星定位系统时间2.3 坐标系统2.3.1 基本概念2.3.2 惯性坐标系(ClS)与协议天球坐标系2.3.3 地固坐标系2.3.4 坐标系换算第3章地球重力场及地球形状的基本理论3.1 地球及其运动的基本概念3.1.1 地球概说3.1.2 地球运动概说3.1.3 地球基本参数:3.2 地球重力场的基本原理3.2.1 引力与离心力3.2.2 引力位和离心力位3.2.3 重力位3.2.4 地球的正常重力位和正常重力3.2.5 正常椭球和水准椭球,总的地球椭球和参考椭球3.3 高程系统3.3.1 一般说明3.3.2 正高系统3.3.3 正常高系统3.3.4 力高和地区力高高程系统3.3.5 国家高程基准3.4 关于测定垂线偏差和大地水准面差距的基本概念3.4.1 关于测定垂线偏差的基本概念3.4.2 关于测定大地水准面差距的基本概念3.5 关于确定地球形状的基本概念3.5.1 天文大地测量方法3.5.2 重力测量方法3.5.3 空间大地测量方法第4章地球椭球及其数学投影变换的基本理论4.1 地球椭球的基本几何参数及其相互关系4.1.1 地球椭球的基本几何参数4.1.2 地球椭球参数间的相互关系4.2 椭球面上的常用坐标系及其相互关系4.2.1 各种坐标系的建立4.2.2 各坐标系间的关系4.2.3 站心地平坐标系4.3 椭球面上的几种曲率半径4.3.1 子午圈曲率半径4.3.2 卯酉圈曲率半径4.3.3 主曲率半径的计算4.3.4 任意法截弧的曲率半径4.3.5 平均曲率半径4.3.6 M,N,R的关系4.4 椭球面上的弧长计算4.4.1 子午线弧长计算公式4.4.2 由子午线弧长求大地纬度4.4.3 平行圈弧长公式4.4.4 子午线弧长和平行圈弧长变化的比较4.4.5 椭球面梯形图幅面积的计算4.5 大地线4.5.1 相对法截线4.5.2 大地线的定义和性质4.5.3 大地线的微分方程和克莱劳方程4.6 将地面观测值归算至椭球面4.6.1 将地面观测的水平方向归算至椭球面4.6.2 将地面观测的长度归算至椭球面4.7 大地测量主题解算概述4.7.1 大地主题解算的一般说明4.7.2 勒让德级数式4.7.3 高斯平均引数正算公式4.7.4 高斯平均引数反算公式4.7.5 白塞尔大地主题解算方法4.8 地图数学投影变换的基本概念4.8.1 地图数学投影变换的意义和投影方程4.8.2 地图投影的变形4.8.3 地图投影的分类4.8.4 高斯投影简要说明4.9 高斯平面直角坐标系4.9.1 高斯投影概述4.9.2 正形投影的一般条件4.9.3 高斯投影坐标正反算公式4.9.4 高斯投影坐标计算的实用公式及算例4.9.5 平面子午线收敛角公式4.9.6 方向改化公式4.9.7 距离改化公式4.9.8 高斯投影的邻带坐标换算4.10通用横轴墨卡托投影和高斯投影族的概念4.10.1 通用横轴墨卡托投影概念4.10.2 高斯投影族的概念4.11兰勃脱投影概述4.11.1 兰勃脱投影基本概念4.11.2 兰勃脱投影坐标正、反算公式4.11.3 兰勃脱投影长度比、投影带划分及应用第5章大地测量基本技术与方法5.1 国家平面大地控制网建立的基本原理5.1.1 建立国家平面大地控制网的方法5.1.2 建立国家平面大地控制网的基本原则5.1.3 国家平面大地控制网的布设方案5.1.4 大地控制网优化设计简介5.2 国家高程控制网建立的基本原理5.2.1 国家高程控制网的布设原则5.2.2 国家水准网的布设方案及精度要求5.2.3 水准路线的设计、选点和埋石5.2.4 水准路线上的重力测量5.2.5 我国国家水准网的布设概况5.3 工程测量控制网建立的基本原理5.3.1 工程泓量控制网的分类5.3.2 工程平面控制网的布设原则5.3.3 工程平面控制网的布设方案5.3.4 工程高程控制网的布设5.4 大地测量仪器5.4.1 精密测角仪器——经纬仪5.4.2 电磁波测距仪5.4.3 全站仪5.4.4 GPS接收机5.4.5 TPS和GPS的集成——徕卡系统1200-超站仪(system1200-SmartStation5.4.6 精密水准测量的仪器——水准仪5.5 电磁波在大气中的传播5.5.1 一般概念5.5.2 电磁波在大气中的衰减5.5.3 电磁波的传播速度5.5.4 电磁波的波道弯曲5.6 精密角度测量方法5.6.1 精密测角的误差来源及影响5.6.2 精密测角的一般原则5.6.3 方向观测法5.6.4 分组方向观测法5.6.5 归心改正5.7 精密的电磁波测距方法5.7.1 电磁波测距基本原理5.7.2 N值解算的一般原理5.7.3 距离观测值的改正……第6章深空在地测量简介主要参考文献。
大地测量学基础ppt课件

3
二、大地水准面
与平均海水面相重合,不受潮汐、风浪及大气压变化影响, 并延伸到大陆下面处处与铅垂线相垂直的水准面称为大地水 准面,由它包围的形体称为大地体,可近似地把它看成是地 球的形状。
我国曾规定采用青岛验潮站求得的1956年黄海平均海水面 作为我国统一高程基准面,1988年改用“1985国家高程基准” 作为高程起算的统一基准。
Z轴:与地球平均自转轴相 重合,亦即指向某一时刻的平 均北极点。
X轴:指向平均自转轴与平 均格林尼治天文台所决定的子 午面与赤道面的交点。
16
五、天文坐标系
1)天文坐标系是以铅垂线为依 据建立起来的。
2)一点的坐标用天文经度 及
天文纬度 表示。
3)所谓天文纬度是P点的铅垂线 与地球赤道面形成的锐角,
A、B两点平均高度(可用近似值代替)
(g
m o
)m
H AB
是AB路线上的正常重力
42
3.3 高程系统概论
3.3.4 国家高程基准 一、高程基准面
1956年黄海高程系统:1957年确定青岛验潮站为我国 基本验潮站,该站1950年至1956年7年间的潮汐资料推求 的平均海水面作为我国的高程基准面。
正常重力并不顾及地球内部质量和密度分布的不规 则,而仅仅与纬度有关,其计算公式为:r=r0- 0.3086H
(r0:平均椭球面上的重力值)
6
四、 正常椭球和水准椭球 总地球椭球和参考椭球
正常椭球的定位和定向:
其中心和地球质心重合 其短轴与地轴重合 起始子午面与起始天文子午面重合
39
铅垂线大地水准面ppt课件.ppt

❖ 海洋测绘学
以海洋和陆地水域为对象进行测量和海图编绘工作
❖ 工程测量学
研究工程建设在规划、设计、施工、运行管理各阶段所进行的测量工作
❖ 制图学
研究地球表面点、线经投影变换后绘制成满足各种不同需要的地图
return
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
测量学的定义
❖ 定义: 研究地球形状大小以及确定地面(包括空中、 地下和海底)点位的科学。
❖ 解释: 测量学是一门科学(学科),而不是一项纯 粹的技术,因为它有自己作为一门学科的独 特的理论体系。
return
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
测量工作的基本概念
测量工作的基本原则
控制测量的概念
测量的基本工作
三项基本工作:测角、量距、测高差(高程) 三个基本元素:角度、距离、高差(高程)
home
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
铅垂线
大地水准 面
地 球 的 形 状 与 大 小
return
Hale Waihona Puke 在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
第三章斯托克司边值理论

大地水准面上扰动位的解
r d
d 2 R 2 2R cos
令x=,a=1,b=2Rcos,c=R2查积分表
xdx ax bx c
2
r d r R cos ln( r R cos )
地水准面上扰动位的解
3 R2
2
2
将上式两边同除以2,并令S(,)
水准面上扰动位的解
2 r 1 R S ( , ) 3 2 5 2 cos r R r R cos 3 2 cos ln 2
上式称为广义斯托克斯函数,当=R时,
称为斯托克斯函数,相应的扰动位
1 T0 ( g 0 0 )S( )d 4R
3-1-2
利用(3-1-1)得
其中 T0 和 0分别为大地水准面上的扰动位和 平均椭球体表面上的正常重力。
0
由于定义平均椭球体表面的正常重力位等于大地 水准面上的重力位,即 W0 U 0 ,所以(6-1-3) 简化为
因为 T0是微小量,在一级近似下我们用 0的全球平均 值 0 来替换它,这相当于省略扁率级的量,所以这种 近似称为球近似,
上述三个公式(6-1-3),(6-1-4)和(6-1-5)统称为布隆斯公 式。
(三) 垂钱偏差
这里的垂线偏差指重力垂线偏差,它是大地水 准面上某点的重力方向与通过该点到平均椭球 体表面的法线方向之间的夹角。垂线偏差除大 小之外,还必须指出偏离方向,这就需要至少 用它在两个方向的投影来描述,一般取向南的 分量 和向西的分量 来表示,如图6-2所示, 轴垂直于平均椭球体表面。
垂线偏差
1 tg g z 1 tg gz T0 x T0 y
垂线偏差
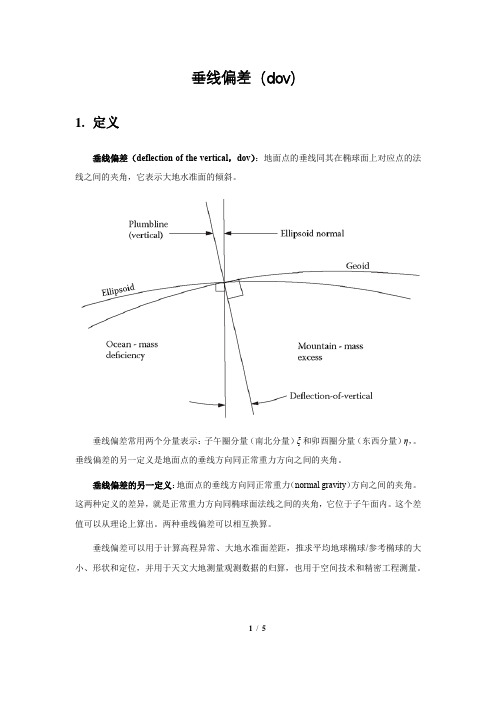
垂线偏差(dov)1.定义垂线偏差(deflection of the vertical,dov):地面点的垂线同其在椭球面上对应点的法线之间的夹角,它表示大地水准面的倾斜。
垂线偏差常用两个分量表示:子午圈分量(南北分量)ξ和卯酉圈分量(东西分量)η,。
垂线偏差的另一定义是地面点的垂线方向同正常重力方向之间的夹角。
垂线偏差的另一定义:地面点的垂线方向同正常重力(normal gravity)方向之间的夹角。
这两种定义的差异,就是正常重力方向同椭球面法线之间的夹角,它位于子午面内。
这个差值可以从理论上算出。
两种垂线偏差可以相互换算。
垂线偏差可以用于计算高程异常、大地水准面差距,推求平均地球椭球/参考椭球的大小、形状和定位,并用于天文大地测量观测数据的归算,也用于空间技术和精密工程测量。
1 / 52.分类:绝对(重力)、相对(天文大地)按选取的椭球不同,垂线偏差可分为绝对垂线偏差和相对垂线偏差。
(1) 绝对垂线偏差(absolute deflection of the vertical)又称重力垂线偏差(gravimetric deflection of the vertical),是垂线同平均地球椭球面(mean earth ellipsoid)法线之间的夹角。
因为平均地球椭球是不变的,所以过地面点的法线或正常重力线也是不变的。
因而垂线偏差具有绝对意义,它可以利用重力异常,按维宁·曼尼兹(Vening Meinesz)公式计算。
在经典的地球形状理论中,需要的是大地水准面上的垂线偏差,因而需将地面点的垂线归算到大地水准面上,组成大地水准面上相应的垂线偏差。
由于这种归算(reduction)同大地水准面和地面间的质量分布有关,而目前尚不能准确地知道这种分布,因此计算大地水准面上的垂线偏差分量,理论上就不可能是严密的。
为避免这种不严密性,可采用Molodensky 理论计算地面点的垂线偏差。
用零次趋近的Molodensky公式计算的地面垂线偏差和用Vening Meinesz公式算出的数值是一样的。
垂线偏差和大地水准面差距课件

重要性
精确定位和测量
垂线偏差和大地的水准面差距是影响 精确定位和测量的关键因素,对于地 理信息系统、导航、地震监测等领域 具有重要意义。
地球科学基础
理解垂线偏差和大地的水准面差距有 助于深入了解地球的重力场、地球自 转等地球科学基础问题。
课程目标
掌握垂线偏差和大地 的水准面差距的基本 概念和原理。
正等。
03
大地水准面差距概念
定义
01
大地水准面差距是指地面点沿正 常重力线到大地水准面的距离。
02
大地水准面是假设的一个静止的 平均海水面,与地球表面相切, 并垂直于地球自转轴。
产生原因
由于地球内部物质散布不均匀,导致 地球重力场不均匀,进而影响大地水 准面的形态。
大地水准面差距的产生还受到地形、 地貌、地质构造、地下水位等因素的 影响。
垂线偏差是地球重力场的重要参数 之一,对于地球科学研究和地球重 力场模型建立具有重要意义。
大地水准面差距在水文和蔼象中的应用
水位监测
大地水准面差距是影响水位监测 的重要因素之一。通过获取大地 水准面差距数据,可以修正水位 监测结果,提高水位监测的精度
。
气象预报
大地水准面差距也会影响气象预 报的准确性。在数值天气预报中 ,需要将大地水准面差距考虑在
06
应用和案例分析
垂线偏差在导航和定位中的应用
航海和航空导航
垂线偏差会影响船舶和飞机的导 航精度,因此需要进行修正。通 过测量垂线偏差,可以计算出修
正值,提高导航的准确性。
卫星定位
卫星定位系统如GPS也会受到垂线 偏差的影响。通过获取垂线偏差数 据,可以对卫星定位结果进行修正 ,提高定位精度。
地球科学研究
第三章-3垂线偏差大地水准面差距的测定分析

六、高程基准面
•就是地面点高程的统一起算面。 •通常采用大地水准面作为高程基准面。 •严格地讲,大地水准面与平均海水面不同。
七、我国的国家高程基准
H85 H56 0.029 m
•1956年黄海高程系统,其水准原点的高程为72.289m
•1985国家高程基准,其水准原点的高程为72.260m
一、建立大地坐标系统必须解决的问题 (回顾)
大地水准面差距
4、利用GPS高程拟合法研究似大地水准面
GPS可以测出大地高(精度约2cm),如果在测区中选 择一定的GPS点同时联测几何水准测量,求出这些点的正 常高H常,于是在这些点上便可求出高程异常:
H H常
代入适当的数学拟合方程中,用最小二乘求解出各系数, 即可得到计算其他点高程异常,如:
( L) cos
• 若已知一点的垂线偏差, 便可将天文纬度和经度换算为大地纬度和经度:
B L sec
2、天文方位角归算为大地方位角的公式
A ( L)sin ( sin A cos A)cot Z天
A ( L)sin 或: A tan
上式称为拉普拉斯方程
在经典大地测量中,只能用实测的天文方位角由拉普拉斯 方程计算大地方位角。而用现代GPS测量技术可以直接算 出大地方位角,而不必再由实测的天文方位角推求。
•地面一点上的重力向量g和相应椭球面上的法线向
量 n之间的夹角定义为该点的垂线偏差u。很显然,
根据所采用的椭球不同可分为绝对垂线偏差及相对 垂线偏差,垂线与总地球椭球(或参考椭球)法线构 成的角度称为绝对(或相对)垂线偏差,它们统称为 天文大地垂线偏差。
•为计算表示方便,垂线偏差分解为子午圈分量ξ和 卯酉圈分量η。
r n2
m0
垂线偏差

定义
同一测站点上铅垂线与椭球面法线之间的夹角u,即是垂线偏差。
垂线偏差u通常用南北方向分量ζ和东西方向分量η表示。如图《垂线偏差》所示:
垂线偏差的另一定义是地面点的垂线方向同正常重力方向之间的夹角。这两种定义的差异,就是正常重力方 向同椭球面法线之间的夹角,它位于子午面内。这个差值可以从理论上算出。两种垂线偏差可以相互换算。
垂线偏差
测
目录
02 分类 04 法
垂线偏差是指同一测站点上铅垂线与椭球面法线之间的夹角u。u通常用南北方向分量ζ和东西方向分量η表 示。地面点的垂线同其在椭球面上对应点的法线之间的夹角,它表示大地水准面的倾斜。垂线偏差通常用两个分 量来表示,一个是子午圈分量ξ,即垂线偏差南北分量;一个是卯酉圈分量η,即垂线偏差东西分量。
在重力资料稀少的情况下,垂线偏差还可以根据地壳均衡假说来计算,这样的垂线偏差称为地形均衡垂线偏 差。
又称天文大地垂线偏差,是垂线和参考椭球面的法线之间的夹角。因为不同的参考椭球过地面点的法线不同, 垂线偏差也各不相同,所以它具有相对意义。相对垂线偏差可以利用天文和大地经纬度来计算。
计算公式
(1)垂线偏差公式: ξ=φ-B,η=(λ-L)cosφ。已知一点的天文和大地经、纬度,就可求得垂线偏差。 (2)拉普拉斯方程: A=α-(λ-L)sinφ-(ξsinA-ηcosA)cotZ(天) 简化 A=α-(λ-L)sinφ或 A=α-ηtanφ (3)这样可以将天文方位角α归算为大地方位角A。 天文纬度φ、经度λ同大地纬度B、经度L的关系:B= φ-ξ;L= λ-ηsecφ 依据上式,便可将天文纬度和经度换算为大地纬度和经度。
垂线偏差法需要先利用卫星测高数据计算海洋上的测高垂线偏差,Sandwell、Olgiati、Hwang先后提出了 不同的测高垂线偏差计算方法,它们也是当前国际上测高垂线偏差的主要计算方法。垂线偏差法的另一重要步骤 是如何利用测高垂线偏差精确计算海洋重力场,Molodenskii、Sandwell、Hwang等在不同时期分别提出了各自 利用垂线偏差法确定海洋重力场的原理,尤其是Molodenskii、 Hwang利用测高垂线偏差计算海域大地水准面和 重力异常的方法在理论上比较严密,在实际工程中应用得比较普遍。
大地水准面差距名词解释

大地水准面差距名词解释大地水准面差距是由于人类活动而引起的相对于真正的大地水准面在高程方向上的变化。
它等于两个假定水准面的差,其值在天文计算中很有用。
与之相似的概念还有地球自转偏向力差距。
名词解释:大地水准面是根据一个已知点的水准位置和高程拟合成的一个椭圆柱面。
其长轴通过地心且垂直于赤道面,称为大地水准面。
是指当地球自转轴的垂线不通过地心时,从某一点观测,地面法线铅垂投影到参考椭球面上所得的椭圆柱面。
按椭圆柱面法线通过地心的假定,可分为理论大地水准面和假定大地水准面。
若不计及椭球体旋转的影响,当地球不自转时,地面上任意两点的连线和地球球面交于一点,此点即为地球椭球体的中心。
此点同时又是地球质量中心、地心、引力中心和大地水准面的重心。
此时地面上各点离椭球体中心的距离称为地球椭球体的半径。
地球椭球体是个近似球体,具有数学公理中的关系式E=M。
大地水准面的这种改变和真正的水准面差距不同。
它只有在两个椭球面的法线不平行或重叠时才能产生。
例如当地球静止在极轨道上时,理论上将在地球表面上产生一个水平椭圆柱面,这个椭圆柱面和原来的大地水准面相比较,其水平位移就会出现大约5°的误差,因而实际上有一个虚假的大地水准面。
这个虚假的大地水准面就叫做地球自转轴相对于地球质心的偏离椭圆柱面。
地球自转轴相对于地球质心的偏离椭圆柱面就是假定大地水准面。
当然,这个虚假的大地水准面必须假设在理论的或更远的时代,由人们所测定出来的,也是十分可靠的,但这只是一个假设而已。
所以,严格地说,它只是理论上的大地水准面,并非真正的大地水准面。
人造卫星所观测到的大地水准面也只是这个理论大地水准面的一个组成部分。
在大地水准面中,理论上的虚假大地水准面和真正的大地水准面是一个差距最大的两个部分。
两个椭圆柱面都有各自的曲率半径,随着椭球体形状的改变而改变,且随纬度的变化而变化。
在高纬度处,理论上的虚假大地水准面与真正的大地水准面的最大差距最大,在低纬度处,两者的差距就小一些。
大地水准面

什么是大地水准面军事辞海中的解释:在全球海洋范围内,与静态海面地形的平均值为零的面相重合并向大陆内部延伸的水准面是地球重力场中一个等位面,也是高程测量中的正高系统的起算面。
因地球表面地形起伏和内部质量分布不均匀,使大地水准面成为略有起伏的曲面。
大地测量学研究的地球形状主要指大地水准面的形状。
汉语词典中的解释:指与平均海水面重合并延伸到大陆内部的水准面。
是正高的基准面。
在测量工作中,均以大地水准面为依据。
因地球表面起伏不平和地球内部质量分布不匀,故大地水准面是一个略有起伏的不规则曲面。
该面包围的形体近似于一个旋转椭球,称为“大地体”,常用来表示地球的物理形状。
大地水准面是是重力等位面,即物体沿该面运动时,重力不做功(如水在这个面上是不会流动的)。
大地水准面是描述地球形状的一个重要物理参考面,也是海拔高程系统的起算面。
大地水准面的确定是通过确定它与参考椭球面的间距--大地水准面差距来实现的。
大地水准面和海拔高程等参数和概念在客观世界中无处不在,在国民经济建设中起着重要的作用。
大地水准面是大地测量基准之一,确定大地水准面是国家基础测绘中的一项重要工程。
它将几何大地测量与物理大地测量科学地结合起来,使人们在确定空间几何位置的同时,还能获得海拔高度和地球引力场关系等重要信息。
大地水准面的形状反映了地球内部物质结构、密度和分布等信息,对海洋学、地震学、地球物理学、地质勘探、石油勘探等相关地球科学领域研究和应用具有重要作用。
大地水准面是测绘工作中假想的包围全球的平静海洋面,与全球多年平均海水面重合,形状接近一个旋转椭球体,是地面高程的起算面。
大地水准面同平均地球椭球面或参考椭球面之间的距离都称为大地水准面差距。
前者是绝对的,也是唯一的;后者则是相对的,随所采用的参考椭球面不同而异。
绝对大地水准面差距是指大地水准面到平均地球椭球面间的距离。
它的数值最大在±100米左右。
绝对大地水准面差距可以利用全球重力异常按斯托克斯积分公式进行数值积分算得,也可以利用地球重力场模型的位系数按计算点坐标进行求和算得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1sin
2
, A垂线偏差计算点至面 的元 球面距离和方位角
说明:⑴假设大地水准面外没有扰动物质,全球重力异常已知; ⑵然而这两个条件都还不能实现,所以重力方法至今也没有得到 独立的应用。 3.天文重力方法 综合利用天文大地方法和重力测量方法来确定垂线偏差
首先建立天文大地点:在这些点上用天文大地测量方法计算各自的 垂线偏差,在计算点周围σ范围内:进行较密的重力测量,内插 确定垂线偏差
在更大的区域Σ内:进行少数重力测量,计算重力垂线偏差, 同通过天文大地测量方法确定的垂线偏差比较。
4.GPS测量方法
在GPS相对定位中,只要测出基线长D,大地方位角A及高程异常
差Δζ,便可求得垂线偏差。计算公式: i i cos Ai i sin Ai
——A、B两点的似大地水准面之差:
A B D 2
3.4.3 大地水准面差距
§3.4 关于测定垂线偏差和大地水准面差距的基本概念 补充知识点: 1、天文经度、天文纬度和天文方位角 天文经度:包含测站垂线的子午面与起始子午面的夹角; 天文纬度:测站垂线的与赤道面的夹角; 天文方位角:包含测站垂线的子午面与测站垂线和照准面所张成的
垂直面的夹角; 天文天顶距:测站垂线与观测方向的夹角
arctaa2n84.280
a1
3、垂线偏差
uarctaa12n a226.4"8
小结
• 掌握基本概念:垂线偏差 。 • 天文坐标和大地坐标的公式转换及推导过程。 • 了解测定垂线偏差基本方法。 垂线偏差的变化 1、垂线偏差随点位的不同而不同。 2、它的变化是均匀的和缓慢的,在微小的范围内可以
将它视为一个常量。
2 球面三角的基本知识
正弦定理:球面三角各边的正弦和对角的正弦成正比。
边的余弦定理:球面三角任意边的余弦等于其他两边的余弦加上这 两边的正弦及其夹角余弦的连乘积。
角的余弦定理:球面三角任意一角的余弦等于其他两角的余弦冠以 负号加上这两角的正弦及其夹边余弦的连乘积。
3.4 垂线偏差和大地水准面差距
测量取得天文坐标(φ,λ),通过垂线偏差公式,计算得到该点
的垂线偏差,也称为赫尔默特垂线偏差。
计算公式:( B , L )
说明:⑴精度高;
( , )
(,)
(L)cos
⑵作业量大,只适用于少数的天文大地点上。
2.重力测量方法实质是借助于大地水准面和地球椭球面上的重力异
常,假设已知全球范围的重力异常,就可按斯托克斯方法求得大
若对设多条基A 线而B 言,则,有则式由上i 式i可c o s 得A i :is in A i( i 1 ,2 , DL ,,n )
从而可用最小二乘法求出垂线偏差 、
说明:这种方法应用是有条件的,比如,地形平坦,基线不长,精
度要求较低。
• 上面是垂线偏差的线段法:是以线段端点高程异常值为观测值, 平均垂线偏差的子午线和卯酉圈上的分量为参数,通过平差计算 得到垂线偏差。
3.4.1 垂线偏差概念
垂线偏差:指地面上一点分别向椭球作法线和向大地水准面作铅垂 线,两条线之间的夹角或指地面上一点的重力向量g与相应椭球面 上的法线向量n之间的夹角。是由于同一点的法线与垂线不一致而 引起的差异。
垂线偏差
, 分别是垂线偏差的子午
分量和卯酉分量
分类:绝对垂线偏差:总地球椭球
相对垂线偏差:参考椭球
解:1、确定平面 由于范围较小,可将这四个点所在的
高程异常区面视为一个平面,这个平面可 用一个方程表示,即
N a 0 a 1 (x x 0 ) a 2 (y y 0 )
x04144,y0004 095000 a0 28.632 a13.1321 06 a23.1271 05
2、垂线偏差的方向
• 还有平面法:以例题说明其原理
例题:四个点分别命名为A、B、C、D,它们的 平面位置及高程异常如表,试计算垂线偏差。
点名 横坐标 纵坐标 高程异常
A 4145158 495585 28.65
B 4144937 496990 28.701
C 4146063 497185 28.704
D 4146430 495124 28.646
地水准面上的垂线偏差。
建立扰动位与垂线偏差的关系,即扰动位与观测量(重力异常)的函
数
重力异常 垂线偏差
维宁.曼尼兹推得了垂线偏差的计算公式:
21
2
0
gQ()coAs ddA
0
21
2
0
Q() cos2 [csec 12sin 32sin2
2
3 12sin2 ln(sin sin2)],
即 siR n 1 (R )siq n co z1s
公式推导
在球面三角形MZZ1中: sin q sin R
sin sin z1
siqn sin siR n /siz1 n
sq i n sin siA n)/( sz i1n
R R 1 ( u cs o A i s u n si c n A ) o cz 1 s ot
A ( L )s i ( n sA i n cA ) o cZ 天 s ot
A(L)sin
ZZ0coAssiA n
此式也是天文经纬度同大地经纬度的关系式。
公式推导 1 垂线偏差对水平方向的影响是:
R - R1
在球面直角三角形R1RM中:
c9 o 0 ( s R 1 [ R ) ] sq i s n 9 i n 0 z 1 ) (
2、推导由于测站所在的天文子午面和测站所在的大地子午面的不 同引起的方位角的变化:即求θ1-θ
3.4.2 垂线偏差测定
• 测定垂线偏差一般有以下几种方法: 1. 天文大地测量方法 2. 重力测量方法 3. 天文重力方法 4. GPS测量方法
1.天文大地测量方法
在天文大地点上,既进行大地测量取得大地坐标(B,L),又进行天文
根据所采用的椭球不同可分为绝对垂线偏差及相对垂线偏差,垂线 同总地球椭球(或参考椭球)法线构成的角度称为绝对(或相对)垂 线偏差,它们统称为天文大地垂线偏差。
▪ 图中,u是垂线偏差,ξ、η分别是u在子午圈和卯酉圈上的分量
uAco A ssiA n
u2 2 2
9 0B(9 0)B
(L)cos
B L sec
