高中数学人教新课标A版必修2 第二章 点、直线、平面之间的位置关系 2.2.3直线与平面平行的性质B
人教A版高中数学必修2《二章 点、直线、平面之间的位置关系 欧几里得《原本》与公理化方法》教案_2

第二章点、直线、平面之间的位置关系阅读与思考:欧几里得与《几何原本》教学目标与教学指导:数学的内容可以粗略地分为代数与几何两大部门。
代数是关于数量关系及数量形式的学问,而几何是关于空间形式的学问,最初主要研究空间的度量、形体关系以至形式演绎。
在数学教学中,几何与代数具有同等重要的地位。
希望通过本专题的学习,了解欧几里得对数学发展的贡献及《几何原本》的主要内容,并将其灵活运用于对教学的指导。
教学内容:1、欧几里得的生平简介:欧几里得(约公元前330-公元前275),古代希腊最杰出的数学家。
生平没有详实的资料流传,出生地也无从查考,现在仅知道他生活在托勒密一世统治时期,曾在亚历山大创办学校并从事教学工作。
他在数学上的贡献在于创立了欧氏几何学。
在总结前人关于几何学实践知识的基础上,集他人研究成果之大,以逻辑推理的方法,将公认的事实定义化和公理化,并予以演绎证明,编著了《几何原本》。
这部著作一直流传至今,对人类活动产生持续的重大影响,至少到19世纪非欧几里得几何出现之前,它一直是几何学的推理、定理和方法的主要源泉,堪称是人类历史上一部伟大的科学著作。
《几何原本》的内容包括算术、平面几何、立体几何,是世界上最早公理化的数学著作。
全书共计13卷,据史料记载,欧几里得还有4部失传的著作:《辩伪术》、《衍论》、《二次曲线》、《曲面一轨迹》。
2、教师生涯:毕竟时光已经流逝了2000多年,到现在为止,我们都无法知道欧几里得出生和去世的准确日子,也不知道他究竟是什么地方人。
只大致了解他是希腊人,生活在埃及托勒密一世统治时期。
因为托勒密一世于公元前323年到公元前285年在位,而后来的大科学家阿基米德又曾经引用过欧几里得的著作,因而判定欧几里得活动的年代比阿基米德要早一些,而阿基米德生活的年代是公元前2世纪,由此推测欧几里得活动的年代大约是公元前330年到公元前275年左右。
欧几里得年青时,曾经在雅典的柏拉图科学院求学,受到了十分良好的教育。
人教A版高中数学必修二第二章 点、直线、平面之间的位置关系

的直线与另一个平面垂直
二面角二 范围 面: 角[的0°平,面18角0°]
专题突破
专题一 空间中的位置关系 1.空间中两直线的位置关系:相交、平行、异面. 2.空间中直线与平面的位置关系:直线在平面内、直线 与平面平行、直线与平面相交. 3.两个平面的位置关系:平行、相交.
[例 1] 下面四个命题中,正确命题的个数是( )
如上图,AB∥平面 CDD′C′,BB′∥平
③ × 面 CDD′C′,AB∩BB′=B,即 AB 与
BB′不平行,③不正确
序号 正误
原因分析
如上图,设直线 l 是平面 ABB′A′内与 AB 平行的任一条直线,l 有无数条,即 AB 与 ④× 平面 ABB′A′内的无数条直线平行,但 AB⊂平面 ABB′A′,④不正确
[解析] ∵AB 为⊙O 直径,C 为⊙O 上一点, ∴BC⊥AC,
DBCA⊂⊥平平面面AABBCC⇒DA⊥BC
BC⊥AC
AC∩DA=A
⇒BACF⊂⊥平平面面DDAACC ⇒
BC⊥
AF⊥DC
BC∩DC=C
⇒ABFD⊥⊂平平面面DDCCBB⇒ BD⊥AF
BD⊥AE
AF∩AE=A
判定定理:一个平面内的两条相交直线与另一个平面平行,
则这两个平面平行 平面与平面平行
性质定理:如果两个平行平面同时和第三个平面相交,那么 它们的交线平行
平面与平面之间的位置关系
判定定理:一个平面过另一个平面的垂线,则这两个平面垂直
平面与平面垂直性质定理:两个平面垂直,则一个平面内垂直于交线
[例2] (2011·江苏高考)如图,在四棱锥P-ABCD中,平 面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是 AP,AD的中点.
新人教A版必修2高中数学第二章点、直线、平面之间的位置关系单元总结

学习本章应着眼于以下几个方面:(1)从图形入手,学会识 图、画图,并注意图形语言、符号语言及文字语言之间的转 化;(2)整体把握空间点、线、面之间的位置关系,在具体的学 习中,对定理的学习要做到细致入微,从条件到结论,必须做 到准确的表达,论证要严谨,有理有据,计算要有依据,尽量 的追求简便;
(3)把握处理立体几何问题的思想方法,即把空间问题转化 为平面问题去解决,化繁为简,这是解决立体几何问题的基本 方法,也是最重要的思想方法;(4)培养处理立体几何问题必备 的三个方面能力:一是空间想象能力,二是逻辑思维能力,三 是推理论证能力.
9、 人的价值,在招收诱惑的一瞬间被决定 。21.4 .421.4 .4Sun day, April 04, 2021 10、低头要有勇气,抬头要有低气。 08:48 :1308 :48:1 308:4 84/4/ 2021 8:48:13 AM 11、人总是珍惜为得到。21.4.408: 48:13 08:48 Apr-2 14-Apr-21 12、人乱于心,不宽余请。08:48:1 308:4 8:130 8:48Sunday , April 04, 2021 13、生气是拿别人做错的事来惩罚自 己。21 .4.42 1.4.40 8:48: 1308: 48:13 April 4, 2021 14、抱最大的希望,作最大的努力。 2021 年4月4 日星期 日上午 8时48 分13秒 08:48 :1321. 4.4 15、一个人炫耀什么,说明他内心缺 少什么 。。20 21年4 月上午 8时48 分21.4 .408: 48Apri l 4, 2021 16、业余生活要有意义,不要越轨。 2021 年4月4 日星期 日8时4 8分13 秒08:4 8:134 April 2021 17、一个人即使已登上顶峰,也仍要 自强不 息。上 午8时4 8分13 秒上午 8时48 分08: 48:13 21.4.4
人教A版高中数学必修2第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系课件

C D
B A
C1 D1
B1 A1
知识小结
实例引 入平面
平面的画 法和表示
点和平面的 位置关系
平面三 个公理
空间图形
文字叙述
符号表示
2.1.2空间中两直线的位置 关系
平面有知识(复习 )
判断下列命题对错: 1、如果一条直线上有一个点在一个平面上,则这条直线上
的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平
直线。(既不相交也不平行的两条直线) 判断:
(1)
m
β
m
l
α
l
直线m和l是异面直线吗?
(2)
,则 与 是异面直线
(3)a,b不同在平面 内,则a与b异面
异面直线的画法:
通常用一个或两个平面来衬托,异面直线
不同在任何一个平面的特点
a
b
b
a
b
a
2、空间中两直线的三种位置关系
1、相交
m P
l
2、平行
m l
b′
平
a′ θ O
移
若两条异面直线所成角为90°,则称它们互相垂直。 异面直线a与b垂直也记作a⊥b 异面直线所成角θ的取值范围:
例 3 在正方体ABCD—A1B1C1D1中指出下列各对线段所
成的角:
D1
C1
1)AB与CC1; 2)A1 B1与AC; A1
B1
3)A1B与D1B1。
1)AB与CC1所成的角 = 9 0°
4、平面的基本性质
公理3 如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
符号表示为:
P l, Pl.
人教版高中数学必修二第二章 点、直线、平面之间的位置关系全章教案

)利用生活中的实物对平面进行描述;的直观图)掌握平面的基本性质及作用;.思考4:当两个平面相交时,你认为下列哪个图形的立体感强?你能指出其画法要点吗?(1)画出交线;(2)被遮挡部分画虚线.说明:为了表示和区分平面,我们可以用适当的字母作为平面的名称,如思考5:直线和平面都可以看成点的集合.那么“点P在直线l在平面α内”,用集合符号可怎样表示?“点P在直线l外”,“点A在平面α外”用集合符号可怎样表示?思考3:如图,当点A、B落在平面α内时,直线置关系如何?由此可得什么结论?公理1 如果一条直线上的两点在一个平面内思考1:空间中,经过两点有且只有一条直线,即两点确定一条直线,那么两思考1:如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所思考2:如果两条不重合的直线有公共点,则其公共点只有一个重合的平面有公共点,其公共点有多少个?这些公共点的位置关系如何?l β= ,有哪些理论作用吗?确定两平面相交的依据,判断多点共线的依据例2: 如图,用符号表示下列图形中点、直线、平面之间的位置关系,l P αβ=且(1)平面的概念、画法、表示方法;(2)文字语言、符号语言、图形语言描述点、直线、平面之间的位置关)了解空间中两条直线的位置关系;(养学生的空间想象能力;(;()异面直线所成角的定义、范围及应用。
思考2:我们把上图中直线A′B与直线CD怎样理解异面直线?关于异面直线的定义,你认为下列哪个说法最合适?A. 空间中既不平行又不相交的两条直线;思考1:设直线a//b,将直线a在空间中作平行移动,在平移过程中a与b思考2:如图, 在长方体ABCD—A′B′C′D′中,BB′∥AA′,DD′∥AA′,那么BB′与DD′平行吗 ?思考3:取一块长方形纸板ABCD,E,F分别为AB,CD的中点,将纸板沿EF 折起,在空间中直线AD与BC的位置关系如何 ?思考4:通过上述实验可以得到什么结论?思考1:在平面上,如果一个角的两边与另一个角的两边分别平行,那么这两思考2:如图,四棱柱ABCD--A′B′C′D′的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何 ?思考3:如图,在空间中AB// A′B′,AC// A′C′,你能证明∠BAC与∠B′A′C′相等吗?例2:如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中1. 空间直线的位置关系;2. 异面直线的概念(既不平行也不相交的两条直线);3. 异面直线画法及判定;对于两条异面直线a,b,经过空间任一点O作直线a′∥a, b′∥b,则 a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)思考3:求异面直线所成角的步骤有哪些?思考1:我们规定两条平行直线的夹角为0°,那么两条异面直线所成的角的思考3:在平面几何中,垂直于同一条直线的两直线互相平行,在空间中这个结论还成立吗 ?例1:如图,在正方体ABCD-A′B′C′D′中.(1)直线A′B和CC′的夹角是多少?(2)哪些棱所在的直线与直线AA′垂直?1、正方体ABCD- A)了解空间中直线与平面的位置关系;((.思考2:对于一条直线和一个平面,就其公共点个数来分类有哪几种可能?思考4:通过上面的观察和分析,直线与平面有三种位置关系,即直线在平面内,直线与平面相交,直线与平面平行.这些位置关系的基本特征是什么? (1)直线在平面内---有无数个公共点;思考7:过平面外一点可作多少条直线与这个平面平行?若直线思考1:拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位思考3:由上面的观察和分析可知,两个平面的位置关系只有两种,即两个平面平行,两个平面相交.这两种位置关系的基本特征是什么?(1)两个平面平行---没有公共点;例1:给出下列四个命题:(1)若直线l上有无数个点不在平面α内,则l∥α.(2)若直线l与平面α平行,则l与平面α内的任意一条直线都平行(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.(4)若直线l在平面α内,且l与平面β平行,则平面α与平面β一、直线与平面有三种位置关系:(1)直线在平面内——有无数个公共点;(2)直线与平面相交——有且只有一个公共点;(3)直线与平面平行——没有公共点.二、两个平面之间有两种位置关系:)理解并掌握直线与平面平行判定定理;(思考3:若将一本书平放在桌面上,翻动书的封面,观察封面边缘所在直线l与桌面所在的平面具有怎样的位置关系?思考4:有一块木料如图,P为面思考5:如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行?思考1:如果直线a与平面α内的一条直线b平行,则直线a与平面α一定思考2:设直线b在平面α内,直线a在平面α外,若a//b,则直线a与直线b确定一个平面β,那么平面α与平面β的位置关系如何?此时若直线a思考3:通过上述分析,我们可以得到判定直线与平面平行的一个定理,你能用文字语言表述出该定理的内容吗?定理若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平思考5:直线与平面平行的判定定理可简述为“线线平行,则线面平行”,在例2 在长方体ABCD—A1B1C1D1中.(1)作出过直线AC且与直线BD1平行的截面,并说明理由.(2)设E,F分别是A1B和B1C的中点,求证直线EF//平面ABCD.2.两个平面平行的基本特征是什么?有什么简单办法判定两个平面平行呢?思考5: 建筑师如何检验屋顶平面与水平面是否平行?思考3:通过上述分析,我们可以得到判定平面与平面平行的一个定理,用文字语言表述出该定理的内容吗?定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行思考4:上述定理通常称为平面与平面平行的判定定理,怎样表述?思考5:在直线与平面平行的判定定理中,“a∥α,b∥β”,可用什么条件例1:在正方体ABCD-A′B′C′例2 :在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,求证:平面DEF//平面ABC.)掌握两个平面平行的性质定理及其应用()使学生掌握直线和平面垂直的定义及判定定理;()掌握直线和平面所成的角及其应用((。
新课标人教A版高中数学必修2知识点总结
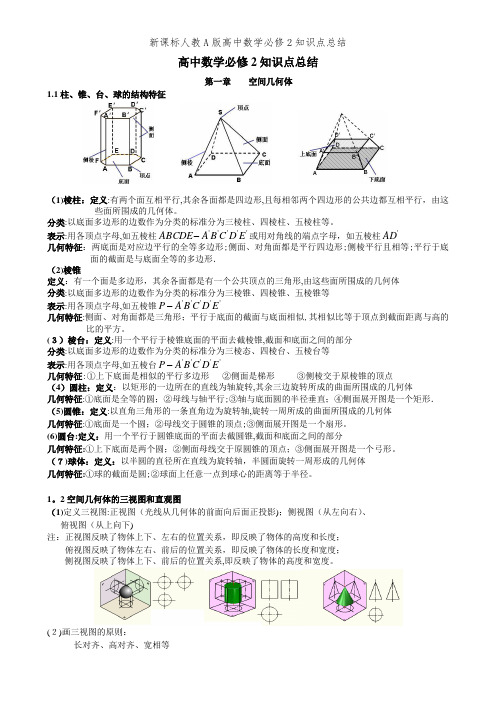
高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''E D C B A ABCDE -或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体 分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分 分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''E D C B A P -几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形. (5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
人教A高二数学必修二第二章点直线平面之间的位置关系212空间中直线与直线之间的位置关系课件共36

2 3 D 2 3
G F C B
在Rt△EFG中,求得∠EGF = 45°,
所以 BC与EG所成的角为45°. (2)因为BF∥AE,
A
所以∠FBG(或其补角)为所求.
在Rt△BFG中,求得∠FBG = 60°,
相交直线 空间两直线的位置关系
平行直线
异面直线
异面直线的定义
异面直线
异面直线的画法 两异面直线所成的角 一作(找)二证三求
边形叫做空间四边形ABCD.
A
相对顶点A与C,B与D的连线AC, BD叫做这个空间四边形的对角线.
B
C
D
【即时训练】
如图所示,在正方体 ABCD-A1B1C1D1 中,判断下列直线的位置关系:
平行 ; (1)直线 A1B 与直线 D1C 的位置关系是________ 异面 ; (2)直线 A1B 与直线 B1C 的位置关系是________ 相交 ; (3)直线 D1D 与直线 D1C 的位置关系是________ 异面 . (4)直线 AB 与直线 B1C 的位置关系是________
b a′ ? O a b′ a′
θ
O
平 移
若两条异面直线所成的角为90°,则称它们互相垂直. 异面直线a与b垂直也记作a⊥b. 异面直线所成的角θ 的取值范围: 0 o < 90 o
例2
如图,已知正方体ABCD-A′B′C′D′.
(1)哪些棱所在直线与直线BA′是异面直线?
(2)直线BA′和CC′的夹角是多少? ( 3 )哪些棱所在的直线与直线AA′垂直? 解 : (1)由异面直线的定义可知, 与直线BA′成异面直线的有直线 B′C′,AD,CC′,DD′,DC,D′C′.
数学:第二章《点、直线、平面之间的位置关系》教案(新人教A版必修2)

点、直线、平面之间的位置关系复习(一)课型:复习课一、教学目标1、知识与技能(1)使学生掌握知识结构与联系,进一步巩固、深化所学知识;(2)通过对知识的梳理,提高学生的归纳知识和综合运用知识的能力。
2、过程与方法利用框图对本章知识进行系统的小结,直观、简明再现所学知识,化抽象学习为直观学习,易于识记;同时凸现数学知识的发展和联系。
3情态与价值学生通过知识的整合、梳理,理会空间点、线面间的位置关系及其互相联系,进一步培养学生的空间想象能力和解决问题能力。
二、教学重点、难点重点:各知识点间的网络关系;难点:在空间如何实现平行关系、垂直关系、垂直与平行关系之间的转化。
三、教学设计(一)知识回顾,整体认识1、本章知识回顾(1)空间点、线、面间的位置关系;(2)直线、平面平行的判定及性质;(3)直线、平面垂直的判定及性质。
2、本章知识结构框图(二)整合知识,发展思维1、刻画平面的三个公理是立体几何公理体系的基石,是研究空间图形问题,进行逻辑推理的基础。
公理1——判定直线是否在平面内的依据;公理2——提供确定平面最基本的依据;公理3——判定两个平面交线位置的依据;公理4——判定空间直线之间平行的依据。
2、空间问题解决的重要思想方法:化空间问题为平面问题;3、空间平行、垂直之间的转化与联系:4、观察和推理是认识世界的两种重要手段,两者相辅相成,缺一不可。
(三)应用举例,深化巩固1、P.73 A 组第1题2、P.74 A 组第6、8题(四)、课堂练习:1.选择题 (1)如图BC 是R t ⊿ABC 的斜边,过A 作⊿ABC 所在平面α垂线AP ,连PB 、PC ,过A 作AD ⊥BC 于D ,连PD ,那么图中直角三角形的个数是( ) (A )4个 (B )6个 (C )7个 (D )8个(2)直线a 与平面α斜交,则在平面α内与直线a 垂直的直线( ) (A )没有 (B )有一条 (C )有无数条 (D )α内所有直线 答案:(1)D (2) C2.填空题(1)边长为a 的正六边形ABCDEF 在平面α内,PA ⊥α,PA =a ,则P 到CD 的距离为 ,P 到BC 的距离为 .(2)AC 是平面α的斜线,且AO =a ,AO 与α成60º角,OC ⊂α,AA '⊥α于A ',∠A 'OC =45º,则A 到直线OC 的距离是 , ∠AOC 的余弦值是 . 答案:(1)a a27,2; (2)42,414a 3.在正方体ABCD -A 1B 1C 1D 1中,求证:A 1C ⊥平面BC 1D .分析:A 1C 在上底面ABCD 的射影AC ⊥BD, A 1C 在右侧面的射影D 1C ⊥C 1D,所以A 1C ⊥BD, A 1C ⊥C 1D,从而有A 1C ⊥平面BC 1D .A A ′ CαOC1课后作业1、阅读本章知识内容,从中体会知识的发展过程,理会问题解决的思想方法;2、P.76 B组第2题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学人教新课标 A 版必修 2 第二章 点、直线、平面之间的位置关系 2.2.3 直线
与平面平行的性质 B 卷
姓名:________
班级:________
成绩:________
一、 单选题 (共 3 题;共 6 分)
1. (2 分) 如图,四棱锥 S—ABCD 的底面为正方形,SD 底面 ABCD,则下列结论中不正确的是
A . AC⊥SB B . AB∥平面 SCD C . SA 与平面 SBD 所成的角等于 SC 与平面 SBD 所成的角 D . AB 与 SC 所成的角等于 DC 与 SA 所成的角 【考点】
2. (2 分) 下列四个结论: ⑴两条不同的直线都和同一个平面平行,则这两条直线平行. ⑵两条不同的直线没有公共点,则这两条直线平行. ⑶两条不同直线都和第三条直线垂直,则这两条直线平行. ⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行. 其中正确的个数为( ) A.0 B.1 C.2 D.3 【考点】
3. (2 分) 设 是两条不同的直线,
是三个不同的平面.有下列四个命题:
①若 ,
,
,则 ;
②若
,
③若
,
,则 ,
; ,则
;
第 1 页 共 13 页
④若
,
,
,则
.
其中错误命题的序号是( )
A . ①④
B . ①③
C . ②③④
D . ②③
【考点】
二、 选择题 (共 5 题;共 10 分)
4. (2 分) (2018 高一上·深圳月考) 已知空间两条不同的直线
正确的是( )
A.若
则
B.若
则
C.
D.若
则
【考点】
和两个不同的平面
,则下列命题
5. (2 分) 已知两个不同的平面 和两条不重合的直线 a,b,则下列四个命题正确的是( ) 【考点】
6. (2 分) (2018 高一上·大连期末) 若
题的是( )
A.若
,则
是两条不同的直线,
B.若
,则
C.若 D.若 【考点】
,则 ,则
是三个不同的平面,则下列为真命
7. (2 分) (2019 高一上·集宁月考) 已知
是两个不同的平面,
第 2 页 共 13 页
是两条不同的直线,给出下列命
题: ①若
,则
面直线,那么 与 相交;④若 ()
A . ①② B . ②③ C . ③④ D.④ 【考点】
②若
,且
,则 ,则
;③
是异
且
.其中正确的命题是
8. (2 分) (2019·浙江模拟) 已知空间两不同直线 、 ,两不同平面 、 ,下列命题正确的是( )
A.若
且
,则
B.若
且
,则
C.若
且
,则
D . 若 不垂直于 ,且 【考点】
,则 不垂直于
三、 填空题 (共 3 题;共 3 分)
9. (1 分) (2021·奉贤模拟) 在棱长为 的正方体
(不包括端点)上的动点,且线段
平行于平面
【考点】
,则四面体
中,点
分别是线段
的体积的最大值是________.
10. (1 分) (2020 高三上·合肥月考) 若命题 若直线 与平面 内的所有直线都不平行,则直线 与
平面 不平行;则命题
是________命题(填“真”或“假”).
【考点】
11. (1 分) (2019 高二下·金山月考) 棱长为 1 的正方体
、
上运动(不包括线段端点),且
.以下结论:①
段
、
的中点,则由线
与
确定的平面在正方体
第 3 页 共 13 页
中,点 、 分别在线段 ;②若点 、 分别为线
上的截面为等边三角形;
③四面体
的体积的最大值为
________.(填序号)
;④直线
与直线
的夹角为定值.其中正确的结论为
【考点】
四、 解答题 (共 3 题;共 30 分)
12. (10 分) 如图,在四棱柱 ABCD-A1B1C1D1 中,已知平面 AA1C1C⊥平面 ABCD,且 AB=BC=CA= ,AD=CD=1.
(1) 求证:BD⊥AA1. (2) 在棱 BC 上取一点 E,使得 AE∥平面 DCC1D1 , 求 【考点】
的值.
13.(10 分)(2018·河北模拟) 如图,四棱锥
平面
,点 是
的中点,棱
与平面
的底面 交于点 .
是边长为 2 的正方形,平面
(1) 求证: (2) 若 【考点】
; 是正三角形,求三棱锥
的体积.
第 4 页 共 13 页
14. (10 分) (2019·长春模拟) 如图,
别是
上的动点,且
.
平面
分
(1) 若平面 (2) 当平面 【考点】
与平面 平面
的交线为 ,求证:
时,求平面
与
; 平面所成的二面角的余弦值.
第 5 页 共 13 页
一、 单选题 (共 3 题;共 6 分)
答案:1-1、 考点: 解析:
参考答案
答案:2-1、 考点:
解析:
答案:3-1、 考点:
解析:
二、 选择题 (共 5 题;共 10 分)
答案:4-1、
考点: 解析:
第 6 页 共 13 页
答案:5-1、 考点: 解析:
答案:6-1、 考点: 解析:
答案:7-1、 考点:
解析: 答案:8-1、 考点:
第 7 页 共 13 页
解析:
三、 填空题 (共 3 题;共 3 分)
答案:9-1、 考点: 解析:
答案:10-1、 考点:
第 8 页 共 13 页
解析: 答案:11-1、 考点: 解析:
四、 解答题 (共 3 题;共 30 分)
答案:12-1、
第 9 页 共 13 页
答案:12-2、
考点: 解析: 答案:13-1、 答案:13-2、
考点: 解析:
第 10 页 共 13 页
答案:14-1、
答案:14-2、
第11 页共13 页
第12 页共13 页
考点:
解析:
第13 页共13 页。
