中考复习专题:中考中“将军饮马”问题的常见模型及典型例题课件(共38张PPT)
将军饮马问题(课堂PPT)

A'
M
C . .A
.B
O
.N
D .B '
.
14
(四)二次轴对称:两点在两相交直线内部
• 例4变式2:如图,OMCN是矩形的台球桌面, 有黑、白两球分别位于B、A两点的位置上,
• 试问怎样撞击白球,使白球A依次碰撞球台 边OM、ON后,反弹击中黑球?
C
B N
M A
O
.
15
(四)二次轴对称:两点在两相交直线内部
M
N
C
C'
∵ 直线MN是点B、B’的对称轴, 点C、C’在对称轴上,∴BC=B’C,BB'C’=B’C’.
∴BC+AC = B’C+AC = B’A.
∴BC ’ +AC ’ = B’C ’ +AC ’
在△AB ’ C’中,AB ’ < AC’+B ’ C’,
∴ BC+AC < BC ’ +AC ’ ,即AC+BC最小.
例4变式2:
M
作 法 :(1)作 点 A关 于 O M 的 对 称 点 A',
点 B关 于 O N的 对 称 点 B'.
. ( 2 ) 连 结 A '和 B ', 交 O M 于 C , 交 O N 于 D 。 A
A.'
则 点 C、 D为 所 求 。
.C
B.
.
N
.D
O
B'
.
16
将军饮马的实质: (1)求最短路线问题------
问:这位将军怎样走路程最短?
A
B
河
.
5
(二)一次轴对称:两点在一条直线同侧
2020中考数学复习 最值问题-将军饮马问题 (51张PPT)

02、将军饮马模型系列 ————“一定两动”之点到点
当P'、N、M、P''共线时,得△PMN周长的最小值,即线段P'P''长,连接OP'、 OP'',可得△OP'P''为等边三角形,所以P'P''=OP'=OP=8.
02、将军饮马模型系列 ————“两定两动”之点到点
在OA、OB上分别取点M、N使得四边 形PMNQ的周长最小。
05、将军过桥
【分析】 考虑MN长度恒定,只要求AM+NB最小值即可。问题 在于AM、NB彼此分离,所以首先通过平移,使AM与 NB连在一起,将AM向下平移使得M、N重合,此时A 点落在A'位置。
问题化为求A'N+NB最小值,显 然,当共线时,值最小,并得出 桥应建的位置.
05、将军过桥
通过几何变换将若干段原本彼此分离线段组合到一起,是解决问题的关键~
此处M点为折点,作点P关于OA对称 的点P',将折线段PM+MN转化为 P'M+MN,即过点P'作OB垂线分别 交OA、OB于点M、N,得PM+MN 最小值(点到直线的连线中,垂线段 最短)
03、几何图形中的将军饮马
寻找几何图形中 端点关于折点所在直线的对称点位置
03、几何图形中的将军饮马 ----正方形中的“将军饮马”
则PC+PD的最小值为( )
A.4
B.5 C.6
D.7
03、几何图形中的将军饮马 ----正方形中的“将军饮马”
【分析】作点C关于P点所在直线AB的对称点C',当C'、P、D共线时, PC+PD最小,最小值为5,故选B.
2020年中考复习 将军饮马问题 讲义

将军饮马(作对称点求最短线段终极版)背景知识:早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.常用知识点:两点之间线段最短,垂线段最短,三角形三边关系,轴对称,平移;解题思路:找对称点,变折线为直线。
常见模型:一、两定点一动点型:如图:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小。
解题思路:连接AB,与直线的交点为点Q,即此时点P运动到点Q处,最小值为AB.证明:运用三角形三边关系:两边之和大于第三边,当A、P、B三点共线可取等于。
在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB的和最小.解题思路:作定点B关于直线l的对称点C,连接AC,交直线于点Q,当点P运动到点Q,最小值为AC.证明:关键是作其中一个定点的对称点,使得PB=PC,求PA+PB的最小值,即求PA+PC的最小值。
再转化为上述题型。
PA-值最大。
引申1:此题型也可以求PB解题思路:延长AB交直线l于点Q,当点P运动到点Q,PBPA-最大值为AB.证明:三角形任意两边之差小于第三边,当A、B、P三点共线可取等于.(提示:如果两定点不在直线的同侧,可以作其中一个定点关于直线l的对称点)PA-值最小。
引申2:此题型也可以求PB解题思路:连接AB,作AB的垂直平分线角l于点P.证明:垂直平分线上的点到线段的两端距离相等,可得PA=PB二.两动点一定点型(两动点在角的两边上)如图,在∠MON 的内部有一点A ,在OM 上找一点B ,在ON 上找一点C ,使得△BAC 周长最短.解题思路:作点A 关于OM 的对称点'A ,作点A 关于ON 的对称点''A ,连接'''A A ,与OM 交于点B , 与ON 交于点C ,连接AB ,AC ,此△ABC 周长最短.证明:两点之间,线段最短变式1:如图:在∠MON 的内部有一点A ,在OM 上找一点B ,在ON 上找一点C ,使得AB +BC 最短.解题思路:作点A 关于OM 的对称点'A ,过点'A 作C A '⊥ON ,交OM 于点B ,交ON 于点C,即为所求。
九年级中考数学复习课件第7单元 数学文化——将军饮马

解:(1)答案依次是:CB′,C′B′,AB′;
赢在 中考
讲 练通
第一部分 教材同步复习
第七单元 图形的变化
数学
数学文化——将军饮马
数学Βιβλιοθήκη 栏目导航【模型介绍】古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位 将军,每天都要巡查河岸一侧的两个军营 A、B,他总是先去 A 营,再到河边饮马,之 后再去 B 营,如图①,他时常想,怎么走才能使每天的路程之和最短呢?
(2)答案依次是:DE, 5;
图⑤:作 B 关于 CD 的对称点 E,则 E 正好在圆周上,
连接 OA、OB、OE、AE,AE 交 CD 于 P,则 AP+BP 最短,
︵
∵∠AOD=60°,B 为AD 的中点,
︵︵
︵
∴AB =BD ,且AB 的度数是 30°,
∴∠AEB=15°(圆周角的度数等于它所对的弧的度数的一半),
大数学家海伦曾用轴对称的方法巧妙的解决了这个问题
栏目导航
如图②,作 B 关于直线 l 的对称点 B′,连接 AB′与直线 l 交于点 C,点 C 就是所 求的位置.请你在下列的阅读、应用的过程中,完成解答.
(1)理由:如图③,在直线 l 上任取一点 C′,连接 AC′,BC′,B′C′. ∵直线 l 是点 B,B′的对称轴,点 C,C′在 l 上. ∴CB=________,C′B=________ ∴AC+CB=AC+CB′=________. 在△AC′B′中,∵AB′<AC′+C′B′. ∴AC+CB<AC′+C′B′.∴AC+CB<AC′+C′B′即 AC+CB 最小
将军饮马(最完整讲义)
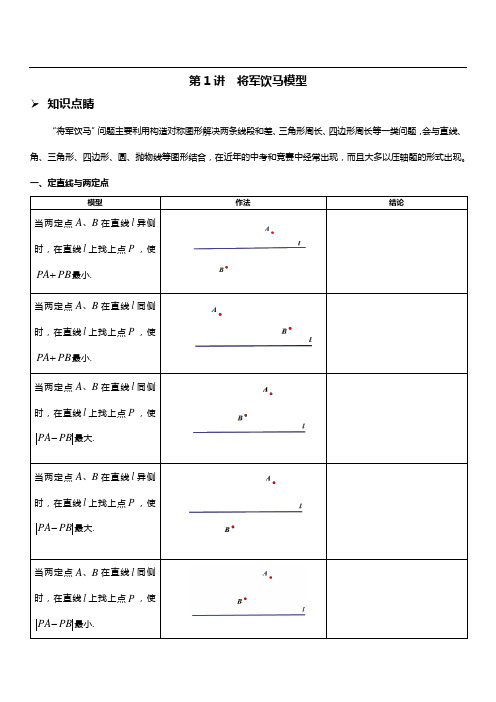
第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现。
一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时,在直线l上找上点P,使PA+最小.PBA、在直线l同侧当两定点B时,在直线l上找上点P,使PA+最小.PBA、在直线l同侧当两定点B时,在直线l上找上点P,使PA-最大.PBA、在直线l异侧当两定点B时,在直线l上找上点P,使PA-最大.PBA、在直线l同侧当两定点B时,在直线l上找上点P,使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部,在OA 上找一点M ,在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部,在OA 上找一点M ,在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部,在OA 上找一点M ,在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部,在射线OA 上找一点P ,使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部,在射线OA 上找一点P ,使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是,在OA 上找一点M ,在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、(M 在左),使NB MN AM ++最小,且d MN =.如图,21//l l ,21l l 、之间的距离为d ,在21l l 、上分别找N M 、两点,使1l MN ⊥,且NB MN AM ++最小.如图,21//l l ,43//l l ,21l l 、之间的距离为1d ,43//l l 之间的距离为2d ,在21l l 、上分别找N M 、两点,使1l MN ⊥,在43l l 、上分别找Q P 、两点,使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图,在⊙O 上找一点N ,在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1:如图,点P 是∠AOB 内任意一点,∠AOB =30°,OP =8,点M 和点N 分别是射线OA 和射线OB 上的动点,则△PMN 周长的最小值.P OBAMN例2:如图,正方形ABCD 的边长是4,M 在DC 上,且DM =1, N 是AC 边上的一动点,则△DMN 周长的最小值.例3:如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且AC :CB =1:3,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为( )A .(2,2)B .5(2,5)2C .8(3,8)3D .(3,3)第3题图 第4题图 第5题图例4:如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( ) A .4B .5C .6D .7例5:如图,在等边△ABC 中,AB =6, N 为AB 上一点且BN =2AN , BC 的高线AD 交BC 于点D ,M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________. PDCBAA BCDMNNMDCBA例6:如图,在Rt △ABD 中,AB =6,∠BAD =30°,∠D =90°,N 为AB 上一点且BN =2AN , M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值.例7:如图,在Rt △ABC 中,∠ACB =90°,AC =6.AB =12,AD 平分∠CAB ,点F 是AC 的中点,点E 是AD 上的动点,则CE +EF 的最小值为( ) A .3 B .4 C . D .第7题图 第8题图 第9题图例8:如图,在锐角三角形ABC 中,BC =4,∠ABC =60°, BD 平分∠ABC ,交AC 于点D ,M 、N 分别是BD ,BC 上的动点,则CM +MN 的最小值是( ) A B .2 C .D .4例9:如图,在菱形ABCD 中,AC =BD =6,E 是BC 的中点,P 、M 分别是AC 、AB 上的动点,连接PE 、PM ,则PE +PM 的最小值是( ) A .6B .C .D .4.5NMDBA E AFCDBNM DCBAEPDCBAM例10:如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( ) A .4(0,)3B .5(0,)3C .(0,2)D .10(0,)3第10题图 第11题图 第12题图例11:如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足13PAB ABCD S S ∆=矩形,则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A .B .C .D 例12:如图,矩形ABCD 中,AB =10,BC =5,点E 、F 、G 、H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为( )A .B .C .D .例13:如图,∠AOB =60°,点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )A B C .6D .3第13题图 第14题图 CBH FGEDCB AA BMOPN例14:如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为 .例15:如图,已知正比例函数y =kx (k >0)的图像与x 轴相交所成的锐角为70°,定点A 的坐标为(0,4),P 为y 轴上的一个动点,M 、N 为函数y =kx (k >0)的图像上的两个动点,则AM +MP +PN 的最小值为___________.第15题图例16:如图,在平面直角坐标系中,矩形ABCD 的顶点B 在原点,点A 、C 在坐标轴上,点D 的坐标为(6,4),E 为CD 的中点,点P 、Q 为BC 边上两个动点,且PQ =2,要使四边形APQE 的周长最小,则点P 的坐示应为______________.例17:如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值.AB CD EFMx例18:如图,正方形ABCD 的面积是12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,求PD+PE 的最小值。
将军饮马(最完整讲义)

第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。
二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点(在左), 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A .例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A (4,4), 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C .,D .第3题图 第4题图 第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5:如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________.A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图 第8题图 第9题图A .例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA .例10: 如图, 矩形ABOC 的顶点A 的坐标为(-4,5), D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图 第11题图 第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图 第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N (3,0)是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15:如图, 已知正比例函数y=kx (k>0)的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为(0, 4), P 为y 轴上的一个动点, M 、N 为函数y=kx (k>0)的图像上的两个动点, 则AM+MP+PN 的最小值为___________.第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为(6, 4), E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17:如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值.x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。
将军饮马问题课件

将军饮马问题类型一、基本模式类型二、轴对称变换得应用(将军饮马问题)2、如图所示,如果将军从马棚M出发,先赶到河OA上得某一位置P,再马上赶到河OB上得某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P与Q),使得总路程MP+PQ+QN最短.【变式】如图所示,将军希望从马棚M出发,先赶到河OA上得某一位置P,再马上赶到河OB 上得某一位置Q。
请为将军设计一条路线(即选择点P与Q),使得总路程MP+PQ最短.3、将军要检阅一队士兵,要求(如图所示):队伍长为a,沿河OB排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N、请问:在什么位置列队(即选择点P与Q),可以使得将军走得总路程MP+PQ+QN最短?4。
如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M得距离与点P到OA 边得距离之与最小5已知∠MON内有一点P,P关于OM,ON得对称点分别就是与,分别交OM, ON于点A、B,已知=15,则△PAB 得周长为( )ﻫA。
15 B 7、5 C。
10 D. 24ﻫ6、已知∠AOB,试在∠AOB内确定一点P,如图,使P到OA、OB得距离相等,并且到M、N两点得距离也相等、7、已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB得周长取最小值时,求∠APB得度数、8、如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C、若P就是BC边上一动点,则DP长得最小值为______.ﻫ练习1、已知点在直线外,点为直线上得一个动点,探究就是否存在一个定点,当点在直线上运动时,点与、两点得距离总相等,如果存在,请作出定点;若不存在,请说明理由、2、如图,在公路得同旁有两个仓库、,现需要建一货物中转站,要求到、两仓库得距离与最短,这个中转站应建在公路旁得哪个位置比较合理?3、已知:、两点在直线得同侧, 在上求作一点,使得最小。
2.将军饮马模型-课件PPT

3
给妹妹讲初中数学
5 真题训练
2023·黑龙江省齐齐哈尔市
4
给妹妹讲初中数学
5 真题训练
2023·黑龙江省绥化市
5
给妹妹讲初中数学
5 真题训练
2023·广西
给妹妹讲初中数学 6
5 真题训练
2023·四川宜宾
给妹妹讲初中数学 7
5 真题训练
2023·湖南省邵阳市
8
给妹妹讲初中数学
5 真题训练
(2个动点不关联,转化为图形到图形的最值问题)
1个图形做对称图形,与另1个图形的最值。
点到点
图形到图形 直线到直线,垂直 直线到圆,过圆心 圆到圆,过两圆圆心
给妹妹讲初中数学 示例图
4 解题技巧
第五步:求最值。
解题技巧
找到图形中的最短值后,根据题意求解值即可。
给妹妹讲初中数学
4 解题技巧
解题技巧
2 模型探究
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
(2019,陕西)
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
给妹妹讲初中数学
4 解题技巧
(2020,云南)
给妹妹讲初中数学
4 解题技巧
(2019,沈阳)
给妹妹讲初中数学
4 解题技巧
1. 找出最值经过的所有点,标记定点和动点。
2. 画出所有动点的运动轨迹。
3. 判断最值的两个端点是动点还是定点。
4. 根据端点情况,做对称点/对称图形。
5. 求最值。
找动点 画轨迹 判两端 做对称 求最值
给妹妹讲初中数学
将军饮马专题ppt课件

第8题图
返回
1 综合训练
1. 如图,在矩形ABCD中,AB=2,AD=1,点E为AB的中点,M、N是CD上的两 动点,且MN=1,则EM+EN的最小值为____。
1 综合训练
2. 如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个 动点,则下列线段的长等于AP+EP最小值的是 ____。
之
间
,
线
段
最
短
2
用模型战试题
每一个试题都是模型,每一种模型都有方法
综合训练
针对训练1
2
1. 如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AB 边上一点,且AE=2,则线段EF+CF的最小值为( B ) A. 3 B. 2 3 C. 2 D. 2
第1题图
返回
2 针对训练2
两动一定型 2
例7
在∠MON的内部 有一点A,在OM上找 一点B,在ON上找一 点C,使得△BAC周长
最短.
在 OM上找一点C,在 ON上找一点D,使 得四边形ABCD周 长最短.
例9
在∠MON的内部 有一点A,在OM上 找一点B,在ON上 找一点C,使得AB +BC最短.
【传说】
早在古罗马时代,传说亚历山大城有一位精通数学 和物理的学者,名叫海伦.一天,一位罗马将军专程 去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去 河岸同侧的军营B开会,应该怎样走才能使路程最短 ?这个问题的答案并不难,据说海伦略加思索就解决 了它.
从此以后,这个被称为“将军饮马”的问题便流传至 今.
A. 3 B. 2 3 C. 3 1 D. 3 2
初中数学-将军饮马问题-公开课课件课件全文

抽象: 如图,在直线MN上找一点P, 使得PA+PB最小?
A
M
B
P
N
思考:在前面研究几何问题的过程中,你是否遇到过与此 相类似求线段的距离最短或者线段和最小的问题? 请举例说明.
垂线段最短 m
思考:在前面研究几何问题的过程中,你是否遇到过与此 相类似求线段的距离最短或者线段和最小的问题的 问题?请举例说明.
使AC+CD+BD+AB最短。
问题特征: 两线两定两动
解决方法:依据两点之间,线段最短,通过两次轴对称, 将三条折线段化为一条直线段.
8/25/ቤተ መጻሕፍቲ ባይዱ024
联系中考
(2019中考) 如图,∠AOB=30°,角内有一点P,PO=10cm, 两边上各有一点Q、R(均不同于点O),则 △PQR的周长的最小值是__
Q A
P
O
B
R
如图所示,直线MN表示一条铁路,铁路两旁各有一 点A和B,表示两个工厂.要在铁路上建一货站,使
´
它到两厂距离之和最短,这个货站应建在何处?
P´ P
方法:在解决选择位置、求最短距离等问题时,通常 转化为“两点之间线段最短”
问题:如图,另一位将军也骑马从城堡A到城堡B,途中马 也要到小溪边饮水一次.问这位将军怎样走路程最短?
M
P
连接AP, 则PA´=PA,
A´
则PA+ PB= PA ´+ PB= A´B
在直线MN上任意取一点P´ 连接AP´,BP´,A´P´,
则AP´=A´P´,则AP´+BP´= A´P´+ BP´
△BA´P´中,A ´B < BP´+A´P´,
中考复习专题:中考中“将军饮马”问题的常见模型及典型例题 优质课件

A B′
CO
Px
B
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
数学活动室
1.如图,正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中
点,点M在BC边上,且BM=6.P为对角线BD上一动点,求|PM-PN|
B A
图1
C
图2
D
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
小小设计家
1.如图所示,钱塘江的一侧有A,B两个工厂。现要在江边建造一 个水厂C,把水送到这两个工厂,要使供水管路线最短。这样可
以节省成本。
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
梳理体系
"将军饮马问题”的模型
【将军饮马问题模型6】异侧两点差的最大值问题
A B′ l P B
|PA-PB|最大问题
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
梳理体系
"将军饮马问题”的模型
【将军饮马问题模型5】同侧两点差的最值问题
A
B l
P (1)
|PA-PB|最大问题
A
B
P
l
(2)
|PA-PB|最小问题
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 优质课件
中考必会几何模型:将军饮马模型
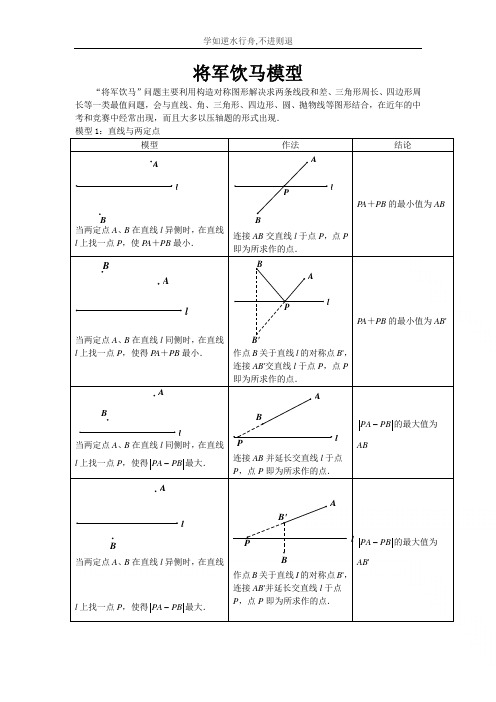
将军饮马模型“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现. 模型1:直线与两定点模型作法结论lB A当两定点A 、B 在直线l 异侧时,在直线l 上找一点P ,使P A +PB 最小.lPAB连接AB 交直线l 于点P ,点P即为所求作的点.P A +PB 的最小值为ABl AB当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得P A +PB 最小.lPB'AB作点B 关于直线l 的对称点B ', 连接AB '交直线l 于点P ,点P 即为所求作的点.P A +PB 的最小值为AB 'l AB当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得PA PB -最大.lPAB连接AB 并延长交直线l 于点P ,点P 即为所求作的点.PA PB -的最大值为ABlAB当两定点A 、B 在直线l 异侧时,在直线l 上找一点P ,使得PA PB -最大.l B'AB P作点B 关于直线I 的对称点B ',连接AB '并延长交直线l 于点P ,点P 即为所求作的点.PA PB -的最大值为AB 'l AB当两定点A 、B 在直线l 同侧时,在直线l 上找一点P ,使得PA PB -最小.l PAB连接AB ,作AB 的垂直平分线交直线l 于点P ,点P 即为所求作的点.PA PB -的最小值为0模型实例例1:如图,正方形ABCD 的面积是12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,则PD +PE 最小值是 .EBC ADP解答:如图所示,∵点B 与点D 关于AC 对称,∴当点P 为BE 与AC 的交点时,PD +PE 最小,且线段BE 的长. ∵正方形ABCD 的面积为12,∴其边长为23∵△ABE 为等边三角形,∴BE =AB =23PD +PE 的最小值为3例2:如图,已知△ABC 为等腰直角三角形,AC =BC =4,∠BCD =15°,P 为CD 上的动点,则PA PB -的最大值是多少?DPPA'B解答:如图所示,作点A 关于CD 的对称点A ′,连接A ′C ,连接A ′B 并延长交CD 于点P ,则点P 就是PA PB -的值最大时的点,PA PB -=A ′B .∵△ABC 为等腰直角三角形,AC =BC 等于4,∴∠ACB =90°. ∵∠BCD =15°,∴∠ACD =75°.∵点A 、A ′关于CD 对称,∴AA ′⊥CD ,AC =CA ′, ∵∠ACD =∠DCA ′=75°,∴∠BCA ′=60°.∵CA ′=AC =BC =4,∴△A ′BC 是等边三角形,∴A ′B =BC =4.∴PA PB -的最大值为4. 练习1.如图,在△ABC 中,AC =BC =2,∠ACB =90°,D 是BC 边的中点,E 是AB 边上一动点,则EC +ED 的最小值是 .DACB E解:解:过点C 作CO⊥AB 于O ,延长CO 到C ',使O C '=OC ,连接D C ',交AB 于E ,连接C 'B ,此时DE+CE=DE+E C '=D C '的值最小.连接B C ',由对称性可知∠C 'BE=∠CBE=45°,∴∠CB C '=90°,∴B C '⊥BC, ∠BC C '=∠B C 'C=45°,∴BC=B C '=2,∵D 是BC 边的中点,∴BD=1, 根据勾股定理可得:D C '=5,故EC+ED 的最小值是5.2.如图,点C 的坐标为(3,y ),当△ABC 的周长最短时,求y 的值.xyB (2,0)A (0,3)O解:解:(1)作A 关于x=3的对称点A ′,连接A ′B 交直线x=3与点C . ∵点A 与点A ′关于x=3对称,∴AC=A ′C .∴AC+BC=A ′C+BC .当点B 、C 、A ′在同一条直线上时,A ′C+BC 有最小值,即△ABC 的周长有最小值. ∵点A 与点A ′关于x=3对称,∴点A ′的坐标为(6,3).设直线BA′的解析式y=kx+b,将点B和点A′的坐标代入得:k=34,b=−32.∴y=34x-32.将x=3代入函数的解析式,∴y的值为3 43.如图,正方形ABCD中,AB=7,M是DC上的一点,且DM=3,N是AC上的一动点,求|DN-MN|的最小值与最大值.C解:解:当ND=NM时,即N点DM的垂直平分线与AC的交点,|DN-MN|=0,因为|DN-MN|≤DM,当点N运动到C点时取等号,此时|DN-MN|=DM=3,所以|DN-MN|的最小值为0,最大值为3于D ,点C 、点D 即为所求.PB OAQ点P 、Q 在∠AOB 内部,在OB 边上找点D ,OA 边上找点C ,使得四边形PQDC周长最小.分别作点P 、Q 关于OA 、OB 的对称点P ′、Q ′,连接P ′Q ′,分别交OA 、OB 于点C 、D ,点C 、D 即为所求.PC +CD +DQ 的最小值为P ′Q ′,所以四边形PQDC 周长的最小值为PQ +P ′Q ′模型实例如图,∠AOB=30°,∠AOB 内有一定点P ,且10OP .在OA 上有一点Q ,OB 上 一点R .若立△PQR 周长最小,则最小周长是多少?解答如图,作点P 分别关于OA 、OB 的对称点E 、F ,连接EF ,分别交OA 、OB 于点Q 、R ,连接OE 、OF 、PE 、PF .EQ OP =,FR RP .△PQR 的周长的最小值为EF 的长.由对称性可得∠EOQ=∠POQ ,∠FOR=∠POR , ∠EOF=2∠AOB=60°. △EOF 是正三角形.10EF OE OP ===.即△PQR 周长最小值为10.OBAP模型2/角与定点1.已知,40MON ,P 为MON 内一定点,A 为OM 上的点,B 为ON 上的点, 当△PAB 的周长取最小值时:(1)找到A 、B 点,保留作图痕迹;(2)求此时APB 等于多少度.如果∠MON =θ,∠APB 又等于多少度?ON1.解答(1)做点P 分别关于OM ON 、的对称点E F 、,连接EF 分别交OM ON 、于点A B 、.点A B 、即为所求,此时△PAB 的周长最小.(2)∵点E 与点P 关于直线OM 对称,点F 与点P 关于ON 对称, ∴∠E =∠APE ,∠F =∠BPF ,∠CPD =180°-∠MON =140°. ∴在△EFP 中,∠E +∠F =180°-140°=40°,∴∠CPA +∠BPD =40°.∴∠APB =100°.如果∠MON =θ, ∴∠CPD =180°-θ,∠E +∠F =θ. 又∵∠PAB =2∠E ,∠PBA =2∠F∴∠PAB +∠PBA =2(∠E +∠F )=2θ ∴∠APB =180°-2θ.ON2.如图,四边形中ABCD ,110BAD ,90BD ,在BC 、CD 上分别找一点M 、N ,使△AMN 周长最小,并求此时+AMN ANM ∠∠的度数.A DBMN2.解答如图,作点A关于BC的对称点A',关于CD的对称点A'',连接A A'''与BC、CD的交点即为所求的点M、N.此时△AMN周长最小.∵∠BAD=110°,∴∠A'+∠A''=180°-110°=70°.由轴对称的性质得:∠A'=∠A AM',∠A''=∠A AN'',∴∠AMN+∠ANM=2(∠A'+∠A'')=2×70°=140°.3.如图,在x轴上找一点C,在y轴上找一点D,使AD CD BC最小,并求直线CD的解析式及点C、D的坐标.yxOB(3,1)A(1,3)3.解答作点A关于y轴的对称点A',点B关于x轴的对称点B',连接A B''分别交x轴、y轴于点C、D,此时AD CD BC++最小.由对称性可知A'(-1,3),B'(3,-1).易求得直线A B''的解析式为2y x=-+,即直线CD的解析式2y x=-+.当0y=时,2x=,∴点C坐标为(2,0).当0x=时,2y=,∴点D坐标为(0,2).4.如图,20MON,A 、B 占分别为射线OM 、ON 上两定点,且2OA ,4OB ,点P 、Q 分别为射线OM 、ON 上两动点,当P 、Q 运动时,线段AQ PQ PB 的最小值是多少?ONB4.解答作A 点关于ON 的对称点A ',点B 关于OM 的对称点B ',连接A B '',分别交OM ON 、于点P Q 、,连接OA '、OB '.则AQ PQ PB A Q PQ PB A B ''''++=++=,此时AQ PQ PB ++最小. 由对称可知,PB PB '=,AQ A Q '=,2OA OA '==,4OB OB '==,20MOB NOA MON ''∠=∠=∠=︒. 60A OB ''∠=︒.作A D '⊥OB '于点D , 在Rt △ODA'中,∴1OD =,A D '=∴413B D '=-=,A B ''=∴AQ PQ PB ++的最小值是模型3两定点一定长模型作法结论如图,在直线l 上找M 、N 两点 (M 在左),使得AM +MN +NB 最 小,且MN =d .将A 向右平移d 个单位到A ′,作A ′关于l 的对称点A ",连接A "B 与直线l 交于点N ,将点N 向左平移d 个单位即为M ,点M ,N 即为所求.AM +MN +NB 的最小值为A "B +d如图,l 1∥l 2,l 1、l 2间距离为d , 在l 1、l 2分别找M 、N 两点,使 得MN ⊥l 1,且AM +MN +NB 最小.将A 向下平移d 个单位到A ,连接A ′B 交直线l 2于点N ,过点N 作MN ⊥l 1,连接AM .点M 、N 即为所求.AM +MN +NB 的最小值为A 'B +d .例题:在平面直角坐标系中,矩形OABC 如图所示,点A 在x 轴正半轴上,点C 在y 轴正半轴上,且OA =6,OC =4,D 为OC 中点,点E 、F 在线段OA 上,点E 在点F 左侧,EF =2.当四边形BDEF 的周长最小时,求点E 的坐标.ABl 2 l 1 A ′NMABl 2 l 1 BAlMNA ′A "BAld解答:如图,将点D 向右平移2个单位得到D '(2,2),作D '关于x 轴的对称点D "(2,-2),连接BD "交x 轴于点F ,将点F 向左平移2个单位到点E ,此时点E 和点F 为所求作的点,且四边形BDEF 周长最小. 理由:∵四边形BDEF 的周长为BD +DE +EF +BF ,BD 与EF 是定值. ∴BF +DE 最小时,四边形BDEF 周长最小, ∵BF +ED =BF +FD '=BF +FD "=BD "设直线BD "的解析式为y =kx +b ,把B (6,4),D "(2,-2)代入,得6k +b =4,2k +b =-2,解得k =32,b =-5,∴直线BD "的解析式为y =32x -5.令y =0,得x =103,∴点F 坐标为(103,0).∴点E 坐标为(43,0).练习1.在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,A (3,0),B (0,4),D 为边OB 的中点. (1)若E 为边OA 上的一个动点,求△CDE 的周长最小值;(2)若E 、F 为边OA 上的两个动点,且EF =1,当四边形CDEF 的周长最小时,求点E 、F 的坐标.解答:(1)如图,作点D 关于x 轴的对称点D ',连接CD '与x 轴交于点E ,连接DE ,由模型可知△CDE 的周长最小.∵在矩形OACB 中,OA =3,OB =4,D 为OB 的中点, ∴D (0,2),C (3,4),D '(0,-2).设直线CD '为y =kx +b ,把C (3,4),D '(0,-2)代入, 得3k +b =4,b =-2,解得k =2,b =-2, ∴直线CD '为y =2x -2. 令y =0,得x =1,学如逆水行舟,不进则退 11 ∴点E 的坐标为(1,0).∴OE =1,AE =2.利用勾股定理得CD =13,DE =5,CE =25,∴△CDE 周长的最小值为13+35.(2)如图,将点D 向右平移1个单位得到D '(1,2),作D '关于x 轴的对称点D ″(1,-2),连接CD ″交x 轴于点F ,将点F 向左平移1个单位到点E ,此时点E 和点F 为所求作的点,且四边形CDEF 周长最小.理由:∵四边形CDEF 的周长为CD +DE +EF +CF ,CD 与EF 是定值,∴DE +CF 最小时,四边形BDEF 周长最小,∴DE +CF =D 'F +CF =FD ″+CF =CD ″, 设直线CD ″的解析式为y =kx +b ,把C (3,4),D (1,-2)代入,得3k +b =4,k +b =-2,解得k =3,b =-5.∴直线CD ″的解析式为y =3x -5,令y =0,得x =53,∴点F 坐标为(53,0),∴点E 坐标为(23,0).2.村庄A 和村庄B 位于一条小河的两侧,若河岸彼此平行,要架设一座与河岸垂直的桥,桥址应如何选择,才使A 与B 之间的距离最短?解答:设l 1和l 2为河岸,作BD ⊥l 2,取BB '等于河宽,连接AB '交l 1于C 1,作C 1C 2⊥l 2于C 2, 则A →C 1→C 2→B 为最短路线,即A 与B 之间的距离最短.为大家整理的资料供大家学习参考,希望对大家能有帮助,非常感谢大家的下载,以后会为大家提供更多实用的资料。
中考复习专题:中考中“将军饮马”问题的常见模型及典型例题 课件(共38张PPT)

(2)点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时.
①求直线PQ的解析式;②求四边形PABQ周长的最小值。
y
y
B.
A
Q
PO
x
B . B′
A
Q
PO
x
A′
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)
典例探究
例7
如图,已知点A(
1 2
,y1),B(2,y2)为反比例函数
y
1 的图 x
象上的两点,动点P(x,0)在x轴正半轴上运动,当AP-BP最大时,点
P的坐标是( D )
A、( 1 ,0) B、( 1 ,0) 2
C、( 3 ,0) 2
D、( 5 ,0) 2
y
A
y x 5 2
B
O
P
P
x
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)
梳理体系
【将军饮马问题模型5】同侧两点差的最值问题
A
B l
P (1)
|PA-PB|最大问题
A
B
P
l
(2)
|PA-PB|最小问题
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)
中考复习专题:中考中“将军饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)
y A
D E OC B x
y
A
C
D
E
C′O C
将军饮马课件

几何最值问题的解决 ——将军饮马
P'N为PM+MN最小值(依据:垂线段最短)
秒杀技巧
对 称一定点,垂 直出最短
模型巧记
将军饮马问题难, 两定一动一直线。 对称转化是关键, 勾股定理帮忙算。
转化思想
模型梳理
B A
A'
对 称一定点 连 接出最短
模型特征: 两个定点,一个动点在一条直线上, 且两个定点在直线的同侧
(简记为:两定一动)
解题步骤:
1.以动点所在直线为对称轴,作一个 定点关于直线的对称点。
2.连接对称点和另一个定点。
则连线即为线段之和的最小值,连线 与动点所在直线的交点即为取得最值 时动点的位置。
x=3
(0,4)
P
4
四边形APCO的周长 =CO+OA+AP+PC =5+AP+PC
四边形APCO周长最小值 =5+BC
1
(1,0)
(5,0)
模型拓展 将军饮马模型系列 ——“一定两动”之点到点
在OA、OB上分别取点M、N,使得△PMN周长最小。 NhomakorabeaP'
思路:此处M、N均为动点,分别作点P关于OAP('' 动点M所在 直线)、OB(动点N所在直线)的对称点,化折线段 PM+MN+NP为P'M+MN+NP'',当P'、M、N、P''共线时, △PMN周长最小。
中考复习专题:中考中“将军饮马”问题的常见模型及典型例题 课件

使得△PBC的周长最小,如果存在,请求出点P的坐标;如果不存在,请
说明理由。
y
C
P
A
B
O
x
【技巧】此类问题有一个动点在一条直线上运动,在直线的一侧有两个 定点,先找出其中一个定点关于这条直线的对称点,然后连接这个对称 点和另一个定点,与已知直线有个交点,这个交点就是使得这个动点到 两个定点距离之和最小的点。
y A
D E OC B x
y
A
C
D
E
C′O C
B
x
数学活动室
1.一次函数 y kx b 的图象与x、y轴分别交于点A(2,0)、B
(0,4).
学 (1)求该函数的解析式;
(2)O为坐标原点,设OA的中点为C,D、P分别为AB、OB上一
以 动点,求△PCD的最小值,并求取得最小值时P点坐标。
y
致
B
用
D P
O CA
x
2020年中考复习专题:中考中“将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)中考复习课件中 考ppt课 件中考 专题复 习课件 优秀课 件
梳理体系
【将军饮马问题模型4】双动点双对称(四边形周长的最小值问题)
P1
M
a
A
B b
N
P2
2020年中考复习专题:中考中“将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)中考复习课件中 考ppt课 件中考 专题复 习课件 优秀课 件
数学活动室
1.如图,在平面直角坐标系中,点O为坐标原点,直线 y x 4 与x轴交于点A,过点A的抛物线 y ax2 bx与直线 y x 4 交于
另一点B,且点B的横坐标为1.
几何模型-将军饮马模型(将军饮马、将军遛马、造桥选址等)-中考数学第二轮总复习课件(全国通用)

是OC上的一点,当△ADE的周长最小时,点E的坐标是( B )
A.(0,4 ) B.(0,5 ) C.(0,2) D.(0,10 )
3
3
3
河边
y
A
C
E E
B
DO
D´ x
针对训练
将军饮马---两定一动
知识点二
如图:已知⊙O的直径CD为2,︵AC的度数为60º,点B是A︵C的中点,在直
径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为__2___
A
B CP
B'
D O 河边
知识点
01 线段之差最短(长)
02
将军饮马
03
将军遛马
04
造桥选址
05
垂线段最短
情境导入
将军遛马---两定两动
知识点三
【引例1】如图,A,B均为驻地,将军某 B´
一天要从驻地A出马,先到草地边某处 M 牧马,再到河边饮马,然后回到驻地B,
这位怎样走路程最短?
图形特征:两定两动; 适用模型:将军遛马(台球两次碰壁); 基本策略:同侧化异侧、折线化直线; 基本方法:N个动点N条河,N次对称跑不脱; 基本原理:两点之间线段最短; 解题关键:根据结论抓点、线.
D 河流 N
草地
C
A´
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以节省成本。
学 (1)请你设计一下水厂应该建造在哪里?
以 (2)若AE=0.5千米,BD=1.5千米,且DE=3千米。求水厂C距离
D处有多远?
B
致
A
用
E.
C
.D
F
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
梳理体系
【将军饮马问题模型3】双动点双对称(三角形周长的最小值问题)
P1 a
M P
N b
P2
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
典例探究
例 5 如图,已知点C(1,0),直线 y x 7与两坐标轴分别交于A、B
两点,D、E分别是AB、OA上的动点。当△CDE的周长最小值时,求: (1)点D、E的坐标; (2)△CDE的周长的最小值是多少?
(3)通过以上解答,充分展开联想,运用数形结合思想,请你尝试解决
下面问题:若 y x2 1
求出这个最小值。
B.
A.
9 x2 4 ,当x为何值时,y的值最小,并
B A
图1
C
图2
D
小小设计家
1.如图所示,钱塘江的一侧有A,B两个工厂。现要在江边建造一 个水厂C,把水送到这两个工厂,要使供水管路线最短。这样可
数学活动室
1.如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在
正方形ABCD内部,在对角线AC上有一点P,使得PD+PE最小,
学
则这个最小值为( B )
A、3
B、2 3
C、2 6
D、 6
以
B
C
典例探究
例 3 阅读并解答下列问题:
(1)如图1所示,直线l 的两侧有A、B两点,在l上求作一点P,使AP+BP
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
的值最小。(要求尺规作图,保留作图痕迹,不写画法和证明)
(2)如图2,A、B两个化工厂位于一段直线形河堤的同侧,A工厂至河堤
的距离AC为1千米,B工厂到河堤的距离BD为2千米,经测量河堤上C、D
两地间的距离为6千米.现准备在河堤边修建一个污水处理厂,为使A、B
两厂到污水处理厂的排污管道最短,污水处理厂应建在距C地多远的地方?
聪明的你,能解决诗中提出的问题:“白日登山望烽火,黄昏饮马傍交河”
情境激疑
【问题】如图,诗中将军在观望烽火之后从山脚下的A点出发,走 到河边饮马后再到B点宿营。请问怎样走才能使总的路程最短?
A
九年级(下)
华东师大版中考第一轮综合复习
梳理体系
【将军饮马问题模型1】异侧两点问题 A P B
梳理体系
? 分别为BC、CD的中点,P是对角线BD上一点,求PM+PN的最小值。
学以致用
例 2 在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,求PE和
PC的长度之和最小值。
A
D
A F' D
P P
PP
F
B
EC
BEM
C
【变式】如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F 为AB上的一点,AF=2,P为AC上一个动点,求PF+PE的最小值。
数学活动室
1.如图,在平面直角坐标系中,点O为坐标原点,直线 y x 4 与x轴交于点A,过点A的抛物线 y ax2 bx与直线 y x 4 交于
另一点B,且点B的横坐标为1.
学 (1)求抛物线的解析式;
以
(2)若P是抛物线对称轴上一动点,当PB+PO最小时,求出点P的 坐标及PB+PO的最小值。
【将军饮马问题模型2】同侧两点问题 A B
P B′
学以致用
例 1 如图,在菱形ABCD的边长为6,∠BAD=60°,点E是AB的中点,
点P是对角线AC上的动点,连结PB,PE,请你求PE+PB的最小值。
D
C
P
P
D
C
M'
PP N
AEB
A MB
【变式】如图,已知菱形ABCD两条对角线的长度分别为6和8,M、N
典例探究
例 4 如图所示,抛物线 y 1 x2 3 x 2和直线 y 1 x 2 相交于A、C
22
2
两点,抛物线与x轴的另一个交点为B,在抛物线的对称轴上是否存在点P,
使得△PBC的周长最小,如果存在,请求出点P的坐标;如果不存在,请
说明理由。
y
C
P
A
B
O
x
【技巧】此类问题有一个动点在一条直线上运动,在直线的一侧有两个 定点,先找出其中一个定点关于这条直线的对称点,然后连接这个对称 点和另一个定点,与已知直线有个交点,这个交点就是使得这个动点到 两个定点距离之和最小的点。
数学源泉
【线段公理】两点之间,线段最短。
A
B
数学源泉
【垂线段的性质】 从直线外一点到这条直线上各点所连的线段中,垂线段 最短。
P
l D
情境激疑
白日登山望烽火,黄昏饮马傍交河。 行人刁斗风沙暗,公主琵琶幽怨多。 野营万里无城郭,雨雪纷纷连大漠。 胡雁哀鸣夜夜飞,胡儿眼泪双双落。 闻道玉门犹被遮,应将性命逐轻车。 年年战骨埋荒外,空见葡萄入汉家。
致
y
用
B
O
Ax
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
中考复习中考专题复习课件ppt课件20 20年中 考复习 专题: 中考中 “将军 饮马” 问题的 常见模 型及典 型例题 课件(共38张PPT)优秀课件精品课 件免费 课件公 开课课 件ppt课 件课件 下载
