哈工大机械原理考研-第5章 轮系例题精解
机械原理第五章章末地地总结

《第五章 轮系及其设计》知识总结小组成员:何春江 陈彦智 陈肯第一节 轮系的分类根据轮系中各个齿轮的轴线位置相对于机架的关系,轮系可分为两大类。
定轴轮系和周转轮系由这两种轮系组合成的轮系称复合轮系(或混合轮系)。
第二节 定轴轮系及其设计本节将主要讨论以下几个问题:1)定轴轮系的运动学分析,主要内容是讨论定轴轮系的传动比计算。
2)定轴轮系的动力学分析,主要内容是讨论定轴轮系的传动效率计算。
一、定轴轮系的传动比计算传动比kkk nn i 111==ωω。
式中ω和n 分别表示轴的角速度和轴的每分钟转数。
轮系的传动比计算,除了需要确定i 1k 的大小之外,还需确定输入轴与输出轴的转向关系。
1)传动比大小的计算定轴轮系的传动比等于组成该轮系的各级齿轮传动比的连乘积。
传动比的大小等于各对相互啮合的齿轮中,所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比。
即积所有主动轮齿数的连乘积所有从动轮齿数的连乘定轴轮系的传动比=2)定轴轮系输入、输出轴转向关系的确定定轴轮系中各轮的转动方向以及输入、输出轴的转动方向可用标注箭头的方法来确定。
两外啮合圆柱齿轮表示转向的箭头方向不是相背,便是相向;两内啮合圆柱齿轮表示转向的箭头方向总是一致的;相啮合的两圆锥齿轮转向的箭头方向不是同时指向节点,便是同时背离节点;蜗轮蜗杆传动方向可根据蜗杆螺旋线的旋向(右旋蜗杆用右手判断、左旋蜗杆用左手判断)和蜗杆的转动方向(用四个指头握住蜗杆、使四指尖的弯曲方向与蜗杆转动的方向一致,这时大姆指表示的方向为蜗轮不动时蜗杆旋进的方向。
但因蜗杆被约束不能旋进,则在啮合点处蜗轮应沿蜗杆旋进的反方向运动)来确定蜗轮的转向。
对于所有齿轮轴线相互平行的定轴轮系,轮系中所有齿轮的转向相对于输入轴的转向,不是相同就是相反。
因此由圆柱齿轮组成的定轴轮系的传动比的大小及输出轴的转向关系可表示为:定轴轮系的传动比=(-1)m积所有主动轮齿数的连乘积所有从动轮齿数的连乘式中:m —轴全部平行的定轴轮系中外啮合齿轮的对数。
机械原理 第五章 轮系

3
3 ´
2 ´
2
4 5
将齿数代入上式,即
300 z 2 z3 z 4 z5 3 40 80 15 1 1 w5 z1 z2 z3 z4 20 30 30
H i 13
100 n H 20 25 200 n H 30 25
nH=-100r/min
2) n1与n3 反向,即用 n1=100r/min,n3= -200r/min代入,
i
H 13
100 n H 20 25 200 n H 30 25
可得
nH=700r/min
4.实现运动的合成与分解 运动输入
5 r 4 H
运 n 动 1 输 出
2 1
3 2 H
运 n3 动 输 出
2L
§5-2 定轴轮系的传动比计算 一、轮系传动比的定义
2
3' 1 3 4 4'
w1
w5
5
(avi)
输入轴与输出轴之间
的角速度之传动比:
i15
w1 n 1 w5 n5
包含两个方面:大小与转向
H 43
3
4
联立求解得:
i14 i1H i4 H
63 1 ( ) 588 6 56
§5-3 混合轮系的传动比
3 1 2 4 H 2'
1、复合齿轮系:既含有定轴齿轮系,又含有行星齿轮系 , 或者含有多个行星齿轮系的传动。 3 H 2' OH 4 4 (1) 6 (2) 5 2 H 3 1
机械原理-轮系集合例题

第5章轮系典型例题例1在图示轮系中,已知各轮齿数为:z1 =z1' = 40,z2=z4=30,z3=z5=100,试求传动比i1H。
解:齿轮1',4,5和系杆H组成了一个差动轮系。
齿轮1,2,3和齿轮5(充当系杆)组成了一个行星轮系。
在由齿轮1,2,3和齿轮5(系杆)组成的行星轮系中由于n 3=0,故有在由齿轮1',4,5和系杆H组成的差动轮系中即分析两个基本轮系的联系,可知n1= n1'(c)将(a),(c)两式代入(b),可得计算结果为正,表明从动系杆H和主动齿轮1的转向相同。
例2 在图示轮系中,已知各轮齿数为:z 1 = 90,z 2 = 60,z 2' = 30,z 3 =30,z 3' = 24,z 4 = 18,z 5 = 60,z 5' = 36,z 6 = 32。
运动从A,B两轴输入,由构件H输出。
已知n A=100r/min,n B=900r/min,转向如图所示。
试求输出轴H的转速n H的大小和方向。
解:齿轮3',4,5和系杆H组成了一个差动轮系齿轮1,2,2',3组成了一个定轴轮系,齿轮5',6组成了另一个定轴轮系。
对于齿轮3',4,5和系杆H组成的差动轮系,有即对于齿轮1,2,2',3组成的定轴轮系,有即对于齿轮5,6组成的定轴轮系,有即分析三个轮系之间的基本联系,有将该结果带入(a)式,可得化简整理后得计算结果为负,说明n H转向与n 5 相同,即n A,n B转向相反。
例3 在图示轮系中,已知齿轮1的转速为n 1 =1650 r/min,齿轮4的转速n4=1000r/min,所有齿轮都是标准齿轮,且z 2=z 5=z 6=20。
求各个齿轮中未知的齿轮齿数。
解:由齿轮1与齿轮3和齿轮6与齿轮4的同轴条件得齿轮1,2,3及系杆H1组成差动轮系;齿轮4,5,6及系杆H2组成行星轮系。
机械原理第五章答案

5.1解:(1)应满足杆长条件,且AD 必不为最短杆AD 为最长杆:c b d a +≤+,360280120+≤+d ,520360≤≤dAD 不为最长杆:d b c a +≤+,d +≤+280360120,200360≥d 所以,d 的取值范围为200mm ≤d ≤520mm(2)如果满足杆长条件,无论AD 如何取值均有曲柄存在,故本解中必不满足杆长条件 ①AD 为最长杆:(安装条件)c b a d ++≤, 760 dc bd a ++ ,360280120++ d ,520 d因此,760520 d <②AD 不是最长杆也不是最短杆:120=>a dd b c a ++ ,d ++280360120 , 200<d因此,200120<<d5.6解:(1)180180341.46618018034k θθ++===--(2)[]min 33γγ=<死点位置如图示。
5.15 解 1 1.251180180201 1.251k k θ--===++ (1)AC2=269.23mm ,AC1=127.95mm(2)取比例尺mm m L /002.0=μ根据已知条件可作出摇杆DC 的一个极限位置DC1,要进行图解还需找出摇杆的另一极限位置。
(3)以D 点为圆心,DC1为半径作圆弧S 。
连接AC1,作∠C1AC2=360,AC2线与圆弧S 可交于两点C2‘,则DC2(或DC2‘)皆为摇杆的另一极限位置。
(4)取摇杆的极限位置为DC1、DC2时,由图可得AC1=24,AC2=58,则1712=-=AC AC AB 412=-=AB AC BC5.8 解:分析:因为是转动导杆机构,ADP 又是对心的曲柄滑块机构,所以曲柄AD 的两个极位必在AP 线上,那么对于转动导杆机构而言,转动曲柄BC 的极位C1和C2也比在AP 线上。
(1)又因 3018011=+-=k k ϑ,两个极位的实际夹角应该是 150。
哈尔滨工业大学 第七版 理论力学 第5章 课后习题答案

第5章 摩 擦5-1 如图5-1a 所示,置于V 型槽中的棒料上作用1力偶,力偶矩m N 15⋅=M 时,刚好能转动此棒料。
已知棒料重力N 400=P ,直径m 25.0=D ,不计滚动摩阻。
求棒料与V 形槽间的静摩擦因数f s 。
(a)(b)图5-1解 圆柱体为研究对象,受力如图5-1b 所示,F s1,F s2为临界最大摩擦力。
0=∑x F ,045cos 2s 1N =°−+P F F (1) 0=∑y F ,045sin 1s 2N =°−−P F F (2) 0=∑O M ,0222s 1s =−+M DF D F(3)临界状态摩擦定律:1N s 1s F f F =(4) 2N s 2s F f F =(5)以上5式联立,化得 0145cos s2s =+°−MPDf f 代入所给数据得01714.4s 2s =+−f f 方程有2根:442.4s1=f (不合理), 223.0s2=f (是解)故棒料与V 形槽间的摩擦因数223.0s =f5-2 梯子AB 靠在墙上,其重力为N 200=P,如图5-2a 所示。
梯长为l ,并与水平面交角°=60θ。
已知接触面间的静摩擦因数均为0.25。
今有1重力为650 N 的人沿梯向上爬,问人所能达到的最高点C 到点A 的距离s 应为多少?AN F As F(a)(b)图5-2解 梯子为研究对象,受力如图5-2b 所示,刚刚要滑动时,A ,B 处都达最大静摩擦力。
人重力N 650=W ,平衡方程: 0=∑x F , 0s N =−A B F F (1) 0=∑y F , 0s N =−−+W P F F B A(2)0=∑A M ,060cos 60sin 60cos 60cos 2s N =°−°−°+°l F l F Ws lPB B (3) 临界补充方程:A s A F f F N s = (4)B s B F f F N s =(5)联立以上5式,解得 N 80012sN =++=f WP F A ,N 200s =A F N 200)(12s N =++=W P f f F sB ,N 50s =B F l PF f W l s B 456.02)3[(N s =−+=5-3 2根相同的匀质杆AB 和BC ,在端点B 用光滑铰链连接,A ,C 端放在不光滑的水平面上,如图5-3a 所示。
机械设计基础第5章 轮系习题解答1
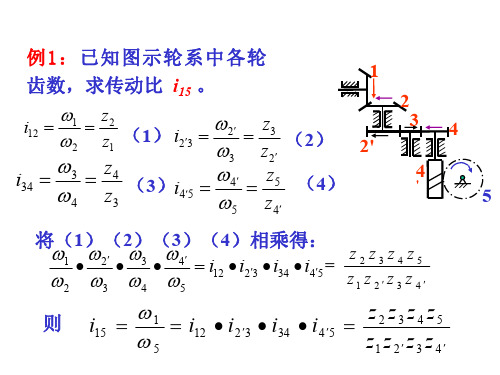
50 nH
8
nH
350 33
10.6r / min
转向与n1方向相同。
n1 1 991909100
nH
1010000000
n1 19091909011 1100 1 nH 1100000 1010000000 100
iH 1
1 i1H
10100000
例题5.4:如图所示的轮系中 ,已知若 z1=20, z2=40,
z2’=20, z3=30,z4=80,试求传动比i1H。
解: 将轮系分解
4 13
1-2为定轴轮系 2-2’共轴
2
H
H-4-3-2’为周转轮系
2’
定轴轮系: i12=ω1/ω2 =-z2/ z1
周转轮系: iH2’4=(1- i2’H) =-z4 /z2’
连接条件: ω2=ω2’
i12 • i2’H
联立解得 i1H
1 H
z2 (1 z4 ) 40 (1 20) 10 z1 z2 20
z2=25,z2'=20,z3=75,齿轮1的转速为200r/min(箭头朝
上),齿轮3的转速为50r/min,求行星架转速的nH大小和
方向。
解: i13H
n1H n3 H
n1 nH n3 nH
z2z3 z1 z2
25 75 25 30 20 8
设n1为正,则n3= -50
200 nH 25
“-”表示齿轮1和行星架H的转向相反。
例5.5 :在图所示的电动卷扬机减速器中,已知各轮齿数
为z1=25,z2=50,z2'=20,z3=60,z3'=18,z4=30,z5=54。 试求传动比i1H。又若电动机的转速为n1=1000r/min,求 转筒的转速。
哈尔滨工业大学机械原理试题精选与解题技巧第5章轮系理论部分

哈尔滨⼯业⼤学机械原理试题精选与解题技巧第5章轮系理论部分第5章轮系及其设计5.1基本要求1.轮系的类型、轮系的功⽤;2.定轴轮系传动⽐的计算;3.周转轮系传动⽐的计算;4.复合轮系传动⽐的计算;5.了解⾏星轮系传动效率的特点;6.设计⾏星轮系时,考虑哪些因素选择⾏星轮系的类型?7.设计⾏星轮系时,各轮齿数和⾏星轮数⽬必须满⾜的四个条件是什么?8.了解⾏星轮系的均载⽅法;9.了解渐开线少齿差⾏星传动、谐波齿轮传动、摆线针轮⾏星传动。
5.2内容提要⼀、本章重点本章重点是定轴轮系、周转轮系及复合轮系传动⽐的计算及设计。
计算齿轮的齿廓曲线与齿廓啮合基本定律是判断给定轮系的类型并确定其传动⽐及转向;设计是根据⼯作要求选择轮系的类型并确定各轮的齿数。
1.轮系的分类(1)定轴轮系组成轮系的各个齿轮的轴线相对于机架的位置都是固定的轮系。
定轴轮系⼜可分为平⾯定轴轮系和空间定轴轮系。
(2)周转轮系组成轮系的各个齿轮中有⼀个或⼏个齿轮的轴线位置是绕着其它齿轮的固定轴线回转的轮系。
周转轮系可按⾃由度的数⽬分为:⾃由度为2的差动轮系和⾃由度为1的⾏星轮系。
基本周转轮系是由两个中⼼轮、⼀个或⼏个⾏星轮和⼀个系杆组成。
该轮系中作为输⼊或输出运动的构件⼜称为基本构件。
(3)复合轮系即包含定轴轮系⼜包含周转轮系或由⼏部分周转轮系组成的复合轮系。
其中把含有定轴轮系和周转轮系的复合轮系称为混合轮系,⽽把由⼏部分周转轮系组成的复合轮系,⼜称为复合周转轮系。
(1)定轴轮系的传动⽐传动⽐⼤⼩的计算:定轴轮系的传动⽐(⾸末两轮的⾓速度之⽐)等于组成该轮系的各对齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之⽐。
即 13142211-===n n n z z z z z z i 积所有主动轮齿数的连乘积所有从动轮齿数的连乘ωω⾸末两轮转向关系的确定及表⽰:定轴轮系⾸末两轮的转向关系通常⽤画箭头法确定,即从已知⾸轮的转向开始,循着运动传递路线,逐对对啮合传动进⾏转向判断,并⽤画箭头法⽰出各主、从动轮的转向,直⾄确定出末轮的转向。
哈工大机械原理考研-第5章 思考题与习题

5.4 复习思考与习题一、思考题1. 在定轴轮系中,如何来确定首、末两轮转向间的关系?2. 何谓周转轮系的“转化机构”?它在计算周转轮系传动比中起什么作用?3. 在差动轮系中,若已知两个基本构件的转向,如何确定第三个基本构件的转向?4. 周转轮系中两轮传动比的正负号与该周转轮系转化机构中两轮传动比的正负号相同吗?5. 计算复合轮系传动比的基本思路是什么?能否通过给整个轮系加上一个公共的角速度H ω-的方法来计算整个轮系的传动比?为什么?6. 如何从复杂的复合轮系中划分各个基本轮系?7. 定轴轮系有哪些功能?设计定轴轮系时应考虑哪几方面的问题? 8. 周转轮系有哪些功能?设计周转轮系时应考虑哪几方面的问题? 9. 什么样的轮系可以进行运动的合成和分解? 10. 周转轮系中各轮齿数的确定需要满足哪些条件?11. 在周转轮系中,H AB i 和AB i 有何区别?它们的符号如何确定?HAω的大小和方向与A ω的大小和方向有何区别?二、习题题5-1 如题5-1图所示轮系中,已知2071==z z ,30832===z z z ,164=z ,606=z ,25=z ,min /14401r n =,求8n 的大小和转向。
题5-1图题5-2 如题5-2图所示的电动三爪卡盘传动轮系,已知各轮齿数为61=z ,252=z , 252='z ,573=z ,564=z ,试求传动比14i 。
题5-3 如题5-3图所示轮系中,已知各轮齿数为281=z ,783=z ,244=z ,806=z ,min /20001r n =。
当分别将轮3或轮6刹住时,试求行星架的转速H n 。
题5-2图 题5-3图题5-4 如题5-4图所示轮系中,2525==z z ,202='z ,组成轮系的各齿轮模数相同。
齿轮1'和3'轴线重合,且齿数相同。
求轮系传动比54i 。
题5-5 如题5-5图所示轮系,已知1z =24, 2z =24,3z =72,4z =89,H 23142'H2314565z =95,6z =24, 7z =30。
《机械设计基础》第5章轮系1解析

Z3
例四:已知马铃薯挖掘中:z1=z2=z3 ,求ω 2, ω 3 z1 2 H 2 H H =-1 i21 ω 2=2 ω H z2 0 H 1 H 3 H 3 H H 2 z1 z 2 i31 (1) =1 ω 3=0 1 H 0 H z 2 z3 模型验证 上式表明轮3的绝对角速度为0,但相对角速度不为0。
3 2 1
J
A
B
5
连接条件:
i A13=(ω1 - ωA ) /(0 -ωA ) =- z 3 / z 1 iB3’5=(ω 3’-ω B )/(ω 5-ω B ) =- z 5/ z 3’ ω 5 =ω A
1 z3 z3' 1 5 (1 )(1 ) 联立解得: i1B A B B z1 z5 =i1A · i5B
H 1 H 1 H H 1 解 1) i13 H i1H 1 0 H 3 H 3
2
H 1 3
z 2 z3 z 60 3 3 z1 z2 z1 20
∴
i1H=4 ,
H 2) i13
齿轮1和系杆转向相同 H 1 nH n1 nH n1 H =-3 1 nH n3 nH n3 两者转向相反。
特别强调:① i13≠ iH13
一是绝对运动、一是相对运动
② i13≠ - z3 /z1
例三:已知图示轮系中 z1=44,z2=40, z2’=42, z3=42,求iH1 解:iH13=(ω 1-ω H)/(0-ω H ) = 1-i1H =z3 /z1z2’ =40×42/44×42 =10/11
iB3’5=(ω 3’-ω B)/(0-ω B) =-z5/ z3’
机械设计基础第5章 轮系习题解答2
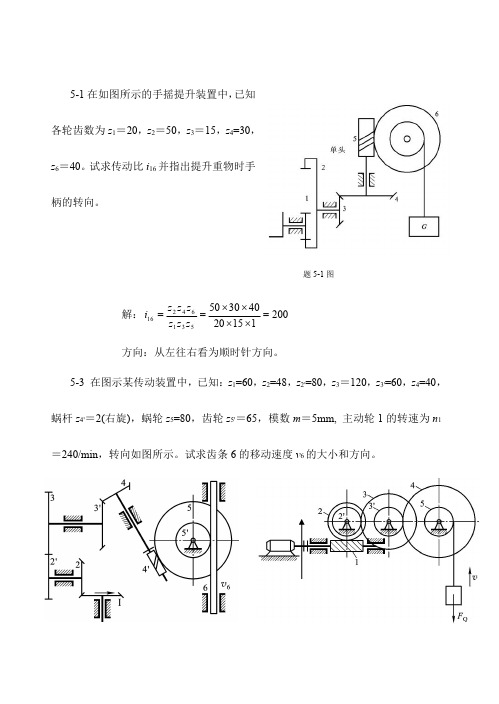
5-1在如图所示的手摇提升装置中,已知各轮齿数为z 1=20,z 2=50,z 3=15,z 4=30,z 6=40。
试求传动比i 16并指出提升重物时手柄的转向。
题5-1图解:2001152040305053164216=⨯⨯⨯⨯==z z z z z z i 方向:从左往右看为顺时针方向。
5-3在图示某传动装置中,已知:z 1=60,z 2=48,z 2'=80,z 3=120,z 3'=60,z 4=40,蜗杆z 4'=2(右旋),蜗轮z 5=80,齿轮z 5'=65,模数m =5mm,主动轮1的转速为n 1=240/min ,转向如图所示。
试求齿条6的移动速度v 6的大小和方向。
题5-3图题5-4图解:齿条的移动方向如图所示,其轮系传动比为:322608060804012048'4'3'2154325115=⨯⨯⨯⨯⨯⨯===z z z z z z z z n n i 则齿轮5’的转速为:min /5.7322401515r i n n ===又齿轮5’分度圆直径为:mm m z d 325565'5'5=⨯==所以齿条的移动速度为:s m n d v /128.0600005.73251000605'56=⨯⨯=⨯=ππ5-4如图所示为一电动卷扬机的传动简图。
已知蜗杆1为单头右旋蜗杆,蜗轮2的齿数z 2=42,其余各轮齿数为z 2'=18,z 3=78,z 3'=18,z 4=55;卷筒5与齿轮4固联,其直径D 5=400mm ,电动机转速。
n 1=1500r/min ,试求:(1)转筒5的转速n 5的人小和重物的移动速度v 。
(2)提升重物时,电动机应该以什么方向旋转?解:1.其轮系传动比为:11.5569500518181557842'3'214324114==⨯⨯⨯⨯===z z z z z z n n i 则齿轮4的转速(即转筒5的转速)为:min /70.211.556150014145r i n n n ====所以重物的移动速度为:s m n D v /057.0600007.2400100060556=⨯⨯=⨯=ππ5-5在如图所示周转轮系中,已知各轮齿数为z 1=60,z 2=20,z 2'=20,z 3=20,z 4=20,z 5=100,试求传动比i 41。
机械原理课后答案——第五章 凸轮机构及其设计

从动件所受正压力方向: 滚子中心与凸轮几何中心的 连线。
力作用点凸轮从图示位置转过90º 后推杆的位移; 图示位置推杆的位移量S0应 是沿推杆的导路方向(与偏距圆 相切)从基圆开始向外量取。 凸轮从图示位置转过90º 后 推杆的位移等于推杆从图示位 置反转90º 后的位移。 推杆从图示位置反转90º 后 的导路方向仍于与偏距圆相切。 其位移量S1 仍是沿推杆的导路 方向从基圆开始向外量取。 凸轮从图示位置转过90º 后推杆的位移:S=S1 -S0
凸轮机构及其设计
习题9-7 9-8 9-9
9-7 试标出 a 图在图示位置时凸轮机构的压力角,凸轮从 图示位置转过90后推杆的位移;标出图b 推杆从图示位置 升高位移s 时,凸轮的转角和凸轮机构的压力角。
a
b
1) a 图在图示位置时凸轮机构的压力角, 凸轮机构的压力角: 在 不计摩擦的情况下,从动件 所受正压力方向与力作用点 的速度方向之间所夹的锐角。
9-8
作出凸轮的理论 廓线和凸轮的基圆。 以A’为圆心,A到滚子 中心的距离为半径作 圆弧,分别交基圆和 理论廓线于C、C’点, 则C’A’C为所求的位 移角。
过C’作公法线 O’C’,过C’作A’C’的 垂线,则两线的夹角 为所求的压力角。
9-9 解:采用等加速等减速运动规律,可使推杆推程阶段 最大加速度最小。其运动线图如下:
v max 2 h / 0 2 16 1 .5 /( 5 π / 6 ) 18.34mm/s
a 4 h 2 / 02 4 16 1 .5 2 /( 5 π / 6 ) 2 21.03mm/s
2
2) 标出图b 推杆从图示位置升高位移s 时,凸轮的转角和 凸轮机构的压力角。
《机械原理》第五章习题轮系及其设计及答案

《机械原理》第五章习题轮系及其设计及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第五章 轮系及其设计习题5 2 在题图52所示的手摇提升装置中,已知各轮齿数为:z 120,z 250,z 315,z 430,z 640,z 718,z 851,蜗杆z 51,右旋,试求传动比i 18并确定提升重物时手柄的转向。
题图525 5 在题图55所示的压榨机中,螺杆4和5为一对旋向相反的螺杆,其螺距分别为6mm 和3mm ,螺杆5旋在螺杆4内,螺杆4与齿轮3固联在一起,螺杆5与盘B 固联在一起,盘B 插在框架两侧的槽内只能沿框架上下移动。
已知各轮齿数为z 118,z 224,z 224,z 364,试求为使盘B 下降19mm ,轴A应转多少转,转向如何答案:转!题图555-6题图5-6所示为手动起重葫芦,已知z l=z2=10,z2=20,z3=40。
设由链轮A至链轮B 的传动效率为= 0. 9,为了能提升Q =1000N的重物,求必须加在链轮A上的圆周力P。
57题图57所示为一灯具的转动装置,已知:n1min,方向如图示,各轮齿数为z160,z2z230,z3 z440,z5120。
求灯具箱体的转速及转向。
5-11 在题图5-11所示的三爪电动卡盘的传动轮系中,各轮齿数为z1=6,z2=z2=25,z3=57,z4=56,求传动比i14。
题图511512 在题图512所示的自行车里程表机构中,C为车轮轴,P为里程表指针。
已知各轮齿数为z117,z323,z419,z420,z524。
设轮胎受压变形后车轮的有效直径为0.7m,当自行车行驶1km时,表上的指针刚好回转一周。
试求齿轮2的齿数。
513 在题图513所示的双螺旋桨飞机的减速器中,已知z126,z220,z430,z518,n115000r/min,求螺旋桨P、Q的转速n P、n Q及转向。
题图513516 题图516所示的减速器中,已知蜗杆1和5的头数均为1,蜗杆1为左旋,蜗杆5为右旋,各轮齿数为z 1=101,z2=99,z 2=z4,z 4=100,z 5=100。
机械第五章习题
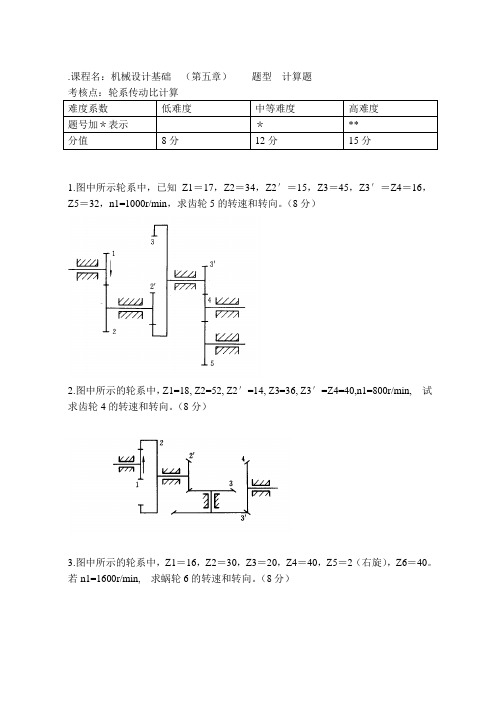
.课程名:机械设计基础(第五章)题型计算题考核点:轮系传动比计算1.图中所示轮系中,已知Z1=17,Z2=34,Z2′=15,Z3=45,Z3′=Z4=16,Z5=32,n1=1000r/min,求齿轮5的转速和转向。
(8分)2.图中所示的轮系中,Z1=18, Z2=52, Z2′=14, Z3=36, Z3′=Z4=40,n1=800r/min,试求齿轮4的转速和转向。
(8分)3.图中所示的轮系中,Z1=16,Z2=30,Z3=20,Z4=40,Z5=2(右旋),Z6=40。
若n1=1600r/min,求蜗轮6的转速和转向。
(8分)5.在图示的轮系中,已知Z1=Z2=Z4=Z5=20,Z3=Z6=60,齿轮1的转速n1=1440r/min,求齿轮6的转速和转向。
(8分)*6.在图示的轮系中,设已知双头右旋蜗杆的转速n1=900r/min,Z2=60,Z2′=25,Z3=20,Z3′=25,Z4=20,Z4′=30,Z5=35,Z5′=28,Z6=135,求轮6的转速和转向。
(12分)*7.在图示的轮系中,已知Z1=15,Z2=25,Z2′=15,Z3=30,Z3′=15,Z4=30,Z4′=2(右旋),Z5=60,Z5′=20,(m=4mm),若n1=1000r/min,求齿轮6的线速度v的大小和方向。
(12分)8.在图示的双级蜗杆传动中,右旋蜗杆1的转向如图,Z1=2,Z2=70,Z2′=2,Z3=60,试求传动比i13和判断蜗轮2和蜗轮3的转向,并以箭头在图中表示。
(8分)*9.图中所示轮系中,已知各标准直齿圆柱齿轮的齿数Z1=Z2=20,Z3′=26,Z4=30,Z4′=20,Z5=39,试计算齿轮3的齿数及传动比i15.(12分)10.图示轮系中,已知Z1=Z2′=15,Z2=45,Z3=30,Z3′=17,Z4=34。
试计算传动比i14及用箭头表示各轮的转向。
(8分)11.图示轮系中,已知Z1=2,Z2′=Z3′=20,Z3=Z4=40,Z2=50,采用右旋蜗杆,若n1=1500r/min,试求轮4的转速和转向。
机械原理课后习题答案-第五章

*
d a mz 2m
1; c
*
mz d
f
2 ha
*
0 . 25
2m
(2)r=mz/2=96mm;rb=rcosα=87.01mm ra=r+ha*m=96+1×8=104mm αa=arccos(rb/ra)=33°13′ ra sa s 2 ra ( inv a inv ) ∴ Sa=4.24mm; r Sk=0,
题5-15解
1.选择传动类型 2. 求 和 x
arccos(
a a
a
m 2
( z 1 z 2 ) 120 mm a
cos ) 29 5 0 2 8
x
( z 1 z 2 )( inv inv ) 2 tg
1 . 2505
20 . 26
73 . 75 60
题5-15解
1
1 2
[ z 1 ( tg a 1 tg ) z 2 ( tg a 2 tg )]
z 1 ( tg a 1 tg )
1 . 03
题5-16解 用等变位修复,小正变位;大负变位
则 inv k s inv 0 . 095426
αk=35°42′
2r
rk=rb/cosαk=107.14mm
题5-8解
αa1=arccos(rb/ra1) =arccos[(z1cosα)/(z1+2ha*)] =31°46′
α
P
N2
O1
B2
N1
αa2=26°14′10″
B1P=B1N1-N1P =mz1/2· cosα(tgαa1-
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.3 例题精选及答题技巧例5-1 某传动装置如例5-1图所示,已知:1z =60,2z =48,'2z =80,3z =120,'3z =60,4z =40,蜗杆'4z =2(右旋),涡轮5z =80,齿轮'5z =65,模数m=5 mm 。
主动轮1的转速为1n =240 r/min ,转向如图所示。
试求齿条6的移动速度6v 的大小和方向。
例5-1图解题要点:这是一个由圆柱齿轮、圆锥齿轮、蜗轮蜗杆、齿轮齿条所组成的定轴轮系。
解:为了求齿条6的移动速度6v 的大小,需要首先求出齿轮5'的转动角速度'5ω。
因此首先计算传动比15i 的大小: 322608060804012048432154325115=⨯⨯⨯⨯⨯⨯==='''z z z z z z z z n n i ===='3224015155i n n n 7.5 r/min 605.7260255⨯==''ππωn =0.785 rad/s 齿条6的移动速度等于齿轮5'的分度圆线速度,即:785.0655212155556⨯⨯⨯===''''ωωmz r v =127.6 mm/s 齿条6的运动方向采用画箭头的方法确定如例5-1图所示。
例5-2 如例5-2图所示,已知各轮齿数为1z 、2z 、3z 、4z 、5z 、6z ,1z 为主动件,转向如图箭头所示,试求:1. 传动比?/11==H H i ωω(列出表达式);22. 若已知各轮齿数1z =2z =4z =5z =20,3z =40,6z =60,求H i 1的大小及转向。
图 5-2解题要点:如例5-2图所示,从结构上看,此轮系由两部分组成,齿轮1、齿轮2、齿轮3组成定轴轮系,齿轮4、5、6及系杆H 组成行星轮系,二者之间属串联关系。
齿轮3和齿轮4属同一构件。
解:1. 根据上面分析,得到如下方程: 1321323113z z z z z z i ===ωω (1) 464634411z z i i HH H H +=-===ωωωω (2) 由式(1)与式(2)解得: ⎪⎪⎭⎫⎝⎛+==4613111z z z z i H H ωω (3) 3. 将1z =4z =20,3z =40,6z =60代入式(3)得: 82060120401=⎪⎭⎫⎝⎛+=H i 转向如例5-2图所示。
例5-3 如例5-3图所示轮系,已知各轮齿数为:1z =25,2z =50,2'z =25,H z =100,4z =50,各齿轮模数相同。
求传动比14i122'34H例5-3图解提要点:如例5-3图轮系,由两部分组成,齿轮1、22'-、3及系杆H 组成行星轮系,齿轮(系杆)H 及齿轮4组成定轴轮系。
解:利用同心条件:1002550252213=++=++='z z z z 对于齿轮1、22'-、3及系杆H 组成行星轮系有: 925251005011121321311=⨯⨯+=+=-=='z z z z i n n i HH H (1) 对于齿轮(系杆)H 及齿轮4组成定轴轮系有: 2110050444-=-=-==H H H z z n n i (2) 由式(1)及式(2)得: 5.421941414114-=⎪⎭⎫⎝⎛-⨯==⋅=⋅=n n n n n n i i i H H H H 计算结果为负,说明1n 的转向与4n 转向相反。
例5-4 如例5-4图所示轮系,已知1z =36,2z =60,3z =23,4z =49,4'z =69,5z =31,6z =131,7z =94,8z =36,9z =167,1n =3549 r/min 。
求2H n 的大小及转向?例5-4图解题要点:如例5-4图所示,此轮系由三部分组成,齿轮1、2、3、4组成定轴轮系,齿轮4'、5、6及系杆H 1组成行星轮系,齿轮7、8、9及系杆H 2组成行星轮系,三者之间属串联关系。
齿轮4和齿轮4'属同一构件,系杆H 1和齿轮7属同一构件。
解:对定轴轮系1,2,3,4有: 31424114z z z z n n i ==(1)齿轮4'、5、6及系杆H 1组成行星轮系: 46164141411''''+=-==z z i n n i H H H (2) 齿轮7、8、9及系杆H 2组成行星轮系: 79279272711z z i n n i H H H +=-==(3) 由式(1)、式(2)及式(3),并考虑到44'=n n ,71n n H =得: )1)(1(794631422121z z z z z z zz n n i H H ++==' (4) 将各轮齿数代入式(4)得: )941671)(691311(233649602121++⨯⨯==H H n n i =28.58 则:58.2835492112==H H i n n =124.19 r/min 。
转向如例5-4图所示。
例5-5 如例5-5图所示轮系,已知1z =30,2z =30,3z =90,1'z =20,4z =30,3'z =40,4'z =30,5z =15。
求AB i 的大小及转向?例5-5图解题要点:如例5-5图所示,此轮系由三部分组成,齿轮4、5、1'(1) 组成定轴轮系及齿轮4'、3'(3)组成定轴轮系将齿轮1、2、3及系杆B 组成差动轮系封闭起来组成封闭式行星轮系。
齿轮4和齿轮4'属同一构件,齿轮1'和齿轮1属同一构件。
解:对于1,2,3,B 组成的差动轮系有: 33090133113-=-=-=--=z z n n n n i B B B(1)5123AB1'44'3'对于4(A )、5、1'(1)组成定轴轮系: 3230204111414=====''''z z n n n n i A 即: A n n 231=' (2) 对于齿轮4'、3'(3)组成定轴轮系: 3430404333434-=-=-===''''z z n n n n i A 即: A n n 433-=' (3) 考虑到11n n =',33n n ='将式(1)及式(2)代入式(3)得:34323-=---B A B A n n n n 解得:33.5316-≈-==B A AB n n i 。
A n 和B n 的转向相反。
例5-6 如例5-6图所示电动卷扬机减速器,已知各轮齿数1z =26,2z =50,2'z =18,3z =94,3'z =18,4z =35,5z =88,求15i例5-6图解题要点:如例5-6图所示,此轮系由两部分组成。
齿轮1、22'-、3及系杆5组成差动轮系,其基本构件3和5被定轴轮系3'、4、5封闭起来了,从而使差动轮系部分的两个基本构件3和5之间保持一定的速比关系,使整个轮系变成了自由度为1的特殊的行星轮系,称为封闭式行星轮系。
齿轮2和齿轮2'属同一构件,齿轮3和齿轮3'属同一构件。
解:对于1,22'- ,3,5组成的差动轮系有:12342'3'511325351513'-=--=z z zz n n n n i (1)对于3'、4、5组成的定轴轮系有: 35535353'''-===z z n n n n i 即: 5353n z z n '-= (2) 将式(1)代入式(2)解得: 11888118269450113521325115+⎪⎭⎫ ⎝⎛+⨯⨯=+⎪⎪⎭⎫ ⎝⎛+==''z z z z z z n n i =60.14 齿轮1和卷筒(齿轮)5转向相同。
例5-7 如例5-7图所示轮系,已知各轮齿数11'=z z =40,42z z ==30,53z z ==100。
求H i 1=?例5-7图解题要点:如解5-7图所示,此轮系由两部分组成。
齿轮1、2、3及系杆5组成行星轮系,其基本构件1和系杆5把齿轮 1'、4、5及系杆H 组成差动轮系封闭起来了,从而使差动轮系部分的两个中心轮1(1')和5之间保持一定的速比关系。
整个轮系是一个由行星轮系把差动轮系中的中心轮1'和5封闭起来组成的封闭式差动轮系。
齿轮1和齿轮1'属同一构件,构件5是前一行星轮系的系杆又是后一差动轮系的中心轮。
解:对于1,2 ,3,5组成的行星轮系有: 40100111135135115+=+=-==z z i n n i =3.5 5.315n n =(1) 对于齿轮 1'、4、5及系杆H 组成差动轮系有:H423151'5.240100155151-=-=-=--='''z z n n n n i H H H(2)考虑到11'=n n 将式(1)代入式(2)得:5.25.311-=--H Hn n n n化简整理后得:244911==H H n n i 。
系杆H 和主动齿轮1的转向相同。
例5-8 如例5-8图所示轮系中,已知各轮齿数为:1z =90,2z =60,2'z =30,3z =30,3'z =24,4z =18,5z =60,5'z =36,6z =32,运动从A ,B 两轴输入,由构件H 输出。
已知A n =100 r/min ,B n =900 r/min ,转向如图所示。
试求输出轴H 的转速H n 的大小和转向。
例5-8图解题要点:如例5-8图所示轮系,由三部分组成,齿轮1、22'-、3组成定轴轮系,齿轮5'、6组成定轴轮系,齿轮3'、4、5及系杆H 组成差动轮系。
齿轮2和齿轮2'属同一构件,齿轮3和齿轮3'属同一构件。
齿轮5和齿轮5'属同一构件。
解:对于齿轮3'、4、5及系杆H 组成差动轮系有: 252460355353-=-=-=--='''z z n n n n i H H H(1)对于齿轮1、22'-、3组成定轴轮系有: 323090306021323113+=⨯⨯+=+=='z z z z n n i 即 1502323133+=+=+=='A n n n n r/min (2) 注意 这是一个由圆锥齿轮所组成的定轴轮系,只能用标箭头的方法确定其转向。
