第六章 多元函数微分学及其应用
多元函数微分法及其应用总结

多元函数微分法及其应用总结多元函数微分法及其应用是高等数学中一个重要的内容。
多元函数是指自变量有两个或者多个的函数,如z=f(x,y)。
而微分法是研究函数的变化率的一种方法。
本文将对多元函数微分法及其应用进行总结。
1. 多元函数微分法的基本概念多元函数的微分可以分为偏导数和全微分两种形式。
对于多元函数z=f(x,y),其偏导数表示函数在某一自变量上的变化率,可以记作∂z/∂x,∂z/∂y。
全微分表示函数在所有自变量上的变化率,可以记作dz。
多元函数的微分法有很多性质和定理,如链式法则、高阶偏导数、隐函数定理等。
2. 多元函数的极值与最值利用多元函数微分法,我们可以求多元函数的极值与最值。
对于多元函数z=f(x,y),其极值、最值的求解步骤大致如下:(1)求函数的偏导数,得到所有的偏导数;(2)令所有的偏导数等于零,求解出关于x和y的方程;(3)求解方程组,得到x和y的解;(4)将解代回原函数,求得z的值;(5)比较求得的z值,得到最大值或最小值。
3. 多元函数的泰勒展开多元函数的泰勒展开是利用多元函数在某一点附近进行近似求解的一种方法。
对于多元函数z=f(x,y),其泰勒展开公式为:f(x+Δx,y+Δy) = f(x,y) + (∂f/∂x)Δx + (∂f/∂y)Δy + 1/2(∂²f/∂x²)(Δx)² + 1/2(∂²f/∂y²)(Δy)² + (∂²f/∂x∂y)ΔxΔy + O(Δx²,Δy²)这里的O(Δx²,Δy²)表示高阶无穷小,Δx和Δy表示自变量的增量。
4. 多元函数微分法的应用多元函数微分法广泛应用于物理学、工程学和经济学等领域。
具体应用如下:(1)在物理学中,多元函数微分法可以用于描述粒子在空间中的运动轨迹,求解最优路径等问题。
(2)在工程学中,多元函数微分法可以用于建模和优化设计,如求解最优结构、最优控制等问题。
多元函数微分学的应用

多元函数微分学的应用一、极值问题多元函数微分学最重要的应用之一是求解极值问题。
通过求取函数的偏导数,我们可以找到函数的极值点。
这对于经济学家、物理学家和其他相关领域的研究者来说是非常重要的。
例如,在经济学中,我们可以使用多元函数微分学来确定产品的最优产量和价格,以使利润最大化。
在物理学中,我们可以使用多元函数微分学来优化力学系统的能量和动量。
二、方向导数与梯度方向导数是一个重要概念,它描述了函数在其中一点沿着一些方向的变化率。
梯度是一个向量,它指向函数值增加最快的方向,并且梯度的模表示函数在其中一点的最大变化率。
方向导数和梯度在工程技术中的应用非常广泛。
例如,在机器学习中,我们可以使用梯度下降算法来优化模型的参数,以最小化损失函数。
三、偏微分方程偏微分方程是描述自然现象的重要数学工具,包括热传导、扩散、波动等。
多元函数微分学为解偏微分方程提供了重要的数学基础。
通过偏微分方程的分析解或数值解,我们可以深入了解自然现象的行为和性质。
例如,在工程技术中,我们可以使用多元函数微分学来解决电磁场、弹性力学和流体力学等方面的问题。
四、约束优化约束优化是指在满足一定条件下找到使目标函数最大或最小的参数的问题。
多元函数微分学是解决约束优化问题的重要工具。
通过拉格朗日乘数法,我们可以将约束优化问题转化为无约束优化问题,并应用多元函数微分学的方法求解。
约束优化问题在经济学、运筹学和供应链管理等领域有着广泛的应用。
例如,在经济学中,我们可以使用约束优化来确定消费者的最优选择。
五、多元函数积分学多元函数微分学与多元函数积分学是紧密相关的。
多元函数微分学提供了计算多元函数导数的方法,而多元函数积分学则通过对函数的积分来研究函数的整体性质。
应用多元函数积分学,我们可以计算多元函数在其中一区域上的平均值、总值和概率密度等。
多元函数积分学在统计学、物理学和金融工程学等领域有广泛的应用。
例如,在统计学中,我们可以使用多元函数积分学来计算多维随机变量的期望和方差。
多元函数微分法及其应用

第九章多元函数微分法及其应用一、基本要求及重点、难点1. 基本要求(1)理解二元函数的概念,了解多元函数的概念。
(2)了解二元函数的极限、连续性概念,有界闭域上连续函数的性质。
(3)理解偏导数和全微分的概念,熟练掌握偏导数的计算,了解全微分存在的必要条件和充分条件。
(4)了解方向导数与梯度的概念及其计算方法。
(5)掌握复合函数一阶偏导数的求法,会求复合函数的二阶偏导数。
(6)会求隐函数(包括由方程组确定的隐函数)的偏导数(主要是一阶)。
(7)了解曲线的切线和法平面及曲面的切平面与法线、并会求出它们的方程。
(8)理解多元函数极值和条件极值的概念,会求二元函数的极值。
了解求条件极值的拉格朗日乘数法,会求解一些较简单的最大值和最小值的应用问题。
2. 重点及难点(1)重点:多元函数概念,偏导数与全微分概念,偏导数计算,微分在几何上的应用,多元函数的极值的计算。
(2)难点:二重极限的定义与计算,多元函数连续;偏导数存在与可微之间的关系;复合函数的高阶偏导数;方向导数、偏导数、梯度之间的关系。
二、内容概述多元函数微分学是一元函数微分学的推广,因此两者之间有许多相似之处,但是要特别注意它们之间的一些本质差别。
1.多元函数的极限和连续(1)基本概念1)点集和区域。
2)多元函数的定义、定义域。
3)二元函数的极限、连续。
(2)基本定理1)多元初等函数在其定义域内是连续的。
2)多元连续函数在有界闭区域上一定有最大值M、最小值m;且必取到最大值M和最小值m之间的任何值。
2.多元函数微分法(1)基本概念偏导数、全微分、高阶偏导数的定义。
(2) 计算方法1) 偏导数:),(y x f z =在),(00y x 处对x 的偏导数x x xz =∂∂,就是一元函数),(0y x f z =在0x x =处的导数;对y 的偏导数x x xz =∂∂(同理)。
2) `全微分:),(y x f z =的全微分dy yzdx x z dz ∂∂+∂∂=3) 复合函数求导法则:画出函数到自变量的路经,然后利用链式迭加法则:即同条路经的偏导数相乘,不同路经的偏导数相加,求出所要的偏导数。
《高等数学教学课件》9.1多元函数微分学法及其应用

在社会科学中的应用(如人口动态学、市场均衡分析等)
在工程科学中的应用(如机器人控制、信号处理等)
总结词:优化和控制
感谢观看
THANKS
全微分的定义
线性性质、可加性、全微分与偏导数的关系、全微分与方向导数的关系。
全微分的性质
全微分的定义与性质
03
梯度的性质
梯度与方向导数的关系、梯度的几何意义。
01
方向导数的定义
在某一方向上函数值的变化率。
02
梯度的定义
方向导数在各个方向上的最大值,表示函数值变化最快的方向。
方向导数与梯度
04
多元函数的极值
在物理科学中的应用(如流体动力学、热传导等)
总结词:揭示内在机制 总结词:预测和政策制定 总结词:复杂系统分析 详细描述:在人口动态学和市场均衡分析等社会科学领域,多元函数微分学也具有广泛的应用。通过建立微分方程模型,我们可以揭示人口动态变化和市场供需关系的内在机制,预测未来的发展趋势。此外,这些模型还可以为政策制定提供依据,帮助政府和企业制定有效的政策和措施。在复杂系统分析中,多元函数微分学也为我们提供了理解和预测系统动态行为的有力工具。
极值点处的函数一阶导数必须为零
如果一个多元函数在某点的所有偏导数都为零,并且该点的二阶导数矩阵正定,那么该点就是函数的极值点。
费马定理是判断多元函数极值点的充分条件,但在实际应用中,需要结合其他条件进行判断,例如函数的单调性、凹凸性等。
极值的充分条件(费马定理)
费马定理的应用
费马定理
最大值与最小值的定义
多元函数的表示方法
可以用数学符号表示,如$z = f(x, y)$,其中$x$和$y$是自变量,$z$是因变量。
多元函数的定义域
多元函数的微分学的应用

多元函数的微分学的应用
多元函数的微分学在实际生活中有多种应用。
以下是其中几个常见的应用:
1. 最值问题:多元函数的微分学可以用来解决最值问题,例如优化问题,找到函数的最大值或最小值。
这种应用广泛用于物流、金融和工程等领域,其中包括确定最小成本生产和最大利润等问题。
2. 等高线图:多元函数的微分学也可以用来绘制等高线图。
等高线图常常用于表示地形,如山地,海底地形,或者用于表示等值线,如等压线,等温线和等高线等。
3. 导航系统:对于导航系统而言,通过多元函数微分学,不仅能够实时计算用户之间的距离,还能推断用户的行车方向,从而更好地指引用户前进方向。
4. 工程应用:对于工程师而言,他们会使用多元函数的微分学去计算关键参数,例如建筑物的结构支持力量、材料的伸缩性,以及各种形态的机器件等。
5. 统计分析:多元函数的微分学也可以帮助人们进行数据建模、数据预测,诸如对群体的群体大小计算以及分析等等。
在这种场合下,多元函数的微分学可帮助人们发现数据之间的关联以执行信息预测等任务。
总之,多元函数的微分学在实践中具有广泛应用,并为许多领域提供了重要的工
具和方法。
多元函数微分学及其应用归纳总结

多元函数微分学及其应用归纳总结一、多元函数的微分与偏导数1. 多元函数的微分定义为函数在其中一点上的线性逼近。
对于二元函数,微分为 dz=f_x*dx+f_y*dy,其中 f_x 和 f_y 分别为函数的偏导数。
对于一般的 n 元函数也可类似定义。
2.多元函数的偏导数表示函数沿着其中一个变量的变化率。
对于二元函数f(x,y),其偏导数f_x表示x方向上的变化率,f_y表示y方向上的变化率。
一般而言,当存在偏导数且连续时,函数在该点可微分。
3.偏导数的计算方法与一元函数相似,利用极限的定义求出偏导数表达式,对于高阶偏导数,可以反复求导。
4.混合偏导数表示函数在二个或二个以上变量上求偏导数后再对另外一个或另外几个变量求偏导数,其次序不影响结果。
二、多元函数的求导法则1. 多元函数的和、差、常数倍法则:设函数 f 和 g 在其中一点连续可导,则(f±g)'=f'±g',(kf)'=kf'。
2.多元函数的乘积法则:设函数f和g在其中一点连续可导,则(f·g)'=f'·g+g'·f。
3.多元函数的商法则:设函数f和g在其中一点连续可导且g不为零,则(f/g)'=(f'·g-g'·f)/g^24. 复合函数求导法则:设函数 y=f(u) 和 u=g(x) 在其中一点可导,则复合函数 y=f(g(x)) 的导数为dy/dx=f'(u)·g'(x),其中 x 和 u 为中间变量。
三、多元函数的极值与梯度1.多元函数的极值包括极大值和极小值。
在二元函数中,极值的必要条件为偏导数为零,充分条件为偏导数存在且满足一定条件。
2.多元函数的梯度是一个向量,其方向与函数在其中一点上变化最快的方向一致,大小表示变化率的大小。
梯度为零的点可能为极值点。
多元函数微分学的几何应用

多元函数微分学的几何应用一、多元函数微分学多元函数微分学是微积分的一个分支,研究的是多个自变量的函数的导数、微分和全微分等概念。
与一元函数微分学不同的是,多元函数在求导时需要通过偏导数来计算,而全微分可以看做多元函数在某一点上的线性近似。
多元函数微分学在实际生活中有着广泛的应用,尤其是在几何学方面。
二、几何应用1. 向量场和梯度向量场是一个函数与向量的映射关系,在几何学中经常用于描述速度场、磁场等。
其中,梯度是向量场的一个重要概念。
梯度表示在某一点上函数变化增加最快的方向。
例如,在平面上的某一点上,一个函数的梯度表示了函数值增加最快的方向及增加的速率。
2. 方向导数和梯度的应用方向导数表示函数在某一点上沿着某一给定方向上的导数。
在平面几何中,方向导数可以用来求解曲面的切平面方程。
具体来说,可以通过梯度和方向向量的点积计算出方向导数,从而得到曲面上某一点的切平面方程。
3. 曲面积分曲面积分是对曲面上的函数进行积分,类似于线积分。
在计算曲面积分时,需要用到曲面的面积元素,这里面积元素的计算需要用到微积分中的偏微分。
具体来说,可以通过将曲面分成小的面元,计算每个面元的面积和函数值,然后将它们累加起来,从而得到曲面上的积分值。
4. 极值和拐点在多元函数中,类似于一元函数中的极值和拐点的概念。
在平面几何中,可以将这些概念应用于曲线的局部特征的分析中。
通过极值和拐点的计算,可以得到曲线上的最大和最小值,以及拐点的位置和拐点的类型等信息。
总之,多元函数微分学在几何学中有着广泛的应用。
通过对向量场、梯度、方向导数、曲面积分、极值和拐点等概念的研究,可以深入分析曲线、曲面的本质特征和局部特征,从而为实际问题的求解提供了精确的数学工具。
多元函数微分学的应用

多元函数微分学的应用一、多元函数微分学在物理学中的应用多元函数微分学在物理学中有重要的应用,可以用于描述和分析物体的运动和力学性质。
例如,当我们研究一个物体在空气中自由落体的过程时,可以通过建立物体的位置、速度和加速度之间的多元函数关系来描述物体的运动规律。
通过对这个多元函数进行微分,我们可以计算出物体的速度和加速度,并进一步研究物体的运动轨迹和运动的特性。
二、多元函数微分学在工程技术中的应用工程技术领域广泛应用多元函数微分学,其中一个重要的应用是工程优化。
通过建立多元函数模型,可以描述工程系统的性能与各种因素之间的关系,例如工程结构的刚度、强度和稳定性与材料、尺寸和几何形状等因素之间的关系。
通过对这些多元函数进行微分,可以找到使性能最优化的设计变量组合,从而优化工程系统的设计。
三、多元函数微分学在经济管理中的应用多元函数微分学在经济管理中也有广泛的应用,可以用于分析和优化经济系统的运行和决策问题。
例如,在经济学中,我们可以建立多元函数模型来描述生产函数、成本函数和效用函数等与经济生产和消费相关的关系。
通过对这些多元函数进行微分,可以分析生产效率、最小化成本和最大化效用的最优决策策略,从而实现经济系统的优化和管理。
四、多元函数微分学在生物学中的应用多元函数微分学也被广泛应用于生物学领域,可以用于描述和分析生物系统中的各种生物过程和生物现象。
例如,在生态学中,我们可以建立多元函数模型来描述种群数量与环境因素之间的关系。
通过对这些多元函数进行微分,可以研究种群的增长速率、极限状态和稳定性等生态学性质,从而深入理解和预测生态系统的动态演化。
总之,多元函数微分学具有广泛的应用领域,可以用于自然科学、工程技术和经济管理等各个领域中的建模、优化和解决实际问题。
通过对多元函数的微分,我们可以深入理解各种系统和过程的特性和规律,从而实现对这些系统和过程的优化和控制。
(完整版)多元函数微分学及其应用习题解答

(((x 2 + y 2 ≤ 1, x+ y }(1- (t + 4) 2 解:令 t=xy , lim = lim= lim 2=- t →0 t →0习题 8-11. 求下列函数的定义域:(1) z =解: x -x - y ;y ≥ 0, y ≥ 0 ⇒ D ={x, y ) y ≥ 0, x ≥ y }x(2) z = ln( y - x) +;1 - x2 - y 2解: y - x ≥ 0, x ≥ 0,1 - x 2 - y 2 ⇒ D ={ x , y ) y > x ≥ 0 且 x2+ y 2 < 1}(3) u = R 2 - x 2 - y 2- z 2 +1x 2 + y 2+ z 2 - r 2(R > r > 0) ;解: 0 ≤ R 2 - x 2 - y 2 - z 2,0 < x 2 + y 2 + z 2 - r 2 ⇒⇒ D = {x , y , z ) r 2< x 2 + y 2 + z 2 ≤ R 2}(4) u = arccoszx 2 + y 2。
解:z2 2 ≠ 0 ⇒ D = {x, y ) z ≤x 2 + y 2 且 x 2 + y 2≠ 02. 求下列多元函数的极限::(1) lim ln( x + e y )x →1 x 2 + y 2y →0;解: limx →1y →0ln( x + e y ) x 2 + y 2 = ln(1+ 1)1= ln 2(2) lim 2 - xy + 4x →0xy y →0;1- 2 - xy + 4 2 t + 4 1 x →0xy t 1 4 y →01 / 28x →0 y →0x →0lim x +y = , m 不同时,极值也不同,所以极限不存在 。
(3) lim sin xyx →0x y →5;sin xy sin xy解: lim = 5lim = 5x →0 x 5xy →5y →01 - cos( x2 + y 2 ) (4) lim( x 2 + y 2 )e x 2 y 2;x →0 y →0解:Q 1 - cos( x 2 + y 2 ) = 2(sinx 2 + y 2 2)2 ,∴ l im x →0 y →01 - cos( x2 + y 2 ) 1= 2 ⋅ ⋅ 0 = 0( x 2 + y 2 )e x 2 y 2 2(5) lim( x 2 + y 2 ) xy 。
第六章 多元函数微分法及其应用部分考研真题及解答

第六章 多元函数微分法及其应用 6.1多元函数06.34) 设()1sin,,0,01arctan xy y yf x y x y xy xπ-=->>+,求 (Ⅰ) ()()lim ,y g x f x y →+∞=(Ⅱ) ()0lim x g x +→6.2偏导数08.3)已知(,)f x y = ( B )(A )(0,0)x f ',(0,0)y f '都存在 (B )(0,0)x f '不存在,(0,0)y f '存在 (C )(0,0)x f '不存在,(0,0)y f '不存在 (D )(0,0)x f ',(0,0)y f '都不存在6.3全微分02.1)考虑二元函数(,)f x y 的下面4条性质:①(,)f x y 在00(,)x y 处连续②(,)f x y 在00(,)x y 处两个偏导数连续③(,)f x y 在00(,)x y 处可微④(,)f x y 在00(,)x y 处两个偏导数存在.若用“P Q ⇒”表示可由性质P 推出Q ,则有 ( A )(A )②⇒③⇒①. (B )③⇒②⇒①. (C )③⇒④⇒①. (D )③⇒①⇒④. 07.2) 二元函数f (x , y )在点(0,0) 处可微的一个充分条件是 ( C ) (A )(,)(0,0)lim [(,)(0,0)]0x y f x y f →-=.(B) 0(,0)(0,0)lim0x f x f x →-=,且0(0,)(0,0)lim 0y f y f y→-=.(C)(,)lim0x y →=.(D) 0lim[(,0)(0,0)]0x x x f x f →''-=,且0lim[(0,)(0,0)]0y y y f y f →''-=.05.34) 设二元函数)1ln()1(y x xez yx +++=+,则=)0,1(dzdy e edx )2(2++ .06.34) 设函数()f u 可微,且()102f '=,则()224Z f x y =-在点(1,2)处的全微分()1,2dz=42dx dy -6.4多元复合函数求导法则05.12) 设函数⎰+-+-++=yx yx dt t y x y x y x u )()()(),(ψϕϕ, 其中函数ϕ具有二阶导数,ψ具有一阶导数,则必有 [ B ](A ) 2222yu x u ∂∂-=∂∂. (B ) 2222y u x u ∂∂=∂∂. (C) 222y uy x u ∂∂=∂∂∂. (D) 222x u y x u ∂∂=∂∂∂. 01.4)设(2),x z e f x y -=--且当0y =时,2,z x =则zx ∂=∂22(2)x y x x y e e ----+ 07.1) 设f (u ,v )为二元可微函数,(,)y x z f x y =,则zx∂∂=112ln .y x f yx f y y -''⋅+⋅07.234) 设f (u ,v )是二元可微函数,(,),y x z f x y =则z z xy x y ∂∂-=∂∂1222.y x f f x y''-+ 09.1)设函数(,)f u v 具有二阶连续偏导数,z=(,)f x xy 则2zx y∂∂∂=12222xf f xyf '''''++ 09.3)设()y x z x e =+,则(1,0)zx ∂∂=2ln 21+ 09农)设(,)f u v 为二元可微函数,(sin(),)xyZ f x y e =+,则zx∂∂=12cos()xy f x y yf e ''++ 01.1)设函数(,)f x y 在点(1,1处可微,且(1,1)(1,1)(1,1)1,2,3,f ff x y ∂∂===∂∂ ()(,(,))x f x f x x ϕ=.求31()x d x dx ϕ=(符合函数求导+求值(1)ϕ) 01.34)设(,,)u f x y z =有连续的一阶偏导数,又函数()y y x =及()z z x =分别由下列两式确定:2xye xy -=和0sin ,x zxt e dt t -=⎰求dudx03.34) 设f (u ,v )具有二阶连续偏导数,且满足12222=∂∂+∂∂v fu f ,又)](21,[),(22y x xy f y x g -=,求.2222yg x g ∂∂+∂∂【详解】v f x u f y x g ∂∂+∂∂=∂∂,.vf y u f x yg ∂∂-∂∂=∂∂ 故 v f vf x v u f xy u f y xg ∂∂+∂∂+∂∂∂+∂∂=∂∂2222222222,.2222222222v f vf y u v f xy u f x yg ∂∂-∂∂+∂∂∂-∂∂=∂∂ 所以 222222222222)()(vf y x u f y x yg x g ∂∂++∂∂+=∂∂+∂∂=.22y x + 04.2) 设22(,)xyz f x y e =-,其中f 具有连续二阶偏导数,求2,,z z zx y x y∂∂∂∂∂∂∂. 【详解】122xy z x f ye f x ∂''=+∂,122xy zy f xe f y∂''=-+∂, 21112222[(2)]xy xy xy zx f y f xe e f xye f x y∂''''''=⋅-+⋅++∂∂2122[(2)]xy xy ye f y f xe ''''+⋅-+⋅ 222111222242()(1)xy xy xy xyf x y e f xye f e xy f '''''''=-+-++++. 05.34)设f (u )具有二阶连续导数,且)()(),(y x yf x y f y x g +=,求.222222yg y x g x ∂∂-∂∂ 【详解】 由已知条件可得)()(2y x f x y f x y x g '+'-=∂∂,)(1)()(242322y xf y y x f x y x y f x y xg ''+''+'=∂∂, )()()(1yx f y x y x f x y f x y g '-+'=∂∂, )()()()(13222222y xf yx y x f y x y x f y x x y f x y g ''+'+'-''=∂∂,所以 222222y g y x g x ∂∂-∂∂=)()()(2222y x f y x y x f x y x y f x y ''+''+')()(222y x f y x x y f x y ''-''- =).(2xyf x y ' 09.2) 设(,,)z f x y x y xy =+-,其中f 具有2阶连续偏导数,求dz 与2z x y∂∂∂【解析】123123,z zf f yf f f xf x y∂∂''''''=++=-+∂∂ 所以123123()()z zdz dx dy f f yf dx f f xf dy x y∂∂''''''=+=+++-+∂∂21112132122233313233.1.(1)..1(1).[.1.(1).]zf f f x f f f x f y f f f x x y∂'''''''''''''''''''=+-+++-++++-+∂∂ 31122331323()()f f f xyf x y f x y f '''''''''''=+-++++- 10.2)设函数(,)f x y μ=具有二阶连续偏导数,且满足等式2222241250x x y y μμμ∂∂∂++=∂∂∂∂,确定a ,b 的值,使等式在变换x ay ξ=+,x by η=+下化简为20μξη∂=∂∂.6.5隐函数的求导公式05.1) 设有三元方程1ln =+-xz e y z xy ,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程 [ D ](A )只能确定一个具有连续偏导数的隐函数z=z(x ,y ).(B)可确定两个具有连续偏导数的隐函数x =x (y ,z)和z=z(x ,y ). (C)可确定两个具有连续偏导数的隐函数y =y (x ,z)和z=z(x ,y ). (D)可确定两个具有连续偏导数的隐函数x =x (y ,z)和y =y (x ,z).(考查隐函数存在定理,只需令F (x ,y ,z)=1ln -+-xz e y z xy , 分别求出三个偏导数y x z F F F ,,,再考虑在点(0,1,1)处哪个偏导数不为0,则可确定相应的隐函数.)10.12)设函数(,)z f x y =,由方程,0y z F x x ⎛⎫=⎪⎝⎭确定,其中F 为可微函数,且20F '≠,则z zxy x y∂∂+=∂∂ ( B ) (A )x (B )z (C )x - (D )z - 04.2) 设函数(,)z z x y =由方程232x z z e y -=+确定, 则3z zx y∂∂+=∂∂2.04.3) 设函数f (u , v )由关系式f [xg (y ) , y ] = x + g (y )确定,其中函数g (y )可微,且g (y ) ≠ 0,则)()(22v g v g vu f'-=∂∂∂.02.34)设函数(,,)u f x y z =有连续偏导数,且(,)z z x y =由方程x y zxe ye ze -=所确定,求du .08.3) 设(,)z z x y =是由方程()22x y z x y z ϕ+-=++所确定的函数,其中ϕ具有2阶导数且1ϕ'≠-时.(1)求dz (2)记()1,z z u x y x y x y ⎛⎫∂∂=- ⎪-∂∂⎝⎭,求u x ∂∂. 【详解】(I) ()()22xdx ydy dz x y z dx dy dz ϕ'+-=++⋅++()()()122dz x dx y dy ϕϕϕ'''⇒+=-++-+ ()()221x dx y dy dz ϕϕϕ''-++-+⇒='+()1ϕ'≠-(II) 由上一问可知22,11z x z yx y ϕϕϕϕ''∂-+∂-+==''∂+∂+, 所以 ()11221222,()()1111z z x y y x u x y x y x y x y x y ϕϕϕϕϕϕ''∂∂-+-+-+=-=-=⋅=''''-∂∂-++-++所以 ()()()()223322(1)2(1)2(12)2(12)11111x z u x x x x ϕϕϕϕϕϕϕϕϕϕϕϕ'-∂''+''-+'''''''∂++-++∂==-=-=-∂''''++++.6.6偏导数的应用01.1)函数(,)f x y 在点(0,0)附近有定义,且(0,0)3,(0,0)1,x y f f ''==则 ( C ) (A )(0,0)|3dz dx dy =+ (B )曲面(,)z f x y =在点(0,0,(0,0))f 的法向量为(3,1,1)(C )曲线(,)0z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的切向量为(1,0,3)(D )曲线(,)z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的切向量为(3,0,1)03.1) 已知函数f (x ,y )在点(0,0)的某个邻域内连续,且1)(),(lim2220,0=+-→→y x xyy x f y x ,则 (A) 点(0,0)不是f (x ,y )的极值点. (B) 点(0,0)是f (x ,y )的极大值点. (C) 点(0,0)是f (x ,y )的极小值点.(D) 根据所给条件无法判断点(0,0)是否为f (x ,y )的极值点. [ A ] 解: 由1)(),(lim2220,0=+-→→y x xyy x f y x 知,分子的极限必为零,从而有f(0,0)=0, 且 222)(),(y x xy y x f +≈- y x ,(充分小时),于是 .)()0,0(),(222y x xy f y x f ++≈-可见当y=x 且x 充分小时,04)0,0(),(42>+≈-x x f y x f ;而当y= -x 且x 充分小时,04)0,0(),(42<+-≈-x x f y x f . 故点(0,0)不是f(x,y)的极值点03.34) 设可微函数f (x ,y )在点),(00y x 取得极小值,则下列结论正确的是 [ A ] (A) ),(0y x f 在0y y =处的导数等于零. (B )),(0y x f 在0y y =处的导数大于零. (C) ),(0y x f 在0y y =处的导数小于零. (D) ),(0y x f 在0y y =处的导数不存在. 06.1234) 设(,)f x y 与(,)x y ϕ均为可微函数,且(,)0y x y ϕ'≠. 已知00(,)x y 是(,)f x y 在约束条件(,)0x y ϕ=下的一个极值点,下列选项正确的是 [ D ] (A )若00(,)0x f x y '=,则00(,)0y f x y '=. (B )若00(,)0x f x y '=,则00(,)0y f x y '≠. (C )若00(,)0x f x y '≠,则00(,)0y f x y '=. (D )若00(,)0x f x y '≠,则00(,)0y f x y '≠.09.2) 设函数(,)z f x y =的全微分为dz xdx ydy =+,则点(0,0)( D ) (A )不是(,)f x y 的连续点 (B )不是(,)f x y 的极值点 (C )是(,)f x y 的极大值点(D )是(,)f x y 的极小值点04.1) 设z =z (x ,y )是由0182106222=+--+-z yz y xy x 确定的函数,求),(y x z z =的极值点和极值.【详解】 因为 0182106222=+--+-z yz y xy x ,所以02262=∂∂-∂∂--x z z x z yy x , 0222206=∂∂-∂∂--+-yz z y z y z y x . 令 ⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂0,0y z xz 得⎩⎨⎧=-+-=-,0103,03z y x y x 故 ⎩⎨⎧==.,3y z y x将上式代入0182106222=+--+-z yz y xy x ,可得⎪⎩⎪⎨⎧===3,3,9z y x 或 ⎪⎩⎪⎨⎧-=-=-=.3,3,9z y x 由于 02)(22222222=∂∂-∂∂-∂∂-xzz x z x z y ,,02222622=∂∂∂-∂∂⋅∂∂-∂∂∂-∂∂--yx zz x z y z y x z y x z02)(22222022222=∂∂-∂∂-∂∂-∂∂-∂∂-yzz y z y z y y z y z ,所以 61)3,3,9(22=∂∂=x zA ,21)3,3,9(2-=∂∂∂=y x zB ,35)3,3,9(22=∂∂=yzC , 故03612>=-B AC ,又061>=A ,从而点(9,3)是z (x ,y )的极小值点,极小值为z (9,3)=3. 类似地,由61)3,3,9(22-=∂∂=---xzA ,21)3,3,9(2=∂∂∂=---y x zB ,35)3,3,9(22-=∂∂=---yzC ,可知03612>=-B AC ,又061<-=A ,从而点(-9, -3)是z (x ,y )的极大值点,极大值为 z (-9, -3)= -3.05.2) 已知函数z =f (x ,y ) 的全微分ydy xdx dz 22-=,并且f (1,1,)=2. 求f (x ,y )在椭圆域}14),{(22≤+=y x y x D 上的最大值和最小值.【详解】 由题设,知x x f 2=∂∂,y yf 2-=∂∂, 于是 )(),(2y C x y x f +=,且 y y C 2)(-=',从而 C y y C +-=2)(,再由f (1,1)=2,得 C =2, 故 .2),(22+-=y x y x f令0,0=∂∂=∂∂y fx f 得可能极值点为x =0,y =0. 且 2)0,0(22=∂∂=xf A ,0)0,0(2=∂∂∂=y x f B ,2)0,0(22-=∂∂=yfC ,042>=-=∆AC B ,所以点(0,0) 不是极值点,从而也非最值点.再考虑其在边界曲线1422=+y x 上的情形:令拉格朗日函数为 )14(),(),,(22-++=y x y x f y x F λλ, 解 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+='=+-=+∂∂='=+=+∂∂=',014,02122,0)1(2222y x F y y y y f F x x x fF y xλλλλλ得可能极值点4,2,0===λy x ;4,2,0=-==λy x ;1,0,1-===λy x ;.1,0,1-==-=λy x 代入f (x ,y )得,2)2,0(-=±f 3)0,1(=±f ,可见z =f (x ,y )在区域}14),{(22≤+=y x y x D 内的最大值为3,最小值为-2.05.4) 求f (x ,y )=222+-y x 在椭圆域}14),{(22≤+=y x y x D 上的最大值和最小值.(同上) 07.1)求函数2222(,)2f x y x y x y =+-在区域22{(,)4,0}D x y x y y =+≤≥上的最大值和最小值。
多元函数微分学及应用

2x3x 2 fdx x 3 h (xdy ydxxdy ydx习题课:多元函数求偏导,多元函数微分的应用多元复合函数、隐函数的求导法?(1)多元复合函数设二兀函数z f(u,v)在点(u o ,v o )处偏导数连续,二元函数 u u(x, y), v v(x, y)在点 (x o , y o )处偏导数连续,并且u o u(x o , y o ),v o v(x o ,y o ),则复合函数 z f (u(x, y), v(x, y))在点(x o ,y o )处可微,且dz — dx —z dyx y计算—f u f v zu f v 代人,xu x v xyu y v yzz f uf v fu f v dzdx dydxdyxy u x v xuyv yf u . uf v , v ,dx dydx dyu x yvxydu dv u v例 1 设 z x 3f xy,—,求一^,二。
x x y解:dz f 3x 2dx x 3df 3x 2 fdx x 3 f |d(xy) f 2 d — xf u o ,v ou x o , y of u o ,v ov x o ,y o(x o ,y o )uxvxf u o , v ou x o , y of u o ,v ov X o , y o(x o ,y o )uy vyz xz y多元函数微分形式的不变性:则将z 看成x, y 的函数,有f (u,v),u u(x, y), v v(x, y),均为连续可微,我们将 dz — dx — dyx y—du ~~ dv 叫做微分形式不变性。
u v例3已知函数y f (x)由方程ax by f x 2 y 2 , a,b 是常数,求导函数。
解:方程ax by f x 2 y 2 两边对x 求导,a b 业 f (x 2 y 2) 2x 2y 业dxdxdy 2xf (x 2 y 2) a dx b 2yf (x 2 y 2)两端分别关于x i 求偏导数得到,并解f, 可得到公式:一yF x x,y F y x, yX iXi例4设函数x x(z), y y(z)由方程组2 2 2 …x y z 12 o 2 2 dx 2y z 1 0确定,求0确定,求导之函数? y(x 1 ,...,x n ),对于方程F(X 1,...,X n ,y(X 1,...,X n ))3x 2fx 3yf i xyf 2 dx x 4 f 1 x 2f 2 dy由微分形式不变性,dz — dx x—dy y 3x f xyf ixyf 2 dx x 4 f 1 x 2 f 2 dy3x 2fx 3yf ixyf 2x 4 f 1 x 2 f 2例2已知y,求亠dydx解考虑二元函数y1 ,vx 应用推论得dy dxdu u dxy dv .vuv dx(In u)u v $ x1x(1 In x).⑵隐函数 若函数 x ,由方程 按隐函数定义有恒等式:F x, y x 0 x, y A F dx0确定, x, y x求导之函数?F x x, yF y x, y x y xF x x,y x oF y x, y x从这是可见:函数y x 可导有一个必要条件是,F y x,y 0.般来说,若函数y y x ,由方程F x, y将y 看作是x 1,...,x n 的函数y y xdx dy dz ,dzdz dz 2 2 2 ,2x2y — 2z解xyz 1dx dy 解方程得:2小2x 2yz 212x dz —4y dz 2zdxdydxdz = 1 4y 2y 2z 1 12yzdy 4xy2x 2x2z4xy8xzdz由此得到dX 3z, dy 2zdz x ' dz yu,v 是由方程uv 1 0 u (x, y)的x, y 的隐函数,在这两个等式两端分别关于0 cosv 」usinv y 1 sinv —u ucosv yx, y 求偏导数,得_v y v yv(x, y)cosv 』 xsinv 』 x usinv — x ucosv 」x得到u vsin uuv cosv得到ycosv,sin v,xxuy xu将这个结果代入前面的式子,得到z u vv uvcosv sin vx xxz u v与v u -vsin v cosvyyyu f (x, y, z,t)⑶ 隐函数函数u u(x,y)由方程 g(y, z,t) 0 确定,求一9x h(z,t) 0变量)? 3 ( 方程)=2(自变量); ),二中(z, t )解这个问题涉及到复合函数微分法与隐函数微分法x, y 是自变量,u,v 是中间变量(u,v 是x, y 的函数),先由z uv 得到zzuzv u vv u x u x v x x x zzuz v u vv uy u yv y y y例5已知函数z z x, y 由参数方程:x u cosvy usinv ,给定,试求—. x y zuv解:函数关系分析:5 ( 一函(u ),二自(x, yz , ,i h 上 g g t 0y ©h)t 丨(乙t )| h yz z 二阶偏导数:一阶导函数的偏导数 f f zf tyz yt yf hf hg u ft zz tyyyg h ghz t tzu f u =5exxy例6 z 2 z(x, y)由 x 2y 2 2 z a 决定,求解: 2x 2^z 0 2y 2zZ oxy x y2zzx z _y xJz yz 2z yz xy23x yzxzx f x,2x ,x,其中函数的二阶偏导数连续,求d 2g x dx 2X\ f(xy,—) y xf lff f5f25yf2fu f2fvf 2ff2fM1222212J121uvu vv u,f 二阶连续可微,求 xy, v2 2 -2xzf u f v1 £y f 1f xuxvxy2zzf 11 f2 2yxx xxyxu,v 为中间变量,都是以r 1 F F f11 「2u因为 v以x,y 为自变量的函数,所以将以上两式代入前式得 f 1uv1fnf 12y fn f 12xxxy f 2uv1七f21f22y f 21—怯xxxy2z 2 fo f1 f2 y T 11122 T22 .xy例9设z z(x, y)二阶连续可微,并且满足方程例10 设u(x, y)2C2,又ux2u 220, u(x,2x) x, u x(x,2x) x ,求yU xx(x,2x), U xy(x,2x) U yy(X,2X)解:u / c \(x,2x) x2 x ,两边对x求导,2z 2z2B -------x y2z若令U X y,试确定v x y 为何值时能变原方程为2z0.u,v看成中间变量,利用链式法则得z z u z vx u x v xz z u z vy u y v y2z z z 2 z2 x x u v 2 u2z z z2 2z2y y u v 2 u2z z zx y x u vz z——zu v u vz z——zu v u v2 2 2z z2- 2 —zu v v u v2 2z 2 z2 2u v v u2 2 2z z z2 2u u v v2B —z v2z _ ~~2= yA 2B 2B2 z~~2 vA 2B0.问题成为方程 A 2Bt Ct20有两不同实根,即要求令 B ■ B2AC, B B2AC ,即可。
高等数学第六章多元函数微分法及应用第三节 全微分

dz f x (1,2)dx f y (1,2)dy 2 0.04 0 0.02 0.08
(1.04)2.02 1.08
V 2rhr r 2h
其余部分是 (r)2 (h)2的高阶无穷小,所以
V 2rhr r 2h o( (r)2 (h)2 )
2020/2/13
线性主部
无穷小量
3
二 全微分的定义
(Definition of total differential)
全微分存在.
xy
例如,
f
(
x,
y)
x2 y2
0
x2 y2 0 .
x2 y2 0
在 点 (0 ,0 )处 f x (0 ,0 ) f y (0 ,0 ) 0
z [ f x (0,0) x f y (0,0) y]
x y , (x)2 (y)2
2020/2/13
14
记全微分为 dz z dx z dy. x y
通常我们把二元函数的全微分等于它的两个 偏微分之和这件事称为二元函数的微分符合叠加 原理.
叠加原理也适用于二元以上函数的情况. 全微分的定义可推广到三元及三元以上函数
du u dx u dy u dz. x y z
2020/2/13
20
证 令 x cos , y sin ,
则 lim xy sin 1
( x , y )(0,0)
x2 y2
lim 2 sin cos sin 1
多元函数微分学的应用

多元函数微分学的应用引言多元函数微分学是微积分的一个重要分支,通过研究多元函数的极限、连续性、可微性、偏导数、全微分以及二阶偏导数等概念和性质,为解决实际问题提供了强大的工具和方法。
本文将介绍多元函数微分学在实际应用中的一些案例和方法。
1. 函数的极限多元函数的极限是多元函数微分学的基础,它描述了函数在某一点处的趋近性。
在实际应用中,我们常常需要确定一个多元函数在某一点的极限,以便对问题进行分析和计算。
对于给定的多元函数f(x,y),如果当点(x,y)趋近于某一点(a,b)时,f(x,y)趋近于一个常数L,则称f(x,y)在点(a,b)处有极限,记为$\\lim_{(x, y) \\to (a, b)} f(x, y) = L$。
2. 函数的连续性函数的连续性是多元函数微分学的另一个重要概念。
一个多元函数f(x,y)在某一点(a,b)处连续,意味着在点(a,b)的任意一个邻域内,函数值和点(a,b)的距离趋近于零。
连续函数在实际应用中具有重要的意义,因为它们能够准确地描述函数的行为和性质。
3. 偏导数与全微分在实际问题中,我们常常需要计算多元函数的偏导数和全微分,以便分析函数的变化率和方向导数。
对于一个多元函数f(x,y),它的偏导数$\\frac{\\partialf}{\\partial x}$和$\\frac{\\partial f}{\\partial y}$分别表示函数在x方向和y方向上的变化率。
全微分df表示函数的微小变化量,它可以用偏导数表示为$df =\\frac{\\partial f}{\\partial x}dx + \\frac{\\partial f}{\\partial y}dy$。
4. 高阶偏导数在多元函数微分学中,我们还可以计算多元函数的高阶偏导数。
高阶偏导数描述了函数的高阶变化率和曲率性质。
例如,一个二阶偏导数$\\frac{\\partial^2 f}{\\partial x^2}$表示函数在x方向上的曲率,而一个二阶偏导数$\\frac{\\partial^2 f}{\\partial x \\partial y}$表示函数在x和y方向上的变化率的关系。
多元函数微分法及其应用

1、多元函数存在的条件存在是指P(x,y)以任何方式趋于P0(x0,y0)时,函数都接近于A,如果P(x,y)以某一特殊方式,例如沿着一条定直线或定曲线趋于P0(x0,y0)时,即使函数接近某一确定值,我们还不能由此断定函数存在。
反过来,如果当P(x,y)以不同方式趋于P0(x0,y0)时,函数趋于不同的值,那么就可以断定这函数的不存在。
例如函数:f(x,y)={0(xy)/(x^2+y^2)x^2+y^2≠02、多元函数的连续性定义设函数f(x,y)在开区域(或闭区域)D内有定义,P0(x0,y0)是D的内点或边界点且P0∈D,如果lim(x→x0,y→y0)f(x,y)=f(x0,y0)则称f(x,y)在点P0(x0,y0)连续。
性质(最大值和最小值定理)在有界闭区域D上的多元连续函数,在D上一定有最大值和最小值。
性质(介值定理)在有界闭区域D上的多元连续函数,如果在D 上取得两个不同的函数值,则它在D上取得介于这两个值之间的任何值至少一次。
3、多元函数的连续与可导如果一元函数在某点具有导数,则它在该点必定连续,但对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续。
这是因为各偏导数存在只能保证点P沿着平行于坐标轴的方向趋于P0时,函数值f(P)趋于f(P0),但不能保证点P按任何方式趋于P0时,函数值f(P)都趋于f(P0)。
4、多元函数可微的必要条件一元函数在某点的导数存在是微分存在的充分必要条件,但多元函数各偏导数存在只是全微分存在的必要条件而不是充分条件,即可微=>可偏导。
5、多元函数可微的充分条件定理(充分条件)如果函数z=f(x,y)的偏导数存在且在点(x,y)连续,则函数在该点可微分。
6.多元函数极值存在的必要、充分条件定理(必要条件)设函数z=f(x,y)在点(x0,y0)具有偏导数,且在点(x0,y0)处有极值,则它在该点的偏导数必为零。
定理(充分条件)设函数z=f(x,y)在点(x0,y0)的某邻域内连续且有一阶及二阶连续偏导数,又fx(x0,y0)=0,fy(x0,y0)=0,令fxx(x0,y0)=0=A,fxy(x0,y0)=B,fyy(x0,y0)=C,则f(x,y)在点(x0,y0)处是否取得极值的条件如下:(1)AC-B2>0时具有极值,且当A0时有极小值;(2)AC-B27、多元函数极值存在的解法(1)解方程组fx(x,y)=0,fy(x,y)=0求的一切实数解,即可求得一切驻点。
第六章多元函数微分学及其应用
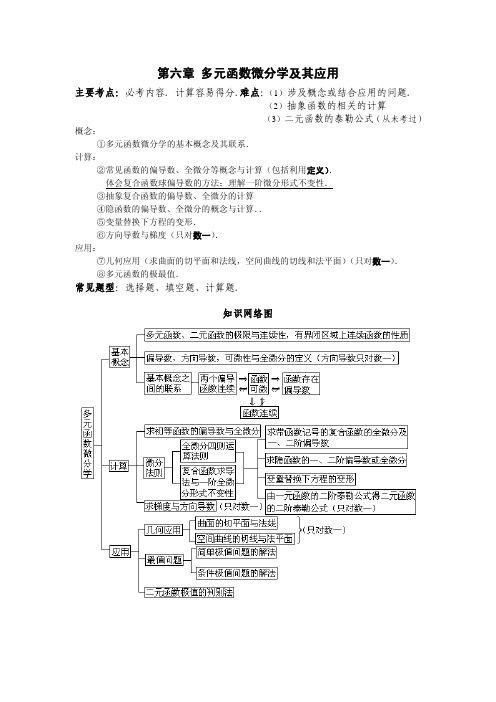
第六章 多元函数微分学及其应用主要考点:必考内容. 计算容易得分.难点:(1)涉及概念或结合应用的问题.(2)抽象函数的相关的计算(3)二元函数的泰勒公式(从未考过)概念:①多元函数微分学的基本概念及其联系.计算:②常见函数的偏导数、全微分等概念与计算(包括利用定义).体会复合函数球偏导数的方法;理解一阶微分形式不变性.③抽象复合函数的偏导数、全微分的计算④隐函数的偏导数、全微分的概念与计算..⑤变量替换下方程的变形.⑥方向导数与梯度(只对数一).应用:⑦几何应用(求曲面的切平面和法线,空间曲线的切线和法平面)(只对数一).⑧多元函数的极最值.常见题型:选择题、填空题、计算题.知识网络图一 多元函数微分学的基本概念及其联系几个概念之间的关系: ⇑⇐⇒⇓连续偏导数方向连续偏导数可微分方向导数存在注意:关注几个典型的例子!!!【例】(97)二元函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,),(22y x y x yx xyy x f 在点(0,0)处 ( ) P87(A )连续,偏导数存在, (B )连续,偏导数不存在,(C )不连续,偏导数存在, (D )不连续,偏导数不存在。
【例】(02)考虑二元函数的下面4条性质: P87(1)在点处连续; (2)在点处的两个偏导数连续; ),(y x f ),(00y x ),(y x f ),(00y x (3)在点处可微; (4)在点处的两个偏导数存在。
),(y x f ),(00y x ),(y x f ),(00y x 【例】(07)二元函数(,)f x y 在点(0,0)处可微的一个充分条件是 ( ) P153(A )()()()(),0,0lim,0,00x y f x y f →−=⎡⎤⎣⎦(B ) ()(),00,0lim0x f x f x →−=,且()()00,0,0lim0y f y f y →−= (C )()(,0,0,00,0lim 0x y f x f →−=(D ) 且()0lim ',0'(0,0)0,x x x f x f →−=⎡⎤⎣⎦()0lim ',0'(0,0)0,y y y f x f →⎡⎤−=⎣⎦ 二常见函数的偏导数、全微分等概念与计算1.利用定义【例】(08) 已知(,)f x y =,则 P153(A ),都存在 (B )不存在,存在 (0,0)x f ′(0,0)y f ′(0,0)x f ′(0,0)y f ′(C )不存在,不存在 (D ),都不存在 (0,0)x f ′(0,0)y f ′(0,0)x f ′(0,0)y f ′【例】32)sin(1)1(x xy x y z ++−=,求)1,2(x z ′。
多元函数微分学的应用

多元函数微分学的应用引言在数学中,多元函数微分学是研究多元函数的变化过程的一门学科。
通过微分学的方法,我们可以研究多元函数的局部性质、极值点和方向导数等重要概念。
多元函数微分学在科学、工程和经济等领域有着广泛的应用。
本文将介绍多元函数微分学的一些应用,并重点讨论最小二乘法和梯度下降法的实际应用。
最小二乘法最小二乘法是一种常用的数据拟合方法,它通过最小化实际观测值与理论模型之间的误差平方和,来寻找最佳的参数估计。
在多元函数微分学中,最小二乘法可以用于拟合多元线性回归模型。
假设我们有一组观测数据$(x_1, y_1), (x_2, y_2), \\ldots, (x_n, y_n)$,其中x x是自变量,x x是因变量。
我们的目标是找到一条直线 $y = a + b_1x_1 + b_2x_2 + \\ldots + b_mx_m$,使得所有观测数据到该直线的距离之和最小。
这可以转化为一个最小二乘问题。
在最小二乘法中,我们引入残差$r_i = y_i - (a + b_1x_{i1} +b_2x_{i2} + \\ldots + b_mx_{im})$,其中,x是截距,x x是斜率系数,x xx是第x组数据的第x个自变量的取值。
我们的目标是找到一组最优的x和x x,使得x x的平方和最小。
最小二乘法可以通过求解线性方程组来得到参数的估计值。
具体而言,我们可以通过计算矩阵的逆来得到参数的最小二乘解。
梯度下降法梯度下降法是一种常用的优化算法,它通过迭代的方式逐步更新参数,以达到函数的最小值。
在多元函数微分学中,梯度下降法可以用于求解多元函数的极值点。
假设我们要求解函数$f(x_1, x_2, \\ldots, x_n)$ 的极小值点,其中x x表示第x个自变量。
梯度下降法的基本思想是:从一个初始点开始,通过迭代更新参数,使得函数的值逐渐减小,直到达到最小值。
梯度下降法的更新规则如下:repeat until convergence {for i from 1 to n {theta_i := theta_i - alpha * (d/dtheta_i J(theta))}}其中,$J(\\theta)$ 是损失函数,$d/d\\theta_iJ(\\theta)$ 是损失函数对第x个参数的偏导数,$\\theta_i$ 是第x个参数的值,$\\alpha$ 是学习率。
第六章-多元函数微分学基础

z
V
O
y
V
V
V
x
图6-3 八卦限示意图
下面将平面上两点间的距离公式推广到空间(证明从略)
设M
1
(
x1
,
y1
,
z1
)和M
2
(
x2
,
y2
,
z2
)为空间两点,
则点M
1与M
间的
2
距离为
M1M 2 (x2 x1)2 ( y2 y1)2 (z2 z1)2 (6-1)
例1 在x轴上求一点P,使它到点A(3,2, 2)的距离为3.
0和G(x, y, z) 0是两个曲面方程,它们交线上的每一点的坐标
都同时满足上述两个曲面方程;反过来,曲时满足上述两个曲面
方程的点都在这条交线上.因此,联立方程组
z
F(x, y, z) 0
L
F(x, y, z) 0 G(x, y, z) 0
G(x, y, z) 0
叫做空间曲线L的一般方程
由两点距离公式知
M1M (x a1)2 ( y b1)2 (z c1)2 M 2M (x a2 )2 ( y b2 )2 (z c2 )2 又因为 M1M M 2M ,故知
(x a1)2 ( y b1)2 (z c1)2 (x a2 )2 ( y b2 )2 (z c2 )2
称上式为平面的一般方程,式中,A, B,C, D分别为变量x, y, z的系数; D为常数 Nhomakorabea.z
p3 c
例2 求过点P1(a, 0, 0), P2 (0,b, 0),
P3 (0, 0, c)的平面方程(其中a,b, c 0)
(见图6 5)
p1 a
高等数学(7)多元函数微分学 - 修正版.

仅考虑二维的情况,二维点可以从平面的任何方向 趋近于定点,对应于这些不同的趋近路线,函数取值 的变化可能千差万别。而在一维情况下,函数自变量 只有两个方向趋近于定点,易于观察和验证。
下面是可以按常规算法求极限的几道例题。
【例6-6】求 lim
xy .
( x, y)(0,0) 1 xy 1
【例6-7】求 lim sin( xy) .
第六章 多元函数微分学及其应用
假设已经搞懂了一元函数的微 分(包括极限、连续和导数概念) 理论,那么这一章的主要任务就 是弄清多元函数微分与一元函数 微分的联系与区别。
其中,从直线到平面的推广或 拓展,是最值得注意的。特别是 与极限概念相关的部分。
6.1多元函数的基本概念
1. N维空间中的点集 2. N维空间中点列的收敛 3. 多元函数的定义 4. 多元函数的极限 5. 多元函数的连续性
(iv)累次极限存在且相等,重极限也可能不存在。
例:当 (x, y) (0,0) 时,观察函数 f ( x, 其累次极限均为0,但重极限不存在。
y)
xy x2 y2
,
(v)两个相互关联的结论:
若重极限与累次极限都存在,则它们不能不相等;
反之,如累次极限存在且不相等,则重极限不能存在。
直观说明:如果两个累次极限不相等,那么从函数 的图像可以看出,在接近z轴的时候,图像一定有 断裂(或上下撕裂)的现象,重极限不可能存在。
满足李普希斯条件。证明该函数是连续的。
讨论:如果二元函数关于每个单个变量是连续函数, 是否可以认为这个函数是连续的二元函数?
xy
f
( x,
y)
x2
y2
0
( x2 y2 0); ( x2 y2=0).
第六单元 多元函数微分学

(应用题) 2)求 曲 面 z xy 在 点 (1, 2 , 2 ) 处 的 切 平 面 方 程 .
解
1)点 (1, 1, 1) 处 t 1, x t 1, y t 2 t , z t 3 t ,
' ' ' 2
当 t 1时 , x t 1, y t 2 , z t 3, 切 线 方 向 为 (1, 2 , 3 )
lim
f ( x0 x , y 0 ) f ( x0 , y 0 ) x
x 0
f x ( x , y ) lim
f ( x h, y ) f ( x, y ) h
h 0
2 z z z z f xx ( x , y ), f yy ( x , y ), 2 2 x x x y y y
y x
z.
证
1)
z x
f (
'
y x
)(
y x
2
)
y x
2
f (
'
y x
),
z y
f (
'
)(
1 x
)
1 x
f (
'
y x
),
x
z x
y
z y
xy x
2
f (
'
y x
)
y x
f (
'
y x
) 0.
16
z x
z x F ' 2
y z
11
3
3) 1 2 2 4
n1 {1, 2, 1}, n 2 {2, 4, 2} 2 n1 , n1 与 n 2 平 行 , 而 1 -1 3 6 ,所以两平面不重合.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( x, y ) ≠ (0,0) ( x, y ) = (0,0)
在点 (0, 0) 处(
)
P87
(B)连续,偏导数不存在, (D)不连续,偏导数不存在。 P87
(1) f ( x, y ) 在点 ( x0 , y 0 ) 处连续; (2) f ( x, y ) 在点 ( x0 , y 0 ) 处的两个偏导数连续; (3) f ( x, y ) 在点 ( x0 , y 0 ) 处可微; (4) f ( x, y ) 在点 ( x0 , y 0 ) 处的两个偏导数存在。 【例】(07)二元函数 f ( x, y ) 在点(0,0)处可微的一个充分条件是 (A)
∂f ∂f du + dv . ∂u ∂v
∂2 z x 1 在 ( 2, ) 点的值__________ 【例】(94) 设 z = e sin ,求 y ∂x∂y π
−x
三 抽象复合函数的偏导数、全微分的计算
几种基本情形: 【例】 (05)设函数 u ( x, y ) = ϕ ( x + y ) + ϕ ( x − y ) + 具有一阶导数,则必有
x y
y x
∂2z 求 。 ∂x∂y
其他方式的考察: 【例】(07)设 f (u , v ) 是二元可微函数, z = f ( , ) ,则 x
y x x y
∂z ∂z − y = _____ . ∂x ∂y
P154
【例】(09) z = f ( x + y , x − y , xy ) ,其中 f 具有 2 阶连续偏导数,求 dz 与
2 2 2
。 P96
【例】 (93)由曲线 ⎨
⎧3x 2 + 2 y 2 = 12 绕 y 轴旋转一周得到的旋转面在点 (0, 3 , 2 ) 处的指 ⎩z = 0
。
向外侧的单位法向量为 【例】 (97)设直线 l:⎨
⎧x + y + b = 0 2 2 在平面 π 上,而平面 π 与曲面 z = x + y 相切 ⎩ x + ay − z − 3 = 0
xz
= 1 ,根据隐函数存在定理,存在点(0,1,1)
( ) P88
2.计算(包括方程组的情形! )
' 【例】 ( 10 )设函数 z ( x, y ) 由方程 F ( , ) = 0 确定,其中 F 为可微函数,且 F2 ≠ 0 ,则
y z x x
x
∂z ∂z + y =( ∂x ∂y
(A)
) (B) z
P97 【例】
于点 (1, -2, 5) , 求 a, b 之值。 (01)设函数 f ( x, y ) 在点(0,0)附近有定义,且 f x′ (0,0) = 3, (A) dz
∂2 z ∂x∂y
P154
【例】 (01) 设函数 z = f ( x, y ) 在点 (1, 1) 处可微, 且 f (1,1) = 1 ,
,1)
= 3,
P89
ϕ ( x ) = f ( x, f ( x, x )) ,求
d 3 ϕ ( x) dx
x =1
x =0
.
【例】(08)设 z = z ( x, y ) 是由方程 x + y − z = ϕ ( x + y + z ) 所确定的函数,其中 ϕ 具有 2 阶导数且 ϕ ′ ≠ −1 时. (1)求 dz (2)记 u ( x, y ) =
1 ⎛ ∂z ∂z ⎞ ∂u . P154 ⎜ − ⎟ ,求 x − y ⎝ ∂x ∂y ⎠ ∂x
∫
x+ y
x− y
ψ (t )dt ,其中 ϕ 具有二阶导数,ψ
( )P88
∂ 2u ∂ 2u (A) 2 = − 2 , ∂x ∂y
∂ 2u ∂ 2u ∂ 2u ∂ 2u (B) 2 = , (C) = , ∂x∂y ∂y 2 ∂x ∂y 2
y x
∂ 2u ∂ 2u = (D) ∂x∂y ∂x 2
。
四 隐函数的偏导数、全微分的概念与计算
1.隐函数存在定理及概念的理解
【例】 (05)设有三元方程 xy − z ln y + e 的一个领域,在此领域内该方程 (A)只能确定一个具有连续偏导数的隐函数 z = z ( x, y ) 。 (B)可确定两个具有连续偏导数的隐函数 y = y ( x, z ) 和 z = z ( x, y ) 。 (C)可确定两个具有连续偏导数的隐函数 x = x ( y , z ) 和 z = z ( x, y ) 。 (D)可确定两个具有连续偏导数的隐函数 y = y ( x, z ) 和 x = x ( y , z ) 。
第六章 多元函数微分学及其应用
主要考点:必考内容. 计算容易得分.难点: (1)涉及概念或结合应用的问题. (2)抽象函数的相关的计算 (3)二元函数的泰勒公式(从未考过)
概念: ①多元函数微分学的基本概念及其联系. 计算: ②常见函数的偏导数、全微分等概念与计算(包括利用定义) . 体会复合函数球偏导数的方法;理解一阶微分形式不变性. ③抽象复合函数的偏导数、全微分的计算 ④隐函数的偏导数、全微分的概念与计算. . ⑤变量替换下方程的变形. ⑥方向导数与梯度(只对数一) . 应用: ⑦几何应用(求曲面的切平面和法线,空间曲线的切线和法平面) (只对数一) . ⑧多元函数的极最值.
x
【例】 (97) 设函数 f (u ) 具有二阶连续导数, 而 z = f (e sin y ) 满足方程 求 f (u )
∂2z ∂2z + = e2x z , ∂x 2 ∂y 2
P90
−2 x
(04)设 f (u , v ) 具有连续偏导数,且满足 f u′ (u , v ) + f v′ (u , v) = uv ,求 y ( x) = e 所满足的一阶微分方程,并求其通解。 【例】 (96)设变换 ⎨ 数a。 (10)设函数 μ = f ( x, y ) 具有二阶连续偏导数,且满足等式 4
三种方法! (C)
P155 (D) − z
y −1
x
−x
【例】 (07)已知函数 f ( a ) 具有二阶导数, 且 f '(0) =1, 函数 y = y ( x ) 由方程 y − xe 确定.设 z = f (ln y − sin x ), 求
=1所
P154
dz dx
2
x =0
,
2
d 2z dx 2
P153
【例】(07) 设 f (u , v ) 为二元可微函数, z = f ( x , y ) ,则
∂z = ∂x
【例】 (09) 设函数 f ( u, v ) 具有二阶连续 偏导数,z = f ( x, xy ) , 则 ..
∂2 z = ∂x∂y
P154
【例】(01)设 z = f ( xy , ) + g ( ) ,其中函数 f 具有二阶连续可导, g 具有二阶连续导数,
2.偏导数与全微分的计算 ∂z ⎛ y ⎞y 【例】(08) 已知 z = ⎜ ⎟ ,则 = _______ ∂x (1,2) ⎝x⎠
【例】(09)设 z = ( x + e ) ,则
y x
x
P153
∂z ∂x
=____________
(1,0)
P153
注意: (1)体会复合函数求偏导数的方法! ! ! (2)一阶微分形式不变性: z = f (u, v ) 可微,则 dz = (3)混合偏导数连续时与求导过程无关。
1.利用定义
【例】(08) 已知 f ( x, y ) = e
x2 + y 4
,则
P153 (B) f x′ (0, 0) 不存在, f y′ (0, 0) 存在 (D) f x′ (0, 0) , f y′ (0, 0) 都不存在 P88
(A) f x′ (0, 0) , f y′ (0, 0) 都存在 (C) f x′ (0, 0) 不存在, f y′ (0, 0) 不存在
常见题型:选择题、填空题、计算题. 知识网络图
一 多元函数微分学的基本概念及其联系
连续 ⇑ 偏导数 ⇐ ⇒ 方向连续偏导数 可微分 ⇓ 方向导数存在
几个概念之间的关系:
注意:关注几个典型的例子!!!
⎧ xy , ⎪ 2 2 【例】 (97) 二元函数 f ( x, y ) = ⎨ x + y ⎪0, ⎩
(C)
( x , y )→( 0,0 )
lim
⎡ f ' y ( x, 0 ) − f ' y (0, 0) ⎤ f 'x ( x, 0 ) − f 'x (0, 0) ⎤ (D) lim ⎡ ⎦ = 0, 且 lim ⎦ = 0, x →0 ⎣ y →0 ⎣
二 常见函数的偏导数、全微分等概念与计算
y
)P154
(A)i. (B)-i. (C)j. (D)-j. 注意: (1)方向导数公式中方向 l 应单位化; 方向 l 可能需计算如曲面的法向量、切线的切向量等 (2)方向导数与梯度的关系:在梯度方向,方向导数取最大值。
七 几何应用(只对数一) (与空解几结合)
1.空间曲线的切线与法平面
【例】 (92)在曲线 x = t , y = −t , z = t 的所有切线中,与平面 x + 2 y + z = 4 平行的切
【例】 (99)设 y = y ( x), z = z ( x) 是由方程 z = xf ( x + y ) 和 F ( x, y , z ) = 0 所确定的函数, 其中 f 和 F 分别具有一阶连续导数和一阶连续偏导数,求
