动力学方程 拉格朗日方程
第十七章 动力学普遍方程

系统的总虚功为 ( Fi FNi FIi ) δ ri 0 利用理想约束条件
得到
i Ii i i
F
i
Ni
δ ri 0
(i 1, 2, , n)
(F F )δ r 0
(i 1, 2, , n)
—— 达朗贝尔-拉格朗日方程
动力学普遍方程的直角坐标形式
(F
i
ix
mi xi ) δxi (Fiy mi yi ) δyi (Fiz mi zi ) δzi 0 i 1, 2, , n
动力学普遍方程的意义和应用
动力学普遍方程是将达朗伯原理和虚位移原理 而得到的,可用来求解质点系的动力学问题。
广义坐标和广义力
由n个质点所 组成的质点系 质点位置坐标 广义坐标 主 动 力
F1 , F2 , , Fn
x1 , y1 , z1 , x2 , y2 , z2 , q1 , q2 , , qN
N 3n S
, xn , yn , zn ,
第i个质点的位矢 虚位移
ri ri (q1 , q2 , , qN )
三、拉格朗日方程
d T T Qk= ( )- k dt q qk
对于主动力为有势力的情况,拉格朗日方程可改 写为:
d L L ( )- =0 k dt q qk
式中:
L=T-V
L称为拉格朗日函数,或动势。
本课件的部分动画来源于西工大的媒 体素材库,在此表示衷心的感谢。部分动 画与图片来源于互联网,版权不明,希望 版权所有人见到后与制作人员联系,我们 表示感谢。
第十七章 动力学普遍方程 和拉格朗日方程
一、动力学普遍方程 二、广义坐标和广义力 三、拉格朗日方程
理论力学 第3章 拉格朗日方程

记
3.1 拉格朗日方程
拉格朗日关系
3.1 拉格朗日方程
由拉格朗日关系
又
3.1 拉格朗日方程
3.1 拉格朗日方程
3.1 拉格朗日方程
(1)动能的显式: 直角坐标 平面极坐标 柱坐标 球坐标
ቤተ መጻሕፍቲ ባይዱ
1 2 T mi r i i 1 2
n
单个质点
x, y , z
r ,
, , z
3.1 拉格朗日方程
[思考2] 滑块作简谐运动
自由度 s 1 ,广义坐标为 :
X x0 cos t l sin
X l cos
Y l cos Y l sin 约束力 T T sin i T cos j
约束力的虚功
3.2 运动积分 诺特定理
3.2 运动积分 诺特定理
讨论:质点在有心力场中的动能和势能
1 2 2 r 2 T m r 2
k 2m V r
2 1 k m 2 2 2 r L T V m r 2 r
广义坐标:r,
L 0
对应一个循环积分:
3.1 拉格朗日方程
(2)系统势能:(以弹簧原长为弹性势能零点,滑块A所在 平面为重力势能零点)
1 2 V kx m2 gl cos 2
(3)拉格朗日函数:
L T V 1 1 1 2 2 2 2 m 2 l m 2 xl cos kx m 2 gl cos ( m1 m 2 ) x 2 2 2
r Fi i q
n
3.1 拉格朗日方程
3.1 拉格朗日方程
动力学普遍方程及拉格朗日方程

O1
x1
δα
l α α l
A
− FIA ⋅ δxA + FIB ⋅ δxB + m1g ⋅ δyA + m1g ⋅ δyB + m2 g ⋅ δyC = 0
根据几何关系,有 根据几何关系,
ωB
δrC
δrB FIB
l m1g
xA = −lsinα yA = lcosα xB = lsinα yB = lcosα yC = 2lcosα
由动力学普遍方程, 由动力学普遍方程,得
∑F ⋅ δr −∑m a ⋅ δr
i =1 i i i =1 i i
n j j
N
N
i
=0
∑F ⋅ δr = ∑Q δ q
i =1 i i j =1
N
Q j ——广义力
n N ∂ri ∂r && ⋅ ∑ δ qj = ∑(∑mi && ⋅ i )δ qj ri ∑miai ⋅ δr i = ∑miri j=1 ∂qj ∂qj i =1 j =1 i =1 i =1
MI2 = J2 α2
J2 = 1 m2 R2 2
α
m2 g
B
x
m1g
ar = Rα2
m2 gsinα ⋅ Rδϕ + FI2ecosα ⋅ Rδϕ − FI2r ⋅ Rδϕ-J2α2 ⋅ δϕ = 0
1 3 sinα ⋅ + (a1cosα − ar ) = 0 g 2
解:4、应用动力学普遍方程 令: δ x ≠ 0,δ ϕ = 0
i i i i i
(i = 1,2, ⋅⋅⋅, N)
动力学普遍方程的直角坐标形式
∑[(F
动力学-拉格朗日方程

§16-1 以广义坐标表示的 质点系平衡条件
不稳定平衡 12
第 十六章 拉格朗日方程
▪ 保守系统平衡的稳定性
§16-1 以广义坐标表示的 质点系平衡条件
不稳定平衡
13
第 十六章 拉格朗日方程
▪ 保守系统平衡的稳定性
§16-1 以广义坐标表示的 质点系平衡条件
随遇平衡 14
其中,令 qk 0, q j 0
则
WF Qkqk
( j 1, 2, , N, j k)
Qk
WF qk
3.
对于保守系统 处于平衡状态
Qk
V qk
0
(k 1,2,, N )
例题
第十六章 拉格朗日方程
例 题 16-1
两均质杆,均长2l,均重P,用铰链连接,跨过半径为r 的光滑圆柱体上,并位于同一铅直面内,求杆的平衡位置。
,
Fyi
V yi
,
Fzi
V zi
WF (Fxixi Fyiyi Fzizi )
V ( xi
xi
V yi
yi
V zi
zi )
V 0
V 0
在势力场中,具有理想约束的质点系的平衡条件是
系统势能在平衡位置处一阶变分为零
6
第 十六章 拉格朗日方程
§16-1 以广义坐标表示的 质点系平衡条件
改写为:l tan3 r tan2 r 0
由此解出θ。
例 题 16-1
18
例题
第十六章 拉格朗日方程
例 题 16-2
图示系统,A重2P,B重P。不计滑轮重及O、E处摩擦, 求平衡时C的重量W及A与水平面之间的摩擦系数 f。
解:系统具有2自由度。 以sA、 sB为广义坐标 (1)当sA改变δsA而δsB=0( B不动),此时δsC= δsA /2
动力学方程 拉格朗日方程

dt
dt
dt
s
1
V q
q
dV dt
dT dV 0 dt dt
T+V=E=恒量
这就是力学体系的能量积分。
可见拉格朗日方程具有能量积分的条件是:受稳定的理想约束的完整系 ,只受保守力而且T、V中不显含t,这时体系的能量守恒。
(3)对于完整的保守的力学体系,受不稳定约束而且T、V 中不显含t情况的分析。
d dt
n i 1
mi
ri
ri q
n i1
mi
ri
ri q
d dt
n i 1
q
1 2
mi
ri
2
n i 1
q
1 2
mi ri 2
令
T
n i 1
1 2
mi ri 2
显然 T 是体系的动能,则有
P
d dt
T
q
T q
即
d dt
T q
T q
Q ,
1, 2, , s
y
Fy
j'
rP
解 方法一:
o
从定义式计算。 将定义式用于极坐标,因 粒子数 n=1,则
Qr
F
r r
r
Q F
F
i'
Fx
x
又因 x= r cos,y=r sin
则
x cos , y sin
r
Qr
F
r r
r
Fx
x r
Fy
y r
y
Fy
j'
F
i'
r P Fx
o
Q= r F(是力矩)
F
r o
拉格朗日动力学方程

拉格朗日动力学方程
拉格朗日动力学(1agrangianDynamics)是一种以势能作为基础的动力学理论,由拉格朗日在18th世纪末提出。
它利用势能和动能,即动量及系统内部动量来描述物理系统的运动。
动力学方程中表达的是系统在特定时刻的状态,它是以物体的位置和速度为变量描述物理系统状态的。
拉格朗日动力学方程是物理系统总动量保守定理的衍生形式,它表示了系统动量的变化规律,是阐明动量守恒原理的有力证明。
它可以表达为:
d1∕dt=F o
其中,d1/dt表示系统的总动量,F表示系统的外力。
拉格朗日动力学方程是物理系统之间相互作用以及物体受到外力影响的动力学的表征。
它的推导不仅展示了动量的守恒,而且它的结构可以作为理解物理系统状态及物体运动的抽象框架。
动力学普遍方程及拉格朗日方程

动力学普遍方程的直角坐标形式
[(F
i
ix
mi xi ) δxi (Fiy mi yi ) δyi (Fiz mi zi ) δzi ] 0 i 1, 2, , N
动力学普遍方程 适用于具有理想约束或双面约束的系统。 动力学普遍方程 既适用于具有定常约束的系统,也适用于 具有非定常约束的系统。 动力学普遍方程 既适用于具有完整约束的系统,也适用于 具有非完整约束的系统。 动力学普遍方程 既适用于具有有势力的系统,也适用于具有 无势力的系统。
(m1 m2 ) g m1lcos
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
y
A ae C2
D
2 ar B
求:1、三棱柱后退的加速度a1; OC 2、圆轮质心C2相对于三棱 柱加速度ar。 解:1、分析运动 三棱柱作平动,加速度为 a1。 圆轮作平面运动,质心的牵连 加速度为ae= a1 ;质心的相对加 速度为ar;圆轮的角加速度为2。
N N ri ri d d ri mi ri mi (ri ) mi ri ( ) q j i 1 dt q j dt q j i 1 i 1 N
N r ri d i r r ( ) mi ri d ri i mi i ri dt q q i 1 i 1 j j dt q q q N
将虚位移原理和达朗贝尔原理综合应用于动力学
★ 建立分析力学的新体系 拉格朗日力学
动力学普遍方程
考察由N个质点的、具有理想约束的系统。根据 达朗贝尔原理,有
Fi FRi mi ai 0
理论力学-拉格朗日方程

d dt
(
L qr
)
L qr
0
24
积分得:
L qr
C
(常数)
(rk)
循环积分
因L = T - U,而U中不显含 qr ,故上式可写成
L qr
qr
(T
U
)
T qr
Pr
C
(常数)
Pr称为广义动量,因此循环积分也可称为系统的广义动量积分。 保守系统对应于循环坐标的广义动量守恒。
能量积分和循环积分都是由保守系统拉格朗日方程积分一 次得到的,它们都是比拉格朗日方程低一阶的微分方程。
12 g
W ( ) M
Q
W (
)
M
T
1 6
2P
9Q g
(R r)2
;
d dt
T
1 6
2P
9Q g
(
R
r)
2
;
T
0
15
代入拉氏方程:
1 2P 9Q (R r)2 0 M
6g
6M
g
(2P 9Q)(R r)2
积分,得:
3M (2 P 9Q )(R r ) 2
gt
2
C1t
C2
代入初始条件,t =0 时, 0 0 , 0 0 得 C1 C2 0
故:
3M
gt 2
(2P9Q)( Rr)2
16
[例2] 与刚度为k 的弹簧相连的滑块A,质量为m1,可在光 滑水平面上滑动。滑块A上又连一单摆,摆长l , 摆锤质量为 m2 ,试列出该系统的运动微分方程。
解:将弹簧力计入主 动力,则系统成为具 有完整、理想约束的 二自由度系统。保守
系统。取x , 为广义
分析力学动力学普遍方程和拉格朗日方程实用课件

圆柱的角速度为 O (设圆柱o的半径为r)
m(l
R )2,
d dt
L
2mR (l
R) 2
m(l
R ) 2
L mR(l R) 2 mg (l R)sin
已求得
d dt
L
2mR (l
R) 2
m(l
R ) 2
L mR(l R) 2 mg (l R)sin
将式上式代入保守系统的拉氏方程
d dt
L
L
0
得摆的运动微分方程
(l R) R 2 g sin 0
M v
P
R'=-R=- ma
此力是摆锤被迫作非惯性运动时产生的“反作用力”, 称为惯性力。
结论:质点在作非惯性运动的任意瞬时,对于施力于它的物 体会作用一个惯性力,该力的大小等于其质量与加速度的乘 积,方向与其加速度方向相反。
若用Fg表示惯性力,则有 Fg =- ma
说明: 1.此力是不是真实的力! 2.此力作用于施力给质点的物体上! 3.此力又称为牛顿惯性力!
拉格朗日
1736 — 1813,法籍 意大利人,数学家、 力学家、天文学家, 十九岁成为数学教 授,与欧拉共同创 立变分法,是十八 世纪继欧拉后伟大 的数学家。
设质点系由n个质点组成,具有s个完整理想约束,则有 N=3n-s个自由度(广义坐标)。
用q1,q2,…qN表示系统的广义坐标,第i个质点质量为mi, 矢径为ri。则
i 1
n
或 (Fi miai ) δri 0 i 1
动力学普遍方程
表明:在理想约束条件下,在任意瞬时,作用于质点系上 的主动力和惯性力在质点系的任意虚位移上所做虚功之和 等于零。
若 Fi X ii Yi j Zik, ai xii yi j zik,
动力学普遍方程及拉格朗日方程讲解

★ 建立分析力学的新体系 拉格朗日力学
动力学普遍方程
考察由N个质点的、具有理想约束的系统。根据 达朗贝尔原理,有
Fi FRi mi ai 0
主动力
(i 1, 2, , N )
惯性力
令系统有任意一组虚位移
δri
系统的总虚功为
(i 1,2, , N )
2 aC g sin 3
0
mgsin x - FIR x M IC
x
R
例 题 2
离心调速器
已知: m1-球A、B 的质量; m2-重锤C 的质量; l-杆件的长度; - O1 y1轴的旋转角速度。 求: - 的关系。
O1 l l FIA m1g l
C
如果将位矢对任意一个广义坐标 qj 求偏导数,再对时间求 导数,则得到
d ri dt q j
2 N 2 ri ri k q q t k 1 q j qk j
ri q j
=
d ri dt q j
第二个拉格朗日关系式
N
ri d T mi ri q j dt i 1 q j
N
T q j
Q j mi ri
i 1
N
ri 0 ( j 1, 2, q j
, n)
ri d T mi ri q j dt i 1 q j
a1
C1
x
解:2、施加惯性力
y
A x OC a1
FI 2 r
MI2
D C2
m2 g FI 2 e
FI1 m1a1
第一类拉格朗日动力学方程

第一类拉格朗日动力学方程第一类拉格朗日动力学方程是描述质点在保守力场中运动的动力学方程,也称为拉格朗日方程。
它可以通过最小作用量原理导出。
设一个质点在平面上的位置用广义坐标q和q'表示,其中q为广义坐标,q'为广义速度。
质点在这个保守力场中的运动可以由拉格朗日函数L(q,q')描述,其表达式为:L(q,q') = T(q,q') - V(q)其中,T(q,q')为质点的动能,V(q)为保守力场中的势能。
根据最小作用量原理,质点的运动路径满足满足驻定作用量条件,即质点在一个时间间隔内的作用量的变分为零。
作用量S的表达式为:S = ∫(t1,t2) L(q,q') dt其中t1和t2为起始和终止时间。
为了推导第一类拉格朗日动力学方程,我们采用变分法。
首先,在时间间隔[t1,t2]上作用量的变分为:δS = ∫(t1,t2) (δL(q,q')/δq)δq dt + ∫(t1,t2) (δL(q,q')/δq')δq' dt使用分部积分法将第二项中的变分δq'转化为对广义坐标q的变分,得到:δS = ∫(t1,t2) [(∂L/∂q - d/dt(∂L/∂q'))δq] dt + [∂L/∂q'δq]在t1到t2的两端值由于作用量的变分为零,所以第二项在起始和终止时间的两个端点为零,即:[∂L/∂q'δq]在t1到t2的两端值 = 0因此,驻定作用量条件可以写成:∫(t1,t2) [(∂L/∂q - d/dt(∂L/∂q'))δq] dt = 0由于δq的任意性,可以得出:∂L/∂q - d/dt(∂L/∂q') = 0这就是第一类拉格朗日动力学方程。
它描述了质点在保守力场中运动的规律,通过求解这个方程,我们可以得到质点的运动轨迹。
动力学-拉格朗日方程
n
n
n
(Fix miaix )xi (Fiy miaiy )yi (Fiz miaiz )zi 0
i 1
i 1
i 1
9
FIr
FI
FIe
MI
mg s
x
例:图示系统:地面光滑, 圆柱(半径为 r )作纯滚动,
求圆柱的角加速度 和滑块
的加速度 a。
Mg
解 :(1) 分析运动,并确定惯性力
应用虚位移原理:
若质点系所受的 约束为理想约束
n
FNi • ri 0
i 1
动力学普遍方程
n
W (Fi FNi FIi ) • ri 0 i 1
n
n
(Fi FIi ) •ri FNi •ri 0
i 1
i 1
n
(Fi FIi ) • ri 0 其中:FIi miai
i 1
yA 2Lsin xB 2l cos
aA yA 2L sin 2L cos2
xB 2l sin 2l cos2 aB
aCn l2 aCt l
FInC mC aCn , FItC mC aCt
M IC JC , M IO JO
mA mB m1, mC m,
11
rA
A
rCC
A
T M
135
M
mg
B
C
D
mg
mg
3
A
T M
mg
sB B
135
C
mg sc
M
D
mg
利用虚位移原理:取虚位移
由投影定理: sB 0
虚位移原理,虚功之和为零:
sc
L
王振发版分析力学第2章动力学普遍方程和拉格朗日方程

二、质点系的达朗伯原理
设质点系由n个质点组成, 第i个质点质量为mi,受力有主动力 Fi ,约束反力FNi ,加速度为ai ,假想地加上其惯性力Fgi=-miai ,则根据质点的达朗伯原理,Fi 、 FNi与Fgi应组成形式上的平衡 力系,即
Fi + FNi +Fgi=0 (i =1,2,…,n )
解得
a((22m m11m m22))rr22si2nJ g
(a) (b)
2. 拉格朗日方程
将动力学普遍方程用广义坐标表示,即可推导出第二类拉 格朗日方程。
m
j &x&j x j
m
j &y&j
Fyj
k i1
i
fi y j
m j &z&j
Fzj
N i1
ri qk
δqk
n
n
动力学普遍方程可写成
Fiδri miaiδri 0
其中
i1
i1
i n1miaiδri i n1mi r ikN 1qrikδqk
Nn
k1 i1
mi ri qrik
δqk
根据虚位移原理中广义力与广义虚位移的表示形式,有
n
N
Fi δri Qkδqk
设质点系由n个质点组成,第i个质点质量为mi,
受主动力Fi,约束反力FNi,加速度为ai,虚加上 M
Fgi
其惯性力Fgi=-miai
则根据达朗伯原理, Fi 、FNi 与Fgi, 应组成形式上的平衡力系,即
FNi
ai Fi
Fi + FNi +Fgi= 0
若质点系受理想约束作用,应用虚位移原理,有
拉格朗日方程式

拉格朗日方程式拉格朗日方程式________________________________拉格朗日方程式(Lagrange equation)是物理学中的一个重要概念,主要描述了摩擦力学系统中的动力学特性。
它也是物理学中一个很重要的数学工具,常用于解决简单和复杂力学系统中的力学问题。
它可以用来计算物体在受到外力作用时的动力学行为,从而对物体的运动进行分析和预测。
#### 一、拉格朗日方程式的定义拉格朗日方程式是一种数学方程,它可以用来描述物体在外力作用下的动力学行为。
它的基本形式是:\begin{equation}m\ddot x=F_{ext}-F_{int}\end{equation}其中,$x$是物体的位置向量,$m$是物体的质量,$F_{ext}$是物体受到的外力,$F_{int}$是物体内部受到的内力。
#### 二、拉格朗日方程式的应用拉格朗日方程式在物理学中有广泛的应用,常用于解决各种复杂的力学问题。
例如,在求解物体在受到外力作用时的运动轨迹、求解物体在受到外力作用时的运动规律等问题中,都可以使用拉格朗日方程式来解决。
此外,它还可以用来求解物体在受到外力作用时的运动轨迹、求解物体在受到外力作用时的能量变化、求解物体在受到外力作用时的内部应力等问题。
#### 三、拉格朗日方程式的推导在求解拉格朗日方程式之前,我们需要先了解一些基本概念。
例如,我们需要了解物体受到外力作用时所发生的力学过程,以及物体在这个过程中所受到的力和应力。
具体来说,我们需要了解物体在受到外力作用时所发生的力学过程,以及物体在这个过程中所受到的各种外力和内部应力。
然后,我们就可以使用牛顿定律和能量守恒定律来推导拉格朗日方程式。
依据牛顿定律,我们可以得到:\begin{equation}m\ddot x=F_{ext}-F_{int}\end{equation}而依据能量守恒定律,我们可以得到:\begin{equation}\frac{dK}{dt}+\frac{dU}{dt}=0\end{equation}其中,$K$是物体的动能,$U$是物体的位能。
动力学普遍方程和拉格朗日方程

由动力学普遍方程(达朗贝尔—拉格朗日原理):
n
(Fi miai ) δ ri 0
i1
n
i1
( Fi
miai )
k j1
ri q j
δqj
0
(23.7)
10
交换求和顺序
k j1
n i1
( Fi
miai )
ri q j
δqj
0
k
j1
n i1
( Fi
miai )
9
推导广义坐标的动力学普遍方程
设完整约束质点系由n个质点组成,系统的自由度为k,其
广义坐标为q1,q2,……,qk,
则各质点相对于定点O的矢径为
ri
ri
(q1,
q2
,,
qk
,t)
(i=1,2,…,n)
(23.5)
各质点的虚位移为
ri
k
ri
j1 q j
δqj
(i=1,2,…,n)
(23.6)
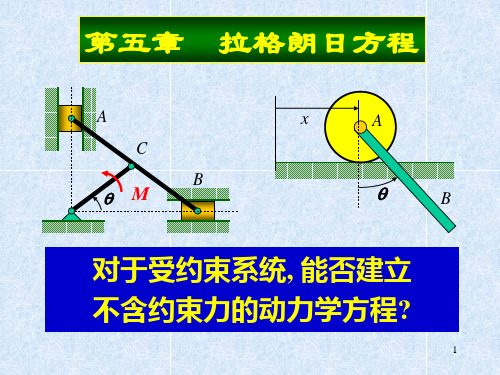
那么能否建立一种不含约束力的非自由质点系的动力学方 程呢?
将达朗贝尔原理和虚位移原理结合起来可以达到这一目的, 因为达朗贝尔原理给出了通过列写形式上的静力学平衡方程求 解质点系的动力学问题的方法,而虚位移原理又建立了不含约 束力的非自由质点系的平衡方程。
3
动力学普遍方程 (general equations of dynamics)
4
第23章 动力学普遍方程和 拉格朗日方程
(general equations of dynamics and lagrange equations)
§23.1 动力学普遍方程 (general equations of dynamics)
拉格朗日方程

方 程
T
1 2
m1 x 2
1 2
(1 2
m1R2 ) 2
1 2
m2 (x
R )2
系统的广义力为
Qx
W (x) x
(m1
m2 )gx k(x L0 )x x
(m1 m2 )g k(x L0 )
Q
W ( )
m2 gR
g
MI
PI
a
QI
Q
MI
PI
P
P
程
s
一、拉格朗日方程
设有n个知点组成的知点系,受完整的理想约束,具有N个自由度,其 位置
可由N个广义坐标 1.2
来确定。则有
拉 格
d ( T ) dt qk
T qk
Qk
(k 1,2,, N )
朗 日
式中
T
程。
1.2
k
x2
拉 格 朗
解:以系统为研究对象,系统具两个
自由度。选取 、 为广义坐标。
x1
x2
系统的动能为
x1 A
kR
B
日 方
T
1 2
m1x12
1 2
m2 x22
1 2
(1 2
m2
R
2
)(
x2 R
)2
1 2
m1x12
3 4
m2 x22
系统的广义力为
程
Qx1
W (1) x1
T
3 4
拉格朗日方程

定义:拉格朗日方程,因约瑟夫·路易斯·拉格朗日而命名,是拉格朗日力学的主要方程,可以用来描述物体的运动,特别适用于理论物理的研究。
拉格朗日方程的功能相等于牛顿力学中的牛顿第二定律。
拉格朗日方程:对于完整系统用广义坐标表示的动力方程,通常系指第二类拉格朗日方程,是法国数学家J.-L.拉格朗日首先导出的。
通常可写成:式中T为系统用各广义坐标qj和各广义速度q'j所表示的动能;Qj为对应于qj 的广义力;N(=3n-k)为这完整系统的自由度;n为系统的质点数;k为完整约束方程个数。
从虚位移原理可以得到受理想约束的质点系不含约束力的平衡方程,而动静法(达朗贝尔原理)则将列写平衡方程的静力学方法应用于建立质点系的动力学方程,将这两者结合起来,便可得到不含约束力的质点系动力学方程,这就是动力学普遍方程。
而拉格朗日方程则是动力学普遍方程在广义坐标下的具体表现形式。
拉格朗日方程可以用来建立不含约束力的动力学方程,也可以用来在给定系统运动规律的情况下求解作用在系统上的主动力。
如果要想求约束力,可以将拉格朗日方程与动静法或动量定理(或质心运动定理)联用。
通常,我们将牛顿定律及建立在此基础上的力学理论称为牛顿力学(也称矢量力学),将拉格朗日方程及建立在此基础上的理论称为拉格朗日力学。
拉格朗日力学通过位形空间描述力学系统的运动,它适合于研究受约束质点系的运动。
拉格朗日力学在解决微幅振动问题和刚体动力学的一些问题的过程中起了重要的作用。
拉格朗日插值公式(外文名Lagrange interpolation formula)指的是在节点上给出节点基函数,然后做基函数的线性组合,组合系数为节点函数值的一种插值多项式。
公式线性插值也叫两点插值,已知函数y = f(x)在给定互异点x0, x1上的值为y0= f(x0),y1= f(x1)线性插值就是构造一个一次多项式P1(x) = ax + b使它满足条件P1(x0) = y0P1(x1) = y1其几何解释就是一条直线,通过已知点A (x0, y0),B(x1, y1)。
物理学中的动力学方程解法

物理学中的动力学方程解法动力学方程是物理学研究中的重要内容,涉及到物质运动的规律与变化。
求解动力学方程是研究物理现象的关键,有多种解法,本文将从不同角度介绍动力学方程的求解方法。
拉格朗日方程法拉格朗日方程法是一种基于能量原理的方法,解决动力学方程问题时不涉及具体物理系统的结构和特征,只考虑给定系统的动力学特征。
一般来说,如果已知系统的拉格朗日函数,则可以通过拉格朗日方程求得系统的运动方程。
拉格朗日方程可以表示为:$$ \frac{d}{dt}\frac{\partial L}{\partial \dot x_i}-\frac{\partialL}{\partial x_i}=Q_i $$其中$L$是拉格朗日函数,$\dot x_i$是$x_i$的变化率,$Q_i$是广义力。
这个方程可以求解出系统的运动方程并且可以与多个粒子或者车体单元相关。
欧拉-拉格朗日方程法欧拉-拉格朗日方程法是一种基于欧拉方程的泛函分析方法,可以用于求解高阶动力学方程。
此方法将欧拉方程与拉格朗日方程相结合,将其转换为更一般和更简单的表达形式。
对于欧拉-拉格朗日方程,可以表示为:$$ \frac{\partial L}{\partial t}-\sum\frac{\partial}{\partialx_i}\frac{\partial L}{\partial (\partial x_i)}=\sum F_i^{\prime}\frac{\partial L}{\partial (\partial x_i)} $$其中,$L$是拉格朗日量,$t$表示时间,$x_i$是广义坐标,$\frac{\partial L}{\partial(\partial x_i)}$是拉格朗日函数中广义坐标的变化率,$F_i$是广义力。
哈密顿方程法哈密顿方程法是一种基于哈密顿函数的动力学方程求解方法,通过求解哈密顿函数的偏导数,可以得到物理系统的微分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则对任一个质点有
Fi iV
分量式为
i
i xi
yi
j zi
k
Fix
V xi
,
Fiy
V yi
,
Fiz
V zi
,
i 1, 2, , n
现在把广义力与势能函数连系起来
Q
n i 1
Fi
ri q
而广义力:
Q
n i 1
Fi
ri q
广义力可以是力,也可以是力矩等,视广义坐标的选择而 定。计算广义力的方法可以有两种:一种方法是从上定义式直 接计算,另一种方法是从主动力所作的虚功来计算。
1、从主动力所作的虚功来计算
W
n i 1
Fi
sn ri
ri q
q
0
令
P
n i 1
mi
ri
ri
q
Q
n i 1
Fi
ri q
(广义力)
s
则
(P Q )q 0
1
因各 q 互相独立,所以 P=Q
改写
Q
Fx
x
Fy
x
r(Fx sin Fy cos )
上式括号中的第一项为
Fx
在 j 方向的投影,第二项
是 Fy在 j 方向的投影。
所以两者之和就是 F 在 j
y
j '
Fy
rP o
方向的投影 F ,因此
F
i'
Fx
x
Q= r F(是力矩)
P
Q
n
mi
i 1
n Fi
i 1
ri
ri q
ri
q
P
n i 1
miri
ri
q
d dt
n i 1
mi
ri qri
n i 1
mi ri ddt
ri q
Fy
rP
Qr r Fx cos r Fy sin r
则
Qr
Wr r
Fx cos
Fy sin
Fr
F
i'
Fx
x
W
(F
Q
r )r 0
(Fx x Fy y)r0
o
y
j '
Fy
rP
F
五、循环积分与能量积分
拉格朗日方程是 s 个二阶常微分方程组,我们希望也像牛顿 力学一样 ,若能首先对微分方程组积分一次 ,找出某些初积分 ( 或叫第一积分 ),使我们对某些问题的求解能简便些 。在某 些情况下,部分的第部广义坐标和 广义速度(广义动量)及时间 t 的函数,即
三、广义动量与广义力的计算
对于单个质点来说,动能对某速度分量的导数是对应的动量分量
T
x
x
1 2
m(
2 x
2 y
2 z
)
mx
与此类比,可以定义广义动量 p 为
T q
p
注意:广义动量可以是线动量,也可以是角动量等等,
视广义坐标的选择而定。
§1.3 拉格朗日方程
为了得到广义坐标表示的完整力学系的动力学方程–––– 拉格朗日方程,需要先导出达朗伯-拉格朗日方程。
一、达朗伯-拉格朗日方程
设受完整约束的力学体系有n个质点,体系中每一个质点都
服从如下形式的牛顿运动定律,设第i个质点受主动力,受约束
反力,则
mi ri
Fi
Ri , i
解 : 设质点的质量为m,因为只有一个质点,故n=1, 自由质点只受有心力作用时,作平面曲线运动,
所以 s=2,取极坐标(r,)为广义坐标,则有
T
1 2
m 2
1 2
m(r2 r 22 )
V km r
L T V
1 m(r2 r22 ) km L(r, r,)
1,
2,
,
n
miri
mi
ri
Fi
Ri
0,
i
1, 2,
:称为达朗伯惯性力或称有效力
,
n
注意:这个达朗伯惯性力与力学中定义过的惯性力不是一个概念,
那里的惯性力是对某一非惯性系而言的,而上式中各质点的 并不相等,所以这里并不存在一个统一的非惯性系。
ri
以
2
r
可见 L 函数中不含 ,所以 是循环坐标,则
p
L
ri ri (q1, q2 , , qs , t)
则
ri
ri q1
q1
ri q2
q2
ri qs
qs
s
ri
1 q
q
代入达朗伯-拉格朗日方程
n
i 1
(
miri
Fi )
s a 1
则
x cos , y sin
r
r
Qr
F
r r
Fx
x r
Fy
y r
y
j '
Fy
F
i'
r P Fx
o
x
Fx cos Fy sin Fr
可见广义力的径向分量就是的径向分量,说明 Qr 是一个力。
另外 x r sin , x r cos
1 i1
Fi
ri
q
s
q Q
1
q
如求Q1,令 q2= q3=…= q s=0,则
n
W1 (
Fi
ri )
q2 q3 qs 0
Q1q1
i 1
Q1
W1 q1
n
(
i1
Fi
i'
Fx
x
r(Fx sin Fy cos ) rF
则
Q
Wθ
rF
两种方法的结果一致
四、保守力学系的拉格朗日方程
实际上,在很多情况下我们仅遇见保守力学系。
对于保守力学系,存在势能
V V (x1, y1, z1, x2 , y2 , z2 , , xn , yn , zn )
可见广义力的横向分量 Q 是力矩。
方法二:从主动力 所作的虚功来计算
x r sin cos r
y r cos sin r
Wr Qr (F
r r )
0
o
(Fx x Fy y) 0
y
j '
由
ri
ri
,
d
ri
ri
q q
dt q q
P
d dt
n i 1
mi
ri
ri q
n i1
mi
ri
ri q
d dt
n i 1
q
则
d dt
L qj
0
pj
L qj
恒量
可见,当L函数中不含某广义坐标 q j 时,这个 q j 即循环坐标
所对应的广义动量
pj
L qj
就是守恒量,称为循环积分。
这表明,对任一循环坐标,都对应有一个循环积分。
[例4] 求一自由质点在有心力场中的循环积分。
d dt
T q
T q
V q
,
1, 2,
,s
d dt
T q
T q
V q
,
1, 2,
,s
注意:一般势能函数不显含时间和速度变量,即
V=V(x1,y1,z1,…,x n,y n,z n)=V(q1,q2,…,q s)
q1=r,q2= 。与此两
广义坐标对应的广义力为 Q r 和Q 。求 Q r与Q , 用两种方法。
解 方法一:
y
j '
Fy
rP o
从定义式计算。
将定义式用于极坐标,因 粒子数 n=1,则
Qr
F
r r
r
Q F
F
i'
Fx
x
又因 x= r cos,y=r sin
则
V 0 q
令 L=T-V ,则
L (T V ) T 与 L (T V ) T V
