计算方法第三章(插值法)解答
插 值 法(3)

第三章 插 值 法在观察或总结某些现象时,往往会发现所关心变量之间存在着某种联系,但是这种联一般很难用解析式表达。
有时即便找出了其解析表达式,由于表达式过于复杂,使用或计算起来也可能十分困难。
于是就想到能否用形式比较简单的函数去近似原来很困难得到或应用起来不便的函数。
本章所讨论的插值法就是函数近似表达的一种方法。
这里介绍的插值方法本身也是以后介绍的方法如:数值积分,数值微分,以及微分方程的数值解的基础。
本章主要介绍插值函数的构造,误差估计及简单介绍方法的收敛性和稳定性。
§1.插值的基本概念插值定义:设f(x)为定义在[a,b]上的函数,n 10x ,,x ,x 为[a,b ]上n+1个互不相同的点,Y为给定的某一个函数类,若Y上有函数y(x),满足:n ,,2,1,0i ),x (f )x (y i i ==(3—1)则称y(x)为f(x)关于节点n 10x ,,x ,x 在Y上的插值函数,点n 10x ,,x ,x 称为插值节点,f(x)称为被插值函数。
包含插值节点的区间[a,b]称为插值区间,条件(3—1)称为插值条件。
关于函数插值,我们要回答以下几个问题:(1)给定了被插函数(即f(x)),插值节点n 10x ,,x ,x 及插值函数类Y,那么满足插值条件的插值函数是否存在?若存在,是否唯一?即插值的存在性与唯一性问题。
(2)如若插值函数存在唯一,如何构造插值函数?即采用何种插值方法问题。
(3)y(x)作为f(x)的近似函数,存在误差R(x)=f(x)-y(x)。
如何估计其误差?当不斯地增加插值节点,那么插值函数列是否收敛被插函数。
现在首先回答第一个问题:由于我们这里介绍的插值函数类Y是多项式类。
故要求插值函数是多项式的情况下,来回答存在性与唯一性问题。
定理:设)x (M n 表示次数不超过n 次的多项式的全体,则满足插值条件(3—1)的,属于函数类Y=)x (M n 的插值多项y(x)存在且唯一。
计算方法 3 牛顿插值

2
分析
显然, L2 ( x0 ) y0,L2 ( x1 ) y1;利用插值 条件, L2 ( x2 ) y2 y1 y0 y 2 y0 ( x2 x0 ) a ( x2 x0 )( x2 x1 ) x1 x0 y2 y0 y1 y0 x2 x0 x1 x0 y1 y0 a L2 y0 ( x x0 ) x2 x1 x1 x0 y2 y0 y1 y0 x2 x0 x1 x0 ( x x0 )( x x1 ) x2 x1
计算方法(2016/2017 第一学期) 贾飞 西南科技大学 制造科学与工程学院
9
牛顿基本插值公式
其中,线性部分 N 1 ( x ) f ( x0 ) f [ x0 , x1 ]( x x0 ) 满足 N 1 ( x0 ) f ( x 0 ) f ( x1 ) f ( x0 ) N 1 ( x1 ) f ( x0 ) ( x1 x0 ) f ( x1 ) x1 x0 N 1 ( x ) 为 f ( x ) 以 x0,x1 为插值结点的 线性插值函数,即: N ( 1 x ) L1 ( x )
西南科技大学
制造科学与工程学院
16
解:构造差商表如下,
xi -2 0 f(xi ) 1阶 17 1 -8 1 17 3 8 1.25 2阶 3阶
1
2
2
19
N 3 ( x ) 17 8( x 2) 3( x 2) x 1.25( x 2) x ( x 1) f 0.9 N 3 (0.9) 1.30375, R3 0.9 1.25 0.9 2 0.9 0.9 1 0.9 2 0.358875
计算方法第三章习题答案

计算方法第三章习题答案计算方法第三章习题答案计算方法是一门涵盖了数值计算和计算机编程的学科,它在现代科学和工程中扮演着重要的角色。
第三章是计算方法课程中的重要章节,主要涉及到数值计算中的误差分析和插值方法。
本文将为大家提供第三章习题的详细答案,帮助读者更好地理解和应用这些概念。
1. 误差分析误差分析是计算方法中非常重要的一部分,它帮助我们理解和评估数值计算中的误差来源。
以下是一些常见的误差类型:- 绝对误差:绝对误差是指数值计算结果与真实值之间的差异。
它可以通过计算两者之差来得到。
- 相对误差:相对误差是指绝对误差与真实值之间的比值。
通常以百分比的形式表示。
- 截断误差:截断误差是由于在计算过程中舍入或截断数字而引入的误差。
它通常是由于计算机的有限精度导致的。
- 舍入误差:舍入误差是由于将无限位数的小数截断为有限位数而引入的误差。
它通常是由于计算机的有限精度或计算方法的近似性质导致的。
2. 插值方法插值方法是一种用于通过已知数据点来估计未知数据点的技术。
以下是一些常见的插值方法:- 线性插值:线性插值是一种简单的插值方法,它假设两个已知数据点之间的未知数据点的取值在直线上。
通过已知数据点的斜率和截距,我们可以计算出未知数据点的值。
- 拉格朗日插值:拉格朗日插值是一种使用多项式来逼近已知数据点的方法。
它通过构造一个满足通过已知数据点的多项式来估计未知数据点的值。
- 牛顿插值:牛顿插值是一种使用差商来逼近已知数据点的方法。
它通过构造一个满足通过已知数据点的差商多项式来估计未知数据点的值。
3. 习题答案以下是一些第三章习题的答案,供大家参考:- 习题1:已知函数f(x)在区间[a, b]上连续,且在[a, b]上的导数存在且连续,证明存在一点c∈(a, b),使得f(b) - f(a) = (b - a)f'(c)。
这是拉格朗日中值定理的一个特例,根据定理的条件,我们可以得到上述结论。
- 习题2:已知函数f(x)在区间[a, b]上连续,且在(a, b)内可导,证明存在一点c∈(a, b),使得f'(c) = (f(b) - f(a))/(b - a)。
计算方法-插值方法实验

实验一插值方法一. 实验目的(1)熟悉数值插值方法的基本思想,解决某些实际插值问题,加深对数值插值方法的理解。
(2)熟悉Matlab 编程环境,利用Matlab 实现具体的插值算法,并进行可视化显示。
二. 实验要求用Matlab 软件实现Lagrange 插值、分段线性插值、三次Hermite 插值、Aitken 逐步插值算法,并用实例在计算机上计算和作图。
三. 实验内容1. 实验题目 (1)已知概率积分dxe y xx ⎰-=22π的数据表构造适合该数据表的一次、二次和三次Lagrange 插值公式,输出公式及其图形,并计算x =0.472时的积分值。
答:①一次插值公式:输入下面内容就可以得到一次插值结果 >> X=[0.47,0.48];Y=[0.4937452,0.5027498]; >> x=0.472;>> (x-X(2))/(X(1)-X(2))*Y(1)+(x-X(1))/(X(2)-X(1))*Y(2)ans =0.495546120000000>>②两次插值公式为:输入下面内容就可以得到两次插值结果>> X=[0.46,0.47,0.48];Y=[0.4846555,0.4937452,0.5027498]; >> x=0.472;>>(x-X(2))*(x-X(3))/((X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(1))*(x-X(3))/((X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(2))*(x-X(1))/((X(3)-X(2))*(X(3)-X(1)))*Y(3)i 0123x 0.46 047 0.48 0.49 y0.4846555 0.4937452 0.5027498 0.5116683ans =0.495552928000000>>③三次插值公式为:输入下面内容就可以得到三次插值结果>> X=[0.46,0.47,0.48,0.49];Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x=0.472;>>(x-X(2))*(x-X(3))*(x-X(4))/((X(1)-X(4))*(X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(4))*( x-X(1))*(x-X(3))/((X(2)-X(4))*(X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(4))*(x-X(2))*( x-X(1))/((X(3)-X(4))*(X(3)-X(2))*(X(3)-X(1)))*Y(3)+(x-X(3))*(x-X(2))*(x-X(1))/(( X(4)-X(1))*(X(4)-X(2))*(X(4)-X(3)))*Y(4)ans =0.495552960000000输入下面内容,绘出三点插值的图:>> X=[0.46,0.47,0.48,0.49];Y=[0.4846555,0.4937452,0.5027498,0.5116683];>> x=linspace(0.46,0.49);>>y=(x-X(2)).*(x-X(3)).*(x-X(4))/((X(1)-X(4))*(X(1)-X(2))*(X(1)-X(3)))*Y(1)+(x-X(4) ).*(x-X(1)).*(x-X(3))/((X(2)-X(4))*(X(2)-X(1))*(X(2)-X(3)))*Y(2)+(x-X(4)).*(x-X(2) ).*(x-X(1))/((X(3)-X(4))*(X(3)-X(2))*(X(3)-X(1)))*Y(3)+(x-X(3)).*(x-X(2)).*(x-X(1) )/((X(4)-X(1))*(X(4)-X(2))*(X(4)-X(3)))*Y(4);>>plot(x,y)(注意上面的“.*”不能用“*”替代);(2)将区间[-5,5]分为10等份,求作211)(x x f +=的分段线性插值函数,输出函数表达式及其图形,并计算x =3.3152时的函数值。
插值法(拉格朗日插值)讲解

因此, Pn(x)在点x0邻近会很好的逼近f(x).
Taylor展开方法就是一种插值方法.
泰勒插值要求提供 f(x) 在点x0处的各阶导数,这仅 仅适用于 f(x) 相当简单的情况.
§1.2 Lagrange插值
• 设函数y = f(x)在区间[a,b]上有定义,且给 出一系列点上的函数值yi=f(xi) (i=0,1,2,…,n), 求作n次多项式pn(x) 使得
定理 (插值多项式的存在唯一性) 满足 P( xi ) yi , i 0, ... , n
的 n 阶插值多项式是唯一存在的。
证明: ( 利用Vandermonde 行列式论证)
a0 a1x0 ... an x0n y0 a0 a1x1 ... an x1n y1 ...
1 xj)
j0
li ( x)
n ji
(x xj) (xi x j )
j0
n
Ln ( x) li ( x) yi i0
插值余项 /* Remainder */
用简单的插值函数L n(x)代替原复杂函数f(x),其 精度取决于截断误差,即插值余项.
设节点 a x0 x1 xn b ,且 f 满足条件 f C n[a,b] , f (n1)在[a , b]内存在, 考察截断误差 Rn( x) f ( x) Ln( x)
Rn(x)
f (n1) ( )
(n 1) !
n
(x xi )
i0
即Rn (x)
f (n1) ( )
(n 1)!
(
x
x0
)(
x
x1
)(
x
计算方法课后习题集规范标准答案

习 题 一3.已知函数y =4, 6.25,9x x x ===处的函数值,试通过一个二次插值函解:0120124, 6.25,9;2, 2.5,3y x x x y y y =======由题意 (1) 采用Lagrange插值多项式220()()j j j y L x l x y ==≈=∑27020112012010*********()|()()()()()()()()()()()()(7 6.25)(79)(74)(79)(74)(7 6.25)2 2.532.255 2.25 2.75 2.7552.6484848x y L x x x x x x x x x x x x x y y y x x x x x x x x x x x x ==≈------=++------------=⨯+⨯+⨯⨯-⨯⨯= 其误差为(3)25(3)25(3)2[4,9]2()(7)(74)(7 6.25)(79)3!3()83max |()|40.0117281|(7)|(4.5)(0.01172)0.008796f R f x x f x R ξ--=---==<∴<=又则(2)采用Newton插值多项式2()y N x =≈ 根据题意作差商表:224(7)2(74)()(74)(7 6.25) 2.64848489495N =+⨯-+-⨯-⨯-≈4. 设()()0,1,...,k f x x k n ==,试列出()f x 关于互异节点()0,1,...,i x i n =的Lagrange 插值多项式。
注意到:若1n +个节点()0,1,...,i x i n =互异,则对任意次数n ≤的多项式()f x ,它关于节点()0,1,...,i x i n =满足条件(),0,1,...,i i P x y i n ==的插值多项式()P x 就是它本身。
可见,当k n ≤时幂函数()(0,1,...,)kf x x k n ==关于1n +个节点()0,1,...,i x i n =的插值多项式就是它本身,故依Lagrange 公式有()00(),0,1,...,nn n k kk i j j j j j i j ii jx x x l x x x k n x x ===≠-=≡=-∑∑∏特别地,当0k =时,有()0001nn n ij j j i j ii jx x l x x x ===≠-=≡-∑∑∏而当1k =时有()000nnn ij j j j j i j ii jx x x l x x x x x ===≠⎛⎫- ⎪=≡ ⎪- ⎪⎝⎭∑∑∏ 5.依据下列函数表分别建立次数不超过3的Lagrange 插值多项式和Newton 插值多项式,并验证插值多项式的唯一性。
化工计算方法-3-插值法

l k 1 ( x k 1 ) 1 l k 1 ( x k ) 0 l k 1 ( x k 1 ) 0
l k 1 ( x k 1 ) 0 l k 1 ( x k ) 0 l k 1 ( x k 1 ) 1
( x xk 1 )( x x k 1 ) lk ( x ) ( xk xk 1 )( x k x k 1 )
xk 1 xk 由两点式可看出, L1(x) 是由两个线性函数 x x k 1 x xk 的线性组合得到的, lk ( x ) , l k 1 ( x ) x k x k 1 x k 1 x k
线性插值多项式可写为 满足
l k ( xk ) 1 l k 1 ( x k ) 0
( x xk 1 )( x xk ) l k 1 ( x ) ( xk 1 xk 1 )( xk 1 xk )
l k ( x k 1 ) 0 lk ( xk ) 1 l k ( xk 1 ) 0
10
3.2.3 n次插值
用 n+1 个 插值节点,构造一个n 次插值多项式 Pn (x) 使通过所有 n+1 个插值节点,即满足 Pn ( x j ) y j (j = 0, 1,…,n) 所以此时的插值基函数应该满足 1 i k lk ( xi ) ( i , k 0, 1, 2, , n) 0 i k 用类似的推导方法,可求得n次插值基函数为 n x xj lk ( x ) ( ) j , k 0, 1, 2, , n j 0 xk x j
• 以直线方程作为插值多项式,即下 式中的 n=1
x3= 30 x4= 40
x5= 50 x6= 60 x7= 70
数值计算方法三次样条插值

4.4 三次样条插值
令
A1
j1 (u )
(1
2
u
x hj
j 1
)(
u
xj hj
)2
A2
j (u )
(1
2
u
x hj
j
)(
u
x hj
j 1
)2
B1
j1 (u )
(u
u x j 1 )(
xj hj
)2
B2
j (u )
(u
x
j )(
u
x hj
j
)2
分段三次Hermite插值算法
I2(x)
I
n
(
x
)
x ( x0 , x1)
x ( x1, x2 ) ...... x ( xn1, xn )
其I中 j xxj1 xxj j yj1xxj xxjj 11yj yj1(xxj1)(yj yj1)/(xj xj1)
缺点:I(x)连续,但不光滑,精度较低,仅在 hm 1jan{xhj xj xj1}足够小才能较好。的逼近
ss((xxn0
) )
f f
( x0 ) (xn )
m0 mn
计算方法讲义 (3)

6月5日
1
考试安排
6月17日(周三)下午14:00~16:00
考试范围:1-7章(上节课内容)
2
综合复习一
往届期末考卷讲评
3
1.(15%) 求一个次数不高于4的多项式
满足下列插值条件: P4(1)=2 , P4(2)=4 ,P4(3)=12 ,P4’(1)=1 ,
P4’(3)=-1
x j1)
(xj
xn )
41
复习:
42
1. 若f(x)=a0xn+a1xn-1+…+an-1x+an有互不相 同的n个实根x1, x2, …, xn. 试证明:
n
j 1
f
xkj '(xj )
0 a01
0kn1 k n1
令g(x) xk
则g(x)的n 1阶均差(差商)
g[x1, x2 , , xn ]
12
定理6说明
切比雪夫多项式
n-1次最佳逼近多项式余项 是切比雪夫多项式进行适
当的放缩(乘系数)
13
第一步:变量代换
设f(x)的三次最佳一致逼近多项式为
P3
(
x),x
[0,1],令x
t
2
1,t
[1,1]
则根据定义有
f
(x)
P3
(x)
F (t)
P3 (t)
1
t
1 2
(t
1) 2 2
(t
1)3 2
其中(x)为[a, b]上的权函数,求积系数为
Ai
ab
(x)li(x)dx
b
a
(x)
n
j0
xxj xi x j
计算方法课件_插值法

P( x) an x an1 x
n
n1
a1 x a0
满足
P( xi ) f ( xi )
(i 0,1,2,, n)
计 则称P(x)为f(x)的n次插值多项式。这种插值法通常 算 称为代数插值法。其几何意义如下图所示 方 法 课 件 y=p(x)
y=f(x)
2016/12/27
算 l0 ( x0 ) 1, l0 ( x1 ) 0 , l0 ( x2 ) 0 方 法 这个问题容易求解。由上式的后两个条件知 : 课 件 x1 , x 2 是 l0 ( x) 的两个零点。于是
1 再由另一条件 l0 ( x0 ) 1 确定系数 c ( x0 x1 )(x0 x2 ) ( x x1 )(x x2 ) 从而导出 l0 ( x) ( x0 x1 )(jkhh x0 x 2 ) 2016/12/27 14
直接由插值条件决定,
y
计 即 a0 , a1 , a 2 满足下面 y0 算 的代数方程组: 方 O x0 法 课 2 a a x a x 0 1 0 2 0 y0 件 该三元一
y=L2(x) y1 x1 y1 x2 y=f(x) x
2 a a x a x 0 1 1 2 1 y1 2 a a x a x 2 2 y2 0 1 2
(i=0,1,2,…,n )
的便于使用的插值多项式P(x),先考察几种简单情形,
线性插值是代数插值的最简单形式。假设给定了函数 近似地代替f(x)。选
x1 的值, f(x)在两个互异的点 x0 , y0 f ( x0 ), y1 f ( x1 )
,现要求用线性函数 p( x) ax b 择参数a和b, 使 p( xi ) f ( xi )(i 0,1) P(x) 为f(x)的线性插值函数 2016/12/27 jkhh 。
计算方法 课后习题答案

,
正规方程组化为:
得 =2.43689 =0.291211
=2.43689所以 =11.45 = =0.291211
=2.43689所以 =11.45 1= =0.291211
12.求函数 在给定区间上对于 的最佳平方逼近多项式:
解:设
(1)
(2)
。
。
13. 上求关于 的最佳平方逼近多项式。
解:Legendre是[-1,1]上的正交多项式
解:1)用梯形公式有:
事实上,
2)Simpson公式
事实上,
3)由Cotes公式有:
事实上,
2.证明Simpson公式 具有三次代数精度。
证明:
而当 时
左侧:
右侧:
左侧不等于右侧。所以Simpson具有三次代数精度.
3.分别用复化梯形公式和复化公式Simpson计算下列积分.
(1) ,(3) ,(4)
注意到这里 是三重零点, 是单零点,故插值余项为
20.求作次数 的多项式 ,使满足条件
并列出插值余项。
解法1:由于在 处有直到一阶导数值的插值条件,所以它是“二重节点”;而在 处有直到二阶导数值的插值条件所以 是“三重节点”。因此利用重节点的差商公式:
可以作出差商表
一阶
二阶
三阶
四阶
0
0
1
1
1
-1
-1
利用 的第1式,可将第2式化为
同样,利用第2式化简第3式,利用第3式化简第4式,分别得
由 式消去 得
进一步整理
由此解出
解得:
因此所求的两点Gauss求积公式:
或依下面的思想:
解(2):令原式对于 准确成立,于是有
插值法例题计算过程

插值法例题计算过程
(原创实用版)
目录
1.插值法的概念与应用
2.插值法例题的解答过程
3.插值法在实际问题中的应用
4.总结
正文
一、插值法的概念与应用
插值法是一种求解未知数值的方法,它通过已知的数据点来预测或推断未知数据点的值。
在数学、工程、物理等学科中都有广泛的应用。
插值法可以分为拉格朗日插值法、牛顿插值法、三次样条插值法等。
二、插值法例题的解答过程
假设我们有一组数据:当折现率为 10% 时,净现值为 121765;当折现率为 12% 时,净现值为 116530。
现在需要求解当折现率为 i 时,净现值的值。
我们可以使用插值法来解决这个问题。
首先,我们假设净现值为120000,然后列出一个方程:
(i-12%)/(10%-12%)=(120000-116530)/(121765-116530)
解这个方程,我们可以得到 i 的值。
三、插值法在实际问题中的应用
插值法在实际问题中有广泛的应用,例如在财务管理中,我们可以使用插值法来计算债券的收益率、股票的预期收益等。
在工程领域,插值法可以用来预测工程项目的进度、成本等。
在物理学中,插值法可以用来预
测物体的运动轨迹等。
四、总结
插值法是一种强大的求解未知数值的方法,它可以通过已知的数据点来预测或推断未知数据点的值。
力学中的计算方法(插值)
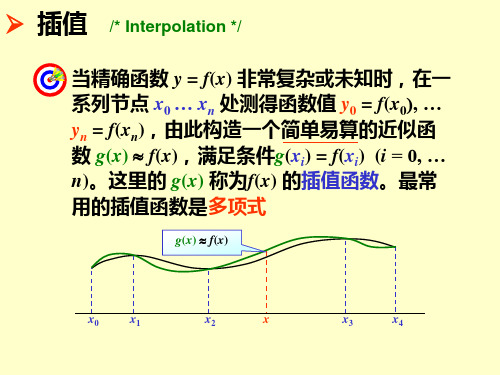
1阶差商 /* the 1st
divided difference of f w.r.t. xi and xj */
f [ xi , x j ] - f [ x j , xk ] f [ xi , x j , xk ] = (i k ) xi - xk
1 + (x - x0) 2 + … … + (x - x0)…(x - xn-1)
n-1
f ( x) = f ( x0 ) f [ x0 , x1 ]( x - x0 ) f [ x0 , x1 , x2 ]( x - x0 )( x - x1 ) ...
f [ x0 , ... , xn ]( x - x0 )...(x - xn-1 )
=
x - x1 y + x 0 - x1 0
x - x0 y = x1 - x 0 1
l ( x) y
i =0 i
1
i
l0(x)
l1(x)
§1 Lagrange Polynomial
n1
希望找到li(x),i = 0, …, n 使得 li(xj)=ij ;然后令
Pn ( x ) =
l (x) y
f [ x, x0 , ... , xn ]( x - x0 )...(x - xn-1 )( x - xn )
2阶差商
§2 Newton’s Interpolation
(k+1)阶差商:
f [ x0 , x1 , ... , xk ] - f [ x1 , ... , xk , xk 1 ] f [ x0 , ... , xk 1 ] = x 0 - x k 1 f [ x0 , ... , xk -1 , xk ] - f [ x0 , ... , xk -1 , xk 1 ] = x k - x k 1
计算方法答案 第三章

第三章 插值法与最小二乘法1. 已知下列表值x 10 11 12 13 lnx 2.3026 2.3979 2.4849 2.5649用线形插值与二次Lagrange 插值计算ln11.75的近似值,并估计误差。
解:(1)线形插值说明:当插值点落在被插区间之内,这种方法称为内插法,此时插值精度较好。
x ],12,11[75.11∈=故选择x 0=11,x 1=12,求线形插值函数。
11001y x l y x l x P ⨯+⨯=∴)()()(=10100101y x x x x y x x x x ⨯--+⨯--=4849.21112113979.2121112⨯--+⨯--x x=2.4849(x-11)-2.3979(x-12))1275.11(3979.2)1175.11(4849.2)75.11(75.11ln 1---=≈∴p =2.46315(2)二次拉格朗日插值选择插值结点:x 12,11,10210===x x P 2211002)()()()(y x l y x l y x l x ++= =212021012101200201021))(())(())(())(())(())((y x x x x x x x x y x x x x x x x x y x x x x x x x x ----+----+----=4849.2)1112)(1012()11)(10(3979.2)1211)(1011()12)(10(3026.2)1210)(1110()12)(11(----+----+----x x x x x x=1.1513(x-11)(x-12)-2.3979(x-10)(x-12)+1.24425(x-10)(x-11))1175.11)(1011075(24245.1)1275.11)(1075.11(3979.2)1275.11)(1175.11(1513.1)75.11(75.11ln 2--+-----=≈∴P =1.15133125.124245.14375.03979.2)1875.0(⨯+⨯+-⨯ =2.4639282. 已知下列表值求f(x)在[0,2]之间零点近似值。
计算物理学(刘金远)第-3-章-函数近似方法(课后习题及答案)

第3章函数近似方法(习题及答案)§3.1插值法【3.1.1】已知sin()x 在030,45,60的值分别为1/2,分别用一次插值和二次插值求0sin(50)近似值。
【3.1.2】误差函数的数据表:x 0.460.470.480.49…f(x)0.48465550.49374520.50274980.5116683…利用二次插值计算:(1)(0.472)f ;(2)()0.5,?f x x ==【3.1.3】【3.1.4】已知列表函数x -101y-15-5-3给出二次插值函数【解】0(0)(1)1()(1)(10)(11)2x x l x x x --==-----;1(1)(1)()(1)(1)(01)(01)x x l x x x +-==--++-2(1)(0)1()(1)(11)(10)2x x l x x x +-==++-2153()(1)5(1)(1)(1)22L x x x x x x x =--+-+--【3.1.5】已知,3)9(,2)4(==f f 用线性插值计算)5(f ,并估计误差。
【解】取插值节点014, 9x x ==,两个插值基函数分别为)9(51)(1010--=--=x x x x x x l )4(51)(0101-=--=x x x x x x l 故有565)4(53)9(52)()()(11001+=-+--=+=x x x y x l y x l x L 2.25655)5()5(1=+=»L f 误差为)(2)95)(45(!2)()5(2x x f f R ¢¢-=--¢¢=【3.1.6】已知(1)2,(1)1,(2)1f f f -===,求()f x 的二次拉格郎日插值多项式【解】22(1)(2)(1)(2)(1)(1)()21(11)(12)(11)(12)(21)(21)1(38)6x x x x x x L x x x --+-+-=++----+-+-=-+【3.1.7】求经过(0,1),(1,2),(2,3)A B C 三点的二次拉格郎日插值多项式【解】22(1)(2)(0)(2)(0)(1)()123(01)(02)(10)(12)(20)(21)1(343)2x x x x x x L x x x ------=++------=-+【3.1.8】编写拉格朗日三点插值程序,绘出)cos(x y =在[p ,0]区间的插值曲线,将[p ,0]区间8等份(9个插值点),由插值函数取25个点绘出插值曲线。
计算方法-插值方法

这都会给研究带来困难。如何解决这类问题?当函数f(x) 比较复杂或根本无法写出解析式时,往往寻求用一个熟悉的 简单函数P(x)的去近似表示f(x),将研究f(x)的问题转化为 研究函数P(x)的问题。
插值
/* Interpolation */
当精确函数 y = f(x) 非常复杂或未知时,在一 系列节点 x0 … xn 处测得函数值 y0 = f(x0), … yn = f(xn),由此构造一个简单易算的近似函 数 g(x) f(x),满足条件g(xi) = f(xi) (i = 0, … n)。这里的 g(x) 称为f(x) 的插值函数。最常 用的插值函数是多项式 …?
分别利用x0, x1 以及 x1, x2 计算
x0
利用 x1 , x2
4
3
~ 5 0 . 00538 R 0.00660 sin 50 0.76008, 1 18
内插 /* interpolation */ 的实际误差 0.00596
n=2
引例及问题综述
• 引例1 血药浓度问题
为试验某种新药的疗效,医生对某人用快速静脉注射方 式一次注入该药300mg后,在一定时间t(h)采取血样,测 得血药浓度C数据如下
试确定血药浓度C与时间t的函数关系。
引例及问题综述
引例2:标准正态分布函数
1 x 2
e
x
u2 2
du
sin x x
2 n 1 i i 2 n 1 i i
Hermite插值也叫带指定微商值的插值,它要构
造一个插值函数 , 不但在给定节点上取函数值 , 而
且取已知微商值,使插值函数和被插函数的密和
程度更好 。
数值分析-计算方法-插值a
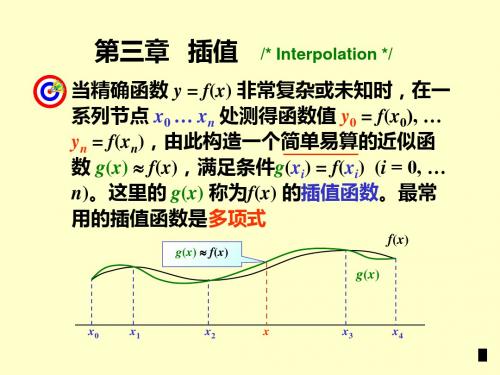
500 5
18
解: n = 1 分别利用x0, x1 以及 x1, x2 计算
x0
x1
x2
利用
x0 6 , x1 4
L 1 (x ) x /6 /4 /4 1 2 x /4 /6 /6 1 2
sin
而
50 0
Lf1内要( (5端1x 8插计)点 ) 通算s,0 常的i.x 7插n 7 优x6值12 2 所于4效,在外果R 1 的推(x 较) 区。f 好(f x 间选)2 ( 。 ! 的择x s )(x ix ,n 6 f)x (( x 4 )) 4 s 2 |( ix x n , 6 )x x ( ( 4 6 )|, 4)
Ln ( xi ) yi , i 0, ... , n
条件:无重合节点,即 i j xi xj
n=1
线性插值
已称知为x拉0 氏, x基1 ;函y0数, y1/*,La求graL n1 g(exB)asa is0 */,a1x 使得
L满1( 足x0 )条 件y0 l,i(Lx1j)(=x1 )ij/*yK1 ronecker Delta */
f(x)L (x) n
f ( ) (n1)
ni
i
项式是唯一存在的。
证明: 由插值条件可知,插值多项式Ln(x)的系数ai满足线性
方程组
1
x 0
xn 0
a0
y 0
1
x 1
xn 1
a1
y 1
1
x n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Aitken(埃特肯)算法 N 0,1,,k , p ( x) L( x) N 0,1,,k ( x)
N 0,1,,k 1, p ( x) N 0,1,,k ( x) x p xk
Neville(列维尔)算法
( x xk )
Ni ,i 1,,k ( x) L( x) Ni ,i 1,,k 1 ( x) Ni 1,i 2,k ( x) Ni ,i 1,,k 1 ( x) xk xi ( x xi )
( x0 , y0 ), ( x1 , y1 )
容易求出,该函数为:
x x0 x x1 y y0 y1 x0 x1 x1 x0
一般插值问题:求过n+1个点
( x0 , y0 ), ( x1 , y1 ),,( xn , yn )
的不超过n次多项式 Ln ( x )。
Ln ( x) yi li ( x )
例子:求方程 x3-2x-5=0 在(2 , 3)内的根 思路: 设 y = f(x) =x3-2x-5 ,其反函数为 x=f -1(y),则 根为x* =f -1(0) 。先用3= f -1(16), 2= f -1(-1)插值,得 N0,1 (y) ≈f -1(y), 计算N0,1 (0)= 2.058823, f(2.058823) = -0.39 ,以-0.39为新的节点,继续……
第三章 插值法
第一节 插值多项式的基本概念
假设已经获得n+1点上的函数值
f xi yi , i 0,1,, n,
即提供了一张数据表
x
y f x
x0
y0
x1
y1
x2
xn
y2
yn
如何利用这张表求 f (x) 在其他给定点上的合 理的近似值呢?
在实验数据的处理、难以计算的函数的逼近、 数值微积分等方面需要解决这样的问题,这是 数值逼近中的一个基本问题。一个自然的想法 是找一个简单易计算的函数(x),使得
称为Newton形式的插值多项式。
差商概念:
设函数 f (x) ,定义函数在两个不同点的一阶差商为
f ( xi , x j )
f ( xi ) f ( x j ) xi x j
, ( xi x j , i j )
三个不同点的二阶差商为:
f ( xi , x j , xk )
例子:用0、90、180、270、360五个点作出sinx 牛顿插值多项式。 做差商表 0 90 180 0 1 0 0.01111 -0.01111 -1.235e-4
270
360
-1
0
-0.01111
0.01111
0
4.572e-7
0
1.235e-4 4.572e-7
差商的性质
差商的计算公式:
n ( x) ( x x0 ) ( x x1 ) ( x xm )
r0 r1
rm
r0 r1 rm n 1
在x0 , x1 ,, xm之间,与x有关
证明思路:构造辅助函数,用罗尔定理。
, P3 ( x1 ) y1, P3 ( x2 ) y2 P3 ( x0 ) y0 , P3( x0 ) y0
2
值得注意的是在较大区间上进行插值时,误差可能会 很大!另外,一般情况下,外推不如内插好!
第二节 Lagrange插值公式 插值条件是
( x0 , y0 ),( x1 , y1 ),,( xn , yn )
Lagrange插值实质上是求通过上面 n+1 个点的 n 次多项式。
一次插值: 问题为求一次多项式,即一次函数,过以下 两点:
( xi ) yi (i 0,1,, n)
将φ(x)作为 f (x) 在一定范围内的近似函数,对于 这个范围内的某个给定点a,取 f (a)≈ φ(a)。这种 近似方法称为插值法。φ(x)称为 f (x)的以{xi} (i=0,1,· · · ,n)为插值节点的插值函数。插值节点上 所给的函数值称为样本值。
例子:用0、30、45、60、90五个点作出sinx 牛顿插值多项式。 做差商表 0 30 45 60 90 0 0.5 0.7071 0.866 1 0.016667 0.013807 0.010595 0.0044658 -0.000063556 -0.00010707 -0.0001362 -0.0000007 -0.00000049
Aitken(埃特肯)算法
x0
x1 x2 x3
N0 N1 N2 N3
N 0,1 ( x) N0,2 ( x) N 0,1,2 ( x) N 0,3 ( x) N 0,1,3 ( x) N 0,1,2,3 ( x)
Neville(列维尔)算法
x0
x1 x2 x3
N0 N1 N2 N3
N 0,1 ( x) N1,2 ( x) N 0,1,2 ( x) N 2,3 ( x) N1,2,3 ( x) N 0,1,2,3 ( x)
差商的计算简表:
x0 f ( x0 ) x1 f ( x1 ) f ( x0 , x1 ) x2 f ( x2 ) f ( x1 , x2 ) f ( x0 , x1 , x2 ) x3 f ( x3 ) f ( x2 , x3 ) f ( x1 , x2 , x3 ) f ( x0 , x1 , x2 , x3 ) x4 f ( x4 ) f ( x3 , x4 ) f ( x2 , x3 , x4 ) f ( x1 , x2 , x3 , x4 ) f ( x0 , x1 , x2 , x3 , x4 )
求过n+1个点的不超过n次多项式的插值多项 式是唯一的。 插值公式的误差为:
f ( n1) ( x ) Rn ( x) f ( x) Ln ( x) ( x x0 )( x x1 )( x xn ) (n 1)!
M n1 max f ( n 1) ( x)
因式定理:多项式P(x)具有r 次因式 (x-a)r 的 充 要条件是 P(a) P(a) P( r1) (a) 0 最一般的插值条件: ( xi ) yi , ( xi ) yi,, ( ri 1) ( xi ) yi( ri 1) xi ri 是 r 重插值节点, r r n 1
φ(xi)=yi 称为插值条件。函数值待求的点称为插值 点。插值节点所界定的范围称为插值区间。如 果所给插值点位于插值区间之内,这种插值过程 称为内插,否则称为外插。 若用多项式来作为插值函数,则称其为插值 多项式。通常用 n 次多项式作为n+1个插值条件 的插值多项式。如果插值条件只是给出节点的函 数值,称为拉格朗日插值,如果既有函数值也有 节点处函数的导数值,称为埃尔米特插值。
f ( x) N n1 ( x) N n ( x) f ( x0 , x1,, xn , x)( x x0 )( x x1 )( x xn )
Rn ( x ) f ( x ) N n ( x ) f ( x0 , x1 ,, xn , x )( x x0 )( x x1 )( x xn )
f (xj ) f ( x0 , x1 ,, xk ) (xj ) j 0 k
k
( x j ) ( x j xi ) k ( x ) ( x xi ) , k
yi 16 -1 xi 3 2 Ni,i+1 (0) Ni,i+1,i+2 (0) Ni,i+1,i+2,i+3 (0) 23
2.096589 2.094529
2.095659 2.094554 2.094553
0.012 2.095659 1.51E-5 2.094553
第四节 牛顿插值 设插值点为 ( x0 , f0 ),( x1, f1 ),( x2 , f 2 ),,( xn , f n ) 插值多项式形如
N n ( x) c0 c1 ( x x0 ) c2 ( x x0 )( x x1 ) cn ( x x0 )( x x1 )( x xn1 )
在点
f ( xi , x j ) f ( x j , xk ) xi xk
x0 , x1 ,, xk , xk 1 处 K+1 阶差商为:
f ( x0 , x1 ,, xk ) f ( x1 , , xk , xk 1 ) f ( x0 , x1 ,, xk , xk 1 ) x0 xk 1
i 0
n
li ( x ) 称为Lagrange插值基函数,满足:
1 , i j li ( x j ) ij , ij 0 , i j
( x x0 )( x xi 1 )( x xi 1 )( x xn ) li ( x) ( xi x0 )( xi xi 1 )( xi xi 1 )( xi xn )
牛顿插值的截断误差:
N n1 ( x) N n ( x) f ( x0 , x1,, xn1 )( x x0 )( x x1 )( x xn )
f ( xn1 ) Nn1 ( xn1 ) Nn ( xn1 ) f ( x0 , x1 ,, xn1 )( xn1 x0 )( xn1 x1 ) ( xn1 xn )
0 1 m
定理:给定上述n+1个插值条件,则n次插值 多项式是存在唯一的。
设函数 y = f (x) 在闭区间 [a , b ]上有n + 1 阶导数, 满足前面的一般插值条件,且插值节点各不相同, 则插值截断误差为
1 ( n 1) Rn ( x) f ( x) Pn ( x) f ( ) n ( x) (n 1)!
