常见超越函数图像及常用放缩函数
高考导数解答题中常见的放缩大法完整版.doc

(高手必备)高考导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟,将复杂的函数求导,再对导函数求导,再求导,然后就没有然后了......如果懂得了最常见的放缩,如:人教版课本中常用的结论⑴sin ,(0,)x x x π<∈,变形即为sin 1x x<,其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下: exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。
例析:(2018年广州一模)x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立,求a 的取值范围。
放缩法:由可得:1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下,供大家参考。
第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥-> (放缩成类反比例函数)1ln 1x x≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+, ()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x +<<+第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x=-,ln y x x =. 拓展阅读:为何高考中总是考这些超越函数呢?和x e xln 因为高考命题专家是大学老师,他们站在高观点下看高中数学,一览无遗。
导数大题中最常用的放缩大法

导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟,将复杂的函数求导,再对导函数求导,再求导,然后就没有然后了......如果懂得了最常见的放缩,如:人教版课本中常用的结论⑴sin ,(0,)x x x π<∈,变形即为sin 1x x<,其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下: exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。
例析:(2018年广州一模)x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立,求a 的取值范围。
放缩法:由可得:1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下,供大家参考。
第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥-> (放缩成类反比例函数)1ln 1x x≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+, ()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x +<<+第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x=-,ln y x x =. 拓展阅读:为何高考中总是考这些超越函数呢?和x e x ln 因为高考命题专家是大学老师,他们站在高观点下看高中数学,一览无遗。
经典数学函数图像大全-数学函数图像
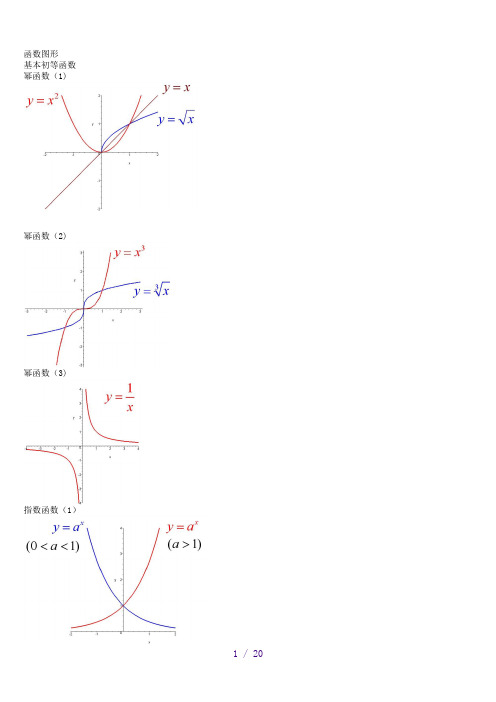
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)双曲函数(3)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(4)双曲函数(5)双曲函数(7)反双曲函数(3)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)反双曲函数(5)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|取整函数 y= [x]极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)(注:文档可能无法思考全面,请浏览后下载,供参考。
高考导数解答题中常见的放缩大法

For personal use only in study and research; not forcommercial use(高手必备)高考导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟,将复杂的函数求导,再对导函数求导,再求导,然后就没有然后了......如果懂得了最常见的放缩,如:人教版课本中常用的结论⑴sin ,(0,)x x x π<∈,变形即为sin 1x x<,其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下: exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。
例析:(2018年广州一模)x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立,求a 的取值范围。
放缩法:由可得:1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下,供大家参考。
第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥->(放缩成类反比例函数)1ln 1x x ≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+, ()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x +<<+第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x =-,ln y x x =. 拓展阅读:为何高考中总是考这些超越函数呢?和x e x ln 因为高考命题专家是大学老师,他们站在高观点下看高中数学,一览无遗。
导数压轴-超越函数的探讨(有详细解答)

(2) 换元处理 (3) 分离函数比较(提取公因式,分离超越式)
例题分析
三角函数
例 1. 已知 f x e1x a cos x,a R (1) 若函数 y f x 在0, 存在单调递增区间,求实数 a 的取值范围
(2)
若
f
2
0
,证明:对于
则有 a
2
sin(
x
4
)min
,因为在
0,
上所以
a
1
即可
对于第二问来说由
f
2
0
我
们不
难得到
a=0 , 进 一 步 则 不 等 号 左 边 即 为
ex2 cosx 1 2e1x sin x cos xcosx 1 0
即
解析几何导数专题
cos
x
1 (ex2
2e1x
sin
x
cos
x)
非是去绝对值后进行求导探求极值点,但是这道题里面难点就在于 a 是参数且
求导后无法得出具体的极值点,结合之前讲的放缩技巧,我们可以先一步使用绝
对值不等式有 a cos2x a 1cos x 1 a cos x a 1cos x 1 ,此时还带着
三 角 函 数 , 因 此 我 们 继 续 使 用 三 角 函 数 放 缩 即 可 当 a1 有
0
而又因为在
x
1,
1 2
上
cos
x
1
0
恒
成 立 所 以 即 证 (ex2 2e1x sin x cos x) 0 即 可 , 即 e2x1 2
2
sin(x
4
)
在
高考常考的超越函数
从而不存在 x0 1满足题意 当 k 1时,令 G(x) f (x) k(x 1), x (0, ) ,
则有 G(x) 1 x 1 k x2 (1 k)x 1
x
x
由 G(x) 0 得, x2 (1 k)x 1 0
解得 x1 1 k
(1 k)2 4
1k
2
0, x2
(1 k)2 4 1
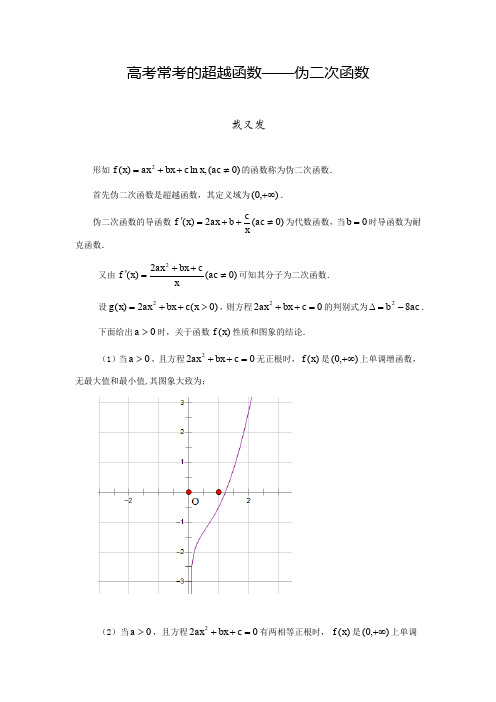
无最大值和最小值,其图象大致为;
(2)当 a 0 ,且方程 2ax2 bx c 0 有两相等正根时, f (x) 是 (0,) 上单调
增函数,无最大值和最小值,其图象大致为;
(3)当 a 0 ,且方程 2ax2 bx c 0 有一正根一负根时,设 x0 为其正根, f (x) 在 (0, x0 ) 上为减函数,在是 (x0 ,) 上是增函数,当 x x0 时, f (x) 取得最小值,其图象
高考常考的超越函数——伪二次函数
戴又发
形如 f (x) ax2 bx c ln x, (ac 0) 的函数称为伪二次函数. 首先伪二次函数是超越函数,其定义域为 (0,) . 伪二次函数的导函数 f (x) 2ax b c (ac 0) 为代数函数,当 b 0 时导函数为耐
x
克函数.
(Ⅰ)讨论函数 f (x) 极值点的个数,并说明理由;
(Ⅱ)若 x 0, f (x) 0 成立,求 a 的取值范围.
解析:(Ⅰ)由题意知,函数 f (x) 的定义域为 (1, ) ,
f (x) 1 a(2x 1) 2ax2 ax a 1 ,
x 1
x 1
令 g(x) 2ax2 ax a 1, x (1, ) ,
所以 x e 是 f (x) 在区间 (1, e] 上的唯一零点。
高考导数解答题中常见的放缩大法

(高手必备)高考导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟,将复杂的函数求导,再对导函数求导,再求导,然后就没有然后了......如果懂得了最常见的放缩,如:人教版课本中常用的结论⑴sin ,(0,)x x x π<∈,变形即为sin 1x x<,其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下: exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。
例析:(2018年广州一模)x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立,求a 的取值范围。
放缩法:由可得:1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下,供大家参考。
第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥-> (放缩成类反比例函数)1ln 1x x≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+, ()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x +<<+第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x=-,ln y x x =. 拓展阅读:为何高考中总是考这些超越函数呢?和x e x ln 因为高考命题专家是大学老师,他们站在高观点下看高中数学,一览无遗。
完整版三角函数公式和图像大全
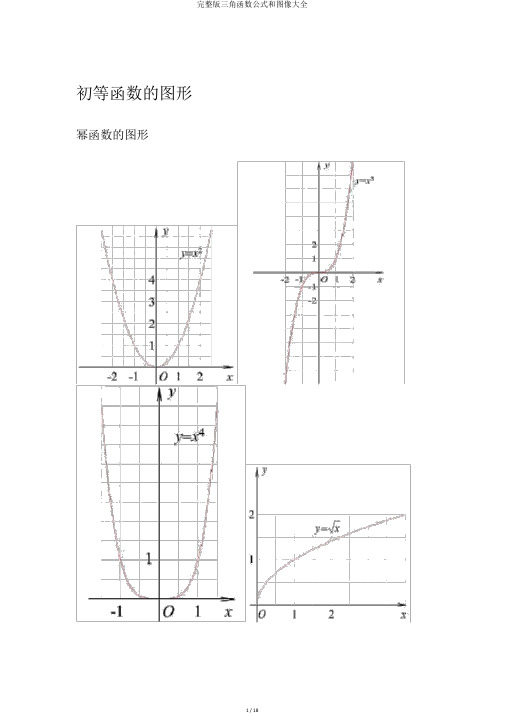
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sin α· csc αcos α· sec αtan α· cot α三角函数的性质函数y=sinx y=cosx y=tanx{x|x∈R 且定义域R R x ≠ k π+,k∈2Z }[-1,1]x=2kπ+时[ -1,1]x=2k π时2Ry max =1 y max =1值域无最大值x=2k π- 时 y min =-1 x=2k π +π时无最小值y min =-12周期性周期为 2π周期为 2π周期为π奇偶性奇函数偶函数奇函数在[ 2kπ- ,2k π+ ]在[ 2kπ-π,在(k π- ,2k π]上都是增2 2 2单调性上都是增函数;在函数;在[2kπ,kπ+)内都是[2kπ+ 2 2k π +π]上都是 2,2k π+π]2 3 减函数 (k ∈Z) 增函数 (k ∈ Z)上都是减函数 (k ∈Z) y=cotx{x|x∈R 且 x ≠ k π∈,kZ }R无最大值无最小值周期为π奇函数在(k π,kπ+π)内都是减函数(k ∈Z)反三角函数的图形反三角函数的性质名称反正弦函数y=sinx(x ∈〔- ,〕的反2 2函数,叫做反正定义弦函数,记作x=arsinyarcsinx 表示属于[- ,]2 2理解且正弦值等于 x的角定义域[-1, 1]值域[- ,]2 2 反余弦函数y=cosx(x ∈〔0, π〕)的反函数,叫做反余弦函数,记作x=arccosyarccosx 表示属于[ 0,π],且余弦值等于x的角[-1, 1][0,π]反正切函数y=tanx(x ∈(-,2)的反函数,叫2做反正切函数,记作x=arctanyarctanx 表示属于(- , ),且正切2 2值等于 x 的角(-∞,+∞)(-,)2 2反余切函数y=cotx(x ∈(0, π的))反函数,叫做反余切函数,记作x=arccotyarccotx 表示属于(0,π)且余切值等于 x 的角(-∞, +∞)(0,π)性单调性在〔 -1,1〕上是质增函数奇偶性arcsin(-x)=-arcsi nx周期性都不是同期函数sin(arcsinx)=x(x∈[ -1,恒等式1])arcsin(sinx)=x(x ∈[- , ])2 2互余恒等arcsinx+arccosx=式在[-1,1]上是减函数arccos(-x)=π-arccosxcos(arccosx)=x(x ∈[ -1,1])arccos(cosx)=x(x ∈[ 0, π])(x ∈[ -1,1])2在(-∞,+∞)上是增在 (-∞,+∞)上数是减函数arctan(-x)=-arcta arccot(- x)= π-anx rccotxtan(arctanx)=x(x cot(arccotx)=x∈ (x ∈R) R)arctan(tanx)=xarccot(cotx)=x ( x∈ (- , ))(x∈(0,π))2 2arctanx+arccotx=(X∈R)2三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanA tanBtan(A-B) =1- tanAtanB tanA tanBcot(A+B) =1 tanAtanBcotAcotB -1cot(A-B) =cotB cotA cotAcotB 1 cotB cotA倍角公式tan2A = 2tanA1 tan2 ASin2A=2SinA?CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式3sin3A = 3sinA-4(sinA) 3cos3A = 4(cosA) -3cosAtan3a = tana ·tan(+a)· tan(-a)33sin( A)=1 cosA 22cos( A)= 1 cosA2 2 tan( A)= 1 cosA 1 cosA 2cot( A )= 1cosA 21 cosAtan( A2)= 1cosA sin A =sin A1 cos A和差化积sina+sinb=2sina b cosab22 sina-sinb=2cosa bsinab2 2cosa+cosb = 2cosa bcosab2 2 cosa-cosb = -2sina bsinab22tana+tanb=sin(ab)cosa cosb积化和差1sinasinb = - [cos(a+b)-cos(a-b)]1cosacosb = [cos(a+b)+cos(a-b)]1 sinacosb = [sin(a+b)+sin(a-b)]1cosasinb =[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(-a) = cosa2 cos(-a) = sina2 sin(+a) = cosa 2cos( +a) = -sina2sin( -πa) = sinacos( π-a) = -cosasin( π +a)-sina=cos( π +a) -=cosasin atgA=tanA =全能公式2tanasina=2 1 (tan a) 221 (tan a) 2cosa=21 (tan a)2 22tanatana=21 (tan a)2 2a?sina+b?cosa= (a 2 b 2) × sin(a+c) [其中 tanc= b]aa?sin(a)-b?cos(a) = (a2b 2) ×cos(a-c) [其中 tan(c)= a]b1+sin(a) =(sin a+cos a)22 2 1-sin(a) = (sin a-cos a)222其他非重点三角函数csc(a) =1sec(a) =sin a 1cos a双曲函数sinh(a)= e a - e -a 2cosh(a)=e ae -a2sinh( a) tg h(a)=cosh(a)公式一设 α为任意角,终边相同的角的同一三角函数的值相等: sin (2k π+α)= sin α cos (2k π+ α) = cos α tan (2k π+α)= tan αcot (2k π+α)= cot α设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sin αcos(π+α)= -cos αtan(π+α)= tan αcot(π+α)= cot α公式三任意角α与 -α的三角函数值之间的关系:sin(-α) = -sin αcos(-α) = cos αtan(-α) = -tan αcot(-α) = -cot α公式四利用公式二和公式三可以获取π-α与α的三角函数值之间的关系:sin(π-α)= sin αcos(π-α)= -cos αtan(π-α)= -tan αcot(π-α)= -cot α公式五利用公式 -和公式三可以获取2π-α与α的三角函数值之间的关系:sin(2π-α)= -sin αcos(2π-α)= cos αtan(2π-α)= -tan αcot(2π-α)= -cot α±α及3±α与 α的三角函数值之间的关系:22sin ( +α)= cos α 2cos ( +α)= -sin α2tan ( +α)= -cot α2cot ( +α)= -tan α2sin ( -α)= cos α2cos ( -α)= sin α2tan ( -α)= cot α2cot ( -α)= tan α 2sin (3+α)= -cos α2cos ( 3+α)= sin α2tan (3+α)= -cot α2cot ( 3+α)= -tan α2sin (3-α) = -cos α2cos ( 3-α)= -sin α2tan (3-α) = cot α2cot (3-α) = tan α2(以上 k ∈ Z)这个物理常用公式我费了半天的劲才输进来 ,希望对大家适用A?sin( ω t+ θ )+ B?sin( 22ω t+A φ )B = 2AB cos() × sintarcsin[(As in Bsin ) A 2 B 2 2 AB cos( )三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b| ≤ |a|+|b||a-b| ≤ |a|+|b||a| ≤ b<=>-≤ a≤ b|a-b| ≥ |a||b|--|a| ≤ a≤ |a|一元二次方程的解-b+√ (b2-4ac)/2a -b-b+√ (b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理鉴识式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)= √-((1cosA)/2) sin(A/2)=- √ ((1-cosA)/2)cos(A/2)= √ ((1+cosA)/2) cos(A/2)=-√ ((1+cosA)/2)tan(A/2)=√-cosA)/((1+cosA)) tan(A/2)=-√ ((1-cosA)/((1+cosA))ctg(A/2)=√ ((1+cosA)/((1-cosA)) ctg(A/2)=-√ ((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前 n 项和1+2+3+4+5+6+7+8+9+⋯ +n=n(n+1)/21+3+5+7+9+11+13+15+⋯ +(2n-1)=n22+4+6+8+10+12+14+⋯ +(2n)=n(n+1)12+22+32+42+52+62+72+82+⋯ +n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+⋯ n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+ ⋯ +n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中 R 表示三角形的外接半径余弦定理b2=a2+c2-2accosB注:角 B 是 a 和 c 的角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}的准方程(x-a)2+(y-b)2=r2 注:( a,b)是心坐的一般方程x2+y2+Dx+Ey+F=0 注: D2+E2-4F>0抛物准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra 是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中 ,S'是直截面面积,L 是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
2022高考数学函数与导数—导数中的放缩问题

函数与导数—导数中的放缩问题专题综述放缩法是解决函数不等式问题的利器,导数压轴题中的函数往往是指数、对数与其他函数综合,或者指对数并存的超越函数,有时直接构造出的函数难以直接求出最值,需要借助放缩解决.利用导数判断函数单调性、解决函数零点问题、不等式证明等问题中都会用到放缩法,使问题难度降低.常用的放缩方式有:①常用不等式放缩:指数放缩、对数放缩、三角放缩;②利用已知题目信息放缩;③根据已知参数范围或常识,减少变量,适当放缩;③利用单调性放缩;④利用基本不等式放缩: 若0a b >>,则211ln ln 2a b a bb ab a b a b-+<<<<-+;⑤由数值大小关系直接放缩,做题时灵活运用.本专题就前3种,重点探究.专题探究探究1:利用不等式放缩函数中有指数、对数、三角函数时,直接求导,导数不等式无法解出,根据函数结构,选择不等式进行放缩,使函数简单化. 常用不等式有:(1)三角函数放缩:①0,,sin tan 2x x x x π⎛⎫∀∈<< ⎪⎝⎭;②21sin 2x x x ≥-;③22111cos 1sin 22x x x -≤≤-(2)指数放缩:①1x e x ≥+;②x e ex ≥(1,y x y ex =+=为函数x y e =图象的两条切线);③()101xe x x ≤≤-;④()10x e x x≤-< (3)对数放缩:①11ln 1x x x -≤≤-;②ln x x e ≤;③1ln x ex ≥-;(1,xy x y e =-=为函数ln y x =图象的两条切线)(4)指对放缩:()()ln 112xe x x x ->+--=(2021安徽省合肥市联考) 已知函数()(ln ),.xe f x a x x a R x=--∈(1)当0a >时,讨论函数()f x 的单调性;(2)当1a =-时,函数1()()()x g x f x x e mx x =+++满足:对任意(0,)x ∈+∞,都有()1g x 恒成立,求实数m 的取值范围.【审题视点】第(2)问显化函数()g x ,恒成立问题回顾常用的方法(专题1.3.7):分离参数、含参讨论单调性等方法,由解析式的具体结构确定方法与细节.【思维引导】分离参数以后,函数中有指、对结构,若直接通过求导判断单调性求最值,方法较困难,利用不等关系1x e x ≥+,得ln ln 1x x e x x +≥++,使难度大大降低.【规范解析】解:(1)()f x 的定义域是(0,)+∞,22()(1)()x x x a xe e ax e x f x a x x x -+-'=--=,当0a >,0x >时,令()0f x '>,则1x <∴()f x 在(0,1)上单调递增,在(1,)+∞上单调递减;(2)当1a =-时,1()()()ln (1)x x g x f x x e mx xe x m x x=+++=-++,()()0,,1x g x ∀∈+∞≥即ln 1ln 1ln 11x x x x xe x e m x x++-+--=-,1.恒成立问题求参:分离参数构造函数求最值;2.构造的函数中有ln x 、ln x x e +,通过求导判断单调性求最值较困难,通过常用不等关系1xe x ≥+,进行放缩,是函数简单化.设()1x F x e x =--,则()1x F x e '=-,令()0F x '>,则0x >∴()f x 在()0,+∞上单调递增,在(),0-∞上单调递减∴()(0)0F x F =,即1(x e x +当且仅当0x =时“=”成立),故ln ln 1(x x e x x +++当且仅当ln 0x x +=时“=”成立), ()ln G x x x =+在(0,)+∞上是增函数,且11()10G e e=-<,(1)10G =>,故存在01(,1)x e∈使得ln 0x x +=成立,故ln 1ln 1ln (ln 1)112x x x e x x x x x++-+-++--=-(当且仅当0x x =时“=”成立),∴2m -,即m 的取值范围是[2,).-+∞【探究总结】常见的不等关系要灵活运用,解题时函数结构复杂,可考虑运用上述不等式进行放缩,使问题简答化.但不等式1,,ln 1,ln xxx e x e ex x x x e≥+≥≤-≤,从图象的角度看,是以直代曲,放缩的程度大,容易出现误差,在使用时要注意.另外若是求参数取值范围问题,要考虑不等式中的等号能否取到.(2021山东省泰安市一模) 已知函数()()ln 2xf x e x k -=-,(k 为常数, 2.718e =⋅⋅⋅是自然对数的底数),曲线()y f x =在点()()1,1f 处的切线与y 轴垂直.(1)求()f x 的单调区间;(2)设()()1ln 1xx x g x e-+=,对任意0x >,证明:()()21x x x g x e e -+<+. 探究2:利用已证结论放缩1.对使用过得不等关系,构造函数证明成立;2.利用不等关系进行替换.恒成立求取值范围的问题,放缩以后,要确保不等式中等号能否取到解答题的上一问中证明的不等式,或者推导过程中证明出的结论,为后续的证明提供放缩的依据.需证明的不等式为关于n 的多项式的和或不等式结构复杂,利用已证结论,进行放缩,使不等式化繁为简,便于构造函数求最值.(2021湖南省郴州市模拟) 已知函数()e (1)ln(1) 1.x f x x x =-++-(1)当0x >时,证明:()0f x >;(2)已知数列{}n a 的通项公式为1e 1nn n na n -=+,证明:12ln (1).n a a a n ++⋅⋅⋅+>+ 【审题视点】第(2)问,出现数列的前n 项和,且不能用常规的求和方法求和,借助第一问的结论对n a 的通项公式进行放缩,便于求和.【思维引导】对第一问的不等式进行变形,观察n a 的结构,进行放缩,能够用已知方法求和.【规范解析】解:(1)由题意得 ()()ln(1)10x f x e x x '=-+->, 设()ln(1)1x g x e x =-+-,则1(1)1()11x xe x g x e x x +-'=-=++, 当0x >时, 1x e >,11x +>,则(1)1x e x +>则(1)1()01x e x g x x +-'=>+, ()g x ∴在()0,+∞上单调递增,故()()00g x g >=,即()0f x '> ()f x ∴在()0,+∞上单调递增,∴当0x >时,()(0)0f x f >=,即()0f x >(2)由(1)知:当0x >时,()(1)ln(1)10x f x e x x =-++->,即1ln(1)1x e x x ->++ 令1x n=,则11ln()1nne n n n n -+>+,12231ln ln ln12n n a a a n++++>+++ 231ln()ln(1)12n n n+=⨯⨯⨯=+ ∴12ln (1)n a a a n ++⋅⋅⋅+>+【探究总结】函数中证明与n 有关的求和问题,或不等式证明问题,要仔细观察不等式结构特点,往往会利用前一问的结论,或者解题过程中的结论.利用已证结论,进行放缩,化繁为简,证明不等式的成立.(2021广东省东莞市联考) 已知函数()ln (1),(0)f x x a x a =-->( 2.718e ≈即自然对数的底数).(1)若函数()f x 在()1,+∞上是单调减函数,求实数a 的取值范围; (2)在(1)的条件下,当n N +∈时,证明:2311111111.2222n e ⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭探究3:利用已知参数范围或常识放缩函数解析中含有参数,且已知参数范围,证明不等式成立,可以从参数的范围入手,使参数取确定的值或利用单调性、其它不等关系,对不等式进行放缩,减少变量,使函数结构简单,易于判断单调性.(2021河北省石家庄联考) 已知函数()(2).x f x e k x =-+(1)讨论函数()f x 的单调性;(2)证明:当0k e <<时,()(1ln )0.f x k x x ++->【审题视点】已知参数范围,证明不等式成立,且函数指对结构都有,若含参讨论难度大,可能要借助放缩,化繁为简.【思维引导】1.对已证不等式进行变形,变形为与n a 通项公式相似的结构;2.对自变量进行替换,得出新的不等式.利用不等式性质进行求和,实现放缩,证明结论.第(2)问不等式的证明,函数中有x e ,ln x ,构造函数求导,含参讨论解导数不等式较困难,可巧妙利用参数的范围,参数取确定的值,进行放缩,求不含参函数的最值较为简单.【规范解析】解:(1)由题意得 ()e .x f x k '=- ①当0k 时,()e 0x f x k '=->,∴函数()f x 在(,)-∞+∞上单调递增;②当0k >时,令()e 0x f x k '=-> 得ln x k >,则()g x '在(0,)+∞上单调递增,且(1)0g '= 当(0,1)x ∈时,()0g x '< 当(1,)x ∈+∞时,()0g x '>)0,10⎫->⎪⎭∴当0k e <<时,()(1ln )0.f x k x x ++->【探究总结】不等式的证明问题中含有参数,若直接构造函数含参讨论,难以解决的情况下,为避开讨论,可以在参数给定的范围内,结合不等式的结构进行第一步的放缩,达到消参的目的,转化为证明不含参的不等式.若不等式的结构依然复杂,在利用常用不等关系、已证结论等方法进一步放缩.(2021湖北省荆州市高三模拟) 已知函数()ln(2).x m f x e x -=-(1)设1x =是函数()f x 的极值点,求m 的值并讨论()f x 的单调性; (2)当2m 时,证明:()ln 2.f x >-专题升华导数解答题中函数多以xe 、ln x 型的函数与其他函数结合的形式出现,考查零点问题、不等式证明问题、恒成立问题等方向时,如果利用常规方法处理时,因函数结构复杂求导判断单调性难度较大,通过放缩将难以处理的函数转化为较为简单的函数进行处理.放缩法较为灵活,要根据不等式的结构、形式等特征,使条件与结论建立联系,选择适当的方法是关键. 1.积累常见的不等结论:如探究1中提及的不等式,解题时需构造函数,证明其正确性,再进行放缩.利用不等式进行放缩,体现了数学中的化归与转化思想,也体现了处理数学问题时以直代曲、以曲代曲的方法.2.巧用已证不等式,顺水推舟:利用已证不等式(或结论) “服务”于后续问题的求解,这类题目最明显的“暗示”,即为证明一个类似于数列求和的不等式,需利用已证不等式进行逐项替换放缩.若题目的第一问证明不等式,在后续解题时,留意是否会利用已证结论.3.已知参数范围:含参不等式的证明时,若因为参数的存在使函数讨论非常复杂,可考虑结合参数范围及其它结论进行放缩.4.其他放缩方法:除了上述三种难度较大的放缩方法以外,单调性、已知结论、基本不等式等.如利用基本不等式进行放缩,化曲为直,()202x x +=≥;和积互化等.不仅仅应用于简化不等式,在解题过程中,也可能用放缩证明代数式的值.长干行·其一[唐]李白妾发初覆额,折花门前剧。
高考导数解答题中常见的放缩大法

For personal use only in study and research; not forcommercial use(高手必备)高考导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟,将复杂的函数求导,再对导函数求导,再求导,然后就没有然后了......如果懂得了最常见的放缩,如:人教版课本中常用的结论⑴sin ,(0,)x x x π<∈,变形即为sin 1x x<,其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下: exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。
例析:(2018年广州一模)x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立,求a 的取值范围。
放缩法:由可得:1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下,供大家参考。
第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥->(放缩成类反比例函数)1ln 1x x ≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+, ()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x +<<+第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x =-,ln y x x =. 拓展阅读:为何高考中总是考这些超越函数呢?和x e x ln 因为高考命题专家是大学老师,他们站在高观点下看高中数学,一览无遗。
高中数学函数图像的平移与缩放技巧分享

高中数学函数图像的平移与缩放技巧分享在高中数学中,函数图像的平移与缩放是一个重要的概念和技巧。
通过平移与缩放,我们可以改变函数图像的位置和形状,从而更好地理解和分析函数的性质。
本文将分享一些关于函数图像平移与缩放的技巧,并通过具体的例子来说明其考点和应用。
一、平移技巧平移是指将函数图像沿着坐标轴的方向移动一定的距离。
平移可以改变函数图像的位置,但不改变其形状。
下面以一道具体的例题来说明平移的技巧。
例题:已知函数f(x)的图像如下图所示,求函数g(x) = f(x - 2)的图像。
(插入图像)解析:要求函数g(x) = f(x - 2)的图像,我们需要将函数f(x)的图像沿着x轴平移2个单位。
具体操作如下:1. 将函数f(x)的图像上的每一个点的横坐标都减去2,即将每个点(x, y)变为(x - 2, y)。
2. 连接新的点,就得到了函数g(x) = f(x - 2)的图像。
通过这个例题,我们可以看出平移的关键就是改变函数图像上的每一个点的横坐标,从而实现整个图像的平移。
这个技巧在解决函数图像平移的问题时非常有用。
二、缩放技巧缩放是指将函数图像沿着坐标轴的方向进行拉伸或压缩,从而改变函数图像的形状和大小。
缩放可以通过改变函数的系数来实现。
下面以一道具体的例题来说明缩放的技巧。
例题:已知函数f(x)的图像如下图所示,求函数g(x) = 2f(x)的图像。
(插入图像)解析:要求函数g(x) = 2f(x)的图像,我们需要将函数f(x)的图像沿着y轴方向进行拉伸。
具体操作如下:1. 将函数f(x)的图像上的每一个点的纵坐标都乘以2,即将每个点(x, y)变为(x,2y)。
2. 连接新的点,就得到了函数g(x) = 2f(x)的图像。
通过这个例题,我们可以看出缩放的关键就是改变函数图像上的每一个点的纵坐标,从而实现整个图像的缩放。
这个技巧在解决函数图像缩放的问题时非常有用。
三、举一反三通过以上的例题,我们可以看出平移与缩放技巧的应用范围是很广的。
2019届高考导数解答题中常见的放缩大法

而
由
对
数
平
均
不
等
式
得
:
x2 x1
(2 x1 ) (2 x2 ) (2 x1 ) (2 x2 ) 2 x1 x2 1
ln(2 x1) ln(2 x2) ln(2 x1) ln(2 x2)
2
2
,矛盾。
由 (x1 1)2 (x2 1)2 0, 4 (x1 x2 ) 0 ,故 x1 x2 2
(2)法一: f (x) (x 2)ex a(x 1)2 0 即 (2 x)ex a(x 1)2 0;
由
f
( x1 )
f
(
x2
)
0
得
(2 (2
x1)e x1 x2 )ex2
a(x1 1)2 a(x2 1)2
,两式相减得
(2 x1)ex1 (2 x2 )ex2 a(x1 x2 )(x1 x2 2),
放缩法:由 ex x 1可得:
e2x ln x 1 xex (ln x 1) e2xln x (ln x 1) 2x ln x 1 (ln x 1) 2
x
x
x
x
高考中最常见的放缩法可总结如下,供大家参考。 第一组:对数放缩
(放缩成一次函数) ln x x 1, ln x x , ln 1 x x
近似函数在这一点的邻域中的值,如果这个点是 0,就是形式比较简单的麦克劳林级数。简而言之,它的功能就 是把超越式近似表示为幂函数。常见的幂级数展示式有:
(放缩成双撇函数)
ln
x
1 2
