第六章 序列相关性kk
第六章 自相关(序列相关)

2 横截面数据中的自相关:一般来说截面数据不容
易出现自相关,但相邻的观测单位之间也可能存在 “溢出效应”(neighborhood effect)。例如,相邻 省份、国家之间的经济活动相互影响(通过贸易、 投资、劳动力流动等);相邻地区的农业产量受到 类似的天气影响而相关;同一社区内的房屋价格存 在相关性;相邻地区的消费倾向有相关性
图 中 实 线 表 示 真 实 的 总 体 回 归 线 。 假 设 扰 动 项 存 在
正 自 相 关 , 即 E ij X >0 , 若 1>0 ( 图 中 左 边 小 椭 圆 形 ) 由 于 存 在 正 自 相 关 , 则 2 >0 的 可 能 性 也 就 很 大 ; 而 若
n-1<0 ( 图 中 右 边 小 椭 圆 形 ) 则 n <0 的 可 能 性 也 就 很 大
此 检 验 被 称 为 B GB 检 验 ( r e u s c h - G o d f r e y )
3B 、 o x P i e r c e Q 检 验
定义残差的各阶样本自相关系数为
t=j+1 ˆ j n
e e
t=1
n
t t-j
2 e t
(j=1,2, ,p)
d ˆ 且 n 正 态 分 布 , j = 1 , 2 , , p j
3 设 定 误 差 m i s s p e c i f i c a t i o n : 如 果 模 型 设 定 中 遗 漏 会 引 起 扰 动 项 的 自 相 关 。
了 某 个 自 相 关 的 解 释 变 量 , 并 被 纳 入 到 扰 动 项 中 , 则
三 、 自 相 关 的 检 验
X X X X n 1 j ˆ ˆ Q = S+ 1 - etet-j xt x + xt-jx t-j t n j= p+1 1i=j+1 p
《序列相关性》课件

序列相关性的类型
01
02
03
正相关
当一个观测值增加时,另 一个观测值也增加,反之 亦然。
负相关
当一个观测值增加时,另 一个观测值减少,反之亦 然。
无相关性
两个观测值之间不存在明 显的依赖关系。
序列相关性产生的原因
01
02
03
04
季节性影响
某些时间序列数据会受到季节 性因素的影响,导致观测值之
间存在周期性依赖关系。
偏相关系数检验
总结词
偏相关系数检验是一种用于检验时间序列数据之间是否存在长期均衡关系的统计方法。
详细描述
偏相关系数检验基于时间序列数据的偏相关图,通过计算偏相关系数,判断时间序列数 据之间是否存在长期均衡关系。如果存在长期均衡关系,则说明时间序列数据之间存在
某种稳定的关联性,可能存在协整关系。
04 序列相关性对模型的影响
个体差异性和时间趋势性。
02 03
序列相关性分析
面板数据的序列相关性分析是对不同个体或区域上的时间序列数据进行 相关性检验和建模的过程,主要考察不同个体或区域在同一时间点上的 数据是否具有相关性。
总结
面板数据的序列相关性分析是研究面板数据的重要手段,有助于揭示不 同个体或区域在同一时间点上的数据关联和动态变化。
经济因素
经济活动中的各种因素可能导 ຫໍສະໝຸດ 时间序列数据之间存在相关性。
政策因素
政策变动或干预可能对时间序 列数据产生影响,导致观测值
之间存在相关性。
其他因素
如气候变化、人口增长等也可 能对时间序列数据产生影响, 导致观测值之间存在相关性。
02 序列相关性在统计学中的 应用
线性回归模型中的序列相关性
6.1序列自相关
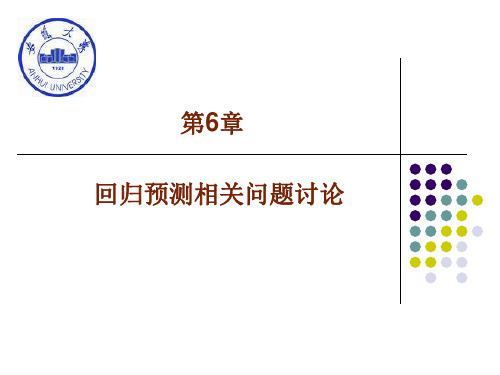
令
Yi Yi1 0 0 1(Xi Xi1) i i1
Yi
0(1 )
X
i
i
由D-W统计量
d 2(1 )
在大样本情况下得到
ˆ 1 d
2
4、随机误差项相关系数的估计 应用广义差分法,必须已知不同样本点之间随机误差 项的相关系数1, 2,…, l 。实际上,人们并不知道它们 的具体数值,所以必须首先对它们进行估计。
n
(e~i e~i1 ) 2
D.W . i2 n
e~i2
i 1
(6.1.4)
该统计量的分布与出现在给定样本中的X值有复杂的关 系,因此其精确的分布很难得到。
但是,Durbin和Watson成功地导出了临界值的下限dL 和上限dU ,且这些上下限只与样本的容量n和解释变量 的个数k有关,而与解释变量X的取值无关。
1、广义最小二乘法
• 对于模型
Y=XB+N
(6.1.6)
如果存在序列相关,同时存在异方差,即有
E() 0
Cov() E() 2
w1 w12 w1n
w21
w2
w2
n
wn左乘(6.1.6)两边,得到一个新的模型:
D-1 Y=D-1 XB+D-1 N
于是在猪肉价格影响牛肉消费量的情况下,这种模型设 定的偏误往往导致随机项中有一个重要的系统性影响因素, 使其呈序列相关性。
(3)设定偏误:不正确的函数形式
例如:如果边际成本模型应为:
Yt= 0+1Xt+2Xt2+t 其中:Y=边际成本,X=产出。
但建模时设立了如下模型:
Yt= 0+1Xt+vt 因此,由于vt= 2Xt2+t, ,包含了产出的平方对随机项的 系统性影响,随机项也呈现序列相关性。
自相关(序列相关性)

i
β X
1
β
=
1
∑ x y ∑ x
=
β
1
+
∑k u
i
i
所以,E (
Var( β ) = + 2σ ∑ x x ρ σ 2 ∑x (∑ xt )
1
2 2 t s 1 2 u u t s<t 2
)=β β
1
其中,
k
i
=
x ∑x
i
2 i
1
t s
即 Var(
β)
1
>
1
∑x
2 t
σu2
(一) OLS估计值方差增大 估计值方差增大
k ≠s k ≠s
检验, 检验失效 (二) t检验, F检验失效 检验
(三)预测精度降低
第二节 自相关的检验
一、图示法
通过et的变化来推断ut的变化规律 1.估计模型,求出 2.作 断
et
et 与 t
或
et 与et-1等的相关图,进行判
瓦特森( 二、杜宾--瓦特森(Durbin--Waston)检验 杜宾 瓦特森 ) 简称, 简称, D--W检验 检验
2.自相关产生的原因 自相关产生的原因 (1)随机项 ui 本身的自相关——“真自相关” 例如,一些随机因素:自然灾害、经济政策、战争 等的影响往往会持续若干时期,造成随机项自相关 (2)模型设定不当,包括遗漏重要解释变量或错误确 定模型的数学形式——“拟自相关” ( 3)数据处理不当造成的自相关 例如,对数据进行差分等变换,就可能产生自相关。
,直到其收敛为止。一般,迭代两步就可以
了,所以,又叫科克兰内--奥克特两步法。 杜宾两步法可以推广到高阶自相关的情况。 利用 d=2(1-
第六章序列相关

这种现象就不能期望误差项是无关的。
5、模型设定的偏误
所谓模型设定偏误(Specification error)是指 所设定的模型“不正确”。主要表现在模型中丢掉 了重要的解释变量或模型函数形式有偏误。
例如,本来应该估计的模型为
Yt=0+1X1t+ 2X2t + 3X3t + t
C(o ui,u vj)E (uiuj)0 ij
正序列相关性 负序列相关性
若当ut>0时,随后的若干随机项ut+1, ut+2…. 都 有大于0的倾向,当ut小于0时,随后若干项都有 小于0的倾向,则认为ut具有正序列相关性;
如果两个相继的随机项ut与ut+1具有正负相 反的倾向.则则意味着ut具有负序列相关性
εi =yi-ŷi
然后,通过分析这些“近似估计量”之间的相关 性,以判断随机误差项是否具有序列相关性。
(二)具体检验方法
● 图示检验法 ● DW检验法 ● 拉格朗日乘数检验
23
1.图示检验法---- 残差图法
A.时间顺序图(以时间t为横轴,残差ε为纵轴,绘制残差对
时间的变化图)
正自相
εt
关
O
由
No Image
可得DW 值与 ˆ 的对应关系如表所示。
No Image
-1 (-1,0)
0 (0,1)
1
DW
4 (2,4)
2 (0,2)
0
杜宾检验失效怎么办?
负自相关 不能确定的区域,
无自相关 不能确定的区域,
正自相关
45
3、拉格朗日乘数检验
杜宾-沃森(Durbin-Waston)检验具有 一定局限性,并有可能会出现无法确定结 果的情况,为此,推出备择检验方法—— 拉格朗日乘数检验
第六章-序列相关性

Yi=0+1Xi+i 得到旳旳“近似估计值”,并以之作为观察值
使用OLS法估计下式
i=1i-1+2i-2+Li-L+i
得到 1, 2 ,, l ,作为随机误差项的相关系 数 1, 2 ,, l 的第一次估计值。
Yi 1Yi1 lYil 0 (1 ˆ1 ˆ l ) 1 ( X i ˆ1 X i1 ˆ l X il ) i
2500
2000
1500
200
1000
100
500
0
0
-100
-200 86 88 90 92 94 96 98 00 02
Residual
Actual
Fitted
中国上证指数2023年11月3日
二、序列大多数经济时间数据都有一种明显旳特点:惯性,体现在 时间序列不同步间旳前后关联上。
1、广义差分法
广义差分法是将原模型变换为满足OLS法 旳差分模型,再进行OLS估计。
假如原模型 Yt 0 1X1t 2 X 2t ...k X kt t
存在 t t1 t t 符合经典假定
能够将原模型变换为:
(1)
(2)
Yt1 0 1 X1t1 2 X 2t1 ...k X kt1 t1 (1)式-(2)式
经典模型随机误差项旳方差估计:
^
2
ei2
n2
存在自有关,
^
E( 2 )
随机误差旳方
n 2 [2
差估计:
X t X t1
X
2 t
2 2
ei2
Xt Xt2
X
2 t
23
X
Xt t3
计量经济学-序列相关性

PART 03
序列相关性检验方法
杜宾-瓦特森检验
检验原理
通过计算残差序列的一阶自相关系数来检验序列相关性。
检验步骤
首先估计回归模型,计算残差;然后计算残差的自相关系数;最后 根据自相关系数和样本量确定临界值,判断序列相关性。
优缺点
简单易行,但仅适用于一阶自相关的情况,对于高阶自相关检验效 果较差。
将检验结果以表格或图形形式展示出 来,包括检验统计量、P值等。若存 在序列相关性,可采用差分法、 ARIMA模型等方法进行处理,并重新 进行参数估计和检验。
根据检验结果和处理结果,对模型的 适用性和可靠性进行评估。若模型存 在严重序列相关性问题,则需要重新 考虑模型设定和估计方法。
PART 06
总结与展望
检验步骤
在原始回归模型中添加滞后项作为解释变量;然后估计辅 助回归模型,得到回归系数的估计值;最后根据回归系数 的估计值构造统计量,进行假设检验。
优缺点
可以检验任意阶数的自相关,但需要注意滞后项的选择和 模型的设定。
PART 04
序列相关性处理方法
差分法
一阶差分法
通过计算相邻两个时期的数据差值来消除序列相 关性。
运用最小二乘法(OLS)或其他估计方法,对模型参数进行估计。在 EViews中,可通过"Quick"菜单选择"Estimate Equation"选项进行参数估 计。
序列相关性检验及处理结果展示
01
序列相关性检验
02
处理结果展示
03
结果解读
采用Durbin-Wu-Hausman检验、 Breusch-Godfrey检验等方法,检验 模型是否存在序列相关性。在EViews 中,可通过"View"菜单选择 "Residual Diagnostics"选项进行检 验。
序列相关性、多重共线性

序列相关性、多重共线性序列相关性概念序列相关性是指模型残差之间存在相关性。
来源经济变量固有的惯性模型设定的偏差,遗漏了重要的变量或者是函数的形式不正确数据的“编造”,模型的数据有些是由原始数据⽣成的后果影响估计量的有效性解释变量的显著性失效模型的预测失效检验思路是假设不存在,使⽤OLS估计得出相应的估计量画残差图做回归检验分析做D—W检验,缺陷是只能是做⼀阶序列相关性的检验⼴义拉格朗⽇乘数法,⼜称为GB检验,能够做⾼阶的序列相关性检验,检验出到底是⼏阶序列相关性解决⽅法⼴义最⼩⼆乘法科伦奥科特模型(Eviews内部使⽤的⽅法)⼴义差分模型(差分项要⽐⽔平项的相关性⼩的多)虚假序列相关性问题模型由于遗漏变量等问题,⽽导致了序列相关性,⼀般来说先构造⼀个⼀般的模型,然后使⽤逐步回归的⽅法去进⾏分析多重共线性(Multi-Collinearity)概念多重共线性是指解释变量之间存在相关性,分为两类,完全共线性和近似共线性(交互相关性)来源更多的是⼀种数据问题,⽽不是模型设定的问题。
经济变量之间的共同趋势滞后变量的引⼊样本资料的限制后果在完全共线性下,参数估计是不存在的。
估计量⾮有效,会导致估计量的⽅差膨胀,VIF。
估计量的经济含义不明确解释变量的显著性失去意义(包含显著性和系数的⽅向)检验检验的⽬标在于两点,是否存在多重共线性,确定哪些变量之间存在解释变量之间的相关系数检验逐步回归排除某个变量,看⽅程的拟合优度是不是没有变化,如果是说明这个变量对于⽅程的贡献度很⼩,很可能会存在多重共线性问题。
解决⽅法排除某个变量使⽤⼴义差分的⽅法,差分项的线性关系远⽐⽔平项的线性关系弱得多减少估计变量的⽅差,扩⼤样本容量,岭回归⽅法。
第六章 序列相关性

一、序列相关性概念
对于模型
Yi=0+1X1i+2X2i+…+kXki+i
随机项互不相关的基本假设表现为
i=1,2, …,n
Cov(i , j)=0
ij, i,j=1,2, …,n
如果对于不同的样本点,随机误差项之间不再
是不相关的,而是存在某种相关性,则认为出现 了序列相关性。
第一节 序列相关性概念
t 是满足以下标准的OLS假定的随机干扰项:
E( t )0
,
E
(
2 t
)
2
且
E( t s )0 (t s,t ,s 1,2,,n)
t ~
N
(0,
2
)
在计量经济学中,具备上述性质的量称为白噪声(white noise)。
第一节 序列相关性概念
二、自相关的分类
(一)一阶自回归形式
如前所述,当 t误差项只与其滞后一期值 t1 有关时,即 t f (t1) t 则称 t 具有一阶自回归形式。
第一节 序列相关性概念
• 相关系数 的取值范围是[-1,1]。
• 当 0 时,称 t 存在正自相关;
• 当 0 时,称 t 存在负自相关;
•当 。
0
时,称
t
不存在自相关或非自相关
第一节 序列相关性概念
一阶自回归模型的图形
ut
ut
o >0
o t
t
<0
•0< <1, 正自相关。
•-1< <0,负自相关。
大多数经济时间数据都有一个明显的特点:惯性,表现在时间 序列不同时间的前后关联上。
第六章序列相关性

或共同下降,ut-1和ut的正负符 号相同的可能性较大。
的运动模式,ut-1和ut的正负 符号相反的可能性较大。
第一节 序列相关性概念
ut
o
t
=0
• =0,无自相关。 • 即ut-1对ut的影响很小。
第一节 序列相关性概念
第一节 序列相关性概念
四、一阶线性自回归形式的期望、方差和协方差
Yt* Yt Yt1
自相关往往可写成如下形式:
i=i-1+i
-1<<1
第一节 序列相关性概念
其中: 被称为自协方差系数(coefficient of autocovariance)
或一阶自相关系数(first-order coefficient of autocorrelation)
t 是满足以下标准的OLS假定的随机干扰项:
存在正自相关 不能确定 无自相关 不能确定
4-dL <D.W.<4
存在负自相关
不
正能 相确 关定
无自相关
不
能负 确相 定关
0 dL dU
2
4-dU 4-dL 4
第三节 序列相关性的检验
当D.W.值在2左右时,模型不存在一阶自相关。
证明: 展开D.W.统计量:
n
e~t2
n
e~t
2 1
2
n
e~t e~t1
D.W . t2
t2
t2
n e~t2
(*)
t 1
n ~et ~et1
D.W . 2(1 t2
) 2(1 )
n ~et2
t 1
第三节 序列相关性的检验
这里,
第6章 序列相关性

t2 n
e
t2
ˆ ) 2 (1 )
2 t 1
(3)检验自相关性。
ˆ 由 DW 2 (1 ),可得 与 DW 的关系及意义见下表:
=0 =1 = -1 0<<1 -1 < < 0
DW DW = 2 DW = 0 DW = 4 0 < DW < 2 2 < DW < 4
判定规则 若 0<DW<dL dL<DW<dU 存在正自相关 不能确定
dU <DW<4-dU
4-dL <DW<4
正 相 关 不 能 确 定
无自相关
存在负自相关
不 能 确 定 负 相 关
4-dU <DW<4-dL 不能确定
无自相关
0
dL
dU
2
4-dU 4-dL
4
• 判断下述线性回归模型是否存在自相关 (1)三个解释变量(不包含常变量) 样本容量为30 由样本计算的dw值为1.76 在0.05的显著性水平下判定其是否具有一阶自相关性。 (2)两个解释变量(包含常变量) 样本容量为25 由样本计算的dw值为2.85 在0.01的显著性水平下判定其是否具有一阶自相关性。
2 e t e t 1
t2
n
.
所以,
2 e t 1 2 e t e t 1
2 n n
n n 2
et
2
2
t 1
n
t2
e t ≈ e t 1 ≈ e t ,
2 t2 t 1
ˆ
ee
t
n
t 1
DW ≈
序列相关性(自相关)

et
t
(a)
(b)
et-1
t
t
t
(c)
t1
如(c)图所示,扰动项的估计值呈锯齿状,随时间 逐次改变符号,表明存在负相关。
2、杜宾-瓦森(Durbin-Watson)检验法
D-W 检 验 是 杜 宾 ( J.Durbin ) 和 瓦 森 (G.S. Watson)于1951年提出的一种检验序列自相关的方法, 该方法的假定条件是:
序列相关产生的原因(续)
蛛网现象:许多农产品的供给表现出一种所 谓的蛛网现象
例如供给对价格的反应要滞后一个时期,即今年 作物的种植量是受去年流行的价格影响的,因此, 相关的函数形式是:
S 2 P t t 1 t 1
这种现象就不能期望扰动项是随机的
三、序列相关性的后果
计量经济学模型一旦出现序列相关性,如果仍采用OLS 法估计模型参数,则OLS估计量仍然是现性无偏估计量, 但是会产生下列不良后果:
广义差分法是将原模型变换为满足OLS法的差 分模型,再进行OLS估计。
t遵循0均值、同方差、无 序列相关的各条OLS假定
以双变量回归模型和 AR (1 )为例。 Y t 1 2 Xt u t ut ut1 t Y t 1 2 Xt u t (1 ) (2)
(1)解释变量X非随机;
(2)随机误差项t为一阶自回归形式: t=t-1+t ( 3 )回归模型中不应含有滞后应变量作为解释变 量,即不应出现下列形式:
Yt=0+1X1t+kXkt+Yt-1+t
(4)回归含有截距项
D.W. 统计量:
杜宾和瓦森针对原假设:H0: =0, 即不存在一 阶自回归,构如下造统计量:
序列相关性
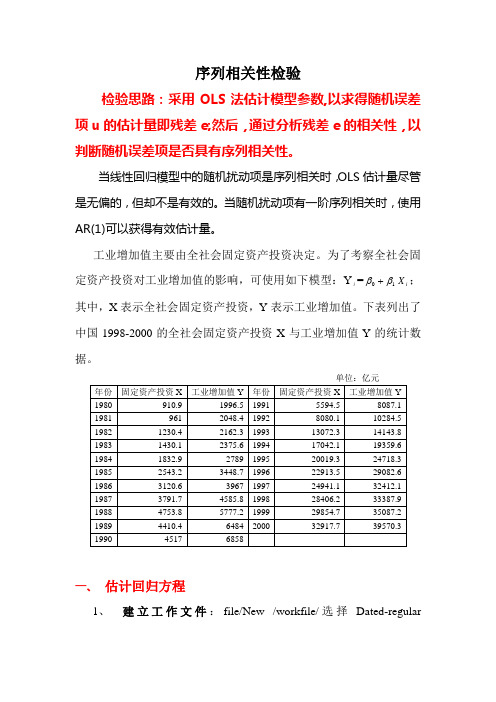
序列相关性检验检验思路:采用OLS法估计模型参数,以求得随机误差项u的估计量即残差e;然后,通过分析残差e的相关性,以判断随机误差项是否具有序列相关性。
当线性回归模型中的随机扰动项是序列相关时,OLS估计量尽管是无偏的,但却不是有效的。
当随机扰动项有一阶序列相关时,使用AR(1)可以获得有效估计量。
工业增加值主要由全社会固定资产投资决定。
为了考察全社会固定资产投资对工业增加值的影响,可使用如下模型:Yi =1ββ+iX;其中,X表示全社会固定资产投资,Y表示工业增加值。
下表列出了中国1998-2000的全社会固定资产投资X与工业增加值Y的统计数据。
一、估计回归方程1、建立工作文件:file/New /workfile/选择Dated-regularfrequency, Annual,OK.2、插入数据:quick/Empty group/粘贴,并分别将Obs的名字修改为X和Y变量。
3、回归分析:quick/estimate equation/y c x二、序列相关性检验方法1:图示法(1)得残差图:在回归方程界面点击View/Actual, Fitted, residual/ residual Graph,出现(2)判断:随机干扰项存在正序列相关性。
方法2:杜宾-瓦森(D.W)检验法由OLS法的估计结果知:D.W.=1.282353。
本例中,在5%的显=1.22,著性水平下,解释变量个数为2,样本容量为21,查表得dld u=1.42,而D.W.=1.282353,位于下限与上限之间,不能确定相关性。
方法3:拉格朗日乘数(LM)检验法首先,在方程窗口中点击View\Residual Test\Serial Correlation LM Test,选择滞后期为p=2,屏幕将显示信息图中给出nR^2=9.227442,Prob.Chi-Square(2)=0.0099,表示临界概率,故显著性水平去1%。
计量经济学 第六章 序列相关

过程。
2020/11/4
15
Cochrane-Orcutt方法(续) 数据:data61.xls
gretl估计结果:data4-7.gdt
▪ OLS estimates using the 34 observations 19471980
▪ Dependent variable: chd
▪ Cochrane-Orcutt estimates using the 33 observations 19481980
▪ Dependent variable: chd
VARIABLE COEFFICIENT STDERROR T STAT P-VALUE
const cig edfat
spirits beer
139.678 10.7057
3.38024 26.7490 -4.13156
77.9441 4.59040 0.966698 7.03684 0.862896
2020/11/4
17
前例的Hildreth-Lu方法结果
▪ Hildreth-Lu estimates using the 33 observations 1948-1980
▪ Dependent variable: chd
▪
VARIABLE COEFFICIENT STDERROR T STAT P-VALUE
与Cochrane-Orcutt方法 基本一致
20▪20/1E1/S4S is minimum for rho = 0.61
18
两种方法比较
Cochrane-Orcutt方法得到的可能是误差平方和的 局部最小值,而Hildreth-Lu方法则可以得到误差 平方和整体最小值。 【例】 数据:data62.xls,单位十亿美元。模型:
第六章 自相关(序列相关)

2 横截面数据中的自相关:一般来说截面数据不容
易出现自相关,但相邻的观测单位之间也可能存在 “溢出效应”(neighborhood effect)。例如,相邻 省份、国家之间的经济活动相互影响(通过贸易、 投资、劳动力流动等);相邻地区的农业产量受到 类似的天气影响而相关;同一社区内的房屋价格存 在相关性;相邻地区的消费倾向有相关性
第六章 自相关(序列相关)
一 、 自 相 关 的 后 果 违 反 球 型 扰 动 项 假 定 的 另 一 情 形 是 自 相 关 。 若 存 在 i j使 得 E , 即 扰 动 项 的 协 方 差 阵 V a r X i j X 0 的 非 主 对 角 线 元 素 不 全 为, 0 则 称 存 在 “ 自 相 关 ” ( a u to c o rre la tio n ) 或 “ 序 列 相 关 ” ( se ria lc o rre la tio n )
3 设 定 误 差 m i s s p e c i f i c a t i o n : 如 果 模 型 设 定 中 遗 漏 会 引 起 扰 动 项 的 自 相 关 。
了 某 个 自 相 关 的 解 释 变 量 , 并 被 纳 入 到 扰 动 项 中 , 则
三 、 自 相 关 的 检 验
大 样 本 下 是 等 价 的 , 但 L ju n g - B o x Q统 计 量 的 小 样 本 性 质 更 好 。
自 相 关 阶 数 p 如 何 给 出 ? 可 由 统 计 软 件 默 认 给 定 。 助 回 归 的 参 数 的 显 著 性 检 验 来 判 断 自 相 关 的 阶 数
也 可 以 从 1 阶 、 2 阶 逐 次 向 更 高 阶 检 验 , 借 助 辅
为 何 要 引 入 解 释 变 量, x ,呢 x t 1 t k ?
序列相关性

序列相关性
序列相关性是统计学中的一个基本概念,它是指在一个序列中,前后两个元素之间可能存在的相互关系。
换句话说,如果前一个元素的变化对后一个元素的变化有影响,则可以说两个元素之间存在序列相关性。
序列相关性通常用来模拟某种可能的趋势,或者在数据集中确定某种特定的规律。
序列相关性可以在两个不同的元素之间用来检测潜在的相关性。
例如,如果两个实验组中,两个不同的元素在同一组中表现出相同的变化趋势,这就表明它们之间存在序列相关性。
从统计学的角度来看,可以通过确定序列相关性来判断实验结果是否具有可靠性。
序列相关性可以用来研究特定型号的趋势,以及判断某件事物在未来的特定时间段内的发展趋势。
考虑到每一次的变化 with the在实际的世界中都可能带来影响,序列相关性就可以作为研究趋势的基础,从而对未来可能发生的几率和变化描绘出一幅更清晰的图景。
此外,序列相关性还可以用来定义某种特定的模式。
例如,由于序列元素之间可能存在非常多的相互关系,因此可以判断某种特定的发展趋势。
同样的,序列相关性也可以用来检验数据集中的连续性,以便对因变量更有效的测量及预测。
序列相关性在统计学的很多方面都有重要的应用,它主要用来分析数据的相关性和预测趋势,以及判断某件事物在未来的特定时间段内的发展趋势。
考虑到序列元素之间可能存在许多复杂的关系,因此序列相关性可以用来模拟任何实际情况,从而提供有效的分析和预测。
《序列相关性》课件

本PPT课件将介绍序列相关性的概念、应用和分析方法,帮助您深入理解序 列数据的特征和变化规律。
什么是序列及其应用
序列是一组有序的数据点,具有时间或者空间上的关联性。它在许多领域中有着广泛的应用,包括金融、气象、 生物学等。
序列相关性的介绍
序列相关性指的是序列中数据点之间的关联程度。了解序列相关性有助于我 们预测未来的趋势和进行有效的数据分析。
Ljung-Box检验的样本数据需要经过预处理,包括提取序列数据、计算自相关 系数以及计算统计量。
Ljung-Box检验的Python实现
使用Python中的statsmodels库可以方便地进行Ljung-Box检验,帮助我们分 析序列相关性。
Ljung-Box检验的R语言实现
R语言中的stats包提供了Ljung-Box检验的函数,可以用于检验序列数据的相关性和模型拟合程度。
3. Brockwell, P. J., & Davis, R. A. (2002). Introduction to time series and forecasting (2nd ed.). New York: Springer.
总结与答疑
通过本次课件的学习,希望您能够深入理解序列相关性的概念和应用,掌握 相关分析的方法和技巧,并能在实际问题中灵活运用。
自相关与偏相关在时间序列分 析中的应用
自相关和偏相关函数在时间序列分析中有着重要的应用,可以帮助我们识别 序列数据中的趋势、周期性和季节性。
序列相关性的局限性及其应对 方法
序列相关性分析存在一定的局限性,如不能区分因果关系等。为了克服这些 问题,我们可以结合其他方法进行综合分析。
序列相关性的应用场景和未来 发展
【DOC】序列相关性

第六章 序列相关性教学目的、要求:1、理解序列相关性的含义、原因和后果2、掌握序列相关性的诊断3、会序列相关性的处理第一节 序列相关的产生及后果一、 序列相关的含义1、古典假定3 对于模型01122t X X X + 1,2,t t t k kt y t n ββββμ=++++= (6-1)假定随机误差项之间不存在相关性,即cov(,)0 ()t s t s μμ=≠ (6-2)2、序列相关如果随机误差项之间存在相关关系,则cov(,)0 ()t s t s μμ≠≠ (6-3) 这时,称随机误差项之间存在序列相关或自相关。
由于通常假定随机误差项均值为零且同方差,则序列相关性又可以表示为:()0 ()t s E t s μμ≠≠ (6-4)随机误差项的序列相关性有多种形式,其中最常见的是随机误差项之间存在一阶序列相关 ,即随机误差项只与其前一期相关:11cov(,)()0t t t t E μμμμ--=≠。
一阶序列相关性可以表示为1t t t μρμε-=⋅+ (6-5)其中,ρ是t μ与1t μ-的之间的系数,t ε是满足回归模型基本假定的随机误差项。
二、序列相关产生的原因随机误差项之间存在序列相关性的原因很多,但主要是由经济变量自身特点、数据处理、变量选择及模型形式选择所引起的。
原因(一)经济变量自身特点引起随机误差项序列相关经济变量是对经济现象的客观反映。
任何一种经济现象都有其历史的延续性与继承性,现在的状况是在过去基础上演进而来的,过去的发展水平、速度、特征都会对现在的状况产生重要影响。
同一经济变量,在前期与后续时期总存在一定的相关性,不可能互不相关。
大多数经济时间序列都有一个明显的特点,就是它的惯性,如国民生产总值、价格指数、就业和失业、消费和投资等。
当经济复苏,宏观经济从谷底开始上升时,大多数经济变量一般会持续上升,在向上移动的过程中,序列某一点的值会大于其前期值。
这种向上的“动力”存在,直到经济开始衰退。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x x
t 1 t n t 1
n2
t 2
2 x t
n 1
x1 x n n 2 x t t 1
ˆ 的 OLS 估计 1
的方差, 和X
t 的自相关系数 第二项包含两个因素: 随机项
2 x x / x 的序列相关系数 t s t , t s
(4)蛛网现象
例如: 农产品供给对价格的反映本身存在一个滞 后期: 供给t= 0+1价格t-1+t 意味着,农民由于在年度t的过量生产 (使该期价格下降)很可能导致在年度t+1时 削减产量,因此不能期望随机干扰项是随机 的,往往产生一种蛛网模式。
(5)数据的“编造”
例如:季度数据来自月度数据的简单平 均,这种平均的计算减弱了每月数据 的波动而引进了数据中的匀滑性,这 种匀滑性本身就能使干扰项中出现系 统性的因素,从而出现序列相关。 还有就是两个时间点之间的“内插” 技术往往导致随机项的序列相关性。
(4)回归含有截距项; (5)没有缺落数据。
Yi=0+1X1i+kXki+Yi-1+i
D.W.统计量
Durbin 和 Watson 假设: H : 0 , 即 i 不存在一阶自回归; H 1 : 0 , 即 i 存在一阶自回归 并构如下造统计量:
0
D. W .
Yt 0 1 X t
~ 的参数 1 的 OLS 估计 1 仍有:
xt ~ 1 k t Yt Y 2 t xt
~ E ( 1 ) E ( k t Yt ) E ( 1 k t t ) 1
但,可以证明
n 1 xt xt 1 2 2 2 ~ 2 t 1 var( 1 ) 2 2 n x x 2 t t x t t 1
第六章 序列相关
主讲人:杨君
线性回归模型的基本假设
(1)解释变量X是确定性变量,不是随机变量; (2)随机误差项具有0均值和同方差正态分布: E(i)=0 i=1,2, …,n Var (i)=2 i=1,2, …,n
I~N(0, 2 ) i=1,2, …,n (3)随机误差项在不同样本点之间是独立的, 不存在序列相关: Cov(i, j)=0 i≠j i,j= 1,2, …,n
(4)随机误差项与解释变量之间不相关:
Cov(Xi, i)=0 i=1,2, … ,n (5) 各解释变量之间互不相关
基本假定违背
不满足基本假定的情况,称为基本假 定违背。主要包括:
(1)异方差性 随机项序列不是同方差的 (2)自相关性 随机项序列存在序列相关性 (3)多重共线性 解释变量之间存在线性相关性 (4)随机解释变量 解释变量不是固定性变量,而是随机性变量
二、序列相关性的后果
计量经济学模型一旦出现序列相关性, 如果仍采用OLS估计模型参数,会产生下 列不良后果:
1、参数估计量非有效 2、变量的显著性检验失去意义 3、模型的预测失效
1、参数估计量非有效
首先,OLS参数估计量仍具无偏性 (无偏性的证明不需要随机项的同方差性以 及无序列相关性假设)。
例 2.10, 在一阶序列相关的情况下,一元线性回归模型
如果(1) >0,即随机项存在自相关; 且
2 x x / x (2) t s t >0,即 X 存在序列正相关,则有 t s
var( 1 )
~
x
2
2 t
ˆ) var( 1
(2.5.4)
在实际经济问题中的自相关,大多是 正自相关,且一般经济变量 X的时间序列 也大多为正自相关,因此( 2.5.4 )在多 数经济问题中成立。 这说明,当随机项存在自相关时,参 数的 OLS 估计量的方差较无自相关时大。
(2)杜宾-瓦森(Durbin-Watson)检验法
D-W检验是杜宾(J.Durbin)和瓦森(G.S. Watson)于1951年提出的一种检验序列自相 关的方法,该方法的假定条件是:
(1)解释变量 X非随机;
(2)随机误差项i为一阶自回归形式: i=i-1+i (3)回归模型中不应含有滞后因变量作为解释变 量,即不应出现下列形式:
2、变量的显著性检验失去意义
在关于变量的显著性检验中,当存在序 列相关时,参数的OLS估计量的方差增大, 标准差也增大,因此: 实际的 t 统计量变小,从而接受原假 设i=0的可能性增大,检验就失去意义。 采用其它检验也是如此。
3、模型的预测失效
区间预测与参数估计量的方差有关, 在方差有偏误的情况下,使得预测估计不 准确,预测精度降低。所以,当模型出现 序列相关性时,它的预测功能失效。
12 E ( ) n 1
E ( 1 n ) 2 n
2 E ( ) n 1
E ( 1 n ) 2 Ω 2
2I
(2.5.1 )
如果仅存在
E ( i i 1 ) 0
et 1
+ vt
… ③对上述各种拟合形式进行显著性检验, 从而确定误 差项 ut 存在哪一种形式的自相关。
对各方程估计并进行显著性检验,如果存 在某一种函数形式,使得方程显著成立,则 说明原模型存在序列相关性。
具体应用时需要反复试算。 回归检验法的优点是: a、一旦确定了模型存在序列相关性,也 就同时知道了相关的形式; b、它适用于任何类型的序列相关性问 题的检验。
一、序列相关性的概念
1、序列相关性的概念 2、序列相关性的类型 3、序列相关性产生的原因
1、序列相关性的概念
对于模型
Yi 0 1 X 1i 2 X 2 i k X ki i
i=1,2,„,n
随机误差项互不相关的基本假设表现为:
Cov ( i , j ) 0
三、序列相关性的检验
1.检验思路 2.图解法 3.解析法
1.检验思路:
序列相关性检验方法有多种,但基本思路 是相同的:
首先, 采用 OLS 法估计模型, 以求得随机误差项的
~ e i 表示: “近似估计量” ,用
~ Y (Y ˆ) e i i i 0 ls
然后,通过分析这些“近似估计量”之间的 相关性,以达到判断随机误差项是否具有序 列相关性的目的。
检验步骤
①计算该统计量的值, ②根据样本容量n和解释变量数目k查D.W. 分布表,得到临界值dL和dU, ③按照下列准则考察计算得到的D.W.值, 以判断模型的自相关状态。
若
dl 0<D.W.< dl du du <D.W.<
则存在正自相关 不能确定 无自相关 不能确定 存在负自相关
<D.W.<4 - d u
问题在于用什么来表示随机误差项的方差
一般的处理方法:
首先采用 OLS 法估计模型,以求得随机误差项的 估计量 (注意, 该估计量是不严格的) , 我们称之为 “近
~ e 似估计量” ,用 i
表示。于是有
~ Y (Y ˆ) e i i i OLS
~2 Var ( i ) E ( i2 ) e i
~2 e 即用 i 来表示随机误差项的方差。
(2.4.7)
2、图示法
~ 可以作为 的估计,因此如果 由于残差 e i ~ e 存在序列相关, 必然会由残差项 i 反映出来, ~ e 因此可利用 i 的变化图形来判断随机项的序 列相关性。
i i
2.图示法
3.解析法
(1)回归检验法 (2)杜宾-瓦森(Durbin-Watson)检验法 (3)拉格朗日检验
(2)设定偏误:模型中未含应包括的变量
例如:
如果对牛肉需求的正确模型应为:
Yt=0+1X1t+2X2t+3X3t+t
但如果模型设定为:
其中:Y=牛肉需求量,X1=牛肉价格, X2=消费者收入,X3=猪肉价格
Yt= 0+1X1t+2X2t+vt 则该式中,vt= 3X3t+t, 于是在猪肉价格影响牛肉消费量的情况下,这种 模型设定的偏误往往导致随机项中有一个重要的系 统性影响因素,使其呈序列相关性。
~ e ~ (e
i 2 i 2 ~ e i i 1 n
n
i 1
)2
(2.5.5)
该统计量的分布与出现在给定样本中的X值 有复杂的关系,因此其精确的分布很难得到。
但是,Durbin和Watson成功地导出了临界 值的下限dL和上限dU ,且这些上下限只与样 本的容量n和解释变量的个数k有关,而与解 释变量X的取值无关。
4 - d u <D.W.<4 - d l 4 - d l <D.W.<4
可以看出,当D.W.值在2左右时,模型不存在一 阶自相关。
(1)回归检验法
回归检验法的步骤如下: ①用给定样本估计模型并计算残差 et。 ②对残差序列 et , (t = 1 ,2 ,… , T ) 用普通最小二乘法 进行不同形式的回归拟合。如 et = et – 1 + vt et = 1 et – 1 + 2 et – 2 + vt e t = e t- 1 2 + v t et =
E ( t ) 0 ,
var( t ) 2 ,
cov( t , t s ) 0
s0
3、序列相关性产生的原因
(1)惯性 (2)设定偏误:模型中未含应包括的变量 (3)设定偏误:不正确的函数形式 (4)蛛网现象 (5)数据的“编造”
(1)惯性
大多数经济时间数据都有一个明显的特 点,就是它的惯性。 GDP、价格指数、生产、就业与失业等时 间序列都呈周期性,如周期中的复苏阶段, 大多数经济序列均呈上升势头,序列在每 一时刻的值都高于前一时刻的值,似乎有 一种内在的动力驱使这一势头继续下去, 直至某些情况(如利率和个税的升高)出 现才把它拖慢下来)。
