预应力钢绞线理论伸长量计算实例
预应力计算 钢绞线伸长量计算 一

预应力计算钢绞线伸长量计算一、主要计算公式1.伸长量计算公式:L=△(P平×L)/(E×A)(1)L△:钢绞线伸长量,㎝P平:钢绞线平均张拉力,N L:钢绞线长度,㎝E:钢绞线弹性模量,MPa 一般图纸中有说明,但以试验室实测数据为准;A:钢绞线截面积,单根φ15.24钢绞线有效截面积为140㎜2 2.平均张拉力P平=P×{1-e-(kL+µθ)}/(KL+µθ) (2) P:张拉端张拉力,单根钢绞线张拉力P=1860×0.75×140=195.3KN K:孔道摩擦影响系数,图纸中有说明;µ:钢绞线与孔道的摩擦系数,图纸中有说明,θ:从张拉端至计算截面的孔道切线转角之和,当有平弯时同样参与计算, Rad(弧度) 二、示例图中L1=5米,L2=8,L3=10;θ1=10.30,θ2=8.10,θ3=5.60 钢绞线为15束,弹性模量E=2.0×105MPa, µ=0.15; k=0.001 计算过程如下:1.θ=(10.3+8.1+5.6)/180×π=0.419(Rad);2.根据P平=P×{1-e-(kL+µθ)}/(KL+µθ) =195.3×15×{1-e-(0.001×23+0.15×0.419)}/(0.001×23+0.15×0.419) =2807.3KN3.根据L=△(P平×L)/(E×A)=(2807.3×23)/(2.0×105×140×15)=15.3㎝三、其它1.一般估计时每米钢绞线按伸长0.6㎝考虑,2.两端张拉时算出一半×2,3.根据校顶报告计算张拉力时采用内差法;4.有平弯时也要参与计算。
5.因为误差极小,所以,可用钢绞线的切线长可代替钢绞线长预应力施工工艺)6)6)6)波纹管铺设波纹管铺设波纹管铺设波纹管铺设、、、、锚垫板安装工艺锚垫板安装工艺锚垫板安装工艺锚垫板安装工艺①波纹管要逐根进行外观检查,表面不得有砂眼,咬口必须牢固、不得有松动现象。
预应力钢绞线伸长量计算实例

预应力钢绞线伸长量计算实例预应力钢绞线是一种用于加固混凝土结构的材料,通过施加预先设计的张力,使钢绞线对混凝土施加压力,提高混凝土的承载能力和抗裂性能。
在预应力构件的设计和施工过程中,准确计算钢绞线的伸长量是非常重要的。
我们需要了解一些基本的概念。
预应力钢绞线的伸长量是指在受到预应力张力作用下,钢绞线的长度增加的量。
预应力钢绞线的伸长量可以通过以下公式来计算:伸长量 = 张力 / 弹性模量 * 截面积 * 长度其中,张力是施加在钢绞线上的预应力力值,弹性模量是钢绞线的材料特性,截面积是钢绞线的横截面积,长度是钢绞线的实际长度。
接下来,我们通过一个实例来说明如何计算预应力钢绞线的伸长量。
假设有一根直径为12.7mm的预应力钢绞线,长度为10m,材料的弹性模量为200 GPa,施加在钢绞线上的预应力为200 kN。
我们需要将钢绞线的直径转换为截面积。
钢绞线的截面积可以通过以下公式计算:截面积= π * (直径/2)^2将直径12.7mm代入公式中,我们可以计算出钢绞线的截面积为:截面积 = 3.14 * (12.7/2)^2 = 127.67 mm^2接下来,我们可以使用上述公式计算钢绞线的伸长量:伸长量 = 200 kN / 200 GPa * 127.67 mm^2 * 10 m将单位进行换算,我们可以得到伸长量的结果:伸长量 = 1.27 mm因此,在给定的条件下,这根预应力钢绞线在受到200 kN的预应力作用下,其长度将增加1.27 mm。
需要注意的是,实际的预应力钢绞线在施加预应力后,可能会有一定的弛松现象,即伸长量会有所减少。
这是由于材料的松弛和损失等因素引起的。
因此,在实际工程中,应该根据具体的材料特性和工程要求进行综合考虑和计算。
总结起来,预应力钢绞线的伸长量是通过施加预应力张力,使钢绞线受压变形而产生的。
通过计算预应力钢绞线的伸长量,可以帮助工程师准确设计和施工预应力构件,确保其安全可靠地工作。
预应力理论伸长量计算实例
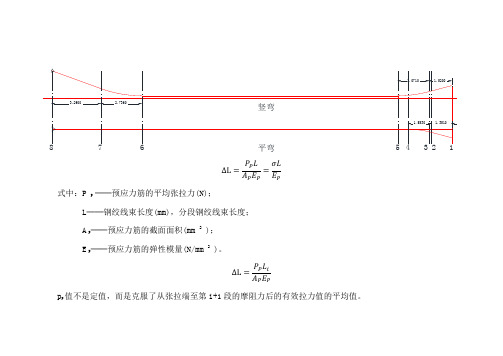
∆L=P P LA P E P=σLE P式中:P P ──预应力筋的平均张拉力(N);L──钢绞线束长度(mm),分段钢绞线束长度;A P──预应力筋的截面面积(mm 2 );E P──预应力筋的弹性模量(N/mm 2 )。
∆L=P P L i A P E Pp p值不是定值,而是克服了从张拉端至第i+1段的摩阻力后的有效拉力值的平均值。
p i+1=p i×e−(kx+μθ)p p=p平均=p i+p i+12式中:χ──从张拉端至计算截面的孔道长度(m);θ──从张拉端至计算截面曲线孔道部分切线的夹角之和(rad);κ──孔道每米局部偏差对摩擦的影响系数;μ──预应力筋与孔道壁的摩擦系数。
平弯又有竖弯,因此各分段钢绞线的分段长度按下列公式计算:长度:L i=√L H2+L Y2角度:θ=√θH2+θY21点锚下控制应力为P1=1395MPa2点控制应力为P2=P1×e−(kx+μθ)χ=L i=√1.3992+1.3992=1.978m κ=0.0015μ=0.15θ=0P2= P1×e−(kx+μθ)=1390.866MPa1-2理论伸长量p p=p平均=p1+p22=1392.933MPaE P=2.0×105MPa∆L=P P L iA P E P=13.8mm3点控制应力为P3=P2×e−(kx+μθ)χ=L i=√0.1742+0.1752=0.2468m κ=0.0015μ=0.15θ=√θH2+θY2=√02+0.26252=0.2625 P3= P2×e−(kx+μθ)=1336.671MPa2-3理论伸长量p p=p平均=p2+p32=1363.768MPaE P=2.0×105MPa∆L=P P L iA P E P=1.7mm4点控制应力为P4=P3×e−(kx+μθ)χ=L i=√1.4072+1.3972=1.9827mκ=0.0015μ=0.15θ=√θH2+θY2=√0.26162+0.26252=0.3706 P4= P3×e−(kx+μθ)=1260.636MPa3-4理论伸长量p p=p平均=p3+p42=1298.653MPaE P=2.0×105MPa∆L=P P L iA P E P=12.9mm5点控制应力为P5=P4×e−(kx+μθ)χ=L i=√0.6872+0.6872=0.9716mκ=0.0015μ=0.15θ=√θH2+θY2=√0.26162+02=0.2616 P5= P4×e−(kx+μθ)=1210.357MPa4-5理论伸长量p p=p平均=p4+p52=1235.496MPaE P=2.0×105MPa∆L=P P L iA P E P=6.0mm6点控制应力为P6=P5×e−(kx+μθ)χ=L i=16.3574mκ=0.0015μ=0.15θ=√θH2+θY2=√02+02=0 P6= P5×e−(kx+μθ)=1181.021MPa5-6理论伸长量p p=p平均=p5+p62=1195.689MPaE P=2.0×105MPa∆L=P P L iA P E P=97.8mm7点控制应力为P7=P6×e−(kx+μθ)χ=L i=2.793mκ=0.0015μ=0.15θ=√θH2+θY2=√02+0.34912=0.3491 P7= P6×e−(kx+μθ)=1116.088MPa6-7理论伸长量p p=p平均=p6+p72=1148.554MPaE P=2.0×105MPa∆L=P P L iA P E P=16.0mm8点控制应力为P8=P7×e−(kx+μθ)χ=L i=3.501mκ=0.0015μ=0.15θ=√θH2+θY2=√02+02=0 P7= P6×e−(kx+μθ)=1110.242MPa7-8理论伸长量p p=p平均=p7+p82=1113.165MPaE P=2.0×105MPa∆L=P P L iA P E P=19.5mm理论伸长量为各段伸长量之和∆L=167.7mm。
40米T梁张拉力及伸长量计算

杨柳河大桥40米预应力T梁张拉计算书编制:复核:审核:2011年3月15日杨柳河大桥40米预应力T梁张拉计算书一、张拉施工方案我合同段施工的阁丫沟大桥40米T梁预应力钢绞线采用高强度低松弛钢铰线,f pk=1860Mpa,公称直径d=15.2mm,公称面积Ay=139mm2,弹性模量Ey=1.95×105Mpa。
40米T梁正弯矩钢束采用8股、9股,钢束控制张拉力σcon=0.75 f pk=1395Mpa。
锚具采用15-8型、15-9型系列整套锚具,管道成孔采用钢波纹管。
所有锚具及钢绞线按材料检验批量抽检,严禁使用无部级以上级别技术鉴定和产品鉴定的材料。
材料要有厂方提供的质量说明书和出厂时间。
钢铰线要防止生锈和影响水泥粘结的油污。
钢铰线下料采用砂轮切割机按加工长度下料,并以22#铁丝编束。
钢筋绑扎结束,装模前由专人对波纹管进行检查,若有孔眼须用胶布缠好,严禁进浆。
预应力张拉前先试压同条件养护砼试件,主梁达到设计强度85%以上且养护龄期不小于7天方可张拉,钢束张拉时应两端对称、均匀张拉,不得集中张拉,并观察主梁的侧弯情况,张拉前先对张拉千斤顶进行校核。
张拉顺序为:50%N2、N3→100%N1→100%N2、N3→100%N4,张拉程序:0-初始应力(10%σk)-σk(持荷2分钟锚固)。
张拉时实行双控,理论伸长量与实际伸长量相差应控制在-6%~+6%之间,否则应分析原因或重新张拉。
张拉严格控制滑丝和断丝,每束不超过1根,累计全片梁小于1%。
张拉完割除钢铰线头,及时压浆。
张拉时做好施工记录。
二、理论伸长值计算1、理论伸长量计算钢铰线采用15.2mm 单根截面面积139mm2标准强度f pk =1860MPa 弹性模量Ey=1.95×105MPa 管道摩擦系数μ=0.25 管道偏差系数K=0.0015锚下控制应力σcon=0.75×f pk=1860×0.75=1395MPa每股控制张拉力1395×139=193905N4股钢绞线控制张拉力N=193905×4=775620N=775.62KN8股钢绞线控制张拉力N=193905×8=1551240N=1551.24KN9股钢绞线控制张拉力N=193905×9=1745145N=1745.15KN计算公式:P P=P(1-e(kx+μθ))/(kx+μθ)△L=P P×L/AP×EP式中:P P--预应力筋平均张拉力(N)P--预应力筋张拉端的张拉力(N)e—常数(e =2.7183)k—孔道摩擦系数(取0.0015)x—从张拉端至计算截面积的孔道长度(米)μ—孔道偏差系数(取0.2)θ—从张拉端至计算截面积曲线孔道部分切线的夹角之和(rad)L--预应力筋的长度(mm)A P --预应力筋的截面面积(mm2)(取139mm2)E P --预应力筋的弹性模量(取1.95*105N/mm2)计算说明:T梁两端对称张拉,所以采用单端计算的方法进行计算。
预应力钢绞线实际伸长量计算方法

预应力钢绞线实际伸长量计算方法范本一:正式风格1.引言本文档介绍了预应力钢绞线实际伸长量的计算方法。
预应力钢绞线在工程中承载重要作用,知道如何准确计算其实际伸长量对工程实施至关重要。
本文将从计算原理、计算步骤以及实例分析等方面进行详细阐述。
2.计算原理预应力钢绞线实际伸长量的计算基于弹性力学理论和预应力破坏准则。
其计算原理主要包括:(1)钢绞线的负应力-应变关系;(2)钢绞线在预应力状态下的伸长量;(3)钢绞线的变形极限。
3.计算步骤(1)根据钢绞线的力学性能参数和工况条件,确定钢绞线的应力状态;(2)根据预应力状态下的应力-应变关系,计算钢绞线的实际应变;(3)根据钢绞线的几何形态和应力-应变关系,计算钢绞线的实际伸长量;(4)考虑到钢绞线的破坏准则,对计算结果进行验证和修正。
4.实例分析以某预应力混凝土梁为例,假设梁的长度为L,采用了n根预应力钢绞线,每根钢绞线的初始预应力为P0。
根据梁的荷载情况和预应力的策略,可以计算出钢绞线的实际应力状态和实际伸长量。
5.附件本文档涉及的附件包括:预应力钢绞线的力学性能参数、预应力混凝土梁的工程图纸以及计算公式等。
6.法律名词及注释(1)预应力:在施工过程中,通过预先施加一定的拉力或压力在结构构件内部产生预设的应力状态,以提高结构的承载能力和使用性能。
(2)钢绞线:由多股钢丝通过扭绞而成的钢缆,用于预应力混凝土结构中的预应力加固。
(3)应变:在外力作用下,物体发生形变的程度。
7.结束语通过本文档,读者可以了解预应力钢绞线实际伸长量的计算方法,并能在工程实践中正确应用。
预应力钢绞线的实际伸长量计算是预应力混凝土工程设计和施工中的重要环节,对于确保结构的安全性和可靠性具有重要意义。
范本二:简洁风格1.计算方法简介本文档旨在介绍预应力钢绞线实际伸长量的计算方法。
预应力钢绞线在工程实践中具有重要作用,因此确切计算其实际伸长量十分必要。
本文将从计算原理、计算步骤以及实例分析等方面进行详细阐述。
预应力钢绞线理论伸长值精确计算实例

预应力钢绞线理论伸长值精确计算实例预应力钢绞线理论伸长值计算结果连续端△L N1= 142.46㎜(142.46÷2=71.23㎜)△L N2= 142.28㎜(142.28÷2=71.14㎜)△L N3= 142.12㎜(142.12÷2=71.06㎜)非连续端△L N1= 142.64㎜(142.64÷2=71.32㎜)△L N2= 142.28㎜(142.28÷2=71.14㎜)△L N3=142.8㎜(142.8÷2=71.4㎜)预应力钢绞线理论伸长值计算书计算依据:根据设计图纸及《钢绞线试验检测报告》,由《桥规》129页公式计算而得出结果:PpL公式:△L=———————ApEp式中:Pp———钢绞线的平均张拉应力(N)直线筋取张拉端的拉力。
L———钢绞线的长度(mm)。
Ap———钢绞线的截面面积(m㎡)。
Ep———钢绞线的弹性模量(N/ m㎡), 根据《钢绞线试验检测报告》取197800(N)。
其中:Pp值(直线筋取张拉端的张拉力),根据《桥规》339页计算而得:Pcon [1—e-(kx+μθ)]公式:Pp=—————————————Kx + μθ式中:Pcon ———钢绞线张拉端的张拉力(N)。
x———从张拉端至计算截面的孔道长度(m)。
θ———从张拉端计算截面曲线孔道部分切线的夹角之和(rad),因为1(rad)=π/ 180°,所以计算弧度角=θ×π/180。
K———孔道每米局部偏差对摩擦系数,由施工规范提供为K=0.0015。
μ———钢绞线与孔道壁的摩擦系数,由施工规范提供为u=0.25。
e———自然对数的底≈2.7182548,常用数学符号。
第一步:先计算正弯矩钢绞线的平均张拉应力和理论伸长值。
一、连续段箱梁的计算A、先计算N1钢绞线。
N1为3束钢绞线,下料长度为20.90m。
1、将N1钢绞线分成三段:AB——直线段,BC——曲线段,CD——直线段2、已知CD段=1.669m(由图纸查得),求AB和BC段长度。
预应力钢绞线实际伸长量计算方法

预应力钢绞线实际伸长量计算方法1、以钢绞线在预应力管道内的长度计算理论伸长量ΔL理为基准时:(1)当采用“行程法”测量伸长量:L实=[(L100%-L10%)+(L20%-L10%)] –ΔL工作长度-ΔL工具锚–ΔL工作锚⑺ L实——钢绞线实际伸长量;L20%——张拉应力为20%б0时,梁段两端千斤顶活塞行程之和;L100%——张拉应力为100%б0时,梁段两端千斤顶活塞行程之和;L10%——张拉应力为10%б0时(即初张应力,规范推荐可取10%-25%),梁段两端千斤顶活塞行程之和;ΔL工作长度——梁段两端千斤顶内钢绞线的无阻伸长量;取理论计算值;ΔL工作锚——梁段两端锚具压缩及钢绞线回缩量;取工艺试验实测值;ΔL工具锚——梁段两端锚具压缩及钢绞线回缩量;取实测值;(2)当采用“直接法”测量伸长量:L实=[(L100%-L10%)+(L20%-L10%)] –ΔL工作长度–ΔL工作锚控制应力*钢绞线截面积*钢绞线的根数=张拉力根据千斤顶和油表的检测报告中的校正方程计算出油表读数即可。
注意:有的需要超张拉来抵消预应力损失,在控制应力中乘以系数即可。
预应力钢绞线伸长量计算方法预应力钢绞线张拉理论伸长量计算公式ΔL=(PpL)/(ApEp)式中:Pp――预应力筋的平均张拉力(N)L――预应力筋的长度(mm)Ap――预应力筋的截面面积(mm2)Ep――预应力筋的弹性模量(N/mm2)Pp=P(1-e-(kx+μθ))/(kx+μθ)式中:Pp――预应力筋平均张拉力(N)P――预应力筋张拉端的张拉力(N)x――从张拉端至计算截面的孔道长度(m)θ――从张拉端至计算截面曲线孔道部分切线的夹角之和(rad)k――孔道每米局部偏差对摩擦的影响系数μ――预应力筋与孔道壁的摩擦系数1、预应力钢绞线张拉实际伸长量ΔL,应建立在初应力后开台量测,测得伸长值还应加上初应力的推算值。
ΔL=ΔL1+ΔL2式中ΔL1从初应力到最大张拉力间的最大伸长值ΔL2初应力以下的推算值关于初应力的取值一般可取张拉控制应力的10—25%。
后张法预应力钢绞线伸长量计算示例
后张法预应力钢绞线伸长量的计算与现场测量控制预应力钢绞线施工时,采用张拉应力和伸长值双控,实际伸长值与理论伸长值误差不得超过6%,后张预应力技术一般用于预制大跨径简支连续梁、简支板结构,各种现浇预应力结构或块体拼装结构。
预应力施工是一项技术性很强的工作,预应力筋张拉是预应力砼结构的关键工序,施工质量关系到桥梁的安全和人身安全,因此必须慎重对待。
一般现行常接触到的预应力钢材主要:有预应力混凝土用钢绞线、PC光面钢丝、刻痕钢丝、冷拔低碳钢丝、精轧螺纹钢等材料。
对于后张法预应力施工时孔道成型方法主要有:金属螺旋管、胶管抽芯、钢管抽芯、充气充水胶管抽芯等方法。
本人接触多的是混凝土预应力钢绞线(PCstrand、1×7公称直径15,24mm,f pk=1860Mpa,270级高强底松弛),成孔方法多采用金属螺旋管成孔,本文就以此两项先决条件进行论述。
1 施工准备:熟悉图纸:拿到施工图纸应先查阅施工说明中关于预应力钢绞线的规格,一般预应力钢束采用ASTMA416-270级低松弛钢绞线,其标准强度为f pk=1860Mpa,1×7公称直径15,24mm,锚下控制力为Δk= f pk Mpa。
根据施工方法确定计算参数:注:摘自《公路桥涵施工技术规范》(JTJ 041-2000)附录G-8根据钢绞线试验结果取得钢绞线实际弹性模量Ep(一般为~×105Mpa)材料检测:金属螺旋管根据《公路桥涵施工技术规范》(JTJ 041-2000)附录G-7之要求检测;锚具根据《公路桥梁预应力钢绞线用YM锚具、连接器规格系列》(JT/T )及《公路桥梁预应力钢绞线用锚具、连接器试验方法及检验规则》(JT/T )之要求检测;钢绞线根据《预应力混凝土用钢绞线》GB/T5224-2003之要求检测2 理论伸长量计算:后张法预应力钢绞线在张拉过程中,主要受到以下两方面的因素影响:一是管道弯曲影响引起的摩擦力,二是管道偏差影响引起的摩擦力;两项因素导致钢绞线张拉时,锚下控制应力沿着管壁向跨中逐渐减小,因而每一段的钢绞线的伸长值也是不相同的。
预应力钢绞线理论伸长量计算方法

预应力筋理论伸长值△L 计算方法计算预应力筋理论伸长值时,将直线段与曲线段拆分开,分段计算各个伸长量,再将各段的伸长值一次相加,可得整个钢绞线的伸长值,具体计算如下:1、预应力筋理论伸长值△L(mm)计算: △L=PP P E A L P式中:Pp ——预应力筋的平均张拉力(N ),直线段取张拉端的拉力,曲线是按下一步的2式计算; L ——预应力筋的长度(mm ); Ap ——预应力筋的截面面积(mm 2); Ep ——预应力筋的弹性模量(N/mm 2); 2、预应力筋的平均张拉Pp (N )计算: Pp=P con ×[1-e-(kx+µθ)]/(kx+µθ)式中:P con ——预应力筋张拉端张拉力(N ); X ——从张拉端至尾端的孔道长度(m );θ ——曲线孔道切线夹角(rad );弧度θ=角度α×л÷180;k ——孔道每米局部偏差对摩擦系数的影响k=0.0015; µ——钢绞线与孔道壁的摩擦系数;取0.2~0.25; e ——取2.718;3、预应力筋张拉端张拉力P coni 经孔道摩擦阻力后尾端的张拉力P wj :P wj=P coni×e-(kx+µθ)式中:P wj——经过长度L后预应力筋的终点处张拉力,N;P coni——预应力筋起点处张拉力,N;注:i、j为连续两断面点;后一段钢绞线张拉端张拉力P con 等于前一段钢绞线尾端张拉力P w;例:以环岛路(太阳岛—仙足岛)衔接改造工程中第一联4×30.5m 底板B2为例计算预应力钢绞线理论伸长量(已知如下图,预应力筋采用7-Φs15.20高强度低松弛钢绞线,标准强度f pk=1860MPa,Ep=195000MPa,控制张拉力б=0.75f pk)解:如上图,B2预应力筋可分成直线AB(L=2173mm)、曲线BC (L=1260mm,θ=90,R=8000,rad=90×л÷180=0.1571)、直线CD(L=33519mm )、曲线DE (L=487mm ,θ=60,R=6000,rad=60×л÷180=0.1047)、直线EF(L=1237mm),1、AB 段:张拉端的控制张拉力:P AB =f pk ×75%×A P ×n=1860×0.75×140×7=1367100NAB 端的平均张拉力:Pp=P AB =1367100N △L AB =PP P E A LP =1367100×2173÷(140×7×195000)=15.56mm2、BC 段:张拉端的控制张拉力:P BC =P WAB =P AB ×e-(kx+µθ)=1367100×e-(0.0015×2.173)=1362651.192NBC 段平均张拉力:Pp=P BC ×[1-e-(kx+µθ)]/(kx+µθ)=1362651.192×[1-e-(0.00151.26+0.250.157)]÷(0.0015×1.26+0.25×0.1571) =1334985.344N △L BC =PP P E A L P =1334985.344×1260÷(140×7×195000)=8.8mm30、CD 段:张拉端的张拉力:P CD =P WBC =P BC ×e-(kx+µθ)=1307696.520NCD 段平均张拉力:Pp=P CD =1307696.520N △L CD =PP P E A L P =229.37mm40、DE 段:张拉端的张拉力:P DE =P WCD =P CD ×e -(kx+µθ)=1243573.025NDE 段平均张拉力:Pp=P DE ×[1-e-(kx+µθ)]/(kx+µθ)=1226992.582N △LDE=PP P E A L P =3.12mm50、EF 段:张拉端的张拉力:P EF =P WDE =P DE ×e-(kx+µθ)=1210560.176NEF 段平均张拉力:Pp=P EF =1210560.176N △L EF =7.836mm则预应力筋B2最终理论伸长量:△LEF=△L AB +△L BC +△L CD +△L DE +△L EF=264.686mm (设计263mm )。
后张法钢绞线理论伸长值计算公式说明及计算示例

后张法钢绞线理论伸长值计算公式说明及计算示例后张法钢绞线理论伸长值计算公式说明及计算示例后张法预应力钢绞线在张拉过程中,主要受到以下两方面的因素影响:一是管道弯曲影响引起的摩擦力,二是管道偏差影响引起的摩擦力,导致钢绞线张拉时,锚下控制应力沿着管壁向梁跨中逐渐减小,因而每一段的钢绞线的伸长值也是不相同的。
《公路桥梁施工技术规范》(JTJ041-2000)中关于预应筋伸长值的计算按照以下公式:ΔL=(1)=(2)式中:ΔL —各分段预应力筋的理论伸长值(mm);—各分段预应力筋的平均张拉力,注意不等于各分段的起点力与终点力的平均值(N);L—预应力筋的分段长度(mm);Ap—预应力筋的截面面积(mm2);Ep—预应力筋的弹性模量(Mpa);P—预应力筋张拉端的张拉力,将钢绞线分段计算后,为每分段的起点张拉力,即为前段的终点张拉力(N);θ—从张拉端至计算截面曲线孔道部分切线的夹角之和,分段后为每分段中各曲线段的切线夹角和(r ad);x—从张拉端至计算截面的孔道长度,整个分段计算时x等于L(m);k—孔道每束局部偏差对摩擦的影响系数(1/m),管道弯曲及直线部分全长均应考虑该影响;μ—预应力筋与孔道壁之间的磨擦系数,只在管道弯曲部分考虑该系数的影响。
从公式(1)可以看出,钢绞线的弹性模量Ep是决定计算值的重要因素,它的取值是否正确,对计算预应力筋伸长值的影响较大。
Ep 的理论值为Ep=(1.9~1.95)×105Mpa,而将钢绞线进行检测试验,弹性模量则常出现Ep’=(1.96~2.04)×105Mpa的结果,这是由于实际的钢绞线的直径都偏粗,而进行试验时并未用真实的钢绞线面积进行计算,采用的是偏小的理论值代入公式进行计算,根据公式Ep=可知,若Ap偏小,则得到了偏大的Ep’值,虽然Ep’并非真实值,但将其与钢绞线理论面积相乘所计算出的ΔL却是符合实际的,所以要按实测值Ep’进行计算。
预应力钢绞线实际伸长量计算方法

预应力钢绞线实际伸长量计算方法1、以钢绞线在预应力管道内的长度计算理论伸长量ΔL理为基准时:(1)当采用“行程法”测量伸长量:L实=[(L100%-L10%)+(L20%-L10%)] –ΔL工作长度-ΔL工具锚–ΔL工作锚⑺L实——钢绞线实际伸长量;L20%——张拉应力为20%б0时,梁段两端千斤顶活塞行程之和;L100%——张拉应力为100%б0时,梁段两端千斤顶活塞行程之和;L10%——张拉应力为10%б0时(即初张应力,规范推荐可取10%-25%),梁段两端千斤顶活塞行程之和;ΔL工作长度——梁段两端千斤顶内钢绞线的无阻伸长量;取理论计算值;ΔL工作锚——梁段两端锚具压缩及钢绞线回缩量;取工艺试验实测值;ΔL工具锚——梁段两端锚具压缩及钢绞线回缩量;取实测值;(2)当采用“直接法”测量伸长量:L实=[(L100%-L10%)+(L20%-L10%)] –ΔL工作长度–ΔL工作锚控制应力*钢绞线截面积*钢绞线的根数=张拉力根据千斤顶和油表的检测报告中的校正方程计算出油表读数即可。
注意:有的需要超张拉来抵消预应力损失,在控制应力中乘以系数即可。
预应力钢绞线伸长量计算方法预应力钢绞线张拉理论伸长量计算公式ΔL=(PpL)/(ApEp)式中:Pp――预应力筋的平均张拉力(N)L――预应力筋的长度(mm)Ap――预应力筋的截面面积(mm2)Ep――预应力筋的弹性模量(N/mm2)Pp=P(1-e-(kx+μθ))/(kx+μθ)式中:Pp――预应力筋平均张拉力(N)P――预应力筋张拉端的张拉力(N)x――从张拉端至计算截面的孔道长度(m)θ――从张拉端至计算截面曲线孔道部分切线的夹角之和(rad)k――孔道每米局部偏差对摩擦的影响系数μ――预应力筋与孔道壁的摩擦系数1、预应力钢绞线张拉实际伸长量ΔL,应建立在初应力后开台量测,测得伸长值还应加上初应力的推算值。
ΔL=ΔL1+ΔL2式中ΔL1从初应力到最大张拉力间的最大伸长值ΔL2初应力以下的推算值关于初应力的取值一般可取张拉控制应力的10—25%。
预应力钢绞线张拉伸长量(公式)计算实例

在工程计算中经常要用到度、分、秒,通常的做法就是插入特殊字符来输入。但是在EXCEL中显示的结果却不近人
符间距太大,看起来就象刚学会写字的人写的东西。其实这是由字体引起来的,一般情况下系统默认的字体是宋
入度分秒的时候,它们之间的间距就会比较大。下面几种字体的效果就比较好: Arial Unicode Ms , Batang , Dotum , Gungsuh , New Gulim , Gulim 。 当然也不只是这几种,大家也可以自己测试一下,找一下其它合适的字体。
A11为通过自定义格式
140°25′35″
140.4263889 2.450902843 输入
转为度 140.4264 140.4264
140.4264
140.4264
一、角度的度分秒与小数点格式互相转换 EXCEL能将角度转换成度"°"分"′"秒"″"格式吗?
如将:120.999722222222°转换成120°59′59″. 32.55°转换成32°33′0″
55转换成32330我知道可以用函数radians将角度转换为弧度但我们工程测量上用到的角度计算是以度分秒比如行计算的在excel中怎样用这些数据进行计算
度
转为度分秒 转为度
转为度分秒
32.55°
32°33′00″
32.55
32°33′0″
120.9997222°
120°59′59″ 120.9997222
120°59′59″
度分秒
转为度
转为弧度
140°25′35″
140.4263889 2.450902843 A8为文本格式输入
理论伸长值计算

预应力钢绞线理论伸长值计算1、按理论计算伸长值△L:NjL LN(1-e-(kx+μθ))/(kx+μθ)△L= =ApEs ApEs从《桥规》查得k=0.0015,μ=0.20,计算得θ1=(3+3.7+8.8+5.1)×2×0.0175=0.721rad1-e-(kx+μθ)=0.176kx+μθ=0.194θ2=(3+5.1+10.3+5.1)×2×0.0175=0.8225rad1-e-(kx+μθ)=0.193kx+μθ=0.214N=1395×140.1×15=2931592.5NL1=32310mm+850 mm =33160mm,L2 =32300mm+850mm=33150mmAp=140.1×15=2101.5 mm2Es=1.96×105计算得:△L1=214.11×2=428.22 mm,△L2=212.79×2=425.58mm2、根据试验室对张拉机压力表校验结果,进行拉力与表读数的换算:设计张拉力为0.75Ryb=0.75×1860×140.1×15=2931592.5N 利用内插法算得拉力如下:①表号029 y=0.0079x-1.3515②表号059 y=0.0078x-0.7561设计拉力百分比拉力(KN表读数20% 586.32 3.28 3.8240% 1172.64 7.91 8.39 60% 1758.96 12.54 12.96 100% 2931.6 21.81 22.11 105% 3078.2 22.97 23.253、张拉记录:张拉时,严格按照设计拉力百分比及相应的拉力进行操作并准确记录伸长值。
即先拉20%(б设),记下伸长值A,再拉至40%(б设),记下伸长值B(利用B-A,记作20%的伸长值),然后拉到100%(б设)持荷2分钟后,将其锚固,记下其伸长值C。
预应力钢绞线理论伸长量计算实例

预应力钢绞线理论伸长量计按两端张拉,采用精确计算法和简化计算分别计算:
如LT40-09图菜子大桥边梁N1,预应力筋采用一束8φ15.24的钢绞线束,张拉控制力
F=195.3×8=1562.4KN,Ay=140×8=1120mm2,Ey=1.95×105Mpa,设孔道采用预埋金属波纹管成型,μ=0.225、k=0.0015。
)
N1立面布置图
1、精确计算:
将40mT梁的半个曲线预应力筋分成三段,采用桥梁规范公式分段计算:
当AB、CD为直线预应力筋时,θ=0
ΔL=(PL/AyEy)×(1-e-kL/KL) 公式①
当BC为曲线预应力筋时,θ=0.01745329252(180/πR)
ΔL=(PL/AyEy)×[]1-e-(KL+μθ)/(KL+μθ) ] 公式②
各段终点力N终=Fi×e-(KL+μθ)公式③
各段平均张拉力P平= Fi×[1-e-(KL+μθ)/(KL+μθ) ] 公式④
各段参数表(表1)
将表1中数据代入公式①、公式②:
分段求得ΔL=2×∑ΔL =273.50mm
2、简化计算:
将表1中的数据代入下式:
ΔL=P L/AyEy ( P近似平均张拉力)公式⑤
分段求得ΔL=2×∑ΔL=273.52mm
通过以上计算可以看出,采用精确计算和简化计算所得的结果相比,两者差值非常小,所以采用简化计算法是完全能满足曲线预应力张拉理论伸长值的计算精度要求的。
预应力钢绞线理论伸长量计算(箱梁)

192962.48 193398.89
27.74 29.25
0.650
0.0000
0.0007
0.999
195300.000 195236.54
4.65
1.067 N4
0.733
0.000 0.087
0.0011 0.0182
0.999 0.982
195173.096 194964.958
195069.01 193202.81
Pp=P(1-e-(KL+μθ))/(KL+μθ)
△L=PpL/(AEp)
0.650
0.0000
0.0007
0.999
195300.000 195236.54
4.65
0.721
0.000
0.0007
0.999
195173.10 195102.75
5.15
0.785 N3
5.252
0.031 0.000
27.32
30m中跨
0.885 0.650
0.0000 0.0000
0.0009 0.0007
0.999 0.999
187964.94 195300.000
187881.79 195236.54
6.09 4.65
0.721
0.000
0.0007
0.999
195173.10 195102.75
5.15
0.0071
0.0067 0.0214 0.0027 0.0007 0.0007 0.0071 0.0051 0.0214 0.0043 0.0007 0.0007
0.993
0.993 0.979 0.997 0.999 0.999 0.993 0.995 0.979 0.996 0.999 0.999
t梁预应力钢绞线伸长值计算实例

△
L1
195.3103 700 140 1.95 105
ห้องสมุดไป่ตู้
5.01mm
A1B1 段:
△L2
194.32 103 9989 140 1.95 105
71.10mm
B1C1 段;
△L3
191.26 103 3540 140 1.95 105
24.80mm
C1D1 段;
△L4 189.00 103 1063 7.36mm 140 1.95 105
△ L4 184.02 103 1639 11.05mm 140 1.95 105
D2 E2 段:
△L4 178.00 103 3200 20.86mm 140 1.95 105
N3 钢束
O3 A3 段:
3
△L1
195.3103 700 140 1.95 105
5.01mm
A3 B3 段;
(MPa) (MPa)
(MPa) (MPa)
N1 7 136.71 3.00 3.09 21.65 273.42 6.85 6.9 43.31 1367.1 37.65 37.39 216.54
N2 8 156.24 3.55 3.63 21.27 312.48 7.95 7.99 43.31 1562.4 43.15 42.83 212.65
N2 钢束
O2 A2 段;
△L1 195.3103 700 5.01mm 140 1.95 105
A2 B2 段;
△L2
194.77 103 5516 140 1.95 105
39.35mm
B2C2 段:
△L3
192.05 103 4272 140 1.95 105
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
预应力钢绞线理论伸长量计按两端张拉,采用精确计算法和简化计算分别计算:
如LT40-09图菜子大桥边梁N1,预应力筋采用一束8φ15.24的钢绞线束,张拉控制力
F=195.3×8=1562.4KN,Ay=140×8=1120mm2,Ey=1.95×105Mpa,设孔道采用预埋金属波纹管成型,μ=0.225、k=0.0015。
)
N1立面布置图
1、精确计算:
将40mT梁的半个曲线预应力筋分成三段,采用桥梁规范公式分段计算:
当AB、CD为直线预应力筋时,θ=0
ΔL=(PL/AyEy)×(1-e-kL/KL) 公式①
当BC为曲线预应力筋时,θ=0.01745329252(180/πR)
ΔL=(PL/AyEy)×[]1-e-(KL+μθ)/(KL+μθ) ] 公式②
各段终点力N终=Fi×e-(KL+μθ)公式③
各段平均张拉力P平= Fi×[1-e-(KL+μθ)/(KL+μθ) ] 公式④
各段参数表(表1)
将表1中数据代入公式①、公式②:
分段求得ΔL=2×∑ΔL =273.50mm
2、简化计算:
将表1中的数据代入下式:
ΔL=P L/AyEy ( P近似平均张拉力)公式⑤
分段求得ΔL=2×∑ΔL=273.52mm
通过以上计算可以看出,采用精确计算和简化计算所得的结果相比,两者差值非常小,所以采用简化计算法是完全能满足曲线预应力张拉理论伸长值的计算精度要求的。
