经济预测与决策实验
经济预测与决策
经济预测与决策摘要：经济预测是指根据现有经济数据、经济指标和信息，对未来一段时间内的经济发展趋势进行预测和预估。
经济预测在国家和地区的经济政策制定和商业决策中起着重要作用。
本论文将介绍经济预测的基本概念和方法，以及决策制定中经济预测的应用。
关键词：经济预测，决策，经济数据，经济指标，趋势一、经济预测的基本概念经济预测，也叫经济预测分析，是指运用统计学、计量经济学和其他方法对未来一定时间内的经济变化趋势进行预测和预估。
经济预测的目的是为政府、企业和个人提供有用的信息，帮助他们做出相应的决策，以适应未来的经济环境。
1.1 经济预测的重要性经济预测是国家和地区经济管理和商业决策的重要依据。
经济预测可以为政府制定宏观经济政策、促进经济发展和稳定、避免经济风险等提供重要的支持和保障。
对企业和个人而言，准确的经济预测可以帮助他们做出准确的商业决策，降低经济风险，增加投资回报。
1.2 经济预测的内容经济预测的内容主要包括宏观经济预测和微观经济预测。
宏观经济预测是指对国家或地区整体经济发展趋势的预测，主要涉及国内生产总值、通货膨胀率、贸易、投资等指标。
微观经济预测则涉及到企业的市场和产品前景等方面的预测。
1.3 经济预测的难点经济预测的难度在于经济环境的多变和经济变量的多元化。
经济环境受社会、政治和自然等多种因素的影响，这些因素可能根据时间、地点和规模的不同所产生的影响也不同。
而经济变量的多元化也会给效果的预测带来很大的困难，因为许多变量并不完全独立，而是相互作用的。
二、经济预测的方法2.1 时间序列方法时间序列方法是运用统计分析技术对经济数据的变化趋势进行分析和判定，进而预测未来的变化趋势。
时间序列方法主要是利用过去的数据来预测未来的趋势，根据这些数据来建立时间序列模型，并为未来的变化预测一个最有可能的值。
2.2 回归方法回归方法是一种通用的预测方法，通常用于预测单个变量对其他变量的影响。
回归方法的基本思想是找到一个可以描述两个变量之间关系的函数，从而预测其中一个变量的值，当其他变量的值给定时。
经济预测与决策仿真实验报告
经济预测与决策仿真实验报告一、实验背景在当今复杂多变的经济环境中，准确的经济预测和明智的决策对于企业、政府和个人都至关重要。
经济预测能够帮助我们提前洞察市场趋势，把握机遇，规避风险；而决策则是基于预测结果，选择最优的行动方案，以实现既定的目标。
为了深入理解和掌握经济预测与决策的方法和技巧，我们进行了本次仿真实验。
二、实验目的本次实验的主要目的是：1、熟悉并运用常见的经济预测方法，如时间序列分析、回归分析等，对经济数据进行预测。
2、通过建立决策模型，综合考虑各种因素，制定最优的经济决策方案。
3、培养对经济数据的敏感度和分析能力，提高解决实际经济问题的能力。
三、实验数据与方法（一）实验数据我们选取了某地区过去五年的经济数据，包括 GDP 增长率、物价指数、失业率、进出口贸易额等指标。
这些数据来源于政府统计部门和相关的经济研究报告。
（二）实验方法1、时间序列分析使用移动平均法和指数平滑法对 GDP 增长率进行预测，观察其短期和中期的趋势变化。
2、回归分析建立多元线性回归模型，以物价指数、失业率等作为自变量，GDP 增长率作为因变量，分析各因素对经济增长的影响。
3、决策树分析构建决策树模型，针对企业的投资决策问题，考虑市场需求、竞争状况、成本等因素，确定最优的投资方案。
四、实验过程与结果（一）时间序列分析1、移动平均法分别计算了 3 期和 5 期移动平均值，并绘制出趋势线。
结果显示，3 期移动平均对短期波动的反应较为灵敏，但中期趋势不够平滑；5 期移动平均则在平滑中期趋势方面表现较好，但对短期变化的捕捉相对滞后。
2、指数平滑法通过调整平滑系数α的值，进行多次预测。
当α取值较大时，预测结果对近期数据的权重较大，能够更快地反映最新的变化；当α取值较小时，预测结果更趋于稳定，但对短期变化的响应较慢。
（二）回归分析经过数据处理和模型拟合，得到回归方程如下：GDP 增长率＝ 05×物价指数 02×失业率＋ 03×进出口贸易额＋常量通过对回归系数的分析，发现物价指数对GDP 增长率有正向影响，失业率有负向影响，进出口贸易额也有正向影响。
经济预测与决策技术第六版课后答案
经济预测与决策技术第六版课后答案1．什么叫经济预测？
经济预测是一门研究经济发展过程及其变动趋势的学科。
2．经济预测与决策有什么关系？
经济计划是为实现经济决策目标而编制的一种经济活动方案，而经济决策的目标又是依
据经济预测的结果而确定的。
3．什么叫宏观经济预测？
宏观经济预测是指对整个国民经济或一个地区、一个部门的经济发展前景的预测，它以整个社会（或地区、部门）的经济发展的总图景作为考察对象。
4．什么叫微观经济预测？
微观经济预测是指对一个企业的经济发展前景或家庭、个人的经济活动的预测，它以单个经济单位的经济活动前景作为考察的对象。
5．什么叫定性经济预测？
定性经济预测是对某一经济现象的未来状态所作的一种描
述，也就是对未来的经济状态提供可能变动的方向而非数量的大小所作出的预测。
6．什么叫定量经济预测？
定量经济预测是运用经济统计的数据资料，根据预测目标中
的经济变量之间的关系，建立起预测模型以推导出预测值。
经济预测与决策课程设计
经济预测与决策 课程设计一、课程目标知识目标：1. 学生能够理解并掌握经济预测的基本概念、原理和方法。
2. 学生能够了解经济决策的类型、过程及其在实际中的应用。
3. 学生能够掌握并运用数据分析技能，对经济数据进行分析，为预测和决策提供依据。
技能目标：1. 学生能够运用所学经济预测方法，对实际问题进行预测分析，并提出合理的预测结果。
2. 学生能够结合实际案例，设计简单的经济决策模型，并运用到实际问题的解决中。
3. 学生能够通过小组合作，进行数据分析，提高团队协作和沟通能力。
情感态度价值观目标：1. 学生能够认识到经济预测与决策在国家和企业经济发展中的重要性，增强对经济学的兴趣和热爱。
2. 学生在学习过程中，培养批判性思维和问题解决能力，形成积极主动探索知识的良好习惯。
3. 学生能够树立正确的价值观，关注国家经济发展，提高社会责任感和使命感。
课程性质：本课程为高中年级经济学选修课程，旨在通过实际案例分析，使学生掌握经济预测与决策的基本知识和技能。
学生特点：高中年级学生具有一定的逻辑思维能力和数学基础，对实际经济问题充满好奇心，喜欢探索和解决问题。
教学要求：教师应注重理论与实践相结合，引导学生运用所学知识解决实际问题，提高学生的分析、预测和决策能力。
通过小组讨论、案例分析等教学手段，培养学生的团队协作和沟通能力。
在教学过程中，关注学生的情感态度价值观的培养，使学生在掌握知识技能的同时，形成正确的价值观。
二、教学内容1. 经济预测基本概念：介绍预测的定义、作用和类型，结合教材第3章相关内容，分析不同预测方法的适用场景。
教学安排：2课时2. 经济预测方法：讲解趋势预测、季节性预测、周期性预测等常用预测方法，结合教材第4章进行案例分析。
教学安排：4课时3. 经济决策类型与过程：介绍个体决策、集体决策等类型，分析决策过程，结合教材第5章实际案例进行讲解。
教学安排：3课时4. 数据分析方法：讲解描述性统计、概率分布、回归分析等数据分析方法，结合教材第6章进行实际操作。
经济统计预测与决策 课程大纲
《经济统计预测与决策》课程大纲一、课程简介1.1 课程背景经济统计预测与决策是一门旨在帮助学生掌握经济数据处理和分析技能，从而进行经济现象的预测和决策制定的课程。
本课程将涵盖经济统计基础、预测模型、决策分析等内容，旨在培养学生对经济现象的敏锐观察和分析能力。
1.2 课程目标通过学习本课程，学生将能够掌握经济数据的收集、整理、分析和解读技能，具备运用统计方法进行经济预测和决策的基本能力，并且理解统计工具在经济领域中的重要作用。
1.3 课程要求本课程的学习需要较强的数理基础，学生应具备一定的数学、统计学和经济学基础知识。
需要有一定的数据处理和编程能力，熟练运用Excel、Python等工具进行数据分析。
二、课程内容2.1 经济统计基础2.1.1 经济数据的类型和特征2.1.2 统计描述和展示经济数据2.1.3 经济数据的抽样调查方法2.2 经济预测模型2.2.1 经济时间序列分析2.2.2 经济指标的预测模型2.2.3 多元回归分析在经济预测中的应用2.3 决策分析方法2.3.1 决策树模型2.3.2 风险分析与决策2.3.3 经济决策中的不确定性分析三、课程教学安排3.1 授课方式本课程采用理论授课与应用实践相结合的授课模式。
课堂上教师将介绍相关理论知识，并通过案例分析和实际数据操作进行教学。
3.2 课程作业学生需要完成课后作业，包括数据分析和模型建立等内容。
部分作业将涉及实际经济数据的处理和分析。
3.3 课程项目本课程将安排实际项目，学生将运用所学知识对实际经济问题进行分析和决策，提高实际应用能力。
四、学习评估4.1 考核方式课程考核将包括平时表现、作业完成情况、期中考试和期末项目报告。
4.2 成绩评定学生成绩将由平时成绩、考试成绩和项目报告综合评定。
平时成绩占比30%，期中考试成绩占比30%，期末项目报告占比40%。
五、课程反馈与改进5.1 教学反馈学生可以通过课程评价表反馈教学质量，并提出建议和意见。
经济预测与决策
经济预测与决策摘要：本文简单介绍了经济预测与决策的概念、分类、基本步骤，并阐述了经济预测与决策的关系。
一、经济预测1、经济预测的基本概念经济预测就是在一定的经济理论指导下，根据经济发展的历史和现状资料、客观的环境条件以及主观的经验教训，对经济的未来发展预先作出科学的推测。
是与未来有关的旨在减少不确定性对经济活动影响的一种经济分析。
它是对将来经济发展的科学认识活动。
经济预测不是靠经验、凭直觉的预言或猜测，而是以科学的理论和方法、可靠的资料、精密的计算及对客观规律性的认识所作出的分析和判断。
这样的预测是一种分析的程序，它可以重复地连续进行下去。
目的是为未来问题的经济决策服务。
为了提高决策的正确性，需要由预测提供有关未来的情报，使决策者增加对未来的了解，把不确定性或无知程度降到最低限度，并有可能从各种备选方案中作出最优决策。
2、经济预测的分类通常分为三类：（1）、按预测的范围，有国民经济预测、企业经济预测，介乎两者之间的部门经济预测和地区经济预测，还有世界经济预测。
（2）、按预测的时效，有短期预测、长期预测及中期预测。
短期预测和长期预测的划分，因预测对象的性质、预测的要求、各国习惯而有所差别。
两者区别的实质性标志在于预测期内的主要因素、经济结构等是否发生了根本性变化。
中期预测则介乎这两者之间。
（3）、按预测的性质，有质的预测和量的预测。
只要求对预测事物有概括性的了解，描述其变化趋势,判断它出现的可能性或不可能性,就采用质的预测。
从一些经济指标的已知值推算另一些指标的未来值，进而说明达到这些数值的概率，就采用量的预测。
其中，预测的变量数值表现为单一数值，称为点值预测；预测的变量数值有一个幅度,处于上限和下限的区间之内,称为区间预测。
3、经济预测的步骤（1）、收集和分析预测所需要的各种资料；（2）、进行各种预测计算，提出轮廓性的初步的预测;（3）、召开预测评论会议,以便起到集思广益、集体判断的作用；（4）、补充和修正预测，发布正式的预测报告。
经济预测与决策
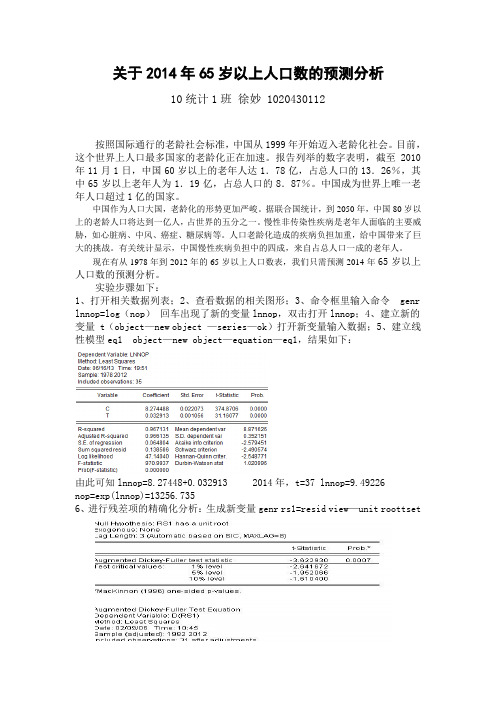
关于2014年65岁以上人口数的预测分析10统计1班徐妙 1020430112按照国际通行的老龄社会标准，中国从1999年开始迈入老龄化社会。
目前，这个世界上人口最多国家的老龄化正在加速。
报告列举的数字表明，截至2010年11月1日，中国60岁以上的老年人达1．78亿，占总人口的13．26％，其中65岁以上老年人为1．19亿，占总人口的8．87％。
中国成为世界上唯一老年人口超过1亿的国家。
中国作为人口大国，老龄化的形势更加严峻。
据联合国统计，到2050年，中国80岁以上的老龄人口将达到一亿人，占世界的五分之一。
慢性非传染性疾病是老年人面临的主要威胁，如心脏病、中风、癌症、糖尿病等。
人口老龄化造成的疾病负担加重，给中国带来了巨大的挑战。
有关统计显示，中国慢性疾病负担中的四成，来自占总人口一成的老年人。
现在有从1978年到2012年的65岁以上人口数表，我们只需预测2014年65岁以上人口数的预测分析。
实验步骤如下：1、打开相关数据列表；2、查看数据的相关图形；3、命令框里输入命令 genr lnnop=log（nop）回车出现了新的变量lnnop，双击打开lnnop；4、建立新的变量 t（object—new object —series—ok）打开新变量输入数据；5、建立线性模型eq1 object—new object—equation—eq1，结果如下：由此可知lnnop=8.27448+0.032913 2014年，t=37 lnnop=9.49226nop=exp(lnnop)=13256.7356、进行残差项的精确化分析：生成新变量genr rs1=resid view—unit roottset由结果可知，P=0.0007<0.05，所以可以建模。
7、下面进行相关性分析View—correlogram由该结果可知，应该用AR秩回归模型，看右边的偏相关函数，由一个不为0所以应该建立一阶秩回归Object—new object—equation——eq2—ok输入：rs1 c ar(1)因为常数C的P值>0.05，可以删去也可以保留，F检验=0.0049所以整个模型显著且可用rs1t =0.4629* rs1t-1第二个方程的残差：genr rs2=resid rs2为第一个方程残差的模型View—correlogram个系数均为0，所以不相关，而且平稳，所以为白噪声。
基于Excel的经济管理预测与决策实验体系设计
理等 实验环境 为微机室 ． 软件环境需要安装 Ｍ ｃｏｏ ｉｒｓｆ ｔ ０ ｉｅ ｘ ｅ ２ ０ ．为保证 Ｅ ｃｌ ｆｃ ｃｌ ｏ ３ Ｅ ｘｅ 中的很 多扩展功能可
分析功能。
三、 实验 的主 要体 系结构
１实验对象和实验环境 ．
本实验 的开设可 以面向经管类本专科学生 ． 专业方 性， 充分利用 了 Ｅ ｃｌ ｘ ｅ 的数据 管理与分 析 、 图表化 的功 向为财务 、 工商管理 、 市场营销 、 、 物流 工业工程 、 城市管
［ 收稿 日 】０ ０ ０ — ２ 期 ２ １— ７ ０ ［ 作者简介 】 傅佳琳 （ ７ 一 ， ， 岛科技大学经济与管理学院讲 １ ５） 青 ９ 女
本 文主要 设 计 与 经济 管理 预 测与 决 策相 关 的 ６个 实验 项 目， 上 机 实验 ． 强 学生 对所 学 知识 的 综合 应 用 ， 强理 论 通过 加 加
教 学与实践教学环节的联 系和衔接 ． 从知识结构上保证课 程体 系的系统性和完整性。
［ 关键词］ 经济管理； 预测与决策； 实验体系； ｘｅ Ｅ ｃ ｌ
从 让学 经管 类专 业设置 经济 管理预 测 与决 策实 能 ． 实际案例 出发 ． 生了解财务和管理 中遇到的
问题 ， 理清问题结构 ， 对问题 中的关系进行量化 。 建立简 验 的意 义 单 的数学 模型 ， 运用计算 机工具 来求得结果 ． 帮助学生 在知识经济 、信息经济逐步取代工业经济的时代 ， 独立建模 能力 、 综合应用理论 知 企业生存环境快速发生变化 ． 各行各业都需要大量 的高 获 得和提 高动手能力 、 预测类 问题和决策类 问题是经济管理 问题 中的 素质 的财务和管理人员 。对于培养经管专业 的学生来 识 能力 。 两大类主要问题 经济管理中的很多数据都带有时间特 说 ． 了理论知识 的系统学习 。 除 还需要 提高其动手解决 即是 随时间变化 的， 这些数 据在不同 的时 间点 上具 问题的实践能力 ．需要把理论知识运用到实际应用 中． 征 。 这些时间点可以是一年 、 一季度或一月 、 一 解决经济管理 中常见 的预测和决策问题 著名教育学家 有不 同的值 ， 在实际工作 中 。 管理 人员需要根据 在过去各时间点 陶行知 曾经说过 ：行是知之始 ， “ 知是行 以成。 正确处理 日． ” 可 好理论与实践的关系是我们开设 这项实验教学 的主要 上 的数据预测其将来值 ．这类 问题属于预测类 问题 ， 以通过外推法或 回归分析来进行预测 决策类问题 主要 目的。对于专业 的经济管理人员来说 ． ｍｃ Ｏ ｅ软件是办 公中最 常使用 的工具 ．其中的 Ｅ ｃｌ 其重要 成员 ． ｘ ｅ是 是 是在一定 目标 的指导下 从各种可供选择 的行动方案 中 决策 目标常常是尽可 能增加 个强大的表格制作和数据处理软件 助其各种编辑 选择一 种加 以实施的过程 ． 借 或尽可能减少成本 。 例如 ， 在盈亏平衡分析中通过 操作 、 务数据 分析方法 、 财 函数 和图表等高级工具 的综 利润 ， ａ ｆ － 得 通过调 合应用 ． 经济管理人员在不需要掌握复杂的编程和较 难 Ｗｈｔｉ分析 ， 到当前销量下 的企业利润状况 ． 整变量 ， 使模型能动态 显示经营状况 ； 最优化 模型一般 的数学推导情况下 ． 就可以处理工作 中遇到的常见的数
经济预测与决策 指数平滑法
《经济预测与决策》作业四要求：用二次移动平均法对2003年的财政支出作出预测解：此步骤如下：（1）绘制散点图（图 1.1）。
由散点图可以看出，用二次移动平均法进行预测。
（图 1.1）（2）取N=4，分别计算)1(t M 和)2(t M ，结果如下表（表1-1）年份 t 财政支出 )1(t M )2(t Mt yˆ i i yy ˆ- tti y y y -1950 1 68.051951 2 122.07 1952 3 172.07 1953 4 219.21 120.73 1954 5 244.11 171.1167 1955 6 262.73 211.7967 1956 7 298.52 242.0167 167.8811 1957 8 295.95 268.4533 208.31 427.3556 131.406 0.444014 1958 9 400.36 285.7333 240.7556 418.8117 18.4517 0.046088 1959 10 543.17 331.61 265.4011 398.1778 144.9922 0.266937 1960 11 643.68 413.16 295.2656 497.1322 146.5478 0.227672 1961 12 356.09 529.07 343.5011 707.8961 351.806 0.987969 1962 13 294.88 514.3133 424.6133 992.9922 698.112 2.367444 1963 14 332.05 431.55 485.5144 738.5633 406.513 1.224252 1964 15 393.79 327.6733 491.6444 296.6389 97.15111 0.246708 1965 16 459.97 340.24 424.5122 -82.2544 542.2244 1.178826 1966 17 537.65 395.27 366.4878 129.5594 408.0906 0.759026 1967 18 439.84 463.8033 354.3944 467.2256 27.3856 0.062263 1968 19 357.84 479.1533 399.7711 737.3256 379.486 1.060491 1969 20 525.86 445.11 446.0756 677.6089 151.749 0.288573 1970 21 649.41 441.18 462.6889 442.6961 206.7139 0.31831 1971 22 732.17 511.0367 455.1478 387.4078 344.7622 0.470877 1972 23 765.86 635.8133 465.7756 650.7589 115.1011 0.15029 1973 24 808.78 715.8133 529.3433 1060.908 252.128 0.311739 1974 25 790.25 768.9367 620.8878 1181.988 391.738 0.495714 1975 26 820.88 788.2967 706.8544 1139.059 318.179 0.387607 1976 27 806.2 806.6367 757.6822 991.9022 185.702 0.230342 1977 28 843.53 805.7767 787.9567 929.0228 85.4928 0.101351 1978 29 1122.09 823.5367 800.2367 850.3267 271.7633 0.242194 1979 30 1281.79 923.94 811.9833 881.7867 400.0033 0.312066 1980 31 1228.83 1082.47 851.0844 1203.832 24.99833 0.020343 1981 32 1138.41 1210.903 943.3156 1660.934 522.524 0.458995 1982 33 1229.98 1216.343 1072.438 1879.873 649.893 0.528377 1983 34 1409.52 1199.073 1169.906 1576.107 166.587 0.118187 1984 35 1701.02 1259.303 1208.773 1271.993 429.0272 0.252218 1985 36 2004.25 1446.84 1224.907 1385.628 618.6217 0.308655 1986 37 2204.91 1704.93 1301.739 2001.673 203.2367 0.092175 1987 38 2262.18 1970.06 1470.358 2712.908 450.728 0.199245 1988392491.212157.1131707.2773219.316728.1060.292271989 40 2823.78 2319.433 1944.034 3281.705 457.925 0.162167 1990 41 3083.59 2525.723 2148.869 3257.931 174.341 0.056538 1991 42 3386.62 2799.527 2334.09 3467.859 81.2394 0.023988 1992 43 3742.2 3097.997 2548.228 3963.118 220.918 0.059034 1993 44 4642.3 3404.137 2807.749 4472.419 169.8811 0.036594 1994 45 5792.62 3923.707 3100.553 4895.106 897.5139 0.154941 1995 46 6823.72 4725.707 3475.28 5981.59 842.13 0.123412 1996 47 7937.55 5752.88 4017.85 7851.773 85.77667 0.010806 1997 48 9233.56 6851.297 4800.764 10090.46 856.895 0.092802 1998 49 10798.18 7998.277 5776.628 11977.63 1179.45 0.109227 1999 50 13187.67 9323.097 6867.484 13552.4 364.729 0.027657 2000 51 15886.5 11073.14 8057.557 15462.13 424.3728 0.026713 2001 52 18902.58 13290.78 9464.837 18612.09 290.4933 0.015368（表1-1）（3）计算线性趋势模型的截距和斜率：14a =2)1(14M -)2(14M =2*13290.78-9464.837=17116.73 14b =2/(N-1)*( )1(14M -)2(14M )=2550.631 于是得到t=14时线性趋势预测模型为：τ+14y=17116.73+5738.92τ(4)计算追溯预测值，并求出平均绝对百分比误差。
《经济预测与决策分析》学期期末论文题目、格式及评分标准
影响吉林省城镇居民收入因素的分析姓名：李威专业：项目管理学号：【摘要】随着改革开放的进行，吉林省在经济发展中显示出了极强的经济活力，省综合实力得到了极大地增强，人们的物质生活的极大丰富。
这些发展为城镇居民收入、消费水平的提高奠定了坚实的基础。
居民的消费理念从过去的单纯追求数量到如今的更加侧重于追求质量。
根据经济学原理中的一般消费理论，收入和价格是决定消费的两要素。
因此采用1980-2008年吉林省城镇居民人均消费支出、城镇居民人均可支配收入、城镇居民消费价格指数，运用计量经济模型对影响吉林省城镇居民人均消费支出的因素进行相关性分析。
在相关性分析的过程中我们不难发现确实随着经济结构的优化，经济体制的发展，人们的收入增加了，消费能力与消费理念也发生了极大地变化。
【关键字】城镇居民可支配收入；经济计量模型；人均生活消费支出；一、问题的提出经济增长的三要素分别是投资、消费、出口。
自改革开放以来，我国的经济得到了突飞猛进的发展，人们的生活水平得到了极大的提高，生活幸福，安居乐业。
虽然在经济建设方面取得了举世瞩目的成绩，但是经济的过速发展的背后却有着很大的我们平时不可见的经济危机。
所以，对居民消费能力的研究在这里就显得尤为重要了。
1980年到2008年的这28年间，吉林省城镇居民的消费水平从358元攀升到11447.8元，消费结构也经历了从贫困型向温饱型和小康型消费的转变，居民消费经历了三次大的消费结构升级。
一是20世纪80年代初，人们只是单纯的追求一些简单的生活用品，以满足温饱为目标的消费结构升级；二是20世纪80年代中期到90年代中期，以家电的普及为标志的发展型消费结构升级；三是20世纪90年代末至今的以多元化的消费为主导的享受型消费结构升级。
到2008年全省城镇人均可支配收入突破16447.8元，居民消费结构继续多样化，向着发展型升级的趋势越来越明显。
二、数据与模型（一）数据的选取吉林省统计局所提供的《吉林省统计年鉴》得到吉林省1980-2008年城镇居民人均消费支出、人均可支配收入数据和消费价格指数，其中表中数据以1980年为基数。
《预测及决策技术应用》课程实验报告
实验报告实验名称：预测与决策技术应用课程实验指导教师：实验日期：实验地点：班级：学号：姓名：实验成绩：实验1 德尔菲预测法【实验题目】某公司为实现某个目标，初步选定了a,b,c,d,e,f 六个工程，由于实际情况的限制，需要从六项中选三项。
为慎重起见，公司共聘请了100位公司内外的专家，请他们选出他们认为最重要的三项工程，并对这三项工程进行排序，专家的意见统计结果如下表。
如果你是最后的决策者，请根据专家给出的意见，做出最合理的决定。
专家意见表排序 1 2 3 a 30 10 20 b 10 10 40 c 16 10 20 d 10 15 0 e 14 46 10 f 20 9 10【实验环境】• Excel【实验目的】• 掌握利用德尔菲法进行定性预测的方法 【实验步骤及结果】本实验中，要求选择3个项目进行排序，则可以按每位专家是同等的预测能力来看待，并规定其专家评选的排在第1位的项目给3分，第2位的项目给2分，第3位的项目给1分，没选上的其余项目给0分。
在本实验中，1T =3分，2T =2分，3T =1分。
上表中，对征询表作出回答的专家人数N=100人：赞成a 项排第1位的专家有30人（即a,1N =30），赞成a 项排第2位的专家有10人（a,2N =10），赞成a 排第3位的有20人（a,3N =20）。
所以，a 项目的总得分为：3*30+2*10+1*20=130分。
同理可以分别计算出：b 项目的总得分为：3*10+2*10+1*40=90分；c 项目的总得分为：3*16+2*10+1*20=88分；d 项目的总得分为：3*10+2*15+1*0=60分；e 项目的总得分为：3*14+2*46+1*10=144分；f 项目的总得分为：3*20+2*9+1*10=88分。
由此，绘制下表。
并从总分按高到低排序，得到前三个项目是e、a、b。
专家意见表排序第1位第2位第3位得分\分排序分值\分 3 2 1工程a 30 10 20 130 2b 10 10 40 90 3c 16 10 20 88 4d 10 15 0 60 6e 14 46 10 144 1f 20 9 10 88 4该方法用统计方法综合专家们的意见，定量表示预测结果。
经济预测与决策分析
经济预测与决策分析经济预测与决策分析是指通过对经济数据和趋势的分析，来预测未来经济发展的趋势，并基于这些预测结果做出相应的决策。
这是一个涉及到经济学、统计学、数学等多个学科的综合性工作。
在当今快速变化的经济环境中，经济预测与决策分析的重要性愈发凸显。
首先，经济预测与决策分析对于政府决策具有重要意义。
政府在制定经济政策时，需要了解当前经济形势以及未来的发展趋势，以便制定出更为科学合理的政策。
例如，通过对GDP、CPI等指标的分析，可以预测通货膨胀压力的增加，从而采取相应的货币政策措施，以保持经济的稳定运行。
其次，经济预测与决策分析对于企业经营决策也具有重要意义。
企业需要根据市场需求的变化来调整生产、销售和投资策略，以适应市场的变化。
通过对市场需求、竞争对手、行业趋势等因素的分析，可以预测市场的发展趋势，从而为企业提供决策参考。
例如，通过对消费者购买力、消费习惯等因素的分析，可以预测到某个产品的市场需求将会增加，企业可以相应地增加生产和投资，以获得更大的市场份额。
此外，经济预测与决策分析对于个人投资决策也具有重要意义。
个人投资者需要根据市场的发展趋势来选择投资品种和时间，以获得更好的投资回报。
通过对股市、货币市场、房地产市场等的分析，可以预测市场的涨跌趋势，从而为个人投资者提供决策参考。
例如，通过对某只股票的基本面和技术面的分析，可以预测到该股票未来的涨跌趋势，个人投资者可以相应地进行买入或卖出操作，以获取更好的投资收益。
然而，经济预测与决策分析也存在一定的局限性。
首先，经济预测本身就存在不确定性。
经济发展受到多种因素的影响，包括政策、自然灾害、国际形势等，这些因素的变化都可能导致预测结果的偏差。
其次，经济预测与决策分析需要大量的数据和专业知识支持，对于一般人来说较为困难。
此外，经济预测与决策分析需要对多个因素进行综合考量，需要在时间和资源有限的情况下做出决策，这也给分析带来了一定的难度。
为了提高经济预测与决策分析的准确性和有效性，需要不断完善分析方法和技术。
经济预测与决策判断预测法
三、联测法（点面联想法） 就是以调查对象的普查资料或抽样资料 为基础，通过分析、判断、联想等来进 行预测的一种方法。
例：设甲，乙两高校08届毕业生的就业 率分别为80%和90%，现对甲高校09届 毕业生的就业情况进行抽样调查，调查 结果为200名毕业生中有120人就业了， 试用联测法预测甲高校09届毕业生的就 业率。
专家会议预测法的缺点
专家会议的主要缺点是易受心理因素的影响。 个别权威的意见，在专家会议上容易左右其他 成员意见； 有些专家由于自尊心，即使个人意见依据不充 分，也不愿意当面修正； 有些专家碍于情面，对自己认为是不正确的判 断，也不愿意发表意见。 另外，因参加会议的人数有限，代表性不够， 影响讨论。
二、头脑风暴法
头脑风暴法是专家会议预测法的具体运用，头脑风暴法又称智暴 法（Brain Storming Method）。这是由奥斯邦（A.F.Osborn）于 1957年提出的。 头脑风暴法是通过一组专家共同开会讨论，进行信息交流和互相 启发，从而激发出专家产生创造性思维，以达到互相补充，并产 生“组合效应”的预测方法。头脑风暴法可分为创业头脑风暴和 质疑头脑风暴两种方法。 创业头脑风暴就是组织专家对所要解决的问题，开会讨论，各持 已见地、自由地发表意见，集思广益，提出所要解决问题的具体 方案。例如，1988年我国纺织工业部曾召开过一次专家会议，来 预测国外春秋时装的流行款式以提高我国纺织品的出口份额。 质疑头脑风暴就是对已制定的某种计划方案，召开专家会议，由 专家提出质疑，去掉不合理的部分，补充不完善的部分，使计划 方案趋于完善。例如，美国国防部曾邀请50名专家，针对美国制 定长远科技规划的工作文件，举行了两周的头脑风暴会议，由专 家提出问题，进行质疑，最后通过讨论形成结论一致的报告。
经济预测与决策教学设计
经济预测与决策教学设计摘要：经济预测与决策是现代经济学中的重要课题，学生对此需要有一定的了解和掌握。
本文将设计一节经济预测与决策的教学内容，以及相应的教学方法和评估方式，旨在帮助学生培养经济预测与决策能力。
第一部分：引言经济预测与决策作为一门重要的学科，对于个人和社会的发展具有重要的意义。
在现代社会中，经济预测与决策的能力已成为各行各业的必备技能之一。
因此，将经济预测与决策纳入教学中，帮助学生培养这方面的能力显得尤为重要。
第二部分：教学内容本节课的教学内容主要包括两个方面：经济预测和经济决策。
对于经济预测，学生需要了解预测的基本概念、方法和技巧。
他们将学习如何运用统计学和经济学的原理，利用历史数据和现有模型进行经济现象的预测。
对于经济决策，学生需要理解决策的基本流程和方法，并学会如何根据经济预测的结果做出合理的决策。
第三部分：教学方法1. 案例分析法：通过真实的案例，让学生了解经济预测与决策在实际问题中的应用。
例如，可以选择一些经济发展中的典型案例，让学生进行分析和讨论，从而培养他们的分析和判断能力。
2. 小组合作学习：将学生分组，让他们进行小组合作学习，共同解决经济预测和决策问题。
通过合作学习，学生可以相互交流，共同思考和解决问题，培养他们的团队合作和沟通能力。
3. 角色扮演：设计一些情景，让学生扮演不同的角色，进行经济决策的模拟。
通过角色扮演，学生可以更好地理解和运用经济预测与决策的概念和方法，提高他们的实践能力。
第四部分：教学评估为了评估学生对经济预测与决策的掌握程度，可以采用以下方式进行评估：1. 课堂讨论：通过课堂上的讨论，评估学生对经济预测和决策概念的理解和应用能力。
2. 个人作业：布置一些与经济预测和决策相关的个人作业，评估学生的独立思考和问题解决能力。
3. 小组项目：要求学生组成小组，开展一项与经济预测和决策相关的小组项目。
评估学生的团队合作和项目管理能力。
第五部分：结论通过本次经济预测与决策的教学设计，学生将有机会了解和掌握经济预测和决策的基本理论和方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
重庆交通大学学生实验报告实验课程名称《经济预测与决策》开课实验室B01机房学院2014 级物流管理专业四班学生姓名陈立新学号631404090402开课时间2015 至2016 学年第二学期实验一一元线性回归预测一、实验目的通过实验掌握一元线性回归预测的数学模型、参数估计方法、误差分析和检验，掌握一元线性回归的点预测和区间预测。
二、实验内容已知某市货物运输量Y（万吨），GDP（亿元，1980年不变价）1985年-1998年的样本观测值见下表：1. 用Excel直接计算一元线性回归模型的参数，要求写出计算过程。
2. 计算可决系数，并根据可决系数分析模型的优劣。
3. 计算F统计量，根据显著性水平α=0.05作F检验。
4. 假如2000年某市以1980为不变价国内生产总值为620亿元，求2000年货物运输量预测值及预测区间。
三、实验步骤xi^2 yi^2 xi*yi b^ a^26143.66 333026001 2950681 26.95415 12596.2729264.94 343175625 3169072 26.95415 12596.2733881.76 338560000 3386888 26.95415 12596.2737927.56 278656249 3250962 26.95415 12596.2739148.58 241584849 3075338 26.95415 12596.2743493.1 253733041 3321993 26.95415 12596.2748867.52 335182864 4047166 26.95415 12596.2760969.49 307020484 4326532 26.95415 12596.2776618.24 468289600 5989952 26.95415 12596.27100096.3 565631089 7524466 26.95415 12596.27132146.8 577921600 8739021 26.95415 12596.27172648.6 582401689 10027503 26.95415 12596.27216951 629508100 11686420 26.95415 12596.27259182.8 600495025 12475496 26.95415 12596.271277340 5.855E+09 83971489 377.3581 176347.7 20169 280.933 91238.6 418227587 599796316954.48 1675777 10330372 0.781002 3684754.517207.31 1736302 8769059 σ^2 270132717557.72 709443 6816567.9 2927060 3127844.917845.59 1328454 5396261.5 σ1207959717929.41 5694969 5013828.9 1710.865 2139591118217.55 5237476 3806472.1 F 1797396618554.75 60885.4 2604420.9 42.79505 346172619251.78 2992152 840499.47 7004340.320057.17 2505339 12409.435 216510221124.02 7070180 912879.98 1306409422394.64 2707218 4955370.1 1498795923795.98 113580 13158119 1571669425150.97 3717.18 24824282 2422045926318.62 3289226 37823126 18804613282360 3.5E+07 125263669 160388387四、实验结果可决系数=0.781002yi=12596.27+26.95415xia^=12596.27b^=26.95F=42.79505F(0.05)=4.75F>F(0.05)方程显著σ=1710.865x=620的预测29307.837值t0.05(12) 2.18预测区间24722.718 33892.96五、实验小结通过实验,我掌握了一元线性回归预测的数学模型、参数估计方法、误差分析和检验，掌握了一元线性回归的点预测和区间预测。
实验二多元线性回归预测一、实验目的通过实验掌握多元线性回归预测的数学模型、参数估计方法、误差分析和检验，掌握多元线性回归的点预测和区间预测。
二、实验内容已知某服装公司的利润与销售额和经营费用有关，现有如下统计数据：1. 根据上面的数据，用Excel中的数据分析直接进行回归。
2. 写出该二元线性回归模型。
3. 写出复相关系数、调整后的可决系数、标准误差，简单判别该预测模型的优劣。
4. 写出F统计量和斜率系数的t统计量，根据显著性水平α=0.05,作F检验和t检验。
5.据估计，未来一年销售额可达460万元，经营费用可控制在100万元，试预测未来一年的利润。
若置信水平为5%，利润可能范围是多少？三、实验步骤SUMMARY OUTPUT回归统计Multiple R 0.95910151R Square 0.919875707Adjusted RSquare 0.905307654标准误差 1.418315633观测值14方差分析df SS MS F SignificanceF回归分析 2 254.0407599 127.0204 63.1433513 9.35E-07 残差11 22.12781157 2.011619总计13 276.1685714Coefficients 标准误差t Stat P-value Lower 95% Upper 95%Intercept 21.31605153 8.626069435 2.47112 0.031059634 2.330201 40.3019 X Variable 1 0.109054091 0.010531302 10.35523 5.21028E-07 0.085875 0.132233 X Variable 2 -0.38786783 0.107699802 -3.60138 0.004159867 -0.62491 -0.15082RESIDUAL OUTPUT观测值预测 Y 残差标准残差1 13.91949835 -1.619498348 -1.241322 14.92875858 1.071241423 0.8210883 15.78803041 -0.088030406 -0.067474 19.07458952 2.12541048 1.6290915 19.47900148 -1.579001479 -1.210286 18.32608747 0.473912529 0.3632467 17.29571233 -1.895712328 -1.453038 17.33159587 1.668404134 1.2788039 18.65980028 1.340199716 1.0272410 19.80486824 -1.404868235 -1.0768111 21.77031327 0.029686728 0.02275412 23.52979124 0.570208761 0.43705513 26.39431467 -0.794314671 -0.6088314 29.8976383 0.102361696 0.078458四、实验结果2．Y=0.109X1-0.388X2+21.3163．复相关系数0.95910151调整后的可决系数0.905307654标准误差1.4183156334．F统计量63.1433513斜率系数的t统计量t1=10.35523 t2=-3.60138F(1,12)=4.75F=63.1433513>F(1,12),方程显著t0.0512=2.18t1>2.18，显著t2<2.18,不显著5.Y=460*0.109-0.388*100+21.316=32.656(28.898,36.414)五、实验小结通过实验我掌握了多元线性回归预测的数学模型、参数估计方法、误差分析和检验，掌握了多元线性回归的点预测和区间预测。
实验三非线性回归预测一、实验目的通过实验掌握非线性回归预测的数学模型、参数估计方法、误差分析和检验，掌握非线性回归的点预测和区间预测。
二、实验内容：1. 对下表所给数据，在Excel中作xy散点图，观察xy的数据适合哪几类曲线？2. 若数据适合二次多项式曲线和幂函数曲线，分别用多元线性回归模型参数估计的方法估计二次多项式模型和幂函数模型的参数，并比较和分析两种模型的优劣。
3. 选择上述模型中更优秀者进行预测。
若2011年的销售量为500千吨，预测当年的利润并给出置信度为95%的区间预测。
三、实验步骤由散点图可以看出，数据适合二次多项式曲线和幂函数曲线二次多项式的回归模型分析幂函数的回归模型分析四、实验结果二次多项式的参数a=0.004 b=0.90 c=-38.48 检验：对于常数c，p=0.17>0.05 不显著对于x1的系数a,p<0.05 显著对于x2的系数b,p<0.05 显著幂函数的参数常数a,p<0.05 显著X的指数b,p<0.05 显著比较之下，幂函数模型更好3.预测区间（499.81，500.19）五、实验小结通过实验我掌握了非线性回归预测的数学模型、参数估计方法、误差分析和检验，掌握了非线性回归的点预测和区间预测方法。
实验四带虚变量的回归预测一、实验目的通过实验掌握带虚变量的回归预测的数学模型、参数估计、误差分析和检验。
二、实验内容1.下表是我国城镇居民家庭抽样调查资料，作散点图，分析该数据的特征。
2.建立带虚变量的线性回归模型，通过多元线性回归的显著性检验t检验，确定一个最合适的预测模型。
3.若某中等收入户人均收入为2808元/年，预测其彩电拥有量。
三、实验步骤四、实验结果T（0.05）8=2.317.964〉2.31，所以显著-7.009〈2.31，所以不显著9.506〉2.31，所以显著Y=52.615+0.013X+38.603D-0.010DX若某中等收入户人均收入为2808元/年，Y=52.615+0.013X，X=2808，Y=89.119其彩电拥有为89.119五、实验小结根据散点图，在图中两变量的关系还是比较直观的，大致可以判断散点图由两条直线组成，所以引入一个虚变量，设定第一条直线的D 为0，第二条直线的D为1，第一条直线由五个点组成，第二条直线也由五个点组成。