生活中的立体图形同步练习题
1.1生活中的立体图形同步训练2024-2025学年鲁教版(五四制)数学六年级上册
1.1 生活中的立体图形同步训练2024-2025学年鲁教版(五四制)数学六年级上册一、单选题1.太阳、西瓜、易拉罐、篮球、橡皮擦、书本中,形状类似圆柱的有()A.1个B.2个C.3个D.4个2.如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,下列说法正确的有()①n棱柱有n个面;①n棱柱有3n条棱;①n棱柱有2n个顶点.A.0个B.1个C.2个D.3个3.下列图形中,立体图形的个数是()A.2B.3C.4D.54.在下面的几何体中:①长方体;①圆柱;①球;①五棱柱;①圆锥;①正方体,可以看成有两个底面的几何体是()A.①①①①B.①①①C.①①①①D.①①①①5.如图,从上面看到的是()A.B.C.D.6.将如图所示的平行四边形绕垂直于一边且过中心的直线旋转一周,形成的几何体是()A.B.C.D.二、填空题7.包围着体的是面,面可以分为和.8.若一个棱柱有12个顶点,则这个棱柱有个侧面.9.用同样大小的正方体木块搭成的立体图形,从前面和上面看到的形状一样,如图所示.搭出这个立体图形至少要用个这样的小正方体木块.10.图中的大矩形长10厘米、宽8厘米,小矩形长6厘米、宽5厘米,以长边中点连线(图中的虚线)为轴,将图中的阴影部分旋转一周得到的几何体的表面积为平方厘米.11.如图,有一个体积为64cm3的魔方,则魔方的表面积为cm2.12.下列说法中,①面数较多的立体图形就是多面体;①长方体是四棱柱,四棱柱是长方体;①长方形绕其一边旋转一周得到的立体图形是圆柱体;①棱锥底面边数与侧棱数相等;①直角三角形绕其一边旋转一周得到的立体图形是圆锥;①棱柱的上、下底面是形状,大小相同的多边形;①圆锥和圆柱的底面都是圆;①由某一图形绕着一条直线旋转一周所得到的几何体,一定不是多面体;①将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球体;其中正确的序号是.三、解答题13.如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连.14.将一个长为8cm,宽为5cm的长方形绕它的一边所在的直线旋转一周,求得到的几何体的体积(结果保留π).15.生活中有哪些几何体可以由平面图形旋转而得到?你能想象它们是由什么平面图形旋转而成的吗?举例说明.16.十九世纪中叶,诞生了一个新的几何学分支…“拓扑学(又称‘位置解析’)”.它所研究的是几何图形这样一些最基本的、最深刻的性质:图形经受剧烈的变形,以致所有度量性质和射影性质都失去之后,这些性质仍然存在.数学家们找到若干个令人叹为观止的实例,例如著名的Mobius带、Klein瓶……请看如图,你能否将正方形图中上方的小方块与下方的对应的小方块用平面内不相交的实线连起来,且要求连线只能在该正方形内部的空白处.17.点动成线,线动成面,面动成体,如图,长方形的长AD=3cm,宽AB=2cm,若将长方形绕BC边所在直线旋转一周,请你解答下列问题:(1)得到的几何体的名称是______;(2)求得到的几何体的侧面积和体积.18.如图所示是由棱为1cm的立方体小木块搭建成的几何体从3个方向看到的形状图.(1)请你观察它是由个立方体小木块组成的;(2)在从上面看到的形状图中标出相应位置上立方体小木块的个数;(3)求出该几何体的表面积(包含底面).。
北师大版数学七年级上册《生活中的立体图形》同步精品练习题

1.1 生活中的立体图形填空题1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.2.图形是由________,__________,____________构成的.3.物体的形状似于圆柱的有________________;类似于圆锥的有______________;类似于球的有_________________.4.围成几何体的侧面中,至少有一个是曲面的是______________.5.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.6.圆柱,圆锥,球的共同点是_____________________________.7.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.8.圆可以分割成_____个扇形,每个扇形都是由___________.9.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形.二、选择题10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形A. 10B. 9C. 8D. 711. 图1-1是由( )图形饶虚线旋转一周形成的13.图1-2绕虚线旋转一周形成的图形是( )14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成A.三角形和扇形B圆和四边形C.圆和三角形D圆和扇形15.下面全由圆形组成的图案是( )三、解答题16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?(1)六面体(2)圆柱(3)圆锥(4)棱锥17.请写出下列几何体的名称( ) ( ) ( )( ) ( )18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?19.动手做一做.将一个长方体切去一部分,看一看剩余的部分是几面体呢?四.开放创新提高题20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形励志名言:1、学习从来无捷径,循序渐进登高峰。
华东师大版七年级数学上册《3.1生活中的立体图形》同步练习题带答案

华东师大版七年级数学上册《3.1生活中的立体图形》同步练习题带答案1.下列图形中,不是立体图形的是()A.圆B.圆柱C.圆锥D.球2.下列所述物体中,是球体的是()A.铅笔B.打足气的自行车内胎C.乒乓球D.电视机3.下列几何体中,不是多面体的是()A.长方体B.正方体C.三棱柱D.圆柱4.下列简单几何体中,属于柱体的有()A.5个B.4个C.3个D.2个5.下列说法中,正确的有()①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆体;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.A.2个B.3个C.4个D.5个6.下列选项中的三个图形全部属于多面体的是()A BC D7.如图所示的多面体是面体,有条棱,个顶点.【能力巩固】8.如图,下列选项中的平面图形绕虚线l旋转一周,可以得到如图所示的立体图形的是()A B C D9.下列立体图形中,有五个面的是()A.四棱锥B.五棱锥C.四棱柱D.五棱柱10.下列说法中,正确的有()①圆锥和圆柱的底面都是圆形;②棱锥底面边数与侧棱数相等;③棱柱的上下底面是形状、大小都相同的多边形;④正方体是四棱柱,四棱柱是正方体.A.1个B.2个C.3个D.4个11.若一个棱柱有10个顶点,则下列说法正确的是()A.这个棱柱有4个侧面B.这个棱柱有5条侧棱C.这个棱柱的底面是十边形D.这个棱柱是一个十棱柱12.若有四个几何体如图所示,则下列说法正确的是()A.①由4个面围成;②由2个面围成;③由3个面围成;④由4个面围成B.①由5个面围成;②由3个面围成;③由4个面围成;④由3个面围成C.①由5个面围成;②由3个面围成;③由4个面围成;④由2个面围成D.①由5个面围成;②由3个面围成;③由4个面围成;④由1个面围成13.用6根完全相同的火柴最多能组成个一样大的三角形,所得几何体的名称是.【素养拓展】14.如图,这是一个正六棱柱,它的底面边长是3 cm,高是6 cm.(1)这个棱柱的侧面积是多少?(2)这个棱柱共有多少条棱?所有棱长的和是多少?(3)这个棱柱共有多少个顶点?(4)通过观察,试用含n的式子表示n棱柱的面数与棱的条数.15.(1)三棱锥有条棱,个面;四棱锥有条棱,个面.(2)十五棱锥有条棱,一百棱锥有个面.(3)有没有一个多棱锥,其棱数是2024,若有,求出它有多少个面;若没有,说明理由.参考答案1.A2.C3.D4.B5.B6.A7.八12 6【能力巩固】8.D9.A10.C11.B12.D13.4三棱锥或四面体【素养拓展】14.解:(1)正六棱柱的侧面积为3×6×6=108(cm2).(2)这个棱柱共有6+6+6=18条棱,所有棱长的和是12×3+6×6=36+36=72(cm).(3)这个棱柱共有12个顶点.(4)n棱柱的面数是(n+2)个,n棱柱棱的条数是3n条.15.解:(1)6;4;8;5.(2)30;101.(3)当2n=2024时,解得n=1012∴n+1=1012+1=1013,即有,它有1013个面.。
数学北师大版七年级上册1.1《生活中的立体图形》同步训练(含解析)

数学北师大版七年级上册1一、选择题1.下面几何体中,全是由曲面围成的是〔〕A.圆柱B.圆锥C.球D.正方体2.以下说法错误的选项是〔〕A. 长方体、正方体都是棱柱B. 三棱柱的正面是三角形C. 直六棱柱有六个正面、正面为矩形D. 球体的三种视图均为异样大小的图形3.以下平面图形中,有五个面的是〔〕A. 四棱锥B. 五棱锥C. 四棱柱D. 五棱柱4.将一个直角三角形绕它的最长边〔斜边〕旋转一周失掉的几何体为〔〕A. B. C. D.5.将四个棱长为1的正方体如图摆放,那么这个几何体的外表积是〔〕A. 3B. 9C. 12D. 18二、填空题6.一个直棱柱有12条棱,那么它是________棱柱.7.一个几何体的面数为12,棱数为30,它的顶点数为________.8.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有________条.9.两个完全相反的长方体的长.宽.高区分为5cm.4cm.3cm,把它们叠放在一同组成个新长方体,在这个新长方体中,体积是________cm3,最大外表积是________cm2.10.一只小蚂蚁从如下图的正方体的顶点A沿着棱爬向有蜜糖的点B,它只能经过三条棱,请你数一数,小蚂蚁有________种匍匐路途.三、解答题11.从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体,失掉一个如图的零件,求:〔1〕这个零件的外表积〔包括底面〕;〔2〕这个零件的体积.12.有3个棱长区分是3cm,4cm,5cm的正方体组分解如下图的图形.其露在外面的外表积是多少?〔整个平面图形摆放在地上〕13.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,失掉的几何体的体积是多少?14.长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,失掉一个几何体,〔1〕求此几何体的体积;〔2〕求此几何体的外表积.〔结果保管π〕15.观察图形,回答以下效果:〔1〕图 是由几个面组成的,这些面有什么特征?〔2〕图②是由几个面组成的,这些面有什么特征?〔3〕图①中共构成了多少条线?这些线都是直的吗?图②呢?〔4〕图①和图②中各有几个顶点?答案解析局部一、选择题1.【答案】C【考点】几何体的外表积【解析】【解答】解:A、圆柱由上下两个平面和正面一个曲面组成,不契合题意;B、圆锥由正面一个曲面和底面一个平面组成,不契合题意;C、球只要一个曲面组成,契合题意;D、正方体是由六个平面组成,不契合题意.故答案为:C.【剖析】圆锥两个面围成,一个曲面,一个平面;圆柱三个面围成,一个曲面,两个平面;正方体由6个面围成,六个面都是平面;球球只要一个曲面组成。
北师大版七年级数学上册 1 1 生活中的立体图形同步练习(含答案)

北师大版七上 1.1 生活中的立体图形一、选择题(共8小题)1. 下列几何体中,属于棱柱的是( )A. ①③B. ①C. ①③⑥D. ①⑥2. 在①球体;②柱体;③圆锥;④棱柱;⑤棱锥中,必是多面体(指由四个或四个以上多边形所围成的立体图形)的是( )A. ①∼⑤都是B. ②和③C. 仅④D. 仅④和⑤3. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学,它有6条棱,则该模型对应的立体图形可能是( )A. 三棱柱B. 四棱柱C. 三棱锥D. 四棱锥4. 下面的说法中,正确的有( )①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④棱柱的侧面一定是长方形(包括正方形);⑤长方体一定是柱体;⑥长方体的面不可能是正方形.A. 2个B. 3个C. 4个D. 5个5. 将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )A. B.C. D.6. 已知长方体ABCD−EFGH如图所示,那么下列直线中与直线AB不平行也不垂直的直线是( )A. EAB. GHC. HCD. EF7. 如图是一个放置在水平试验台上的锥形瓶,从上往下看该立体图形得到的平面图形是( )A. B.C. D.8. 如图为正方体的一种展开图,各面都标有数字,则数字为−2的面与其对面上的数字之积是( )A. −12B. 0C. −8D. −10二、填空题(共5小题)9. 请完善本课时的知识结构图.10. 已知长方体的长、宽、高之比是5:4:3,如果用一根长为48厘米的铁丝全部用于制作这个长方体模型框架,正好用完,那么此长方体的体积是立方厘米.11. 一个棱柱有18条棱,则它有个面.12. 把下面立体图形的标号写在相对应的括号里:长方体:;棱柱体:;圆柱体:;球体:;圆锥体:.13. 有一些具体物体,分别是:①三棱镜、②方砖、③笔筒、④铅锤、⑤粮囤,它们的形状如图1所示;图2中是一些立体图形.请将图1中物体形状对应的序号填入图2中与之类似的立体图形下面的括号内.三、解答题(共7小题)14. 如图,说出下列各几何体的名称,哪些可以由平面图形的旋转得到?15. 将实物与相应的几何体用线连接起来.16. 如图,上面一行是一些具体的实物图形,下面一行是一些立体图形,试用线连接立体图形和类似的实物图形.17. 请根据要求完成下表:18. 你能否将下列几何体进行分类?并说出分类的依据.19. 如图所示的图形是我们常见的一些几何体,请你把每个几何体的名称写在它的下面.;;;;;;.20. 如图,上面一行是一些具体的实物图形,下面一行是一些立体图形,试用线连接立体图形和类似的实物图形.答案1. C2. D3. C 【解析】侧面是三角形,说明它是棱锥,底面是三角形,说明它是三棱锥,故选:C.4. B5. C【解析】图是一个直角梯形,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆,因此得到的立体图形应该是一个圆台.6. C7. B8. A9. 8,12,3,相等,6,长方形,3,形状,大小10. 6011. 812. ②⑤⑧,②④⑤⑧,①⑥,⑦⑨,③⑩13. ③,④,②,①,⑤14. (1)正方体;(2)圆锥;(3)三棱柱;(4)四棱柱;(5)球体;(6)五棱柱;(7)圆柱;(8)长方体;(9)长方体;(10)四棱锥;(2)(5)(7)可以由平面图形旋转得到.15.16. 如图所示:17.名称三棱锥长方体三棱柱圆柱圆锥球包含的平面图形三角形长方形三角形、长方形圆圆/18. 答案不唯一,如按柱体、锥体、球分,柱体有:①③④⑤⑥⑧,锥体有:②,球有:⑦.19. 长方体;球;圆柱;圆锥;三棱柱;正方体;四棱柱20. 如图所示:。
生活中的立体图形同步练习2024—2025学年东华师大版数学七年级上册

3.1生活中的立体图形同步练习一、单选题1.下列几何体,都是由平面围成的是( )A .圆柱B .三棱柱C .圆锥D .球2.用一个平面去截圆锥,得到的截面形状不可能是( )A .B .C .D . 3.以AB 为轴旋转一周后得到的立体图形是( )A .B .C .D . 4.如图所示的两个长方体容器中液体体积相同,根据图中信息,以下结论正确的是()A .8136(5)x x =+B .()81365x x =-C .甲容器中液体的体积为405D .乙容器中液面的高度为105.下列说法不正确的是( ).①长方体一定是柱体;①八棱柱有10个面;①六棱柱有12个顶点;①用一个平面去截几何体,若得到的图形是三角形,则这个几何体一定有一个面的形状是三角形.A.①B.①C.①①D.①①6.下列几何体中,圆锥是()A.B.C.D.7.下面几何体中,是圆锥的为()A.B.C.D.8.用一个平面去截下列几何体,截面不可能是圆的是()A.B.C.D.9.将一个直角三角形绕一条直角边所在的直线旋转一周后得到的几何体可能是()A.B.C.D.10.将一张正方形纸片按图①、图①所示的方式依次对折后,再沿图①中的虚线剪裁,最后将图①中的纸片打开铺平,所得到的图案是()A.B.C.D.二、填空题11.如图,这个几何体的名称为.12.用平面去截下列几何体:①三棱柱;①正方体;①圆柱;①圆锥;①球,则截面的形状可能是三角形的有个.13.一个棱长为6cm的正方体,它是由216个棱长为1cm的小正方体组成的,点P为上底面ABCD的中心,如果挖去(如图)的阴影部分为四棱锥,剩下的部分还包括个完整的棱长是1cm的小正方体.14.如果一个棱柱有12个顶点,那么它的面的个数是.15.已知一个直角三角形的两直角边分别是3和4,将这个直角三角形绕它的直角边所在直线旋转一周,可以得到圆锥,则圆锥的体积是 .(213π圆锥V r h =,结果保留π) 16.如图,一个正方体截去一个角后,剩下的几何体面的个数和棱的条数的和是 .三、解答题17.下列几何体可以由平面图形绕其中一条直线旋转一周得到吗?18.我们知道,将一个长方形绕它的一条边所在的直线旋转一周,得到的几何体是圆柱.现有一个长为6cm ,宽为4cm 的长方形,将这个长方形绕某条边所在直线旋转一周,求所得圆柱的体积是多少?(结果保留π)19.用一个平面去截一个正方体,请你画出三种不同的截面情况.20.如图,图①所示的几何体叫三棱柱,它有6个顶点,9条棱,5个面,图①和图①所示的几何体分别是四棱柱和五棱柱.(1)四棱柱有 个顶点, 条棱, 个面;(2)五棱柱有 个顶点, 条棱, 个面;(3)那么n 棱柱有 个顶点, 条棱, 个面.21.五棱柱、六棱柱各有多少个面?多少个顶点?多少条棱?猜测七棱柱的情形并设法验证你的猜测.22.如图1至图3是将正方体截去一部分后得到的多面体.(1)根据要求填写表格:面数(f)顶点数(v)棱数(e)图1图2图3(2)猜想f、v、e三个数量间有何关系;(3)根据猜想计算,若一个多面体有顶点数2013个,棱数4023条,试求出它的面数.。
1.1生活中的立体图形 北师大版初中数学七年级上册同步练习(含详细答案解析)

1.1生活中的立体图形北师大版初中数学七年级上册同步练习一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.用棱长1厘米的正方体木块,摆成底面积是12平方厘米,高是2厘米的长方体,可以摆成()种不同的形状.A. 1B. 2C. 3D. 42.把一个棱长是4分米的正方体钢坯削成一个最大的圆柱,这个圆柱的体积是( )A. 18.84dm3B. 28.26dm3C. 50.24dm3D. 100.48dm23.如图,将大正方体一个顶点处的一个小正方体去掉后表面积与原表面积比较,( )A. 现在表面积大B. 原来表面积大C. 一样大4.由4个棱长均为1的小正方形组成如图所示的几何体,这个几何体的表面积为( )A. 18B. 15C. 12D. 65.下面现象能说明“面动成体”的是( )A. 流星从空中划过留下的痕迹B. 扔一块小石子,小石子在空中飞行的路线C. 时钟秒针旋转时扫过的痕迹D. 将一枚硬币竖立在桌面,击打一侧使其快速旋转,就会看到一个“球”6.一根长方体木料,长2米,宽和厚都是5米,把它锯成1米长的两段,表面积增加了()平方米.A. 50B. 40C. 45D. 257.下列几何体中,棱锥是( )A. B. C. D.8.如图,如果以直角三角形的一条直角边为轴旋转一周得到一个圆锥,这个圆锥的体积最大是______立方厘米.( )A. 37.68B. 50.24C. 78.5D. 6289.下列几何体都是由平面围成的是( )A. 圆锥B. 五棱锥C. 圆柱D. 球10.下面的几何体中,全是由曲的面围成的是( )A. 圆柱B. 圆锥C. 球D. 正方体11.2023年长沙国际马拉松在芙蓉中路(贺龙体育中心东广场旁)起跑,来自国内外的26000名跑友汇成一片红色的海洋驰骋在长马赛道上,他们用脚步丈量星城,感受一江两岸、山水洲城的魅力.图①是此次全程马拉松男子组颁奖现场.图②是领奖台的示意图,则此领奖台从正面看到的平面图形是( )A. B.C. D.12.如图,大正方体木块的体积是64cm3,把它切成大小相等的8个小正方体,则所有小正方体的表面积之和为 ( )A. 192cm2B. 194cm2C. 196cm2D. 212cm2二、填空题:本题共4小题,每小题3分,共12分。
北师大版七年级数学上册1.1生活中的立体图形同步练习题
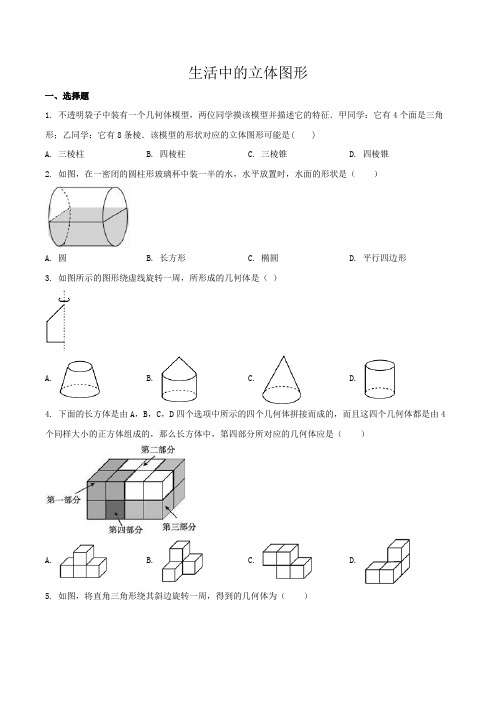
13.生活中常见的几何体有正方体、长方体、三棱柱、圆锥、五棱柱、三棱锥、球,是柱体的有_______;是锥体的有______;是球的有______.
14.如图,长方形 的长 为 ,宽 为 ,将长方形绕 边所在直线旋转后形成的立体图形的体积是_____ .
15.将如图所示的平面图形折成一个正方体形的盒子,折好以后,与1相对的数是_____.
3. 如图所示的图形绕虚线旋转一周,所形成的几何体是( )
A. B. C. D.
4.下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A. B. C. D.
5.如图,将直角三角形绕其斜边旋转一周,得到的几何体为()
(2)若将这个长方形纸片绕AB边所在直线旋转一周,则形成的几何体的体积是cm3(结果保留π);
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留π).
21.如图,如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),观察该图,探究其中的规律.
A. B. C. D.
6.将四个棱长为1的正方体如图摆放,则这个几何体的表面积是( )
A.3B.9C.12D.18
7.观察下图,把左边 图形绕着给定的直线旋转一周后,可能形成的立体图形是()
A. B. C. D.
8.笔尖在纸上快速滑动写出一个又一个字,用数学知识解释 ( )
A.点动成线B.线动成面C.面动成体D.以上答案都不对
二、填空题
9.圆柱是由_____个面组成的,其中______个平面,_____个曲面,圆锥是由______个面组成的.
1.1 生活中的立体图形 同步练习(word版含答案)

1.1 生活中的立体图形一.选择题1.下列说法错误的是()A.长方体和正方体都是四棱柱B.五棱柱的底面是五边形C.n棱柱有n条侧棱,n个面D.若棱柱的底面边长相等,则它的各个侧面面积相等2.如图所示的平面图形绕直线l旋转一周,可以得到的立体图形是()A. B. C. D.3.如图,一个有盖的圆柱形玻璃杯中装有半杯水,若任意放置这个水杯,则水面的形状不可能是()A. B. C. D.4.下列关于长方体面的四个说法错误的是()A.长方体的每个面都是长方形B.长方体中每两个面都互相垂直C.长方体中相对的两个面的面积相等D.长方体中与一个面垂直的面有四个5.如图所示立方体中,过棱BB1和平面CD1垂直的平面有()A.1个 B.2个 C.3个 D.0个6.如图,模块①由15个棱长为1的小正方体构成,模块②﹣⑥均由4个棱长为1的小正方体构成.现在从模块②﹣⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是()A.模块②,⑤,⑥ B.模块③,④,⑥ C.模块②,④,⑤ D.模块③,⑤,⑥7.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是()A.正方体 B.球 C.圆锥 D.圆柱体8.将下列各选项中的平面图形绕轴旋转一周,可得到如图所示的立体图形的是()A. B. C. D.9.面与面相交,形成的是()A.点 B.线 C.面 D.体10.将下面的直角梯形绕直线l旋转一周,可以得到如图立体图形的是()A.B. C. D.11.将下列图形绕着直线旋转一周正好得到如图所示的图形的是()A. B. C. D.12.将一个棱长为3的正方体的表面涂上颜色,分割成棱长为1的小正方体(如图).设其中一面、两面、三面涂色的小正方体的个数分别为为x1、x2、x3,则x1、x2、x3之间的关系为()A.x1﹣x2+x3=1 B.x1+x2﹣x3=1 C.x1﹣x2+x3=2 D.x1+x2﹣x3=2二.填空题13.若一个正方体所有棱的和是60cm,则它的体积是cm3.14.一个棱柱共有18个顶点,所有的侧棱长的和是72厘米,则每条侧棱长是厘米.15.第一行的图形绕虚线转一周,能形成第二行的某个几何体,用线连起来.16.如图所示图形绕图示的虚线旋转一周,(1)能形成,(2)能形成,(3)能形成.17.棱柱侧面的形状可能是一个三角形(判断对错)18.五棱柱有个面,个顶点,条侧棱,n棱柱有个面,个顶点,条棱.19.将一个半圆绕它的直径所在的直线旋转一周得到的几何体是.20.某产品是长方体,它的长、宽、高分别为10cm、8cm、6cm,将12个这种产品摆放成一个大的长方体,则此大长方体的表面积最少为cm2.21.10个棱长为1的正方体,如果摆放成如图所示的上下三层,那么该物体的表面积为;依图中摆放方法类推,继续添加相同的正方体,如果该物体摆放了上下100层,那么该物体的表面积为.22.将如图所示半圆形薄片绕轴旋转一周,得到的几何体是,这一现象说明.三.解答题23.底面半径为10cm,高为40cm的圆柱形水桶中装满了水.小明先将桶中的水倒满3个底面半径为3cm,高为5cm的圆柱形杯子,如果剩下的水倒在长、宽、高分别为50cm,20cm和12cm 的长方体容器内,会满出来吗?若没有满出来,求出长方体容器内水的高度(π取3).24.(1)用斜二侧画法补画下面的图形,使之成为长方体的直观图(虚线表示被遮住的线段;只要在已有图形基础上画出长方体,不必写画法步骤).(2)在这一长方体中,从同一顶点出发的三条棱出发的三条棱的棱长之比是5:7:2,其中最长的棱和最短的棱长之差为10cm,求这个长方体的棱长和总和.25.棱长为a的正方体,摆放成如图所示的形状.(1)如果这一物体摆放三层,试求该物体的表面积;(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.26.如图是一个长为4cm,宽为3cm的长方形纸片(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是,这能说明的事实是.(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.27.探究:将一个正方体表面全部涂上颜色(1)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体,我们把仅有i个面涂色的小正方体的个数记为x i,那么x3=,x2=,x1=,x0=;(2)如果把正方体的棱四等分,同样沿等分线把正方体切开,得到64个小正方体,那么x3=,x2=,x l=,x0=;(3)如果把正方体的棱n等分(n≥3),然后沿等分线把正方体切开,得到n3个小正方体,那么:x3=,x2=,x1=,x0=;参考答案一.选择题1.C.2.C.3.C.4.B.5.A.6.A.7.D.8.A.9.B.10.B.11.A.12.C.二.填空题13.125.14.8.15..16.圆柱;圆锥;球.17.×.18.7,10,5,(n+2),2n,3n.19.球20.1936.21.30300.22.球,面动成体.三.解答题23.解:3×102×40﹣3×32×5×3=12000﹣405=11595(cm3),长方体的容积为:50×20×12=12000cm3.∵12000>11595,∴不会满出来.11595÷(50×20)=11.595cm.∴长方体容器内水的高度11.595cm.24.解:(1)如图所示:(2)设这三条棱的棱长分别为5xcm、7xcm、2xcm,7x﹣2x=10,解得:x=2,则棱长的总和为4(7×2+5×2+2×2)=112cm.25.解:(1)6×(1+2+3)•a2=36a2.故该物体的表面积为36a2;(2)6×(1+2+3+…+20)•a2=1260a2.故该物体的表面积为1260a2.26.解:(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;(2)绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;(3)绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.故答案为:圆柱;面动成体.27.解:(1)根据长方体的分割规律可得x3=8,x2=12,x1=6,x0=1;(2)把正方体的棱四等分时,顶点处的小正方体三面涂色共8个;有一条边在棱上的正方体有24个,两面涂色;每个面的正中间的4个只有一面涂色,共有24个;正方体正中心处的8个小正方体各面都没有涂色.故x3=8,x2=24,x1=24,x0=8;(3)由以上可发现规律:三面涂色8,二面涂色12(n﹣2),一面涂色6(n﹣2)2,各面均不涂色(n﹣2)3。
1.1+生活中的立体图形同步练习++2024-2025学年北师大版(2024)七年级数学+上册+
1.1生活中的立体图形一、单选题1.汽车的雨刷把玻璃上的水滴刷得很干净,属于以下哪个几何知识的实际应用()A.点动成线B.线动成面C.面动成体D.面是平的2.将图中的直角三角形绕最长的边旋转一周可以得到的一个几何体,从正面看这个几何体所得到的平面图形是()A. B.C. D.3.如图,平面图形绕直线l旋转一周后,可以得到的立体图形是()A.B.C.D.4.对于如图所示的几何体,说法正确的是()A.几何体是三棱锥B.几何体有6条侧棱C.几何体的侧面是三角形D.几何体的底面是三角形5.“笔尖在纸上快速滑动写出数字9”运用数学知识解释这一现象为()A.点动成线B.线动成面C.面动成体D.面与面相交得线6.下列说法不正确的是()A.长方体是四棱柱;B.八棱柱有16条棱;C.五棱柱有7个面;D.直棱柱的每个侧面都是长方形.7.下列说法中正确的是()A.正方体和长方体是特殊的四棱柱,也是特殊的六面体B.棱柱底面边数和侧面数不一定相等C.棱柱的侧面可能是三角形D.长方体是四棱柱,四棱柱是长方体8.下列说法不正确的是()A.篮球的表面、水桶的侧面都是曲面B.正方体有八个顶点,经过每个顶点有两条面与面的交线C.晴朗的夜空中一颗流星划过,给我们留下一条美丽的亮线,这说明点动成线D.在中国地图上,锦州可被看作一个点9.如图所示的图形中,属于棱柱的有()A.1个B.2个C.3个D.4个二、填空题1.笔尖在纸上运动就形成了线,夜晚的流星划过天空会留下一道明亮的光线,这都可以说明.2.在正方体、长方体、圆柱、圆锥、球、六棱柱、六棱锥中属于柱体有个.3.如图是一个几何体,请你描述这个几何体的特点(写出三点):.4.如图,线段AB是正方体的一条棱,则与AB在同一平面内且与AB垂直的棱有条.5.如图是由棱长为1厘米的小正方体木块搭成的几何体.至少还需要个这样的小正方体才能搭成一个正方体.三、解答题1.如图所示的图形是一个棱柱,请问:(1)这个棱柱由几个面围成?各面的交线有几条?它们是直的还是曲的?(2)这个棱柱的底面和侧面各是什么形状?(3)该棱柱有几个顶点?2.如图是一张长方形纸片,长方形的长为6cm,宽为4cm,若将此长方形纸片绕它的一边所在直线旋转一周,得到一个几何体.(1)这个几何体的名称是,这个现象用数学知识解释为;(2)求得到的这个几何体的体积(结果保留π)3.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题.(1)根据上面的多面体模型,直接写出表格中的m,n的值,则m=______,n=______.(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______.(3)一个多面体的面数等于顶点数,且这个多面体有30条棱,求这个多面体的面数.5.图中的棱柱、圆锥分别是由几个面围成的?它们是平的还是曲的?。
北师大版七年级数学上册 1 1 生活中的立体图形同步练习(Word版含答案)

北师大版七年级上 1.1 生活中的立体图形一、选择题(共10小题)1. 如图所示,几何体的主视图是( )A. B.C. D.2. 图中几何体的俯视图是( )A. B.C. D.3. 用4个小立方体搭成如图摆放的几何体,下面视图是几何体主视图的是( )A. B.C. D.4. 如图,由三个小立方体搭成的几何体的俯视图是( )A. B.C. D.5. 如图是某物体的三视图,则这个物体的形状是( )A. 四面体B. 直三棱柱C. 直四棱柱D. 直五棱柱6. 如图是一个几何体的三视图,则该几何体的展开图可以是( )A. B.C. D.7. 如图,立体图形由小正方体组成,这个立体图形有小正方体( )A. 9个B. 10个C. 11个D. 12个8. 将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )A. B.C. D.9. 下列四个图形中是正方体的平面展开图的是( )A. B.C. D.10. 已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为( )A. πB. 4πC. π或4πD. 2π或4π二、填空题(共5小题)11. 下列图形中,是平面图形的有,是立体图形的有.12. 如图所示,将图沿实线折起来得到一个正方体,那么“5”的对面是(填编号).13. 有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,则结果是.(填“溢出”“刚好装满”“未装满”)14. 如图,已知某几何体的三视图,则这个几何体是.15. 在市委、市政府的领导下,全市人民齐心协力,努力将我市创建为“全国文明城市”,为此学生小红特制了一个正方体玩具,其展开图如图所示,则原正方体中与“文”字所对的面上标的字应是.三、解答题(共5小题)16. 将图①的正方体切去一块,不同的切法可以得到图②−⑤的几何体,它们各有多少个面?多少条棱?多少个顶点?17. 如图所示是由几个小正方块所组成的几何体俯视图,小正方形中的数字表示在该位置小正方块的个数,请你画出这个几何体的正视图和左视图.18. 如图是一个食品包装盒的表面展开图.(1)请写出这个包装盒的多面体形状的名称.(2)请根据图中所标的尺寸,计算这个多面体的表面积和体积.19. 如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图.20. 如图中的一些积木是由16块棱长为2cm的正方体堆成的,它的表面积是多少平方厘米?答案1. A2. D3. C4. A5. B6. A7. C8. C【解析】图是一个直角梯形,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆, 因此得到的立体图形应该是一个圆台.9. B10. C【解析】题意可知,圆柱底面圆的周长为 4π 或 2π,∴ 圆柱底面圆的半径为 2 或 1,∴ 圆柱底面圆的面积为 4π 或 π.11. ①②④⑤⑥⑧,③⑦⑨【解析】根据平面图形和立体图形的区别,进行辨别即可.12. 113. 未装满14. 四棱锥15. 城16. 图形面(个)棱(条)顶点(个)②71510③7149④7138⑤712717. 如图所示:18. (1)长方体.(2)表面积是4ab+2b2,体积是ab2.19. 如图所示:20. 上面和下面的面积为2×9×(2×2)=72(cm2);前面和后面的面积为2×7×(2×2)=56(cm2);两个侧面的面积为2×8×(2×2)=64(cm2);中间缺口处还有2个面,其面积为2×(2×2)=8(cm2).因为72+56+64+8=200(cm2),所以这个几何体的表面积为200cm2.。
北师大七年级上1.1.1认识生活中的立体图形同步练习(含答案)
1.1.1 认识生活中的立体图形1.下列图形中,不是立体图形的是( )A.球 B.圆柱 C.圆 D.圆锥2.下面物体中,最接近圆柱的是( )图13.与生活中的汽油桶的形状近似的图形是( )A.圆锥 B.长方形 C.球 D.圆柱4.下列几何体为三棱柱的是( )图25.下列几何体中与其他不同类的是( )A.长方体 B.正方体 C.三棱柱 D.圆柱6.(1)下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.图3(2)将这些几何体分类,并写出分类的理由.7.如图4所示的图形中,属于棱柱的有( )图4A.2个 B.3个 C.4个 D.5个8.下列有六个面的几何体有( )①长方体;②四棱柱;③正方体;④三棱柱.A.1个B.2个C.3个D.4个9.一个正六棱柱所有侧棱长的和是18厘米,则每条侧棱的长为________厘米.10.如图5,有一个棱长是4 cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )图5A.变大了 B.变小了C.没变 D.无法确定变化情况11.有两个完全相同的长方体,长、宽、高分别是5 cm,4 cm,3 cm,把它们叠放在一起组成一个新的长方体,在这些新的长方体中,表面积最小的是________cm2.12.如图6,现有一长方体水槽,装入一些水,然后固定底面的一边慢慢倾斜但不能使水从水槽中流出.(1)请你先实践操作一下,再说说你所见到的立体图形有哪些?(2)在这个变化中,你认为其中什么没有变化?图613.新年晚会的会场上悬挂了许多五彩缤纷的小装饰品,其中有各种各样的立体图形,如图7:图7请你数一数上图中每个多面体具有的顶点数(V),棱数(E)和面数(F),并把结果计入下表中.名称各面形状顶点数(V)面数(F)棱数(E)V+F-E正四面体正三角形正方体正方形正八面体正三角形正十二面体正五边形201230 2第1课时认识生活中的立体图形1.C 2.C 3.D4.D5.D6.解:(1)球圆柱圆锥长方体三棱柱(2)答案不唯一,如按柱体、锥体、球体来分:圆柱、长方体、三棱柱为柱体;圆锥为锥体;球为球体.按照有无曲的面来分:球、圆柱、圆锥有曲的面;长方体、三棱柱无曲的面.按照有无顶点来分:圆锥、长方体、三棱柱有顶点;球、圆柱无顶点.7.B8.C9.310.C11.14812.解:(1)长方体、四棱柱、三棱柱.(2)水的体积不变,即水槽中的水构成的柱体的体积不变.13.解:从左到右,从上到下依次填:4,4,6,2;8,6,12,2;6,8,12,2.。
1.1.2 生活中的立体图形 第2课时 北师大版七年级数学上册同步练习(含答案)

1.1.2生活中的立体图形一.选择题。
1.下面图形中,以直线为轴旋转一周,可以得到圆柱体的是( )A.B.C.D.2.如图,下面的平面图形绕轴旋转一周,可以得到圆柱体的是( )A.B.C.D.3.“节日的焰火”可以说是( )A.面与面交于线B.点动成线C.面动成体D.线动成面4.把一枚硬币在桌面上竖直快速旋转后所形成的几何体是( )A.圆柱B.圆锥C.球D.正方体5.下面现象说明“线动成面”的是( )A.旋转一扇门,门在空中运动的痕迹B.扔一块小石子,石子在空中飞行的路线C.天空划过一道流星D.汽车雨刷在挡风玻璃上面画出的痕迹6.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )A.B.C.D.7.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )A.①②③④B.①②③C.②③④D.①③④二.填空题(共5小题)8.粉笔在黑板上划过写出一个又一个字母,画出一个个图案,这说明 .9.长为4,宽为2的矩形绕其一边旋转构成一个圆柱的最大体积为 .(结果保留π)10.一个直角三角形的两条直角边的长分别为3厘米和4厘米,绕它的直角边所在的直线旋转所形成几何体的的体积是 立方厘米.(结果保留π)三.解答题(共4小题)11.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,其中一条直角边旋转一周,得到了一个几何体,请计算出几何体的体积.(锥体体积=底面积×高)12.如图是一个长为4cm,宽为3cm的长方形纸片(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.1.1.2生活中的立体图形参考答案与试题解析一.选择题。
北师大版七年级数学上册《1.1生活中的立体图形》同步测试题及答案

北师大版七年级数学上册《1.1生活中的立体图形》同步测试题及答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.下列立体图形中,是圆锥的是()A.B.C.D.2.下列图形中是多面体的有()A.(1)(2)(4)B.(2)(4)(6)C.(2)(5)(6)D.(1)(3)(5)3.子弹从枪膛中射出去的轨迹像是一条线,这个现象可以用数学知识解释为()A.点动成线B.线动成面C.面动成体D.以上都不对4.一个印有“你要探索数学”字样的立方体纸盒表面展开图如图1所示,若立方体纸盒是按图2展开,则印有“索”字在几号正方形内()A.①B.①C.①D.①5.几何图形都是由点、线、面、体组成的,点动成线,线动成面,面动成体,下列生活现象中可以反映“线动成面”的是()A.笔尖在纸上移动划过的痕迹B.长方形绕一边旋转一周形成的几何体C.流星划过夜空留下的尾巴D.汽车雨刷的转动扫过的区域6.如图,下列图形中属于棱柱的有()A.2B.3C.4D.57.夜晚时,我们看到的流星划过属于()A.点动成线B.线动成面C.面动成体D.以上答案都不对8.一个直角三角形绕它的一边所在直线旋转一周所得到的几何体一定是()A.圆锥B.圆柱C.圆锥或圆柱D.以上都不对9.观察下面四个图形是圆锥的是()A.B.C.D.10.在①球体;①柱体;①锥体;①棱柱;①棱锥中,必是多面体的是() A.①~①B.①①C.①D.①①11.一个棱柱有18条棱,那么它的底面一定是()A.五边形B.六边形C.十边形D.十五边形12.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是().A.B.C.D.二、填空题13.一个正方体有个面,条棱,个顶点.14.今年十一国庆节当晚,香港以“富兴百业贺国庆,盈聚慧城耀香江”为主题,在维多利亚港举行国庆烟花汇演,庆祝中华人民共和国成立74周年.绚烂的焰火可以看成由点运动形成的,这个现象说明.15.如果长方形的长和宽分别为6和4,那么以长方形的一边为轴旋转一周所得的几何体的体积为(结果保留 ).16.如图的几何体有个面,条棱,个顶点,它是由简单的几何体和组成的.17.如图,有一个盛有水的正方体玻璃容器,从内部量得它的棱长为30 cm,容器内的水深为8 cm.现把一块长,宽,高分别为15 cm,10 cm,10 cm的长方体实心铁块平放进玻璃容器中,容器内的水将升高cm.三、解答题18.小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=13底面积×高)19.请把下图中的平面图形与其绕所画直线旋转一周之后形成的立体图形用线连接起来.20.将一个长方形分别沿它的长和宽所在的直线旋转一周,回答下列问题:(1)旋转后将得到什么几何体?(2)若长方形的长和宽分别为6cm和4cm,求旋转后两个几何体的体积.(结果保留π)21.请你观察下列几种简单多面体模型,解答下列问题:多面体面数(F)棱数(E)四面体46长方体612正八面体8(1)计算长方体棱数,可依据长方体有6个面,每个面均为四边形即有4条棱,得出总棱数为12;请你猜想多面体面数、形状、棱长之间的数量关系,完成以下计算:①如图所示,正八面体的每一个面都是三角形,则正八面体有__________条棱;①正十二面体的每一个面都是正五边形,则它共有__________条棱;(2)如下图,一种足球(可视作简单32面多面体)是由32块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长相等,已知图中足球有90条棱;某体育公司采购630张牛皮用于生产这种足球,已知一张牛皮可用于制作30个正五边形或者制作20个正六边形,要使裁剪后的五边形和六边形恰好配套,应怎样计划用料才能制作尽可能多的足球?22.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:多面体顶点数(V)面数(F)棱数(E)四面体44①长方体8612正八面体①812正十二面体201230(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.(3)一个多面体的面数与顶点数相同,且有12条棱,则这个多面体的面数是.23.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题.(1)根据上面的多面体模型,直接写出表格中的m,n的值,则m=______,n=______.多面体顶点数(V)面数(F)棱数(E)四面体446长方体m612正八面体n812正十二面体201230(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______.(3)一个多面体的面数等于顶点数,且这个多面体有30条棱,求这个多面体的面数.参考答案1.A【分析】本题考查常见的几何体.熟记常见的几何体,是解题的关键.根据圆锥的特征,进行判断即可.【详解】解:A、是圆锥,符合题意;B、是球体,不符合题意;C、是圆柱体,不符合题意;D、是长方体,不符合题意;故选:A.2.B【分析】多面体指四个或四个以上多边形所围成的立体.【详解】解:(1)圆锥有2个面,一个曲面,一个平面,不是多面体;(2)正方体有6个面,故是多面体;(3)圆柱有3个面,一个曲面两个平面,不是多面体;(4)三棱锥有4个面,故是多面体;(5)球有1个曲面,不是多面体;(6)三棱柱有5个面,故是多面体.故是多面体的有(2)(4)(6)故选:B.【点睛】本题考查多面体的定义,关键点在于:多面体指四个或四个以上多边形所围成的立体.3.A【分析】根据“点动成线”的概念直接回答即可.【详解】解:子弹从枪膛中射出去的轨迹可以看作点动成线的实际应用;故选A【点睛】此题考查了点、线、面、体,正确理解点线面体的概念是解题的关键.4.A【详解】试题分析:正方体的表面展开图的特征:相对面展开后间隔一个正方形.由图可得印有“索”字在①号正方形内,故选A.考点:正方体的表面展开图点评:本题属于基础应用题,只需学生熟练掌握正方体的表面展开图的特征,即可完成.5.D【分析】根据点动成线,线动成面,面动成体即可一一判定.【详解】解:A.笔尖在纸上移动划过的痕迹,反映的是“点动成线”,故不符合题意;B.长方形绕一边旋转一周形成的几何体,反映的是“面动成体”,故不符合题意;C.流星划过夜空留下的尾巴,反映的是“点动成线”,故不符合题意;D.汽车雨刷的转动扫过的区域,反映的是“线动成面”,故符合题意.故选:D【点睛】本题考查了点动成线,线动成面,面动成体,理解和掌握点动成线,线动成面,面动成体是解决本题的关键.6.B【分析】根据有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,由此可选出答案.【详解】解:根据棱柱的定义可得①符合棱柱定义的有第一、二、四个几何体都是棱柱,共3个,其余都不是棱柱.故选①B.【点睛】本题考查棱柱的定义,属于基础题,掌握基本的概念是关键.7.A【分析】把流星视为点,流星的轨迹是一条线,符合点动成线的原理.【详解】①把流星视为点,流星的轨迹是一条线,符合点动成线的原理①选A.【点睛】本题考查了点动成线的原理,正确理解题意是解题的关键.8.D【分析】此题考查面与体的关系,正确理解面与体的关系是解题的关键.由平面图形绕某条直线旋转一周可得到体,据此依次判断.【详解】解:将直角三角形绕一边所在的直线旋转一周形成的几何体不一定是圆锥,以斜边所在的直线为轴旋转一周所得到的几何体是两个圆锥组成的组合体,不是圆锥故选:D9.C【分析】根据圆锥的定义:圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥,进行判断即可.【详解】解:A、不是圆锥,故错误;B、不是圆锥,故错误;C、是圆锥,故正确;D、不是圆锥,故错误;故选C.【点睛】本题主要考查了圆锥的定义,解题的关键在于能够熟练掌握圆锥的定义.10.D【详解】解:①球体只有一个曲面,故球体不是多面体;①柱体,圆柱有三个面,故柱体不一定是多面体;①锥体,圆锥有两个面,故锥体不一定是多面体;①棱柱至少有两个底面,三个侧面,故棱柱是多面体;①棱锥至少有一个底面,三个侧面,故棱锥是多面体.故选D.11.B【分析】根据题意利用n棱柱中棱的条数为3n,由棱的总条数为18,进行计算即可求出答案.【详解】解:n棱柱有3n条棱,又18÷3=6,因此底面是六边形.故选:B.【点睛】本题考查认识立体图形,熟练掌握棱柱的顶点、面数和棱的条数是正确判断的前提.12.B【分析】根据点动成线,线动成面,面动成体进行判断即可.【详解】解:绕轴旋转一周,可得到图中所示的立体图形的是:故选:B.【点睛】此题主要考查了点、线、面、体,关键是掌握面动成体.点、线、面、体的运动组成了多姿多彩的图形世界.13.612 8【分析】根据正方体的特征:正方体有6个面、12条棱、8个顶点,每个面都是正方形,而且面积相等,每条棱的长度都相等,正方体是特殊的长方体.据此解答.【详解】解:正方体有6个面,有12条棱,有8个顶点,一个正方体所有面的大小相等;每条棱长度都相等;故答案为6,12,8.【点睛】本题考查正方体,解题关键是理解并掌握正方体的特征.14.点动成线【分析】根据点,线,面,体的关系得出答案.【详解】绚烂的烟花可以看成由点运动形成的,这个现象说明了点动成线.故答案为:点动成线.15.96π或144π【分析】由题意易得可分两种情况进行求解,即①若以长方体的长为轴,旋转一周,则得到高为6,底面半径为4的圆柱,①若以长方体的宽4为轴,旋转一周,则得到高为4,底面半径为6的圆柱;然后进行求解即可.【详解】解:①若以长方体的长为轴,旋转一周,则得到高为6,底面半径为4的圆柱,其体积为24696ππ⨯⨯=;①若以长方体的宽4为轴,旋转一周,则得到高为4,底面半径为6的圆柱,其体积为264144ππ⨯⨯=.故答案为:96π或144π.【点睛】本题主要考查几何初步,关键是由平面图形得到几何体,进而求解即可.16.9 16 9 四棱锥四棱柱【详解】观察这个几何体可知,它有9个面,16条棱,9个顶点,它是由简单的几何体四棱锥和四棱柱组成的.17.315或1【分析】根据题意列出式子,进行计算即可【详解】解:设长方体浸入水面的高度为xcm,则水面升高了(x-8)cm 当以15 cm,10 cm为底面积浸入水中时:30308+1510x=3030x⨯⨯⨯⨯解得:3 x=95故水面升高了:339-8=155(cm)当以10 cm,10 cm为底面积浸入水中时:30308+1010x=3030x⨯⨯⨯⨯解得:x=9故水面升高了:9-8=1(cm)故答案为:315或1【点睛】此题主要考查了有理数乘除的应用,根据题意得出式子进行计算是解题关键.18.几何体的体积为:96πcm3或128πcm3或76.8πcm3.【分析】根据三角形旋转是圆锥,可得几何体;根据圆锥的体积公式,分类讨论可得答案.【详解】解:以8cm为轴,得:以8cm为轴体积为13×π×62×8=96π(cm3);以6cm为轴,得:以6cm为轴的体积为13×π×82×6=128π(cm3);以10cm为轴,得以10cm 为轴的体积为13×π(245)2×10=76.8π(cm 3). 故几何体的体积为:96πcm 3或128πcm 3或76.8πcm 3.【点睛】本题考查了点线面体,利用三角形旋转是圆锥是解题关键.19.见解析【分析】本题考查了点线面体,熟记各种图形旋转得出的立体图形是解题关键.直角三角形绕直角边旋转一周得到的立体图形是圆锥,长方形绕一边旋转一周得到的立体图形是圆柱,直角梯形绕如图所示的一边旋转一周得到的立体图形是圆台,半圆绕直径旋转一周得到的立体图形是球.【详解】解:如图所示:20.(1)圆柱(2)396cm π 3144cm π【分析】(1)根据平面图形中矩形旋转一周可得到圆柱求解即可;(2)根据绕长方形的长旋转一周得到圆柱的高为6cm ,圆柱底面半径为4cm ;绕长方形的宽旋转一周得到的圆柱的高为4cm ,底面半径为6cm ,分别利用圆柱的体积公式求解即可.【详解】(1)解:由题意可得,旋转后将得到圆柱答:旋转后将得到的几何体是圆柱;(2)解:由题意可得,绕长方形的长旋转一周得到圆柱的高为6cm ,圆柱底面半径为4cm①236496V cm ππ=⨯⨯=圆柱绕长方形的宽旋转一周得到的圆柱的高为4cm ,底面半径为6cm①2246144V cm ππ=⨯⨯=圆柱答:旋转后两个几何体的体积分别为396cm π 3144cm π.21.(1)12;30(2)用于制作30个正五边形的牛皮共180张,用于制作20个正六边形的牛皮共450张.【分析】本题考查了几何体中点、棱、面之间的关系以及二元一次方程组的应用与整除问题,解题的关键是审清题意.(1)根据每一个面有三条棱,每二个面共用一条棱即可求解,即:棱数=面数32⨯÷.(2)设一个足球有黑皮x 块,白皮y 块,根据二个面共用一条棱,结合题意可列方程组,求得每个足球黑皮块数与白皮块数;然后再设用于制作正五边形的需要m 张,用于制作正六边形的需要n 张,依据题意建立方程组,求得m 与n 的最大整数值,并检验是否符合题意即可得到答案.【详解】(1)解:①正八面体的每一个面都是三角形,则每一个面有三条棱,故八个面共有2438=⨯条棱,但每两个面共用一条棱,因此正八面体棱数是:24212÷=(条).①根据①的思路可知,正十二面体共有棱数:125302⨯=(条). 故答案为:12;30.(2)设一个足球有黑皮x 块,白皮y 块,根据题意得: 5690232x y x y +=⨯⎧⎨+=⎩,解得:1220x y =⎧⎨=⎩ 设630张牛皮中,用于制作正五边形的需要m 张,用于制作正六边形的需要n 张,依据题意得:63030201220m n m n +≤⎧⎪⎨=⎪⎩,解得:180450m n ≤⎧⎨≤⎩(m 、n 为整数) m 、n 取最大的整数并经过检验知,180,450m n ==正好符合题意①最多制作2045020n =(个)足球,且正好将630张牛皮全部用完. 答:用于制作30个正五边形的牛皮共180张,用于制作20个正六边形的牛皮共450张.22.(1)6,6;(2)V+F -E=2;(3)7.【分析】(1)观察图形即可得出结论;(2)观察可得:顶点数+面数-棱数=2;(3)代入(2)中的式子即可得到面数【详解】解:(1)观察图形,四面体的棱数为6;正八面体的顶点数为6;多面体顶点数(V)面数(F)棱数(E)四面体446长方体8612正八面体6812正十二面体201230(2)观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;(3)由题意得:F+F-12=2,解得F=7.故答案为:(1)6,6;(2)V+F-E=2;(3)7.【点睛】本题考查多面体的顶点数,面数,棱数之间的关系及灵活运用.23.(1)8;6(2)V+F-E=2(3)这个多面体的面数为16【分析】(1)观察图形即可得出结论;(2)观察可得:顶点数+面数-棱数=2;(3)将所给数据代入(2)中的式子即可得到面数.【详解】(1)解:观察图形,长方体的定点数为8;正八面体的顶点数为6;多面体顶点数(V)面数(F)棱数(E)四面体446长方体8612正八面体6812正十二面体201230故答案为:8;6;(2)解:观察表格可以看出:顶点数+面数-棱数=2,关系式为:V+F-E=2;(3)解:由题意得:F+F-30=2解得F=16①这个多面体的面数为16.【点睛】本题主要考查多面体的顶点数,面数,棱数之间的关系及灵活运用,正确理解题意是解题的关键.。
1 生活中的立体图形同步练习含答案

第一章丰富的图形世界1 生活中的立体图形A基础知识训练1.(2016•丽水中考)下列图形中,属于立体图形的是()2.(2016•滨湖中学月考)下列说法正确的是()①教科书是长方形;②教科书是长方体,也是棱柱;③教科书的表面是长方形.A.①②B.①③C.②③D.①②③3. (2016•阴平中学月考)如图所示为8个立体图形.其中,是柱体的序号为;是锥体的序号为;是球的序号为.4.如图,在长方体ABCD-EFGH中,与平面ADHE垂直的棱共有条.5.(2016•枣庄实验期中)汽车的雨刷把玻璃上的雨水刷干净,是运用了的原理.6.如图,把下列物体和与其相似的图形连接起来.B基本技能训练1(2016•台儿庄39中模拟)下面图形中为圆柱的是()2.(2016•龙口期中)若一个棱柱有10个顶点,则下列说法正确的是()A.这个棱柱有4个侧面B.这个棱柱有5条侧棱C.这个棱柱的底面是十边形D.这个棱柱是一个十棱柱3.(2015•本溪二模)将如图所示的几何图形,绕直线l旋转一周得到的立体图形()4.硬币在桌面上快速地转动时,看上去象球,这说明了.5.(2016•枣庄十五中月考)如图:将一个长方形形沿它的长或宽所在的直线l旋转一周,回答下列问题:(1)得到什么几何体?(2)长方形的长和宽边分别为6厘米和4厘米,分别绕它的长或宽所在直线旋转一周,得到不同的几何体,它们的体积分别为多少?(结果保留π)6.(2016•丹东七中月考)已知一个长方体的长为4cm,宽为3cm,高为5cm,请求出:(1)长方体所有棱长的和.(2)长方体的表面积.7.(能力提升题)将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:(1)其中三面涂色的小正方体有个,两面涂色的小正方体有个,各面都没有涂色的小正方体有个;(2)如果将这个正方体的棱n等分,所得的小正方体中三面涂色的有个,各面都没有涂色的有个;(3)如果要得到各面都没有涂色的小正方体100个,那么至少应该将此正方体的棱等分.附答案:1.1生活中的立体图形A基础知识训练1.【解析】选C.A、角是平面图形,故A错误;B、圆是平面图形,故B错误;C、圆锥是立体图形,故C正确;D、三角形是平面图形,故D错误.2.【解析】选C.因为教科书是一个空间实物体,是长方体所以不能说它是一个长方形,因为有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱所以它是棱柱.教科书的表面是一个长方形.3.【解析】是柱体的序号为①②⑤⑦⑧;是锥体的序号为④⑥;是球的序号为③.答案:①②⑤⑦⑧,④⑥,③.4.【解析】与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.答案:45.【解析】汽车的雨刷把玻璃上的雨水刷干净,是运用了线动成面的原理,答案:线动成面.6.【解析】如图:B基本技能训练1.【解析】选D.由圆柱的特征可知,D是圆柱.2.【解析】选B.一个棱柱有10个顶点,则它是五棱柱,五棱柱有5个侧面,有5条侧棱,底面是五边形.3.【解析】选C.绕直线l旋转一周,可以得到的圆台.4.【解析】硬币在桌面上快速地转动时,看上去象球,这说明了面动成体.答案:面动成体.5.解:(1)得到的图形是圆柱形;(2)绕宽旋转得到的圆柱的底面半径为6cm,高为4cm,体积=π×62×4=144πcm3;绕长旋转得到的圆柱底面半径为4cm,高为6cm,体积=π×42×6=96πcm3.6.解:长方体的长、宽、高分别为4cm,3cm,5cm,(1)这个长方体的棱长总和为4×(4+3+5)=48cm,(2)长方体的表面积为:2×(4×3+4×5+3×5)=2×47=94cm2.7. 解:(1)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体.观察其中三面被涂色的有8个,两面涂色的有12个;各面都没有涂色的有1个,故答案为:8,12,1;(2)根据正方体的棱三等分时三面被涂色的有8个,有1个是各个面都没有涂色的,正方体的棱四等分时三面被涂色的有8个,有8个是各个面都没有涂色的,所以正方体的棱n等分时三面被涂色的有8个,有(n-2)3个是各个面都没有涂色的,故答案为:8,(n-2)3;(3)由(2)得将这个正方体的棱n等分,有(n-2)3个是各个面都没有涂色的,所以(n-2)3=100,解得6<n<7,∴至少应该将此正方体的棱7等分,故答案为:7.。
4.1《生活中的立体图形》同步练习
4.1生活中的立体图形一.填空题:1.立体图形的各个面都是__________的面,这样的立体图形称为多面体;2.物体的形状似于圆柱的有____________,类似于圆锥的有_______________,类似于球的有__________________;(各举一例)3.围成几何体的侧面中,至少有一个是曲面的是______________;(举一例)4.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都__________;5.圆柱、圆锥、球的共同点是_____________________________;6.在乒乓球、橄榄球、足球、羽毛球、冰球中,是球体的有;7.将下列几何体分类,柱体有:,锥体有(填序号);8.长方体由_____________个面______________条棱_____________个顶点;二.选择题9.以下立体图形中是棱柱的有()(A)①⑤(B)①②③(C)①②④⑤(D)①②⑤10.下列说法中,正确的是()(A)正方体不是棱柱(B)圆锥是由3个面围成(C)正方体的各条棱都相等(D)棱柱的各条棱都相等11.按组成面的平或曲划分,与圆锥为同一类几何体的是()(A)正方体(B)长方体(C)球(D)棱柱12.一个正方体锯掉一个角后,顶点的个数是()(A)7个(B)8个(C)9个(D)7个或8个或9个或10个三.解答题:13. ⑴下面这些基本图形和你很熟悉,试一试在括号里写出它们的名称.()()()()()⑵将这些几何体分类,并写出分类的理由.参考答案一、1.平;2.略;3.略;4.8,3,相等;5.都有一个面是曲面;6.乒乓球、足球;7.(1)(2)(3),(5)(6);8.6,12,8;二、9.A;10.C;11.C;12.D;三、13.(1)(从左至右)球、圆柱、圆锥、长方体、三棱柱;(2)按面分:曲面:球、圆柱、圆锥;平面:长方体、三棱柱;按柱体分:圆柱、长方体、三棱柱;球;圆锥;。
生活中的立体图形全章同步习题

第1课时几何图形1 三、平行练习一一三基的巩固一、课前小测一一简约的导入1.你能说出右图中包含哪些平面图形吗?0 0中1 L□W2.与红砖、足球相类似的图形是()A.长方形、圆B.长方体、圆C.长方形、球D.长方体、球二、典例探究一一核心的知识例1下列各图中,实物的形状对应哪些立体图形? 把相应的实物与图形用线连起来.3.如图是一些具体的图形一一三棱镜、方砖、帆布帐篷、笔筒、铅锤、粮囤、天文台;下图中是一些立体图形,找出与下图的立体图形类似的实物,填在括号内。
4.下图中的几何图形可看作哪些简单的图形组成5.请说出右图中的茶叶盒中包含哪些平面图形。
例3.如图中的立体图形分别是由几个面围成的,们是平面茶叶苴四、变式练习一一拓展的思维例4.在一个圆椎上切去一个小圆锥所得到的立体 图形是()6.如图,上面是一些具体的物体,下面是一些立体 图形,试找出与下面立体图形相类似的实物(用 线连接).A B C D变式1.如图,用一个平面去截长方体,则截面形 状为()-±27 口 O 口 △上二ABC D变式2.图⑴是正方体木块,把它切去一块,可能 得到(2)、(3)、(4)、(5)所示的图形,问(2)、(3)、 (4)、(5)图中切掉的部分可能是其他几块中的哪一 块?8 .下列各立体图形的表面中包含哪些平面图形?请 指出来。
9 .如图是一个正六棱柱,它的底面边长是3 cm,高 是 6 cm,变式3.如果你按照下面的步骤做,当你完成到第 五步的时候,将纸展开,会得到图形()(1)这个棱柱共有多少个面?计算它的侧面积。
(2)这个棱柱共有多少条棱?所有棱的长是多少?(3) 这个棱柱共有多少个顶点?五、课时作业一一必要的再现7.写出下列立体图形的名称.第2课时几何图形2一、课前小测一简约的导入1 .判断(1)圆柱、圆锥的底面都是圆.( )(2)棱柱的侧面是四边形.( ) (3)棱柱的侧面是三角形.()2 .如图,图(1)是哪一个几何体从上往下看所看到的图形( )例2从上面观察以下四个实物,得到什么平面图形,请将相应的图形连接起来:例3右图是一个由9个正方体组成的立体图形,分别从正面,左面,上面观察,各能得到 什么平面图形?二、典例探究一一核心的知识例1下图是一个立体图形,从左面看得到图2图形, 那么从正面看和从上面看可以得到什么样的图形 呢? 请画出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生活中的立体图形
一.填空题
1.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,
时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.
2.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成___
_______个三角形.
3.围成几何体的侧面中,至少有一个是曲面的是______________.
4.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.
5.圆柱,圆锥,球的共同点是_____________________________.
6.圆可以分割成_____个扇形,每个扇形都是由___________________.
7.立体图形的各个面都是__________的面,这样的立体图形称为多面体.
8.物体的形状似于圆柱的有________________;类似于圆锥的有_____________________;
类似于球的有__________________.
9.图形是由________,__________,____________构成的.
二.选择题
10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形
A. 10
B. 9
C. 8
D. 7
11. 图1-1是由( )图形饶虚线旋转一周形成的
A B C D 图1-1
13.图1-2绕虚线旋转一周形成的图形是 ( )
图1-2
A B C D
14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成
A.三角形和扇形B圆和四边形 C.圆和三角形D圆和扇形
15.下面全由圆形组成的图案是( )
A B C D
三解答题
16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?
(1)六面体(2)圆柱(3)圆锥(4)棱锥
( ) ( )
( ) ( ) ( )
18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?
19.动手做一做.
将一个长方体切去一部分,看一看剩余的部分是几面体呢?
四.开放创新提高题
20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?
21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形。
