张量分析第一章PPT课件
张量分析——初学者必看PPT

§A-2 矢量的基本运算
A 张量分析
四、矢量的并乘(并矢)
a ai ei , b b j e j
并乘
ab ai ei b j e j ai b j ei e j
a2b1e2 e1 a2b2 e2 e2 a2b3e2 e3 a3b1e3e1 a3b2 e3e2 a3b3e3e3
ab a1b1e1e1 a1b2 e1e2 a1b3e1e3
§A-3 坐标变换与张量的定义
A 张量分析
x x cos y sin y x sin y cos
x x cos y sin y x sin y cos
约定
S ai xi a j x j
用拉丁字母表示3维,希腊字母表2维
一、求和约定和哑指标
§ A-1 指标符号
双重求和
Aij xi y j
i 1 j 1
3
3
Aij xi y j A11x1 y1 A12 x1 y2 A13 x1 y3 A21x2 y1 A22 x2 y2 A23 x2 y3 A31x3 y1 A32 x3 y2 A33 x3 y3
两个二阶张量点积的结果为一个新的二阶张量,这 相当于矩阵相乘
§A-4 张量的代数运算
A 张量分析
五、张量的双点积
两个张量点积的结果仍为张量。新张量的阶数是 原两个张量的阶数之和减 4
A : B ( Aijk ei e j ek )( Brster es et ) Aijk Brst jr ks ei et Aijk B jkt ei et S
A B ( Aijk ei e j ek ) ( Brst er es et ) Aijk Brst ei e j kr es et Aijk Bkst ei e j es et S
张量分析TensorAnalysisppt课件

的切线方向。矢量 r 可以取作曲线坐标系的基矢量(协变基矢量):
xi
gi
r xi
zj xi
ij
注意:对于在曲线坐标系中的每一点,都有三个基 矢量。
ቤተ መጻሕፍቲ ባይዱ
基矢量一般不是单位矢量,彼此也不正交;
基矢量可以有量纲,但一点的三个基矢量的量纲可以不同;
基矢量不是常矢量,它们的大小和方向依赖于它们所在点的坐标。
利用克罗内克符号,上式可写成:
ds2 ijdxidxj
克罗内克符号的一些常用性质:
ijxi xj
x j xi
j i
ijki kj
D) 置换符号
置换符号eijk=eijk定义为:
1
e ijk
e ijk
1
0
当i,j,k是1,2,3的偶置换(123,231,312) 当i,j,k是1,2,3的奇置换(213,132,321) 当i,j,k的任意二个指标相同
i,j,k的这些排列分别叫做循环排列、逆循环排列和非循环排列。
D) 置换符号(续)
置换符号主要可用来展开三阶行列式:
a11 a1 2 a3 1 aa12 a22 a32 a11a22a33a12a23a3 1a13a1 2a32
a13 a23 a33 a11a23a32 a12a1 2a33 a13a1 2a32
量 Ai ,在坐标系yi中有三个分量 Âi ,它们由以下的变换法则相联系;
AˆiyAjxxyij
逆变矢量用上标表示;因此上标也称为逆变指标。
(3) 协变矢量(一阶协变张量)
一个量被称为协变矢量或一阶协变张量,若它在坐标系 xi 中有三个分 量 Ai ,在坐标系yi中有三个分量 Âi ,其变换法则相为;
张量分解学习PPT课件

.
26
CP分解
张量的低秩近似
◦ 然而在低秩近似方面,高阶张量的性质比矩阵SVD差
Kolda给出了一个例子,一个立方张量的最佳秩-1近似并不 包括在其最佳秩-2近似中,这说明张量的秩-k近似无法渐进 地得到
下面的例子说明,张量的“最佳”秩-k近似甚至不一定存在
X a1ob 1oc2a1ob2oc1a2ob 1oc1
纤维:x i j :
.
6
基本概念及记号
切片(slice)
水平切片:X i : :
侧面切片:X : j :
正面切片:X ::k ( X k )
.
7
基本概念及记号
内积和范数
◦ 设 X,Y¡I1× I2× L× IN
内积:
I1 I2
IN
X,Y
L x y i1i2LiN i1i2LiN
i11i21 iN1
R
X§A,B,C¨arobrocr r1
X
c1 b 1
c2 b2
L
cR b R
a1
a2
aR
三阶张量的CP分解
.
20
CP分解
CP分解的矩阵形式
◦ 因子矩阵:秩一张量中对应的向量组成的矩阵,如
A a 1 a2 LaR
◦ 利用因子矩阵,一个三阶张量的CP分解可以写成展开形式
X (1) A C e B T X (2) B C e A T X (3) C B e A T
◦ 对于高阶张量,有
X ┈ λ ;A (1 ),A (2 ),L ,A (N ) Rra ( r 1 )o a ( r 2 )o L o a ( r N ) r 1
其展开形式为
X ( n ) A ( n ) d i a g ( λ ) A ( N ) e L e A ( n 1 ) e A ( n 1 ) e L e A ( 1 )T
最新第1章-张量分析(清华大学张量分析-你值得拥有)PPT课件

1 、g
2
P
其中 g 1 、g 2 不一定是单位矢量。
矢量 P 可表示为:
P P1 g1 P 2 g2
2
P g P g 1
斜角直线坐标系的基矢量与矢量分量
➢ 平面内斜角直线坐标系的协变基矢量和逆变基矢量
P P g :哑指标
x2
( x 1 , x 2 ) Einstein求和约定
r
g2
如何计算 u(vw)?
vw
观察右图,可知 vw正交于
u
v 、w 构成的平面,而 u(vw)
w
正交于 vw,因此,u(vw)
一定在 v 、w 构成的平面
v
u (v w) v w
u(vw)
(u w)v (u v)w (uv) w
数形结合
矢量及其代数运算
➢矢量的乘法 矢量的混合积
uv wuvw群u论的v轮w换次序不变性w
张
gij gi gj gij gi gj
量
可证明:
分 析
g ij g ji
gij g ji
的
称 g i j 为度量张量的协变分量
起
称 g i j 为度量张量的逆变分量
点
gi gij g j gi = g ij g j
协变基矢量在逆变基矢量下分解 逆变基矢量在协变基矢量下分解
斜角直线坐标系的基矢量与矢量分量
※ 根据几何图形直接确定
由对偶条件可知, g 1 与 g 2 、g 3 均正交,因此正交于 g 2 与 g 3 所
确定的平面;其模的大小等于
g1 1
g1 cos
g1 g1
2 g2
2
g3
斜角直线坐标系的基矢量与矢量分量
张量分析.ppt

(A2 5)
3.混合积
1 基矢量混合积
(ei e j ) ek ei j rer ek ei j rδr k
ei j k
(A2 7)
故也有定义
ei jk (ei e j ) ek ei (e j ek )
2 矢量混合积
(a b) c ei jk aibjek crer ei jk aibjcrδk r
第一节 问题的提出 第二节 矢量的基本运算 第三节 坐标变换及张量的定义
自然法则与坐标无关,坐标系的引入方便 分析,但也掩盖了物理本质; 坐标系引入后的相关表达式冗长
引入张量方法
§A-1 指标符号
x1,x2xn 记作 xi (i 1,2,n)
下标符号 i 称为指标;n 为维数 指标 i 可以是下标,如 xi
e1 e2 e3 ei j tet ei j kek
a11 a12 a13
(比较: A a21 a22 a23 ei jk a1ia2 j a3k )
a31 a32 a33
特别地:
e1 e2 e12kek e123e3 e3
2 两个任意矢量的叉积
a b aiei bje j aibjei e j aibjei j kek ei j k aibjek c
0 0 1 31 32 33
ij Ai
1 j A1
2 j A2
3 j A3
A1 A2
A3
Aj
j 1 j2 j3
ds2 dx2 dy2 dz2 dxidxi ijdxidx j
性质:
ijij ii 11 22 33 3
Aijij Aii Ajj A11 A22 A33
22
23
~ yx
数学张量分析PPT课件

第6页/共92页
右散度表示为: diva a
diva a
ei i a je j
ij
a j xi
ai xi
iai
a1 a2 a3 x1 x2 x3
显然 diva diva
今后对于矢量场的左散度和右散度不加区别
第7页/共92页
张量的散度
关于二阶张量场 T T的P左散度定义为:
间点的位置。两者由下列坐标变换联系起来:
xi xi xi' i, i ' 1,2,3
第23页/共92页
若 xi'是的线性函数,则 x i' 也是一个斜角坐标,而且坐标变换为:
xi
Ai i'
x i'
x i
x i'
xi'
这里
Ai i'
为变换系数,它是常数。
若 x i不是 xi' 的线性函数,则 xi' 称为曲线坐标。
标量的梯度:
标量函数:
f f (r)
则梯度为:
f gradf eii f
展开后有:
原式 1 f e1 2 f e2 3 f e3
f i f j f k x y z
第1页/共92页
矢量的梯度: 左梯度
grad a a (i ei )(a j ej ) (eii )(a j e j )
a ai gi ai gi
由 eijk 的定义可知,下列混合积等式成立:
gig jgk gi g j gk gig jgk eijk gig jgk gi g j gk gig jgk eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk 由此定义可知
弹性力学张量分析学习—对于初学者很有用PPT课件

符号ij 与erst
➢ erst 符号 (排列符号或置换符号,Eddington)
➢ 定义(笛卡尔坐标系)
1
e rst
1
0
当r, s, t为正序排列时 当r, s, t为逆序排列时 当r, s, t中两个指标值相同时
或
erst
1rssttr
2
(1,2,3)及其轮流换位得到的(2,3,1)和(3,1,2)称为正序排列。 (3,2,1)及其轮流换位得到精的选(课2件,1,3)和(1,3,2)称为逆序排列。
ij
1 0
(i = j) (i, j=1, 2, …, n) (i j)
➢ 特性
1. 对称性,由定义可知指标 i 和 j 是对称的,即
ij ji
精选课件 29
符号ij 与erst
2. ij 的分量集合对应于单位矩阵。例如在三维空间
11 12 13 1 0 0
21
22
23
0
1
0
31 32 33 0 0 1
3
➢ 分解式记法: uu1e1u2e2u3e3 uiei i1
➢ 分量记法: u i
精选课件
Appendix A.1
8
张量基本概念
➢ 指标符号用法
1. 三维空间中任意点 P 的坐标(x, y, z)可缩写成 xi , 其中x1=x, x2=y, x3=z。
2. 两个矢量 a 和 b 的分量的点积(或称数量积)为:
d s2 d x 1 2 d x 22 d x 32
可简写成: ds2 dxi dxi
场函数 f (x1, x2, x3) 的全微分: f
d f xi d xi
精选课件 24
最新张量分析第一章ppt课件

0,当 i , j , k 中有取值相同者.
1
1
3
2
3
2
偶排列
奇排列
21
矢量叉积 a b ( a 2 b 3 a 3 b 2 ) e 1 ( a 1 b 2 a 2 b 1 ) e 3 ( a 3 b 1 a 1 b 3 ) e 2 用置换符号可写成
a b c ( ijka jb k ) ( c i)
23
1.2 恒等式 ijk istjs kt jt ks
第一种证明:
11 12 13 1 0 0
1r 1s 1t
I 21 22 23 0 1 0 1 rst I 2r 2s 2t rst
31 32 33 0 0 1
3r 3s 3t
ir is it ijkrst jr js jt
a b abco s
点积满足
abba
a ( b c ) a b a c
11
(5)矢量的叉积
e1 e2 e3 aba1 a2 a3
b1 b2 b3
(a2b3a3b2)e1(a1b2a2b1)e3(a3b1a1b3)e2
注意:
a b b a
axb
O
b
a -axb
12
质量守恒,动量守恒,能量守恒,热力学基本定律 3)连续介质的本构方程
描述各种连续介质模型对外部作用的响应;
3
第一章 连续介质力学的数学基础
重点掌握: 1. 张量的概念 满足坐标变换规律 运算法则 2 .证明一些恒等式 3 .梯度,散度,旋度等概念
7
第一章 连续介质力学的数学基础
1.1 矢量
1.1.1矢量的概念
在三维欧几里得空间内, 具有大小和方向 的有向 线段.
第一章张量分析基础知识

第⼀章张量分析基础知识晶体物理性能南京⼤学物理系由于近代科学技术的发展,单晶体⼈⼯培养技术的成熟,单晶体的各⽅⾯物理性能(如⼒、声、热、电、磁、光)以及它们之间相互作⽤的物理效应,在各尖端科学技术领域⾥,都得到了某些应⽤.特别是⽯英⼀类压电晶体作为换能器、稳定频率的晶体谐振器、晶体滤波器等在电⼦技术中,⽐较早地在⼯业规模上进⾏⼤批⽣产和⼴泛应⽤.激光问世的四⼗多年来,单晶体在激光的调制、调Q、锁模、倍频、参量转换等光电技术应⽤中,已成单晶体应⽤中极为活跃的领域.《晶体物理性能》是我系晶体物理专业的专业课程之⼀,⽬的就是希望对晶体特别是光电技术中使⽤的晶体(包括基质晶体与⾮线性光学晶体)的有关物理性能及其应⽤⽅⾯的基本知识,有⼀个了解.对今后从事光电晶体的⽣长、检测和应⽤的⼯作,在分析问题、解决问题⽅⾯有所帮助,同时要在今后⼯作中不断从实践和理论两个⽅⾯扩⼤知识领域,有⼀个基础.考虑到本专业属于晶体材料性质的专业特点,本课程不仅对晶体物理性能的各个⽅⾯作深⼊全⾯的介绍,也将侧重于激光晶体有关的⼀些性能及其应⽤.鉴于以上考虑,《晶体物理性能》讲义将以离⼦晶体为主要对象,以光电技术上应⽤为线索组织内容,共分为⼋章.着重于从宏观⾓度结合微观机制介绍晶体基本物理性能以及各种交互作⽤过程的物理效应和它们在光电技术中的某些应⽤,包括弹性与弹性波(第⼆章),晶体光学中的各向异性(第五章),压电与铁电现象(第四章),电光效应(第七章),光学参量过程(第六章),声光效应(第⼋章).由于晶体物理性能的各向异性的特点和晶体对称性有密切关系,通常正确、⽅便地描述这些物理性能必须使⽤张量来表⽰.因此,在第⼀章,我们介绍了关于张量分析基础知识⽅⾯的内容.由于⽔平有限,实践经验缺乏,时间仓促,因⽽内容安排不妥、取舍不当、错误之处⼀定很多,希望同学们提出宝贵意见,批评指正.第⼀章张量的基础知识§1.1标量、⽮量和⼆阶张量…………………………………………………………………2§1.2坐标变换和变换矩阵……………………………………………………………………§1.3正交变换矩阵的性质……………………………………………………………………§1.4晶体对称操作的变换矩阵……………………………………………………………§1.5⼆阶张量的变换与张量的定义………………………………………………………§1.6张量的⾜符互换对称…………………………………………………………………§1.7张量的矩阵表⽰和矩阵的代数运算…………………………………………………§1.8⼆阶对称张量的⼏何表⽰和⼆阶张量的主轴………………………………………§1.9⼆阶对称张量主轴的确定……………………………………………………………§1.10晶体张量与晶体对称性的关系………………………………………………………第⼆章晶体的弹性与弹性波§2.1弹性性质与原⼦间⼒…………………………………………………………………§2.2应变……………………………………………………………………………………§2.3应⼒……………………………………………………………………………………§2.4推⼴的虎克定律、弹性系数…………………………………………………………§2.5⽴⽅晶体的弹性系数…………………………………………………………………§2.6各向同性材料的弹性系数……………………………………………………………§2.7弹性扰动的传播――弹性波…………………………………………………………§2.8简谐振动和驻波……………………………………………………………………§2.9弹性常数及振动衰减因⼦的测量⽅法……………………………………………第三章晶体的介电性质§3.1介质中的宏观电场强度与极化强度………………………………………………§3.2晶体中的有效场……………………………………………………………………§3.3⾼频电场的介电极化(光的⾊散与吸收)………………………………………§3.4介电常数的测量……………………………………………………………………§3.5离⼦晶体的静电击穿………………………………………………………………§3.6激光的电击穿(激光的电击穿损伤)……………………………………………第四章铁电与压电物理§4.1铁电体的⼀般性质…………………………………………………………………§4.2常⽤铁电体的实验规律……………………………………………………………§4.3铁电体的相变热⼒学………………………………………………………………§4.4铁电体相变的微观机制……………………………………………………………§4.5晶体的压电效应……………………………………………………………………§4.6压电⽅程和机电耦合系数…………………………………………………………§4.7压电晶体的应⽤实例――⽯英……………………………………………………第五章晶体光学§5.1光学各向异性晶体…………………………………………………………………§5.2各向异性介质中光的传播…………………………………………………………§5.3折射椭球与折射率曲⾯……………………………………………………………§5.4晶体表⾯上的折射…………………………………………………………………§5.5晶体偏光⼲涉及其应⽤……………………………………………………………第六章倍频与参量频率转换§6.1⾮线性极化…………………………………………………………………………§6.2⾮线性极化系数……………………………………………………………………§6.3⾮线性介质中电磁场耦合⽅程……………………………………………………§6.4光倍频………………………………………………………………………………§6.5光倍频的相匹配……………………………………………………………………§6.6第II类相匹配………………………………………………………………………§6.7⾓度匹配和温度匹配扫描实验曲线………………………………………………§6.8内腔倍频……………………………………………………………………………§6.9光参量放⼤…………………………………………………………………………§6.10参量振荡器…………………………………………………………………………§6.11参量振荡器的调谐⽅法……………………………………………………………§6.12参量频率上转换……………………………………………………………………§6.13⾮线性材料的性能要求……………………………………………………………第七章电光效应及其应⽤§7.1线性电光效应………………………………………………………………………§7.2两种典型材料的电光效应…………………………………………………………§7.3电光滞后……………………………………………………………………………§7.4电光调制原理………………………………………………………………………§7.5实际调制器的⼏个问题……………………………………………………………§7.6晶体电光开关………………………………………………………………………§7.7电光Q开关…………………………………………………………………………§7.8电光偏转……………………………………………………………………………§7.9电光材料……………………………………………………………………………§7.10晶体均匀性的实验检测……………………………………………………………§7.11晶体的激光损伤……………………………………………………………………§7.12晶体均匀性实验检测………………………………………………………………第⼋章声光效应及其应⽤§8.1弹光效应……………………………………………………………………………§8.2声光交互作⽤产⽣的衍射现象……………………………………………………§8.3声光交互作⽤的理论………………………………………………………………§8.4声光效应在⼀些物理常数测量中的应⽤…………………………………………§8.5声光调制器…………………………………………………………………………§8.6声光偏转器…………………………………………………………………………§8.7声光调Q……………………………………………………………………………§8.8声光材料……………………………………………………………………………附录A.32点群投影图…………………………………………………………………………B.各阶张量在不同点群中的矩阵形式……………………………………………………C.主要常数表………………………………………………………………………………D.单轴晶体中光线离散⾓α的推导………………………………………………………E.双轴晶体中双折射⾯相差Γ的推导……………………………………………………F.贝塞尔函数的基本性质…………………………………………………………………第⼀章张量分析基础知识以前学的课程中,有关⼒学、热学、电学、光学等的性质都是以各向同性介质来表述的或以⼀维问题来说明问题,这对于突出某些物理现象的微观的物理原因⽅⾯是必要的,但晶体物理性能是讲晶体中的⼒学、电学、光学、声学、磁学、热学等物理性能,⽽晶体的各向异性却是⼀种很普遍的特性,特别是很多现象如热电、压电、电光、声光、⾮线性光学效应……等等物理现象则完全因为晶体具有各向异性性质才能表现出来.因此,晶体结构对称性和这些性质之间的关系成为问题的主要⽅⾯。
流体力学-第一讲 场论与张量分析初步ppt精选课件

•
标量场(scalar
field):f
(r,t)
• 向量场(vector field):g (r,t) g=f(r,t)
• 均匀场(homogeneous field):f c
• •
非 定均常匀流场场((nstoen-adhyomfoigeelndou)s:ffi(erl)d): field):f(r,t)
a x b x a yb y a zb z 标量
18.06.2021
ppt精选版
9
1
如a、b正交 ,则
abab0
2
如a、b平行 ,则
aba b
3 4
如 分a在 配b正 律交 ab投 c影 aba表 用 b示 ac
m a b a m b m a b
a
ax2ay 2az2
散度是标量,而不是向量。
diav l
im sa dsaxayaz a
v 0 v x y z
于是Gauss定理可以写作:
sa n d s sa d s v( a x x a y y a z z)d v v( a )dv
18.06.2021
ppt精选版
28
div A 0 的场称为无源场。其性质:
运动学 动力学
以实际流体为主
18.06.2021
ppt精选版
2
主要内容:
第一章 场论与张量分析初步
第二章 流体运动学
第三章 流体力学基本方程组
第四章 粘性流动基础
第五章 Navier-Stokes 方程的解
第六章 边界层理论
第七章 流体的旋涡运动
第八章 湍流理论
18.06.2021
ppt精选版
3
张量分析第一章

主要掌握:应力张量,应力张量的对称性,变换规律,主应力,主 方向,剪应力,应力偏张量等
第三章 连续介质运动学
4
主要掌握:物质坐标与空间坐标,物质导数,随波导数,速度张 量,速度分解定理等.
第四章 连续介质力学基本定律
三大守恒定律:质量守恒,动量守恒,能量守恒,状态方程,熵 不等式,热力学两大定律.
间位置的变化及各邻近点距离的变化;研究随时间变化 的物理量的时间变化率. 2)连续介质满足的物理基本定律
质量守恒,动量守恒,能量守恒,热力学基本定律 3)连续介质的本构方程
描述各种连续介质模型对外部作用的响应;
3
课程内容
第一章 连续介质力学中的数学模型
主要掌握:张量的概念,张量的表示方法以及张量的运算规律等
O
b
a -axb
12
(6)并矢 定义 ab ai eibj ej ai bj eiej
展开共9项, ei e j 可视为并矢的基
ai bj 为并矢的分解系数或分量
13
1.1.3 Einstein求和约定
在同一项内的一个指标的重复,将表示对该指标 在它的范围上遍历求和.
自由指标:无重复出现的指标,取值域1,2,3(三维空间中) 哑标: 重复出现一次且仅重复一次的指标为求和指标或 为哑标.
ds2 dx2 dy2 dz2 dxidxi ijdxidx j
ij jk ik
aiij a j
xi x j
xi, j
ij
19
例: Aijbj
分量形式:
Ai1b1 Ai2b2 Ai3b3
uii
u11 u22 u33
k
1 2 3
张量分析-第1讲LJ

a2 F3 a3 F2 a c b1 a b c1 a3 F1 a1 F3 a c b2 a b c2 a1 F2 a2 F1 a c b3 a b c3
所以有: a b c a c b a b c
g1和g 2
g1和g 2 不是单位矢量,即它们有量纲的, 一般地说,
其长度也不为单位长度。此外它们也并不正交。 矢量F可以在 g1和g 2 上分解:
F F g1 F g 2
1 2
(平行四边形法则)
则有: F g 1 F 1g 1 g 1 F 2 g 2 g 1
F g 1 F 1g 1 g 1 F 2 g 2 g 1
e2 b2 c2
e3
e3 b3 b2 c3 b3 c2 e 1 b3 c1 b1c3 e 2 b1c2 b2 c1 e 3 c3
b3 a 2 F3 a3 F2 e 1 a3 F1 a1 F3 e 2 a1 F2 a 2 F1 e 3 F3
j 1
F2 ' e 2 ' e1 F1 e 2 ' e 2 F2 e 2 ' e 3 F3 2 ' j F j
j 1 3
3
F3' e 3' e1 F1 e 3' e 2 F2 e 3' e 3 F3 3' j F j
j 1
矢量场函数的散度: 矢量场函数的旋度:
i F x Fx j y Fy
Fx Fy Fz F z y x
k Fz Fy Fx Fz Fy Fx i k j y z y z z x x Fz
张量第一章

系中也必为零。
2、设,为r阶张量,方程
为张量方程。在张量方程中的每一项都有相同的张量特性。因此在
所有能够容许变换到的坐标系普遍有效。
若将张量方程两边同乘以变换系数,则
所以方程具有张量性质。
张量分析的重要性在于,由物理关系得到的方程如果是张量方程,
那它就在所有容许变换的坐标系成立了,避免了它在各种不同坐标系中
张量相乘提高了阶数,又称为张量外积。
3、 张量的缩并 对r阶张量进行缩并,就是对张量的某两个指标求和(如使j=k),
所得到的仍是张量,阶数比缩并前的原张量少2,即变为r-2阶张量。 缩并使张量降阶,又称为张量内积。 例如:对三阶张量,使j=k,缩并为 缩并也可由乘法定义。
例:对的j、k进行缩并,则 二阶张量缩并后得到标量,是它的不变量。
变换,则这九个量的集合称二阶张量,每个元素称张量分量。 为单位二阶张量
二阶张量分量可组成一个二阶张量矩阵。 二阶张量的另一个定义: 设,为任意矢量的分量,若九个分量能与它们构成标量
则这九个分量定义一个二阶张量。 高阶张量定义: 在三维空间中,当直角坐标系旋转变换到时,基矢量和坐标按前述
规律变化。如果中确定的个分量与在中确定的之间服从相同的变换规 律,即按式
个张量中的每一个分量,它们所组成的集合仍然是一个张量,称为第一 个张量乘以第二个张量的乘积。积张量的阶数等于因子张量阶数之和。
例如:一矢量乘以一个二阶张量,乘积为 = 为一个三阶张量。
张量乘法服从分配律和结合律,但不服从交换律。 高阶张量的乘积也可表示为不变式。张量与的乘积表示为(,可以 是任意阶张量)
五:求导的简化法
数量场Φ的梯度
向量场散度:
向量场的旋度:
§1.2 坐标变换
【张量分析ppt课件】张量分析课件第一章 线性空间-50页精选文档

(2)∵ x y z ( x 1 y 1 ) z 1 , , ( x n y n ) z n
( x 1 y 1 z 1 , ,x n y n z n )
x ( y z ) ( x 1 ( y 1 z 1 ) , , ( x n ( y n z n ))
( x 1 y 1 z 1 , ,x n y n z n )
∴ x + (y + z )= ( x + y )+ z = x + y + z (4)∵ o(0, ,0)V0 x o (x 1 0 , x n 0 )(x1, ,xn)
∴ xox
(5)∵ ()x ()(x 1 , ,xn) (()x 1 , ,()xn)
∴
(x 1 , ,xn) (x 1 ), ,)xn)
第一章 线性空间
若记实数集合为F,F中的元素记为a、b、c、…。
则加法法则将F中的任意两个元素 a, bF ; c F
+ (a, b)c
abc
乘法法则将F中的任意两个元素 a, bF ; c F
× (a, b)c
abc
显然具有加法法则和乘法则所确定的实数集中元
素间确定关系使得实数集构成一个空间。并记为:
所有以x点为起点的矢量按:
u x yu x z(y 1 x 1 , ,y n x n ) (z 1 x 1 , ,z n x n )
(y 1 ( x 1 ) (z 1 x 1 ) ,,(y n x n ) (z n x n ))
u xy (y1x1, ,ynxn) ((y1x1) ,,(ynxn)) F
a, b,xF
(6) (a b ) x a x b x
a, b,xF
张量分析
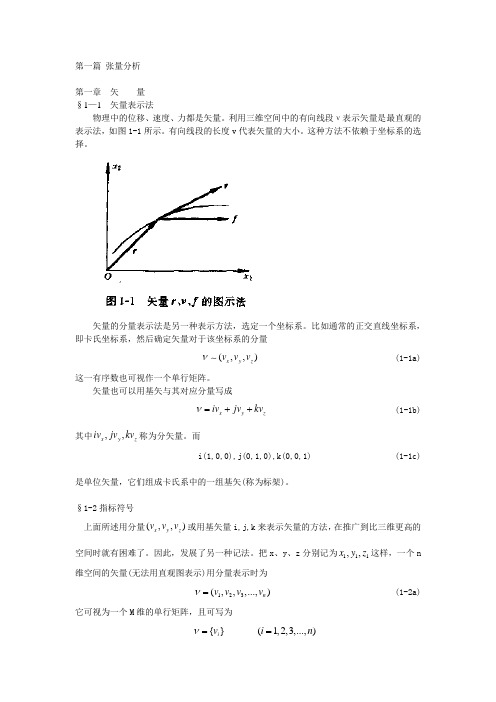
第一篇 张量分析第一章 矢 量 §1—1 矢量表示法物理中的位移、速度、力都是矢量。
利用三维空间中的有向线段ν表示矢量是最直观的表示法,如图1-1所示。
有向线段的长度v 代表矢量的大小。
这种方法不依赖于坐标系的选择。
矢量的分量表示法是另一种表示方法,选定一个坐标系。
比如通常的正交直线坐标系,即卡氏坐标系,然后确定矢量对于该坐标系的分量(,,)x y z v v v ν(1-1a)这一有序数也可视作一个单行矩阵。
矢量也可以用基矢与其对应分量写成x y z iv jv kv ν=++ (1-1b)其中,,x y z iv jv kv 称为分矢量。
而i(1,0,0),j(0,1,0),k(0,0,1) (1-1c)是单位矢量,它们组成卡氏系中的一组基矢(称为标架)。
§1-2指标符号上面所述用分量(,,)x y z v v v 或用基矢量i,j,k 来表示矢量的方法,在推广到比三维更高的空间时就有困难了。
因此,发展了另一种记法。
把x 、y 、z 分别记为111,,x y z 这样,一个n 维空间的矢量(无法用直观图表示)用分量表示时为123(,,,...,)n v v v v ν= (1-2a)它可视为一个M 维的单行矩阵,且可写为{}i v ν= (1,2,3,...,)i n =同理,基矢i,j,k 可分别写为123,,e e e ,n 维空间的基矢i e (1,2,3,...,)i n =。
而与式(1-1b)对应的写法为112233n n e v e v e v e v ν=++++ (1-2b)相应的分矢量为11,,,i i e v e v ,其中1e =(0,…,0,1,0,…,0) (1-2c)↑ 顺序第i 个这里i 叫做v 的下标,也有记作jv (如本书第三章以后章节所出现)的,这时j 称为上标。
有些量比矢量更复杂,只用一个下(或上)指标还不够,还要采用更多的指标,比如,,,ij ij ijk A B C ,等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主要掌握:应力张量,应力张量的对称性,变换规律,主应力,主 方向,剪应力,应力偏张量等
第三章 连续介质运动学
4
主要掌握:物质坐标与空间坐标,物质导数,随波导数,速度张 量,速度分解定理等.
第四章 连续介质力学基本定律
三大守恒定律:质量守恒,动量守恒,能量守恒,状态方程,熵 不等式,热力学两大定律.
ax
x2
ay
a a 1 e 1 a 2 e 2 a 3 e 3
a
a12a22a32
9
1.1.2 矢量和,差与积
(1) 矢量和 (平行四边形法则)
abba (ab)ca(bc)
(2)矢量差
aba(b)
(3) 矢量与标量的积满足结合律和分配律
ma
m(nb)(mn)b
a
m ( a b ) m ( b a ) m a m b
10
(4)矢量的点积
标量 a b a 1 b 1 a 2 b 2 a 3 b 3
a b abcos
点积满足
abba
a (b c ) a b a c
11
(5)矢量的叉积
e1 e2 e3 aba1 a2 a3
b1 b2 b3
(a2b3a3b2)e1(a1b2a2b1)e3(a3b1a1b3)e2
Wrong Right
17
(6) Kronecker 符号 Delta
ij
ij
1 0
i j i j
几个重要式子:
A ij ij A ii A jj A 1 1 A 2 2 A 3 3
ij ijii1 12 23 3 3
18
ijai 1ja1 2 ja2 3 ja3 aa12
a3
第五章 本构方程
本构概念,本构方程遵循的一些理论
5
考核方法:平时作业和出勤情况占 30%; 期末考试占70%。
参考书目: 1) 冯元祯,连续介质力学导论,重庆大学出版社 2) 吕洪生等编著,连续介质力学基础,国防科技
大学出版社
6
第一章 连续介质力学的数学基础
重点掌握: 1. 张量的概念 满足坐标变换规律 运算法则 2 .证明一些恒等式 3 .梯度,散度,旋度等概念
aibi a jb j a ijb j a ik bk
(2)连续介质的研究对象是三维连续体,
i , j , k 取值范围为1,2,3
15
(3) 同一项中重复出现的指标不能超过两次.
( a 1 1 a 2 2 a 3 3 ) ( b 1 1 b 2 2 b 3 3 ) a i ib i i
张量分析与连续介质力学
授课对象:工程力学本科生 学时: 48 任课教师: 任会兰 副教授
1
连续介质力学 研究对象:大量粒子构成的系统的宏观力学行为.
可视为连续体
统计平均值
宏观物理量随物质点的变化而改变----场(应力 场,应变场,速度场,位移场和温度场……
连续体模型—固体,流体
2
1)变形几何和运动学 研究连续介质变形的几何性质,确定物体各部分空
应写成 a i i b j j
(4)同一等式中,同一文字指标在其中的一项单独出现, 则它在其他某项内重复出现,对该项也不求和.
fi Tii
f1 T11 f2 T 22
f3 T 33
16
(5) 不能改变某一项的自由标,但所有项的自由标可以 改变.
如 ajixi bj
akixi bj akixi bk
哑标: 重复出现一次且仅重复一次的指标为求和指标或 为哑标.
如
ai
a'
ji j
a b a 1 b 1 a 2 b 2 a 3 b 3 a ib i
a 11a 1 1 ' 2a 1 2 ' 3a 1 3 ' aii a11a22a33
14
几个注意事项:
(1)求和指标不区分该指标表示的各个分量,而是 一种约定的求和标记.
j 1 j 2 j 3
aj
ds2 dx2 dy2 dz2 dxidxi ijdxidxj
ijjk ik
aiij a j
xi x j
xi, j
ij
19
例: A i j b j
u i i
k xk
xi Cij z j
分量形式:
Ai1b1Ai2b2Ai3b3
u11u22u33
1 2 3
间位置的变化及各邻近点距离的变化;研究随时间变化 的物理量的时间变化率. 2)连续介质满足的物理基本定律
质量守恒,动量守恒,能量守恒,热力学基本定律 3)连续介质的本构方程
描述各种连续介质模型对外部作用的响应;
3
课程内容
第一章 连续介质力学中的数学模型
主要掌握:张量的概念,张量的表示方法以及张量的运算规律等
22
1.1.5三矢量之积 三矢量标量积(混合积)
a (b c ) (a ie i)( ijkb jc k )e i
x1 x2 x3
x1 C11z1 C12z2 C13z3 x2 C21z1 C22z2 C23z3 x3 C31z1 C32z2 C33z3
20
1.1.4 置换符号 { ijk }
1, 当 i , j , k 是1,2,3的偶排列
123,231,312
i j k -1,当 i , j , k 是1,2,3的奇排列
132,321,213
0,当 i , j , k 中有取值相同者.
1
1
3
2
3
2
偶排列
奇排列
21
矢量叉积 a b ( a 2 b 3 a 3 b 2 ) e 1 ( a 1 b 2 a 2 b 1 ) e 3 ( a 3 b 1 a 1 b 3 ) e 2 用置换符号可写成
a b c ( ijka jb k) (c i)
7
第一章 连续介质力学的数学基础
1.1 矢量
1.1.1矢量的概念
在三维欧几里得空间内, 具有大小和方向 的有向 线段.
矢量的表示
粗体字或字母上箭头
矢量相等
大小和方向相同
单位矢量
大小为1
零矢量
大小为0
8
图形表示
矢量 a (a1,a2,a3)
分量: 小
x3 a
a
O
a az
注意:
abba
axb
O
b
a -axb
12
(6)并矢 定义 a ba ieibjeja ibjeiej
展开共9项, e i e j 可视为并矢的基
a i b j 为并矢的分解系数或分量
13
1.1.3 Einstein求和约定
在同一项内的一个指标的重复,将表示对该指标 在它的范围上遍历求和.
自由指标:无重复出现的指标,取值域1,2,3(三维空间中)
