高考数学基础训练题三角函数函数图像与性质、函数y=Asin(wx+φ)的图像性质及应用
新高考数学考点12 y=Asin(wx+φ)的图像与性质考点分类讲义练习题附解析1

考点12 y=Asin(wx+φ)的图像与性质1、了解三角函数的周期性,画出 y =sin x , y =cos x , y =tan x 的图像,并能根据图像理解正弦函数、余弦函数在[ 0 ,2π ],正切函数的性质(如单调性、最大值和最小值、图像与 x 轴的交点等)2. 了解三角函数 y = A sin ( ωx + φ )的实际意义及其参数 A , ω ,φ 对函数图像变化的影响;能画出 y = A sin (ωx +φ )的简图,能由正弦曲线 y =sin x 通过平移、伸缩变换得到 y = A sin ( ωx + φ )的图像 .3. 会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型 .1. 三角函数的图像与性质是高考中的必考点,对这部分内容的考查,高考中大多以中、低档题为主,主要集中于对函数的周期、图像、单调性、值域(或最值)等几个方面的考查 . 要解决此类问题,要求学生熟练地掌握三角函数的图像,及正弦函数、余弦函数、正切函数的最基本的性质,并能运用这些性质去熟练地解题 .2. 利用三角函数的性质解决问题时,要重视化归思想的运用,即将复杂的三角函数转化为基本的正弦、余弦、正切函数来处理1、函数 f ( x ) = A sin ( ωx + φ )的图像的平移和伸缩变换以及根据图像确定 A , ω ,φ 问题是高考的热点,题型多样,难度中低档,主要考查识图、用图的能力,同时考查利用三角公式进行三角恒等变换的能力 . 2、要牢牢记住函数 f ( x ) = A sin ( ωx + φ )的图像和性质。
1、【2020年江苏卷】.将函数y =πsin(2)43x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.【答案】524x π=-【解析】3sin[2()]3sin(2)6412y x x πππ=-+=- 72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈当1k =-时524x π=-故答案为:524x π=-2、【2020年全国1卷】设函数()cos π()6f x x ω=+在[π,π]-的图像大致如下图,则f (x )的最小正周期为( )A. 10π9 B.7π6 C. 4π3D. 3π2【答案】C【解析】由图可得:函数图象过点4,09π⎛⎫-⎪⎝⎭, 将它代入函数()f x 可得:4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭又4,09π⎛⎫-⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点, 所以4962πππω-⋅+=-,解得:32ω=所以函数()f x 的最小正周期为224332T πππω=== 故选:C3、【2020年全国3卷】16.关于函数f (x )=1sin sin x x+有如下四个命题: ①f (x )的图像关于y 轴对称. ②f (x )的图像关于原点对称. ③f (x )的图像关于直线x =2π对称. ④f (x )的最小值为2.其中所有真命题的序号是__________. 【答案】②③【解析】对于命题①,152622f π⎛⎫=+= ⎪⎝⎭,152622f π⎛⎫-=--=- ⎪⎝⎭,则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()f x 的图象不关于y 轴对称,命题①错误;对于命题②,函数()f x 的定义域为{},x x k k Z π≠∈,定义域关于原点对称,()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭,所以,函数()f x 的图象关于原点对称,命题②正确;对于命题③,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭, 11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭,则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()f x 的图象关于直线2x π=对称,命题③正确;对于命题④,当0x π-<<时,sin 0x <,则()1sin 02sin f x x x=+<<, 命题④错误. 故答案为:②③.4、【2020年天津卷】8.已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭.给出下列结论: ①()f x 的最小正周期为2π;②2f π⎛⎫⎪⎝⎭是()f x 的最大值; ③把函数sin y x =的图象上所有点向左平移3π个单位长度,可得到函数()y f x =的图象. 其中所有正确结论的序号是 A. ① B. ①③C. ②③D. ①②③【答案】B【解析】因为()sin()3f x x π=+,所以周期22T ππω==,故①正确;51()sin()sin 122362f ππππ=+==≠,故②不正确; 将函数sin y x =的图象上所有点向左平移3π个单位长度,得到sin()3y x π=+的图象, 故③正确. 故选:B.5、【2020年山东卷】.下图是函数y = sin(ωx +φ)的部分图像,则sin(ωx +φ)= ( )A. πsin(3x +)B. πsin(2)3x - C. πcos(26x +)D. 5πcos(2)6x - 【答案】BC【解析】由函数图像可知:22362T πππ=-=,则222T ππωπ===,所以不选A, 当2536212x πππ+==时,1y =-∴()5322122k k Z ππϕπ⨯+=+∈, 解得:()223k k ϕππ=+∈Z ,即函数的解析式为:2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭ 故选:BC.6、【2019年高考全国Ⅰ卷理数】函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为 A .B .C .D .【答案】D 【解析】由22sin()()sin ()()cos()()cos x x x xf x f x x x x x-+----===--+-+,得()f x 是奇函数,其图象关于原点对称,排除A .又22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+,排除B ,C ,故选D . 7、【2019年高考全国Ⅰ卷理数】关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数②f (x )在区间(2π,π)单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A .①②④ B .②④ C .①④D .①③【答案】C 【解析】()()()()sin sin sin sin ,f x x x x x f x f x -=-+-=+=∴为偶函数,故①正确.当ππ2x <<时,()2sin f x x =,它在区间,2π⎛⎫π ⎪⎝⎭单调递减,故②错误. 当0πx ≤≤时,()2sin f x x =,它有两个零点:0,π;当π0x -≤<时,()()sin sin f x x x =--2sin x =-,它有一个零点:π-,故()f x 在[],-ππ有3个零点:0-π,,π,故③错误.当[]()2,2x k k k *∈ππ+π∈N时,()2sin f x x =;当[]()2,22x k k k *∈π+ππ+π∈N时,()sin sin 0f x x x =-=,又()f x 为偶函数,()f x ∴的最大值为2,故④正确.综上所述,①④正确,故选C .8、【2019年高考全国Ⅱ卷理数】下列函数中,以2π为周期且在区间(4π,2π)单调递增的是A .f (x )=|cos2x |B .f (x )=|sin2x |C .f (x )=cos|x |D .f (x )=sin|x |【答案】A【解析】作出因为sin ||y x =的图象如下图1,知其不是周期函数,排除D ; 因为cos cos y x x ==,周期为2π,排除C ;作出cos2y x =图象如图2,由图象知,其周期为π2,在区间(4π,2π)单调递增,A 正确; 作出sin 2y x =的图象如图3,由图象知,其周期为π2,在区间(4π,2π)单调递减,排除B ,故选A .图1图2图39、【2019年高考全国Ⅲ卷理数】设函数()f x =sin (5x ωπ+)(ω>0),已知()f x 在[]0,2π有且仅有5个零点,下述四个结论:①()f x 在(0,2π)有且仅有3个极大值点 ②()f x 在(0,2π)有且仅有2个极小值点③()f x 在(0,10π)单调递增 ④ω的取值范围是[1229510,)其中所有正确结论的编号是 A .①④ B .②③ C .①②③ D .①③④【答案】D【解析】①若()f x 在[0,2π]上有5个零点,可画出大致图象, 由图1可知,()f x 在(0,2π)有且仅有3个极大值点.故①正确;②由图1、2可知,()f x 在(0,2π)有且仅有2个或3个极小值点.故②错误;④当()f x =sin (5x ωπ+)=0时,5x ωπ+=k π(k ∈Z ),所以ππ5k x ω-=, 因为()f x 在[0,2π]上有5个零点,所以当k =5时,π5π52πx ω-=≤,当k =6时,π6π52πx ω-=>,解得1229510ω≤<,10、【2019年高考天津卷理数】已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B . CD .2【答案】C【解析】∵()f x 为奇函数,∴(0)sin 0,=π,,0,f A k k k ϕϕ==∴∈∴=Z 0ϕ=; 又12π()sin,2π,122g x A x T ωω=∴==∴2ω=,又π()4g =2A =,∴()2sin 2f x x =,3π()8f =故选C. 11、【2018年高考江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称,则ϕ的值是________. 【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ,所以2πππππ()326k k k +=+=-+∈Z ,ϕϕ,因为ππ22-<<ϕ,所以π0,.6k ==-ϕ 【名师点睛】由对称轴得2πππππ()326k k k +=+=-+∈Z ,ϕϕ,再根据限制范围求结果.函数()sin y A x B =++ωϕ(A >0,ω>0)的性质:(1)max min ,y A B y A B =+=-+; (2)最小正周期2πT =ω;(3)由()ππ2x k k +=+∈Z ωϕ求对称轴; (4)由()ππ2π2π22k x k k -+≤+≤+∈Z ωϕ求增区间;由()π3π2π2π22k x k k +≤+≤+∈Z ωϕ求减区间.12、【2019年高考浙江卷】设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值; (2)求函数22[()][()]124y f x f x ππ=+++的值域. 【答案】(1)π2θ=或3π2;(2)[1-+. 【解析】(1)因为()sin()f x x θθ+=+是偶函数,所以,对任意实数x 都有sin()sin()x x θθ+=-+, 即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+, 故2sin cos 0x θ=, 所以cos 0θ=. 又[0,2π)θ∈, 因此π2θ=或3π2. (2)2222ππππsin sin 124124y fx f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 2136212sin 22222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎫⎝⎭⎝⎭=+=--⎪⎪⎝⎭π1223x ⎛⎫=-+ ⎪⎝⎭.因此,函数的值域是[1+.题型一 三角函数的性质1、(2020届山东省枣庄市高三上学期统考)设函数2sin cos ()(,0)x x xf x a R a ax +=∈≠,若(2019)2f -=,(2019)f =( )A .2B .-2C .2019D .-2019【答案】B 【解析】因为2sin cos ()x x xf x ax +=,所以22sin()cos()sin cos ()()x x x x x xf x f x ax ax---+-==-=-, 因此函数()f x 为奇函数,又(2019)2f -=,所以(2019)(2019)2f f =--=-. 故选B2、(2020届山东省枣庄市高三上学期统考)已知函数()cos()(0)f x x ωϕω=+>的最小正周期为π,且对x ∈R ,()3f x f π⎛⎫⎪⎝⎭恒成立,若函数()y f x =在[0,]a 上单调递减,则a 的最大值是( )A .π6B .π3C .2π3D .5π6【答案】B 【解析】因为函数()()cos f x x ωϕ=+的最小正周期为π,所以22πωπ==,又对任意的x ,都使得()3f x f π⎛⎫≥ ⎪⎝⎭, 所以函数()f x 在3x π=上取得最小值,则223k πϕππ+=+,k Z ∈, 即2,3k k Z πϕπ=+∈,所以()cos 23f x x π⎛⎫=+ ⎪⎝⎭, 令222,3k x k k Z ππππ≤+≤+∈,解得,63k x k k Z ππππ-+≤≤+∈ ,则函数()y f x =在0,3π⎡⎤⎢⎥⎣⎦上单调递减,故a 的最大值是3π. 故选B3、(2020届山东省潍坊市高三上期中)已知函数()sin cos f x x x =+,则( ) A .()f x 的最小正周期为πB .()y f x =图象的一条对称轴方程为4x π=C .()f x 的最小值为2-D .()f x 的0,2π⎡⎤⎢⎥⎣⎦上为增函数【答案】B 【解析】()sin cos )4f x x x x π=+=+,对A ,()f x ∴的最小正周期为2π,故A 错误;对B ,()42f ππ==()y f x ∴=图象的一条对称轴方程为4x π=,故B 正确;对C ,()f x 的最小值为,故C 错误; 对D ,由[0,]2x π∈,得3[,]444x πππ+∈,则()f x 在[0,]2π上先增后减,故D 错误. 故选:B .4、(2020届山东实验中学高三上期中)已知函数()sin 2f x a x x =的图象关于直线12x π=-对称,若()()124f x f x ⋅=-,则12a x x -的最小值为( )A .4π B .2π C .πD .2π【答案】B 【解析】()f x 的图象关于直线12x π=-对称,(0)()6f f π∴=-,即-1a =,则()sin 222sin 26f x x x x π⎛⎫=-=- ⎪⎝⎭,12()()4f x f x =-,1()2f x ∴=,2()2f x =-或1()2f x =-,2()2f x =,即1()f x ,2()f x 一个为最大值,一个为最小值, 则12||x x -的最小值为2T, T π=,12||x x ∴-的最小值为2π, 即12a x x -的最小值为2π.故选:B .5、(2020届山东省滨州市三校高三上学期联考)设函数()sin 23f x x π⎛⎫=- ⎪⎝⎭,则下列结论正确的是( )A .π-是()f x 的一个周期B .()f x 的图像可由sin 2y x =的图像向右平移3π得到 C .()f x π+的一个零点为6x π=D .()y f x =的图像关于直线1712x π=对称 【答案】ACD 【解析】()sin 23f x x π⎛⎫=- ⎪⎝⎭的最小正周期为π,故π-也是其周期,故A 正确;()f x 的图像可由sin 2y x =的图像向右平移6π得到,故B 错误;()77()()sin sin 066323f f ππππππ⎛⎫+==-== ⎪⎝⎭,故C 正确; sin sin 17175()1262sin 132f πππππ⎛⎫⎛⎫⎛⎫-=== ⎪ =⎪ ⎪⎝⎭⎝⎭⎝⎭,故D 正确. 故选:ACD6、.(2020届江苏省南通市如皋市高三下学期二模)已知函数()()()sin 0f x x ωϕω=+>,将函数()y f x =的图象向右平移π4个单位长度后,所得图象与原函数图象重合,则ω的最小值等于__________.【答案】4【解析】由题得12=,4,()42n n n Z ππωω⨯⨯∴=∈, 因为0>ω,所以ω的最小值等于4.故答案为:47、(2020届江苏南通市高三基地学校第一次大联考数学试题)已知函数()2sin()(0)3f x x πωω=+>的图象关于点,02π⎛⎫⎪⎝⎭对称,则ω的最小值为_____. 【答案】43. 【解析】由题意可得,32k k Z ππωπ⨯+=∈,求得22,3k k Z ω=-∈, 又0>ω,则ω的最小值为43, 故答案为:43. 8、(2019南京学情调研)已知函数f(x)=2sin (2x +φ)⎝⎛⎭⎫-π2<φ<π2的图像关于直线x =π6对称,则f(0)的值为________.【答案】. 1【解析】由题意,f ⎝⎛⎭⎫π6=2sin ⎝⎛⎭⎫2×π6+φ=±2,即sin ⎝⎛⎭⎫π3+φ=±1,又因为-π2<φ<π2, -π6<π3+φ<5π6,所以π3+φ=π2,即φ=π6,所以f(x)=2sin ⎝⎛⎭⎫2x +π6,f(0)=1.9、(2019苏锡常镇调研)函数()cos()(0)3f x x πωω=->的图像关于直线2x π=对称,则ω的最小值为 .【答案】.32【解析】解法1:根据余弦函数的图像及性质,令ππωk x =-3,Z k ∈得ωππk x +=3,令23πωππ=+k 得k 232+=ω,Z k ∈,又因为0>ω,所以当0=k 时ω取得最小值为.32 解法2:由条件可得1)2(±=πf ,即1)32cos(±=-πωπ,则ππωπk =-32,Z k ∈,解得k 232+=ω,Z k ∈,又因为0>ω,所以当0=k 时ω取得最小值为.32解后反思:利用整体思想,结合三角函数的图像及性质是解决这类问题的关键!10、(2019苏州期初调查) 已知函数f(x)=sin (2x +φ)(0≤φ<π)的一条对称轴是x =-512π,则φ=________.【答案】 π3【解析】因为函数f(x)的一条对称轴是x =-512π,所以2×⎝⎛⎭⎫-5π12+φ=k π+π2,k ∈Z ,则φ=k π+4π3,k ∈Z ,又因为0≤φ<π,所以φ=π3.11、(2019南京、盐城二模)若函数f(x)=2sin (ωx +φ)(ω>0,0<φ<π)的图像经过点⎝⎛⎭⎫π6,2,且相邻两条对称轴间的距离为π2,则f ⎝⎛⎭⎫π4的值为________.【答案】.3【解析】由相邻两条对称轴间的距离为π2,知其最小正周期T =2×π2=π,从而得ω=2πT =2ππ=2,又f(x)=2sin (2x +φ)的图像经过点⎝⎛⎭⎫π6,2,所以2sin ⎝⎛⎭⎫π3+φ=2,解得φ=2k π+π6(k ∈Z ),又因为0<φ<π,所以φ=π6,故f (x )=2sin ⎝⎛⎭⎫2x +π6,即有f ⎝⎛⎭⎫π4=2sin 2π3= 3.题型二 三角函数图像的变换1、(2020届山东师范大学附中高三月考)为了得函数23y sin x π⎛⎫=+ ⎪⎝⎭的图象,只需把函数2y sin x =的图象( ) A .向左平移6π个单位 B .向左平移3π单位 C .向右平移6π个单位 D .向右平移3π个单位【答案】A 【解析】不妨设函数2y sin x =的图象沿横轴所在直线平移ϕ个单位后得到函数23y sin x π⎛⎫=+⎪⎝⎭的图象. 于是,函数2y sin x =平移ϕ个单位后得到函数,sin 2()y x ϕ=+,即sin(22)y x ϕ=+, 所以有223k πϕπ=+,6k πϕπ=+,取0k =,6π=ϕ.答案为A . 2、(2020届山东省枣庄、滕州市高三上期末)将曲线()cos 2y f x x =上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移4π个单位长度,得到曲线cos 2y x =,则6f π⎛⎫= ⎪⎝⎭( )A .1B .-1C D .【答案】D 【解析】把cos 2y x =的图象向左平移4π个单位长度,得cos 2()cos(2)sin 242y x x x ππ=+=+=-的图象,再把所得图象各点的横坐标变为原来的12倍,纵坐标不变,得图象的函数式为sin(22)sin 4y x x =-⨯=-, sin 42sin 2cos 2()cos 2y x x x f x x =-=-=,∴()2sin 2f x x =-,∴()2sin63f ππ=-=.故选:D.3、(2020届山东省潍坊市高三上学期统考)将函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0a a >个单位得到函数()πcos 24g x x ⎛⎫=+ ⎪⎝⎭的图像,则a 的值可以为( )A .5π12B .7π12C .19π24D .41π24【答案】C【解析】由题意知,3()cos(2)sin(2)44g x x x ππ=+=+,其图像向左平移a 个单位得到函数3()sin(22)4f x x a π=++, 而函数()πsin 23f x x ⎛⎫=+⎪⎝⎭,所以有32243a k πππ+=+5224a k ππ=-+,取1k =得1924a π=.答案选C.4、(2020届浙江省宁波市余姚中学高考模拟)函数f(x)=sin(wx +φ)(w >0,φ<2π)的最小正周期是π,若将该函数的图象向右平移6π个单位后得到的函数图象关于直线x =2π对称,则函数f(x)的解析式为( )A .f(x)=sin(2x +3π) B .f(x)=sin(2x -3π) C .f(x)=sin(2x +6π) D .f(x)=sin(2x -6π) 【答案】D【解析】因为函数()()f x sin ωx φ=+的最小正周期是π,所以2ππω=,解得ω2=,所以()()f x sin 2x φ=+, 将该函数的图像向右平移π6个单位后,得到图像所对应的函数解析式为ππy sin 2x φsin 2x φ63⎡⎤⎛⎫⎛⎫=-+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 由此函数图像关于直线πx 2=对称,得: πππ2φk π232⨯+-=+,即πφk π,k Z 6=-∈,取k 0=,得πφ6=-,满足πφ2<,所以函数()f x 的解析式为()πf x sin 2x 6⎛⎫=-⎪⎝⎭,故选D. 5、(2020·蒙阴县实验中学高三期末)关于函数()22cos cos(2)12f x x x π=-+-的描述正确的是( )A .其图象可由2y x =的图象向左平移8π个单位得到 B .()f x 在(0,)2π单调递增C .()f x 在[]0,π有2个零点D .()f x 在[,0]2π-的最小值为【答案】ACD【解析】由题:()22cos cos(2)1cos 2sin 2)24f x x x x x x ππ=-+-=+=+,由2y x =的图象向左平移8π个单位,得到)))84y x x ππ=+=+,所以选项A 正确;令222,242k x k k Z πππππ-≤+≤+∈,得其增区间为3[,],88k k k Z ππππ-+∈ ()f x 在(0,)8π单调递增,在(,)82ππ单调递减,所以选项B 不正确;解()0,2,4f x x k k Z ππ=+=∈,得:,28k x k Z ππ=-∈,[0,]x π∈, 所以x 取37,88ππ,所以选项C 正确;3[,0],2[,],sin(2)[24444x x x πππππ∈-+∈-+∈-,()[f x ∈, 所以选项D 正确. 故选:ACD6、(2020届山东省枣庄市高三上学期统考)将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度得到()g x 图象,则下列判断正确的是( ) A .函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B .函数()g x 图象关于直线712x π=对称 C .函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D .函数()g x 图象关于点,03π⎛⎫⎪⎝⎭对称 【答案】ABD【解析】函数()sin 23f x x π⎛⎫=+⎪⎝⎭的图像向右平移2π个单位长度得到()ππsin 223g x x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦2πsin 23x ⎛⎫=- ⎪⎝⎭.由于7π7π2ππsin sin 112632g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,故7π12x =是()g x 的对称轴,B 选项正确. 由于π2π2πsin sin 00333g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,故,03π⎛⎫ ⎪⎝⎭是()g x 的对称中心,D 选项正确.由π2ππ2232x -≤-≤,解得π7π1212x ≤≤,即()g x 在区间π7π,1212⎡⎤⎢⎥⎣⎦上递增,故A 选项正确、C 选项错误. 故选:ABD.7、(2019无锡期末) 已知直线y =a(x +2)(a>0) 与函数 y =|cos x|的图像恰有四个公共点A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),D(x 4,y 4), 其中 x 1<x 2<x 3<x 4,则x 4+1tan x 4=________. 【答案】-2【解析】根据图形可得直线y =a(x +2)与函数y =-cos x 的图像相切于点(x 4,-cos x 4),其中x 4∈⎝⎛⎭⎫π4,π.因为y =sin x ,由导数的几何意义可得a =sin x 4=-cos x 4-0x 4+2,化简得x 4+1tan x 4=-2.8、(2020届江苏省南通市高三下学期3月开学考试)将函数()πsin 6f x x ω⎛⎫=- ⎪⎝⎭(0>ω)的图象向左平移π3个单位长度后,所得图象关于直线πx =对称,则ω的最小值为______. 【答案】12【解析】将函数f (x )=sin (ωx 6π-)(ω>0)的图象向左平移3π个单位后,可得函数y =sin (ωx 36πωπ+-)的图象,再根据所得图象关于直线x =π对称,可得ωπ36πωπ+-=k π2π+,k ∈Z , ∴当k =0时,ω取得最小值为12, 故答案为12.题型三 三角函数的解析式1、(2020届山东省滨州市高三上期末)已知函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭,则( )A .把()y f x =的图象向右平移6π个单位得到函数2sin 2y x =的图象 B .函数()f x 在区间,02π⎛⎫- ⎪⎝⎭上单调递减C .函数()f x 在区间[]0,2π内有五个零点D .函数()f x 在区间0,3π⎡⎤⎢⎥⎣⎦上的最小值为1 【答案】D【解析】因为函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭, 所以2sin 23πϕ⎛⎫+= ⎪⎝⎭,因此2,32k k Z ππϕπ+=+∈,所以2,6k k Z πϕπ=+∈,因此()2sin(2)2sin 222sin 266f x x x k x ππϕπ⎛⎫⎛⎫=+=++=+ ⎪ ⎪⎝⎭⎝⎭;A 选项,把()y f x =的图象向右平移6π个单位得到函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象,故A 错; B 选项,由3222,262k x k k Z πππππ+≤+≤+∈得2,63k x k k Z ππππ+≤≤+∈,即函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的单调递减区间是:2,,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,故B 错; C 选项,由()2sin 206f x x π⎛⎫=+= ⎪⎝⎭得2,6x k k Z ππ+=∈,即,122k x k Z ππ=-+∈, 因此[]0,2x π∈,所以5111723,,,12121212x ππππ=,共四个零点,故C 错; D 选项,因为0,3x π⎡⎤∈⎢⎥⎣⎦,所以52,666x πππ⎡⎤+∈⎢⎥⎣⎦,因此1sin 2,162x π⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,所以[]2sin 21,26x π⎛⎫+∈ ⎪⎝⎭,即()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的最小值为1,故D 正确;故选:D.2、(2020·浙江温州中学3月高考模拟)已知()sin()f x A x ωφ=+(0,04,)2A πωφ><<<)过点1(0,)2,且当6x π=时,函数()f x 取得最大值1.(1)将函数()f x 的图象向右平移6π个单位得到函数()g x ,求函数()g x 的表达式; (2)在(1)的条件下,函数2()()()2cos 1h x f x g x x =++-,求()h x 在[0,]2π上的值域.【答案】(1)()sin(2)6g x x π=-;(2)[1,2]-.【解析】 (1)由函数()f x 取得最大值1,可得1A =,函数过10,2⎛⎫ ⎪⎝⎭得12sin φ=,,26ππφφ<= 12,6662f k k Z ππππωπ⎛⎫=⇒+=+∈ ⎪⎝⎭,∵04ω<<,∴2ω=()26f x sin x π⎛⎫=+ ⎪⎝⎭,()266g x f x sin x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭.(2) ()22226h x x cos x sin x π⎛⎫=+=+⎪⎝⎭, 710,,2,21266626x x sin x πππππ⎡⎤⎛⎫∈≤+≤-≤+≤ ⎪⎢⎥⎣⎦⎝⎭,12226sin x π⎛⎫-≤+≤ ⎪⎝⎭,值域为[]1,2-.。
1.8函数y=Asin(wx+φ)的图象基础练习题

3.A
【分析】
由三角函数图象平移的规律即可得解.
【详解】
若将函数 的图象向右平移 个单位,
所得函数图象对应的函数表达式是 .
故选:A.
4.A
【分析】
根据图象求出 即可得到函数解析式.
【详解】
显然 ,
因为 ,所以 ,所以 ,
由 得 ,
所以 ,即 , ,
因为 ,所以 ,
所以 .
故选:A
【点睛】
【点睛】
本题考查三角函数的伸缩变换,属于基础题.
7.C
【分析】
根据左加右减的原则,可得平移后的解析式为 ,化简整理,即可得出结果.
【详解】
将函数 的图象向右平移 个单位长度,所得图象的函数解析式为
,整理得 .
故选C
【点睛】
本题主要考查三角函数的图像变换问题,熟记平移原则即可,属于基础题型.
8.D
【分析】
【详解】
(1)由已知得 ,解得 .
将点 代入解析式, ,可知 ,
由 可知 ,于是 .
(2)令
解得 ,
于是函数 的单调递增区间为 .
【点睛】
本题考查正弦函数的图像和性质,基础题.
21.(1) ;(2)当 时, ;当 时, .
【分析】
(1)先由周期为 求出 ,再根据 , 进行求解即可;
(2)先求出 ,可得 ,进而求解即可
15.2
【分析】
根据所给的相邻的零点可求周期,从而得到 的值.
【详解】
因为 , 是函数 两个相邻的零点,
故 ,所以 ,故 ,
故答案为:2.
【点睛】
本题考查三角函数的图象性质,一般地,相邻两个零点之间的距离为半周期,相邻两条对称轴之间的距离也是半周期.
高考数学函数y=Asin(ωx+φ)的图象和性质

§3.3 函数y=Asin(ωx+φ)的图象和性质
知识清单
2
1.函数y=Asin(ωx+φ)和y=Acos(ωx+φ)的最小正周期都是① | ω | .
2.函数y=Atan(ωx+φ)的最小正周期是② | ω | .
3.y=Asin(ωx+φ)的有关概念
4.用五点法画y=Asin(ωx+φ)一个周期内的简图 用五点法画y=Asin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表 所示:
(1)求A、B,确定函数的最大值M和最小值m,则A=
M
2
m
,B=
M
2
m
.
(2)求ω,确定函数的周期T,则ω=2T .
(3)求φ,常用代入法.
例1
已知函数f(x)=Asin(ωx+φ)
A>0,ω>0,|φ|<
2
,x∈R
的部分图象如
图所示.
(1)求f(x)的解析式;
(2)若g(x)=
3
f
5.确定y=Asin(ωx+φ)+k(A>0,ω>0,|φ|<π)中的参数的方法:
在由图象求解析式时,若最大值为M,最小值为m,则A= M m ,k= M m ,ω
2
2
由周期T确定,即由ω=2 求出,φ由特殊点的坐标确定.
T
方法技巧
方法 1 根据图象确定函数解析式
求函数y=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π)的解析式的步骤:
=2sin 2x.
∵tan α=3,
∴g(α)=2sin
三角函数y=Asin(wx+φ)的图像和性质

专题:三角函数)sin(ϕ+=wx A y 的图像和性质一、知识点总结1、函数sin y x =的图象上所有点向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 2、函数sin y x =的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数sin y x ω=的图象;再将函数sin y x ω=的图象上所有点向左(右)平移ϕω个单位长度,得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 3、函数()()sin 0,0y x ωϕω=A +A >>的性质: ①振幅:A ;②周期:2πωT =;③频率:12f ωπ==T ;④相位:x ωϕ+;⑤初相:ϕ. ⑥函数()sin y x ωϕ=A ++B ,当1x x =时,取得最小值为min y ;当2x x =时,取得最大值为max y ,则()max min 12y y A =-,()max min 12y y B =+,()21122x x x x T=-< 二、课前热身1.函数())4f x x π=-(x ∈R )的最小正周期为2. 满足21)4sin(=-πx 的x 的集合为_____3. 已知函数sin()y A x ωϕ=+(0,||A ϕπ><)的一段图象如下图所示,则函数的解析式 . 4. 要得到)32sin(π-=x y 的图像,只要将y=sin2x 的图像向___移动___单位 5. 函数y=cos(2x-3π) 的单调递增区间是____________________ 6. 若函数()3sin 2f x x ω=+(0ω>)在区间3,34ππ⎡⎤-⎢⎥⎣⎦上是增函数,则ω的取值范围是 ___7. 函数y=3sin (2x-6π)-2(2π≤x ≤32π)的值域为___________8. 关于函数()4sin(2)3f x x π=+(x R ∈),有下列命题① 由12()()0f x f x ==得12x x -必是π的整数倍; ② ()y f x =的表达式可改为()4cos(2)6f x x π=-;③ ()y f x =的图象关于点(,0)6π-对称;④ ()y f x =的图象关于直线6x π=-对称.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上) 三、典例分析例1:函数sin(A y =ωx )ϕ++B (0,0,>><ωπϕA )的最大值为22,最小值为-2,周期为32π,图象过点(0,42-),求此函数解析式例2:已知函数)2,0[],21,23[,1sin 2)(2πθθ∈-∈-+=x x x x f (1)当6πθ=时,求f(x)的最大值和最小值;(2)求θ的范围,使f(x)在区间]21,23[-上是单调递减函数。
高考数学函数y=Asin(ωx+φ)的图像及三角函数的应用

课堂考点探究
[思路点拨]根据≤x≤可得≤2x-≤,由此讨论函数g(x)的单调区间和取值范围.
例3 已知函数f(x)=sin+4cos2x,将函数f(x)的图像先向右平移个单位长度,再向下平移2个单位长度,得到函数g(x)的图像.(2)求函数g(x)在区间上的单调递减区间及取值范围.
课堂考点探究
课堂考点探究
变式题 (1)(多选题)函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图像如图4-25-4所示,则下列结论正确的是( )A.函数f(x)的最小正周期为πB.函数f(x)图像的一条对称轴为直线x=C.函数f(x)的单调递减区间为,k∈ZD.当x∈时,函数f(x)的取值范围为
课前基础巩固
[解析]将(0,1)代入函数f(x)的解析式,可得2sin φ=1,即sin φ=.因为|φ|<,所以φ=.
例1 (1)(多选题)为得到函数y=cos的图像,只需将y=cos 2x的图像上所有的点( ) A.横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位长度B.横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位长度C.向右平移个单位长度,再将横坐标伸长到原来的2倍(纵坐标不变)D.向右平移个单位长度,再将横坐标伸长到原来的2倍(纵坐标不变)
图4-25-4
课堂考点探究
(2)[2021·全国甲卷] 已知函数f(x)=2cos(ωx+φ)的部分图像如图4-25-5所示,则满足条件>0的最小正整数x为 .
Asin(ωx+φ)的图像与性质练习(含解析)
专题4.5 函数y=Asin(ωx+φ)的图象与性质【考试要求】1.结合具体实例,了解y=A sin(ωx+φ)的实际意义;能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响;2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型.【知识梳理】1。
用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示.2.函数y=A sin(ωx+φ)的有关概念3.函数y=sin x的图象经变换得到y=A sin(ωx+φ)的图象的两种途径4。
三角函数应用(1)用正弦函数可以刻画三种周期变化的现象:简谐振动(单摆、弹簧等),声波(音叉发出的纯音),交变电流。
(2)三角函数模型应用题的关键是求出函数解析式,可以根据给出的已知条件确定模型f(x)=A sin(ωx+φ)+k中的待定系数。
(3)把实际问题翻译为函数f(x)的性质,得出函数性质后,再把函数性质翻译为实际问题的答案。
【微点提醒】1。
由y=sin ωx到y=sin(ωx+φ)(ω>0,φ〉0)的变换:向左平移错误!个单位长度而非φ个单位长度。
2。
函数y=A sin(ωx+φ)的对称轴由ωx+φ=kπ+错误!(k∈Z)确定;对称中心由ωx+φ=kπ(k∈Z)确定其横坐标。
3.音叉发出的纯音振动可以用三角函数表达为y=A sin ωx,其中x表示时间,y表示纯音振动时音叉的位移,错误!表示纯音振动的频率(对应音高),A表示纯音振动的振幅(对应音强)。
4。
交变电流可以用三角函数表达为y=A sin(ωx+φ),其中x表示时间,y表示电流,A表示最大电流,错误!表示频率,φ表示初相位。
【疑误辨析】1.判断下列结论正误(在括号内打“√"或“×”)(1)将函数y=3sin 2x的图象左移错误!个单位长度后所得图象的解析式是y=3sin错误!.()(2)利用图象变换作图时“先平移,后伸缩"与“先伸缩,后平移”中平移的长度一致.()(3)函数y=A cos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为错误!.( )(4)由图象求解析式时,振幅A的大小是由一个周期内图象中最高点的值与最低点的值确定的。
高中 函数y=Asin(ωx+φ)的图象及性质 知识点+例题 全面
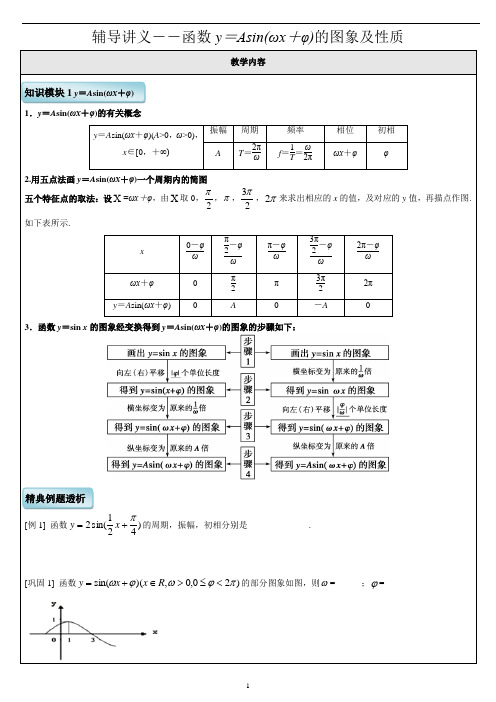
辅导讲义――函数y =Asin(ωx +φ)的图象及性质教学内容1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图 五个特征点的取法:设X =ωx +φ,由X 取0,2π,π,23π,π2来求出相应的x 的值,及对应的y 值,再描点作图.如下表所示.x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:[例1] 函数)421sin(2π+=x y 的周期,振幅,初相分别是______________.[巩固1] 函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则ω=______;ϕ=______知识模块1 y =A sin(ωx +φ)精典例题透析[巩固] 若关于x 的方程01sin sin 2=+-+m x x 有解,则实数m 的取值范围为_____________.[例5] 要得到)21sin(x y -=的图象,只需将)621sin(π--=x y 的图象_______________.[巩固1] 为得到函数)3cos(π+=x y 的图象,只需将函数x y sin =的图象_____________________.[巩固2] 为得到函数)62sin(π-=x y 的图象,只需将函数x y 2cos =的图象_____________________.[例6] 已知函数x x f πsin )(=的图象的一部分如左图,则右图的函数图象所对的函数解析式为_____________.[巩固1] 函数)0,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式为____________.[巩固2] 已知函数),0,)(sin()(πϕπωϕω<<->∈+=R x x A x f 的部分图象如图所示,则函数)(x f 的解析式 是_______________.[例7] 设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号)[例](1)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则ω=_____,φ=_______.(2)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.[巩固] 如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.题型三:函数y =A sin(ωx +φ)的性质[例] (2014·重庆改编)已知函数f (x )=3sin(ωx +φ)(ω>0,-π2≤φ<π2)的图象关于直线x =π3对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)当x ∈[0,π2]时,求函数y =f (x )的最大值和最小值.[巩固] 已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω,A >0,0<φ<π2)的最大值为2,最小正周期为π,直线x =π6是其图象的一条对称轴.(1)求函数f (x )的解析式;(2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间.1.(2013·山东)将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A .3π4B .π4C .0D .-π42.(2013·浙江)函数f (x )=sin x cos x +32cos 2x 的最小正周期和振幅分别是__________.3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是______________.4.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是_____________.5.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是_________________.6.设偶函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,△KLM 为等腰直角三角形,∠KML =90°, KL =1,则f (16)的值为________.,7.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6) (x =1,2,3,…,12,A >0)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值 为________℃.夯实基础训练。
函数y=Asin(wx+φ)的性质与图象(典型题型)高一数学(北师大版2019必修第二册)

∴在规定的8∶00至20∶00之间,有6个小时时间可供冲浪者运动,即9∶00至15∶00.
题型五: 用方程思想求三角函数图象的解析式
第一步:根据图象确定第一个平衡点、第二个平衡点或最高点、最低点.第二步:将“ωx+φ ”作为一个整体,找到对应的值.第三步:列方程组求解.第四步:写出所求的函数解析式.
1.6函数y=Asin(x+)的性质与图象(典型题型)
横向伸缩
横向伸缩
温故知新
温故知新
0
温故知新
方法一
向左(>0)(右<0)平移|φ|个单位长度
各点的横坐标伸长(0<<1)(缩短>1)原来的
各点的纵坐标伸长(A>1)(缩短0<A<1)原来的A倍
倍
五.函数
在物理学中的几何意义
表示离开平衡位置的最大距离,
t(时)
0
3
6
9
12
15
18
21
24
y(米)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b. (1)根据以上数据,求函数y=Acosωt+b(ω>0)的最小正周期T,振幅A及函数表达式. (2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8∶00至20∶00之间,有多少时间可供冲浪者进行运动?
横坐标不变
纵坐标伸长到原来的 倍
向左平移
纵坐标不变
横坐标缩短到原来的 倍
变换二:
例2. 如何由 y=sinx 的图象得到 的图象?
新高考数学考点12 y=Asin(wx+φ)的图像与性质考点分类讲义练习题附解析3

考点12 y=Asin(wx+φ)的图像与性质1、了解三角函数的周期性,画出 y =sin x , y =cos x , y =tan x 的图像,并能根据图像理解正弦函数、余弦函数在[ 0 ,2π ],正切函数的性质(如单调性、最大值和最小值、图像与 x 轴的交点等)2. 了解三角函数 y = A sin ( ωx + φ )的实际意义及其参数 A , ω ,φ 对函数图像变化的影响;能画出 y = A sin (ωx +φ )的简图,能由正弦曲线 y =sin x 通过平移、伸缩变换得到 y = A sin ( ωx + φ )的图像 .3. 会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型 .1. 三角函数的图像与性质是高考中的必考点,对这部分内容的考查,高考中大多以中、低档题为主,主要集中于对函数的周期、图像、单调性、值域(或最值)等几个方面的考查 . 要解决此类问题,要求学生熟练地掌握三角函数的图像,及正弦函数、余弦函数、正切函数的最基本的性质,并能运用这些性质去熟练地解题 .2. 利用三角函数的性质解决问题时,要重视化归思想的运用,即将复杂的三角函数转化为基本的正弦、余弦、正切函数来处理1、函数 f ( x ) = A sin ( ωx + φ )的图像的平移和伸缩变换以及根据图像确定 A , ω ,φ 问题是高考的热点,题型多样,难度中低档,主要考查识图、用图的能力,同时考查利用三角公式进行三角恒等变换的能力 . 2、要牢牢记住函数 f ( x ) = A sin ( ωx + φ )的图像和性质。
1、【2020年江苏卷】.将函数y =πsin(2)43x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.2、【2020年全国1卷】设函数()cos π()6f x x ω=+在[π,π]-的图像大致如下图,则f (x )的最小正周期为( )A.10π9 B.7π6 C. 4π3D. 3π2 3、【2020年全国3卷】16.关于函数f (x )=1sin sin x x+有如下四个命题:①f (x )的图像关于y 轴对称. ②f (x )的图像关于原点对称. ③f (x )的图像关于直线x =2π对称. ④f (x )的最小值为2.其中所有真命题的序号是__________. 4、【2020年天津卷】8.已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭.给出下列结论: ①()f x 的最小正周期为2π; ②2f π⎛⎫⎪⎝⎭是()f x 的最大值; ③把函数sin y x =的图象上所有点向左平移3π个单位长度,可得到函数()y f x =的图象. 其中所有正确结论的序号是 A. ①B. ①③C. ②③D. ①②③5、【2020年山东卷】.下图是函数y = sin(ωx +φ)的部分图像,则sin(ωx +φ)= ( )A. πsin(3x +)B. πsin(2)3x - C. πcos(26x +)D. 5πcos(2)6x - 6、【2019年高考全国Ⅰ卷理数】函数f (x )=2sin cos ++x xx x 在[,]-ππ的图像大致为A .B .C .D .7、【2019年高考全国Ⅰ卷理数】关于函数()sin |||sin |f x x x =+有下述四个结论:①f (x )是偶函数②f (x )在区间(2π,π)单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A .①②④ B .②④ C .①④D .①③8、【2019年高考全国Ⅱ卷理数】下列函数中,以2π为周期且在区间(4π,2π)单调递增的是A .f (x )=|cos2x |B .f (x )=|sin2x |C .f (x )=cos|x |D .f (x )=sin|x |9、【2019年高考全国Ⅲ卷理数】设函数()f x =sin (5x ωπ+)(ω>0),已知()f x 在[]0,2π有且仅有5个零点,下述四个结论:①()f x 在(0,2π)有且仅有3个极大值点 ②()f x 在(0,2π)有且仅有2个极小值点 ③()f x 在(0,10π)单调递增④ω的取值范围是[1229510,) 其中所有正确结论的编号是 A .①④ B .②③ C .①②③D .①③④10、【2019年高考天津卷理数】已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2- B. CD .211、【2018年高考江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称,则ϕ的值是________.12、【2019年高考浙江卷】设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值; (2)求函数22[()][()]124y f x f x ππ=+++的值域.题型一 三角函数的性质1、(2020届山东省枣庄市高三上学期统考)设函数2sin cos ()(,0)x x xf x a R a ax +=∈≠,若(2019)2f -=,(2019)f =( )A .2B .-2C .2019D .-20192、(2020届山东省枣庄市高三上学期统考)已知函数()cos()(0)f x x ωϕω=+>的最小正周期为π,且对x ∈R ,()3f x f π⎛⎫⎪⎝⎭恒成立,若函数()y f x =在[0,]a 上单调递减,则a 的最大值是( )A .π6B .π3C .2π3D .5π63、(2020届山东省潍坊市高三上期中)已知函数()sin cos f x x x =+,则( ) A .()f x 的最小正周期为πB .()y f x =图象的一条对称轴方程为4x π=C .()f x 的最小值为2-D .()f x 的0,2π⎡⎤⎢⎥⎣⎦上为增函数4、(2020届山东实验中学高三上期中)已知函数()sin 2f x a x x =的图象关于直线12x π=-对称,若()()124f x f x ⋅=-,则12a x x -的最小值为( ) A .4πB .2π C .πD .2π5、(2020届山东省滨州市三校高三上学期联考)设函数()sin 23f x x π⎛⎫=- ⎪⎝⎭,则下列结论正确的是( )A .π-是()f x 的一个周期B .()f x 的图像可由sin 2y x =的图像向右平移3π得到 C .()f x π+的一个零点为6x π=D .()y f x =的图像关于直线1712x π=对称 6、.(2020届江苏省南通市如皋市高三下学期二模)已知函数()()()sin 0f x x ωϕω=+>,将函数()y f x =的图象向右平移π4个单位长度后,所得图象与原函数图象重合,则ω的最小值等于__________.7、(2020届江苏南通市高三基地学校第一次大联考数学试题)已知函数()2sin()(0)3f x x πωω=+>的图象关于点,02π⎛⎫⎪⎝⎭对称,则ω的最小值为_____. 8、(2019南京学情调研)已知函数f(x)=2sin (2x +φ)⎝⎛⎭⎫-π2<φ<π2的图像关于直线x =π6对称,则f(0)的值为________.9、(2019苏锡常镇调研)函数()cos()(0)3f x x πωω=->的图像关于直线2x π=对称,则ω的最小值为 .10、(2019苏州期初调查) 已知函数f(x)=sin (2x +φ)(0≤φ<π)的一条对称轴是x =-512π,则φ=________.11、(2019南京、盐城二模)若函数f(x)=2sin (ωx +φ)(ω>0,0<φ<π)的图像经过点⎝⎛⎭⎫π6,2,且相邻两条对称轴间的距离为π2,则f ⎝⎛⎭⎫π4的值为________.题型二 三角函数图像的变换1、(2020届山东师范大学附中高三月考)为了得函数23y sin x π⎛⎫=+ ⎪⎝⎭的图象,只需把函数2y sin x =的图象( ) A .向左平移6π个单位 B .向左平移3π单位 C .向右平移6π个单位 D .向右平移3π个单位2、(2020届山东省枣庄、滕州市高三上期末)将曲线()cos 2y f x x =上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移4π个单位长度,得到曲线cos 2y x =,则6f π⎛⎫= ⎪⎝⎭( )A .1B .-1C D .3、(2020届山东省潍坊市高三上学期统考)将函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0a a >个单位得到函数()πcos 24g x x ⎛⎫=+ ⎪⎝⎭的图像,则a 的值可以为( )A .5π12B .7π12C .19π24D .41π244、(2020届浙江省宁波市余姚中学高考模拟)函数f(x)=sin(wx +φ)(w >0,φ<2π)的最小正周期是π,若将该函数的图象向右平移6π个单位后得到的函数图象关于直线x =2π对称,则函数f(x)的解析式为( )A .f(x)=sin(2x +3π) B .f(x)=sin(2x -3π) C .f(x)=sin(2x +6π) D .f(x)=sin(2x -6π)5、(2020·蒙阴县实验中学高三期末)关于函数()22cos cos(2)12f x x x π=-+-的描述正确的是( )A .其图象可由2y x =的图象向左平移8π个单位得到 B .()f x 在(0,)2π单调递增C .()f x 在[]0,π有2个零点D .()f x 在[,0]2π-的最小值为6、(2020届山东省枣庄市高三上学期统考)将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移2π个单位长度得到()g x 图象,则下列判断正确的是( ) A .函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B .函数()g x 图象关于直线712x π=对称 C .函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D .函数()g x 图象关于点,03π⎛⎫⎪⎝⎭对称7、(2019无锡期末) 已知直线y =a(x +2)(a>0) 与函数 y =|cos x|的图像恰有四个公共点A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),D(x 4,y 4), 其中 x 1<x 2<x 3<x 4,则x 4+1tan x 4=________. 8、(2020届江苏省南通市高三下学期3月开学考试)将函数()πsin 6f x x ω⎛⎫=- ⎪⎝⎭(0>ω)的图象向左平移π3个单位长度后,所得图象关于直线πx =对称,则ω的最小值为______.题型三 三角函数的解析式1、(2020届山东省滨州市高三上期末)已知函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫⎪⎝⎭,则( ) A .把()y f x =的图象向右平移6π个单位得到函数2sin 2y x =的图象B .函数()f x 在区间,02π⎛⎫- ⎪⎝⎭上单调递减C .函数()f x 在区间[]0,2π内有五个零点D .函数()f x 在区间0,3π⎡⎤⎢⎥⎣⎦上的最小值为12、(2020·浙江温州中学3月高考模拟)已知()sin()f x A x ωφ=+(0,04,)2A πωφ><<<)过点1(0,)2,且当6x π=时,函数()f x 取得最大值1.(1)将函数()f x 的图象向右平移6π个单位得到函数()g x ,求函数()g x 的表达式; (2)在(1)的条件下,函数2()()()2cos 1h x f x g x x =++-,求()h x 在[0,]2π上的值域.解析附后考点12 y=Asin(wx+φ)的图像与性质1、【答案】524x π=-【解析】3sin[2()]3sin(2)6412y x x πππ=-+=- 72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈当1k =-时524x π=-故答案为:524x π=-2、【答案】C【解析】由图可得:函数图象过点4,09π⎛⎫-⎪⎝⎭, 将它代入函数()f x 可得:4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭又4,09π⎛⎫-⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点, 所以4962πππω-⋅+=-,解得:32ω=所以函数()f x 的最小正周期为224332T πππω=== 故选:C 3、【答案】②③【解析】对于命题①,152622f π⎛⎫=+= ⎪⎝⎭,152622f π⎛⎫-=--=- ⎪⎝⎭,则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()f x 的图象不关于y 轴对称,命题①错误;对于命题②,函数()f x 的定义域为{},x x k k Z π≠∈,定义域关于原点对称,()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭,所以,函数()f x 的图象关于原点对称,命题②正确;对于命题③,11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭, 11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭,则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()f x 的图象关于直线2x π=对称,命题③正确;对于命题④,当0x π-<<时,sin 0x <,则()1sin 02sin f x x x=+<<, 命题④错误. 故答案为:②③. 4、【答案】B【解析】因为()sin()3f x x π=+,所以周期22T ππω==,故①正确;51()sin()sin 122362f ππππ=+==≠,故②不正确; 将函数sin y x =的图象上所有点向左平移3π个单位长度,得到sin()3y x π=+的图象, 故③正确. 故选:B. 5、【答案】BC【解析】由函数图像可知:22362T πππ=-=,则222T ππωπ===,所以不选A, 当2536212x πππ+==时,1y =-∴()5322122k k Z ππϕπ⨯+=+∈, 解得:()223k k ϕππ=+∈Z ,即函数的解析式为:2sin 22sin 2cos 2sin 236263y x k x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫=++=++=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.而5cos 2cos(2)66x x ππ⎛⎫+=-- ⎪⎝⎭ 故选:BC. 6、【答案】D 【解析】由22sin()()sin ()()cos()()cos x x x xf x f x x x x x-+----===--+-+,得()f x 是奇函数,其图象关于原点对称,排除A .又22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+,排除B ,C ,故选D . 7、【答案】C 【解析】()()()()sin sin sin sin ,f x x x x x f x f x -=-+-=+=∴为偶函数,故①正确.当ππ2x <<时,()2sin f x x =,它在区间,2π⎛⎫π ⎪⎝⎭单调递减,故②错误. 当0πx ≤≤时,()2sin f x x =,它有两个零点:0,π;当π0x -≤<时,()()sin sin f x x x =--2sin x =-,它有一个零点:π-,故()f x 在[],-ππ有3个零点:0-π,,π,故③错误.当[]()2,2x k k k *∈ππ+π∈N时,()2sin f x x =;当[]()2,22x k k k *∈π+ππ+π∈N时,()sin sin 0f x x x =-=,又()f x 为偶函数,()f x ∴的最大值为2,故④正确.综上所述,①④正确,故选C . 8、【答案】A【解析】作出因为sin ||y x =的图象如下图1,知其不是周期函数,排除D ; 因为cos cos y x x ==,周期为2π,排除C ;作出cos2y x =图象如图2,由图象知,其周期为π2,在区间(4π,2π)单调递增,A 正确; 作出sin 2y x =的图象如图3,由图象知,其周期为π2,在区间(4π,2π)单调递减,排除B ,故选A .图1图2图39、【答案】Df x在[0,2π]上有5个零点,可画出大致图象,【解析】①若()f x在(0,2π)有且仅有3个极大值点.故①正确;由图1可知,()f x在(0,2π)有且仅有2个或3个极小值点.故②错误;②由图1、2可知,()10、【答案】C【解析】∵()f x 为奇函数,∴(0)sin 0,=π,,0,f A k k k ϕϕ==∴∈∴=Z 0ϕ=; 又12π()sin,2π,122g x A x T ωω=∴==∴2ω=,又π()4g =2A =,∴()2sin 2f x x =,3π()8f =故选C. 11、【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ,所以2πππππ()326k k k +=+=-+∈Z ,ϕϕ,因为ππ22-<<ϕ,所以π0,.6k ==-ϕ【名师点睛】由对称轴得2πππππ()326k k k +=+=-+∈Z ,ϕϕ,再根据限制范围求结果.函数()sin y A x B =++ωϕ(A >0,ω>0)的性质:(1)max min ,y A B y A B =+=-+; (2)最小正周期2πT =ω;(3)由()ππ2x k k +=+∈Z ωϕ求对称轴; (4)由()ππ2π2π22k x k k -+≤+≤+∈Z ωϕ求增区间;由()π3π2π2π22k x k k +≤+≤+∈Z ωϕ求减区间.12、【答案】(1)π2θ=或3π2;(2)[1-.【解析】(1)因为()sin()f x x θθ+=+是偶函数,所以,对任意实数x 都有sin()sin()x x θθ+=-+, 即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+, 故2sin cos 0x θ=, 所以cos 0θ=. 又[0,2π)θ∈, 因此π2θ=或3π2. (2)2222ππππsin sin 124124y f x f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 213621cos 2sin 222222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭=+=-- ⎪ ⎪⎝⎭π123x ⎛⎫=+ ⎪⎝⎭.因此,函数的值域是[122-+.题型一 三角函数的性质1、【答案】B 【解析】因为2sin cos ()x x xf x ax+=, 所以22sin()cos()sin cos ()()x x x x x xf x f x ax ax ---+-==-=-, 因此函数()f x 为奇函数,又(2019)2f -=,所以(2019)(2019)2f f =--=-. 故选B 2、【答案】B 【解析】因为函数()()cos f x x ωϕ=+的最小正周期为π,所以22πωπ==,又对任意的x ,都使得()3f x f π⎛⎫≥ ⎪⎝⎭, 所以函数()f x 在3x π=上取得最小值,则223k πϕππ+=+,k Z ∈, 即2,3k k Z πϕπ=+∈,所以()cos 23f x x π⎛⎫=+ ⎪⎝⎭, 令222,3k x k k Z ππππ≤+≤+∈,解得,63k x k k Z ππππ-+≤≤+∈ ,则函数()y f x =在0,3π⎡⎤⎢⎥⎣⎦上单调递减,故a 的最大值是3π. 故选B3、【答案】B 【解析】()sin cos )4f x x x x π=+=+, 对A ,()f x ∴的最小正周期为2π,故A 错误;对B ,()42f ππ==()y f x ∴=图象的一条对称轴方程为4x π=,故B 正确;对C ,()f x 的最小值为,故C 错误; 对D ,由[0,]2x π∈,得3[,]444x πππ+∈,则()f x 在[0,]2π上先增后减,故D 错误. 故选:B . 4、【答案】B 【解析】()f x 的图象关于直线12x π=-对称,(0)()6f f π∴=-,即-1a =,则()sin 222sin 26f x x x x π⎛⎫=-=- ⎪⎝⎭,12()()4f x f x =-,1()2f x ∴=,2()2f x =-或1()2f x =-,2()2f x =,即1()f x ,2()f x 一个为最大值,一个为最小值, 则12||x x -的最小值为2T, T π=,12||x x ∴-的最小值为2π, 即12a x x -的最小值为2π.故选:B . 5、【答案】ACD 【解析】()sin 23f x x π⎛⎫=- ⎪⎝⎭的最小正周期为π,故π-也是其周期,故A 正确;()f x 的图像可由sin 2y x =的图像向右平移6π得到,故B 错误;()77()()sin sin 066323f f ππππππ⎛⎫+==-== ⎪⎝⎭,故C 正确; sin sin 17175()1262sin 132f πππππ⎛⎫⎛⎫⎛⎫-=== ⎪ =⎪ ⎪⎝⎭⎝⎭⎝⎭,故D 正确. 故选:ACD 6、【答案】4【解析】由题得12=,4,()42n n n Z ππωω⨯⨯∴=∈, 因为0>ω,所以ω的最小值等于4.故答案为:4 7、【答案】43. 【解析】由题意可得,32k k Z ππωπ⨯+=∈,求得22,3k k Z ω=-∈, 又0>ω,则ω的最小值为43, 故答案为:43. 8、【答案】. 1【解析】由题意,f ⎝⎛⎭⎫π6=2sin ⎝⎛⎭⎫2×π6+φ=±2,即sin ⎝⎛⎭⎫π3+φ=±1,又因为-π2<φ<π2, -π6<π3+φ<5π6,所以π3+φ=π2,即φ=π6,所以f(x)=2sin ⎝⎛⎭⎫2x +π6,f(0)=1.9、【答案】.32【解析】解法1:根据余弦函数的图像及性质,令ππωk x =-3,Z k ∈得ωππk x +=3,令23πωππ=+k 得k 232+=ω,Z k ∈,又因为0>ω,所以当0=k 时ω取得最小值为.32 解法2:由条件可得1)2(±=πf ,即1)32cos(±=-πωπ,则ππωπk =-32,Z k ∈,解得k 232+=ω,Z k ∈,又因为0>ω,所以当0=k 时ω取得最小值为.32解后反思:利用整体思想,结合三角函数的图像及性质是解决这类问题的关键!10、【答案】π3【解析】因为函数f(x)的一条对称轴是x =-512π,所以2×⎝⎛⎭⎫-5π12+φ=k π+π2,k ∈Z ,则φ=k π+4π3,k ∈Z ,又因为0≤φ<π,所以φ=π3.11、【答案】.3【解析】由相邻两条对称轴间的距离为π2,知其最小正周期T =2×π2=π,从而得ω=2πT =2ππ=2,又f(x)=2sin (2x +φ)的图像经过点⎝⎛⎭⎫π6,2,所以2sin ⎝⎛⎭⎫π3+φ=2,解得φ=2k π+π6(k ∈Z ),又因为0<φ<π,所以φ=π6,故f (x )=2sin ⎝⎛⎭⎫2x +π6,即有f ⎝⎛⎭⎫π4=2sin 2π3= 3.题型二 三角函数图像的变换1、【答案】A 【解析】不妨设函数2y sin x =的图象沿横轴所在直线平移ϕ个单位后得到函数23y sin x π⎛⎫=+⎪⎝⎭的图象. 于是,函数2y sin x =平移ϕ个单位后得到函数,sin 2()y x ϕ=+,即sin(22)y x ϕ=+, 所以有223k πϕπ=+,6k πϕπ=+,取0k =,6π=ϕ.答案为A . 2、【答案】D 【解析】把cos 2y x =的图象向左平移4π个单位长度,得cos 2()cos(2)sin 242y x x x ππ=+=+=-的图象,再把所得图象各点的横坐标变为原来的12倍,纵坐标不变,得图象的函数式为sin(22)sin 4y x x =-⨯=-, sin 42sin 2cos 2()cos 2y x x x f x x =-=-=,∴()2sin 2f x x =-,∴()2sin63f ππ=-=.故选:D. 3、【答案】C【解析】由题意知,3()cos(2)sin(2)44g x x x ππ=+=+,其图像向左平移a 个单位得到函数3()sin(22)4f x x a π=++, 而函数()πsin 23f x x ⎛⎫=+⎪⎝⎭,所以有32243a k πππ+=+5224a k ππ=-+,取1k =得1924a π=.答案选C.4、【答案】D【解析】因为函数()()f x sin ωx φ=+的最小正周期是π,所以2ππω=,解得ω2=,所以()()f x sin 2x φ=+, 将该函数的图像向右平移π6个单位后,得到图像所对应的函数解析式为ππy sin 2x φsin 2x φ63⎡⎤⎛⎫⎛⎫=-+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 由此函数图像关于直线πx 2=对称,得: πππ2φk π232⨯+-=+,即πφk π,k Z 6=-∈,取k 0=,得πφ6=-,满足πφ2<,所以函数()f x 的解析式为()πf x sin 2x 6⎛⎫=- ⎪⎝⎭,故选D. 5、【答案】ACD【解析】由题:()22cos cos(2)1cos 2sin 2)24f x x x x x x ππ=-+-=+=+,由2y x =的图象向左平移8π个单位,得到)))84y x x ππ=+=+,所以选项A 正确;令222,242k x k k Z πππππ-≤+≤+∈,得其增区间为3[,],88k k k Z ππππ-+∈ ()f x 在(0,)8π单调递增,在(,)82ππ单调递减,所以选项B 不正确;解()0,2,4f x x k k Z ππ=+=∈,得:,28k x k Z ππ=-∈,[0,]x π∈, 所以x 取37,88ππ,所以选项C 正确;3[,0],2[,],sin(2)[1,244442x x x πππππ∈-+∈-+∈-,()[f x ∈, 所以选项D 正确. 故选:ACD6、【答案】ABD【解析】函数()sin 23f x x π⎛⎫=+⎪⎝⎭的图像向右平移2π个单位长度得到()ππsin 223g x x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦2πsin 23x ⎛⎫=- ⎪⎝⎭.由于7π7π2ππsin sin 112632g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,故7π12x =是()g x 的对称轴,B 选项正确. 由于π2π2πsin sin 00333g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,故,03π⎛⎫ ⎪⎝⎭是()g x 的对称中心,D 选项正确.由π2ππ2232x -≤-≤,解得π7π1212x ≤≤,即()g x 在区间π7π,1212⎡⎤⎢⎥⎣⎦上递增,故A 选项正确、C 选项错误. 故选:ABD.7、【答案】-2【解析】根据图形可得直线y =a(x +2)与函数y =-cos x 的图像相切于点(x 4,-cos x 4),其中x 4∈⎝⎛⎭⎫π4,π.因为y =sin x ,由导数的几何意义可得a =sin x 4=-cos x 4-0x 4+2,化简得x 4+1tan x 4=-2.8、【答案】12【解析】将函数f (x )=sin (ωx 6π-)(ω>0)的图象向左平移3π个单位后,可得函数y =sin (ωx 36πωπ+-)的图象,再根据所得图象关于直线x =π对称,可得ωπ36πωπ+-=k π2π+,k ∈Z , ∴当k =0时,ω取得最小值为12,故答案为12.题型三 三角函数的解析式1、【答案】D【解析】因为函数()2sin(2)f x x ϕ=+的图象过点,26A π⎛⎫ ⎪⎝⎭, 所以2sin 23πϕ⎛⎫+=⎪⎝⎭,因此2,32k k Z ππϕπ+=+∈, 所以2,6k k Z πϕπ=+∈, 因此()2sin(2)2sin 222sin 266f x x x k x ππϕπ⎛⎫⎛⎫=+=++=+ ⎪ ⎪⎝⎭⎝⎭; A 选项,把()y f x =的图象向右平移6π个单位得到函数2sin 26y x π⎛⎫=-⎪⎝⎭的图象,故A 错; B 选项,由3222,262k x k k Z πππππ+≤+≤+∈得2,63k x k k Z ππππ+≤≤+∈,即函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的单调递减区间是:2,,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦,故B 错; C 选项,由()2sin 206f x x π⎛⎫=+= ⎪⎝⎭得2,6x k k Z ππ+=∈,即,122k x k Z ππ=-+∈, 因此[]0,2x π∈,所以5111723,,,12121212x ππππ=,共四个零点,故C 错; D 选项,因为0,3x π⎡⎤∈⎢⎥⎣⎦,所以52,666x πππ⎡⎤+∈⎢⎥⎣⎦,因此1sin 2,162x π⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦,所以[]2sin 21,26x π⎛⎫+∈ ⎪⎝⎭,即()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的最小值为1,故D 正确; 故选:D.2、【答案】(1)()sin(2)6g x x π=-;(2)[1,2]-.【解析】 (1)由函数()f x 取得最大值1,可得1A =,函数过10,2⎛⎫ ⎪⎝⎭得12sin φ=,,26ππφφ<= 12,6662f k k Z ππππωπ⎛⎫=⇒+=+∈ ⎪⎝⎭,∵04ω<<,∴2ω= ()26f x sin x π⎛⎫=+ ⎪⎝⎭,()266g x f x sin x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭.(2) ()22226h x x cos x sin x π⎛⎫=+=+ ⎪⎝⎭, 710,,2,21266626x x sin x πππππ⎡⎤⎛⎫∈≤+≤-≤+≤ ⎪⎢⎥⎣⎦⎝⎭, 12226sin x π⎛⎫-≤+≤ ⎪⎝⎭,值域为[]1,2-.。
高中数学三角函数函数yasin(ωxφ)的图象与性质函数y=asin(ωx+φ)的图象与性质

跟踪演练 1 要得到 y=cos2x-π4的图象,只要将 y=sin 2x 的
图象( )
A.向左平移π8个单位
B.向右平移π8个单位
C.向左平移π4个单位
D.向右平移π4个单位
第十二页,共三十页。
解析 y=sin 2x=cosπ2-2x=cos2x-π2 =cos2x-π4=cos2x-π8-π4 若设 f(x)=sin 2x=cos 2x-π8-π4, 则 fx+π8=cos2x-π4,∴向左平移π8个单位.
第二十七页,共三十页。
(2)y=sin x―周―期―变―换→y=sin ωx―相―位―变―换→
y=sin[ω(x+ωφ )]=sin(ωx+φ)―振―幅―变―换→
y=Asin(ωx+φ). 注意:两种途径的变换顺序不同,其中变换的量也有所不同: (1)是先相位变换后周期变换,平移|φ|个单位.(2)是先周期变换 后相位变换,平移|ωφ|个单位.
指出其变换步骤.
第二页,共三十页。
1 预习(yùxí)导学
实
2 课堂(kètáng)讲义
3 当堂(dānɡ tánɡ)检测
功
第三页,共三十页。
挑战自我,点点落
重点难点,个个击破 当堂训练,体验成
[知识(zhī shi)链接]
1.“五点法”作图 画正弦函数 y=sin x,x∈[0,2π]的图象,五个关键点是 (0,0), π2,1,(π,0),32π,-1,(2π,0) .
第二十六页,共三十页。
课堂(kètáng)小结
1.由y=sin x的图象,通过变换可得到函数y=Asin(ωx+φ)(A>0,ω>0)
的图象,其变化(biànhuà)途径有两条:
(1)y=sin x―相―位―变―换→y=sin(x+φ)―周―期―变―换→ y=sin(ωx+φ)―振―幅―变―换→y=Asin(ωx+φ).
高中数学:“剖析”函数y=asin(wxφ)的图像及性质

高中数学:“剖析”函数y=asin(wxφ)的图像及性质“老师,为什么我用五点法作图,总是会出错呢?不是这里错,就是那里错!”“老师,我觉得在高中数学函数y=Asin(wx+φ)中,函数图像的变化是最容易错的,很多时候我都把几倍的变换弄成是几分之一的变换,真是头都大了!”“老师,有的题目稍微复杂一点,我就连解析式都求不出来了。
”……在高中数学中,函数y=Asin(wx+φ)的相关知识确实是很难,不仅要考虑的东西非常多,而且很多知识点都非常容易弄错。
在本省重点中学从事高中数学教学13年,教学实践还算是有些丰富,一直以来,这个知识点都是同学们最大的难点,我总是会话最多的时间去讲评、去给同学们做练习。
但是,同学们的吸收效率还是非常不理想,于是,我就自己花时间去总结。
学过这个内容的同学都知道,这个知识点的复杂以及考题的多变,很多时候类似的题目,同学们的答题效果也是非常不理想。
为了帮助同学们更好的学习,让同学们掌握方法才是关键,我自己抽出时间来总结了这个知识点。
我总结出了高中数学中国年y=Asin(wx+φ)的三个考点,并且选择了典型的例子给同学们讲解。
高中数学中,y=Asin(wx+φ)的考题变幻无常,同学们看了我举的例子以后一定要自己在做一些练习,强化一下,相信同学们一定会有所进步的。
一、用“五点法”作函数y=Asin(wx+φ)(A>0,W>0)的图像。
五点,及最高点、最低点以及与坐标轴的三个交点,凭这五点,即可完成一个函数图像的绘制。
这是解答函数题目的一个非常重要的步骤,考得最多。
二、三角函数图象的变换。
在高中数学中,函数图像的变换也是非常常考的点,在这一部分,同学们一定要分清楚w和φ不同倍数时的纵坐标和横坐标的变化。
三、函数y=Asin(wx+φ)的物理意义。
在高中数学的函数中,y=Asin(wx+φ)的物理意义比较简单,主要就是考它的周期和振幅、频率及相位。
以上三个就是高中数学中,函数y=Asin(wx+φ)的考点,同学们一定要把这3点吃透,这样在考试之中也会轻松很多。
函数y=Asinωxφ的图象

2023函数y=asinωxφ的图象pptcontents •函数y=asinωxφ的简介•函数y=asinωxφ的图象•函数y=asinωxφ的应用•其他类型的三角函数图象•对于学习函数的建议目录01函数y=asinωxφ的简介1asinωxφ的定义与性质23asinωxφ是正弦型函数,其中ω和φ是常数。
asinωxφ的定义域为x ∈ (-∞,+∞),值域为y ∈ [-1,1]。
函数y=asinωxφ的周期为2π/ω。
数学表达式为y=asin(ωx+φ),其中a为振幅,ω为角频率,φ为初相。
表达式中的ωx+φ表示将自变量x乘以角频率ω,再加上初相φ。
函数y=asinωxφ的数学表达式当a>1时,函数y=asinωxφ的图象呈现振幅较大的正弦型曲线。
当a<1时,函数y=asinωxφ的图象呈现振幅较小的正弦型曲线。
当a=1时,函数y=asinωxφ的图象呈现标准的正弦型曲线。
当ω>1时,函数y=asinωxφ的图象呈现周期较小的正弦型曲线。
当0<ω<1时,函数y=asinωxφ的图象呈现周期较大的正弦型曲线。
函数y=asinωxφ的图象及性质02函数y=asinωxφ的图象图形描述函数$y=asin\omega x\varphi$的图象是一个正弦曲线,随着$\omega$的增大,曲线的振幅逐渐增大,周期逐渐减小。
变化趋势当$x$逐渐增大时,$y$的值先逐渐增大,到达最大值后逐渐减小,当$y$达到最小值时,$x$的值也达到最大值。
函数y=asinωxφ的图象及变化趋势周期性定义函数$y=asin\omega x\varphi$的图象呈现周期性变化,周期是$\frac{2\pi}{\omega}$。
周期性变化每个周期内的图形完全相同,只是相位相差$\frac{\pi}{\omega}$,随着$x$增大,相位逐渐增大,新的周期逐渐开始。
函数y=asinωxφ的周期性变化函数$y=asin\omega x\varphi$的最大值是$1$,最小值是$-1$。
函数y=Asin(wx+φ)的图象与性质(图文运用)

函数sin()(0,0)y A x A ωϕω=+>>的图象【学习目标】1、理解sin()(0,0)y A x A ωϕω=+>>函数中,,A ωϕ的涵义;2、能根据sin()(0,0)y A x A ωϕω=+>>的部分图象求出其中的参数,并能简单应用;3、渗透数形结合思想,一题多解、一题多变思想. 【学习重点】三角函数的图形变换及相关题型的求解. 【学习难点】已知图形求参数,其中参数φ的求解. 一、自主学习1、若函数sin()(0,0)y A x A ωϕω=+>>表示一个振动量,则这个振动的振幅为 , 周期为 ,初相为 ,频率为 ,相位为 .2、“五点法”作图“五点法”作sin()y A x ωϕ=+的简图,主要是通过变量代换,设z x ωϕ=+由z 取 , , , , 来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象.2、平移变换:由函数sin y x =的图象经怎样的变换可得到函数sin()y x b ϕ=++的图象? . 3、伸缩变换:(纵向伸缩)由函数sin y x =的图象经怎样的变换可得到函数sin (0)y A x A =>的图象? . 4、伸缩变换:(横向伸缩)由函数sin y x =的图象经怎样的变换可得到函数sin (0)y x ωω=> 的图象? . 5、函数sin y x =象到函数sin()(0,0)y A x A ωϕω=+>>的图象变换.得到sin()y x ωϕ=+的图象得到sin()y x ϕ=+的图象画出sin y x =的图象得到sin()y A x ωϕ=+的图得到sin()y x ωϕ=+的图象得到sin y x ω=的图象画出sin y x =的图象得到sin()y A x ωϕ=+的图6、如何根据条件求函数sin()(0,0)y A x A ωϕω=+>>的解析式?二、课前热身 1、函数2sin(3)7y x π=+的振幅是 ,相位是 ,初相是 ,周期是 .2、为了得到函数R x x y ∈+=),3cos(的图象,只需把余弦曲线上所有的点向 (左或右)平行移动 个单位长度. 3、要得到函数sin(2)3y x π=-的图象,只要sin 2y x =的图象向 (左或右)平行移动个单位长度.4、把函数sin(2)6y x π=+的图象向右平移3π个单位后,所得图象对应函数解析式为 .5、要得到函数sin()26x y π=-+的图象,可由sin()2xy =-的图象向 (左或右)平行移动 个单位长度.6、把函数sin y x =的图象上所有的点的纵坐标变为原来的13倍(横坐标不变)所得图象的解析式为 .7、将函数sin y x =的图象上所有点向左平移3π个单位长度,再把所得图象上各点横坐标变为原来的5倍,则最后所得图象的解析式为 .三、典型例题分析例1、作出函数3sin(2),3y x x R π=+∈的简图,说明它与sin y x =图象之间的关系.变式练习:已知函数13sin()24y x π=-(1)用五点法作出函数的图象;(2)说明它由sin y x =图象经过怎么样的变化得到的;(3)求此函数的振幅、周期和初相;(4)求此函数的对称轴、对称中心坐标。
2023年高考数学微专题练习专练20函数y=Asinωx φ的图像及三角函数模型含解析理

专练20 函数y =A sin (ωx +φ)的图像及三角函数模型命题范围:三角函数的解析式、三角函数的图像变换.[基础强化]一、选择题1.要得到函数y =sin (4x -π3)的图像,只需将函数y =sin4x 的图像( )A .向左平移π12个单位B .向右平移π12个单位C .向左平移π3个单位D .向右平移π3个单位2.把函数y =cos2x +1的图像上所有的点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是( )3.将函数y =sin (2x +π5)的图像向右平移π10个单位长度,所得图像对应的函数( )A .在区间⎣⎢⎡⎦⎥⎤-π4,π4上单调递增B .在区间⎣⎢⎡⎦⎥⎤-π4,0上单调递减C .在区间⎣⎢⎡⎦⎥⎤π4,π2上单调递增D .在区间⎣⎢⎡⎦⎥⎤π2,π上单调递减 4.函数y =A sin (ωx +φ)的部分图像如图所示,则( ) A .y =2sin (2x -π6)B .y =2sin (2x -π3)C .y =2sin (x +π6)D .y =2sin (x +π3)5.[2022·江西省南昌市第十中学月考]将函数y =sin2x +3cos2x 的图像沿x 轴向左平移φ(φ>0)个单位后,得到关于y 轴对称的图像,则φ的最小值为( )A .π12B .π6C .π4D .5π12 6.函数y =2sin (ωx +φ)(ω>0,-π2<φ<π2)的部分图像如图所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π37.[2021·全国乙卷]把函数y =f (x )图像上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得曲线向右平移π3个单位长度,得到函数y =sin (x -π4)的图像,则f (x )=( )A.sin (x 2-7π12)B.sin (x 2+π12)C.sin (2x -7π12)D.sin (2x +π12)8.已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是( )A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 29.[2022·安徽省示范高中皖北协作区联考]将函数f (x )=2sin (2x -π3)的图像向右平移π6个单位后所得到的函数记为g (x ),则下列结论中正确的是( )A .g (x )的对称中心为(k π2+π6,0)(k ∈Z )B .g (x )=2sin (2x +π3)C .g (x )在(π12,7π12)上单调递减D .g (x )的图像关于x =π12对称二、填空题 10.已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)的一段图像如图所示,则函数f (x )的解析式为f (x )=________.11.[2022·南昌市模拟]已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π2)的图像与x 轴在原点右侧的第一个交点为(1,0),在y 轴右侧的第一个最高点为(3,2),则f (-1)=________.12.将函数f (x )=sin (ωx +φ)(ω>0,-π2≤φ<π2)图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π6个单位长度得到y =sin x 的图像,则f (π6)=________.[能力提升]13.[2022·安徽芜湖模拟]已知函数f (x )=A cos (ωx +φ)+b (A >0,ω>0,|φ|<π2)的大致图像如图所示,将函数f (x )的图像上点的横坐标拉伸为原来的3倍后,再向左平移π2个单位长度,得到函数g (x )的图像,则函数g (x )的单调递增区间为( )A .[-3π2+3k π,3k π](k ∈Z )B .[3k π,3k π+3π2](k ∈Z )C.[-7π4+3k π,-π4+3k π](k ∈Z )D .[-π4+3k π,5π4+3k π](k ∈Z )14.[2022·陕西省西安中学模拟]已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)的部分图像如图所示,现将f (x )的图像向左平移π12个单位长度得到y =g (x )的图像,则方程2g (x )=2在[0,2π]上实数解的个数为( )A .5B .6C .7D .815.[2022·西南大学附中模拟]水车在古代是进行灌溉引水的工具,亦称“水转筒车”,是一种以水流作动力,取水灌田的工具.据史料记载,水车发明于隋而盛于唐,距今已有1000多年的历史,是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为R 的水车,一个水斗从点A (3,-33)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.经过t 秒后,水斗旋转到P 点,设点P 的坐标为(x ,y ),其纵坐标满足y =f (t )=R sin (ωt +φ)(t ≥0,ω>0,|φ|<π2),则下列叙述正确的是( )A .水斗作周期运动的初相为-π6B .在水斗开始旋转的60秒(含)中,其高度不断增加C .在水斗开始旋转的60秒(含)中,其最高点离平衡位置的纵向距离是3 3D .当水斗旋转100秒时,其和初始点A 的距离为616.[2022·全国甲卷(理),11]设函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π3在区间(0,π)恰有三个极值点、两个零点,则ω的取值范围是( )A .⎣⎢⎡⎭⎪⎫53,136B .⎣⎢⎡⎭⎪⎫53,196C .⎝ ⎛⎦⎥⎤136,83D .⎝ ⎛⎦⎥⎤136,196 专练20 函数y =A sin (ωx +φ)的 图像及三角函数模型1.B ∵y =sin (4x -π3)=sin ⎣⎢⎡⎦⎥⎤4(x -π12),∴要得到y =sin (4x -π3)的图像,只需将y =sin4x 的图像向右平移π12个单位.2.A y =cos2x +1――→横坐标伸长2倍纵坐标不变y =cos x +1――→向左平移1个单位长度y =cos (x +1)+1――→向下平移1个单位长度y =cos (x +1).函数图像过(π2-1,0),结合选项可知,选A.3.A 将y =sin (2x +π5)的图像向右平移π10个单位长度,得到y =sin ⎣⎢⎡⎦⎥⎤2(x -π10)+π5=sin2x ,令2k π-π2≤2x ≤2k π+π2(k ∈Z ),得k π-π4≤x ≤k π+π4(k ∈Z ),∴y =sin2x在⎣⎢⎡⎦⎥⎤k π-π4,k π+π4(k ∈Z )上单调递增,当k =0时,得到y =sin2x 的一个单调增区间为⎣⎢⎡⎦⎥⎤-π4,π4,故A 正确,B 不正确,由2k π+π2≤2x ≤2k π+32π(k ∈Z ),得y =sin2x 的单调减区间为⎣⎢⎡⎦⎥⎤k π+π4,k π+34π(k ∈Z ),结合选项可知C 、D 不正确.4.A 由图知A =2,T 2=π3-(-π6)=π2,∴T =π,∴ω=2.将(π3,2)坐标代入,得2×π3+φ=2k π+π2,k ∈Z ,∴φ=2k π-π6,k ∈Z .取k =0,得φ=-π6.5.A ∵函数y =sin2x +3cos2x =2sin (2x +π3),将函数y =sin2x +3cos2x 的图像沿x 轴向左平移φ个单位后,得到函数y =2sin (2x +2φ+π3),因为函数是偶函数,∴2φ+π3=k π+π2(k ∈Z )∴φ=k π2+π12(k ∈Z ).当k =0时,φ=π12.则φ的最小值为π12.6.A 由题意得512π+π3=34T ,∴T =π,又T =2πω,∴ω=2,又当x =512π时,2sin (2×512π+φ)=2,∴φ=-π3+2k π(k ∈Z ),又-π2<φ<π2,∴φ=-π3.7.B 依题意,将y =sin ⎝⎛⎭⎪⎫x -π4的图像向左平移π3个单位长度,再将所得曲线上所有点的横坐标扩大到原来的2倍,得到f (x )的图像,所以y =sin ⎝⎛⎭⎪⎫x -π4将其图像向左平移π3个单位长度→y =sin ⎝⎛⎭⎪⎫x +π12的图像――→所有点的横坐标扩大到原来的2倍f (x )=sin ⎝⎛⎭⎪⎫x 2+π12的图像.8.D y =sin (2x +2π3)=cos (2x +2π3-π2)=cos (2x +π6)=cos ⎣⎢⎡⎦⎥⎤2(x +π12),由y =cos x 的图像得到y =cos2x 的图像,需将曲线C 1上各点的横坐标缩短到原来的12,纵坐标不变;由y =cos2x 的图像得到y =cos ⎣⎢⎡⎦⎥⎤2(x +π12)的图像,需将y =cos2x 的图像上的各点向左平移π12个单位长度,故选D.9.D 函数f (x )=2sin (2x -π3)的图像向右平移π6个单位得到g (x )=2sin [2(x -π6)-π3]=2sin (2x -2π3), g (x )=2sin (2x -2π3)=2sin (2x +π3-π)=-2sin (2x +π3),B 选项错误. 2x +π3=k π,x =k π2-π6,所以g (x )的对称中心为(k π2-π6,0)(k ∈Z ),A 选项错误.π12<x <7π12,π6<2x <7π6,π2<2x +π3<3π2,所以g (x )=-2sin (2x +π3)在(π12,7π12)上递增,C 选项错误.g (π12)=-2sin (π6+π3)=-2sin π2=-2,所以g (x )的图像关于x =π12对称,D 选项正确.10.2sin (2x +3π4)解析:由题图可知,f (x )max =2,f (x )min =-2, 故A =2, 最小正周期T =2×⎣⎢⎡⎦⎥⎤3π8-(-π8)=π,故ω=2ππ=2,所以f (x )=2sin (2x +φ). 又曲线y =f (x )过点(-π8,2),所以2sin ⎣⎢⎡⎦⎥⎤2×(-π8)+φ=2, 即φ-π4=π2+2k π,k ∈Z .又|φ|<π,所以φ=3π4.故函数f (x )的解析式为f (x )=2sin (2x +3π4).11.-2解析:由与x 轴在原点右侧的第一个交点为(1,0),在y 轴右侧的第一个最高点为(3,2)知T 4=3-1,T =8,或3T 4=3-1,T =83,当T =8时,ω=2πT =π4,A =2,∴f (x )=2sin (π4x +φ),代入点(1,0),2sin (π4+φ)=0,又|φ|<π2,∴φ=-π4,f (x )=2sin (π4x -π4),f (-1)=-2;当T =83时,ω=2πT =3π4,A =2,∴f (x )=2sin (3π4x +φ),代入点(1,0), 2sin (3π4+φ)=0,又|φ|<π2,∴φ=π4,f (x )=2sin (3π4x +π4),f (-1)=-2.综上,f (-1)=-2. 12.22解析:由题意得将y =sin x 的图像向左平移π6个单位,得到y =sin (x +π6),再纵坐标不变,横坐标伸长为原来的2倍,得到y =sin (12x +π6),即f (x )=sin (12x +π6),∴f (π6)=sin π4=22.13.C 依题意,⎩⎪⎨⎪⎧A +b =1,-A +b =-3,解得⎩⎪⎨⎪⎧A =2,b =-1,故f (x )=2cos (ωx +φ)-1, 而f (π12)=1,f (π3)=-1,∴T 4=π3-π12=π4, 故T =π=2πω,则ω=2;∴2cos (π6+φ)-1=1,故π6+φ=2k π(k ∈Z ), 又|φ|<π2,故φ=-π6,∴f (x )=2cos (2x -π6)-1;将函数f (x )的图像上点的横坐标拉伸为原来的3倍后, 得到y =2cos (23x -π6)-1,再向左平移π2个单位长度,得到g (x )=2cos (23x +π3-π6)-1=2cos (23x +π6)-1,令-π+2k π≤23x +π6≤2k π(k ∈Z ),故-7π4+3k π≤x ≤-π4+3k π(k ∈Z ),故函数g (x )的单调递增区间为[-7π4+3k π,-π4+3k π](k ∈Z ). 14.B 根据函数f (x )=A sin (ωx +φ),(A >0,ω>0,|φ|<π)的部分图像, 可得12·2πω=11π12-7π12,∴ω=3.所以f (x )=A sin (3x +φ),结合五点法作图,3×7π12+φ=2π+2k π,k ∈Z ,∴φ=π4+2k π,k ∈Z ,因为|φ|<π,∴φ=π4,故f (x )=A sin (3x +π4).再把点(π2,-1)代入,可得-1=A sin ⎝ ⎛⎭⎪⎫3π2+π4,即-1=-A cos π4,∴A =2,所以f (x )=2sin (3x +π4).现将f (x )的图像向左平移π12个单位长度,得到函数y =g (x )=2sin [3(x +π12)+π4]=2cos3x ,因为2g (x )=2,即cos3x =12,所以3x =π3+2k 1π,k 1∈Z 或3x =-π3+2k 2π,k 2∈Z ,解得x =π9+2k 1π3,k 1∈Z 或x =-π9+2k 2π3,k 2∈Z ,因为x ∈[0,2π],所以x =π9或7π9或13π9或5π9或11π9或17π9, 故方程2g (x )=2在[0,2π]上实数解的个数为6个. 15.D 由A (3,-33), 知R =32+(-33)2=6, 又T =120,所以ω=2πT =π60.当t =0时,点P 在点A 位置,有-33=6sin φ, 解得sin φ=-32, 又|φ|<π2,所以φ=-π3,故A 错误;可知f (t )=6sin (π60t -π3),当t ∈(0,60]时,π60t -π3∈(-π3,2π3],所以函数f (t )先增后减,故B 错误; 当t ∈(0,60]时,π60t -π3∈(-π3,2π3],sin (π60t -π3)∈(-32,1], 所以点P 到x 轴的距离的最大值为6,故C 错误;11 当t =100时,π60t -π3=4π3, P 的纵坐标为y =-33,横坐标为x =-3,所以|PA |=|-3-3|=6,故D 正确.16.C 因为f (x )=sin ⎝⎛⎭⎪⎫ωx +π3,结合选项,只考虑ω>0.当ωx +π3=π2+k π(k ∈Z ),即x =π6ω+k πω(k ∈Z )时,f (x )取得极值.又因为f (x )在区间(0,π)上恰有三个极值点,所以⎩⎪⎨⎪⎧π6ω+2πω<π,π6ω+3πω≥π,解得136<ω≤196.当ωx +π3=k π(k ∈Z ),即x =-π3ω+k πω(k ∈Z )时,f (x )=0.又因为f (x )在区间(0,π)上恰有两个零点,所以⎩⎪⎨⎪⎧-π3ω+2πω<π,-π3ω+3πω≥π,解得53<ω≤83.综上可得,ω的取值范围是⎝ ⎛⎦⎥⎤136,83.故选C.。
函数y=Asin(wx+φ)的图象与性质练习题

函数y=Asin(wx+φ)的图象与性质练习题函数y =A sin(ωx +?)的图象及应⽤1.满⾜sin(x-4π)≥21的x 的集合是()A .?∈+≤≤+Z k k x k x ,121321252|ππππB .∈+≤≤-Z k k x k x ,1272122|ππππC .?∈+≤≤+Z k k x k x ,65262|ππππD .∈+≤≤Z k k x k x ,622|πππ∪?∈+≤≤+Z k k x k x ,)1(2652|πππ2.要得到函数cos(21)y x =+的图象,只要将函数cos 2y x =的图象() A. 向左平移1个单位 B. 向右平移1个单位 C. 向左平移12 个单位 D.向右平移 12个单位3、函数y =cos x 的图象向左平移3π个单位,横坐标缩⼩到原来的12,纵坐标扩⼤到原来的3倍,所得的函数图象解析式为 ( ) (A) y =3cos(12x +3π) (B) y =3cos(2x +3π) (C) y =3cos(2x +23π) (D) y =13cos(12x +6π)4.已知函数f (x )=sin ?ωx +π3(ω>0)的最⼩正周期为π,则该函数的图象( )A .关于点? ??π3,0对称 B .关于直线x =π4对称C .关于点? ??π4,0对称 D .关于直线x =π3对称5、下列函数中,图像的⼀部分如右图所⽰的是(A )sin()6y x π=+ (B )sin(2)6y x π=- (C )cos(4)3y x π=- (D )cos(2)6y x π=-6、函数y =2sin(ωx +φ),|φ|<2π的图象如图所⽰,则 ((A) ω=1011,φ=6π(B) ω=1011,φ= -6π(C) ω=2,φ=6π (D) ω=2,φ= -6π 7、(2010·福建卷)将函数f (x )=sin(ωx +φ)的图象向左平移π2个单位,若所得图象与原图象重合,则ω的值不可能等于( )A .4B .6C .8D .128、函数y =xsin x,x ∈(-π,0)∪(0,π)的图象可能是下列图象中的( )9.函数y=-xcosx 的部分图像是()C10、锐⾓△ABC 中,sinA 和cosB 的⼤⼩关系是() A 、sinA=cosB B 、sinA <cosB C 、sinA >cosB D 、不能确定11、若A 、B 是锐⾓△ABC 的两个内⾓,则点P (cosB ﹣sinA ,sinB ﹣cosA )在()A 、第⼀象限B 、第⼆象限C 、第三象限D 、第四象限12、下列函数中,在[0,]内是增函数且以π为最⼩正周期的函数是()A 、y=|sinx|B 、y=tan2xC 、y=sin2xD 、y=cos4x13.)32sin(3π+-=x y 的振幅为初相为14、函数y =sin2x 的图象向右平移φ(φ>0)个单位,得到的图象恰好关于直线x =6π对称,则φ的最⼩值是 .15.把函数y=cos(x+34π)的图象向右平移φ个单位,所得的图象正好关于y 对称,则φ的最⼩正值为10.)32sin(3π+-=x y 的振幅为初相为16.已知函数f (x )=sin(ωx +φ)? ?ω>0,-π2≤φ≤π2的图象上的两个相邻的最⾼点和最低点的距离为22,则ω=________.17.已知函数f (x )=3sin ? ?ωx -π6(ω>0)和g (x )=2cos(2x +φ)+1的图象的对称轴完全相同.若x ∈?0,π2,则f (x )的取值范围是________.18、已知函数y =A sin(ωx +φ)(A >0,ω>0)的图象过点P π12,0,图象上与点P 最近的⼀个最⾼点是Qπ3,5. (1)求函数的解析式; (2)指出函数的增区间; (3)求使y ≤0的x 的取值范围.19.函数f (x )=A sin(ωx +φ)? ?A >0,ω>0,0<φ<π2的部分图象如图所⽰.(1)求f (x )的解析式;(2)设g (x )=f ?x -π122,求函数g (x )在x ∈-π6,π3上的最⼤值,并确定此时x 的值.。
6.3 函数y=Asin(wx+φ)的图象与性质

13.已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( )
A. 1B.2C.1/2D. 1/3
14.把函数 ( )的图象上所有点向左平行移动 个单位长度,
再把所得图象上所有点的横坐标缩短到原来的 倍(纵坐标不变),得到的
归纳2:函数y = Asin(wx+),(A>0,w>0)的图像可以看作是先把y = sinx的图像上所有的点向左(>0)或向右(>1)平移||个单位,再把所得各点的横坐标缩短(w>1)或伸长(0<w<1)到原来的 倍(纵坐标不变),再把所得各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍,(横坐标不变)。即:平移变换→周期变换→振幅变换。
例1:作函数y = 3sin(2x+ )的简图。
例2.函数y=Asin(wx+)(A>0,w>0)图像和函数y=sinx图像的关系。
归纳1:先把函数y = sinx的图像上的所有点向左平行移动 个单位,得到y=sin(x+ )的图像,再把y = sin(x + )的图像上所有的点的横坐标缩短到原来的 倍(纵坐标不变),得到y= sin(2x + )的图像,再把y = sin(2x + )的图像上所有的点的纵坐标伸长到原来的3倍(横坐标不变),从而得到y = 3sin(2x + )图像。
9.画出下列函数在长度为一个周期的闭区间上的简图
(1) (2) ;
(3) (4)
10.为了得到函数 的图象,只需把余弦曲线上所有的点( )
高考 函数y=Asin (ωx+φ)的图像及三角函数模型的简单应用 详解

函数y =A sin (ωx +φ)的图像及三角函数模型的简单应用A 组 基础必做1.把函数y =sin x 的图像上所有点的横坐标缩小到原来的一半,纵坐标保持不变,再把所得函数图像向左平移π4个单位,得到的函数图像的解析式是( )A .y =cos 2xB .y =-sin 2xC .y =sin ⎝ ⎛⎭⎪⎫2x -π4D .y =sin ⎝ ⎛⎭⎪⎫2x +π4解析 由y =sin x 图像上所有点的横坐标缩小到原来的一半,纵坐标保持不变,所得图像的解析式为y =sin 2x ,再向左平移π4个单位得y =sin 2x +π4,即y =cos 2x 。
答案 A2.(2016·上饶模拟)已知函数y =A cos ⎝⎛⎭⎪⎫π2x +φ(A >0)在一个周期内的图像如图所示,其中P ,Q 分别是这段图像的最高点和最低点,M ,N 是图像与x 轴的交点,且∠PMQ =90°,则A 的值为()A. 3B. 2 C .1D .2解析 依题意QM =QN =12PQ ,又∠PMQ =90°,可得△MNQ 是等边三角形,又由于MN 等于半个周期长,MN =12×2ππ2=2。
所以A=32×2=3。
答案 A3.为了得到函数y =sin 3x +cos 3x 的图像,可以将函数y =2cos 3x 的图像( )A .向右平移π4个单位 B .向左平移π4个单位 C .向右平移π12个单位D .向左平移π12个单位解析 y =sin 3x +cos 3x =2cos ⎝ ⎛⎭⎪⎫3x -π4=2cos ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫x -π12,因此需将函数y =2cos 3x 的图像向右平移π12个单位。
故选C 。
答案 C4.(2016·青岛模拟)函数f (x )=A sin(ωx +φ)其中A >0,|φ|<π2的图像如图所示,为了得到g (x )=sin 2x 的图像,则只需将f (x )的图像( )A .向右平移π6个长度单位 B .向左平移π6个长度单位 C .向右平移π3个长度单位 D .向左平移π3个长度单位解析 由已知中函数f (x )=A sin(ωx +φ)的图像过点⎝ ⎛⎭⎪⎫π3,0和点⎝ ⎛⎭⎪⎫7π12,-1,易得:A =1,T =4⎝ ⎛⎭⎪⎫7π12-π3=π,即ω=2,即f (x )=sin(2x +φ),将点⎝ ⎛⎭⎪⎫7π12,-1代入可得,7π6+φ=3π2+2k π,k ∈Z 。
高考数学专题复习:函数y=Asin(ωx+φ)的图像和性质

高考数学专题复习:函数y=Asin(ωx+φ)的图像和性质一、单选题1.将函数sin 2()4y x x π⎛⎫=+∈ ⎪⎝⎭R 的图象向右平移8π个单位长度,再把所得图象上各点的横坐标缩短到原来的12,纵坐标不变,则所得图象的函数解析式为( ) A .cos y x =B .cos 4y x =C .sin y x =D .sin 4y x =2.若函数()()sin 046f x x πωω⎛⎫=-<< ⎪⎝⎭的图象向左平移3π个单位长度后关于y 轴对称,则ω=( )A .2B .12C .1D .33.函数π()sin 2+4f x x ⎛⎫= ⎪⎝⎭的图像,向右平移π4个单位长度后得到函数()g x 的解析式为( )A .()sin 2g x x =B .π()sin(2+)4g x x =C .π()sin(2)4g x x =-D .3π()sin(2)4g x x =+4.已知函数()sin f x x =,函数()g x 的图象可以由函数()f x 的图象先向右平移6π个单位长度,再将所得函数图象保持纵坐标不变,横坐标变为原来的1(0)ωω>得到.若方程1()2g x =在(0,)π上恰有6个根,则ω的取值范围是( )A .195,3⎛⎤⎥⎝⎦B .195,3⎡⎫⎪⎢⎣⎭C .2913,62⎛⎤ ⎥⎝⎦D .2913,62⎡⎫⎪⎢⎣⎭5.()sin 23πf x x ⎛⎫=- ⎪⎝⎭的图象向左平移ϕ个单位,恰与()5sin 26g x x π⎛⎫=+ ⎪⎝⎭的图象重合,则ϕ的取值可能是( )A .3π B .512π C .2π D .712π 6.为了得到sin 2y x =,x ∈R 的图象,只需把cos 2y x =,x ∈R 图像上所有的点( ). A .向左平移π4个单位长度B .向右平移π4个单位长度C .向左平移π2个单位长度D .向右平移π2个单位长度7.将函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位长度,再向上平移1个单位长度,得到()g x 的图象,若()()129g x g x ⋅=,且[]12,0,2x x π∈,则12x x -的值为( )A .2πB .πC .2π D .4912π8.设函数()sin (0)6f x x πωωω⎛⎫=++> ⎪⎝⎭的图象如图,则函数f (x )的图象的对称轴方程为( )A .3x k ππ=+(k ∈Z ) B .26k x ππ=+(k ∈Z ) C .26k x ππ=-(k ∈Z ) D .3x k ππ=-(k ∈Z )9.已知函数()πsin()cos 3x f x x =+的图像向右平移3π个单位,再将图像上所有点的横坐标缩小到原来的一半,纵坐标不变,得到函数g (x )的图象,若()()()121214g x x x x g ⋅=≠,则12||x x -的最小值为( ) A .π 4B .2πC .πD .2π10.已知函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭,()sin g x x =,要得到函数()y f x =的图象,只需将函数y g x 的图象上的所有点( )A .横坐标缩短为原来的12,再向左平移π3个单位得到B .横坐标缩短为原来的12,再向左平移π6个单位得到C .横坐标伸长为原来的2倍,再向左平移π3个单位得到D .横坐标伸长为原来的2倍,再向左平移π6个单位得到11.要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( )A .向左平移3π个单位; B .向左平移6π个单位;C .向右平移3π个单位; D .向右平移6π个单位12.已知函数()()0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象如图所示,则下列说法正确的个数为( )①3πϕ=;②()f x 在区间,03π⎛-⎫⎪⎝⎭上单调递增;③()f x 的一条对称轴为512x π=;④要想将()f x 变成一个偶函数,可以将()f x 的图象向左平移12π个单位.A .1个B .2个C .3个D .4个二、填空题13.将函数()sin 2f x x =的图像向左平移()0ϕϕ>个单位得到函数()cos2g x x =的图像,则ϕ的最小值是________.14.已知函数1()4sin 26f x x ππ⎛⎫=+ ⎪⎝⎭,将函数f (x )的图象上所有点的横坐标变成原来的12倍,纵坐标不变,得到函数g (x )的图象,且当x ∈1,3a ⎡⎤-⎢⎥⎣⎦时,()[]2,4g x ∈-,则a 的取值范围是________.15.将函数()cos 2f x x =的图象向左平移(0)ϕϕ>个单位长度,得到函数()g x 的图象.若函数()g x 的图象关于原点对称,则ϕ的一个取值为________.16.已知函数π()sin()(0,0,||)2f x A x A ωϕωϕ=+>><的部分图象如图所示,()sin(2)g x A x ωϕ=-,给出以下说法:①将()y f x =的图象向左平移34个单位长度可以得到()g x 的图象;②()g x 的图象关于直线x =1对称; ③()g x 的图象关于点5(,0)2成中心对称;④()g x 在719(,)44上单调递减.其中所有正确说法的编号是________ 三、解答题 17.已知函数sin ωφf xA xB (其中A ,ω,ϕ,B 均为常数,0A >,0>ω,2πϕ<)的部分图象如图所示.(1)求函数()f x 的解析式及其递增区间;(2)若先将函数()f x 图象上所有点的横坐标变为原来的12倍(纵坐标不变),再将图象向左平移m (0m >)个单位长度,得到函数()g x 的图象,若()g x 是偶函数,求实数m 的最小值.18.已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示:(1)求函数()f x 的解析式;(2)将函数()y f x =的图像上各点的横坐标缩短到原来的12,纵坐标不变,得到函数()y g x =的图像,求函数()y g x =在区间0,4⎡⎤⎢⎥⎣⎦π上的最大值及函数取最大值时相应的x 值.19.已知函数()()sin (0,0,02)f x A x A ωϕωϕπ=+>><<的部分图象如图所示.(1)求函数()f x 的解析式;(2)若()()((0,))2g x f x t t π=+∈为偶函数,求t 的值.20.已知函数()2sin f x x ω=其中常数0>ω.(1)若()y f x =在2,43ππ⎡⎤-⎢⎥⎣⎦上单调递增,求ω的取值范围;(2)令2ω=,将函数()y f x =的图象向左平移6π个单位长度,再向上平移1个单位长度,得到函数()y g x =的图象,区间[],a b (,a b ∈R 且a b <)满足:()y g x =在[],a b 上至少含有100个零点,在所有满足上述条件的[],a b 中,求b a -的最小值.21.某同学用“五点法”画函数()sin()0,||2f x A x πωϕωϕ⎛⎫=+>< ⎪⎝⎭在某一周期内的图象时,列表并填入的部分数据如下表:(1)请写出上表的122x x y ,,及函数()f x 的解析式;(2)将函数()f x 的图象向右平移3π个单位,再将所得图象上各点的横坐标缩小为原来的12,纵坐标不变,得到函数()g x 的图象,求()g x 的解析式及()12log y g x ⎡=⎢⎣⎦的定义域.22.已知函数()2cos(2)(0)f x x ϕϕπ=+<<. (1)若π=ϕ,完成下列表格并在给定的坐标系中,画出函数f (x )在[0,]π上的图象;(2)若f (x )为奇函数,求ϕ;(3)在(2)的前提下,将函数f (x )的图象向右平移6π个单位长度后,再将得到的图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数g (x )的图象,求g (x )的单调递减区间.参考答案1.D 【分析】根据图象平移,伸缩变换的原则,结合所给方程,化简整理,即可得答案. 【详解】将sin 2()4y x x π⎛⎫=+∈ ⎪⎝⎭R 的图象向右平移8π个单位长度,得到图象的解析式为sin 2sin 284y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,再将sin 2y x =的图象上各点的横坐标缩短到原来的12,纵坐标不变,则所得图象的函数解析式为sin 4y x =, 故选:D . 2.A 【分析】先求出平称后的函数解析式,再由其图像关于y 轴对称,可得其为偶函数,从而可求出ω的值 【详解】解:函数()()sin 046f x x πωω⎛⎫=-<< ⎪⎝⎭的图象向左平移3π个单位长度后的解析式为sin sin 3636y x x πππωπωω⎡⎤⎛⎫⎛⎫=+-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,因为其图像关于y 轴对称, 所以,362k k Z πωπππ-=+∈,解得32,k k Z ω=+∈, 因为04ω<<,所以2ω=, 故选:A 3.C 【分析】由平移变换得解析式.【详解】向右平移π4个单位长度后得:()sin 2()sin(2)444g x x x πππ⎡⎤=-+=-⎢⎥⎣⎦.故选:C . 4.A 【分析】由图象变换得出()g x 的表达式,求出1()2g x =的解,正数解从小到大排序后,π大于第六个解,不小于第7个解,由此可得结论. 【详解】由题意()sin()6g x x πω=-,由1sin()62x πω-=,得(1)66k x k ππωπ-=+-,1(1)66k x k πππω⎡⎤=++-⎢⎥⎣⎦,k Z ∈, (1)66k k πππ++-中正数依次为3π,π,73π,3π,133π,5π,193π,…,1()2g x =在(0,)π上恰有6个根,则5193πππωω<≤,解得1953ω<≤.故选:A . 5.D 【分析】首先根据平移规律,写出平移后的图象,再根据两图象重合,列式求ϕ的值. 【详解】()sin 23πf x x ⎛⎫=- ⎪⎝⎭的图像向左平移ϕ个单位后得()sin 23y x πϕ⎡⎤=+-⎢⎥⎣⎦,0ϕ>,与图象()5sin 26g x x π⎛⎫=+ ⎪⎝⎭重合,所以522,36k k Z ππϕπ-=+∈,解得:7,12k k Z πϕπ=+∈, 当0k =时,712πϕ=. 故选:D 6.B 【分析】由诱导公式可得cos 2sin(2)2y x x π==+,结合sin()y A x ωϕ=+的图像变换规律即可得出结论.【详解】由诱导公式可得cos 2sin(2)sin 2()24y x x x ππ==+=+,所以将函数图像上的点向右平移4π个单位长度,即可得到sin 2y x =的图像. 故选:B 7.B 【分析】根据函数sin()y A x ωϕ=+的图象变换规律,求得()g x 的解析式,再利用正弦函数的最大值,可得1()g x 和2()g x 相差一个周期的整数倍,从而判断1232x ππ+=,22232x πππ+=+或1232x ππ+=,22232x πππ+=+,进而求得12x x -的值.【详解】解:将函数()2sin(2)6f x x π=+的图象向左平移12π个单位,再向上平移1个单位,得到()2sin(2)13g x x π=++的图象.若12()()9g x g x ⋅=,则1()g x 和2()g x 都取得最大值3, 故1()g x 和2()g x 相差一个周期的整数倍. 由[]12,0,2x x π∈,则122,2,43333x x πππππ⎡⎤++∈+⎢⎥⎣⎦, 故1232x ππ+=,22232x πππ+=+, 或1232x ππ+=,22232x πππ+=+,所以12x x π-= 故选:B . 8.B 【分析】由图象得2ω=,再由正弦函数的对称轴方程可得答案. 【详解】 由图象可知,132ω+=,所以2ω=,所以 ()sin 226f x x π⎛⎫=++ ⎪⎝⎭,令()262x k k Z πππ+=+∈得()26k x k Z ππ=+∈, 故选:B. 9.B 【分析】先对函数化简,得1()sin 223f x x π⎛⎫=+ ⎪⎝⎭,再利用三角函数图像变换规律求出()1sin 423g x x π⎛⎫=- ⎪⎝⎭,由()()()121214g x x x x g ⋅=≠,可得1x 与2x 都是波峰或波谷的横坐标,从而可得答案 【详解】因为()sin cos 3f x x x π⎛⎫=+= ⎪⎝⎭1sin cos 2x x x ⎛⎫+= ⎪ ⎪⎝⎭1cos24x x =111sin 2sin 22223x x x π⎛⎫⎛⎫+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭的图像向右平移3π个单位得1sin 2233y x ππ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦1sin 223x π⎛⎫=- ⎪⎝⎭,再将图像上所有点的横坐标缩小到原来的一半得到()1sin 423g x x π⎛⎫=- ⎪⎝⎭,因为()()1214g x g x ⋅=,所以()()1212g x g x ==或()()1212g x g x ==-,因为1x 与2x 都是波峰或波谷的横坐标,所以12min2x x T π-==,故选:B . 10.B 【分析】根据正弦函数图象变化前后的解析式,确定图象的变换过程. 【详解】由()πsin 2()6f x x =+,而()sing x x =,∴将函数yg x 的图象上的所有点横坐标缩短为原来的12,再向左平移π6个单位得到()y f x =.故选:B 11.B 【分析】根据两个函数的解析式的特征,结合正弦型函数图像的变换性质进行求解即可.【详解】因为sin 2sin[2]36y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,所以要得到函数sin 23y x π⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像向左平移6π个单位即可, 故选:B 12.C 【分析】先根据图象特征求ω和ϕ,判断①正确,得到解析式,再利用代入验证法判断②正确③错误,利用图象平移判断④正确,即得正确说法的个数. 【详解】由图象知,7ππ2π4π123T ω⎛⎫=-== ⎪⎝⎭,所以2ω=,函数()()2f x x ϕ=+, 由图象过π,03⎛⎫⎪⎝⎭知,2,3k k Z πϕππ⨯+=+∈,而2πϕ<,故π3ϕ=,故①正确,()32πin f x x ⎛⎫=+ ⎪⎝⎭.,03x π⎛⎫∈- ⎪⎝⎭时,222,,333x πππππ⎛⎫⎛⎫+∈⊆ ⎪ ⎪⎝⎭⎝-⎭-,所以函数单调递增,②正确;512x π=时,37πsin 2sin 16x π⎛⎫+=≠± ⎪⎝⎭,所以512x π=不是对称轴,③错误;()32πin f x x ⎛⎫=+ ⎪⎝⎭向左平移12π个单位得ππ2221232πy x x x ⎡⎤=⎢⎥⎣⎦⎛⎫⎛⎫=+++= ⎪ ⎪⎝⎭⎝⎭是偶函数,所以④正确.综上,说法正确的个数为3个. 故选:C. 13.4π【分析】将cos 2x 化为sin 22x π⎛⎫+ ⎪⎝⎭,进而通过平移得到答案.【详解】由已知可得sin 2()cos2sin 22x x x πϕ⎛⎫+==+ ⎪⎝⎭,∴222k πϕπ=+,∴,4k k πϕπ=+∈Z ,∵0ϕ>,∴ϕ的最小值是4π. 故答案为:4π. 14.1,13⎡⎤⎢⎥⎣⎦【分析】利用图象变换知识可得()4sin()6g x x ππ=+,结合正弦函数的图象与性质可得结果.【详解】由题意可得()4sin()6g x x ππ=+,当1,3x a ⎡⎤∈-⎢⎥⎣⎦时,(),666x a πππππ⎡⎤+∈-+⎢⎥⎣⎦,又()[]2,4g x ∈-,结合正弦函数的图象可得7266a ππππ≤+≤,所以113a ≤≤.故答案为:1,13⎡⎤⎢⎥⎣⎦.15.4π 【分析】根据平移后的可得函数()cos(22)g x x ϕ=+,根据题意可得(0)0g =可得22k πϕπ=+,取一值即可得解. 【详解】将函数()cos 2f x x =的图象向左平移(0)ϕϕ>个单位长度, 可得()cos(22)g x x ϕ=+,由函数()g x 的图象关于原点对称, 可得(0)cos(2)0g ϕ==, 所以22k πϕπ=+,42k ππϕ=+, 当0k =时,4πϕ=.故答案为:4π 16.①②③ 【分析】由给定的函数图象求出ω和ϕ并写出()f x ,()g x 的解析式,然后对四个命题逐一分析判断作答.【详解】令函数()f x 周期为T ,观察图象得75()3244T =--=,即6T =,则23T ππω==, 又当74x =时,()f x 取得最大值,于是有72()342k k Z ππϕπ⋅+=+∈,因||2ϕπ<,则有0,12k πϕ==-,所以()sin(),()sin()31236f x A xg x A x ππππ=-=+,因33()sin[()]sin()4341236f x A x A x ππππ+=+-=+,即g (x )的图象可以由y =f (x )的图象向左平移34个单位长度得到,①正确; 由()362x k k Z ππππ+=+∈得函数()g x 图象的对称轴为13()x k k Z =+∈,于是得直线x =1是g (x )图象的一条对称轴,②正确; 由()36x k k Z πππ+=∈得13()2x k k Z =-∈,()g x 图象的对称中心为1(3,0)()2k k Z -∈,则点5(,0)2是()g x 图像的一个对称中心,③正确; 当719(,)44x ∈时,37(,)3644x ππππ+∈,所以()g x 在7(,4)4单调递减,在19(4,)4上单调递增,④错误.故答案为:①②③17.(1)()sin 223f x x π⎛⎫=-+ ⎪⎝⎭;递增区间为:5(,)()1212k k k Z ππππ-++∈;(2)524π. 【分析】(1)根据图象可得函数的解析式为()sin 223f x x π⎛⎫=-+ ⎪⎝⎭,再解不等式222232k x k πππππ-<-<+,即可得到答案;(2)由题意()()sin 423g x x m π⎡⎤=+-+⎢⎥⎣⎦,()g x sin 4423x m π⎛⎫=+-+ ⎪⎝⎭,由()g x 是偶函数,得432m k πππ-=+,k ∈Z ,从而求得答案;【详解】 (1)由图可知:3112A -==,3122B +==,31173212122T πππ⎛⎫=--= ⎪⎝⎭, 所以2T ππω==,所以2ω=,所以()()sin 22f x x ϕ=++.由1111sin 21126f ππϕ⎛⎫⎛⎫=++=⎪⎪⎝⎭⎝⎭,得113262k ππϕπ+=+,k ∈Z , 所以23k πϕπ=-,k ∈Z ,因为2πϕ<,所以3πϕ=-.所以()sin 223f x x π⎛⎫=-+ ⎪⎝⎭.递增区间为:5(,)()1212k k k Z ππππ-++∈.(2)由题意:()()sin 423g x x m π⎡⎤=+-+⎢⎥⎣⎦,()g x sin 4423x m π⎛⎫=+-+ ⎪⎝⎭因为()g x 是偶函数,所以432m k πππ-=+,k ∈Z ,所以5424k m ππ=+,k ∈Z , 因为0m >,所以当0k =时,m 的最小值为524π. 18.(1)2sin 23y x π⎛⎫=+ ⎪⎝⎭;(2)24x π=时,函数()g x 在0,4⎡⎤⎢⎥⎣⎦π区间上的最大值为2.【分析】(1)根据函数的最值求出A 的值,根据函数的最小正周期求出ω的值,根据函数的最值点求出ϕ的值即得解;(2)首先求出()2sin 43g x x π⎛⎫=+ ⎪⎝⎭,再根据不等式的性质和三角函数的图象和性质求出最大值及函数取最大值时相应的x 值. 【详解】解:(1)如图可知,2,4126A T πππ⎡⎤⎛⎫==⨯--= ⎪⎢⎥⎝⎭⎣⎦,∴22Tπω==. ∵2sin 22122πϕπϕ⎧⎛⎫⨯+= ⎪⎪⎪⎝⎭⎨⎪<⎪⎩, ∴3πϕ=,即函数解析式为2sin 23y x π⎛⎫=+ ⎪⎝⎭;(2)根据图象变换原则得()2sin 43g x x π⎛⎫=+ ⎪⎝⎭,∵0,4x π⎡⎤∈⎢⎥⎣⎦,∴44,333x πππ⎡⎤+∈⎢⎥⎣⎦,∴2sin 4[3x π⎛⎫+∈ ⎪⎝⎭,当432x ππ+=,即24x π=时,函数()g x 在0,4⎡⎤⎢⎥⎣⎦π区间上的最大值为2.19.(1)())3f x x π=+;(2)12π.【分析】(1)利用函数图象信息求出A ,周期T 而得ω,再由最小值点求出ϕ即可作答; (2)利用正余弦型函数的奇偶性列式计算即得. 【详解】(1)由图知A =函数()f x 周期为T ,则373()41264T πππ=--=,T π=,于是得22T πω==,则()()2f x x ϕ=+,由77())1212f ππϕ⋅+=7322,122k k Z ππϕπ⋅+=+∈,解得2,3k k Z πϕπ=+∈,而02ϕπ<<,则3πϕ=,所以函数()f x的解析式为())3f x x π=+;(2)由(1)知()()2)3x t g x f x t π=+++=为偶函数,从而有2,32t k k Z πππ+=+∈,解得,122k t k Z ππ=+∈,又(0,)2t π∈,所以12t π=.20.(1)(30,4⎤⎥⎦;(2)1483π. 【分析】(1)求出()()2sin 0f x x ωω=>的单调递增区间,根据42232ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩解不等式组可得答案;(2)求出()g x 的零点相邻间隔依次为3π和23π,利用三角函数的性质进行求解即可.【详解】(1)由()2222k x k k Z πππωπ-≤≤+∈得()2222k k x k Z ππππωωωω-≤≤+∈,()2sin f x x ω=的单调递增区间为()22,22k k k Z ππππωωωω⎡⎤-+∈⎢⎥⎣⎦, 若()y f x =在2,43ππ⎡⎤-⎢⎥⎣⎦上单调递增,所以令0k =,则22x ππωω-≤≤()0ω>, 根据题意有42232ππωππω⎧-≥-⎪⎪⎨⎪≤⎪⎩,解得304ω<≤所以ω的取值范围是(30,4⎤⎥⎦.(2)由()2sin 2f x x =可得,()2sin 212sin 2163g x x x ππ⎡⎤⎛⎫⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由()0g x =可得1sin 232x π⎛⎫+=- ⎪⎝⎭,4x k ππ∴=-或712x k k Z ππ=-∈,,即()g x 的零点相邻间隔依次为3π和23π,故若()y g x =在[],a b 上至少含有100个零点,则b a -的最小值为21484950333πππ⨯+⨯=. 21.(1)1224π7π,,33x x y ===1π()23f x x ⎛⎫=+ ⎪⎝⎭;(2)()π6g x x ⎛⎫=+ ⎪⎝⎭;2π2π,2π,Z 3k k k ⎛⎫+∈ ⎪⎝⎭.【分析】(1)利用五点法依次代入计算参数,,A ωϕ,即得解析式,再代入计算解得122x x y ,,即可; (2)先利用图象变换得到()g x 的解析式,再根据对数的性质得到()g x ,即解不等式π1sin 62x ⎛⎫+> ⎪⎝⎭,即得结果.【详解】解:(1)依题意可知,20332πωϕππωϕ⎧-+=⎪⎪⎨⎪+=⎪⎩,解得123ωπϕ⎧=⎪⎪⎨⎪=⎪⎩,又ππsin 32f A A ⎛⎫=== ⎪⎝⎭1π()23f x x ⎛⎫=+ ⎪⎝⎭,故由11ππ23x +=,21π3π232x +=,解得124π7π,33x x ==,又2221π3π()232f x y x ⎛⎫+== ⎪⎝⎭= (2)函数()f x 的图象向右平移3π个单位,得到1ππ1π23326y x x ⎡⎤⎛⎫⎛⎫=-+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再将所得图象上各点的横坐标缩小为原来的12,纵坐标不变,得到函数()π6g x x ⎛⎫=+ ⎪⎝⎭; 函数()12log y g x ⎡=⎢⎣⎦中,()0g x >,即()g x 所以()π6g x x ⎛⎫=+> ⎪⎝⎭π1sin 62x ⎛⎫+> ⎪⎝⎭,所以ππ5π2π2π,Z 666k x k k +<+<+∈,解得2π2π2π,Z 3k x k k <<+∈, 所以()12log y g x ⎡=⎢⎣⎦的定义域为2π2π,2π,Z 3k k k ⎛⎫+∈ ⎪⎝⎭. 22.(1)答案见解析;(2)2ϕπ=;(3)52,2()66k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z . 【分析】(1)先填表,再作出函数的图象; (2)由题得2k πϕπ=+,给k 取值即得解;(3)求出()2sin 3g x x π⎛⎫=-- ⎪⎝⎭,再利用复合函数单调性原理和三角函数的图象求解.【详解】解:(1)函数f (x )在[0,]π的图象如下:(2)由()2cos(2)f x x ϕ=+,因为f (x )为奇函数,则2k πϕπ=+,又0ϕπ<<,所以2ϕπ=. (3)由(2)知()2sin 2f x x =-,向右平移6π个单位长度后,再将得到的图象上各点的横坐标变为原来的2倍后,可得()2sin 3g x x π⎛⎫=-- ⎪⎝⎭.由22232k x k πππππ--+,得522()66k x k k ππππ-++∈Z . 从而可得g (x )的单调递减区间为52,2()66k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十四、三角函数函数图像与性质、函数sin()y A wx ϕ=+的图像性质及应用
1.求下列函数的定义域 (1)x
x y cos 2cos 1+=; (2)x y 2sin =. (3)y =tan ⎝ ⎛⎭⎪⎫
π4-x
2.求下列函数的最小正周期
(1))23πsin(x y -=; (2))4
π
2πtan(+=x y ; (3)y =|sin x |
(4) y =3cos ⎝ ⎛⎭⎪⎫
x 2-π4 (5))]1(2
πcos[)2πcos(-=x x y (6)f (x )=(1+3tan x )cos x
3.若函数cos()3y x πω=+(0)ω>的图象相邻两条对称轴间距离为2
π
,则ω等于 .
4.已知函数f (x )=sin x +cos x ,f ′(x )是f (x )的导函数.求f ′(x )及函数y =f ′(x )的最小正周期;
5.函数)3π
21sin(2-=x y 的一条对称轴方程为( )
A .3π4-=x
B .6π5-=x
C .3π-=x
D .3
π
2=x
6.函数sin(2)3
y x π
=+图像的对称轴方程可能是( )
A .6x π=-
B .12x π=-
C .6x π=
D . 12x π
=
7.y =sin ⎝ ⎛⎭
⎪⎫
x -π4的图象的一个对称中心是( ).
A .(-π,0) B.⎝ ⎛⎭⎪⎫-3π4,0 C.⎝ ⎛⎭⎪⎫3π2,0 D.⎝ ⎛⎭
⎪⎫π2,0
8.求函数)3
π
2cos(-=x y 的对称轴方程和对称中心的坐标
9.已知函数()2sin()f x x ωϕ=+对任意x 都有()(),66f x f x ππ
+=-则()6f π等于( )
A . 2或0
B . 2-或2
C . 0
D . 2-或0
10.函数)3π
2sin(+=x y 的图象( )
A .关于点(3π,0)对称
B .关于直线4π
=x 对称
C .关于点(4π,0)对称
D .关于直线3
π
=x 对称
11.函数y =tan ⎝ ⎛
⎭
⎪⎫2x +π4的图象与x 轴交点的坐标是 .
12.求下列函数的单调区间
(1))3
π
21cos(-=x y
(2)]0,π[),6
π
2sin(2-∈+=x x y
(3)x x y 2sin 32cos -=
(4))23π
sin(2x y -=
(5)y sin(2)6x π
=++1
(6)]),0[)(26
sin(2ππ
∈-=x x y
(7)y =2|cos x | (8))4sin 2cos 4cos
2(sin log 2
1π
π
x x y -=
13.设函数f (x )=sin ()2x +φ (-π<φ<0),y =f (x )图象的一条对称轴是直线x =π
8. (1)求φ; (2)求函数y =f (x )的单调增区间.
14.求下列函数的值域 (1) y =cos2x +cos x
(2))3π
2,6π(,sin 2-∈=x x y
(3))3
π
,2π(),3π2cos(2-∈+=x x y
(4)x x y 2cos 32sin -= )
66(π
π≤≤-x
(5) y =2sin ⎝ ⎛
⎭
⎪⎫2x +π3 (-π6<x <π6)(6)y =sin 2x +sin x -1
15.函数x x y cos 3sin +=在区间]2
,0[π
上的最小值为 .
16.函数)2
π
sin(sin 3)(x x x f ++=的最大值是______.
17.已知函数()sin sin(),2
f x x x x R π
=++∈.
(I)求()f x 的最小正周期; (II)求()f x 的的最大值和最小值;
18.试述如何由sin y x =的图像得到1sin(2)33
y x π
=+的图像。
反之呢?
19.把函数y =sin x (x ∈R )的图象上所有的点向左平行移动3
π
个单位长度,再把所得图象上所有点的横 坐标缩短到原来的
2
1
倍(纵坐标不变),得到的图象所表示的函数是 . 20.将函数sin()()6y x x R π=+∈的图象上所有的点向左平行移动4π
个单位长度,再把图象上各点的横
坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为 . 21.将函数sin y x =的图像上所有的点向右平行移动
10
π
个单位长度,再把所得各点的横坐标伸长到原
来的2倍(纵坐标不变),所得图像的函数解析式是 . 22.为了得到函数)6
2sin(π
-=x y 的图象,可以将函数x y 2cos =的图象( )
A .向右平移
6π个单位长度 B .向右平移3π
个单位长度 C .向左平移6π个单位长度 D .向左平移3
π
个单位长度
23.为了得到函数y =sin (2x +1)的图像,只需把函数y =sin 2x 的图像上所有的点( ) A .向左平行移动12个单位长度 B .向右平行移动1
2个单位长度 C .向左平行移动1个单位长度 D .向右平行移动1个单位长度 24.为了得到函数y =sin 3x +cos 3x 的图像,可以将函数y =2cos 3x 的图像( ) A .向右平移π4个单位 B .向左平移π
4个单位 C .向右平移π12个单位 D .向左平移π
12个单位
25.函数y =cos(2x +φ)(-π≤φ<π)的图象向右平移π2个单位后,与函数y =sin ⎝ ⎛
⎭⎪⎫2x +π3的图象重合,则
φ=_ _.
26.将函数y =3sin ⎝ ⎛
⎭⎪⎫2x +π3的图像向右平移π2个单位长度,所得图像对应的函数( )
A .在区间⎣⎢⎡⎦⎥⎤π12,7π12上单调递减
B .在区间⎣⎢⎡⎦⎥⎤
π12,7π12上单调递增
C .在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递减
D .在区间⎣⎢⎡⎦⎥⎤
-π6
,π3上单调递增
27.函数y =-xc os x 的部分图象是( )
28.函数)2
π
2π(lncos <<-
=x x y 的图象( )
29.设函数f (x )=sin(ωx +φ)(ω>0,0<φ<π2)的部分图象如图所示,直线x =π
6是它的一条对称轴,则函数f (x )的解析式为( )
A .f (x )=sin ⎝ ⎛⎭⎪⎫x +π3
B .f (x )=sin ⎝ ⎛
⎭⎪⎫2x -π6
C .f (x )=sin ⎝ ⎛⎭⎪⎫4x +π3
D .f (x )=sin ⎝ ⎛
⎭
⎪⎫2x +π6
30.函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0,0<φ<π
2)的部分图象如图所示.求f (x )的解析式;
31.已知函数y =sin(ωx +φ)(ω>0,-π≤φ<π)的图象如图所示,则φ=________.
32.已知函数y =sin(ωx +φ)(ω>0,|φ|<π)的图象如图所示,则φ=________.
33.已知函数f (x )=A cos(ωx +φ) 的图象如图所示,f (π2)=-2
3,则f (0)=________.
34.下列函数中,图像的一部分如右图所示的是( )
A .
sin()6y x π=+ B .cos(2)6
y x π
=- C .cos(4)3y x π=- D .sin(2)6
y x π
=-
35.已知函数)sin(φϖ+=x A y 在同一周期内,当3π
=x 时有最大值2,当x=0时有最小值-2,那么函
数的解析式为_______________.
36.已知函数f (x )=A sin(ωx +φ) (A >0,ω>0,|φ|<π
2)的部分图象如图所示. (1)求函数f (x )的解析式;
(2)如何由函数y =2sin x 的图象通过适当的变换得到函数f (x )的图象.
37.函数)3
2sin(3)(π
-
=x x f 的图象为C ,如下结论中正确的是________ (写出所有正确结论的编号).
① 图象C 关于直线π12
11=x 对称; ② 图象C 关于点)0,3
2(π
对称;
③ 函数125,
12()(π
π-
在区间x f )内是增函数;
④ 由x y 2sin 3=的图象向右平移3
π
个单位长度可以得到图象C.
38.设函数y =sin(ωx +φ) (ω>0,φ∈(-π2,π2))的最小正周期为π,且其图象关于直线x =π
12对称,则 在下面四个结论中:
① 图象关于点⎝ ⎛⎭⎪⎫π4,0对称; ②图象关于点⎝ ⎛⎭⎪⎫
π3,0对称;
③在⎣⎢⎡⎦⎥⎤0,π6上是增函数; ④在⎣⎢⎡⎦⎥⎤
-π6,0上是增函数,
所有正确结论的编号为________.。
