布莱克舒尔斯期权定价模型
布莱克-舒尔斯期权定价模型

几何布朗运动的离散形式
第一节 证券价格的变化过程
四、证券价格的变化过程
几何布朗运动的基本特征: 在短时间 t 后,证券价格比率的变化值
S t t S
S 因此: S
S S
为:
也具有正态分布特征,其均值为 t , 方差为 2t ,标准差为 t 即: S ~ ( t ,
通
布
朗
运
动
变量X遵循普通布朗运动:
dx adt bdz adt b dt
a和b均为常数,dz遵循标准布朗运动。 漂移率a:单位时间内变量z均值的变化值。 方差率b2:单位时间的方差
普通布朗运动的离差形式
x at b t
第一节 证券价格的变化过程
二、布朗运动
对普通布朗运动的理解:
Hale Waihona Puke dx adt bdzx at b t 遵循普通布朗运动的变量x是关于时间和dz的动态 过程
第一项adt为确定项,它意味着x的期望漂移率是每单位
时间为a 第二项bdz是随机项,它表明对x的动态过程添加的噪音。 这种噪音是由维纳过程的b倍。
在任意时间长度T后,x值的变化也具有正态分布特 征,其均值为aT,方差为 b 2T ,标准差b T 。 标准布朗运动的漂移率a为0,方差率为1。
第二节 布莱克-舒尔斯期权定价模型
一、布莱克-舒尔斯微分方程
由于证券价格S遵循几何布朗运动,因此有:
dS Sdt Sdz
其在一个小的时间间隔 t 中,S的变化值 S 为:
S S t S z
设f是依赖于S的衍生证券的价格,则f一定是S和t的函 数,根据伊藤引理可得: f f 1 2 f 2 2 f df ( S S )dt Sdz 2 S t 2 S S
第六章 布莱克-舒尔斯期权定价模型

因此,z(T)-z(0)也具有正态分布特征,其均值为0,方差为 N Δ t =T,标准差 。 T
若变量x 遵循普通布朗运动:dx adt bdz 其中:1、a和b均为常数,dz遵循标准布朗运动。 2、a为漂移率(Drift Rate),是指单位时间内变量 z均值的变化值。 3、b2为方差率(Variance Rate),是指单位时间的方差。 普通布朗运动的离差形式为 x at b t ,显然,Δx也 2 具有正态分布特征,其均值为 at ,标准差为 b t,方差为 b t
1965年,法玛(Fama)提出了著名的效 率市场假说。该假说认为,投资者都力图利用 可获得的信息获得更高的报酬;证券价格对新 的市场信息的反应是迅速而准确的,证券价格 能完全反应全部信息;市场竞争使证券价格从 一个均衡水平过渡到另一个均衡水平,而与新 信息相应的价格变动是相互独立的
1、弱式效率市场假说认为,证券价格变动的历史不包含任何对 预测证券价格未来变动有用的信息,也就是说不能通过技术分析 获得超过平均收益率的收益。 2、半强式效率市场假说认为,证券价格会迅速、准确地根据可 获得的所有公开信息调整,因此以往的价格和成交量等技术面信 息以及已公布的基本面信息都无助于挑选价格被高估或低估的证 券。 3、强式效率市场假说认为,不仅是已公布的信息,而且是可能 获得的有关信息都已反映在股价中,因此任何信息(包括“内幕 信息”)对挑选证券都没有用处。 根据众多学者的实证研究,发达国家的证券市场大体符合弱式效 率市场假说。
普通布朗运动
1、显然,遵循普通布朗运动的变量x是关于时间和dz的动态过程, 其中第一项adt为确定项,它意味着x的期望漂移率是每单位时间为 a。第二项bdz是随机项,它表明对x的动态过程添加的噪音。这种 噪音是由维纳过程的 b倍给出的。 b T
Chapter11布莱克休尔斯莫顿期权定价模型

衍生证券的定价。
Copyright© Zheng Zhenlong & Chen Rong, 2008
19
观察布莱克-舒尔斯微分方程,我们可以发现,受制于主观的 风险收益偏好的标的证券预期收益率并未包括在衍生证券的价值决 定公式中。这意味着,无论风险收益偏好状态如何,都不会对f的值 产生影响。因此我们可以作出一个可以大大简化我们工作的假设: 在对衍生证券定价时,所有投资者都是风险中性的。尽管这只是一 个人为的假定,但通过这种假定所获得的结论不仅适用于投资者风 险中性情况,也适用于投资者厌恶风险的所有情况。
11
由上一页的推导可知证券价格对数服从正态分布。如果
一个变量的自然对数服从正态分布,则称这个变量服从对数
正态分布。这表明ST服从对数正态分布。根据对数正态分布 的特性,以及符号的定义,我们可以得到 E(ST ) Se (T t) 和 var(ST ) S 2e 2(T t) [e 2 (T t) 1]
S S S 2 S 2 t
代入式 dG ( G a G 1 2G b 2 )dt G bdz我们就可得到 G ln S 所
x
t 2 x 2
x
遵循的随机过程为 dG d ln S ( 2 )dt dz
2
由于dlnS是股票的连续复利收益率,得出的公式说明股票的连续
复利收益率服从期望值 ( 2 )dt ,方差为 2dt 的正态分布。
2、在任意时间长度T后x值的变化也具有正态分布特征,其均值为 aT,标准差为 b T,方差为b2T。
Copyright© Zheng Zhenlong & Chen Rong, 2008
6
普通布朗运动假定漂移率和方差率为常数,若把变量 x的漂移率和方差率当作)dz
布莱克—舒尔斯期权定价

显然,S0=1OO,X=105,r=0.20,T-t=0.50,σ=0.05 用公式计算:d1=1.47 ; d2=1.43 查正态分布数值表(标准正态曲线下的面积—累积概率):
N(d1)=N(1.47)=0.9292; N(d2)=N(1.43)=0.9236
用公式计算:
C = $5.17
5)标的物股票的价格波动率 越大,看涨期权
的价值越高
关于波动率:在这个公式中,最难理解的莫过于
波动率(),其实这是期权定价法中最重要的 变量。这个变量体现的是:金融市场上,吸收了 全部当前“信息”之后,对未来该股票价格走势 的“不确定性”的判断。
也就是说,越小,说明市场对该股票价格的判断就越明 确,市场上投资人相信其价格在未来不会出现大的波动, 投资人根据当前市场上掌握的信息,可以比较容易地判断 该股票未来价格走势,因而该股票未来价格的不确定性也 就越低。
~
S363
~
S364
~
~
1
Rt 365
St
~
St 1
每天的收益率
1
~
R
~
S365
~
S0
~
S1
S0
~
S2
~
S1
~
S365
~
S364
1
~
R1
365
1
~
R2
365
1
~
R365
365
年利率
利用连续计息方式计息的连续复利
rt 365
log
1
二叉树各个阶段股票价格的变化是互相独立的, 而且变化的概率分布是同分布的,因此满足条件1
二叉树定价中所分阶数越来越多,适当的选择二 叉树中的u和d,使他们都足够快的趋于1,当所 分阶数趋于无穷大时,股票的价格变化就趋向于 对数正态分布(收益率变化趋于正态分布)
第六章布莱克-舒尔斯期权定价模型
第六章 布莱克-舒尔斯期权定价模型一、 影响期权价值的主要因素由前面的分析知道决定期权价值(价格)C V 的因素是到期的股票市场价格m S 和股票的执行价格X 。
但是到期m S 是未知的,它的变化还要受价格趋势和时间价值等因素的影响。
1)标的股票价格与股票执行价格的影响。
标的股票市场价格越高,则买入期权的价值越高,卖出期权的价值越低;期权的执行价越高,则买入的期权价值越低,卖出期权的价值越高。
2)标的股票价格变化范围的影响。
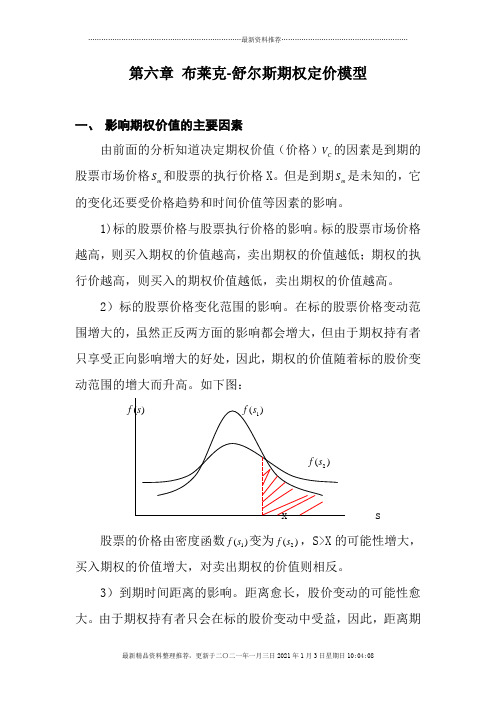
在标的股票价格变动范围增大的,虽然正反两方面的影响都会增大,但由于期权持有者只享受正向影响增大的好处,因此,期权的价值随着标的股价变动范围的增大而升高。
如下图:)(s f )(1s f)(2s fx s股票的价格由密度函数)(1s f 变为)(2s f ,S>X 的可能性增大,买入期权的价值增大,对卖出期权的价值则相反。
3)到期时间距离的影响。
距离愈长,股价变动的可能性愈大。
由于期权持有者只会在标的股价变动中受益,因此,距离期权到期的时间越长,期权的价值就越高。
4)利率的影响。
利率越高,则到期m S 的现值就越低,使得买入期权价值提高,而卖出期权价值降低。
5)现金股利的影响。
股票期权受到股票分割或发放股票股利的保护,期权数量也适应调整,而不受影响,但是期权不受现金股利的保护,因此当股票的价格因公司发放现金股利而下降时,买入期权的价值下降,卖出期权的价值便上升。
二、布莱克-舒尔斯期权定价模型的假设条件B-S 模型是反映欧式不分红的买入期权定价模型,它的假定条件,除了市场无摩擦(例如无税、无交易成本、可以无限制自由借贷等)以外,还有:1. 股票价格是连续的随机变量,所以股票可以无限分割。
2. T 时期内各时段的预期收益率r i 和收益方差σi 保持不变。
3. 在任何时段股票的复利收益率服从对数正态分布,即在t 1-t 2时段内有: ()()()2221211()ln ,()S t N t t t t S t μσ⎛⎫-- ⎪⎝⎭ 因为股票的价格可以用随机过程{},...2,1)(=t t S 表示,其中S (t )表示第t 日股票的价格,它是一个随机变量. 则第t 日股票的收益率(年收益率)为R t :3651)1()(t R t S t S +=-股票的年收益率(单利)R 应该是:)3651()3651)(3651()364()365()1()0()2()1()0()365(136521R R R S S S S S S S S R +++===+ 为了简化计算两边同时取自然对数可得:∑=+=+3651)3651()1(t t R In R In 设r ,r 1,r 2,…,r 365为和R ,R 1,R 2,…,R 365相对应的连续复利。
布莱克舒尔斯默顿期权定价模型

• dz项可以消除。
其它方程
•BSM 微分方程
f t
rS
f S
1 2S2
2
2 f S 2
rf
• BSM 期权定价公式
c SN (d1) Xer(T t) N (d2 )
10.2 股票价格的变化过程
•人们通常用形如公式
dS dt dz
的几S何布朗运动来描绘股票价格的随机变化过程。
这是期权定价模型的基础性假设。也好似金融中最主 要的假设。 最重要的是dz项,它代表影响股票价格变化的随机因 素。通常被成为标准布朗运动(Standard Brownian Motion)或维纳过程(Wiener Process)。
15
• 由特征1知道,z 本身也具有正态分布。均 值为零,标准差为 t ,方差为 t
• 由特征2知道,遵循标准布朗运动的变量具有 独立增量的性质。
维纳过程的性质
进一步发现,变量z在一段较长时间T-t中的变化情形。用 z(T)-z(t)表示变量z在T-t中的变化量,即N个长度为 t的小时
间间隔中z的变化总量,其中N=(T-t)/t
N
z(T ) z(t) i t i1
• Z(T) − Z(t) 也服从正态分布
Z(T) − Z(t)均值等于0
方差等于N t =T − t
标准差等于√T − t
方差可加性
可知
• 1)在任意长度的时间T-t中,遵循标准布朗 运动的变量的变化值服从均值为0,标准差为
√T − t。 • 2)在任意长度的时间间隔T-t中,方差具有可
• 1973年,美国芝加哥大学教授 Fischer Black(费雪.布莱克)& Myron Scholes(梅隆.舒尔 斯)发表了《期权与公司负债定价》疑问,提 出了著名的B-S定价模型,用于确定欧式股票 期权价格,在学术界和实务界引起了强烈反响 ;同年,Robert C. Merton(罗伯特.莫顿)独立地 提出了一个更为一般化的模型。舒尔斯和默顿 由此获得了1997年的诺贝尔经济学奖。
第六章布莱克-舒尔斯期权定价模型

(二)风险中性定价原理
假设所有投资者都是风险中性的,那么 所有现金流量都可以通过无风险利率进 行贴现求得现值。
尽管风险中性假定仅仅是为了求解布莱 克——舒尔斯微分方程而作出的人为假 定,但通过这种假定所获得的结论不仅 适用于投资者风险中性情况,也适用于 投资者厌恶风险的所有情况。
Copyright©Zhenlong Zheng 2003, Department of Finance, Xiamen University
特征1:和z t的关系满足(6.1):
z t
(6.1)
其中,代表从标准正态分布(即均值为0、
标准差为1.0的正态分布)中取的一个随
机值。
Copyright©Zhenlong Zheng 2003, Department of Finance, Xiamen University
标准布朗运动(2)
特征2:对于任何两个不同时间间隔,t 和 z的值相互独立。
考察变量z在一段较长时间T中的变化情
形,我们可得: N z(T ) z(0) i t (6.2) i 1
当0时,我们就可以得到极限的标准布
朗运动: dz dt
(6.3)
Copyright©Zhenlong Zheng 2003, Department of Finance, Xiamen University
2
(6.11)
证券价格对数G遵循普通布朗运动,且:
ln
Hale Waihona Puke STlnS
~ [(
2
2
)(T
t),
T t]
Copyright©Zhenlong Zheng 2003, Department of Finance, Xiamen University
布莱克—舒尔斯期权定价模型

布莱克—舒尔斯期权定价模型期权定价是现代金融学中一项非常重要的内容,同时也是一个比较复杂、难度较大的问题。
目前关于期权定价主要有两种方法:(1)二项式模式;(2)布莱克—舒尔斯期权定价模型(B-S 模型)。
较为适用的是布莱克—舒尔斯期权定价模型。
布莱克—舒尔斯期权定价模型是美国经济学家布莱克—舒尔斯于1973年提出来的。
这是现代金融学金融衍生工具研究领域的一个重大突破,布莱克—舒尔斯因此获得了1997年诺贝尔经济学奖。
1、 基本原理:(模型建立的基础)期权的完全套期保值功能,即期权具备完全消除股票投资组合中市场风险的套期保值功能。
2、 假设条件:(1) 市场是无摩擦的:即不计佣金费用,无交易成本,没有卖空限制,可以根据市场情况经常地调整套期保值的比率,调整期权与股票的比率。
(2) 在期权到期前,股票不支付股利。
(3) 在期权到期前,无风险利率r 和股票收益的方差2σ保持不变。
(4) 股票价格变化是连续的,不会发生突然及大的波动。
3、 基本公式:在上述原理及假设条件的基础上,布莱克—舒尔斯提出了这样一个公式:TTr X S T d d TTr X S d d N Xe d N S C rT σσσσσ)5.0()/ln()5.0()/ln()()(20122012100-+=-=++=-=-其中:其中:0C 为期权价格;0S 为股票当前的价格;)(d N 为服从于标准正态分布的随机变量小于d 的概率;即:}{)1,0(,N Y d y P -<X 为协定价格;e 为2.71828;r 为无风险利率(以连续复利计算) t 为距离到期日所剩的时间,单位为年 σ为股票收益率的标准差。
在这个公式中,)(1d N 、)(2d N 代表期权到期是处于实值的概率,也就是能够执行给投资者带来实质性收益的概率。
如果假定1)()(21==d N d N ,也就是看涨期权极其有可能被执行。
公式的解释:期权价值=内在价值+时间价值期权到期前处于三种状态,虚值—平价—实值时间价值虚值 协定 实值 价格(平价) 从这个图形可以看出,随着股价的进一步升高,期权到期被执行的可能性越来越大,相应地,期权的内在价值越来越大,其价格波动的可能性即时间价值越来越小。
布莱克斯克尔斯期权定价模型

2
当时,该模型是为了解决金融衍生品,特别是期 权定价的问题而建立的。
3
金融衍生品是一种金融合约,其价值取决于其他 金融资产或指标。
模型发展历程
布莱克斯克尔斯模型的发展得益于许多重要的突破,其 中包括
无套利原则:模型利用无套利原则,这意味着在市场上 不能通过买卖资产来赚取无风险利润。
欧式期权定价:该模型适用于欧式期权,即只能在到期 日行使的期权。
THANKS
感谢观看
研究前景展望
随着金融市场的不断发展和全球化进程的加速,布莱克斯克尔斯期权定价模型的应用前景将更加广泛 。例如,在跨境资本流动、国际金融市场分析以及企业风险管理等领域,布莱克斯克尔斯模型都有着 广泛的应用前景。
随着金融创新和科技进步的不断推进,未来的研究也可以探索将布莱克斯克尔斯模型与其他金融理论 和模型相结合,以得到更加全面和准确的金融市场分析和风险管理方法。例如,可以将布莱克斯克尔 斯模型与风险管理、投资组合优化等理论相结合,以得到更加全面和实用的金融解决方案。
与随机波动率模型的比较
总结词
考虑了波动率随机性,但模型更加复杂。
详细描述
相比于随机波动率模型,布莱克斯克尔斯模型能够更好地刻画波动率的随机性和 自相关性,从而更准确地预测金融衍生品价格的变动。但是,这也使得模型的数 学表达式更加复杂,需要更多的计算资源和更精细的数值计算技术。
与跳跃扩散模型的比较
总结词
考虑了价格跳跃,但跳跃参数难以确定。
详细描述
跳跃扩散模型相比于布莱克斯克尔斯模型,能够更好地刻画金融衍生品价格的 跳跃行为,从而更准确地预测价格变动。但是,跳跃扩散模型的参数更加难以 确定,需要更多的历史数据和更精细的统计方法。
06
布莱克-舒尔斯期权定价模型

布莱克-舒尔斯期权定价模型布莱克-舒尔斯期权定价模型是一种用于计算欧式期权的理论定价模型。
该模型于1973年由费舍尔·布莱克和麦伦·舒尔斯提出,并且在同年被罗伯特·默顿-米勒进一步完善和发展。
布莱克-舒尔斯期权定价模型的基本原理是通过建立股票和债券的投资组合,获得一个无风险的合成证券,该合成证券与欧式期权具有相同的收益率。
该模型的关键假设包括资产价格满足几何布朗运动、市场无摩擦、无交易成本和无道德风险等。
根据这些假设,布莱克-舒尔斯期权定价模型的基本公式可以表示为:C = S*N(d1) - X*e^(-rt)*N(d2),其中C表示期权的价格,S是标的资产(如股票)的当前价格,X是期权的行权价格,r是无风险利率,t是期权的剩余期限,e是自然常数(约等于2.71828),N(d1)和N(d2)分别表示标准正态分布的累积分布函数。
在该公式中,d1=(ln(S/X) + (r+σ^2/2)t) / (σ*√t),d2=d1-σ*√t。
其中σ是标的资产的波动率,它衡量标的资产的波动程度。
布莱克-舒尔斯期权定价模型的优点是可以较为准确地计算欧式期权的理论定价,并且可以用于不同类型的期权,如看涨期权、看跌期权等。
它在金融市场中得到了广泛的应用,并为投资者和金融机构提供了重要的参考依据。
然而,布莱克-舒尔斯期权定价模型也存在一些限制。
首先,该模型基于一系列假设,不一定适用于所有市场和资产。
其次,该模型仅适用于欧式期权,而不适用于美式期权等其他类型的期权。
最后,该模型假设市场无摩擦和无道德风险,这在实际市场中并不总是成立。
综上所述,布莱克-舒尔斯期权定价模型为计算欧式期权的理论价格提供了一个重要的工具,但在实际应用中需要对假设进行谨慎评估,并结合其他方法进行综合分析和决策。
布莱克-舒尔斯期权定价模型是金融领域中非常重要且广泛应用的一种定价模型。
它的提出对于金融市场的发展和期权的交易产生了巨大的影响。
布莱克-舒尔斯-默顿期权定价模型培训

布莱克-舒尔斯-默顿期权定价模型培训布莱克-舒尔斯-默顿期权定价模型(Black-Scholes-Merton option pricing model)是金融学中最经典的期权定价模型之一。
该模型由费舍尔·布莱克(Fisher Black)、默顿·舒尔斯(Myron Scholes)和罗伯特·默顿(Robert Merton)三位学者于1973年共同提出,他们因此获得了1997年诺贝尔经济学奖。
该模型被广泛用于期权定价和风险管理。
布莱克-舒尔斯-默顿模型建立在一系列假设之上,其中包括市场允许短期空头交易、无风险利率保持恒定、市场流动性足够充足、期权不考虑红利支付等。
该模型的核心思想是使用风险中性估值来确定期权的价格,基于期权的风险与标的资产价格的相关性。
模型的数学公式为:C = S_0 * N(d1) - X * e^(-rT) * N(d2)P = X * e^(-rT) * N(-d2) - S_0 * N(-d1)其中,C为看涨期权的价格,P为看跌期权的价格,S_0是标的资产的现价,X是期权的行权价,r是无风险利率,T是期权的到期时间,N()是正态分布函数,d1和d2是根据数学公式计算得出的变量。
这个模型基于对资本市场和期权市场的理性行为假设,即市场参与者会根据可得的信息做出最优决策。
它可以用来估计欧式期权的价格,即只在到期日时才能行使的期权。
但该模型不能直接应用于美式期权,因为美式期权可以在任何时间行使。
为了使用布莱克-舒尔斯-默顿模型进行期权定价,需要计算d1和d2的值。
这两个值可以通过期权定价的一系列参量(如标的资产价格、行权价、无风险利率、到期时间和标的资产的波动率)来计算。
这些参量的准确估计对期权定价的精确性至关重要。
布莱克-舒尔斯-默顿模型的优点在于提供了一种快速而相对准确的期权定价方法,为投资者提供了一个公平的市场价值。
然而,该模型也存在一些限制,例如,该模型假设市场流动性充足,但实际市场可能存在流动性不足的情况。
布莱克 斯科尔斯期权定价模型

经济领域术语
01 发展历程
03 定价方法
目录
0--由布莱克与斯科尔斯在20世纪70年代提出。该模型认为,只有股价的当前值与未 来的预测有关;变量过去的历史与演变方式与未来的预测不相关。模型表明,期权价格的决定非常复杂,合约期 限、股票现价、无风险资产的利率水平以及交割价格等都会影响期权价格。
理论前驱
理论前驱
1、巴施里耶(Bachelier,1900) 巴施里耶2、斯普伦克莱(Sprenkle,1961) 3、博内斯(Boness,1964) 4、萨缪尔森(Samuelson,1965)
定价方法
定价方法
(1)Black—Scholes公式 (2)二项式定价方法 (3)风险中性定价方法 (4)鞅定价方法等
主要模型
B-S模型
二项式模型
B-S模型
期权定价模型基于对冲证券组合的思想。投资者可建立期权与其标的股票的组合来保证确定报酬。在均衡时, 此确定报酬必须得到无风险利率。期权的这一定价思想与无套利定价的思想是一致的。所谓无套利定价就是说任 何零投入的投资只能得到零回报,任何非零投入的投资,只能得到与该项投资的风险所对应的平均回报,而不能 获得超额回报(超过与风险相当的报酬的利润)。从Black-Scholes期权定价模型的推导中,不难看出期权定价 本质上就是无套利定价。
谢谢观看
假设条件 1、标的资产价格服从对数正态分布; 2、在期权有效期内,无风险利率和金融资产收益变量是恒定的; 3、市场无摩擦,即不存在税收和交易成本; 4、金融资产在期权有效期内无红利及其它所得(该假设后被放弃); 5、该期权是欧式期权,即在期权到期前不可实施。
二项式模型
二项式模型的假设主要有: 1、不支付股票红利。 2、交易成本与税收为零。 3、投资者可以以无风险利率拆入或拆出资金。 4、市场无风险利率为常数。 5、股票的波动率为常数。 假设在任何一个给定时间,金融资产的价格以事先规定的比例上升或下降。如果资产价格在时间t的价格为S, 它可能在时间t+△t上升至uS或下降至dS。假定对应资产价格上升至uS,期权价格也上升至Cu,如果对应资产价 格下降至dS,期权价格也降至Cd。当金融资产只可能达到这两种价格时,这一顺序称为二项程序。
布莱克-舒尔斯模型

布莱克-舒尔斯模型
布莱克-舒尔斯模型(Black-Scholes Model),简称BS模型,是一种为期权或权证等金融衍生工具定价的数学模型,由美国经济学家迈伦·舒尔斯(Myron Scholes)与费雪·布莱克(Fischer Black)首先提出,并由罗伯特·墨顿(Robert C. Merton)完善。
该模型就是以迈伦·舒尔斯和费雪·布莱克命名的。
1997年迈伦·舒尔斯和罗伯特·墨顿凭借该模型获得诺贝尔经济学奖。
然而它假设价格的变动,会符合高斯分布(即俗称的钟形曲线),但在财务市场上经常出现符合统计学肥尾现象的事件,这影响此公式的有效性。
B-S模型5个重要假设
1.金融资产价格服从对数正态分布,而金融资产收益率服从正态
分布;
2.在期权有效期内,无风险利率和金融资产收益变量是恒定的;
3.市场无摩擦,即不存在税收和交易成本;
4.金融资产在期权有效期内无红利及其它所得(该假设后被放弃);
5.该期权是欧式期权,即在期权到期前不可实施。
模型
其中:
Ln:自然对数;
C:期权初始合理价格;
L:期权交割价格;
S:所交易金融资产现价;
T:期权有效期;
r:连续复利计无风险利率H;
:年度化方差;
N():正态分布变量的累积概率分布函数。
第六章布莱克舒尔斯期权定价模型
第六章 布莱克-舒尔斯期权定价模型一、 影响期权价值的主要因素由前面的分析知道决定期权价值(价格)的因素是到期的股票市场价格和股票的执行价格X 。
但是到期是未知的,它的变化还要受价格趋势和时间价值等因素的影响。
1)标的股票价格与股票执行价格的影响。
标的股票市场价格越高,则买入期权的价值越高,卖出期权的价值越低;期权的执行价越高,则买入的期权价值越低,卖出期权的价值越高。
2)标的股票价格变化范围的影响。
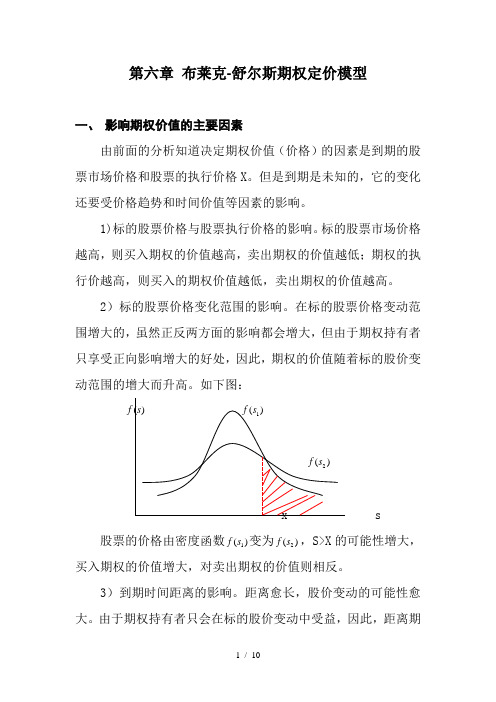
在标的股票价格变动范围增大的,虽然正反两方面的影响都会增大,但由于期权持有者只享受正向影响增大的好处,因此,期权的价值随着标的股价变动范围的增大而升高。
如下图:)(s f )(1s f)(2s fx s股票的价格由密度函数)(1s f 变为)(2s f ,S>X 的可能性增大,买入期权的价值增大,对卖出期权的价值则相反。
3)到期时间距离的影响。
距离愈长,股价变动的可能性愈大。
由于期权持有者只会在标的股价变动中受益,因此,距离期权到期的时间越长,期权的价值就越高。
4)利率的影响。
利率越高,则到期的现值就越低,使得买入期权价值提高,而卖出期权价值降低。
5)现金股利的影响。
股票期权受到股票分割或发放股票股利的保护,期权数量也适应调整,而不受影响,但是期权不受现金股利的保护,因此当股票的价格因公司发放现金股利而下降时,买入期权的价值下降,卖出期权的价值便上升。
二、布莱克-舒尔斯期权定价模型的假设条件B-S 模型是反映欧式不分红的买入期权定价模型,它的假定条件,除了市场无摩擦(例如无税、无交易成本、可以无限制自由借贷等)以外,还有:1. 股票价格是连续的随机变量,所以股票可以无限分割。
2. T 时期内各时段的预期收益率r i 和收益方差σi 保持不变。
3. 在任何时段股票的复利收益率服从对数正态分布,即在t 1-t 2时段内有: ()()()2221211()ln ,()S t N t t t t S t μσ⎛⎫-- ⎪⎝⎭ 因为股票的价格可以用随机过程{},...2,1)(=t t S 表示,其中S (t )表示第t 日股票的价格,它是一个随机变量. 则第t 日股票的收益率(年收益率)为R t :3651)1()(t R t S t S +=-股票的年收益率(单利)R 应该是:)3651()3651)(3651()364()365()1()0()2()1()0()365(136521R R R S S S S S S S S R +++===+ 为了简化计算两边同时取自然对数可得:∑=+=+3651)3651()1(t t R In R In 设r ,r 1,r 2,…,r 365为和R ,R 1,R 2,…,R 365相对应的连续复利。
(完整)BLACK-SCHOLES期权定价模型

BLACK—SCHOLES期权定价模型Black-Scholes期权定价模型(Black-Scholes Option Pricing Model),1997年10月10日,第二十九届诺贝尔经济学奖授予了两位美国学者,哈佛商学院教授罗伯特·默顿(RoBert Merton)和斯坦福大学教授迈伦·斯克尔斯(Myron Scholes)。
他们创立和发展的布莱克-斯克尔斯期权定价模型(Black Scholes Option Pricing Model)为包括股票、债券、货币、商品在内的新兴衍生金融市场的各种以市价价格变动定价的衍生金融工具的合理定价奠定了基础,特别是为评估组合保险成本、可转换债券定价及认股权证估值等提供了依据。
斯克尔斯与他的同事、已故数学家费雪·布莱克(Fischer Black)在70年代初合作研究出了一个期权定价的复杂公式(看涨和看跌)。
与此同时,默顿也发现了同样的公式及许多其它有关期权的有用结论。
结果,两篇论文几乎同时在不同刊物上发表。
所以,布莱克—斯克尔斯定价模型亦可称为布莱克—斯克尔斯—默顿定价模型(含红利的)。
默顿扩展了原模型的内涵,使之同样运用于许多其它形式的金融交易。
瑞士皇家科学协会(The Royal Swedish Academyof Sciencese)赞誉他们在期权定价方面的研究成果是今后25年经济科学中的最杰出贡献。
(一)B—S模型有5个重要的假设1、金融资产收益率服从对数正态分布;(股票价格走势遵循几何布朗运动)2、在期权有效期内,无风险利率和金融资产收益变量是恒定的;3、市场无摩擦,即不存在税收和交易成本;4、该期权是欧式期权,即在期权到期前不可实施;5、金融资产在期权有效期内无红利及其它所得(该假设后被放弃);6、不存在无风险套利机会;7、证券交易是持续的;8、投资者能够以无风险利率借贷。
(二)荣获诺贝尔经济学奖的B-S定价公式)()(21d N Le d SN c rT --=其中:C-期权初始合理价格 L —期权交割价格 S —所交易金融资产现价 T —期权有效期r -连续复利计无风险利率2σ—年度化方差(波动率)N ()—正态分布变量的累积概率分布函数,(标准正态分布 μ=0)在此应当说明两点:第一,该模型中无风险利率必须是连续复利形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 布莱克-舒尔斯期权定价模型一、 影响期权价值的主要因素由前面的分析知道决定期权价值(价格)C V 的因素是到期的股票市场价格m S 和股票的执行价格X 。
但是到期m S 是未知的,它的变化还要受价格趋势和时间价值等因素的影响。
1)标的股票价格与股票执行价格的影响。
标的股票市场价格越高,则买入期权的价值越高,卖出期权的价值越低;期权的执行价越高,则买入的期权价值越低,卖出期权的价值越高。
2)标的股票价格变化范围的影响。
在标的股票价格变动范围增大的,虽然正反两方面的影响都会增大,但由于期权持有者只享受正向影响增大的好处,因此,期权的价值随着标的股价变动范围的增大而升高。
如下图: )(s f )(1s f)(2s fx s股票的价格由密度函数)(1s f 变为)(2s f ,S>X 的可能性增大,买入期权的价值增大,对卖出期权的价值则相反。
3)到期时间距离的影响。
距离愈长,股价变动的可能性愈大。
由于期权持有者只会在标的股价变动中受益,因此,距离期权到期的时间越长,期权的价值就越高。
4)利率的影响。
利率越高,则到期m S 的现值就越低,使得买入期权价值提高,而卖出期权价值降低。
5)现金股利的影响。
股票期权受到股票分割或发放股票股利的保护,期权数量也适应调整,而不受影响,但是期权不受现金股利的保护,因此当股票的价格因公司发放现金股利而下降时,买入期权的价值下降,卖出期权的价值便上升。
二、布莱克-舒尔斯期权定价模型的假设条件B-S 模型是反映欧式不分红的买入期权定价模型,它的假定条件,除了市场无摩擦(例如无税、无交易成本、可以无限制自由借贷等)以外,还有:1. 股票价格是连续的随机变量,所以股票可以无限分割。
2. T 时期内各时段的预期收益率r i 和收益方差σi 保持不变。
3. 在任何时段股票的复利收益率服从对数正态分布,即在t 1-t 2时段内有:()()()2221211()ln ,()S t N t t t t S t μσ⎛⎫-- ⎪⎝⎭因为股票的价格可以用随机过程{},...2,1)(=t t S 表示,其中S (t )表示第t 日股票的价格,它是一个随机变量. 则第t 日股票的收益率(年收益率)为R t :3651)1()(t R t S t S +=-股票的年收益率(单利)R 应该是:)3651()3651)(3651()364()365()1()0()2()1()0()365(136521R R R S S S S S S S S R +++===+为了简化计算两边同时取自然对数可得:∑=+=+3651)3651()1(t tR In R In设r ,r 1,r 2,…,r 365为和R ,R 1,R 2,…,R 365相对应的连续复利。
则根据单复利之间的关系In(1+R)=r 有:∑∑===+=+=365136513651)3651()1(t t tt rR In R In r同理,对任何时间间隔T 都有:∑∑===-==T t Tt t r T t S t S In T S T S In r 011))1()((1))0()((由中心极限定理知))0()((S T S In 服从正态分布。
即有: ))0()((S T S In ~),(2T T N σμ 式中μ,2σ分别为r t 的数学期望和方差 令))0()((S T S In y =,则y ~),(2T T N σμ,而y e S T S )0()(=进行简单的变量替换,可以求出S (T )的数学期望为:)21exp()0())((2T T S T S E σμ+=对于股票的二叉树定价来说,如果从t=0时刻到t=T ,时刻,所分的阶段数趋于无限大时,股票的价格也趋于对数正态分布。
即股票的二叉树定价和对数正态分布定价是一致的。
因为二叉树定价时股票的价格变化的规律是:⎩⎨⎧-=-qdq u t S t S 1)1()(按照概率按照概率所以 ⎩⎨⎧-=-qdq u t S t S In 1ln ln ))1()((按照概率按照概率即T t t S t S ,,2,1))1()(ln(=-服从两点分布且相互独立. 所以∑=-=Tt t S t S S T S 1))1()(ln())0()(ln(服从二项分布.当+∞→T ,二项分布趋近于正态分布。
即在一定的条件下,股票的二叉树定价和对数正态分布定价是一致的。
B-S 定价模型是二叉树定价模型的极限式。
三、布莱克-舒尔斯期权定价模型的直观理解 作为无现金股利的欧式买权定价模式是:012()()rT C S N d Xe N d -=-式中C 是买权价格,S 0是期初股票价格,N (·)是累计正态分布函数,201ln S r Td σ⎛⎫⎛⎫++ ⎪ ⎪=2021ln 2S r TX d d σσ⎛⎫⎛⎫+- ⎪ ⎪==-为了更容易从经济意义上理解B-S 定价模型,我们可以从现实直观的角度来作一些解释:已知 max(,0)T T C S X =-式中T C 为到期T 时买权的价格,T S 为到期标的股票市场价格X 为期权协定的执行价格。
则有 )]0,[m ax ()(X S E C E T T -=设到期XS T>的概率为P ,此时X S X S T T -=-)0,m ax (则有 ]0)1[(])([)(⨯-+->=P X X S S E P C E T T T])([X X S S E P T T ->⨯=考虑到期初的期权合理定价等于)(T C E 的现值而有)(T rt C E e C -=])([X X S S E eP T T rt->⨯⨯=- (1)式中C:期初期权合理价格,r :无风险连续复利率,t 到期时间长度这里关键的问题,要找出P 和)(X S S E T T >的表达式。
1) 由于0000()[()]1T T T S S XX P S X P P S S S S ⎛⎫>=>=- ⎪⎝⎭等价收益率2ln()()1X r TN σ--=-20ln()()S r T N σ+-==)(2d N 这是由于正态分布的对称性其中T S 服从对数正态分布S X 服从对数正态分布(0S 为常数))ln(0S X 服从正态分布。
收益率平均为*u ,22*σ+=ur 或22*σ-=r u 。
而且2σ和r 是以年为基础计算的,但期权通常不超一年。
T 为分数,应用2,rT Tσ代替2σ和r 。
即2()2r T σ-为新正态分布的期望值。
2) 由于T T XTT T dS S f SX S S E )(][⎰∞=>其中)(T S f 为对数正态分布密度函数212(ln )21S u T T TX S e dS S σ-∞-=⎰其中u 为T S ln 的均值,2σ是T S ln 的方差令S S T =ln)()(2121210ln 2)(2)(ln 2222d N d N e S ds edS ee rtxu S S u S xS ===⎰⎰∞----∞σσσπσπ其中注意到:22)]([2)(22222σσσσ++---=--u u S u S S 并且,r u e S e022=+σ式中t d d ttr X S d σσσ-=++=12201,)2()ln(将以上计算结果代入(1)式,得])()([)(2102X d N d N eS ed N C rtrt-⨯⨯=-)()(210d N Xed N S rt--=这便是有名的Black-Scholes 期权定价公式。
举例:已知股票期初市价500=S ,协议执行价X=45,距到期日时间t=3个月=0.25年无风险利率r=10%,2σ=0.16,4.0=σ则有: 7520.025.04.025.0)216.01.0()4550ln()2()ln(201=⨯⨯++=++=t t r X S d σσ 5520.025.04.07520.012=⨯-=-=t d d σ查正态分布表:N(1d )=N(0.7520)=0.7740 N(2d )=N(0.552)=0.709556.77095.0457740.05025.01.0=⨯-⨯=⨯-e C一般地,期权交易市场上买入的价格即由B-S 公式定价,如果实际市场价格比计算的价值低,说明期权的价格被低估,存在套利机会,可以买入期权。
四、B-S 期权定价模型微分方程推导的基本思路①随机方程(某变量以某种不确定的方式随时间变化) ②马尔可夫过程(随机过程变量的未来预测值只与该变量的当前值有关,而与该变量的过去值无关时,该随机过程称为马尔可夫过程) ③基本维纳过程(在t ∆内变量Z 的变化满足:εt Z ∆=∆,其中ε满足标准正态分布N(0,1)的一个随机值。
且两个不同的Z t ∆∆,的值相互独立) ④一般维纳过程(变量X 满足:εt badt bdz adt dx ∆+=+=)如图:一般维纳过程基本维纳过程⑤伊腾过程(S 遵循ITO 过程,即有dZ t S b dt t S a dS ),(),(+=变量G 是S 、t 的函数,G=F(S ,t),则G 也是ITO 过程,并且有:bdZ SGdt b S G t G a S G dG ∂∂+∂∂+∂∂+∂∂=)21(222 ⑥股票价格的ITO 过程(股价S 的变动可用瞬时期望漂移率为:uS ,瞬时方差率为22S σ的ITO 过程,即Sdz uSdt dS σ+=,即dz udt SdSσ+= 其中当股价的方差率恒为0时,则有uSdt dS =,得ut e S S 0=说明当方差率为0时,股价得单位时间为u 的连续复利方式增长。
五、关于对数正态分布我们已经知道很多独立同分布的随机变量之和趋于正态分布。
那么许多独立同分布随机变量的连乘积便服从于对数正态分布,即i ni n x X 1lim =∞→∏= 对数正态分布因为令x y ln =则∑∏=====ni i ni i x x x y 11ln ln ln 这是n 个随机变数之和,根据中心极限定理,y 趋于正态分布,如图:设1000=S ,每年增长10%则有 对数正态分布的密度函数100 110 121 200Xt r S x )1(0+=对数分布图:100200而且rt e x rt==ln ln 1 2 3 n lnxlnx0 1r 2r r n 2nr对数正态分布的密度函数:222)(ln 21σπσu x ex --x>0=)(x f0 x 0≤其中u 为x ln 的均值,2σ为x ln 的方差 注意到: 202σ+==u re S e EX所以 22σ+=u r 22σ-=r u考虑r 常指年利率,而期权利率常是几个月,如三个月25.0<t ,t r u )2(2σ-=。
