多项式四则运算
多项式运算初中数学知识点之多项式的四则运算法则

多项式运算初中数学知识点之多项式的四则运算法则多项式是数学中一个重要的概念,也是初中数学中需要掌握的知识点之一。
在多项式的学习中,四则运算是必不可少的一部分。
本文将介绍多项式的四则运算法则,以及它们的应用。
一、多项式的基本概念首先,我们来回顾一下多项式的基本概念。
多项式是由一系列代数式通过加法和减法运算组合而成的表达式。
它的形式可以表示为:P(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0其中,P(x)为多项式的表示形式,an, an-1, …, a1, a0为常数项,n为多项式的次数,x为变量。
二、多项式的四则运算法则1. 多项式的加法运算多项式的加法运算规则非常简单,只需要将对应的系数相加即可。
例如,对于两个多项式 P(x) = 3x^2 + 2x + 1 和 Q(x) = 2x^2 + 4x + 3,它们的和为:P(x) + Q(x) = (3x^2 + 2x + 1) + (2x^2 + 4x + 3)= 3x^2 + 2x^2 + 2x + 4x + 1 + 3= 5x^2 + 6x + 42. 多项式的减法运算多项式的减法运算也遵循类似的规则,即将对应的系数相减。
例如,对于两个多项式 P(x) = 3x^2 + 2x + 1 和 Q(x) = 2x^2 + 4x + 3,它们的差为:P(x) - Q(x) = (3x^2 + 2x + 1) - (2x^2 + 4x + 3)= 3x^2 - 2x^2 + 2x - 4x + 1 - 3= x^2 - 2x - 23. 多项式的乘法运算多项式的乘法运算是比加法和减法复杂一些的运算。
多项式的乘法运算需要使用分配律的原理,将每一项相乘后再进行合并。
例如,对于两个多项式 P(x) = 3x + 2 和 Q(x) = 2x^2 + 4x + 3,它们的乘积为:P(x) * Q(x) = (3x + 2) * (2x^2 + 4x + 3)= 3x * 2x^2 + 3x * 4x + 3x * 3 + 2 * 2x^2 + 2 * 4x + 2 * 3= 6x^3 + 12x^2 + 9x + 4x^2 + 8x + 6= 6x^3 + 16x^2 + 17x + 64. 多项式的除法运算多项式的除法运算是最为复杂的一种运算,需要使用长除法的方法进行计算。
多项式的加减乘除四则运算
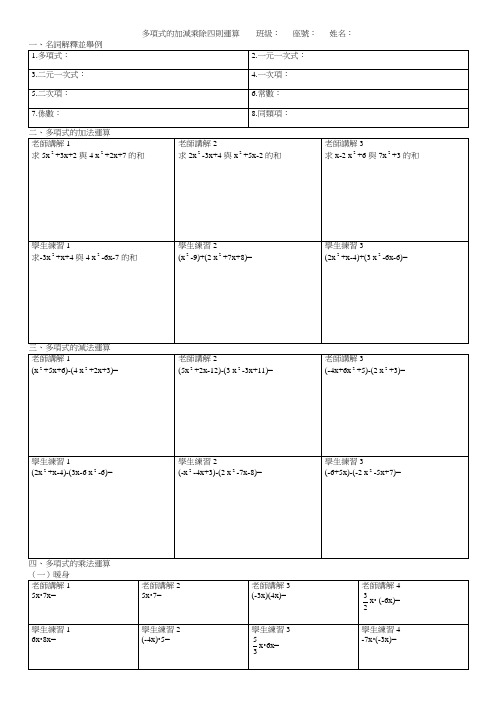
多項式的加減乘除四則運算班級:座號:姓名:
五、多項式的除法運算
四、十字交乘法(三項式) 班級:座號:姓名:
2
2. x2項的係數「不是1」的十字交乘法
二、完全平方數:背1~20的平方
三、平方根的定義
四、利用方格紙畫圖,作出面積是2 平方單位、5 平方單位、18平方單位的正方形-----介紹無理數
五、非完全平方數的平方根:根號引入的必須
六、利用方格紙畫圖,作出1、2、3、4、5、……. 、n
七、正數、零、負數的平方根
(一)正數:
(二)零:
(三)負數:
八、利用標準分解式計算平方根
九、十分逼近法:求無理數的近似值
十、電算器求平方根
一元二次方程式班級:座號:姓名:
5. a x2+bx+c=0,a和b 和c是常數(、十字交乘法)
6. 綜合題
7. 應用問題。
补充教材:多项式的四则运算

多项式的四则运算【1】下列何者为x 的多项式?(A) x 2+2x +y1 (B) x 2+x +2 (C) x 2y +3++y y x(D) x 2+1+x (E)11+x +2x +1。
[解答]:(A)(C)【详解】:x 的多项式需x 的乘方是0或自然数。
(B)中x =x 21,乘方21非自然数。
(D)中x 没有次数。
(E)中11+x =(x +1)-1均非x 之多项式。
【2】f(x)=2x 3-5x 2-8x +a ,g(x)=x 2-4x +b ,f(x)是g(x)的倍式,则a = ,b =[解答]:a =6,b =2【详解】:3-5x 2-8x +a 是g(x)=x 2-4x +b 的倍式,即g(x)整除f(x),用综合除法 b余式为0,故4-2b =0,a -3b =0得b =2,a =6【3】18x 4-3x 3-7x 2+11x -3除以3x 2+2x -1的商为 ,余式为 。
[解答]:6x 2-5x +3,0【4】设多项式f(x)被ax -b(a ≠0)除之商为q(x),余式为r ,下列何者为真?(A)以x -ab除f(x)之余式为ar 。
(B) f(bx)被ax -1除之余式为r 。
(C) f(bx)被ax -1除之商为bq(x)。
(D) af(x)被x -ab除之余式为ar 。
(E) xf(x)被x -a b 除之余式为abr。
[解答]:(B)(D)(E)【详解】:由已知f(x)=(ax -b)q(x)+r ,(A) f(x)=(x -ab).aq(x)+r ,商为aq(x),余式r 。
(B) f(bx)=(abx -b)q(bx)+r =(ax -1).bq(bx)+r ,商为bq(bx),余式r 。
(C)商为bq(bx),非bq(x)。
(D) af(x)=(ax -b)aq(x)+ar =(x -ab)a 2q(x)+ar ,商为a 2q(x),余式ar 。
多项式地四则运算

适用标准多 式的四 运算 回 上 的知 :〔1〕 式: 含有一些数和字母的乘法〔包含乘法〕运算的式子叫做 式注意: 的一个数字和字母也是 式1:以下 式各是几次 式?它 的系数各是多少?2ab 、5m 5 n 3 、 0.75v 2 t 2 、 xyz 、3xy10( 2〕同 式〔同 〕 :假如在几个 式中,不论它 的系数是不是同样,只需它 所含的字母同样, 并且同样字母的指数也分 同样, 那么, 几个 式就叫做同 式, 称同注意:全部的常数都是同2:〔 1〕以下各 中的两个 是不是同 , 什么?1ab 3 和4 b 3 a 4abc 和 4ab0.2x 2 y 和 0.2xy 233和mn2x 3和 2 x212和-6mn把以下各 式按同 分 ,能分出几 ?3-7 、 6x 、 1x 3y 、2 、xyz 、0.5yx 3、 5zyx 、x y、 0.1x 、 9 yxz 、 10yx325( 3〕多 式:由有限个 式的代数和 成的式子,叫做多 式 :多 式里的每个 式叫做多 式的常数 :不含字母的 ,叫做常数例 如 : 3x 0 . 5x 2、2 x 33x 2、 xy 3x5y 1 、 a 2 ab b 2、2 x3 y 3 2.13x 2 8z ⋯⋯⋯⋯都是多 式 7( 4〕归并同 : 把同 式的相加和相减。
其法 是把同 式的系数相加和相减,而 式中的字母及 些字母的乘方指数不 , 归并同 的依据是交 律、 合律以及分派律因为 式是一些数与拥有数系运算通性的字母的方 所 成的, 就是 , 式加、 乘足交 律、乘 足交 律、 合律以及分派律 3:归并以下同 〔1〕 x 2x 3x 4 x〔2〕2xy2xy 23xy22xy 2〔3〕7 x32x35x30.5 x30.7 x3归并以下各式中的同〔1〕4x28x 5 3x26x 2〔2〕4a2+3b22ab 4a22b2b2〔3〕x5x34x22x52x23x4〔4〕a2bc10abc215a2bc abc22a2bc 3abc2把 (a b) 作一个因式,归并同〔1〕5(a b) 4(a b) 10(a b)〔2〕3(a b)2( a b) 2(a b) 2( a b)34(a b) 2(a b) 3(5〕元数:代数学中,经常把字母 x、 y、z⋯⋯未知数,在多式中,所含的不一样未知数的个数,称个多式的元数数:归并同此后,多式所含式的个数,称个多式的数多式次数:多式归并同后,所含各式中最高次的次数,就称个多式的次数4:将以下多式先归并同,而后按所含字母降次摆列,并指出它的元数、次数、数〔1〕2x51x5 3 x52〔2〕3x24x27 x3x31〔3〕3 2 y2 3 y 4 y33y2 2 y35〔4〕1x2 5 x2 1 x4x x37 362〔5〕2 y223 y349 y33y 222y 2 y y 1〔6〕5xy3x4y x68x3y42y 1〔按x降次摆列〕知识点一:多项式的值新课内容:任何一个多项式,就是一个用加、减、乘方运算把数和未知数连结起来的式子。
初中数学多项式的四则运算公式定理

初中数学多项式的四则运算公式定理1 单项式与多项式仅含有一些数和字母的乘法(包括乘方)运算的式子叫做单项式单独的一个数或字母也是单项式单项式中的数字因数叫做这个单项式(或字母因数)的数字系数,简称系数当一个单项式的系数是1或-1时,〝1〞通常省略不写一个单项式中,所有字母的指数的和叫做这个单项式的次数如果在几个单项式中,不管它们的系数是不是相同,只要他们所含的字母相同,并且相同字母的指数也分别相同,那么,这几个单项式就叫做同类单项式,简称同类项所有的常数都是同类项12 多项式有有限个单项式的代数和组成的式子,叫做多项式多项式里每个单项式叫做多项式的项,不含字母的项,叫做常数项单项式可以看作是多项式的特例把同类单项式的系数相加或相减,而单项式中的字母的乘方指数不变在多项式中,所含的不同未知数的个数,称做这个多项式的元数经过合并同类项后,多项式所含单项式的个数,称为这个多项式的项数所含个单项式中最高次项的次数,就称为这个多项式的次数13 多项式的值任何一个多项式,就是一个用加、减、乘、乘方运算把数和未知数连接起来的式子14 多项式的恒等对于两个一元多项式f(x)、g(x)来说,当未知数x同取任一个数值a时,如果它们所得的值都是相等的,即f(a)=g(a),那么,这两个多项式就称为是恒等的记为f(x)==g(x),或简记为f(x)=g(x) 性质1 如果f(x)==g(x),那么,对于任一个数值a,都有f(a)=g(a) 性质2 如果f(x)==g(x),那么,这两个多项式的个同类项系数就一定对应相等15 一元多项式的根一般地,能够使多项式f(x)的值等于0的未知数x的值,叫做多项式f(x)的根2 多项式的加、减法,乘法21 多项式的加、减法22 多项式的乘法单项式相乘,用它们系数作为积的系数,对于相同的字母因式,那么连同它的指数作为积的一个因式3 多项式的乘法多项式与多项式相乘,先用一个多项式等每一项乘以另一个多项式的各项,再把所得的积相加23 常用乘法公式公式I 平方差公式(a+b)(a-b)=a^2-b^2两个数的和与这两个数的差的积等于这两个数的平方差公式II 完全平方公式(a+b)^2=a^2+2ab+b^2(a-b)^2=a^2-2ab+b^2两数(或两式)和(或差)的平方,等于它们的平方和,加上(或减去)它们积的2倍3 单项式的除法两个单项式相除,就是它们的系数、同底数的幂分别相除,而对于那些只在被除式里出现的字母,连同它们的指数一起作为商的因式,对于只在除式里出现的字母,连同它们的指数的相反数一起作为商的因式一个多项式处以一个单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
多项式的定义及四则运算

多项式的定义及四则运算多项式是数学中常见的一种函数。
它由若干个单项式组成,每个单项式都是由常数项和变量的一次或多次幂组成。
例如,$x^3+3x^2+2x+1$就是一个多项式。
本文将介绍多项式的定义及其四则运算。
1. 多项式的定义在数学中,多项式的定义如下:一个多项式$f(x)$是由若干单项式相加或相减而成的。
每个单项式可以有系数和一个或多个变量的一次或多次幂。
多项式的次数是最高次单项式的次数,并且多项式中所有单项式的次数都不能超过最高次数。
例如,$x^3+3x^2+2x+1$的次数是3。
2. 多项式的四则运算(1) 加法多项式加法是指将两个多项式的各项系数对应相加,形成一个新的多项式。
例如,$(x^2+3x-4)+(2x^2+5x+1)=3x^2+8x-3$。
(2) 减法多项式减法是指将两个多项式的各项系数对应相减,形成一个新的多项式。
例如,$(x^2+3x-4)-(2x^2+5x+1)=-x^2-2x-5$。
(3) 乘法多项式乘法是指将两个多项式的每一项相乘,并将结果相加,形成一个新的多项式。
例如,$(x^2+3x-4)\times(2x^2+5x+1)=2x^4+11x^3-5x^2-7x-4$。
(4) 除法多项式除法是指将一个多项式整除另一个多项式并得到商和余数。
例如,$(2x^2+3x-4)\div(x-2)=2x+7$,余数是$-10$。
3. 多项式的常见形式多项式有几种常见的形式。
例如:(1) 一般式:$a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$。
(2) 二次式:$ax^2+bx+c$,其中$a,b,c$都是实数且$a\neq0$。
(3) 因式分解式:$a(x-p_1)(x-p_2)...(x-p_n)$,其中$a$是常数,$p_1,p_2,...,p_n$是不同的实数。
(4) 标准式:$y=a(x-h)^2+k$,其中$a,h,k$是实数,$a\neq0$。
初等数学--多项式

初等数学--多项式
•多项式的四则运算
•多项式的最大公因子
多项式
代数中多项式的应用十分广泛,比如经济领域、工程领域、科学领域等。
本章介绍什么是多项式,它的数学运算是怎样的。
多项式的四则运算
单项式、二项式、三项式、多项式
单项式:只有一个项的表达式
二项式:有两个项的表达式
三项式:有三个项的表达式
多项式:有两个及以上的项的表达式
多项式的次数
这里我们讨论是只含有一个变量的多项式的次数。
多项式的次数和项的次数取决于变量的指数。
•项的次数是变量的指数值
•常数项的次数为0
•多项式的次数是最高次数项对应的次数
四则运算
•多项式的加减即是合并同类项 - 有相同指数的变
量对应的系数进行加减
•多项式的乘除 - 变量之间指数相加或相减,常数
项与一般项的系数相乘
同类项中指数相加,常数项与一般项系数相乘
系数相乘,同变量项的指数相加
单项式与三项式相乘
二项式相乘(多项式相乘过程相同)
不同项式相乘
项的乘除
多项式的最大公因子
因式分解与我们前面讲到的求分数分母的最小公倍数比较类似,这里是把多项式分解几个因子项相乘的形式。
因式分解是找到多个表达式之间的最大公因子,它的方法与找最小公倍数类似。
【参考出等数学22-分数】
对于24, 36 经过因子树或梯形模型找到的最大公因子是12,即
24 = 12 * 2
36 = 12 * 3
对于含变量的因式分解,12x2 与 18x3 可知,它们的最大公因子是6x2。
多项式的四则运算

摘要在算法程序的设计与编写过程中,根据对本题的要求分析,结合设计对象的特点,实现一元多项式的加、减、乘、除以及对多项式求导、求值的相关计算。
根据一元多项式的结构特点和运算规则。
本程序中采用了链表的存储与实现,采用链表可以很方便的对其中的结点进行插入、删除等操作。
通过链表的合并即可完成多项式的四则运算。
1 引言:1.1 待处理问题的问题背景:本题要求对从键盘上输入的任意两个一元多项式,能够分别对每个多项式进行降幂排序并输出,实现对这两个多项式的加、减、乘、除等相关运算。
在具体实现时,可采用链式存储结构将多项式中的每一项连接起来,从而表达出整个多项式,其中每一项是一个一元多项式,通过每一项系数与指数的输入设定,可以实现对整个多项式的设定,再通过建立单链表,结点来存储每一项的系数与指数,通过链表完成多项式的存储,对每个多项式分别建立一个链表,通过链表的加减乘除运算规则实现连标的合并,最终得到计算结果。
2需要完成的任务:根据题目要求,本程序需要实现对两个一元多项式的四则运算以及对多项式进行赋值求值运算、求导运算等相关计算,要求正确输出运算结果,对不满足输入要求的数据有一定的反应。
3设计:3.1核心算法的设计与说明:3.1.1 一元多项式的定义:有多个单项式的代数和就构成了多项式,一元多项式就是只含有一个变元的多项式。
所以由定义可知有n个单项式组成的一元多项式来说,它的运算是满足交换率的,所以可进行降幂排序,只需将它的所有指数相比较,然后将指数大的放前面,小的放后面即可完成排序。
3.1.2本题的核心算法:首先调用建表函数,CreatePolyn建立两个一元多项式,然后对两个一元多项式进行降幂排序,该过程的实现主要由insert()函数实现,然后调用相应的计算函数: 加(AddPolyn)、减(SubtractPolyn)、(MultiplyPolyn)、除(DevicePolyn)、导数(Derivative)、求值(ValuePolyn)。
多项式的运算与应用

又 f (x) 除以 x-2 的余式为 4,故由余式定理知 f (2) = 4
代入 x = 1 及 x = 2
得
f f
(1) a b 2 ,即 (2) 2a b 4
a b 2
2a
b
4
,可解得
a b
2 0
所以 f ( x) ( x 1)( x 2)q( x) 2x
r
(ax
b)
1 a
q(
x)
r
所以 f (x) 除以 ax-b 的商式是 1 q( x),余式仍然是 r。 a
Page 16/36
5 p.86
若多项式 f ( x) 2x3 x2 3x 4 a( x 1)3 b( x 1)2 c( x 1) d, 其中 a,b,c,d 是常数,试求: (1) a,b,c,d 之值。
(2) 题目条件表示 x4 与 x3 的系数皆为 0
因此 a 2 0,且 b 1 0,故 a 2,b 1
故此多项式为 x2 (2)2 1 3 x2 2 即常数项为 2
多项式的定义 p.76 ~ p.78
Page 4/36
两多项式相等: 当两多项式相对应的每一单项的系数都相同,则称这 两个多项式相等。
将此式改写成
f (x)
2g(
x )
1 2
q(
x)
r(
x)
这表示 f (x) 除以 2g(x) 的商式是 1 q( x) , 2
余式仍然是 r (x)
Page 10/36
数学中的代数运算

数学中的代数运算代数是数学中的一个重要分支,研究数的性质和运算规律,它的核心就是代数运算。
代数运算是指通过一系列运算法则对数进行操作和变换,以求出结果或解决问题。
在数学中,代数运算包括四则运算、指数运算、多项式运算等,下面将针对这些代数运算进行详细阐述。
一、四则运算四则运算是最基本、最常见的运算方式,包括加法、减法、乘法和除法。
下面将逐个进行说明。
1. 加法运算加法是最基础的运算,其运算法则为“两数相加,结果为和”。
例如,对于两个数a和b,它们的和可以表示为a + b。
在加法运算中,顺序可以变化,即满足交换律。
例如,a + b = b + a。
2. 减法运算减法是加法的逆运算,也是常见的运算方式。
其运算法则为“被减数减去减数,结果为差”。
例如,对于两个数a和b,它们的差可以表示为a - b。
需要注意的是,在减法运算中,减数必须小于或等于被减数,否则结果将会为负数。
减法运算不满足交换律,即a - b不等于b - a。
3. 乘法运算乘法是指将两个数相乘得到一个新的数,结果称为积。
乘法的运算法则为“两数相乘,结果为积”。
例如,对于两个数a和b,它们的积可以表示为a * b。
在乘法运算中,顺序可以变化,即满足交换律。
例如,a * b = b * a。
4. 除法运算除法是乘法的逆运算,其运算法则为“被除数除以除数,结果为商”。
例如,对于两个数a和b,它们的商可以表示为a / b。
在除法运算中,除数不能为0,否则结果将无意义。
除法运算不满足交换律,即a / b不等于b / a。
二、指数运算指数运算是指将一个数乘以自身多次得到的运算方式,其中,第一个数称为底数,第二个数称为指数。
指数运算可以用于表示大数字或进行数的近似计算等。
1. 正整数指数运算正整数指数运算是指指数为正整数的运算方式。
例如,对于一个数a,它的n次方可以表示为a的n次方,记作a^n。
在正整数指数运算中,底数不为0,指数为正整数。
例如,2^3表示2的3次方,即2 * 2 * 2。
多项式的四则运算解读

(4) (a b)(a 2 ab b 2 ) a 3 b3
(5) (a b)(a 2 ab A與B, 若A除以B的商式為Q,餘式為R, 即 A B Q R, 則 A B Q R 或 A Q R B B
第一章
數與式
1-2 多項式的四則運算
1-2
多項式的四則運算
1. 多項式
2. 多項式的相等
3. 多項式的乘法公式 4. 多項式的除法定理
多項式
每一個x的一元多項式,都可以寫 成如:
f ( x) an x n an1x n1 a1x a0
若an≠0,則an稱為領導係數,
多項式f (x)的次數為n次,
多項式的除法
多項式的除法須注意下列事項:
(1) 商式Q的次數為被除式 A 的次數減除式 B 的次數。 (2) 若餘式 R = 0,則 B 整除 A。 (3) 若餘式 R 0,R 的次數一定小於除式 B 的次數。
…… b1 x b0
若 f ( x) g ( x) ,則
an bn,an1 bn1 ,…… ,a1 b1,a0 b0
多項式的乘法公式
(1) (a b) 2 a 2 2ab b 2
(2) (a b) 2 a 2 2ab b 2
a0稱為常數項。
常數多項式
c (c 0),稱為零次多項式
f(x)=
0,稱為零多項式
零次多項式的次數為0,零多項式不
規定它的次數。
多項式的相等
設多項式
f ( x) an x n an1 x n1 …… a1 x a0 g ( x) bn x bn1 x
n n1
练习:多项式的运算与应用

(2) 常数项为 f(0)=(0-0+0+1)3=1
(3) f(-1)=(-1+2-1+1)3=13=1
偶次项系数和为 f(1)+f(-1)=1+1=1
2
2
(4) 奇次项系数和为 f(1)-f(-1)=1-1=0
2
2
上一题 下一题
主题 2 多项式的四则运算
例题 6 多项式的加法
计算下列各式: (1) (3x2-2x-3)+(x3+5x-4)。 (2) (2x4+x3+1)+(2x4-x3+2x2+1)。 解■ (1) (3x2-2x-3)+(x3+5x-4)
(2) 设 a,b,c,d 是实数,若多项式(a-1)x3+bx2+(c+2)x+d 为零多项式,试求 a,b,c,d 的值。
解■ (1) f(x)最高次项为 x3,故 deg(f(x))=3 又 x2 项的系数为-2,常数项为 4
(2) 因(a-1)x3+bx2+(c+2)x+d 为零多项式 得 a-1=0,b=0,c+2=0,d=0 故 a=1,b=0,c=-2,d=0
1-1) 6+ 5+ 0+ 1
6- 6
11+ 0
11- 11
11 + 1
11 - 11
12
商式为 6x2+11x+11,余式为 12
例题 9 多项式的除法
试求下列各式的商式及余式: (3) (3x3+4x2+2x+7)÷(x2+x-2)。
解■ (3)
3+1
1+1-2)3 + 4 + 2 + 7
五入)
例题 13 连续综合除法
解■ (1) 计算 f(x)对 x+2 的连续综合除法 1 +3 +0 -5 + 8 -2 -2 -2 +4 + 2 1 +1 -2 -1 +10 ……e -2 +2 +0 1 -1 +0 -1 ……d -2 +6 1 -3 +6 ……c -2 1 -5 ……b a f(x)=(x+2)4-5(x+2)3+6(x+2)2-(x+2)+10
初中数学多项式的四则运算

初中数学多项式的四则运算
各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢
单项式与多项式
仅含有一些数和字母的乘法运算的式子叫做单项式单独的一个数或字母也是单项式
单项式中的数字因数叫做这个单项式的数字系数,简称系数
当一个单项式的系数是1或-1时,“1”通常省略不写
一个单项式中,所有字母的指数的和叫做这个单项式的次数
如果在几个单项式中,不管它们的系数是不是相同,只要他们所含的字母相同,并且相同字母的指数也分别相同,那么,这几个单项式就叫做同类单项式,简称同类项所有的常数都是同类项
1多项式
有有限个单项式的代数和组成的式
子,叫做多项式
多项式里每个单项式叫做多项式的项,不含字母的项,叫做常数项
单项式可以看作是多项式的特例
把同类单项式的系数相加或相减,而单项式中的字母的乘方指数不变
在多项式中,所含的不同未知数的个数,称做这个多项式的元数经过合并同类项后,多项式所含单项式的个数,称为这个多项式的项数所含个单项式中最高次项的次数,就称为这个多项式的次数
2多项式的值
任何一个多项式,就是一个用加、减、乘、乘方运算把已知数和未知数连接起来的式子
3多项式的恒等
对于两个一元多项式f、g来说,当未知数x同取任一个数值a时,如果它们所得的值都是相等的,即f=g,那么,这两个多项式就称为是恒等的记为f==g,或简记为f=g
各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢。
初中数学多项式的四则运算公式定理_公式总结

初中数学多项式的四则运算公式定理_公式总结1 单项式与多项式仅含有一些数和字母的乘法(包括乘方)运算的式子叫做单项式单独的一个数或字母也是单项式单项式中的数字因数叫做这个单项式(或字母因数)的数字系数,简称系数当一个单项式的系数是1或-1时,“1”通常省略不写一个单项式中,所有字母的指数的和叫做这个单项式的次数如果在几个单项式中,不管它们的系数是不是相同,只要他们所含的字母相同,并且相同字母的指数也分别相同,那么,这几个单项式就叫做同类单项式,简称同类项所有的常数都是同类项12 多项式有有限个单项式的代数和组成的式子,叫做多项式多项式里每个单项式叫做多项式的项,不含字母的项,叫做常数项单项式可以看作是多项式的特例把同类单项式的系数相加或相减,而单项式中的字母的乘方指数不变在多项式中,所含的不同未知数的个数,称做这个多项式的元数经过合并同类项后,多项式所含单项式的个数,称为这个多项式的项数所含个单项式中最高次项的次数,就称为这个多项式的次数13 多项式的值任何一个多项式,就是一个用加、减、乘、乘方运算把已知数和未知数连接起来的式子14 多项式的恒等对于两个一元多项式f(x)、g(x)来说,当未知数x同取任一个数值a时,如果它们所得的值都是相等的,即f(a)=g(a),那么,这两个多项式就称为是恒等的记为f(x)==g(x),或简记为f(x)=g(x)性质1 如果f(x)==g(x),那么,对于任一个数值a,都有f(a)=g(a)性质2 如果f(x)==g(x),那么,这两个多项式的个同类项系数就一定对应相等15 一元多项式的根一般地,能够使多项式f(x)的值等于0的未知数x的值,叫做多项式f(x)的根2 多项式的加、减法,乘法21 多项式的加、减法22 多项式的乘法单项式相乘,用它们系数作为积的系数,对于相同的字母因式,则连同它的指数作为积的一个因式3 多项式的乘法多项式与多项式相乘,先用一个多项式等每一项乘以另一个多项式的各项,再把所得的积相加23 常用乘法公式公式I 平方差公式(a+b)(a-b)=a^2-b^2两个数的和与这两个数的差的积等于这两个数的平方差公式II 完全平方公式(a+b)^2=a^2+2ab+b^2(a-b)^2=a^2-2ab+b^2两数(或两式)和(或差)的平方,等于它们的平方和,加上(或减去)它们积的2倍3 单项式的除法两个单项式相除,就是它们的系数、同底数的幂分别相除,而对于那些只在被除式里出现的字母,连同它们的指数一起作为商的因式,对于只在除式里出现的字母,连同它们的指数的相反数一起作为商的因式一个多项式处以一个单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加。
多项式的四则运算

多项式的四则运算一、单项式与多项式1 仅含有一些数和字母的乘法(包括乘方)运算的式子叫做单项式单独的一个数或字母也是单项式单项式中的数字因数叫做这个单项式(或字母因数)的数字系数,简称系数当一个单项式的系数是1或-1时,“1”通常省略不写一个单项式中,所有字母的指数的和叫做这个单项式的次数如果在几个单项式中,不管它们的系数是不是相同,只要他们所含的字母相同,并且相同字母的指数也分别相同,那么,这几个单项式就叫做同类单项式,简称同类项所有的常数都是同类项2 多项式有有限个单项式的代数和组成的式子,叫做多项式多项式里每个单项式叫做多项式的项,不含字母的项,叫做常数项单项式可以看作是多项式的特例把同类单项式的系数相加或相减,而单项式中的字母的乘方指数不变在多项式中,所含的不同未知数的个数,称做这个多项式的元数经过合并同类项后,多项式所含单项式的个数,称为这个多项式的项数所含个单项式中最高次项的次数,就称为这个多项式的次数3 多项式的值任何一个多项式,就是一个用加、减、乘、乘方运算把已知数和未知数连接起来的式子4 多项式的恒等对于两个一元多项式f(x)、g(x)来说,当未知数x同取任一个数值a时,如果它们所得的值都是相等的,即f(a)=g(a),那么,这两个多项式就称为是恒等的记为f(x)==g(x),或简记为f(x)=g(x)性质1 如果f(x)==g(x),那么,对于任一个数值a,都有f(a)=g(a)性质2 如果f(x)==g(x),那么,这两个多项式的个同类项系数就一定对应相等5 一元多项式的根一般地,能够使多项式f(x)的值等于0的未知数x的值,叫做多项式f(x)的根二、多项式的加、减法,乘法1 多项式的加、减法2 单项式的乘法单项式相乘,用它们系数作为积的系数,对于相同的字母因式,则连同它的指数作为积的一个因式3 多项式的乘法多项式与多项式相乘,先用一个多项式等每一项乘以另一个多项式的各项,再把所得的积相加4 常用乘法公式公式I :平方差公式(a+b)(a-b)=a^2-b^2两个数的和与这两个数的差的积等于这两个数的平方差公式II :完全平方公式(a+b)^2=a^2+2ab+b^2(a-b)^2=a^2-2ab+b^2两数(或两式)和(或差)的平方,等于它们的平方和,加上(或减去)它们积的2倍三、单项式的除法两个单项式相除,就是它们的系数、同底数的幂分别相除,而对于那些只在被除式里出现的字母,连同它们的指数一起作为商的因式,对于只在除式里出现的字母,连同它们的指数的相反数一起作为商的因式。
高中数学核心素养新版教案

高中数学核心素养新版教案
教学内容:多项式的四则运算
教学目标:
1. 能够熟练进行多项式的加法、减法、乘法和除法运算。
2. 能够应用多项式的四则运算解决实际问题。
3. 培养学生的逻辑思维能力和分析问题的能力。
教学重点和难点:
1. 多项式的乘法运算及乘法的规则。
2. 多项式的除法运算及除法的规则。
教学步骤:
一、导入(5分钟)
介绍本节课的教学内容和目标,引出多项式的四则运算。
二、讲解(15分钟)
1. 多项式的加法和减法规则。
2. 多项式的乘法规则和应用。
3. 多项式的除法规则和注意事项。
三、练习(20分钟)
1. 练习多项式的加法和减法。
2. 练习多项式的乘法。
3. 练习多项式的除法。
四、拓展(10分钟)
运用多项式的四则运算解决实际问题,提高学生的应用能力。
五、总结(5分钟)
总结本节课的内容,强化学生对多项式四则运算的理解。
六、作业布置(5分钟)
布置相关作业,梳理知识点。
七、课后反思(5分钟)
反思教学过程,总结教学效果,并做相应调整。
教学工具:教材、黑板、彩色粉笔、练习册等。
教学方法:讲解、练习、拓展、总结、课后反思。
教学评价:根据学生的课堂表现和作业成绩进行评价,及时反馈学生的学习情况。
多项式的四则运算

1§多項式的四則運算z ,y ,x 等,經過加、減、乘的運算後所形成之式子,就叫多項式。
2.定義:形如∑=--=++++=nk k k n n nn x a a x a xa x a x p 0111...)( ,其中n 是正整數或零;a a a a n n ,,...,,11-都是數,此式子稱為x 的多項式,此時k a 稱為k 次項的係數, a 稱為常數項。
係數可以是整數、有理數、實數或複數。
3.所有整係數多項式所成集合稱為整係數多項式集,以][x Z 表示。
同理,以][],[],[x C x R x Q 分別表有理係數多項式集、實係數多項式集、複係數多項式集。
4.次數:當0≠n a 時,n 叫做多項式)(x p 的次數,以n x p =)(deg 表示,而n a 稱為)(x p 的領導(首項)係數。
5.常數多項式:只有0a 項的多項式稱之,有兩種:(1)零多項式:即為0,沒有次數。
(2)零次多項式:除零多項式外之常數多項式,其次數為0。
6.排列方式:多項式之次數由小而大的排列方式稱為升冪排列,反之則稱為降冪排列。
7.多項式相等:設n n x a x a x a a x p ++++= 2210)(,m m x b x b x b b x q ++++= 2210)(為兩多項式,其中0,≠m n b a ,則)()(x q x p =的充要條件為n m =且i b a i i ∀=,。
※0111)(a x a x a x a x f n n n n ++++=-- ,0 N n ∈,0≠n a ,n x f =))(deg(,n a :領導係數若0))(deg(=x f ⎩⎨⎧≠=:零次多項式,:零多項式,)(0)(00x f a x f a※多項式之文字符號不可在絕對值,分母,根號。
2(A)x + 3 (B) 2x + 1 (C) x 2 +3x + 1 (D)x1(E) | x |。
1-4-1多项式-多项式的四则运算

除法原理:
設 f (x) 與 g(x) 是兩個多項式且 g(x) = (x − c) 不是零多項式,
則有唯一的多項式 q(x) 與 r(x) ,
使得 f (x) = g(x)q(x) + r(x)
且 r(x) = 0 或 deg r(x) < deg g(x) 。
【問題】
若 f (x) 除以 (ax − b) 之商為 q(x) 、餘式為 r ,則 f (x) 除以 (x − b ) 之商及餘式各為 a
141多项式多项式的四则运算多项式的运算多项式运算若多项式2x的四次方四则运算四则混合运算练习题四则混合运算若多项式x的平方多项式的次数四则运算练习题
4-1 多項式-多項式的四則運算
【定義】 多項式的定義: x 與實數的加減乘所組成的式子稱為 x 的多項式,即形如 f (x) = an x n + an−1xn−1 + " + a1x + a0 的式子,稱為 x 的多項式,其中 an , an−1,", a1, a0 稱為多項式 f (x) 的係數,且若 an ≠ 0 時, an 稱為領導(首項)係 數, a0 稱為常數項。 次數: f (x) 中係數非零者中,次數最高者稱為 f (x) 的次數,記為 deg f (x) = n ,此時 f (x) 稱為 n 次多項式。 單項式: 只含一個項的多項式。 常數多項式: f (x) = c, c ≠ 0 時,稱零次多項式,其次數為零次。 f (x) = 0 時,稱零多項式,不 定義次數。 多項式的相等: 設 f (x) = an x n + an−1x n−1 + " + a1x + a0 , g(x) = bm x m + bm−1x m−1 + " + b1x + b0 ,則 f (x) = g(x) 的充要條件為 n = m, an = bm ,", a1 = b1, a0 = b0 。 【性質】 多項式的排列方法有: 1. 遞增排列(升羃排列),形如 f (x) = a0 + a1x + " + an−1x n−1 + an x n 。 2. 遞減排列(降羃排列),形如 f (x) = an x n + an−1x n−1 + " + a1x + a0 。 多項式的呈現方法有: 1. 因式形(多用於求解),形如 f (x) = (x − x1 )(x − x2 )"(x − xn ) 。 2. 層套形(多用於計算器求值),形如 f (x) = x(x(ax + b) + c) + d 。 若一個多項式 f (x) 的每項係數都屬於同一個集合 S ,就稱 f (x) 是布於 S 的多項 式,記為 f (x) ∈ S[x]。一般討論的有 Z ,Q, R,C 等情形,即整系數多項式、有理系 數多項式、實系數多項式、複數系數多項式、,且在各種集合中的因式分解方法 不盡相同。 【定義】 多項式的加法、減法: 設 f (x) = an x n + an−1x n−1 + " + a1x + a0 , g(x) = bm x m + bm−1x m−1 + " + b1x + b0 , n ≥ m ,則 f (x) + g(x) = (an + bn )x n + " + (am + bm )x m + " + (a1 + b1 )x + (a0 + b0 ) f (x) − g(x) = (an − bn )x n + " + (am − bm )x m + " + (a1 − b1 )x + (a0 − b0 ) 且 deg( f (x) + g(x)) ≤ max(deg f (x), deg g(x)) 。 多項式的乘法: 設 f (x) = an x n + an−1x n−1 + " + a1x + a0 , g(x) = bm x m + bm−1x m−1 + " + b1x + b0 , n ≥ m ,則 f (x) × g(x) = anbm x n+m + " + (a1b0 + a0b1 )x + a0b0 。 且當 f (x) ≠ 0, g(x) ≠ 0 時, deg( f (x) × g(x)) = deg f (x) + deg g(x) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多项式四则运算运行图:源代码:// 多项式加减乘除-02.cpp : 定义控制台应用程序的入口点。
//#include "stdafx.h"int _tmain(int argc, _TCHAR* argv[]){return 0;}#include<stdio.h>#include<malloc.h>typedef struct Polynomial{float coef;int expn;struct Polynomial *next;}*Polyn,Polynomial;void Insert(Polyn p,Polyn h){if(p->coef==0)free(p);else{Polyn q1,q2;q1=h;q2=h->next;while(q2&&p->expn<q2->expn){q1=q2;q2=q2->next;}if(q2&&p->expn==q2->expn){q2->coef+=p->coef;free(p);if(!q2->coef){q1->next=q2->next;free(q2);}}else{p->next=q2;q1->next=p;}}}Polyn CreatePolyn(Polyn head,int m){int i;Polyn p;p=head=(Polyn)malloc(sizeof(struct Polynomial));head->next=NULL;for(i=0;i<m;i++){p=(Polyn)malloc(sizeof(struct Polynomial));printf("请输入第%d项的系数与指数:",i+1);scanf_s("%f %d",&p->coef,&p->expn);Insert(p,head);}return head;}void DestroyPolyn(Polyn p){Polyn q1,q2;q1=p->next;q2=q1->next;while(q1->next){free(q1);q1=q2;q2=q2->next;}}void PrintPolyn(Polyn P){Polyn q=P->next;int flag=1;if(!q){putchar('0');printf("\n");return;}while (q){if(q->coef>0&&flag!=1)putchar('+');if(q->coef!=1&&q->coef!=-1){printf("%g",q->coef);if(q->expn==1) putchar('X');elseif(q->expn)printf("X^%d",q->expn);}else{if(q->coef==1){if(!q->expn)putchar('1');else if(q->expn==1)putchar('X');else printf("X^%d",q->expn);}if(q->coef==-1){if(!q->expn)printf("-1");else if(q->expn==1)printf("-X");else printf("-X^%d",q->expn);}}q=q->next;flag++;}printf("\n");}int compare(Polyn a,Polyn b){if(a&&b){if(!b||a->expn>b->expn)return 1;elseif(!a||a->expn<b->expn)return -1;elsereturn 0;}else if(!a&&b)return -1;elsereturn 1;}Polyn AddPolyn(Polyn pa,Polyn pb){Polyn qa=pa->next;Polyn qb=pb->next;Polyn headc,hc,qc;hc=(Polyn)malloc(sizeof(struct Polynomial));hc->next=NULL;headc=hc;while(qa||qb){qc=(Polyn)malloc(sizeof(struct Polynomial));switch(compare(qa,qb)){case 1:{qc->coef=qa->coef;qc->expn=qa->expn;qa=qa->next;break;}case 0:{qc->coef=qa->coef+qb->coef;qc->expn=qa->expn;qa=qa->next;qb=qb->next;break;}case -1:{qc->coef=qb->coef;qc->expn=qb->expn;qb=qb->next;break;}}if(qc->coef!=0){qc->next=hc->next;hc->next=qc;hc=qc;}else free(qc);}return headc;}Polyn SubtractPolyn(Polyn pa,Polyn pb){Polyn h=pb;Polyn p=pb->next;Polyn pd;while(p){p->coef*=-1;p=p->next;}pd=AddPolyn(pa,h);for(p=h->next;p;p=p->next)p->coef*=-1;return pd;}float ValuePolyn(Polyn head,float x){Polyn p;int i;float sum=0,t;for(p=head->next;p;p=p->next){t=1;for(i=p->expn;i!=0;){if(i<0){t/=x;i++;}else{t*=x;i--;}}sum+=p->coef*t;}return sum;}Polyn MultiplyPolyn(Polyn pa,Polyn pb){Polyn hf,pf;Polyn qa=pa->next;Polyn qb=pb->next;hf=(Polyn)malloc(sizeof(struct Polynomial));hf->next=NULL;for(;qa;qa=qa->next){for(qb=pb->next;qb;qb=qb->next){pf=(Polyn)malloc(sizeof(struct Polynomial));pf->coef=qa->coef*qb->coef;pf->expn=qa->expn+qb->expn;Insert(pf,hf);}}return hf;}#include<stdlib.h>#include<stdio.h>#include<malloc.h>struct list{int zhishu;int xishu;struct list *next;};typedef struct list node; typedef node *link;void free_list(link head){link pointer;while(head!=NULL){pointer=head;head=head->next;free(pointer);}}link rev(link head){link p1,p2;p1=head->next;p2=p1->next;p1->next=NULL;while(p2!=NULL){head->next=p2;p2=p2->next;head->next->next=p1;p1=head->next;}return head;}link find_list(link head,int key) {link p0;p0=head->next;while(p0!=NULL){return p0;p0=p0->next;}return p0;}link find2_list(link head,int key){link p0;p0=head;while(p0!=NULL){if((p0->next->zhishu==key)&&(p0->next->xishu!=0)) return p0;p0=p0->next;}return p0;}link clearzero(link head){link p0,pp;p0=head;while(p0!=NULL){if((p0->next->xishu==0)&&(p0->next->zhishu!=0)){pp=p0->next;p0->next=pp->next;free(pp);}p0=p0->next;}return head;}int max_list(link head1,link head2){link p1;link p2;int temp=-10000;p1=head1->next;p2=head2->next;while(p1!=NULL){if(p1->zhishu>temp)p1=p1->next;};while(p2!=NULL){if(p2->zhishu>temp)temp=p2->zhishu;p2=p2->next;};return temp;}link add_list(link head1,link head2){link pointer1;link pointer2;link pointer3;link new1;link new2;link head3;int a=0;int i=0;head3=(link)malloc(sizeof(node));if(head3==NULL){printf("Memory allocate Failure!\n");}else{head3->next=NULL;head3->zhishu=0;head3->xishu=0;};pointer1=head1->next;pointer2=head2->next;pointer3=head3;if((pointer1->zhishu)>=(pointer2->zhishu)){i=pointer2->zhishu;}else{i=pointer1->zhishu;};while(1){if(i>max_list(head1,head2))break;a=0;if(find_list(head1,i)!=NULL){new2=find_list(head1,i);a=a+new2->xishu;};if(find_list(head2,i)!=NULL){new2=find_list(head2,i);a=a+new2->xishu;};if(a!=0){new1=(link)malloc(sizeof(node));new1->zhishu=i;new1->xishu=a;new1->next=NULL;pointer3->next=new1;pointer3=new1;};i=i+1;};return head3;}link init_list(link head){head=(link)malloc(sizeof(node));if(head==NULL)printf("Memory allocate Failure!\n");else{head->next=NULL;head->zhishu=0;head->xishu=0;}return head;}link jianfa(link head11,link head22){link p2;p2=head22->next;while(p2!=NULL){p2->xishu=(-1)*(p2->xishu);p2=p2->next;}return add_list(head11,head22);}link chufa(link head1,link head2){link head3=NULL,tp,new1,p3,p2,new2;link temp=NULL;head3=(link)malloc(sizeof(node));head3->next=NULL;head3->zhishu=0;head3->xishu=0;temp=(link)malloc(sizeof(node));temp->next=NULL;temp->zhishu=0;temp->xishu=10;init_list(head3);init_list(temp);p3=head3;while(1){if((head1->next->zhishu)<(head2->next->zhishu)){p3->next=head1;break;};new1=(link)malloc(sizeof(node));new1->zhishu=(head1->next->zhishu)-(head2->next->zhishu);new1->xishu=(head1->next->xishu)/(head2->next->xishu);new1->next=NULL;p3->next=new1;p3=new1;tp=temp;p2=head2->next;while(p2!=NULL){if((p2->xishu==0)&&(p2->zhishu==0)){break;};new2=(link)malloc(sizeof(node));new2->zhishu=p2->zhishu+p3->zhishu ;new2->xishu=(p2->xishu)*(p3->xishu) ;new2->next=NULL;tp->next=new2;tp=new2;p2=p2->next;};head1=jianfa(rev(head1),rev(temp));head1=rev(head1);free_list(temp->next);temp->next=NULL;};return head3 ;}link chengfa(link head1,link head2){link p1,p2,p3,new1,p,tp,p31;link head3=NULL;head3=(link)malloc(sizeof(node));if(head3==NULL){printf("Memory allocate Failure!\n");}else{head3->next=NULL;head3->zhishu=0;head3->xishu=0;};p1=head1->next;p2=head2->next;p3=head3;while(p1!=NULL){p2=head2->next;while(p2!=NULL){new1=(link)malloc(sizeof(node));new1->zhishu=p1->zhishu+p2->zhishu;new1->xishu=(p1->xishu)*(p2->xishu);new1->next=NULL;p3->next=new1;p3=new1;p2=p2->next;}p1=p1->next;}p3=head3->next;while(p3!=NULL){p=p3;p31=p3;while(p31!=NULL){if(find2_list(p31,p->zhishu)!=NULL){new1=find2_list(p31,p->zhishu);p->xishu=p->xishu+new1->next->xishu;tp=new1->next;new1->next=tp->next;free(tp);};p31=p31->next;};p3=p3->next;};return clearzero(head3);}void print_list(link head){link pointer;pointer=head->next;printf(" ");while(pointer!=NULL){printf("%d x^%d ",pointer->xishu,pointer->zhishu);if(pointer->next!=NULL)printf("+");pointer=pointer->next;}printf("\n");}/*****************************************************/ /*void print_list(link head){link pointer;pointer=head->next;printf("(zhishu , xishu)\n");while(pointer!=NULL){printf("%d , %d\n",pointer ->zhishu,pointer->xishu);pointer=pointer->next;}printf("\n"); }/*****************************************************/ link create_list(link head){link new1;link pointer;head=(link)malloc(sizeof(node));if(head==NULL)printf("Memory allocate Failure!\n");else{head->next=NULL;head->zhishu=0;head->xishu=0;pointer=head;while(1){new1=(link)malloc(sizeof(node));printf("输入指数和系数:");scanf_s("%d %d",&(new1->zhishu),&(new1->xishu));if (new1->xishu==0){printf("多项式输入完毕。
