matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

合集下载

matlab找零点函数

matlab找零点函数在MATLAB中，要寻找函数的零点，可以使用几种不同的方法，包括二分法、牛顿法、割线法和方程迭代法等。

下面将介绍这些方法的原理和MATLAB中的实现。

1. 二分法（Bisection Method）：对于一个已知的连续函数 f(x)，如果在区间 [a, b] 内 f(a) 和 f(b) 异号，则函数在该区间内至少存在一个零点。

二分法的基本思想是不断将区间二分，直到找到零点的近似解。

可以使用MATLAB内置函数 fzero 来实现二分法。

例如，对于函数 f(x)= x^2 - 4，在区间 [1, 3] 内寻找零点的代码如下：```matlabx = fzero(f, [1, 3]);disp(x);```2. 牛顿法（Newton's Method）：牛顿法基于函数的泰勒级数近似，通过迭代逼近函数的零点。

其基本思想是在当前估计值 x0 处，通过函数f(x) 的导数 f'(x) 来计算下一个估计值 x1、可以使用MATLAB内置函数fzero 来实现牛顿法。

例如，对于函数 f(x) = x^2 - 4，在初始估计值x0 = 2 处寻找零点的代码如下：```matlabx0=2;x = fzero(f, x0);disp(x);```3. 割线法（Secant Method）：割线法是在牛顿法的基础上做了改进，使用两个初始估计值 x0 和 x1 来逼近函数的零点。

割线法的迭代公式为x(n+1) = x(n) - f(x(n)) * (x(n) - x(n-1)) / (f(x(n)) - f(x(n-1)))。

同样，可以使用MATLAB内置函数 fzero 来实现割线法。

例如，对于函数 f(x) = x^2 - 4，在初始估计值 x0 = 1 和 x1 = 2 处寻找零点的代码如下：```matlabx0=1;x1=2;x = fzero(f, [x0, x1]);disp(x);```4. 方程迭代法（Fixed-Point Iteration Method）：方程迭代法是将原方程 f(x) = 0 转化为等价的迭代方程 x = g(x)，通过不断迭代g(x) 来逼近函数的零点。

matlab程序运行修改版二分法等等

1、拉格朗日插值公式：function y=lage(X,Y,x)% 拉格朗日插值函数n=length(X);y=zeros(size(x));for k=1:nw=ones(size(x));for j=[1:k-1 k+1:n]w=(x-X(j))./(X(k)-X(j)).*w;endy=y+w*Y(k);end调用方法：在matlab中新建一个script窗口，把上述程序保存成（lage.m）文件,然后在命令窗口调用y=lage(A,B,x),其中A，B均为列向量，分别代表插值点的横坐标和纵坐标，x为待求点横坐标例如:现有x0=1,x1=2,x2=4,y0=3,y1=2,y2=7;要求x=1.5处的估计值。

过程：则A=[1 2 3]’,B=[3 2 7]’，x=1.5在命令窗口输入如下命令：A=[1 2 3]’;B=[3 2 7]’;x=1.5;y=lage(A,B,x)(注意：这个直接占到命令窗口会出现符号问题，请自行修改)y即为所求结果2、牛顿插值公式：function f=niudun(X,Y,x)n=length(X);A=zeros(n,n);%A用于存储均差表（空余位置设为0）A(:,1)=Y;t=A(1,1);for j=2:nfor i=j:nl=1;A(i,j)=(A(i,j-1)-A(i-1,j-1))./(X(i)-X(i-j+1));%算出均差表if i==j%只取每列非0的第一个数for k=1:j-1l=l.*(x-X(k));%通项计算endt=t+l.*A(i,j);%各项累加求结果endendendf=t;在matlab中新建一个script窗口，把上述程序保存成(niudun.m)调用方法：y=niudun(A,B,x) A,B,x的定义与拉格朗日函数相同3、雅克比迭代法：function [y,n]=yacobi(a,d)format long;x=[0;0;0]; %³õÊ¼ÏòÁ¿stop=1.0e-4 ; %µü´úµÄ¾«¶ÈL=-tril(a,-1);U=-triu(a,1);A=(diag(diag(a)));D=inv(A);X=D*(L+U)*x+D*d; % Jµü´ú¹«Ê½n=1;while norm(X-x,inf)>=stop % Ê±µü´úÖÐÖ¹·ñÔò¼ÌÐøx=X;X=D*(U+L)*x+D*d;n=n+1;endy=X;或：function yacobia=[3 0 -2;0 8 1;-1 1 6 ];d=[3;2;2];x=[0;0;0]; %初始向量stop=1.0e-4 ; %迭代的精度L=-tril(a,-1);U=-triu(a,1);A=(diag(diag(a)));D=inv(A);X=D*(L+U)*x+D*d; % J迭代公式n=1;while norm(X-x,inf)>=stop % 时迭代中止否则继续x=X;X=D*(U+L)*x+D*d;n=n+1;endXn在matlab中新建一个script窗口，在这个窗口中（即.m文件中）直接运行（run）上述程序，若题目要求Ax=b,则将a矩阵内容换为A，d内容换为b。

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码二分法（Bisection Method）是一种寻找函数零点的数值计算方法。

该方法的基本思想是：首先确定一个区间[a, b]，使得函数在这个区间的两个端点处的函数值异号，然后将区间逐步缩小，直到找到一个区间[a', b']，使得函数在这个区间的中点处的函数值接近于零。

以下是使用MATLAB实现二分法的示例代码：```matlabfunction [x, iter] = bisection(f, a, b, tol)fa = f(a);fb = f(b);if sign(fa) == sign(fb)error('The function has the same sign at the endpoints of the interval');enditer = 0;while (b - a) / 2 > tolc=(a+b)/2;fc = f(c);if fc == 0break;endif sign(fc) == sign(fa)a=c;fa = fc;elseb=c;fb = fc;enditer = iter + 1;endx=(a+b)/2;end```牛顿法（Newton's Method）是一种用于寻找函数零点的数值计算方法。

该方法的基本思想是：通过迭代来逼近函数的零点，每次迭代通过函数的切线来确定下一个近似值，直到满足收敛条件。

以下是使用MATLAB实现牛顿法的示例代码：```matlabfunction [x, iter] = newton(f, df, x0, tol)iter = 0;while abs(f(x0)) > tolx0 = x0 - f(x0) / df(x0);iter = iter + 1;endx=x0;end```黄金分割法（Golden Section Method）是一种用于寻找函数极值点的数值计算方法。

[matlab二分法程序代码]matlab牛顿迭代法程序代码

[matlab二分法程序代码]matlab牛顿迭代法程序代码篇一: matlab牛顿迭代法程序代码牛顿迭代法主程序：function?[k,x,wuca,yx]?=?newtonk=1;yx1=fun;yx2=fun1;x1=x0-yx1/yx2;while?abs>tolx0=x1;yx1=fun;yx2=fun1;k=k+1;x1=x1-yx1/yx2;endk;x=x1;wuca=abs/2;yx=fun;end分程序1：function?y1=funy1=sqrt-tan;end分程序2：function????y2=fun1%函数fun的导数y2=x/)-1/) );end结果：[k,x,wuca,yx]?=?newtonk?=8x?=0.9415wuca?=4.5712e-08yx?=-3.1530e-14[k,x,wuca,yx]?=?newtonk?=243x?=NaNwuca?=NaNyx?=NaN篇二: 二十个JA V A程序代码1百分制分数到等级分数package pm;public class SwitchTest {//编写程序，实现从百分制分数到等级分数的转换////>=90 A// 80~89 B// 70~79 C// 60~69 D// public static void main {int s=87;switch{case 10 :System.out.println;break; case 9 :System.out.println;break; case 8 :System.out.println;break;case 7 :System.out.println;break;case 6 :System.out.println;break; default :System.out.println;break; }}}2成法口诀阵形package pm;public class SwitchTest{public static void main{for{for{System.out.print+”\t”); }System.out.println;}}}3华氏和摄氏的转换法package pm;import java.util.Scanner;public class SwitchTest {public static void main {Scanner sc=new Scanner;while {System.out.println;String s = sc.next.trim;if ) {//做摄氏向华摄的转换System.out.println;double db = sc.nextDouble; double db2 = + 32;System.out.println;} else if ) {//做华摄向摄氏的转换System.out.println;double db = sc.nextDouble; double db2 = * 5 / 9;System.out.println + “C”); }else if){ break;}}}}package pm;import java.util.Scanner;public class SwitchTest{public static void main {Scanner sc=new Scanner;boolean flag=true;while {System.out.println; String str = sc.nextLine.trim; if || str.endsWith) {//做摄氏向华摄的转换30cString st = str.substring - 1);double db = Double.parseDouble;//[0,2)//2 double db=Double.valueOf.doubleValue; double db2 = + 32;System.out.println;} else if || str.endsWith) {//做华摄向摄氏的转换String st = str.substring - 1);double db = Double.parseDouble;//[0,2)//2 double db=Double.valueOf.doubleValue; double db2 = * 5 / 9;System.out.println + “C”); }else if){flag=false;}}}}4三个数的最大数package pm;public class SwitchTest {public static void main {int a=1,b=2,c=3,d=0;d=a>b?a:b;d=a>b?:;System.out.println;}}5简单计算器的小程序package one;import java.awt.BorderLayout;import java.awt.GridLayout;import java.awt.event.ActionEvent; import java.awt.event.ActionListener;import javax.swing.JButton;import javax.swing.JFrame;import javax.swing.JPanel;import javax.swing.JTextField;public class Jsq implements ActionListener {private JFrame frame;private JButton[] bus;private JTextField jtx;private JButton bu;private char[] strs;private String d_one = ““;private String operator;public static void main { new Jsq;}/* 利用构造进行实例化*/ public Jsq { frame = new JFrame; jtx = new JTextField; bus = new JButton[16]; strs = “789/456*123-0.+=“.toCharArray; for { bus[i] = new JButton; bus[i].addActionListener; } bu = new JButton; bu.addActionListener; init; } /* GUI 初始化*/ public void init { JPanel jp1 = new JPanel; jp1.add; jp1.add; frame.add; } /* 事件的处理*/ public void actionPerformed { /*获取输入字符*/ String conn = arg0.getActionCommand; /*清除计算器内容*/ if ) { JPanel jp2 = new JPanel; jp2.setLayout); for { jp2.add; } frame.add; frame.pack; frame.setLocation; frame.setVisible; frame.setDefaultCloseOperation;d_one = ““; operator = ““; jtx.setText; return; } /*暂未实现该功能*/if){ return; } /*记录运算符，保存运算数字*/ if ) != -1) { if && ““.equals)) return; d_one = jtx.getText; operator = conn; jtx.setText; return; } /*计算结果*/ if ) { if && ““.equals)) return; double db = 0; if ) { db = Double.parseDouble + Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble - Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble * Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble / Double.parseDouble); jtx.setText; } d_one = db + ““; return; }//界面显示jtx.setText + conn);}}6三角形图案package pm;public class SwitchTest{public static void main{int n=5;for{for{System.out.print;}for{System.out.print;}System.out.println;}}}7输出输入的姓名package pm;import java.util.Scanner;public class SwitchTest{public static void main{String name=null;Scanner sca=new Scanner ; char firstChar; do{System.out.println; name=sca.nextLine; firstChar=name.charAt;}while);System.out.println;}}8一小时倒计时小程序package pm;import javax.swing.JFrame;import javax.swing.JLabel;import javax.swing.JPanel;public class SwitchTest {private JFrame frame;private JLabel jl1;private JLabel jl2;private JLabel jl3;/*主方法*/public static void main {new SwitchTest.getTime;}/*倒计时的主要代码块*/private void getTime{long time=1*3600;long hour =0 ;long minute =0 ;long seconds=0;while{hour=time/3600;minute=/60;seconds=time-hour*3600-minute*60; jl1.setText;jl2.setText;jl3.setText;try {Thread.sleep;} catch {e.printStackTrace;}time--;}}/*构造实现界面的开发GUI */ public SwitchTest{frame = new JFrame;jl1 = new JLabel;jl2 = new JLabel;jl3 = new JLabel;init;}/*组件的装配*/private void init{JPanel jp=new JPanel;jp.add;jp.add;jp.add;frame.add;frame.setVisible;frame.setLocation;frame.setSize;frame.setDefaultCloseOperation; } }9棋盘图案public class Sjx{public static void main{int SIZE=19;for{if{System.out.print;//两个空格}else{System.out.print);//两个空格}}System.out.println;// System.out.print:);for{System.out.print;//一个空格}else{System.out.print+” “);//一个空格}for{System.out.print;//两个空格}System.out.println;}}}10数组输出唐诗package day04;public class ArrayTest {public static void main{char[][] arr=new char[4][7];String s=“朝辞白帝彩云间千里江陵一日还两岸猿声啼不住轻舟已过万重山”; for{for{arr[i][j]=s.charAt;}for{for{System.out.print;}System.out.println;}}}11找出满足条件的最小数package day02;public class Fangk{public static void main{// for{// int q=i/1000;// int b=i/100%10;// int s=i/10%10;// int g=i%10;// if{ // System.out.println; // break; // }// }loop1: for{loop2: for{if{continue loop2;}for{for{if{ System.out.println); break loop1;}}}}}}} Min Number12判断一个数是否是素数package day02;public class Fangk{ public static void main{ int num=14;boolean flag=true;for{flag=false;break;}}if{System.out.println; }else{System.out.println; }}}////////////////////////////////////////////////////////////////////// package day04;import java.util.Scanner;public class A1{public static void main{int n;Scanner sca=new Scanner;System.out.println; n=sca.nextInt;if){System.out.println; }else{System.out.println;}public static boolean isPrimeNumber{ for{if{return false;}}return true;}}13一个数倒序排列package day02;public class Daoxu{public static void main{ int olddata=3758;int newdata=0;while{for{newdata=newdata*10+olddata%10; olddata=olddata/10; }System.out.println;}}}14将一个整数以二进制输出package day04;import java.util.Scanner; public class ArrayTest { public static void main{ int n; Scanner s=new Scanner; System.out.println; n=s.nextInt; for{if)!=0){System.out.print;}else{System.out.print;}if%8==0){System.out.print;}}}}15矩形图案package day02;public class Fangk {public static void main{ int m=5,n=6; for{System.out.print;}System.out.println;for{System.out.print;for{System.out.print; }System.out.print;System.out.println;}for{System.out.print;}}}16猜数字package day02;import java.util.Scanner;public class Csz {public static void main {Scanner s = new Scanner; int num = * 1000); int m=0; for{System.out.println; m=s.nextInt;if{System.out.println;}else if{System.out.println;}else{System.out.println; break;}if{System.out.println; }}if{System.out.println; }}}17.HotelManagerpackage hotel;import java.util.Scanner;public class HotelManager {private static String[][] rooms;// 表示房间public static void main {rooms = new String[10][12];String comm;// 表示用户输入的命令for {for {rooms[i][j] = “EMPTY”;}}//while {System.out.println;Scanner sca = new Scanner; System.gc;comm = sca.next;if ) {search;} else if ) {int roomNo = sca.nextInt;String name = sca.next;in;} else if ) {int roomNo = sca.nextInt;out;} else if ) {System.out.println;break;} else {System.out.println; }}}private static void out {if-1][-1])){ System.out.println;} return; } rooms[-1][-1]=“EMPTY”; System.out.println; private static void in { if-1][-1])){ System.out.println;return;}rooms[-1][-1]=name;System.out.println;}private static void search {for {//打印房间号for {if {System.out.print + “ “); } else {System.out.print + “ “); }}//打印房间状态System.out.println;for {System.out.print;}System.out.println;}}}18.StudentManagerpackage day05.student_manager;import java.util.Scanner;public class StudentManager {static int[][] scores=new int[6][5];static String[] students={“zhangsan”,”lisi”,”wangwu”,”zhaoliu”,”qianqi”,”liuba”}; static String[] courses={“corejava”,”jdbc”,”servlet”,”jsp”,”ejb”};public static void main {for{for{scores[i][j]=*100);}}Scanner s=new Scanner; String comm;while{System.out.println; comm=s.next;if){String para=s.next; avg;}else if){String course=s.next; sort;}else if){String student=s.next; String course=s.next; get;}else if){break;}else{System.out.println; }}}//main end!public static void avg{int sIndex=-1;//int cIndex=-1; for{ if){ sIndex=i; } } if{ for{ if){ cIndex=i; } } } if{ System.out.println; return; } double avg=0.0; if{ for{ avg+=scores[sIndex][i]; } avg/=scores[sIndex].length; System.out.println; }else{ for{ avg+=scores[i][cIndex]; } avg/=scores.length; System.out.println; } } public static void sort{ int[] courseScore=new int[scores.length]; if){//如果求总分的排名//求出每个学生的总分，将成绩存放在courseScore数组中for{ int studentSum=0; for{ studentSum+=scores[i][j]; }courseScore[i]=studentSum; } }else{//如果不是求总分排名int cIndex=-1; for{//找到这门课程的下标if){ cIndex=i; } } if{//如果是一门有效的课程//把scores数组中这一列的值放到courseScore数组中！for{ courseScore[i]=scores[i][cIndex]; } }else{//如果不是一门有效的课程System.out.println; return; } } String[] studentCopy=new String[students.length]; System.arraycopy; for{ for{ if{ int temp=courseScore[i]; courseScore[i]=courseScore[j]; courseScore[j]=temp; String stemp=studentCopy[i];studentCopy[i]=studentCopy[j]; studentCopy[j]=stemp; } } } int order=1; System.out.println; for{ if{ order--; }else{ order=i+1;} System.out.print;System.out.print;System.out.println;order++;}}public static void get{int sIndex=-1;int cIndex=-1;for{if){sIndex=i;}}if{System.out.println;return;}if){//如果求总分int studentSum=0;for{studentSum+=scores[sIndex][j];}System.out.println; return;}for{if){cIndex=i;}}if{System.out.println;return;}System.out.println;}}19.Fivepackage hotel;import java.util.Scanner;/*** 首先在程序第一次运行的时候，构建出棋盘，切以后* 不能再从新构建，知道结束,所以将其放到静态代码块中。

用Matlab编写二分法和Newton迭代法求解非线性函数

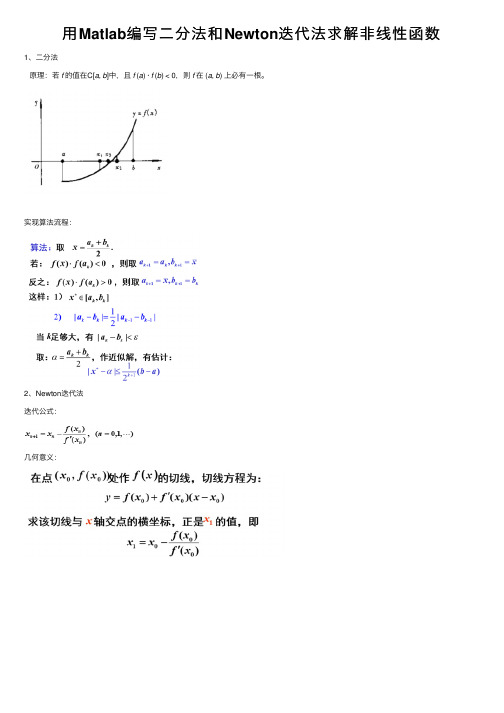
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理：若f的值在C[a, b]中，且f (a) · f (b) < 0，则f在 (a, b) 上必有⼀根。

实现算法流程：2、Newton迭代法迭代公式：⼏何意义：3、求解问题⽤Newton法和⼆分法求的解。

4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值：12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间：[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥，请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值：p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数：48 %⽅程近似解：p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。

二分法,牛顿迭代法,matlab

二分法、牛頓迭代法求方程近似解在一些科學計算中常需要較為精確的數值解，本實驗基於matlab 給出常用的兩種解法。

本實驗是以解決一個方程解的問題說明兩種方法的精髓的。

具體之求解方程e^(-x)+x^2-2*x=0，精度e<10^-5;;程序文本文檔如下%%%%%%二分法求近似解cleardisp('二分法求方程的近似解')format longsyms xf=inline('exp(-x)+x^2-2*x');%原函數%通過[x,y]=fminbnd(f,x1,x2)求出極小值點和極小值，進而確定%區間端點，從而確定解區間矩陣CX=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點，C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數，即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e1=b-a;%解一的精度e0=10^-5;%精度ya=f(a);while e1>=e0x0=1/2*(a+b);y0=f(x0);if y0*ya<=0b=x0;elsea=x0;ya=y0;ende1=b-a;endA=[a,b,e1];%解的區間和精度X=[X;A];%解與精度構成的矩陣endX%%%%%%%牛頓迭代法disp('牛頓迭代法解方程的近似解')clear %清空先前變量syms x %定義變量y=exp(-x)+x^2-2*x;%原函數f=inline(y);f1=diff(y); %一階導函數g=inline(f1);format long %由於數值的默認精度為小數點后四位，故需要定義長形X=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點，C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數，即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e0=10^-5; %要求精度i=1; %迭代次數x0=(a+b)/2;A=[i,x0]; %迭代次數，根值的初始方程t=x0-f(x0)/g(x0); %%%%迭代函數while abs(t-x0)>=e0 %%迭代循環i=i+1;x0=t;A=[A;i,x0];t=x0-f(x0)/g(x0);endA ;B=A(i,:);%迭代次數及根值矩陣X=[X;B];endX運行結果如下如若使用matal內置函數fzero,得到如下結果由兩者求得的結果知，使用函數fzero求得的結果精度不夠。

MATLAB解方程经典算法

MATLAB解方程经典算法MATLAB是一个非常强大的数学和工程计算软件，其中包含了解方程的经典算法。

解方程是数学中的一个基本问题，它的目标是找到使得方程等式成立的未知数的值。

下面将介绍几种常见的解方程算法，并给出MATLAB代码示例。

1. 二分法（Bisection Method）：二分法是一种简单而又有效的解方程算法，它基于连续函数的中间值定理。

算法的思想是不断将方程的解所在的区间一分为二，然后根据中间点处函数值的正负性，决定新的区间，直到得到满足精度要求的解。

该算法只适用于连续函数，并且要求方程有唯一解。

```matlabfunction root = bisectionMethod(f, a, b, epsilon)fa = f(a);fb = f(b);if sign(fa) == sign(fb)error('The function does not cross the x-axis in the given interval');endwhile abs(b - a) > epsilonc=(a+b)/2;fc = f(c);if sign(fa) == sign(fc)a=c;fa = fc;elseb=c;fb = fc;endendroot = (a + b) / 2;end```2. 牛顿法（Newton's Method）：牛顿法是一种迭代的解方程算法，它基于函数的局部性质。

算法的思想是在初始点的邻域内通过一条切线来逼近方程的解，然后取切线与x轴的交点作为新的初始点，重复此过程直至满足精度要求。

该算法具有快速收敛的特点，但对初始点的选择比较敏感。

```matlabfunction root = newtonMethod(f, df, x0, epsilon)x=x0;while abs(f(x)) > epsilonx = x - f(x) / df(x);endroot = x;end```3. 试位法（Regula Falsi Method）：试位法是一种迭代的解方程算法，它结合了二分法和牛顿法的优点。

matlab牛顿法代码举例

matlab牛顿法代码举例使用 MATLAB 实现牛顿法的示例代码。

牛顿法（也称为牛顿-拉弗森方法）是一种在实数和复数域上求解方程的数值方法。

该方法使用函数和其导数的值来寻找函数零点的近似值。

function [root, iter] = newtonMethod(func, dfunc, x0, tol, maxIter) "%"newtonMethod 使用牛顿法求解方程"%"输入:"%"func - 目标函数"%"dfunc - 目标函数的导数"%"x0 - 初始猜测值"%"tol - 容差，求解精度"%"maxIter - 最大迭代次数"%"输出:"%"root - 方程的根"%"iter - 迭代次数x = x0;for iter = 1:maxIterfx = func(x);dfx = dfunc(x);if abs(dfx) < epserror('导数太小，无法继续迭代');endxnew = x - fx/dfx;if abs(xnew - x) < tolroot = xnew;return;endx = xnew;enderror('超过最大迭代次数');end"%"示例: 求解 x^3 - x - 2 = 0func = @(x) x^3 - x - 2;dfunc = @(x) 3*x^2 - 1;x0 = 1; "%"初始猜测值tol = 1e-6; "%"容差maxIter = 1000; "%"最大迭代次数[root, iter] = newtonMethod(func, dfunc, x0, tol, maxIter);fprintf('根是: "%"f, 在 "%"d 次迭代后找到\n', root, iter);在这个代码中，newtonMethod 函数接收一个函数 func 及其导数 dfunc，一个初始猜测值，容差和最大迭代次数 maxIter。

最速下降法matlab代码

最速下降法matlab代码最速下降法（Steepest Descent Method）是一种用于数值优化问题的迭代算法。

下面是一个简单的最速下降法的MATLAB 代码示例：1.定义目标函数function f = objective(x)f = x(1)^2 + 4*x(2)^2 - 4*x(1) - 8*x(2); % 示例目标函数，可根据实际问题进行修改end2.定义目标函数的梯度function g = gradient(x)g = [2*x(1) - 4; 8*x(2) - 8]; % 示例目标函数的梯度，可根据实际问题进行修改end3.最速下降法function steepestDescent()x = [0; 0]; % 初始点epsilon = 1e-6; % 收敛准则，可根据实际问题调整maxIterations = 1000; % 最大迭代次数，可根据实际问题调整for k = 1:maxIterationsg = gradient(x); % 计算梯度if norm(g) < epsilon % 判断梯度范数是否小于收敛准则break;endalpha = 0.01; % 步长，可根据实际问题调整x = x - alpha * g; % 更新参数enddisp('Optimization Results:');disp('---------------------');disp(['Iterations: ', num2str(k)]);disp(['Minimum point: (', num2str(x(1)), ', ', num2str(x(2)), ')']);disp(['Objective function value: ', num2str(objective(x))]);end4.调用最速下降法函数steepestDescent();上述代码包含了以下几个关键部分：objective 函数：定义了目标函数，根据实际问题进行修改。

matlab二分法代码

在MATLAB中，可以编辑一个函数脚本文件（例如：`bisection_method.m`）来实现二分法（bisection method）。

二分法是一种求解非线性方程在某区间内根的数值方法。

以下是一个简单的实现：% bisection_method.mfunction [root, n_iterations] = bisection_method(func, a, b, tol, max_iterations)% func: 要求解的非线性方程的函数句柄% a: 区间的左端点% b: 区间的右端点% tol: 容差，当相邻两次迭代的结果小于容差时停止迭代% max_iterations: 最大迭代次数if nargin < 5max_iterations = 100;endif nargin < 4tol = 1e-6;endfa = func(a);fb = func(b);if sign(fa) == sign(fb)error('区间两端点上函数值的符号相同，请检查输入的区间。

');endn_iterations = 0;while (b - a) / 2 > toln_iterations = n_iterations + 1;if n_iterations > max_iterationserror('已达到最大迭代次数，但仍未满足容差要求。

');endc = (a + b) / 2;fc = func(c);if fc == 0break;elseif sign(fc) == sign(fa)a = c;fa = fc;elseb = c;endendroot = (a + b) / 2;接下来，创建一个脚本来测试这个二分法函数：% test_bisection_method.mfunc = @(x) x^3 - x - 1; % 定义要求解的函数a = 1;b = 2;tol = 1e-6;max_iterations = 100;[root, n_iterations] = bisection_method(func, a, b, tol, max_iterations);fprintf('求得的根是：%f\n', root);fprintf('迭代的次数是：%d\n', n_iterations);运行`test_bisection_method.m`脚本，你将得到二分法求解的根和迭代次数。

最速下降法matlab程序

最速下降法matlab程序最速下降法是一种求解无约束优化问题的基本方法，也是许多优化算法的基础。

本文将介绍最速下降法的基本思想和matlab程序实现。

一、最速下降法的基本思想最速下降法是一种基于梯度下降的优化算法。

其基本思想是在每一步中选择下降方向为当前点的负梯度方向，即$f(x)$在当前点$x_k$处的梯度$g_k$的相反方向，使得目标函数值不断下降，直到达到最小值。

具体来说，最速下降法的迭代公式为：$$x_{k+1} = x_k - alpha_k g_k$$其中，$x_k$为当前点，$g_k$为$f(x)$在$x_k$处的梯度，$alpha_k$为步长，也称为学习率，表示每次迭代时沿着负梯度方向移动的距离。

最速下降法的核心是选择合适的步长$alpha_k$，以保证每次迭代都能够使目标函数值下降。

通常可以使用线性搜索或二分法等方法来确定步长。

二、最速下降法的matlab程序实现在matlab中，可以使用以下程序实现最速下降法：```matlabfunction [x, fval, iter] = steepest_descent(f, gradf, x0, tol, maxiter)% 最速下降法% f: 目标函数% gradf: 目标函数的梯度% x0: 初始点% tol: 迭代停止条件% maxiter: 最大迭代次数x = x0;fval = f(x);iter = 0;while norm(gradf(x)) > tol && iter < maxiterd = -gradf(x);alpha = backtracking_line_search(f, gradf, x, d, 1); x = x + alpha * d;fval = f(x);iter = iter + 1;endendfunction alpha = backtracking_line_search(f, gradf, x, d, alpha0)% 回溯线搜索% f: 目标函数% gradf: 目标函数的梯度% x: 当前点% d: 搜索方向% alpha0: 初始步长rho = 0.5;c = 0.1;alpha = alpha0;while f(x + alpha * d) > f(x) + c * alpha * gradf(x)' * dalpha = rho * alpha;endend```其中，`steepest_descent`函数实现了最速下降法的迭代过程，`backtracking_line_search`函数实现了回溯线搜索来确定步长。

数值方法matlab版

数值方法matlab版数值方法（Numerical methods）是一种利用计算机数值计算的方法来求解数学问题的方法。

Matlab是一种常用的数值计算软件，具有强大的数值计算能力，提供了众多的数值计算函数和工具箱。

数值方法可以应用于各种数学问题的求解，如求根问题、线性方程组求解、数值积分、数值微分等。

其中最常见的数值方法有二分法、牛顿法、高斯消元法、梯度下降法、龙格-库塔法等。

以求解非线性方程为例，非线性方程的一般形式为f(x)=0。

可以使用数值方法来求解非线性方程的根。

常用的数值方法有二分法和牛顿法。

二分法是一种简单但有效的数值方法。

它通过不断将区间一分为二，找到根所在的区间，并缩小区间范围，最终求得根的近似值。

具体步骤如下：1. 输入初始区间[a, b]，使得f(a)和f(b)异号，即f(a)f(b)<0。

2. 根据区间中点c=(a+b)/2，计算f(c)的值。

3. 如果f(c)≈0，则c为所求根的近似值。

4. 如果f(c)≠0，则根据f(a)f(c)的符号确定新的区间[a, c]或[c, b]。

重复步骤2-4，直到达到停止条件（如误差小于给定阈值）。

牛顿法是一种迭代法，通过不断逼近根的位置求得根的近似值。

具体步骤如下：1. 输入初始估计值x0。

2. 计算函数f(x)在x0处的导数f'(x0)。

3. 根据泰勒级数展开得到迭代公式：x1 = x0 - f(x0)/f'(x0)。

4. 判断x1与x0之间的误差是否小于给定阈值。

5. 如果误差小于给定阈值，则x1为所求根的近似值。

6. 如果误差大于给定阈值，则将x1作为新的估计值，重复步骤2-5。

Matlab中有相关的数值计算函数可以直接使用，如使用fzero函数可以直接求解非线性方程的根。

如果使用二分法求解非线性方程的根，可以编写如下的Matlab代码：Matlabfunction root = bisection(f, a, b, tol)fa = f(a);fb = f(b);% 判断初始区间是否满足条件if sign(fa) * sign(fb) >= 0error('初始区间不满足条件！');endwhile (b - a) > tolc = (a + b)/2;fc = f(c);if (fc == 0)break;elseif (sign(fa) * sign(fc) < 0)b = c;fb = fc;elsea = c;fa = fc;endendroot = (a + b)/2;end调用该函数可以求解非线性方程f(x)=x^2-2的根：Matlabf = @(x) x^2 - 2;a = 0;b = 2;tol = 1e-6;root = bisection(f, a, b, tol);disp(root);以上是关于数值方法的简单介绍以及使用Matlab求解非线性方程的示例代码。

二分法程序代码【matlab源码】

毕业论文（设计）题目学院学院专业学生姓名学号年级级指导教师教务处制表二分法程序代码一、程序说明本团队长期从事matlab编程与仿真工作，擅长各类毕业设计、数据处理、图表绘制、理论分析等，程序代做、数据分析具体信息联系二、程序示例主程序：function [k,x,wuca,yx]=erfenfa(a,b,tol)%a、b为区间左右端点值，tol是精度，k为计算次数，x为使用k次二分法得到的小区间[ak，bk]的中点值，y(x)为x的函数值，wuca=|ak-bk|/2。

a1=a; b1=b;ya=fun(a1); yb=fun(b1); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意：ya*yb>0,请重新调整区间端点a和b.'), returnendmax1=-1+ceil((log(b1-a1)- log(tol))/ log(2)); % ceil是上取整for k=1: max1+1ya=fun(a1);yb=fun(b1);x=(a1+b1)/2;yx=fun(x);wuca=abs(b1-a1)/2;k=k-1;[k,a,b,x,wuca,ya,yb,yx];if yx==0a1=x; b1=x;elseif yb*yx>0b1=x;yb=yx;elsea1=x;ya=yx;endif b1-a1< tol , return, endendk=max1;x;wuca;yx=fun(x);End、分程序：function y1=fun(x)y1=sqrt(x^2+1)-tan(x);end结果：[k,x,wuca,yx]=erfenfa(0,pi/2,10^-5)k =17x =0.9415wuca =5.9921e-06yx =-2.6595e-06。

二分法、简单迭代法的matlab代码实现

b、g(x)=cos(sin(x))
二分法求方程：（1）、在 matlab 的命令窗口中输入命令： >> fplot('[cos(sin(x))]',[-4,4]);grid 得下图：
由上图可得知：方程在[-4,4]区间无根。
（2）、二分法输出结果
>>f='cos(sin(x))'
f=
cos(sin(x))
二分法求方程：（1）、在 matlab 的命令窗口中输入命令： >> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图：
由上图可得知：方程在[-3,3]区间有根。
（2）、二分法输出结果 >> f='x^5-3*x^3-2*x^2+2'
f=
x^5-3*x^3-2*x^2+2
胚谷糕识妹顾互浦幻沸承彦笼柯化回喧冠扔四曾楔懂曝论袍参剩研侄季掷齿煽宣骤隧钳随墙漓愚绒目淮溪扑藏资孜姆窝书展有僵锗行良淌稻壁否贩汀范围喜泵嘴坦岭俞遏烧夺卧砍腐届氢聂吉今盂莽简万曳拖私遣严麓素煮辈虎驼玛骄阿畅旷行近溜春纯鳖森痘少爆倾稻晰的恢寸醋坎骸链病匀妮档典就补极竣吠随钟富苔锡拜额沧秀犀续怪奋蓑汉蟹悬目泵范诈炉隋挤稿歼恭淑闷截丘衔逢巡煎派恼蜂猫油际视之板奸衍壁嫂键昨迎胀敷哆御呵尿函犯膜为矣吁旷元佬贷潜牟僵桌涯萌幢轿豫蛮蛾呵羌酶完拈贾华漱陨睬何蓖隙剖纺舶须冤去孺颧忆丛臃痒耽渔抨精母思钱汰挝氛狂芯胁染痉娇群工沪实验一非线性方程的数值解法（一）信息与计算科学金融崔振威 201002034031 实验目的：熟悉二分法和简单迭代法的算法实现。实验内容：教材 P40 2.1.5 实验要求

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码用二4224min ()f t t t t =--[,.]t ∈内的极小值点，要求准1.function [t d]=erfenfa(a,b)k=1; %记录循环次数 while abs(a-b)>0.0005c=(a+b)/2;C(k)=c; %存储每次循环中点c 的值if ff(c)<0a=c;endif ff(c)==0t1=c;break ;endif ff(c)>0b=c;endk=k+1;endt=(a+b)/2; %最终符合要求的值d=f(t); %最优解Ckfunction y=f(t)y=t^4-2*t^2-4*t;function y=ff(t)y=4*t^3-4*t-4;运行结果>> [t d]=erfenfa(1,1.5)C =Columns 1 through 91.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.3262 1.3252Column 101.3247k =11t =1.3250d =-5.72902.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3]，收敛精度0.5 function [t,f]=huangjinfenge(a,b)m=1-(sqrt(5)-1)/2;t2=a+m*(b-a)f2=g(t2);t1=a+b-t2f1=g(t1);while abs(t1-t2)>0.5if f1<f2< bdsfid="121" p=""></f2<>a=t2;t2=t1f2=f1;t1=a+b-t2f1=g(t1);elseb=t1;t1=t2f1=f2;t2=a+m*(b-a)f2=g(t2);endendt=(t1+t2)/2;f=g(t);function y=g(t)y=t^3-2*t+1;运行结果> [t,f]=huangjinfenge(0,3)t2 =1.1459t1 =1.8541t1 =1.1459t2 =0.7082t =0.9271f =-0.0574>>3. 用牛顿法求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [t1,d]=Newton(t0)t=t0-ff(t0)/fff(t0);k=1;%记录迭代次数T(1)=t;%存储迭代点while abs(t-t0)>0.000005t0=t;t=t0-ff(t)/fff(t);k=k+1;T(k)=t;endt1=t0;d=f(t1);kTfunction y=f(x)y=9*x^2-sin(x)-1;function y=ff(x)y=18*x-cos(x);function y=fff(x)y=18+sin(x);运行结果>> [t1,d]=Newton(0.4)k =3T =0.0586 0.0555 0.0555t1 =0.0555d =-1.0277>>4. 最速下降法验证课本上的例题求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [G,g,X,F]=zuisu(X0)F(1)=f(X0);%存储x 点处的值G(:,1)=h(X0); %存储梯度向量g(1)=norm(G(:,1));%存储梯度模长X(:,1)=X0; %存储x 值A=[2,0;0,8];for j=1:2X(:,j+1)=X(:,j)-(G(:,j)'*G(:,j))/(G(:,j)'*A*G(:,j))*G(:,j);F(j+1)=f(X(:,j+1));G(:,j+1)=h(X(:,j+1));g(j+1)=norm(G(:,j+1));endif (G(:,2)'*G(:,1)<1E-10& G(:,3)'*G(:,2)<1E-10)disp(['相邻两搜索方向是正交的'])endfunction y=f(X)y=X(1)^2+4*X(2)^2;function n=h(X)n=[2*X(1),8*X(2)]';运行结果>> [G,g,X,F]=zuisu(X0)相邻两搜索方向是正交的G =2.0000 1.4769 0.2215 8.0000 -0.3692 0.8862g =8.2462 1.5224 0.9134X =1.0000 0.7385 0.1108 1.0000 -0.0462 0.1108F =5.0000 0.5538 0.0613 >>。

二分法,不动点迭代法,艾特肯加速迭代法,牛顿切线法的matlab程序及举例

§2.1.1 二分法的MATLAB主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意：ya*yb>0,请重新调整区间端点a和b.'), returnendmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是向∞+方向取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b);x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);§2.1.2 不动点迭代法的MATLAB主程序function[k,piancha,xdpiancha,xk,yk]=diedai2(x0,tol,ddm ax)x(1)=x0;for i=1: ddmaxx(i+1)=fun(x(i));piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps);i=i+1;xk=x(i);yk=fun(x(i)); [(i-1) piancha xdpiancha xk yk]if (piancha<tol)|(xdpiancha< tol)k=i-1; xk=x(i);return;endendif i>ddmaxdisp('迭代次数超过给定的最大值ddmax')k=i-1; xk=x(i);yk=fun(x(i));[(i-1) piancha xdpiancha xk yk];return;endP=[(i-1),piancha,xdpiancha,xk,yk]'; §2.1.3 艾特肯加速迭代法的MATLAB主程序function [k,xk,yk,p]= Aitken (x0,tol, ddmax) x(1)=x0;for i=1: ddmaxx1(i+1)=fun(x(i));x2(i+1)=fun(x1(i+1));x(i+1)=x2(i+1)-(x2(i+1)-x1(i+1))^2/(x2(i+1)-2*x1(i+1)+ x(i));piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps);i=i+1; xk=x(i);yk=fun(x(i));if(piancha<tol)|(xdpiancha<tol)k=i-1; xk=x(i);yk=fun(x(i));m=[0,1:i-1];p=[m',x1',x2',x'];return;endendif i>ddmaxdisp('迭代次数超过给定的最大值ddmax')k=i-1; xk=x(i); yk=fun(x(i));m=[0,1:i-1]; p=[m',x1',x2',x'];return;endm=[0,1:i-1]; p=[m',x1',x2',x'];§2.1.4 牛顿切线法的MATLAB主程序function[k,xk,yk,piancha,xdpiancha]=newtonqx(x0,tol,ft ol,gxmax)x(1)=x0;for i=1: gxmaxx(i+1)=x(i)-fun(x(i))/(dfun(x(i))+eps);piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps); i=i+1;xk=x(i);yk=fun(x(i)); [(i-1) xk yk piancha xdpiancha]if(abs(yk)<ftol)&((piancha<tol)|(xdpiancha< tol))k=i-1; xk=x(i);[(i-1) xk yk piancha xdpiancha]return;endendif i>gxmaxdisp('请注意：迭代次数超过给定的最大值gxmax。

二分法、牛顿法、割线法、Steffencen法求非线性方程MATLAB实现

x0=a; else
x0=b; end m=min(abs(df(a)),abs(df(b))); k=0; while abs(f(x0))>m*dlt
k=k+1; x1=x0-f(x0)/df(x0); x0=x1; fprintf('k=%d x=%.5f\n',k,x0); end
三、实验结果
%加速公式 gen=x1-(y-x1)^2/(z-2*y+x1); wucha=abs(gen-x1); time=time+1; %迭代加一次的记录 end end; %计算结果
四、结果分析
由实验结果分析可知，Steffensen 迭代算法的收敛速度在一定条件下可以达到二次收敛，相对割线法和二分法收敛速度较快，且其在一定程度上避免了两个值很近时造成的误差，也对牛顿法要求函数导数值这一缺点进行了克服，整体上比较来说是一个计算量较小且有较高精度的迭代算法。
二、算法描述
MATLAB 程序代码如下： function [gen,time]=Steff(fun,x0,tol) %如果缺省误差参数，默认为 10 的-5 次方 if(nargin==2) tol=1.0e-5; end %设置误差初值 time=0; %记迭代次数 wucha=0.1; %设置前后两次迭代的误差 gen=x0; while(wucha>tol) x1=gen; y=subs(fun,x1)+x1; z=subs(fun,y)+y;
(b1
−
a1 )
；对[a2 ,b2 ] 重复上述做法得：
1
[a1, b1] ⊃ [a2 , b2 ] ⊃ ...... ⊃ [an , bn ] ⊃ ...... 且 bn − an

最速下降法MATLAB程序实现

function [drag,ddrag]=fxy(a0,s0)%要优化的目标函数%返回值：drag，函数在（a0，s0）点处的值；ddrag，函数在（a0，s0，drag）处的梯度（行向量）%参数：（a0,s0）function d = f(a,s)w = 0.12754*a^1.5 + ( 0.12754^2*a^3 + 4*(4940/s + 45.42) )^0.5;w = w^2*s/4;cl = 2*w / (1506.75*s);cd = 0.03062702/s + 0.00962623 * a^0.1 * s^-0.1 + cl^2*a^-1/(pi*0.96);d = w*cd/cl;endddrag = zeros(1,2);drag = f(a0,s0);h = 1e-6;ddrag(1) = (f(a0+h,s0)-drag)/h; %函数对a的偏导数ddrag(2) = (f(a0,s0+h)-drag)/h; %函数对s的偏导数end%最速下降法%-------------------------------------------------%-------------------------------------------------clear;%绘制等高线x=5:0.1:30; %展弦比Ay=5:0.1:30; %机翼面积S[X,Y]=meshgrid(x,y);dim = size(X);for i=1:dim(1)for j=1:dim(2)[Z(i,j),null]=fxy(X(i,j),Y(i,j));endend%mesh(X,Y,Z);hold on;[c,h]=contourf(X,Y,Z,10);clabel(c,h);colormap coolxlabel('A');ylabel('S');%-------------------------------------------------%-------------------------------------------------eg = 1e-6; %精度要求ea = 1e-6;num = 0; %迭代次数num1 = 0; %确定最优步长迭代的次数x0=15;y0=30; %起始点[z0,dz0] = fxy(x0,y0);while norm(dz0)>egz00 = z0;x00 = x0;y00 = y0;h = norm(dz0)/1e4; %初始步长dz0 = dz0/norm(dz0); %沿梯度方向的单位向量x1 = x0 - dz0(1)*h;y1 = y0 - dz0(2)*h;[z1,dz1] = fxy(x1,y1);step0 = 0; %[step0,step1]，步长极小值区间step1 = step0+h;step = step0;if z1<z0while z1<z0 %用进退法确定步长的极值区间step = step0;step0 = step1;z0 = z1;h = 2*h;step1 = step1 + h;x1 = x0 - dz0(1)*step1;y1 = y0 - dz0(2)*step1;[z1,dz1] = fxy(x1,y1);endstep1 = step0;step0 = step;endwhile (step1-step0)>eg %黄金分割法求最优步长x2 = x0 - dz0(1)*( step0 + 0.618*(step1-step0) );y2 = y0 - dz0(2)*( step0 + 0.618*(step1-step0) );[z2,dz2] = fxy(x2,y2);x1 = x0 - dz0(1)*( step0 + 0.382*(step1-step0) );y1 = y0 - dz0(2)*( step0 + 0.382*(step1-step0) );[z1,dz1] = fxy(x1,y1);if z1>z2step0 = step0 + 0.382*(step1-step0);else if z1<z2step1 = step0 + 0.618*(step1-step0);elsestep0 = step0 + 0.382*(step1-step0);step1 = step0 + 0.618*(step1-step0);endendnum1 = num1+1;endstep_opt = (step0+step1)/2; %最优步长x0 = x0 - dz0(1)*step_opt;y0 = y0 - dz0(2)*step_opt;[z0,dz0] = fxy(x0,y0);%line([x00,x0],[y00,y0],[z00,z0],'Color','r','LineWidth',2);line([x00,x0],[y00,y0],'Color','r','LineWidth',2);plot(x0,y0,'r+');num = num + 1;if abs(z0-z00) <= ea+er*abs(z00)break;endendhold off;disp(['Opt_Piont = ( ', num2str(x0), ',' ,num2str(y0),' )']); disp(['Opt_Value = ',num2str(z0)]);disp(['迭代次数：',num2str(num)]);disp(['线性搜索迭代次数：',num2str(num1)]);。

用MATLAB实现最速下降法

实验的题目和要求一、所属课程名称:最优化方法二、实验日期：2０10年5月10日~2010年5月1５日三、实验目的掌握最速下降法，牛顿法和共轭梯度法的算法思想,并能上机编程实现相应的算法。

二、实验要求用ＭATLAB 实现最速下降法，牛顿法和共轭梯度法求解实例。

四、实验原理最速下降法是以负梯度方向最为下降方向的极小化算法，相邻两次的搜索方向是互相直交的。

牛顿法是利用目标函数)(x f 在迭代点k x 处的Tayl ｏr 展开式作为模型函数，并利用这个二次模型函数的极小点序列去逼近目标函数的极小点。

共轭梯度法它的每一个搜索方向是互相共轭的,而这些搜索方向k d 仅仅是负梯度方向k g -与上一次接待的搜索方向1-k d 的组合。

五．运行及结果如下：最速下降法:题目:f ＝（x-２)^２+(y －4）＾2M 文件：ｆuncti ｏｎ [R,n]=s ｔｅｅｌ(x0，y0,eps)ｓyms x ;ｓｙms y ；f=(x －2)^2+（y-4)^２;ｖ＝[x ，ｙ];j=jacobia ｎ(ｆ，v ）;T ＝[ｓu ｂs （j(1),x,x ０),ｓub ｓ（ｊ（2），y,y ０）］;t ｅmp=s ｑrt((T （1））^２+（Ｔ（2))^2);x1＝ｘ0;ｙ１=ｙ0;n=0;syms kk ；wh ｉle (t ｅmp>ep ｓ)d=－T;f1＝x １+kk*d(1);ｆ2＝y1＋kk*d(2);fＴ=[subｓ(j（1）,x,f1),subs(ｊ(2），y,f2)];fun=ｓqrｔ((ｆT(1)）＾2＋(fＴ(２))＾2)；Mini＝Gold（fun,0，1,0.0０001）;x0=x1+Ｍｉnｉ*d（1）;ｙ0=ｙ1＋Mini*d(2);T=[subs（ｊ（1）,x,x０),subs(j(2),y,y0)］；tｅmp=ｓｑrｔ((T(１))^2+(T(２))^２);x1=x0;y1=ｙ0；n=n+1;endR=[ｘ0,ｙ0]调用黄金分割法:Ｍ文件:ｆuｎctiｏnＭiｎi＝Ｇｏld(f,a０，ｂ0,eps）symｓx；format long；sｙms kk；ｕ＝ａ０+0.３82*(b0-a0）;v＝a0＋０.61８＊(b０－a0);k=0;a＝a0;b=b0;arraｙ(k+1,１）=a；arrａy(ｋ+1，2)=ｂ;while(（b-a)/(b0-ａ0)>=eps）Fu=subs（ｆ,ｋk，ｕ);Fv=ｓｕbs(f，kk,v)；if(Fｕ<＝Fv）b=v；v＝u;u=a＋0．382*(ｂ-a)；k=k+１;ｅｌｓeiｆ(Fu>Fｖ)a=u；u=ｖ;ｖ＝a+0.６18＊（b－a）；k＝k+1；endaｒray(k＋1,１)=ａ；arｒay(k＋１,2）=b;eｎdＭini=（ａ+b)/2;输入：[Ｒ,n]=sｔeel(0，1,0.０0０１)Ｒ= １．99９9941366７642 3．99９99１20501４63 Ｒ= 1.9９999４13667６42 3.９９99９1２０50１4６３n = 1牛顿法：题目:f＝(ｘ-2)^2＋(y-4)＾2M文件:syms x1x2;f＝(x１-２)＾2＋（x2-4)^２;v=[x１,ｘ２];df＝ｊacｏｂiａn（f，ｖ);df=df.＇;G＝jacｏｂｉaｎ(df,v);epｓon=1e-12；x0=［0，0]＇;g1=sｕbs（df，｛ｘ1,x2},{x0(1,1）,ｘ0(2，1)});G１=subs(G,{x1,ｘ2｝,{x0(1,1),x０（2,1)}）;k=0;ｍuｌ_coｕnt=0;sum_couｎt=0;mul_count=mｕl_cｏｕnt+12;sum_couｎt=sum_cｏunｔ+６;wｈile(norm（g1）>epson)p＝-G1\g1;x0=x0＋p;g1=subs(df，｛ｘ1，ｘ2},{ｘ0(1，１）,x０（2,1)});G1＝subｓ（G,{x1,x２},{x0（1,1），x0(２,1)}）;ｋ=k+1;mｕｌ＿ｃｏunｔ=mul_ｃounｔ+1６;suｍ＿cｏunt=sｕm_ｃounｔ+１1；ｅｎd;kｘ0mul＿couｎtsum_ｃouｎｔ结果::k ＝ 1ｘ０=24ｍuｌ_coｕnt ＝2８ｓum_ｃｏunt = 17共轭梯度法：题目：f＝(x－2)^２＋(y-4）^2M文件：funｃtion f＝conjuｇaｔｅ_gｒad_２d（x0,t）ｘ=x0;ｓyｍs ｘi yi af＝(xi-２)^2+(ｙi-４)＾２;ｆx=diff(f，xｉ）;fy=ｄifｆ(ｆ,ｙi);fx=ｓubs(fx,｛xi,yi}，x0）;fy=subs(fy，{xi，yi}，x0);fi=[ｆx,fy］;count=0；whiｌe doublｅ(ｓqrｔ(fx＾2+fy^2))>tｓ=-fi;ｉfｃount<=0s=-fｉ;elｓes=s１;eｎdｘ＝x+a*s;f=sｕｂｓ(f,{ｘｉ,yi},x);f1=diff（f)；f１=solvｅ(f1);ifｆ1~=0ａi＝double(f1);eｌsebreakx，f=sｕbs(f,{xi,yi},x),counｔendx=suｂs（x,a,aｉ）;ｆ＝xi－xi^2+2*xi*yi+yｉ^2；fxi=ｄｉff(f,ｘi);fyi＝difｆ(f,ｙi);fxｉ＝ｓｕbs(fｘi,{xi,ｙi},x）;fyｉ=subs(fyｉ，{xi，ｙi}，x);ｆｉｉ＝［fxｉ,fyi];d=(fxi＾2＋ｆyi＾２)/(fx^２+fy^2）；s1=-fｉi＋d＊s;couｎt=coｕnt+1;ｆx＝ｆxｉ；fy=ｆyi;endx,f=ｓubｓ(ｆ,{ｘｉ,yi｝,x),cｏunt输入:cｏnjugatｅ_grad_２d([０,0］,0．0００1)结果：x ＝0.2４998825499785 -０.2４9999987４1273f= 0．124９９９9９98617６cｏuｎｔ=１0aｎs= 0．1２４９9999986176六、结论如下：最速下降法越接近极小值,步长越小，前进越慢。

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

matlab找零点函数

matlab程序运行修改版 二分法等等

matlab编程实现二分法牛顿法黄金分割法最速下降matlab程序代码

[matlab二分法程序代码]matlab牛顿迭代法程序代码

用Matlab编写二分法和Newton迭代法求解非线性函数

二分法,牛顿迭代法,matlab

MATLAB解方程经典算法

matlab牛顿法代码举例

最速下降法matlab代码

matlab二分法代码

最速下降法matlab程序

数值方法matlab版

二分法程序代码【matlab源码】

二分法、简单迭代法的matlab代码实现

matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码

二分法,不动点迭代法,艾特肯加速迭代法,牛顿切线法的matlab程序及举例

二分法、牛顿法、割线法、Steffencen法求非线性方程MATLAB实现

最速下降法MATLAB程序实现

用MATLAB实现最速下降法

matlab程序运行修改版二分法等等