解析几何同步练习(椭圆及其标准方程2a)1
高中解析几何辅导练习:椭圆的的方程及其性质

训练四 椭圆的的方程及其性质一.概念:1.椭圆的定义及第二定义; 2.椭圆的标准方程; 3.椭圆的性质;4.椭圆的焦半径;5.直线与椭圆的问题.二. 例题1、(5分)(2001全国文7)若椭圆经过原点,且焦点为)0,3(),0,1(21F F ,则其离心率为(A )43 (B )32 (C )21 (D )41 2、(5分)(2004河南理7)椭圆1422=+y x 的两个焦点为F 1、F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则||2PF =( )A .23B .3C .27 D .4 3、(4分)(2004湖南文15)F 1,F 2是椭圆C :14822=+x x 的焦点,在C 上满足PF 1⊥PF 2的点P 的个数为__________.4、(4分)(2004重庆理16)对任意实数K ,直线:y kx b =+与椭圆:)20(sin 41cos 23πθθθ<≤⎩⎨⎧+=+=y x 恒有公共点,则b 取值范围是_______________5.过椭圆14922=+y x 内一点D (1,0)引动弦AB ,求弦AB 的中点M 的轨迹方程。
6.椭圆141622=+y x 上有两点P 、Q ,O 是原点,若OP 、OQ 斜率之积为41-。
求证22||||OQ OP +为定值。
训练题四: 椭圆及其性质1、(5分)(2004春安徽理3)已知F 1、F 2为椭圆22221x y a b+=(0a b >>)的焦点;M 为椭圆上一点,MF 1垂直于x 轴,且∠F 1MF 2=600,则椭圆的离心率为( )(A )21 (B )22 (C )33 (D )23 2、(5分)(2004湖北理6)已知椭圆191622=+y x 的左、右焦点分别为F 1、F 2,点P 在椭圆上,若P 、F 1、F 2是一个直角三角形的三个顶点,则点P 到x 轴的距离为( )A .59B .3C .779D .49 3、(5分)(2004福建理4)已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若△ABF 2是正三角形,则这个椭圆的离心率是( )A .33B .32C .22D .23 4、(5分)(2004重庆理10)已知双曲线22221,(0,0)x y a b a b-=>>的左,右焦点分别为12,F F ,点P 在双曲线的右支上,且12||4||PF PF =,则此双曲线的离心率e 的最大值为:( )A .43B .53C .2D .735.一个圆的圆心在椭圆的右焦点2F 上,且过椭圆的中心D (0,0),该圆与椭圆交于点P ,设1F 是椭圆的左焦点,直线1PF 恰好与圆相切于点P ,则椭圆的离心率是( )A .13-B .32-C .22D .23 6.设椭圆1204522=+y x 的两个焦点分别为1F 和2F ,P 为椭圆上一点,并且21PF PF ⊥,则||||||21PF PF -等于( )A .56B .52C .531 D .532 7.过点M (-2,0)的直线l 与椭圆2222=+y x 交于1P 、2P 两点,线段21P P 的中点为P ,设直线l 的斜率为)0(11≠k k ,直线OP 的斜率为2k ,则21k k 的值为( )A .2B .-2C .21D .21- 8.方程1)4csc(3322=+-παy x 表示椭圆时,α适合的条件是( ) A .παπ4743≤≤ B .παπ4743<< C .)(472432Z ∈+<<+k k k ππαππ D .)(4743Z ∈+<<+k k k ππαππ 9.设b ≥2a>0,则曲线122=+by ax 上对两焦点张角为直角的点有( )A .0个B .0个或2个C .2 个或4个D .0个或2个或4个10.点P 在椭圆284722=+y x 上,则点P 到直线3x-2y-16=0的距离的最大值是( ) A .13132 B .131316 C .131324 D .131328 11、已知双曲线22154x y -=,若将该双曲线绕着它的右焦点逆时针旋转90︒后,所得双曲线的一条准线方程是 ( )(A )43y =- (B )43y = (C )163y = (D )163y =- 12、直线10x y --=与实轴在y 轴上的双曲线22(0)x y m m -=≠的交点在以原点为中心、边长为2且各边分别平行于坐标轴的正方形的内部,则m 的取值范围是 ( )(A )01m << (B )0m < (C )10m -<< (D )1m <-13.△ABC 中,三边a 、c 、b 成等差数列,且a>c>b ,若A (-1,0),B (1,0),则动点C 的轨迹方程为____________。
《解析几何》第10讲 椭圆及其标准方程

椭圆及其标准方程
1.椭圆的定义
文字语言:
平 面 内 与 两 个 定 点 F1 , F2 的 距 离 的 和 等 于 常 数 ( 大 于
|F1F2|)的点的轨迹叫做椭圆.
符号语言:
平面内点M满足|MF1|+|MF2|=2a(2a>|F1F2|),点M的轨 迹叫做椭圆.
2.椭圆的标准方程
标准 方程
且△F1AB的面积为9, 则b= 3 .
2
2
的焦点,点P在椭圆上满足 ∠F1 PF2=90°,
P
m
F1
2c
n
F2
例题 3. 已知中心在原点的椭圆 C 的右焦点为 F(1,0), 1 D . 离心率等于 ,则 C 的方程是 2 x2 y2 x2 y2 A. + =1 B. + =1 3 4 4 3 x2 y2 x2 y2 C. + =1 D. + =1 4 2 4 3
x y 1 上一点 例题2. 已知椭圆 16 9 P 到一个焦点的距离为 3 , 则它到
另一个焦点的距离是
2
2
5
.
变式1. 已知椭圆中心为原点,一个焦点 F1(3,0),过F2的直线与椭圆交于AB,且 △F1AB的周长为16, 椭圆的方程是 .
已知F1 , F2是椭圆 2 2 1 a b
x 2 y2 2+ 2= 1(a>b>0) a b
y2 x2 2+ 2=1(a>b>0) a b
图形
性 质
范 围
-a≤x≤a -b≤y≤b
-b≤x≤b -a≤y≤a
x y 例题 1. 若方程 + =1 表示椭圆, 则 5- k k - 3 k 的取值范围是
2
2
椭圆及其标准方程(一)1
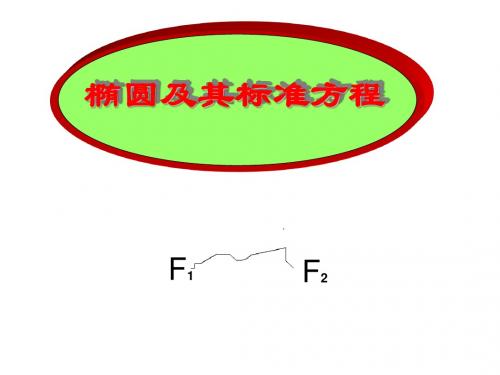
b a c 5 4 9
2 2 2 2 2
x y 1 ∴ 所求的椭圆的标准方程为 25 9
2
2
教材例1 求适合下列条件的椭圆的标准方程:
(2)两个焦点的坐标分别是(0,-2)、(0,2), 并且椭圆经过点 3 , 5
2 2
解:∵ 椭圆的焦点在y轴上,
教材例2 :
2c=6, 2a=16-6=10,c=3,a=5, b a c 5 3 16. 但当点A在直线BC上,即y=0时,A、B、C三点不能 构成三角形,所以点 A的轨迹方程是: 2 2
2 2 2 2 2
x y 1. ( y 0). 25 16
教材例3: 如图,已知一个圆的圆心为坐标原点,
所以 ( x c) 2 y 2 2a ( x c) 2 y 2 两边平方得 : ( x c) 2 y 2 4a 2 4a ( x c) 2 y 2 ( x c) 2 y 2 即 : a 2 cx a ( x c) 2 y 2
2 2
y x ∴ 所求的椭圆的标准方程为 1 10 6
b a c 10 4 6 2 2
2
已知B、C是两个定点,|BC|=6, 且△ABC的周长等于16,求顶点A的轨迹方程。 分析:在解析几何里,求符合某种条件的点的轨 迹方程,要建立适当的坐标系。为选择适当的坐标系, 常常需要画出草图。 经画图分析,点A的轨迹是椭圆。 Y 解:建立如图坐标系,使 A x轴经过点B、C,原点O与 BC的中点重合。 O C X |BC|=6 ,|AB|+|AC|=16-6=10, B 所以点A的轨迹是椭圆,
教材例1 求适合下列条件的椭圆的标准方程:
第二关 以解析几何中与椭圆相关的综合问题为解答题-(解析版)

压轴解答题第二关 以解析几何中与椭圆相关的综合问题【名师综述】纵观近三年的高考题,解析几何题目是每年必考题型,主要体现在解析几何知识内的综合及与其它知识之间的综合,且椭圆考查的最多,,同时可能与平面向量、导数相交汇,每个题一般设置了两个问,第(1)问一般考查曲线方程的求法,主要利用定义法与待定系数法求解,而第(2)问主要涉及最值问题、定值问题、对称问题、轨迹问题、探索性问题、参数范围问题等.这类问题综合性大,解题时需根据具体问题,灵活运用解析几何、平面几何、函数、不等式、三角知识,正确构造不等式,体现了解析几何与其他数学知识的密切联系.类型一 中点问题典例1已知椭圆()2222:10x y C a b a b+=>>的离心率13e =,焦距为2.(1)求椭圆C 的方程;(2)过点()0,2Q 作斜率为()0k k ≠的直线l 与椭圆C 交于A 、B 两点,若x 轴上的一点E 满足AE BE =,试求出点E 的横坐标的取值范围.【来源】河南省温县第一高级中学2021-2022学年高三上学期1月月考文科数学试题 【答案】(1)22198x y ;(2)220,12⎡⎫⎛⎤⎪ ⎢⎥⎪ ⎣⎭⎝⎦. 【解析】(1)由已知可求得a 、c 的值,可求得b 的值,由此可得出椭圆C 的标准方程;(2)设点设()11,A x y 、()22,B x y ,将直线l 的方程与椭圆C 的方程联立,列出韦达定理,求出线段AB 的中点G 的坐标,由题意可知EG AB ⊥,可得1EG k k=-,可得出m 关于k 的表达式,分0k <、0k >两种情况讨论,结合基本不等式可求得m 的取值范围.(1)解:由已知得1322c a c ⎧=⎪⎨⎪=⎩,所以,1c =,3a =,2228b a c =-=,因此,椭圆C 的方程为22198x y .(2)解:根据题意可知直线l 的方程为2y kx =+,设()11,A x y 、()22,B x y , 线段AB 的中点为()00,G x y ,设点(),0E m ,使得AE BE =,则EG AB ⊥.联立222198y kx x y =+⎧⎪⎨+=⎪⎩得()228936360k x kx ++-=,()()22223614498288940k k k ∆=++=+>,由韦达定理可得1223698k x x k +=-+,所以,021898k x k -=+,00216298y kx k =+=+, 因为EG AB ⊥,所以,1EGk k =-,即221601981898k k k m k -+=---+, 则2228989k m k k k--==++,当0k >时,89298122k k +≥⨯=22k =20m ≤<; 当0k <时,()()8889929122k k k k k k⎡⎤+=--+≤--⋅-⎢⎥--⎣⎦ 当且仅当22k =20m <≤综上所述,点E 的横坐标的取值范围为220,12⎡⎫⎛⎤⎪ ⎢⎥⎪ ⎣⎭⎝⎦. 【点睛】方法点睛:圆锥曲线中取值范围问题的五种求解策略:(1)利用圆锥曲线的几何性质或判别式构造不等关系,从而确定参数的取值范围;(2)利用已知参数的范围,求新的参数的范围,解这类问题的核心是建立两个参数之间的等量关系; (3)利用隐含的不等关系建立不等式,从而求出参数的取值范围; (4)利用已知的不等关系建立不等式,从而求出参数的取值范围;(5)利用求函数值域的方法将待求量表示为其他变量的函数,求其值域,从而确定参数的取值范围.【举一反三】已知椭圆C :()222210y x a b a b+=>>的焦距与椭圆2213x y +=的焦距相等,且C 经过抛物线()212y x =- (1)求C 的方程;(2)若直线y kx m =+与C 相交于A ,B 两点,且A ,B 关于直线l :10x ty ++=对称,O 为C 的对称中心,且AOB 10k 的值. 【答案】(1)22142y x +=;(2)3k = 【解析】(1)由题意:()212y x =-(2,焦距为22故22222112a ba b ⎧+=⎪⎨⎪-=⎩,解得:24a =,22b =,所以C 的方程为:22142y x +=; (2)因为直线y kx m =+与C 相交于A ,B 两点,且A ,B 关于直线l :10x ty ++=对称,故直线l 垂直AB ,所以k t =,联立22142y kx my x =+⎧⎪⎨+=⎪⎩可得()2222240k x kmx m +++-=,设()11,A x y ,()22,B x y ,AB的中点为()00,P x y ,则()228240k m∆=+->,022km xk =-+,00222my kx m k =+=+,因为()00,P x y 在直线l :10x ky ++=上,所以2221022km km k k -++=++,即2m k k ⎛⎫=-+ ⎪⎝⎭,所以22480k k ⎛⎫∆=-> ⎪⎝⎭,即:22k >,()()()2222222212122k k AB k k k k +-∆=+=++,O 到直线AB 的距离()222211m d k k k ==++,()2241102AOBk SAB d -===,解得:23k =,3k =类型二 垂直问题典例2 已知椭圆1C :22221x y a b +=(0a b >>)的离心率为22,1C 的长轴是圆2C :222x y +=的直径.(1)求椭圆的标准方程;(2)过椭圆1C 的左焦点F 作两条相互垂直的直线1l ,2l ,其中1l 交椭圆1C 于P ,Q 两点,2l 交圆2C 于M ,N 两点,求四边形PMQN 面积的最小值.【来源】广东省肇庆市2021届高三二模数学试题【答案】(1)2212x y +=;(2)2.【解析】(1)由222a =,得2a =由2c e a ==,得1c =,所以1b =.所以椭圆的方程为2212x y +=.(2)由(1)可得()1,0F -.①当过点F 的直线1l 的斜率不存在时,22MN =2PQ =这时11222222PMQN S MN PQ ==⨯=. ②当过点F 的直线1l 的斜率为0时,2MN =,22PQ =, 这时112222222PMQN S MN PQ ==⨯⨯=③当过点F 的直线1l 的斜率存在且不为0时,设直线1l 的方程为1x my =-,()11,P x y ,()22,Q x y .由22112x my x y =-⎧⎪⎨+=⎪⎩,整理可得()222210m y my +--=. 12222m y y m +=+,12212y y m -=+. 所以())222212121222211142m m y m y y y y m PQ +=+-=++-=+.直线2l 的方程为0mx y m ++=,坐标原点O 到2l 的距离21d mm =+所以2222222211m m MN m m +=-=++22211122221222PMQN m S MN PQ m m +===-++由222m +>,得2122122m->+,即(2,22PMQN S ∈. 综上所述,四边形PMQN 的面积的最小值为2.【举一反三】已知椭圆222:1(1)x C y a a+=>,离心率6e .直线:1l x my =+与x 轴交于点A ,与椭圆C 相交于,E F 两点.自点,E F 分别向直线3x =作垂线,垂足分别为11,E F .(Ⅰ)求椭圆C 的方程及焦点坐标;(Ⅱ)记1AEE ,11AE F ,1AFF 的面积分别为1S ,2S ,3S ,试证明1322S S S 为定值.【答案】(Ⅰ)椭圆C 的方程为2213x y +=,焦点坐标为(2,0)±;(Ⅱ)证明见解析. 【解析】(Ⅰ)由题意可知1b =,又63c e a ==,即22123a a -=.解得23a =.即3a =. 所以222c a b =-=.所以椭圆C 的方程为2213x y +=,焦点坐标为(2,0)±.(Ⅱ)由221330x my x y =+⎧⎨+-=⎩得22(3)220m y my ++-=,显然m R ∈. 设()11,E x y ,()22,F x y ,则12122222,33m y y y y m m --+==++,()113,E y ,()123,F y ,因为13112211(3)(3)22S S x y x y =-⋅-12121(2)(2)4my my y y =--21212121[42()]4m y y m y y y y =-++ 22221222(42)4333m m m m m m ---=-⋅+⋅+++2223(2)(3)m m +=+, 又因为22221212121[2]()42S y y y y y y =⨯-=+-()22224833m m m =+++()222248243m m m ++=+()22212243m m +=+.所以22213222223(2)1(3)12(2)4(3)m S S m m S m ++==++. 类型三 面积问题典例3如图,已知椭圆221:12x y Γ+=和抛物线22:3x y Γ=,斜率为正的直线l 与y 轴及椭圆1Γ依次交于P 、A 、B 三点,且线段AB 的中点C 在抛物线2Γ上.(1)求点P 的纵坐标的取值范围;(2)设D 是抛物线2Γ上一点,且位于椭圆1Γ的左上方,求点D 的横坐标的取值范围,使得PCD 的面积存在最大值.【来源】浙江省2022届高三水球高考命题研究组方向性测试Ⅴ数学试题 【答案】(1)3,22⎛⎫⎪⎝⎭;(2)323,2⎛-- ⎝⎭. 【解析】(1)设直线l 的方程为()0,0y kx b k b =+>>,则()0,P b ,将直线l 的方程与椭圆的方程联立,可求得点C 的坐标,将点C 的坐标代入抛物线的方程,可得出()223214k b k +=,结合0∆>可得出2k 的取值范围,进而可求得b 的取值范围,即可得解;(2)设点()23,3D t t ,计算得出PCD 的面积239142416t S t k k ⎛⎫-=-+- ⎪⎝⎭,令1u k =,记()()32424f u u t u t =-+--,则60u <()f u ',分析可知函数()f u 在6⎛ ⎝⎭内有唯一的极值点,且为极大值点,结合已知条件可得出关于t 的不等式组,解出t 的取值范围,即可得出点D 的横坐标的取值范围.(1)解:由题意可设直线l 的方程为()0,0y kx b k b =+>>,则()0,P b ,联立2222y kx b x y =+⎧⎨+=⎩可得()222214220k x kbx b +++-=, ()()()2222221682118210k b k b k b ∆=-+-=+->,可得2221b k <+,① 设点()11,A x y 、()22,B x y ,由韦达定理可得122421kb x x k +=-+,21222221b x x k -=+,设点()00,C x y ,则12022221x x kb x k +==-+,00221by kx b k =+=+, 将点C 的坐标代入抛物线2Γ的方程得224630k b k --=,则()223214k b k+=,代入①可得()22249212116k k k +<+,可得42161890k k -->,解得232k >, 因此()222321333,24242k b k k +⎛⎫==+∈ ⎪⎝⎭. 因此,点P 的纵坐标的取值范围是3,02⎛⎫⎪⎝⎭.(2)解:设点()23,3D t t,则点D 到直线l 的距离为22223311tk t bd k k -+==++,221kb k PC +=PCD 的面积()22331221kb t tk b S PC d k --=⋅=+,② 将()223214k b k +=代入②得239142416t S t k k ⎛⎫-=-+- ⎪⎝⎭, 令1u k =,记()()32424f u u t u t =-+--,则60u <()22342f u u t '=-+-, 因为()f u '在6⎛ ⎝⎭上单调递减,所以,函数()f u 在6⎛ ⎝⎭内有唯一的极值点,且为极大值点,所以,()2204206440f t f t ⎧=->⎪⎨=-<⎪⎭'⎝⎩',可得2112t <<,③ 因为点D 在椭圆1Γ的左上方,则2409182t t t <⎧⎨+>⎩,④ 由③④可得21t -<<D 的横坐标的取值范围是323,⎛- ⎝⎭. 【点睛】方法点睛:圆锥曲线中的最值问题解决方法一般分两种:一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.【举一反三】已知椭圆C :22221(x y a b a b+=>>0)的右焦点F 与右准线l :x =4的距离为2.(1)求椭圆C 的方程;(2)若直线():0m y kx t t =+≠与椭圆C 相交于A ,B 两点,线段AB 的垂直平分线与直线m 及x 轴和y 轴分别相交于点D ,E ,G ,直线GF 与右准线l 相交于点H .记AEGF ,ADGH 的面积分别为S 1,S 2,求12S S 的值.【来源】江苏省苏州中学等四校2021-2022学年高三下学期期初联合检测数学试题 【答案】(1)22184x y +=;(2)12 【解析】(1)根据已知条件求得,,a b c ,由此求得椭圆C 的方程.(2)结合根与系数关系求得D 点坐标,进而求得,,E G H 点坐标,利用“中点”求得面积比.(1)依题意2222242a c a c ca b c ⎧=⎪⎪⎪-=⎨⎪=+⎪⎪⎩,解得22,2a b c ===,所以椭圆方程为22184x y +=. (2)右焦点()2,0F .直线():0m y kx t t =+≠,由于线段AB 的垂直平分线与,x y 轴都相交,所以0k ≠,由22184y kx tx y =+⎧⎪⎨+=⎪⎩消去y 并化简得()222124280k x ktx t +++-=,设()()1122,,,A x y B x y , 则()1212122242,21212kt tx x y y k x x t k k -+=+=++=++, 所以222,1212ktt D k k -⎛⎫ ⎪++⎝⎭.线段AB 的垂直平分线的方程为22121212t kt y x k k k ⎛⎫-=-⋅+ ⎪++⎝⎭,令0y =,解得22,01212E kt kt x E k k --⎛⎫=⇒ ⎪++⎝⎭, 令0x =,解得220,1212G t t y G k k --⎛⎫=⇒ ⎪++⎝⎭. 所以,D G 关于E 点对称,所以DE EG =, 所以ADEAEGSS=.直线GF 的方程为()20120220tk y x --+-=--,令4x =,解得224,1212H t t y H k k ⎛⎫=⇒ ⎪++⎝⎭, 所以,G H 关于F 对称,所以GF FH =, 所以AGFAFHSS=.结合图象可知:1212S S =.【点睛】本题求四边形AEGF 和四边形ADGH 的面积比,常规的方法是借助弦长公式和点到直线距离来求面积,但本题用这个方法很难.在解题的过程中,求出,,,,D E G F H 的坐标后,要注意观察坐标间的对称性,结合对称性来求面积比,将问题求解大大简化.类型四 范围与定值问题典例4已知椭圆C :()2222 1x y a b c a b +=>>2()2,1P .(1)求C 的方程;(2)若A ,B 是C 上两点,直线AB 与曲线222x y +=相切,求AB 的取值范围. 【来源】重庆市2022届高三下学期开学考试数学试题【答案】(1)22163x y +=;(2)22,3⎡⎤⎣⎦ 【解析】(1)根据已知条件求得,,a b c ,由此求得椭圆C 的方程.(2)对直线AB 的斜率分成不存在,0k =,0k ≠三种情况进行分类讨论,结合弦长公式、基本不等式求得AB 的取值范围.(1)依题意22222224116,3c aa b c a b a b c ⎧=⎪⎪⎪+=⇒===⎨⎪=+⎪⎪⎩所以椭圆C 的方程为22163x y +=.(2)圆222x y +=的圆心为()0,0,半径2r =当直线AB 的斜率不存在时,直线AB 的方程为2x 2x = 2222163x y x y ⎧=⎪⇒=⎨+=⎪⎩2222163x y x y ⎧=-⎪⇒=⎨+=⎪⎩ 所以22AB =当直线AB 的斜率为0时,直线AB 的方程为2y 2y =-2222163y x x y ⎧=⎪⇒=⎨+=⎪⎩2222163y x x y ⎧=-⎪⇒=⎨+=⎪⎩ 所以22AB =当直线AB 的斜率0k ≠时,设直线AB 的方程为,0y kx b kx y b =+-+=, 由于直线AB 和圆222x y +=()2222211b b k k =++.22163y kx b x y =+⎧⎪⎨+=⎪⎩,消去y 并化简得()222124260k x kbx b +++-=, ()()222222164122648248k b k b k b ∆=-+-=+- ()22248248213280k k k =+-⨯+=+>.设()()1122,,,A x y B x y 则2121222426,1212kb b x x x x k k --+=⋅=++, 所以()2222212122242614141212kb b AB k x x x x k k k --⎛⎫=++-=+-⋅ ⎪++⎝⎭()2422224242232845112222144144112k k k k k k k k k k ++++++++++2212122144k k=+>++另一方面,由于22221144448k k k k +⋅+≥=,当且仅当222114,2k k k ==时等号成立. 所以2211212131844k k++=++,即223AB ≤. 综上所述,AB 的取值范围是22,3⎡⎤⎣⎦.【举一反三】已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为(2,0)F ,过点F 且垂直于x 轴的直线与椭圆相交所得的弦长为2. (1)求椭圆C 的方程;(2)过椭圆内一点P (0,t ),斜率为k 的直线l 交椭圆C 于M ,N 两点,设直线OM ,ON (O 为坐标原点)的斜率分别为k 1,k 2,若对任意k ,存在实数λ,使得12k k k λ+=,求实数λ的取值范围. 【来源】江苏省扬州大学附中2021届高三下学期2月检测数学试题【答案】(1)22142x y +=;(2)[2,)+∞. 【解析】(1)椭圆2222:1(0) x y C a b a b+=>>的右焦点为(2,0)F ,则2c =∵过点F 且垂直于x 轴的直线与椭圆相交所得的弦长为2,22221c y a b ∴+=,解得2b y a =±,222b a∴=,即2b a =,∴2222a b c a =+=+, 解得2a =,∴椭圆的方程为22142x y +=,(2)设直线l 的方程为y kx t =+.由221? 42x y y kx t ⎧+=⎪⎨⎪=+⎩,消元可得()222214240k x ktx t +++-=, 设()()1122,,,M x y N x y ,则122421kt x x k -+=+,21222421t x x k -=+, 而121212*********y y kx t kx tk k k t x x x x x x ⎛⎫+++=+=+=++ ⎪⎝⎭1222124422242x x kt kk t k t x x t t +--=+⋅=+⋅=--, 由12k k k λ+=,242kk t λ-=-, 因为此等式对任意的k 都成立,所以242t λ-=-,即242t λ=-. 由题意得点(0,)P t 在椭圆内,故202t ≤<,即4022λ≤-<,解得2λ≥,故实数λ的取值范围为[2,)+∞.典例5 已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点与短轴的两个端点组成的三角形是等腰直角三角形,点(10,1)P 是椭圆C 上一点. (1)求椭圆C 的标准方程;(2)设(,)R s t 是椭圆C 上的一动点,由原点O 向22()()4x s y t -+-=引两条切线,分别交椭圆C 于点P ,Q ,若直线,OP OQ 的斜率均存在,并分别记为12,k k ,求证:12k k ⋅为定值. 【来源】云南省昭通市2022届高三期末数学(理)试题 【答案】(1)22:1126x y C +=;(2)证明见解析【解析】(1)由椭圆的性质得出b c =,再将(10,1)P 代入椭圆方程,结合222a b c =+得出椭圆C 的标准方程;(2)设直线1:OP y x k =,直线2:OQ y k x =,根据距离公式得出12,k k 是方程()2224240s k stk t --+-=的两根,由韦达定理结合点(,)R s t 在椭圆上,得出12k k ⋅为定值.(1)解:由已知有222222,(10)11,,b c b a b c =⎧⎪⎪+=⎨⎪=+⎪⎩解得22212,6,6,a b c ⎧=⎪=⎨⎪=⎩ ∴椭圆C 的方程为22:1126x y C +=.(2)证明:设直线1:OP y x k =,直线2:OQ y k x = 又直线OP 为圆R 12121k s t k -=+,化简可得()222114240s k stk t --+-=,同理可得()222224240s k stk t --+-=,∴12,k k 是方程()2224240s k stk t --+-=的两根,由()240,0s -≠∆>,可知212244t k k s -⋅=-, 又(,)R s t 在椭圆上,即22162t s =-,∴22122212412442s t k k s s --⋅===---,∴12k k ⋅为定值12-. 【举一反三】已知椭圆2222:1(0)x y C a b a b +=>>经过两点33,M ⎭,242N ⎝⎭. (1)求椭圆C 的方程:(2)A 、B 分别为椭圆C 的左、右顶点,点P 为圆224x y +=上的动点(P 不在坐标轴上),P A 与PB 分别与椭圆C 交E 、F 两点,直线EF 交x 轴于H 点,请问点P 的横坐标与点H 的横坐标之积是否为定值?若是,求出这个定值;若不是,说明理由.【来源】江西省景德镇市2022届高三第二次质检数学(理)试题【答案】(1)22143x y +=(2)点P 的横坐标与点H 的横坐标之积为定值,定值为4 【解析】(1)将两点代入椭圆方程解方程求出,a b 的值,确定椭圆方程(2)设P A 与PB 直线与椭圆联立,求出E 、F 两点的坐标表达式,写出直线EF 方程,求出与x 轴的交点H 点的坐标,联立两条直线求出P 点的坐标,计算乘积判断是否为定值(1)将,M N 点坐标代入椭圆方程得:222233141421216a b a b⎧+=⎪⎪⎨⎪+=⎪⎩ ,解得:2234a b =⎧=⎪⎨⎪⎩ ,所以椭圆方程为22143x y +=(2)根据圆方程为224x y +=可知,AB 为圆的直径,点P 在圆上,所以PA PB ⊥,设直线PA 方程为:()2,0y k x k =+≠,联立()222143y k x x y ⎧=+⎪⎨+=⎪⎩ 得:()2222341616120k x k x k +++-=,所以221612234A E E k x x x k -⋅=-=+,所以228634E k x k -+=+,代入直线得:21234E k y k =+;同理设直线PB 方程为:()12y x k =--,联立()2212143y x k x y ⎧=--⎪⎪⎨⎪+=⎪⎩得:2222416163120x x k k k ⎛⎫+-+-= ⎪⎝⎭,则22221612161224343B F F k k x x x k k--⋅===++, 所以228643F k x k -=+,21243Fk y k =+, 所以2337E F EFE F y y k k x x k --==- ,直线EF 的方程为:222212338634734k k k y x k k k ⎛⎫--+-=- ⎪++⎝⎭,令0y =得:()()()()222222222234661278666343334333433H k k k k k k x k k k k k k -++-++=-⋅+==+-+-+-, 联立直线PA ,PB ()()212y k x y x k =+⎧⎪⎨=--⎪⎩得:22221P k x k -=+,所以222222664133P H k k x x k k -+⋅=⋅=+-,所以点P 的横坐标与点H 的横坐标之积为定值,定值为4【精选名校模拟】1.已知椭圆2222C :1(0)x y a b a b+=>>的离心率为12,直线1:22l y x =-+与椭圆C 有且仅有一个公共点A .(Ⅰ)求椭圆C 的方程及A 点坐标;(Ⅱ)设直线l 与x 轴交于点B .过点B 的直线与C 交于E ,F 两点,记点A 在x 轴上的投影为G ,T 为BG 的中点,直线AE ,AF 与x 轴分别交于M ,N 两点.试探究||||TM TN ⋅是否为定值?若为定值,求出此定值;否则,请说明理由.【来源】湖南省长沙市第一中学、广东省深圳实验学校2021届高三下学期联考数学试题【答案】(1)2231,1,432x y A ⎛⎫+= ⎪⎝⎭;(2)||||TM TN ⋅为定值94 【解析】(1)设椭圆C 的半焦距为c ,则12c a =,则224a c =,22223b a c c =-=, 所以椭圆C 的方程为:2222143x y c c+=,将椭圆C 的方程与直线l 的方程联立得:222430x x c -+-=, 所以244(43)0c ∆=-⨯-=,解得:21c =,所以24a =,23b =,故椭圆C 的方程为22143x y +=,此时将21c =代入222430x x c -+-=得:2210x x -+=, 所以1x =,此时32y =。
高二数学椭圆的标准方程2
♦ 1求动点轨迹方程的一般步骤: (1)建立适当的坐标系,用有序实数对表示曲线 上任意一点M的坐标; (2)写出适合条件P的点M的集合;(可以省略, 直接列出曲线方程) (3)用坐标表示条件P(M),列出方程 f ( x, y) 0 (4)化方程 f ( x, y) 0 为最简形式; (5)证明以化简后的方程的解为坐标的点都是 曲线上的点(可以省略不写,如有特殊情况,可以 适当予以说明)
2 2
y + =1 m - 1 3- m
.
2
2
表示焦点在y轴上的椭圆,则m的取值范 围是 (1,2)
练习:求适合下列条件的椭圆的标准方程:
(1)a= 6 ,b=1,焦点在x轴上; (2)焦点为F1(0,-3),F2(0,3),且a=5. (3)两个焦点分别是F1(-2,0)、F2(2,0),且过 P(2,3)点; (4)经过点P(-2,0)和Q(0,-3).
F(±c,0)
F(0,±c)
c2=a2-b2
注: 共同点:椭圆的标准方程表示的一定是焦点在坐标轴上, 中心在坐标原点的椭圆;方程的左边是平方和,右边是1. 2 不同点:焦点在x轴的椭圆 x 项分母较大. 2 y 焦点在y轴的椭圆 项分母较大.
练习:
1.口答:下列方程哪些表示椭圆? 若是,则判定其焦点在何轴? 并指明 a 2 , b 2 ,写出焦点坐标.
2
解:设|PB|=r.
∵圆P与圆A内切,圆A的半径为10. ∴两圆的圆心距|PA|=10-r, 即|PA|+|PB|=10(大于|AB|). ∴点P的轨迹是以A、B两点为焦点的椭圆. ∴2a=10, 2c=|AB|=6, ∴ a= 5, c= 3. ∴b2=a2-c2=25-9=16.
x y = 1. 即点P的轨迹方程为 25 16
人教新课标版(A)高二选修1-1 2.1.1椭圆及其标准方程(一)同步练习题

人教新课标版(A )高二选修1-1 2.1.1 椭圆及其标准方程(一)同步练习题【基础演练】题型一:椭圆的定义平面内与两个定点1F 、2F 距离的和等于常数(大于|F F |21)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,请根据以上知识解决以下1~4题。
1. 到两定点1F (-2,0)和2F (2,0)的距离之和为4的点M 的轨迹是A. 椭圆B. 线段C. 圆D. 以上都不对2. 椭圆125y 9x 22=+的焦点为1F 、2F ,AB 是椭圆过焦点1F 的弦,则△2ABF 的周长是A. 20B. 12C. 10D. 6 3. 椭圆1y 25x 22=+上一点P 到一个焦点的距离为2,则点P 到另一个焦点的距离为A. 5B. 6C. 7D. 84. 命题甲:动点P 到两定点A 、B 的距离之和()为常数且a ,0a a 2|PB ||PA |>=+; 命题乙:P 点的轨迹是椭圆,则命题甲是命题乙的A. 充分不必要条件B. 必要不充分条件C. 充分且必要条件D. 既不充分又不必要条件题型二:椭圆的标准方程椭圆的两种标准方程1b y a x 2222=+,1bx a y 2222=+中都有:(1)0b a >>;(2)222b a c -=或222c b a +=;(3)焦点坐标(c ±,0)或(0,c ±);(4)2x 与2y 所对应的分母,哪个大,焦点就在哪个轴上,请用以上知识解决以下5~8题。
5. 椭圆116y 32x 22=+的焦距等于A. 312B. 8C. 6D. 46. 若方程1a y ax 222=-表示焦点在y 轴上的椭圆,则a 的取值范围是A. 0a <B. 0a 1<<-C. 1a <D. 无法确定7. 椭圆0ab by ax 22=++(0b a <<)的焦点坐标是A. ()0,b a -±B. ()0,a b -±C. ()b a ,0-±D. ()a b ,0-±8. 椭圆112y 13x 22=+上一点到两个焦点的距离和为A. 26B. 24C.134D. 132题型三:椭圆的标准方程的应用 紧扣标准方程的两种方式,焦点位置取决于两个分母哪个大,特别注意看似非标准形式的标准形式,如11k y kx 222=--,这说明01k <-,另外注意c 2|PF ||PF |21>+的约束条件,请用以上知识解决以下9~10题。
人教B版高中数学选择性必修第一册精品课件 第二章 平面解析几何 分层作业21 椭圆的标准方程

2.[探究点一](多选题)已知在平面直角坐标系中,点A(-3,0),B(3,0),点P为一
动点,且|PA|+|PB|=2a(a≥0),下列说法中正确的是( AC )
A.当a=2时,点P的轨迹不存在
B.当a=4时,点P的轨迹是椭圆,且焦距为3
C.当a=4时,点P的轨迹是椭圆,且焦距为6
D.当a=3时,点P的轨迹是以AB为直径的圆
.
15.已知椭圆C:
2 2
+ =1内有一点M(2,3),F1,F2分别为椭圆的左、右焦
25 16
点,P为椭圆C上的一点,求:
(1)|PM|-|PF1|的最大值与最小值;
(2)|PM|+|PF1|的最大值与最小值.
解 (1)由椭圆
2
C:25
+
2
=1 可知
16
a=5,b=4,c=3,
则 F1(-3,0),F2(3,0),
256
2
2
2
即 144=1 + 2 -r1r2=(r1+r2) -3r1r2=400-3r1r2,则 r1r2= ,
所以△ =
1 2
1
r1r2sin
2
1
60°=
2
×
256
3
×
设点 P 到 x 轴的距离为 d,则△ =
1 2
3
2
=
64 3
.
3
3
1
64 3
32 3
×|F1F2|×d=6d,故 6d= 3 ,解得 d= 9 .
根据椭圆的定义可知,点B的轨迹是以A(-1,0),C(1,0)为焦点,以4为长轴长的
椭圆,
故顶点 B
高中数学椭圆及其标准方程解析几何同步练习1苏教版选修2-1

分析几何同步练习(椭圆及其标准方程)知识重点:①定义: | PF1 | |PF2 | 2a 2a | F1F2 | ;②标准方程:x2 y 2 1 a b 0; y 2 x 2 1 a b 0 。
一、选择题a2 b 2 a 2 b21、若点 P 到两定点 F1(-4 , 0),F2( 4, 0)的距离和是8,则动点 P 的轨迹为[ ]A. 椭圆B. 线段 F1F2C.直线 F1F2D. 不可以确立2. 以下说法正确的个数是[ ]①平面内与两个定点 F 、F 的距离和等于常数的点的轨迹是椭圆②与两个定点 F 、F 的距离1 2 1 2的和等于常数(大于| F 1F2|)的点的轨迹是椭圆③方程x2 y21(a>c>0)表示焦c 2 a 2 c 2y2 x2点在 x 轴上的椭圆④方程1(a>0,b>0)表示焦点在y轴上的椭圆a2 b2A. 13.椭圆 x 2 y 2 1的焦距为2,则m的值等于[ ]m 4或34. 过点( 3, -2 )且与x2 y2 1 有同样焦点的椭圆是[ ] 9 4A. x2 y2 1B. x2 y 2 1C. x 2 y 2 1D. x 2 y 2 115 10 225 100 10 15 100 225 5.已知方程x2 my2 1 表示焦点在y轴上的椭圆,则m 的取值范围是[ ]A. m<1 B . -1<m<1 C .m>1 D .0<m<16. 椭圆 ax2+by2 +ab=0( a<b<0)的焦点坐标是[ ]A. (a b,0)B. ( 0, a b )C.( b a ,0)D.(0, b a )二、填空题7. 假如椭圆x2 y 2 1上一点P到焦点F1的距离等于6,则点 P 到另一个焦点100 36F2的距离是;8 过椭圆 C:x 2 y21 的焦点引垂直于x 轴的弦,则弦长为a 2 b2三、解答题:9.求经过点A(0,2) 和 B( 1, 3 )的椭圆的标准方程210. 椭圆的两个焦点 F1、F2在 x 轴上,以 | F1F2| 为直径的圆与椭圆的一个交点为(3, 4),求椭圆标准方程 .11.已知点P在以坐标轴为对称轴的椭圆上,点P到两个焦点的距离分别为 4 5,2 5,过3 3 P作焦点所在轴的垂线恰巧过椭圆的一个焦点,求椭圆的方程参照答案一、选择题:BAAA DD二、填空题:1、 14; 2 、2b2。
【配套K12】高中数学第二章圆锥曲线与方程2.2椭圆2.2.1椭圆及其标准方程优化练习

2.2.1 椭圆及其标准方程[课时作业][A 组 基础巩固]1.椭圆x 225+y 29=1上一点M 到焦点F 1的距离为2,则M 到另一个焦点F 2的距离为( ) A .3B .6C .8D .以上都不对 解析:由椭圆的定义知|MF 1|+|MF 2|=10,∴|MF 2|=10-2=8,故选C.答案:C 2.(2015·高考广东卷)已知椭圆x 225+y 2m 2=1(m >0)的左焦点为F 1(-4,0),则m =( ) A .2B .3C .4D .9解析:由左焦点为F 1(-4,0)知c =4,又a =5,∴25-m 2=16,解得m =3或-3,又m >0,故m =3.答案:B3.椭圆x 216+y 27=1的左、右焦点为F 1、F 2,一直线过F 1交椭圆于A ,B 两点,则△ABF 2的周长为( )A .32B .16C .8D .4 解析:∵|AF 1|+|AF 2|=8,|BF 1|+|BF 2|=8.又∵|AF 1|+|BF 1|=|AB |,∴△ABF 2的周长为|AB |+|AF 2|+|BF 2|=(|AF 1|+|AF 2|)+ (|BF 1|+|BF 2|)=16.故选B. 答案:B4.方程x 2sin 2+cos 2-y 2cos 2-sin 2=1所表示的曲线是( ) A .焦点在x 轴上的椭圆B .焦点在y 轴上的椭圆C .焦点在x 轴上的双曲线D .焦点在y 轴上的双曲线解析:∵π2<2<3π4,∴sin 2>0,cos 2<0 且|sin 2|>|cos 2|,∴sin 2+cos 2>0,cos 2-sin 2<0且sin 2-cos 2>sin 2+cos 2,故表示焦点在y 轴上的椭圆. 答案:B5.已知椭圆x 24+y 2=1的焦点为F 1、F 2,点M 在该椭圆上,且MF 1→·MF 2→=0,则点M 到x 轴的距离为( ) A.233B.263C.33D. 3解析:由MF 1→·MF 2→=0,得MF 1⊥MF 2,可设|MF 1→|=m ,|MF 2→|=n ,在△F 1MF 2中,由m 2+n 2=4c 2得(m +n )2-2mn =4c 2,根据椭圆的定义有m +n =2a ,所以2mn =4a 2-4c 2,故mn =2b 2,即mn =2,∴S △F 1MF 2=12·mn =1,设点M 到x 轴的距离为h ,则12×|F 1F 2|×h =1,又|F 1F 2|=23,故h =33,故选C. 答案:C6.已知椭圆的中心在原点,一个焦点为(0,-23)且a =2b ,则椭圆的标准方程为________. 解析:由c =23,a =2b ,a 2=b 2+c 2,∴3b 2=12,b 2=4,a 2=16,∴标准方程为y 216+x 24=1. 答案:y 216+x 24=1 7.已知椭圆的两焦点为F 1(-2,0),F 2(2,0),P 为椭圆上的一点,且|F 1F 2|是|PF 1|与|PF 2|的等差中项.该椭圆的方程是________.解析:由题意知椭圆焦点在x 轴上,c =2,|F 1F 2|=4,由于|F 1F 2|是|PF 1|与|PF 2|的等差中项,∴|PF 1|+|PF 2|=2|F 1F 2|=8,∴a =4,b 2=a 2-c 2=42-22=12,故椭圆的方程为x 216+y 212=1. 答案:x 216+y 212=1 8.若F 1,F 2是椭圆x 29+y 27=1的两个焦点,A 为椭圆上一点,且∠F 1AF 2=45°,则△AF 1F 2的面积为________.解析:如图所示,|F 1F 2|=22,|AF 1|+|AF 2|=6,由|AF 1|+|AF 2|=6,得|AF 1|2+|AF 2|2+2|AF 1||AF 2|=36.又在△AF 1F 2中,|AF 1|2+|AF 2|2-|F 1F 2|2=2|AF 1||AF 2|cos 45°,∴36-2|AF 1||AF 2|-8=2|AF 1||AF 2|,∴|AF 1||AF 2|=282+2=14(2-2). ∴S △AF 1F 2=12|AF 1||AF 2|sin 45° =12×14(2-2)×22=7(2-1). 答案:7(2-1)9.已知点P (3,4)是椭圆x 2a 2+y 2b2=1(a >b >0)上一点,F 1,F 2是椭圆左、右焦点,若PF 1⊥PF 2,试求:(1)椭圆方程;(2)△PF 1F 2的面积.解析:(1)由PF 1⊥PF 2,可得|OP |=c ,得c =5.设椭圆方程为x 2a +y 2a -25=1,代入P (3,4), 得9a 2+16a 2-25=1,解得a 2=45. ∴椭圆方程为x 245+y 220=1. (2)S △PF 1F 2=12|F 1F 2||y P |=5×4=20. 10.已知B ,C 是两个定点,|BC |=8,且△ABC 的周长等于18,求这个三角形的顶点A 的轨迹方程.解析:以过B ,C 两点的直线为x 轴,线段BC 的垂直平分线为y 轴,建立直角坐标系xOy ,如图所示.由|BC |=8,可知点B (-4,0),C (4,0),c =4.由|AB |+|AC |+|BC |=18,|BC |=8,得|AB |+|AC |=10.因此,点A 的轨迹是以B ,C 为焦点的椭圆,这个椭圆上的点与两焦点的距离之和2a =10,但点A 不在x 轴上.由a =5,c =4,得b 2=a 2-c 2=25-16=9.所以点A 的轨迹方程为x 225+y 29=1(y ≠0).[B 组 能力提升]1.已知方程x 2|m |-1+y 22-m=1表示焦点在y 轴上的椭圆,则m 的取值范围是( ) A .m <2B .1<m <2C .m <-1或1<m <32D .m <-1或1<m <2 解析:由题意得⎩⎪⎨⎪⎧ |m |-1>0,2-m >0,|m |-1<2-m ,解得m <-1或1<m <32.故选C. 答案:C2.椭圆x 212+y 23=1的焦点为F 1和F 2,点P 在椭圆上.如果线段PF 1的中点在y 轴上,那么|PF 1|是|PF 2|的( )A .7倍B .5倍C .4倍D .3倍 解析:不妨设F 1(-3,0),F 2(3,0),由条件知P ⎝ ⎛⎭⎪⎫3,±32,即|PF 2|=32, 由椭圆定义知|PF 1|+|PF 2|=2a =43,则|PF 1|=732, 即|PF 1|=7|PF 2|,故选A.答案:A 3.已知曲线C :x 2k -5+y 23-k =-1,则“4≤k <5”是“曲线C 表示焦点在y 轴上的椭圆”的________条件.解析:将曲线C 的方程化为:x 25-k +y 2k -3=1,若曲线C 是焦点在y 轴上的椭圆, 则k -3>5-k >0,即4<k <5,故“4≤k <5”是“曲线C 表示焦点在y 轴上的椭圆”的必要不充分条件.答案:必要不充分4.在平面直角坐标系中,A (4,0),B (-4,0),且sin A +sin B sin C =54,则△ABC 的顶点C 的轨迹方程为________.解析:在△ABC 中,由正弦定理|BC |=2R sin A ,|AC |=2R sin B ,|AB |=2R sin C ,∴|BC |+|AC ||AB |=54,又|AB |=8,∴|BC |+|AC |=10>8,由椭圆的定义2a =10,a =5,c =4, ∴b 2=a 2-c 2=9,又C 与AB 不共线,∴顶点C 的轨迹方程为x 225+y 29=1(y ≠0). 答案:x 225+y 29=1(y ≠0) 5.△ABC 的三边a ,b ,c 成等差数列,且a >b >c ,A ,C 的坐标分别为(-1,0),(1,0),求顶点B 的轨迹方程.解析:由已知得b =2,又a ,b ,c 成等差数列,∴a +c =2b =4,即|AB |+|BC |=4,∴点B 到定点A ,C 的距离之和为定值4,由椭圆定义知B 点的轨迹为椭圆的一部分,其中a ′=2,c ′=1.∴b ′2=3.又a >b >c ,∴顶点B 的轨迹方程为x 24+y 23=1(-2<x <0). 6.动圆C 与定圆C 1:(x +3)2+y 2=32内切,与定圆C 2:(x -3)2+y 2=8外切,A 点坐标为⎝ ⎛⎭⎪⎫0,92. (1)求动圆C 的圆心C 的轨迹方程;(2)若轨迹C 上的两点P ,Q 满足AP →=5AQ →,求|PQ |的值.解析:(1)如图,设动圆C 的半径为R ,则|CC 1|=42-R ,①|CC 2|=22+R ,②①+②得,|CC 1|+|CC 2|=62>6=|C 1C 2|,由椭圆的定义知C 点的轨迹是以C 1,C 2为焦点,长轴长为62的椭圆,其轨迹方程为x 218+y 29=1. (2)设P (x 1,y 1),Q (x 2,y 2),则AP →=⎝ ⎛⎭⎪⎫x 1,y 1-92,AQ →=⎝⎛⎭⎪⎫x 2,y 2-92. 由AP →=5AQ →可得⎝⎛⎭⎪⎫x 1,y 1-92=5⎝ ⎛⎭⎪⎫x 2,y 2-92, 所以x 1=5x 2,y 1=5y 2-92×5+92=5y 2-18, ③由P ,Q 是椭圆C 上的两点,得 ⎩⎪⎨⎪⎧ x 2218+y 229=1, ④25x 2218+y 2-29=1, ⑤由④、⑤得y 2=3,将y 2=3代入③,得y 1=-3, 将y 2=3代入④,得x 2=0,所以x 1=0, 所以P (0,-3),Q (0,3),|PQ |=6.。
备战2022年高考数学复习之解析几何知识讲解专练05 椭圆(原卷版)

专题05 椭圆一相关知识点1.椭圆的定义把平面内到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点的集合叫作椭圆.这两个定点叫作椭圆的焦点,两焦点间的距离叫作椭圆的焦距.集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数.(1)当2a>|F1F2|时,P点的集合是椭圆;(2)当2a=|F1F2|时,P点的集合是线段;(3)当2a<|F1F2|时,P点不存在.2.椭圆的标准方程和几何性质标准方程x2a2+y2b2=1(a>b>0)x2b2+y2a2=1(a>b>0)图形性质范围-a≤x≤a,-b≤y≤b -b≤x≤b,-a≤y≤a 对称性对称轴:坐标轴,对称中心:(0,0)顶点A1(-a,0),A2(a,0),B1(0,-b),B2(0,b)A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)轴长轴A1A2的长为2a,短轴B1B2的长为2b焦距|F1F2|=2c离心率e=ca,e∈(0,1)a,b,c的关系c2=a2-b23.i.点P(x0,y0)和椭圆的位置关系(1)点P(x0,y0)在椭圆内⇔x20a2+y20b2<1.(2)点P(x0,y0)在椭圆上⇔x20a2+y20b2=1.(3)点P(x0,y0)在椭圆外⇔x20a2+y20b2>1.ii.焦点三角形椭圆上的点P(x0,y0)与两焦点构成的△PF1F2叫做焦点三角形.r1=|PF1|,r2=|PF2|,∠F 1PF 2=θ,△PF 1F 2的面积为S ,则在椭圆x 2a 2+y 2b2=1(a >b >0)中:(1)当r 1=r 2时,即点P 的位置为短轴端点时,θ最大;(2)S =b 2ta n θ2=c |y 0|,当|y 0|=b 时,即点P 的位置为短轴端点时,S 取最大值,最大值为bc .(3) S △PF 1F 2=12|PF 1||PF 2|·sin θ,当|y 0|=b ,即P 为短轴端点时,S △PF 1F 2取最大值为bc .(4)焦半径公式:|PF 1|=a +ex 0,|PF 2|=a -ex 0. (5)4c 2=|PF 1|2+|PF 2|2-2|PF 1||PF 2|·cos θ. (6)a -c ≤|PF 1|≤a +c .(7)焦点三角形的周长为2(a +c ). (8)过点P (x 0,y 0)的切线方程为x 0x a 2+y 0y b2=1.(9)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a 是斜边长,a 2=b 2+c 2. (10)已知过焦点F 1的弦AB ,则△ABF 2的周长为4a . 4.椭圆中点弦的斜率公式若M (x 0,y 0)是椭圆x 2a 2+y 2b 2=1(a >b >0)的弦AB (AB 不平行y 轴)的中点,则有k AB ·k OM =-b 2a 2,即k AB =-b 2x 0a 2y 0.5.弦长公式:直线与圆锥曲线相交所得的弦长 (1)|AB |=1+k 2|x 1-x 2|=(1+k 2)[(x 1+x 2)2-4x 1x 2] =1+1k2|y 1-y 2|=⎝⎛⎭⎫1+1k 2[(y 1+y 2)2-4y 1y 2](k 为直线斜率). (2)焦点弦(过焦点的弦):最短的焦点弦为通径长2b 2a,最长为 2a .题型一 椭圆的定义及其应用1.过椭圆4x 2+y 2=1的一个焦点F 1的直线与椭圆交于A ,B 两点,则A 与B 和椭圆的另一个焦点F 2构成的△ABF 2的周长为2.已知动点P (x ,y )的坐标满足x 2+(y +7)2+x 2+(y -7)2=16,则动点P 的轨迹方程为________.3.如图所示,一圆形纸片的圆心为O ,F 是圆内一定点,M 是圆周上一动点,把纸片折叠使M 与F 重合,然后抹平纸片,折痕为CD ,设CD 与OM 交于点P ,则点P 的轨迹是( )A .椭圆B .双曲线C .抛物线D .圆题型二 椭圆的标准方程类型一 利用椭圆定义求椭圆的标准方程1.已知动点M 到两个定点A (-2,0),B (2,0)的距离之和为6,则动点M 的轨迹方程为2.在△ABC 中,A (-4,0),B (4,0),△ABC 的周长是18,则顶点C 的轨迹方程是A.x 225+y 29=1(y ≠0) B .y 225+x 29=1(y ≠0) C.x 216+y 29=1(y ≠0) D .y 216+x 29=1(y ≠0)3.已知两圆C 1:(x -4)2+y 2=169,C 2:(x +4)2+y 2=9,动圆在圆C 1内部且和圆C 1相内切,和圆C 2相外切,则动圆圆心M 的轨迹方程为4.与圆C 1:(x +3)2+y 2=1外切,且与圆C 2:(x -3)2+y 2=81内切的动圆圆心P 的轨迹方程为_______.5.已知A (-1,0),B 是圆F :x 2-2x +y 2-11=0(F 为圆心)上一动点,线段AB 的垂直平分线交BF 于点P ,则动点P 的轨迹方程为6.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1、F 2,离心率为33,过F 2的直线l 交C 于A 、B 两点.若△AF 1B 的周长为43,则C 的方程为7.已知A ⎝⎛⎭⎫-12,0,B 是圆⎝⎛⎭⎫x -122+y 2=4(F 为圆心)上一动点,线段AB 的垂直平分线交BF 于点P ,则动点P 的轨迹方程为________.8.已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为32,且椭圆G 上一点到两个焦点的距离之和为12,则椭圆G 的方程为9.已知点P 是圆F 1:(x +1)2+y 2=16上任意一点(F 1是圆心),点F 2与点F 1关于原点对称.线段PF 2的垂直平分线m 分别与PF 1,PF 2交于M ,N 两点.求点M 的轨迹C 的方程.类型二 利用待定系数法求椭圆标准方程1.若直线x -2y +2=0经过椭圆的一个焦点和一个顶点,则该椭圆的标准方程为________.2.已知椭圆C 经过点A (2,3),且点F (2,0)为其右焦点,则椭圆C 的标准方程为____________.3.已知椭圆的中心在原点,离心率e =12,且它的一个焦点与抛物线y 2=-4x 的焦点重合,则此椭圆方程为4.设椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点与抛物线y 2=16x 的焦点相同,离心率为63,则此椭圆的方程为________.5.已知椭圆的中心在坐标原点,长轴长是8,离心率是34,则此椭圆的标准方程是6.已知椭圆C 的中心在原点,一个焦点F (-2,0),且长轴长与短轴长的比是2∶3,则椭圆C 的方程是________________.7.过点(3,-5),且与椭圆y 225+x 29=1有相同焦点的椭圆的标准方程为________.8.过点A (3,-2)且与椭圆x 29+y 24=1有相同焦点的椭圆的方程为9.与椭圆9x 2+4y 2=36有相同焦点,且短轴长为2的椭圆的标准方程为10.已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点⎝⎛⎭⎫-32,52,(3,5),则椭圆方程 为11.与椭圆x 24+y 23=1有相同的离心率且经过点(2,-3)的椭圆方程为12.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为10,一个焦点的坐标是(-5,0),则椭圆的标准方程为________.13.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,离心率为33,过F 2的直线l 交C 于A ,B 两点,若△AF 1B 的周长为43,则C 的方程为14.椭圆E 的焦点在x 轴上,中心在原点,其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点,则椭圆E 的标准方程为15.已知点P 在以坐标轴为对称轴的椭圆上,且P 到两焦点的距离分别为5,3,过P 且与长轴垂直的直线恰过椭圆的一个焦点的椭圆的标准方程为________.16.已知中心在坐标原点的椭圆过点A (-3,0),且离心率e =53,则椭圆的标准方程为________.17.已知椭圆的中心在原点,焦点在x 轴上,离心率为55,且过P (-5,4),则椭圆的方程为________.18.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的长轴长为6,且两焦点恰好将长轴三等分,则此椭圆的标准方程为19.一个椭圆的中心在原点,焦点F 1,F 2在x 轴上,P (2,3)是椭圆上一点,且|PF 1|,|F 1F 2|,|PF 2|成等差数列,则椭圆的标准方程为20.设F 1,F 2为椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点,经过F 1的直线交椭圆C 于A ,B 两点,若△F 2AB是面积为43的等边三角形,则椭圆C 的方程为__________.21.设F 1,F 2分别是椭圆E :x 2+y 2b 2=1(0<b <1)的左、右焦点,过点F 1的直线交椭圆E 于A ,B 两点.若|AF 1|=3|F 1B |,AF 2⊥x 轴,则椭圆E 的方程为________.22.如图,已知椭圆C 的中心为原点O ,F (-5,0)为C 的左焦点,P 为C 上一点,满足|OP |=|OF |且|PF |=6,则椭圆C 的方程为23.已知椭圆x 2a 2+y 2b2=1(a >b >0),F 1,F 2分别为椭圆的左、右焦点,A 为椭圆的上顶点,直线AF 2交椭圆于另一点B .(1)若∠F 1AB =90°,求椭圆的离心率;(2)若AF 2→=2F 2B →,AF 1→·AB →=32,求椭圆的方程.题型三 椭圆的几何性质类型一 识别椭圆相关性质概念1.椭圆x 216+y 225=1的焦点坐标为2.已知椭圆的标准方程为x 2+y 210=1,则椭圆的焦点坐标为 3.椭圆x 210-m +y 2m -2=1的焦距为4,则m 等于4.椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(-10,0),则焦点坐标为________.5.曲线C 1:x 225+y 29=1与曲线C 2:x 225-k +y 29-k=1(k <9)的( )A .长轴长相等B .短轴长相等C .离心率相等D .焦距相等6.已知椭圆x 2a 2+y 2b2=1(a >b >0)的一个焦点是圆x 2+y 2-6x +8=0的圆心,且短轴长为8,则椭圆的左顶点为____________.7.椭圆x 29+y 24+k =1的离心率为45,则k 的值为8.椭圆x 24+y 2=1的左、右焦点分别为F 1,F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则|PF 2|等于9.椭圆mx 2+ny 2+mn =0(m <n <0)的焦点坐标是10.已知椭圆x 2+(m +3)y 2=m (m >0)的离心率e =32,求m 的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标.类型二 求离心率的值(或范围)1.椭圆x 29+y 24=1的离心率是2.若椭圆C :x 2a 2+y 2b 2=1(a >b >0)的短轴长等于焦距,则椭圆的离心率为3.已知椭圆C :x 2a 2+y 24=1的一个焦点为(2,0),则C 的离心率为________.4.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)和直线l :x 4+y3=1,若过C 的左焦点和下顶点的直线与直线l 平行,则椭圆C 的离心率为5.若椭圆x 24+y 2m =1上一点到两焦点的距离之和为m -3,则此椭圆的离心率为6.焦点在x 轴上的椭圆方程为x 2a 2+y 2b 2=1(a >b >0),短轴的一个端点和两个焦点相连构成一个三角形,该三角形内切圆的半径为b3,则椭圆的离心率为7.若一个椭圆长轴的长、短轴的长和焦距成等比数列,则该椭圆的离心率是8.如图,F 1,F 2是双曲线C 1:x 2-y 28=1与椭圆C 2的公共焦点,点A 是C 1,C 2在第一象限内的交点,若|F 1F 2|=|F 1A |,则C 2的离心率是A.23B.45C.35D.259.已知F 是椭圆x 2a 2+y 2b2=1(a >b >0)的左焦点,A 为右顶点,P 是椭圆上的一点,PF ⊥x 轴,若|PF |=34|AF |,则该椭圆的离心率是________.10.已知椭圆x 2a 2+y 2b2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y轴于点P .若AP ―→=2PB ―→,则椭圆的离心率是11.设椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,P 是C 上的点,PF 2⊥F 1F 2,∠PF 1F 2=30°,则C 的离心率为12.已知F 1,F 2是椭圆C 的两个焦点,P 是C 上的一点.若PF 1⊥PF 2,且∠PF 2F 1=60°,则C 的离心率为13.P 是椭圆x 2a 2+y 2b 2=1(a >b >0)上的一点,A 为左顶点,F 为右焦点,PF ⊥x 轴,若tan ∠P AF =12,则椭圆的离心率e 为14.直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为15.如图,底面直径为12 cm 的圆柱被与底面成30°角的平面所截,截口是一个椭圆,则这个椭圆的离心率为16.已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线bx -ay+2ab =0相切,则C 的离心率为17.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率等于13,其焦点分别为A ,B ,C 为椭圆上异于长轴端点的任意一点,则在△ABC 中,sin A +sin B sin C=________.18.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左顶点为M ,上顶点为N ,右焦点为F ,若NM ―→·NF ―→=0,则椭圆的离心率为19.已知椭圆x 2a 2+y 2b2=1(a >b >0)的右顶点和上顶点分别为A ,B ,左焦点为F .以原点O 为圆心的圆与直线BF 相切,且该圆与y 轴的正半轴交于点C ,过点C 的直线交椭圆于M ,N 两点.若四边形F AMN 是平行四边形,则该椭圆的离心率为20.已知F 1,F 2分别是椭圆的左、右焦点,现以F 2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M ,N ,若过F 1的直线MF 1是圆F 2的切线,则椭圆的离心率为21.已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为22.设椭圆C :x 2a 2+y 2b2=1(a >b >0)的右焦点为F ,过点F 的直线l 与椭圆C 相交于A ,B 两点,直线l 的倾斜角为60°,AF →=2FB →.则椭圆C 的离心率是________.23.已知F 1,F 2分别是椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为椭圆上一点, 且PF 1―→·(OF 1―→+OP ―→)=0(O 为坐标原点),若|PF 1―→|=2|PF 2―→|,则椭圆的离心率为24.椭圆x 2a 2+y 2b 2=1(a >b >0),F 1,F 2为椭圆的左、右焦点,O 为坐标原点,点P 为椭圆上一点, |OP |=24a ,且|PF 1|,|F 1F 2|,|PF 2|成等比数列,则椭圆的离心率为25.椭圆C 的两个焦点分别是F 1,F 2,若C 上的点P 满足|PF 1|=32|F 1F 2|,则椭圆C 的离心率e 的取值范围是26.在椭圆x 2a 2+y 2b2=1(a >b >0)中,F 1,F 2分别是其左、右焦点,若|PF 1|=2|PF 2|,则该椭圆离心率的取值范围是27.过椭圆C :x 2a 2+y 2b2=1(a >b >0)的左顶点A 且斜率为k 的直线交椭圆C 于另一个点B ,且点B 在x 轴上的射影恰好为右焦点F 2,若13<k <12,则椭圆的离心率的取值范围是__________.28.如图,椭圆的中心在坐标原点O ,顶点分别是A 1,A 2,B 1,B 2,焦点分别为F 1,F 2,延长B 1F 2与A 2B 2交于P 点,若∠B 1P A 2为钝角,则此椭圆的离心率的取值范围为______.29.已知F 1,F 2是椭圆的两个焦点,满足MF →1·MF →2=0的点M 总在椭圆内部,则椭圆离心率的取值范围是________.30.已知F 1,F 2是椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右两个焦点,若椭圆上存在点P 使得PF 1⊥PF 2,则该椭圆的离心率的取值范围是31.设椭圆C :x 2a 2+y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,点E (0,t )(0<t <b ).已知动点P 在椭圆上,且点P ,E ,F 2不共线,若△PEF 2的周长的最小值为4b ,则椭圆C 的离心率为32.已知椭圆和双曲线有共同的焦点F 1,F 2,P 是它们的一个交点,且∠F 1PF 2=2π3,记椭圆和双曲线的离心率分别为e 1,e 2,则3e 21+1e 22=33.已知F 1,F 2分别是椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点,若椭圆C 上存在点P ,使得线段PF 1的中垂线恰好经过焦点F 2,则椭圆C 离心率的取值范围是34.已知椭圆x 2a 2+y 2b2=1(a >b >c >0,a 2=b 2+c 2)的左、右焦点分别为F 1,F 2,若以F 2为圆心,b -c 为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且|PT|的最小值不小于32(a-c),则椭圆的离心率e的取值范围是____.35.已知F1,F2分别是椭圆x2a2+y2b2=1(a>b>0)的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A,B 上下两点,若△ABF2是锐角三角形,则该椭圆的离心率e的取值范围是36.如图,椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.(1)若|PF1|=2+2,|PF2|=2-2,求椭圆的标准方程;(2)若|PF1|=|PQ|,求椭圆的离心率e.37.已知椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1(-c,0),F2(c,0),若椭圆上存在点P使1-cos 2∠PF1F21-cos 2∠PF2F1=a2c2,求该椭圆的离心率的取值范围.38.已知椭圆x2a2+y2b2=1(a>b>0)的左焦点为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点.过F ,B ,A 三点的圆的圆心坐标为(p ,q ).(1)当p +q ≤0时,求椭圆的离心率的取值范围;(2)若点D (b +1,0),在(1)的条件下,当椭圆的离心率最小时,(MF →+OD →)·MO →的最小值为72,求椭圆的方程.类型三 求参数的值(或范围)1.若焦点在y 轴上的椭圆x 2m +y 22=1的离心率为12,则m 的值为________.2.若方程x 25-m +y 2m +3=1表示椭圆,则m 的取值范围是3.已知方程x 22-k +y 22k -1=1表示焦点在y 轴上的椭圆,则实数k 的取值范围是4.方程kx 2+4y 2=4k 表示焦点在x 轴上的椭圆,则实数k 的取值范围是5.若x 2+ky 2=2表示焦点在y 轴上的椭圆,则实数k 的取值范围是________.6.如果方程x 2a 2+y 2a +6=1表示焦点在x 轴上的椭圆,则实数a 的取值范围是________.7.“2<m <6”是“方程x 2m -2+y 26-m=1表示椭圆”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件8.已知椭圆mx 2+4y 2=1的离心率为22,则实数m 等于9.设e 是椭圆x 24+y 2k =1的离心率,且e =23,则实数k 的值是________.10.“m >n >0”是“方程mx 2+ny 2=1表示焦点在y 轴上的椭圆”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 11.已知椭圆x 24+y 2b2=1(0<b <2)的左、右焦点分别为F 1,F 2,过F 1的直线l 交椭圆于A ,B 两点, 若|BF 2|+|AF 2|的最大值为5,则b 的值是12.设A ,B 是椭圆C :x 23+y 2m=1长轴的两个端点,若C 上存在点M 满足∠AMB =120°,则m 的取值范围是13.椭圆x 24+y 2=1的左,右焦点分别为F 1,F 2,点P 为椭圆上一动点,若∠F 1PF 2为钝角,则点P 的横坐标的取值范围是________________.14.已知动点M 到定点F 1(-2,0)和F 2(2,0)的距离之和为4 2.(1)求动点M 的轨迹C 的方程;(2)设N (0,2),过点P (-1,-2)作直线l ,交C 于不同于N 的两点A ,B ,直线NA ,NB 的斜率分别为k 1,k 2,求k 1+k 2的值.类型四 焦点三角形1.椭圆C :x 225+y 216=1的左、右焦点分别为F 1,F 2,过F 2的直线交椭圆C 于A ,B 两点,则△F 1AB 的周长为________.2.过椭圆x 24+y 2=1的左焦点F 1作直线l 交椭圆于A ,B 两点,F 2是椭圆右焦点,则△ABF 2的周长为3.已知△ABC 的顶点B ,C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是________.4.已知点F 1,F 2分别为椭圆C :x 24+y 23=1的左、右焦点,若点P 在椭圆C 上,且∠F 1PF 2=60°,则|PF 1|·|PF 2|=5.F 1,F 2是椭圆x 29+y 27=1的两个焦点,A 为椭圆上一点,且∠AF 1F 2=45°,则△AF 1F 2的面积为6.如图,椭圆x 2a 2+y 24=1(a >2)的左、右焦点分别为F 1,F 2,点P 是椭圆上的一点,若∠F 1PF 2=60°,那么△PF 1F 2的面积为7.已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1⊥PF 2,若△PF 1F 2的面积为9,则b =________.8.设F 1,F 2为椭圆x 29+y 25=1的两个焦点,点P 在椭圆上,若线段PF 1的中点在y 轴上,则|PF 2||PF 1|的值为9.已知点P 是椭圆x 25+y 24=1上y 轴右侧的一点,且以点P 及焦点F 1,F 2为顶点的三角形的面积等于1,则点P 的坐标为10.已知F 1,F 2是长轴长为4的椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 是椭圆上一点, 则△PF 1F 2面积的最大值为________.11.P 为椭圆x 225+y 29=1上一点,F 1,F 2分别是椭圆的左焦点和右焦点,过P 点作PH ⊥F 1F 2于点H ,若PF 1⊥PF 2,则|PH |=12.设F 1,F 2分别为椭圆x 24+y 2=1的左、右焦点,点P 在椭圆上,且|PF 1→+PF 2→|=23,则∠F 1PF 2等于13.设P 为椭圆C :x 249+y 224=1上一点,F 1,F 2分别是椭圆C 的左、右焦点,且△PF 1F 2的重心为 点G ,若|PF 1|∶|PF 2|=3∶4,那么△GPF 1的面积为14.设椭圆x 29+y 25=1的左、右焦点分别为F 1,F 2,过焦点F 1的直线交椭圆于A (x 1,y 1),B (x 2,y 2)两点,若△ABF 2的内切圆的面积为π,则|y 1-y 2|=15.设椭圆x 216+y 212=1的左、右焦点分别为F 1,F 2,点P 在椭圆上,且满足PF 1→·PF 2→=9,则|PF 1|·|PF 2|的值为16.已知△ABC 的顶点B ,C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是17.椭圆x 29+y 22=1的左、右焦点分别为F 1,F 2,点P 在椭圆上,若|PF 1|=4,则∠F 1PF 2的大小为18.已知椭圆的长轴长为10,两焦点F 1,F 2的坐标分别为(3,0)和(-3,0).(1)求椭圆的标准方程;(2)若P 为短轴的一个端点,求△F 1PF 2的面积.19.已知F 1,F 2分别为椭圆x 22+y 2=1的左、右焦点,过F 1的直线l 与椭圆交于不同的两点A ,B ,连接AF 2和BF 2.(1)求△ABF 2的周长;(2)若AF 2⊥BF 2,求△ABF 2的面积.类型五 与椭圆的几何性质有关的最值问题1.以椭圆上一点和两个焦点为顶点的三角形的面积的最大值为1,则椭圆长轴长的最小值为2.已知F 是椭圆5x 2+9y 2=45的左焦点,P 是此椭圆上的动点,A (1,1)是一定点,则|P A |+|PF |的最大值为 ,最小值为 .3.已知P 为椭圆x 225+y 216=1上的一点,M ,N 分别为圆(x +3)2+y 2=1和圆(x -3)2+y 2=4上的点,则|PM |+|PN |的最小值为________.4.在平面直角坐标系xOy 中,P 是椭圆y 24+x 23=1上的一个动点,点A (1,1),B (0,-1), 则|P A |+|PB |的最大值为5.设F 1,F 2分别是椭圆x 225+y 216=1的左、右焦点,P 为椭圆上任一点,点M 的坐标为(6,4), 则|PM |+|PF 1|的最大值为________.6.设P 是椭圆x 225+y 29=1上一点,M ,N 分别是两圆:(x +4)2+y 2=1和(x -4)2+y 2=1上的点, 则|PM |+|PN |的最小值、最大值分别为________.7.若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP →·FP →的最大值为8.已知点F 1,F 2是椭圆x 2+2y 2=2的左,右焦点,点P 是该椭圆上的一个动点,那么|PF 1→+PF 2→|的最小值是9.如图,焦点在x 轴上的椭圆x 24+y 2b 2=1的离心率e =12,F ,A 分别是椭圆的一个焦点和顶点,P 是椭圆上任意一点,则PF →·P A →的最大值为________.。
椭圆的常见题型及解法二

椭圆的常见题型及解法(二)一对称问题平面解析几何常遇到含参数的对称问题,常困扰学生思维.其实平面解析几何所有的对称只有以下四类,分别为“点关于点对称”;“点关于直线对称”;“曲线关于点对称”;“曲线关于直线对称”.①点A 关于B 的对称点为C ,点B 为A 、C 的中点,由中点坐标公式有:⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧+=+=11112222y b y x a x y y b x x a ; ②设点A(x 1,y 1)关于直线 :ax+by+c=0的对称点为C(x,y),由AC 直线与 垂直,且AB的中点在 上,有:()();222202212211222211221111⎪⎪⎩⎪⎪⎨⎧+---=+---=⇒⎪⎪⎩⎪⎪⎨⎧=++++-=⎪⎭⎫ ⎝⎛-⨯--b a bc abx y b a y b a acaby x a b x c y y b x x a b a x x y y(当直线 中a=0或b=0时,上面结论也正确)③曲线F(x,y)=0关于点B(a,b)对称的曲线,在曲线F(x,y)=0上任取一点A(x 1,y 1),它关于点B(a,b)的对称点为C(x,y).其实点A 为主动点,点C 为从动点,由中点坐标公式有:⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧+=+=y b y xa x y yb x x a 22221111,代入到主动点的方程中,得对称曲线方程:0)2,2(=--y b x a F .④曲线F(x,y)=0关于点ax+by+c=0对称的曲线, 在曲线F(x,y)=0上任取一点A(x 1,y 1),它关于直线ax+by+c=0的对称点为C(x,y),则有:()()⎪⎪⎩⎪⎪⎨⎧+---=+---=⇒⎪⎪⎩⎪⎪⎨⎧=++++-=⎪⎭⎫ ⎝⎛-⨯--2222122221111122220221b a bcabx y b a y b a acaby x a b x c y y b x x a b a x x y y ,代入到主动点的方程中,得对称曲线方程:()()0)22,22(22222222=+---+---b a bcabx y b a b a ac aby x a bF .圆锥曲线上存在两点关于某直线对称,求某参变量的取值范围.这一类问题求解时,必须同时确保: ⑴垂直;⑵平分⑶存在,下面就实例说明三个确保的实施.例1.已知椭圆C: 191622=+y x ,试确定m 的取值范围,使得对于直线 :m x y +=4在椭圆C 上存在不同的两点关于直线 对称.解:椭圆上存在两点A,B 关于直线 m x y +=4对称, 设直线AB 为:n x y +-=41(确保垂直). 设直线AB 与椭圆有两个不同的交点()()2211,,,y x B y x A .0728451916412222=-+-⇒⎪⎪⎩⎪⎪⎨⎧=++-=n nx x y x n x y ()()072854422>-⨯⨯--=∆n n (确保存在)即:()10,10102-∈⇒<n n ()1545421nn x x =--=+ AB 两点的中点的横坐标为,52221n x x =+纵坐标为n n n 1095241=+⨯- 则点⎪⎭⎫⎝⎛n n 109,52在直线 m x y +=4上,m n n +⨯=524109. (确保平分).107n m -=⇒ 把上式代入(1)中,得:.1010710107<<-m 变式训练(2010年安徽理19):已知椭圆E 经过点A (2,3),对称轴为坐标轴,焦点F 1,F 2在x 轴上,离心率.21=e (I )求椭圆E 的方程;(II )求21AF F ∠的角平分线所在直线l 的方程;(III )在椭圆E 上是否存在关于直线l 对称的相异两点?若存在,请找出;若不存在,说明理由.本题考查椭圆的定义及标准方程,椭圆的简单几何性质,直线的点斜式方程与一般方程,点到直线的距离公式,点关于直线的对称等基础知识;考查解析几何的基本思想、综合运算能力、探究意识与创新意识.解:(I )设椭圆E 的方程为22221x y a b+=2222222211,,2,3,221.43c e a c b a c e a x yc e ====-=∴+=由即得椭圆方程具有形式 将A (2,3)代入上式,得22131,2,c c c+==解得 ∴椭圆E 的方程为22 1.1612x y += (II )解法1:由(I )知12(2,0),(2,0)F F -,所以直线AF 1的方程为:3(2),3460,4y x x y =+-+=即 直线AF 2的方程为: 2.x =由点A 在椭圆E 上的位置知,直线l 的斜率为正数. 设(,)P x y l 为上任一点,则|346||2|.5x y x -+=- 若346510,280x y x x y -+=-+-=得(因其斜率为负,舍去). 所以直线l 的方程为:210.x y --= 解法2:121212121(2,3),(2,0),(2,0),(4,3),(0,3).114(4,3)(0,3)(1,2).535||||2,:32(1),210.A F F AF AF AF AF AF AF k l y x x y -∴=--=-∴+=--+-=-∴=∴-=---=即(III )解法1:假设存在这样的两个不同的点1122(,)(,),B x y C x y 和2121121200001,.2(,),,,22BC y y BC l k x x x x y y BC M x y x y -⊥∴==-++==设的中点为则由于M 在l 上,故00210.x y -+= ①又B ,C 在椭圆上,所以有222211221 1.16121612x y x y +=+=与 两式相减,得222221210,1612x x y y --+=即12211221()()()()0.1612x x x x y y y y +-+-+=将该式写为122112211108262x x y y y y x x +-+⋅+⋅⋅=-,并将直线BC 的斜率BC k 和线段BC 的中点,表示代入该表达式中, 得0000110,320.812x y x y -=-=即 ② ①×2—②得202,3x y ==,即BC 的中点为点A ,而这是不可能的. ∴不存在满足题设条件的点B 和C. 解法2:假设存在1122(,),(,)B x y C x y l 两点关于直线对称, 则1,.2BC l BC k ⊥∴=-221,1,21612x y BC y x m =-++=设直线的方程为将其代入椭圆方程得一元二次方程2222134()48,120,2x x m x mx m +-+=-+-=即 则12x x 与是该方程的两个根, 由韦达定理得12,x x m +=于是121213()2,22m y y x x m +=-++= ∴B ,C 的中点坐标为3(,).24m m又线段BC 的中点在直线321,1, 4.4my x m m =-∴=-=上得即B ,C 的中点坐标为(2,3),与点A 重合,矛盾. ∴不存在满足题设条件的相异两点.二 中点弦问题例1、过椭圆141622=+y x 内一点)1,2(M 引一条弦,使弦被M 点平分,求这条弦所在直线的方程。
解析几何综合问题圆与椭圆双曲线抛物线等一轮复习专题练习(二)含答案新人教版高中数学名师一点通

高中数学专题复习
《解析几何综合问题圆与椭圆双曲线抛物线等》
单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I 卷(选择题)
请点击修改第I 卷的文字说明 评卷人
得分 一、选择题
1.以抛物线24y x =的焦点为圆心,且过坐标原点的圆的方程为( )
A .22x +y +2x=0
B .22x +y +x=0
C .22x +y -x=0
D .22x +y -2x=0(汇编福建理) 第II 卷(非选择题)
请点击修改第II 卷的文字说明 评卷人
得分 二、填空题
2.椭圆21)0,0(12222
=>>=+e b a b y a x 的离心率,右焦点F (c,0),方程
02=-+c bx ax 的两个根分别为x 1,x 2,则点P (x 1,x 2)在与圆222=+y x 的位置。
2021年高中数学 2.2 椭圆及其标准方程(二)同步练习 理(普通班)新人教A版选修2-1

2021年高中数学 2.2 椭圆及其标准方程(二)同步练习 理(普通班)新人教A 版选修2-1一、选择题1.将椭圆C 1∶2x 2+y 2=4上的每一点的纵坐标变为原来的一半,而横坐标不变,得一新椭圆C 2,则C 2与C 1有( ) A .相等的短轴长 B .相等的焦距 C .相等的离心率D .相等的长轴长2.若椭圆的短轴为AB ,它的一个焦点为F 1,则满足△ABF 1为等边三角形的椭圆的离心率是( )A.14B.12C.22D.32 3.椭圆C 1:x 225+y 29=1和椭圆C 2:x 29-k +y 225-k=1 (0<k <9)有( )A .等长的长轴B .相等的焦距C .相等的离心率D .等长的短轴4.椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点,则椭圆离心率为( )A.22 B.32 C.53 D.635.已知椭圆的对称轴是坐标轴,离心率为13,长轴长为12,则椭圆方程为( )A.x 24+y 26=1B.x 26+y 24=1 C.x 236+y 232=1或x 232+y 236=1 D.x 236+y 232=1 6.椭圆x 2a 2+y 2b 2=1和x 2a 2+y 2b 2=k (k >0)具有( )A .相同的长轴B .相同的焦点C .相同的顶点D .相同的离心率二、填空题7.已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为32,且G 上一点到G 的两个焦点的距离之和为12,则椭圆G 的方程为________.8.经过椭圆x 2a 2+y 2b 2=1(a >b >0)的焦点且垂直于椭圆长轴的弦长为________.三、解答题9.已知椭圆x 2+(m +3)y 2=m (m >0)的离心率e =32,求m 的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标.10.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率e =32,连接椭圆的四个顶点得到的菱形的面积为4.求椭圆的方程.2.2.2 一、选择题 1.[答案] C[解析] 把C 1的方程化为标准方程,即C 1:2x2+4y2=1,从而得C 2:2x2+y 2=1.因此C 1的长轴在y 轴上,C 2的长轴在x 轴上.e 1=22=e 2,故离心率相等,选C. 2.[答案] D[解析] △ABF 1为等边三角形, ∴2b =a ,∴c 2=a 2-b 2=3b 2∴e =a c =a2c2=4b23b2=23.3.[答案] B[解析] 依题意知椭圆C 2的焦点在y 轴上,对于椭圆C 1:焦距=2=8,对于椭圆C 2:焦距=2=8,故答案为B. 4.[答案] A[解析] 由题意知b =c ,∴a =c ,∴e =a c =22.5.[答案] C[解析] ∵长轴长2a =12,∴a =6,又e =31∴c =2,∴b 2=a 2-c 2=32,∵焦点不定,∴方程为36x2+32y2=1或32x2+36y2=1.6.[答案] D[解析] 椭圆a2x2+b2y2=1和a2x2+b2y2=k (k >0)中,不妨设a >b ,椭圆a2x2+b2y2=1的离心率e 1=a a2-b2,椭圆a2k x2+b2k y2=1(k >0)的离心率e 2=a a2-b2=a a2-b2.二、填空题7. [答案] 36x2+9y2=1[解析] 设椭圆G 的标准方程为a2x2+b2y2=1 (a >b >0),半焦距为c ,则3,∴3a =6,∴b 2=a 2-c 2=36-27=9,∴椭圆G 的方程为36x2+9y2=1.8. [答案] a 2b2[解析] ∵垂直于椭圆长轴的弦所在直线为x =±c ,由=1y2,得y 2=a2b4,∴|y |=a b2,故弦长为a 2b2. 三、解答题9. [解析] 椭圆方程可化为m x2+m +3m=1, ∵m -m +3m=m +3m +2>0,∴m >m +3m.即a 2=m ,b 2=m +3m ,c ==m +3m +2.由e =23得,m +3m +2=23,∴m =1. ∴椭圆的标准方程为x 2+41=1,∴a =1,b =21,c =23.∴椭圆的长轴长为2,短轴长为1;两焦点坐标分别为F 1(-23,0),F 2(23,0);四个顶点分别为A 1(-1,0),A 2(1,0),B 1(0,-21),B 2(0,21).10.[解析] 由e =a c =23,得3a 2=4c 2,再由c 2=a 2-b 2,得a =2b .由题意可知21×2a ×2b =4,即ab =2. 解方程组ab =2,a =2b ,得a =2,b =1,所以椭圆的方程为4x2+y 2=1.21914 559A 喚 21021 521D 初21299 5333 匳26741 6875 桵35225 8999 覙39074 98A2 颢H B38628 96E4 雤36395 8E2B踫31653 7BA5 箥22276 5704 圄。
解析几何同步练习(椭圆及其标准方程2A)

解析几何同步练习(椭圆及其标准方程2A )知识要点: ①定义: ()||22||||2121F F a a PF PF >=+;② 标准方程:()012222>>=+b a b y a x ;()012222>>=+b a bx a y 。
一、选择题1、已知椭圆的焦点是21,F F ,P 是椭圆上一个动点,如果延长P F 1到Q ,使得2PF PQ =,那么动点Q 的轨迹是[ ]A 圆B 椭圆C 直线D 线段2. △ABC 的两个顶点坐标A (-4,0),B (4,0),△ABC 的周长是18,则顶点C 的轨迹方程是 A. 192522=+y x B.192522=+x y (y ≠0) C.)0(191622≠=+y y x D.192522=+y x (y ≠0) 3.已知△ABC 的三边AB ,BC ,AC 的长依次成等差数列,且|AB|>|AC|,B (-1,0)C(1,0)则顶A 的轨迹方程为[ ] A. 13422=+y x B.13422=+y x (x>0) C.13422=+y x (x<0) D.13422=+y x (x>0y ≠0) 4.椭圆的方程为19222=+y ax ,它的两个焦点分别为F 1、F 2,若| F 1F 2|=8,弦AB 过F 1 则△ABF 2的周长为[ ] A.10 B.20 C.241 D.441二、填空题5.过点F 1(0,2)且与圆F 2:x 2+(y+2)2=36内切的动圆圆心的轨迹方程为 . 6.P 点在椭圆1204522=+y x 上,F 1、F 2是两个焦点,若21PF PF ⊥,则P 点的坐标是 7.P 是椭圆16410022=+y x 上的一点,F 1和F 2是焦点,若 6021=∠PF F , 则21F PF ∆的面积为 。
8. 如图,F 1,F 2分别为椭圆12222=+by a x的左、右焦点, 点P 在椭圆上,△POF 2是面积为3的正三角形,则b2 的值是三、解答题9.一动圆与圆x 2+y 2+6x+5=0外切,同时与圆x 2+y2-6x-91=0内切,求动圆圆心的轨迹.10.如图,线段AB 的两个端点A ,B 分别在x 轴上,y 轴上滑动,|AB|=5点M 是AB 上一点,且|AM|=2,点M 随线段AB 的运动而变化,求点M 的轨迹方程.参考答案一、选择题: ADDB二、填空题:1、15922=+x y ; 2、()4,3±±; 3、3364; 4、32。
人教A版高中数学选修一解析几何同步练习(椭圆及其标准方程1A).docx

解析几何同步练习(椭圆及其标准方程1A )知识要点: ①定义:()||22||||2121F F a a PF PF >=+;②标准方程:()012222>>=+b a b y a x ;()012222>>=+b a bx a y 。
一、选择题1、若点P 到两定点F 1(-4,0),F 2(4,0)的距离和是8,则动点P 的轨迹为 [ ]A.椭圆B.线段F 1F 2C.直线F 1F 2D.不能确定2.下列说法正确的个数是 [ ] ①平面内与两个定点F 1、F 2的距离和等于常数的点的轨迹是椭圆②与两个定点F 1、F 2的距离的和等于常数(大于| F 1F 2|)的点的轨迹是椭圆③方程122222=-+c a y c x (a>c>0)表示焦点在x 轴上的椭圆④方程12222=+bx a y (a>0,b>0)表示焦点在y 轴上的椭圆A .1B.2C.3D.43.椭圆1422=+y m x 的焦距为2,则m 的值等于 [ ]A.5或3B.8C.5D.164.过点(3,-2)且与14922=+y x 有相同焦点的椭圆是 [ ]A.1101522=+y x B. 110022522=+y x C. 1151022=+y x D.122510022=+y x5.已知方程122=+my x 表示焦点在y 轴上的椭圆,则m 的取值范围是 [ ] A .m<1 B .-1<m<1 C .m>1 D .0<m<16.椭圆ax 2+by 2+ab=0(a<b<0)的焦点坐标是 [ ]A.()0,b a -±B.(0,b a -±)C.(a b -±,0)D.(0,a b -±)二、填空题7.如果椭圆13610022=+y x 上一点P 到焦点F 1的距离等于6,则点P 到另一个焦点 F 2的距离是 ;8过椭圆C :12222=+by a x 的焦点引垂直于x 轴的弦,则弦长为三、解答题:9.求经过点A(0,2)和B(3,21)的椭圆的标准方程10.椭圆的两个焦点F 1、F 2在x 轴上,以| F 1F 2|为直径的圆与椭圆的一个交点为(3,4),求椭圆标准方程.11.已知点P在以坐标轴为对称轴的椭圆上,点P到两个焦点的距离分别为352,354,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程参考答案一、选择题: BAAA DD二、填空题:1、14;2、ab 22。
人教A版高中数学选修一解析几何同步练习(椭圆及其标准方程1A).docx

高中数学学习材料唐玲出品解析几何同步练习(椭圆及其标准方程1A )知识要点: ①定义:()||22||||2121F F a a PF PF >=+;②标准方程:()012222>>=+b a b y a x ;()012222>>=+b a bx a y 。
一、选择题1、若点P 到两定点F 1(-4,0),F 2(4,0)的距离和是8,则动点P 的轨迹为 [ ]A.椭圆B.线段F 1F 2C.直线F 1F 2D.不能确定2.下列说法正确的个数是 [ ] ①平面内与两个定点F 1、F 2的距离和等于常数的点的轨迹是椭圆②与两个定点F 1、F 2的距离的和等于常数(大于| F 1F 2|)的点的轨迹是椭圆③方程122222=-+c a y c x (a>c>0)表示焦点在x 轴上的椭圆④方程12222=+bx a y (a>0,b>0)表示焦点在y 轴上的椭圆A .1B.2C.3D.43.椭圆1422=+y m x 的焦距为2,则m 的值等于 [ ]A.5或3B.8C.5D.164.过点(3,-2)且与14922=+y x 有相同焦点的椭圆是 [ ]A.1101522=+y x B. 110022522=+y x C. 1151022=+y x D.122510022=+y x5.已知方程122=+my x 表示焦点在y 轴上的椭圆,则m 的取值范围是 [ ] A .m<1 B .-1<m<1 C .m>1 D .0<m<16.椭圆ax 2+by 2+ab=0(a<b<0)的焦点坐标是 [ ]A.()0,b a -±B.(0,b a -±)C.(a b -±,0)D.(0,a b -±)二、填空题7.如果椭圆13610022=+y x 上一点P 到焦点F 1的距离等于6,则点P 到另一个焦点 F 2的距离是 ;8过椭圆C :12222=+by a x 的焦点引垂直于x 轴的弦,则弦长为三、解答题:9.求经过点A(0,2)和B(3,21)的椭圆的标准方程10.椭圆的两个焦点F 1、F 2在x 轴上,以| F 1F 2|为直径的圆与椭圆的一个交点为(3,4),求椭圆标准方程.11.已知点P在以坐标轴为对称轴的椭圆上,点P到两个焦点的距离分别为352,354,过P作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程参考答案一、选择题: BAAA DD二、填空题:1、14;2、ab 22。
椭圆及其标准方程

故由椭圆的标准方程可知P点的轨迹方程是:
x2 25(y=0)
小结
教学重点
求椭圆的标准方程
教学难点
待定系数法的应用
课后作业
(一)课本第95页:第二题,第三题(2)(3)
(二)预习椭圆的几何性质
谢谢大家
椭圆及其标准方程(2)
曾都一中 宋旭
教学重点
求椭圆的标准方程
教学难点
待定系数法的应用
在一次校园足球赛中有一位足球爱好者 兼数学教师的我在绕足球场最近的一条路 道上跑步,目的是一边看足球赛一边锻炼身 体.但我发现了一个很奇怪的现象-我距离 两个队的守门员的距离之和总是不变的(两 个守门员都站在固定的位置,且他们两个人 相距80m),在好奇心的驱使下,我专门去 测量了一下这个距离,刚好是100m。
80m
问题: 设两守门圆所在的位置分别为A,B;足球爱好者为P; 已知|AB|=80;|PA|+|PB|=100 . 求P点的轨迹方程?
分析:在解析几何里,求符合某种条件的点的轨迹,要建立适
当的坐标系。为选择适当的坐标系,常常需画出草图。
y P 解:如图建立坐标系,使x轴经过点A,B;原点 O与AB的中点重合。由已知|PA|+|PB|=100 可知P点的轨迹是椭圆,且2c=80;2a=100 ∴c=40;a=50,b =a -c =900 A 0 B x 故由椭圆的标准方程可知P点的轨迹方程是: x2 y2 + 2500 900
练习
已知B,C是两个定点,|BC|=6,且⊿ABC 的周长等于16,求顶点A的轨迹方程?
y A 解:如图建立坐标系,使x轴经过点B,C;原点 O与BC的中点重合。由已知|AB|+|AC|=100 可知P点的轨迹是椭圆, 且2c=6;2a=16-6=10 B 0 C x ∴c=3;a=5,b =a -c =16。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析几何同步练习(椭圆及其标准方程2A )
知识要点: ①定义: ()||22||||2121F F a a PF PF >=+;
② 标准方程:()012222>>=+b a b y a x ;()0122
22>>=+b a b
x a y 。
一、选择题
1、已知椭圆的焦点是21,F F ,P 是椭圆上一个动点,如果延长P F 1到Q ,使得2PF PQ =,那么动点Q 的轨迹是 [ ]
A 圆
B 椭圆
C 直线
D 线段
2. △ABC 的两个顶点坐标A (-4,0),B (4,0),△ABC 的周长是18,则顶点C 的轨迹方程是 A. 192522=+y x B.1925
2
2=+x y (y ≠0) C.)0(191622≠=+y y x D.1925
2
2=+y x (y ≠0) 3.已知△ABC 的三边AB ,BC ,AC 的长依次成等差数列,且|AB|>|AC|,B (-1,0)C (1,0)则顶A 的轨迹方程为 [ ] A. 13422=+y x B.13422=+y x (x>0)C.13422=+y x (x<0) D.134
2
2=+y x (x>0y ≠0) 4.椭圆的方程为19222
=+y a
x ,它的两个焦点分别为F 1、F 2,若| F 1F 2|=8,弦AB 过F 1 则△ABF 2的周长为 [ ] A.10 B.20 C.241 D.441
二、填空题
5.过点F 1(0,2)且与圆F 2:x 2+(y+2)2=36内切的动圆圆心的轨迹方程
为 .
6.P 点在椭圆120
452
2=+y x 上,F 1、F 2是两个焦点,若21PF PF ⊥,则P 点的坐标是 7.P 是椭圆164
10022
=+y x 上的一点,F 1和F 2是焦点,若 6021=∠PF F , 则21F PF ∆的面积为 。
8. 如图,F 1,F 2分别为椭圆12222=+b
y a x 的左、右焦点, 点P 在椭圆上,△POF 2是面积为3的正三角形,则b
2 的值是
三、解答题
9.一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹.
10.如图,线段AB的两个端点A,B分别在x轴上,y轴上滑动,|AB|=5点M是AB上一点,且|AM|=2,点M随线段AB的运动而变化,求点M的轨迹方程.
参考答案
一、选择题: ADDB
二、填空题:
1、15
92
2=+x y ; 2、()4,3±±; 3、3364; 4、32。
三、解答题:
1、127362
2=+y x ;
2、14922=+y x 。
