第7章 函数(function)与过程(procedure)
第7章VB过程和参数传递

VB程序设计教程
沈美莉 马银晓 陈孟建 编著
10
Function过程 第二节 Function过程
二、调用Function过程 调用 过程
Function过程的调用比较简单,可以象一个函数一样调用,其调用格式为: <过程名> = ([<实参表列>]) 【例题5.16】 编写一个求最大公约数(GCD)的函数过程,并调用该函数。 【程序代码】 (1)创建GCD函数 Function gcd(ByVal x As Integer, ByVal y As Integer) As Integer Dim reminder As Integer Do While y <> 0 reminder = x Mod y x = y y = reminder Loop gcd = x End Function
VB程序设计教程
沈美莉 马银晓 陈孟建 编著
5
Sub过程 第一节 Sub过程
二、调用sub过程 调用 过程 调用Sub过程有两种方法,一种方法是使用Call调用过程语句来调 用过程,另一种方法是将过程名作为一个语句来使用。 call调用语句 1.用call调用语句 (1)格式 Call 过程名 [(<实参表>)] (2)功能 Call语句把程序控制传递到一个Visual Basic语言的Sub过程。 Call语句调用一个过程时,如果过程本身没有参数,则<实参表> 和括号可以省略;否则,应给出相应的实际参数,并把参数放在 括号中。实际参数是传递给sub过程的变量或常数的。 例如: Call ppa(a,b)
VB程序设计教程
沈美莉 马银晓 陈孟建 编著
18
第三节 参数的传递
例如: Function fac(a,b) …… …… fac = fa End Function 调用fac函数时,可以使用以下语句来完成: Private Sub Command1_Click() …… …… Call fac(x,y) End sub 以上程序中的a和b是两个形式参数,而 x和y是两个实际参数。这样就完成了形参 与实参的结合,其关系如下图所示。
高等数学名词(中英文)

高等数学名词(中英文)第一章函数与极限Chapter1 Function and Limit 集合set元素element子集subset空集empty set并集union交集intersection差集difference of set基本集basic set补集complement set直积direct product笛卡儿积Cartesian product开区间open interval闭区间closed interval半开区间half open interval有限区间finite interval区间的长度length of an interval无限区间infinite interval领域neighborhood领域的中心centre of a neighborhood 领域的半径radius of a neighborhood 左领域left neighborhood右领域right neighborhood映射mappingX到Y的映射mapping of X ontoY 满射surjection单射injection一一映射one-to-one mapping双射bijection算子operator变化transformation函数function逆映射inverse mapping复合映射composite mapping自变量independent variable 因变量dependent variable定义域domain函数值value of function函数关系function relation值域range自然定义域natural domain单值函数single valued function多值函数multiple valued function单值分支one-valued branch函数图形graph of a function绝对值函数absolute value符号函数sigh function整数部分integral part阶梯曲线step curve当且仅当if and only if(iff)分段函数piecewise function上界upper bound下界lower bound有界boundedness无界unbounded函数的单调性monotonicity of a function 单调增加的increasing单调减少的decreasing单调函数monotone function函数的奇偶性parity(odevity) of a function 对称symmetry偶函数even function奇函数odd function函数的周期性periodicity of a function周期period反函数inverse function直接函数direct function复合函数composite function中间变量intermediate variable函数的运算operation of function基本初等函数basic elementary function初等函数elementary function幂函数power function指数函数exponential function对数函数logarithmic function三角函数trigonometric function反三角函数inverse trigonometric function常数函数constant function双曲函数hyperbolic function双曲正弦hyperbolic sine双曲余弦hyperbolic cosine双曲正切hyperbolic tangent反双曲正弦inverse hyperbolic sine反双曲余弦inverse hyperbolic cosine反双曲正切inverse hyperbolic tangent极限limit数列sequence of number收敛convergence收敛于a converge to a发散divergent极限的唯一性uniqueness of limits收敛数列的有界性boundedness of a convergent sequence子列subsequence函数的极限limits of functions函数当x趋于x0时的极限limit of functions as x approaches x0左极限left limit右极限right limit单侧极限one-sided limits水平渐近线horizontal asymptote无穷小infinitesimal无穷大infinity铅直渐近线vertical asymptote夹逼准则squeeze rule单调数列monotonic sequence高阶无穷小infinitesimal of higher order低阶无穷小infinitesimal of lower order同阶无穷小infinitesimal of the same order等阶无穷小equivalent infinitesimal 函数的连续性continuity of a function增量increment函数在x0连续the function is continuous at x0左连续left continuous右连续right continuous区间上的连续函数continuous function函数在该区间上连续function is continuous on an interval不连续点discontinuity point第一类间断点discontinuity point of the first kind第二类间断点discontinuity point of the second kind初等函数的连续性continuity of the elementary functions定义区间defined interval最大值global maximum value (absolute maximum)最小值global minimum value (absolute minimum)零点定理the zero point theorem介值定理intermediate value theorem第二章导数与微分Chapter2 Derivative and Differential速度velocity匀速运动uniform motion平均速度average velocity瞬时速度instantaneous velocity圆的切线tangent line of a circle切线tangent line切线的斜率slope of the tangent line位置函数position function导数derivative可导derivable函数的变化率问题problem of the change rate of a function导函数derived function左导数left-hand derivative右导数right-hand derivative单侧导数one-sided derivatives在闭区间[a, b]上可导is derivable on the closed interval [a,b]切线方程tangent equation角速度angular velocity成本函数cost function边际成本marginal cost链式法则chain rule隐函数implicit function显函数explicit function二阶函数second derivative三阶导数third derivative高阶导数nth derivative莱布尼茨公式Leibniz formula对数求导法log- derivative参数方程parametric equation相关变化率correlative change rata微分differential可微的differentiable函数的微分differential of function自变量的微分differential of independent variable微商differential quotient间接测量误差indirect measurement error绝对误差absolute error相对误差relative error第三章微分中值定理与导数的应用Chapter3 Mean Value Theorem ofDifferentials and the Application ofDerivatives罗马定理Rolle’s theorem费马引理Fermat’s lemma拉格朗日中值定理Lagrange’s mean value theorem驻点stationary point稳定点stable point 临界点critical point辅助函数auxiliary function拉格朗日中值公式Lagrange’s mean value formula柯西中值定理Cauchy’s mean value theorem 洛必达法则L’Hospital’s Rule0/0型不定式indeterminate form of type 0/0 不定式indeterminate form泰勒中值定理Taylor’s mean value theorem 泰勒公式Taylor formula余项remainder term拉格朗日余项Lagrange remainder term麦克劳林公式Maclaurin’s formula佩亚诺公式Peano remainder term凹凸性concavity凹向上的concave upward, cancave up凹向下的,向上凸的concave downward’ concave down拐点inflection point函数的极值extremum of function极大值local(relative) maximum最大值global(absolute) mximum极小值local(relative) minimum最小值global(absolute) minimum目标函数objective function曲率curvature弧微分arc differential平均曲率average curvature曲率园circle of curvature曲率中心center of curvature曲率半径radius of curvature渐屈线evolute渐伸线involute根的隔离isolation of root隔离区间isolation interval切线法tangent line method第四章不定积分Chapter4 Indefinite Integrals原函数primitive function(anti-derivative)积分号sign of integration被积函数integrand积分变量integral variable积分曲线integral curve积分表table of integrals换元积分法integration by substitution分部积分法integration by parts分部积分公式formula of integration by parts 有理函数rational function真分式proper fraction假分式improper fraction第五章定积分Chapter5 Definite Integrals曲边梯形trapezoid with曲边curve edge窄矩形narrow rectangle曲边梯形的面积area of trapezoid with curved edge积分下限lower limit of integral积分上限upper limit of integral积分区间integral interval分割partition积分和integral sum可积integrable矩形法rectangle method积分中值定理mean value theorem of integrals函数在区间上的平均值average value of a function on an integvals牛顿-莱布尼茨公式Newton-Leibniz formula微积分基本公式fundamental formula of calculus换元公式formula for integration by substitution递推公式recurrence formula反常积分improper integral 反常积分发散the improper integral is divergent反常积分收敛the improper integral is convergent无穷限的反常积分improper integral on an infinite interval无界函数的反常积分improper integral of unbounded functions绝对收敛absolutely convergent第六章定积分的应用Chapter6 Applications of the DefiniteIntegrals元素法the element method面积元素element of area平面图形的面积area of a luane figure直角坐标又称“笛卡儿坐标(Cartesian coordinates)”极坐标polar coordinates抛物线parabola椭圆ellipse旋转体的面积volume of a solid of rotation旋转椭球体ellipsoid of revolution, ellipsoid of rotation曲线的弧长arc length of acurve可求长的rectifiable光滑smooth功work水压力water pressure引力gravitation变力variable force第七章空间解析几何与向量代数Chapter7 Space Analytic Geometry andVector Algebra向量vector自由向量free vector单位向量unit vector零向量zero vector相等equal平行parallel向量的线性运算linear poeration of vector三角法则triangle rule平行四边形法则parallelogram rule交换律commutative law结合律associative law负向量negative vector差difference分配律distributive law空间直角坐标系space rectangular coordinates坐标面coordinate plane卦限octant向量的模modulus of vector向量a与b的夹角angle between vector a and b方向余弦direction cosine方向角direction angle向量在轴上的投影projection of a vector onto an axis数量积,外积,叉积scalar product,dot product,inner product曲面方程equation for a surface球面sphere旋转曲面surface of revolution母线generating line轴axis圆锥面cone顶点vertex旋转单叶双曲面revolution hyperboloids of one sheet旋转双叶双曲面revolution hyperboloids of two sheets柱面cylindrical surface ,cylinder圆柱面cylindrical surface准线directrix抛物柱面parabolic cylinder二次曲面quadric surface 椭圆锥面dlliptic cone椭球面ellipsoid单叶双曲面hyperboloid of one sheet双叶双曲面hyperboloid of two sheets旋转椭球面ellipsoid of revolution椭圆抛物面elliptic paraboloid旋转抛物面paraboloid of revolution双曲抛物面hyperbolic paraboloid马鞍面saddle surface椭圆柱面elliptic cylinder双曲柱面hyperbolic cylinder抛物柱面parabolic cylinder空间曲线space curve空间曲线的一般方程general form equations of a space curve空间曲线的参数方程parametric equations of a space curve螺转线spiral螺矩pitch投影柱面projecting cylinder投影projection平面的点法式方程pointnorm form eqyation of a plane法向量normal vector平面的一般方程general form equation of a plane两平面的夹角angle between two planes点到平面的距离distance from a point to a plane空间直线的一般方程general equation of a line in space方向向量direction vector直线的点向式方程pointdirection form equations of a line方向数direction number直线的参数方程parametric equations of a line两直线的夹角angle between two lines垂直perpendicular直线与平面的夹角angle between a line and a planes平面束pencil of planes平面束的方程equation of a pencil of planes 行列式determinant系数行列式coefficient determinant第八章多元函数微分法及其应用Chapter8 Differentiation of Functions ofSeveral Variables and Its Application一元函数function of one variable多元函数function of several variables内点interior point外点exterior point边界点frontier point,boundary point聚点point of accumulation开集openset闭集closed set连通集connected set开区域open region闭区域closed region有界集bounded set无界集unbounded setn维空间n-dimentional space二重极限double limit多元函数的连续性continuity of function of seveal连续函数continuous function不连续点discontinuity point一致连续uniformly continuous偏导数partial derivative对自变量x的偏导数partial derivative with respect to independent variable x高阶偏导数partial derivative of higher order 二阶偏导数second order partial derivative混合偏导数hybrid partial derivative全微分total differential偏增量oartial increment偏微分partial differential 全增量total increment可微分differentiable必要条件necessary condition充分条件sufficient condition叠加原理superpostition principle全导数total derivative中间变量intermediate variable隐函数存在定理theorem of the existence of implicit function曲线的切向量tangent vector of a curve法平面normal plane向量方程vector equation向量值函数vector-valued function切平面tangent plane法线normal line方向导数directional derivative梯度gradient数量场scalar field梯度场gradient field向量场vector field势场potential field引力场gravitational field引力势gravitational potential曲面在一点的切平面tangent plane to a surface at a point曲线在一点的法线normal line to a surface at a point无条件极值unconditional extreme values条件极值conditional extreme values拉格朗日乘数法Lagrange multiplier method 拉格朗日乘子Lagrange multiplier经验公式empirical formula最小二乘法method of least squares均方误差mean square error第九章重积分Chapter9 Multiple Integrals二重积分double integral可加性additivity累次积分iterated integral体积元素volume element三重积分triple integral直角坐标系中的体积元素volume element in rectangular coordinate system柱面坐标cylindrical coordinates柱面坐标系中的体积元素volume element in cylindrical coordinate system球面坐标spherical coordinates球面坐标系中的体积元素volume element in spherical coordinate system反常二重积分improper double integral曲面的面积area of a surface质心centre of mass静矩static moment密度density形心centroid转动惯量moment of inertia参变量parametric variable第十章曲线积分与曲面积分Chapter10 Line (Curve) Integrals andSurface Integrals对弧长的曲线积分line integrals with respect to arc hength第一类曲线积分line integrals of the first type对坐标的曲线积分line integrals with respect to x,y,and z第二类曲线积分line integrals of the second type有向曲线弧directed arc单连通区域simple connected region复连通区域complex connected region格林公式Green formula第一类曲面积分surface integrals of the first type对面的曲面积分surface integrals with respect to area 有向曲面directed surface对坐标的曲面积分surface integrals with respect to coordinate elements第二类曲面积分surface integrals of the second type有向曲面元element of directed surface高斯公式gauss formula拉普拉斯算子Laplace operator格林第一公式Green’s first formula通量flux散度divergence斯托克斯公式Stokes formula环流量circulation旋度rotation,curl第十一章无穷级数Chapter11 Infinite Series一般项general term部分和partial sum余项remainder term等比级数geometric series几何级数geometric series公比common ratio调和级数harmonic series柯西收敛准则Cauchy convergence criteria, Cauchy criteria for convergence正项级数series of positive terms达朗贝尔判别法D’Alembert test柯西判别法Cauchy test交错级数alternating series绝对收敛absolutely convergent条件收敛conditionally convergent柯西乘积Cauchy product函数项级数series of functions发散点point of divergence收敛点point of convergence收敛域convergence domain和函数sum function幂级数power series幂级数的系数coeffcients of power series阿贝尔定理Abel Theorem收敛半径radius of convergence收敛区间interval of convergence泰勒级数Taylor series麦克劳林级数Maclaurin series二项展开式binomial expansion近似计算approximate calculation舍入误差round-off error,rounding error欧拉公式Euler’s formula魏尔斯特拉丝判别法Weierstrass test三角级数trigonometric series振幅amplitude角频率angular frequency初相initial phase矩形波square wave谐波分析harmonic analysis直流分量direct component基波fundamental wave二次谐波second harmonic三角函数系trigonometric function system傅立叶系数Fourier coefficient傅立叶级数Forrier series周期延拓periodic prolongation正弦级数sine series余弦级数cosine series奇延拓odd prolongation偶延拓even prolongation傅立叶级数的复数形式complex form of Fourier series第十二章微分方程Chapter12 Differential Equation解微分方程solve a differential equation常微分方程ordinary differential equation偏微分方程partial differential equation,PDE 微分方程的阶order of a differential equation 微分方程的解solution of a differential equation 微分方程的通解general solution of a differential equation初始条件initial condition微分方程的特解particular solution of a differential equation初值问题initial value problem微分方程的积分曲线integral curve of a differential equation可分离变量的微分方程variable separable differential equation隐式解implicit solution隐式通解inplicit general solution衰变系数decay coefficient衰变decay齐次方程homogeneous equation一阶线性方程linear differential equation of first order非齐次non-homogeneous齐次线性方程homogeneous linear equation 非齐次线性方程non-homogeneous linear equation常数变易法method of variation of constant 暂态电流transient state current稳态电流steady state current伯努利方程Bernoulli equation全微分方程total differential equation积分因子integrating factor高阶微分方程differential equation of higher order悬链线catenary高阶线性微分方程linear differential equation of higher order自由振动的微分方程differential equation of free vibration强迫振动的微分方程differential equation of forced oscillation串联电路的振荡方程oscillation equation of series circuit二阶线性微分方程second order lineardifferential equation线性相关linearly dependence线性无关linearly independence二阶常系数齐次线性微分方程second order homogeneous linear differential equation with constant coefficient二阶变系数齐次线性微分方程second order homogeneous linear differential equation with variable coefficient特征方程characteristic equation无阻尼自由振动的微分方程differential equation of free vibration with zero damping 固有频率natural frequency 简谐振动simple harmonic oscillation,simple harmonic vibration微分算子differential operator待定系数法method of undetermined coefficient共振现象resonance phenomenon欧拉方程Euler equation幂级数解法power series solution数值解法numerial solution勒让德方程Legendre equation微分方程组system of differential equations常系数线性微分方程组system of linear differential equations with constant coefficientV、X、Z:Value of function :函数值Variable :变数Vector :向量Velocity :速度Vertical asymptote :垂直渐近线Volume :体积X-axis :x轴x-coordinate :x坐标x-intercept :x截距Zero vector :函数的零点Zeros of a polynomial :多项式的零点T:Tangent function :正切函数Tangent line :切线Tangent plane :切平面Tangent vector :切向量Total differential :全微分Trigonometric function :三角函数Trigonometric integrals :三角积分Trigonometric substitutions :三角代换法Tripe integrals :三重积分S:Saddle point :鞍点Scalar :纯量Secant line :割线Second derivative :二阶导数Second Derivative Test :二阶导数试验法Second partial derivative :二阶偏导数Sector :扇形Sequence :数列Series :级数Set :集合Shell method :剥壳法Sine function :正弦函数Singularity :奇点Slant asymptote :斜渐近线Slope :斜率Slope-intercept equation of a line :直线的斜截式Smooth curve :平滑曲线Smooth surface :平滑曲面Solid of revolution :旋转体Space :空间Speed :速率Spherical coordinates :球面坐标Squeeze Theorem :夹挤定理Step function :阶梯函数Strictly decreasing :严格递减Strictly increasing :严格递增Sum :和Surface :曲面Surface integral :面积分Surface of revolution :旋转曲面Symmetry :对称R:Radius of convergence :收敛半径Range of a function :函数的值域Rate of change :变化率Rational function :有理函数Rationalizing substitution :有理代换法Rational number :有理数Real number :实数Rectangular coordinates :直角坐标Rectangular coordinate system :直角坐标系Relative maximum and minimum :相对极大值与极小值Revenue function :收入函数Revolution , solid of :旋转体Revolution , surface of :旋转曲面Riemann Sum :黎曼和Riemannian geometry :黎曼几何Right-hand derivative :右导数Right-hand limit :右极限Root :根P、Q:Parabola :拋物线Parabolic cylinder :抛物柱面Paraboloid :抛物面Parallelepiped :平行六面体Parallel lines :并行线Parameter :参数Partial derivative :偏导数Partial differential equation :偏微分方程Partial fractions :部分分式Partial integration :部分积分Partiton :分割Period :周期Periodic function :周期函数Perpendicular lines :垂直线Piecewise defined function 分段定义函数Plane :平面Point of inflection :反曲点Polar axis :极轴Polar coordinate :极坐标Polar equation :极方程式Pole :极点Polynomial :多项式Positive angle :正角Point-slope form :点斜式Power function :幂函数Product :积Quadrant :象限Quotient Law of limit 极限的商定律Quotient Rule :商定律M、N、O:Maximum and minimum values :极大与极小值Mean Value Theorem :均值定理Multiple integrals :重积分Multiplier :乘子Natural exponential function 自然指数函数Natural logarithm function 自然对数函数Natural number :自然数Normal line :法线Normal vector :法向量Number :数Octant :卦限Odd function :奇函数One-sided limit :单边极限Open interval :开区间Optimization problems :最佳化问题Order :阶Ordinary differential equation :常微分方程Origin :原点Orthogonal :正交的L:Laplace transform :Leplace 变换Law of Cosines :余弦定理Least upper bound :最小上界Left-hand derivative :左导数Left-hand limit :左极限Lemniscate :双钮线Length :长度Level curve :等高线L'Hospital's rule 洛必达法则Limacon :蚶线Limit :极限Linear approximation:线性近似Linear equation :线性方程式Linear function :线性函数Linearity :线性Linearization :线性化Line in the plane :平面上之直线Line in space :空间之直线Lobachevski geometry 罗巴切夫斯基几何Local extremum :局部极值Local maximum and minimum 局部极大值与极小值Logarithm :对数Logarithmic function :对数函数I:Implicit differentiation :隐求导法Implicit function :隐函数Improper integral :瑕积分Increasing/Decreasing Test 递增或递减试验法Increment :增量Increasing Function :增函数Indefinite integral :不定积分Independent variable :自变数Indeterminate from :不定型Inequality :不等式Infinite point :无穷极限Infinite series :无穷级数Inflection point :反曲点Instantaneous velocity :瞬时速度Integer :整数Integral :积分Integrand :被积分式Integration :积分Integration by part :分部积分法Intercepts :截距Intermediate value of Theorem 中间值定理Interval :区间Inverse function :反函数Inverse trigonometric function反三角函数Iterated integral :逐次积分H:Higher mathematics 高等数学/高数E、F、G、H:Ellipse :椭圆Ellipsoid :椭圆体Epicycloid :外摆线Equation :方程式Even function :偶函数Expected Valued :期望值Exponential Function :指数函数Exponents , laws of :指数率Extreme value :极值Extreme Value Theorem :极值定理Factorial :阶乘First Derivative Test :一阶导数试验法First octant :第一卦限Focus :焦点Fractions :分式Function :函数Fundamental Theorem of Calculus :微积分基本定理Geometric series :几何级数Gradient :梯度Graph :图形Green Formula :格林公式Half-angle formulas :半角公式Harmonic series :调和级数Helix :螺旋线Higher Derivative :高阶导数Horizontal asymptote :水平渐近线Horizontal line :水平线Hyperbola :双曲线Hyper boloid :双曲面D:Decreasing function :递减函数Decreasing sequence :递减数列Definite integral :定积分Degree of a polynomial :多项式之次数Density :密度Derivative :导数of a composite function :复合函数之导数of a constant function :常数函数之导数directional :方向导数domain of :导数之定义域of exponential function :指数函数之导数higher :高阶导数partial :偏导数of a power function :幂函数之导数of a power series :羃级数之导数of a product :积之导数of a quotient :商之导数as a rate of change :导数当作变率right-hand :右导数second :二阶导数as the slope of a tangent 导数看成切线之斜率Determinant :行列式Differentiable function 可导函数Differential :微分Differential equation :微分方程partial :偏微分方程Differentiation :求导法implicit :隐求导法partial :偏微分法term by term :逐项求导法Directional derivatives :方向导数Discontinuity :不连续性Disk method :圆盘法Distance :距离Divergence :发散Domain :定义域Dot product :点积Double integral :二重积分change of variable in二重积分之变数变换in polar coordinates :极坐标二重积分C:Calculus :微积分differential :微分学integral :积分学Cartesian coordinates :笛卡儿坐标一般指直角坐标Cartesian coordinates system 笛卡儿坐标系Cauch’s Mean Value Theorem 柯西均值定理Chain Rule :连锁律Change of variables :变数变换Circle :圆Circular cylinder :圆柱Closed interval :封闭区间Coefficient :系数Composition of function :函数之合成Compound interest :复利Concavity :凹性Conchoid :蚌线Cone :圆锥Constant function :常数函数Constant of integration :积分常数Continuity :连续性at a point :在一点处之连续性of a function :函数之连续性on an interval :在区间之连续性from the left :左连续from the right :右连续Continuous function :连续函数Convergence :收敛interval of :收敛区间radius of :收敛半径Convergent sequence :收敛数列series :收敛级数Coordinate:s:坐标Cartesian :笛卡儿坐标cylindrical :柱面坐标polar :极坐标rectangular :直角坐标spherical :球面坐标Coordinate axes :坐标轴Coordinate planes :坐标平面Cosine function :余弦函数Critical point :临界点Cubic function :三次函数Curve :曲线Cylinder:圆柱Cylindrical Coordinates :圆柱坐标A、B:Absolute convergence :绝对收敛Absolute extreme values :绝对极值Absolute maximum and minimum 绝对极大与极小Absolute value :绝对值Absolute value function :绝对值函数Acceleration :加速度Antiderivative :反导数Approximate integration :近似积分Approximation :逼近法by differentials :用微分逼近linear :线性逼近法by Simpson’s Rule :Simpson法则逼近法by the Trapezoidal Rule 梯形法则逼近法Arbitrary constant :任意常数Arc length :弧长Area :面积under a curve :曲线下方之面积between curves :曲线间之面积in polar coordinates :极坐标表示之面积of a sector of a circle :扇形之面积of a surface of a revolution 旋转曲面之面积Asymptote :渐近线horizontal :水平渐近线slant :斜渐近线vertical :垂直渐近线Average speed :平均速率Average velocity :平均速度Axes, coordinate :坐标轴Axes of ellipse :椭圆之轴Binomial series :二项级数微积分专有名词中英文对照absolutely convergent 绝对收敛absolute value 绝对值algebraic function 代数函数analytic geometry 解析几何antiderivative 不定积分approximate integration 近似积分approximation 近似法、逼近法arbitrary constant 任意常数arithmetic series/progression (AP)算数级数asymptotes (vertical and horizontal)(垂直/水平)渐近线average rate of change 平均变化率base 基数binomial theorem 二项式定理,二项展开式Cartesian coordinates 笛卡儿坐标(一般指直角坐标)Cartesian coordinates system 笛卡儿坐标系Cauch’s Mean Value Theorem 柯西均值定理chain rule 链式求导法则calculus 微积分学closed interval integral 闭区间积分coefficient 系数composite function 复合函数conchoid 蚌线continuity (函数的)连续性concavity (函数的)凹凸性conditionally convergent 有条件收敛continuity 连续性critical point 临界点cubic function 三次函数cylindrical coordinates 圆柱坐标decreasing function 递减函数decreasing sequence 递减数列definite integral 定积分derivative 导数determinant 行列式differential coefficient 微分系数differential equation 微分方程directional derivative 方向导数discontinuity 不连续性discriminant (二次函数)判别式disk method 圆盘法divergence 散度divergent 发散的domain 定义域dot product 点积double integral 二重积分ellipse 椭圆ellipsoid 椭圆体epicycloid 外摆线Euler's method (BC)欧拉法expected valued 期望值exponential function 指数函数extreme value heorem 极值定理factorial 阶乘finite series 有限级数fundamental theorem of calculus 微积分基本定理geometric series/progression (GP)几何级数gradient 梯度Green formula 格林公式half-angle formulas 半角公式harmonic series 调和级数helix 螺旋线higher derivative 高阶导数horizontal asymptote 水平渐近线horizontal line 水平线hyperbola 双曲线hyper boloid 双曲面implicit differentiation 隐函数求导implicit function 隐函数improper integral 广义积分、瑕积分increment 增量increasing function 增函数indefinite integral 不定积分independent variable 自变数inequality 不等式ndeterminate form 不定型infinite point 无穷极限infinite series 无穷级数infinite series 无限级数inflection point (POI) 拐点initial condition 初始条件instantaneous rate of change 瞬时变化率integrable 可积的integral 积分integrand 被积分式integration 积分integration by part 分部积分法intercept 截距intermediate value of Theorem :中间值定理inverse function 反函数irrational function 无理函数iterated integral 逐次积分Laplace transform 拉普拉斯变换law of cosines 余弦定理least upper bound 最小上界left-hand derivative 左导数left-hand limit 左极限L'Hospital's rule 洛必达法则limacon 蚶线linear approximation 线性近似法linear equation 线性方程式linear function 线性函数linearity 线性linearization 线性化local maximum 极大值local minimum 极小值logarithmic function 对数函数MacLaurin series 麦克劳林级数maximum 最大值mean value theorem (MVT)中值定理minimum 最小值method of lagrange multipliers 拉格朗日乘数法modulus 绝对值multiple integral 多重积分multiple 倍数multiplier 乘子octant 卦限open interval integral 开区间积分optimization 优化法,极值法origin 原点orthogonal 正交parametric equation (BC)参数方程partial derivative 偏导数partial differential equation 偏微分方程partial fractions 部分分式piece-wise function 分段函数parabola 抛物线parabolic cylinder 抛物柱面paraboloid :抛物面parallelepiped 平行六面体parallel lines 并行线parameter :参数partial integration 部分积分partiton :分割period :周期periodic function 周期函数perpendicular lines 垂直线piecewise defined function 分段定义函数plane 平面point of inflection 反曲点point-slope form 点斜式polar axis 极轴polar coordinates 极坐标polar equation 极坐标方程pole 极点polynomial 多项式power series 幂级数product rule 积的求导法则quadrant 象限quadratic functions 二次函数quotient rule 商的求导法则radical 根式radius of convergence 收敛半径range 值域(related) rate of change with time (时间)变化率rational function 有理函数reciprocal 倒数remainder theorem 余数定理Riemann sum 黎曼和Riemannian geometry 黎曼几何right-hand limit 右极限Rolle's theorem 罗尔(中值)定理root 根rotation 旋转secant line 割线second derivative 二阶导数second derivative test 二阶导数试验法second partial derivative 二阶偏导数series 级数shell method (积分)圆筒法sine function 正弦函数singularity 奇点slant 母线slant asymptote 斜渐近线slope 斜率slope-intercept equation of a line 直线的斜截式smooth curve 平滑曲线smooth surface 平滑曲面solid of revolution 旋转体symmetry 对称性substitution 代入法、变量代换tangent function 正切函数tangent line 切线tangent plane 切(平)面tangent vector 切矢量taylor's series 泰勒级数three-dimensional analytic geometry 空间解析几何total differentiation 全微分trapezoid rule 梯形(积分)法则。
第7章 函数与预处理命令

例如:求两个数的最大值。 int max(int x,int y) { int z; 没有形式参数 z = x > y ? x : y; 为无参函数 return( z ); }
龙诚数码:
9
形参也可以这样定义 int max(x,y) int x,y; { int z; z = x > y ? x : y; return( z ); }
龙诚数码:
【例7.1】求一个整数的立方。
int cube (int x) /* 函数定义 */ { return (x * x * x); } main( ) 程序的执行总是 { int f, a; 从main函数开始 printf("\nEnter an integer number:"); scanf("%d", &a); 函数调用 f = cube (a); printf("%d * %d * %d = %d\n", a, a, a, f); 程序运行情况如下: } Enter an integer number:2 2*2*2=8
a=9,b=5
14
龙诚数码:
2.函数的类型与函数的返回值
15
【例7.6】输出两个数中的大数。 ⑴ 函数的类型 max(int x,int y) 说明: { int z; ①函数的类型 z=x>y?x:y; 决定了函数返 return (z); /* 返回z的值 */ 回值的类型。 } 若省略函数的 main( ) 类型,系统默 { int a,b,c; 认其为int型。 scanf("%d,%d",&a,&b); ②无返回值的 c=max(a,b); 函数应将其类 printf("max is %d\n",c); 型定义为void } (空)类型。
第7章 数据库高级对象的使用

3、视图的优点
1.视点集中 用户只关心它感兴趣的某些特定数据和他们所负责的特定任务。
2.简化操作 视图大大简化了用户对数据的操作。因为在定义视图时,若视图本身就 是一个复杂查询的结果集,这样在每一次执行相同的查询时,不必重新 写这些复杂的查询语句,只要一条简单的查询视图语句即可。可见视图 向用户隐藏了表与表之间的复杂的连接操作。
SCHEMABINDING | VIEW_METADATA }
2、用SQL语句定义视图
【例7-1】已知学生表的数据如图7-1所示。
创建一个视图,视图中只包含信安152班的数据,SQL语 句如下: CREATE VIEW VW_信安152 AS SELECT * FROM 学生 WHERE 班级='信安152' 通过Select语句查询视图中的数据,语句如下: SELECT * FROM VW_信安152
运行程序过程: EXEC prcShopper '000002' /*返回ID号为000002的购物者所购买的 玩具及数量。*/
提示:存储过程可以带多个输入参数,之间用逗号格开。
二、存储过程
RETURN语句从一个存储过程返回值
【例7-8】带输入参数的存储过程,并且报告执行的结果,根据输入的购物者的ID号, 返回购物者的名字、所订购的玩具的名字和订购数量。 CREATE PROCEDURE prcShopper1 @ShopperId CHAR(6) AS BEGIN
JOIN Toys ON OrderDetail.cToyId = Toys.cToyId END
调用该存储过程方法是:
EXEC prcOrders
/*运行(调用)存储过程*/
二、存储过程
EDA技术课后参考答案(陈炳权_曾庆立)之欧阳德创编

答案由个人做出,可能有不全或错误之处,欢迎大家批评指正。
第一章1.EDA的英文全称及其中文含义是什么?答:EDA是Electronic Design Automation,其中文含义是“电子设计自动化”。
2.什么叫EDA技术?简述EDA技术的发展历程。
答:EDA技术有狭义和广义之分,狭义EDA技术就是以大规模可编程逻辑器件为设计载体,以硬件描述语言为系统逻辑描述的主要表达方式,以计算机、大规模可编程逻辑器件的开发软件及实验开发系统为设计工具,通过有关的开发软件,自动完成用软件的方式设计的电子系统到硬件系统的逻辑编译、逻辑化简、逻辑分割、逻辑综合及优化、逻辑布局布线、逻辑仿真,直至完成对于特定目标芯片的适配编译、逻辑映射、编程下载等工作,最终形成集成电子系统或专用集成芯片的一门新技术,或称为IES/ASIC自动设计技术。
3.简述用EDA技术设计电路的设计流程。
答EDA设计流程包括:设计准备、设计输入、设计处理、设计校验、器件编程、器件测试和设计验证。
4.什么叫”综合”和”网表文件”?答:(A)在电子设计领域中综合的概念可以表示为:将用行为和功能层次表达的电子系统转换为低层次的便于具体实现的模块组合装配的过程。
(1)从自然语言转换到VHDL 语言算法表示,即自然语言综合。
(2)从算法表示转换到寄存器传输级(RegisterTransport Level,RTL),即从行为域到结构域的综合,即行为综合。
(3)从 RTL 级表示转换到逻辑门(包括触发器)的表示,即逻辑综合。
(4)从逻辑门表示转换到版图表示(ASIC 设计),或转换到FPGA 的配置网表文件,可称为版图综合或结构综合。
综合在电子设计自动化中处于核心地位。
(B)文件是描述电路的连接关系的文件,一般以文本文件的形式存在。
英文为netlist file格式有cdl, spice, aucdl...等5.从使用的角度来讲,EDA技术主要包括几个方面的内容?这几个方面在整个电子系统的设计中分别起什么作用?答: EDA技术的学习主要应掌握4个方面的内容:① 大规模可编程逻辑器件;② 硬件描述语言;③ 软件开发工具;④ 实验开发系统。
Pascal基本教程 第一至十一章甄选

Pascal基本教程第一至十一章(优选.)Pascal基本教程2008-04-19 18:18来自Pascal语言中文网的一份pascal入门教程,适合Pascal初学者阅读。
第一章Pascal语言概述与预备知识第二章Pascal语言基础知识第三章顺序结构程序设计第四章选择结构程序设计第五章循环结构程序设计第六章枚举型和子界型第七章数组第八章函数和过程第九章集合与记录第十章指针第十一章文件Pascal基本教程第一章2008-04-19 18:20第一章Pascal语言概述与预备知识1 关于Turbo PascalPascal是一种计算机通用的高级程序设计语言。
它由瑞士Niklaus Wirth教授于六十年代末设计并创立。
以法国数学家命名的Pascal语言现已成为使用最广泛的基于DOS的语言之一,其主要特点有:严格的结构化形式;丰富完备的数据类型;运行效率高;查错能力强。
正因为上述特点,Pascal语言可以被方便地用于描述各种算法与数据结构。
尤其是对于程序设计的初学者,Pascal语言有益于培养良好的程序设计风格和习惯。
IOI(国际奥林匹克信息学竞赛)把Pascal语言作为三种程序设计语言之一,noi(全国奥林匹克信息学竞赛)把pascal语言定为唯一提倡的程序设计语言,在大学中Pascal语言也常常被用作学习数据结构与算法的教学语言。
在Pascal问世以来的三十余年间,先后产生了适合于不同机型的各种各样版本。
其中影响最大的莫过于Turbo pascal系列软件。
它是由美国Borland公司设计、研制的一种适用于微机的Pascal编译系统。
该编译系统由1983年推出1.0版本发展到1992年推出的7.0版本,其版本不断更新,而功能更趋完善。
下面列出Turbo Pascal编年史出版年代版本名称主要特色1983Turbo Pascal 1.0Turbo Pascal 2.0Turbo-87 Pascal提高实数运算速度并扩大值域1985Turbo Pascal 3.0增加图形功能Turbo BCD Pascal特别适合应用于商业1987Turbo Pascal 4.0提供集成开发环境(IDE),引入单元概念1988Turbo Pascal 5.0增加调试功能1989Turbo Pascal 5.5支持面向对象的程序设计(OPP)1990Turbo Pascal 6.0提供面向对象的应用框架和库(Turbo Vision)1992Turbo Pascal 7.0面向对象的应用系统、更完善的IDETurbo Vision 2.01993Borland Pascal 7.0开发Object Windows库、(For Windows)提供对OLE多媒体应用开发的支持1995DelphiVisual PascalTurbo Pascal语言是编译型程序语言,它提供了一个集成环境的工作系统,集编辑、编译、运行、调试等多功能于一体。
_fortran-第七章 过程

Fortran 提供了一个特定机制,使得可以在构建 最终的程序前容易地独立开发和调试子任务。 可以把每个子任务作为独立的程序单元来编码, 该独立程序单元被称为外部过程( external procedure) ,每个外部过程都可以独立于程序 中的其它子任务(过程)来进行编译、调试。 Fortran 中有两种外部过程:子程序 ( subroutine) 和函数子程序( function subprogram)(或者就叫函数, function)
7.1 子程序
SUBROUTINE 语句标志着子程序的开始,定义了子 程序名和相关参数表。子程序名必须遵循标准的 Fortran 命名规则由字母和数字组成,最大长度可以 到31 个字符,但第一个字符必须是字母。参数表含 有一系列变量和/或数组,这些变量、数组的值将从 调用程序传递给子程序。这些变量被称为形参 (dummy agument ,形式参数),子程序实际上没有 为它们真正分配任何内存空间。对从调用程序单元传 递来的实际参数(实参)来说它们仅仅是占位符。
每个子程序是一个独立的程序单元,它开始于 SUBROUTINE 语句,结束于END SUBROUTINE 语句。 当程序调用子程序时,调用程序的执行暂时被 挂起,子程序执行部分开始运行。当运行到子 程序的RETURN 语句或END SUBROUTINE 语 句时,调用程序又开始运行调用子程序语句下 面的程序代码。 任何可执行程序单元都可以调用子程序,包括 另一个子程序。(但是,子程序不能调用它自 身,除非它被定义为递归类型(recursive) )。
Fortran95/2003程序设计
第七章 过程
本章学习目标: • 学习Fortran 语言中的过程如何帮助实现好的程序设 计 • 了解子程序与函数的不同 • 掌握创建和调用子程序 • 理解并学会使用INTENT 属性 • 理解使用地址传递方案实现变量传递 • 理解显式结构的形参数组、不定结构的形参数组和不 定大小的形参数组之间的区别 • 理解为什么不再使用不定大小的数组 • 掌握在过程之间使用模块实现共享数据 • 理解显式接口,以及为什么在模块内部定义过程更好 • 能创建并且调用用户自定义函数 • 掌握如何把Fortran 过程调用参数传递给其他过程。
《EDA技术及应用》朱正伟-三,四,五章部分课后题答案

第三章3-5设计一个4选1多路选择器,当选择输入信号分别取“00”、“01”、“10”和“11”时,输出信号分别与一路输入信号相连。
LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY MAX4_1 ISPORT(A,B,C,D,S1,S2 : IN STD_LOGIC;Y : OUT STD_LOGIC);END ENTITY MAX4_1;ARCHITECTURE HF1 OF MAX4_1 ISSIGNAL SS : STD_LOGIC_VECTOR (0 TO 1);BEGINSS<=S2&S1;PROCESS(SS)BEGINCASE SS ISWHEN "00" => Y<=A;WHEN "01" => Y<=B;WHEN "10" => Y<=C;WHEN "11" => Y<=D;WHEN OTHERS => NULL;END CASE;END PROCESS;END HF1;3-6设计一个7人表决电路,参加表决者7人,同意为1,不同意为0,同意者过半则表决通过,绿指示灯亮;表决不通过则红指示灯亮。
设计思路:根据7人表决电路设计要求,7人中至少有4个通过才可以表决通过,故可以在程序中设置一个变量TEMP,使其在表决电路中遇1则加1,遇0则加0(设计中1表示通过,0表示不通过)。
当TEMP>=4时,表示表决通过,当TEMP<4时表决不通过。
LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY VOTE7 ISPORT (MEN:IN STD_LOGIC_VECTOR(6 DOWNTO 0);OUTPUT: OUT BIT);END VOTE7;ARCHITECTURE BEHA VE OF VOTE7 ISBEGINPROCESS(MEN)V ARIABLE TEMP: INTEGER RANGE 0 TO 7;BEGINTEMP:=0;FOR I IN 0 TO 6 LOOPIF(MEN(I)='1')THENTEMP:=TEMP+1;ELSETEMP:=TEMP;END IF;END LOOP;CASE TEMP ISWHEN 0 TO 3 =>OUTPUT<='0';WHEN 4 TO 7 =>OUTPUT<='1';END CASE ;END PROCESS;END BEHA VE;第四章4-6试写出4选1多路选择器VHDL描述。
VHDL习题解答

V H D L习题解答(共15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--VHDL 程序设计教程习题参考解答第一章习题参考答案1.什么是VHDLVHDL的实现有哪几种形态硬件描述语言(Hardware Description Language,HDL),顾名思义,是电子系统硬件行为描述、结构描述、数据流描述的语言。
VHDL语言的英文全名是Very High Speed Integrated Circuit Hardware Description Language,即超高速集成电路硬件描述语言。
2.简述VHDL的发展史。
1981年6月VHDL工作小组成立,提出了一个满足电子设计各种要求的能够作为工业标准的硬件描述语言。
1983年第三季度,由IBM公司、TI公司、Inter metrics公司签约,组成开发小组,工作任务是提出语言版本和开发软件环境。
1986年IEEE标准化组织开始工作,讨论VHDL语言标准,历时一年有余,于1987年12月通过标准审查,版本宣布实施,即IEEE STD 1076-1987。
1993年经过重新修订,发布版本,从而形成新的标准即IEEE STD 1076-1993。
2006年VHDL发布版本;2008年8月,VHDL 版本发布,解决了版本中发现的多个问题。
2009年1月,IEEE公布了VHDL 的标准版本,最新VHDL标准IEEE 1076-2008在2009年1月实施。
3. 详述VHDL设计IP模块的流程。
第1种设计形态,VHDL程序以IP模块的形态存在,VHDL-IP设计流程如图所示。
IP模块是与集成电路工艺无关的芯片设计方案,可以移植到不同的设计环境。
IP产品形态有规范,有IP包装规则和复用规则,是原生态的芯片硬件设计产品。
图 VHDL-IP设计流程4. 简答VHDL设计用FPGA实现的意义。
可编程器件FPGA具有容量大、密度高等特点,是科学实验、小批量生产、样机研制的载体。
VB第7章过程

6
第七章 过程
6.1 引言
1. 引例 2. 过程的定 义与使用
2)过程的定义与使用
定义过程
首先用户必须自定义一个子过程,这个子过 程通常可以完成一个特定的功能,该子过程以一 个名字来标识,可以被其他过程调用,其名字后 面的变量表称为形式参数。
用户自定义子过程与事件过程的区别是: 事件过程的名字是有一定规律的,且不能 改变,即控件名_事件名,而用户自定义 的过程名则由用户自己定义。事件过程的 参数是由系统根据事件给出,面用户自定 义的过程则是根据用户的需要。
辽宁科技大学 < Visual Basic 程序设计>教学课件③ 2007-2
10
第七章 过程
6.2 Sub过程
2)Sub过程的调用
1. Sub过程 的定义 2. Sub过程 的调用
格式:
Call 过程名 (实参列表) 或 过程名 实参列表
说明: ① 实参的个数、类型、顺序应与相应的形参保 持一致,子过程中如果没有形参,则调用中 也无实参。 ② 第2种调用方式与第1种相比,结果一样,只 是去掉Call和一对括号( )。
辽宁科技大学 < Visual Basic 程序设计>教学课件③ 2007-2
9
第七章 过程
6.2 Sub过程
1)Sub过程的定义
1. Sub过程 的定义 2. Sub过程 的调用
Sub过程说明 (1) 在VB中,Sub过程又称为子过程。 (2)子过程名、参数列表、语句块等与函数过程 的要求基本相同。 (3)子过程定义格式中“Sub过程名”和“End Sub”是必不可少的,子过程由“Sub”开始定义, 由End Sub结束,在这两者之间的程序便是能完 成某个功能的程序主体。 (4)在子过程中如果没有形参,调用时括号() 必须省略。
vb过程7.1-7.3

盐城工学院
Visual Basic 程序设计
7.1.2 通用过程
一般形式 ([参数列表 参数列表]) [ Private | Public ] Sub 过程名 ([参数列表]) 局部变量和常数声明] [局部变量和常数声明] 语句块 [ Exit Sub ] 语句块 End Sub
盐城工学院
Visual Basic 程序设计
盐城工学院
Visual Basic 程序设计
通用Sub Sub过程调用 7.3.2 通用Sub过程调用
Call语句 Call语句 <过程名 过程名> 实在参数表) Call <过程名> (实在参数表) • 实参是传送给被调用的Sub过程的变量、常 实参是传送给被调用的Sub过程的变量、 Sub过程的变量 数或表达式; 数或表达式; • 它的个数、类型和顺序,应与被调过程的形 它的个数、类型和顺序, 参相配; 参相配; • 有多个参数时,用逗号隔开; 有多个参数时,用逗号隔开; • 无参数时,括号可省 无参数时,
盐城工学院
Visual Basic 程序设计
7.1 Sub过程 过程
7.1.1 事件过程 –事件过程是为窗体或控件编写的代码 事件过程是为窗体或控件编写的代码 –由VB中的事件调用而执行 由VB中的事件调用而执行 –保存在窗体模块中 保存在窗体模块中 –分为窗体事件过程和控件事件过程 分为窗体事件过程 分为窗体事件过程和
盐城工学院
Visual Basic 程序设计
7.3 .2过程调用 过程调用
直接用过程名 实参1 [,实参2 过程名 [ 实参1 [,实参2 . . . ] ] • 不需要关键字Call 不需要关键字Call • 实参表不需要加括号
C13第7章 函数(3)

例7-27 汉诺塔问题。
设A座上有n个盘子。 座上有n个盘子。 如果n 如果n为1时,即A座上只有一个盘子,则把它直接移到C座上 座上只有一个盘子,则把它直接移到C 否则,用下面三步完成任务: 否则,用下面三步完成任务: 第一步, 第一步,把A座上的n-1个盘子先利用C座移动到B座上。 座上的n 个盘子先利用C座移动到B座上。 第二步, 第二步,把A座上仅有的第n个盘子移动到C座上。 座上仅有的第n个盘子移动到C座上。 第三步,把B座上的n-1个盘子利用A座移动到C座上。 第三步, 座上的n 个盘子利用A座移动到C座上。
分析upstairs(4)的运行情况
upstairs(4) upstairs(3) + upstairs(2) upstairs(2) + upstairs(1)
Hale Waihona Puke 程序的输出为void main( ) { printf(“4阶楼梯有 种不同的走法 阶楼梯有%d种不同的走法 阶楼梯有 种不同的走法\n”, upstairs(4));}
例7-24
例7-25
编写一个递归函数isPalin判断字符数组中的字符串是 编写一个递归函数isPalin判断字符数组中的字符串是 isPalin 否为回文,是则返回1 不是返回0 否为回文,是则返回1,不是返回0。
例7-27
汉诺塔问题。
古代有一个梵塔,塔内有3个标示为A 古代有一个梵塔,塔内有3个标示为A、B、C的座,A座 的座, 上有5个大小不等的盘子,大的在下面,小的在上面, 上有5个大小不等的盘子,大的在下面,小的在上面,如 图7-8所示。现要求把5个盘子从A座移动到C座,每次只允 所示。现要求把5个盘子从A座移动到C 许移动一个盘子,在移动过程中可以利用B座,但是3个座 许移动一个盘子,在移动过程中可以利用B 但是3 上要始终保持大盘在下面,小盘在上面。 上要始终保持大盘在下面,小盘在上面。
vb第7章过程jh

4. 过程的调用
Private Sub Command1_Click() Dim a As Integer Dim b As Integer a = Val(InputBox("请输入第一个加数")) b = Val(InputBox("请输入第二个加数")) Call Add(a, b) Call Add(100, 200) Add 400, 500 End Sub Private Sub Add(x As Integer, y As Integer) Dim z As Integer z=x+y Print x; "+"; y; "="; z End Sub
7.2 Sub子过程
(2)定义一行输出10个星号的过程:
Private Sub f2()
Dim i% For i=1 To 10 Print "*"; Next i
End Sub 过程可以有参数,也可以不带任何参数。没有参 数的过程称为无参过程。
7.2 Sub子过程
(3)定义一个过程,要完成的功能是:已知两 整型数据x、y,计算这两个数的和并输出。
7.2 Sub子过程
2. 建立Sub过程
(1)在代码窗口中直接定义
(2)利用“工具”菜单下的“添加过程”命令
定义
7.2 Sub子过程
3.过程定义举例
(1)定义一行输出n个星号的过程: Private Sub f1(n As Integer) Dim i% For i=1 To n Print "*"; Next i Print End Sub 该过程的名字是f1,参数只有一个,是一个整型变量n, 它限制了一行输出“*”的个数。
常用算法表示工具
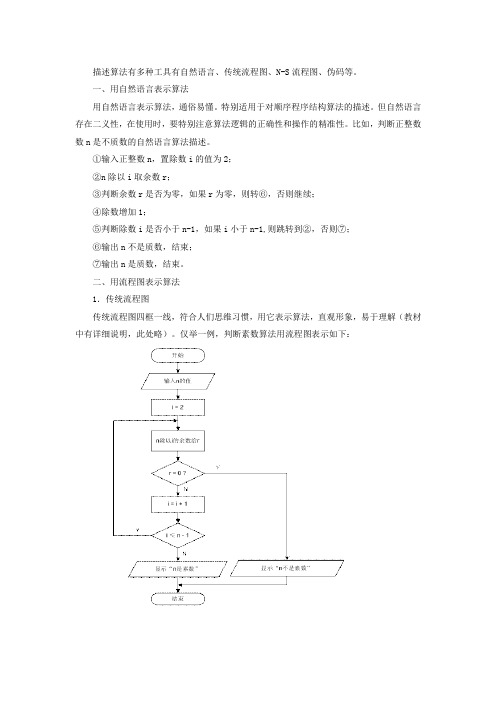
描述算法有多种工具有自然语言、传统流程图、N-S流程图、伪码等。
一、用自然语言表示算法用自然语言表示算法,通俗易懂。
特别适用于对顺序程序结构算法的描述。
但自然语言存在二义性,在使用时,要特别注意算法逻辑的正确性和操作的精准性。
比如,判断正整数数n是不质数的自然语言算法描述。
①输入正整数n,置除数i的值为2;②n除以i取余数r;③判断余数r是否为零,如果r为零,则转⑥,否则继续;④除数增加1;⑤判断除数i是否小于n-1,如果i小于n-1,则跳转到②,否则⑦;⑥输出n不是质数,结束;⑦输出n是质数,结束。
二、用流程图表示算法1.传统流程图传统流程图四框一线,符合人们思维习惯,用它表示算法,直观形象,易于理解(教材中有详细说明,此处略)。
仅举一例,判断素数算法用流程图表示如下:选择结构:当条件P成立时,则执行A语句,否则执行B语句。
当型循环结构:当条件P1成立时,则循环执行A语句。
直到型循环结构:循环执行A语句,直到条件P1成立为止。
三、伪代码表示算法用流程图表示算法,直观易懂,但画起来比较费劲,在设计一个算法时,可能要反复修改,而修改流程图是比较麻烦的,因此,流程图适用于表示一个算法,但在设计算法的过程中使用却不是很理想,尤其当算法比较复杂、需要反复修改时。
为设计算法时方便,就产生了伪代码。
伪代码是介于自然语言和机器语言之间用文字和符号来描述算法的,它不用图形符号,因此书写方便,格式紧凑,也比较好懂。
虽然伪代码不是一种实际的编程语言,但是在表达能力上类似于编程语言,同时避免了描述技术细节带来的麻烦,所以伪代码更适合描述算法,故被称为“算法语言”或“第一语言”。
伪代码便于向计算机语言算法(如C语言、Java)过渡。
伪代码的7个主要部分:(1) 算法名称(2)指令序列(3)输入/输出(4)分支选择(5)赋值(6)循环(7)算法结束1.算法名称两种表示算法的伪代码:过程(Procedure)函数(Function)过程和函数的区别是:过程是执行一系列的操作,不需要返回操作的结果,无返回数据;函数是执行一系列的操作后,要将操作的结果返回,有返回数据。
VB教程第7章教案

创建通用过程的方法
通用过程(Sub/Function)过程可以保存在两种模块中: 过程可以保存在两种模块中: 通用过程 过程可以保存在两种模块中 窗体模块(.frm)和标准模块(.bas) 和标准模块 窗体模块
(1) 在窗体模块中创建通用过程: 在窗体模块中创建通用过程:
可以在代码窗口中直接键入来创建Sub过程 过程 可以在代码窗口中直接键入来创建 选择"工具"菜单中的"添加过程"命令 选择"工具"菜单中的"添加过程"
程序运行结果
例7.1 主页
Sub过程的定义和调用 Sub过程的定义和调用
1. Sub过程定义格式: 过程定义格式: 过程定义格式
[Private|Public | Static] Sub 过程名 参数表 | 过程名([参数表 参数表]) 语句块 [Exit Sub] End Sub
2. 调用 调用Sub过程有以下两种方法: 过程有以下两种方法: 过程有以下两种方法
(1) 使用 使用Call语句.格式: 语句. 语句 格式: Call 过程名 [实参表]) 过程名([实参表] 直接使用过程名,格式: (2) 直接使用过程名,格式: 过程名[实参表] 过程名[实参表] 例如,调用名为SubCal的过程: 例如,调用名为SubCal的过程: SubCal的过程 Call SubCal(10) SubCal 10
主页
例7.2
计算5! 计算5! + 10!
因为计算5!和 都要用到阶乘 都要用到阶乘n! = × × × × 因为计算 和10!都要用到阶乘 (n!=1×2×3×…×n) 所以把计算n!编成 编成Sub过程 所以把计算 编成 过程 采用Print直接在窗体上输出结果,程序代码: 采用 直接在窗体上输出结果,程序代码: 直接在窗体上输出结果 Private Sub Form_Load() Show Dim y As Long, s As Long Call Jc(5, y) Private Sub Jc(n As Integer, t As Long) s=y Dim i As Integer Call Jc(10, y) t=1 s=s+y For i = 1 To n Print "5! + 10! ="; s t=t*i End Sub Next i 程序运行结果: 例 程序运行结果: 7.2 End Sub 5! + 10! = 3628920 注意参数n及 的调用情况 注意参数 及t的调用情况
vb第7章过程

……
Call fact End Sub
Private Sub Command1_Click(Index As Integer) Dim a As Integer, b As Integer, c As Integer, tot As Long n = Index Select Case n Sub fact(m As Integer, Case 0 a=5 total As Long) Call fact(a, tot) Dim i As Integer Label1.Caption = a & "!=" & tot total = 1 Case 1 For i = 1 To m a=6 total = total * i Call fact(a, tot) Next I Label1.Caption = a & "!=" & tot End Sub Case 2 a=8 Call fact(a, tot) Label1.Caption = a & "!=" & tot Case 3 a = 5: b = 6: c = 8 Call fact(a, tot) s = tot Call fact(b, tot) s = s + tot Call fact(c, tot) s = s + tot Label1.Caption = a & "!+" & b & "!+" & c & "!=" & s End Select
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fun ction与 proced ure 之 间 的 差 异 在 于 :funct ion的 返 回 值 永 远 只 有 一 个 ,而 procedure的 返 回 值 却 可 以 不 只 一 个 。 Function 所 有 的 参 数 都 是 input 信 号 , 而 procedure的参数却可以是input、output,甚至inout。Function的返回值置于 参数声明之外,而procedure的返回值是放在参数声明之内的。图7-1所示即为上 面所述的差异。
library ieee; use ieee.std_logic_1164.all;
entity V7_1 is port(a,b : in bit; c : out std_logic);
end V7_1;
architecture a of V7_1 is
function bit2std(Inb : bit ) return std_logic is
还 有 一 点 就 是 在 子 程 序 中 所 有 的 语 句 都 是 像 在 process中 的 sequential logic, 所 以 在 第 6章 中 所 使 用 到 的 语 法 都 能 在 子 程 序 中 使 用 。 现 在 让 我 们 看 看子程序的特性。
7-1 Function 的声明及使用
VHDL是一种数据类型检查非常严格的语言,比如说bit的数据类型包含’0’ 与’1’两种逻辑状态,而std_logic的数据类型包含了’0’与’1’及其他七种逻辑状 态,若是一个设计中有bit的数据类型及std_logic的数据类型如下:
signal a, b :bit; signal c, d :std_logic; 那你能做以下方式的指定吗? a <= c and d; 答案是否定的。也许你会认为是因为信号c和信号d的范围比较宽,信号a 的范围比较窄,那么反过来表示: C <= a and b; 总该可以了吧!结果答案仍是否定的。为什么呢?信号c的数据类型是 std_logic,总共有九种不同的逻辑状态。信号a和信号b的数据类型是bit,再怎 么样都不会超过std_logic的九种不同的逻辑状态啊!为什么答案还是否定的呢? 问题就在于这一节开始就提到的,VHDL是一种数据类型检查非常严格的语言,只 要是数据类型不同,即使是范围再宽也不能做指定,惟一的办法是将数据类型转 换成一样的,这便是function的功能之一。我们可以看看下面的例子:
声明: function SHIFT_LEFT( arg : signed; count :natural )
return signed; 内容: function SHIFT_LEFT ( arg : signed; count : natural )
return signed is begin
if (arg’length < 1) then return nas;
在看完function的声明及内容的描述,相信要如何写一个function已不是 难事,至于function该怎么调用呢?非常简单,只要看看以下例子就明白了。
O <= max (a, b); 这是延续前面求最大值的例子,只要将输入信号放在参数中,再将 function的返回值指定给输出信号就成了。
7-2 类型转换的 Function
Function所 有 的 参 数 都 是 input信 号 ,惟 一 的 输 出 值 就 是 此 function的 处 理 结果。Function的语法如下:
语法: function Function_Name(parameters:parameters ‘type;…)return
return_type is function 声明区; begin Function 结构区; end Function_Name; 实例: function max( Ina: integer; Inb: integer) return integer is
variable MaxValue : integer begin
if Ina > Inb then MaxValue := Ina;
else MaxValue := Inb;
End if; return MaxValue; end max; 上 面 的 例 子 是 一 个 比 较 两 个 输 入 值 , 并 返 回 其 中 较 大 值 的 function。在 function中 声 明 了 一 个 内 部 参 数 MaxValue,比 较 时 若 Ina大 于 Inb,会 将 信 号 Ina 的 值 指 定 给 MaxValue , 否 则 会 将 信 号 Inb 的 值 指 定 给 MaxValue 。 最 后 再 将 MaxValue的值当做返回值输出。 我们可以将上面的例子稍做修改,描述方式看起来会更简单。
constant NAS: signed ( 0 downto 1) := (others => ‘0’); 这是一个非常特殊的常数,其数据类型为signed,但注意其范围却是(0
downto 1),这就有些令人搞不清楚了。Downto的用法不是大的数值在前,小的 数值在后吗?为什么会有( 0 downto 1)呢?事实上真的没有,所以在此声明前特 别加了一段批注为null range array constants,这就符合在检查arg的长 度时,若其长度小于1要返回nas了。
return std_logic_vector
不 管 这 个 function 的 内 容 是 什 么 , 其 返 回 值 就 已 经 不 是 signed , 而 是 std_logic_vector了。为了让其返回值由std_logic_vector变成signed,需要将 此function以括号括起来,再在其前面加上signed,这么一来就能将原先数据类 型为std_logic_vector的输出编程signed了。另外function XSLL的第一个参数 其 数 据 类 型 为 std_logic_vector, 而 SHIFT_LEFT 的 第 一 个 参 数 其 数 据 类 型 为 signed , 可 使 用 相 同 的 方 法 , 在 function XSLL 的 第 一 个 参 数 前 加 上 std_logic_vector,将其数据类型由signed转成std_logic_vector。
在 上 面 的 例 子 中 ,我 们 用 了 两 个 语 句 来 做 func tion的 调 用 ,先 是 声 明 了 一 个 内部信号bitc,并 将 信 号 a与 信 号 b做 逻 辑 上 and的 结 果 指 定 给 信 号 bitc。接 着 再 调 用 function bit2std,将 信 号 bitc转 换 成 std_logic的 数 据 类 型 并 指 定 给 信 号 c。这样的写法并没有错,不过你可以再精简一点,就像下面的写法:
begin if Inb = '0' then return '0'; else return '1'; end if;
end function;
signal bitc : bit;
begin
bitc <= a and b; c <= bit2std(bitc);
end a; 在architecture之后声明了一个function bit2std,其只有一个数据类型为
c <= bit2std (a and b ); 因为a and b之后仍是一个数据类型为bit的信号,只不过少了一道手续罢了。 然而在看完7-1节中的function SHIFT_LEFT后,不知你是否会有个疑问,那 就是“是不是有一个function其名称为std_logic_vector或signed呢?”不然为 什 么 用 std_logic_vector(a)就 能 将 原 先 不 是 std_logic_vector的 信 号 a转 变 成 数 据 类 型 为 std_logic_vector呢 ? 答 案 是 否 定 呢 。那 之 前 所 说 的 ”VHD L是 一 种 数 据 类型检查非常严格的语言”不就有些矛盾了吗?事实上并没有,我们先来看看下 面的64.all; use ieee.std_logic_unsigned.all; use ieee.numeric_std.all;
在看完判断arg长度的if语句之后,后面接着就是一个返回值的语句: return signed (XSLL (std_logic_vector(arg) , count )); 由 于 在 之 前 就 已 经 声 明 了 这 个 Function返 回 值 的 数 据 类 型 是 signed,因 此 我们要看看XSLL这个Function的返回值是什么,先看看它的声明。 function XSLL (arg: std_logic_vector; count: natural)
end if; return signed ( XSLL(std_logic_vector(arg),count)); end SHIFT_LEFT;
这 是 一 个 将 输 入 参 数 移 位 几 个 bit的 function,它 有 两 个 参 数 ,一 个 是 要 被 shift的 数 值 arg, 其 数 据 类 型 为 signed。 一 个 是 要 shift几 个 bit的 count, 其 数 据 类 型 为 natural。 Function一 开 始 会 检 查 arg的 长 度 , 若 是 长 度 小 于 1, 表 示其根本不存在,所以返回值是nas。Nas是在numeric_std的package body 内声明的一个常数,其内容为:
