Matlab(R2009a版)-第8讲 计算方法的MATLAB实现
#Matlab-第8讲 计算方法的MATLAB实现

14.05.2019
8.2.2 线性方程组求解中的变换
• 上三角变换 • U=triu(x)返回矩阵x的上三角部分; • U=triu(x,k)返回第k条对角线以上部分的元 素。
14.05.2019
11
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> triu(a) • ans = • • • 12 0 0 -3 3 3 -1 0 1
14.05.2019
20
Jacobi迭代法
14.05.2019
21
Jacobi.m
• function s=jacobi(a,b,x0,eps) • %jacobi迭代法皆线性方程组 • %a为系数矩阵,b为方程组ax=b中的右边的矩阵b, x0为迭代初值 • if nargin==3 • eps=1.0e-6; • elseif nargin<3 • error • return • end
14.05.2019
31
不动点迭代法
14.05.2019
32
staticiterate.m
• function s=staticiterate(x,eps) • %不动点迭代法解非线性方程组,x为迭代初值, eps为允许误差 • if nargin==1 • eps=1.0e-6; • elseif nargin<1 • error • return • end
14.05.2019
4
程序实例
• • • • • • • • • >> fzero('x^3-3*x-1',2) ans = 1.8794 >> fzero('x^3-3*x-1',[1,4]) ans = 1.8794 >> fzero('x^3-3*x-1',[2,4]) ??? Error using ==> fzero The function values at the interval endpoints must differ in sign.
如何使用MATLAB进行数值计算

如何使用MATLAB进行数值计算使用MATLAB进行数值计算一、引言数值计算是现代科学与工程领域中不可或缺的一部分,它能够解决许多实际问题,包括求解方程、优化问题和模拟实验等。
而MATLAB作为一种功能强大的数值计算软件,被广泛应用于各个领域。
本文将介绍如何使用MATLAB进行数值计算,并结合实例进行说明。
二、MATLAB基础首先,我们需要了解MATLAB的基本操作和语法,以便能够熟练运用。
MATLAB使用矩阵和数组来存储和处理数据,因此,熟悉矩阵和数组操作是非常重要的。
MATLAB中的矩阵和数组是通过方括号来定义的,例如:A = [1 2 3; 4 5 6; 7 8 9]表示一个3x3的矩阵A,其中每个元素由空格或分号隔开。
我们可以使用括号或索引来访问矩阵中的元素。
例如,要访问矩阵A的第二行第三列的元素,可以使用A(2,3)。
MATLAB提供了大量内置的数学函数,包括算术运算、三角函数、指数和对数函数等。
这些函数可以直接应用于矩阵和数组,简化了数值计算的过程。
三、方程求解方程求解是数值计算中的一个重要任务,MATLAB提供了多种方法来求解方程,包括代数方法和数值方法。
1. 代数方法对于一些简单的方程,例如一元一次方程或二次方程,可以直接使用MATLAB内置的解方程函数进行求解。
例如,对于一元一次方程ax + b = 0,可以使用solve函数来求解。
代码示例:syms x;eqn = a*x + b == 0;sol = solve(eqn, x);其中,syms x;指定x为符号变量,eqn为方程表达式,sol为方程的解。
2. 数值方法对于一些复杂的方程,无法用解析方法求解。
这时,可以使用数值方法来近似求解。
MATLAB提供了多种数值求解方法,包括二分法、牛顿法和割线法等。
这些方法可以通过迭代逼近的方式求解方程的根。
代码示例:f = @(x) x^2 - 4;x0 = 2;x = fzero(f, x0);其中,f为方程的表达式,x0为初始猜测值,x为方程的根。
Matlab(R2009a版)_MATLAB简述

结束迭代;否则,转(5);
(5)若k=n则令:X(0)X(k1),转(2)开始新的一轮迭代,
否则转(6), (6)构造新的迭代方向:
k
f ( X ) (k1) 2 f (X (转k) )(23)
并令k=k+1,
S (.k 1 ) f( X (k 1 ))kS (k )
4-4 共轭梯度法
例题:用MATLAB使用共轭梯度法求解无约束优化问题,已知:
(2)产生中间插入点并计算其函数值
x1a0.38(b2a),f1f(x1) x2a0.61(b8a),f2f(x2) (3)比较函数值 f1和 f 2,确定区间的取舍:
若 f1 f2 ,则新区间 a,ba,x2
令 bx2,x2x 1,f2f1 记 N0 0
若 f1 f2 ,则新区间 a,bx1,b
➢编辑已有的M文件:
从MATLAB命令窗口的Flie菜单中选择
Open M-file命令。
21
函数文件
函数文件是另一种形式的M文件,每一个函数文 件都定义一个函数。Matlab提供的标准函数大部分 是由函数文件定义的。
函数文件的基本结构 函数文件由function语句引导,其基本结构为: function 输出形参表 = 函数名(输入形参表) 注释说明部分 函数体语句 其中,以function开头的一行为引导行,表示该M 文件是一个函数文件。 当输出形参多于一个时,应该用方括号括起来。
>> syms x; >> f=sin(x)+3*x^2; >> g=diff(f,x)
13
符号表达式的替换
用给定的数据替换符号表达式中的指定的符号变量
subs(f,x,a) 用 a 替换字符函数 f 中的字符变量 x a 是可以是 数/数值变量/表达式 或 字符变量/表达式
MATLAB中的数学计算方法详解

MATLAB中的数学计算方法详解在科学研究和工程领域中,数学计算方法的应用是不可避免的。
MATLAB作为一种强大的数学工具,提供了丰富的数学函数和算法,为用户提供了便捷的数学计算方式。
本文将详细介绍MATLAB中常用的数学计算方法,包括数值计算、符号计算以及优化算法等。
一、数值计算方法数值计算是MATLAB中应用最广泛的数学计算方法之一。
它通过将数值代入数学模型,利用数值逼近的方式求得近似解。
MATLAB提供了各种数值计算函数,如插值、积分、微分等。
下面我们将介绍其中几种常用的数值计算方法。
1. 插值方法插值是一种通过已知数据点来估计未知数据点的方法。
在MATLAB中,可以使用interp1函数实现一维数据的插值。
该函数支持多种插值方法,例如线性插值、样条插值等。
用户只需提供已知的数据点和插值点,即可得到插值结果。
2. 数值积分方法数值积分是计算定积分近似值的方法。
在MATLAB中,可以使用quad函数来进行一维定积分计算。
该函数采用自适应的数值积分算法,能够适应不同类型的函数。
用户只需提供被积函数和积分区间,即可得到积分结果。
3. 数值微分方法数值微分是计算函数导数的方法。
在MATLAB中,可以使用diff函数对函数进行数值微分。
该函数可以计算一阶和二阶导数,还支持多点数值微分和符号数值微分。
通过数值微分,可以方便地求得函数在给定点的导数近似值。
二、符号计算方法符号计算是指在计算过程中处理符号表达式而不是数值。
MATLAB的Symbolic Math Toolbox提供了强大的符号计算功能,可以进行代数操作、求解方程、求导、积分等。
下面我们将介绍几种常用的符号计算方法。
1. 代数操作在MATLAB中,可以使用符号计算功能进行代数操作,如多项式求解、多项式展开、多项式化简等。
通过定义符号变量和符号表达式,可以进行各种代数计算,方便用户进行复杂的代数操作。
2. 方程求解MATLAB的符号计算工具箱提供了solve函数用于求解方程。
使用Matlab进行数值计算和数值方法

使用Matlab进行数值计算和数值方法近年来,数值计算和数值方法在科学研究和工程实践中的重要性日益凸显。
数值计算和数值方法作为一种通过计算机模拟和近似求解数学问题的手段,已经广泛应用于各个领域,如物理学、化学、工程学、经济学等。
而Matlab作为一种常用的科学计算软件,具有简单易学、功能强大、可扩展性强等优点,成为了数值计算和数值方法的首选工具。
一、Matlab的基本使用Matlab是一种基于矩阵运算的数学软件,它提供了丰富的数值计算函数库和直观的交互式编程环境,使得数值计算变得更加简单快捷。
在使用Matlab进行数值计算时,我们首先需要了解一些基本的概念和操作。
1. 数组和矩阵Matlab中最基本的数据结构是数组和矩阵。
数组是一种只有一个维度的数据结构,而矩阵则是二维的。
我们可以使用Matlab中的命令来创建和操作数组和矩阵,例如可以使用"zeros"来创建一个全零矩阵,使用"eye"来创建一个单位矩阵,使用"rand"来创建一个随机矩阵等。
2. 数值计算函数库Matlab提供了丰富的数值计算函数库,包括数值积分、微分方程求解、线性代数运算等。
这些函数库使得我们能够轻松地进行各种数值计算操作。
例如,我们可以使用"integral"来进行数值积分,使用"ode45"来求解常微分方程,使用"eig"来计算矩阵的特征值等。
3. 图形绘制除了数值计算,Matlab还提供了强大的图形绘制功能。
我们可以使用Matlab中的绘图函数来绘制各种图形,如曲线图、散点图、三维图等。
这样可以更直观地观察和分析数值计算的结果。
二、数值方法的应用数值方法是指通过数值计算的手段来近似求解数学问题的方法。
在实际科学研究和工程实践中,常常会遇到一些复杂的数学问题,无法直接通过解析的方式求出精确解。
这时候,数值方法便可以派上用场。
matlab第八讲数值计算

quad('sin(x)./x',0,1) %注意./ Warning: Divide by zero. In inlineeval at 13 In inline.subsref at 25 In quad at 62
ans =
0.9461
quad('sin(x)./x',eps,1) ans =
运行结果: p=
0.5057 1.1225 s=
R: [2x2 double] df: 3 normr: 0.0052
作业
1.求函数
1
y e 3 sin 3t
在[0,π]的零点
2. 求一元函数y=x2-2x-5极小值点
多元函数y=(x1-1)2+(x2-2)2极小值点
3.解方程组 1 1 1 6 0 4 1x 5
1 sin xdx
0x
matlab命令: x=eps:0.001:1; %eps表示什么? y=sin(x)./x; %注意./ trapz(x,y) ans =
0.9461
由于辛普森公式quad、科特斯公式quad8这二种方法依 据的积分法不同于梯形法,因此它们的语法就和 trapz 不 同;
fval = 2.6131e-010
[x,fval]=fminunc('x(1)^2+x(2)^2-x(1)*x(2)+2*x(1)-4*x(2)',[2,2])
x= 02
fval = -4
四、数值积分
梯形方法trapz 辛普森公式quad 科特斯公式quad8 精度依次提高
梯形方法
观察f(x)与x轴的交点,大致可以看出有四个穿越x轴的交点, 具体位置不是很清楚,所以希望图像能够局部放大,以便看 得更加清楚
在Matlab中实现数值计算与优化算法

在Matlab中实现数值计算与优化算法数值计算与优化算法在工程和科学领域中扮演着重要的角色。
而Matlab作为一种强大的数值计算和数据分析工具,提供了丰富的函数和工具箱,可以方便地实现各种数值计算和优化算法。
本文将介绍在Matlab中实现数值计算和优化算法的一些常用方法和技巧。
1. 数值计算基础在进行数值计算之前,首先需要了解一些数值计算的基本概念和方法。
Matlab 提供了丰富的数学函数,例如矩阵运算、符号计算等。
通过使用这些函数,我们可以进行矩阵运算、数值积分、微分、微分方程求解等操作。
2. 数值计算方法在实际的数值计算中,我们经常需要解决一些复杂的问题,例如求解非线性方程、最小化函数、解线性方程组等。
Matlab提供了多种数值计算方法,例如牛顿法、拟牛顿法、全局优化算法等。
这些方法可以帮助我们高效地解决各种数值计算问题。
3. 数值优化算法数值优化是指在给定约束条件下求解最优解的问题。
在实际应用中,数值优化算法经常被用于解决一些优化问题,例如最小二乘法、线性规划、非线性规划等。
Matlab提供了多个优化工具箱,例如Optimization Toolbox和Global Optimization Toolbox,可以帮助我们实现各种数值优化算法。
4. 遗传算法遗传算法是一种模拟自然选择和遗传机制的优化算法。
在遗传算法中,通过适应度评价、选择、交叉和变异等操作,逐步搜索解空间,最终找到最优解。
Matlab 提供了一个遗传算法优化工具箱,可以方便地实现遗传算法。
5. 粒子群优化算法粒子群优化算法是一种模拟鸟群觅食行为的优化算法。
在粒子群优化算法中,通过模拟粒子在解空间中的运动,寻找最优解。
Matlab提供了一个粒子群优化工具箱,可以方便地实现粒子群优化算法。
6. 约束优化算法约束优化是指在给定约束条件下求解最优解的问题。
在实际应用中,约束优化经常被用于解决一些复杂的问题,例如最小化函数、最大化函数、多目标优化等。
Matlab(R2009a版)_MATLAB简述课件

学习交流PPT
18
命令文件和函数文件的区别
➢命令文件没有输入参数,也不返回输出参数;函 数文件可以带输入参数,也可以返回输出参数。
➢命令文件对工作空间中的变量进行操作,文件中 所有命令的执行结果也返回工作空间中;函数文 件中定义的变量为局部变量,当函数文件执行完 毕时,这些变量也被清除。
➢在调用函数时,MATLAB用两个永久变量nargin和 nargout分别记录调用该函数时的输入实参和输出 实参的个数。只要在函数文件中包含这两个变量, 就可以准确地知道该函数文件被调用时的输入输出 参数个数,从而决定函数如何进行处理。
10
代数方程求解
solve(f,v):求方程关于指定自变量的解,f 可以是用字符串表示的方程、符号表达式或符号 方程; solve 也可解方程组(包含非线性); 得不到解析解时,给出数值解。
学习交流PPT
11
符号计算
syms x y z %建立符号变量 [x,y,z]=solve(2*x+3*y-z-2,8*x+2*y+3*z-
(t + y)/(b + y) + (b^2*t - 4*a*c)^(1/2)
学习交流PPT
16
>> f2=subs(f1,b,y) f2 =
(t + y)/(2*y) + (t*y^2 - 4*a*c)^(1/2) >> f3=subs(f2,t,2) f3 =
(y + 2)/(2*y) + (2*y^2 - 4*a*c)^(1/2) >> f4=subs(f3,y,3) f4 =
学习交流PPT
6
MATLAB数值计算教程

MATLAB数值计算教程第一章:MATLAB入门1.1 MATLAB简介MATLAB(Matrix Laboratory)是一款强大的数值计算软件,广泛用于工程、科学和金融领域。
它的特点是简单易用、高效快速,并且拥有丰富的工具箱和函数库。
1.2 MATLAB环境搭建要使用MATLAB进行数值计算,首先需要安装MATLAB软件,并进行必要的配置。
通过官方网站下载安装程序,根据提示进行安装即可。
安装完成后,打开MATLAB环境,即可开始使用。
1.3 MATLAB基本操作在MATLAB环境中,可以通过命令行窗口输入和执行命令,也可以使用脚本文件进行批量处理。
常用的基本操作包括变量赋值、算术运算、函数调用等。
例如,使用"="符号赋值变量,使用"+"、"-"、"*"、"/"等符号进行算术运算。
第二章:向量和矩阵操作2.1 向量操作在MATLAB中,向量是一种特殊的矩阵,可以通过一组有序的元素构成。
向量可以进行基本的算术运算,如加法、减法、乘法、除法,还可以进行向量的点积、叉积等操作。
可以使用内置函数和运算符来实现。
2.2 矩阵操作矩阵是MATLAB中最常用的数据结构之一,使用矩阵可以进行多个向量的组合和运算。
可以进行矩阵的加法、减法、乘法、除法等操作,也可以进行矩阵的转置、求逆、求特征值等操作。
MATLAB提供了大量的函数和工具箱来支持矩阵的操作。
第三章:数值计算方法3.1 数值积分数值积分是一种用数值方法计算定积分的方法。
在MATLAB 中,可以使用内置函数来进行数值积分,如trapz函数和quad函数。
也可以使用Simpson法则、复合辛普森法等方法实现数值积分。
3.2 数值微分数值微分是一种用数值方法计算导数的方法。
在MATLAB中,可以使用内置函数进行数值微分,如diff函数和gradient函数。
matlab第八讲教案

西南科技大学本科生课程备课教案计算机技术在安全工程中的应用---- Matlab入门及应用授课教师:徐中慧班级:专业:安全技术及工程第八章绘图课型:新授课教具:多媒体教学设备,matlab教学软件一、目标与要求掌握matlab中二维绘图、三维绘图、子图等相关图形绘制功能。
二、教学重点与难点本堂课教学的重点在于引导学生在编写matlab程序时能够熟练运用绘图的相关函数实现相应的功能。
三、教学方法本课程主要通过讲授法、演示法、练习法等相结合的方法来引导学生掌控本堂课的学习内容。
四、教学内容课后习题讲解(1)用switch/case,menu结构编写程序求解下列问题:提示用户输入入学时间是一年、二年、三年还是四年,输入数据是字符串。
根据输入数据决定期末考试的时间。
其中,一年级周一考试,二年级周二考试,三年级周三考试,四年级周四考试。
Input=menu('Enter a value for your grade',‘one year','two years','three years','four years'); switch In put case 1disp('Mo nday')case 2disp('Tuesday')case 3disp('Wed nesday')case 4disp('Thursday')end(2)编写程序,提示用户输入购买方糖的数量,输入数据是糖的块数。
计算购买方糖的费用。
价格确定方法是:1块=$0.75;2块=1.25; 3块=1.65。
当多于3块时,总费用=$1.65+$0.30*(购买数量-3)。
sugar =input( 'Enter a value for quantityof sugar\n');switch sugarcase 1fprintf( '%3.0f lump sugar costs $0.75\n' ,sugar)case 2fprintf( '%3.0f lump sugar cost $1.25\n' ,sugar)case 3fprintf( '%3.0f lump sugar cost $1.65\n' ,sugar) otherwiseoutput=1.65+0.3*(sugar-3);fprintf( '%3.0f lump sugars cost $%4.2f\n' ,sugar,output)end3)用 for 循环结构求矢量元素的和,已知矢量 x 等于x=[1 23 43 72 87 56 98 33]用函数 sum 检查计算结果,并用 while 重写一遍程序。
计算方法matlab

计算方法matlab计算方法matlab是一种非常有用的工具,可以用于解决各种计算问题,包括矩阵计算、符号运算、数值求解等。
在本文中,我们将分步骤阐述如何使用计算方法matlab进行计算。
1.安装matlab首先,你需要从官方网站上下载matlab,并安装到你的电脑中。
在安装过程中,你需要选择你的操作系统、硬件配置等信息。
安装完成后,你需要输入许可证号码才能使用matlab软件。
2.打开matlab在windows中,使用matlab可以直接在桌面上找到matlab的图标,双击即可打开软件。
在其他操作系统中,你可以在终端中输入matlab命令来打开软件。
3.使用matlab进行计算使用matlab进行计算的方法有很多种。
你可以使用matlab的命令行模式,直接在命令行中输入想要计算的式子,matlab会返回计算结果。
例如,输入"2+3",回车后,matlab会返回"5"这个结果。
你还可以使用matlab的脚本文件来进行计算。
脚本文件是可以存储若干行matlab命令的纯文本文件。
你可以打开一个脚本文件,把要计算的命令写到文件中,然后运行这个脚本文件,matlab会按照命令执行计算,并输出结果。
4.使用matlab进行矩阵计算matlab是一种非常强大的矩阵计算工具。
在matlab中,你可以使用矩阵运算符号"+"、"-"、"*"、"/"等来进行矩阵的加减乘除运算。
例如,你可以输入" A=[1 2;3 4]; B=[5 6;7 8]; C=A*B",将矩阵A和B相乘,matlab会返回结果矩阵C。
此外,matlab还提供了很多高级的矩阵计算函数,如行列式det()、逆矩阵inv()、特征值eig()、奇异值分解svd()等。
5.使用matlab进行符号计算除了数值计算,matlab还支持符号计算。
第八讲MATLAB符号计算

% 定义符号变量 % 定义数值变量
% 计算符号表达式值 % 计算数值表达式值
% 计算符号表达式值 % 计算数值表达式值
% 计算符号表达式值 % 计算数值表达式值
ans = 1/2*3^(1/2) ans = 0.8660 ans = 2*2^(1/2)
ans = 2.8284 ans =(3+2^(1/2))^(1/2) ans = 2.1010
(2)syms函数
syms函数的一般调用格式为:
syms var1 var2 … varn 函数定义符号变量var1,var2,…,varn等。用这 种格式定义符号变量时不要在变量名上加字符 分界符(‘),变量间用空格而不要用逗号分隔。
>> syms a b c d
❖ 符号计算的结果是符号或符号表达式,如果其 中的符号要用具体数值代替,可以用subs函数, 例如将A中的符号a以数值5代替,可以用
8.1 符号计算基础
MATLAB中符号计算函数是数值计算函数的重载, 符号计算工具箱采用的函数和数值计算的函数有一 部分同名,为得到准确的在线帮助,应该用 help sym/函数名 例如: help sym/inv
8.1.1 符号对象
1. 建立符号变量和符号常数 (1)sym函数
sym函数用来建立单个符号变量和符号表达式,例如, a=sym(‘a’) 建立符号变量a,此后,用户可以在表达式 中使用变量a进行各种运算。 >> rho = sym('(1+sqrt(5))/2')
8.3 符号积分
8.3.1不定积分
在MATLAB中,求不定积分的函数是int,其调 用格式为:int(f,x)
int 函数求函数 f 对变量 x 的不定积分。参数x可 以缺省,缺省原则与diff函数相同。
如何使用Matlab技术进行数值计算

如何使用Matlab技术进行数值计算概述:Matlab是一种强大的数值计算和数据分析工具,广泛应用于科学、工程和金融等领域。
本文将介绍一些基本的Matlab技术,以帮助读者了解如何使用Matlab进行数值计算。
一、矩阵运算Matlab最大的优势之一是其强大的矩阵运算功能。
通过建立和操作矩阵,可以进行向量运算、线性方程组求解、特征值和特征向量计算等。
例如,假设我们需要解决一个线性方程组Ax=b,其中A是一个3x3的已知系数矩阵,b是一个已知向量,x是未知向量。
我们可以使用Matlab的“\”运算符来求解:x = A \ b;除此之外,Matlab还提供了许多其他的矩阵运算函数,如矩阵乘法(*)、矩阵转置(')、求逆矩阵(inv(A))等。
二、绘图和数据可视化Matlab提供了丰富的绘图函数,可以帮助我们对数据进行可视化分析。
通过绘制线图、散点图、柱状图、等高线图等,我们可以更直观地理解数据的规律和趋势。
例如,我们可以使用Matlab的“plot”函数来绘制一个简单的二维线图:x = linspace(0, 2*pi, 100);y = sin(x);plot(x, y);此外,Matlab还支持自定义图形的样式、添加标题、轴标签和图例等。
通过适当的数据可视化,我们可以更好地理解和解释数据。
三、数值积分和微分在数学和工程领域,积分和微分是常见的数值计算问题。
Matlab提供了许多函数来计算数值积分和微分,如“quad”和“diff”。
例如,我们可以使用Matlab的“quad”函数来计算一个函数在给定区间上的数值积分:f = @(x) x^2 + 2*x + 1;integral = quad(f, 0, 1);类似地,我们可以使用“diff”函数来计算一个函数在给定点上的数值导数:f = @(x) exp(x);x = linspace(0, 1, 100);dx = diff(f(x))./diff(x);四、非线性方程求解非线性方程的求解在科学和工程中经常遇到。
Matlab(R2009a版)MATLAB绘图基础

2020/2/29
73
2020/2/29
74
程序实例
2020/2/29
5
2020/2/29
6
向量绘图实例
• >> t=0:0.1:10; • >> y=sin(t); • >> plot(y)
2020/2/29
7
2020/2/29
8
向量绘图实例
• >> t=1:1:10; • >> y=sin(t); • >> plot(y)
2020/2/29
MATLAB2009 从入门到精通
课程主要内容
• 第1章 MATLAB简介 • 第2章 数值运算 • 第3章 单元数组和结构 • 第4章 字符串 • 第5章 符号运算 • 第6章 MATLAB绘图基础 • 第7章 程序设计 • 第8章 计算方法的MATLAB实现 • 第9章 优化设计 • 第10章 SIMULINK仿真初探
• bar(x,y,width)设置条形的相对宽度和控制在一组内 条形的间距。默认值为0.8,如用户没指定x,则 同一组内的条形有很小的间距,若设置为1,则同 组的条形相互接触。
• bar(x,y,’color’)定义条形颜色。
2020/2/29
67
• bar(x,y,’style’)用style定义条形类型,可以取 值’group’或’stack’。其中’group’为默认的显 示模式,表示若y为n*m阶的矩阵,则bar显示n组, 每组有m个垂直条形的条形图。’stack’表示对矩 阵y的每一个行向量显示在一个图形中,条形的高 度为该行向量中的分量和。其中同一条图中的每 个分量用不同的颜色显示出来,从而可以显示每 个分量在向量中的分布。
如何通过MATLAB进行复杂计算

如何通过MATLAB进行复杂计算MATLAB是一个强大的科学计算软件,可用于许多不同的领域,包括工程、自然科学、数学和金融等。
由于其简单易用的界面和广泛的支持,MATLAB已成为许多工程师、科学家和学生的首选软件。
在本文中,将介绍如何使用MATLAB进行复杂计算。
1.了解MATLAB的基础知识在开始使用MATLAB之前,了解MATLAB的基本知识非常重要。
MATLAB可以用于数值计算和符号计算。
数值计算可以用于执行数学和科学计算,符号计算可以用于求解代数方程和微积分问题。
了解所需要的计算类型将有助于确定如何使用MATLAB。
2.使用MATLAB计算向量和矩阵MATLAB是为矩阵运算而设计的,因此可以轻松地执行向量和矩阵计算。
使用MATLAB进行向量或矩阵运算非常简单。
要创建向量,请在MATLAB命令窗口中输入要使用的向量,并按回车键。
例如,要创建长度为5的向量[1,2,3,4,5],只需在命令窗口中输入“[1,2,3,4,5]”并按回车键即可。
要创建矩阵,请在命令窗口中输入矩阵并按回车键。
矩阵的行数和列数用分号分隔。
例如,要创建一个3×3的矩阵,其中第一行为[1,2,3],第二行为[4,5,6],第三行为[7,8,9],请输入“[1,2,3; 4,5,6; 7,8,9]”并按回车键。
3.使用MATLAB执行基本操作MATLAB可以用于执行许多基本操作,例如加、减、乘、除等等。
要使用MATLAB执行这些基本操作,请输入相应的运算符并按回车键。
例如,要计算2 + 3,输入“2 + 3”并按回车键。
要计算2×3,输入“2 * 3”并按回车键。
4.使用MATLAB计算函数MATLAB内置了许多函数,可以轻松地执行各种计算。
要使用MATLAB内置函数,请输入函数名称及其参数,并按回车键。
例如,要计算sin(π/2),输入“sin(pi/2)”并按回车键。
您还可以使用MATLAB绘图函数来可视化计算结果。
最优化计算方法及其matlab程序实现

最优化计算方法及其matlab程序实现最优化计算是一种通过寻找最佳解决方案来解决问题的方法。
在许多实际问题中,我们希望找到使某个目标函数达到最大或最小值的变量取值。
最优化计算可以应用于各种领域,如工程、经济、物理等。
在最优化计算中,我们首先需要定义一个目标函数,它描述了我们要优化的问题。
目标函数可以是线性的也可以是非线性的,具体取决于问题的性质。
然后,我们需要确定变量的取值范围和约束条件。
最后,我们使用最优化算法来搜索最佳解。
常用的最优化算法包括梯度下降法、牛顿法、拟牛顿法等。
这些算法基于不同的原理和策略,在不同的问题中表现出不同的性能。
选择合适的最优化算法对于获得高效的求解结果非常重要。
接下来,我们将介绍如何使用Matlab编写程序来实现最优化计算方法。
Matlab是一种功能强大的数值计算和编程环境,它提供了丰富的工具箱和函数来支持最优化计算。
我们需要定义目标函数。
在Matlab中,我们可以使用函数句柄来表示目标函数。
例如,假设我们要最小化一个简单的二次函数f(x) = x^2,我们可以定义一个函数句柄如下:```matlabf = @(x) x^2;```然后,我们可以使用Matlab提供的最优化函数来搜索最佳解。
例如,使用fminsearch函数来实现梯度下降法:```matlabx0 = 1; % 初始值x = fminsearch(f, x0);```在上述代码中,x0是变量的初始值,fminsearch函数将根据梯度下降法来搜索最佳解,并将结果存储在变量x中。
除了梯度下降法,Matlab还提供了其他常用的最优化函数,如fminunc、fmincon等。
这些函数具有不同的功能和参数,可以根据具体的问题选择合适的函数来求解。
除了单变量最优化,Matlab还支持多变量最优化。
在多变量最优化中,目标函数和约束条件可以是多元函数。
我们可以使用Matlab 提供的向量和矩阵来表示多变量的取值和约束条件。
MATLAB计算方法与实现
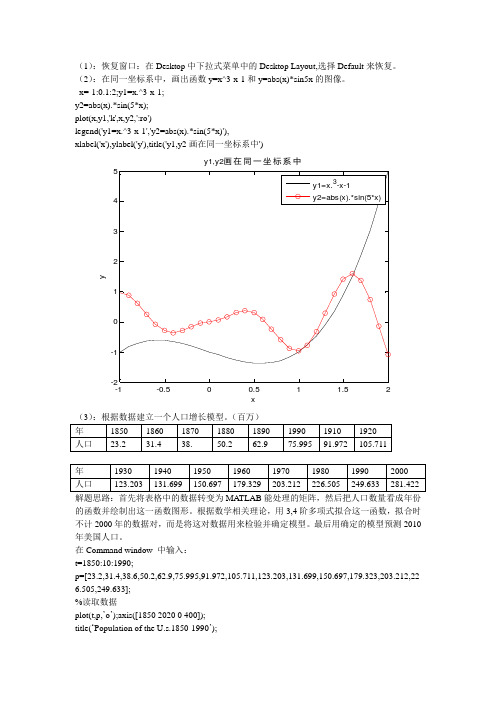
(1):恢复窗口:在Desktop 中下拉式菜单中的Desktop Layout,选择Default 来恢复。
(2):在同一坐标系中,画出函数y=x^3-x-1和y=abs(x)*sin5x 的图像。
x=-1:0.1:2;y1=x.^3-x-1; y2=abs(x).*sin(5*x); plot(x,y1,'k',x,y2,':ro')legend('y1=x.^3-x-1','y2=abs(x).*sin(5*x)'),xlabel('x'),ylabel('y'),title('y1,y2画在同一坐标系中')-1-0.500.51 1.52xyy1,y2画在同一坐标系中(3):根据数据建立一个人口增长模型。
(百万)的函数并绘制出这一函数图形。
根据数学相关理论,用3,4阶多项式拟合这一函数,拟合时不计2000年的数据对,而是将这对数据用来检验并确定模型。
最后用确定的模型预测2010年美国人口。
在Command window 中输入: t=1850:10:1990;p=[23.2,31.4,38.6,50.2,62.9,75.995,91.972,105.711,123.203,131.699,150.697,179.323,203.212,226.505,249.633]; %读取数据plot(t,p,’o ’);axis([1850 2020 0 400]); title(‘Population of the U.s.1850-1990’);ylabel(‘Millions ’);%绘制出数据的函数图形并加以修饰f1=polyfit(t,p,3);f2=polyfit(t,p,4);%对数据做3,4阶多项式拟合,结果分别为f1和f2 v=[polyval(f1,2000),polyval(f2,2000)];%计算当t=2000时多项式f1,f2的值 abs(v-251.422) %计算两个模型与2000年人口数的绝对误差。
Matlab中的数值计算实践技巧

Matlab中的数值计算实践技巧在数学和工程领域中,Matlab是一种广泛使用的数值计算软件。
它的灵活性和功能强大使得它成为许多科学家和工程师的首选工具。
然而,在实践中,由于Matlab提供了许多不同的功能和技术,有时候我们可能会在使用时遇到一些问题。
本文将介绍一些在Matlab中的数值计算实践中经常遇到的技巧和解决方案。
第一部分:数值计算的基础在开始介绍一些高级技巧之前,我们首先需要了解一些数值计算的基础知识。
数值计算是利用数值方法来近似解决数学问题的过程。
在Matlab中,我们可以使用一些内置的函数来执行一些基本的数值计算操作,比如加减乘除和求幂等。
另外,Matlab还提供了一些常用的数学函数,例如三角函数、指数函数和对数函数等。
这些函数在数值计算中非常重要,我们可以利用它们来进行各种复杂的计算。
第二部分:数值计算的优化技巧在进行复杂的数值计算时,性能往往是一个关键因素。
为了提高计算效率,我们可以采用一些优化技巧。
其中一个常用的技巧是向量化运算。
在Matlab中,向量化运算可以显著减少循环的数量,从而提高计算速度。
例如,如果我们需要对一个向量中的每个元素进行运算,我们可以使用向量化的方式,而不是使用循环来逐个处理。
另外一个常见的优化技巧是矩阵分解。
许多数值计算问题可以转化为矩阵分解的形式,例如线性方程组的求解和特征值问题的求解。
在Matlab中,我们可以使用一些内置的函数来实现这些分解,并且这些函数通常会采用一些高效的算法来提高计算速度。
第三部分:数值计算的问题与解决方案在进行数值计算时,我们可能会遇到一些问题。
在这一部分,我们将介绍一些常见的问题,并给出一些解决方案。
第一个问题是数值不稳定性。
由于计算机的有限精度,有些计算可能会引入一些误差。
当计算过程中的误差累积到一定程度时,可能会导致结果的不稳定性。
为了解决这个问题,我们可以使用一些数值稳定性较好的算法,或者对问题进行一些转化来避免误差的累积。
如何在MATLAB中进行数值计算

如何在MATLAB中进行数值计算MATLAB是一种用于数值计算和科学计算的程序设计语言和环境。
它提供了各种函数和工具箱,用于处理数值计算问题,包括线性代数、数值积分、数值微分、常微分方程求解、优化、插值等。
下面将介绍如何在MATLAB中进行数值计算的基本步骤和常用函数。
首先,启动MATLAB软件,创建一个新的脚本文件(.m文件),用于编写和保存MATLAB代码。
1.数值计算基础在MATLAB中进行数值计算的基本单位是矩阵和向量。
可以使用MATLAB提供的各种函数来创建和操作矩阵和向量。
例如,可以使用"zeros"函数创建一个全零的矩阵,使用"ones"函数创建一个全一的矩阵,使用"rand"函数生成一个随机矩阵。
2.线性代数计算MATLAB提供了丰富的线性代数函数,用于处理线性方程组、矩阵运算和特征值计算等问题。
例如,可以使用"inv"函数计算矩阵的逆,使用"det"函数计算矩阵的行列式,使用"eig"函数计算矩阵的特征值和特征向量。
3.数值积分MATLAB提供了多种数值积分方法,用于计算函数的定积分。
可以使用"quad"函数进行一维数值积分,使用"quad2d"函数进行二维数值积分,使用"quad3d"函数进行三维数值积分。
4.数值微分MATLAB提供了多种数值微分方法,用于计算函数的导数和偏导数。
可以使用"diff"函数计算函数的导数,使用"gradient"函数计算函数的梯度,使用"hessian"函数计算函数的Hessian矩阵。
5.常微分方程求解MATLAB提供了多种数值方法,用于求解常微分方程组。
可以使用"ode45"函数求解一阶常微分方程,使用"ode15s"函数求解刚性常微分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019/2/16 1
课程主要内容
• • • • • • • • • • 第1章 MATLAB简介 第2章 数值运算 第3章 单元数组和结构 计 第8章 计算方法的MATLAB实现 第9章 优化设计 第10章 SIMULINK仿真初探
16
2019/2/16
• 对角变换
• U=diag(x)返回矩阵x主对角线上的元素,返回结 果是一列向量形式; • U=diag(x,k)返回第k条对角线上的元素值。 • 当x为向量时生成矩阵。
2019/2/16
17
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> diag(a) • ans = • • • 12 3 1
12x1 3x2 3x3 15 18x1 3x2 x3 15 x x x 6 1 2 3
2019/2/16
9
程序实例
• • • • • • • • • • • • >> a=[12 -3 3;-18 3 -1;1 1 1]; >> b=[15;-15;6]; >> x1=a\b x1 = 1.0000 2.0000 3.0000 >> x2=inv(a)*b x2 = 1 2 3
2019/2/16
14
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> tril(a) • ans = • • • 12 0 0 -18 3 0 1 1 1
2019/2/16
15
程序实例
• • • • • • • • • • >> tril(a,1) ans = 12 -3 0 -18 3 -1 1 1 1 >> tril(a,-1) ans = 0 0 0 -18 0 0 1 1 0
2
2019/2/16
第8章 计算方法的MATLAB实现
• 随着计算机的迅速发展与广泛运用,在众多的领 域,科学计算方法的应用越来越广泛了,而 MATLAB在进行科学计算方面有着无与伦比的优 势。本章介绍MATLAB在计算方法中的运用。
2019/2/16
3
8.1 方程求根
• • • • roots见多项式求根;roots(多项式系数矩阵) fzero可求解非线性方程,它的格式为: fzero(‘function’,x0) 其中function为求解的方程,x0为估计的根,x0可 为标量或长度为2的向量,为向量时函数的两端的 值应该符号相反,此时求区间上的解。只能求解 x0附近的一个解。即使在某个区间内有多个解, 但是区间端点符号相同的话仍然出错。
2019/2/16
7
8.2.1 直接解法
• 关于线性方程组的直接解法有许多种,比如Gauss 消去法、列主元消去法、平方根法等。而在 MATLAB中,线性方程组的直接解法只需用符号 “/”或“\”就解决问题。还可以使用逆阵函数来求 解: x=inv(A)*B。
2019/2/16
8
程序实例
• 求解下列方程组
2019/2/16
5
程序实例
• • • • • • • • • >> fzero('x^2-3*x+2',0) ans = 1.0000 >> fzero('x^2-3*x+2',3) ans = 2.0000 >> fzero('x^2-3*x+2',[0,4]) ??? Error using ==> fzero The function values at the interval endpoints must differ in sign.
2019/2/16
18
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> diag(a,1) • ans = • -3 • -1 • >> diag(a,-1)
• ans = • -18 • 1
2019/2/16 19
8.2.3 迭代解法
• 迭代解法非常适用于求解大型稀疏系数矩阵的方 程组,在线性方程组常用的迭代解法主要有Jacobi 迭代法、Gauss-Seidel迭代法。
2019/2/16
12
程序实例
• • • • • • • • • • >> triu(a,1) ans = 0 -3 3 0 0 -1 0 0 0 >> triu(a,-1) ans = 12 -3 3 -18 3 -1 0 1 1
2019/2/16
13
• 下三角变换
• U=tril(x)返回矩阵x的下三角部分; • U=tril(x,k)返回第k条对角线以上下部分的元素。
2019/2/16
4
程序实例
• • • • • • • • • >> fzero('x^3-3*x-1',2) ans = 1.8794 >> fzero('x^3-3*x-1',[1,4]) ans = 1.8794 >> fzero('x^3-3*x-1',[2,4]) ??? Error using ==> fzero The function values at the interval endpoints must differ in sign.
10
2019/2/16
8.2.2 线性方程组求解中的变换
• 上三角变换
• U=triu(x)返回矩阵x的上三角部分; • U=triu(x,k)返回第k条对角线以上部分的元素。
2019/2/16
11
程序实例
• >> a=[12 -3 3;-18 3 -1;1 1 1]; • >> triu(a) • ans = • • • 12 0 0 -3 3 3 -1 0 1
2019/2/16
6
8.2 线性方程组数值解法
• 线性方程组的求解不仅在工程技术领域涉及到, 而且在其他的许多领域也经常碰到,因此这是一 个应用相当广泛的课题。 • 关于线性方程组的数值解法一般分为两类:一类 是直接法,就是在没有舍入误差的情况下,通过 有限步四则运算求得方程组准确解的方法。另一 类是迭代法,就是先给定一个解的初始值,然后 按一定的法则逐步求出解的各个更准确的近似值 的方法。
