射影平面
射影平面

区别起见,称平面上原有的点为有穷远点(通常点),记作P
约定1.1 (3) 按约定(1), (2)添加无穷远点之后,平面上全体 无穷远点构成一条直线,称为无穷远直线(理想直线),记作l∞
区别起见,称平面上原有的直线为有穷远直线(通常直线),l
给平行线添加交点!
§ 1.2 拓广平面
一、中心射影 二、无穷远元素
目标: 改造空间,使得中心射影成为双射 途径: 给平行直线添加交点 要求: 不破坏下列两个基本关系
两条相异直线确定惟一一个点(交点)
} 点与直线的关联关系
两个相异点确定惟一一条直线(连线)
§ 1.2 拓广平面
二、无穷远元素
约定1.1 (1) 在每一条直线上添加惟一一个点,此点不是该直 线上原有的点. 称为无穷远点(理想点),记作P∞
总结:在平面上添加无穷远元素之后,没有破坏点与直线 的关联关系,同时使得中心射影成为一一对应.
§ 1.2 拓广平面
理解约定1.1(1), (2)
1、对应平面上每一方向,有惟一无穷远点. 平行的直线交于同 一无穷远点;交于同一无穷远点的直线相互平行.
2、每一条通常直线上有且仅有一个无穷远点. 3、平面上添加的无穷远点个数=过一个通常点的直线数. 4、不平行的直线上的无穷远点不同. 因而,对于通常直线:
定理1.16 在拓广平面上, 点与直线的关联关系成立: (1) 两个相异的拓广点确定惟一一条拓广直线; (2) 两条相异的拓广直线确定惟一一个拓广点.
四、拓广直线、拓广平面的基本性质及模型 1、拓广直线(射影仿射直线)
(1) 拓广直线的封闭性 欧氏直线:向两个方向无限伸展 拓广直线:向两方前进最终都到达同一个无穷远点
[高等教育]射影平面
![[高等教育]射影平面](https://img.taocdn.com/s3/m/8b526b3c48d7c1c708a14594.png)
4、每一组平行平面有且仅有一条交线为无穷远直线;过同一 条无穷远直线的平面相互平行. 因而,对于通常平面:
平行
无穷远直线
两平面
交于惟一
不平行
有穷远直线
空间中任二平面必相交于唯一直线
§ 2.1 射影平面
三、射影平面
定义1.24 通常点和无穷远点统称拓广点; 添加无穷远点后的直线和无穷远直线统称为拓广直线(射影仿 射直线); 添加无穷远直线后的平面称为拓广平面(射影仿射平面).
§ 2.1 射影平面
(2) 拓广直线的拓扑模型
§ 2.1 射影平面
(3) 射影直线上点的分离关系
欧氏直线:一点区分直线为两个部分。 射影直线:一点不能区分直线为两个部分。 欧氏直线:两点确定直线上的一条线段。 射影直线:两点不能确定直线上的一条线段。
点偶A,B分离点偶C,D
点偶A,B不分离点偶C,D
平行
无穷远点
两直线 不平行 交于惟一 有穷远点
平面上任二直线总相交
5、空间中每一组平行直线交于惟一无穷远点. 6、任一直线与其平行平面交于惟一无穷远点.
§ 2.1 射影平面
理解约定1.1(3)
1、无穷远直线为无穷远点的轨迹. 无穷远直线上的点均为无穷 远点;平面上任何无穷远点均在无穷远直线上.
2、每一条通常直线与无穷远直线有且仅有一个交点为该直线 上的无穷远点.
§ 2.1 射影平面
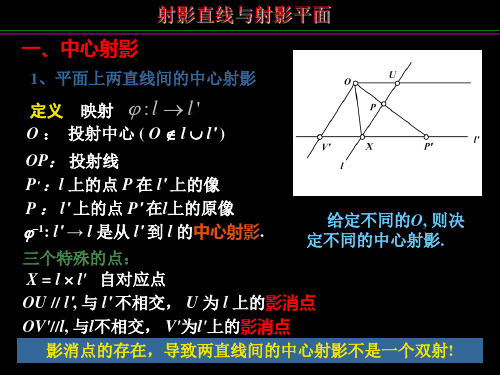
一、中心射影
2、平面到平面的中心射影
定义1.23 : '
O投射中心(O ')
OP 投射线 P' π 上的点P 在π'上的像 P π' 上的点P'在π上的像
第二章射影平面

第二章射影平面本章是在欧氏平面的基础上,通过引进无穷远元素的方法来建立射影平面。
然后又在欧氏平面上引进齐次坐标,并介绍了对偶原理。
§1 射影直线与射影平面1.1 中心射影与无穷远元素定义1.1 设两条直线a和a′在同一平面内,O是两直线外一点,A为直线a上任一点,A与O连线交直线a′于A′,如此得到的直线a与a′的对应叫做以O为射心的中心射影。
A′叫做A从O投射到a′上的对应点。
OA叫投射线,O叫投射中心,简称射心。
显然,A也叫A′从O投射到a上的对应点。
选取射心不同,就会得到不同的中心射影。
如果,a和a′相交于点C,则C是自对应点(二重点)。
在欧氏平面上,中心射影不是一一的。
如果a上点P使OP∥a′,则P没有对应点。
同样,在a′上也存在一点Q′,使OQ′∥a,则Q′的对应点也不存在。
点P和Q′叫影消点。
类似的,我们可以定义两平面间的中心射影。
而且,如果两平面有交线l,则交线l上的每一点都是自对应点(二重点),l叫自对应直线(二重直线)。
另外,在两平面间的中心射影下,不但存在影消点(该点与射心连线平行于另一平面),还存在影消线(影消点的轨迹)。
1为使中心射影成为一一对应,我们必须引进新的元素,从而将欧氏平面加以扩充。
于是,我们约定:约定1在平面内的一组平行直线上引进唯一一点叫无穷远点,此点在组中每一条直线上,记作:P∞。
平面上原有的点称为有穷远点。
由此可知,一组平行直线有且只有一个公共点,即无穷远点。
另外,一条直线a与同它平行的平面交于无穷远点。
这是因为过直线a作与已知平面相交的平面,则交线平行于直线a,即两条直线相交于无穷远点。
约定2平面内所有无穷远点的集合叫做无穷远直线,记作:l∞。
平面内原有的直线称为有穷远直线。
可以证明,一组平行平面相交于一条无穷远直线。
约定3空间里所有无穷远点的集合叫做无穷远平面,记作:π∞。
空间中原有平面叫有穷远平面。
定义1.2无穷远点,无穷远直线,无穷远平面统称为无穷远元素。
初学者如何理解射影平面

影平 面定义的理解 , 最后利用射 影平 面的模型来揭示射影平面的结 构, 想象它的形状 , 帮助初 学者更好地理解射影
平 面 的结 构 与 性 质 。
[ 关键词 ] 射影几何 ; 射影平 面; 解 理 [ 中图分类号 ] 0 8 . 15 1 [ 文献标识码 ] A [ 文章编号] 17 92 (07 ZO — 1 1 0 62— 0 1 2 0 ) J 1 00 — 3
因此本文从射影平面上的无穷远点无穷远直线射影直线的理解入手在理解这些抽象概念的同时即理解射影平面上元素的特点接着理解射影平面的定义最后给出射影平面的模型以帮助理解射影平面的形象
维普资讯
第2 7卷增刊第 1 期
20 07年 8月
河池学 院学报
J RN F HE HIUNI RS Y OU AL O C VE n
[ 作者简介] 李彩凤(9 3一) 女 , 17 , 广西合浦人 , 河池学 院数学系讲师, 主要研究方向为函数论 。
在射影几何的基本 内容中 , 初学者对 射影平面尤感兴趣 , 但又觉得其极为抽象 、 以理解 , 难 这主要是与我们 的直观认识不
一
致引起 的。因此 , 本文从射影平面上的无 穷远点 、 无穷远直 线 、 射影直 线的理解 入手 , 在理解这 些抽 象概念 的同时 , 即理 解
V J 7Sp l et yI u o 1 o. u p m n r s eN . 2 e a s
Au . 0 7 g20
初 学 者如 何 理解 射 影 平 面
李彩 凤
( 池学 院 河 数 学 系 ,广 西 宜州 5 60 4 3 0 J
[ 摘
要 ] 对射影平 面的理解是从局部到整体的扩展过程 。先从 无穷远元素 、 影直线的理解入手 , 射 再到射
射影平面中的直线、椭圆、抛物线和双曲线

射影平面中的直线、椭圆、抛物线和双曲线在射影平面中,直线是一条与无穷远直线有且仅有一个交点的闭曲线(如下图中的绿色、红色、青色、蓝色四条闭曲线,就分别是通过OA、OB、OC、OD的四条直线)。
“与无穷远直线有且只有一个交点”,是直线的拓扑不变性质。
射影平面无论怎样拓扑变形,直线的这一性质不会改变,所以,如果一条闭曲线不符合“与无穷远直线有且只有一个交点”的条件,就可以肯定它不是直线。
当然,这只是直线的必要条件,并不是直线的充分条件。
一条闭曲线,单单符合这一条件,还不能肯定它一定是直线。
直线还必须满足一定的方程。
一条直线,可以通过射影变换(注意:射影变换与拓扑变形不是一回事),变成另一条直线。
一条直线,也可以通过射影变换,变成无穷远直线。
在射影平面中,椭圆是一条与无穷远直线没有一个交点的闭曲线(如下图中的黄色闭曲线),抛物线是一条与无穷远直线有一个切点的闭曲线(如下图中的橙色闭曲线),双曲线是一条与无穷远直线有两个交点的闭曲线(如下图中的紫色闭曲线)。
“与无穷远直线没有交点”,是椭圆的拓扑不变性质;“与无穷远直线有一个切点”,是抛物线的拓扑不变性质;“与无穷远直线有两个交点”,是双曲线的拓扑不变性质。
射影平面无论怎样拓扑变形,这些性质都不会改变,所以,如果一条闭曲线不符合这样的条件,就可以肯定它不是椭圆、抛物线或双曲线。
当然,这只是椭圆、抛物线和双曲线的必要条件,并不是椭圆、抛物线和双曲线的充分条件。
一条闭曲线,单单符合这些条件,还不能肯定它一定是椭圆、抛物线和双曲线。
椭圆、抛物线和双曲线还必须满足一定的方程。
通过射影变换,椭圆可以变成抛物线,抛物线可以变成双曲线,双曲线可以变成椭圆。
在射影变换下,任何两条二次曲线(椭圆、抛物线或双曲线),都可以互相变来变去。
但是,二次曲线(椭圆、抛物线或双曲线),不可能通过射影变换,变成直线。
直线也不可能通过射影变换,变成二次曲线(椭圆、抛物线或双曲线)。
167;13射影平面

图形Σ
作对偶变换
图形Σ'
互为对偶图形
§ 1.4 平面对偶原则
一、平面对偶原则
2. 基本对偶图形举例
(1) 点
(1)' 直线
(2) 点列(共线点集) l(P)
(2)' 线束(共点线集)
L( p)
(3) 点场(共面点集)
(3)' 线场(共面线集)
(4) 简单n点形:n个点(其中无 三点共线)及其两两顺次连线 构成的图形.
§ 1.3 射影平面
一、实射影平面(二维实射影空间) 二、实射影平面的模型 三、射影坐标变换 四、实射影直线(一维实射影空间)
§ 1.3 射影平面
五、复射影平面、实-复射影平面
实射影平面
三维实向量类: RP2 , (RP2 )*
复射影平面
三维复向量类: CP2 , (CP2 )*
实-复射影平面
将实射影平面嵌入到复射影平面中(作为 其子空间),即带有虚元素的实射影平面
Desargues定理画图过程演示
提示:从现在起,画图要预先设计、思考,否则天大的 纸也摆不下一张图!真尴尬耶!
§ 1.5 Desargues定理
今日作业 P.35: 1(图1.19, 1.22); 4; 5
祝同学们国庆节快乐!
The Class is over. Goodbye!
课件作者:南师大数科院周兴和
若两个三点形对应边的交点共线, 则称这对对应三点形具有透视轴, 透视轴也称为Desargues 线.
有趣 请问你是怎样画出这两个图的?
问题 存在透视中心 存在透视轴?
画图过程演示
§ 1.5 Desargues定理
一、Desargues定理 1、两个三点形的对应关系
射影几何三大入门定理

射影几何三大入门定理1. 定理一:射影平面的基本性质射影几何是研究投影关系的一门数学分支,它研究的对象是射影空间和射影平面。
在射影几何中,有三个重要的入门定理,这些定理对于理解和应用射影几何具有重要意义。
首先,我们来讨论第一个定理:射影平面的基本性质。
1.1 射影平面的定义在介绍定理之前,我们需要先了解什么是射影平面。
射影平面是指一个由点和直线构成的集合,满足以下条件:•任意两条直线有且只有一个交点;•任意两个不同的点确定一条直线。
1.2 定理一的表述定理一指出,在射影平面中,存在以下基本性质:•任意两个不同的直线交于唯一一点;•任意两个不同的点确定唯一一条直线。
1.3 定理一的证明第一个性质:任意两个不同的直线交于唯一一点假设在射影平面中存在两个不同的直线L1和L2,在L1上取两个不同的点A和B,在L2上取两个不同的点C和D。
我们需要证明线段AB和CD的交点是唯一的。
根据射影平面的定义,任意两个不同的点确定唯一一条直线,所以线段AB确定了一条直线L3,线段CD也确定了一条直线L4。
由于L3和L4都与L1和L2相交,所以它们一定有一个公共交点P。
假设还存在另一个不同于P的交点Q,那么根据射影平面的定义,线段PQ也应该与直线L1相交。
但是根据前面的假设,A、B、C、D四个点在射影平面中是不共面的,所以直线PQ与直线L1没有交点。
这与假设矛盾,因此我们得出结论:任意两个不同的直线在射影平面中交于唯一一点。
第二个性质:任意两个不同的点确定唯一一条直线假设在射影平面中存在两个不同的点A和B,在A上取两条不同的直线L1和L2,在B上取两条不同的直线L3和L4。
我们需要证明直线AB和CD(其中C为L1与L3的交点,D为L2与L4的交点)是唯一相交的。
根据射影平面的定义,任意两条直线有且只有一个交点,所以线段AB与L1和L2分别有唯一的交点C和D。
假设还存在另一条直线EF与A、B两点相交,并且E和F分别是直线EF与L1和L2的交点。
射影平面六讲一一第一讲

以下我們將 ξ1 和 ξ2 固定, 而令 ξ0 變 化。 以 (ξ0, ξ1, ξ2) 為齊次座標的點 P 的非齊 次座標為 (ξ1/ξ0, ξ2/ξ0)。 設 P0 為以 (ξ1, ξ2) 為非齊次座標的點。 連接原點和 P0 成一直線 l。 對一切 ξ0, P 點始終在直線 l 上。 當 ξ0 取負值, 且其絕對值很大時, P 很接近原點, 但和 P0 在原點的異側。 當 ξ0 取負值時, P 仍維持和 P0 在原點的異側, 而且隨 |ξ0| 變 小而漸行漸遠。 當它變成 0 時, 點 P 沒有定 義。 當它變成正數時, 它又有定義了, 成為和 P0 在原點同側的 l 上的一點。 ξ0 取很小的 正值 時, P 離原點很遠。 當 ξ0 增加到 1 時, P 便和 P0 重合。 當 ξ0 增加超過 1 時, P 點逐漸靠近原點。 這些想法提示我們在直線 l 上增加一點, 以(0, ξ1, ξ2) 為其齊次座標。
現在設想 l 為 G 上的一定線, Q 為 G 上 l 外之一定點, P 為在 l 上的一動點。 當 P 不斷向前移動 (即與 Poncelet 在窗之異側向 遠離窗之方向移動) 時, σP 從直線 j 的下方 向上移動。 當 P 漸行漸遠之時, 直線 QP 漸 漸接近於平行的位置, 而點 σP 也漸漸從直 線 j 的下方接近於j。 若令 P 向後移動, 則 σP 從直線 j 的上方向下移動。 當 P 漸行漸 遠之時, 直線 QP 和點 σP 的狀況也和上文 所述的相當類似。 這種考慮使 Poncelet 想到 在平面上添加一些 無限遠點 (points at infinity), 作為平行線的交點, 便可把平行線的 觀念統合在不平行線的觀念以內。 添加無限 遠點後, 歐氏平面便變成了 射影平面 (projective plane)。 以下我們不用 Poncelet 的
2.1射影平面

§ 1 射影直线和射影平面
定义1.5 如果把仿射直线上的非无穷远点与 无穷远点同等看待而不加区分那么这条直线就 叫做射影直线
圆
墨比乌斯带
定义1.6 在仿射平面上,如果对于普通元素和 无穷远元素不加区分,即可得到射影平面
§ 1 射影直线和射影平面
五、射影直线、射影平面的基本性质
1、射影直线
欧氏直线:一点区分直线为两个部分。
§ 1 射影直线和射影平面
1.4 德萨格(Desargues)定理 应用举例
例2 证明:三角行的三中线点共.
§ 1 射影直线和射影平面
1.4 德萨格(Desargues)定理
今 天 作 业
P28 : 5
O投射中心(O l l ')
OP 投射线 P' l 上的点P在l'上的像 P l' 上的点P'在l上的像 因此 ,φ–1: l' → l是 l' 到 l 的中心射影 三个特殊的点: X=l×l' 自对应点(不变点) OU与l'不相交, U为l上的影消点 OV'与l不相交, V'为l'上的影消点 影消点的存在,导致两直线间的中心射影不是一个一一对应
§ 1 射影直线和射影平面
1.4 德萨格定理
德萨格(Desargues)定理
如果两个三点形对应顶点的连线交于 一点,则对边的交点在一直线上.
A
X
C
Y
C
B
A
B Z
O
A
X
C
B Z Y
C
B
A
o
L
A
l
L
A
X
C
§ 13 射影平面

(1). 点x在直线u上 x在u上. (1)'. 直线u过点x u过x.
(对 uj xj 0两边取共轭即得结论)
(2). 虚点x在实直线u上 x在 (2)'. 虚直线u过实点x u过x. u上.
(3). 实直线上的点或为实点或 为成对出现的共轭虚点.
(3)' . 过实点的直线或为实直线 或为成对出现的共轭虚直线.
u3 0.
(3) 无穷远直线上的点 (A, B,0)
Au1 Bu2 0.
(4)-(8) Thm. 1.5-Thm. 1.9
(1)' 直线 [A, B,C]
Ax1 Bx2 Cx3 0.
(2)' 无穷远直线 [0,0,1]
x3 0.
(3)' 过原点的直线 [A, B,0]
Ax1 Bx2 0.
§ 1.4 平面对偶原则
一、平面对偶原则 1、基本概念 2、对偶图形举例
3、作一图形的对偶图形 例 1 作下列图形的对偶图形(P.32,例1.12).
翻译
点 P,Q
2个 直线 p, q
2条
直线 l, a,b,c, d
5条 点 L, A, B,C, D
5个
关联关系 (1) P, Q在l上;
关联关系 (1) ' p, q过点L;
(2). 对偶运算 过一点作一直线
在一直线上取一点
(3). 对偶变换 互换对偶元素地位、作对偶运算
(4). 对偶图形 在射影平面上,设已知由点、直线及其关联关系
构成的图形Σ,若将Σ中各元素改为其对偶元素、各运算改为其对 偶运算(即对Σ作对偶变换),则得到另一个图形Σ'. 称Σ、 Σ'为一对 对偶图形.
射影平面
定义 如果将通常的点与无穷远点不加区别,通常的直线与 无穷远直线不加区别,则仿射直线就叫射影直线,仿射平面 就叫射影平面。在射影直线上,通常的点和拓广点都叫点。
通常直线:两点确定直线上的一条线段。
射影直线:两点不能确定直线上的一条线段。
射影直线与射影平面
2、射影平面
(1) 射影平面的封闭性(从两个方面理解) (i) 任一直线划分通常平面为两个不同的区域 任一直线不能划分射影平面为两个不同的区域 (ii) 两条相交直线划分通常平面为四个不同的区域 两条相交直线划分射影平面为两个不同的区域
若两个三点形对应边的交点共线, 则称 这对对应三点形具有透视轴, 透视轴也 称为Desargues 线.
Desargues透视定理
2、Desargues透视定理
定理 (Desargues透视定理及其逆) 对于两个对应三点形, 存在 Desargues点存在Desargues线.
或者叙述如下:
迪沙格定理 如果两个三点形对应 顶点的连线交于一点,则对应边的 交点共线。
Desargues透视定理
(2)三点形 ABC 和 A'B'C' 共面 如图,设这个平面是 。
Desargues透视定理
此时,过 O 作一条异面直线 l ,然后在 l 上任取两点 S 和 S' 。
考虑三点形 SBC 和 S'B'C' ,则这两个三点形异面(否则,如 果它们共面,则这个平面必须是 ,于是 S, S' 就在 上,这 与 l 为异面直线矛盾)。
2射影平面

a1x1 a2 x2 a3x3 0, (a12 a22 0)
(1.3)
给出,并且任何一个这样的方程都对应着π上的一条直
线。
我们把无穷远点的几何轨迹称为无穷远直线,根据 无穷远点的齐次坐标的特点,无穷远直线可由方程
x3 0 来表示。
(1.4)
于是,射影平面上,任何方程
a1x1 a2 x2 a3x3 0,
x1, x2, x3的所有直线,故又称为点的线方程。经过定点
的所有直线称为线束。
射影平面
定义:一个具有线结构的集合(即规定了它 的哪些子集为线)称为一个射影平面,如果 存在从它中心直线把的保持结构的一一对 应. 注:这里所说的“保持线结构”,也就是
“保持 点线的关联关系”.
(1.5)
其中,a12 a22 a32 0 都是某条直线的方程。如果 a12 a22 0 ,则称为射影直线。如果 a1 a2 0 , 则 (1.5)表示无穷远直线。方程(1.5)称为直线的普通方程。
在射影平面上,任何两条直线都相交,这是因为线性方程
组
ba11xx11
a2 x2 b2 x2
a3x3 b3x3
0, 0.
(1.6)
总有非零解。特别地,两条平行直线交于无穷远点 。
对于射影直线而言,如果它的方程为(1.5),则无穷远
点 a2 ,a1,0 在此射影直线上,且是此射影直线上的唯一
的无穷远点。实际上(a2 ) : a1 表示仿射坐标中的直线 a1x a2 y a3 0 的方向,因而直观上,射影直线就是欧 氏平面上的直线添加上此直线的方向所得到的。
表示同一直线当且仅当存在非零实数λ,使
(a1, a2 , a3 ) b1,b2 ,b3 . 于是我们可以用直线方程的
第二章射影平面
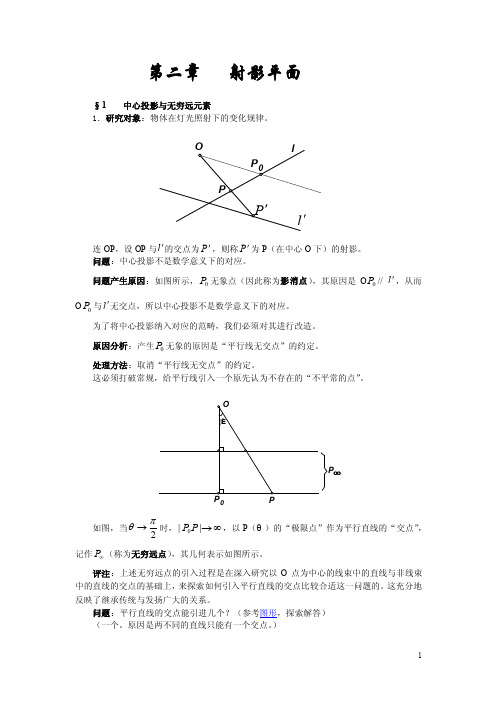
第二章 射影平面§1 中心投影与无穷远元素1.研究对象:物体在灯光照射下的变化规律。
连OP ,设OP 与l '的交点为P ',则称P '为P (在中心O 下)的射影。
问题:中心投影不是数学意义下的对应。
问题产生原因:如图所示,0P 无象点(因此称为影消点),其原因是O 0P // l ',从而O 0P 与l '无交点,所以中心投影不是数学意义下的对应。
为了将中心投影纳入对应的范畴,我们必须对其进行改造。
原因分析:产生0P 无象的原因是“平行线无交点”的约定。
处理方法:取消“平行线无交点”的约定。
这必须打破常规,给平行线引入一个原先认为不存在的“不平常的点”。
如图,当2πθ→时,∞→||0P P ,以P (θ)的“极限点”作为平行直线的“交点”,记作∞P (称为无穷远点),其几何表示如图所示。
评注:上述无穷远点的引入过程是在深入研究以O 点为中心的线束中的直线与非线束中的直线的交点的基础上,来探索如何引入平行直线的交点比较合适这一问题的。
这充分地反映了继承传统与发扬广大的关系。
问题:平行直线的交点能引进几个?(参考图形,探索解答) (一个。
原因是两不同的直线只能有一个交点。
)o o无穷远点的引进是一个创新的过程,需要大胆的想象力。
而直线上的无穷远点只能引进一个则是原来的原则“两直线只有一个交点”的要求所至。
无穷远点根据研究需要而引入,又是原系统的规则的延伸,从而“无穷远点”又受到原系统的规则的“约束”,这充分体现了继承与发展的关系。
对照一维中心投影,请自行考虑二维中心投影的相应问题。
2. 无穷远元素规定一 在平面内对任何一组平行线引入唯一一点叫做无穷远点(记作∞P )与之对应,此点在组中每一直线上而不在组外的任何直线上。
规定二 平面内无穷远点的集合是一条直线,叫做无穷远直线,记作∞l 。
规定三 空间里所有无穷远点的集合是一个平面,叫做无穷远平面,记作∞π。
有限域上的射影平面

有限域上的射影平面史逸(南京师范大学数学与计算机科学学院2004级1班)摘要:定义有限射影平面,利用射影几何与群论的方法推导有限射影平面上的一系列性质, 并由此证明存在任意阶的多项式方程在Z p上无解。
关键词:有限域;射影平面;射影变换;群在定义射影平面时,我们约定点与直线为一对无定义的基本元素,在点的集合与直线的集合之间有一个关系称为关联关系。
对所谓的关联关系,给出如下约定:约定1. 1.当点P与直线l 有关联关系时,下列说法等价:点P与直线l 相关联;直线l 与点P相关联;点P在直线l 上。
直线l 通过点P。
2. 当点P与直线l 没有关联关系时,下列说法等价:点P与直线l 不关联;直线l 与点P不关联;点P不在直线l 上。
直线l 不通过点P。
定义1.设集合π为两个不交的非空集合P与L的并集。
P的元素称为π的点。
L的元素称为π的直线。
而且,在点与直线之间有一个关系称为关联关系,满足下述公理:公理P 存在一对双射φ:P →FP²,ψ:L →(FP²)* ,对于任意的P∈P和任意的l ∈L,若φ(P)= x ,ψ(l )= u ,则点P与直线l 相关联←→u1x1 + u2x2 + u3x3= 0 ,这里F为Z p。
称π为一以P为点集,L为直线集的一个有限域F上的射影平面或称为有限域F上的二维射影空间,简称有限射影平面,记作π=(P ,L)。
满足公理P的一对双射(φ,ψ)称为有限域F上的射影平面上的一个射影坐标映射,并分别称φ和ψ为点坐标映射和线坐标映射,点和直线的坐标映射像分别称为点和直线的坐标。
对于固定的有限域F,任意有限射影平面都同构与有限域F上的射影平面的算术模型,即πF =(FP²,(FP²)*),则任意两有限域F上的射影平面都相互同构,下面我们就以πF =(FP²,(FP²)*)为具体模型阐述有限域F上的射影平面的性质。
我们约定F为整数集Z模p(p为素数)同余类所生成的有限域Z p ,射影平面为πF =(FP²,(FP²)*)。
射影平面知识点总结

射影平面知识点总结射影平面是射影几何的基本概念,它是在射影空间的基础上引入的一种几何结构。
射影平面是一种具有射影性质的空间,它拥有特殊的性质和结构,因此在几何学和代数学中有着重要的应用。
本文将对射影平面的基本知识点进行介绍和总结,包括射影平面的定义、性质、构造方法以及相关定理和定律等内容。
一、射影平面的定义射影平面是指一个由点、直线和射线组成的空间结构,它是由二维实射影空间定义的。
在射影平面中,任意两条不共线的直线都有且只有一个交点,这是射影平面的基本性质之一。
另外,射影平面满足幂零定理,即任意两条相交的直线在其交点处的切线都是无穷远的。
在代数几何中,射影平面可以通过将欧几里德平面上的点扩充为射线上的点,从而得到一个射影平面。
这样的扩充是通过引入无穷远点的方式来实现的,因此射影平面上的点包括有限远的点和无穷远的点。
二、射影平面的性质1. 射影平面是紧致的。
这意味着射影平面上的任意闭曲线都可以用有限个闭曲线来覆盖。
2. 射影平面是连通的。
任意两点之间都存在一条直线。
3. 射影平面是欧几里德平面的紧致化,因此它具有相同的拓扑性质。
4. 射影平面上的直线都是闭曲线。
这意味着任意两条直线的交点都是封闭的。
5. 射影平面是一种紧致性空间,可以用带权和的方式来描述其拓扑结构。
三、射影平面的构造射影平面可以通过多种方式进行构造,其中最常见的方法包括射影坐标系的引入、齐次坐标系的应用以及仿射几何的推广等。
以下是射影平面的几种常见构造方法:1. 射影坐标系的引入。
通过引入射影坐标系,可以将欧几里德平面上的点扩充为射线上的点,从而得到一个射影平面。
2. 齐次坐标系的应用。
齐次坐标系是射影几何中常用的坐标系,它可以用于描述射影空间中的点、直线和射线等基本几何元素。
3. 仿射几何的推广。
通过将仿射几何的概念推广到射影几何中,可以得到一个射影平面的构造方法。
四、射影平面的相关定理和定律1. 帕斯卡定理。
帕斯卡定理是射影几何中的重要定理,它描述了射影平面上的六点共线的条件。
有限射影平面

1、2、有限射影平面我们先看一个有趣的问题:有一位好客的女主人打算邀请7位朋友来家里聚会,每次聚会她只想邀请3位宾客,但是她希望其中的任何两位朋友都恰好在一次聚会上见面,那么她应该怎样安排呢?这样的安排是否存在?我们简单试一下就会发现,任何两次聚会中必须有一位相同的朋友被邀请到.换句话说,如果第一次邀请A、B、C,第二次邀请D、E、F,这样安排是行不通的.下面我们给出一种可行的安排方案:第一次邀请A、B、C;第二次,邀请A、D、E;第三次,邀请A、F、G;第四次,邀请B、D、F;第五次,邀请B、E、G;第六次,邀请C、D、G;第七次,邀请C、E、F.我们可以用下面的一个图形来表示这个邀请方案:上面的图形是非常有名的!它是由数学家G.Fano在1892年提出的,实际上,它就是定义在二元域上的二阶射影平面PG(2,2).射影几何的研究始自法国数学家G.Desargues的1639年的著作,但是在当时并没有引起人们的重视.一直到两个世纪后,由于法国著名数学家J.V.Poncelet著作(1822)的发表,射影几何才开始受到数学界的重视,更使其成为19世纪几何学研究的重点.射影几何学在古典几何学中是最基础的、最广泛的而且是最自由的.它是公理化数学的典型之一例,也可以说它是现代数学的先驱.定义射影平面(P,L)是由点集合P和线集合L构成的,它是满足下面条件的平面1、任意两个点决定一条直线,每条直线上至少有两个点;2、任意两条直线都相交;3、存在4点集,使其中的任意三个点不在一条直线上.注意,定义中的条件3是为了排除射影平面只有一条直线的平凡情形的.定理4.1设(P,L)为射影平面,其中点集合P含v个点,线集合L有b条线,则存在2一整数k 2,使v b k k 1,而且每条直线上有k 1个点,过每个点有k 1条线.我们称上述定理中的k为射影平面(P,L)的阶数.在有限射影几何中一个非常重要的核心问题是:对给定的自然数k,k阶射影平面是否存在?如果存在,则有几种类型?定理4.22阶射影平面是唯一的.证明由于是2阶射影平面,所以只能有7个点,不妨设点集合为{0,1,2,3,4,5,6}.因为过点1有三条直线,不妨设它们为{1,2,4},{1,3,0},{1,6,5}.又过点2也有三条直线,而其中的一条已为{1,2,4},所以另外的两条直线可设为{2,3,5}和{2,0,6}.由射影平面的定义,点4和点0应该决定一条直线,而且其上的另外一点为点5.同理,点3和点4也决定一条直线,其上的另外一点为点6.则其决定的射影平面如图示:我们很容易验证,上图与前面的Fano图形是一致的,即2阶射影平面唯一.下面我们再给出3阶射影平面的图示:其中13条直线分别为{1,2,3,11},{4,5,6,11},{7,8,9,11},{1,4,7,13},{2,5,8,13},{3,6,9,13},{1,5,9,12},{2,6,7,12},{3, 4,8,12},{1,6,8,10},{2,4,9,10},{3,5,7,10}, {10,11,12,13}.n定理4.3如果给定的自然数k p,p为素数,则k阶射影平面存在.证明的方法是利用有限域上的线性空间去构造k阶射影平面.我们在后面的章节会给出详细的证明.通过上述的定理,我们知道2,3,4,5,7,8,9阶射影平面是存在的,而且进一步知道,2,3,4,5,7,8阶射影平面是唯一的,9阶射影平面至少有4种.6阶射影平面不存在.1991年加拿大的林永康(Clement Lam)教授研究小组,利用计算机证明了不存在10阶射影平面,但是严格的数学逻辑证明目前还没有.至于其它阶数的射影平面是否存在,目前还不知到.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
射影平面3.1 中心投影与无穷远元素 知识点解析 中心投影定义. 影消点、影消线的概念影消点没有中心投影;影消线也没有投影. 无穷远点、无穷远直线的概念.仿射直线、射影直线、仿射平面、射影平面的概念.平行的两个平面相交于无穷远直线上,任何一个平面与无穷远平面相交于一条无穷直线上,一条直线与平行平面相交于一个无穷远点.在仿射平面上,任何两条直线有并且只有一个交点.两条有穷远直线若不平行则交于有穷远点,若平行则交于无穷远点,一有穷远直线与无穷远直线交于无穷远点.解题指导(习题选解) 练习3-11. 证明:中心投影一般不保持共线三点的简比. 证明反证法.假设中心投影保持共线三点的简比,则在中心投影下,三角形的中位线仍为三角形的中位线,于是推出中心投影把平行线变成平行线,这与中心投影不保持直线的平行性矛盾.所以,中心投影一般不保持共线三点的简比.4.设21:ππσ→是平面1π与2π之间的中心投影.试讨论1π上两条平行直线的象在2π中是否平行,不平行有什么性质?同样,2π上的两条平行直线在1π中的原象是否为平行直线?解当投影线垂直于这对平行线时,其象在2π中是平行的;当投影线不垂直于这对平行线时,其象在2π中不平行.同理,当投影线垂直于这对平行线时,其原象在1π中是平行的;当投影线不垂直于这对平行线时,其象在1π中不平行.5.试证明:中心投影不保持直线上两个线段之比.证明同第1题.(略). 3.2图形的射影性质 知识点解析透视对应、中心透视的概念透视对应把l 上的影消点Q 投影到l '上无穷远点∞'P ,把l 上的无穷远点∞P 投影到l '上影消点Q '.中心投影把π上的影消线l 投影到π'上无穷远直线∞'l ,同时把π上的无穷远直线∞l 投影到π'上影消线l '.定义3.1图形在中心投影下不变的性质(不变的量),叫做图形的射影性质. 同素性和结合性都是射影不变性质;平行性质和单比不是射影不变性质,它们在中心投影下会改变. 如果中心射影把平面π上的直线l 投影成平面π'上的无穷远直线,如图1所示,那么平面π上两条相交直线a 与b ,若交点在影消线l 上,则它们 的象是π'上的两条平行线a '与b ';反过来,平面π'上两条平行线,它们的原象是π上的两条相交于l 的直线.利用中心投影把一直线投影成无穷远直线,可 以用来证明一些几何问题. 解题指导(习题选解) 练习3-21. 求证:一直线与和它平行的平面交于一个无穷远点证明如果一条直线平行一个平面,则这个平面内有无数条直线与它平行,因为两条直线交于无穷远点,所以,这条直线与这个平面交于无穷远点.2.证明:相交于影消线上的二直线,象为二平行直线.证明设二直线1l 和2l 交于P 点,P 点在影消线上,1l 和2l 经射影对应,对应直线为1l '和2l ',则P 点对应无穷远点. 由于射影对应保持结合性不变,所以P 的对应点是1l '和2l '的交点,即无穷远点,也就)(图1是1l '∥2l '. 3.设OX ,OY ,OZ 为三条定直线,A ,B 为二定点,其连线过O ,点R 为OZ 上的动点,且直线RA ,RB 分别交OX ,OY 于点P ,Q ,求证:PQ 通过AB 上一定点.分析这个题目是要证明PQ 的连线通过AB 上一定点,属于三线共点问题,只涉及点和直线的结合性,可以利用“射影到无穷远”.取OAB 所在直线为影消线,经过中心投影之后,∞∞∞B A O 为无穷远直线,如图所示,则2211R P P R ,1221R R Q Q 为平行四边形.于是有2121//R R P P2121//R R Q Q所以2121//Q Q P P即四边形2211P Q Q P 为平行四边形,11Q P ∥22Q P .则11Q P 通过∞M ,由中心射影保持结合性不变可知,PQ 通过AB 上一定点. 4.在一个平面内的影消线上取定两点A ,B ,C 为该平面内的任意一点,求证∠ACB 投影后是一个常量.分析如图所示,平面α上的 ∠ACB 经射影后,在β平面 上射影成∠B C A '''. 因为A ,B 为影消线上两点,OMY2R 1P 1R BAZ2Q 1Q 2P X )图题(第32R 1R ZY X2P 1P ∞B ∞A ∞M ∞O 2Q 1Q所以OA ∥β,且OA ∥A C '',OB ∥β,且OB ∥B C '',所以∠B C A '''=∠ACB . 而∠ACB 为定角.由于∠ACB 经投影后,不论C 取在平面上任何位置,其射影成的角∠B C A '''永远等于定角∠ACB ,所以为定值.注意:由于射影中心O 和影消线AB 所成平面一定平行于平面β,所以,利用有关立体几何的平面与平面平行的定理,就可以证明此题.3.3笛沙格定理 知识点解析三点形、三线形概念定理3.1(笛沙格定理) 如果两个三点形对应顶点的连线交于一点,则对应边的交点在一条线上.定理3.2 如果两个三点形对应边的交点在一条线上,则对应顶点的连线交于一点(共点).解题指导(习题选解) 练习3-31.三角形ABC 的顶点A ,B ,C 分别在共点的三直线α,β,γ上移动.证明:AB 和BC 分别通过定点P 与Q 时,CA 也通过PQ 上的一个定点.证明如图所示.设三角形C B A ''' 是满足条件的另一个三角形,在三角形ABC 和C B A '''中,由于对应点的连线l ,m ,n 共点O ,由笛沙格定理可知,对应边的交点P ,Q ,R 共线,即AC 与C A ''的交点R 必在直线PQ 上,于是R 为定点.2.若三角形ABC 的二顶点B 与C 分别在定直线α与β上移动,三边AB 、BC 、C A题图)(第1ABB 'P ClA 'C 'OQRn m分别通过共线的定点P ,Q ,R ,求证顶点A证明根据图形(见第2题图)可知,Λ),,,(21ΛB B B),,,(21ΛC C C ,则Λ),,,(21ΛB B B P ),,,(21ΛC C C R在这两个射影线束中,PR 是自对应元素,所以Λ),,,(21ΛB B B P ),,,(21ΛC C C R两透视对应的线束对应直线的交点Λ,,,21A A A 共线.3.设A ,B ,C ,D 为平面上的 四点,R CD AB =⨯(AB 与CD 的交点 为R ),P AD BC =⨯,Q BD AC =⨯. 试证:BC 与QR 的交点1A ,CA 与RP 的 交点1B ,AB 与PQ 的交点1C 在同一直线上.证明如图所示.在三角形ABC 和PQR 中,对应顶点的连线AP ,BQ ,CR 共点于S ,由笛沙格定理,对应边的交点1A ,1B ,1C 共线.3.4齐次坐标 知识点解析 一维齐次坐标),(21x x ,其中1x ,2x 满足x x x =21)0(2≠x 二维齐次坐标),,(321x x x ,其中1x ,2x ,3x 满足x x x =31,y x x=32)0(3≠x ,),(y x 是欧氏平面内的笛氏坐标.)0,,(21x x (1x ,2x 不同时为0)是一个无穷远点的齐次坐标.A题图)(第21题图)(第3),,(321x x x )0(3≠x 是一个有穷远点的齐次坐标.)0,0,0(不表示一个点的齐次坐标.)0,,1(k 为一组直线kx y =上的无穷远点的齐次坐标.直线方程欧氏坐标系下直线方程为)0(02221321≠+=++a a a y a x a其中),(y x 是直线上点的非齐次坐标.点),(y x 的齐次坐标为),,(321x x x ,其中1x ,2x ,3x 满足x x x =31,y x x=32. 直线的齐次方程为)0(022********≠+=++a a x a x a x a过原点的直线的齐次方程为)0(022212211≠+=+a a x a x a无穷远直线的齐次方程为03=x无穷远直线无非齐次方程. 齐次线坐标 直线的齐次方程为0332211=++x u x u x u321,,u u u 叫做直线的齐次线坐标,记为],,[321u u u .]0,0,1[是y 轴的齐次线坐标. ]0,1,0[是x 轴的齐次线坐标. ]1,0,0[是无穷远直线的齐次线坐标.定理3.3一点),,(321x x x X =在一直线],,[321u u u u =上的充分必要条件为0332211=++x u x u x u直线0332211=++x u x u x u 的非齐次坐标为31u u u =,32u uv =. 所有不通过原点的直线方程都可以写成01=++vy ux两点),,(321a a a A =,),,(321b b b B =的连线的方程为0321321321=b b b a a a x x x即0)()()(312213311312332=-+-+-x b a b a x b a b a x b a b a两点),,(321a a a A =,),,(321b b b B =的连线的坐标为),,(122131132332b a b a b a b a b a b a ---解题指导(习题选解) 练习3-41.试求出下面各点的齐次坐标. (1))0,0(,)0,1(,)1,0(,)35,2(. (2)以43为方向的无穷远点。
(3)013=++y x 上的无穷远点.解(1)利用公式x x x =31,y x x=32,取13=x ,得 )1,0,0(,)1,0,1(,)1,1,0(,)1,35,2(.(2)利用:)0,,1(k 为一组直线kx y =上的无穷远点的齐次坐标,得)0,43,1( (3)利用:)0,,1(k 为一组直线kx y =上的无穷远点的齐次坐标,得)0,3,1(-2.求下列直线上的无穷远点.(1)04321=-+x x x (2)0221=+x x (3)0332=-x x (4)0521=+x x解利用)0,,(21x x (1x ,2x 不同时为0)是一个无穷远点的齐次坐标.(1)令03=x ,取12-=x ,则11=x ,于是04321=-+x x x 上无穷远点的坐标为)0,1,1(-.同理,(2)令03=x ,取12-=x ,则21=x ,于是,0221=+x x 上无穷远点的坐标为)0,1,2(-.(3)令03=x ,这时02=x ,取11=x ,于是,0332=-x x 上无穷远点的坐标为)0,0,1(.(4)令03=x ,取12-=x ,则51=x ,于是,0221=+x x 上无穷远点的坐标为)0,1,5(-.注意:直线上的无穷远点不是唯一的. 4.写出下面直线的坐标. (1)x 轴;(2)y 轴;(3)无穷远直线;(4)过原点且斜率为2的直线. 解(1)]0,1,0[是x 轴的齐次线坐标; (2)]0,0,1[是y 轴的齐次线坐标; (3)]1,0,0[是无穷远直线的齐次线坐标;(4)利用)0,,1(k 为一组直线kx y =上的无穷远点的齐次坐标.于是,过原点且斜率为2的直线的坐标为)0,2,1(.3.5对偶原则知识点解析平面射影几何对偶原理:在射影平面上,点与直线的每一个射影命题都对应着另一个对偶命题,如果两个命题之一成立,那么另一个也成立.解题指导(习题选解) 练习3-52.写出下面命题的对偶命题.设一个变动的三点形,它的两边各通过一个定点,且三顶点在共点的三条定直线上.求证:第三边也通过一个定点.解对偶命题:设一个变动的三点形,它的两顶点各通过一条定直线,且三条边分别通过共线的三点.求证:第三个顶点也通过一条定直线.3.求两点01143321=-+u u u ,0135321=+-u u u 的连线的坐标. 解利用两点),,(321a a a A =,),,(321b b b B =的连线的方程为0321321321=b b b a a a x x x两点),,(321a a a A =,),,(321b b b B =的连线的坐标为),,(122131132332b a b a b a b a b a b a ---代入得)1,2,1()29,58,29(1351143321=---=--x x x4.求过两直线]1,1,1[,]3,1,2[的交点与点032321=++u u u 的直线的坐标. 解直线]1,1,1[,]3,1,2[的交点为)1,1,2(312111321-=x x x 点)1,1,2(-与点032321=++u u u 的直线的坐标为)4,2,1()8,4,2(132112321-=--=-x x x .。
