第五讲---平面上取点线,平面的辅助投影;线面相对位置
合集下载
机械制图——第一章投影法和点、线、平面的投影

表示重影点时,看不见点的投影,其代号用圆括号括起来,例 如上面所述的C点的正投影看不见,可表示为a’(c’)。
两个空间的点,发生重影的条件: 两对坐标值相等,一对坐标值不相等.
Xa = Xc Za = Zc Ya > Yc
a'(c') Yc
Za/Zc C A
c" a"
c Ya
a Xa/Xc
a'(c') Za/Zc
(三)两点的相对位置
如图1-8所示,两个点的投影沿左右、前后、上下三个方向 所反映的坐标差,即这两个点对应投影面W、V、H的距离差, 能反映两点的相对位置;反之,若已知两点的相对位置和其中 一点的投影,也能作出另一点的投影。
两点的相对位置
A(XA,YA,ZA) 和 B(XB,YB,ZB) 两点的相对位置: 如:b’→ a’ : a’(△X=Xa-Xb ,△Z =Za-Zb )
投影法分为两类: 中心投影法 平行投影法(称平行光源)
二、中心投影法
如图所示,点 S(投射中心)射 出过A点射线,在 投影面 P形成 a点的投影图案, 该方法称为:
中心投影法。
三、平行投影法
如图所示,投射线(由平行光源)平行投射,在投影面P形 成的投影图案,称为平行投影法。
平行投影法又可分为:
正投影法:投影线(平行光源)垂至于投影面的投影法
例:过C点作水平线CD与AB相交。
c●
k
a
b d
a
d
先作正面投影
k c●
b
⒊ 两直线交叉
b′
c′
a′ X
a
V
d′
c′
O
a′
AC
d
a
两个空间的点,发生重影的条件: 两对坐标值相等,一对坐标值不相等.
Xa = Xc Za = Zc Ya > Yc
a'(c') Yc
Za/Zc C A
c" a"
c Ya
a Xa/Xc
a'(c') Za/Zc
(三)两点的相对位置
如图1-8所示,两个点的投影沿左右、前后、上下三个方向 所反映的坐标差,即这两个点对应投影面W、V、H的距离差, 能反映两点的相对位置;反之,若已知两点的相对位置和其中 一点的投影,也能作出另一点的投影。
两点的相对位置
A(XA,YA,ZA) 和 B(XB,YB,ZB) 两点的相对位置: 如:b’→ a’ : a’(△X=Xa-Xb ,△Z =Za-Zb )
投影法分为两类: 中心投影法 平行投影法(称平行光源)
二、中心投影法
如图所示,点 S(投射中心)射 出过A点射线,在 投影面 P形成 a点的投影图案, 该方法称为:
中心投影法。
三、平行投影法
如图所示,投射线(由平行光源)平行投射,在投影面P形 成的投影图案,称为平行投影法。
平行投影法又可分为:
正投影法:投影线(平行光源)垂至于投影面的投影法
例:过C点作水平线CD与AB相交。
c●
k
a
b d
a
d
先作正面投影
k c●
b
⒊ 两直线交叉
b′
c′
a′ X
a
V
d′
c′
O
a′
AC
d
a
工程制图 平面的投影-线面相对位置解读
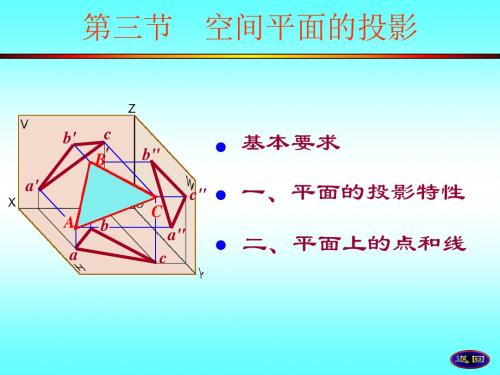
(2) p'与x、z轴的夹角反映α、 角的真实大小 (3) p、 p为平面P的类似形
(一)投影面的垂直面
2.铅垂面:只垂直于H面,倾斜于V面和W面的平面
z p' p' p" O
P
p"
x
yW
p
p
yH
投影特性 :(1) H面投影积聚为一条线p
(2) p与x、 y轴的夹角反映β、角的真实大小 (3) p'、 p为平面P的类似形
b'
b' c'
z b"
c'
b" a' c" x O a"
c" yW
B
a'
A
a 投影特性:
C
b
c
b
a" a c yH
(1) 一般平面的三面投影既不反映实形也没有积聚性。 (2) 其三面投影均为空间平面的类似形,且面积缩小。
平面投影特性判断
正平面
铅垂面
侧平面
正平面
正垂面
侧平面
侧垂面
一般位置平面
二、平面上的点和线
C
D A B
A C F a
D
D A B a C K E B F b c(f) d(e)
K
F
E
d(e) a b
E
c(f)
c(f)
k
d(e)
k
b
一
二
三
一、平行问题
1.直线与平面平行
直线与平面平行具有下列几何关系: 若直线与平面平行<- ->该直线必平行于平面上的一条直线; 当平面垂直于投影面时<- ->该直线的投影必然与平面具有积聚性 的投影平行。
(一)投影面的垂直面
2.铅垂面:只垂直于H面,倾斜于V面和W面的平面
z p' p' p" O
P
p"
x
yW
p
p
yH
投影特性 :(1) H面投影积聚为一条线p
(2) p与x、 y轴的夹角反映β、角的真实大小 (3) p'、 p为平面P的类似形
b'
b' c'
z b"
c'
b" a' c" x O a"
c" yW
B
a'
A
a 投影特性:
C
b
c
b
a" a c yH
(1) 一般平面的三面投影既不反映实形也没有积聚性。 (2) 其三面投影均为空间平面的类似形,且面积缩小。
平面投影特性判断
正平面
铅垂面
侧平面
正平面
正垂面
侧平面
侧垂面
一般位置平面
二、平面上的点和线
C
D A B
A C F a
D
D A B a C K E B F b c(f) d(e)
K
F
E
d(e) a b
E
c(f)
c(f)
k
d(e)
k
b
一
二
三
一、平行问题
1.直线与平面平行
直线与平面平行具有下列几何关系: 若直线与平面平行<- ->该直线必平行于平面上的一条直线; 当平面垂直于投影面时<- ->该直线的投影必然与平面具有积聚性 的投影平行。
平面的投影—平面对投影面的相对位置(工程制图)

三、投影面垂直面
2.铅垂面—垂直于H面Z,倾斜于V,W面 V
C
A
W
cቤተ መጻሕፍቲ ባይዱ
a
x
z ba
o
a
X
O
ac B
c
b
b
Y
YH
投影特性:1) abc积聚为一条线。 2)a’b’c’ , a”b”c”为ABC的类似形。 3)反应平面与V、 W的倾角
c
b
YW
6.2平面对投影面的相对位置
三、投影面垂直面
3.侧垂面—垂直于W面,倾Z斜于H,V面
投影面垂直面
6.2平面对投影面的相对位置
三、投影面垂直面 空间位置:垂直于一个投影面,倾斜于另外两个投影面 正垂面—垂直V面,倾斜H、W面的平面
铅垂面—垂直H面,倾斜V、W面的平面
侧垂面—垂直W面,倾斜V、H面的平面
投影特性: 1)在平面所垂直的投影面上的投影积聚为一条直线;它与相应投影轴的夹 角反应该平面与其他两个投影面的倾角 2)另外两个投影面上的投影为空间平面的类似形,且小于实形。
6.2平面对投影面的相对位置
三、投影面垂直面
1.正垂面—垂直于V面,倾斜于H,W面
Z
bz
c
c
b
V
b
a
a
c C
a
B b”W c”
x
c
o
YW
X
Ac
O a”
a
a
b
b
YH
Y
投影特性:1) abc 积聚为一条线。
2) abc, abc为 ABC的类似形。
3)反应平面与H、 W的倾角
6.2平面对投影面的相对位置
X
o
机械制图平面的投影及相对位置 ppt课件

k●
c
a
●1(2)
n
投影积聚成一个点,故交点K 的水平投影也积聚在该点上。
2.作图
用面上取点法
b
mk(●●n2) ●
c
a
1
① 求交点 ② 判别可见性(V面) 用重影点判断
点Ⅰ位于平面上,在前;点Ⅱ位
于MN上,在后。故k 2为不可见。
ppt课件
⒉两平面相交(实物)
两平面相交其交线为直线,交线是两平面的共有线, 同时交线上的点都是两平面的共有点,交线是两平面可见与 不可见的分界线。
要讨论的问题:
① 求两平面的交线 方法: ⑴ 确定两平面的两个共有点。 ⑵ 确定一个共有点及交线的方向。
② 判别两平面之间的相互遮挡的可见性。
只讨论两平面中至少有一个处于特殊位置的情况(即 两种情况:一个平面处于特殊,两个平面都处于特殊)。
ppt课件
(1)两平面都为特殊平面
ppt课件
例1:求两平面的交线MN,并判别可见性。
c 点n,即为两平面的两个共有点的 正面投影,故mn是MN的正面投
影。
2.作图
●m
n●
h ① 求交线 ② 判别可见性(H面)
a f
c
mnb’在e’f’h’上面, 故水平投影mnb可见,其他可见
性可根据投影特点得出。
ppt课件
⑶
b
KN后面的蓝色
平面的投影
f
m
●
d
k ●
n
●
e
ppt课件
(2). 其中一平面为特殊平面
V
b n c H
m B
a
N
P
E
M
C
F
A
H
工程制图-5-点线面相对位置讲解学习

B
△ZC 1
g′
c′
g c
1 b
60 °
A = A0 c C
B0
△ZC 1
【例题7】已知等边△ABC与H面的倾角α=30°,高BD长
30mm,试完成该等边△ABC的两面投影。
△ZB
D
a′
a
b′
B0
d′
d α
作图步骤
1、作等边△ABC高
c′
的实长最大倾斜线
2、直角三角形法求作 BD的Z坐标差
c
等边△ABC 高BD的实长
工程制图-5-点线面相对位置
【基本作图一】一般线与投影面垂直面相交
b
V
´ n´
N
B
a
k
´
´
m´
A
K
ab
n
x
c´
n
M
C
k
c
a
k
m
H
b
m
c
【基本作图二】投影面垂直线与一般面相交 a′ e′
V
e´
a´
b´
k´ E A
b′
f´ E K B
F
aC
b
e(f )(k)
c
H
b
k′ 1′
f′
c′
a
1
e(f) (k)
2′
c′
1′
a′
2
a
c
b′
作图步骤
1、过点A作直线AB 的垂直面AⅠⅡ;
2、在垂直面AⅠⅡ上, 运用平面定线方法确定 AC边;
3、连线完成直角三 角形ABC的投影。 b
1
【例题3】作一直线与两交叉直线AB和CD相交,同时与直 线EF平行。
一章投影法和点直线平面的投影 PPT资料共31页

[例题2] 已知点A在点B之前5毫米,之上9毫米,之右8 毫米,求点A的投影。
a
a
9
8 a
5
§1- 4 重影点的投影
a
d(c)
b
A
C
D
B
a(b)
c
d
更多精品资源请访问
docin/sanshengshiyuan doc88/sanshenglu
[例题1] 已知点A的正面与侧面投影,求点A的水平投影。
a
不注 画: 出因 平为 面平 边面 框是 。无
限 大 的 , 所 以 一 般
五、特殊点的投影
V
b
Bb
a
b
Cc
c
Aa
a c
X
O
b
c
a
H
§1-3 两点的相对位置
a
b
B
A
a
b
b a
两点中x值大的点 —— 在左 两点中y 值大的点 —— 在前 两点中z 值大的点 —— 在上
点在一个投影面上的投
P
影不能确定点的空间位置。
● b B1
B2 ●
B3 ●
解决办法?
●
采用多面投影。
§1-2 三投影面体系中点的投影
一、三投影面体系的建立 二、三投影面体系中点的投影 三、点的直角坐标与三面投影的关系 四、三投影面体系中点的投影规律 五、特殊点的投影
一、三投影面体系的建立
Z
OW
§1-2 点的投影
§1-1 点在一个投影面中的投影 §1-2 三投影面体系中点的投影 §1-3 两点的相对位置 §1-4 重影点的投影
例题1
例题2
§1-1 点在一个投影面上的投影
【精品】线、面相对位置ppt课件

试过点K作水平线AB平行于ΔCDE平面
c
f
e b k a
d
d f c
e
a
k
b
二、两平面平行
P E
D
F
C
S B
A
若一平面内的相交两直线对应平行于另一平面内的相交两直线, 则此两平面平行
已知定平面由平行两直线AB和CD给定。试过点K作一
平面平行于已知平面 。
a
s
d
f
k
e
m
n
b
c
r
c
b m
r n
d
Ⅳ 影面上的可见性。
B
K
ⅢA
f
1
a
b
k4 E
2 c (3) e
H
直线EF与平面 ABC相交,判别可见性。
b
f
( 2
1
)
4
k a
3
c
e
f
2
c
a
1
k ( 3) 4
b
e
注意: 利用重影点判别可见性
以正垂面为辅助平面求线面交点
SV m
c
步骤:
1
1、 过MN作正
垂平面S。
k b
2、求S平面与
2
ΔABC的交线 ⅠⅡ。
V
D
B
d
c
k
L A
K
E
C
a
F bl
ck
e
d
c
H
k
e
b l
f
a
lb a f
一般位置平面与特殊位置平面相交
V
D
B
d
c
k
机械制图平面的投影及相对位置课件

03
投影规律
在正投影中,物体的前面与正面投影面相交,得到前视图;物体的上面
与水平投影面相交,得到俯视图;物体的左面与左侧投影面相交,得到
左视图。
机件的视图表达
机件视图的选择
根据机件的结构特点和工作位置,选择合适的视图表达方式,如 主视图、俯视图、左视图等。
剖视图的应用
对于内部结构较为复杂的机件,剖视图是一种有效的表达方式,通 过剖切平面将内部结构展示出来。
机械制图平面的投影及相对位置课件
目录 Contents
• 平面投影的基本概念 • 平面间的相对位置 • 平面上的点和线 • 平面投影的实际应用 • 总结与复习
01
平面投影的基本概念
平面的表示方法
几何元素表示法
包含两平行直线表示法
通过三个非共线的几何元素(点、直 线、平面)来确定一个平面的位置。
03
平面上的点和线
点在平面上的投影
点的投影
点在平面上的投影是指该点在平面上的垂直投影,可以通过确定点的坐标和投影 角度来计算。
点的投影特性
点的投影具有真实性、类似性和积聚性的特性,这些特性决定了投影的形状和大 小。
线在平面上的投影
线的投影
线在平面上的投影是指该线在平面上的垂直投影,可以通过 确定线的起点和终点以及投影角度来计算。
3
材料和技术要求
在零件图中,需要注明零件的材料、热处理要求 、表面处理等,以便于加工制造和质量控制。
05
总结与复习
重点回顾
平面投影的基本原
理
掌握平面在三投影面体系中的投 影特性,包括投影面积、投影形 状和投影位置。
特殊位置平面的判
定
能够根据平面的投影特性判断其 属于哪个位置的平面(正垂面、 侧垂面、一般位置平面)。
点线面的投影ppt课件

Y
6
[二] 点的三面投影
z
a
a
az
x
ax o
ay
45
a
ay
投影特性:
垂直关系
aa,,aa,,
OX OZ
yW 相等关系
a ax a,,az
yH 7
三投影面体系中点的投影规律
Z
V a
az
V
a
y
x
a
X
ax
z
O W X ax
Z
W
az
a
O ay YW
a H
ay
ay
YH a
YH
1. aaz = aay = x
b
c
B
C
a
X
O
直线上的点具有两个特性:
A cb c
a
1 从属性 若点在直线上,则点的各个投影必在 直线的各同面投影上。
2 定比性 属于线段上的点分割线段之比等于其 投影之比。
例1 判断 E、F点是不是在直线AB上。
a, e,
f , b,
a e
f b
E点在AB直线上 F点不在AB直线上
10
例2 试判断K点是否在直线EF上。
a
a
X
O
YW
a YH
例题2 已知点 A的正面投影和侧面投影, 求其水平投影。
z
a
a
x
O
yW
a yH
注: 这是二求三问题的基础。
8
三 点的投影与直角坐标的关系
投影面→坐标面 投影轴→坐标轴 轴的交点O→坐标原点
距离的关系:
Aa=Xa
X
Aa =Ya
投影 坐标
第五讲---平面上取点线,平面的辅助投影;线面相对位置资料
c
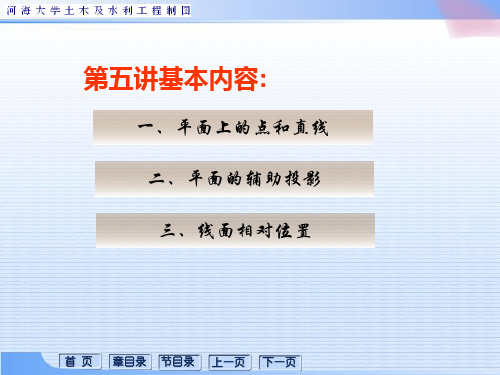
分析:ABCD
b k
d
既然是平面, 则它的对角线必相交。
作图:
a a b k d
1)连接a′、c′和b′、d′,得交点k′;
2)连接b、d,在bd上求出 k,并连接a、k; 3)在ak上求出c,连接b、c 和d、c,即得该平面的水平 投影;
下一页
c
首 页 章目录 节目录 上一页
例 完成平面的水平投影
本节结束
作业:
P15,P16(去掉3-35),P17(去掉3-42) 下次课内容: 轴测投影
首 页
章目录
节目录
上一页
下一页
k n
首 页
章目录
节目录
上一页
下一页
定理2(逆) 若一直线的水平投影垂直于属于平面的水平线的 水平投影;直线的正面投影垂直于属于平面的正平线的正面投 影,则直线必垂直于该平面。
首 页
章目录
节目录
上一页
下一页
[例题7] 平面由 BDF给定,试过定点K作平面的法线。
n c a
k
k
a c n
第五讲基本内容:
一、平面上的点和直线
二、平面的辅助投影 三、线面相对位置
首 页
章目录
节目录
上一页
下一页
一、平面上的点和直线
(1)平面上取任意直线
如何判断直线在平面内?
方法一:
若一直线通过平面上的两点, 则此直线必在该平面内。
方法二:
若一直线通过平面上的一点,且 平行于该平面上的另一直线, 则此直 线在该平面内。
首 页 章目录 节目录 上一页 下一页
n
b
c
判断直线的可见性 b n
a
m
分析:ABCD
b k
d
既然是平面, 则它的对角线必相交。
作图:
a a b k d
1)连接a′、c′和b′、d′,得交点k′;
2)连接b、d,在bd上求出 k,并连接a、k; 3)在ak上求出c,连接b、c 和d、c,即得该平面的水平 投影;
下一页
c
首 页 章目录 节目录 上一页
例 完成平面的水平投影
本节结束
作业:
P15,P16(去掉3-35),P17(去掉3-42) 下次课内容: 轴测投影
首 页
章目录
节目录
上一页
下一页
k n
首 页
章目录
节目录
上一页
下一页
定理2(逆) 若一直线的水平投影垂直于属于平面的水平线的 水平投影;直线的正面投影垂直于属于平面的正平线的正面投 影,则直线必垂直于该平面。
首 页
章目录
节目录
上一页
下一页
[例题7] 平面由 BDF给定,试过定点K作平面的法线。
n c a
k
k
a c n
第五讲基本内容:
一、平面上的点和直线
二、平面的辅助投影 三、线面相对位置
首 页
章目录
节目录
上一页
下一页
一、平面上的点和直线
(1)平面上取任意直线
如何判断直线在平面内?
方法一:
若一直线通过平面上的两点, 则此直线必在该平面内。
方法二:
若一直线通过平面上的一点,且 平行于该平面上的另一直线, 则此直 线在该平面内。
首 页 章目录 节目录 上一页 下一页
n
b
c
判断直线的可见性 b n
a
m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章目录 节目录 上一页 下一页
首 页
例1 已知平面由相交的两直线AB、AC 所确定, 试在平面内任作一条直线。 解法一 (利用方法一)
b m a m a n b c a c n c a b d
解法二 (利用方法二)
b c d
有无数个解。
首 页 章目录 节目录 上一页 下一页
例2 在平面ABC 内作一条水平线,使其到 H 面的距离为20mm。
a m 20 n c b b
c m a
首 页 章目录 节目录 上一页
n
问题:本题有几个解? 结论:唯一解!
下一页
(2)平面上取点
面上取点的方法——定点先定线
即:找出过此点而又在平面内的一条直线作为 辅助线,然后再在该直线上确定点的位置。
例1 已知K点在平面ABC上,求K点的水平投影。
b k● a a 利用平面的积聚性求解
一、直线与平面相交只有一个交点
二、两平面的交线是直线
三、特殊位置线面相交 四、一般位置平面与特殊位置平面相交 五、直线与一般位置平面相交 六、两一般位置平面相交
首 页
章目录
节目录
上一页
下一页
一、直线与平面相交
A
K
B
直线与平面相交只有一个交点,它是直线与平面的共有点。
首 页 章目录 节目录 上一页 下一页
(四)点、线、面综合题 1.熟练掌握点、线、面的基本作图方法; 2.能对一般画法几何综合题进行空间分析,了解综合题的一般解题 步骤和方法。
首 页 章目录 节目录 上一页 下一页
直线与平面平行,平面与平面平行
一、直线与平面平行
几何条件 若平面外的一条直线与平面内的一条直线平行,则该直线与该 平面平行。这是解决直线与平面平行作图问题的依据。
f
b
a
a
b f
首 页 章目录 节目录 上一页 下一页
二、两平面平行
E D F C
B A
若属于一平面的相交两直线对应平行于属于另一平面的相交两 直线,则此两平面平行
首 页 章目录 节目录 上一页 下一页
[例题3 ]
试判断两平面是否平行
s n r
m
n m
s r
首 页
结论:两平面平行 章目录 节目录 上一页 下一页
b2 d2
e2 c2
e1 e
d
e
首 页 章目录 节目录
d
上一页 下一页
[例题] 求平面ABC与平面ABD的夹角。
a' d'
b' c' a1(b1) a b d1
c d c1
首 页
章目录
节目录
上一页
下一页
三、线面相对位置
(一)平行问题
1.熟悉线、面平行,面、面平行的几何条件; 2.熟练掌握线、面平行,面、面平行的投影特性及作图方法。 (二)相交问题 1.熟练掌握特殊位置线、面相交(其中直线或平面的投影具有积聚 性)交点的求法和作两个面的交线(其中一平面的投影具有积聚性)。 2.熟练掌握一般位置线、面相交求交点的方法;掌握一般位置面、 面相交求交线的作图方法。 3.掌握利用重影点判别投影可见性的方法。 (三)垂直问题 掌握线面垂直、面面垂直的投影特性及作图方法。
两平面垂直
两平面不垂直
首 页
章目录
节目录
上一页
下一页
[例题12] 平面由 BDF给定,试过定点K作已知平面的垂面。
h
g
c
a
a
c
g
h
首 页 章目录 节目录 上一页 下一页
[例题13] 试判断 ABC与相交两直线KG和KH所给定的平面是否 垂直。
f d
f
d
首AD 页 直线不在 章目录 ABC 节目录 上一页 下一页 结论:因为 平面上,所以两平面不垂直。
首 页
章目录
节目录
上一页
下一页
二、平面的辅助投影
三个基本问题
(一) 把一般位置平面变为投影面垂直面
(二) 把投影面垂直面变为投影面平行面
(三) 把一般位置平面变为投影面平行面
首 页
章目录
节目录
上一页
下一页
(一) 把一般位置平面变为投影面垂直面
b
d
b1
a
c b d c
D
V X d1H1 H a1 a c1
例题13
首 页
章目录
节目录
上一页
下一页
直线与平面垂直的几何条件:若一直线垂直于一平面,则必垂直于属于该
平面的一切直线。
首 页
章目录
节目录
上一页
下一页
定理1 若一直线垂直于一平面、则直线的水平投影必垂直于属 于该平面的水平线的水平投影;直线的正面投影必垂直于属于 该平面的正平线的正面投影。 n k
c
k
首 页 章目录
●
b c
上一页 下一页
节目录
例2
已知M点在平面EFG上,求M点的水平投影。
f m
●
h g
e f h g
e
●
m
通过在面内作 辅助线求解
首 页
章目录
节目录
上一页
下一页
例3 如图所示,已知一般位置平面ABCD的正面投影和 AB、
AD两条边的水平投影ab和ad,补全该面的水平投影。
首 页 章目录 节目录 上一页 下一页
[例题8] 试过定点K作特殊位置平面的法线。
h
h h
h h
首 页
h
(c)
(a)
章目录
节目录
上一页
下一页
(b)
两平面垂直的几何条件 若一直线垂直于一定平面,则包含这条直线的所有平面 都垂直于该平面。 A
D
首 页
章目录
节目录
上一页
下一页
反之,两平面相互垂直,则由属于第一个平面的任意一 点向第二个平面作的垂线必属于第一个平面。
首 页
例题4
章目录
例题5
节目录 上一页 下一页
一、直线与平面平行
若一直线平行于属于定平面的一直线,则该直线与平面平行
首 页 章目录 节目录 上一页 下一页
[例题1]
试判断直线AB是否平行于定平面
gAB不平行于定平面 首 页 章目录 节目录 上一页 下一页
[例题2] 试过点K作水平线AB平行于ΔCDE平面
章目录
节目录
上一页
下一页
四、一般位置平面与特殊位置平面相交
求两平面交线的问题可以看作是求两个共有点的问题, 由于特殊位置平面的某个投影有积聚性,交线可直接求出。
一般位置平面与特殊位置平面相交
判断平面的可见性
首 页
章目录
节目录
上一页
下一页
m
M B K F m C P
b
f n k l
c
d
c
首 页 章目录 节目录 上一页 下一页
[例题]
求点S到平面ABC的距离
k1
s1 距离
首 页
章目录
节目录
上一页
下一页
[例题] 已知E到平面ABC的距离为N,求E点的正面投影e。 [选讲]
d e
N
d
首 页 章目录 节目录 上一页 下一页
(二) 把投影面垂直面变为投影面平行面
c1 V1 a1
c
分析:ABCD
b k
d
既然是平面, 则它的对角线必相交。
作图:
a a b k d
1)连接a′、c′和b′、d′,得交点k′;
2)连接b、d,在bd上求出 k,并连接a、k; 3)在ak上求出c,连接b、c 和d、c,即得该平面的水平 投影;
下一页
c
首 页 章目录 节目录 上一页
例 完成平面的水平投影
b1
首 页
X1
章目录
节目录
上一页
下一页
c1 b1 a1
首 页
章目录
节目录
上一页
下一页
(三) 把一般位置平面变为投影面平行面 a2 b2 d2 d c2 实形
d
首 页 章目录 节目录 上一页 下一页
[例题] 已知E点在平面ABC上,距离A、B为15,求点E的投影。 a2
15
第五讲基本内容:
一、平面上的点和直线
二、平面的辅助投影 三、线面相对位置
首 页
章目录
节目录
上一页
下一页
一、平面上的点和直线
(1)平面上取任意直线
如何判断直线在平面内?
方法一:
若一直线通过平面上的两点, 则此直线必在该平面内。
方法二:
若一直线通过平面上的一点,且 平行于该平面上的另一直线, 则此直 线在该平面内。
a k b
a l
A L
N b n k a l
m f
f
c
n
c PH
首 页
章目录
节目录
上一页
下一页
判断平面的可见性
首 页
章目录
节目录
上一页
下一页
结果
判断平面的可见性
首 页
章目录
节目录
上一页
下一页
直线与平面垂直、两平面垂直
一、直线与平面垂直 几何条件 定理1 定理2 例题7 例题8 例题9 例题10 二、两平面垂直 几何条件 例题11 例题12
有关线、面平行的作图问题有:判别已知线面是否平行;作直线与已 知平面平行;包含已知直线作平面与另一已知直线平行。
例题1
例题2
二、平面与平面平行 几何条件 若一个平面内的相交二直线与另一个平面内的相交二直线对应 平行,则此两平面平行。这是两平面平行的作图依据。 两面平行的作图问题有:判别两已知平面是否相互平行;过一点作一 平面与已知平面平行;已知两平面平行,完成其中一平面的所缺投影。 例题3
首 页
例1 已知平面由相交的两直线AB、AC 所确定, 试在平面内任作一条直线。 解法一 (利用方法一)
b m a m a n b c a c n c a b d
解法二 (利用方法二)
b c d
有无数个解。
首 页 章目录 节目录 上一页 下一页
例2 在平面ABC 内作一条水平线,使其到 H 面的距离为20mm。
a m 20 n c b b
c m a
首 页 章目录 节目录 上一页
n
问题:本题有几个解? 结论:唯一解!
下一页
(2)平面上取点
面上取点的方法——定点先定线
即:找出过此点而又在平面内的一条直线作为 辅助线,然后再在该直线上确定点的位置。
例1 已知K点在平面ABC上,求K点的水平投影。
b k● a a 利用平面的积聚性求解
一、直线与平面相交只有一个交点
二、两平面的交线是直线
三、特殊位置线面相交 四、一般位置平面与特殊位置平面相交 五、直线与一般位置平面相交 六、两一般位置平面相交
首 页
章目录
节目录
上一页
下一页
一、直线与平面相交
A
K
B
直线与平面相交只有一个交点,它是直线与平面的共有点。
首 页 章目录 节目录 上一页 下一页
(四)点、线、面综合题 1.熟练掌握点、线、面的基本作图方法; 2.能对一般画法几何综合题进行空间分析,了解综合题的一般解题 步骤和方法。
首 页 章目录 节目录 上一页 下一页
直线与平面平行,平面与平面平行
一、直线与平面平行
几何条件 若平面外的一条直线与平面内的一条直线平行,则该直线与该 平面平行。这是解决直线与平面平行作图问题的依据。
f
b
a
a
b f
首 页 章目录 节目录 上一页 下一页
二、两平面平行
E D F C
B A
若属于一平面的相交两直线对应平行于属于另一平面的相交两 直线,则此两平面平行
首 页 章目录 节目录 上一页 下一页
[例题3 ]
试判断两平面是否平行
s n r
m
n m
s r
首 页
结论:两平面平行 章目录 节目录 上一页 下一页
b2 d2
e2 c2
e1 e
d
e
首 页 章目录 节目录
d
上一页 下一页
[例题] 求平面ABC与平面ABD的夹角。
a' d'
b' c' a1(b1) a b d1
c d c1
首 页
章目录
节目录
上一页
下一页
三、线面相对位置
(一)平行问题
1.熟悉线、面平行,面、面平行的几何条件; 2.熟练掌握线、面平行,面、面平行的投影特性及作图方法。 (二)相交问题 1.熟练掌握特殊位置线、面相交(其中直线或平面的投影具有积聚 性)交点的求法和作两个面的交线(其中一平面的投影具有积聚性)。 2.熟练掌握一般位置线、面相交求交点的方法;掌握一般位置面、 面相交求交线的作图方法。 3.掌握利用重影点判别投影可见性的方法。 (三)垂直问题 掌握线面垂直、面面垂直的投影特性及作图方法。
两平面垂直
两平面不垂直
首 页
章目录
节目录
上一页
下一页
[例题12] 平面由 BDF给定,试过定点K作已知平面的垂面。
h
g
c
a
a
c
g
h
首 页 章目录 节目录 上一页 下一页
[例题13] 试判断 ABC与相交两直线KG和KH所给定的平面是否 垂直。
f d
f
d
首AD 页 直线不在 章目录 ABC 节目录 上一页 下一页 结论:因为 平面上,所以两平面不垂直。
首 页
章目录
节目录
上一页
下一页
二、平面的辅助投影
三个基本问题
(一) 把一般位置平面变为投影面垂直面
(二) 把投影面垂直面变为投影面平行面
(三) 把一般位置平面变为投影面平行面
首 页
章目录
节目录
上一页
下一页
(一) 把一般位置平面变为投影面垂直面
b
d
b1
a
c b d c
D
V X d1H1 H a1 a c1
例题13
首 页
章目录
节目录
上一页
下一页
直线与平面垂直的几何条件:若一直线垂直于一平面,则必垂直于属于该
平面的一切直线。
首 页
章目录
节目录
上一页
下一页
定理1 若一直线垂直于一平面、则直线的水平投影必垂直于属 于该平面的水平线的水平投影;直线的正面投影必垂直于属于 该平面的正平线的正面投影。 n k
c
k
首 页 章目录
●
b c
上一页 下一页
节目录
例2
已知M点在平面EFG上,求M点的水平投影。
f m
●
h g
e f h g
e
●
m
通过在面内作 辅助线求解
首 页
章目录
节目录
上一页
下一页
例3 如图所示,已知一般位置平面ABCD的正面投影和 AB、
AD两条边的水平投影ab和ad,补全该面的水平投影。
首 页 章目录 节目录 上一页 下一页
[例题8] 试过定点K作特殊位置平面的法线。
h
h h
h h
首 页
h
(c)
(a)
章目录
节目录
上一页
下一页
(b)
两平面垂直的几何条件 若一直线垂直于一定平面,则包含这条直线的所有平面 都垂直于该平面。 A
D
首 页
章目录
节目录
上一页
下一页
反之,两平面相互垂直,则由属于第一个平面的任意一 点向第二个平面作的垂线必属于第一个平面。
首 页
例题4
章目录
例题5
节目录 上一页 下一页
一、直线与平面平行
若一直线平行于属于定平面的一直线,则该直线与平面平行
首 页 章目录 节目录 上一页 下一页
[例题1]
试判断直线AB是否平行于定平面
gAB不平行于定平面 首 页 章目录 节目录 上一页 下一页
[例题2] 试过点K作水平线AB平行于ΔCDE平面
章目录
节目录
上一页
下一页
四、一般位置平面与特殊位置平面相交
求两平面交线的问题可以看作是求两个共有点的问题, 由于特殊位置平面的某个投影有积聚性,交线可直接求出。
一般位置平面与特殊位置平面相交
判断平面的可见性
首 页
章目录
节目录
上一页
下一页
m
M B K F m C P
b
f n k l
c
d
c
首 页 章目录 节目录 上一页 下一页
[例题]
求点S到平面ABC的距离
k1
s1 距离
首 页
章目录
节目录
上一页
下一页
[例题] 已知E到平面ABC的距离为N,求E点的正面投影e。 [选讲]
d e
N
d
首 页 章目录 节目录 上一页 下一页
(二) 把投影面垂直面变为投影面平行面
c1 V1 a1
c
分析:ABCD
b k
d
既然是平面, 则它的对角线必相交。
作图:
a a b k d
1)连接a′、c′和b′、d′,得交点k′;
2)连接b、d,在bd上求出 k,并连接a、k; 3)在ak上求出c,连接b、c 和d、c,即得该平面的水平 投影;
下一页
c
首 页 章目录 节目录 上一页
例 完成平面的水平投影
b1
首 页
X1
章目录
节目录
上一页
下一页
c1 b1 a1
首 页
章目录
节目录
上一页
下一页
(三) 把一般位置平面变为投影面平行面 a2 b2 d2 d c2 实形
d
首 页 章目录 节目录 上一页 下一页
[例题] 已知E点在平面ABC上,距离A、B为15,求点E的投影。 a2
15
第五讲基本内容:
一、平面上的点和直线
二、平面的辅助投影 三、线面相对位置
首 页
章目录
节目录
上一页
下一页
一、平面上的点和直线
(1)平面上取任意直线
如何判断直线在平面内?
方法一:
若一直线通过平面上的两点, 则此直线必在该平面内。
方法二:
若一直线通过平面上的一点,且 平行于该平面上的另一直线, 则此直 线在该平面内。
a k b
a l
A L
N b n k a l
m f
f
c
n
c PH
首 页
章目录
节目录
上一页
下一页
判断平面的可见性
首 页
章目录
节目录
上一页
下一页
结果
判断平面的可见性
首 页
章目录
节目录
上一页
下一页
直线与平面垂直、两平面垂直
一、直线与平面垂直 几何条件 定理1 定理2 例题7 例题8 例题9 例题10 二、两平面垂直 几何条件 例题11 例题12
有关线、面平行的作图问题有:判别已知线面是否平行;作直线与已 知平面平行;包含已知直线作平面与另一已知直线平行。
例题1
例题2
二、平面与平面平行 几何条件 若一个平面内的相交二直线与另一个平面内的相交二直线对应 平行,则此两平面平行。这是两平面平行的作图依据。 两面平行的作图问题有:判别两已知平面是否相互平行;过一点作一 平面与已知平面平行;已知两平面平行,完成其中一平面的所缺投影。 例题3
