形式语言与自动机理论试题答案解析
《形式语言与自动机》(王柏、杨娟编著)课后习题答案-推荐下载

P2
9.对应图(a)(b)的状态转换图写出正则式。(图略) (1) 由图可知 q0=aq0+bq1+a+ε
q1=aq2+bq1 q0=aq0+bq1+a =>q1=abq1+bq1+aaq0+aa =(b+ab) q1+aaq0+aa =(b+ab) *( aaq0+aa)
=>q0=aq0+b(b+ab) *( aaq0+aa ) +a+ε
(2) 由生成式得:
S=aA+B ①
A=bB+cC ② B=a+bB ③ C=D+abB ④ D=dB ⑤ 由③得 B=b*a ⑥ 将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦ 将⑥⑦代入② A=b+a+c(d+b+a) ⑧ 将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a
=ab+a+acd+acab+a+b*a
4.对下列文法的生成式,找出其正则式 (1) G=({S,A,B,C,D},{a,b,c,d},P,S),生成式 P 如下:
S→aA S→B
A→abS A→bB
B→b B→cC
C→D D→bB
D→d
(2) G=({S,A,B,C,D},{a,b,c,d},P,S),生成式 P 如下:
S→aA S→B
P: S→aS S→bS S→ε
(2) 右线性文法 G=({S},{a,b},P,S)
P: S→aS S→bS S→abb
形式语言与自动机Chapter6练习参考解答

Chapter 6 练习参考解答Exercise 6.2.1 设计PDA 使它接受下列语言,你可以使用以终结状态方式接受或者以空栈方式接受中方便的一个。
b) 所有由0,1 构成的,并且任何前缀中 1 的个数都不比0 的个数多的串的集合。
c) 所有0,1 个数相同的0,1 串的集合。
参考解答:b)构造以终态方式接受的PDA P = (Q,艺,r , S , q o, Z o, F),其中Q={q o};状态q o表示当前扫描过的输入串的任何前缀中1的个数不比0的个数多;工={0 , 1};r ={ Z o, X};下推栈中,X的个数表示当前扫描过的输入串中o的个数比1 的个数多多少;F={q o};S (q o,o, Z o)={( q o,X Z o)}, S (q o,o, X)={( q o,X X)}, S (q o,1, X)={( qo, )}.c)构造以空栈方式接受的PDA P = (Q, 2 , r , S , q o, Z o),其中Q={q o, q i };状态q o表示当前扫描过的输入串的任何前缀中o的个数不少于1 的个数,状态q1 表示当前扫描过的输入串的任何前缀中 1 的个数不少于o 的个数;2 ={o, 1};r ={ Z o, X };下推栈中,X的个数表示当前扫描过的输入串中o的个数比i 的个数或 1 的个数比o 的个数多多少;S(q o,o, Z o)={( q o,X Z o)}, S(q o,1, Z o)={( q1,X Z o)};S (q i,O, Z o)={( q o,X Z o)}, S (q i,1, Z o)={( q i,X Z o)};S (q o,O, X)={( q o,X X)}, S (q o,1, X)={( q o, )};S(q1,o, X)={( q 1, )},S(q1,1, X)={( q 1, X X)} ;S(q o, , Z o)={( q o, )},S(q1, , Z o)={( q1, )}.Exercise 6.3.2 把下面的文法S aAAA aS | bS | a转换成以空栈方式接受同样语言的PDA 。
形式语言与自动机理论_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年

形式语言与自动机理论_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.令字母表【图片】, 则克林闭包【图片】中元素的长度为?参考答案:只能是有限的2.由字符0和1构成且含有奇数个1的DFA,至少需要几个状态?参考答案:23.双栈PDA可以接受任意图灵机接受的语言。
参考答案:正确4.由某字母表【图片】中的字符构成的全部正则表达式的集合,也可以看做是一个语言,则该语言为:参考答案:上下文无关语言5.由字符0和1构成且含有奇数个1和偶数个0的DFA,至少需要几个状态?参考答案:46.字符串的长度可以是任意的,那么也可以是无穷长的。
参考答案:错误7.设【图片】和【图片】是字母表【图片】上的任意语言且【图片】是无穷的,则两个语言的连接【图片】一定是无穷的。
参考答案:错误8.每一个有穷的语言都是正则语言。
参考答案:正确9.任何正则语言都是上下文无关语言。
参考答案:正确10.任意有穷集合的克林闭包一定是无穷集合。
参考答案:错误11.递归可枚举语言是可判定的语言。
参考答案:错误12.任何有限的语言都是上下文无关语言。
参考答案:正确13.NFA处于某个状态q且输入某字符a时,如果状态转移函数未定义,则NFA会:参考答案:停止自动机的运行,并拒绝该串。
14.有穷自动机有了空转移(不消耗输入串的状态跳转), 改变了它识别语言的能力。
参考答案:错误15.对同一个语言,可能存在两个不同的有穷自动机识别。
参考答案:正确16.带有空转移的非确定有穷自动机中,对于某一个状态,是否可以同时存在“对某字符a的非确定性”和“空转移”?参考答案:可以。
17.图灵机是算法的好模型。
参考答案:错误18.确定的图灵机与非确定的图灵机等价。
参考答案:正确19.由字符0和1构成且含有偶数个1的DFA,至少需要几个状态?参考答案:220.如果一个语言是不可判定的,那么它的补也一定是不可判定的参考答案:错误21.确定的有穷自动机中,“确定的”含义是:参考答案:状态转移是确定的22.由字符0和1构成且长度为偶数的全部字符串的DFA,至少需要几个状态?参考答案:223.集合的克林闭包与正比包一定不相等参考答案:错误24.设【图片】是字母表【图片】上的任意语言,则语言【图片】的闭包【图片】一定是无穷的。
形式语言与自动机蒋宗礼答案

形式语言与自动机蒋宗礼答案形式语言与自动机蒋宗礼答案【篇一:形式语言第四章参考答案(蒋宗礼)】p> 解:所求正则表达式为:(0+1)*。
+⑵ {0, 1}。
解:所求正则表达式为:(0+1)+。
⑶ { x│x∈{0,1}且x中不含形如00的子串 }。
解:根据第三章构造的fa,可得所求正则表达式为:1*(01+)*(01+0+1)。
⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。
++ +q1为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)* 将以上5个正则表达式用“+”号相连,就得到所要求的正则表达式。
⑺ { x│x∈{0,1}且当把x看成二进制数时,x模5与3同余和x为0时,│x│=1且x≠0时,x的首字符为1}。
解:先画出状态转移图,设置5个状态q0、q1、q2、q3、q4,分别表示除5的余数是0、1、2、3、4的情形。
另外,设置一个开始状态q.由于要求x模5和3同余,而3模5余3,故只有q3可以作为终态。
由题设,x=0时,│x│=1,模5是1,不符合条件,所以不必增加关于它的状态。
下面对每一个状态考虑输入0和1时的状态转移。
q: 输入1,模5是1,进入q1。
+q0: 设x=5n。
输入0,x=5n*2=10n,模5是0,故进入q0输入1,x=5n*2+1=10n+1,模5是1,故进入q1q1:设x=5n+1。
输入0,x=(5n+1)*2=10n+2,模5是2,故进入q2输入1,x=(5n+1)*2+1=10n+3,模5是3,故进入q3 q2:设x=5n+2。
形式语言与自动机答案蒋宗礼

形式语言与自动机答案蒋宗礼【篇一:形式语言第四章参考答案(蒋宗礼)】p> 解:所求正则表达式为:(0+1)*。
+⑵ {0, 1}。
解:所求正则表达式为:(0+1)+。
⑶ { x│x∈{0,1}且x中不含形如00的子串 }。
解:根据第三章构造的fa,可得所求正则表达式为:1*(01+)*(01+0+1)。
⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。
++ +q1为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)*将以上5个正则表达式用“+”号相连,就得到所要求的正则表达式。
⑺ { x│x∈{0,1}且当把x看成二进制数时,x模5与3同余和x为0时,│x│=1且x≠0时,x的首字符为1}。
解:先画出状态转移图,设置5个状态q0、q1、q2、q3、q4,分别表示除5的余数是0、1、2、3、4的情形。
另外,设置一个开始状态q.由于要求x模5和3同余,而3模5余3,故只有q3可以作为终态。
由题设,x=0时,│x│=1,模5是1,不符合条件,所以不必增加关于它的状态。
下面对每一个状态考虑输入0和1时的状态转移。
q: 输入1,模5是1,进入q1。
+q0: 设x=5n。
输入0,x=5n*2=10n,模5是0,故进入q0输入1,x=5n*2+1=10n+1,模5是1,故进入q1q1:设x=5n+1。
输入0,x=(5n+1)*2=10n+2,模5是2,故进入q2输入1,x=(5n+1)*2+1=10n+3,模5是3,故进入q3 q2:设x=5n+2。
形式语言与自动机 形式语言与自动机理论-蒋宗礼-第三章参考答案

形式语言与自动机形式语言与自动机理论-蒋宗礼-第三章参考答案导读:就爱阅读网友为您分享以下“形式语言与自动机理论-蒋宗礼-第三章参考答案”的资讯,希望对您有所帮助,感谢您对的支持!因此我们只需要证明对任何的2NFA M1?(Q1,?,?1,F1,q0),都存在FAM2?(Q2,?,?2,F2,q0)与之等价。
对于任何的2NFA M1?(Q1,?,?1,F1,q0),构造FA M2?(Q2,?,?2,F2,q0),按三个方式构造?2:1.如果q?Q1,a??,?1(q,a)?{p,R},则?2(q,a)?p;2.如果q?Q1,a??,?1(q,a)?{p,S},则如果??1(p,a)?{o,R},则?2(q,a)?o;如果??1(p,a)?{o,S},则重复第二步;如果??1(p,a)?{o,L},则对于集合A = {r|b?Q1,?1(r,b)?(o,R)},?2(q,a)?r,r?A。
3.如果q?Q1,a??,?1(q,a)?{p,L},则设集合 A = {r|b?Q1,?1(r,b)?(p,R)},?2(q,a)?r,r?A*************************************************** ****************************28.证明定理3-8:Moore机与Mealy机等价(郭会02282015)证明:不妨设Moore机M1=(Q1,?,?,?1,?1,q01),Mealy机M2=(Q2,?,?,?2,?2,q02),则根据Moore机和Mealy机等价的定义知,必须证明:T1(x)??1(q0)T2(x),其中T1(x)和T2(x)分别表示M1和M2关于x的输出。
??Moore机M1,?Mealy机M2,使M2与M1等价(1)构造M2,?2??1,q02?q01,Q2?Q1?q?Q1?{q01},?1(q)?a,?q'?Q1且?b??,?1(q',b)=q,就构造?2(q',b)=a(2)证明?x??*,?1(q0)T2(x)?T1(x)不妨设x?x1x2……xn,则?i?N,(i?1,2……n)则M1的输出为:T1(x)??1(q0)?1(?1(q0,x1))……?1(?1((…?1(q0,x1),x2)…),xn)由题意可知?1(q0,x1),?1(?1(q0,x1),x2),…,?1(……?1 (?1(q0,x1),x2) xn) 均为Moore机中的状态,由(1)中的构造假设知,M2的输出为:T2(x)??2(q0,x1)?2(?2(q0,x1),x2)…?2(……?2(?2(q0,x1),x2) ? ?1(q0,x1)?1(?1(q0,x1),x2)…?1(……?1(?1(q0,x1),x2) xn) xn) ?T1(x)??1(q0)T2(x)??Mealy机M2,?Moore机M1,使M1与M2等价(1)构造M1,q01?q02Q1?Q2?{qij|??2(qi,a)?qj,其中qi,qj?Q2,a??}?1?{?|?(qi,a)?qij,?(qij,?)?qj其中?2(qi,a)?qj}?1?{?|?1(qi,a)?qij,?1(qij,?)?qj,?(qij)??2(qi,a) }(2)证明?x??*,T1(x)=?1(q0)T2(x)不妨设x?x1x2……xn,则?i?N,(i?1,2……n)则M1的输出为:T2(x)??2(?2(q0,x1))……?2(?2((…?2(q0,x1),x2)…),xn) 由题意可知?2(q0,x1),?2(?2(q0,x1),x2),…,?2(……?2 (?2(q0,x1),x2) xn) 均为Mealy机中的状态,由(1)中的构造假设知,M1的输出为:T1(x)??1(q0)?1(?2(q0,x1))?1(?1(q0,x1),x2)…?1(……?1(?1(q 0,x1),x2) xn)??1(q0)?2(?2(q0,x1))……?2(?2((…?2(q0,x1),x2)…),xn) ?T1(x)??1(q0)T2(x)综上所述,Moore机与Mealy机等价第三章作业答案1.已知DFA M1与M2如图3-18所示。
形式语言与自动机课后习题答案部分

– 产生语言{0x|x{0, 1}*}的文法
• S0A;
– G: S0A A|0A|1A
2013-7-24 (C)Guohong Fu, CS@HLJU 11
G F H
课后作业二 (cont.)
• 习题8(3)的解答
– 分析:语言的特点
• {11x11|x*}{111, 11};
– 产生语言{x|x{0, 1}*}的文法
G F H
课后作业二 (cont.)
• pp.84:习题 8
设={0, 1},构造产生下列语言的文法 (1) 所有以0开头的串; (3) 所有以11开头,以11结尾的串;
• 8(1)解答
– 分析语言的特点: {0x|x{0, 1}*}; – 产生子语言{x|x{0, 1}*}的文法
• A|0A|1A;
– 习题 15(1) --- -NFANFA
2013-7-24
(C)Guohong Fu, CS@HLJU
20
G 课后作业四 (cont.) F H pp.128 习题 11(1) 构造与NFA M等价的DFA M
2013-7-24 (C)Guohong Fu, CS@HLJU 2
G F H – – – –
课后作业一
• pp.39-41:L基本概念
习题 21 ---字母表 习题 22 --- 前/后缀 习题 23 --- 前/后缀 习题 28(1)(2)(10) --- L的描述
2013-7-24
(C)Guohong Fu, CS@HLJU
用自然语言描述下列文法定义的语言
G: AaaA|aaB BBcc|D#cc DbbbD|#
• 解题思路
– 观察每个产生式及其组合产生的子语言的特点; – 根据开始符的产生式将它们并起来就是整个文法产生的语言;
《形式语言与自动机》期末复习题及答案(一)

形式语言与自动机期末复习题及答案(一)1.有图灵机 M=(Q, ∑, Γ, δ,q 0 , B , F) 接受语言{w t w│w ∈{a, b}*},按照下图说明其接受过程。
(本题15分 )[q 1[q 6,B]答:abtab 的分析过程:[q 1,B]abtab├a [q 2,a]btab├ab [q 2,a]tab├abt [q 3,a]ab├ ab [q 4,B]tab├a [q 5,B]btab├[q 6,B]abtab├a [q 1,B]btab ├ab [q 2,b]tab├abt [q 3,b]ab ├abta [q 3,b]b ├abt [q 4,B]ab├a [q 5,B]btab ├ab [q 7,B]tab ├abt [q 8,B]ab├abta [q 8,B]b ├abtab [q 8,B]B├abta [q 9,B]b 接受abtab√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√√2.简述《形式语言与自动机》课程的主要内容。
(本题10分)答:语言的文法描述;RL (RG 、FA 、RE 、RL 的性质 );CFL (CFG(CNF 、GNF)、PDA 、CFL 的性质);TM (基本TM 、构造技术、TM 的修改);CSL (CSG 、LBA )。
3.简述《形式语言与自动机》课程的学习目的和基本要求。
(本题10分) 答:本专业人员4种基本的专业能力:计算思维能力、算法的设计与分析能力、程序设计和实现能力、计算机软硬件系统的认知、分析、设计与应用能力。
其中计算思维能力包括:逻辑思维能力和抽象思维能力、构造模型对问题进行形式化描述、理解和处理形式模型。
本课程应使学生掌握如下知识:正则语言、下文无关语言的文法、识别模型及其基本性质、图灵机的基本知识。
锻炼培养如下能力:形式化描述和抽象思维能力、了解和初步掌握“问题、形式化描述、自动化(计算机化)”这一最典型的计算机问题求解思路。
形式语言与自动机课后习题答案部分PPT69页

16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
《形式语言与自动机》(王柏、杨娟编著)课后习题答案

形式语言与自动机课后习题答案第二章4.找出右线性文法,能构成长度为1至5个字符且以字母为首得字符串。
答:G={N,T,P,S}其中N={S,A,B,C,D} T={x,y} 其中x∈{所有字母} y∈{所有得字符} P如下: S→x S→xA A→y A→yBB→y B→yC C→y C→yD D→y6.构造上下文无关文法能够产生L={ω/ω∈{a,b}*且ω中a得个数就是b得两倍}答:G={N,T,P,S}其中N={S} T={a,b} P如下:S→aab S→aba S→baaS→aabS S→aaSb S→aSab S→SaabS→abaS S→abSa S→aSba S→SabaS→baaS S→baSa S→bSaa S→Sbaa7.找出由下列各组生成式产生得语言(起始符为S)(1)S→SaS S→b(2)S→aSb S→c(3)S→a S→aE E→aS答:(1)b(ab)n /n≥0}或者L={(ba)n b/n≥0}(2) L={a n cb n /n≥0}(3)L={a2n+1 /n≥0}第三章1.下列集合就是否为正则集,若就是正则集写出其正则式。
(1)含有偶数个a与奇数个b得{a,b}*上得字符串集合(2)含有相同个数a与b得字符串集合(3)不含子串aba得{a,b}*上得字符串集合答:(1)就是正则集,自动机如下题(2)。
(3) 就是正则集先瞧L’为包含子串aba得{a,b}*上得字符串集合显然这就是正则集,可以写出表达式与画出自动机。
(略)则不包含子串aba得{a,b}*上得字符串集合L就是L’得非。
根据正则集得性质,L也就是正则集。
4.对下列文法得生成式,找出其正则式(1)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→abS A→bBB→b B→cCC→D D→bBD→d(2)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→cC A→bBB→bB B→aC→D C→abBD→d答:(1) 由生成式得:S=aA+B ①A=abS+bB ②B=b+cC ③C=D ④D=d+bB ⑤③④⑤式化简消去CD,得到B=b+c(d+bB)即B=cbB+cd+b =>B=(cb)*(cd+b) ⑥将②⑥代入①S=aabS+ab(cb)*(cd+b)+(cb)*(cd+b) =>S=(aab)*(ab+ε)(cb)*(cd+b) (2) 由生成式得:S=aA+B ①A=bB+cC ②B=a+bB ③C=D+abB ④D=dB ⑤由③得 B=b*a ⑥将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦将⑥⑦代入② A=b+a+c(d+b+a) ⑧将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a=ab+a+acd+acab+a+b*a5、为下列正则集,构造右线性文法:(1){a,b}*(2)以abb结尾得由a与b组成得所有字符串得集合(3)以b为首后跟若干个a得字符串得集合(4)含有两个相继a与两个相继b得由a与b组成得所有字符串集合答:(1)右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→ε(2) 右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→abb(3) 此正则集为{ba*}右线性文法G=({S,A},{a,b},P,S)P: S→bA A→aA A→ε(4) 此正则集为{{a,b}*aa{a,b}*bb{a,b}*, {a,b}*bb{a,b}*aa{a,b}*}右线性文法G=({S,A,B,C},{a,b},P,S)P: S→aS/bS/aaA/bbBA→aA/bA/bbCB→aB/bB/aaCC→aC/bC/ε7、设正则集为a(b a)*(1)构造右线性文法(2)找出(1)中文法得有限自b动机答:(1)右线性文法G=({S,A},{a,b},P,S)P: S→aA A→bS A→ε(2)自动机如下:)9、对应图(a)(b)得状态转换图写出正则式。
形式语言与自动机理论-蒋宗礼-第四章参考答案

1.写出表示下列语言的正则表达式。
(吴贤珺02282047)⑴{0, 1}*。
解:所求正则表达式为:(0+1)*。
⑵{0, 1}+。
解:所求正则表达式为:(0+1)+。
⑶{ x│x∈{0,1}+ 且x中不含形如00的子串 }。
解:根据第三章构造的FA,可得所求正则表达式为:1*(01+)*(01+0+1)。
⑷{ x│x∈{0,1}*且x中不含形如00的子串 }。
解:根据上题的结果,可得所求正则表达式为:ε+1*(01+)*(01+0+1)。
⑸{ x│x∈{0,1}+ 且x中含形如10110的子串 }。
解:所求正则表达式为:(0+1)*10110(0+1)*。
⑹ { x│x∈{0,1}+ 且x中不含形如10110的子串 }。
解:根据第三章的习题,接受x的FA为:要求该FA对应的正则表达式,分别以q0、q1、q2、q3、q4为终结状态考虑:q为终态时的正则表达式:(0*(11*0(10)*(ε+111*11*0(10)*)0)*)*q为终态时的正则表达式:0*1(1*(0(10)*111*1)*(0(10)*00*1)*)*1q为终态时的正则表达式:0*11*0((10)*(111*11*0)*(00*11*0)*)*2q为终态时的正则表达式:0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)*3q为终态时的正则表达式:0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)*4将以上5个正则表达式用“+”号相连,就得到所要求的正则表达式。
⑺ { x│x∈{0,1}+ 且当把x看成二进制数时,x模5与3同余和x为0时,│x│=1且x≠0时,x的首字符为1}。
解:先画出状态转移图,设置5个状态q0、q1、q2、q3、q4,分别表示除5的余数是0、1、2、3、4的情形。
另外,设置一个开始状态q.由于要求x模5和3同余,而3模5余3,故只有q3可以作为终态。
形式语言与自动机理论蒋宗礼第一章参考复习资料

第一章参考答案1.1 请用列举法给出下列集合。
(吴贤珺02282047)⑴ 你知道的各种颜色。
解:{红,橙,黄,绿,青,蓝,紫}⑵ 大学教师中的各种职称。
解:{助教,讲师,副教授,教授}⑶ 你所学过的课程。
解:{语文,数学,英语,物理,化学,生物,历史,地理,政治}⑷ 你的家庭成员。
解:{ 父亲,母亲,妹妹,我}⑸ 你知道的所有交通工具。
解:{ 汽车,火车,飞机,轮船,马车}⑹ 字母表{a , b} 上长度小于 4 的串的集合。
解:{a,b,aa,bb,ab,ba,aaa,aab,aba,abb,baa,bab,bba,bbb}⑺ 集合{1,2,3,4} 的幂集。
解:{①,{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4}, {1,3,4},{2,3,4},{1,2,3,4} }⑻ 所有的非负奇数。
解: {135,7,…}⑼0〜100的所有正整数。
解: {1,2,3, (100)(10) 1〜10之间的和为10的整数集合的集合。
解:设所求的集合为A,集合A中的元素为A i (i=1,2,3,…),A i也是集合,A i中的元素在1〜10之间,并且和为10。
根据集合元素的彼此可区分性,可以计算出A i中元素的最多个数,方法是:把 1 开始的正整数逐个相加,直到等于10(即10=1+2+3+4),这样,A i中最多有4个元素。
原因是:从最小的1开始,每次加入新的元素都只依次增加1,这样相加的和最小,要加到10,元素个数就最多。
求出最大的I A i 1= 4后,再求出元素个数为3, 2, 1的集合就可以了。
故A={{10},{1,9},{2,8},{3,7},{4,6},{1,2,7},{1,3,6},{1,4,5},{2,3,5},{1,2,3,4}}1.2 请用命题法给出下列集合2.(1){x|0 x 100且x z}(2) {x|x {a,b}*且|x| 4}(3) {B|B {1,2,3,4}}(4) {L|L {a,b}*}(5) {x|x 2n 1,n N}(6) {(a,b)|a b 10且a,b [4,9]}⑺{x|x {0,*,且x中0的个数是1的个数的两倍}(8){x|x {0,*,且x中 1 的个数是10}(9){ x|x {0,1}*,且x中倒数第十个字符为1}|A||(10){A| x i A,x i [1,10],i [1,|A|], x i=10}i11.3 给出下列集合的幂集. ( 02282075 冯蕊)(1) ①⑵{①}(3) {①,{①}}⑷{ & ,0,00}(5) {0,1}解答:(1) {①}(2) {①,{①}}⑶{①,{①},{{①}},{①,{①}}}⑷{①,{ & },{0},{00},{ & ,0},{ & ,00},{0,00},{ & ,0,00}}①,{0},{1},{0,1}}1.4.列出集合{0,1 ,2,3,4}中(褚颖娜02282072)( 1) 所有基数为3 的子集{0,1,2},{0,1,3},{0,1,4},{0,2,3,} ,{0 ,2,4} ,.{1 ,2,3} ,{1 ,2,4},{1,3,4} ,{0,3,4},{2,3,4}(2) 所有基数不大于 3 的子集①,{0} , {1} , {2} , {3} , {4} , {3 , 4} , {2 , 4} , {2 , 3}, {1 , 4} , {1 , 3}, {0 , 4} ,{0 ,3} ,{0 ,2} ,{1 ,2} ,{0 ,1} ,{0 ,1,2} ,{0 ,1,3}{0,1,4},{0,2,3,},{0,2,4},.{1 ,2,3},{1 ,2,4},{1 ,3,4},{0,3,4},{2,3,4}1.5 解答:1、3、8、10、11、12、16正确1.6 证明下列各题目02282081 刘秋雯) 1) A=B iff A 是B的子集且B是A的子集证明:充分条件:•/ A=B则由集合相等的定义知对于任何x € A,有x € B••• A为B的子集同理, B 为 A 的子集必要条件:••• A为B的子集•对于任何x € A,都有x € B又••• B为A的子集,•对于任何x€ B 有,x€ A由集合相等的定义知,A=B2) 如果A为B的子集,则|A| 〈=|B|证明:A 为B 的子集,则对于任何x€ A 有x€ B,•存在一个集合C使B=A U C 且A n C为空集则|B|=|A|+|C| |C|〉=0• |A|〈=|B|3) 如果A为B的真子集,则|A| 〈=|B|证明:(1)当 A 为有穷集合时,因为 A 为B 的真子集,且则对于任何x€ A 有x€ B,且存在€ B的x,此x不€ A•存在一个非空集合 C ,使B=A U C 且A n C 为空集则|B|=|A|+|C| 且|C|> =1• |A|〈|B|(2)当A为无穷集合,因为A为B的真子集,则 B 一定也为无穷集合,|A| = s, |B|=m• |A|=|B|综合( 1),(2)所述,|A|<=|B|4) 如果A是有穷集且A为B的真子集则|A| 〈 |B|证明:见上题证明( 1 )5) 如果A为B的子集,则对于任何x € A,有x€ B证明:若A为B的子集,则由子集定义可知,对于任何x€ A,有x€ B6) 如果A是B的真子集,则对于任何x€ A,有x € B,并且存在x€ B,但x不€ A证明:由真子集的定义可证7)如果A为B的子集,B为C的子集,贝U A为C的子集证明:A为B的子集,B为C的子集则对于任何x € A,则x都€ B, 且,又对于任何y € B,贝Uy€ C,「.对于任何x€ A,x€ C••• A为C的子集8)如果A为B的真子集,B为C的真子集,贝U A为C的真子集证明:A为B的真子集,B为C的真子集则对于任何x € A,则x都€ B,且,存在x€ B 但次x 不€ A,又对于任何y€ B,则y€ C,存在y € C但此y不€ B,•••对于任何x€ A,x € C,存在x€ C.x不€ A• A为C的真子集9)如果A为B的子集,B为C的真子集,贝U A为C的真子集证明:因为 A 为 B 的子集, B 为 C 的真子集则对于任何x € A,x都€ B,且x都€ C又对于任何y€ B,则y€ C,存在y € C但此y不€ B,则y不€ A•••对于任何x€ A,x € C,存在x€ C.x不€ A• A为C的真子集10)如果A为B的真子集,B为C的子集,贝U A为C的真子集证明:A为B的真子集,B为C的子集则对于任何x € A,则x都€ B,且存在x€ B 但次x 不€ A,又对于任何y€ B,贝U y€ C•••对于任何x€ A,x € C,存在x€ C.x不€ A• A为C的真子集11)如果A=B 则|A| = |B|证明:A=B ,则A 与B 所含元素相同• |A|=|B|12)如果A为B的子集,B为C的真子集,或如果A为B的真子集集,为C的子则A为C的真子集证明:证明见9,101.7 A = {1,2,3,4,5,6} B = {1,3,5} C = {2,4,6} U = {0,1,2,3,4,5,6,7,8,9}(1). A B={1,3,5} = B(2) .(A B) C={1,3,5} {2,4,6}={1,2,3,4,5,6} = A(3) .(A B) (U C)={1,3,5} {0,135,7,8,9}={0,135,7,8,9} = C(4) .A-B-C={2,4,6} -{2,4,6}⑸.A X B X C XA X =⑹.(A B) A C A={1,3,5} {0,7,8,9} {0,7,8,9}={0,1,3,5,7,8,9} = C(7). ABAC=A B C=A {(a,b)|(a B,b C)或(a B,b C)或(a B,b C)}C)} ={(a,b,c)|(a A,b B,c C)或(a A,b B,c C)或(a A,b B,c(8). A B (A B) C=A A C=A C=A={1 , 2, 3, 4, 5, 6}1. 8对论域U上的集合A、B、C,证明以下结论成立。
2008-2009第一学期形式语言与自动机考查试卷(A)-答案-open

2008—2009第一学期形式语言与自动机考查试卷(A)参考答案及评分标准(院系:计算机科学技术 专业:计算机科学技术 年级:2006 考核形式:开卷)(一)填空题(本大题共10个空,每空3分,总计30分)(3) 设r=1*Φ,则L(r)= Φ。
解答:步骤不清或中间步骤出错者可酌情扣去1分(1)分析语言的特点:----------------------------------------------------------------------4语言L可分为两个子语言,即L1={0n1n|n≥0}和L2={1n0n|n≥0},且L=L1⋃L2。
因此,为了构造产生L的文法,可分别先构造产生子语言L1和L2的文法,然后利用L= L1⋃L2两个文法合在一起即可。
(2)构造产生子语言L1={0n1n|n≥0}的文法G1:A→0A1|ε;-------------------------3(3)构造产生子语言L2={1n0n|n≥0}的文法G2:B→1B0|ε;-------------------------3(4)由于L=L1⋃L2,因此在G1和G2基础上引入产生式S→A|B,即得到产生L的文法G:------------------------------------------------------------------------------4S→A|BA→0A1|εB→0B1|ε四、等价转换题(本大题共1小题,每小题12分,总计12分)将下列CFG G 等价转化为乔姆斯基范式(要求给出具体步骤)G: S→ASA|aBA→B|SB→b|ε解答:步骤不清或中间步骤出错时可酌情扣1分(1) 化简:删除B→ε后得------------------------------------------------------------------2S→ASA|aB|aA→B|S|εB→b(2) 化简:删除A→ε后得------------------------------------------------------------------2S→ASA|aB|a|AS|SA|SA→B|SB→b(3) 化简:删除S→S和A→B后得-------------------------------------------------------1S→ASA|aB|a|AS|SAA→b|SB→b(4) 化简:删除A→S后得-----------------------------------------------------------------1S→ASA|aB|a|AS|SAA→b| ASA|aB|a|AS|SAB→b(5) 转化为CNF:A→B1B2…B m和A→a-----------------------------------------------3引入变量A a和产生式A a→a将(4)中产生式转化为S→ASA|A a B|a|AS|SAA→b| ASA|A a B|a|AS|SAB→bA a→a(6)转化为CNF:A→BC和A→a形式---------------------------------------------------3引入变量A1和产生式A1→SA将(5)中产生式转化为S→AA1|A a B|a|AS|SAA→b| AA1|A a B|a|AS|SAA1→SAB→bA a→a五、构造题(本大题共1小题,每小题14分,总计14分)构造确定型下推自动机 M,使得L(M)={0n1m0n|m≥0,n≥1}。
形式语言与自动机理论--第三章参考答案
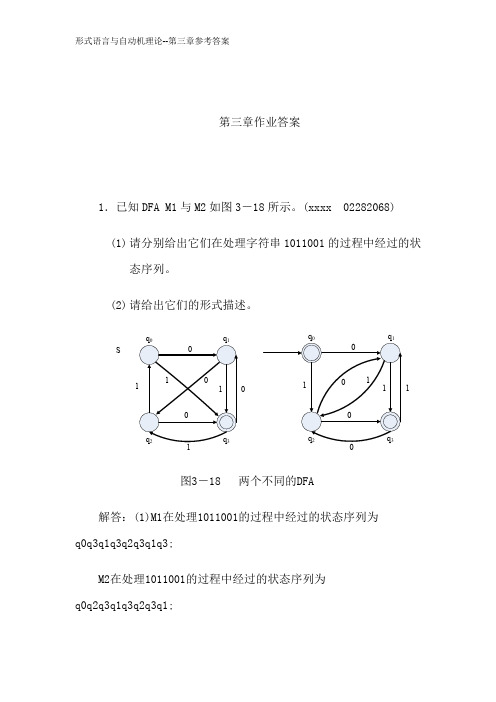
第三章作业答案1.已知DFA M1与M2如图3-18所示。
(xxxx 02282068) (1) 请分别给出它们在处理字符串1011001的过程中经过的状态序列。
(2) 请给出它们的形式描述。
Sq q1q q图3-18 两个不同的DFA解答:(1)M1在处理1011001的过程中经过的状态序列为q0q3q1q3q2q3q1q3;M2在处理1011001的过程中经过的状态序列为q0q2q3q1q3q2q3q1;(2)考虑到用形式语言表示,用自然语言似乎不是那么容易,所以用图上作业法把它们用正则表达式来描述:M1: [01+(00+1)(11+0)][11+(10+0)(11+0)]* M2: (01+1+000){(01)*+[(001+11)(01+1+000)]*} *******************************************************************************2.构造下列语言的DFA( xx02282085 ) (1){0,1}*,1(2){0,1}+,1(3){x|x{0,1}+且x 中不含00的串}(设置一个陷阱状态,一旦发现有00的子串,就进入陷阱状态)(4){ x|x{0,1}*且x中不含00的串}(可接受空字符串,所以初始状态也是接受状态)(5){x|x{0,1}+且x中含形如10110的子串}(6){x|x{0,1}+且x中不含形如10110的子串}(设置一个陷阱状态,一旦发现有00的子串,就进入陷阱状态)(7){x|x{0,1}+且当把x看成二进制时,x模5和3同余,要求当x为0时,|x|=1,且x0时,x的首字符为1 }1.以0开头的串不被接受,故设置陷阱状态,当DFA在启动状态读入的符号为0,则进入陷阱状态2.设置7个状态:开始状态qs,q0:除以5余0的等价类,q1:除以5余1的等价类,q2:除以5余2的等价类,q3:除以5余3的等价类,q4:除以5余4的等价类,接受状态qt3.状态转移表为(8){x|x{0,1}+且x的第十个字符为1}(设置一个陷阱状态,一旦发现x的第十个字符为0,进入陷阱状态)(9){x|x{0,1}+且x以0开头以1结尾}(设置陷阱状态,当第一个字符为1时,进入陷阱状态)(10){x|x{0,1}+且xxx至少含有两个1}(11){x|x{0,1}+且如果x以1结尾,则它的xx为偶数;如果x以0结尾,则它的xx为奇数}可将{0,1}+的字符串分为4个等价类。
形式语言与自动机理论-蒋宗礼-参考答案

2.1回答下面的问题: (周期律 02282067) (1)在文法中,终极符号和非终极符号各起什么作用?✓ 终结符号是一个文法所产生的语言中句子的中出现的字符,他决定了一个文法的产生语言中字符的范围。
✓ 非终结符号又叫做一个语法变量,它表示一个语法范畴,文法中每一个产生式的左部至少要还有一个非终结符号,(二,三型文法要求更严,只允许左部为一个非终结符号)他是推导或归约的核心。
(2)文法的语法范畴有什么意义?开始符号所对应的语法范畴有什么特殊意义? ✓ 文法的非终结符号A 所对应的语法范畴代表着一个集合L (A ),此集合由文法产生式中关于A 的产生式推导实现的✓ 开始符号所对应的语法范畴则为文法G = {V ,T ,P ,S}所产生的语言L (G )={w S T w w **|⇒∈且}(3)在文法中,除了的变量可以对应一个终极符号行的集合外,按照类似的对应方法,一个字符串也可以对应一个终极符号行集合,这个集合表达什么意义?✓ 字符串对应的终极符号行集合表示这个字符串所能推导到的终极字符串集合,为某个句型的语言。
(4)文法中的归约和推导有什么不同?✓ 推导:文法G = {V ,T ,P ,S},如果,)(,,*T VP ∈∈→δγβα则称γαδ在G 中推导出了γβδ。
✓ 归约:文法G = {V ,T ,P ,S},如果,)(,,*T VP ∈∈→δγβα则称γβδ在G 中归约到γαδ。
✓ 这他们的定义,我个人理解两个概念从不同角度看待文法中的产生式,推导是自上而下(从产生式的左边到右边),而归约是自下而上(从产生式的右边到左边),体现到具体实际中,如编译中语法分析时语法树的建立,递归下降,LL (1)等分析法采用自开始符号向下推导识别输入代码生成语法树,对应的LR (1),LALR 等分析法则是采用自输入代码(相当于文法中语言的句子)自底向上归约到开始符号建立语法树,各有优劣。
(5)为什么要求定义语言的字母表上的语言为一个非空有穷集合? ✓ 非空:根据字母表幂的定义:εε,}{0∑=为字母表中0个字符组成的。
形式语言与自动机理论试题答案解析
形式语言与自动机理论试题答案解析一、按要求完成下列填空1. 给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集 (2x4')(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}2. 设∑={0,1},请给出∑上的下列语言的文法 (2x5') (1)所有包含子串01011的串 S →X01011YX →ε|0X|1X Y →ε|0Y|1Y(2)所有既没有一对连续的0,也没有一对连续的1的串 A →ε|A ’|A ”A’ →0|01|01A ’ A ” →1|10|10A ”3. 构造识别下列语言的DFA 2x6'(1) {x|x {0,1}+且x 以0开头以1结尾} (设置陷阱状态,当第一个字符为1时,进入陷阱状态)1S110,10(2) {x|x{0,1}+且x 的第十个字符为1}(设置一个陷阱状态,一旦发现x 的第十个字符为0,进入陷阱状态)1S0,10,10,10,10,110,0,10,10,10,10,1二、判断(正确的写T ,错误的写F ) 5x2'1R 和2R 是集合{a,b,c,d,e}上的二元关系,则3231321)(R R R R R R R ⊆( T )任取(x.,y),其中x,y },,,,{e d c b a ∈,使得321)(),(R R R y x ∈。
)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒2.对于任一非空集合A ,Φ⊆A2 ( T ) 3.文法G :S A|AS A a|b|c|d|e|f|g 是RG ( F )2型语言1型语言0型语言 ( F )5.s (rs+s )*r=rr *s (rr *s )* ( F )不成立,假设r,s 分别是表示语言R ,S 的正则表达式,例如当R={0},S={1}, L(s(rs+s)*r)是以1开头的字符串,而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*) 所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立三、设文法G 的产生式集如下,试给出句子aaabbbccc 的至少两个不同的推导(12分)。
形式语言与自动机理论试题
形式语言与自动机理论试题一、按要求完成下列填空1.给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集 (2x4')(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}2.设∑={0,1},请给出∑上的下列语言的文法 (2x5')(1)所有包含子串01011的串 S →X01011YX →ε|0X|1X Y →ε|0Y|1Y(2)所有既没有一对连续的0.也没有一对连续的1的串 A →ε|A ’|A ”A’ →0|01|01A ’ A ” →1|10|10A ”3.构造识别下列语言的DFA 2x6'(1) {x|x ∈{0.1}+且x 以0开头以1结尾}(设置陷阱状态.当第一个字符为1时.进入陷阱状态)1S110,10(2) {x|x ∈{0.1}+且x 的第十个字符为1}(设置一个陷阱状态.一旦发现x 的第十个字符为0.进入陷阱状态)1S0,10,10,10,10,110,0,10,10,10,10,1二、判断(正确的写T.错误的写F ) 5x2'1.设1R 和2R 是集合{a,b,c,d,e}上的二元关系.则3231321)(R R R R R R R ⊆( T )任取(x.,y),其中x,y },,,,{e d c b a ∈.使得321)(),(R R R y x ∈。
)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒2.对于任一非空集合A.Φ⊆A2 ( T ) 3.文法G :S A|AS A a|b|c|d|e|f|g 是RG ( F )4.3型语言2型语言1型语言0型语言 ( T )5.s (rs+s )*r=rr *s (rr *s )* ( F )不成立.假设r,s 分别是表示语言R.S 的正则表达式.例如当R={0}.S={1},L(s(rs+s)*r)是以1开头的字符串.而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*)所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立三、设文法G 的产生式集如下.试给出句子aaabbbccc 的至少两个不同的推导(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形式语言与自动机理论试题答案解析
一、按要求完成下列填空
1.给出集合{Φ,{Φ}}和集合{ε,0,00}的幂集(2x4')
(1) {Φ,{Φ},{{Φ}},{Φ,{Φ}}}
(2) {Φ,{ε},{0},{00},{ε,0},{ε,00},{0,00},{ε,0,00}}
2.设∑={0,1},请给出∑上的下列语言的文法(2x5')
(1)所有包含子串01011的串
S→X01011Y
X→ε|0X|1X
Y→ε|0Y|1Y
(2)所有既没有一对连续的0,也没有一对连续的1的串
A→ε|A’|A”
A’→0|01|01A’
A”→1|10|10A”
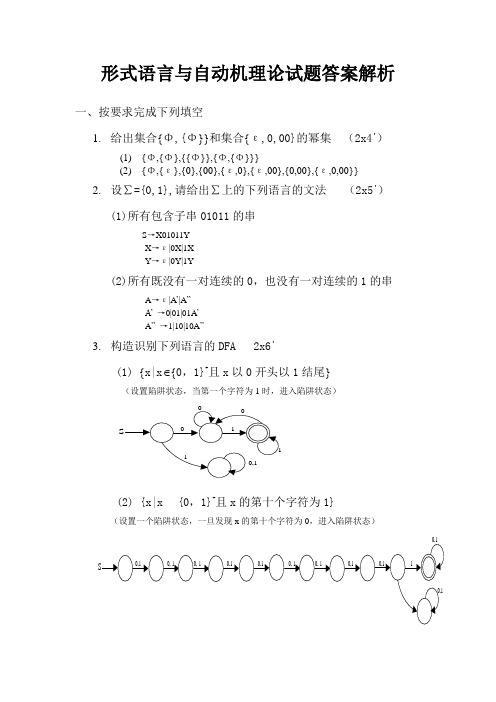
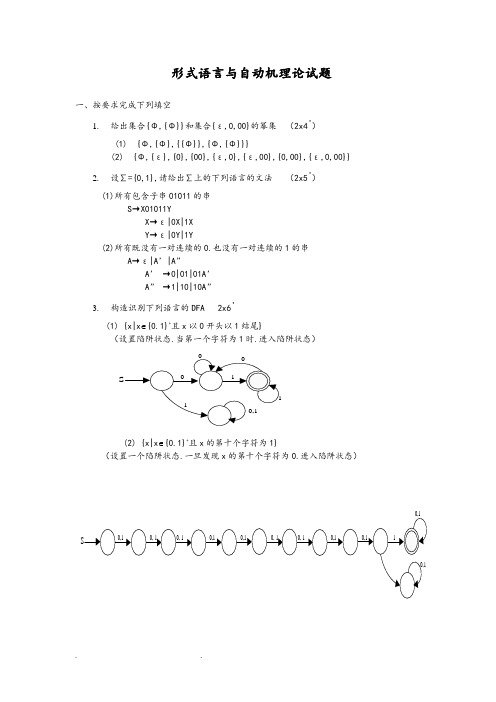
3.构造识别下列语言的DFA 2x6'
(1) {x|x∈{0,1}+且x以0开头以1结尾}
(设置陷阱状态,当第一个字符为1时,进入陷阱状态)
(2) {x|x∈{0,1}+且x的第十个字符为1}
(设置一个陷阱状态,一旦发现x的第十个字符为0,进入陷阱状态)
二、判断(正确的写T ,错误的写F ) 5x2'
1.设1R 和2R 是集合{a,b,c,d,e}上的二元关系,则
3231321)(R R R R R R R ⊆ ( T )
任取(x.,y),其中x,y },,,,{e d c b a ∈,使得321)(),(R R R y x ∈。
)),(),((321R y z R R z x z ∈∧∈∃⇒ },,,,{e d c b a z ∈ )),(),(),((321R y z R z x R z x z ∈∧∈∧∈∃⇒
)),(),(()),(),((3231R y z R z x z R y z R z x z ∈∧∈∃∧∈∧∈∃⇒ 3231),(),(R R y x R R y x ∈∧∈⇒ 3231),(R R R R y x ∈⇒
2.对于任一非空集合A ,Φ⊆A
2 ( T ) 3.文法G :S A|AS A a|b|c|d|e|f|g 是RG ( F ) 4.3型语言
2型语言
1型语言
0型语言 ( F )
5.s (rs+s )*r=rr *s (rr *s )* ( F )
不成立,假设r,s 分别是表示语言R ,S 的正则表达式,例如当R={0},S={1}, L(s(rs+s)*r)是以1开头的字符串,而L(rr*s(rr*s)*)是以0开头的字符串.L(s(rs+s)*r) ≠ L(rr*s(rr*s)*) 所以s(rs+s)*r ≠ rr*s(rr*s)*,结论不成立
三、设文法G 的产生式集如下,试给出句子aaabbbccc 的至少两个不同的推导(12分)。
aSBC
aBC S |→ ab aB →
bB →bb CB →BC bC →bc cC →cc
推导一: S=>aSBC
=>aaSBCBC =>aaaBCBCBC =>aaabCBCBC =>aaabBCCBC =>aaabbCCBC =>aaabbCBCC =>aaabbBCCC =>aaabbbCCC =>aaabbbcCC =>aaabbbccC =>aaabbbccc
推导二:
S=>aSBC
=>aaSBCBC =>aaaBCBCBC
=>aaaBBCCBC =>aaaBBCBCC
=>aaabBCBCC
=>aaabbCBCC
=>aaabbBCCC =>aaabbbCCC =>aaabbbcCC
=>aaabbbccC =>aaabbbccc
四、判断语言{n n n 010|n>=1}是否为RL ,如果是,请构造出它的有穷描述(FA,RG 或者RL );如果不是,请证明你的结论(12分)
解:设L={n n n 010|n>=1}。
假设L 是RL ,则它满足泵引理。
不妨设N 是泵引理所指的仅依赖于 L 的正整数,取Z=N N N 010 显然,Z ∈L 。
按照泵引理所述,必存在u ,v ,w 。
由于|uv|<=N,并且|v|>=1,所以v 只可能是由0组成的非空串。
不妨设v=k 0,k>=1 此时有u=j k N --0 ,w=N N j 010 从而有uv i w=N N j i k j k N 010)0(0-- 当i=2时,有uv 2w=N N k N 010+ 又因为k>=1, 所以 N+k>N 这就是说N N k N 010+不属于L , 这与泵引理矛盾。
所以,L 不是RL 。
五、构造等价于下图所示DFA 的正则表达式。
(12分)
答案(之一):(
01+(1+00)((1+00*1)0)*((1+00*1)1)
)*
(ε+(1+00)((1+00*1)0)*00*)
去掉q 3:
去掉q 1
3Y
2Y
Y
S
30
.
去掉q 2:
去掉q 0:
六、设M=({210,,q q q },{0,1},{0,1,B},{δ},0q ,B,{2q }),其中δ的定义如下:
δ(0q ,0)=(0q ,0,R ) δ(0q ,1)=(1q ,1,R ) δ(1q ,0)=(1q ,0,R ) δ(1q ,B )=(2q ,B ,R )
请根据此定义,给出M 处理字符串00001000,10000的过程中ID 的变化。
(10分)
解:处理输入串00001000的过程中经历的ID 变化序列如下:
0q 00001000
00q 0001000 000q 001000 0000q 01000 00000q 10000
000011q 0000
0000101q 00
00001001q 0
000010001q
00001000B 2q
处理输入串10000的过程中经历的ID 变化序列如下: 0q 10000 11q 00000 101q 000 1001q 00 10001q 0 100001q
10000B 2q
七、根据给定的NFA ,构造与之等价的DFA 。
(14分) NFA M 的状态转移函数如下表
q 0
ε
X
Y
ε+(1+00)((1+00*1)0)*00*
01+(1+00)((1+00*1)0)*((1+00*1)1)
X
Y
(01+(1+00)((1+00*1)0)*((1+00*1)1))* (ε+(1+00)((1+00*1)0)*00*)
解答:。
