鲍威尔法概述及算例求解

合集下载

819韦尔奇-鲍威尔算法

韦尔奇-鲍威尔算法Welsh–Powell Algorithm
决定一个图的色数是一个难题（准确地讲，它是一个NP完全问题），目前尚不存在有效的方法
因此在对图进行点着色时常采用近似算法——尽管不能得到最优结果，但是算法的执行却是快捷有效的。

下面将介绍韦尔奇-鲍威尔（Welch-Powell）点着色算法：
韦尔奇-鲍威尔算法Welch-Powell (G)
输入：图G
输出：图G 的一个点着色方案
1. 将图中顶点按度数不增的方式排成一个序列
2. 使用一种新颜色对序列中的第一个顶点进行着色，并且按照序列次序，对与已着色顶点不邻接的每一顶点着同样的颜色，直至序列末尾。

然后从序列中去掉已着色的顶点得到一个新的序列
3. 对新序列重复步骤2直至得到空序列
acgbdef cgbef
gbe
e
c
a
g d
f
b
e
要说明的是，韦尔奇-鲍威尔算法并不总能得到最少颜色数目的染色方案。

韦尔奇-鲍威
尔算法共使
用四种颜色
1
3
5
7 2 4 6 8
韦尔奇-鲍威
尔算法共使
用两种颜色
1
2
3
4 5 6 7 8
E nd。

机械优化设计鲍威尔法编程

鲍威尔法求解二维函数极小值的程序说明一题目利用鲍威尔法求函数221212112(,)242f x x x x x x x =+--的极小值点。

二鲍威尔法基本思想:1) 给定初始点0x ，选取初始方向组，它由n 各线性无关的向量00012,...n d d d 所组成。

2) 从0k x 出发，顺次沿12,,...k k k n d d d 作一维搜索得12,,...k k k n x x x 。

接着以k n x 为起点，沿方向10k k k n n d x x +=-移动一个0k k n x x -的距离，得到 01,,k k k n n x x x +分别称为一轮迭代的始点，终点和反射点。

始点，终点，反射点所对应的函数值分别表示为同时计算各中间点处的函数值，并记为因此有002,n F f F f ==计算n 个函数值之差，记作1i i i f f -∆=-其中最大者记作1max m i m m f f -∆=∆=-3) 根据是否满足判别条件和来确定是否要对原方向组进行替换。

若不满足判别条件，则下轮迭代应对原方向组进行替换，将1k n d +补充到原方向组的最后位置，而除掉k m d 。

即新方向组为1k d ，2k d ，…，1k m d -，1k m d +，…，k n d ，1kn d +作为下轮迭代的搜索方向。

下轮迭代的始点取1k n d +方向进行一维搜索得极小点10k x +。

4) 判断是否满足收敛准则。

若满足则取10k x +为极小点，否则应置1k k =+，返回2，继续进行下一轮迭代。

改进后的鲍威尔法程序框图如下：三用鲍威尔法求函数程序如下：//鲍威尔法Dlg.cpp:implementationfile//#include"stdafx.h"#include"鲍威尔法.h"#include"鲍威尔法Dlg.h"#ifdef_DEBUG#definenewDEBUG_NEW#undefTHIS_FILEstaticcharTHIS_FILE[]=__FILE__;#endif///////////////////////////////////////////////////////////////////////////// //CAboutDlgdialogusedforAppAboutclassCAboutDlg:publicCDialog{public:CAboutDlg();//DialogData//{{AFX_DATA(CAboutDlg)enum{IDD=IDD_ABOUTBOX};//}}AFX_DATA//ClassWizardgeneratedvirtualfunctionoverrides//{{AFX_VIRTUAL(CAboutDlg)protected:virtualvoidDoDataExchange(CDataExchange*pDX);//DDX/DDVsupport //}}AFX_VIRTUAL//Implementationprotected://{{AFX_MSG(CAboutDlg)//}}AFX_MSGDECLARE_MESSAGE_MAP()};CAboutDlg::CAboutDlg():CDialog(CAboutDlg::IDD){//{{AFX_DATA_INIT(CAboutDlg)//}}AFX_DATA_INIT}voidCAboutDlg::DoDataExchange(CDataExchange*pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CAboutDlg)//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CAboutDlg,CDialog)//{{AFX_MSG_MAP(CAboutDlg)//Nomessagehandlers//}}AFX_MSG_MAPEND_MESSAGE_MAP()///////////////////////////////////////////////////////////////////////////// //CMyDlgdialogCMyDlg::CMyDlg(CWnd*pParent/*=NULL*/):CDialog(CMyDlg::IDD,pParent){//{{AFX_DATA_INIT(CMyDlg)m_x01=0.0f;m_x02=0.0f;m_x1=0.0f;m_x2=0.0f;//}}AFX_DATA_INIT//NotethatLoadIcondoesnotrequireasubsequentDestroyIconinWin32 m_hIcon=AfxGetApp()->LoadIcon(IDR_MAINFRAME);}voidCMyDlg::DoDataExchange(CDataExchange*pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CMyDlg)DDX_Text(pDX,IDC_x01,m_x01);DDX_Text(pDX,IDC_x02,m_x02);DDX_Text(pDX,IDC_x1,m_x1);DDX_Text(pDX,IDC_x2,m_x2);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CMyDlg,CDialog)//{{AFX_MSG_MAP(CMyDlg)ON_WM_SYSCOMMAND()ON_WM_PAINT()ON_WM_QUERYDRAGICON()//}}AFX_MSG_MAPEND_MESSAGE_MAP()///////////////////////////////////////////////////////////////////////////// //CMyDlgmessagehandlersBOOLCMyDlg::OnInitDialog(){CDialog::OnInitDialog();//Add"About..."menuitemtosystemmenu.//IDM_ABOUTBOXmustbeinthesystemcommandrange.ASSERT((IDM_ABOUTBOX&0xFFF0)==IDM_ABOUTBOX);ASSERT(IDM_ABOUTBOX<0xF000);CMenu*pSysMenu=GetSystemMenu(FALSE);if(pSysMenu!=NULL){CStringstrAboutMenu;strAboutMenu.LoadString(IDS_ABOUTBOX);if(!strAboutMenu.IsEmpty()){pSysMenu->AppendMenu(MF_SEPARATOR);pSysMenu->AppendMenu(MF_STRING,IDM_ABOUTBOX,strAboutMenu);}}//Settheiconforthisdialog.Theframeworkdoesthisautomatically//whentheapplication'smainwindowisnotadialogSetIcon(m_hIcon,TRUE); //SetbigiconSetIcon(m_hIcon,FALSE); //Setsmallicon//TODO:AddextrainitializationherereturnTRUE;//returnTRUEunlessyousetthefocustoacontrol}voidCMyDlg::OnSysCommand(UINTnID,LPARAMlParam){if((nID&0xFFF0)==IDM_ABOUTBOX){CAboutDlgdlgAbout;dlgAbout.DoModal();}else{CDialog::OnSysCommand(nID,lParam);}}//Ifyouaddaminimizebuttontoyourdialog,youwillneedthecodebelow//todrawtheicon.ForMFCapplicationsusingthedocument/viewmodel,//thisisautomaticallydoneforyoubytheframework.voidCMyDlg::OnPaint(){if(IsIconic()){CPaintDCdc(this);//devicecontextforpaintingSendMessage(WM_ICONERASEBKGND,(WPARAM)dc.GetSafeHdc(),0);//CentericoninclientrectangleintcxIcon=GetSystemMetrics(SM_CXICON);intcyIcon=GetSystemMetrics(SM_CYICON);CRectrect;GetClientRect(&rect);intx=(rect.Width()-cxIcon+1)/2;inty=(rect.Height()-cyIcon+1)/2;//Drawtheicondc.DrawIcon(x,y,m_hIcon);}else{CDialog::OnPaint();}}//Thesystemcallsthistoobtainthecursortodisplaywhiletheuserdrags//theminimizedwindow.HCURSORCMyDlg::OnQueryDragIcon(){return(HCURSOR)m_hIcon;}voidCMyDlg::OnOK(){//TODO:Addextravalidationhere//CDialog::OnOK();UpdateData(true);inti,n;doubleh1,h2,h3,m,flag,X00[2][1],d01[2][1],d02[2][1],d03[2][1];//确定键的执行程序doubleX01[2][1],X02[2][1],X03[2][1];doubleF0,F1,F2,F3,e1,e2,em;doubleX[2][1];doublef0,f1,f2,f3;X00[0][0]=m_x01;//对初始搜索点进行赋值X00[1][0]=m_x02;d01[0][0]=1,d01[1][0]=0;//初始索索方向的确定d02[0][0]=0,d02[1][0]=1;i=1;do{F0=(X00[0][0]*X00[0][0]+2*X00[1][0]*X00[1][0]-4*X00[0][0]-2*X00[0][0]*X00[1][0]),f0=F0;//初始点函数值h1=(4*d01[0][0]+2*d01[0][0]*X00[1][0]+2*d01[1][0]*X00[0][0])/(2*d01[0][0]*d01[0][0]+//确定搜索方向4*d01[1][0]*d01[1][0]-4*d01[1][0]*d01[0][0]);X01[0][0]=X00[0][0]+h1*d01[0][0],X01[1][0]=X00[1][0]+h1*d01[1][0];F1=(X01[0][0]*X01[0][0]+2*X01[1][0]*X01[1][0]-4*X01[0][0]-2*X01[0][0]*X01[1][0]),f1=F1;//确定F的函数值h2=(4*d02[0][0]+2*d02[0][0]*X01[1][0]+2*d02[1][0]*X01[0][0])/(2*d02[0][0]*d02[0][0]+//确定搜索步长4*d02[1][0]*d02[1][0]-4*d02[1][0]*d02[0][0]);X02[0][0]=X01[0][0]+h2*d02[0][0];X02[1][0]=X01[1][0]+h2*d02[1][0];F2=(X02[0][0]*X02[0][0]+2*X02[1][0]*X02[1][0]-4*X02[0][0]-2*X02[0][0]*X02[1][0]),f2=F2;//确定F2的函数值e1=f0-f1;//进行判定e2=f1-f2;if(e1>e2)em=e1,m=1;elseem=e2,m=2;//////////////////////////////////////////////////////////////////////////////d03[0][0]=X02[0][0]-X00[0][0];d03[1][0]=X02[1][0]-X00[1][0];X03[0][0]=2*X02[0][0]-X00[0][0];X03[1][0]=2*X02[1][0]-X00[1][0];F3=(X03[0][0]*X03[0][0]+2*X03[1][0]*X03[1][0]-4*X03[0][0]-2*X03[0][0]*X03[1][0]),f3=F3;//确定F3的函数值while(F3>=F0&&(F0-2*F2+F3)*(F0-F2-em)*(F0-F2-em)>=0.5*(F0-F3)*(F0-F3))//不满足判别条件{i++;if(F2<F3){X00[0][0]=X02[0][0],X00[1][0]=X02[1][0];//以函数最小者作为下轮迭代的始点F0=(X00[0][0]*X00[0][0]+2*X00[1][0]*X00[1][0]-4*X00[0][0]-2*X00[0][0]*X00[1][0]),f0=F0;//进行第二轮搜索h1=(4*d01[0][0]+2*d01[0][0]*X00[1][0]+2*d01[1][0]*X00[0][0])/(2*d01[0][0]*d01[0][0]+//确定步长4*d01[1][0]*d01[1][0]-4*d01[1][0]*d01[0][0]);X01[0][0]=X00[0][0]+h1*d01[0][0],X01[1][0]=X00[1][0]+h1*d01[1][0];F1=(X01[0][0]*X01[0][0]+2*X01[1][0]*X01[1][0]-4*X01[0][0]-2*X01[0][0]*X01[1][0]),f1=F1;//确定函数值h2=(4*d02[0][0]+2*d02[0][0]*X01[1][0]+2*d02[1][0]*X01[0][0])/(2*d02[0][0]*d02[0][0]+//确定步长4*d02[1][0]*d02[1][0]-4*d02[1][0]*d02[0][0]);X02[0][0]=X01[0][0]+h2*d02[0][0];X02[1][0]=X01[1][0]+h2*d02[1][0];F2=(X02[0][0]*X02[0][0]+2*X02[1][0]*X02[1][0]-4*X02[0][0]-2*X02[0][0]*X02[1][0]),f2=F2;//确定函数值e1=f0-f1;e2=f1-f2;if(e1>e2)em=e1,m=1;//进行判断elseem=e2,m=2;d03[0][0]=X02[0][0]-X00[0][0];//确定新的搜索方向d03[1][0]=X02[1][0]-X00[1][0];X03[0][0]=2*X02[0][0]-X00[0][0];X03[1][0]=2*X02[1][0]-X00[1][0];F3=(X03[0][0]*X03[0][0]+2*X03[1][0]*X03[1][0]-4*X03[0][0]-2*X03[0][0]*X03[1][0]),f3=F3;//确定函数值}else{X00[0][0]=X03[0][0],X00[1][0]=X03[1][0];F0=(X00[0][0]*X00[0][0]+2*X00[1][0]*X00[1][0]-4*X00[0][0]-2*X00[0][0]*X00[1][0]),f0=F0;h1=(4*d01[0][0]+2*d01[0][0]*X00[1][0]+2*d01[1][0]*X00[0][0])/(2*d01[0][0]*d01[0][0]+4*d01[1][0]*d01[1][0]-4*d01[1][0]*d01[0][0]);X01[0][0]=X00[0][0]+h1*d01[0][0],X01[1][0]=X00[1][0]+h1*d01[1][0];F1=(X01[0][0]*X01[0][0]+2*X01[1][0]*X01[1][0]-4*X01[0][0]-2*X01[0][0]*X01[1][0]),f1=F1;h2=(4*d02[0][0]+2*d02[0][0]*X01[1][0]+2*d02[1][0]*X01[0][0])/(2*d02[0][0]*d02[0][0]+4*d02[1][0]*d02[1][0]-4*d02[1][0]*d02[0][0]);X02[0][0]=X01[0][0]+h2*d02[0][0];X02[1][0]=X01[1][0]+h2*d02[1][0];F2=(X02[0][0]*X02[0][0]+2*X02[1][0]*X02[1][0]-4*X02[0][0]-2*X02[0][0]*X02[1][0]),f2=F2;e1=f0-f1;e2=f1-f2;if(e1>e2)em=e1,m=1;elseem=e2,m=2;d03[0][0]=X02[0][0]-X00[0][0];d03[1][0]=X02[1][0]-X00[1][0];X03[0][0]=2*X02[0][0]-X00[0][0];X03[1][0]=2*X02[1][0]-X00[1][0];F3=(X03[0][0]*X03[0][0]+2*X03[1][0]*X03[1][0]-4*X03[0][0]-2*X03[0][0]*X03[1][0]),f3=F3;}}if(m=1)d01[0][0]=d03[0][0],d01[1][0]=d03[1][0];else{if(m=2)d02[0][0]=d03[0][0],d02[1][0]=d03[1][0];}h3=(4*d03[0][0]+2*d03[0][0]*X02[1][0]+2*d03[1][0]*X02[0][0])/(2*d03[0][0]*d03[0][0]+4*d03[1][0]*d03[1][0]-4*d03[1][0]*d03[0][0]);X00[0][0]=X02[0][0]+h3*d03[0][0];X00[1][0]=X02[1][0]+h3*d03[1][0];if(i=2)break;}while(abs(X02[0][0]-X00[0][0])>0.001&&abs(X02[1][0]-X00[1][0])>0.001);//输出极小值点X[0][0]=X00[0][0],X[1][0]=X00[1][0];m_x1=X[0][0];m_x2=X[1][0];UpdateData(false);}程序运行结果：四结论由该程序的运行结果可知，要求函数的极小值的在（10,5）处。

鲍威尔算法

一阶导数
变尺度法
d k = − Ak g k
A =A
k
k −1
+ ∆A
k −1
一阶导数，使 A k ≈ [G k ]−1
(d j )T ( g k − g k +1 ) = (d j )T G ( x k +1 − x k ) = 0
取 d k = x k +1 − x k 这说只要沿dj 方向分别对函作两次一维搜索，得到两个极小点xk 和xk+1 ，那么这两点的连线所给出的方向dk就是与dj一起对G共轭的方向。
k x0k , xnk , xn+1（ xnk+1 = xnk + ( xnk − x0k ) = 2 xnk − x0k ）
分别称为一轮迭代的始点、终点和反射点。
f i = f ( xik ) (i = 0,1, 2,L, n) 记：
∆ i = f i −1 − f i (i = 1, 2,L, n)
因此 F0 = f 0 , F2 = f n
则在循环中函数下降最多的第m次迭代是
∆ m = max ∆ i = f m−1 − f m
1≤i ≤ n
k 相应的方向为d m 。
为了构成共轭性好的方向组，须遵循下列准则：在k次循环中，若满足条件：
F3 < F0
和 ( F0 − 2 F2 + F3 )( F0 − F2 − ∆ m ) 2 < 0.5∆ m ( F0 − F3 ) 2
1 d3 方向进行一维搜索得沿
4 x = 2
2
f ( x 2 ) = −8
检验终止条件
x 2 − x02 = (4 − 3.8) 2 + (2 − 1.7) 2 = 0.36 > ε

优化设计-鲍威尔法

Ⅱ、鲍威尔法缺陷
• 当某一循环方向组中的矢量系出现线性相关的情况（退化、病态）时，搜索过程在降维的空间进行，致使计算不能收敛而失败。
e3
新一轮搜索方向
新一轮搜索 e3 方向和原方
向线性相关
e2
e2
(1)
X0
(1)
S4
(1)
X3
(1)
S4
(1)
X3
e1
(1)
X1
(1)
X2
e1
(1)
X0
(1)
X1
1 1
2 0.5
沿 S (1) 作一维搜索：
x (1) 3
x (1) 2
(1) 3
S
(1)
3 1.5
(1) 3
2 0.5
3 1.5
2 3(1) 0.5
(1) 3
代入f(X),令dfd(3(31(1)) ) 0 得
(1) 3
=
2 5
故有
19
x (1) 3
5
17
，
f (x3(1) ) 7.9
第一个方向S1(k)的办法，而是计算函数值并根
据是否满足条件计算：
Sk (n)
➢ f1=f(Xk(0))
X2
f3
➢ f2=f(Xk(n)) ➢ f3=f(Xk(n+2))
X (n2) k
f2
X (n1) k
X k(n)
f1
2
X k (0)
1
X k (1)
X1
• 找出前一轮迭代法中函数值下降最多的方向 m及下降量△m，即：
10
故以
x(2) 0
x
(1)为新起点，沿（

机械优化设计——鲍威尔法

机械优化设计——鲍威尔法机械优化设计是指在构筑机械产品或系统时，通过优化设计、算法分析等手段，使得机械产品或系统达到最佳的性能和效率。

鲍威尔法（Broyden-Fletcher-Goldfarb-Shanno algorithm，简称BFGS算法）是一种求解非线性最优化问题的拟牛顿法，广泛应用于机械优化设计中。

鲍威尔法是由四位科学家共同提出的，在非线性优化问题中具有很高的效率和可靠性。

它与传统的牛顿法相比，具有更好的收敛性能和更小的存储需求。

鲍威尔法是一种迭代的方法，通过不断更新设计变量的值，使得目标函数的值不断接近最优值。

鲍威尔法的核心思想是利用目标函数的梯度信息来指导方向和步长的选择。

在每一次迭代中，鲍威尔法通过构造一个正定的Hessian矩阵的近似来逼近目标函数的二次泰勒展开式，从而求取方向。

而步长的选择则通过线方法来确定，确保目标函数值在每次迭代中都能够下降。

在机械优化设计中，鲍威尔法可以应用于多种问题，如结构优化、参数优化等。

以结构优化为例，鲍威尔法可以通过不断调整结构的几何形状或内部结构的参数，来使得结构的重量最小或强度最大。

在进行参数优化时，鲍威尔法可以通过调整设计变量的取值，使得可以在给定约束条件下，最大化或最小化一些性能指标。

机械优化设计中的鲍威尔法需要满足一定的数学条件才能保证其收敛性和稳定性。

首先，目标函数必须是连续可微的。

其次，初始设计点的选取对于迭代过程的收敛性也有一定的影响。

一般情况下，选择一个合适的初始设计点可以加快鲍威尔法的收敛速度。

总结起来，鲍威尔法是机械优化设计中一种常用的求解非线性最优化问题的方法。

它可以通过迭代更新设计变量的值，使得目标函数达到最优值。

鲍威尔法不仅具有较好的收敛性能和计算效率，而且对于各种类型的机械优化设计问题都具有很好的适应性。

机械优化设计鲍威尔法编程

机械优化设计鲍威尔法编程鲍威尔法（Powell's method）是一种常用于机械优化设计的迭代算法，它基于步长的方向进行，进而找到局部或全局最优解。

该算法主要用于解决无约束优化问题，即不涉及约束条件的优化设计。

下面将详细介绍鲍威尔法的编程实现。

鲍威尔法的基本思路是在迭代过程中通过多次步长方向，找到全局最优解。

具体步骤如下：1.初始化：设置初始点x0和迭代次数k=0。

2.计算方向：选择一个初始的方向d0和步长α，并将d0归一化为单位向量。

3. 求解新的迭代点：通过计算当前点xk加上步长α乘以方向dk，得到新的迭代点xk+14. 更新方向：计算新的方向dk+15. 判断是否达到终止条件：如果达到了终止条件，则输出当前点xk+1为最优解；否则，令k=k+1，返回第3步继续进行迭代。

下面给出一个使用Python编程实现鲍威尔法的示例代码：```pythonimport numpy as npdef powell_method(f, x0, alpha, eps, max_iter):#初始化x=x0d = np.eye(len(x0))k=0while k < max_iter:#计算方向和步长g=f(x)d_norm = np.linalg.norm(d, axis=0) d = d / d_normalpha = alpha / d_norm#求解新的迭代点x_new = x + alpha * d#更新方向g_new = f(x_new)delta = g_new - gd = np.roll(d, -1, axis=0)d[-1] = (x_new - x) / alpha#判断终止条件if np.linalg.norm(delta) < eps: return x_new#更新迭代点x = x_newk+=1return x#示例函数，目标是求解f(x)=(x[0]-1)^2+(x[1]-2)^2 def f(x):return (x[0] - 1) ** 2 + (x[1] - 2) ** 2#设置初始点、步长、终止条件和最大迭代次数x0 = np.array([0.0, 0.0])alpha = 0.1eps = 1e-6max_iter = 100#调用鲍威尔法进行优化设计x_opt = powell_method(f, x0, alpha, eps, max_iter) #输出最优解print("Optimal solution: ", x_opt)print("Optimal value: ", f(x_opt))```在上述代码中，目标函数f(x)为示例函数，可以根据具体的优化设计问题进行修改。

鲍威尔算法

gk
dj
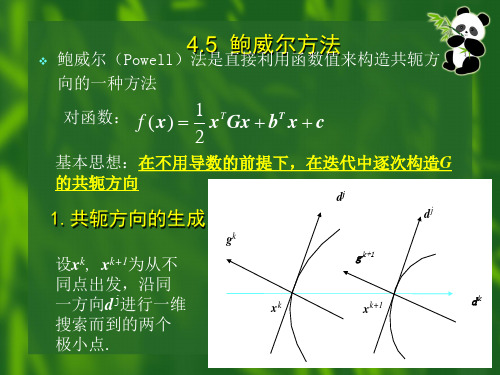
设xk,
xk+1为从不
x
k
g k+1 dk
同点出发，沿同一方向dj进行一维搜索而到的两个极小点.
x
k+1
梯度和等值面相垂直的性质, dj和 xk, xk+1两点处的梯度gk,gk+1之间存在关系:
(d j )T g k = 0, (d j )T g k +1 = 0
另一方面，对于上述二次函数，其xk, xk+1 两点处的梯度可表示为: g k = Gx k + b, g k +1 = Gx k +1 + b 因而有
由于满足Powell条件，则淘汰函数值下降量最 d30 大的方向e1，下一轮的基本方向组为e2，。构成新的方向
3 1 2 d = x − x = − = 1.5 1 0.5
0 3 0 2 0 0
d30 方向一维搜索得极小点和极小值沿 3.8 1 x = ， f ( x1 ) = −7.9 1.7
3.96 3.8 4.12 x = 2x − x = 2 − 1.7 = 2.18 1.94
1 3 1 2 1 0
1 F3 = f ( x3 ) = −7.964
检验Powell条件，淘汰函数值下降量最大的方 1 d30 ，d3 。向e2，下一轮的基本方向组应为构成新的方向 3.96 3.8 0.16 1 1 1 d 3 = x 2 − x0 = − 1.7 = 0.24 1.94
1 1 d 2 = x 2 − x0
1 0
x2 d1
1 x0
x1 2
x*
0 x2

鲍威尔算法实验报告

一、实验目的1. 理解鲍威尔算法的基本原理和步骤。

2. 掌握鲍威尔算法在求解非线性方程组中的应用。

3. 分析鲍威尔算法的收敛速度和精度。

二、实验原理鲍威尔算法是一种迭代算法，用于求解非线性方程组。

该算法的基本思想是利用相邻迭代的残差向量构造一个线性方程组的系数矩阵，进而求出近似解。

具体步骤如下：1. 初始化：选择初始点 \( x_0 \) 和 \( x_1 \)，计算初始残差向量\( \mathbf{r}_0 = f(x_0) \) 和 \( \mathbf{r}_1 = f(x_1) \)。

2. 构造系数矩阵：根据残差向量 \( \mathbf{r}_0 \) 和 \( \mathbf{r}_1 \) 构造系数矩阵 \( \mathbf{A} \)。

3. 求解线性方程组：求解线性方程组 \( \mathbf{A} \mathbf{x} =\mathbf{r}_1 \)，得到系数 \( \mathbf{x} \)。

4. 更新近似解：根据系数 \( \mathbf{x} \) 更新近似解 \( x_2 = x_1 +\mathbf{x} \)。

5. 检查收敛性：计算新的残差向量 \( \mathbf{r}_2 = f(x_2) \)，如果满足收敛条件，则停止迭代；否则，返回步骤2。

三、实验内容1. 选择非线性方程组：设非线性方程组为\[\begin{cases}f_1(x_1, x_2) = x_1^2 + x_2^2 - 1 = 0 \\f_2(x_1, x_2) = x_1^3 - x_2 - 1 = 0\end{cases}\]2. 选择初始点：取 \( x_0 = (0, 0) \) 和 \( x_1 = (1, 1) \)。

3. 运行鲍威尔算法：根据上述步骤，编写程序求解该非线性方程组。

四、实验结果与分析1. 实验结果：经过多次迭代，鲍威尔算法得到近似解为 \( x_1 \approx 0.5285 \)，\( x_2 \approx 0.8572 \)。

鲍威尔法

鲍威尔法二级斜齿轮减速器的优化设计姓名：王剑锋学号：109011159班级：机制096班一、基本原理前已述及，对于n维无约束最优化问题，采用原始共轭方向法在产生n个共轭方向时，有可能是线性相关或接近线性相关的，如遇这种情况，会导致在降维空间寻优使迭代计算不能收敛到真正最优点而失败。

鲍威尔在1964年提出了对上述原始共轭方向法的改进方法—鲍威尔共轭方向法。

这个改进方法与原始共轭方向法的关键区别是在构成第k + 1环基本方向组时，不再总是不管好坏一律去掉前一环的第一个方向，并再将前一环的新生方向补于最后，而是首先判断前一环的基本方向组是否需要更换；如需更换，还要进一步判断前一环原基本方向组中沿某一个方向作一维搜索函数值下降量最大，去掉该方向再将新生方向补入最后构成第k+1环的基本方向组以避免线性相关并最接近共轭。

判别前一环基本方向组是否需要更换的依据，则按导出的下列两个条件式。

（1）（2）是否得到满足来进行处理，式中各符号的涵义可参阅图5-13(P62)说明如下——k环起始点的函数值；——k环沿基本方向组依次一维搜索后的终点的函数值；——对的映射点的函数值，；——k环基本方向组中沿诸方向一维搜索所得各目标函数值下降量中之最大者，对应方向。

若条件式（1）或(2)中至少有一个成立，则第k +1环的基本方向组仍用原来第k环的基本方向组。

k十1环的初始点应选取、两点中函数值小者，亦即当时，取；时，取。

若式(1)及式(2)均不成立，则去掉原来第k环基本方向组中函数值下降量最大的方向，再将第k环所产生的新生方向补入k+1环基本方向组的最后，即以构成第k+l环的基本方向组。

k+1环的初始点应取第k环中沿方向一维搜索的极小点，亦即取。

图2显示了二维正定二次函数用鲍威尔共轭方向法求极小点的搜索路线，其几何意义亦完全可推广到n维正定二次函数。

二、迭代过程及算法框图鲍威尔共轭方向法的具体迭代步骤如下:(1)给定初始点，迭代精度，维数n，。

数据分析知识：数据分析中的鲍威尔法

数据分析知识：数据分析中的鲍威尔法在数据分析中，鲍威尔法（Box-Jenkins方法）是一种常用的时间序列分析方法。

它的主要目的是利用历史数据来预测未来数据，以便制定在合适的时间做出相应决策的策略。

本文将对于鲍威尔法进行详细介绍。

一、鲍威尔法鲍威尔法是由英国统计学家George Box和美国统计学家GM Jenkins于1970年提出来的。

它是一种识别、估计和预测时间序列模型的方法，包括（AR）自回归模型、（MA）移动平均模型和（ARIMA）自回归移动平均模型等。

定量的时间序列数据越来越广泛地应用于经济、金融、气象等日常领域和科学研究中，准确预测和解释时间序列数据的变化越来越重要。

鲍威尔法的基本思路是把观察到的时间序列数据转变成计算机可以处理的数据模型，然后利用这些模型来预测未来的数据。

这样，它可以帮助我们更好地理解与预测一系列未知的数据，包括预测市场趋势、月销量、流量分析、旅游业务、未来的气温和气候变化等。

二、鲍威尔法模型的建立鲍威尔法的建立是一个动态迭代过程，包含模型的建立、模型诊断、模型修正和模型的应用等步骤。

下面，我们将详细讲述具体流程。

1.模型的建立首先，我们需要定义时间序列模型的“参数集”，包括“自回归”参数、“移动平均”参数和“截距”参数等。

自回归是指复杂系统内部的历史行为会影响未来行为的现象，移动平均是指未来行为可能会受到突发事件或预测错误影响的现象。

基于已有的数据，我们需要计算各个参数的值，建立时间序列模型。

2.模型诊断在模型诊断的过程中，我们需要评估和诊断模型的各个方面和参数选择的合理性，以确定模型是否能够有效预测未来数据。

其中，常用的诊断工具包括统计检验、残差诊断以及预测诊断等。

通过对时间序列数据的观察和诊断，可以找出模型中可能存在的错误和不一致之处，并根据诊断的结果及时地修正和更新模型。

3.模型修正在模型修正的过程中，如果我们发现时间序列的参数集合不足以对未来数据进行准确的预测，我们需要对模型进行修正。

鲍威尔法的基本原理

鲍威尔法的基本原理在数学优化领域，鲍威尔法（Powell's Method）是一种求解无约束优化问题的重要方法。

它以其独特的思路和有效的性能，在众多优化算法中占据了一席之地。

要理解鲍威尔法，首先得清楚什么是无约束优化问题。

简单来说，就是在没有任何限制条件的情况下，寻找一个函数的最小值或最大值。

比如说，我们有一个函数 f(x)，目标就是找到那个能让 f(x)取到最小或最大的 x 值。

鲍威尔法的核心思想在于通过一系列的线性搜索来逐步逼近最优解。

它不是一下子就找到最终的答案，而是一步一步地靠近。

具体来看，鲍威尔法从一个初始点开始。

这个初始点可以是随意选择的，但通常会根据问题的特点和一些先验知识来进行合理的设定。

然后，它会沿着一组给定的方向进行搜索。

这些方向是怎么来的呢？一开始，鲍威尔法会选择一组固定的线性无关的方向。

比如说，在二维空间中，可能就是 x 轴和 y 轴的方向；在三维空间中，可能就是 x、y、z 轴的方向。

随着算法的进行，这些方向会不断地更新和优化。

在每次的迭代中，鲍威尔法会沿着当前的方向进行线性搜索，找到函数值下降最快的点。

这个过程就像是在黑暗中摸索，沿着一个方向走，看看哪里更低。

当完成一轮沿着所有给定方向的搜索后，鲍威尔法会根据这一轮搜索的结果来更新方向。

它会把这一轮中函数值下降最多的方向保留下来，然后用新产生的方向替换掉原来的某个方向。

新产生的方向是通过把这一轮搜索的起点和终点连接起来得到的。

这样做的目的是为了让新的方向更能反映函数的特性，从而更有效地引导搜索朝着最优解的方向前进。

比如说，如果在一轮搜索中，沿着某个方向函数值下降得特别多，那么这个方向就被认为是比较好的方向，会被保留。

而新产生的方向则是基于这一轮搜索的整体效果，希望能够捕捉到函数的变化趋势，更好地指导下一轮的搜索。

鲍威尔法的一个重要特点是它不需要计算目标函数的导数。

这在一些情况下是非常有用的，因为计算导数可能会很复杂，甚至有时候根本无法计算。

机械优化设计鲍威尔法

机械优化设计鲍威尔法
机械优化设计鲍威尔法（Powell method）是一种常用的非线性优化
算法，它以鲍威尔的名字命名，用于解决无约束非线性优化问题。

该方法
在各个领域都有广泛的应用，如工程优化设计、机器学习等。

下面将详细
介绍机械优化设计鲍威尔法的原理及应用。

鲍威尔法的具体步骤如下：
1.初始化参数：选择初始设计参数和方向。

2.寻找一维极小值点：沿着方向找到目标函数在该方向上的极小值点。

3.更新方向：通过比较前后两个极小值点的差异来更新方向。

4.迭代优化：重复步骤2和步骤3，直到达到指定的收敛条件。

鲍威尔法的优点是收敛速度较快、计算量较小，同时可以处理非线性
的优化问题。

然而，该方法也存在一些不足之处，如可能陷入局部最优解、对初值敏感等。

机械优化设计鲍威尔法在工程领域中有广泛的应用。

例如，在机械结
构设计中，可以利用鲍威尔法来优化结构参数，以满足特定的性能指标。

在汽车工业中，可以使用鲍威尔法来优化车辆的燃油效率和性能。

在航空
航天领域，可以利用该方法来优化飞行器的飞行性能。

此外，该方法还可
以用于机器学习中的参数优化，如调整神经网络的权重和偏置等。

总之，机械优化设计鲍威尔法是一种常用的非线性优化算法，通过迭
代逼近最优解。

虽然该方法有一些不足之处，但在实际应用中具有广泛的
适用性，尤其在工程优化设计和机器学习等领域。

通过使用该方法，可以
优化设计参数，改进性能指标，提高工程效率和产品质量。

鲍威尔法

根据这一原理构造的迭代算法称为鲍威尔基本算法。
（二）鲍威尔法的缺陷
鲍威尔基本算法不可能对每一个都起作用，因为在迭代过程中的n个搜索方向有时会变成线性相关的，而不能形成共轭方向，导致随后的迭代搜索在降维（退化）的空间中进行，可能求不到极小点，故而进行改进。
（三）鲍威尔修正算法
为了避免这种“退化”现象的发生，鲍威尔对这一算法进行了修正。即在每一轮产生新的搜索方向后，首先判断原搜索方向组是否可以直接用下一轮迭代的方向组，若可以，即用。否则，还要进一步判断原搜索方向组中哪个方向上的函数值下降量最大，然后再用新搜索方向替换这个下降量最大的搜索方向，以保证逐次生成共轭方向，即每一轮迭代的搜索方向组线性无关。
并求出（5）计算判断
是否成立若成立，则由出发沿方向进行一维搜索，求出目标函数f(x)的极小点，并作为k+1轮的初始点，然后进行 k+1轮搜索，挤掉，同时把放在方向组的最后构成新一轮的方向组。
（6）若上述判断条件不成立，则k+1轮的初始点和方向组为 = 即此时k+1轮的n个搜索方向全部用第k轮的搜索方向。（7）每轮迭代结束，都应检验收敛条件，若能满足：
鲍威尔法
鲍威尔（Powell）法又称方向加速度法，它是利用共轭方向可以加快收敛速度的性质形成的一种搜索方法。该方法不用对目标函数求导，当目标函数的导数不连续时也能应用，因此，鲍威尔法是一种十分有效的直接搜索法。
一共轭方向的概念与共轭向量的性质

（一）共轭方向设A为n阶实对称正定矩阵，若有两个n维向量和能满足 A =0 则称向量与对矩阵A共轭，共轭向量的方向称为共轭方向。
二鲍威尔法
（一）鲍威尔法的基本原理和迭代过程

MATLAB鲍威尔算法

MATLAB鲍威尔算法鲍威尔算法（Broyden-Fletcher-Goldfarb-Shanno, BFGS）是用于非线性优化问题的一种数值优化算法。

它是一种拥有全局收敛性和快速收敛速度的准牛顿法。

BFGS算法的基本思想是通过近似二次函数来逼近原函数的局部结构，并利用此近似函数来求解极值。

它通过建立二次模型来估计目标函数的海森矩阵的逆（或近似逆），然后使用逆海森矩阵来更新方向。

算法的基本步骤如下：1.初始化参数：给定初始点x_0，设定精度要求ε，设置迭代次数k=0，以及初始H_0=I。

2.计算梯度：计算目标函数在当前点x_k的梯度g_k。

3.求解方向：计算方向d_k=-H_k*g_k，其中H_k表示当前的逆海森矩阵。

4.一维：在方向上进行一维线，求解最优步长α_k。

5.更新参数：更新参数x_{k+1}=x_k+α_k*d_k。

6.判断停止条件：如果，g_{k+1}，<ε，则停止迭代。

7. 更新逆海森矩阵：更新逆海森矩阵H_{k+1} = H_k + \frac{y_k* y_k^T}{y_k^T * s_k} - \frac{H_k * s_k * s_k^T * H_k}{s_k^T *H_k * s_k}，其中y_k = g_{k+1} - g_k，s_k = x_{k+1} - x_k。

8.如果迭代次数k超过预设迭代次数或者步长α_k小于预设步长，则停止迭代。

BFGS算法通过逆海森矩阵的更新来逼近目标函数的局部曲率，从而实现更快的收敛速度。

在每一次迭代中，BFGS算法更新逆海森矩阵，使其逐渐收敛到目标函数的真实海森矩阵的逆。

由于逆海森矩阵的计算复杂度为O(n^2)，其中n为变量的维度，BFGS算法在高维问题中的计算效率较低。

需要注意的是，BFGS算法只适用于无约束的非线性优化问题。

对于带有线性等式约束或者线性不等式约束的优化问题，需要使用相应的约束处理方法来进行求解。

总之，BFGS算法是一种拥有全局收敛性和快速收敛速度的准牛顿法。

机械优化设计鲍威尔法编程

pSysMenu->AppendMenu(MF_STRING, IDM_ABOUTBOX, strAboutMenu);
}
}
// Set the icon for this dialog. The framework does this automatically
// when the application's main window is not a dialog
UpdateData(true);
int i,n;
double h1,h2,h3,m,flag,X00[2][1],d01[2][1],d02[2][1],d03[2][1]; //确定键的执行程序
double X01[2][1],X02[2][1],X03[2][1];
double F0,F1,F2,F3,e1,e2,em;
// the minimized window.
HCURSOR CMyDlg::OnQueryDragIcon()
{
return (HCURSOR) m_hIcon;
}
void CMyDlg::OnOK()
{
// TODO: Add extra validation here
//CDialog::OnOK();
F1=(X01[0][0]*X01[0][0]+2*X01[1][0]*X01[1][0]-4*X01[0][0]-2*X01[0][0]*X01[1][0]),f1=F1; //确定F的函数值
h2=(4*d02[0][0]+2*d02[0][0]*X01[1][0]+2*d02[1][0]*X01[0][0])/(2*d02[0][0]*d02[0][0]+ //确定搜索步长

机械优化设计鲍威尔法编程

机械优化设计鲍威尔法编程鲍威尔法编程，又称行进法、射线法，是一种无约束极值问题的最优化算法。

其核心思想是通过不断更新方向，寻找函数极小值点。

鲍威尔法编程结合了线和模式的特点，具有全局能力和局部能力，因此在机械优化设计中得到广泛应用。

在机械优化设计中，通常需要考虑多个设计参数对机械性能的影响。

鲍威尔法编程可以通过不断迭代的方式，寻找最佳的设计参数组合，以达到设计要求。

其具体步骤如下：1.初始化设计参数和步长。

2.计算当前设计参数下的目标函数值。

3.在当前方向上进行线，找到使目标函数值下降的步长。

4.更新设计参数，将方向和步长相乘加到当前设计参数上。

5.检查当前设计参数的变化是否满足终止条件，如果满足则结束，否则返回步骤26.返回最佳设计参数组合及对应的目标函数值。

下面以一个简单的机械优化设计案例为例进行详细说明。

假设有一个弹簧悬挂系统，需要设计合适的弹簧刚度和阻尼系数来满足特定的振动要求。

目标函数为最小化系统振动幅值。

首先，需要定义设计参数和目标函数。

设计参数可以选择弹簧刚度和阻尼系数。

目标函数可以定义为系统振动幅值的平方。

其次，需要确定方向和初始步长。

对于弹簧刚度和阻尼系数来说，方向可以选择正方向和负方向。

初始步长可以根据经验或试验来确定。

然后，根据鲍威尔法编程的步骤，进行迭代。

首先，初始化设计参数和步长。

然后，计算当前设计参数下的目标函数值。

接下来，根据当前方向和步长进行线，找到使目标函数值下降的步长。

再更新设计参数，将方向和步长相乘加到当前设计参数上。

最后，检查当前设计参数的变化是否满足终止条件，如果满足则结束，否则返回到线步骤继续。

最后，得到最佳的设计参数组合及对应的目标函数值。

可以根据实际情况进行设计参数的调整和优化，以获得更好的机械性能。

总之，鲍威尔法编程是一种常用的机械优化设计方法。

通过不断迭代的方式，寻找最佳的设计参数组合，以满足设计要求。

其原理和步骤相对简单，但需要结合具体问题进行参数的选择和调整。

十一、Powell算法（鲍威尔算法）原理以及实现

⼗⼀、Powell算法（鲍威尔算法）原理以及实现⼀、介绍 Powell算法是图像配准⾥⾯的常⽤的加速算法，可以加快搜索速度，⽽且对于低维函数的效果很好，所以本篇博客主要是为了介绍Powell算法的原理以及实现。

由于⽹上已经有了对于Powell算法的讲解，所以我只是把链接放出来（我觉得⾃⼰⽬前还没有这个讲解的能⼒），⼤家⾃⼰去了解。

放在这⾥主要也是为了节省⼤家搜索的时间。

（都是我⾟⾟苦苦搜出来的^-^）。

⼆、预备知识了解⼀维搜索算法：进退法，消去法，黄⾦分割法阅读以下博客：三、鲍威尔算法具体原理阅读这⾥：参考博客：原理与例⼦（⼀个例⼦的计算过程）：四、matlab代码实现⼀个简单函数的求解代码来源：这个代码的程序与思路很是简洁，我觉得写得很好。

原⽂代码放在这⾥：⽂件：MyPowell.m　function MyPowell()syms x1 x2 x3 a;f=10*(x1+x2-5)^4+(x1-x2+x3)^2 +(x2+x3)^6;error=10^(-3);D=eye(3);x0=[000]';for k=1:1:10^6MaxLength=0;x00=x0;m=0;if k==1,s=D;endfor i=1:3x=x0+a*s(:,i);ff=subs(f,{x1,x2,x3},{x(1),x(2),x(3)});t=Divide(ff,a); %调⽤了进退法分割区间aa=OneDemensionslSearch(ff,a,t); %调⽤了0.618法进⾏⼀维搜索 xx=x0+aa*s(:,i);fx0=subs(f,{x1,x2,x3},{x0(1),x0(2),x0(3)});fxx=subs(f,{x1,x2,x3},{xx(1),xx(2),xx(3)});length=fx0-fxx;if length>MaxLength,MaxLength=length;m=m+1;endx0=xx;endss=x0-x00;ReflectX=2*x0-x00;f1=subs(f,{x1,x2,x3},{x00(1),x00(2),x00(3)});f2=subs(f,{x1,x2,x3},{x0(1),x0(2),x0(3)});f3=subs(f,{x1,x2,x3},{ReflectX(1),ReflectX(2),ReflectX(3)});if f3<f1&&(f1+f3-2*f2)*(f1-f2-MaxLength)^2<0.5*MaxLength*(f1-f3)^2x=x0+a*ss;ff=subs(f,{x1,x2,x3},{x(1),x(2),x(3)});t=Divide(ff,a);aa=OneDemensionslSearch(ff,a,t);x0=x0+aa*ss;for j=m:(3-1),s(:,j)=s(:,j+1);ends(:,3)=ss;elseif f2>f3, x0=ReflectX;endendif norm(x00-x0)<error,break;endk;x0;endopx=x0;val=subs(f,{x1,x2,x3},{opx(1),opx(2),opx(3)});disp('最优点：');opx'disp('最优化值：');valdisp('迭代次数：');k ⽂件 Divide.m ：%对任意⼀个⼀维函数函数进⾏区间分割，使其出现“⾼—低—⾼”的型式function output=Divide(f,x,m,n)if nargin<4,n=1e-6;endif nargin<3,m=0;endstep=n;t0=m;ft0=subs(f,{x},{t0});t1=t0+step;ft1=subs(f,{x},{t1});if ft0>=ft1t2=t1+step;ft2=subs(f,{x},{t2});while ft1>ft2t0=t1;%ft0=ft1;t1=t2;ft1=ft2;step=2*step;t2=t1+step;ft2=subs(f,{x},{t2});endelsestep=-step;t=t0;t0=t1;t1=t;ft=ft0;%ft0=ft1;ft1=ft;t2=t1+step;ft2=subs(f,{x},{t2});while ft1>ft2t0=t1;%ft0=ft1;t1=t2;ft1=ft2;step=2*step;t2=t1+step;ft2=subs(f,{x},{t2});endendoutput=[t0,t2];View Code ⽂件：OneDemensionslSearch.mfunction output=OneDemensionslSearch(f,x,s,r)if nargin<4,r=1e-6;enda=s(1);b=s(2);a1=a+0.382*(b-a);fa1=subs(f,{x},{a1});a2=a+0.618*(b-a);fa2=subs(f,{x},{a2});while abs((b-a)/b)>r && abs((fa2-fa1)/fa2)>rif fa1<fa2b=a2;a2=a1;fa2=fa1;a1=a+0.382*(b-a);fa1=subs(f,{x},{a1});elsea=a1;a1=a2;fa1=fa2;a2=a+0.618*(b-a);fa2=subs(f,{x},{a2});endendop=(a+b)/2;%fop=subs(f,{x},{op});output=op;View Code 全部放到同⼀个⼯程⽬录⾥⾯，设置为当前⽬录，然后输⼊Powell即可运⾏得到结果。

机械优化设计方法——鲍威尔法,坐标轮换法

鲍威尔法
机械优化设计方法——鲍威尔法
鲍威尔(Powell)法是直接利用函数值来构造共扼方向的一种共扼方向法。基本思想是在不用求导数的前提下，在迭代中逐次构造Hessian矩阵G的共扼方向。
原始共轭法的缺点
对于n维无约束最优化问题，采用原始共轭方向法在产生n个共轭方向时，有可能是线性相关或接近线性相关的，遇这种情况，会导致在降维空间寻优使迭代计算不能收敛到真正最优点而失败。
(4)判断是否满足收敛准则。
即
X k 1 X k
。若满足，则
X k1 0
为
极小点，否则应置 k k 1 ，返回，
继续进行下一轮迭代。
计算 f (X ) x12 25x22 的极小值
解：选取初始点为 X 0 2,2T,初试搜索方向
为 d10 1,0T，d20 0,1 T。初始点处的函数
值
F1
f
(
X
0 0
)
104
第一轮迭代：沿 d10 方向进行一维搜
索，得
X10
X
0
1d10
2
1
1 0
2
1
2
将
X
0 1
代入原方程得：
f1 f (X10) (2 1)2 2522 4 41 12 100
最佳步长
：
df ( d
)
4
21
0
1 2
X10
2 2
210
0 2
X
0 1
鲍威尔法计算步骤与程序原理
(1)任选一初始点 X 0 ,
X
0 0
X
0
，选取初
试方向组，它由n个线性无关的向量

鲍威尔法概述及算例求解

鲍威尔法
鲍威尔（Powell）法又称方向加速度法，它是利用共轭方向可以加快收敛速度的性质形成的一种搜索方法。该方法不用对目标函数求导，当目标函数的导数不连续时也能应用，因此，鲍威尔法是一种十分有效的直接搜索法。
一共轭方向的概念与共轭向量的性质

（一）共轭方向设A为n阶实对称正定矩阵，若有两个n维向量和能满足 A =0 则称向量与对矩阵A共轭，共轭向量的方向称为共轭方向。
根据这一原理构造的迭代算法称为鲍威尔基本算法。
（二）鲍威尔法的缺陷
鲍威尔基本算法不可能对每一个都起作用，因为在迭代过程中的n个搜索方向有时会变成线性相关的，而不能形成共轭方向，导致随后的迭代搜索在降维（退化）的空间中进行，可能求不到极小点，故而进行改进。
（三）鲍威尔修正算法
为了避免这种“退化”现象的发生，鲍威尔对这一算法进行了修正。即在每一轮产生新的搜索方向后，首先判断原搜索方向组是否可以直接用下一轮迭代的方向组，若可以，即用。否则，还要进一步判断原搜索方向组中哪个方向上的函数值下降量最大，然后再用新搜索方向替换这个下降量最大的搜索方向，以保证逐次生成共轭方向，即每一轮迭代的搜索方向组线性无关。
并求出（5）计算判断
是否成立若成立，则由出发沿方向进行一维搜索，求出目标函数f(x)的极小点，并作为k+1轮的初始点，然后进行 k+1轮搜索，挤掉，同时把放在方向组的最后构成新一轮的方向组。
（6）若上述判断条件不成立，则k+1轮的初始点和方向组为 = 即此时k+1轮的n个搜索方向全部用第k轮的搜索方向。（7）每轮迭代结束，都应检验收敛条件，若能满足：

（二）共轭向量的性质设A为n×n阶实对称正定矩阵，（i=1,2,…n）是关于A的n个互相共轭的非零向量，对于正定二次函数f(x)的极小化寻优问题，从任何初始点出发，依次沿方向经n次一维搜索即可收敛到极小点 = 沿n元二次正定函数的n个共轭方向进行n次一维搜索就可达到目标函数的极小点。