江苏南通市2018届高三数学第二次调研试卷含答案
江苏省南通市2018届高考第二次调研数学试卷含答案

4. 如图是一个算法流程图,则输出的 S 的值为 ▲ . 5. 在长为 12 cm 的线段 AB 上任取一点 C,以线段 AC,BC 为邻边作矩形,则该矩形的面 积 大于 32 cm2 的概率为 ▲ . 6. 在 △ ABC 中,已知 AB 1 ,, AC 2
B 45 ,则 BC 的长为 ▲ .
m 的取值范围是
▲
. ▲
. 14.已知 a 为常数,函数 f ( x)
x ax
2
的最小值为 2 ,则 a 的所有值为 3 1 x
2
▲
. 二、解答题:本大题共 6 小题,共计 90 分.请在答题卡指定区域内作答.解答时应写出文 字说明、 证明过程或演算步骤. 15.(本小题满分 14 分) 在平面直角坐标系xOy 中,设向量a cos ,sin , b sin , cos ,
y2 1 有公共的渐近线,且经过 3
7. 在平面直角坐标系 xOy 中,已知双曲线 C 与双曲线 x 2 点
P 2 , 3 ,则双曲线 C 的焦距为
▲
.
8. 在平面直角坐标系 xOy 中,已知角 , 的始边均为 x 轴的非负半轴,终边分别经过 点
A ( 1 ,2 ) , B ( 5 , 1 ) ,则 tan( ) 的值为
c 1, 3 . 2 2
(1)若 a b c ,求 sin ( ) 的值; (2)设 5π , 0 π ,且 a // b c ,求 的值. 6 16.(本小题满分 14 分) 如图,在三棱柱 ABC A 1 B 1 C 1 中, AB AC ,点 E , F 分别在棱 BB 1 , CC 1 上(均异 于 端点) ,且 ∠ ABE ∠ ACF, AE ⊥ BB 1 , AF⊥CC1. A (第 A F C C1 B16 1 1 题) E B 求证:(1)平面 AEF⊥平面 BB1C1C; (2)BC // 平面 AEF.
江苏地区南通,徐州,扬州,泰州,淮安,宿迁六市2018年度高三第二次调研数学试题

2018届高三模拟考试试卷(十三)数学2018.3(满分160分,考试时间120分钟)参考公式:柱体的体积公式V柱体=Sh,其中S为柱体的底面积,h为高.一、填空题:本大题共14小题,每小题5分,共70分.1. 已知集合U={-1,0,1,2,3},A={-1,0,2},则∁U A=________.2. 已知复数z1=a+i,z2=3-4i,其中i为虚数单位.若z1z2为纯虚数,则实数a的值为________.3. 某班40名学生参加普法知识竞赛,成绩都在区间[40,100]上,其频率分布直方图如图所示,则成绩不低于60分的人数为________.(第3题) (第4题)4. 如图是一个算法流程图,则输出的S的值为________.5. 在长为12 cm的线段AB上任取一点C,以线段AC,BC为邻边作矩形,则该矩形的面积大于32 cm2的概率为________.6. 在△ABC中,已知AB=1,AC=2,B=45°,则BC的长为________.7. 在平面直角坐标系xOy 中,已知双曲线C 与双曲线x 2-y 23=1有公共的渐近线,且经过点P(-2,3),则双曲线C 的焦距为________.8. 在平面直角坐标系xOy 中,已知角α,β的始边均为x 轴的非负半轴,终边分别经过点A(1,2),B(5,1),则tan(α-β)的值为________.9. 设等比数列{a n }的前n 项和为S n .若S 3,S 9,S 6成等差数列,且a 8=3,则a 5的值为________. 10. 已知a ,b ,c 均为正数,且abc =4(a +b),则a +b +c 的最小值为________. 11. 在平面直角坐标系xOy 中,若动圆C 上的点都在不等式组⎩⎪⎨⎪⎧x ≤3,x -3y +3≥0,x +3y +3≥0表示的平面区域内,则面积最大的圆C 的标准方程为______________.12. 设函数f(x)=⎩⎪⎨⎪⎧e -x -12,x >0,x 3-3mx -2,x ≤0(其中e 为自然对数的底数)有3个不同的零点,则实数m 的取值范围是________.13. 在平面四边形ABCD 中,已知AB =1,BC =4,CD =2,DA =3,则AC →·BD →的值为________. 14. 已知a 为常数,函数f(x)=x a -x 2-1-x 2的最小值为-23,则a 的所有值为________.二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)在平面直角坐标系xOy 中,设向量a =(cos α,sin α),b =(-sin β,cos β),c =(-12,32).(1) 若|a +b|=|c|,求sin(α-β)的值;(2) 设α=5π6,0<β<π,且a ∥(b +c ),求β的值.16. (本小题满分14分)如图,在三棱柱ABC A 1B 1C 1中,AB =AC ,点E ,F 分别在棱BB 1,CC 1上(均异于端点),且∠ABE =∠ACF ,AE ⊥BB 1,AF ⊥CC 1.求证:(1) 平面AEF ⊥平面BB 1C 1C ; (2) BC ∥平面AEF.17. (本小题满分14分)如图,在平面直角坐标系xOy 中,B 1,B 2是椭圆x 2a 2+y 2b 2=1(a >b >0)的短轴端点,P 是椭圆上异于点B 1,B 2的一动点.当直线PB 1的方程为y =x +3时,线段PB 1的长为42.(1) 求椭圆的标准方程;(2) 设点Q 满足:QB 1⊥PB 1,QB 2⊥PB 2.求证: △PB 1B 2与△QB 1B 2的面积之比为定值.18. (本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿虚线l1,l2裁剪成A,B,C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:方案①:以l1为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;方案②:以l2为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与l1或l2垂直)作为正四棱柱的两个底面.(1) 设B,C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2) 设l1的长为x dm,则当x为多少时,能使按方案②制成的正四棱柱的体积最大?19. (本小题满分16分)设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且q≠1,d ≠0.记c i=a i+b i(i=1,2,3,4).(1) 求证:数列c1,c2,c3不是等差数列;(2) 设a1=1,q=2.若数列c1,c2,c3是等比数列,求b2关于d的函数关系式及其定义域;(3) 数列c1,c2,c3,c4能否为等比数列?并说明理由.20. (本小题满分16分) 设函数f(x)=x -asin x(a >0).(1) 若函数y =f(x)是R 上的单调增函数,求实数a 的取值范围;(2) 设a =12,g(x)=f(x)+bln x +1(b ∈R ,b ≠0),g ′(x)是g(x)的导函数.① 若对任意的x >0,g ′(x)>0,求证: 存在x 0,使g(x 0)<0; ② 若g(x 1)=g(x 2)(x 1≠x 2),求证: x 1x 2<4b 2.2018届高三模拟考试试卷(十三) 数学附加题(满分40分,考试时间30分钟)21. 【选做题】 在A ,B ,C ,D 四小题中只能选做2题,每小题10分,共20分.若多做,则按作答的前两题计分.解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修41:几何证明选讲)如图,A ,B ,C 是圆O 上的3个不同的点,半径OA 交弦BC 于点D.求证:DB ·DC +OD 2=OA 2.B. (选修42:矩阵与变换)在平面直角坐标系xOy 中,已知A(0,0),B(3,0),C(2,2).设变换T 1,T 2对应的矩阵分别为M =⎣⎢⎢⎡⎦⎥⎥⎤1002,矩阵N =⎣⎢⎢⎡⎦⎥⎥⎤2001,求对△ABC 依次实施变换T 1,T 2后所得图形的面积.C. (选修44:坐标系与参数方程)在极坐标系中,求以点P(2,π3)为圆心且与直线l :ρsin(θ-π3)=2相切的圆的极坐标方程.D. (选修45:不等式选讲)已知a ,b ,c 为正实数,且a +b +c =12,求证:1-a +c c (a +2b )≥2.【必做题】 第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22. 在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3×3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖总金额为X 元.(1) 求概率P(X =600);(2) 求X 的概率分布及数学期望E(X).23. 已知(1+x)2n +1=a 0+a 1x +a 2x 2+…+a 2n +1x 2n +1,n ∈N *.记T n =(2k +1)a n -k .(1) 求T 2的值;(2) 化简T n 的表达式,并证明:对任意的n ∈N *,T n 都能被4n +2整除.2018届高三模拟考试试卷(十三)(六市联考)数学参考答案及评分标准1. {1,3}2. 433. 304. 1255. 13 6.2+627. 43 8. 979. -6 10. 811. (x -1)2+y 2=4 12. (1,+∞) 13. 10 14. 4,1415. 解:(1) 因为a =(cos α,sin α),b =(-sin β,cos β),c =(-12,32),所以|a|=|b|=|c|=1,且a ·b =-cos αsin β+sin αcos β=sin(α-β).(3分) 因为|a +b|=|c|,所以|a +b|2=c 2,即a 2+2a ·b +b 2=1, 所以1+2sin(α-β)+1=1,即sin(α-β)=-12.(6分)(2) 因为α=5π6,所以a =(-32,12).故b +c =(-sin β-12,cos β+32).(8分)因为a ∥(b +c ),所以-32(cos β+32)-12(-sin β-12)=0.化简得12sin β-32cos β=12,所以sin(β-π3)=12.(12分)因为0<β<π,所以-π3<β-π3<2π3.所以β-π3=π6,即β=π2.(14分)16. 证明:(1) 在三棱柱ABC A 1B 1C 1中,BB 1∥CC 1. 因为AF ⊥CC 1,所以AF ⊥BB 1.(2分) 又AE ⊥BB 1,AE ∩AF =A ,AE ,AF ⊂平面AEF ,所以BB 1⊥平面AEF.(5分) 因为BB 1⊂平面BB 1C 1C ,所以平面AEF ⊥平面BB 1C 1C.(7分) (2) 因为AE ⊥BB 1,AF ⊥CC 1,∠ABE =∠ACF ,AB = AC , 所以Rt △AEB ≌Rt △AFC.所以BE =CF.(9分)又由(1)知,BE ∥CF ,所以四边形BEFC 是平行四边形.故BC ∥EF.(11分) 又BC ⊄平面AEF ,EF ⊂平面AEF ,所以BC ∥平面AEF.(14分)17. 解:设P(x 0,y 0),Q(x 1,y 1).(1) 在y =x +3中,令x =0,得y =3,从而b =3.(2分) 由⎩⎪⎨⎪⎧x 2a 2+y29=1,y =x +3得x 2a 2+(x +3)29=1,所以x 0=-6a 29+a2.(4分)因为PB 1=x 20+(y 0-3)2=2|x 0|, 所以42=2·6a 29+a2,解得a 2=18. 所以椭圆的标准方程为x 218+y 29=1.(6分)(2) (方法1)直线PB 1的斜率为kPB 1=y 0-3x 0,由QB 1⊥PB 1,所以直线QB 1的斜率为kQB 1=-x 0y 0-3.于是直线QB 1的方程为y =-x 0y 0-3x +3.同理,QB 2的方程为y =-x 0y 0+3x -3.(8分) 联立两直线方程,消去y ,得x 1=y 20-9x 0.(10分)因为P(x 0,y 0)在椭圆x 218+y 29=1上,所以x 2018+y 209=1,从而y 20-9=-x 202.所以x 1=-x 02.(12分)所以S △PB 1B 2S △QB 1B 2=⎪⎪⎪⎪⎪⎪x 0x 1=2.(14分)(证法2)设直线PB 1,PB 2的斜率为k ,k ′,则直线PB 1的方程为y =kx +3. 由QB 1⊥PB 1,直线QB 1的方程为y =-1kx +3.将y =kx +3代入x 218+y 29=1,得(2k 2+1)x 2+12kx =0,因为P 是椭圆上异于点B 1,B 2的点,所以x 0≠0,从而x 0=-12k2k 2+1.(8分)因为P(x 0,y 0)在椭圆x 218+y 29=1上,所以x 2018+y 209=1,从而y 20-9=-x 202.所以k ·k ′=y 0-3x 0·y 0+3x 0=y 20-9x 20=-12,得k ′=-12k .(10分)由QB 2⊥PB 2,所以直线QB 2的方程为y =2kx -3. 联立⎩⎪⎨⎪⎧y =-1k x +3,y =2kx -3则x =6k 2k 2+1,即x 1=6k 2k 2+1.(12分)所以S △PB 1B 2S △QB 1B 2=⎪⎪⎪⎪⎪⎪x 0x 1=⎪⎪⎪⎪⎪⎪-12k2k 2+16k 2k 2+1=2.(14分)18. 解:(1) 设所得圆柱的半径为r dm, 则(2πr +2r)×4r =100,(4分) 解得r =52(π+1)2(π+1).(6分)(2) 设所得正四棱柱的底面边长为a dm ,则⎩⎪⎨⎪⎧a ≤x2,a ≤100x -4a ,即⎩⎪⎨⎪⎧a ≤x2,a ≤20x .(9分)(方法1)所得正四棱柱的体积V =a 2x ≤⎩⎪⎨⎪⎧x 34,0<x ≤210,400x ,x>210.(11分)记函数p(x)=⎩⎪⎨⎪⎧x 34,0<x ≤210,400x ,x>210,则p(x)在(0,210]上单调递增,在[210,+∞)上单调递减, 所以当x =210时,p max (x)=2010.所以当x =210,a =10时,V max =2010 (dm 3).(14分)(方法2)2a ≤x ≤20a ,从而a ≤10.(11分)所得正四棱柱的体积V =a 2x ≤a 2(20a)=20a ≤2010.所以当a =10,x =210时,V max =2010 (dm 3).(14分)答:(1) 圆柱的底面半径为52(π+1)2(π+1) dm ;(2) 当x 为210时,能使按方案②制成的正四棱柱的体积最大.(16分)【评分说明】① 直接“由x ·(2x +x2)=100得x =210时正四棱柱的体积最大”给2分;② 方法1中的求解过程要体现V ≤p(x)≤210,凡写成V =p(x)≤210的最多得5分,其他类似解答参照给分.19. (1) 证明:假设数列c 1,c 2,c 3是等差数列,则2c 2=c 1+c 3,即2(a 2+b 2)=(a 1+b 1)+(a 3+b 3).因为b 1,b 2,b 3是等差数列,所以2b 2=b 1+b 3,从而2a 2=a 1+a 3.(2分)因为a 1,a 2,a 3是等比数列,所以a 22=a 1a 3. 所以a 1=a 2=a 3,这与q ≠1矛盾,从而假设不成立. 所以数列c 1,c 2,c 3不是等差数列.(4分) (2) 解:因为a 1=1,q =2,所以a n =2n -1.因为c 22=c 1c 3,所以(2+b 2)2=(1+b 2-d)(4+b 2+d),即b 2=d 2+3d.(6分)由c 2=2+b 2≠0,得d 2+3d +2≠0,所以d ≠-1且d ≠-2.又d ≠0,所以b 2=d 2+3d ,定义域为{d ∈R |d ≠-1,d ≠-2,d ≠0}.(8分)(3) 解:(解法1)设c 1,c 2,c 3,c 4成等比数列,其公比为q 1,则⎩⎪⎨⎪⎧a 1+b 1=c 1 ①,a 1q +b 1+d =c 1q 1②,a 1q 2+b 1+2d =c 1q 21 ③,a 1q 3+b 1+3d =c 1q 31④.(10分)将①+③-2×②,得a 1(q -1)2=c 1(q 1-1)2 ⑤,将②+④-2×③,得a 1q(q -1)2=c 1q 1(q 1-1)2 ⑥,(12分) 因为a 1≠0,q ≠1,由⑤得c 1≠0,q 1≠1. 由⑤⑥得q =q 1,从而a 1=c 1.(14分)代入①得b 1=0. 再代入②得d =0,与d ≠0矛盾. 所以c 1,c 2,c 3,c 4不成等比数列.(16分)(解法2)假设数列c 1,c 2,c 3,c 4是等比数列,则c 2c 1=c 3c 2=c 4c 3.(10分)所以c 3-c 2c 2-c 1=c 4-c 3c 3-c 2,即a 3-a 2+d a 2-a 1+d =a 4-a 3+d a 3-a 2+d .两边同时减1,得a 3-2a 2+a 1a 2-a 1+d =a 4-2a 3+a 2a 3-a 2+d .(12分)因为等比数列a 1,a 2,a 3,a 4的公比为q(q ≠1),所以a 3-2a 2+a 1a 2-a 1+d =q (a 3-2a 2+a 1)a 3-a 2+d.又a 3-2a 2+a 1=a 1(q -1)2≠0,所以q(a 2-a 1+d)=a 3-a 2+d ,即(q -1)d =0.(14分) 这与q ≠1,且d ≠0矛盾,所以假设不成立. 所以数列c 1,c 2,c 3,c 4不能为等比数列.(16分)20. (1) 解:由题意,f ′(x)=1-acos x ≥0对x ∈R 恒成立. 因为a>0,所以1a≥cos x 对x ∈R 恒成立.因为(cos x)max =1,所以1a≥1,从而0<a ≤1.(3分)(2) 证明:① g(x)=x -12sin x +bln x +1,所以g ′(x)=1-12cos x +bx .若b<0,则存在-b 2>0,使g ′(-b 2)=-1-12cos(-b2)<0,不合题意,所以b>0.(5分)取x 0=e -3b,则0<x 0<1.此时g(x 0)=x 0-12sin x 0+bln x 0+1<1+12+bln e -3b +1=-12<0.所以存在x 0>0,使g(x 0)<0.(8分)② 依题意,不妨设0<x 1<x 2,令x 2x 1=t ,则t>1.由(1)知函数y =x -sin x 单调递增,所以x 2-sin x 2>x 1-sin x 1. 从而x 2-x 1>sin x 2-sin x 1. (10分)因为g(x 1)=g(x 2),所以x 1-12sin x 1+bln x 1+1=x 2-12sin x 2+bln x 2+1,所以-b(ln x 2-ln x 1)=x 2-x 1-12(sin x 2-sin x 1)>12(x 2-x 1),所以-2b>x 2-x 1ln x 2-ln x 1>0.(12分)下面证明x 2-x 1ln x 2-ln x 1>x 1x 2,即证明t -1ln t>t ,只要证明ln t -t -1t<0 (*).设h(t)=ln t -t -1t (t>1),所以h ′(t)=-(t -1)22t t <0在(1,+∞)上恒成立.所以h(t)在(1,+∞)上单调递减,故h(t)<h(1)=0,从而(*)得证.所以-2b>x 1x 2, 即x 1x 2<4b 2.(16分)2018届高三模拟考试试卷(十三)(六市联考)数学附加题参考答案及评分标准21. A. 证明:延长AO 交圆O 于点E ,则BD ·DC =DE ·DA =(OD +OE)·(OA -OD).(5分) 因为OE =OA ,所以DB ·DC =(OA +OD)·(OA -OD)=OA 2-OD 2. 所以DB ·DC +OD 2=OA 2.(10分)B. 解:依题意,依次实施变换T 1,T 2所对应的矩阵NM =⎣⎢⎢⎡⎦⎥⎥⎤2 00 1⎣⎢⎢⎡⎦⎥⎥⎤1 00 2=⎣⎢⎢⎡⎦⎥⎥⎤2 00 2.(5分)则⎣⎢⎢⎡⎦⎥⎥⎤2 00 2⎣⎢⎢⎡⎦⎥⎥⎤00=⎣⎢⎢⎡⎦⎥⎥⎤00,⎣⎢⎢⎡⎦⎥⎥⎤2 00 2⎣⎢⎢⎡⎦⎥⎥⎤30=⎣⎢⎢⎡⎦⎥⎥⎤60,⎣⎢⎢⎡⎦⎥⎥⎤2 00 2⎣⎢⎢⎡⎦⎥⎥⎤22=⎣⎢⎢⎡⎦⎥⎥⎤44. 所以A(0,0),B(3,0),C(2,2)分别变为点A ′(0,0),B ′(6,0),C ′(4,4). 从而所得图形的面积为12×6×4=12.(10分)C. 解:以极点为原点,极轴为x 轴的非负半轴,建立平面直角坐标系xOy. 则点P 的直角坐标为(1,3).(2分)将直线l :ρsin ⎝ ⎛⎭⎪⎫θ-π3=2的方程变形为ρsin θcos π3-ρcos θsin π3=2,化为普通方程,得3x -y +4=0.(5分)所以P(1,3)到直线l :3x -y +4=0的距离为4(3)2+(-1)2=2.故所求圆的普通方程为(x -1)2+(y -3)2=4.(8分)化为极坐标方程,得ρ=4sin ⎝ ⎛⎭⎪⎫θ+π6.(10分)D. 证明:因为a ,b ,c 为正实数,所以1-a +c c (a +2b )=a +2b +3c c (a +2b )=(a +c )+2(b +c )ac +2bc ≥2ac +4bcac +2bc=2(当且仅当a =b =c 取“=”).(10分)22. 解:(1)从3×3表格中随机不重复地点击3格,共有C 39种不同情形, 则事件“X =600”包含两类情形: 第一类是3格各得奖200元;第二类是1格得奖300元,1格得奖200元,1格得奖100元.其中第一类包含C 34种情形,第二类包含C 11·C 14·C 14种情形, 所以P(X =600)=C 34+C 11·C 14·C 14C 39=521.(3分)(2) X 的所有可能值为300,400,500,600,700,则P(X =300)=C 34C 39=484=121,P(X =400)=C 11·C 24C 39=2484=27,P(X =500)=C 11·C 24+C 14·C 24C 39=3084=514,P(X =700)=C 11·C 24C 39=684=114.所以X 的概率分布列为所以E(X)=300×121+400×27+500×514+600×521+700×114=500.(10分)23. 解:由二项式定理,得a i=C i2n+1(i=0,1,2,…,2n+1).(1) T2=a2+3a1+5a0=C25+3C15+5C05=30.(2分)(2) 因为(n+1+k)C n+1+k2n+1=(n+1+k)·(2n+1)!(n+1+k)!(n-k)!=(2n+1)·(2n)!(n+k)!(n-k)!=(2n+1)C n+k2n,(4分)(8分)T n=(2n+1)C n2n=(2n+1)(C n-12n-1+C n2n-1)=2(2n+1)C n2n-1.因为C n2n-1∈N*,所以T n能被4n+2整除.(10分)。
江苏省南通市高三第二次调研测试数学Word版含答案

(第4题)南通市2018届高三第二次调研测试数学Ⅰ参考公式:柱体的体积公式V Sh =柱体,其中S 为柱体的底面积,h 为高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.. 1. 已知集合{}{} 1012 3 10 2 U A =-=-,,,,,,,,则UA = ▲ .2. 已知复数12i 34i z a z =+=-,,其中i 为虚数单位.若12z z 为纯虚数,则实数a 的值为 ▲ . 3. 某班40名学生参加普法知识竞赛,成绩都在区间[]40100,上,其频率分布直方图如图所示,则成绩不低于60分的人数为 ▲ .4. 如图是一个算法流程图,则输出的S 的值为 ▲ ./分(第3题)5. 在长为12 cm 的线段AB 上任取一点C ,以线段AC ,BC 为邻边作矩形,则该矩形的面积大于32 cm 2的概率为 ▲ .6. 在ABC △中,已知145AB AC B ===︒,,则BC 的长为 ▲ .7. 在平面直角坐标系xOy 中,已知双曲线C 与双曲线2213y x -=有公共的渐近线,且经过点()2P -,则双曲线C 的焦距为 ▲ .8. 在平面直角坐标系xOy 中,已知角αβ,的始边均为x 轴的非负半轴,终边分别经过点(12)A ,,(51)B ,,则tan()αβ-的值为 ▲ . 9. 设等比数列{}n a 的前n 项和为n S .若396S S S ,,成等差数列,且83a =,则5a 的值为▲ .10.已知a b c ,,均为正数,且4()abc a b =+,则a b c ++的最小值为 ▲ .11.在平面直角坐标系xOy 中,若动圆C上的点都在不等式组33030x x x ⎧⎪+⎨⎪+⎩≤,≥,≥表示的平面区域内,则面积最大的圆C 的标准方程为 ▲ .12.设函数31e 02()320x x f x x mx x -⎧->⎪=⎨⎪--⎩≤,,,(其中e 为自然对数的底数)有3个不同的零点,则实数m 的取值范围是 ▲ .13.在平面四边形ABCD 中,已知1423AB BC CD DA ====,,,,则AC BD ⋅的值为 ▲ . 14.已知a为常数,函数()f x 的最小值为23-,则a 的所有值为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在平面直角坐标系xOy 中,设向量()cos sin αα=,a ,()sin cos ββ=-,b,()12=-c . (1)若+=a b c ,求sin ()αβ-的值;(2)设5π6α=,0πβ<<,且()//+a b c ,求β的值.16.(本小题满分14分)如图,在三棱柱ABC -A 1B 1C 1中,AB = AC ,点E ,F 分别在棱BB 1 ,CC 1上(均异于端点),且∠ABE =∠ACF ,AE ⊥BB 1,AF ⊥CC 1. 求证:(1)平面AEF ⊥平面BB 1C 1C ;(2)BC // 平面AEF .17.(本小题满分14分)如图,在平面直角坐标系xOy 中,B 1,B 2是椭圆22221(0)y x a b a b+=>>的短轴端点,P 是椭圆上异于点B 1,B 2的一动点.当直线PB 1的方程为3y x =+时,线段PB 1的长为 (1)求椭圆的标准方程;(2)设点Q 满足:11QB PB ⊥,22QB PB ⊥.求证:△PB 1B 2与△QB 1B 2的面积之比为定值.18.(本小题满分16分)AA 1B 1C 1B C FE(第16题)0(第17题)(第18题)将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿虚线l 1,l 2裁剪成A ,B ,C 三个矩形(B ,C 全等),用来制成一个柱体.现有两种方案: 方案①:以1l 为母线,将A 作为圆柱的侧面展开图,并从B ,C 中各裁剪出一个圆形作为圆柱的两个底面;方案②:以1l 为侧棱,将A 作为正四棱柱的侧面展开图,并从B ,C 中各裁剪出一个正方形(各边分别与1l 或2l 垂直)作为正四棱柱的两个底面.(1)设B ,C 都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设1l 的长为x dm ,则当x 为多少时,能使按方案②制成的正四棱柱的体积最大?19.(本小题满分16分)设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(i = 1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域;(3)数列1234c c c c ,,,能否为等比数列?并说明理由.20.(本小题满分16分)设函数()sin (0)f x x a x a =->.(1)若函数()y f x =是R 上的单调增函数,求实数a 的取值范围;(2)设1()()ln 1(0)2a g x f x b x b b ==++∈≠R ,,,()g x '是()g x 的导函数.① 若对任意的0()0x g x '>>,,求证:存在0x ,使0()0g x <;② 若1212()()()g x g x x x =≠,求证:2124x x b <.南通市2018届高三第二次调研测试数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.................... 若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-1:几何证明选讲](本小题满分10分)如图,A ,B ,C 是⊙O 上的3个不同的点,半径OA 交弦BC 于点D . 求证:22DB DC OD OA ⋅+=.B .[选修4-2:矩阵与变换](本小题满分10分)在平面直角坐标系xOy 中,已知(00)(30)(22)A B C ,,,,,.设变换1T ,2T 对应的矩阵分别为1002⎡⎤=⎢⎥⎣⎦M ,2001⎡⎤=⎢⎥⎣⎦N ,求对△ABC 依次实施变换1T ,2T 后所得图形的面积. ABDOC(第21—A 题)C .[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点()23P π,为圆心且与直线l :()sin 23ρθπ-=相切的圆的极坐标方程.D .[选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 为正实数,且12a b c ++=2.【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3⨯3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3元.(1)求概率(600)P X =;(2)求X 的概率分布及数学期望()E X .23.(本小题满分10分) 已知212012(1)n x a a x a x ++=+++ (21)21n n a x+++,*n ∈N .记0(21)nn n k k T k a -==+∑.(1)求2T 的值;(2)化简n T 的表达式,并证明:对任意的*n ∈N ,n T 都能被42n +整除.(第22题)(第4题)南通市2018届高三第二次调研测试 数学学科参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共计70分. 1. 已知集合{}{} 1012 3 10 2 U A =-=-,,,,,,,,则UA = ▲ .【答案】{}13,2. 已知复数12i 34i z a z =+=-,,其中i 为虚数单位.若12z z 为纯虚数,则实数a 的值为 ▲ . 【答案】433. 某班40名学生参加普法知识竞赛,成绩都在区间[]40100,上,其频率分布直方图如图 所示,则成绩不低于60分的人数为 ▲ .【答案】304. 如图是一个算法流程图,则输出的S 的值为▲ . 【答案】1255. 在长为12 cm 的线段AB 上任取一点C ,以线段AC ,BC 为邻边作矩形,则该矩形的面积大于32 cm 2的概率为 ▲ .【答案】136. 在ABC △中,已知145AB AC B ===︒,,则BC 的长为 ▲ ./分(第3题)7. 在平面直角坐标系xOy 中,已知双曲线C 与双曲线2213y x -=有公共的渐近线,且经过点()2P -,则双曲线C 的焦距为 ▲ .【答案】8. 在平面直角坐标系xOy 中,已知角αβ,的始边均为x 轴的非负半轴,终边分别经过点 (12)A ,,(51)B ,,则tan()αβ-的值为 ▲ . 【答案】979. 设等比数列{}n a 的前n 项和为n S .若396S S S ,,成等差数列,且83a =,则5a 的值为▲ . 【答案】6-10.已知a b c ,,均为正数,且4()abc a b =+,则a b c ++的最小值为 ▲ . 【答案】811.在平面直角坐标系xOy 中,若动圆C上的点都在不等式组33030x x x ⎧⎪+⎨⎪+⎩≤,≥,≥表示的平面区域内,则面积最大的圆C 的标准方程为 ▲ . 【答案】22(1)4x y -+=12.设函数31e 02()320x x f x x mx x -⎧->⎪=⎨⎪--⎩≤,,,(其中e 为自然对数的底数)有3个不同的零点, 则实数m 的取值范围是 ▲ . 【答案】()1+∞,13.在平面四边形ABCD 中,已知1423AB BC CD DA ====,,,,则AC BD ⋅的值为 ▲ . 【答案】1014.已知a为常数,函数()f x 的最小值为23-,则a 的所有值为 ▲ .【答案】144,二、解答题:本大题共6小题,共计90分. 15.(本小题满分14分)在平面直角坐标系xOy 中,设向量()cos sin αα=,a ,()sin cos ββ=-,b ,()12=-c .(1)若+=a b c ,求sin ()αβ-的值;(2)设5π6α=,0πβ<<,且()//+a b c ,求β的值.解:(1)因为()cos sin αα=,a ,()sin cos ββ=-,b,()12=-c ,所以1===a b c ,且cos sin sin cos sin ()αβαβαβ⋅=-+=-a b . …… 3分因为+=a b c ,所以22+=a bc ,即a 2 + 2 a ⋅b + b 2 = 1,所以12sin ()11αβ+-+=,即1sin ()2αβ-=-. …… 6分(2)因为5π6α=,所以()12=,a .依题意,()1sin cos 2ββ+=--+,b c . …… 8分因为()//+a b c,所以)()11cos sin 022ββ---=.化简得,11sin 22ββ-=,所以()π1sin 32β-=. …… 12分因为0πβ<<,所以ππ2π333β-<-<. 所以ππ36β-=,即π2β=. …… 14分16.(本小题满分14分)如图,在三棱柱ABC -A 1B 1C 1中,AB = AC ,点E ,F 分别在棱BB 1 ,CC 1上(均异 于端点),且∠ABE =∠ACF ,AE ⊥BB 1,AF ⊥CC 1. 求证:(1)平面AEF ⊥平面BB 1C 1C ;(2)BC // 平面AEF .证明:(1)在三棱柱ABC -A 1B 1C 1中,BB 1 // CC 1.因为AF ⊥CC 1,所以AF ⊥BB 1. …… 2分又AE ⊥BB 1,AE AF A =,AE ,AF ⊂平面AEF , 所以BB 1⊥平面AEF . …… 5分AA 1B 1C 1BCF E(第16题)又因为BB 1⊂平面BB 1C 1C ,所以平面AEF ⊥平面BB 1C 1C . …… 7分 (2)因为AE ⊥BB 1,AF ⊥CC 1,∠ABE =∠ACF ,AB = AC , 所以Rt △AEB ≌Rt △AFC .所以BE = CF . …… 9分 又由(1)知,BE // CF .所以四边形BEFC 是平行四边形.从而BC // EF . …… 11分 又BC ⊄平面AEF ,EF ⊂平面AEF ,所以BC // 平面AEF . …… 14分17.(本小题满分14分)如图,在平面直角坐标系xOy 中,B 1,B 2是椭圆22221(0)y x a b a b+=>>的短轴端点,P 是椭圆上异于点B 1,B 2的一动点.当直线PB 1的方程为3y x =+时,线段PB 1的长为 (1)求椭圆的标准方程;(2)设点Q 满足:11QB PB ⊥,22QB PB ⊥.求证:△PB 1B 2与△QB 1B 2的面积之比为定值. 解:设()00P x y ,,()11Q x y ,.(1)在3y x =+中,令0x =,得3y =,从而b = 3…… 2 由222193y x a y x ⎧+=⎪⎨⎪=+⎩, 得()222319x x a ++=. 所以20269a x a =-+. …… 4分因为10PB x =,所以2269a a=+,解得218a =. 所以椭圆的标准方程为221189y x +=. …… 6分 (2)方法一:直线PB 1的斜率为1003PB y k x -=, (第17题)由11QB PB ⊥,所以直线QB 1的斜率为1003QB x k y =--. 于是直线QB 1的方程为:0033x y x y =-+-. 同理,QB 2的方程为:0033x y x y =--+. …… 8分 联立两直线方程,消去y ,得20109y x x -=. …… 10分因为()00P x y ,在椭圆221189y x +=上,所以22001189x y +=,从而220092x y -=-. 所以012x x =-. …… 12分 所以1212012PB B QB B S xS x ∆∆==. …… 14分 方法二:设直线PB 1,PB 2的斜率为k ,k ',则直线PB 1的方程为3y kx =+. 由11QB PB ⊥,直线QB 1的方程为13y x k=-+.将3y kx =+代入221189y x +=,得()2221120k x kx ++=, 因为P 是椭圆上异于点B 1,B 2的点,所以00x ≠,从而0x =21221k k -+.…… 8分 因为()00P x y ,在椭圆221189y x +=上,所以22001189x y +=,从而220092x y -=-. 所以2000200033912y y y k k x x x -+-'⋅=⋅==-,得12k k '=-. …… 10分 由22QB PB ⊥,所以直线2QB 的方程为23y kx =-.联立1323y x k y kx ⎧=-+⎪⎨⎪=-⎩,则2621k x k =+,即12621k x k =+. …… 12分 所以1212201212212621PB B QB B k S xk S x kk ∆∆-+===+. …… 14分18.(本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿 虚线l 1,l 2裁剪成A ,B ,C 三个矩形(B ,C 全等),用来制成一个柱体.现有两种方案:(第18题)方案①:以1l 为母线,将A 作为圆柱的侧面展开图,并从B ,C 中各裁剪出一个圆形作为圆柱的两个底面;方案②:以1l 为侧棱,将A 作为正四棱柱的侧面展开图,并从B ,C 中各裁剪出一个正方形(各边分别与1l 或2l 垂直)作为正四棱柱的两个底面.(1)设B ,C 都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设1l 的长为x dm ,则当x 为多少时,能使按方案②制成的正四棱柱的体积最大? 解:(1)设所得圆柱的半径为r dm ,则()2π24100r r r +⨯=, …… 4分 解得r =. …… 6分(2)设所得正四棱柱的底面边长为a dm ,则21004x a a a x ⎧⎪⎨⎪-⎩≤≤,,即220.x a a x ⎧⎪⎨⎪⎩≤≤,…… 9分 方法一:所得正四棱柱的体积3204400x x V a x x x⎧<⎪=⎨⎪>⎩≤≤,, ……11分记函数304()400x x p x x x⎧<⎪=⎨⎪>⎩≤,,则()p x 在(0,上单调递增,在)⎡+∞⎣上单调递减,所以当x =max ()p x =所以当x =a =max V =dm 3. …… 14分 方法二:202a x a ≤≤,从而a ……11分所得正四棱柱的体积()222020V a x a a a==≤≤.所以当a x =max V =dm 3. …… 14分答:(1 dm ;(2)当x 为 …… 16分 【评分说明】①直接“由()21002x x x ⋅+=得,x =2分;②方法一中的求解过程要体现()p x V ≤≤()p x V =≤的最多得5分, 其它类似解答参照给分.19.(本小题满分16分)设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(i = 1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. 解:(1)假设数列123c c c ,,是等差数列, 则2132c c c =+,即()()()2211332a b a b a b +=+++.因为12b b ,,3b 是等差数列,所以2132b b b =+.从而2132a a a =+. …… 2分又因为12a a ,,3a 是等比数列,所以2213a a a =. 所以123a a a ==,这与1q ≠矛盾,从而假设不成立.所以数列123c c c ,,不是等差数列. …… 4分 (2)因为11a =,2q =,所以12n n a -=.因为2213c c c =,所以()()()2222214b b d b d +=+-++,即223b d d =+,…… 6分 由2220c b =+≠,得2320d d ++≠,所以1d ≠-且2d ≠-.又0d ≠,所以223b d d =+,定义域为{}120d d d d ∈≠-≠-≠R ,,.…… 8分 (3)方法一:设c 1,c 2,c 3,c 4成等比数列,其公比为q 1, 则1111111221111331111=2=3=.a b c a q b d c q a q b d c q a q b d c q +=⎧⎪++⎪⎨++⎪⎪++⎩①②③④,,, …… 10分将①+③-2×②得,()()2211111a q c q -=-,⑤将②+④-2×③得,()()22111111a q q c q q -=-,⑥ …… 12分 因为10a ≠,1q ≠,由⑤得10c ≠,11q ≠.由⑤⑥得1q q =,从而11a c =. …… 14分 代入①得10b =.再代入②,得0d =,与0d ≠矛盾.所以c 1,c 2,c 3,c 4不成等比数列. …… 16分方法二:假设数列1234c c c c ,,,是等比数列,则324123c c c c c c ==. …… 10分 所以32432132c c c c c c c c --=--,即32432132a a d a a d a a d a a d -+-+=-+-+. 两边同时减1得,321432213222a a a a a a a a d a a d-+-+=-+-+. …… 12分 因为等比数列a 1,a 2,a 3,a 4的公比为q ()1q ≠,所以()321321213222q a a a a a a a a d a a d-+-+=-+-+. 又()23211210a a a a q -+=-≠,所以()2132q a a d a a d -+=-+,即()10q d -=. …… 14分 这与1q ≠,且0d ≠矛盾,所以假设不成立.所以数列1234c c c c ,,,不能为等比数列. …… 16分20.(本小题满分16分)设函数()sin (0)f x x a x a =->.(1)若函数()y f x =是R 上的单调增函数,求实数a 的取值范围;(2)设1()()ln 1(0)2a g x f x b x b b ==++∈≠R ,,,()g x '是()g x 的导函数.① 若对任意的0()0x g x '>>,,求证:存在0x ,使0()0g x <;② 若1212()()()g x g x x x =≠,求证:2124x x b <. 解:(1)由题意,()1cos 0f x a x '=-≥对x ∈R 恒成立,因为0a >,所以1cos x a≥对x ∈R 恒成立,因为()max cos 1x =,所以11a ≥,从而01a <≤. …… 3分(2)①()1sin ln 12g x x x b x =-++,所以()11cos 2b g x x x '=-+.若0b <,则存在02b ->,使()()11cos 0222b b g '-=---<,不合题意,所以0b >. …… 5分 取30e b x -=,则001x <<.此时()30000111sin ln 11ln 10222b g x x x b x b e -=-++<+++=-<.所以存在00x >,使()00g x <. …… 8分 ②依题意,不妨设120x x <<,令21x t x =,则1t >. 由(1)知函数sin y x x =-单调递增,所以2211sin sin x x x x ->-.从而2121sin sin x x x x ->-. …… 10分因为()()12g x g x =,所以11122211sin ln 1sin ln 122x x b x x x b x -++=-++,所以()()()2121212111ln ln sin sin 22b x x x x x x x x --=--->-. 所以212120ln ln x x b x x -->>-. ……12分下面证明2121ln ln x x x x ->-1ln t t ->()ln 0t <*.设())ln 1h t t t =>,所以()210h t -'=<在()1+∞,恒成立.所以()h t 在()1+∞,单调递减,故()()10h t h <=,从而()*得证.所以2b -> 即2124x x b <. ……16分数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.................... 若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-1:几何证明选讲](本小题满分10分)如图,A ,B ,C 是⊙O 上的3个不同的点,半径OA 交弦BC 于点D . 求证:22DB DC OD OA ⋅+=. 证明:延长AO 交⊙O 于点E ,则()()DB DC DE DA OD OE OA OD ⋅=⋅=+⋅-.…… 5分因为OE OA =,所以()()22DB DC OA OD OA OD OA OD ⋅=+⋅-=-. 所以22DB DC OD OA ⋅+=. …… 10分B .[选修4-2:矩阵与变换](本小题满分10分)ABDC(第21—A 题)EO在平面直角坐标系xOy 中,已知(00)(30)(22)A B C ,,,,,.设变换1T ,2T 对应的矩 阵分别为1002⎡⎤=⎢⎥⎣⎦M ,2001⎡⎤=⎢⎥⎣⎦N ,求对△ABC 依次实施变换1T ,2T 后所得图形的面积. 解:依题意,依次实施变换1T ,2T 所对应的矩阵=NM 201020010202⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. …… 5分 则20000200⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,20360200⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,20240224⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. 所以(00)(30)(22)A B C ,,,,,分别变为点(00)(60)(44)A B C ''',,,,,. 从而所得图形的面积为164122⨯⨯=. (10)分C .[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点()23P π,为圆心且与直线l :()sin 23ρθπ-=相切的圆的极坐标方程.解:以极点为原点,极轴为x 轴的非负半轴,建立平面直角坐标系xOy .则点P 的直角坐标为()1. …… 2分 将直线l :()sin 23ρθπ-=的方程变形为:sin cos cos sin 233ρθρθππ-=,40y -+=. …… 5分所以()1P 到直线l 40y -+=2=.故所求圆的普通方程为()(2214x y -+=. …… 8分化为极坐标方程得,()π4sin 6ρθ=+. …… 10分D .[选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 为正实数,且12a b c ++=2.证明:因为a ,b ,c 为正实数,==2=(当且仅当a b c ==取“=”). …… 10分【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应 写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3⨯3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X 元.(1)求概率()600P X =;(2)求X 的概率分布及数学期望()E X .解:(1)从3⨯3表格中随机不重复地点击3格,共有39C 种不同情形. 则事件:“600X =”包含两类情形: 第一类是3格各得奖200元;第二类是1格得奖300元,一格得奖200元,一格得奖100元,其中第一类包含34C 种情形,第二类包含111144C C C ⋅⋅种情形.所以()3111414439C C C C 560021C P X +⋅⋅===. …… 3分 (2)X 的所有可能值为300,400,500,600,700.则()3439C 413008421C P X ====,()121439C C 242400847C P X ⋅====,(第22题)()1212144439C C C C 3055008414C P X ⋅+⋅====,()121439C C 637008442C P X ⋅====. 所以X 的概率分布列为:…… 8分所以()12553300400500600700500217142142E X=⨯+⨯+⨯+⨯+⨯=(元). …… 10分23.(本小题满分10分) 已知212012(1)n x a a x a x ++=+++ (21)21n n a x+++,*n ∈N .记0(21)nn n k k T k a -==+∑.(1)求2T 的值;(2)化简n T 的表达式,并证明:对任意的*n ∈N ,n T 都能被42n +整除. 解:由二项式定理,得21C i i n a +=(i =0,1,2,…,2n +1).(1)210221055535C 3C 5C 30T a a a =++=++=; …… 2分(2)因为()()()()()12121!1C 11!!n kn n n k n k n k n k ++++++=++⋅++-()()()()212!!!n n n k n k +⋅=+-()221C n kn n +=+,…… 4分 所以()021nn n k k T k a -==+∑()21021C nn kn k k -+==+∑()121021C nn k n k k +++==+∑()()12102121C nn k n k n k n +++==++-+⎡⎤⎣⎦∑()()112121021C21C nnn k n kn n k k n k n ++++++===++-+∑∑()()12210221C21C nnn kn knn k k n n ++++===+-+∑∑()()()2212112212C 21222n n n n n n +=+⋅⋅+-+⋅⋅ ()221C n n n =+. …… 8分()()()()1221212121C 21C C 221C n n n nn n n n n T n n n ----=+=++=+.因为21C n n *-∈N ,所以n T 能被42n +整除. …… 10分。
江苏省南通、徐州、扬州、泰州、淮安、宿迁六市2018届高三数学3月第二次调研(二模)试题
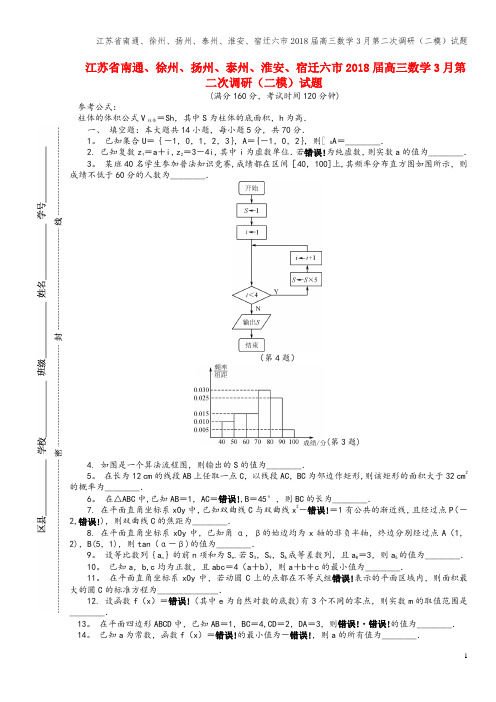
江苏省南通、徐州、扬州、泰州、淮安、宿迁六市2018届高三数学3月第二次调研(二模)试题(满分160分,考试时间120分钟)参考公式:柱体的体积公式V柱体=Sh,其中S为柱体的底面积,h为高.一、填空题:本大题共14小题,每小题5分,共70分.1。
已知集合U={-1,0,1,2,3},A={-1,0,2},则∁U A=________.2. 已知复数z1=a+i,z2=3-4i,其中i为虚数单位.若错误!为纯虚数,则实数a的值为________.3。
某班40名学生参加普法知识竞赛,成绩都在区间[40,100]上,其频率分布直方图如图所示,则成绩不低于60分的人数为________.(第4题)(第3题)4. 如图是一个算法流程图,则输出的S的值为________.5。
在长为12 cm的线段AB上任取一点C,以线段AC,BC为邻边作矩形,则该矩形的面积大于32 cm2的概率为________.6。
在△ABC中,已知AB=1,AC=错误!,B=45°,则BC的长为________.7. 在平面直角坐标系xOy中,已知双曲线C与双曲线x2-错误!=1有公共的渐近线,且经过点P(-2,错误!),则双曲线C的焦距为________.8. 在平面直角坐标系xOy中,已知角α,β的始边均为x轴的非负半轴,终边分别经过点A(1,2),B(5,1),则tan(α-β)的值为________.9。
设等比数列{a n}的前n项和为S n.若S3,S9,S6成等差数列,且a8=3,则a5的值为________.10。
已知a,b,c均为正数,且abc=4(a+b),则a+b+c的最小值为________.11。
在平面直角坐标系xOy中,若动圆C上的点都在不等式组错误!表示的平面区域内,则面积最大的圆C的标准方程为______________.12. 设函数f(x)=错误!(其中e为自然对数的底数)有3个不同的零点,则实数m的取值范围是________.13。
江苏省南通市2018届高三第二次调研数学测试含答案

(第4题)江苏省南通市2018届高三第二次调研测试数学学科参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共计70分.1. 已知集合{}{} 1012 3 10 2 U A =-=-,,,,,,,,则U A =ð ▲ .【答案】{}13,2. 已知复数12i 34i z a z =+=-,,其中i 为虚数单位.若12z 为纯虚数,则实数a 的值为 ▲ . 【答案】433. 某班40名学生参加普法知识竞赛,成绩都在区间[]40100,上,其频率分布直方图如图 所示,则成绩不低于60分的人数为 ▲ .【答案】304. 如图是一个算法流程图,则输出的S 的值为▲ . 【答案】1255. 在长为12 cm 的线段AB 上任取一点C ,以线段AC ,BC 为邻边作矩形,则该矩形的面积大于32 cm 2的概率为 ▲ .【答案】136. 在ABC △中,已知145AB AC B ===︒,,则BC 的长为 ▲ .7. 在平面直角坐标系xOy 中,已知双曲线C 与双曲线2213y x -=有公共的渐近线,且经过成绩/分(第3题)点()2P -,则双曲线C 的焦距为 ▲ .【答案】8. 在平面直角坐标系xOy 中,已知角αβ,的始边均为x 轴的非负半轴,终边分别经过点(12)A ,,(51)B ,,则tan()αβ-的值为 ▲ . 【答案】979. 设等比数列{}n a 的前n 项和为n S .若396S S S ,,成等差数列,且83a =,则5a 的值为▲ . 【答案】6-10.已知a b c ,,均为正数,且4()abc a b =+,则a b c ++的最小值为 ▲ . 【答案】811.在平面直角坐标系xOy 中,若动圆C上的点都在不等式组33030x x x ⎧⎪+⎨⎪++⎩≤,≥,≥表示的平面区域内,则面积最大的圆C 的标准方程为 ▲ . 【答案】22(1)4x y -+=12.设函数31e 02()320x x f x x mx x -⎧->⎪=⎨⎪--⎩≤,,,(其中e 为自然对数的底数)有3个不同的零点, 则实数m 的取值范围是 ▲ . 【答案】()1+∞,13.在平面四边形ABCD 中,已知1423AB BC CD DA ====,,,,则AC BD ⋅的值为 ▲ . 【答案】1014.已知a为常数,函数()f x =的最小值为2-,则a 的所有值为 ▲ .【答案】144,二、解答题:本大题共6小题,共计90分. 15.(本小题满分14分)在平面直角坐标系xOy 中,设向量()cos sin αα=,a ,()sin cos ββ=-,b ,()12=-c .(1)若+=a b c ,求sin ()αβ-的值;(2)设5π6α=,0πβ<<,且()//+a b c ,求β的值.解:(1)因为()cos sin αα=,a ,()sin cos ββ=-,b,()12=-c ,所以1===a b c ,且cos sin sin cos sin ()αβαβαβ⋅=-+=-a b . …… 3分因为+=a b c ,所以22+=a bc ,即a 2 + 2 a ⋅b + b 2= 1,所以12sin ()11αβ+-+=,即1sin ()2αβ-=-. …… 6分(2)因为5π6α=,所以()12=,a .依题意,()1sin cos 2ββ+=--,b c . …… 8分因为()//+a b c,所以)()11cos sin 022ββ---=.化简得,11sin ββ=,所以()π1sin 32β-=. …… 12分因为0πβ<<,所以ππ2π333β-<-<. 所以ππβ-=,即π2β=. …… 14分16.(本小题满分14分)如图,在三棱柱ABC -A 1B 1C 1中,AB = AC ,点E ,F 分别在棱BB 1 ,CC 1上(均异 于端点),且∠ABE =∠ACF ,AE ⊥BB 1,AF ⊥CC 1. 求证:(1)平面AEF ⊥平面BB 1C 1C ;(2)BC // 平面AEF .证明:(1)在三棱柱ABC -A 1B 1C 1中,BB 1 // CC 1.因为AF ⊥CC 1,所以AF ⊥BB 1. …… 2分又AE ⊥BB 1,AE AF A =,AE ,AF ⊂平面AEF , 所以BB 1⊥平面AEF . …… 5分 又因为BB 1⊂平面BB 1C 1C ,所以平面AEF ⊥平面BB 1C 1C . …… 7分AA 1B 1C 1BCF E(第16题)(2)因为AE ⊥BB 1,AF ⊥CC 1,∠ABE =∠ACF ,AB = AC , 所以Rt △AEB ≌Rt △AFC .所以BE = CF . …… 9分 又由(1)知,BE // CF .所以四边形BEFC 是平行四边形.从而BC // EF . …… 11分 又BC ⊄平面AEF ,EF ⊂平面AEF ,所以BC // 平面AEF . …… 14分17.(本小题满分14分)如图,在平面直角坐标系xOy 中,B 1,B 2是椭圆22221(0)y x a b a b+=>>的短轴端点,P 是椭圆上异于点B 1,B 2的一动点.当直线PB 1的方程为3y x =+时,线段PB 1的长为 (1)求椭圆的标准方程;(2)设点Q 满足:11QB PB ⊥,22QB PB ⊥.求证:△PB 1B 2与△QB 1B 2的面积之比为定值. 解:设()00P x y ,,()11Q x y ,. (1)在3y x =+中,令0x =,得3y =,从而b = 3…… 2 由222193y x a y x ⎧+=⎪⎨⎪=+⎩, 得()222319x x a ++=. 所以20269a x a =-+. …… 4分因为10PB x =,所以2269a a+,解得218a =.所以椭圆的标准方程为221189y x +=. …… 6分 (2)方法一:直线PB 1的斜率为1003PB y k x -=, (第17题)由11QB PB ⊥,所以直线QB 1的斜率为1003QB x k y =--. 于是直线QB 1的方程为:0033x y x y =-+-. 同理,QB 2的方程为:0033x y x y =--+. …… 8分 联立两直线方程,消去y ,得20109y x x -=. …… 10分因为()00P x y ,在椭圆221189y x +=上,所以22001x y +=,从而22009x y -=-.所以012x x =-. …… 12分 所以1212012PB B QB B S xS x ∆∆==. …… 14分方法二:设直线PB 1,PB 2的斜率为k ,k ',则直线PB 1的方程为3y kx =+. 由11QB PB ⊥,直线QB 1的方程为13y x k=-+.将3y kx =+代入221189y x +=,得()2221120k x kx ++=, 因为P 是椭圆上异于点B 1,B 2的点,所以00x ≠,从而0x =21221k k -+.…… 8分 因为()00P x y ,在椭圆221189y x +=上,所以22001189x y +=,从而220092x y -=-.所以2000200033912y y y k k x x x -+-'⋅=⋅==-,得12k k '=-. …… 10分 由22QB PB ⊥,所以直线2QB 的方程为23y kx =-.联立1323y x k y kx ⎧=-+⎪⎨⎪=-⎩,则2621k x k =+,即12621k x k =+. …… 12分 所以121201212212621PB B QB B k S x k S x kk ∆∆-+===+. …… 14分18.(本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿 虚线l 1,l 2裁剪成A ,B ,C 三个矩形(B ,C 全等),用来制成一个柱体.现有两种方案:(第18题)方案①:以1l 为母线,将A 作为圆柱的侧面展开图,并从B ,C 中各裁剪出一个圆形作为圆柱的两个底面;方案②:以1l 为侧棱,将A 作为正四棱柱的侧面展开图,并从B ,C 中各裁剪出一个正方形(各边分别与1l 或2l 垂直)作为正四棱柱的两个底面.(1)设B ,C 都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设1l 的长为x dm ,则当x 为多少时,能使按方案②制成的正四棱柱的体积最大? 解:(1)设所得圆柱的半径为r dm ,则()2π24100r r r +⨯=, …… 4分 解得r …… 6分(2)设所得正四棱柱的底面边长为a dm ,则21004x a a a x ⎧⎪⎨⎪-⎩≤≤,,即220.x a a x ⎧⎪⎨⎪⎩≤≤,…… 9分 方法一:所得正四棱柱的体积3204400x x V a x x x⎧<⎪=⎨⎪>⎩≤≤,, ……11分记函数304()400x x p x x x⎧<⎪=⎨⎪>⎩≤,,则()p x 在(0,上单调递增,在)⎡+∞⎣上单调递减,所以当x =max ()p x =所以当x =a =max V =dm 3. …… 14分 方法二:202ax a ≤≤,从而a ……11分所得正四棱柱的体积()222020V a x a a a==≤≤.所以当a =x =max V =dm 3. …… 14分答:(1 dm ;(2)当x 为 …… 16分 【评分说明】①直接“由()21002x x x ⋅+=得,x =2分;②方法一中的求解过程要体现()p x V ≤≤()p x V =≤5分, 其它类似解答参照给分.19.(本小题满分16分)设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(i = 1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. 解:(1)假设数列123c c c ,,是等差数列, 则2132c c c =+,即()()()2211332a b a b a b +=+++.因为12b b ,,3b 是等差数列,所以2132b b b =+.从而2132a a a =+. …… 2分 又因为12a a ,,3a 是等比数列,所以2213a a a =. 所以123a a a ==,这与1q ≠矛盾,从而假设不成立.所以数列123c c c ,,不是等差数列. …… 4分 (2)因为11a =,2q =,所以12n n a -=.因为2213c c c =,所以()()()2222214b b d b d +=+-++,即223b d d =+,…… 6分 由2220c b =+≠,得2320d d ++≠,所以1d ≠-且2d ≠-.又0d ≠,所以223b d d =+,定义域为{}120d d d d ∈≠-≠-≠R ,,.…… 8分(3)方法一:设c 1,c 2,c 3,c 4成等比数列,其公比为q 1, 则1111111221111331111=2=3=.a b c a q b d c q a q b d c q a q b d c q +=⎧⎪++⎪⎨++⎪⎪++⎩①②③④,,, …… 10分将①+③-2×②得,()()2211111a q c q -=-,⑤将②+④-2×③得,()()22111111a q q c q q -=-,⑥ …… 12分 因为10a ≠,1q ≠,由⑤得10c ≠,11q ≠.由⑤⑥得1q q =,从而11a c =. …… 14分 代入①得10b =.再代入②,得0d =,与0d ≠矛盾.所以c 1,c 2,c 3,c 4不成等比数列. …… 16分方法二:假设数列1234c c c c ,,,是等比数列,则324123c c c c c c ==. …… 10分 所以32432132c c c c --=,即32432132a a d a a d -+-+=. 两边同时减1得,321432213222a a a a a a a a d a a d-+-+=-+-+. …… 12分 因为等比数列a 1,a 2,a 3,a 4的公比为q ()1q ≠,所以()321321213222q a a a a a a a a d a a d-+-+=-+-+.又()23211210a a a a q -+=-≠,所以()2132q a a d a a d -+=-+,即()10q d -=. …… 14分 这与1q ≠,且0d ≠矛盾,所以假设不成立.所以数列1234c c c c ,,,不能为等比数列. …… 16分20.(本小题满分16分)设函数()sin (0)f x x a x a =->.(1)若函数()y f x =是R 上的单调增函数,求实数a 的取值范围;(2)设1()()ln 1(0)a g x f x b x b b ==++∈≠R ,,,()g x '是()g x 的导函数.① 若对任意的0()0x g x '>>,,求证:存在0x ,使0()0g x <;② 若1212()()()g x g x x x =≠,求证:2124x x b <. 解:(1)由题意,()1cos 0f x a x '=-≥对x ∈R 恒成立,因为0a >,所以1cos x a≥对x ∈R 恒成立,因为()max cos 1x =,所以11a ≥,从而01a <≤. …… 3分(2)①()1sin ln 12g x x x b x =-++,所以()11cos 2b g x x x'=-+.若0b <,则存在0b ->,使()()11cos 0222b b g '-=---<,不合题意,所以0b >. …… 5分 取30ebx -=,则001x <<.此时()30000111sin ln 11ln 10222g x x x b x b e -=-++<+++=-<.所以存在00x >,使()00g x <. …… 8分 ②依题意,不妨设120x x <<,令21x t x =,则1t >. 由(1)知函数sin y x x =-单调递增,所以2211sin sin x x x x ->-.从而2121sin sin x x x x ->-. …… 10分因为()()12g x g x =,所以11122211sin ln 1sin ln 122x x b x x x b x -++=-++,所以()()()2121212111ln ln sin sin 22b x x x x x x x x --=--->-. 所以212120ln ln x x b x x -->>-.……12分下面证明2121x x -1t ->()ln 0t <*.设()()ln 1h t t t =>,所以()210h t -'=<在()1+∞,恒成立.所以()h t 在()1+∞,单调递减,故()()10h t h <=,从而()*得证.所以2b - 即2124x x b <. ……16分数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.................... 若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,A ,B ,C 是⊙O 上的3个不同的点,半径OA 交弦BC 于点D . 求证:22DB DC OD OA ⋅+=. 证明:延长AO 交⊙O 于点E ,则()()DB DC DE DA OD OE OA OD ⋅=⋅=+⋅-.…… 5分因为OE OA =,所以()()22DB DC OA OD OA OD OA OD ⋅=+⋅-=-. 所以22DB DC OD OA ⋅+=. …… 10分B .[选修4-2:矩阵与变换](本小题满分10分)在平面直角坐标系xOy 中,已知(00)(30)(22)A B C ,,,,,.设变换1T ,2T 对应的矩 阵分别为1002⎡⎤=⎢⎥⎣⎦M ,2001⎡⎤=⎢⎥⎣⎦N ,求对△ABC 依次实施变换1T ,2T 后所得图形的面积. ABDC(第21—A 题)EO解:依题意,依次实施变换1T ,2T 所对应的矩阵=NM 201020010202⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. …… 5分 则20000200⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,20360200⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,20240224⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. 所以(00)(30)(22)A B C ,,,,,分别变为点(00)(60)(44)A B C ''',,,,,. 从而所得图形的面积为164122⨯⨯=. …… 10分C .[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点()23P π,为圆心且与直线l :()sin 2ρθπ-=相切的圆的极坐标方程.解:以极点为原点,极轴为x 轴的非负半轴,建立平面直角坐标系xOy .则点P 的直角坐标为()1. …… 2分将直线l :()sin 23ρθπ-=的方程变形为:sin cos cos sin 233ρθρθππ-=,40y -+=. …… 5分所以()1P 到直线l 40y -+=2=.故所求圆的普通方程为()(2214x y -+=. …… 8分化为极坐标方程得,()π4sin 6ρθ=+. …… 10分D .[选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 为正实数,且12a b c ++=2.证明:因为a ,b ,c 为正实数,=2a c b c +++=2=(当且仅当a b c ==取“=”). …… 10分【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应 写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3⨯3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X 元.(1)求概率()600P X =;(2)求X 的概率分布及数学期望()E X .解:(1)从3⨯3表格中随机不重复地点击3格,共有39C 种不同情形. 则事件:“600X =”包含两类情形: 第一类是3格各得奖200元;第二类是1格得奖300元,一格得奖200元,一格得奖100元,其中第一类包含34C 种情形,第二类包含111144C C C ⋅⋅种情形.所以()3111414439C C C C 560021C P X +⋅⋅===. …… 3分 (2)X 的所有可能值为300,400,500,600,700.则()3439C 413008421C P X ====,()121439C C 242400847C P X ⋅====, ()1212144439C C C C 3055008414C P X ⋅+⋅====,()121439C C 637008442C P X ⋅====. 所以X 的概率分布列为:(第22题)…… 8分所以()12553300400500600700500217142142E X=⨯+⨯+⨯+⨯+⨯=(元). …… 10分23.(本小题满分10分) 已知212012(1)n x a a x a x ++=+++ (21)21n n a x+++,*n ∈N .记0(21)nn n k k T k a -==+∑.(1)求2T 的值;(2)化简n T 的表达式,并证明:对任意的*n ∈N ,n T 都能被42n +整除. 解:由二项式定理,得21C i i n a +=(i =0,1,2,…,2n +1).(1)210221055535C 3C 5C 30T a a a =++=++=; …… 2分(2)因为()()()()()12121!1C 11!!n kn n n k n k n k n k ++++++=++⋅++-()()()()212!!!n n n k n k +⋅=+-()221C n kn n +=+,…… 4分 所以()021nn n k k T k a -==+∑()21021C nn kn k k -+==+∑()121021C nn k n k k +++==+∑()()12102121C nn k n k n k n +++==++-+⎡⎤⎣⎦∑()()1121210021C21C nnn kn kn n k k n k n ++++++===++-+∑∑()()12210221C21C nnn kn knn k k n n ++++===+-+∑∑()()()2212112212C 21222n n n n n n +=+⋅⋅+-+⋅⋅ ()221C n n n =+.…… 8分()()()()1221212121C 21C C 221C n n n nn n n n n T n n n ----=+=++=+. 因为21C n n *-∈N ,所以n T 能被42n +整除. …… 10分。
江苏省南通市2018届高考第二次调研数学试卷及答案

i <4i ←i + 1结束N YS ←S ×5输出S 开始 S ←1i ←1南通市2018届高三第二次调研测试数学Ⅰ参考公式:柱体的体积公式V Sh =柱体,其中S 为柱体的底面积,h 为高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知集合{}{} 1012 3 10 2 U A =-=-,,,,,,,,则U A =ð▲. 2.已知复数12i 34i z a z =+=-,,其中i 为虚数单位.若12z z 为纯虚数,则实数a 的值为▲. 3.某班40名学生参加普法知识竞赛,成绩都在区间[]40100,上,其频率分布直方图如图所示, 则成绩不低于60分的人数为▲.4.如图是一个算法流程图,则输出的S 的值为▲.5.在长为12 cm 的线段AB 上任取一点C ,以线段AC ,BC 为邻边作矩形,则该矩形的面积 大于32 cm 2的概率为▲.6.在ABC △中,已知1245AB AC B ==︒,,则BC 的长为▲.7.在平面直角坐标系xOy 中,已知双曲线C 与双曲线2213y x -=有公共的渐近线,且经过点()23P -,,则双曲线C 的焦距为▲.成绩/分 组距40 5060 70 80 90 100 0.0050.010 0.0150.025 0.030 (第3题)8.在平面直角坐标系xOy 中,已知角αβ,的始边均为x 轴的非负半轴,终边分别经过点 (12)A ,,(51)B ,,则tan()αβ-的值为▲.9.设等比数列{}n a 的前n 项和为n S .若396S S S ,,成等差数列,且83a =,则5a 的值为▲. 10.已知a b c ,,均为正数,且4()abc a b =+,则a b c ++的最小值为▲. 11.在平面直角坐标系xOy 中,若动圆C 上的点都在不等式组3330330x x x y ⎧⎪+⎨⎪+⎩≤,≥,≥表示的平面区域内,则面积最大的圆C 的标准方程为▲.12.设函数31e 0()320x x f x x mx x -⎧->⎪=⎨⎪--⎩≤,,,(其中e 为自然对数的底数)有3个不同的零点,则实数 m 的取值范围是▲.13.在平面四边形ABCD 中,已知1423AB BC CD DA ====,,,,则AC BD ⋅的值为▲. 14.已知a 为常数,函数22()1xf x a x x =---的最小值为23-,则a 的所有值为▲.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字说明、 证明过程或演算步骤. 15.(本小题满分14分)在平面直角坐标系xOy 中,设向量()cos sin αα=,a ,()sin cos ββ=-,b ,()312=-,c .(1)若+=a b c ,求sin ()αβ-的值;(2)设5π6α=,0πβ<<,且()//+a b c ,求β的值.16.(本小题满分14分)如图,在三棱柱ABC -A 1B 1C 1中,AB = AC ,点E ,F 分别在棱BB 1 ,CC 1上(均异于 端点),且∠ABE =∠ACF ,AE ⊥BB 1,AF ⊥CC 1. 求证:(1)平面AEF ⊥平面BB 1C 1C ;(2)BC // 平面AEF .17.(本小题满分14分)如图,在平面直角坐标系xOy 中,B 1,B 2是椭圆22221(0)y x a b a b+=>>的短轴端点,P 是椭圆上异于点B 1,B 2的一动点.当直线PB 1的方程为3y x =+时,线段PB 1的长为42 (1)求椭圆的标准方程;AA 11C 1B CFE(第16题)l 1l 2 AB C(第18题)(2)设点Q 满足:11QB PB ⊥,22QB PB ⊥.求证:△PB 1B 2与△QB 1B 2的面积之比为定值.18.(本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿虚线l 1,l 2裁剪成A ,B ,C 三个矩形(B ,C 全等),用来制成一个柱体.现有两种方案: 方案①:以1l 为母线,将A 作为圆柱的侧面展开图,并从B ,C 中各裁剪出一个圆形作为圆 柱的两个底面;方案②:以1l 为侧棱,将A 作为正四棱柱的侧面展开图,并从B ,C 中各裁剪出一个正方形 (各边分别与1l 或2l 垂直)作为正四棱柱的两个底面.(1)设B ,C 都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设1l 的长为x dm ,则当x 为多少时,能使按方案②制成的正四棱柱的体积最大?19.(本小题满分16分)设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,.记i i i c a b =+(i = 1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由.20.(本小题满分16分)设函数()sin (0)f x x a x a =->.(1)若函数()y f x =是R 上的单调增函数,求实数a 的取值范围;(2)设1()()ln 1(0)2a g x f xb x b b ==++∈≠R ,,,()g x '是()g x 的导函数. (第17题)0B 1B 2PQOP xy①若对任意的0()0x g x '>>,,求证:存在0x ,使0()0g x <;② 若1212()()()g x g x x x =≠,求证:2124x x b <.南通市2018届高三第二次调研测试数学Ⅱ(附加题)若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,A ,B ,C 是⊙O 上的3个不同的点,半径OA 交弦BC 于点D . 求证:22DB DC OD OA ⋅+=.B .[选修4-2:矩阵与变换](本小题满分10分)换1T ,2T 在平面直角坐标系xOy 中,已知(00)(30)(22)A B C ,,,,,.设变对应的矩阵分别为1002⎡⎤=⎢⎥⎣⎦M ,2001⎡⎤=⎢⎥⎣⎦N ,求对△ABC 依次实施变换1T ,2T 后所得图形的面积.C .[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点()23P π,为圆心且与直线l :()sin 23ρθπ-=相切的圆的极坐标方程.D .[选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 为正实数,且12a b c ++=()122a c c a b-++.ABDOC(第21—A 题)i < 4i ←i + 1N YS ←S ×5 输出S开始 S ←1i ←1【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出 文字说明、证明过程或演算步骤. 22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张 如图所示的3⨯3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元, 点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖总金额为X 元. (1)求概率(600)P X =;(2)求X 的概率分布及数学期望()E X .23.(本小题满分10分) 已知212012(1)n x a a x a x ++=+++ (21)21n n a x+++,*n ∈N .记0(21)nn n k k T k a -==+∑.(1)求2T 的值;(2)化简n T 的表达式,并证明:对任意的*n ∈N ,n T 都能被42n +整除.南通市2018届高三第二次调研测试 数学学科参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共计70分.1.已知集合{}{} 1012 3 10 2 U A =-=-,,,,,,,,则U A =ð▲.【答案】{}13,2.已知复数12i 34i z a z =+=-,,其中i 为虚数单位.若12z z 为纯虚数,则实数a 的值为▲. 【答案】433.某班40名学生参加普法知识竞赛,成绩都在区间[]40100,上,其频率分布直方图如图所示,则成绩不低于60分的人数为▲.【答案】30组距0.0150.025 0.0304.如图是一个算法流程图,则输出的S 的值为▲. 【答案】1255.在长为12 cm 的线段AB 上任取一点C ,以线段AC ,BC 为邻边作矩形,则该矩形的面积大于32 cm 2的概率为▲. 【答案】136.在ABC △中,已知1245AB AC B ==︒,,则BC 的长为▲.26+7.在平面直角坐标系xOy 中,已知双曲线C 与双曲线2213y x -=有公共的渐近线,且经过点()23P -,,则双曲线C 的焦距为▲. 【答案】438.在平面直角坐标系xOy 中,已知角αβ,的始边均为x 轴的非负半轴,终边分别经过点 (12)A ,,(51)B ,,则tan()αβ-的值为▲.【答案】99.设等比数列{}n a 的前n 项和为n S .若396S S S ,,成等差数列,且83a =,则5a 的值为▲. 【答案】6-10.已知a b c ,,均为正数,且4()abc a b =+,则a b c ++的最小值为▲. 【答案】811.在平面直角坐标系xOy 中,若动圆C 上的点都在不等式组3330330x x x y ⎧⎪+⎨⎪+⎩≤,≥,≥表示的平面区域内,则面积最大的圆C 的标准方程为▲. 【答案】22(1)4x y -+=12.设函数31e 0()320x x f x x mx x -⎧->⎪=⎨⎪--⎩≤,,,(其中e 为自然对数的底数)有3个不同的零点, 则实数m 的取值范围是▲.【答案】()1+∞,13.在平面四边形ABCD 中,已知1423AB BC CD DA ====,,,,则AC BD ⋅的值为▲. 【答案】1014.已知a 为常数,函数22()1xf x a x x =---的最小值为23-,则a 的所有值为▲.【答案】144,二、解答题:本大题共6小题,共计90分. 15.(本小题满分14分)在平面直角坐标系xOy 中,设向量()cos sin αα=,a ,()sin cos ββ=-,b , ()312=-c .(1)若+=a b c ,求sin ()αβ-的值;(2)设5π6α=,0πβ<<,且()//+a b c ,求β的值.解:(1)因为()cos sin αα=,a ,()sin cos ββ=-,b ,()31=-c ,所以1===a b c ,且cos sin sin cos sin ()αβαβαβ⋅=-+=-a b . ……3分因为+=a b c ,所以22+=a bc ,即a 2+ 2a ⋅b + b 2= 1,所以12sin ()11αβ+-+=,即1sin ()2αβ-=-.……6分(2)因为5π6α=,所以()31=,a .依题意,()31sin cos 2ββ+=--,b c .……8分因为()//+a b c ,所以)()3311cos sin 0ββ---=.化简得,311sin ββ=,所以()π1sin β-=.…… 12分因为0πβ<<,所以ππ2π333β-<-<.所以ππ36β-=,即π2β=.…… 14分16.(本小题满分14分)如图,在三棱柱ABC -A 1B 1C 1中,AB = AC ,点E ,F 分别在棱BB 1 ,CC 1上(均异 于端点),且∠ABE =∠ACF ,AE ⊥BB 1,AF ⊥CC 1. 求证:(1)平面AEF ⊥平面BB 1C 1C ;(2)BC // 平面AEF .AB CFE证明:(1)在三棱柱ABC -A 1B 1C 1中,BB 1 // CC 1. 因为AF ⊥CC 1,所以AF ⊥BB 1.…… 2分 又AE ⊥BB 1,AEAF A =,AE ,AF ⊂平面AEF ,所以BB 1⊥平面AEF .…… 5分又因为BB 1⊂平面BB 1C 1C ,所以平面AEF ⊥平面BB 1C 1C .…… 7分 (2)因为AE ⊥BB 1,AF ⊥CC 1,∠ABE =∠ACF ,AB = AC , 所以Rt △AEB ≌Rt △AFC . 所以BE = CF .…… 9分 又由(1)知,BE // CF . 所以四边形BEFC 是平行四边形. 从而BC // EF .…… 11分又BC ⊄平面AEF ,EF ⊂平面AEF , 所以BC // 平面AEF .…… 14分17.(本小题满分14分)如图,在平面直角坐标系xOy 中,B 1,B 2是椭圆22221(0)y x a b a b+=>>的短轴端点,P 是椭圆上异于点B 1,B 2的一动点.当直线PB 1的方程为3y x =+时,线段PB 1的长为42 (1)求椭圆的标准方程;(2)设点Q 满足:11QB PB ⊥,22QB PB ⊥.求证:△PB 1B 2与△QB 1B 2的面积之比为定值. 解:设()00P x y ,,()11Q x y ,.(1)在3y x =+中,令0x =,得3y =,从而b = 3. …… 2分由222193y x a y x ⎧+=⎪⎨⎪=+⎩,得()222319x x a ++=. 所以20269a x a =-+.…… 4分因为()22100032PB x y x =+-,所以2264229a a +,解得218a =. 所以椭圆的标准方程为221189y x +=.…… 6分 (2)方法一: 直线PB 1的斜率为1003PB y k -=, (第17题)0由11QB PB ⊥,所以直线QB 1的斜率为100QB x k =-. 于是直线QB 1的方程为:003x y x =-+. 同理,QB 2的方程为:0033x y x y =--+.…… 8分 联立两直线方程,消去y ,得20109y x x -=.…… 10分因为()00P x y ,在椭圆221189y x +=上,所以22001189x y +=,从而22009x y -=-. 所以012x x =-.…… 12分 所以1212012PB B QB B S xS x ∆∆==.…… 14分 方法二:设直线PB 1,PB 2的斜率为k ,k ',则直线PB 1的方程为3y kx =+. 由11QB PB ⊥,直线QB 1的方程为13y x k=-+.将3y kx =+代入221189y x +=,得()2221120k x kx ++=, 因为P 是椭圆上异于点B 1,B 2的点,所以00x ≠,从而0x =21221k k -+.…… 8分 因为()00P x y ,在椭圆221189y x +=上,所以22001189x y +=,从而220092x y -=-. 所以2000200033912y y y k k x x x -+-'⋅=⋅==-,得12k k '=-.…… 10分 由22QB PB ⊥,所以直线2QB 的方程为23y kx =-.联立1323y x k y kx ⎧=-+⎪⎨⎪=-⎩,则2621k x k =+,即12621k x k =+.…… 12分 所以121220112212621PB B QB B k S x k kk ∆∆-+===+.…… 14分18.(本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿 虚线l 1,l 2裁剪成A ,B ,C 三个矩形(B ,C 全等),用来制成一个柱体.现有两种方案: 方案①:以1l 为母线,将A 作为圆柱的侧面展开图,并从B ,C 中各裁剪出一个圆形作为圆柱的两个底面;方案②:以1l 为侧棱,将A 作为正四棱柱的侧面展开图,并从B ,C 中各裁剪出一个正方l 1l 2 AB C(第18题)形(各边分别与1l 或2l 垂直)作为正四棱柱的两个底面.(1)设B ,C 都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设1l 的长为x dm ,则当x 为多少时,能使按方案②制成的正四棱柱的体积最大? 解:(1)设所得圆柱的半径为r dm ,则()2π24100r r r +⨯=, …… 4分 解得()()52π1r +=.…… 6分(2)设所得正四棱柱的底面边长为a dm , 则21004x a a a x ⎧⎪⎨⎪-⎩≤≤,,即220.x a a x ⎧⎪⎨⎪⎩≤≤,…… 9分 方法一:所得正四棱柱的体积3202104400210.x x V a x x x⎧<⎪=⎨⎪>⎩≤≤,,……11分 记函数302104()400210.x x p x x x⎧<⎪=⎨⎪>⎩≤,, 则()p x 在(0210⎤⎦,上单调递增,在)210⎡+∞⎣上单调递减,所以当210x =max ()2010p x =所以当210x =10a =max V =2010dm 3.…… 14分 方法二:202a x a≤≤,从而10a 11分所得正四棱柱的体积()2220202010V a x a a ==≤≤.所以当10a =210x =max V =2010dm 3.…… 14分答:(1()()52π1+dm ;(2)当x 为210 16分 【评分说明】①直接“由()21002x x x ⋅+=得,210x =2分;②方法一中的求解过程要体现()210p x V ≤≤()210p x V =≤的最多得5分, 其它类似解答参照给分.19.(本小题满分16分)设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(i = 1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. 解:(1)假设数列123c c c ,,是等差数列,则2132c c c =+,即()()()2211332a b a b a b +=+++.因为12b b ,,3b 是等差数列,所以2132b b b =+.从而2132a a a =+.……2分 又因为12a a ,,3a 是等比数列,所以2213a a a =. 所以123a a a ==,这与1q ≠矛盾,从而假设不成立.所以数列123c c c ,,不是等差数列.……4分 (2)因为11a =,2q =,所以12n n a -=.因为2213c c c =,所以()()()2222214b b d b d +=+-++,即223b d d =+,……6分 由2220c b =+≠,得2320d d ++≠,所以1d ≠-且2d ≠-.又0d ≠,所以223b d d =+,定义域为{}120d d d d ∈≠-≠-≠R ,,.……8分 (3)方法一:设c 1,c 2,c 3,c 4成等比数列,其公比为q 1, 则1111111221111331111=2=3=.a b c a q b d c q a q b d c q a q b d c q +=⎧⎪++⎪⎨++⎪⎪++⎩①②③④,,,……10分将①+③-2×②得,()()2211111a q c q -=-,⑤将②+④-2×③得,()()22111111a q q c q q -=-,⑥……12分 因为10a ≠,1q ≠,由⑤得10c ≠,11q ≠. 由⑤⑥得1q q =,从而11a c =.……14分 代入①得10b =.再代入②,得0d =,与0d ≠矛盾. 所以c 1,c 2,c 3,c 4不成等比数列.……16分方法二:假设数列1234c c c c ,,,是等比数列,则324123c c c ==.……10分 所以32432132c c c c c c c c --=--,即32432132a a d a a d a a d a a d -+-+=-+-+.两边同时减1得,321432213222a a a a a a -+-+=.……12分 因为等比数列a 1,a 2,a 3,a 4的公比为q ()1q ≠,所以()321321213222q a a a a a a a a d a a d-+-+=-+-+.又()23211210a a a a q -+=-≠,所以()2132q a a d a a d -+=-+,即()10q d -=. ……14分这与1q ≠,且0d ≠矛盾,所以假设不成立.所以数列1234c c c c ,,,不能为等比数列.……16分20.(本小题满分16分)设函数()sin (0)f x x a x a =->.(1)若函数()y f x =是R 上的单调增函数,求实数a 的取值范围;(2)设1()()ln 1(0)2a g x f x b x b b ==++∈≠R ,,,()g x '是()g x 的导函数.①若对任意的0()0x g x '>>,,求证:存在0x ,使0()0g x <;② 若1212()()()g x g x x x =≠,求证:2124x x b <. 解:(1)由题意,()1cos 0f x a x '=-≥对x ∈R 恒成立,因为0a >,所以1cos x a≥对x ∈R 恒成立,因为()max cos 1x =,所以11a ≥,从而01a <≤.……3分(2)①()1sin ln 12g x x x b x =-++,所以()11cos 2b g x x x'=-+.若0b <,则存在02b ->,使()()11cos 0222b b g '-=---<,不合题意,所以0b >.……5分 取30ebx -=,则001x <<.此时()30000111sin ln 11ln 10b g x x x b x b e -=-++<+++=-<.所以存在00x >,使()00g x <.……8分 ②依题意,不妨设120x x <<,令21x t =,则1t >. 由(1)知函数sin y x x =-单调递增,所以2211sin sin x x x x ->-. 从而2121sin sin x x x x ->-.……10分因为()()12g x g x =,所以11122211sin ln 1sin ln 1x x b x x x b x -++=-++,所以()()()2121212111ln ln sin sin 22b x x x x x x x x --=--->-.所以212120x x b -->>.……12分下面证明211221x x x x ->1t t ->()1ln 0t t t-<*.设()()1ln 1t h t t t t-=>,所以()2102t h t t t-'=<在()1+∞,恒成立.所以()h t 在()1+∞,单调递减,故()()10h t h <=,从而()*得证.所以122b x x ->2124x x b <.……16分数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.................... 若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,A ,B ,C 是⊙O 上的3个不同的点,半径OA 交弦BC 于点D . 求证:22DB DC OD OA ⋅+=. 证明:延长AO 交⊙O 于点E ,则()()DB DC DE DA OD OE OA OD ⋅=⋅=+⋅-.……5分因为OE OA =,所以()()22DB DC OA OD OA OD OA OD ⋅=+⋅-=-. 所以22DB DC OD OA ⋅+=.……10分B .[选修4-2:矩阵与变换](本小题满分10分)在平面直角坐标系xOy 中,已知(00)(30)(22)A B C ,,,,,.设变换1T ,2T 对应的矩 阵分别为1002⎡⎤=⎢⎥⎣⎦M ,2001⎡⎤=⎢⎥⎣⎦N ,求对△ABC 依次实施变换1T ,2T 后所得图形的面积.ABDC(第21—A 题)EO解:依题意,依次实施变换1T ,2T 所对应的矩阵=NM 201020010202⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦.……5分则20000200⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,20360200⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,20240224⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. 所以(00)(30)(22)A B C ,,,,,分别变为点(00)(60)(44)A B C ''',,,,,. 从而所得图形的面积为164122⨯⨯=.……10分C .[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点()23P π,为圆心且与直线l :()sin 23ρθπ-=相切的圆的极坐标方程.解:以极点为原点,极轴为x 轴的非负半轴,建立平面直角坐标系xOy .则点P 的直角坐标为()13,.……2分将直线l :()sin 23ρθπ-=的方程变形为:sin cos cos sin 2ρθρθππ-=,340x y -+=.……5分 所以()13P ,到直线l 340x y -+=()()224231=+-.故所求圆的普通方程为()(22134x y -+=.……8分化为极坐标方程得,()π4sin 6ρθ=+.……10分D .[选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 为正实数,且12a b c ++=()122a c c a b-++.证明:因为a ,b ,c 为正实数, ()()12322a c a b cc a b c a b-+++=++2a cbc +++=2=(当且仅当a b c ==取“=”).……10分【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3⨯3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X 元. (1)求概率()600P X =;(2)求X 的概率分布及数学期望()E X .解:(1)从3⨯3表格中随机不重复地点击3格,共有39C 种不同情形. 则事件:“600X =”包含两类情形: 第一类是3格各得奖200元;第二类是1格得奖300元,一格得奖200元,一格得奖100元,其中第一类包含34C 种情形,第二类包含111144C C C ⋅⋅种情形. 所以()3111414439C C C C 560021C P X +⋅⋅===.……3分 (2)X 的所有可能值为300,400,500,600,700.则()3439C 41300C P X ====,()121439C C 242400C P X ⋅====, ()1212144439C C C C 3055008414C P X ⋅+⋅====,()121439C C 637008442C P X ⋅====. 所以X 的概率分布列为:X 300 400 500 600 700 P12127514 521 342……8分所以()12553300400500600700500217142142E X=⨯+⨯+⨯+⨯+⨯=(元). ……10分23.(本小题满分10分) 已知212012(1)n x a a x a x ++=+++ (21)21n n a x+++,*n ∈N .记0(21)nn n k k T k a -==+∑.(1)求2T 的值;(2)化简n T 的表达式,并证明:对任意的*n ∈N ,n T 都能被42n +整除. 解:由二项式定理,得21C i i n a +=(i =0,1,2,…,2n +1).(1)210221055535C 3C 5C 30T a a a =++=++=;…… 2分(2)因为()()()()()12121!1C 11!!n kn n n k n k n k n k ++++++=++⋅++-()()()()212!!!n n n k n k +⋅=+-()221C n kn n +=+, …… 4分所以()021nn n k k T k a -==+∑()21021C nn kn k k -+==+∑ ()121021C nn k n k k +++==+∑ ()()12102121C nn k n k n k n +++==++-+⎡⎤⎣⎦∑ ()()112121021C21C nnn kn kn n k k n k n ++++++===++-+∑∑()()12210221C21C nnn kn knn k k n n ++++===+-+∑∑()()()2212112212C 21222n n n n n n +=+⋅⋅+-+⋅⋅ ()221C n n n =+. …… 8分()()()()1221212121C 21C C 221C n n n nn n n n n T n n n ----=+=++=+. 因为21C n n *-∈N ,所以n T 能被42n +整除.…… 10分。
江苏省南通市2018届高考第二次调研数学试卷含答案

上..
1. 已知集合 U
1,0 ,1,2 ,3 ,A
1 ,0 ,2 ,则 e U A ▲ .
2. 已知复数 z1
a i ,z2
3 4 i ,其中 i 为虚数单位. 若 z1 为纯虚数, 则实数 a 的值为 z2
▲
.
3. 某班 40 名学生参加普法知识竞赛,成绩都在区间
40 ,100 上,其频率分布直方图如图所
0.5 毫米签字笔填写
3. 作答试题必须用书写黑色字迹的 0.5 毫米签字笔写在答题卡上的指定位置,在其它位 置作答一律无效。如有作图需要,可用 2B 铅笔作答,并请加黑、加粗,描写清楚。
参考公式: 柱体的体积公式 V柱体 Sh ,其中 S 为柱体的底面积, h 为高.
一、填空题:本大题共 14 小题,每小题 5 分,共计 70 分.请把答案填写在答题.卡.相.应.位.置..
c
1 2
,
3 2
.
(1)若 a b
c ,求 sin () 的值;(2)设56π, 0
π,且 a // b c ,求 的值.
16.(本小题满分 14 分)
如图,在三棱柱 ABC A1B1C1 中, AB AC ,点 E, F 分别在棱 BB 1 , CC 1 上(均异
于
端点),且∠ ABE ∠ ACF , AE ⊥ BB 1, AF ⊥ CC 1. 求证:( 1)平面 AEF ⊥平面 BB1C1C;
( 1)求证:数列 c1 ,c2 ,c3 不是等差数列; ( 2)设 a1 1, q 2 .若数列 c1 ,c2 ,c3 是等比数列,求 b2 关于 d 的函数关系式及其定义 域; ( 3)数列 c1 ,c2 ,c3 ,c4 能否为等比数列?并说明理由.
江苏省2018届高三数学二模试卷 含解析

2018年江苏省高考数学二模试卷一、填空题:本大题共14个小题,每小题5分,共计70分,请把答案直接填写在答题卡相应的位置上.1.已知集合A={x||x|<2},B={﹣1,0,1,2,3},则集合A∩B中元素的个数为.2.已知复数z满足(2﹣3i)z=3+2i(i是虚数单位),则z的模为.3.已知一组数据8,10,9,12,11,那么这组数据的方差为.4.运行如图所示的伪代码,其输出的结果S为.5.袋中有形状、大小都相同的四只球,其中有1只红球,3只白球,若从中随机一次摸出2只球,则这2只球颜色不同的概率为.6.已知,那么tanβ的值为.7.已知正六棱锥的底面边长为2,侧棱长为,则该正六棱锥的表面积为.8.在三角形ABC中,,则的最小值为.9.已知数列{a n}的首项为1,等比数列{b n}满足,且b1018=1,则a2018的值为.10.已知正数a,b满足2ab+b2=b+1,则a+5b的最小值为.11.已知函数,若方程f(x)=﹣x有且仅有一解,则实数a的取值范围为.12.在平面直角坐标系xOy中,点A(3,0),动点P满足PA=2PO,动点Q(3a,4a+5)(a ∈R),则线段PQ长度的最小值为.13.已知椭圆的离心率为,长轴AB上2018个等分点从左到右依次为点M1,M2,…,M2018,过M1点作斜率为k(k≠0)的直线,交椭圆C于P1,P2两点,P1点在x轴上方;过M2点作斜率为k(k≠0)的直线,交椭圆C于P3,P4两点,P3点在x 轴上方;以此类推,过M2018点作斜率为k(k≠0)的直线,交椭圆C于P4189,P4180两点,P4189点在x轴上方,则4180条直线AP1,AP2,…,AP4180的斜率乘积为.14.已知函数f(x)=x|x﹣a|,若对任意x1∈[2,3],x2∈[2,3],x1≠x2恒有,则实数a的取值范围为.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.在△ABC中,角A、B、C分别是边a、b、c的对角,且3a=2b.(Ⅰ)若B=60°,求sinC的值;(Ⅱ)若,求sin(A﹣B)的值.16.如图,平行四边形ABCD⊥平面CDE,AD⊥DE.(I)求证:DE⊥平面ABCD;(Ⅱ)若M为线段BE中点,N为线段CE的一个三等分点,求证:MN不可能与平面ABCD 平行.17.已知椭圆的离心率为e,直线l:y=ex+a与x,y轴分别交于A、B点.(Ⅰ)求证:直线l与椭圆C有且仅有一个交点;(Ⅱ)设T为直线l与椭圆C的交点,若AT=eAB,求椭圆C的离心率;(Ⅲ)求证:直线l:y=ex+a上的点到椭圆C两焦点距离和的最小值为2a.18.如图,,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t km,且半径增大到81km 时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.(Ⅰ)当无人侦察机在CD上飞行t分钟至点E时,试用t和θ表示无人侦察机到O点的距离OE;(Ⅱ)若无人侦察机在C点处雷达就开始开机,且θ=,则雷达是否能测控到无人侦察机?请说明理由.19.已知数列{a n }满足.数列{a n }前n 项和为S n .(Ⅰ) 求数列{a n }的通项公式;(Ⅱ)若a m a m +1=a m +2,求正整数m 的值; (Ⅲ)是否存在正整数m ,使得恰好为数列{a n }中的一项?若存在,求出所有满足条件的m 值,若不存在,说明理由.20.已知函数f (x )=xlnx ﹣ax 2+a (a ∈R ),其导函数为f ′(x ). (Ⅰ)求函数g (x )=f ′(x )+(2a ﹣1)x 的极值;(Ⅱ)当x >1时,关于x 的不等式f (x )<0恒成立,求a 的取值范围.三.附加题部分【选做题】(本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.)A .[选修4-1几何证明选讲](本小题满分10分) 21.若AB 为定圆O 一条弦(非直径),AB=4,点N 在线段AB 上移动,∠ONF=90°,NF 与圆O 相交于点F ,求NF 的最大值.B .[选修4-2:矩阵与变换](本小题满分10分) 22.已知矩阵,若矩阵A 属于特征值6的一个特征向量为=,属于特征值1的一个特征向量为=.求A 的逆矩阵.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.过点P (﹣3,0)且倾斜角为30°的直线和曲线ρ2cos2θ=4相交于A 、B 两点.求线段AB 的长.D .[选修4-5:不等式选讲](本小题满分0分) 24.设 x ,y ,z ∈R +,且x +y +z=1,求证:.四.[必做题](第25题、第26题,每题10分,共20分.解答时应写出文字说明、证明过程或演算步骤)25.一个袋中有若干个红球与白球,一次试验为从中摸出一个球并放回袋中,摸出红球概率为p ,摸出白球概率为q ,摸出红球加1分,摸出白球减1分,现记“n 次试验总得分为S n ”. (Ⅰ)当时,记ξ=|S 3|,求ξ的分布列及数学期望;(Ⅱ)当时,求S 8=2且S i ≥0(i=1,2,3,4)的概率.26.数列{a n }各项均为正数,,且对任意的n ∈N *,有.(Ⅰ)求证:;(Ⅱ)若,是否存在n∈N*,使得a n>1,若存在,试求出n的最小值,若不存在,请说明理由.2018年江苏省高考数学二模试卷参考答案与试题解析一、填空题:本大题共14个小题,每小题5分,共计70分,请把答案直接填写在答题卡相应的位置上.1.已知集合A={x||x|<2},B={﹣1,0,1,2,3},则集合A∩B中元素的个数为3.【考点】交集及其运算.【分析】求出A中不等式的解集确定出A,找出A与B的交集,即可作出判断.【解答】解:由A中不等式解得:﹣2<x<2,即A=(﹣2,2),∵B={﹣1,0,1,2,3},∴A∩B={﹣1,0,1},则集合A∩B中元素的个数为3,故答案为:32.已知复数z满足(2﹣3i)z=3+2i(i是虚数单位),则z的模为1.【考点】复数代数形式的乘除运算.【分析】根据向量的复数运算和向量的模即可求出.【解答】解:(2﹣3i)z=3+2i,∴z====i,∴|z|=1,故答案为:1.3.已知一组数据8,10,9,12,11,那么这组数据的方差为2.【考点】极差、方差与标准差.【分析】先求出这组数据的平均数,由此能求出这组数据的方差.【解答】解:∵一组数据8,10,9,12,11,∴这组数据的平均数=(8+10+9+12+11)=10,这组数据的方差为S2= [(8﹣10)2+(10﹣10)2+(9﹣10)2+(12﹣10)2+(11﹣10)2]=2.故答案为:2.4.运行如图所示的伪代码,其输出的结果S为15.【考点】程序框图.【分析】由已知中的程序代码可得:程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案【解答】解:当l=1时,满足进行循环的条件,S=3,l=4;当l=4时,满足进行循环的条件,S=9,l=7;当l=7时,满足进行循环的条件,S=15,l=10;当l=10时,不满足进行循环的条件,故输出的S值为15.故答案为:155.袋中有形状、大小都相同的四只球,其中有1只红球,3只白球,若从中随机一次摸出2只球,则这2只球颜色不同的概率为.【考点】古典概型及其概率计算公式.【分析】先求出基本事件总数,再求出这2只球颜色不同包含的基本事件个数,由此能求出这2只球颜色不同的概率.【解答】解:∵袋中有形状、大小都相同的四只球,其中有1只红球,3只白球,从中随机一次摸出2只球,∴基本事件总数n==6,这2只球颜色不同包含的基本事件个数m==3,∴这2只球颜色不同的概率为p==.故答案为:.6.已知,那么tanβ的值为3.【考点】两角和与差的正切函数.【分析】由已知,利用同角三角函数基本关系式可求cosα,tanα的值,利用两角和的正切函数公式即可化简求值.【解答】解:∵,∴cosα=﹣=﹣,tanα==﹣2,∴tan(α+β)===,整理可得:tanβ=3.故答案为:3.7.已知正六棱锥的底面边长为2,侧棱长为,则该正六棱锥的表面积为+12.【考点】棱柱、棱锥、棱台的侧面积和表面积.【分析】利用勾股定理可得侧面三角形的斜高h,利用等腰三角形与等边三角形的面积计算公式即可得出.【解答】解:侧面三角形的斜高h==2,∴该正六棱锥的表面积S=+6×=+12,故答案为: +12.8.在三角形ABC中,,则的最小值为.【考点】平面向量数量积的运算.【分析】可根据条件得到,而由可得到,两边平方并进行数量积的运算便可得到,这样根据不等式a2+b2≥2ab即可得出的范围,从而得出的范围,即得出的最小值.【解答】解:根据条件,=;∴;由得,;∴;∴==,当且仅当即时取“=”;∴;∴的最小值为.故答案为:.9.已知数列{a n}的首项为1,等比数列{b n}满足,且b1018=1,则a2018的值为1.【考点】等比数列的通项公式.【分析】由已知结合,得到a2018=b1b2…b2018=(b1b2018)•(b2b2018)…(b1018b1018)•b1018,结合b1018=1,以及等比数列的性质求得答案.【解答】解:,且a1=1,得b1=,b2=,∴a3=a2b2=b1b2,b3=,∴a4=a3b3=b1b2b3,…a n=b1b2…b n.﹣1∴a2018=b1b2…b2018=(b1b2018)•(b2b2018)…(b1018b1018)•b1018,∵b1018=1,∴b1b2018=b2b2018=…=b1018b1018=(b1018)2=1,∴a2018=1,故答案为:1.10.已知正数a,b满足2ab+b2=b+1,则a+5b的最小值为.【考点】基本不等式.【分析】正数a,b满足2ab+b2=b+1,可得:a=>0.则a+5b=+5b=+,利用基本不等式的性质即可得出.【解答】解:∵正数a,b满足2ab+b2=b+1,∴a=>0.则a+5b=+5b=+≥+=,当且仅当b=,a=2时取等号.故答案为:.11.已知函数,若方程f(x)=﹣x有且仅有一解,则实数a的取值范围为a≥﹣1或a=﹣2..【考点】根的存在性及根的个数判断.【分析】根据指数函数的图象,结合图象的平移可知当a≥﹣1时,2x+a在x≤0时,与y=﹣x 有一交点,而x++a在x>0无交点,符合题意;再考虑当a<﹣1时的情况,结合图象的平移和二次函数的知识求出a的取值.【解答】解:根据指数函数的图象易知:当a≥﹣1时,y=2x+a在x≤0时,与y=﹣x有一交点,y=x++a在x>0与y=﹣x无交点,符合题意;当a<﹣1时,只需x++a=﹣x有且仅有一根,△=a2﹣8=0,解得a=﹣2.故答案为a≥﹣1或a=﹣2.12.在平面直角坐标系xOy中,点A(3,0),动点P满足PA=2PO,动点Q(3a,4a+5)(a ∈R),则线段PQ长度的最小值为0.【考点】两点间距离公式的应用.【分析】求出圆的方程并化为标准形式,由条件求得点Q(3a,4a+5)到圆心(﹣1,0)的距离d的最小值,将d的最小值减去圆的半径,即为所求.【解答】解:∵点A(3,0),动点P满足PA=2PO,设P(x,y),则有(x﹣3)2+y2=4x2+4y2,∴(x+1)2+y2=4,表示以(﹣1,0)为圆心、半径等于2的圆.点Q(3a,4a+5)到圆心(﹣1,0)的距离d==≥,故距离d可以是2,此时PQ=0,故线段PQ长度的最小值为0.13.已知椭圆的离心率为,长轴AB上2018个等分点从左到右依次为点M1,M2,…,M2018,过M1点作斜率为k(k≠0)的直线,交椭圆C于P1,P2两点,P1点在x轴上方;过M2点作斜率为k(k≠0)的直线,交椭圆C于P3,P4两点,P3点在x 轴上方;以此类推,过M2018点作斜率为k(k≠0)的直线,交椭圆C于P4189,P4180两点,P4189点在x轴上方,则4180条直线AP1,AP2,…,AP4180的斜率乘积为﹣2﹣2018.【考点】椭圆的简单性质.【分析】运用椭圆的离心率公式,可得a2=2b2=2c2,设M n的坐标为(t,0),直线方程为y=k (x﹣t),代入椭圆方程,运用韦达定理,再由直线的斜率公式,化简整理,可得•=,再由等分点,设出t的坐标,化简整理,计算即可得到所求值.【解答】解:由题意可得e==,可得a2=2b2=2c2,设M n的坐标为(t,0),直线方程为y=k(x﹣t),代入椭圆方程x2+2y2=2b2,可得(1+2k2)x2﹣4tk2x+2k2t2﹣2b2=0,即有x1+x2=,x1x2=,•=•======,可令t=﹣,﹣,…,﹣,﹣,0,,,…,,,即有AP1,AP2,…,AP4180的斜率乘积为•(•…•)••(•…•)=﹣.故答案为:﹣2﹣2018.14.已知函数f(x)=x|x﹣a|,若对任意x1∈[2,3],x2∈[2,3],x1≠x2恒有,则实数a的取值范围为[3,+∞).【考点】分段函数的应用.【分析】根据凸函数和凹函数的定义,作出函数f(x)的图象,利用数形结合进行求解即可.【解答】解:满足条件有的函数为凸函数,f(x)=,作出函数f(x)的图象,由图象知当x≤a时,函数f(x)为凸函数,当x≥a时,函数f(x)为凹函数,若对任意x1∈[2,3],x2∈[2,3],x1≠x2恒有,则a≥3即可,故实数a的取值范围是[3,+∞),故答案为:[3,+∞)二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.在△ABC中,角A、B、C分别是边a、b、c的对角,且3a=2b.(Ⅰ)若B=60°,求sinC的值;(Ⅱ)若,求sin(A﹣B)的值.【考点】两角和与差的正弦函数;正弦定理;余弦定理.【分析】(Ⅰ)利用正弦定理化简已知可得3sinA=2sinB,由已知可求sinA,利用大边对大角可得A为锐角,可求cosA,利用三角形内角和定理,两角和的正弦函数公式即可求sinC的值.(Ⅱ)由已知及正弦定理可求a=,余弦定理可求c=,利用余弦定理可得cosB=0,从而可求sinB=1,sinA=,利用大边对大角及同角三角函数基本关系式可求cosA,利用两角差的正弦函数公式即可计算得解.【解答】(本题满分为14分)解:(Ⅰ)在△ABC中,∵3a=2b,∴3sinA=2sinB又∵B=60°,代入得3sinA=2sin60°,解得sinA=.∵a:b=2:3,∴A<B,即cosA=,∴sinC=sin(A+B)=sinAcosB+cosAsinB=.…(Ⅱ)∵3a=2b,可得:a=,,∴==,解得:c2=,c=,∴cosB===0,可得:sinB=1,∵3sinA=2sinB=2,可得:sinA=,A为锐角,可得cosA==.∴sin(A﹣B)=sinAcosB﹣cosAsinB=﹣cosA=﹣.…16.如图,平行四边形ABCD⊥平面CDE,AD⊥DE.(I)求证:DE⊥平面ABCD;(Ⅱ)若M为线段BE中点,N为线段CE的一个三等分点,求证:MN不可能与平面ABCD 平行.【考点】直线与平面垂直的判定;直线与平面平行的性质.【分析】(1)在平面ABCD内过A作CD的垂线AP,则AP⊥平面CDE,于是AP⊥DE,结合AD⊥DE,得出DE⊥平面ABCD;(2)使用反证法证明,假设MN∥平面ABCD,由线面平行的性质得MN∥BC,与已知矛盾.【解答】证明:(1)过A作AP⊥CD,垂足为P,∵平面ABCD⊥平面CDE,平面ABCD∩平面CDE=CD,AP⊂平面ABCD,AP⊥CD,∴AP⊥平面CDE,∵DE⊂平面CDE,∴AP⊥DE,又∵DE⊥AD,AD⊂平面ABCD,AP⊂平面ABCD,AD∩AP=A,∴DE⊥平面ABCD.(2)假设MN∥平面ABCD,∵MN⊂平面BCE,平面BCE∩平面ABCD=BC,∴MN∥BC,∴,与M是BE的中点,N是CE的三等分点相矛盾.∴MN不可能与平面ABCD平行.17.已知椭圆的离心率为e,直线l:y=ex+a与x,y轴分别交于A、B点.(Ⅰ)求证:直线l与椭圆C有且仅有一个交点;(Ⅱ)设T为直线l与椭圆C的交点,若AT=eAB,求椭圆C的离心率;(Ⅲ)求证:直线l:y=ex+a上的点到椭圆C两焦点距离和的最小值为2a.【考点】椭圆的简单性质.【分析】(Ⅰ)将直线l:y=ex+a代入椭圆方程,运用判别式,结合离心率公式,化简整理即可得证;(Ⅱ)由直线l:y=ex+a,可得A(﹣,0),B(0,a),运用向量共线的坐标表示,解方程可得离心率;(Ⅲ)设F2(c,0)关于直线y=ex+a的对称点为F'(m,n),运用两直线垂直的条件:斜率之积为﹣1和中点坐标公式,求得F'的坐标,计算|F'F1|,即可得到所求最小值.【解答】解:(Ⅰ)证明:直线l:y=ex+a代入椭圆,可得(b2+a2e2)x2+2ea3+a4﹣a2b2=0,可得判别式为4a2e6﹣4(b2+a2e2)(a4﹣a2b2)=﹣4(a4b2﹣a2b4﹣a4e2b2)=﹣4[a2b2(a2﹣b2)﹣a2c2b2]=0,即有直线l与椭圆C有且仅有一个交点;(Ⅱ)由直线l:y=ex+a,可得A(﹣,0),B(0,a),由(Ⅰ)可得x T=﹣=﹣=﹣ea,由=e,可得﹣ea+=e(0+),即e2+e﹣1=0,解得e=(负的舍去):(Ⅲ)证明:设F2(c,0)关于直线y=ex+a的对称点为F'(m,n),即有=﹣,=+a,结合e=,b2+c2=a2,解得m=﹣c,n=2a,即为F'(﹣c,2a),则|F'F1|=2a.故直线l:y=ex+a上的点到椭圆C两焦点距离和的最小值为2a.18.如图,,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t km,且半径增大到81km 时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.(Ⅰ) 当无人侦察机在CD 上飞行t 分钟至点E 时,试用t 和θ表示无人侦察机到O 点的距离OE ;(Ⅱ)若无人侦察机在C 点处雷达就开始开机,且θ=,则雷达是否能测控到无人侦察机?请说明理由.【考点】解三角形的实际应用. 【分析】(I )在△OCE 中,CE=15t ,使用余弦定理表示出OE ;(II )令f (t )=OE 2﹣r 2,通过导数判断f (t )的单调性计算f (t )的最小值,判断OE 与测控半径r 的大小关系. 【解答】解:(I )在△OCE 中,CE=15t ,OC=90,由余弦定理得OE 2=OC 2+CE 2﹣2OC •CEcos θ=8100+225t 2﹣2700tcos θ. ∴OE=.(II )令f (t )=OE 2﹣r 2=225t 2﹣1350t +8100﹣9t 3,令r=3t =81,解得t=9.∴0≤t ≤9 ∴f ′(t )=﹣27t 2+450t ﹣1350=﹣27(t ﹣)2+1875﹣1350<0.∴f (t )在[0,9]上是减函数.f (9)=225×92﹣1350×9+8100﹣9×93>0. ∴当0≤t ≤9时,f (t )>0,即OE >r . ∴雷达不能测控到无人侦察机.19.已知数列{a n }满足.数列{a n }前n 项和为S n .(Ⅰ) 求数列{a n }的通项公式;(Ⅱ)若a m a m +1=a m +2,求正整数m 的值; (Ⅲ)是否存在正整数m ,使得恰好为数列{a n }中的一项?若存在,求出所有满足条件的m 值,若不存在,说明理由. 【考点】数列的求和;数列递推式.【分析】(Ⅰ)化简可得数列{a n }的奇数项构成以1为首项,2为公差的等差数列,数列{a n }的偶数项构成以2为首项,3为公比的等比数列,从而写出通项公式;(Ⅱ)分类讨论即方程的解;=3m﹣1﹣1+m2,从而可得(Ⅲ)化简S2m=1+2+3+6+…+2m﹣1+2•3m﹣1=3m﹣1+m2,S2m﹣1=1+,从而讨论求值.【解答】解:(Ⅰ)∵,∴数列{a n}的奇数项构成以1为首项,2为公差的等差数列,数列{a n}的偶数项构成以2为首项,3为公比的等比数列,故a n=;=m•2•m﹣1=m+2,(Ⅱ)若m为奇数,则a m a m+1无解;=(m+1)2•m﹣2=2•m,若m为偶数,则a m a m+1即=2,解得,m=2;综上所述,m=2;(Ⅲ)由题意知,S2m=1+2+3+6+…+2m﹣1+2•3m﹣1=(1+3+5+…+2m﹣1)+(2+6+18+…+2•3m﹣1)=•m+=3m﹣1+m2,=1+2+3+6+…+2m﹣1S2m﹣1=(1+3+5+…+2m﹣1)+(2+6+18+…+2•3m﹣2)=•m+﹣2•3m﹣1=3m﹣1﹣1+m2,故==1+,若m=1,则=3=a3,若=1时,即m=2时,=2=a2,所有满足条件的m值为1,2.20.已知函数f(x)=xlnx﹣ax2+a(a∈R),其导函数为f′(x).(Ⅰ)求函数g(x)=f′(x)+(2a﹣1)x的极值;(Ⅱ)当x>1时,关于x的不等式f(x)<0恒成立,求a的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的极值.【分析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出满足条件的a的范围即可.【解答】解:(Ⅰ)由题知x>0,f'(x)=lnx﹣2ax+1,则g(x)=f'(x)+2a(x﹣1)=lnx﹣x+1,,当0<x<1时,,g(x)为增函数;当x>1时,,g(x)为减函数.所以当x=1时,g(x)有极大值g(1)=0,g(x)无极小值.(Ⅱ)由题意,f'(x)=lnx﹣2ax+1,(ⅰ)当a≤0时,f'(x)=lnx﹣2ax+1>0在x>1时恒成立,则f(x)在(1,+∞)上单调递增,所以f(x)>f(1)=0在(1,+∞)上恒成立,与已知矛盾,故a≤0不符合题意.(ⅱ)当a>0时,令φ(x)=f'(x)=lnx﹣2ax+1,则,且.①当2a≥1,即时,,于是φ(x)在x∈(1,+∞)上单调递减,所以φ(x)<φ(1)=1﹣2a≤0,即f'(x)<0在x∈(1,+∞)上成立.则f(x)在x∈(1,+∞)上单调递减,所以f(x)<f(1)=0在x∈(1,+∞)上成立,符合题意.②当0<2a<1,即时,>1,,若,则φ'(x)>0,φ(x)在上单调递增;若,则φ'(x)<0,φ(x)在上单调递减.又φ(1)=1﹣2a>0,所以φ(x)>0在上恒成立,即f'(x)>0在上恒成立,所以f(x)在上单调递增,则f(x)>f(1)=0在上恒成立,所以不符合题意.综上所述,a的取值范围.三.附加题部分【选做题】(本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.)A.[选修4-1几何证明选讲](本小题满分10分)21.若AB为定圆O一条弦(非直径),AB=4,点N在线段AB上移动,∠ONF=90°,NF与圆O相交于点F,求NF的最大值.【考点】与圆有关的比例线段.【分析】由NF=,线段OF的长为定值,得到需求解线段ON长度的最小值,由此能求出结果.【解答】解:∵ON⊥NF,∴NF=,∵线段OF的长为定值,即需求解线段ON长度的最小值,弦中点到圆心的距离最短,此时N为BE的中点,点F与点B或E重合,∴|NF|max=|BE|=2.B.[选修4-2:矩阵与变换](本小题满分10分)22.已知矩阵,若矩阵A属于特征值6的一个特征向量为=,属于特征值1的一个特征向量为=.求A的逆矩阵.【考点】特征向量的意义.【分析】根据矩阵特征值和特征向量的性质代入列方程组,求得a、b、c和d的值,求得矩阵A,丨A丨及A*,由A﹣1=×A*,即可求得A﹣1.【解答】解:矩阵A属于特征值6的一个特征向量为=,∴=6,即=,属于特征值1的一个特征向量为=.∴=,=,∴,解得:,矩阵A=,丨A丨==6,A*=,A﹣1=×A*=,∴A﹣1=.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.过点P(﹣3,0)且倾斜角为30°的直线和曲线ρ2cos2θ=4相交于A、B两点.求线段AB 的长.【考点】简单曲线的极坐标方程.【分析】过点P(﹣3,0)且倾斜角为30°的直线的参数方程为:(t为参数).曲线ρ2cos2θ=4即ρ2(cos2α﹣sin2α)=4,把y=ρsinθ,x=ρcosθ代入化为直角坐标方程.把直线参数方程代入可得:t2﹣6t+10=0,利用|AB|=|t1﹣t2|=即可得出.【解答】解:过点P(﹣3,0)且倾斜角为30°的直线的参数方程为:(t为参数),曲线ρ2cos2θ=4即ρ2(cos2α﹣sin2α)=4化为x2﹣y2=4,把直线参数方程代入可得:t2﹣6t+10=0,∴t1+t2=6,t1t2=10.∴|AB|=|t1﹣t2|===.D.[选修4-5:不等式选讲](本小题满分0分)24.设x,y,z∈R+,且x+y+z=1,求证:.【考点】不等式的证明.【分析】由x,y,z∈R+,且x+y+z=1,可得+≥2=2x,同理可得+≥2y, +≥2z,累加即可得证.【解答】证明:由x,y,z∈R+,且x+y+z=1,可得+≥2=2x,同理可得+≥2y,+≥2z,三式相加,可得+++x+y+z≥2(x+y+z),即为++≥x+y+z,则++≥1成立.四.[必做题](第25题、第26题,每题10分,共20分.解答时应写出文字说明、证明过程或演算步骤)25.一个袋中有若干个红球与白球,一次试验为从中摸出一个球并放回袋中,摸出红球概率为p,摸出白球概率为q,摸出红球加1分,摸出白球减1分,现记“n次试验总得分为S n”.(Ⅰ)当时,记ξ=|S3|,求ξ的分布列及数学期望;(Ⅱ)当时,求S8=2且S i≥0(i=1,2,3,4)的概率.【考点】离散型随机变量的期望与方差;列举法计算基本事件数及事件发生的概率;离散型随机变量及其分布列.【分析】(Ⅰ)当时,ξ=|S3|的可能取值为1,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.(Ⅱ)由题意前8次试验5次摸到红球,3次摸到白球,并且满足下列条件:若第一次和第三次摸到红球,其余六次可任意有3次摸到红球,另3次摸到白球;若第一次和第二次摸到红球,第二次摸到白球,则后五次可任意三次摸到红球,另两次摸到白球.由此能求出S8=2且S i≥0(i=1,2,3,4)的概率.【解答】解:(Ⅰ)当时,ξ=|S3|的可能取值为1,3,P(ξ=1)=+=,P(ξ=3)==,∴ξ的分布列为:ξ 1 3PEξ==.(Ⅱ)∵,S8=2且S i≥0(i=1,2,3,4),∴前8次试验5次摸到红球,3次摸到白球,并且满足下列条件:若第一次和第三次摸到红球,其余六次可任意有3次摸到红球,另3次摸到白球,若第一次和第二次摸到红球,第二次摸到白球,则后五次可任意三次摸到红球,另两次摸到白球,∴S8=2且S i≥0(i=1,2,3,4)的概率:p=()•()5•()3=.26.数列{a n}各项均为正数,,且对任意的n∈N*,有.(Ⅰ)求证:;(Ⅱ)若,是否存在n∈N*,使得a n>1,若存在,试求出n的最小值,若不存在,请说明理由.【考点】数列递推式.【分析】(1)把已知数列递推式取倒数,可得,然后利用累加法证得答案;=a n+a n2>a n,然后利用放缩法得a1<a2<…a2018(2)把代入已知递推式,得a n+1<1<a2018<a2019<…,从而说明存在n∈N*,使得a n>1,且n的最小值为2018.【解答】(1)证明:由,得,即,∴,,…,累加得:,即,∵a n>0,∴;∴数列a n单调递增,=a n+a n2>a n,(2)解:当时,a n+1得,=a n+a n2,得由a n+1,∴,∵a i>0(i=1,2,…,2018),∴,则a2018<1;又,∴×2018=1.即a2018>1.即数列{a n}满足a1<a2<…a2018<1<a2018<a2019<…,综上所述,存在n∈N*,使得a n>1,且n的最小值为2018.2018年10月17日。
优质金卷:江苏省南通、徐州、扬州等六市2018届高三第二次调研(二模)测试数学试题(解析版)

1.{}13,【解析】∵集合{}{}10123102U A =-=-,,,,,,, ∴{}1,3U C A = 故答案为{}1,3.3.30【解析】根据频率分布直方图可得成绩不低于60分的学生的频率为()0.0150.0300.0250.005100.75+++⨯=.∴成绩不低于60分的学生的人数为为400.7530⨯=. 故答案为30.4.125【解析】模拟执行程序可得: 1S =, 1i =,满足条件4i <,执行循环体, 155S =⨯=, 112i =+=,满足条件4i <,执行循环体, 5525S =⨯=, 213i =+=,满足条件4i <,执行循环体,255125S =⨯=, 314i =+=,不满足条件4i <,退出循环,输出S 的值为125.故答案为125.点睛:识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构; (2)要识别、运行程序框图,理解框图所解决的实际问题; (3)按照题目的要求完成解答并验证. 5.13【解析】设AC x =,则12BC x =-,矩形的面积为()21212S AC BC x x x x =⨯=-=-.∵21232x x -> ∴48x <<由几何概率的求解公式可得:该矩形的面积大于232cm 的概率为841123P -==. 故答案为13. 点睛:(1)当试验的结果构成的区域为长度、面积、体积等时,要考虑使用几何概型求解;(2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域;(3)几何概型有两个特点:一是无限性,二是等可能性,基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的的区域是有限的,因此可用“比例解法”求解几何概型的概率.7.∵双曲线C 与双曲线2213y x -=有公共的渐近线 ∴设双曲线C 的方程为22(0)3y x λλ-=>∵双曲线C 经过点()2P - ∴413λ=-=∴双曲线C 的方程为22139x y -=∴双曲线C的焦距为=故答案为9.-6【解析】设等比数列{}n a 的公比为q .∵396S S S ,,成等差数列 ∴9362S S S =+,且1q ≠.∴()()()9361112111111a q a q a q qq q---=+---,即63210qq --=.∴312q =-或31q =(舍去) ∵83a = ∴8533612a a q ===-- 故答案为6-.10.8【解析】∵a b c ,,均为正数,且()4abc a b =+∴()4a b c ab+=∴()4448a b a b c a b a b abb a +++=++=+++≥+=,当且仅当2a =, 2b =时取等号∴a b c ++的最小值为8故答案为8.点睛:本题主要考查等差中项的应用以及利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用≥或≤时等号能否同时成立). 11.()2214x y -+=【解析】由约束条件作出可行域如图所示:由对称性可知,圆C 的圆心在x 轴上,设(),0C a3a -,解得1a =或9a =(舍去).∴面积最大的圆的标准方程为()2214x y -+=. 故答案为()2214x y -+=.12.()1+∞,【解析】当0x >时, ()12x f x e -=-,画出函数图象如图所示:∴函数()f x 此时有1个零点∵函数()f x 在R 上有3个不同的零点∴当0x ≤时, ()332f x x mx =--有2个不同的零点∵()233f x x m '=-∴令()0f x '=,则20x m -=,若0m ≤,则函数()f x 为增函数,不合题意,故0m >.∴函数()f x 在(,-∞上为增函数,在(⎤⎦上为减函数,即()max 3222f x =--=.点睛:已知函数有零点求参数取值范围常用的方法和思路:(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解. 13.10【解析】取AC 中点O ,连接BO , DO .∴()()()()()1122AC BD AC BO OD AC BO AC OD BC BA BC BA DC DA DC DA ⋅=⋅+=⋅+⋅=-+--+ ()222212BC BA DA DC =-+- ∵1423AB BC CD DA ====,,, ∴()116194102AC BD ⋅=-+-= 故答案为10.14.144,【解析】由题意得函数()f x 为奇函数. ∵函数()f x =∴()f x'=①当01a <<时,函数()f x的定义域为⎡⎣,由()0f x '>得x ≤<x<≤,由()0f x '<得x <<函数()f x在⎡⎢⎣,上为增函数,在⎛⎝上为减函数. ∵(f =,f=, ∴()min 23f x f ===-,则14a = ②当1a >时,函数()fx 的定义域为[]1,1-,由()0f x '>得x << ()0fx '<得1x -≤<1x <≤,函数()f x在⎛ ⎝上为增函数,在1,⎡-⎢⎣,⎤⎥⎦为减函数. ∵f ⎛= ⎝()1f =∴()min23f x f ===-,则4a =.综上所述, 14a =或4a =. 故答案为4, 14. 15.(1) 12-;(2) π2β=.试题解析:(1)∵向量()cos ,sin a αα=, ()sin ,cos b ββ=-, 1,2c ⎛=- ⎝ ∴1a b c ===,且()cos sin sin cos sin a b αβαβαβ⋅=-+=-. ∵a b c += ∴22a bc +=,即2221a a b b +⋅+=.∴()12sin 11αβ+-+=,即()1sin 2αβ-=-. (2)∵5π6α= ∴31,2a ⎛⎫=-⎪⎪⎝⎭依题意, 1sin ,cos 2b c ββ⎛+=--+ ⎝. ∵a // ()b c +∴11cos sin 022ββ⎫⎛⎫---=⎪ ⎪⎪⎝⎭⎭,化简得, 11sin 22ββ=. ∴π1sin 32β⎛⎫-= ⎪⎝⎭. ∵0πβ<<∴ππ2π333β-<-<. ∴ππ36β-=,即π2β=.16.(1)证明见解析;(2)证明见解析.试题解析:证明:(1)在三棱柱111ABC A B C -中, 1BB // 1CC . ∵1AF CC ⊥ ∴1AF BB ⊥又∵1AE BB ⊥, AE AF A ⋂=, AE , AF ⊂平面AEF . ∴1BB ⊥平面AEF 又∵1BB ⊂平面11BB C C ∴平面AEF ⊥平面11BB C C(2)∵1AE BB ⊥, 1AF CC ⊥, ABE ACF ∠=∠, AB AC = ∴Rt AEB ∆≌Rt AFC ∆ ∴BE CF =又由(1)知, BE // CF .∴四边形BEFC 是平行四边形,从而BC // EF . 又∵BC ⊄平面AEF , EF ⊂平面AEF ∴BC //平面AEF .17.(1)221189x y +=;(2)证明见解析.从而求得0x ,再由P 在椭圆上,得k 与k '的数量关系,从而表示出直线2QB 的方程,即可求得1x ,进而求得12122PB B QB B S S ∆∆=.试题解析:设()00P x y ,, ()11Q x y ,. (1)在3y x =+中,令0x =,得3y =,从而b =3.由2221{ 93x y a y x +==+,得()222319x xa ++=. ∴20269a x a =-+.∵1PB ==∴2269a a =+,解得218a =. ∴椭圆的标准方程为221189x y +=.联立两直线方程,消去y ,得20109y x x -=.∵()00P x y ,在椭圆221189x y +=上∴22001189x y +=,从而220092x y -=-. ∴012x x =-. ∴121212PB B QB B S x S x ∆∆==. 方法二:设直线1PB , 2PB 的斜率为k , k ',则直线1PB 的方程为3y kx =+. 由11QB PB ⊥,直线1QB 的方程为13y x k=-+. 将3y kx =+代入221189x y +=,得()2221120k x kx ++=, ∵P 是椭圆上异于点1B , 2B 的点 ∴00x ≠,从而0x = 21221kk -+.∵()00P x y ,在椭圆221189x y +=上 ∴22001189x y +=,从而220092x y -=-.∴2000200033912y y yk kx x x-+-⋅='⋅==-,得12kk'=-.点睛:本题主要考查椭圆标准方程、直线与椭圆的位置关系以及圆锥曲线的定值问题,属于难题. 探索圆锥曲线的定值问题常见方法有两种:①从特殊入手,先根据特殊位置和数值求出定值,再证明这个值与变量无关;②直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.18.(1)r=(2) .【解析】试题分析:(1)设所得圆柱的半径为rdm,根据矩形薄铁皮的面积为1002dm,即可求得r的值;(2)设所得正四棱柱的底面边长为a dm,根据题意得2 {20.x aax≤≤,.方法一:表示出正四棱柱的体积324{400xxV a xxx<≤=≤>,,,构造函数,求得单调性,即可求得函数的最大值,从而得体积最大值及x的值;方法二:表示出x的范围,从而得到a的范围,再表示出正四棱柱的体积,即可求得最大值及x的值.试题解析:(1)设所得圆柱的半径为rdm,则()2π24100r r r+⨯=,解得r=(2)设所得正四棱柱的底面边长为a dm ,则2{ 1004x a a a x ≤≤-,,即2{20.x a a x≤≤,方法一:所得正四棱柱的体积3204{ 400x x V a x x x<≤=≤>,,记函数()304{ 400x x p x x x<≤=>,,则()p x在(0上单调递增,在)⎡+∞⎣上单调递减.∴当x =时, ()max p x =.∴当x =,a = max V =dm 3.(2)当x为时,能使按方案②制成的正四棱柱的体积最大. 19.(1)证明见解析;(2)答案见解析;(3)答案见解析.【解析】试题分析:(1)假设数列123c c c ,,是等差数列,则2132c c c =+,即()()()2211332a b a b a b +=+++,根据12b b ,, 3b 是等差数列及12a a ,, 3a 是等比数列,找出矛盾,假设不成立;(2)由11a =, 2q =得12n n a -=,根据数列123c c c ,,是等比数列得2213c c c =,化简求得223b d d =+,再根据2220c b =+≠,即可求得d 得范围;(3)方法一:设1c , 2c , 3c , 4c 成等比数列,其公比为1q ,则1111111221111331111={ 2=3=.a b c a q b d c q a q b d c q a q b d c q +=++++++,①,②,③④,解方程组即可;方法二:假设数列1234c c c c ,,,是等比数列,则324123c c c c c c ==,化简得()321321213222q a a a a a a a a d a a d -+-+=-+-+,即可求得()10q d -=,与1q ≠,且0d ≠矛盾,故可得证.(2)∵11a =, 2q = ∴12n n a -=. ∵2213c c c =∴()()()2222214b b d b d +=+-++,即223b d d =+, 由2220c b =+≠,得2320d d ++≠. ∴1d ≠-且2d ≠-. 又∵0d ≠,∴223b d d =+,定义域为{}120d R d d d ∈≠-≠-≠,,. (3)方法一:设1c , 2c , 3c , 4c 成等比数列,其公比为1q ,则1111111221111331111={ 2=3=.a b c a q b d c q a q b d c q a q b d c q +=++++++,①,②,③④将①+③-2×②得, ()()2211111a q c q -=-,⑤ 将②+④-2×③得, ()()22111111a q q c q q -=-,⑥ ∵10a ≠, 1q ≠,由⑤得10c ≠, 11q ≠. 由⑤⑥得1q q =,从而11a c =. 代入①得10b =.再代入②,得0d =,与0d ≠矛盾. ∴1c , 2c , 3c , 4c 不成等比数列.∵等比数列1a , 2a , 3a , 4a 的公比为()1q q ≠ ∴()321321213222q a a a a a a a a d a a d-+-+=-+-+.又∵()23211210a a a a q -+=-≠∴()2132q a a d a a d -+=-+,即()10q d -=.这与1q ≠,且0d ≠矛盾. ∴假设不成立.∴数列1234c c c c ,,,不能为等比数列. 点睛:用反证法证明命题的基本步骤:①反设,设要证明的结论的反面成立.作反设时要注意把结论的所有反面都要写出来,不要有遗漏; ②归谬,从反设出发,通过推理得出与已知条件或公理、定理矛盾的结论; ③否定反设,从而得出原命题结论成立.20.(1) 01a <≤;(2)①.证明见解析;②.证明见解析.【解析】试题分析:(1)由题意, ()1cos 0f x a x '=-≥对x R ∈恒成立,根据0a >,等价为1cos x a ≥对x R ∈恒成立,即可求得a 得取值范围;(2)①分别求得()g x 与()g x ',若0b <,则存在02b->,使02b g ⎛⎫-< ⎪⎝⎭',从而得0b >,取30e b x -=,则001x <<,即可证明()00g x <;②不妨设120x x <<,令21x t x =,则1t >,由(1)知函数sin y x x =-单调递增,则2211sin sin x x x x ->-,从而2121sin sin x x x x ->-,根据()()12g x g x =,推出212120ln ln x x b x x -->>-,只需证明2121ln ln x xx x ->-ln 0t <成立,设())ln 1h t t t =>,求得函数()h t 的单调性,即可证明.(2)①()1sin ln 12g x x x b x =-++,则()11cos 2b g x x x=-+'. 若0b <,则存在02b ->,使11cos 0222b b g ⎛⎫⎛⎫-=---'< ⎪ ⎪⎝⎭⎝⎭,不合题意. ∴0b >. 取30ebx -=,则001x <<.此时()30000111sin ln 11ln 10222b g x x x b x b e -=-++<+++=-<.∴存在00x >,使()00g x <.下面证明2121ln ln x x x x ->-1ln t t ->,只要证明()ln 0*t <. 设())ln 1h t t t =>,则()0h t '=<在()1+∞,恒成立. ∴()h t 在()1+∞,单调递减,故()()10h t h <=,从而()*得证. ∴2b ->,即2124x x b <.点睛:利用导数证明不等式常见类型及解题策略:(1)构造差函数()()()h x f x g x =-.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式;(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.21.证明见解析【解析】试题分析:延长AO 交⊙O 于点E ,则()()DB DC DE DA OD OE OA OD ⋅=⋅=+⋅-,根据OE OA =,即可得证.试题解析:证明:延长AO 交⊙O 于点E ,则()()DB DC DE DA OD OE OA OD ⋅=⋅=+⋅-. ∵OE OA =,∴()()22DB DC OA OD OA OD OA OD ⋅=+⋅-=-.∴22DB DC OD OA ⋅+=. 22.12【解析】试题分析:依次实施变换1T , 2T 所对应的矩阵NM = 201020010202⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,分别求得点A , B , C 在此矩阵的作用下变换后的点,即可求得面积.23.π4sin 6ρθ⎛⎫=+⎪⎝⎭【解析】试题分析:以极点为原点,极轴为x 轴的非负半轴,建立平面直角坐标系xOy ,得点P 的直角坐标,再根据{x cos y sin ρθρθ==的直线l 的普通方程,从而可得点P 到直线l 的距离,即可求得所求圆的普通方程,再化为极坐标方程.试题解析:以极点为原点,极轴为x 轴的非负半轴,建立平面直角坐标系xOy . 则点P的直角坐标为()1. 将直线l : sin 23πρθ⎛⎫-= ⎪⎝⎭的方程变形为: sin cos cos sin 233ππρθρθ-=,化为普通方程得40y -+=.∴()1P 到直线l :40y -+=的距离为:2=.∴所求圆的普通方程为()(2214x y -+=,化为极坐标方程得, π4sin 6ρθ⎛⎫=+ ⎪⎝⎭.24.证明见解析【解析】试题分析:由a,b,c,且12a b c++==,再根据基本不等式即可得证.试题解析:证明:∵a,b,c为正实数2==≥=(当且仅当a b c==取“=”).25.(1)521;(2)答案见解析.【解析】试题分析:(1)从3⨯3表格中随机不重复地点击3格,共有39C种不同情形,再将事件分类,根据古典概型概率公式求得概率;(2)先确定X的所有可能值为300,400,500,600,700,再分别求出对应的概率,列出分布列,最后根据数学期望公式求期望.(2)X的所有可能值为300,400,500,600,700.则()3439C41300C8421P X====,()121439C C242400C847P X⋅====,()1212144439C C C C305500C8414P X⋅+⋅====,()121439C C63700C8442P X⋅====.∴X的概率分布列为:∴()12553300400500600700500217142142E X=⨯+⨯+⨯+⨯+⨯=(元).点睛:求解离散型随机变量的数学期望的一般步骤为:第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义; 第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率; 第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值. 26.(1)30;(2)证明见解析.试题解析:由二项式定理,得21C i i n a +=(i =0,1,2,…,2n+1).(1)210221055535C 3C 5C 30T a a a =++=++=;(2)∵()()()()()()()()()()121221!212!1C 121C 1!!!!n k n k n nn n n n k n k n n k n k n k n k ++++++⋅++=++⋅==+++-+-∴()()()12121002121C21C nnnn k n kn n kn n k k k T k ak k -++-++====+=+=+∑∑∑ ()()()()11121212102121C21C21C nnnn kn kn kn n n k k k n k n n k n +++++++++===⎡⎤=++-+=++-+⎣⎦∑∑∑()()()()()()122122122011221C21C 2212C 21221C 22nnn kn k n nn n nn n n k k n n n n n +++++===+-+=+⋅⋅+-+⋅⋅=+∑∑.∴()()()()1221212121C 21C C 221C n n n nn n n n n T n n n ----=+=++=+.∵*21C n n N -∈∴n T 能被42n +整除.。
高三数学-2018年南通市高三第二次调研考 精品

2018年南通市高三第二次调研考试注意事项:1.答卷前,考生先将自己的姓名、考试证号等填写清楚,并认真核准答题卡表头及答题纸密封线内规定填写或填涂的项目.2.第Ⅰ卷选择题部分的答案必须使用2B 铅笔填涂在答题卡上;第Ⅱ卷非选择题部分的答案必须使用黑色签字笔书写在答题纸上,字体工整、笔迹清楚.3.请按照题号顺序在各题目的答题区域内作答,书写不能超出横线或方格,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效. 保持卡面和答题纸清洁,不折叠、不破损.数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷满分150分,考试时间120分钟. 参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率k n kk n n P P C k P --=)1()(正棱锥、圆锥的侧面积公式S 锥体侧=cl 21其中c 表示底面周长,l 表示斜高或母线长球的体积公式V 球=334R π 其中R 表示球的半径 第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题每小题5分;共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 命题“若a >b ,则a -8>b -8”的逆否命题是A .若a <b ,则a -8<b -8B .若a -8>b -8,则a >bC .若a ≤b ,则a -8≤b -8D .若a -8≤b -8,则a ≤b2. 椭圆13422=+y x 的右焦点到直线y =33x 的距离是 A .21 B .23 C .1 D .33. 在等比数列{a n }中,a 5a 7=6,a 2+a 10=5,则1810a a 等于 A .-32或-23 B .32 C .23D .32或23 4. 将函数y=sin2x 的图象按向量a 平移后得到函数y=sin(2x -π4)的图象,则向量a 可以是 A .(π4,0) B .(π8,0) C .(-π4,0) D .(-π8,0) 5. 如图,长方体ABCD —A 1B 1C 1D 1中,∠DAD 1=45,∠CDC 1=30,那么异面直线AD 1与DC 1所成角的大小为 A. B.2 C. D.2 6.∑∑==1010)(n nk knC的值等于A .1022B .1023C .2186D .2187 7. 已知sinα>0,cosα>0,且sinαcosα>41,则α的取值范围是 A .(2k π+12π,2k π+125π ), k ∈Z B .(k π+12π,k π+125π), k ∈ZC .(2k π+6π,2k π+3π ), k ∈Z D .(k π+6π,k π+3π), k ∈Z 8. 定义在R 上的函数f (x )对任意的实数x ,满足f (x +1)=- f (x -1),则下列结论一定成立的是 A .f (x )是以4为周期的周期函数 B .f (x )是以6为周期的周期函数 C .f (x )的图象关于直线x =1对称 D .f (x )的图象关于点(1,0)对称9. 甲、乙两人玩猜骰子游戏.游戏的规则是:有三个骰子(每个骰子都是正方体,其六个面上分别标有数字1,2,3,4,5,6),乙先从1,2,3,4,5,6这六个数中报一个,然后由甲掷这三个骰子各一次,如果三个骰子中至少有1个骰子的向上一面的数字恰好是乙所报的这个数,那么乙获胜,否则甲获胜.若骰子任意一面向上的概率均等,则乙获胜的概率是A .21631 B .21691 C .21 D .21612510.已知平面上点P ∈{(x ,y )|16)sin 2()cos 2(22=-+-ααy x (α∈R )},则满足条件的点P在平面上所组成图形的面积是A .36πB .32πC .16πD .4π1A (第5题)第Ⅱ卷(非选择题,共100分)二、填空题:本大题共4小题;每小题4分,共16分. 11.函数f (x )=6cos x +cos2x 的最小值是 .12.已知椭圆2212516x y +=与双曲线22221x y m n-=(m >0,n >0)具有相同的焦点F 1,F 2,设两曲线的一个交点为Q ,∠QF 1F 2=90°,则双曲线的离心率为 .13.函数f (x )=lg (x 2-ax -1)在区间(1,+∞)上是单调增函数,则a 的取值范围是 . 14.设函数f (x )定义域为R .若存在与x 无关的正常数M ,使|f (x )| ≤M|x |对一切实数x 均成立,则称f (x )为有界泛函.在函数f (x )=2x ,g (x )=x 2,h (x )=2x ,v (x )=x sin x 中,属于有界泛函的有 . 三、解答题:本大题共6小题;共84分.解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)已知S n 是等比数列{a n }的前n 项和,S 3,S 9,S 6成等差数列. (1)求数列{a n }的公比q ;(2)问a 4,a 7的等差中项是数列{a n }中的第几项?请说明理由. 16.(本小题满分14分)已知向量a =(1,2),b =(-2,1),k ,t 为正实数,向量x = a +(t 2+1)b ,y =-k a +t1b . (1)若x ⊥y ,求k 的最小值;(2)是否存在正实数k ,t ,使x ∥y ?若存在,求出k 的取值范围;若不存在,请说明理由. 17.(本小题满分15分)在四棱锥P —ABCD 中,AD ⊥AB ,CD ∥AB ,PD ⊥底面ABCD ,ABAD直线P A 与底面ABCD 成60°角,点M 、N 分别是P A 、PB 的中点. (1)求二面角P —MN —D 的大小; (2)如果△CDN 为直角三角形,求CDAB的值.AC AD AN AMP AB A(第17题)18.(本小题满分13分)如图,已知A 、B 、C 是一条直路上的三点,AB 与BC 各等于1km ,从三点分别遥望塔M ,在A 处看见塔在北偏东45°方向,在B 处看见塔在正东方向,在点C 处见塔在南偏东60°方向,求塔到直路ABC 的最短距离. 19.(本小题满分15分)设定义在R 上的函数43201234()f x a x a x a x a x a =++++(其中i a ∈R ,i =0,1,2,3,4),当x =-1时,f (x )取得极大值23,并且函数y=f (x+1)的图象关于点(-1,0)对称. (1)求f (x );(2)试在函数f (x )的图象上求两点,使这两点为切点的切线互相垂直,且切点的横坐标都在区间[上;(3)若)1321,23n n n n n nx y --==(n ∈N +),求证:4|()()|3n n f x f y -<.20.(本小题满分13分)设M 是椭圆C :141222=+y x 上的一点,P 、Q 、T 分别为点M 关于y 轴、原点、x 轴的对称点, N 为椭圆C 上异于点M 的另一点,且MN ⊥MQ ,QN 与PT 的交点为E ,当M 沿椭圆C 运动时,求动点E 的轨迹方程.(第18题)。
2018南通市二模数学试题及答案

则 …………………………12分
解得 .所以,圆 的方程为 .…………………14分
18.(本小题满分16分)
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的
半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
15.(本小题满分14分)
如图,平面 平面 ,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO
的中点, , .求证:
(1) 平面 ;
(2) ∥平面 .
【证明】由题意可知, 为等腰直角三角形,
为等边三角形.…………………2分
(1)因为 为边 的中点,所以 ,
因为平面 平面 ,平面 平面 ,
量 = , , =(x,y),当实数λ满足x=λ x1+(1-λ)x2时,记向
量 =λ +(1-λ) .定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
平面 ,所以 面 .…………………5分
因为 平面 ,所以 ,
在等腰三角形 内, , 为所在边的中点,所以 ,
又 ,所以 平面 ;…………………8分
(2)连AF交BE于Q,连QO.
因为E、F、O分别为边PA、PB、PC的中点,
所以 ,且Q是△PAB的重心,…………………10分
于是 ,所以FG//QO.…………………12分
由 ,得 ,………………5分
于是 ,因为 ,所以 .………………7分
(2)因为 ,由(1)知 .………………9分
因为△ABC的面积为 ,所以 ,于是 .①
在△ABC中,设内角A、B的对边分别是a,b.
由余弦定理得 ,所以 .②
江苏省南通市高三第二次调研测试数学Word版含答案

江苏省南通市高三第二次调研测试数学Word版含答案数学I参考公式:柱体的体积公式V柱体Sh,其中S为柱体的底面积,h为高.、填空题:本大题共14小题,每小题5分,共计70分•请把答案填写在答题卡相应位置5. 在长为12 cm 的线段AB 上任取一点 C ,以线段AC , BC 为邻边作矩形,则该矩形的面上. 1. 已知集合U 1,0 , 1 , 2 , 3 , A 1,0 , 2. 已知复数Za i , Z 23 4i ,其中i 为虚数单位3. 某班40名学生参加普法知识竞赛,成绩都在区间 示,则成绩不低于60分的人数为 ▲.若勺为纯虚数,则实数a 的值为 ▲ Z 2上,其频率分布直方图如图所4. 如图是一个算法流程图,则输出的 S 的值为一.40 , 1002频率0.015 0.010 0.0050.030 0.025 (第 4 题)大于32 cm 2的概率为 ▲ •6. 在厶ABC 中,已知 AB 1 , AC 2 , B 45,则BC 的长为 ▲.27.在平面直角坐标系 xOy 中,已知双曲线 C 与双曲线x 2占 1有公共的渐近线,且经过3占 八、、P 2, 3 ,则双曲线C 的焦距为 ▲& 在平面直角坐标系 xOy 中,已知角 ,的始边均为x 轴的非负半轴,终边分别经过 占 八、、A(1 , 2) , B (5 , 1),则 tan( )的值为 ▲. 9.设等比数列 a n 的前n 项和为S n.若S 3,& , S 6成等差数列,且a 83,则a 5的值为▲.实数m 的取值范围是▲.iur uun ,亠13. 在平面四边形ABCD 中,已知AB 1 , BC 4 , CD 2 , DA 3,则AC BD 的值为 ▲ 14.已知a 为常数,函数f(x) -x 。
的最小值为 2,则a 的所有值为▲J a x 2 J 1 x 2 3二、解答题:本大题共 6小题,共计90分.请在答题卡指定区域.内作答.解答时应写出文字 说明、证明过程或演算步骤.10. 已知a , b , c 均为正数,且 abc4( a b),则a b c 的最小值为11.在平面直角坐标系xOy 中,若动圆C 上的点都在不等式组x < 3,x . 3y 3》0,表示的平面区x 3y 3> 0内,则面积最大的圆C 的标准方程为12.设函数f(x)(其中e 为自然对数的底数)有3个不同的零点,则3x 3mx15. (本小题满分14分)在平面直角坐标系xOy中,设向量a cos , sin , b sin , cosc32(1)若ab c,求sin ()的值;(2)设5 n"6,0 n,且a〃b c ,求的值18. (本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为 虚线 16.(本小题满分14分) 如图, 在三棱柱 ABC A 1B 1C 1中,AB AC ,点E ,F 分别在棱 BB i , CC i 上(均异端点) ,且/ ABE / ACF , AE 丄 BB 1, AF 丄 CC 1. 求证: (1)平面AEF(2) BC // 平面 AEF .17.(本小题满分14分)如图,在平面直角坐标系 xOy 中,B 1,2B 2是椭圆Xa 2y _1( a b 0)的短轴端点,P 是 椭圆上异于点B 1, B 2的一动点•当直线 PB 1的方程为x 3时,线段PB 1的长为4.2 .(1)求椭圆的标准方程; (2)设点 Q 满足:QB PB , QB 2PB 2.求证:△ PB 1B 2与厶QB 1B 2的面积之比为定值.100 dm 2的矩形薄铁皮(如图),并沿(第 16 题)11, 12裁剪成A, B, C三个矩形(B, C全等),用来制成一个柱体•现有两种方案:方案①:以h为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;方案②:以h为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与h或12垂直)作为正四棱柱的两个底面.(1 )设B, C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设l i的长为x dm,则当x为多少时,能使按方案②制成的正四棱柱的体积最大?(第18题)19. (本小题满分16分)设等比数列a1, a2, a3, a4的公比为q,等差数列b1, b2, b3, b4的公差为d,且q 1, d 0 . 记G a i b i (i 1, 2, 3, 4).(1)求证:数列c, , g , C3不是等差数列;(2)设q 1 , q 2 .若数列q , c, , C3是等比数列,求b2关于d的函数关系式及其定义域;(3)数列G , C2 , C3 , C4能否为等比数列?并说明理由.20. (本小题满分16分)设函数 f ( x ) x asin x ( a 0).(1)若函数y f(x)是R上的单调增函数,求实数a的取值范围;(2)设a 舟,g( x ) f ( x) bl nx 1 (b R , b 0) , g ( x)是g(x )的导函数.① 若对任意的x 0 , g ( x) 0 ,求证:存在x0,使g( X。
江苏省南通市海门中学2018届高三第二次教学质量调研数学试题 含答案

海门中学2018届高三第二次教学质量调研数学试卷一、填空题:每小题5分,共70分.请把答案直接填写在答题纸相应位置上......... 1.已知集合}3,2,0,1{,02|-=⎭⎬⎫⎩⎨⎧>-=B x x x A ,则=B A ▲ . 2.已知复数z 满足i z i =+)43((i 为虚数单位),则=||z ▲ . 3.函数x x x x f ln )23()(2++=的零点的集合为 ▲ .4.若31tan ),2,0(,=∈απβα,21)tan(=+βα,则=+βα2 ▲ . 5.将函数)32sin(π+=x y 图像上的点),12(t P π-,向右平移)0(>k k 个单位长度得到点'P ,若'P 在函数x y 2sin =的图像上,则k 的最小值为 ▲ .6.已知函数⎩⎨⎧<++-≥+=0),cos(0,sin )(22x x x x x x x f α是奇函数,则=αcos ▲ . 7.若双曲线),(132222R n m nm y n m x ∈=--+的焦距为4,则实数n 的取值范围为 _____▲ .8.若实数y x ,满足⎪⎩⎪⎨⎧≤≥-+≤+-40301y y x y x ,则y x -2)21(的最大值为 ▲ . 9.设n S 是公差不为零的等差数列}{n a 的前n 项和,若25242322a a a a +=+,且279=S ,则数列}{n a 的通项公式=n a ▲ .10.已知圆:C 0422=-+x y x 及点)2,1(),0,1(B A -,直线l 平行于AB ,与圆C 相交于N M ,两点,AB MN =若直线l 与直线AB 在圆心C 的同侧,则直线l 的方程为____▲ .11.若0,0>>b a ,且直线06=-+by ax 与直线052)3(=+--y x b 垂直,则b a 2131+的最小值为 ▲ .12.设R m ∈,若过点),2(m 存在三条直线与曲线x x y 33-=相切,则实数m 的取值范围是 ▲ .13.在ABC ∆中,2=AB ,060=∠A ,点D 满足DB CD 2=,且337=AD ,则=∙ ▲ .14.在ABC ∆中,2tan 2tan 2tan222CB A ++的最小值为 ▲ . 二、解答题:本大题共6小题,共计90分.请在答题纸指定区域.......内作答,解答时应写出必要的文字说明、证明过程或演算步骤. 15. (本题满分14分)在ABC ∆中,c b a ,,分别是角C B A ,,所对的边,若bc A 23)3sin(=+π (1)求角B 的大小;(2)若2,32==c b ,求ABC ∆的面积。
2018南通市高三二模(含答案)

南通市2018届高三第二次调研测试英语第一部分听力 (共两节,满分20分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What makes the girl study harder?A. To get a toy. B. To work as a model. C. To earn money for a car. 2. What does the man want to do? A. Stop to ask for directions. B. Drive to the tall building. C. Write down the correct address. 3. How much will the woman pay for the skirt? A. $30.B. $70.C. $100.4. What is the woman worried about at first?A. The man ’s memory.B. The size of the house.C. The cleanliness of the hotel. 5. What does the woman think of the man ’s schedule? A. Too flexible. B. Too realistic.注意事项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共14页。
本次考试满分为120分,考试时间为120分钟。
考试结束后,请将答题纸(卡)交回。
2. 答题前,请您务必将自己的姓名、考试号等用书写黑色字迹的0.5毫米签字笔填写在答题纸(卡)上。
江苏省南通徐州扬州泰州淮安宿迁六市2018届高三数学3月第二次调研(二模)试题
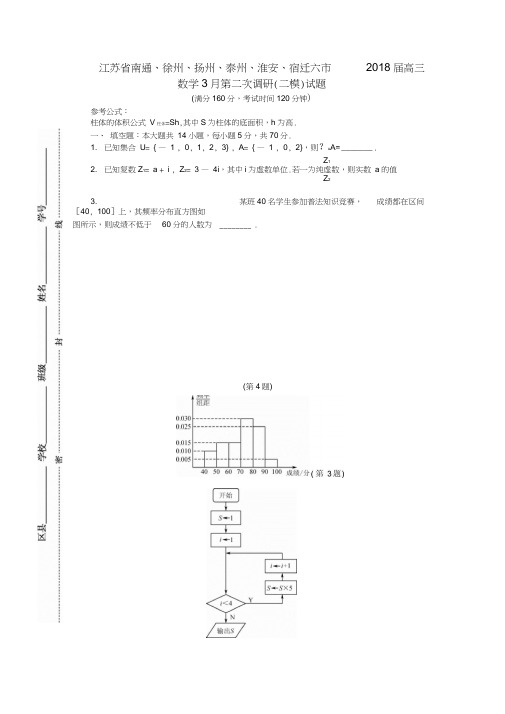
江苏省南通、徐州、扬州、泰州、淮安、宿迁六市2018届高三数学3月第二次调研(二模)试题(满分160分,考试时间120分钟)参考公式:柱体的体积公式V柱体=Sh,其中S为柱体的底面积,h为高.一、填空题:本大题共14小题,每小题5分,共70分.1. 已知集合U= { —1 , 0, 1, 2, 3} , A= { —1 , 0, 2},则?u A= _______ .Z12. 已知复数Z1= a + i , Z2= 3 —4i,其中i为虚数单位.若一为纯虚数,则实数a的值Z23. 某班40名学生参加普法知识竞赛,成绩都在区间[40, 100]上,其频率分布直方图如图所示,则成绩不低于60分的人数为 ________ .(第4题)*4. 如图是一个算法流程图,则输出的S的值为_________ .5. 在长为12 cm的线段AB上任取一点C,以线段AC, BC为邻边作矩形,则该矩形的面积大于32 cm2的概率为 ________ .6. 在厶ABC中,已知AB= 1, AC=Q2, B= 45°,贝U BC的长为_______ .27. 在平面直角坐标系xOy中,已知双曲线C与双曲线x2—y3 = 1有公共的渐近线,且经过点P( —2,⑴),则双曲线C的焦距为 __________ .8. 在平面直角坐标系xOy中,已知角a , B的始边均为x轴的非负半轴,终边分别经过点A(1, 2) , B(5 , 1),则tan( a —3 )的值为___________ .9. 设等比数列{a n}的前n项和为S n.若S, S o, S成等差数列,且a8= 3,贝U a5的值为10. ____________________________________________________________________ 已知a, b, c均为正数,且abc = 4(a + b),贝U a + b+ c的最小值为__________________________x w 3,11. 在平面直角坐标系 xOy 中,若动圆C 上的点都在不等式组x — 3y + 3>0,表示的 -x + ”J 3y + 3》0 平面区域内,则面积最大的圆C 的标准方程为 _______________ • e J 舟,x > 0,12. 设函数f(x) =2(其中e 为自然对数的底数)有3个不同的零点,x 3 — 3mx — 2, x w 0则实数m 的取值范围是 _________ • 13. 在平面四边形 ABCD 中,已知AB= 1 ,BC = 4, CD= 2, DA= 3,则云C ・§D 的值为•x 214. 已知a 为常数,函数 f(x) = 2 2的最小值为一 了则a 的所有值为yj a — x —寸 1 — x3二、 解答题:本大题共 6小题,共90分.解答时应写出必要的文字说明、证明过程或 演算步骤.15. (本小题满分14分)在平面直角坐标系 xOy 中,设向量 a = (cos a, sin a ) , b = ( — sin 3 , cos 3 ), c =(—1 -2)(2, 2 )•(1) 若 |a + b| = |c|,求 sin( a — 3 )的值;5 n(2) 设 a =, O v 3 V n ,且 a II (b + c ),求 3 的值.16. (本小题满分14分)如图,在三棱柱 ABC -A1BG 中,AB= AC,点E , 且/ ABE=Z ACF AE ± BB , AF 丄 CC.求证:(1) 平面AEFL 平面BBGC ;17. (本小题满分14分)2 2x y如图,在平面直角坐标系 xOy 中,B, B 2是椭圆二+ 2= 1(a >b >0)的短轴端点,P 是椭a b圆上异于点B i , B 2的一动点.当直线 PB 的方程为y = x + 3时,线段PB 的长为 谑.(1) 求椭圆的标准方程;F 分别在棱BB , CG 上(均异于端点),(2) 设点Q满足:QB丄PB, QB丄PB>.求证:△ PB1B2与厶QBE的面积之比为定值.将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm2的矩形薄铁皮(如图),并沿虚线l i,12裁剪成A, B, C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:方案①:以1 i为母线,将A作为圆柱的侧面展开图,并从B, C中各裁剪出一个圆形作为圆柱的两个底面;方案②:以1 2为侧棱,将A作为正四棱柱的侧面展开图,并从B, C中各裁剪出一个正方形(各边分别与I i或I 2垂直)作为正四棱柱的两个底面.(1)设B, C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设I 1的长为x dm,则当x为多少时,能使按方案②制成的正四棱柱的体积最大?设等比数列a i, a2, a3, a4的公比为q,等差数列b i, b2, b3, b4的公差为d,且q z 1, d 工0.记C i = a i + b i(i = 1, 2, 3, 4).(1) 求证:数列c i, C2, C3不是等差数列;(2) 设a i= 1, q= 2.若数列c i, C2, C3是等比数列,求b2关于d的函数关系式及其定义域;(3) 数列C1, C2, C3, C4能否为等比数列?并说明理由.设函数f(x) = x—asin x(a > 0).(1) 若函数y = f(x)是R上的单调增函数,求实数a的取值范围;1(2) 设a = 2,g(x) = f(x) + bln x + 1(b € R, b 丰 0) , g ' (x)是g(x)的导函数.① 若对任意的x>0, g' (x) >0,求证:存在x o,使g(x o) v 0;2② 若g(x i) = g(x 2)(x X2),求证:x i X2 v 4b .\数学附加题(满分40分,考试时间30分钟)21. 【选做题】 在A , B , C, D 四小题中只能选做 2题,每小题10分,共20分.若多做,则按作答的前两题计分•解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修41:几何证明选讲)如图,A , B, C 是圆O 上的3个不同的点,半径 OA 交弦BC 于点D.求证:DB- DO 0D=oA.标方程.D.(选修45:不等式选讲)1B. (选修42:矩阵与变换)在平面直角坐标系 xOy 中,已知 _ 1 0 [ - 2 阵分别为M=,矩阵N=L 0 2 II 0 积.A (0 , 0) ,B (3 , 0) ,C (2 , 2).设变换「,T 2对应的矩 0I,求对△ ABC 依次实施变换 T 1, T 2后所得图形的面C. (选修44:坐标系与参数方程)在极坐标系中,求以点p (2, n 为圆心且与直线 I : p sin( 0 —-—) = 2相切的圆的极坐31 — a + c c ( ,a +2 jb )已知a, b, c为正实数,且 a + b + c= ?,求证:【必做题】第22, 23题,每小题10分,共20分•解答时应写出必要的文字说明、证明过程或演算步骤.22. 在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3X3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖总金额为X元.⑴求概率P(X = 600);.(2) 求X的概率分布及数学期望E(X)23. 已知(1 + x)2n+1= a°+ a i x+ a?x2+…+ a2n+ i x2n +1, n€ N.记T n = * = '> (2k + 1)a n-k.(1) 求T2的值;(2) 化简T n的表达式,并证明:对任意的n€ N*, T n都能被4n+ 2整除.n 弩.所以 3 —n=n ,即 即 3 =n .(“ 分)33336 216. 证明:(1) 在三棱柱 ABC -A 1B 1C 中,BB // CG.因为AF 丄CC ,所以AF 丄BB 1.(2 分) 又 AE 丄 BB 1,AE A AF = A ,AE, AF?平面 AEF,所以 BB 丄平面 AEF.(5 分) 因为BB?平面BBCC,所以平面 AEFL 平面 BBCC.(7分) (2) 因为 AE1BB 1,AF 丄 CG ,/ ABE=Z ACF AB = AC , 所以 Rt △ AE 匪 Rt △ AFC.所以 BE = CF.(9 分)又由(1)知,BE// CF,所以四边形 BEFC 是平行四边形.故 BC// EF.(11分) 又BC?平面AEF, EF?平面 AEF,所以BC//平面 AEF.(14分)17. 解:设 P (x o ,y o ),Q (X 1,yj .(1)在 y = x + 3 中,令 x = 0,得 y = 3,从而 b = 3.(2 分)2 2所以椭圆的标准方程为 18+ 9 = 1.(6分)⑵(方法1)直线PB 的斜率为kPB 1 =也二^,由QB 丄PB ,所以直线 QB 的斜率为kQBX 0X 0y 。
高三数学第二次调研测试试题
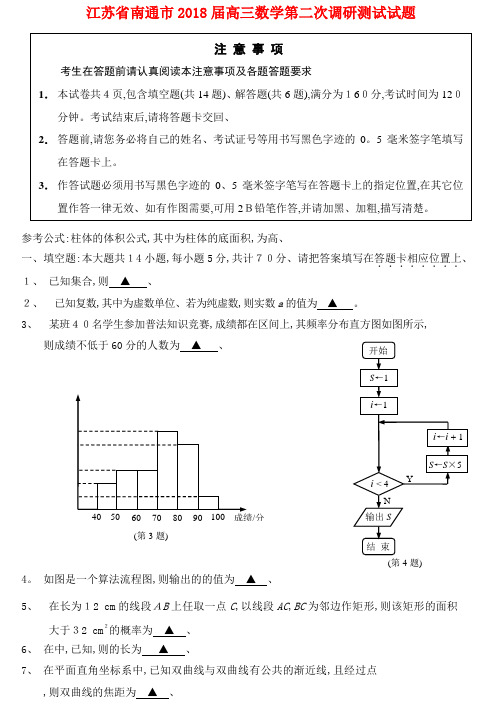
(第4题)江苏省南通市2018届高三数学第二次调研测试试题参考公式:柱体的体积公式,其中为柱体的底面积,为高、一、填空题:本大题共14小题,每小题5分,共计70分、请把答案填写在答题卡相应位置上........、 1、 已知集合,则 ▲ 、2、 已知复数,其中为虚数单位、若为纯虚数,则实数a 的值为 ▲ 。
3、 某班40名学生参加普法知识竞赛,成绩都在区间上,其频率分布直方图如图所示, 则成绩不低于60分的人数为 ▲ 、4。
如图是一个算法流程图,则输出的的值为 ▲ 、5、 在长为12 cm 的线段AB 上任取一点C ,以线段AC ,BC 为邻边作矩形,则该矩形的面积 大于32 cm 2的概率为 ▲ 、 6、 在中,已知,则的长为 ▲ 、7、 在平面直角坐标系中,已知双曲线与双曲线有公共的渐近线,且经过点,则双曲线的焦距为 ▲ 、/分(第3题)8、 在平面直角坐标系xOy 中,已知角的始边均为x轴的非负半轴,终边分别经过点 ,,则的值为 ▲ 、9、 设等比数列的前n 项和为、若成等差数列,且,则的值为 ▲ 、 10、已知均为正数,且,则的最小值为 ▲ 。
11、在平面直角坐标系xOy 中,若动圆上的点都在不等式组表示的平面区域 内,则面积最大的圆的标准方程为 ▲ 、12、设函数(其中为自然对数的底数)有3个不同的零点,则实数 的取值范围是 ▲ 、13、在平面四边形中,已知,则的值为 ▲ 、14。
已知为常数,函数的最小值为,则的所有值为 ▲ 、二、解答题:本大题共6小题,共计90分、请在答题卡指定区域.......内作答、解答时应写出文字说明、 证明过程或演算步骤。
15、(本小题满分14分)在平面直角坐标系中,设向量,,、 (1)若,求的值; (2)设,,且,求的值、16。
(本小题满分14分)如图,在三棱柱ABC A1B1C 1中,AB AC ,点E,F分别在棱BB 1 ,C C1上(均异于端点),且∠A BE∠AC F,AE ⊥BB 1,AF ⊥CC 1、求证:(1)平面AEF ⊥平面BB 1C1C ;(2)BC // 平面AEF 、17、(本小题满分14分)如图,在平面直角坐标系xOy 中,B1,B 2是椭圆的短轴端点,P 是椭圆上异于点B1,B2的一动点、当直线PB 1的方程为时,线段PB 1的长为、AA 1B 1C 1B C FE(第16题)l 1l 2 AB C(第18题)0(1)求椭圆的标准方程;(2)设点Q满足:、求证:△PB 1B 2与△QB 1B 2的面积之比为定值、18、(本小题满分16分)ﻩ将一铁块高温融化后制成一张厚度忽略不计、面积为100 dm 2的矩形薄铁皮(如图),并沿虚线l 1,l 2裁剪成A,B,C 三个矩形(B ,C 全等),用来制成一个柱体、现有两种方案:方案①:以为母线,将A作为圆柱的侧面展开图,并从B ,C 中各裁剪出一个圆形作为圆 柱的两个底面;方案②:以为侧棱,将A 作为正四棱柱的侧面展开图,并从B ,C 中各裁剪出一个正方形 (各边分别与或垂直)作为正四棱柱的两个底面、(1)设B ,C 都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设的长为dm,则当为多少时,能使按方案②制成的正四棱柱的体积最大?19、(本小题满分16分)设等比数列a 1,a2,a 3,a 4的公比为q ,等差数列b1,b 2,b 3,b4的公差为d,且、 记(i1,2,3,4)、(1)求证:数列不是等差数列;(2)设,、若数列是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列能否为等比数列?并说明理由、(第17题)0B 1B 2PQO xy20。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏南通市2018届高三数学第二次调研试卷(含答案)南通市2018届高三第二次调研测试数学Ⅰ参考公式:柱体的体积公式,其中为柱体的底面积,为高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.已知集合,则▲.2.已知复数,其中为虚数单位.若为纯虚数,则实数a的值为▲.3.某班40名学生参加普法知识竞赛,成绩都在区间上,其频率分布直方图如图所示,则成绩不低于60分的人数为▲.4.如图是一个算法流程图,则输出的的值为▲.5.在长为12cm的线段AB上任取一点C,以线段AC,BC 为邻边作矩形,则该矩形的面积大于32cm2的概率为▲.6.在中,已知,则的长为▲.7.在平面直角坐标系中,已知双曲线与双曲线有公共的渐近线,且经过点,则双曲线的焦距为▲.8.在平面直角坐标系xOy中,已知角的始边均为x轴的非负半轴,终边分别经过点,,则的值为▲.9.设等比数列的前n项和为.若成等差数列,且,则的值为▲.10.已知均为正数,且,则的最小值为▲.11.在平面直角坐标系xOy中,若动圆上的点都在不等式组表示的平面区域内,则面积最大的圆的标准方程为▲.12.设函数(其中为自然对数的底数)有3个不同的零点,则实数的取值范围是▲.13.在平面四边形中,已知,则的值为▲.14.已知为常数,函数的最小值为,则的所有值为▲.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)在平面直角坐标系中,设向量,,.(1)若,求的值;(2)设,,且,求的值.16.(本小题满分14分)如图,在三棱柱ABCA1B1C1中,ABAC,点E,F分别在棱BB1,CC1上(均异于端点),且∠ABE∠ACF,AE⊥BB1,AF⊥CC1.求证:(1)平面AEF⊥平面BB1C1C;(2)BC//平面AEF.17.(本小题满分14分)如图,在平面直角坐标系xOy中,B1,B2是椭圆的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为时,线段PB1的长为.(1)求椭圆的标准方程;(2)设点Q满足:.求证:△PB1B2与△QB1B2的面积之比为定值.18.(本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100dm2的矩形薄铁皮(如图),并沿虚线l1,l2裁剪成A,B,C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:方案①:以为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;方案②:以为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与或垂直)作为正四棱柱的两个底面.(1)设B,C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设的长为dm,则当为多少时,能使按方案②制成的正四棱柱的体积最大?19.(本小题满分16分)设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且.记(i1,2,3,4).(1)求证:数列不是等差数列;(2)设,.若数列是等比数列,求b2关于d的函数关系式及其定义域;(3)数列能否为等比数列?并说明理由.20.(本小题满分16分)设函数.(1)若函数是R上的单调增函数,求实数a的取值范围;(2)设,是的导函数.①若对任意的,求证:存在使;②若,求证:.南通市2018届高三第二次调研测试数学Ⅱ(附加题)21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)如图,A,B,C是⊙O上的3个不同的点,半径OA交弦BC于点D.求证:.B.[选修4-2:矩阵与变换](本小题满分10分)在平面直角坐标系xOy中,已知.设变换,对应的矩阵分别为,,求对△ABC依次实施变换,后所得图形的面积.C.[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点为圆心且与直线:相切的圆的极坐标方程.D.[选修4-5:不等式选讲](本小题满分10分)已知a,b,c为正实数,且,求证:.【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的33表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖总金额为X元.(1)求概率;(2)求的概率分布及数学期望.23.(本小题满分10分)已知…,.记.(1)求的值;(2)化简的表达式,并证明:对任意的,都能被整除.南通市2018届高三第二次调研测试数学学科参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共计70分.1.已知集合,则▲.【答案】2.已知复数,其中为虚数单位.若为纯虚数,则实数a的值为▲.【答案】3.某班40名学生参加普法知识竞赛,成绩都在区间上,其频率分布直方图如图所示,则成绩不低于60分的人数为▲.【答案】304.如图是一个算法流程图,则输出的的值为▲.【答案】1255.在长为12cm的线段AB上任取一点C,以线段AC,BC 为邻边作矩形,则该矩形的面积大于32cm2的概率为▲.【答案】136.在中,已知,则的长为▲.【答案】7.在平面直角坐标系中,已知双曲线与双曲线有公共的渐近线,且经过点,则双曲线的焦距为▲.【答案】8.在平面直角坐标系xOy中,已知角的始边均为x轴的非负半轴,终边分别经过点,,则的值为▲.【答案】9.设等比数列的前n项和为.若成等差数列,且,则的值为▲.【答案】10.已知均为正数,且,则的最小值为▲.【答案】811.在平面直角坐标系xOy中,若动圆上的点都在不等式组表示的平面区域内,则面积最大的圆的标准方程为▲.【答案】12.设函数(其中为自然对数的底数)有3个不同的零点,则实数的取值范围是▲.【答案】13.在平面四边形中,已知,则的值为▲.【答案】1014.已知为常数,函数的最小值为,则的所有值为▲.【答案】二、解答题:本大题共6小题,共计90分.15.(本小题满分14分)在平面直角坐标系中,设向量,,.(1)若,求的值;(2)设,,且,求的值.解:(1)因为,,,所以,且.……3分因为,所以,即a22abb2&# 61472;1,所以,即.……6分(2)因为,所以.依题意,.……8分因为,所以.化简得,,所以.……12分因为,所以.所以,即.……14分16.(本小题满分14分)如图,在三棱柱ABCA1B1C1中,ABAC,点E,F分别在棱BB1,CC1上(均异于端点),且∠ABE∠ACF,AE⊥BB1,AF⊥CC1.求证:(1)平面AEF⊥平面BB1C1C;(2)BC//平面AEF.证明:(1)在三棱柱ABCA1B1C1中,BB1//CC1.因为AF⊥CC1,所以AF⊥BB1.……2分又AE⊥BB1,AEAF,AE,AF平面AEF,所以BB1⊥平面AEF.……5分又因为BB1平面BB1C1C,所以平面AEF⊥平面BB1C1C.……7分(2)因为AE⊥BB1,AF⊥CC1,∠ABE∠ACF,ABAC,所以△AEB≌△AFC.所以BECF.……9分又由(1)知,BECF.所以四边形BEFC是平行四边形.从而BCEF.……11分又BC平面AEF,EF平面AEF,所以BC//平面AEF.……14分17.(本小题满分14分)如图,在平面直角坐标系xOy中,B1,B2是椭圆的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为时,线段PB1的长为.(1)求椭圆的标准方程;(2)设点Q满足:.求证:△PB1B2与△QB1B2的面积之比为定值.解:设,.(1)在中,令,得,从而b3.……2分由得.所以.……4分因为,所以,解得.所以椭圆的标准方程为.……6分(2)方法一:直线PB1的斜率为,由所以直线QB1的斜率为.于是直线QB1的方程为:.同理,QB2的方程为:.……8分联立两直线方程,消去y,得.……10分因为在椭圆上,所以,从而.所以.……12分所以.……14分方法二:设直线PB1,PB2的斜率为k,,则直线PB1的方程为.由直线QB1的方程为.将代入,得,因为P是椭圆上异于点B1,B2的点,所以,从而. (8)分因为在椭圆上,所以,从而.所以,得.……10分由,所以直线的方程为.联立则,即.……12分所以.……14分18.(本小题满分16分)将一铁块高温融化后制成一张厚度忽略不计、面积为100dm2的矩形薄铁皮(如图),并沿虚线l1,l2裁剪成A,B,C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:方案①:以为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;方案②:以为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与或垂直)作为正四棱柱的两个底面.(1)设B,C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;(2)设的长为dm,则当为多少时,能使按方案②制成的正四棱柱的体积最大?解:(1)设所得圆柱的半径为dm,则,……4分解得.……6分(2)设所得正四棱柱的底面边长为dm,则即……9分方法一:所得正四棱柱的体积……11分记函数则在上单调递增,在上单调递减,所以当时,.所以当,时,dm3.……14分方法二:,从而.……11分所得正四棱柱的体积.所以当,时,dm3.……14分答:(1)圆柱的底面半径为dm;(2)当为时,能使按方案②制成的正四棱柱的体积最大.……16分【评分说明】①直接“由得,时正四棱柱的体积最大”给2分;②方法一中的求解过程要体现,凡写成的最多得5分,其它类似解答参照给分.19.(本小题满分16分)设等比数列a1,a2,a3,a4的公比为q,等差数列b1,b2,b3,b4的公差为d,且.记(i1,2,3,4).(1)求证:数列不是等差数列;(2)设,.若数列是等比数列,求b2关于d的函数关系式及其定义域;(3)数列能否为等比数列?并说明理由.解:(1)假设数列是等差数列,则,即.因为是等差数列,所以.从而.……2分又因为是等比数列,所以.所以,这与矛盾,从而假设不成立.所以数列不是等差数列.……4分(2)因为,,所以.因为,所以,即,……6分由,得,所以且.又,所以,定义域为.……8分(3)方法一:设c1,c2,c3,c4成等比数列,其公比为q1,则……10分将①+③-2×②得,将②+④-2×③得,……12分因为,,由⑤得,.由⑤⑥得,从而.……14分代入①得.再代入②,得,与矛盾.所以c1,c2,c3,c4不成等比数列.……16分方法二:假设数列是等比数列,则.……10分所以,即.两边同时减1得,.……12分因为等比数列a1,a2,a3,a4的公比为q,所以.又,所以,即.……14分这与且矛盾,所以假设不成立.所以数列不能为等比数列.……16分20.(本小题满分16分)设函数.(1)若函数是R上的单调增函数,求实数a的取值范围;(2)设,是的导函数.①若对任意的,求证:存在使;②若,求证:.解:(1)由题意,对恒成立,因为,所以对恒成立,因为,所以,从而.……3分(2)①,所以.若,则存在,使,不合题意,所以.……5分取,则.此时.所以存在,使.……8分②依题意,不妨设,令,则.由(1)知函数单调递增,所以.从而.……10分因为,所以,所以.所以.……12分下面证明,即证明,只要证明.设,所以在恒成立.所以在单调递减,故,从而得证.所以,即.……16分数学Ⅱ(附加题)21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)如图,A,B,C是⊙O上的3个不同的点,半径OA交弦BC于点D.求证:.证明:延长交⊙O于点E,则.……5分因为,所以.所以.……10分B.[选修4-2:矩阵与变换](本小题满分10分)在平面直角坐标系xOy中,已知.设变换,对应的矩阵分别为,,求对△ABC依次实施变换,后所得图形的面积.解:依题意,依次实施变换,所对应的矩阵.……5分则,,.所以分别变为点.从而所得图形的面积为.……10分C.[选修4-4:坐标系与参数方程](本小题满分10分)在极坐标系中,求以点为圆心且与直线:相切的圆的极坐标方程.解:以极点为原点,极轴为轴的非负半轴,建立平面直角坐标系.则点的直角坐标为.……2分将直线:的方程变形为:,化为普通方程得,.……5分所以到直线:的距离为:.故所求圆的普通方程为.……8分化为极坐标方程得,.……10分D.[选修4-5:不等式选讲](本小题满分10分)已知a,b,c为正实数,且,求证:.证明:因为a,b,c为正实数,所以(当且仅当取“=”).……10分【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的33表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.(2)求的概率分布及数学期望.解:(1)从33表格中随机不重复地点击3格,共有种不同情形.则事件:“”包含两类情形:第一类是3格各得奖200元;第二类是1格得奖300元,一格得奖200元,一格得奖100元,其中第一类包含种情形,第二类包含种情形.所以.……3分(2)X的所有可能值为300,400,500,600,700.则,,,.所以的概率分布列为:X300400500600700P……8分所以(元).……10分23.(本小题满分10分)已知…,.记.(2)化简的表达式,并证明:对任意的,都能被整除.解:由二项式定理,得(i0,1,2,…,2n+1).(1);……2分(2)因为,……4分所以.……8分.因为,所以能被整除.……10分。
