习题课时序逻辑电路分析
电工电子技术-时序逻辑电路的分析

最后还要检查一下得到的状态转换表是否包含Q1的组合状态共有8种,而根 据上述计算过程列出的状态转换表中缺少Q3Q2Q1=111这一状态, 将此状态代入状态方程和输出方程得
QQ32nn11
0 0
Q1n1 0
Y 1
将这一计算结果补充到表中后得完整的状态转换表。
【例15-3】试列出例15-2所示电路的状态转换表。
【解】由图可见,该电路无输入逻辑变量(注意:不要
把CP当作输入逻辑变量,因为它只是控制触发器状态转换的
操作信号),所以电路的次态和输出只取决于电路的初态。
设电路的初态为Q3Q2Q1=000,代入电路状态方程和输出方程
得
QQ32
n1 n1
0 0
Q1n1 1
(3)根据逻辑图写出输出方程为:
Y Q2Q3
2.描述时序电路状态转换全部过程的方法
(1)状态转换表 将任何一组输入变量及电路初态的取值代入状态方程和
输出方程,即可得出电路的次态和初态下的输出值;以得到 的次态作为新的初态,和这时的输入变量取值一起再代入状 态方程和输出方程进行计算,又得到一组新的次态和输出值。 如此继续下去,将所有的计算结果列成真值表的形式,即可 得到状态转换表。
时还进一步将状态转换表的内容表示成状态转换图的形式。 下图为图例15-2所示电路的状态转换图。在状态转换图
中以圆圈表示电路的各个状态,以箭头表示状态转换的方向。 同时,在箭头旁注明状态转换前的输入变量取值和输出值。 通常将输入变量取值写在斜线以上(无输入变量时无需标 注),输出值写在斜线以下。
Y Q2Q3
74LS161的功能表如下表所示:
【解】(1)由给定逻辑图写出电路的驱动方程为:
J J
1 2
第06章时序逻辑电路习题解

[题6.20]分析图P 6.20给出的电路,说明这是多少进制的计数器,两片之间是多少进制。 74LSl61的功能表见表6.3.4。
解:这是采用整体置数法接成的计数器。 在出现LD'=0信号以前,两片74LSl61均按十六进制计数。即第(1)片到第(2) 片为十六进制。当第(1)片计为2,第(2)片计为5时产生LD'=0信号,待下一个 CLK信号到达后两片74LSl61同时被置零,总的进制为 5 X 16+2+1=83 故为八十三进制计数器。
图A 6.12
[题6.13]试分析图P 6.13的计数器在M=1和M=0时各为几进制。
解:图P6.13电路是采用同步置数法用74160接成的可变进制计数器。在M=1的 状态下,当电路进入Q3Q2Q1Q0=1001(九)以后,LD'=0。下一个CLK到达时将 D3D2D1D0=0100(四)置入电路中,使Q3Q2Q1Q0=0100,再从0100继续作加 法计数。因此,电路在0100到1001这六个状态间循环,构成六进制计数器。同 理,在M=0的情况下,电路计到1001后置入0010(二),故形成八进制计数器。
[题6.6]分析图P 6.6给出的时序电路,画出电路的状态转换图,检查电路能否自启动,说 明电路实现的功能。A为输入变量。
解:由电路图写出驱动方程为 J1=K1=1 J2=K2=A Q1 将上述驱动方程代入JK触发器的特性方程,得到状态方程 Q1*=Q1' Q2*=A Q1 Q2 输出方程为 Y=AQ1Q2+A'Q1'Q2' 根据状态方程和输出方程画出的状态转换图如图A 6.6所示。因为不存在无效 状态,所以电路不存在自启动与否的问题。 当A=0时电路对CLK脉冲作二进制加法计数,A=1时作二进制减法计数。
5-2时序逻辑电路的分析

X=1 Z
X Q1n
n Q2 1Q1n1
Z
0 0 1 1
0 1 0 1
0 1 0 1
0 1 1 0
1 0 1 0
0 0 0 1
1 0 1 0
1 0 0 1
1 0 1 0
0 0 0 1
状态图
n Qn1Q1 1 / Z 2 X=0 X=1
0 0 0 1 1 0 1 1
n 2
n 1
X/Z Q2Q1 0/0 00 00
4. 确定和说明电路的逻辑功能
5.2.2 同步时序逻辑电路的分析举例1
先介绍相对简单的Moore型时序逻辑电路,再介绍相对复 杂的Mealy型时序逻辑电路
例1 试分析下图所示时序电路的逻辑功能。
解:由电路图可知,此为同步时序逻辑电路,无输入信号
所以,属Moore型 1.写出各触发器的驱动方程和输出方程。
D0 Q2 Q0
D1 Q1
n1
D 2= Q 0 Q 1
Q
Q
n 1 0 n 2 n 0
D
n 0
Q Q CP0 Q CP0
Q
n1 1
n1 2
Q CP1 Q CP1
n 1 n 1
n 1 n 0 n 2
Q
Q Q CP2 Q CP2
(3)列电路状态转换真值表
Y 输出方程: 1 Q1 , Y2 Q2
驱动方程:
1J >C1
Y1
Q1
1J >C1 1K
Y2
Q2
J1 Q2 , K1 1 J 2 Q1 , K2 1
CP
1K
5.2.2 同步时序逻辑电路的分析举例1
6.2 时序逻辑电路的分析

Y =A Q1Q0
(4) 画出状态图
Q1Q0
A/Y 0/0
1/1
1/0
0/0
11
1/0
10
0/0
重庆工学院
《数字电子技术》
(5) 画出时序图
CP
1
2
3
4
5
6
7
8
9 ①
1 0
n Q1n Qo
n Q1n1 Q0 1 / Y
A=0 00/0 01/0 10/0 11/0
A=1 01/0 10/0 11/0 00/1
重庆工学院
《数字电子技术》
例2 试分析如图所示时序电路的逻辑功能。
X 解:1.了解电路组成。 电路是由两个JK触发 “1” CP 器组成的同步时序电路。 1J Q1 =1 1J Q
>C1
1K FF1 Q1
>C1
1K FF2 Q & Y
2.写出下列各逻辑方程式:
激励方程 J1=K1=1
J2=K2=X Q1 输出方程 Y=Q2Q1
重庆工学院
《数字电子技术》
6.2.1 分析同步时序逻辑电路的一般步骤:
1. 了解电路的组成:
观察电路的输入、输出信号、触发器的类型等 2. 根据给定的时序电路图,写出下列各逻辑方程式:
(1)输出方程; (2)各触发器的激励方程;
(3)状态方程:将每个触发器的驱动方程代入其特
性方程得状态方程。 3. 列出状态转换表或画出状态图和波形图; 4. 确定电路的逻辑功能。
重庆工学院
《数字电子技术》
(3) 根据状态方程组和输出方程列出状态表
n Q0
1
n A Q0
n Q1n Qo
时序逻辑电路习题解答解读

自我测验题1.图T4.1所示为由或非门构成的基本SR锁存器,输入S、R的约束条件是。
A.SR=0B.SR=1C.S+R=0D.S+R=1QG22QRS图T4.1图T4.22.图T4.2所示为由与非门组成的基本SR锁存器,为使锁存器处于“置1”状态,其RS⋅应为。
A.RS⋅=.RS⋅=10D.RS⋅=113.SR锁存器电路如图T4.3所示,已知X、Y波形,判断Q的波形应为A、B、C、D 中的。
假定锁存器的初始状态为0。
XYXYABCD不定不定(a)(b)图T4.34.有一T触发器,在T=1时,加上时钟脉冲,则触发器。
A.保持原态B.置0C.置1D.翻转5.假设JK触发器的现态Q n=0,要求Q n+1=0,则应使。
A.J=×,K=0B.J=0,K=×C.J=1,K=×D.J=K=16.电路如图T4.6所示。
实现AQQ nn+=+1的电路是。
A AA AA .B .C .D .图T4.67.电路如图T4.7所示。
实现n n Q Q =+1的电路是 。
CPCPCPA .B .C .D .图T4.78.电路如图T4.8所示。
输出端Q 所得波形的频率为CP 信号二分频的电路为。
1A .B .C .D .图T4.89.将D 触发器改造成TTQ图T4.9A .或非门B .与非门C .异或门D .同或门 10.触发器异步输入端的作用是。
A .清0B .置1C .接收时钟脉冲D .清0或置1 11.米里型时序逻辑电路的输出是。
A .只与输入有关B.只与电路当前状态有关C.与输入和电路当前状态均有关D.与输入和电路当前状态均无关12.摩尔型时序逻辑电路的输出是。
A.只与输入有关B.只与电路当前状态有关C.与输入和电路当前状态均有关D.与输入和电路当前状态均无关13.用n只触发器组成计数器,其最大计数模为。
A.n B.2n C.n2D.2 n14.一个5位的二进制加计数器,由00000状态开始,经过75个时钟脉冲后,此计数器的状态为:A.01011B.01100C.01010D.00111图T4.1516.电路如图T4.16所示,假设电路中各触发器的当前状态Q2Q1Q0为100,请问在时钟作用下,触发器下一状态Q2 Q1 Q0为。
时序逻辑电路习题解答
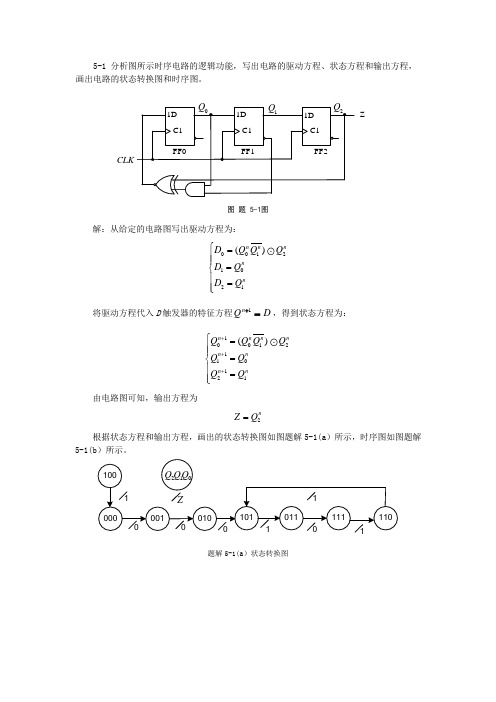
5-1 分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图。
CLKZ图 题 5-1图解:从给定的电路图写出驱动方程为:00121021()n n nn n D Q Q Q D Q D Q ⎧=⎪⎪=⎨⎪=⎪⎩将驱动方程代入D 触发器的特征方程D Qn =+1,得到状态方程为:10012110121()n n n n n n n n Q Q Q Q Q Q Q Q +++⎧=⎪⎪=⎨⎪=⎪⎩由电路图可知,输出方程为2nZ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-1(a )所示,时序图如图题解5-1(b )所示。
题解5-1(a )状态转换图1Q 2/Q ZQ题解5-1(b )时序图综上分析可知,该电路是一个四进制计数器。
5-2 分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
YA图 题 5-2图解:首先从电路图写出驱动方程为:()0110101()n n n n nD AQ D A Q Q A Q Q ⎧=⎪⎨==+⎪⎩将上式代入触发器的特征方程后得到状态方程()101110101()n n n n n n nQ AQ Q A Q Q A Q Q ++⎧=⎪⎨==+⎪⎩电路的输出方程为:01n nY AQ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-2所示YA题解5-2 状态转换图综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态“00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3 已知同步时序电路如图(a)所示,其输入波形如图 (b)所示。
试写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
X(a) 电路图1234CLK5678X(b)输入波形 图 题 5-3图解:电路的驱动方程、状态方程和输出方程分别为:00101100011011011, ,n n n n n n n n n nJ X K X J XQ K XQ X Q XQ XQ XQ Q XQ XQ XQ Y XQ ++⎧==⎪⎨==⎪⎩⎧=+=⎪⎨⎪=+=+⎩= 根据状态方程和输出方程,可分别做出1110,n n Q Q ++和Y 的卡诺图,如表5-1所示。
数字逻辑设计第6章 时序逻辑电路习题与解答
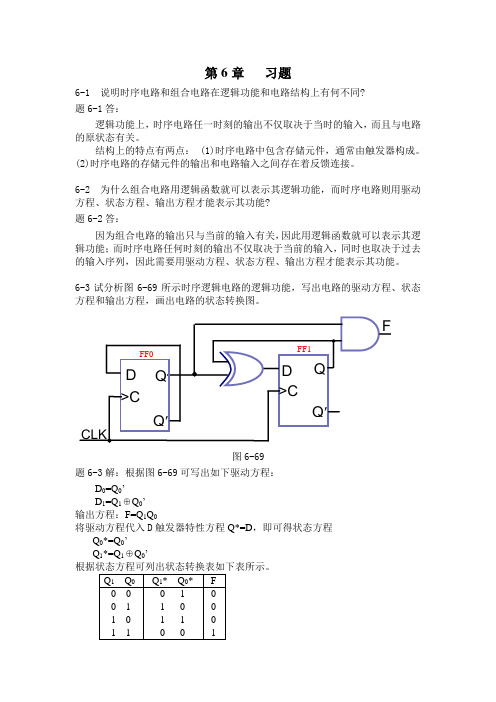
L’/C 为 1 时,装入无效,161 对输入的 CLK 进行计数。 L’/C 为 1 或为 O 时,装入有效,而装入值为 D3=Q2,D2=Q1,D1=Q0,D0=串 行输入数据,所以该电路的功能将数据左移,低位补的是串行输入数据。 6-11 试分析图 6-74 的计数器在 C=1 和 C=0 时各为几进制计数器?
第 6 章 习题
6-1 说明时序电路和组合电路在逻辑功能和电路结构上有何不同?
题 6-1 答:
逻辑功能上,时序电路任一时刻的输出不仅取决于当时的输入,而且与电路 的原状态有关。
结构上的特点有两点: (1)时序电路中包含存储元件,通常由触发器构成。 (2)时序电路的存储元件的输出和电路输入之间存在着反馈连接。
Q2Q1Q0
000
/0
/1
001
/0
010
/0
101
/0
100
/0
011
由状态转换图可画出 Q2Q1Q0 和输出 F 的状态卡诺图如下:
Q1Q0 Q2 00 01 11 10
00
0
10
Q1Q0
Q2
00
01 11 10
00
10
0 10
11 0 X X
(a)Q2 卡诺图
Q1Q0 Q2 00 01 11 10
6-3 试分析图 6-69 所示时序逻辑电路的逻辑功能,写出电路的驱动方程、状态 方程和输出方程,画出电路的状态转换图。
F
FF0
DQ >C 1 Q
CLK
FF1
DQ >C 1 Q
图 6-69
题 6-3 解:根据图 6-69 可写出如下驱动方程:
时序逻辑电路典型例题分析

第六章时序逻辑电路典型例题分析第一部分:例题剖析触发器分析例1在教材图6.1所示的基本RS触发器电路中,若⎺R、⎺S 的波形如图P6.1(a)和(b),试分别画出对应的Q和⎺Q端的波形。
解:基本RS触发器,当⎺R、⎺S同时为0时,输出端Q、⎺Q均为1,当⎺R=0、⎺S=1时,输出端Q为0、⎺Q为1,当⎺R=⎺S=1时,输出保持原态不变,当⎺R=1、⎺S=0时,输出端Q为1、⎺Q为0,根据给定的输入波形,输出端对应波形分别见答图P6.1(a)和(b)。
需要注意的是,图(a)中,当⎺R、⎺S同时由0(见图中t1)变为1时,输出端的状态分析时不好确定(见图中t2),图中用虚线表示。
例2 在教材图6.2.3(a)所示的门控RS触发器电路中,若输入S 、R和E的波形如图P6.2(a)和(b),试分别画出对应的输出Q和⎺Q端的波形。
解:门控RS触发器,当E=1时,实现基本RS触发器功能,即:R=0(⎺R=1)、S=1(⎺S=0),输出端Q为1、⎺Q为0;R=1(⎺R=0)、S=0(⎺S=1)输出端Q为0、⎺Q为1;当E=0时,输出保持原态不变。
输出端波形见答图P6.2。
例3在教材图6.2.5所示的D锁存器电路中,若输入D、E的波形如图P6.3(a)和(b)所示,试分别对应地画出输出Q和Q端的波形。
解:D锁存器,当E=1时,实现D锁存器功能,即:Q n+1=D,当E=0时,输出保持原态不变。
输出端波形见答图P6.3。
例4在图P6.4(a)所示的四个边沿触发器中,若已知CP、A、B的波形如图(b)所示,试对应画出其输出Q端的波形。
设触发器的初始状态均为0。
解:图中各电路为具有异步控制信号的边沿触发器。
图(a)为边沿D触发器,CP上升沿触发,Q1n+1= A,异步控制端S D接信号C(R D=0),当C=1时,触发器被异步置位,输出Q n+1=1 ;图(b)为边沿JK触发器,CP上升沿触发,Q2n+1= A⎺Q2n +⎺BQ2n,异步控制端⎺R D接信号C(⎺S D =1),当C=0时,触发器被异步复位,输出Q n+1=0;图(c)为边沿D触发器,CP下降沿触发,Q3n+1= A,异步控制端⎺S D接信号C(⎺R D =1),当C=0时,触发器被异步置位,输出Q n+1=1;图(d)为边沿JK触发器,CP下降沿触发,Q4n+1= A⎺Q4n +⎺BQ4n,异步控制端R D接信号C(S D =0),当C=1时,触发器被异步复位,输出Q n+1=0。
时序逻辑电路的分析方法

Z
1
1 1
0
1 1
1
0 1
0 1 0 1 1 0 1 0
0 1 0 1 1 0 1 0
0 1 1 0 1 0 0 1
1 0 1 0 1 0 1 0
J1 K1 X Q0
1 当现态Q0为0时,J0=K0=11 1 Q0n+1=/Qn 1 当现态Q1为0时,J1=K1=00 1 Q1n+1=Qn 0 0 Z X Q1 1 输出Z:当X=0,Z =1 1 当:X=1,Q1=0,Z=0
0 /1 1/ 0 假定计数器的初始状态Q1Q0=00 1/1 0 /1 外输入 X 的输入电平序列为111100001 3 1/1 2 每一个CP脉冲为一个节拍,共九个CP 0 /1 求时序电路的响应 将时序电路的状态以十进 制数表示,00→0,01→1 ② 利用状态转换图作出时序电 ,10→2 11→3,然后作 路响应序列,然后作时序图。 出响应序列。
★状态转换真值表反映时序电路输入、触发器现态与次态之间的关系。
3、列出电路状态转换表,画出状态转换图 什么是状态转换表? 以真值表的形式,表示电路的次态/输出(Q1n+1, Q0n+1/Z),与现态和输入(Q1Q0和X)之间的函数关系。 由状态转换真值表作出电路状态转换表: X Q Q Q Q Z a、列Q1Q0全部组合 0 0 0 0 1 1 b、顶部标注输入X的可能状态 0 0 1 1 0 1 现态00,输入为0,次态01,输出为1 0 1 0 1 1 1 现态00,输入为1,次态11,输出为0 0 1 1 0 0 1
1 0 n+1 1 0 n+1
1 1 1 1
0 0 1 1
时序逻辑电路习题解答

5-1分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图和时序图。
解:从给定的电路图写出驱动方程为:D o (Q 0Q i n)e Q 2D i Q 01D 2 Q i nQ 01 1(Q 0Q n)eQ ;Q i n 1Q 0Q 21Q ;由电路图可知,输出方程为Z Q ;CLK将驱动方程代入D 触发器的特征方程Q n 1D ,得到状态方程为:5-1(a )所示,时序图如图题解Z图题5-1图根据状态方程和输出方程,画出的状态转换图如图题解题解5-1(a )状态转换图综上分析可知,该电路是一个四进制计数器。
5-2分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
解:首先从电路图写出驱动方程为:D o A& D i A Qg :A (Q : Q i n)将上式代入触发器的特征方程后得到状态方程Q 0 1AQ :Q :1 AQ 0Q :A (Q nQ :)电路的输出方程为:CLKQ i12345——-A1 11 t----------- 1------------ 1|| 1 » 1 1 1----------- 1 ---------- 1 --------------►CLK0 Q 2/Z 仝题解5-1(b )时序图0 Q o 胃AY图题5-2图丫AQoQ;根据状态方程和输出方程,画出的状态转换图如图题解5-2 所示综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态" 00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3已知同步时序电路如图(a )所示,其输入波形如图 (b )所示。
试写出电路的驱动方 程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
CLK 1 2345678(b )输入波形 图题5-3图解:电路的驱动方程、状态方程和输出方程分别为:J 。
时序逻辑电路例题分析

QA JA QAKA
计数脉冲CP
(7) 检验该计数电路能否自动启动。
本计数电路有三个触发器,可有八个状态组合,可是 只用去六个,尚有两 个未利用,因此需要检验一下, 若不能自行启动要进行修改。
例2 试用主从JK触发器设计一个时序电路,要求该电路的输入Z 与CP之间的关系应满足图示的的波形图。
解:由波形图可以看出这是一个三进制的计数器。
Q1
C1
C1
CP
Q0
Q1
解:输出方程: Y
=
n
X Q1
=
X
Q1n
驱动方程:T0 = 1 T1 = X Q0n
状态方程: Q1n1 = T1 Q1n = X Q0n Q1n Q0n = T0 Q0n = 1 Q0n = Q0n
状态表:
输入
Q1n1 = X Q0n Q1n
X
Q0n = Q0n
0
Y = X Q1n
0 0
QQ10nn=1
= 1
11 =0
1
=
1
0 1 1
Y = 11=1
1
1
现态
Q1n Q0n
00 01 10 11 00 01 10 11
次 态 输出
Q Q n1 n1 10
Y
01
1
10
1
11
1
00
1
11
0
00
0
01
1
10
1
0/1
画
00
01 CP
状 态 图
0/0
X
0/1 1/0 1/1 0/1 Q0
74LS161
CO 1
LD
CR
D0 D1 D2 D3
5.2时序逻辑电路分析

4. 计算状态转换表
Q Q Q3n Q2n Q1n
Q n1
3
n1 2
n1 1
Y
0
0
00
0
1
0
0
0
10
1
0
0
0
1
00
1
1
0
0
1
11
0
0
0
1
0
01
0
1
0
1
0
11
1
0
0
1
1
00
0
0
1
1
1
10
0
0
1
Q n1 1
Q2
Q3
Q1
Y=Q2Q3
Q n1 2
Q1
Q2
Q1
Q3
Q2
Q n1 3
Q1
Q2
Q3
Q2Q3
5. 画状态转换图
Q Q Q3n Q2n Q1n
Q n1 n1 n1 Y
321
0
0
00
0
1
0
0
0
10
1
0
0
0
1
00
1
1
0
0
1
11
0
0
0
1
0
01
0
1
0
1
0
11
1
0
0
1
1
00
0
0
1
1
1
10
0
0
1
CP Q3 Q2 Q1 Y
00000 10010 20100 30110
41000 51010 61101
时序逻辑电路分析举例

时序逻辑电路分析例题解:1、列出驱动方程:丿严K严1J2= K2= AQ{+A Q2、列出状态方程:将驱动方程代入JK触发器的特性方程。
=JQ1 + K'Q得: Q\ = Q\Q; = AQ[Q!2 + + A0Q3、列出输出方程:Y = AQ;Q^A,Q.Q24、列出状态转换表:(1)当A二1 时:根据:Q;=Q(; O;=a@+QQ;= Q[Qi得:(2)当A二0 时:根据:e;=Q[;6、说明电路实现的逻辑功能:此电路是一个可逆4进制(二位二进制)计数器,CLK是计数脉冲输入端,A 是加减控制端,Y是进位和借位输出端。
当控制输入端A为低电平0时,对输入的脉冲进行加法计数,计满4个脉冲,Y输出端输出一个高电平进位信号。
当控制输入端A为高电平1时,对输入的脉冲进行减法计数,计满4个脉冲,Y输岀端输出一个高电平借位信号。
2、如图所示时序逻辑电路,试写出驱动方程、状态方程,画出状态图,说明该电路的功能。
解:驱动方程J.=X®Q^{J,=X ㊉Q;;A=I k=i状态方程er* =(X ㊉0 広"=XQ;'Q'^ + XQ;l Q;;Q;r =(X ㊉Q;'= XQ;'Q;; + XQ;Q;;输出方程Z = (x㊉0也1、状态转换表,如表所示。
状态转换图,略。
2、这是一个3进制加减讣数器,当X二0时为加计数器,计满后通过Z向高位进位;X二1时为减计数器,计满后通过Z向高位借位;能自启动。
例30),要求(1)画出状态转换图。
(2)画出时序图。
(3)说明是多少进制计数器。
答:(1)(2)时序图4、分析下图所示时序逻辑电路,写出电路的驱动方程、状态方程和输出方程, 画岀电路的状态转换图,说明电路实现的的逻辑功能。
A为输入变量。
解:(1)列写方程驱动方程:触发器的驱动方程为:D、= Q[ D2 = A㊉© ㊉Q2(2)列写方程驱动方程:触发器的特性方程为:Q"=D将驱动方程代入特性方程可得状态方程为:CLK-CPQ = D = Q{Q; = 2 = A ㊉© ㊉Q(3)列写输出方程:Y = A(Q i Q2+AQ;Q,2(4)列出状态转换表:当A二1时:根据:Q; =Q;; 0;= 00+00;Y = Q\Q1得:当A=0时:根据:Q: = Q;;Y = 得:(5)画状态转换图:(6)说明电路实现的逻辑功能:(2分)此电路是一个可逆4进制计数器,CLK是计数脉冲输入端,A是加减控制端,Y 是进位和借位输出端。
时序逻辑电路 课后答案
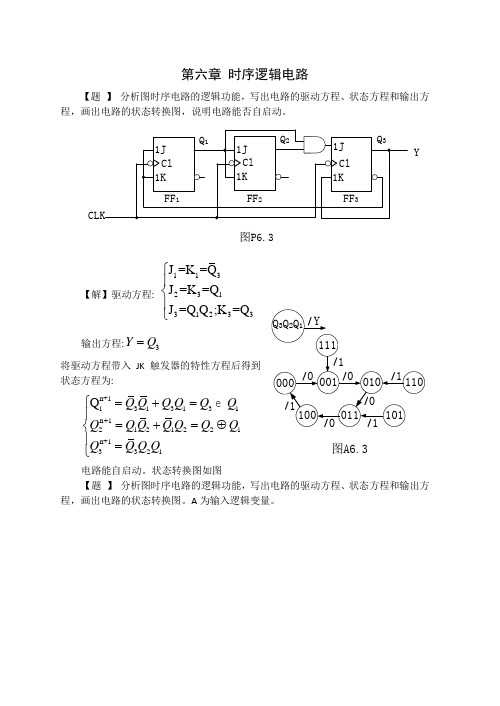
第六章 时序逻辑电路【题 】 分析图时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩e 电路能自启动。
状态转换图如图【题 】分析图时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQQ A Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图1图A6.5【题 】 分析图时序电路的逻辑功能,画出电路的状态转换图,检查电路能否自启动,说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212Q Q Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图。
A =0时作二进制加法计数,A =1时作二进制减法计数。
01图A6.6【题 】 分析图时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=•=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000,由状态方程可得:状态转换图如图。
5.3时序逻辑电路的分析
列表有两种方法: 列表有两种方法:
画状态图和时序图
CP
Q2Q1
00 01
Q1
Q2
10 4. 由状态图和时序图可确定: 由状态图和时序图可确定: 该时序电路为同步三进制计数器。 该时序电路为同步三进制计数器。 同步三进制计数器
试分析下图所示时序电路的逻辑功能。 例2 试分析下图所示时序电路的逻辑功能。 解:由电路图可知,此为同步时序逻辑电路,有输入信号X 由电路图可知,此为同步时序逻辑电路,有输入信号 所以, 所以,属Mealy型 型 1.写出各触发器的驱动方程和输出方程。 写出各触发器的驱动方程和输出方程。 写出各触发器的驱动方程和输出方程
n Y = Q2 Q1n 输出方程: 输出方程:
驱动方程: 驱动方程:
J 1 = K1 = 1
1
X
J1 Q1
>C1
=1 & J2 Q2
>C1
Y
J 2 = K2 = X ⊕ Q
n 1
CP
K1
K2
2.将驱动方程代入特性方程,求得次态方程。 将驱动方程代入特性方程,求得次态方程 将驱动方程代入特性方程
J 1 = K1 = 1
/0
11 /1
/0
10
1
Z
(4) 分析逻辑功能分析 分析逻辑功能分析
CP Q0 Q1 Z
00 /0 01
/0
11 /1
/0
10
由状态图和时序图可知,此电路是一个: 异步四进制减法计数器。 异步四进制减法计数器 序列信号发生器。输出序列脉冲信号Z的重复周期 序列信号发生器 为4TCP,脉宽为1TCP。
例题
试分析下图所示时序电路的逻辑功能。 例1 试分析下图所示时序电路的逻辑功能。 解:由电路图可知,此为同步时序逻辑电路,无输入信号 由电路图可知,此为同步时序逻辑电路, 所以, 所以,属Moore型 型 1.写出各触发器的驱动方程和输出方程。 写出各触发器的驱动方程和输出方程。 写出各触发器的驱动方程和输出方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 课
例题一
画出图1 所示电路的状态图和时序图(设初始状态为00,X为输 入控制信号,可分别分析X=0和X=1时的情况)。
2013-8-3
时序电路
2
例题二
画出图2 所示电路的状态图,简要说明电路的功能特点。
2013-8-3
时序电路
3
例题三
分析图3 所示电路的逻辑功能。
2013-8-3
图6 (a)(b) 所示电路的计数长度N是多少?能否自启动?
图6 (a)
2013-8-3
时序电路
9
图6 (b)
2013-8-3
时序电路 10
认 真 复 习
迎 接 考 试
数 字 电 路
2013-8-3 时序电路 11
时序电路
4
例题四
画出图3(a)电路中B、C端的波形。输入端A、CP波形如图(b) 所示,触发器起始状态为零状态。2013-8-3Fra bibliotek时序电路5
2013-8-3
时序电路
6
例题五
分析图5(a) (b)所示电路的逻辑功能。
图5(a)
2013-8-3
时序电路
7
图5 (b)
2013-8-3
时序电路
8
例题六
