理论力学试题及问题详解
理论力学试题及问题详解

理论力学试题与答案一、是非题〔每题2分。
正确用√,错误用×,填入括号内。
〕1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,如此此力系必然平衡。
〔〕2、力对于一点的矩不因力沿其作用线移动而改变。
〔〕3、在自然坐标系中,如果速度υ = 常数,如此加速度α = 0。
〔〕4、虚位移是偶想的,极微小的位移,它与时间,主动力以与运动的初始条件无关。
〔〕5、设一质点的质量为m,其速度 与x轴的夹角为α,如此其动量在x轴上的投影为mv x=mvcos a。
〔〕二、选择题〔每题3分。
请将答案的序号填入划线内。
〕1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时〔如图〕,圆柱处于极限平衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A = N B;②N A > N B;③N A < N B。
3、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,假如给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是。
①半径为L/2的圆弧; ②抛物线; ③椭圆曲线; ④铅垂直线。
4、在图示机构中,杆O 1 A //O 2 B ,杆O 2 C //O 3 D ,且O 1 A = 20cm ,O 2 C = 40cm ,CM = MD = 30cm ,假如杆AO 1 以角速度 ω = 3 rad / s 匀速转动,如此D 点的速度的大小为cm/s ,M 点的加速度的大小为cm/s 2。
① 60; ②120; ③150; ④360。
5、曲柄OA 以匀角速度转动,当系统运动到图示位置〔OA//O 1 B 。
AB |OA 〕时,有A V B V ,A αB α,ωAB 0,εAB 0。
理论力学试题库及答案(通用篇)

理论力学试题库及答案(通用篇)一、理论力学试题库(通用篇)试题一:已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3,y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二:一质点沿圆周运动,其半径为 r,角速度为ω,角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三:一质点从静止开始沿直线运动,受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六:一质点在重力作用下做自由落体运动,求质点在任意时刻 t 的速度和位移。
试题七:一质点在水平地面上受到一斜向上的拉力F,拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十:一质点在水平地面上受到一恒力 F 的作用,力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一:t = 2s 时,速度 v = (4t, 8t - 1) = (8, 15) m/s;加速度 a = (8, 8) m/s²。
答案二:质点在任意时刻 t 的速度v = (rω, 0),加速度a = (0, rα)。
答案三:质点在任意时刻 t 的速度 v = (F/m)t,位移 s = (F/m)t²/2。
答案四:质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt)),加速度 a = (-rω²sin(ωt), rω²cos(ωt))。
理论力学大一试题及答案

理论力学大一试题及答案一、选择题(每题5分,共20分)1. 牛顿第一定律描述的是:A. 物体在没有外力作用下将保持静止或匀速直线运动B. 物体在受到外力作用下将改变其运动状态C. 物体在受到外力作用下将保持匀速直线运动D. 物体在受到外力作用下将保持静止答案:A2. 根据动量守恒定律,以下说法正确的是:A. 系统内所有物体的动量之和在没有外力作用下保持不变B. 系统内所有物体的动量之和在有外力作用下保持不变C. 系统内所有物体的动量之和在有外力作用下将增加D. 系统内所有物体的动量之和在有外力作用下将减少答案:A3. 角动量守恒的条件是:A. 系统不受外力矩B. 系统受外力矩C. 系统内力矩之和为零D. 系统内力矩之和不为零答案:A4. 以下哪项不是能量守恒定律的表述:A. 能量既不能被创造,也不能被消灭B. 能量可以以多种形式存在C. 能量可以以多种形式相互转化D. 能量在转化过程中总量会增加答案:D二、填空题(每题5分,共20分)1. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成________。
答案:反比2. 一个物体在水平面上以初速度v0运动,受到大小为F的恒定摩擦力作用,其加速度为a=________。
答案:-F/m3. 一个质量为m的物体从高度h自由下落,其下落过程中的重力势能变化量为________。
答案:-mgh4. 根据动能定理,一个物体的动能变化量等于外力对物体做的功,即ΔK=________。
答案:W三、计算题(每题15分,共30分)1. 一个质量为2kg的物体从静止开始,受到一个大小为10N的水平拉力作用,求物体在5秒内的位移。
解:根据牛顿第二定律,F=ma,得a=F/m=10/2=5m/s²。
根据位移公式s=1/2at²,得s=1/2*5*5²=62.5m。
答案:62.5m2. 一个质量为5kg的物体从高度10m自由下落,求物体落地时的速度。
理论力学考试题及答案详解

理论力学考试题及答案详解一、选择题(每题2分,共10分)1. 牛顿第一定律又称为惯性定律,它指出:A. 物体在受力时,会改变运动状态B. 物体在不受力时,会保持静止或匀速直线运动C. 物体在受力时,会做圆周运动D. 物体在受力时,会保持原运动状态答案:B2. 根据胡克定律,弹簧的弹力与弹簧的形变量成正比,比例系数称为:A. 弹性系数B. 刚度系数C. 硬度系数D. 柔度系数答案:A3. 在理论力学中,一个系统动量守恒的条件是:A. 系统外力为零B. 系统外力和内力都为零C. 系统外力和内力之和为零D. 系统外力和内力之差为零答案:C4. 一个物体做自由落体运动,其加速度为:A. 0B. g(重力加速度)C. -gD. 取决于物体的质量答案:B5. 刚体的转动惯量与以下哪个因素无关?A. 质量B. 质量分布C. 旋转轴的位置D. 物体的形状答案:A二、填空题(每空2分,共10分)6. 一个物体受到三个共点力平衡,如果撤去其中两个力,而保持第三个力不变,物体的加速度将________。
答案:等于撤去的两个力的合力除以物体质量7. 根据动能定理,一个物体的动能等于工作力与物体位移的________。
答案:标量乘积8. 在光滑水平面上,两个冰球相互碰撞后,它们的总动能将________。
答案:守恒9. 一个物体在水平面上做匀速圆周运动,其向心力的方向始终________。
答案:指向圆心10. 刚体的角速度与角动量的关系是________。
答案:成正比三、简答题(共20分)11. 什么是达朗贝尔原理?请简述其在解决动力学问题中的应用。
答案:达朗贝尔原理是分析动力学问题的一种方法,它基于牛顿第二定律,用于处理作用在静止或匀速直线运动的物体上的力系。
在应用达朗贝尔原理时,可以将物体视为受力平衡的状态,即使物体实际上是在加速运动。
通过引入惯性力的概念,可以将动力学问题转化为静力学问题来求解。
12. 描述一下什么是科里奥利力,并解释它在地球上的表现。
(完整版)理论力学习题集册答案解析
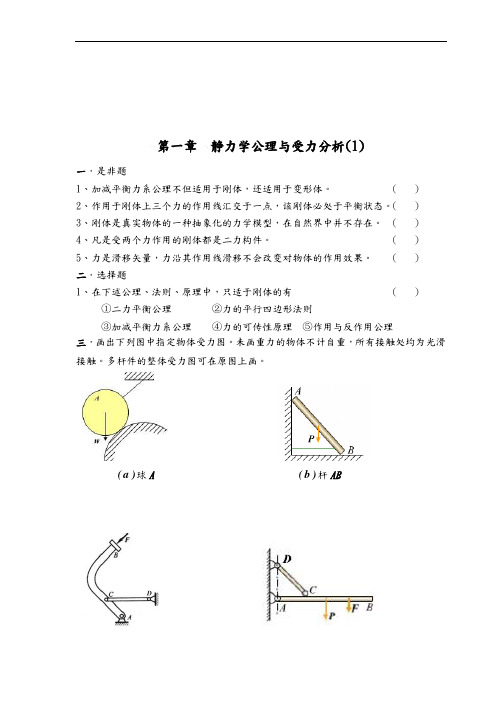
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆AB)a(球A )d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体 )b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学考试试卷(附答案)

理论力学考试试卷(附答案)一、 名词解释(每个4分,共20分)1、刚化原理2、加减平衡力系公理3、相对运动、牵连运动4、质点系动量守恒定理5、质点系动能定理二、 单项选择题(每个4分,共20分)1、已知F1、F2、F3、F4为作用于刚体上A 、B 、C 、D 四点的平面一般力系,其力矢关系如下图所示为平行四边形,由此可知 ( )。
2(A )力系可以合成为一个力偶 (B )力系可以合成为一个力(C )力系可以合成为一个力和一个力偶 (D )力系的合力为零,力系平衡2、物块重P ,与水面的摩擦角o20m ϕ=,其上作用一力Q ,且已知P=Q ,方向如图,则物块的状态为( )。
(A )静止(非临界平衡状态) (B )临界平衡状态(C )滑动状态 (D )不能确定 3、图(a )、(b)为两种结构,那么( )。
(A )图(a )为静不定,图(b )为静定 (B )图(a )、(b )均为静不定 (C )图(a )、(b )均为静定 (D )图(a )为静定,图(b )为静不定4、点作匀变速曲线运动是指( )。
(A )点的加速度大小a =常量 (B )点的加速度a =常矢量(C )点的切向加速度大小τa =常量 (D )点的法向加速度大小na =常量5、边长为a 2的正方形匀质薄板,截去四分之一后悬挂在A 点,今若使BC 边保持水平,则点A 距右端的距离x= ( )。
(A) a (B) 3a /2 (C) 6a /7 (D)5a /6三、计算题(15分)结构的尺寸及荷载如下图所示,已知q=1.5kN/m ,试求支座A 的反力。
(a)(b)a aaaxBAC四、计算题(15分)已知P=5kN ,试求图示桁架中1、2、3杆的内力。
五、计算题(15分)在图示机构中,已知m r B O A O 4.021===,AB O O =21,A O 1杆的角速度4rad s ω=,角加速度22rad s α=,求三角板C 点的加速度,并画出其方向。
理论力学习题及解答1
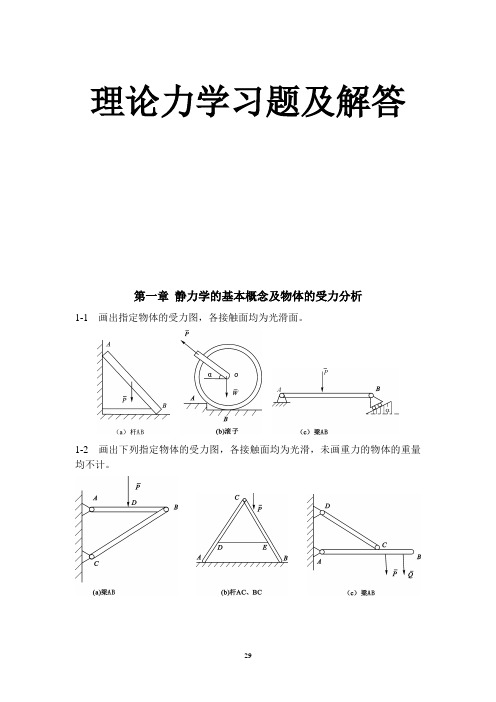
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
理论力学试题及答案

理论力学试题及答案1. 题目:速度与加速度的关系问题:在理论力学中,速度和加速度之间存在着怎样的关系?解答:速度和加速度是物体运动过程中的两个重要物理量,它们之间存在一定的数学关系。
根据牛顿第二定律,物体的加速度等于物体所受合外力的大小与物体的质量之比。
即:a = F/m其中,a表示物体的加速度,F表示物体所受的合外力,m表示物体的质量。
在一维直线运动的情况下,物体的速度和加速度之间的关系可以通过对速度对时间的导数来表示:a = dv/dt其中,a表示物体的加速度,v表示物体的速度,t表示时间。
综上所述,速度和加速度之间的关系可以用以下公式表示:a = dv/dt = F/m这表明,速度和加速度的关系由物体所受合外力和物体的质量共同决定。
2. 题目:牛顿的三大定律问题:简要介绍牛顿的三大定律。
解答:牛顿的三大定律是经典力学的基础,它们描述了物体运动的原理和规律。
第一定律,也被称为惯性定律,表明如果物体受到的合外力为零,则物体将保持静止或匀速直线运动状态。
换句话说,物体的速度只有在受到外力作用时才会改变。
第二定律,也被称为运动定律,表明物体的加速度与物体所受的合外力成正比,与物体的质量成反比。
即 F = ma,其中F表示物体所受的合外力,m表示物体的质量,a表示物体的加速度。
第三定律,也被称为作用-反作用定律,表明任何两个物体之间都存在相互作用力,且作用力和反作用力在大小上相等、方向上相反。
换句话说,所有力都是成对出现的,并且它们互相抵消。
这些定律为解释物体运动和相互作用提供了基本原理,广泛适用于各种力学问题的分析和解决。
3. 题目:动能与势能的转化问题:动能和势能之间如何相互转化?解答:在物体的运动过程中,动能和势能可以相互转化。
动能是物体由于运动而具有的能量,而势能是物体由于位置而具有的能量。
当物体在运动过程中加速度不变时,动能和势能之间可以通过以下公式相互转化:动能(K)= 1/2 mv^2势能(PE)= mgh其中,m表示物体的质量,v表示物体的速度,g表示重力加速度,h表示物体所处的高度。
理论力学试卷及答案解析

2
学号_________________________ 姓名_________________________ 专业班级__________________________
五、(10 分)如图,曲柄 OA=r,以角速度 4rad s 绕 O 轴转动。 O1C // O2D ,O1C=O2D
=r,求杆 O1C 的角速度。
2
G20
FCD 4
2kN 5.66kN (4 分)
n
Fix 0
i 1
FAx FCD cos 45 G 0 FAx 14 kN (4 分)
5
D
P
YB
n
Fiy 0
FAy FCD sin 45 G 0
FAy 6 kN (4 分)
XB
B
i 1
C
三、(16 分)解:研究杆 CBD,画受力图(2 分),列方程
n
m Az (Fi ) 0
i 1
FBx AB FDX AD 0
(2 分) 对象:DE 杆,受力如图示(2 分)
YA
Q
XA A mA
得 FDx 0
Y’B X’B
B
6
n
Fix 0
i 1
FDx FFx 0
n
mDz (Fi ) 0
i 1
M FFy DF 0
n
Fiy 0
i 1
A
O
C
B
1m
3m
4
课程名称:理论力学( A 卷) 一、(10 分)
销 C 与刚架 AC 一起作为研究对象(2 分) 销 C 与哪边刚架一起作为研究对象, 集中载荷 P 就画在哪边刚架的铰 C 上。 销 C 与刚架 CB 一起作为研究对象(2 分) 专门分析销 C 的受力(4 分) 整体受力图(2 分)
理论力学期末精彩试题及问题详解

一、填空题(共15分,共 5题,每题3 分)1. 如图所示的悬臂梁结构,在图中受力情况下,固定端A处的约束反力为:M A = ;F Ax = ;F Ay = 。
2. 已知正方形板ABCD作定轴转动,转轴垂直于板面,A点的速度v A=10cm/s,加速度a A=2,方向如图所示。
则正方形板的角加速度的大小为。
AA BD题1图题2图3. 图示滚压机构中,曲柄OA = r,以匀角速度绕垂直于图面的O轴转动,半径为R的轮子沿水平面作纯滚动,轮子中心B与O轴位于同一水平线上。
则有ωAB = ,ωB = 。
4. 如图所示,已知圆环的半径为R,弹簧的刚度系数为k,弹簧的原长为R。
弹簧的一端与圆环上的O点铰接,当弹簧从A端移动到B端时弹簧所做的功为;当弹簧从A端移动到C端时弹簧所做的功为。
o BC题3图题4图5. 质点的达朗贝尔原理是指:作用在质点上的、和在形式上组成平衡力系。
二、选择题(共20分,共 5 题,每题4 分) 1. 图示机构中,已知均质杆AB 的质量为m ,且O 1A =O 2B =r ,O 1O 2=AB =l ,O 1O =OO 2=l /2,若曲柄转动的角速度为ω,则杆对O 轴的动量矩L O 的大小为( )。
A. L O = mr 2ω B. L O = 2mr 2ωC. L O = 12mr 2ω D. L O = 02. 质点系动量守恒的条件是:( )A. 作用于质点系上外力冲量和恒为零B. 作用于质点系的内力矢量和为零C. 作用于质点系上外力的矢量和为零D. 作用于质点系内力冲量和为零3. 将质量为m 的质点,以速度 v 铅直上抛,试计算质点从开始上抛至再回到原处的过程中质点动量的改变量:( ) A. 质点动量没有改变B. 质点动量的改变量大小为 2m v ,方向铅垂向上C. 质点动量的改变量大小为 2m v ,方向铅垂向下D. 质点动量的改变量大小为 m v ,方向铅垂向下4. 图示的桁架结构,铰链D 处作用一外力F ,下列哪组杆的内力均为零? ( ) A. 杆CG 与杆GF B. 杆BC 与杆BG C. 杆BG 与杆BF D. 杆EF 与杆AF5. 如图所示,已知均质光球重为Q ,由无重杆支撑,靠在重为P 的物块M 上。
理论力学题库及答案详解

理论力学题库及答案详解一、选择题1. 在经典力学中,牛顿第一定律描述的是:A. 物体在没有外力作用下,将保持静止或匀速直线运动状态B. 物体在受到外力作用时,其加速度与所受合力成正比,与物体质量成反比C. 物体的动量守恒D. 物体的角动量守恒答案:A2. 以下哪一项不是牛顿运动定律的内容?A. 惯性定律B. 力的作用与反作用定律C. 动量守恒定律D. 力的独立作用定律答案:C二、填空题1. 根据牛顿第二定律,物体的加速度 \( a \) 与作用力 \( F \) 和物体质量 \( m \) 的关系是 \( a = \frac{F}{m} \)。
2. 一个物体在水平面上以初速度 \( v_0 \) 滑行,摩擦力 \( f \) 与其质量 \( m \) 和加速度 \( a \) 的关系是 \( f = m \cdot a \)。
三、简答题1. 简述牛顿第三定律的内容及其在实际问题中的应用。
答案:牛顿第三定律,也称为作用与反作用定律,指出作用力和反作用力总是成对出现,大小相等、方向相反,作用在两个不同的物体上。
在实际问题中,如火箭发射时,火箭向下喷射气体产生向上的推力,这是作用力;而气体向下的反作用力则推动火箭向上运动。
2. 解释什么是刚体的转动惯量,并给出计算公式。
答案:刚体的转动惯量是描述刚体绕某一轴旋转时惯性大小的物理量,其计算公式为 \( I = \sum m_i r_i^2 \),其中 \( m_i \) 是刚体各质点的质量,\( r_i \) 是各质点到旋转轴的垂直距离。
四、计算题1. 一个质量为 \( m \) 的物体在水平面上以初速度 \( v_0 \) 滑行,受到一个大小为 \( \mu mg \) 的摩擦力作用,求物体滑行的距离\( s \)。
答案:首先应用牛顿第二定律 \( F = ma \),得到 \( \mu mg = ma \)。
解得加速度 \( a = \mu g \)。
《理论力学》章节典型例题(含详解)—精品文档
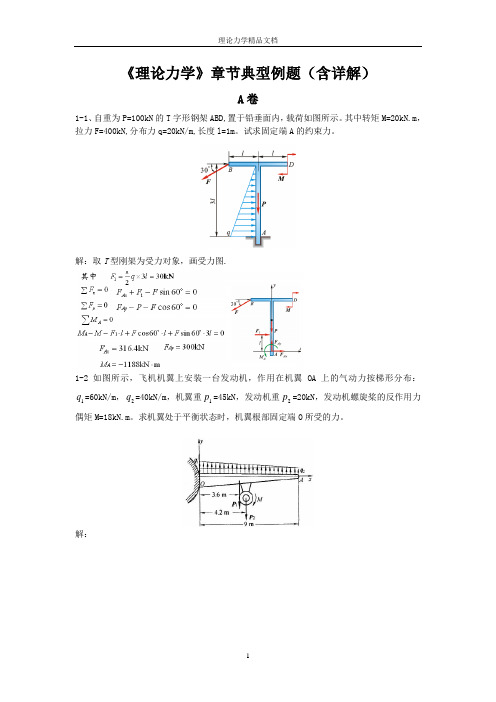
《理论力学》章节典型例题(含详解)A 卷1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的内力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不计,作用力D求各杆的内力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
(完整word版)理论力学历年试卷讲解
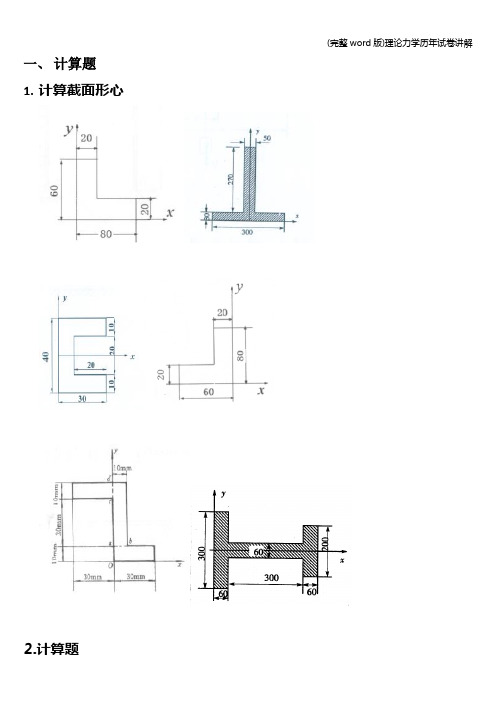
一、计算题1.计算截面形心2.计算题1)如图0230,100,30G N T N α===。
物块与固定面的摩檫系数0.5s f =,问物块处于何种状态?摩檫力F 为多少?2)物体A 重10G N =,放在粗糙的水平固定面上,它与固定面之间的静摩擦因数0.2s f =,动摩擦系数0.18d f =。
今在该物体上施加6F N =的力,030α=,试判断物体A处于何种状态?并求作用在物体上的摩擦力。
3)一物块重N G 200=,现有一水平力N F N 900=作用于该物快并使物块贴于墙上,已知物块与墙之间的摩擦系数2.0=S f ,18.0=d f 。
问物块处于何种状态?摩擦力F 为多少?4)用绳拉一重475N 的物体,拉力150T F N =。
若静摩擦因数0.4s f =,试判断该物体处于何种状态及此时摩擦力的大小? 略)解:设物块静止,此时的支反力为N F 摩擦力为f F (图此时有,0,cos300x Tf F F F =-=∑即需要NF FαAT W30°03cos30150129.92f T F F N ==⨯=的摩擦力,方能使物块静止 而所能提供的最大静摩擦力为max f s N F f F =由平衡方程000,sin 300sin 3047575400yT N N T FW F F F W F N=-++==-=-=∑解出故:max 0.4400160129.9f s N fF f F N F N ==⨯=>=所以,物块静止,摩擦力为129.9f F N =5)钟摆简化如图所示。
已知均质细长杆和均质圆盘的质量分别为1m 和2m ,杆长为l ,圆盘直径为d 。
求钟摆对于通过悬挂点O 的水平轴的转动惯量和动量矩。
6)带传动机构如图所示。
已知带轮及胶带都是均质的,胶带质量为m ,带轮质量均为1m ,带轮半径为r ,带轮1O 转动的角速度为ω。
求带传动系统的动量及系统的动能。
7)已知一质量为m 、半径为r 的均质圆轮在水平面上作纯滚动,质心C 的速度为v 。
《理论力学》考试试题解答解析

z
C
E
D
F
O
30°
By
A
x
2012~2013 学年第一学期《理论力学》考试试题及解答
2、圆盘以匀角速度ω 绕定轴 O 转动,如图所示,盘上动点 M 在半 径为 R 的圆槽内以速度 v 相对圆盘作等速圆周运动,以圆盘为动系, 求点 M 的科氏加速度。
M v
ω R
O
2012~2013 学年第一学期《理论力学》考试试题及解答
l2 R2
R l2 R2
轮
aB R
r 2
l2 R2
2011~2012 学年第二学期《理论力学》考试试题及解答
五、如图所示两均质圆轮质量均为 m ,半径为 R ,A 轮绕固定轴 O
转动,B 轮在倾角为θ 的斜面上作纯滚动,B 轮中心的绳绕到 A 轮
上。若 A 轮上作用一力偶矩为 M 的力偶,忽略绳子的质量和轴承
《理论力学》考试试题 及解答
2012~2013 学年第一学期《理论力学》考试试题及解答
一、简单计算题(每题5分,共15分) 1、正三棱柱的底面为等腰三角形,OA=OB=a,在平面ABED内
有一沿对角线AE作用的力F,F与AB边的夹角θ=30º,大小为F。 求该力在x、y、z 轴上的投影及对y、z 轴的矩。
五、图示纯滚动的均质圆轮与物块 A 的质量均为 m ,圆轮半径为 r , 斜面倾角为θ,物块 A 与斜面间的摩擦系数为 f 。 杆 OA 与斜面平 行,不计杆的质量。试求:⑴ 物块 A 的加速度;⑵ 圆轮所受的摩 擦力;⑶ 杆 OA 所受的力。(20分)
A
O
θ
2012~2013 学年第一学期《理论力学》考试试题及解答
A
D
u O
理论力学考研试题分析及答案

理论力学考研试题分析及答案试题:一、选择题(每题3分,共30分)1. 在经典力学中,牛顿第一定律又称为()A. 惯性定律B. 作用力与反作用力定律C. 力与加速度定律D. 能量守恒定律2. 一个物体的质量为2kg,受到的合外力为10N,根据牛顿第二定律,该物体的加速度为()A. 5 m/s²B. 10 m/s²C. 20 m/s²D. 50 m/s²3. 一个质点在水平面上做匀速圆周运动,其向心力的方向是()A. 指向圆心B. 指向圆外C. 沿着切线方向D. 沿着半径方向4. 根据能量守恒定律,一个物体在只有重力做功的情况下,其()A. 动能保持不变B. 机械能保持不变C. 势能保持不变D. 总能量保持不变5. 两个物体组成的系统,如果系统内力远大于外力,则系统的()A. 动量守恒B. 能量守恒C. 角动量守恒D. 质量守恒6. 一个物体从静止开始自由下落,下落时间为t秒,其位移与时间的关系为()A. s = 1/2 gtB. s = gtC. s = 1/2 gt²D. s = 2gt²7. 在光滑水平面上,一个物体受到一个恒定的水平力F作用,该物体将做()A. 匀速直线运动B. 匀加速直线运动C. 匀减速直线运动D. 变加速直线运动8. 一个物体在竖直平面内做圆周运动,到达最高点时,其速度至少为()A. 零B. 根号(gR)C. 根号(2gR)D. 无法确定9. 根据牛顿第三定律,两个相互作用的物体间的力()A. 大小相等,方向相反B. 大小不等,方向相反C. 大小相等,方向相同D. 大小不等,方向相同10. 一个物体在斜面上下滑,斜面的倾角为θ,摩擦系数为μ,若物体下滑的加速度为a,则μ与θ的关系为()A. μ = tanθ - a/gB. μ = a/g - tanθC. μ = a/g + tanθD. μ = tanθ + a/g答案:一、选择题1. A2. A3. A4. B5. A6. C7. B8. B9. A10. A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
()2、力对于一点的矩不因力沿其作用线移动而改变。
()3、在自然坐标系中,如果速度υ = 常数,则加速度α = 0。
()4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。
()5、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mv x =mvcos a。
()二、选择题(每题3分。
请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时(如图),圆柱处于极限平衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A = N B;②N A > N B;③N A < N B。
3、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是 。
①半径为L/2的圆弧; ②抛物线; ③椭圆曲线; ④铅垂直线。
4、在图示机构中,杆O 1 A //O 2 B ,杆O 2 C //O 3 D ,且O 1 A = 20cm ,O 2 C = 40cm ,CM = MD = 30cm ,若杆AO 1 以角速度 ω = 3 rad / s 匀速转动,则D 点的速度的大小为 cm/s ,M 点的加速度的大小为 cm/s 2。
① 60; ②120; ③150; ④360。
5、曲柄OA 以匀角速度转动,当系统运动到图示位置(OA//O 1 B 。
AB |OA )时,有A V B V ,A αB α,ωAB 0,εAB 0。
①等于; ②不等于。
三、填空题(每题5分。
请将简要答案填入划线内。
)1、已知A 重100kN ,B 重25kN ,A 物与地面间摩擦系数为0.2。
端较处摩擦不计。
则物体A 与地面间的摩擦力的大小为 。
2、直角曲杆O1AB以匀有速度ω1绕O1轴转动,则在图示位置(AO1垂直O1 O2)时,摇杆O2 C的角速度为。
3、均质细长杆OA,长L,重P,某瞬时以角速度ω、角加速度绕水平轴O转动;则惯性力系向O点的简化结果是(方向要在图中画出)。
四、计算题(本题15分)在图示平面结构中,C处铰接,各杆自重不计。
已知:q c = 600N/m,M = 3000N·m,L1 = 1 m,L2 = 3 m。
试求:(1)支座A及光滑面B的反力;(2)绳EG的拉力。
五、计算题(本题15分)机构如图G已知:OF = 4h/g,R = 3h/3,轮E作纯滚动;在图示位置AB杆速度为v,φ= 60°,且E F|OC。
试求:(1)此瞬时ωOC及ωE(ωE为轮E的角速度) (2)求 OC。
六、计算题(本题12分)在图示机构中,已知:匀质轮C 作纯滚动,半径为r 、重为P C ,鼓轮B 的内径为r 、外径为R ,对其中心轴的回转半径为ρ,重为P B ,物A 重为P A 。
绳的CE 段与水平面平行,系统从静止开始运动。
试求:物块A 下落s 距离时轮C 中心的速度。
七、计算题(本题18分)机构如图,已知:匀质轮O 沿倾角为β的固定斜面作纯滚动,重为P 、半径为R ,匀质细杆OA 重Q ,长为,且水平初始的系统静止,忽略杆两端A ,O 处的摩擦,试求:(1)轮的中心O 的加速度α。
(2)用达朗伯原理求A 处的约束反力及B 处的摩擦力(将这二力的大小用加速度α表示即可)。
一、结构如图所示,由AB 、BC 杆件构成,C 端放在理想光滑水平面上,AB 杆上作用力偶M ,BC 杆上作用均布载荷q ,已知KN 10=F ,KNm 5=M ,m KN 2=q ,各杆自重不计,试求A 、C 处约束反力以及销钉B 对BC 杆作用力。
解:A以BC 杆为对象:∑=0BM, 02222=⋅⋅-⋅q F CkN 4=C F∑=0x F ,02222=⋅⋅-q F Bx∑=0y F ,02222=+⋅⋅-C By F q F 0=By F以AB 梁为对象:∑=0xF,0=-Bx Ax F FkN 4=Ax F∑=0y F ,0=--F F F By AykN 10=Ay F∑=0AM, 04=⋅-+F M M Am kN 35⋅=A M二、OA 杆长l 1,绕O 轴定轴转动,带动长为l 2的套筒AB 在O 1D 杆上滑动。
若设置如图所示的参考基T ][y x =e ,杆OA 的连体基T 11][y x =e ,套筒AB 的连体基T 222][y x=e ,并假设i r 为第i 个构件上待求点相对于参考基的坐标阵,O r 为基点坐标阵,i A 为第i 个构件连体基相对于参考基的方向余弦阵,i ρ为构件i 上待求点相对于自身连体基的坐标阵,试利用关系式i i O A ρA r r +=写出机构运动到图示位形时:(1) OA 杆和套筒AB 相对于参考基的位形;(2)套筒AB 的上B 点相对于参考基的位置坐标阵。
y解:图示瞬时方向余弦阵⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒︒︒-︒=2/22/22/22/245cos 45sin 45sin 45cos 1A ,⎥⎦⎤⎢⎣⎡=011l ρ ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒-︒-︒--︒-=2/32/12/12/3)30cos()30sin()30sin()30cos(2A ,⎥⎦⎤⎢⎣⎡=022l ρ (1)OA 杆的位形[]T14/00π=q⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2/22/22/22/20002/22/22/22/211111l l l l l y x y x O O A A 套筒AB 的位形[]T11T1622226/⎥⎦⎤⎢⎣⎡-=-=ππl l y x q AA(2)B 点的位置坐标阵⎥⎥⎦⎤⎢⎢⎣⎡-+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)2()32(2123222202/32/12/12/32121212122112l l l l l l l l l y x y x A A B B三、半径为r 的圆盘与长度为l 的直杆AB 在盘心A 铰接,圆盘沿水平面纯滚,AB 杆B 端沿铅直墙壁滑动。
在图示位置,圆盘的角速度为ω,角加速度为α,杆与水平面的夹角为θ,试求该瞬时杆端B 的速度和加速度。
解:(1) 球速度,速度瞬心C 如图 θsin l AC =,θcos l BC =ωr v A = (2分)θωωsin l r AC v A AB ==(2分) θωθωθωcot sin cos ⋅==⋅=r l r l BC v AB B(2分) (图1分)(2) 球加速度 (图2分)αr a A = (1分)θωθωω22222n sin )sin (l r l r l AB a ABBA ==⋅=(1分)以A 点为基点求B 点加速度n t BA BA A B a a a a ++= (*)式(*)向ξ轴投影:n cos sin BA A B a a a --=-θθ(2分)θωθαθωθαθ322222sin cot )sin cos (sin 1l r r l r r a B +=+=(2分) 四、图示系统,均质圆盘1O 、2O 质量均为m ,半径均为R ,圆盘2O 上作用已知力偶M ,使圆盘绕2O 轴转动,通过自重不计的水平绳带动圆盘1O 在水平面上纯滚。
试完成: (1) 用拉格朗日方程求盘心1O 的加速度; (2) 求水平绳的张力;(3) 滑轮1O 与地面的静摩擦力。
解:(1) 求加速度选2O 轮的转角2ϕ为广义坐标21T T T +=)(222212122321222121212ωωωωmR mR J J O S +=+= )3(2221241ωω+=mR (4分) 由运动学知212ωωR R =,或2/21ϕϕ= (1分)Aa代入动能得 2222222241167)43(ϕϕϕmR mR T =+= (1分)广义力:M Q =2ϕ(1分) 代入拉氏方程222d d ϕϕϕQ T T t =∂∂-∂∂ ,有M mR =2287ϕ ,得:2278mRM =ϕ (2分) 又由运动学知圆盘的角加速度 221742mR M==ϕϕ盘心1O 的加速度: mR M R a O 7411==ϕ (1分)(2) 求绳的张力(5分) [法一]以2O 轮为研究对象由R F M L O T 2-= ,即R F M J O T 22-=ϕ 得:RMR M R M mR R M F 7374212T =-=-=ϕ [法二]或以1O 轮为研究对象由R F L S 2T = ,即R F J S 2T 1⋅=ϕ得:RMmR F 73431T ==ϕ (2) 求摩擦力(5分) 以1O 轮为研究对象 [法一]运用质心运动定理S T 1F F ma +=, RMR M mR M mF ma F 773742T 1S =-=-=[法二]对动点D 运用动量矩定理 )(1F M v m v L D O D D=⨯+R F mv R J O C t20)(S d d 1⋅=+⋅+-,即R F ma R mR O 221S 121⋅=⋅+-ϕ 得:RMmR M mR mR M mR R F 7)742174(2122S =-=五、图示机构,在铅垂面内,曲柄OA 和连杆AB 是相同的均质杆,长l AB OA ==,自重不计,滑块B 重G ,曲柄OA 上作用一力偶M ,使机构静止平衡。
已知静止平衡时曲柄OA 与水平线TSF夹角为ϕ,试用虚位移原理求机构平衡时力偶M 。
解:虚功方程 0δδδδ=+++ϕM y F y F y F C Cy D Dy B By或 0δδδδ11=---C D B y G y G y G M ϕ (*) (5分)B 、C 、D 三点的y 坐标为 ϕsin 2l y B =,ϕsin 21l y C =,ϕsin 23l y D = (3分)求变分: ϕϕδcos 2δ⋅=l y B ,ϕϕδcos δ21⋅=l y C ,ϕϕδcos δ23⋅=l y D (1分) 代入(*)式 0δcos δcos δcos 2δ231211=⋅-⋅-⋅⋅-ϕϕϕϕϕϕϕl G l G l G M 或 0cos 2cos 21=-⋅-ϕϕl G l G M (1分) 得: ϕcos )(21l G G M +⋅=六、一边长为 a 的正立方体所受的力系如图所示,其中F F =1,F F 22=,试用坐标矩阵法求力系向O 点简化的结果。
