Matlab数学实验(上)
数学实验(MATLAB)课后习题答案
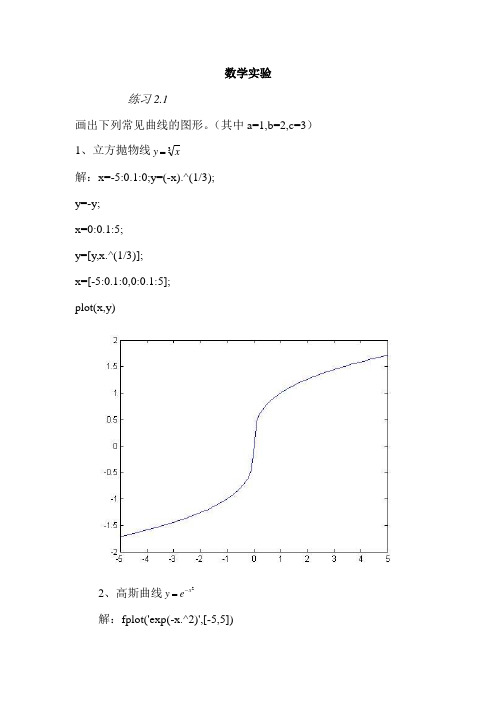
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
matlab数学实验

《管理数学实验》实验报告班级姓名实验1:MATLAB的数值运算【实验目的】(1)掌握MATLAB变量的使用(2)掌握MATLAB数组的创建,(3)掌握MA TLAB数组和矩阵的运算。
(4)熟悉MATLAB多项式的运用【实验原理】矩阵运算和数组运算在MA TLAB中属于两种不同类型的运算,数组的运算是从数组元素出发,针对每个元素进行运算,矩阵的运算是从矩阵的整体出发,依照线性代数的运算规则进行。
【实验步骤】(1)使用冒号生成法和定数线性采样法生成一维数组。
(2)使用MA TLAB提供的库函数reshape,将一维数组转换为二维和三维数组。
(3)使用逐个元素输入法生成给定变量,并对变量进行指定的算术运算、关系运算、逻辑运算。
(4)使用MA TLAB绘制指定函数的曲线图,将所有输入的指令保存为M文件。
【实验内容】(1)在[0,2*pi]上产生50个等距采样数据的一维数组,用两种不同的指令实现。
0:(2*pi-0)/(50-1):2*pi 或linspace(0,2*pi,50)(2)将一维数组A=1:18,转换为2×9数组和2×3×3数组。
reshape(A,2,9)ans =Columns 1 through 71 3 5 7 9 11 132 4 6 8 10 12 14Columns 8 through 915 1716 18reshape(A,2,3,3)ans(:,:,1) =1 3 52 4 6ans(:,:,2) =7 9 118 10 12 ans(:,:,3) =13 15 17 14 16 18(3)A=[0 2 3 4 ;1 3 5 0],B=[1 0 5 3;1 5 0 5],计算数组A 、B 乘积,计算A&B,A|B,~A,A= =B,A>B 。
A.*Bans=0 0 15 121 15 0 0 A&Bans =0 0 1 11 1 0 0 A|Bans =1 1 1 11 1 1 1~Aans =1 0 0 00 0 0 1A==Bans =0 0 0 01 0 0 0A>=Bans =0 1 0 11 0 1 0(4)绘制y= 0.53t e -t*t*sin(t),t=[0,pi]并标注峰值和峰值时间,添加标题y= 0.53t e -t*t*sint ,将所有输入的指令保存为M 文件。
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
MATLAB数学实验答案(全)

MATLAB数学实验答案(全)第⼀次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作⼆维、三维⼏何图形,能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。
补充命令vpa(x,n) 显⽰x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项(要求将结果⽤向量的形式给出)。
数学实验1 MATLAB操作基础

1.1.2 MATLAB命令形式 命令形式
在工作空间或MATLAB命令窗口中输入 命令窗口中输入MATLAB 在工作空间或 命令窗口中输入 认可的任何命令,按回车键都可执行其操作. 认可的任何命令,按回车键都可执行其操作 如“4+7”、“4-7”、“4*7”、“4/7”、 “4^5”, 、 、 、 、 , 等按回车键后可显示其结果. “sqrt(5)”等按回车键后可显示其结果 等按回车键后可显示其结果
随机抽取10 名学生的高等数学课程成绩, 例1.2.2 随机抽取 名学生的高等数学课程成绩, 并统计他们中的最高分、 并统计他们中的最高分、最低分以及他们的平均 成绩。 成绩。
math=[88,90,77,69,92,80,74,66,95,85]; %产生 维向量 产生10维向量 产生 mathaver=sum(math)/10 %计算平均成绩 计算平均成绩 h=max(math) l=min(math) %求出最高分 求出最高分 %求出最低分 求出最低分
第一章 MATLAB使用说明 1.1 MATLAB窗口环境与命令形式
1.1.1 Matlab 的窗口环境
当前工 作目录 当前工 作空间 命令 提示符 命令窗口 输入命令的 历史记录
运行MATLAB创建一个或多个窗口
a) 命令区 命令区(Command Window)是用户使用的主 是用户使用的主 要场所,此时,可以输入变量、 要场所,此时,可以输入变量、数组及运算命 进行一些简单的运算; 键搜索、 令,进行一些简单的运算;用↑↓←→键搜索、 键搜索 修改以前使用过的命令操作, 清除窗口; 修改以前使用过的命令操作 用 clc清除窗口 清除窗口 寻求有关帮助; 用help sqrt ( help input …)寻求有关帮助 寻求有关帮助 b) 编辑区 编辑区(Editor\Debugger Window)编制各种 编制各种 M-文件,存盘 文件, 文件 存盘(Save)、运行(Run)等. 、运行( )
重庆大学数学实验一 matlab的基本应用 参考答案

《数学实验》第一次上机实验1. 设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ,其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵,试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R E A 。
程序及结果:E=eye(3); %创建单位矩阵E% R=rand(3,2); %创建随机矩阵R% O=zeros(2,3); %创建0矩阵% S=diag(1:2); %创建对角矩阵% A=[E,R;O,S]; %创建A 矩阵%B=[E,(R+R*S);zeros(2,3),S^2] %计算等号右边的值%A^2 %计算等号左边的值%运行结果:B =1.00 0 0 1.632.74 0 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.00 ans =1.00 0 0 1.632.740 1.00 0 1.81 1.90 0 0 1.00 0.25 0.29 0 0 0 1.00 0 0 0 0 0 4.002.某零售店有9种商品的单件进价(元)、售价(元)及一周的销量如表1.1,问哪种商品的利润最大,哪种商品的利润最小;按收入由小到大,列出所有商品及其收入;求这一周该10种商品的总收入和总利润。
表1.11)程序:a=[7.15 8.25 3.20 10.30 6.68 12.03 16.85 17.51 9.30]; b=[11.10 15.00 6.00 16.25 9.90 18.25 20.80 24.15 15.50]; c=[568 1205 753 580 395 2104 1538 810 694];s=sum((b-a).*c)i=b.*cmax((b-a).*c)min((b-a).*c)[m,n]=sort(b.*c)2)运行结果:s =4.6052e+004i =1.0e+004 *0.6305 1.8075 0.4518 0.9425 0.3911 3.8398 3.1990 1.95621.0757ans =1.3087e+004ans =1.2719e+003m =1.0e+004 *0.3911 0.4518 0.6305 0.9425 1.0757 1.8075 1.9562 3.1990 3.8398n =5 3 1 4 9 2 8 7 63. 近景图将x的取值范围局限于较小的区间内可以画出函数的近景图,用于显示函数的局部特性。
(完整word版)Matlab数学实验报告

Matlab 数学实验报告一、实验目的通过以下四组实验,熟悉MATLAB的编程技巧,学会运用MATLAB的一些主要功能、命令,通过建立数学模型解决理论或实际问题。
了解诸如分岔、混沌等概念、学会建立Malthu模型和Logistic 模型、懂得最小二乘法、线性规划等基本思想。
二、实验内容2.1实验题目一2.1.1实验问题Feigenbaum曾对超越函数y=λsin(πx)(λ为非负实数)进行了分岔与混沌的研究,试进行迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图2.1.2程序设计clear;clf;axis([0,4,0,4]);hold onfor r=0:0.3:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.5)for i=101:150plot(r,x(i),'k.');endtext(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end加密迭代后clear;clf;axis([0,4,0,4]);hold onfor r=0:0.005:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.1)for i=101:150plot(r,x(i),'k.');endend运行后得到Feigenbaum图2.2实验题目二2.2.1实验问题某农夫有一个半径10米的圆形牛栏,长满了草。
他要将一头牛拴在牛栏边界的桩栏上,但只让牛吃到一半草,问拴牛鼻子的绳子应为多长?2.2.2问题分析如图所示,E为圆ABD的圆心,AB为拴牛的绳子,圆ABD为草场,区域ABCD为牛能到达的区域。
问题要求区域ABCD等于圆ABC的一半,可以设BC等于x,只要求出∠a和∠b就能求出所求面积。
MATLAB数学实验报告

MATLAB数学实验报告姓名:李帆班级:机械(硕)21学号:2120104008第一次数学实验报告——线性规划问题一,实验问题1,某饲养场饲养动物出售,设每头动物每天至少需要700g蛋白质,30g矿物质,100mg 维生素。
现有五种饲料可供选择,各种饲料的每千克营养成分含量和单价如下表。
是确定既能满足动物生长的营养需要,游客是费用最省的选用饲料方案。
2,某工厂生产甲、乙、丙三种产品,单位产品所需工时分别为2、3、1个;单位产品所需原料分别为3、1、5公斤;单位产品利润分别为2、3、5元。
工厂每天可利用的工时为12个,可供应的原料为15公斤。
为使总利润为最大,试确定日生产计划和最大利润。
二,问题分析1,1)该题属于采用线性规划的方式求出最优解的数学问题。
该题有以下特点,1.目标函数有线性,是求目标函数的最小值;2.约束条件为线性方程组;3.未知变量都有非负限制。
1,2)求解该类问题的方法有图解法,理论解法和软件解法。
图解法常用于解变量较少的线性规划问题。
理论解法要构建完整的理论体系。
目前用于解线性规划的理论解法有:单纯形法,椭球算法等。
在此,我们采用单纯形法的MATLAB软件解法来求解该问题。
1,3)此题中,要求既要满足动物生长的营养需要,又要使费用最省,则使每种饲料的选用量为变量,以总费用的最小值为所求量,同时每种饲料的使用量要符合营养成分的要求。
1,4)在此,首先确定建立线性规划模型。
设饲料i选用量为xi公斤,i=1,2,3,4,5.则有模型:Minz=0.2x1+0.7x2+0.4x3+0.3x4+0.8x5s.t. {3x1+2x2+6x4+18x5>=700;x1+0.5x2+0.2x3+2x4+0.5x5>=300.5x1+x2+0.2x3+2x4+0.8x5>=100Xj>=0,j=1,2,3,4,5解之得:x1=x2=x3=0X4=39.74359X5=25.14603Zmin=32.435902, 1)该问题与第一题分析步骤相似,故只在此写出其线性规划模型Z=2x+3y+5z2x+3y+z<=123x+y+5z<=15三,程序设计流程图第一题:c=[0.2,0.7,0.4,0.3,0.8]A=[3,2,1,6,18;1,0.5,0.2,2,0.5;0.5,1,0.2,2,0.8;1,0,0,0,0;0,1 ,0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1]b=[700,30,100,0,0,0,0,0][x,fval]=linprog(c,-A,-b)c =0.2000 0.7000 0.4000 0.3000 0.8000A =3.0000 2.0000 1.0000 6.0000 18.00001.0000 0.5000 0.20002.0000 0.50000.5000 1.0000 0.2000 2.0000 0.80001.0000 0 0 0 00 1.0000 0 0 00 0 1.0000 0 00 0 0 1.0000 00 0 0 0 1.0000b =700 30 100 0 0 0 0 0Optimization terminated.x =0.0000-0.00000.000039.743625.6410fval =32.4359第二题c=[-2 -3 -5]A=[2 3 1;3 1 5]b=[12;15]lb=[0 0 0][x,Z,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。
MATLAB数学实验100例题解
一元函数微分学实验1 一元函数的图形(基础实验)实验目的 通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析 函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧。
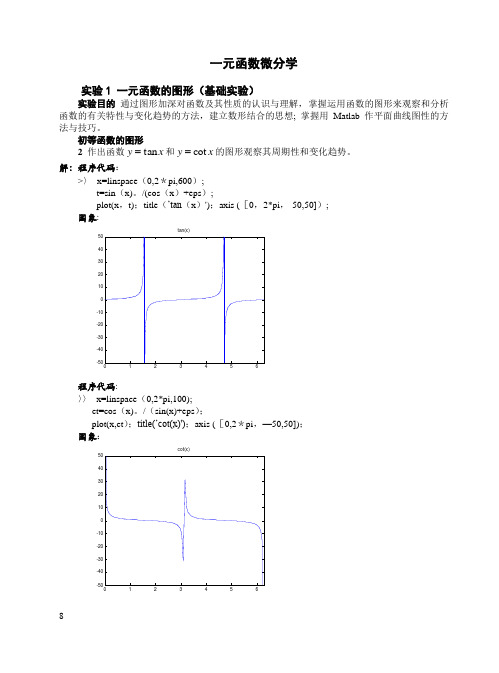
初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势。
解:程序代码:>〉 x=linspace (0,2*pi,600); t=sin (x)。
/(cos (x )+eps );plot(x ,t);title (’tan (x )');axis ([0,2*pi ,-50,50]); 图象:程序代码: 〉〉 x=linspace (0,2*pi,100); ct=cos (x)。
/(sin(x)+eps ); plot(x,ct );title(’cot(x)');axis ([0,2*pi ,—50,50]); 图象:cot(x)4在区间]1,1[-画出函数xy 1sin =的图形。
解:程序代码:>> x=linspace (-1,1,10000);y=sin(1。
/x ); plot (x,y ); axis ([-1,1,—2,2]) 图象:二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形:解:程序代码:>〉 t=linspace(0,2*pi,100); plot(cos(t ).*cos (5*t ),sin(t )。
*cos(3*t)); 图象:极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解:程序代码:〉〉 t=0:0.01:2*pi ; r=exp (t/10);polar(log(t+eps ),log (r+eps)); 图象:90270分段函数作图10 作出符号函数x y sgn =的图形。
01 实验一 MATLAB的基本用法

x=linspace(0,pi,5) ↙ x= 0 0.7854 1.5708 2.3562 3.1416 logspace(0,2,11) ↙ ans = Columns 1 through 7 1.0000 1.5849 2.5119 3.9811 15.8489 Columns 8 through 11 25.1189 39.8107 63.0957 100.0000
16
矩阵的裁剪
基于matlab的数学实验-高等数学中的若干问题1

基于MATLAB的数学实验——高等数学中的若干问题(一)§1.1数列及其极限1.1.1引言极限(Limit )是高等数学中应用最普遍的基本概念之一,因而,正确地理解和把握极限的概念是非常重要的,借助于直观的想象和解释,不仅可以帮助我们理解和把握这一表述抽象的数学定义,而且对利用极限定义的其他数学概念如微分(Differential)、积分(Integral)和无穷级数的敛散性(Convergence and Divergence of Infinite Series)等重要概念的理解也是有帮助的。
1.1.2数列的收敛与发散例1.1让我们首先考察如下的数列:xnnn=+sin()12,n=12,, (1.1)如果我们把xn 看成是沿x轴运动的点P在t n=时刻所处的位置,那么容易看出(也容易证明),随着时间t→+∞,动点P趋近于原点0。
这个事实可借助于软件MATLAB直观地观察到,应用如下程序sequence01.m:%CONVERGENCE AND LIMIT OF SEQUENCEk=700;n=1:3:k;x=sin(n)./(10+n);e=input('Input epsilon, Please: epsilon=')t=e\10;for m=1:t;if m>1/e;N=mbreakendendplot(n,x)hold ontitle('CONVERGENCE AND LIMIT OF SEQUENCE')gtext('xn = sin(n)/(10+n)')QQ:121681692Email:*****************可得到图1.1:用上述程序还可以对任意给定的ε>0,求出N,使得当n N>时,满足不等式:xn -<0ε。
此外,我们还可以使用MATLAB程序文件seqnummovie1.m和seqnummovie2.m演示动点P趋近于原点0的动态过程。
高等数学实验matlab

式函数a0+a1x+a2x2作为经验公式n ),此时偏差平方和函数为
W=
(a
0
+a1xi
+a
2
x
2 i
-yi
)
2
i=1
其中n为数据点的数目。要使偏差平方和函数W最小,需要
n
n
n
na0 a1 xi a2 xi2 yi
i 1
i 1
i 1
a0
n
xi a1
n
xi2 a2
n
xi3
即拟合函数为 y=14.7391+0.1973139x-0.000339492x2
从图1-10可以看出拟合效果比较好,但是是否还可以更好呢? 一般而言,拟合次数的提高可以使得拟合效果变好,但是并 不是次数越高越好。现在提高拟合次数,将基函数由1,x,x2 修改为{1,x,x2,x3}(三次拟合),{1,x,x2,x3,x4}(四次拟合 )……,得到拟合图1-5至图1-9。
67
101
135
202
259
336
404
25.72
32.29
34.03
39.45
43.15
43.46
40.83
471 30.75
【实验方案】
设y代表土豆产量,x代表氮肥的施肥量。显然,y和x之间应该 有某种关系,假设y与x之间的关系为函数关系,则问题就转 化拟为合已问知题数。据点(xi,yi)位置关系,寻找函数y=y(x)。这就是数据
设计性实验
实验一 数据拟合问题 实验二 复利问题
第1章函数与极限—设计性实验
实验一 数据拟合问题
【实验目的】 1.加深对函数基本概念的理解 2.讨论了函数的实际应用问题 3.掌握Matlab软件中有关函数、画图等命令 【实验要求】 掌握函数基本知识,Matlab软件
MATLAB数学实验课后答案

数学实验MATLAB参考答案(重要部分)P20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)P20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a 与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码P20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)T =11.5813P20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)fmin =-1.3907 %最小值min_index =54 %最小值点编址>> x(min_index)ans =0.6500 %最小值点>> [f1,x1_index]=min(abs(f)) %求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; %删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) %求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500P20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6579 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)ans =505 505 505 505 505 505 505 505 505 505 >> sum(diag(z))ans =505>> z(:,2)/sqrt(3)ans =57.157746.188046.765450.229553.693613.85642.88683.46416.928210.3923>> z(8,:)=z(8,:)+z(3,:)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3423 5 82 89 91 48 30 32 39 6683 87 101 115 119 83 87 101 115 11910 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59P 40 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)xbar =72.4000s =12.1124P 40 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=n计算结果m=37clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度P 40 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocP 40 ex5c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)P 40 ex6(1)clear;fplot('x^2*sin(x^2-x-2)',[-2,2])x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2])(2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20);[theta,fai]=meshgrid(theta,fai); x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page41, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page41,ex8分别使用which trapz, type trapz, dir C:\MATLAB7\toolbox\matlab\datafun\ page41,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1);mesh(x,y,p)page41, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16];>> X=lyap(A,C)X =1.0000 -1.0000 -0.0000 -1.00002.0000 1.0000 -0.0000 1.0000 7.0000Chapter 3%Exercise 1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 %一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000%矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Exercise 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) %[A,b]为增广矩阵ans =3ans =3 %可见方程组唯一解>> x=A\bx =2.38301.48942.0213Exercise 2(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b]) ans =3ans =3 %可见方程组唯一解>> x=A\bx =-0.4706-0.2941Exercise 2(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 %可见方程组无解>> x=A\bx =0.3311-0.1219 %最小二乘近似解Exercise 2(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 %rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 %一个特解Exercise 3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11%通解kx+x0 Exercise 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 %成比例,说明x是最大特征值对应的特征向量Exercise 5%用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]'; >> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.0100 0.1200 0.0400 0.0900 >> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500 -0.0900 0.8000 -0.0100 -0.1200 -0.0400 0.9100 >> D=[17 17 17]';x=A\D x =37.569625.786224.7690%Exercise 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a) ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766%Exercise 6(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i%Exercise 6(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887%Exercise 6(4)、(以n=5为例)%关键是矩阵的定义%方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda%方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a%方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] %下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.5865 0.0015 -0.0075 0.0286 -0.0977 0.3173 >> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.9237 0.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.0000 0.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 7.4495 0 00 0 0 5.0000 00 0 0 0 2.5505%Exercise 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a) v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v %验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) %也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 %特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) %对应相同特征值的特征向量成比例ans =2.44912.44912.4491%Exercise 7(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i %v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 -1 0d =1 1 00 1 10 0 1 %jordan标准形不是对角的,所以不可对角化%Exercise 7(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887%本题用jordan不行, 原因未知%Exercise 7(4)参考6(4)和7(1), 略%Exercise 8 只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. %Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0]>> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) %1,2,4行为最大无关组3>> b=a([1 2 4],:)';c=a([3 5],:)'; >> b\c %线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000%Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 %v确实是正交矩阵%Exercise 11%设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下%20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; %i1=i3+i4;i5=i2+i3;i6=i4+i5;%计算如下>> A=[1 0 0 2 0 0 0 0 0;0 0 1 0 3 0 0 0 0;1 0 -1 0 0 -3 0 0 0;1 -1 0 0 0 0 -4 0 0;0 -1 1 0 0 0 0 -5 0;0 1 0 0 0 0 0 0 -3;0 0 0 1 0 -1 -1 0 0;0 0 0 0 -1 -1 0 1 0;0 0 0 0 0 0 -1 -1 1];>>b=[20 5 0 0 0 0 0 0 0]'; A\bans =13.34536.44018.54203.3274-1.18071.60111.72630.42042.1467%Exercise 12>> A=[1 2 3;4 5 6;7 8 0];>> left=sum(eig(A)), right=sum(trace(A))left =6.0000right =6>> left=prod(eig(A)), right=det(A) %原题有错, (-1)^n应删去left =27.0000right =27>> fA=(A-p(1)*eye(3,3))*(A-p(2)*eye(3,3))*(A-p(3)*eye(3,3))fA =1.0e-012 *0.0853 0.1421 0.02840.1421 0.1421 0-0.0568 -0.1137 0.1705>> norm(fA) %f(A)范数接近0ans =2.9536e-013%Exercise 1(1)roots([1 1 1])%Exercise 1(2)roots([3 0 -4 0 2 -1])%Exercise 1(3)p=zeros(1,24);p([1 17 18 22])=[5 -6 8 -5];roots(p)%Exercise 1(4)p1=[2 3];p2=conv(p1, p1);p3=conv(p1, p2);p3(end)=p3(end)-4; %原p3最后一个分量-4roots(p3)%Exercise 2fun=inline('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x'); fzero(fun,2)】%Exercise 3fun=inline('x^4-2^x');fplot(fun,[-2 2]);grid on;fzero(fun,-1),fzero(fun,1),fminbnd(fun,0.5,1.5)%Exercise 4fun=inline('x*sin(1/x)','x');fplot(fun, [-0.1 0.1]);x=zeros(1,10);for i=1:10, x(i)=fzero(fun,(i-0.5)*0.01);end;x=[x,-x]%Exercise 5fun=inline('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fsolve(fun,[0 0 0])%Exercise 6fun=@(x)[x(1)-0.7*sin(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))];[a,b,c]=fsolve(fun,[0.5 0.5])%Exercise 7clear; close; t=0:pi/100:2*pi; x1=2+sqrt(5)*cos(t); y1=3-2*x1+sqrt(5)*sin(t);x2=3+sqrt(2)*cos(t); y2=6*sin(t);plot(x1,y1,x2,y2); grid on; %作图发现4个解的大致位置,然后分别求解y1=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fsolve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exercise 8(1)clear;fun=inline('x.^2.*sin(x.^2-x-2)');fplot(fun,[-2 2]);grid on; %作图观察x(1)=-2;x(3)=fminbnd(fun,-1,-0.5);x(5)=fminbnd(fun,1,2);fun2=inline('-x.^2.*sin(x.^2-x-2)');x(2)=fminbnd(fun2,-2,-1);x(4)=fminbnd(fun2,-0.5,0.5);x(6)=2feval(fun,x)%答案: 以上x(1)(3)(5)是局部极小,x(2)(4)(6)是局部极大,从最后一句知道x(1)全局最小, x(2)最大。
北科大Matlab_数学实验报告1~6次(全)

《数学实验》报告实验名称 Matlab 基础知识学院专业班级姓名学号2014年 6月一、【实验目的】1.认识熟悉Matlab这一软件,并在此基础上学会基本操作。
2.掌握Matlab基本操作和常用命令。
3.了解Matlab常用函数,运算符和表达式。
4.掌握Matlab工作方式和M文件的相关知识。
5.学会Matlab中矩阵和数组的运算。
二、【实验任务】P16 第4题编写函数文件,计算1!nkk =∑,并求出当k=20时表达式的值。
P27第2题矩阵A=123456789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,B=468556322⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,计算A*B,A.*B,并比较两者的区别。
P27第3题已知矩阵A=5291⎡⎤⎢⎥⎣⎦,B=1292⎡⎤⎢⎥⎣⎦,做简单的关系运算A>B,A==B,A<B,并做逻辑运算(A==B)&(A<B),(A==B)&(A>B)。
P34 第1题用11114357π=-+-+……公式求π的近似值,直到某一项的绝对值小于-610为止。
三、【实验程序】P16 第4题function sum=jiecheng(n) sum=0;y=1;for k=1:nfor i=1:ky=y*i;endsum=sum+y;endsumP27第2题>>A=[1 2 3;4 5 6;7 8 9]>>B=[4 6 8;5 5 6;3 2 2]>>A*BP27第3题>> A=[5 2;9 1];B=[1 2;9 2];>>A>B>>A==B>>A<B>> (A==B)&(A<B)>> (A==B)&(A>B)P34 第1题t=1;pi=0;n=1;s=1;while abs(t)>=1e-6pi=pi+t;n=n+2;s=-s;t=s/n;endpi=4*pi;四、【实验结果】P16 第4题P27第2题两者的区别:A*B是按正规算法进行矩阵的计算, A.*B是对应元素相乘。
matlab实验一实验报告

matlab实验一实验报告实验一:Matlab实验报告引言:Matlab是一种强大的数学软件工具,广泛应用于科学计算、数据分析和工程设计等领域。
本实验旨在通过使用Matlab解决实际问题,探索其功能和应用。
一、实验目的本次实验的主要目的是熟悉Matlab的基本操作和常用函数,了解其在科学计算中的应用。
二、实验内容1. 数值计算在Matlab中,我们可以进行各种数值计算,包括基本的加减乘除运算,以及更复杂的矩阵运算和方程求解。
通过编写相应的代码,我们可以实现这些功能。
例如,我们可以使用Matlab计算两个矩阵的乘积,并输出结果。
代码如下:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A * B;disp(C);```2. 数据可视化Matlab还提供了强大的数据可视化功能,可以将数据以图表的形式展示出来,更直观地观察数据的规律和趋势。
例如,我们可以使用Matlab绘制一个简单的折线图,来展示某个物体在不同时间下的位置变化。
代码如下:```matlabt = 0:0.1:10;x = sin(t);plot(t, x);xlabel('Time');ylabel('Position');title('Position vs. Time');```3. 图像处理Matlab还可以进行图像处理,包括图像的读取、处理和保存等操作。
我们可以通过Matlab对图像进行增强、滤波、分割等处理,以及进行图像的压缩和重建。
例如,我们可以使用Matlab读取一张图片,并对其进行灰度化处理。
代码如下:```matlabimg = imread('image.jpg');gray_img = rgb2gray(img);imshow(gray_img);```三、实验结果与分析在本次实验中,我们成功完成了数值计算、数据可视化和图像处理等任务。
Matlab数学实验报告

实验一 Matlab基本操作1.实验课程名称数学实验2.实验项目名称Matlab基本操作3.实验目的和要求了解Matlab的基本知识,熟悉其上机环境,掌握利用Matlab进行基本运算的方法。
4.实验内容和原理内容:三角形的面积的海伦公式为:area=)s-sa--)()(s(csb其中: s=(a+b+c)/2原理:将一般数学问题转化成对应的计算机模型并进行处理的能力。
了解Matlab的基本功能,会进行简单的操作。
5.主要仪器设备计算机与Windows 2000/XP系统;Matlab等软件。
6.操作方法与实验步骤步骤:(1)在M文件编辑窗口输入以下程序,并以文件名”area_helen.m”保存:a= input(‘a=‘) ; b= input(‘b=‘) ; c= input(‘c=‘) ;s= (a+b+c)/2;area=sqrt (s* (s-a) * (s-b) * (s-c))(2)在命令窗口输入文件名“area_helen”,按回车键,即可运行上面的程序,输入三边长,立即可得三角形面积(3)第二题在命令窗口输入b=6;a=3;c=a*b,d=c-2*b(4) 按回车键,即可运行上面的程序7.实验结果与分析<1> a=3; b=4; c=5;时,aera=6 当a为3,b为4,c为5时,s=6,aera=6<2> c= 18,d=6,a为3,b为6时,c=18,d=6实验二 Matlab的数值计算1.实验课程名称数学实验2.实验项目名称Matlab的数值计算3.实验目的和要求了解一些简单的矩阵、向量、数组和多项式的构造和运算方法实例,懂得编写简单的数值计算的Matlab程序。
熟悉一些Matlab的简单程序,会用Matlab的工具箱,懂得Matlab的安装和简单的使用。
4.实验内容和原理内容:从函数表:)1(),5.0(),2( ,0x 1x 021x 1x f(x) 32-⎪⎩⎪⎨⎧≤≤<>+=f f f x x求设)1(),2( ,1211)(2-⎩⎨⎧≤>+=f f x xx x x f 求设 原理:利用矩阵、向量、数组、和多项式的构造和运算方法,用常用的几种函数进行一般的数值问题求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
how are you
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
6.1.3
(二)变量 1.符号变量
MATLAB常用的常量、变量与函数
提问:符号变量创建的格式是什么?
(1)sym a:表示一次创建一个符号变量. (2)syms a b c :表示一次创建多个符号变量. (3)sym(‘x’):表示创建一个符号变量, 它可以是字符、字符串、表达式或字符表达式;
+
点
十字号
s
d
正方形
菱形
o(字母)
*
圆圈
星号
h
p
六角形
五角星
x(字母)
叉号
>
右三角
6.2 6.1 MATLAB MATLAB 中函数 数 运算与作图的实验 学实验(上)
经济数学
6.2 MATLAB中函数运算与作图的实验
6.2.1
(三)作图实验
b
c
运算实验
2.二维图形带参数的图 调用格式:plot(x,y,’参数’):表示给图形添加 颜色、确定线型及数据点的图标等常用参数表 m 蓝色 紫红色
青色 r 红色
g
k
绿色
黑色
w
y
白色
黄色
实线(默认)
点画线
:
--
点连线
虚线
.
设置当前路径
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
6.1.2
(二)命令窗口
MATLAB基本知识介绍
如图是MATLAB的命令窗口,其中“>>”为运算提示符,表示
MATLAB正处在准备状态。当在提示符后输入一段运算式并按 【Enter】键后,MATLAB将给出计算结果,然后再进入准备状态。
经济数学
6.1 MATLAB数学软件简介
6.1.2
(四)当前目录窗口
MATLAB基本知识介绍
在当前目录窗口中可显示或改变当前目录,还可以显示
当前目录下的文件并提供搜索功能。
此窗口有4个按钮控件: 显示并改变当前目录控件 进入所显示的目录的上一级目录
在当前目录中创建一个新的子目录
在当前目录的文件中查找
3
x 1
)
(2)展开 x 1
(答案:x 3 3x 2 3x 1 )
2 x 1x 2) x 3x 2 (答案: (3)分解
(4)求
sin x cos x x 在 3 1 x2
处的值(答案: 12.0962)
6.2 6.1 MATLAB MATLAB 中函数 数 运算与作图的实验 学实验(上)
例题
例如:计算在的值。 >> syms x; >> x=pi/3; >> cos(x) >> ans = 0.5000
函数(变量)
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.2 MATLAB中函数运算与作图的实验
6.2.1
(一)算术运算
+ -
运算实验
MATLAB中提供的常用算术运算符有: 加 减
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
6.1.2
(六) 程序编辑器
MATLAB基本知识介绍
编写好之后以“ logotu.m” 文件名保存。在 MATLAB 主命令窗口中执行命令: MATLAB输入命令 >> logotu
6.1 MATLAB数 学实验(上) 学软件介绍
上机练习
(1)建立一个命令M文件:在同一坐标呢,画出一条正弦曲线和一条余
弦曲线,要求正弦曲线用红色实线、数据点用“+”号显示。
(2)建立一个函数M文件:求函数 f x (保留有效数四位)
x
在 x 3 与 x 30 的近似值
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
打开所选数据的矩阵编辑器
删除所选数据 MATLAB在执行M文件时, 将把M文件的数据保存到对应的工 作间中。 6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
6.1.2
(六) 程序编辑器
MATLAB基本知识介绍
1.M文件的建立 提问:什么是M文件? 编写MATLAB的程序文件就称M文件。M文件分为:命令文件和函数文件 提问:M文件建立的步骤是什么? 1)进入程序编辑器(MATLAB Editor/Debug): 从“File”菜单中选择“New”及“M-file”项或单击“New M-file”按 扭; 2)输入程序:在“MATLAB Editor/Debug”窗口输入MATLAB程序; 3)保存程序:单击“save”按扭,出现一个对话框, 在文件名一框中键入一个文件名,单击“保存”按扭.
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
6.1.2
(三)历史窗口
MATLAB基本知识介绍
在默认设置下,历史窗口中会保留自安装起所有命令的 历史记录,并表明使用时间以方便使用者查询。双击某一行 命令,即在命令窗口中执行该行命令。
Hale Waihona Puke 6.1 MATLAB数 学实验(上) 学软件介绍
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
6.1.3
(二)变量
2.给变量赋值
MATLAB常用的常量、变量与函数
提问:给变量赋值的基本格式是什么? [变量名=]表达式[ ;]
例题
例如:把(5*1.06+4*2.45)/(5+4)赋给a。 >> a=(5*1.06+4*2.45)/(5+4) >> ans = 1. 6778
知识点:
主要内容
经济数学
第6章
基本要求
不定积分
了解原函数提出的背景; 理解并掌握不定积分概念,了解定积分的几何意义; 掌握不定积分的性质,熟记基本积分公式; 掌握不定积分的直接积分法,凑微分法,第二换元积 分法(根号中为一次函数)、分部积分法,会求不定 积分。 理解与掌握不定积分在经济问题中的应用,会用不 定积分解决简单的经济问题。 约8学时
经济数学
6.1 MATLAB数学软件简介
6.1.2
(六) 程序编辑器
MATLAB基本知识介绍
例题
例2 创建一个函数式文件, 文件名为%fibfun.m。 计算第n个Fibonnaci数。 在Medit窗口中写以下内容: %fibfun.m function f=fibfun(n) if n>2 f=fibfun(n-1)+fibfun(n-2); else f=1; end 编写好之后以“fibfun.m” 文件名保存。 在MATLAB主命令窗口中 执行命令: >> fibfun(3) 得到结果为 ans =
6.2 MATLAB中函数运算与作图的实验
6.2.1
(二) 函数运算
运算实验
除了简单的四则运算外,MATLAB还提供了几种常 用的函数运算命令:
expand simple
符号表达式的展开 寻找符号表达式的 最简型
factor simplify
符号表达式因式 分解 符号表达式化简
例题
x 2 3x 2 例5 化简 x 1
经济数学
6.2 MATLAB中函数运算与作图的实验
6.2.1
(三)作图实验 1、二维图形基本图 调用格式:plot(x,y):表示作函数 y f ( x) 的图形;
plot(x,sin(x)) plot(x, sin(x), x, cos(x))
运算实验
6.2 6.1 MATLAB MATLAB 中函数 数 运算与作图的实验 学实验(上)
第四章 不定积分
经济数学
6.1
6.1.1 6.1.2 6.1.3
MATLAB数学软件介绍
MATLAB功能介绍 MATLAB基本知识介绍 MATLAB常用的常量、变量与函数
主要内容
经济数学
6.1 MATLAB数学软件简介
6.1.1 MATLAB功能介绍
常见软件
目前最常见的几种软件: 1. Mathacd 2.Matlab 3. Mathematica
经济数学
第 6章
6.1 6.2 6.3 6.4
MATLAB数学实验(上)
MATLAB数学软件介绍 MATLAB中函数运算与作图的实验 MATLAB中求极限与导数的实验 MATLAB中求不定积分与定积分的 实验
目录
经济数学
第6章 MATLAB数学实验(上)
MATLAB功能介绍 基本窗口介绍 MATLAB 数学软件介绍 MATLAB基本知识介绍 M 文件建立、保存与调用 常用常量、变量与函数介绍 算术运算 运算实验 函数运算 MATLAB中函数运算与作图实验 二维图形 作图实验 三维图形 求x a的极限 求极限实验 求x a的左、右极限 MATLAB中求极限与导数实验 求一阶导数 求导数实验 求高阶导数 求极值的实验 求不定积分实验 MATLAB 中求不定积分与定积分的实验 求区间 a, b 的定积分 求定积分实验 求广义积分
6.1 MATLAB数 学实验(上) 学软件介绍
经济数学
6.1 MATLAB数学软件简介
