03命题逻辑的推理理论 ppt课件
离散数学课件03命题逻辑的推理理论

((┐p∧┐q)∨p) ∨ q
((┐p∨p )∧(┐q∨p)) ∨ q
(┐q∨p) ∨ q 1
精选课件ppt
由定理 3.1可知, 推理正确。
15
推理定律--重言蕴含式
(1) A (A∨B)
附加律
(2) (A∧B) A
化简律
(3) (A→B)∧A B
假言推理
(4) (A→B)∧┐B ┐A
拒取式
(5) (A∨B)∧┐B A
析取三段论
(6) (A→B) ∧ (B→C) (A→C)
假言三段论
(7) (AB) ∧ (BC) (A C)
等价三段论
(8) (A→B)∧(C→D)∧(A∨C) (B∨D) (A→B)∧(┐A→B)∧(A∨┐A) B
构造性二难 构造性二难
(特殊形式)
(9)(A→B)∧(C→D)∧(┐B∨┐精D选)课件pp(t ┐A∨┐C) 破坏性二难16
只要不出现(3)中的情况,推理就是正确的,因而判断 推理是否正确,就是判断是否会出现(3)中的情况。
推理正确,并不能保证结论B一定为真。
精选课件ppt
8
例题
例3.1 判断下列推理是否正确。(真值表法)
(1) {p,p→q}├ q (2) {p,q→p}├ q
正确 不正确
p q p(p→q) q p(q→p)
推理是指从前提出发推出结论的思维过程。
前提是已知命题公式集合。
结论是从前提出发应用推理规则推出的命题公式。
证明是描述推理正确或错误的过程。
要研究推理,首先应该明确什么样的推理是有效的或 正确的。
精选课件ppt
4
命题逻辑的推理理论
概念
描述问题 的句子
命题逻辑的推理理论课件(离散数学)

一、自然推理系统P
自然推理系统P由三个部分组成:
1.
字母表:命题变项符号;联结词符号;括
号和逗号。
2.
命题公式。
3.
推理规则。
22
二、推理规则
(1) 前提引入规则 (2) 结论引入规则 (3) 置换规则 (4) 假言推理规则 AB A \B (5) 附加规则 A \AB (6) 化简规则 AB \A (7) 拒取式规则 AB B \A (8) 假言三段论规则 AB BC \AC
30
四、附加前提证明法
例6:用附加前提证明法构造证明下面的推
理: 2是素数或合数。若2是素数,则 2 是 无理数。若 2 是无理数,则4不是素数。所 以,如果4是素数,则2是合数。
31
四、附加前提证明法
解: 设 p:2是素数, q:2是合数,
r: 2 是无理数,s:4是素数 推理形式结构 前提:pq, pr, rs 结论:sq
40
五、归谬法
解:命题符号化
p:小张守第一垒 q:小李向B队投球
r:A队取胜
s:A队成为联赛第一名
推理的形式结构如下:
( p q ) r , r s , s , p 结论: q
前提:
41
五、归谬法
证一:归谬法(略) 证二:直接法 ① r s 前提引入
② s
③r
前提引入
5
前提是有限个公式的集合,而不是序列 。
二、推理的有效性
A1A2… Ak
0 0
B
0 1
推理的有效性 有效 有效
1
1
0
有效
无效
6
二、推理的有效性
定义:若对于每组赋值,当 A1A2…Ak
逻辑学第一章 逻辑、命题、推理ppt课件

二、逻辑学的研究对象 逻辑学是一门古老的科学,至今已有2000多年的
历史。它有三个发源地,这就是古代的中国、印度和 希腊。
其研究对象主要是思维的形式结构及其规律的简 单操作的逻辑方法。
表一:三种原创哲学的比较
印度哲学 中国哲学 古希腊哲学
研究内容 人生哲学 社会伦理哲学 自然哲学和认识论
研究及思维方式 说教
“如果……那么……”是不变的部分,是这一类命题所共同 具有的,不变部分是“p”和“q”所表示的各不相同的具体 思维内容间共同的联系方式。
[例7] 所有违法行为都是要受法律追究的, 所有偷税行为都是违法行为, 所以,所有偷税行为都是要受法律追究的。
[例8] 所有公民都是民事权利的主体, 超计划生育的孩子是公民, 所以,超计划生育的孩子是民事权利的主体。
思维形式结构本身无所谓真假,但其中的变项代入具体内容后,
便形成了逻辑上有真有假的具体思想。
同一思维形式结构在不同的代入下,成为有不同内容的具体思
想。这些具体思想事实上是真是假,即是否符合客观事物情况,逻
辑学并不能解决。
逻辑学关心的是,当变项代入具体内容时,基于思维形式结构
的不同,其真假情况所表现出的规律性。
例如“所有S是P”、“如果P,那么q”等。 逻辑学便是论证逻辑规律,分析逻辑矛盾,说明什么样的思维
具有形式结构上的正确性或可靠性,是合乎逻辑的。
综上所述,逻辑学是研究思维的形式结构及其规律和
简单的逻辑方法的学说。推理形式及其有效性的判定是它 的核心内容。
第二节 逻辑学的渊源
一、感性认识
Heraclitus(约前540年—前480年) 古希腊哲学家、爱非斯派的创始人
引论
逻辑
逻辑学 性质意义
离散数学课件-3-命题逻辑的推理理论

第三章 命题逻辑的推理理论§1 推理的形式结构推理:从前提出发推出结论的思维过程。
前提:已知命题公式集合。
结论:从前提出发应用推理规则推出的命题公式。
定义设A1, A2, …, A k, B都是命题公式,若命题公式A1∧A2∧…∧A k→B是重言式,则称由前提A1, A2, …, A k推出结论B的推理是有效的或正确的,并称B是有效的结论。
推理的形式结构记为{A1,A2,…,A k}A B推理正确,记为{ A1,A2,…,A k }⊨B推理无效,记为{ A1,A2,…,A k }⊭B注①推理正确,结论未必为真。
②推理只注重结构。
例判断下述推理的正确性。
(1) {p, p→q}⊢ q(2) {p, q→p}⊢ q解 (1) p∧(p→q)→q⇔p∧(¬p∨q)→q⇔(p∧¬p)∨(p∧q)→q⇔p∧q→q⇔¬ (p∧q)∨q⇔¬p∨(¬q∨q)⇔¬p∨1⇔1故{p, p→q }⊨ q(2) p∧(q→p)→q让q =0,可得q→p =1,再取p =1可得p∧(q→p)=1 由此得p∧(q→p)→q有成假赋值1 0,故{ p, q→p }⊭ q判断推理正确性:1.真值表法。
2.等值演算法。
3.主析取范式法。
4.构造证明。
例判断下述推理是否正确?(1)若a能被4整除,则a能被2整除。
a能被4整除。
所以a能被2整除。
(2)若下午气温超过30℃,则王小燕必去游泳。
若她去游泳,则她就不去看电影了。
所以,若王小燕没去看电影,则下午气温必超过了30℃。
解(1) p:a能被4整除q:a能被2整除前提:p→q,p结论:q推理的形式结构:{p→q,p} A q前面已证此推理正确。
(2) p:下午气温超过30℃q:王小燕去游泳r:王小燕去看电影前提:p→q, q→¬r结论:¬ r→p推理的形式结构:{p→q,q→¬r} A(¬r→p)因为,(p→q)∧(q→¬ r)→(¬r→p)⇔m1∨m3∨m4∨m5∨m6∨m7主析取范式显然不是重言式,故推理不正确。
3 命题逻辑的推理理论
(7)拒取式规则
AB B A
(8) 假言三段论规则
AB BC AC
(9)析取三段论规则
AB B A
(10)构造性二难推理规则
AB CD AC BD
(11)破坏性二难推理规则
AB CD BD AC
(12) 合取引入规则
A B AB
证明方法: ◦ 直接证明法 ◦ 附加前提法 ◦ 归谬法(或称反证法)
(2) 联结词符号: ┐, , , , (3) 括号与逗号:( ),, 2. 合式公式(同合取联接词定义)
3. 推理规则
(1)前提引入规则 在证明的任何步骤上都可以引入前提。
(2)结论引入规则 在证明的任何步骤上所得到的结论都可以作为后继证明的前提。
(3)置换规则 在证明的任何步骤上,命题公式中的子公式都可以用与之等值的公
1、用不同的方法验证下面推理是否正确。对于正确的推理还 要在P系统中给出证明。 (1) 前提:pq, q
结论:p (2) 前提:qr, pr
结论:qp
(1)不正确。 验证答案,只需证明(pq)qp不是重言式。 方法一 等值演算
(pq)qp ((pq)q)p (pq)qp ((pq)(qq))p pq 易知10是成假赋值,故(pq)qp不是重言式,所以推理不正确。
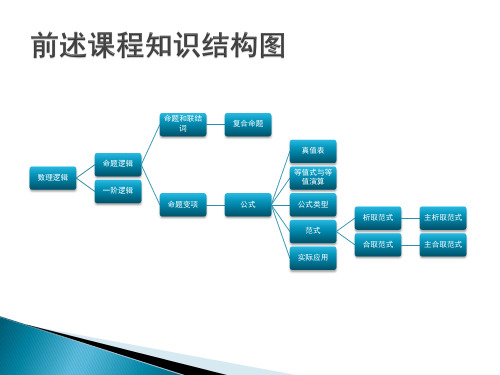
数理逻辑
命题逻辑 一阶逻辑
命题和联结 词
命题变项
复合命题 公式
真值表 等值式与等
值演算 公式类型
范式
实际应用
析取范式 合取范式
主析取范式 主合取范式
根据下列真语句,请判断是谁谋害了张先生? (1)A、B、C三人中至少有一人。 (2)如果张先生生前未饮过麻醉剂,那不是C。 (3)如果张先生曾饮过麻醉剂,那不是A。 (4)如果是A谋害的,那么B也参加了。 (5)如果作案在落雨前,则是A谋害的。 (6)如果作案不在落雨前,张先生临死前搏斗过。 (7)张先生临死前搏斗过,就不是B谋害的。 (8)经过法医解剖化验,张先生死前曾饮过麻醉剂。
3第三章 命题逻辑的推理理论

从语言角度, 推理分为语义和语法两种。 从语言角度, 推理分为语义和语法两种。 语义(semantics)推理注重内涵的正确性 也就是从真 语义(semantics)推理注重内涵的正确性, 也就是从真 推理注重内涵的正确性, 要推出真的结论来, 的前提出发要推出真的结论来 推理过程考虑得少, 的前提出发要推出真的结论来, 推理过程考虑得少,关 心的是结论的正确性。 心的是结论的正确性。 语法推理则注重形式上的有效, 注重推理过程是否符 语法推理则注重形式上的有效, 注重推理过程是否符 则注重形式上的有效 合某些事先规定的逻辑规则, 结论是严格遵循规则 合某些事先规定的逻辑规则, 若结论是严格遵循规则 有效的 得到的, 那便是有效 得到的, 那便是有效的。 数理逻辑主要采用语法推理, 数理逻辑主要采用语法推理, 它关心的是结论的有效 不关心前提的实际真值, 性,而不关心前提的实际真值, 当然语法推理作为一 种推理方法, 种推理方法, 它必须能反映客观事物中真实存在的逻 辑关系, 语法推理必须保证语义上的正确性 必须保证语义上的正确性。 辑关系, 即 语法推理必须保证语义上的正确性。
3、2.1节给出的24个等值式中的每个都可以 2.1节给出的 个等值式中的每个都可以 节给出的24 派生出两条推理定律。 派生出两条推理定律。 例如:双重否定律 A⇔¬¬A ⇔¬¬A 例如: 可以产生两条推理定律 A⇒¬¬A ¬¬A ¬¬A ¬¬A ⇒A
§3.2 自然推理系统P 自然推理系统P
由上一节知识可知,可以利用真值表法、等值演算法 由上一节知识可知,可以利用真值表法、 真值表法 和主析取范式法三种方法来判断推理是否正确。 和主析取范式法三种方法来判断推理是否正确。 三种方法来判断推理是否正确 但是,当推理中包含的命题变项较多时,以上三种 命题变项较多时 但是,当推理中包含的命题变项较多 方法的演算量太大。因此对于由前提A1, A2,…,Ak推 方法的演算量太大。因此对于由前提A B的正确推理应给出严谨的证明。 正确推理应给出严谨的证明。 证明是一个描述推理过程的命题公式序列, 证明是一个描述推理过程的命题公式序列,其中的每 是一个描述推理过程的命题公式序列 个公式是已知前提或者是由某些前提应用推理规则得 个公式是已知前提或者是由某些前提应用推理规则得 已知前提或者是 到的结论。 到的结论。
离散数学第三章 命题逻辑的推理理论

推理实例
例1 判断下面推理是否正确 (1) 若今天是 号,则明天是 号. 今天是 号. 所以 明天是 号. 若今天是1号 则明天是5号 今天是1号 所以, 明天是5号 (2) 若今天是 号,则明天是 号. 明天是 号. 所以 今天是 号. 若今天是1号 则明天是5号 明天是5号 所以, 今天是1号 解 设 p:今天是 号,q:明天是 号. :今天是1号 :明天是5号 → ∧ → (1) 推理的形式结构 (p→q)∧p→q 推理的形式结构: 用等值演算法 (p→q)∧p→q → ∧ → ⇔ ¬((¬p∨q)∧p)∨q ¬ ∨ ∧ ∨ ∨¬q∨ ⇔ ¬p∨¬ ∨q ⇔ 1 ∨¬ 由定理3.1可知推理正确 由定理 可知推理正确
19
练习1: 练习 :判断推理是否正确
1. 判断下面推理是否正确 判断下面推理是否正确: (1) 前提:¬p→q, ¬q 前提: → 结论: 结论:¬p ∧¬q→¬ 推理的形式结构: ¬ → ∧¬ →¬p 解 推理的形式结构 (¬p→q)∧¬ →¬ 方法一:等值演算法 方法一: (¬p→q)∧¬ →¬ ∧¬q→¬ ¬ → ∧¬ →¬p ∧¬q)∨¬ ⇔ ¬((p∨q)∧¬ ∨¬ ∨ ∧¬ ∨¬p ∧¬q)∨ ∨¬ ∨¬p ⇔ (¬p∧¬ ∨q∨¬ ¬ ∧¬ ∨¬p ⇔ ((¬p∨q)∧(¬q∨q))∨¬ ¬ ∨ ∧ ¬ ∨ ∨¬ ⇔ ¬p∨q ∨ 易知10是成假赋值,不是重言式,所以推理不正确 易知 是成假赋值,不是重言式,所以推理不正确. 是成假赋值
16
例4 前提:¬(p∧q)∨r, r→s, ¬s, p 前提: ∧ ∨ → 结论: 结论:¬q 证明 用归缪法 ①q 结论否定引入 ② r→s → 前提引入 ③ ¬s 前提引入 ②③拒取式 ④ ¬r ②③拒取式 ⑤ ¬(p∧q)∨r ∧ ∨ 前提引入 ④⑤析取三段论 ⑥ ¬(p∧q) ∧ ④⑤析取三段论 ∨¬q ⑦ ¬p∨¬ ∨¬ ⑥置换 ①⑦析取三段论 ⑧ ¬p ①⑦析取三段论 ⑨p 前提引入 ⑧⑨合取 ¬p∧p ∧ ⑧⑨合取
《离散数学》课件-第3章命题逻辑的推理理论

判断方法一:真值表法
真值表的最后一列全为1,所以((p∨q)∧┐p) →q为重言式。因而推理正确。
判断方法二:等值演算法
((p∨q)∧┐p)→q ⇔ ((p∧┐p)∨(q∧┐p))→q ⇔ ( q∧┐p )→q ⇔ ┐q∨p∨q ⇔1
因为((p∨q)∧┐p)→q为重言式,所 以推理正确。
判断方法三:主析取范式法
★ ★★
可见,如果能证明★★是重言式,则★也是重言式。 在★★中,原来的结论中的前件A已经变成前提了,称A为 附加前提。称这种将结论中的前件作为前提的证明方法为 附加前提法。
例:在自然推理系统P中构造下面推理的证明 如果小张和小王去看电影,则小李也去看电影。小
赵不去看电影或小张去看电影。小王去看电影。所 以,当小赵去看电影时,小李也去。
前提引入
② ┐s
前提引入
③ ┐p
①②拒取式(A→B)∧┐B⇒┐A
④ p∨q
B)∧┐B⇒A
⑥ q→r
前提引入
⑦r
⑤⑥假言推理(A→B)∧A⇒B
⑧ r∧(p∨q) ⑦④合取引入
(2)前提:┐p∨q,r∨┐q,r→s 结论:p→s
证明:
① ┐p∨q 前提引入
② p→q
①置换
(A→B)∧(C→D)∧(┐B∨┐D) ⇒(┐A∨┐C)
(12)合取引入规则:若证明的公式序列中出现过 A和B,则A∧B是A和B的有效结论。
推理规则(12个)
(1)前提引入规则 (2)结论引入规则(隐规则) (3)置换规则:等值置换 (4)假言推理规则:(A→B)∧A⇒B (5)附加规则:A⇒(A∨B) (6)化简规则:A∧B ⇒A (7)拒取式规则:(A→B)∧┐B⇒┐A (8)假言三段论规则:(A→B)∧(B→C)⇒(A→C) (9)析取三段论规则:(A∨B)∧┐B⇒A (10)构造性二难推理规则 (11)破坏性二难推理规则 (12)合取引入规则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
((┐p∧┐q)∨p) ∨ q
((┐p∨p )∧(┐q∨p)) ∨ q
(┐q∨p) ∨ q 1
2020/12/27
由定理 3.1可知, 推理正确。
17
推理定律--重言蕴含式
(1) A (A∨B)
附加律
(2) (A∧B) A
化简律
(3) (A→B)∧A B
假言推理
(4) (A→B)∧┐B ┐A
拒取式
(5) (A∨B)∧┐B A
析取三段论
(6) (A→B) ∧ (B→C) (A→C)
假言三段论
(7) (AB) ∧ (BC) (A C)
等价三段论
(8) (A→B)∧(C→D)∧(A∨C) (B∨D) (A→B)∧(┐A→B)∧(A∨┐A) B
构造性二难 构造性二难
(特殊形式)
(290)20(/1A2→/27 B)∧(C→D)∧(┐B∨┐D) (┐A∨┐C) 破坏性二难18
关于推理定律的几点说明
A,B,C为元语言符号,代表任意的命题公式。 若一个推理的形式结构与某条推理定律对应的蕴涵
式一致,则不用证明就可断定这个推理是正确的。
2.1节给出的24个等值式中的每一个都派生出两条推 理定律。例如双重否定律A A产生两条推理定 律A A和 AA。
由九条推理定律可以产生九条推理规则,它们构成了 推理系统中的推理规则。
认识世界的渐进过程
2020/12/27
7
有效推理的定义
定义3.1 设A1,A2,…,Ak和B都是命题公式,若对于 A1,A2,…,Ak和B中出现的命题变项的任意一组赋值, (1)或者A1∧A2 ∧…∧Ak为假; (2)或者当A1∧A2 ∧…∧Ak为真时,B也为真; 则称由前提A1,A2,…,Ak推出B的推理是有效的或正确 的,并称B是有效结论。
离散数学
第3章 命题逻辑的推理理论
本章说明
本章的主要内容
–推理的形式结构
–自然推理系统P
本章与后续各章的关系
–本章是第五章的特殊情况和先行准备
2020/12/27
2
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
q
00
0
0
0
0
1
0
1
0
10
0
0
1
11
1
1
1
2020/12/27
0 1 0 1
11
有效推理的等价定理
定理3.1 命题公式A1,A2,…,Ak推B的推理正确当且仅当 (A1∧A2∧…∧Ak )→B 为重言式。
说明 该定理是判断推理是否正确的另一种方法。
2020/12/27
12
定理3.1的证明
(1)证明必要性。若A1,A2,…,Ak推B的推理正确, 则对于A1,A2,…,Ak,B中所含命题变项的任意一组赋值,不会出
只要不出现(3)中的情况,推理就是正确的,因而判断 推理是否正确,就是判断是否会出现(3)中的情况。
推理正确,并不能保证结论B一定为真。
2020/12/27
10
例题
例3.1 判断下列推理是否正确。(真值表法)
(1) {p,p→q}├ q (2) {p,q→p}├ q
正确 不正确
p q p(p→q) q p(q→p)
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
4
3.1 推理的形式结构 3.2 自然推理系统P 本章小结 习题 作业
2020/12/27
5
3.1 推理的形式结构
数理逻辑的主要任务是用数学的方法来研究数学中的 推理。
推理是指从前提出发推出结论的思维过程。
2020/12/27
8
关于有效推理的说明
由前提A1,A2,…,Ak推结论B的推理是否正确 与诸前提的排列次序无关。
由={推A1B,的A推2,理…记,为A┣k}B 若推理是正确的,记为 ╞ B 若推理是不正确的,记为 B
2020/12/27
9
关于有效推理的说明
设A1,A2,…,Ak,B中共出现n个命题变项,对于任何 一组赋值α1α2…αn(αi=0或者1,i=1,2,…,n),前提 和结论的取值情况有以下四种: (1) A1∧A2 ∧…∧Ak为0,B为0。 (2) A1∧A2 ∧…∧Ak为0,B为1。 (3) A1∧A2 ∧…∧Ak为1,B为0。 (4) A1∧A2 ∧…∧Ak为1,B为1。
要求
Г={G1, G2, …,Gn} Г H
也就是 G1∧G2∧…∧Gn→H 为永真公式
因而 真值表技术、演绎法和 间接证明方法
2020/12/27
15
判断推理是否正确的方法
真值表法 等值演算法 主析取范式法
说明 当命题变项较少时,这三种方法比较方便。
思考 是否有其他的证明方法?
2020/12/27
前提是已知命题公式集合。
结论是从前提出发应用推理规则推出的命题公式。
证明是描述推理正确或错误的过程。
要研究推理,首先应该明确什么样的推理是有效的或 正确的。Βιβλιοθήκη 2020/12/276
命题逻辑的推理理论
概念
描述问题 的句子
判断
对概念的肯 定与否定的 判断
推理
从一个或多 个前提推出 结论的思维 过程
2020/12/27
13
推理的形式结构
(1) 设={ A1, A2, …, Ak},记为┣B。
(2) A1A2…AkB
(3)
前提: 结论:
A1, B
A2,
…
, Ak
说明 当推理正确时, 形式(1)记为 ╞ B。
形式(2)记为A1A2…AkB。 表示蕴涵式为重言式。
2020/12/27
14
判断有效结论的常用方法
16
例题
例3.2 判断下列推理是否正确。(等值演算法)
(1) 下午马芳或去看电影或去游泳。她没去看电影,所以,她 去游泳了。
解:设p:马芳下午去看电影,q:马芳下午去游泳。
前提: p∨q,┐p 结论: q 推理的形式结构: ((p∨q)∧┐p)→q
((p∨q)∧┐p)→q
┐((p∨q)∧┐p) ∨ q
现A1∧A2∧…∧Ak为真,而B为假的情况, 因而在任何赋值下,蕴涵式(A1∧A2∧…∧Ak )→B均为真,故它
为重言式。 (2)证明充分性。若蕴涵式(A1∧A2∧…∧Ak)→B为重言式, 则对于任何赋值此蕴涵式均为真,因而不会出现前件为真后件
为假的情况, 即在任何赋值下,或者A1∧A2∧…∧Ak为假, 或者A1∧A2∧…∧Ak和B同时为真,这正符合推理正确的定义。
