第三章命题逻辑推理理论
合集下载
离散数学课件03命题逻辑的推理理论
((┐p∧┐q)∨p) ∨ q
((┐p∨p )∧(┐q∨p)) ∨ q
(┐q∨p) ∨ q 1
精选课件ppt
由定理 3.1可知， 推理正确。
15
推理定律--重言蕴含式
(1) A (A∨B)
附加律
(2) (A∧B) A
化简律
(3) (A→B)∧A B
假言推理
(4) (A→B)∧┐B ┐A
拒取式
(5) (A∨B)∧┐B A
析取三段论
(6) (A→B) ∧ (B→C) (A→C)
假言三段论
(7) (AB) ∧ (BC) (A C)
等价三段论
(8) (A→B)∧(C→D)∧(A∨C) (B∨D) (A→B)∧(┐A→B)∧(A∨┐A) B
构造性二难 构造性二难
(特殊形式)
(9)(A→B)∧(C→D)∧(┐B∨┐精D选)课件pp(t ┐A∨┐C) 破坏性二难16
只要不出现(3)中的情况，推理就是正确的，因而判断 推理是否正确，就是判断是否会出现(3)中的情况。
推理正确，并不能保证结论B一定为真。
精选课件ppt
8
例题
例3.1 判断下列推理是否正确。（真值表法）
(1) {p,p→q}├ q (2) {p,q→p}├ q
正确 不正确
p q p(p→q) q p(q→p)
推理是指从前提出发推出结论的思维过程。
前提是已知命题公式集合。
结论是从前提出发应用推理规则推出的命题公式。
证明是描述推理正确或错误的过程。
要研究推理，首先应该明确什么样的推理是有效的或 正确的。
精选课件ppt
4
命题逻辑的推理理论
概念
描述问题 的句子
《逻辑学》第三章 命题的自然推理
基本真值联结词 ¬ 否定 ∧ 合取 ∨ 析取 蕴涵 等值
5种基本真值形式
¬ p 否定式
p ∧q 合取式 pq 蕴涵式 pq 等值式
p∨q 析取式 真值函项
函数讲的是数值关系，一个函数的值依赖于其中变数的值 y＝f（x），即y的值f（x）由x的取值决定。 与函数类比 真值函项讲的是真值（真假）关系，一个真值形式的值依 赖其变项的值，如p∧q的值，由p和q的值决定。 每一真值形式都是真值函项；真值形式与真值函项的数目并不一样多， 真值形式的数目无限，真值函项数却是确定的；不同的真值形式，表 达相同的真值函项；真值函项是对公式中变项的真假组合的真值断定， 变项组合数2n，对每一组合有真假两种断定，故真值函项数为22n。 当n（变项数）为1时，其真假组合为2，对真假组合的断定有4种可 能，即真值函项有4个；变项数为2，则真值函项有16个；变项数为3， 则真值函项为256个。
f9 f8 的矛盾式
f13 f4 的矛盾式
f14 f3 的矛盾式 f15 f2 的矛盾式
f10
f12
f7 的矛盾式
f5 的矛盾式
f11 f6 的矛盾式
f16
f1 的矛盾式
随着变项数目的增加，函项数也增加，当变项数目为3时，函项数目达 到256个。但不管函项数是多少，重言式的函项只是一个，矛盾式的函 项也是一个，其余均是可满足式。真值函项有3类，那么，表达真值函 项的真值形式也有3类：重言式（永真式）、矛盾式（永假式）和可满 足式（可真可假式）。当然，每一类真值函项包括很多的真值形式， 而同一类真值函项的真值形式是等值的。
但逻辑学难以对付诸如相关性、顺序等影响命题真假的因素。逻辑研究 撇开逻辑联结词在自然语言中的非真值意义，仅从复合命题与支命题之 间的真假制约关系来考虑逻辑联结词，这样，逻辑联结词就成为真值联 结词；命题的逻辑形式也就成为真值形式。
法律逻辑学第三章 简单命题及推理
第一节 命题的概述
一 ,定义 命题是对思维对象有所断定的一种思维形式 二,命题的逻辑特征 1,对思维对象有所肯定或否定 所谓断定,要么对思维对象有所肯定,要么对思维对象 有所否定,即肯定或否定思维对象具有什么性质. 2,有真假 学术界关于逻辑真与经验真问题.(形式真与事实真) 逻辑从命题形式上研究命题的逻章要点
命题-语句-直言命题-真假关系-对当关系-项 的周延性-推理-对当关系推理-命题变形规则推理换质推理-换位推理-换质位推理-换位质推理-戾换 推理-三段论-三段论组成,公理,规则,格与式, 省略形式-关系命题-关系的性质-关系推理
三,命题与语句
联系: 命题作为思维形式是离不开语句而赤裸裸的存在着;命题的形成,存在,巩固和 表达都离不开语句.语句离开命题则是毫无意义的音节或笔划的堆积.命题是语句的 思维内容和逻辑基础,语句则是命题的物质外壳和表达形式. 区别: ①命题属于思想范畴,是客体的反映,语句属于语言范畴,是用来表达思想的音 节或符号.二者属于不同对象领域. ②任何命题都要用语句表达,但并非所有语句表达命题,陈述句,反诘句,感叹 句,祈使句在一定语境中可以间接表达命题. 同一命题可以用不同语句表达. 例如:我是一名教师——I am a teacher. 2,在同一民族语言中同一命题因交际的目的,对象,语境不同,也可以表达不同 的语句. 如:a一切事物都包含着矛盾 b事物总有矛盾. c难道有不包含矛盾的事物. 3,同一语句可以表达不同的命题. 例如:鸡不吃了 我看见白头翁 学生不能欺骗老师
同一素材下A 同一素材下A,E,I,O真假关系由下表来表示
推知 推知 已知真 A E I O T F 不定 F F T F 不定 T F T 不定 F T 不定 T O I E A A E I O 已知假
一 ,定义 命题是对思维对象有所断定的一种思维形式 二,命题的逻辑特征 1,对思维对象有所肯定或否定 所谓断定,要么对思维对象有所肯定,要么对思维对象 有所否定,即肯定或否定思维对象具有什么性质. 2,有真假 学术界关于逻辑真与经验真问题.(形式真与事实真) 逻辑从命题形式上研究命题的逻章要点
命题-语句-直言命题-真假关系-对当关系-项 的周延性-推理-对当关系推理-命题变形规则推理换质推理-换位推理-换质位推理-换位质推理-戾换 推理-三段论-三段论组成,公理,规则,格与式, 省略形式-关系命题-关系的性质-关系推理
三,命题与语句
联系: 命题作为思维形式是离不开语句而赤裸裸的存在着;命题的形成,存在,巩固和 表达都离不开语句.语句离开命题则是毫无意义的音节或笔划的堆积.命题是语句的 思维内容和逻辑基础,语句则是命题的物质外壳和表达形式. 区别: ①命题属于思想范畴,是客体的反映,语句属于语言范畴,是用来表达思想的音 节或符号.二者属于不同对象领域. ②任何命题都要用语句表达,但并非所有语句表达命题,陈述句,反诘句,感叹 句,祈使句在一定语境中可以间接表达命题. 同一命题可以用不同语句表达. 例如:我是一名教师——I am a teacher. 2,在同一民族语言中同一命题因交际的目的,对象,语境不同,也可以表达不同 的语句. 如:a一切事物都包含着矛盾 b事物总有矛盾. c难道有不包含矛盾的事物. 3,同一语句可以表达不同的命题. 例如:鸡不吃了 我看见白头翁 学生不能欺骗老师
同一素材下A 同一素材下A,E,I,O真假关系由下表来表示
推知 推知 已知真 A E I O T F 不定 F F T F 不定 T F T 不定 F T 不定 T O I E A A E I O 已知假
3形式逻辑-第三章 简单命题及其推理(上)
例如：从“他们都不是学生”可推出一 个等值命题：“他们都是非学生”。
A、E、I、O都可以按上述方法进行换质 法变形推理：
原命题 SAP SEP SIP SOP
换质命题 SE﹁P SA﹁P SO﹁P SI﹁P
⑵换位法，改变原命题主项和谓项的位 置而推出一个新命题的推理方法。
步骤:第一，只更换主、谓项的位置；第 二，换位命题的主、谓项不得扩大原命 题中的对应项的周延情况。
(2) 按照前提和结论一般性程度的不同，可以把推理分为演 绎、归纳和类比。演绎是由一般性的前提推到个别性的结论； 演绎推理的前提必须蕴涵结论，即一个正确的演绎推理的前提 如果是真的，则结论一定是真的，所以它一定是必然性推理。 归纳是由个别性的前提推到一般性的结论；类比是由个别性的 前提推到个别性的结论。归纳和类比就是所说的或然性推理。
2.命题和语句
(1)命题是表达判断的语句，但并非所有语句都表达 命题。只有能区分其真或假的语句才构成命题。
语句主要有四种，即陈述句、疑问句、祈使句和感 叹句。其中陈述句一般是能区分真假的，它是命题的最 基本语言形式；疑问句、祈使句、感叹句一般不直接表 达判断，所以不是命题；但反诘疑问句、预设句因为隐 含着判断，所以是命题。
(2)一类推理的正确性，必须分析到简单命题即原子命题所包含 的概念即词项才能判定，则这种推理就称为简单命题推理即词 项推理。相应的逻辑称为词项逻辑。
例如：所有谎言是不可信的
所有S是P
有些谎言是不可信的
有些S是P
另一类推理的正确性，如果只要分析到其中所包含的简单命 题即原子命题为止即可判定，那么这类推理就称为复合命题推 理即命题推理。相应的逻辑称为命题逻辑。
直言命题A、E、I、O四种形式的换 质位情况归纳如下:
A、E、I、O都可以按上述方法进行换质 法变形推理：
原命题 SAP SEP SIP SOP
换质命题 SE﹁P SA﹁P SO﹁P SI﹁P
⑵换位法，改变原命题主项和谓项的位 置而推出一个新命题的推理方法。
步骤:第一，只更换主、谓项的位置；第 二，换位命题的主、谓项不得扩大原命 题中的对应项的周延情况。
(2) 按照前提和结论一般性程度的不同，可以把推理分为演 绎、归纳和类比。演绎是由一般性的前提推到个别性的结论； 演绎推理的前提必须蕴涵结论，即一个正确的演绎推理的前提 如果是真的，则结论一定是真的，所以它一定是必然性推理。 归纳是由个别性的前提推到一般性的结论；类比是由个别性的 前提推到个别性的结论。归纳和类比就是所说的或然性推理。
2.命题和语句
(1)命题是表达判断的语句，但并非所有语句都表达 命题。只有能区分其真或假的语句才构成命题。
语句主要有四种，即陈述句、疑问句、祈使句和感 叹句。其中陈述句一般是能区分真假的，它是命题的最 基本语言形式；疑问句、祈使句、感叹句一般不直接表 达判断，所以不是命题；但反诘疑问句、预设句因为隐 含着判断，所以是命题。
(2)一类推理的正确性，必须分析到简单命题即原子命题所包含 的概念即词项才能判定，则这种推理就称为简单命题推理即词 项推理。相应的逻辑称为词项逻辑。
例如：所有谎言是不可信的
所有S是P
有些谎言是不可信的
有些S是P
另一类推理的正确性，如果只要分析到其中所包含的简单命 题即原子命题为止即可判定，那么这类推理就称为复合命题推 理即命题推理。相应的逻辑称为命题逻辑。
直言命题A、E、I、O四种形式的换 质位情况归纳如下:
3 命题逻辑的推理理论
（7）拒取式规则
AB B A
（8） 假言三段论规则
AB BC AC
（9）析取三段论规则
AB B A
（10）构造性二难推理规则
AB CD AC BD
（11）破坏性二难推理规则
AB CD BD AC
（12） 合取引入规则
A B AB
证明方法： ◦ 直接证明法 ◦ 附加前提法 ◦ 归谬法（或称反证法）
（2） 联结词符号： ┐， ， ， ， （3） 括号与逗号：( )，， 2. 合式公式（同合取联接词定义）
3. 推理规则
（1）前提引入规则 在证明的任何步骤上都可以引入前提。
（2）结论引入规则 在证明的任何步骤上所得到的结论都可以作为后继证明的前提。
（3）置换规则 在证明的任何步骤上，命题公式中的子公式都可以用与之等值的公
1、用不同的方法验证下面推理是否正确。对于正确的推理还 要在P系统中给出证明。 （1） 前提：pq, q
结论：p （2） 前提：qr, pr
结论：qp
（1）不正确。 验证答案，只需证明(pq)qp不是重言式。 方法一 等值演算
(pq)qp ((pq)q)p (pq)qp ((pq)(qq))p pq 易知10是成假赋值，故(pq)qp不是重言式，所以推理不正确。
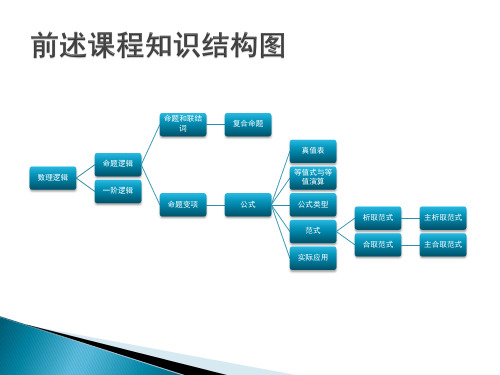
数理逻辑
命题逻辑 一阶逻辑
命题和联结 词
命题变项
复合命题 公式
真值表 等值式与等
值演算 公式类型
范式
实际应用
析取范式 合取范式
主析取范式 主合取范式
根据下列真语句，请判断是谁谋害了张先生？ (1)A、B、C三人中至少有一人。 (2)如果张先生生前未饮过麻醉剂，那不是C。 (3)如果张先生曾饮过麻醉剂，那不是A。 (4)如果是A谋害的，那么B也参加了。 (5)如果作案在落雨前，则是A谋害的。 (6)如果作案不在落雨前，张先生临死前搏斗过。 (7)张先生临死前搏斗过，就不是B谋害的。 (8)经过法医解剖化验，张先生死前曾饮过麻醉剂。
3第三章 命题逻辑的推理理论
从语言角度, 推理分为语义和语法两种。 从语言角度, 推理分为语义和语法两种。 语义(semantics)推理注重内涵的正确性 也就是从真 语义(semantics)推理注重内涵的正确性, 也就是从真 推理注重内涵的正确性, 要推出真的结论来, 的前提出发要推出真的结论来 推理过程考虑得少, 的前提出发要推出真的结论来, 推理过程考虑得少,关 心的是结论的正确性。 心的是结论的正确性。 语法推理则注重形式上的有效, 注重推理过程是否符 语法推理则注重形式上的有效, 注重推理过程是否符 则注重形式上的有效 合某些事先规定的逻辑规则, 结论是严格遵循规则 合某些事先规定的逻辑规则, 若结论是严格遵循规则 有效的 得到的, 那便是有效 得到的, 那便是有效的。 数理逻辑主要采用语法推理, 数理逻辑主要采用语法推理, 它关心的是结论的有效 不关心前提的实际真值, 性，而不关心前提的实际真值, 当然语法推理作为一 种推理方法, 种推理方法, 它必须能反映客观事物中真实存在的逻 辑关系, 语法推理必须保证语义上的正确性 必须保证语义上的正确性。 辑关系, 即 语法推理必须保证语义上的正确性。
3、2.1节给出的24个等值式中的每个都可以 2.1节给出的 个等值式中的每个都可以 节给出的24 派生出两条推理定律。 派生出两条推理定律。 例如：双重否定律 A⇔¬¬A ⇔¬¬A 例如： 可以产生两条推理定律 A⇒¬¬A ¬¬A ¬¬A ¬¬A ⇒A
§3.2 自然推理系统P 自然推理系统P
由上一节知识可知，可以利用真值表法、等值演算法 由上一节知识可知，可以利用真值表法、 真值表法 和主析取范式法三种方法来判断推理是否正确。 和主析取范式法三种方法来判断推理是否正确。 三种方法来判断推理是否正确 但是，当推理中包含的命题变项较多时，以上三种 命题变项较多时 但是，当推理中包含的命题变项较多 方法的演算量太大。因此对于由前提A1, A2,…,Ak推 方法的演算量太大。因此对于由前提A B的正确推理应给出严谨的证明。 正确推理应给出严谨的证明。 证明是一个描述推理过程的命题公式序列， 证明是一个描述推理过程的命题公式序列，其中的每 是一个描述推理过程的命题公式序列 个公式是已知前提或者是由某些前提应用推理规则得 个公式是已知前提或者是由某些前提应用推理规则得 已知前提或者是 到的结论。 到的结论。
逻辑学导论第三章
14
也可以用否定词、等值把矛盾关系表述如下：
◦ （1）SAP↔¬SOP ◦ （2）SEP↔¬SIP ◦ （3）SIP↔¬SEP ◦ （4）SOP↔¬SAP
15
差等关系
◦ 亦称“从属关系”，指A与I、E与O之间的关系。我们可 以把它概括为：如果全称命题真，则相应的特称命题真； 如果特称命题假，则相应的全称命题假；如果全称命题假， 则相应的特称命题真假不定；如果特称命题真，则相应的 全称命题真假不定。
SAP 等 关 系 差 等 关 系 关 系 SIP 下反对关系 SOP 矛 盾 盾 矛 关 反对关系 系 差 等 关 关 系 系 差 SEP 差 等 关
差 a （某个 S） 是P 差
系 系 a（某个 S） 不是 P
等
等
关
19
直言命题中词项的周延性
◦ 在直言命题中，若断定了一个词项的全部外延，则称它是 周延的，否则是不周延的。由此可知，直言命题中词项的 周延性有下述特点：
41
以上五条三段论规则是基本的，用它们就足以把有 效的三段论与无效的三段论区分开来。为明确和方 便起见，有时还从它们证明、推导出一些规则，例 如：
◦ （6）两个特称前提不能得结论。 ◦ （7）如果两个前提中有一个特称，结论必然特称。
42
根据三段论的一般规则，还可以证明有关三段论的 一些定理，例如：
◦ 定理 一个结论全称的正确三段论，其中项不能周延两次。
43
三段论的特殊规则
第一格规则：
◦ （1）小前提必须肯定。 ◦ （2）大前提必须全称。
44
第二格规则：
◦ （1）两个前提必须有一个否定。 ◦ （2）大前提必须全称。
45
第三格规则：
◦ （1）小前提必须肯定。 ◦ （2）结论必须特称。
第三章推理的形式结构
充分性: 若蕴涵式(A1∧A2∧…∧Ak)→B为重言式，则对于任何赋 值此蕴涵式均为真，因而不会出现前件为真后件为假 的情况，即在任何赋值下，或者A1∧A2∧…∧Ak为假， 或者A1∧A2∧…∧Ak和B同时为真，这正符合定义3.1中 推理正确的定义。 由此定理知，推理形式： 前提：A1,A2,…,Ak 结论：B 是有效的当且仅当(A1∧A2∧…∧Ak)→B为重言式。
以引入前提。
（2） 结论引入规则：在证明的任何步骤上所得 到的结论都可以作为后继证明的前提。 （3） 置换规则：在证明的任何步骤上，命题公 式中的子公式都可以用与之等值的公式置换，得到 公式序列中的又一个公式。
（4） 假言推理规则
（5） 附加规则：
（6） 化简规则：
（7） 拒取式规则：
（8） 假言三段论规则：
A1,A2,…,Ak和B中出现的命题变项的任意一组赋值，
或者A1∧A2 ∧…∧Ak为假，或者当A1∧A2 ∧…∧Ak为 真时，B也为真，则称由前提A1,A2,…,Ak推出B的推 理是有效的或正确的，并称B是有效结论。 其中，前提是一个有限的公式集合，记为Г。 将由Г推B的推理记为Г├ B。 若推理是正确的，则记为Г B，否则记为Г B。
（9） 析取三段论规则：
（10） 构造性二难推理：
（11） 破坏性二难推理规则：
（12） 合取引入规则：
P中的证明就是由一组P中公式作为前提，利用P 中的规则，推出结论。当然此结论也为P中公式。
例3.3 在自然推理系统P中构造下面推理的证明： (1)前提：p∨q,q→r,p→s,┐s 结论：r∧(p∨q) 证明： ① p→s ② ┐s 前提引入
结论的否定 前提引入 前提引入 ②③析取三段 前提引人 ④⑤拒取式 ⑥置换 前提引入 ⑦⑧析取三段
第三章.命题逻辑
第三章命题逻辑重点：掌握数理逻辑中命题的翻译及命题公式的定义；利用真值表技术和公式转换方式求公式的主析取范式和主合取范式；利用规则、基本等价和蕴涵公式、三种不同的推理方法完成命题逻辑推理；难点：如何正确地掌握对语言的翻译，如何利用推理方法正确的完成命题推理。
数理逻辑是用数学方法来研究推理的形式结构和推理规律的数学学科，它与数学的其他分支、计算机学科、人工智能、语言学等学科均有十分密切的联系，并且益显示出它的重要作用和更加广泛的应用前景。
要很好地使用计算机，就必须学习逻辑。
数理逻辑分五大部分。
在离散数学中仅介绍命题逻辑和谓词逻辑。
命题逻辑是谓词逻辑的基础，只有掌握了命题逻辑，才能学好谓词逻辑。
对于命题逻辑，下面从六个知识点来加以阐述。
3.1 命题符号化及联系结词1 命题有确切真值的陈述句称为命题。
所谓确切真值是指在具体的环境，具体的时间，具体的对象，具体的位置等情况下能唯一确定真值的。
命题分为两种：(1) 简单命题：不能分解为更为简单的句子的命题。
(2)复合命题：能够分解为更为简单的命题。
2 命题联结词关于联结词，有如下几点要注意：（1）此联结词是联结的句子与句子之间的联结，而非单纯的名记号、形容词、数词等的联结；（2）此联结词是两个句子真值之间的联结词，而非句子的具体含义的联结，两句子之间可以无任何的内在联系；（3）联结词与自然语言之间的对应并非一一对应，如合取联结词“∧”对应了自然语言中的“既……又……”、“不仅……而且……”、“虽然……但是……”、“并且”、“和”、“与”等。
如蕴涵联结词“→”，P →Q 对应了自然语言中的“加P 则Q ”，“只要P 就Q ”，“P 仅当Q ”，“只有Q 才P ”，“除非Q 否则乛P ”等。
如等价联结词“←→ ”对应了自然语言中的“等价”、“并且仅当”、“充分必 ”等。
如析取联结词∨是对应相容的或(中兼的或)。
3.2 命题公式及分类一般称具有确切真值的简单命题叫命题常量，用P ，Q ，R ，…等表示。
命题逻辑的推理理论
10:44:53
16
直接证明法
(2) 写出证明的形式结构
前提：(pq)r, rs, s
结论：pq (3) 证明 ① r s ② s ③ r ④ (p q) r 前提引入 前提引入 ①②拒取式 前提引入
⑤ (p q)
⑥ pq
③④拒取式
⑤置换
10:44:53
17
附加前提证明法
可见，推理的有效性是一回事，前提与结论的 真实与否是另一回事。所谓推理有效，指它的结 论是它的前提的合乎逻辑的结果，也即，如果它 的前提都为真，那么所得结论也必然为真，而并 不是要求前提或结论一定为真或为假。如果推理 是有效的话，那么不可能它的前提都为真时而它 的结论为假。
10:44:53
4
推理的形式结构
10:44:53
25
练习1解答
方法二：主析取范式法， (pq)qp ((pq)q)p pq M2 m0m1m3 未含m2, 不是重言式, 推理不正确.
10:44:53
26
10:44:53
27
练习1解答
(2) 前提：qr, pr 结论：qp 解 推理的形式结构： (qr)(pr)(qp) 用等值演算法
附加前提证明法: 适用于结论为蕴涵式
欲证
前提：A1, A2, …, Ak
结论：CB 前提：A1, A2, …, Ak, C 结论：B
等价地证明
理由：(A1A2…Ak)(CB) ( A1A2…Ak)(CB) ( A1A2…AkC)B
(A1A2…AkC)B
10:44:53
8
推理定律——重言蕴涵式
1. A (AB)
附加律
2. (AB) A
3. (AB)A B 4. (AB)B A
离散数学最全最新答案--屈婉玲
第一章命题逻辑基本概念课后练习题答案4.将下列命题符号化，并指出真值：（1）p∧q,其中，p:2是素数，q:5是素数,真值为1；（2）p∧q,其中，p:是无理数，q:自然对数的底e是无理数,真值为1；（3）p∧┐q,其中，p:2是最小的素数，q:2是最小的自然数,真值为1；（4）p∧q,其中，p:3是素数，q:3是偶数,真值为0；（5）┐p∧┐q,其中，p:4是素数，q:4是偶数,真值为0.5.将下列命题符号化，并指出真值：（1）p∨q,其中，p:2是偶数，q:3是偶数,真值为1；（2）p∨q,其中，p:2是偶数，q:4是偶数,真值为1；（3）p∨┐q,其中，p:3是偶数，q:4是偶数,真值为0；（4）p∨q,其中，p:3是偶数，q:4是偶数,真值为1；（5）┐p∨┐q,其中，p:3是偶数，q:4是偶数,真值为0；6.（1）(┐p∧q)∨(p∧┐q),其中，小丽从筐里拿一个苹果，q：小丽从筐里拿一个梨；（2）(p∧┐q)∨(┐p∧q),其中，p：刘晓月选学英语，q：刘晓月选学日语；.7.因为p与q不能同时为真.13.设p:今天是星期一，q:明天是星期二，r:明天是星期三：（1）p→q，真值为1（不会出现前件为真，后件为假的情况）；（2）q→p，真值为1（也不会出现前件为真，后件为假的情况）；（3）p q，真值为1；（4）p→r，若p为真，则p→r真值为0，否则，p→r真值为1.16 设p、q的真值为0；r、s的真值为1，求下列各命题公式的真值。
（1）p∨(q∧r)⇔0∨(0∧1) ⇔0（2）（p↔r）∧(﹁q∨s) ⇔（0↔1）∧(1∨1) ⇔0∧1⇔0.⌝p∧⌝q∧r）↔(p∧q∧﹁r) ⇔（1∧1∧1）↔ (0∧0∧0)⇔0（3）（⌝r∧s）→(p∧⌝q) ⇔（0∧1）→(1∧0) ⇔0→0⇔1(4)（π是无理数。
并且，如果3是无理数，则2也是无理数。
另外6能被2整除，6才能被4整除。
”17．判断下面一段论述是否为真：“π是无理数1答：p:q: 3是无理数02是无理数 1r:s: 6能被2整除1t: 6能被4整除0命题符号化为：p∧(q→r)∧(t→s)的真值为1，所以这一段的论述为真。
形式逻辑学第三章简单命题及其推理
1、换质推理 原则：
第一，改变前提命题的质。
第二，将前提命题的谓项变为它的矛盾概 念。
第三，前提命题的量项和主、谓项的位置 保持不变。
• SAPSE¯P
• 甲超市里的食品都是经过检疫的，所以， 甲超市里的食品都不是没经过检疫的。
• 所有高科技产品都是高附加值的，所以， 所有高科技产品都不是没有高附加值的。
• 有的细菌不是有害的，所以，有的细菌 是无害的。
• 有些青年人是大学生，所以，有些青年 人是非大学生。
2、换位推理 原则： 第一，改变主、谓项的位置。
第二，在前提中不周延的概念，在结论中 也不得周延。
第三，不改变前提命题的质。
• SAPPIS
• 伟大的领袖都是著名的政治家，所以， 有的著名的政治家是伟大的领袖。
3、所有的人都享有基本人权，所以，并 非所有的人都不享有基本人权。
4、人不能两次踏入同一条河流，所以， 并非人能够两次踏入同一条河流。
3、下反对关系推理
• ¬SIPSOP • ¬SOP SIP
1、并非有的非洲国家是有核武器的国家， 所以，有的非洲国家不是有核武器的国 家。
2、并非有些反刍动物不是哺乳纲动物，所 以，有些反刍动物是哺乳纲动物。
狐狸是动物 猫不是狐狸 所以，猫不是动物
四、两个否定前提不能推出结论
第三章 简单命题及其推理
第一节 命题与推理概述 第二节 性质命题 第三节 性质命题直接推理 第四节 三段论 第五节 关系命题
第一节 命题与推理概述
一、什么是命题 二、命题的种类 三、命题和语句 四、什么是推理 五、推理的种类
一、什么是命题
1、命题定义 就是人们在认知过程中，对思维对 象属性进行肯定或否定断定的思维 形式。
第三章直言命题及其推理
喜欢下雨的人 “雨越下得大，我越高兴。” “你一定是个乐天派。” “不，我是卖雨伞的。”
比我多去一次 爸爸教育小华说：“你越来越不像话了，晚 上也不复习功课，只知道往俱乐部跑。我到俱乐 部下棋，十次倒有九次看到你!小华回答说，“那， 那您比我还多去一一次呢!” 毛病 妻子拿着一叠账单向丈夫抱怨说：“都煤气费怎么付？” “都怪我不好，我的毛病是：有钱就要花。” 丈夫作了一番检查，见妻子消了一点气又补充了 一句：“而你的毛病是：没钱也要花。”
联项的语言形式可以省略一部分，前提和结论的位置不是固 定的。
3、推理的正确性
逻辑性
正确的推理或者合符逻辑的推理必须满足两个条件： （1） 前提真实 （2） 形式正确 4、推理的种类 合符规律和规则的形式 (两种分类)
非模态 推理 演绎推理 必然性 推理 A 推理 或然性 推理 模态推理 完全归纳推理 不完全归纳推理 类比推理
+ +
+ +
+ +
(1)A—E: A判断真，E判断就假；E判断真，A判断就假。
A判断假，E判断可真可假，E判断假，A判断可真可假。 不可同真，但可同假。 反对关系 (2)A— I 全称判断真，特称判断就真，特称判断真，全称判断不定。 E—O 全称判断假，特称判断不定，特称判断假，全称判断必假。 可能同真，也可能同假。 差等关系
3.同一判断可由不同的语句表达
这是因为语言具有民族性和地域性。 例： 不同语言的语句： 我是学生 I am a pupil. 同一语言中的不同语句也可以表达相同的判断。 湖南大学是千年学府。 湖南大学难道不是千年学府吗？
在使用判断时，我们要注意选择最佳的语句以便获得最佳的效果。
例： 阿凡提解梦： 陛下所有的家人都会比陛下先死 陛下将比所有的家人都长寿
《逻辑学》第三章 命题的自然推理
f9 f8 的矛盾式
f13 f4 的矛盾式
f14 f3 的矛盾式 f15 f2 的矛盾式
f10
f12
f7 的矛盾式
f5 的矛盾式
f11 f6 的矛盾式
f16
f1 的矛盾式
随着变项数目的增加，函项数也增加，当变项数目为3时，函项数目达 到256个。但不管函项数是多少，重言式的函项只是一个，矛盾式的函 项也是一个，其余均是可满足式。真值函项有3类，那么，表达真值函 项的真值形式也有3类：重言式（永真式）、矛盾式（永假式）和可满 足式（可真可假式）。当然，每一类真值函项包括很多的真值形式， 而同一类真值函项的真值形式是等值的。
常见的重言式（逻辑规律）
见教科书p83－84
3.2 命题的真值判定方法
真值表方法
真值表的作用
定义作用：5个基本真值形式的真值 表定义了5个真值形式。如，什么是 合取式？回答是，每一支命题为真， 则它为真的 那种真值形 p q p∧q 式，这正是 t t t 合取式的真 值表反映的 f t f 情况。 f f t f f f
AB
例1 1. p q 2. q r 3. P 4. q 5. r 6. pr 例2 1. p q 2. ¬ q 3. P 4. q 5. q∧¬ q 6. ¬ p / ∴ p r AP 1,3 _ 2,4 _ 3,5 +
例3 1. p q 2. r s 3. p∨r 4. P 5.q 6. q∨s 7. r 8. s 9. q∨s 10. q∨s
判定作用： 1、判定一个公式的性质（重言 式，矛盾式或可满足式）； 2、判定任意多个公式的关系 （等值或矛盾等）； 3、判定一个推理是否有效，即 它是否一个重言的蕴涵式或 等值式。
真值表的作法
离散数学第三章 命题逻辑的推理理论
3
推理实例
例1 判断下面推理是否正确 (1) 若今天是 号，则明天是 号. 今天是 号. 所以 明天是 号. 若今天是1号 则明天是5号 今天是1号 所以, 明天是5号 (2) 若今天是 号，则明天是 号. 明天是 号. 所以 今天是 号. 若今天是1号 则明天是5号 明天是5号 所以, 今天是1号 解 设 p：今天是 号，q：明天是 号. ：今天是1号 ：明天是5号 → ∧ → (1) 推理的形式结构 (p→q)∧p→q 推理的形式结构: 用等值演算法 (p→q)∧p→q → ∧ → ⇔ ¬((¬p∨q)∧p)∨q ¬ ∨ ∧ ∨ ∨¬q∨ ⇔ ¬p∨¬ ∨q ⇔ 1 ∨¬ 由定理3.1可知推理正确 由定理 可知推理正确
19
练习1： 练习 ：判断推理是否正确
1. 判断下面推理是否正确 判断下面推理是否正确: (1) 前提：¬p→q, ¬q 前提： → 结论： 结论：¬p ∧¬q→¬ 推理的形式结构: ¬ → ∧¬ →¬p 解 推理的形式结构 (¬p→q)∧¬ →¬ 方法一：等值演算法 方法一： (¬p→q)∧¬ →¬ ∧¬q→¬ ¬ → ∧¬ →¬p ∧¬q)∨¬ ⇔ ¬((p∨q)∧¬ ∨¬ ∨ ∧¬ ∨¬p ∧¬q)∨ ∨¬ ∨¬p ⇔ (¬p∧¬ ∨q∨¬ ¬ ∧¬ ∨¬p ⇔ ((¬p∨q)∧(¬q∨q))∨¬ ¬ ∨ ∧ ¬ ∨ ∨¬ ⇔ ¬p∨q ∨ 易知10是成假赋值，不是重言式，所以推理不正确 易知 是成假赋值，不是重言式，所以推理不正确. 是成假赋值
16
例4 前提：¬(p∧q)∨r, r→s, ¬s, p 前提： ∧ ∨ → 结论： 结论：¬q 证明 用归缪法 ①q 结论否定引入 ② r→s → 前提引入 ③ ¬s 前提引入 ②③拒取式 ④ ¬r ②③拒取式 ⑤ ¬(p∧q)∨r ∧ ∨ 前提引入 ④⑤析取三段论 ⑥ ¬(p∧q) ∧ ④⑤析取三段论 ∨¬q ⑦ ¬p∨¬ ∨¬ ⑥置换 ①⑦析取三段论 ⑧ ¬p ①⑦析取三段论 ⑨p 前提引入 ⑧⑨合取 ¬p∧p ∧ ⑧⑨合取
推理实例
例1 判断下面推理是否正确 (1) 若今天是 号，则明天是 号. 今天是 号. 所以 明天是 号. 若今天是1号 则明天是5号 今天是1号 所以, 明天是5号 (2) 若今天是 号，则明天是 号. 明天是 号. 所以 今天是 号. 若今天是1号 则明天是5号 明天是5号 所以, 今天是1号 解 设 p：今天是 号，q：明天是 号. ：今天是1号 ：明天是5号 → ∧ → (1) 推理的形式结构 (p→q)∧p→q 推理的形式结构: 用等值演算法 (p→q)∧p→q → ∧ → ⇔ ¬((¬p∨q)∧p)∨q ¬ ∨ ∧ ∨ ∨¬q∨ ⇔ ¬p∨¬ ∨q ⇔ 1 ∨¬ 由定理3.1可知推理正确 由定理 可知推理正确
19
练习1： 练习 ：判断推理是否正确
1. 判断下面推理是否正确 判断下面推理是否正确: (1) 前提：¬p→q, ¬q 前提： → 结论： 结论：¬p ∧¬q→¬ 推理的形式结构: ¬ → ∧¬ →¬p 解 推理的形式结构 (¬p→q)∧¬ →¬ 方法一：等值演算法 方法一： (¬p→q)∧¬ →¬ ∧¬q→¬ ¬ → ∧¬ →¬p ∧¬q)∨¬ ⇔ ¬((p∨q)∧¬ ∨¬ ∨ ∧¬ ∨¬p ∧¬q)∨ ∨¬ ∨¬p ⇔ (¬p∧¬ ∨q∨¬ ¬ ∧¬ ∨¬p ⇔ ((¬p∨q)∧(¬q∨q))∨¬ ¬ ∨ ∧ ¬ ∨ ∨¬ ⇔ ¬p∨q ∨ 易知10是成假赋值，不是重言式，所以推理不正确 易知 是成假赋值，不是重言式，所以推理不正确. 是成假赋值
16
例4 前提：¬(p∧q)∨r, r→s, ¬s, p 前提： ∧ ∨ → 结论： 结论：¬q 证明 用归缪法 ①q 结论否定引入 ② r→s → 前提引入 ③ ¬s 前提引入 ②③拒取式 ④ ¬r ②③拒取式 ⑤ ¬(p∧q)∨r ∧ ∨ 前提引入 ④⑤析取三段论 ⑥ ¬(p∧q) ∧ ④⑤析取三段论 ∨¬q ⑦ ¬p∨¬ ∨¬ ⑥置换 ①⑦析取三段论 ⑧ ¬p ①⑦析取三段论 ⑨p 前提引入 ⑧⑨合取 ¬p∧p ∧ ⑧⑨合取
《离散数学》课件-第3章命题逻辑的推理理论
判断方法一：真值表法
真值表的最后一列全为1，所以（（p∨q）∧┐p） →q为重言式。因而推理正确。
判断方法二：等值演算法
（（p∨q）∧┐p）→q ⇔ （（p∧┐p）∨（q∧┐p））→q ⇔ （ q∧┐p ）→q ⇔ ┐q∨p∨q ⇔1
因为（（p∨q）∧┐p）→q为重言式，所 以推理正确。
判断方法三：主析取范式法
★ ★★
可见，如果能证明★★是重言式，则★也是重言式。 在★★中，原来的结论中的前件A已经变成前提了，称A为 附加前提。称这种将结论中的前件作为前提的证明方法为 附加前提法。
例：在自然推理系统P中构造下面推理的证明 如果小张和小王去看电影，则小李也去看电影。小
赵不去看电影或小张去看电影。小王去看电影。所 以，当小赵去看电影时，小李也去。
前提引入
② ┐s
前提引入
③ ┐p
①②拒取式（A→B）∧┐B⇒┐A
④ p∨q
B）∧┐B⇒A
⑥ q→r
前提引入
⑦r
⑤⑥假言推理（A→B）∧A⇒B
⑧ r∧（p∨q） ⑦④合取引入
（2）前提：┐p∨q，r∨┐q，r→s 结论：p→s
证明：
① ┐p∨q 前提引入
② p→q
①置换
（A→B）∧（C→D）∧（┐B∨┐D） ⇒（┐A∨┐C）
（12）合取引入规则：若证明的公式序列中出现过 A和B，则A∧B是A和B的有效结论。
推理规则（12个）
（1）前提引入规则 （2）结论引入规则（隐规则） （3）置换规则：等值置换 （4）假言推理规则：（A→B）∧A⇒B （5）附加规则：A⇒（A∨B） （6）化简规则：A∧B ⇒A （7）拒取式规则：（A→B）∧┐B⇒┐A （8）假言三段论规则：（A→B）∧（B→C）⇒（A→C） （9）析取三段论规则：（A∨B）∧┐B⇒A （10）构造性二难推理规则 （11）破坏性二难推理规则 （12）合取引入规则
第三章性质命题及其推理
3、三段论前提、形式与结论的联系情况 三段论前提、
（1）前提真实，形式正确，结论必然真实。 前提真实，形式正确，结论必然真实。 （2）前提真实，形式错误，结论可真可假。 前提真实，形式错误，。 前提虚假，形式正确，结论可真可假。 （4）前提虚假，形式错误，结论可真可假。 前提虚假，形式错误，结论可真可假。
三、换质位法 定义： 1、定义：把换质法和换位法结合起来交 互使用的命题变形法。 互使用的命题变形法。 规则： 2、规则：同时遵守换质法和换位法的规 则。 公式：原命题（推出） 3、公式：原命题（推出）换质位命题 SAP——SE非P——非PES； ——SE非 ——非 SE SEP——SA非P——非PES； ——SA非 ——非 SA SIP——SO非P——（不能换位）； ——SO非 ——（不能换位）； SO SOP——SI非P——非PIS。 ——SI非 ——非 SI
1、A与E的关系（特点：量同质异） A E 反对关系： 反对关系 不能同真（一个真，另一个必假）； 可以同假（一个假，另一个可真可假）。 2、I与O的关系（特点：量同质异） I O 下反对关系： 下反对关系 不能同假（一个假，另一个必真）； 可以同真（一个真，另一个可真可假）。
3、A与O、E与I的关系（特点：量质皆异） A O E I 矛盾关系： 矛盾关系 不能同真（一个真，另一个必假）； 不能同假（一个假，另一个必真）。 4、A与I、E与O的关系（特点：量异质同） A I E O 差等关系： 差等关系 全称真，特称必真； 全称假，特称可真可假； 特称假，全称必假； 特称真，全称可真可假。
4、三段论推理必须明确的几点认识 只有前提真实并且形式正确的推理， （1）只有前提真实并且形式正确的推理， 才能推出必然真实的结论；除此之外， 才能推出必然真实的结论；除此之外，其它 情况的结论都是不必然真的。 情况的结论都是不必然真的。 前提真实并且结论也真实的推理， （2）前提真实并且结论也真实的推理，其 形式未必正确；但是， 形式未必正确；但是，形式正确而结论虚假 的推理，其前提一定包含有虚假命题。 的推理，其前提一定包含有虚假命题。 检验命题真假要靠科学知识， （3）检验命题真假要靠科学知识，检验形 式正误要靠逻辑知识； 式正误要靠逻辑知识；推理有逻辑性只是指 推理的形式本身正确，不等于说“ 推理的形式本身正确，不等于说“从前提能 够推出必然真的结论” 够推出必然真的结论”。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
14.09.2020
8
只要证明蕴涵式(p ∧ (p q)) q为重言式即可。 三种方式证明：真值表、 等值演算、 主析取范式。 例：判断下列推理是否正确。 1、今天小李或去网吧或去教室。他没去教室，所以
他去网吧了。 设 p：小李去网吧。q：小李去教室。则
前提：p ∨ q , q 结论：p 推理的形式结构： ((p ∨ q) ∧ q) p
<AX(I)，R(I)>为I 的形式演算系统
14.09.2020
17
自然推理系统 P 定义如下： 1、字母表
（1）命题变项符号：p,q,r,… （2）联结词符号： ，∧，∨，， （3）括号与逗号：() , 2、合式公式 定义同1.6 3、推理规则
14.09.2020
3
3.1 推理的形式结构
关于定义3.1的说明： （1）由前提A1，A2，…Ak 推 B 的推理
记作{A1，A2，…Ak}∧ B,称为推理的形式结构。 若推理正确，记作{A1，A2，…Ak}|=B ，
否则：记作{A1，A2，…Ak}|≠B。
14.09.2020
4
3.1 推理的形式结构
14.09.2020
9
（1）真值表
p q p∨q q (p∨q)∧q
00 0 1
0
01 1 0
0
10 1 1
1
11 1 0
0
((p∨q)∧q) p 1 1 1 1
14.09.2020
10
（2）等值演算法： ((p∧ q) ∧ q) p
((p∧ q )∧ (q∧ q)) p (p∧ q ) p (p∧ q )∧ p p∧ q∧ p 1
14.09.2020
15
8.构造性二难 (A→B)∧ (C→D)∧ ( A∧ C) (B∧ D)
(特殊形式) (A→B)∧ ( A→B)∧ ( A∧ A) B
9.破坏性二难 (A→B)∧ (C→D)∧ ( B∧ D)
( A∧ C)
判断推理是否正确，上述三种方法演算量太大， 故而应给出严谨的证明。证明是一个描述推理过 程的命题公式的序列，其中的每个公式或者是已 知前提，或者由某些前提应用推理规则得到的结 论.要构造出严谨的证明必须在形式系统中证明。
14.09.2020
16
3.2 自然推理系统P
定义3.2 一个形式系统 I 由下列四个部分组成： （1）非空的字母表集，记作A（I）。 （2）A(I)符号构造的合式公式集，记作E(I)。 （3）E(I)中一些特殊的公式组成的公理集,记作AX(I)。 （4）推理规则集，记作R(I)。 可以将I 记作为4元组<A(I),E(I),AX(I),R(I)> 其中< A(I)，E(I) >是I 的形式语言系统
14.09.2020
13
3、若下午气温超过30◦C，则王小燕必去游泳。若她 去游泳，她就不去看电影了。所以，若王小燕没去 看电影，下午气温必超过了30◦C。
p：下午气温超过30◦C
q：王小燕去游泳
r：王小燕去看电影
前提：p q，q r 结论： r p 形式结构： ((p q)(q r)) ( r p)
(2)对于任一组赋值，前提和结论的取值有以下四种 情况： ① {A1，A2，…Ak}为0，B为0。 ② {A1，A2，…Ak}为0，B为1。 ③ {A1，A2，…Ak}为1，B为0。 ④ {A1，A2，…Ak}为1，B为1。
结论: ① ② ④ 情况下的推理是正确的. ③ 情况下的推理是错误的.
14.09.2020
所以，推理正确，即((p∧ q)∧ q) p
14.09.2020
12
例：判断下列推理是否正确。 2、若a能被4整除，则天下雨。现在天下雨，所以a
能被4整除。 设 p： a能被4整除。q：天下雨。则， 前提：p q , q 结论：p 推理的形式结构： ((p q) ∧ q) p
答案： 此推理不正确
0
1
1
0
1
1
结论: (1) 式正确. (2)式推理不正确.
14.09.2020
7
定理3.1 命题公式A1，A2，…Ak 推 B 的推理正确当 且仅当 (A1 ∧ A2 ∧ … ∧ Ak) B为重言式。
（证明参见课本） 本书中, 一般采用(A1 ∧ A2 ∧ … ∧ Ak) B作为推 理的形式结构, 并且把它写成下面的形式. 前提：p , p q 结论：q 推理的形式结构： (p ∧(p q)) q
所以，推理正确，即((p∧ q)∧ q) p
14.09.2020
11
（3）主析取范式法： ((p ∧ q) ∧ q) p ((p ∧ q) ∧ q) ∧ p (p ∧ q) ∧ q ∧ p ( p ∧ q ) ∧ q ∧ p (p∧ q )∧ q∧ (p∧ p)∧ p∧ (q∧ q ) (p∧ q )∧ (q∧ p)∧ (q∧ p)∧ (p∧ q)∧ ( p∧ q ) m0 ∧ m1 ∧ m2 ∧ m3
第三章 命题逻辑的推理理论
14.09.2020
1
3.1 推理的形式结构
所谓推理是指从前提出发推出结论的思维过程. 本节所要研究的内容是以什么样的形式来进行 推理, 什么样的推理过程才是正确的推理过程, 也 就是说什么样的推理才是有效的推理.
14.09.2020
2
3.1 推理的形式结构
定义3.1 设A1,A2,…,Ak,B都是命题公式，若对于 A1,A2,…,Ak,B中出现的命题变项的任意一组赋值， 或者A1∧ A2∧ … ∧ Ak为假，或者当A1∧ A2∧ … ∧ Ak为真时，B也为真，则称由前提A1,A2,…,Ak推 出B的推理是有效的或正确的，并称B是有效的结 论。
5
3.1 推理的形式结构
（3）推理正确, 并不能保证结论B一定为真, 这与数 学上的推理是不同的.
判断下列推理是否正确 (1) {p,pq}∧ q (2) {p,qp}∧ q
14.09.2020
6
3.1 推理的形式结构
pq
00 01 10 11
p∧(pq) q
0
Hale Waihona Puke 0010
0
1
1
p∧(qp) q
0
0
14.09.2020
14
推理定律
1.附加律
A (A ∧ B)
2.化简律 (A ∧ B) A
3.假言推理 (A→B) ∧ A B
4.拒取式 (A→B) ∧ B A
5.析取三段论 (A ∧ B) ∧ B A
6.假言三段论 (A→B) ∧ (B→C) (A→C)
7.等价三段论 (A B) ∧ (B C) ((A C)