s曲线与方程
非线性回归分析常见曲线及方程

非线性回归分析常见曲线及方程Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】非线性回归分析回归分析中,当研究的因果关系只涉及和一个时,叫做一元回归分析;当研究的因果关系涉及因变量和两个或两个以上自变量时,叫做多元回归分析。
此外,回归分析中,又依据描述自变量与因变量之间因果关系的表达式是线性的还是非线性的,分为线性回归分析和非线性回归分析。
通常线性回归分析法是最基本的分析方法,遇到非线性回归问题可以借助数学手段化为线性回归问题处理两个现象变量之间的相关关系并非线性关系,而呈现某种非线性的曲线关系,如:双曲线、二次曲线、三次曲线、幂函数曲线、指数函数曲线(Gompertz)、S型曲线(Logistic) 对数曲线、指数曲线等,以这些变量之间的曲线相关关系,拟合相应的回归曲线,建立非线性回归方程,进行回归分析称为非线性回归分析常见非线性规划曲线1.双曲线1bay x =+2.二次曲线3.三次曲线4.幂函数曲线5.指数函数曲线(Gompertz)6.倒指数曲线y=a/e b x其中a>0,7.S型曲线(Logistic)1e x ya b-=+8.对数曲线y=a+b log x,x>09.指数曲线y=a e bx其中参数a>01.回归:(1)确定回归系数的命令[beta,r,J]=nlinfit(x,y,’model’,beta0)(2)非线性回归命令:nlintool(x,y,’model’, beta0,alpha)2.预测和预测误差估计:[Y,DELTA]=nlpredci(’model’, x,beta,r,J)求nlinfit 或lintool所得的回归函数在x处的预测值Y及预测值的显着性水平为1-alpha的置信区间Y,DELTA.例2 观测物体降落的距离s与时间t的关系,得到数据如下表,求s关于t的回归方程2ˆct=.+btas+解:1. 对将要拟合的非线性模型y=a/e b x,建立M文件如下:function yhat=volum(beta,x)yhat=beta(1)*exp(beta(2)./x);2.输入数据:x=2:16;y=[ 10];beta0=[8 2]';3.求回归系数:[beta,r ,J]=nlinfit(x',y','volum',beta0); beta即得回归模型为:1.064111.6036e x y-=4.预测及作图:[YY,delta]=nlpredci('volum',x',beta,r ,J); plot(x,y,'k+',x,YY,'r')2.非线性函数的线性化曲线方程曲线图形变换公式变换后的线性函数by ax=ln ln ln c a v x u y=== u c bv +=bx y ae =ln ln c a u y==u c bv +=b xe y a=1ln ln x c a v u y===u c bv +=ln y a b x +=ln v x u y== u bv +=a。
型曲线和S型曲线增长率和增长速度

型曲线和S型曲线增长率和增长速度增长率和增长速度这两个概念在习题中经常把增长率看作增长速度,这种模糊处理没有科学性。
包括很多资料都没有很好区分;增长率是个百分率,没有“单位”,而增长速率有“单位”,“个(株)/年”。
我举个例子来说明这个问题:“一个种群有1000个个体,一年后增加到1100”,则该种群的增长率为[(1100-1000)/1000]*100%=10%。
而增长速率为(1100-1000)/1年=100个/年。
增长率和增长速率没有大小上的相关性。
增长率:增长率是指单位时间内种群数量变化率,即种群在单位时间内净增加的个体数占个体总数的比率。
增长率=(现有个体数-原有个体数)/原有个体数=出生率—死亡率=(出生数-死亡数)/(单位时间×单位数量)。
在“J”型曲线增长的种群中,增长率保持不变;而在“S”型增长曲线中增长率越来越小。
增长速率:增长速率是指单位时间种群增长数量。
增长速率=(现有个体数-原有个体数)/增长时间=(出生数-死亡数)/单位时间]。
种群增长速率就是曲线上通过每一点的切线斜率,不论是“J”型曲线还是“S”型曲线上的斜率总是变化着的。
在“J”型曲线增长的种群中,增长速率是逐渐增大。
在“S”型曲线增长的种群中,“增长速率”是该曲线上“某点”的切线的斜率,斜率越大,增长速率就越大,且斜率最大时在“ 1/2K”。
之后增长变慢,增长速率是逐渐减小。
在“S”曲线到达K值时,增长速率就为0.分析过程一对J型曲线的分析1.模型假设在食物和空间条件充裕、气候适宜、没有敌害等条件下,种群的数量每年以一定的倍数增长,第二年是第一年的λ倍。
2.对模型假设的分析从模型假设不难得出λ=现有个体数/原有个体数。
结合增长率的概念和定义式不难看出,此时增长率等于(λ-1),λ不变,增长率(λ-1)也就不变。
再看增长速率,由于一段时间内种群内个体基数不断增大,故这段时间内净增加的个体数(Ntλ-Nt)不断增多,除以时间以后即为增长速率,可以看出增长速率是不断增大的。
详解电机S曲线加减速控制
详解电机S曲线加减速控制1、S型曲线1.1 简介Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。
Sigmoid函数也叫Logistic函数,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
该S型函数有以下优缺点:优点是平滑,而缺点则是计算量大。
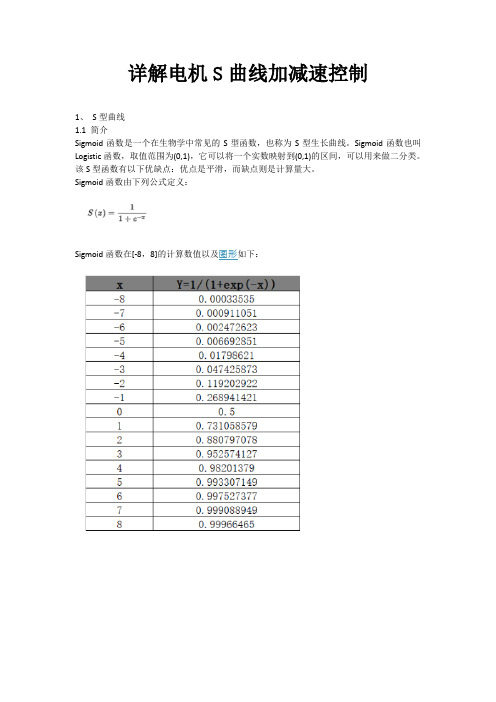
Sigmoid函数由下列公式定义:Sigmoid函数在[-8,8]的计算数值以及图形如下:由以上数据与图形可见,S型曲线就是指图形中变化阶段的曲线呈现一个英文字母'S'型,该曲线无限趋向于0和1,即取值范围为(0,1)。
1.2 曲线延伸为了更直观地观察A、B、a、b分量对函数的影响,我整理了一下对应的曲线图,如下所示:由图可见,A、B分量影响的是曲线的取值范围,而a、b分量影响的则是曲线的平滑程度。
2、应用场景–电机加减速控制2.1 简介电机加减速,顾名思义,即电机以加速方式启动,速度达到预设目标速度后保持一段时间匀速转动,随后又开始以减速方式转动直至电机以一个较低的速度停止转动。
一方面,电机加减速可以避免电机急开急停,进而可能对电机造成一定损坏;另一方面,也可以防止电机在高驱动速度不能起步的情况,即高驱动速度会出现空转、丢步现象。
因而,在电机需要达到一个较高的速度时,通常需要采用慢速加速驱动的方法,简而言之,就是需要有一个加速过程。
例如:步进电机驱动负载可以按目标速度起动,若目标速度超过自身起动脉冲频率时,则该情况下不能起动。
因而,只有当起动频率比电机起动脉冲频率低时才能正常起动,采取加速的方式使速度线性地增加到目标速度,这种方法则称为慢速加速驱动。
2.2 T型与S型目前,在电机加减速控制上,普遍的加减速方法主要有T型加减速和S型加减速,实现方法则有公式法或查表法。
S型加减速相对于T型加减速更加平稳,对电机和传动系统的冲击更小,即S型加减速的优点是启动和停止都很平滑,不会有很大的冲击,但是也并非不存在缺点,缺点就是启动和停止的时间比较长。
s型曲线回归方程

S型曲线回归方程:从概念到实践1.S型曲线回归方程的概念与特点S型曲线回归方程,或称为Sigmoid回归方程,是一种广泛使用的数学模型,特别是在生物学、医学和社会科学领域。
S型曲线描述了在饱和之前,随着自变量(通常是输入)的增加,因变量(通常是输出)的增长速率如何变化。
其特点是因变量最终会达到一个最大值或饱和点。
2.常见S型曲线及其对应的数学模型几种常见的S型曲线包括:⏹Logistic 函数:(y = \frac{1}{1 + e^{-x}})⏹Hyperbolic tangent:(y = \tanh(x))⏹Growth model:(y = \frac{a}{1 + e^{-x}})1.求解S型曲线回归方程的方法与步骤步骤如下:⏹收集数据:获取描述自变量和因变量之间关系的观察数据。
⏹数据清洗:处理缺失值、异常值和离群点。
⏹选择合适的S型曲线模型:根据数据特性选择合适的数学模型。
⏹参数估计:使用最小二乘法、梯度下降法等优化算法估计模型的参数。
⏹模型拟合:将选择的模型应用于数据,并观察其拟合效果。
⏹评估模型:使用R-squared、MSE等指标评估模型的性能。
1.应用场景举例及其实际意义举例来说,在生物学中,S型生长曲线可以描述生物种群随时间的变化,帮助理解种群的增长和生态学特性。
在社会学中,可以用S型曲线描述某种社会现象的普及程度,如新技术或新观念的采纳和传播。
2.曲线拟合优化技巧和参数选择为了提高模型的拟合效果,可以使用以下优化技巧:⏹选择正确的损失函数:损失函数决定了模型试图最小化的目标,比如均方误差(MSE)或者交叉熵等。
⏹正则化:这是一种防止模型过拟合的技术,通过对模型参数施加惩罚项来避免参数过大。
常用的正则化项包括L1正则化和L2正则化。
⏹参数选择:参数的选择应该根据具体情况进行,有时候需要做一些试验来找到最优的参数。
常见的参数选择方法有网格搜索和随机搜索。
1.异常值处理与敏感性分析方法在应用S型曲线回归时,需要对异常值进行处理。
曲面方程及其方程

o y
将 z z, y1 x2 y2 代入 f ( y1, z) 0
f ( y,z) 0
x
0
得旋转曲面 的方程: f ( x2 y2 , z) 0,
即为 yoz 坐标面上的已知曲线 f ( y, z) 0绕z 轴
旋转一周的旋转曲面方程.
由此可见:绕 z 轴旋转,z 坐标不动,将 y 换成 x2 y2.
z x2 y2 cot
o y
令 b cot,则
x
z b x2 y2.
③ 旋转双曲面
x x
双曲线
x2 a2
z2 c2
1
y 0
o
z
oo
z
y
y
绕 x轴旋转而成的曲面:
x2 a2
y2 c2
z2
1
双叶双曲面
绕z轴旋转而成的曲面:
x
2
a2
y2
z2 c2
1
单叶双曲面
x2 a2
y2 c2
z
母线 L
oo
x
准线C'
y
准线C
(2) 母线平行于坐标轴的柱面方程的特征
方程中缺少一个变量 (该坐标轴的变量)
如:F ( x, y) 0
z
表示母线 // z 轴的柱面. 事实上, M( x, y, z) 过点M 作垂直于 xoy 面 的垂线,则此垂线与 C 的交点M1(x, y, 0)的坐标 必满足 :F ( x, y) 0.
F(x, y, z) 0
z
曲面 S 叫做方程 F( x, y, z ) = 0 的图形.
S
曲面的实例:
oy
水桶的表面、台灯的罩子面等. x
s曲线最简单又准的方法

s曲线最简单又准的方法S曲线是一种常用的曲线拟合方法,在生命科学、统计学、经济学等领域有广泛的应用。
下面介绍一种最简单又准确的S曲线拟合方法。
步骤一:数据处理首先,需要对实验数据进行处理。
对于S曲线拟合,通常需要将原始数据先进行log转换。
如果数据中含有0值,需要进行加一平滑操作,即将所有数据加上1再进行log转换。
步骤二:确定拟合方程在S曲线拟合方法中,经典的拟合方程为Logistic方程。
Logistic方程是S曲线的一种,其表述形式为:y = a / (1 + e^(-b(x-c)))其中,y表示反应变量的值,x表示自变量的值,a、b、c分别是拟合参数。
步骤三:参数估计估计拟合参数是S曲线拟合的核心步骤。
常用的参数估计方法有最小二乘法和最大似然估计法,其中最大似然估计法的效果更好。
对于最大似然估计法,我们需要先将Logistic方程进行变形,得到:ln(y/(1-y)) = ln(a/(a-y)) = b(x-c)则,最大似然函数为L = ∏[y^yi(1-y)i-y^ia-yi]对数最大似然函数为l = ∑[yi ln(y/(a-y))+(i-yi)ln((1-y)/y)]然后,使用牛顿迭代法来求解参数。
在迭代过程中需要计算一阶导数和二阶导数。
迭代过程在R软件中可以使用glm函数实现。
步骤四:拟合效果评价在拟合参数后,需要对拟合效果进行评价。
常用的指标有AIC、BIC、残差均方根误差等。
对于拟合效果差的模型,可以考虑使用泊松回归或者贝叶斯方案进行改进。
总结S曲线是一种常用的曲线拟合方法。
本文介绍的S曲线最简单又准的方法包括:数据处理、确定拟合方程、参数估计和拟合效果评价。
在实际应用中,需要根据数据的特点进行参数的选择和模型的修改。
s型曲线算法

S型曲线算法一般是指S型曲线控制法(逻辑斯谛方程),即常微分方程:dN/dt=rN(K-N)/K。
当N=K/2时,dN/dt达到最大值,N增长最快。
K/2是N的一个重要的特殊情况。
S型曲线相对于T型曲线,S型曲线的速度不会突变。
S型曲线的原始公式如下:y=K/(1+Exp(a-b x))(K>0,b>0)Exp是指数函数,由这个公式可以看出y会随着x的增大,逼近K。
把这个公式应用到电机控制之中,K看成最大的速度Vmax,x看成时间t的变量,那么t=0时,就是电机的初始速度,即V0=Vmax/(1+Exp(a-b(0)))=Vmax/(1+Exp(a))。
反推求出a与V0,Vmax之间的关系,a=In((Vmax-V0)/V0)。
b决定曲线的快慢,b越大V变化越快,也就越快接近Vmax。
各种曲线的方程

1.碟形弹簧圓柱坐标方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t2.葉形线.笛卡儿坐標标方程:a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))3.螺旋线(Helical curve)圆柱坐标(cylindrical)方程:r=ttheta=10+t*(20*360)z=t*34.蝴蝶曲线球坐标方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 85.渐开线采用笛卡尔坐标系方程:r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=06.螺旋线.笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t7.对数曲线笛卡尔坐标系方程:z=0x = 10*ty = log(10*t+0.0001)8.球面螺旋线采用球坐标系方程:rho=4theta=t*180phi=t*360*209.双弧外摆线卡迪尔坐标方程:l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)10.星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^311.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*36012.圆内螺旋线采用柱座标系方程:theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)13.正弦曲线笛卡尔坐标系方程:x=50*ty=10*sin(t*360)z=014.太阳线(这本来是做别的曲线的,结果做错了,就变成这样了)15.费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做16.Talbot 曲线卡笛尔坐标方程:theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b17.4叶线(一个方程做的,没有复制)18.Rhodonea 曲线采用笛卡尔坐标系方程:theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)19. 抛物线笛卡儿坐标方程:x =(4 * t)y =(3 * t) + (5 * t ^2) z =020.螺旋线圓柱坐标方程:r = 5theta = t*1800z =(cos(theta-90))+24*t21.三叶线圆柱坐标方程:a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta) y=(a+b)*sin(theta)-b*sin((a/b+1)*theta) z=023. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c) y=b*sin(theta)24.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta) y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)25.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta) y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)a=10x = a*(2*cos(t*360)+cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360))27.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)柱坐标a=100theta = t*400r = a*theta30.对数螺线柱坐标theta = t*360*2.2 a = 0.005r = exp(a*theta)31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x) for x32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/234.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/235.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+137.八字曲线x = 2 * cos ( t *(2*180)) y = 2 * sin ( t *(5*360)) z = 038.螺旋曲线r=t*(10*180)+1 theta=10+t*(20*180) z=t39.圆x = cos ( t *(5*180)) y = sin ( t *(5*180)) z = 040.封闭球形环绕曲线rho=2theta=360*tphi=t*360*1041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180)) y = 100*t * sin ( t *(5*180)) z = 042.蛇形曲线x = 2 * cos ( (t+1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t+1)柱坐标theta = t*360r=10+(8*sin(theta))^244.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)45.梅花曲线柱坐标r=10+(3*sin(theta*2.5))^246.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^247.改一下就成为空间感更强的花曲线了;) theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^248.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*1249.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2 z = t*1650 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+t theta=t*360*10z=t*1051 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)52 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*1053.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3 z=t^3*(t+1)54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*2055. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)56.梅花曲线theta=t*360r=100+50*cos(5*theta) z=2*cos(5*theta)57.桃形曲线rho=t^3+t*(t+1) theta=t*360phi=t^2*360*10*1058.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+2459.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*36061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2) z=sin(ang2)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*664.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8) y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*865.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)66. ufo (漩涡线)球坐标:rho=t*20^2 theta=t*log(30)*60 phi=t*720067. 手把曲线thta0=t*360 thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1) x=r*cos(thta0)y=r1*sin(thta1)z=068.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*569. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
种群增长的S型曲线

预测和控制种群数量
准确预测种群数量变化,并采取有效措施控制种群数量, 以防止种群过度增长或濒危灭绝,是保护生物多样性的关 键挑战。
未来发展
1 2 3
深入研究种群增长机制
环境资源
环境资源是种群增长的限制因素之一,资源的可用性和可获得性 影响种群的生长和存活率。
空间限制
空间限制也是影响种群增长的重要因素,种群数量受到栖息地大小 和可用空间的影响。
竞争与捕食
种内竞争和捕食是影响种群增长的另一个因素,它们可以降低出生 率和存活率,从而影响种群增长。
02
种群增长的s型曲线模型
04
种群增长s型曲线的挑战 与未来发展
挑战
环境容量限制
种群增长在达到环境容量上限后,增长速度会逐渐减缓, 最终趋于稳定。理解并预测种群增长的上限是保护生态平 衡的重要挑战。
环境变化适应性
气候变化、环境污染等因素可能导致种群生存环境的改变 ,如何提高种群的适应性和生存能力是当前面临的重要挑 战。
资源竞争
实例二:某水域的鱼类种群增长
总结词
鱼类种群增长呈现s型曲线,受到食物、 空间和繁殖能力的限制。
VS
详细描述
在某水域的鱼类种群增长过程中,随着时 间的推移,鱼类数量也呈现出s型曲线的 增长趋势。起初,由于食物充足和空间广 阔,鱼类种群数量迅速增长。然而,当鱼 类数量接近环境承载力时,食物和空间的 限制开始发挥作用,繁殖能力也受到限制 ,导致种群增长速度减缓,最终趋于稳定 。
种群增长的s型曲线
目 录
• 种群增长的基础知识 • 种群增长的s型曲线模型 • 种群增长s型曲线的应用 • 种群增长s型曲线的挑战与未来发展 • 实例分析
S形增长曲线及幂增长的曲线拟合及回归方程

S 形增长和幂增长的曲线拟合的例子1. S 形增长S 形增长也称为逻辑斯谛(Logistic)增长。
其满足微分方程dN dt= rN (K−N K) = rN - rKN 2 (1) 其中r 是增长率,K 是增长空间,N 是数量,t 是时间。
在初始时刻数量为N 0 ,这个方程的解为:N =K1+ (K−N 0N 0) e −rt(2) 如何确定和估计K 是很重要的,但是没有很好的方法来确定K 值。
常用的方法是把(2)式变换为:Ln( KN − 1) =Ln(K−N 0N 0) - rt 这是Y = a + b X 的形式,但是K 并没有完全分离出来。
做代换 Y= Ln( KN − 1) ,X=t ,a= Ln(K−N 0N 0) ,b=-r 后,是 Y=a+bX (3) 的形式,可用线性回归确定a 和b,b =∑X i Y i i=n i=1− (∑X i ) (∑Y i ) / n i=n i=1 i=n i=1∑X i 2 i=n i=1− (∑X i ) (∑X i ) / n i=n i=1i=n i=1 (4)a =(∑Y i ) / n i=n i=1−b (∑X i ) / n i=ni=1 (5)由 a= Ln(K−N 0N 0) 得K−N 0N 0= e a K=N 0 e a + N 0 (6)和 r=-b 因而确定K 和r 。
先给定一个K ,算出a 和b,用(6)式算出K ,继续这样的过程,得出几组K 和r ,并对每组K 和r 算误差的绝对值,即:∑Abs(N −N i )i=n i=1 。
用误差的绝对值 ∑Abs(N −N i )i=ni=1 作为衡量指标,并选取 ∑Abs(N −N i )i=n i=1 为最小的一组K 和r 来确定回归方程。
下面是样本数据:ti Ni ti Ni ti Ni1 0.43 26 1.35 51 7.422 0.24 27 1.16 52 8.923 0.37 28 1.22 53 8.364 0.52 29 1.12 54 10.765 0.80 30 0.91 55 9.456 1.43 31 1.15 56 7.657 1.01 32 1.12 57 8.328 1.06 33 1.46 58 10.159 0.74 34 1.51 59 14.7610 0.92 35 1.58 60 13.4311 0.52 36 1.64 61 23.9912 0.38 37 2.35 62 20.6913 0.33 38 2.70 63 24.9714 0.53 39 5.11 64 31.5215 0.85 40 10.66 65 28.516 1.08 41 20.36 66 2317 1.30 42 15.10 67 26.9718 1.33 43 7.28 68 30.7119 1.14 44 6.5720 0.81 45 10.8321 0.74 46 11.8822 1.05 47 9.2523 1.04 48 8.7824 1.29 49 8.6025 1.33 50 8.50用转换数据做线性回归,有如下结果K rAbs(N-Ni) 31.84 0.0690 176.5 45.15 0.0716 173.9 68.76 0.0723 194.1 108.32 0.0697 191.2 163.470.0684191.1对应于 ∑Abs(N −N i )i=n i=1 的较小值173.9的K=45.15 ,r=0.0716 ,其拟合曲线如下:新的方法是偏导方程组迭代法 设拟合曲线方程为 y =x 11+(x 1−N0N 0) e −x 2t(7) 对给定的样本数据(t i ,y i ),求出(x 1,x 2)使得Q=∑ (y −y i )2i=n i=1 = ∑ (x 11+(x 1−N 0N 0) e −x 2t −y i )2i=n i=1 为最小。
空间中的曲面和曲线

柱面,
平行于 x 轴;
平行于 y 轴;
平行于 z 轴;
准线 xoz 面上的曲线 l3.
母线
柱面,
准线 xoy 面上的曲线 l1.
母线
准线 yoz 面上的曲线 l2.
母线
故所求方程为
例1. 求动点到定点
方程.
特别,当M0在原点时,球面方程为
解: 设轨迹上动点为
即
依题意
距离为 R 的轨迹
表示上(下)球面 .
例:
求曲线
绕 z 轴旋转的曲面与平面
的交线在 xoy 平面的投影曲线方程.
解:
旋转曲面方程为
交线为
此曲线向 xoy 面的投影柱面方程为
此曲线在 xoy 面上的投影曲线方程为
,它与所给平面的
截线方程为
解
如图,
例
解答
交线方程为
在 面上的投影为
空间曲线的一般方程、参数方程.
( 必要时需作图 ).
三、柱面
引例. 分析方程
表示怎样的曲面 .
的坐标也满足方程
解:在 xoy 面上,
表示圆C,
沿曲线C平行于 z 轴的一切直线所形成的曲面称为圆
故在空间
过此点作
柱面.
对任意 z ,
平行 z 轴的直线 l ,
表示圆柱面
在圆C上任取一点
其上所有点的坐标都满足此方程,
定义3.
(1) 曲面 S 上的任意点的坐标都满足此方程;
则 F( x, y, z ) = 0 叫做曲面 S 的方程,
曲面 S 叫做方程 F( x, y, z ) = 0 的图形.
两个基本问题 :
(1) 已知一曲面作为点的几何轨迹时,
第九章 酶动力学

Hill常数不同的酶反应速率与底物浓度的关系曲线
v
vmax
Km
ES
I
KI
EI S
k1 ES
k2 E P
k-1
I v [S] vmax
KI’
[S] Km (1 [I ] ) KI
EIS
Km 不变 vmax 降低
+抑制剂
1/v
Vmax/(1+[I]/KI)
[S]
(1+[I]/KI)/Vmax
-1/Km
斜率=Km/vmax
斜率= Km(1+[I]/KI)/vmax
米氏酶的双倒数作图
Eadie-Hofstee作图
Hanes-Wolff 作图
酶抑制剂作用的动力学
酶抑制剂的类型 ① 可逆性抑制剂。以次级键与酶可逆结合,使用透析
或超滤就可去除它们,让酶恢复活性; ② 不可逆性抑制剂。也被称为酶灭活剂,以强的化学
键(通常是共价键)与酶不可逆结合,可导致酶有 效浓度的降低,因此一旦失活就不可逆转。如果想 恢复酶的活性,唯一的手段只能是补充新酶。 酶抑制剂对米氏酶动力学性质的影响
2. 负协同性的优势 呈现负协同效应的别构酶(h=0.5)要将其反应速率从 Vmax的 10% 增加到 90%,需要将底物浓度提高6561倍 。如此大幅度的提高就意味着该酶对底物浓度的变化 极度不敏感。
c语言的s曲线

c语言的s曲线S曲线是一种常见的数学曲线,它的形状像字母"S",因此得名。
在C语言中,我们可以使用数学函数和循环结构来绘制S曲线。
要绘制S曲线,我们首先需要了解曲线的数学表达式。
S曲线的数学表达式可以用一个参数方程表示:x = ty = 1 / (1 + e^(-t))其中,t是一个变量,e是自然对数的底数。
在C语言中,我们可以使用math.h头文件中的exp()函数来计算e的幂。
exp()函数的原型如下:double exp(double x);exp()函数返回e的x次幂的值。
接下来,我们可以使用循环结构来计算和绘制S曲线上的点。
我们可以选择一个合适的步长,然后在给定的范围内逐步计算x和y的值。
下面是一个使用C语言绘制S曲线的示例代码:```c#include <stdio.h>#include <math.h>int main() {double t, x, y;double step = 0.1;double start = -10.0;double end = 10.0;for (t = start; t <= end; t += step) {x = t;y = 1 / (1 + exp(-t));printf("x = %.2f, y = %.2f\n", x, y);}return 0;}```在这个示例代码中,我们使用了一个for循环来计算S曲线上的点。
变量t从start开始,每次增加step,直到达到end为止。
在每次循环中,我们计算x和y的值,并使用printf()函数打印出来。
你可以根据需要调整step、start和end的值来控制曲线的精细程度和范围。
运行这段代码,你将看到一系列的(x, y)坐标对,它们代表了S曲线上的点。
你可以将这些点连接起来,就可以得到完整的S曲线。
绘制S曲线是C语言中一个有趣且有挑战性的任务。
s型曲线回归方程

s型曲线回归方程全文共四篇示例,供读者参考第一篇示例:S型曲线回归方程是一种常用的统计方法,用于描述一种变量随着另一种变量而变化的趋势。
这种曲线通常呈现出一种“S”形状,故得名S型曲线回归方程。
在许多领域,如经济学、生物学和医学等,S型曲线回归方程被广泛应用于数据分析和预测中。
本文将对S型曲线回归方程进行介绍和解释,希望能够帮助读者更好地理解和运用这一方法。
一、什么是S型曲线回归方程S型曲线回归方程是一种非线性回归方程,通常用于描述一种变量随着自变量的变化而呈现出S型的变化趋势。
在统计学中,回归分析是一种用来研究自变量和因变量之间关系的方法,通过建立数学模型来描述二者之间的函数关系。
而S型曲线回归方程则是其中一种常见的非线性回归模型。
S型曲线回归方程通常由一个或多个参数构成的数学函数表达式来表示,其形式可以是logistic方程、Gompertz方程等。
这些方程在不同领域和研究对象中有着不同的应用。
在经济学中,S型曲线回归方程常被用来描述市场需求和供给的变化;在生物学和医学中,它常被用来分析生物生长和药物吸收等过程。
S型曲线回归方程具有以下几个显著的特点:1. S型变化趋势:S型曲线回归方程通常呈现出一种S形状的变化趋势,即在自变量较小时,因变量的增长速度较慢;随着自变量的增加,因变量的增长速度迅速加快,最终趋于平稳。
这种曲线形状很好地描述了许多实际现象的变化规律。
2. 参数拟合:S型曲线回归方程需要对其参数进行拟合来找到最优的拟合曲线。
这通常需要使用数学优化方法,如最小二乘法等,来求解最佳参数值。
3. 非线性关系:与线性回归方程不同,S型曲线回归方程是一种非线性关系模型,其在描述复杂的变化趋势时具有更好的适应性和拟合性。
4. 预测能力:通过S型曲线回归方程,我们可以预测因变量随着自变量的变化趋势,从而对未来的数据进行预测和分析。
S型曲线回归方程在实际应用中具有广泛的应用领域和价值。
以下是几个常见的应用场景:1. 市场需求预测:在经济学中,市场需求通常呈现出S型变化趋势,因此S型曲线回归方程可以用来预测市场需求随着价格变化的关系,为决策提供依据。
s参数曲线

S参数,也被称为散射参数,是表征无源网络特性的一种模型。
在射频、微波和信号完整性领域有着广泛的应用。
S参数是一个复数矩阵,它反映了在频域范围内的反射信号/传输信号的特性(幅度/相位)。
S参数包含两类主要参数:反射参数如S11,S22等;以及传输参数如S12,S21等。
例如,S11为输入反射系数,也就是输入回波损耗;S22为输出反射系数,也就是输出回波损耗。
相反,S12为反向传输系数,也称为隔离;而S21为正向传输系数,也被解释为增益。
为什么我们需要使用S参数呢?原因在于,天线是无线网络中最重要的元器件,它是物理网络与无线电波(空中)的唯一接口。
而天线的关键性能参数包括回波损耗和电压驻波比(VSWR)。
S参数可以帮助我们对这些性能进行测量。
特别地,S11(输入匹配)、S22(输出匹配)、S21(增益/损耗)、S12(隔离度)等测量项目的测试结果可以很方便地导入到电子仿真工具。
s曲线与方程

2 x x1 2 y y1 2 0 联立,得 ,解得 y y1 x x1 3x y 2 x1 2 y x 3y 2 1 , 由Q在双曲线上, 2 2 2 2 2 x y 知x -y =1,可得 1 1 1
2
所以 点M轨迹方程为 2 1 2 x- 2 4 y 1
点评: 在这个题目中,有两个动点Q,M,其中Q为主 动点,M为从动点;主动点Q在已知曲线上运 y 动。也就是说这种问题的辨别特征是: Q 【1】有主动点和从动点两种动点 M 【2】主动点在已知曲线上运动 A • 这种根据已知动点的轨迹方程,求另外一点 的轨迹方程的方法称为代入法或相关点法. • 一般地,定比分点问题,对称问题或能转化 为这两类的轨迹问题,都可用相关点法 .
2 2 2
• 练3 过双曲线x2-y2=1上一动点Q引直线x +y=2的垂线,垂足为M,求线段QM的中点P 的轨迹方程.
• • • • [分析] 题目中的Q,M均为动点,因而其 中点P也为动点,由条件中的中点和垂直关 系可得到坐标关系,最后将坐标代入曲线 方程,即得到QM中点P的轨迹方程.
[解析] 设 QM 中点为 P(x ,y),Q(x 1,y1),由中点关系 得: M 点坐标为(2x -x 1,2y-y1). ∴2x -x 1+2y-y1=2. 又 QM 垂直于直线 x +y=2, y-y1 ∴ =1 即 y-y1=x -x 1. x -x 1 ② ①
解 设C(x,y)
OC x, y OA t (OB OA) ( 1 t, 2t)
x 1 t y 2t 消去 t , 得
点C的轨迹方程为2x-y-2=0
[点评]
用参数法求轨迹方程时,一要
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参数法求曲线方程
• 例4 在平面直角坐标系中, A O(0,0) (1,0)B(2,2)若点C满足, OC OA t (OB OA) 其中 t R 求点C轨迹方程
3x y 2 x 3 y 2 1 所以 2 2 2 2 3x y 2 x 3 y 2 1 故所求轨迹方程为 2 2
2 2
课堂小结 想一想:今天在课堂上你学到了什么?
求曲线的方程常用的几种方法
(1)直接法 (2)定义法
(3)相关点法
(4)参数法
课后作业:
1.已知点Q是曲线
yx
2 上的动点,点A
的坐标为(1,0),求线段QA的中点P的轨迹
方程. 2.若直线y=kx+b交抛物线
2
x y 于A、
B两点,已知|AB|= 4 5,线段AB的中点纵
坐标等于-5,求k,b的值.
2 x x1 2 y y1 2 0 联立,得 ,解得 y y1 x x1 3x y 2 x1 2 y x 3y 2 1 , 由Q在双曲线上, 2 2 2 2 2 x y 知x -y =1,可得 1 1 1
2
学后反思
本题运用了参数法求轨迹.当动点P的坐标x、y之
间的直接关系不易建立时,可适当地选取中间变量t,并用t表
x f t 示动点的坐标x、y,从而得到动点轨迹的参数方程 y g t
消去参数t,便可得到动点P的轨迹方程.其中应注意方程的等
价性和参数t与动点P(x,y)关系的密切性.
设P(x,y),则
1 2 x 2 k 2 k y 2 1 k k
…
(1) (2)
…
由(2) 2 (1),得 y 2 x 8即 y 2 x 8
2
2
2
故线段AB的中点P的轨迹方程为 y 2 x 8
解 设C(x,y)
OC x, y OA t (OB OA) ( 1 t, 2t)
x 1 t y 2t 消去 t , 得
点C的轨迹方程为2x-y-2=0
[点评]
用参数法求轨迹方程时,一要
选好参数,将动点的横、纵坐标表示成参 数的形式;二要掌握消参的技巧.
请做下面变式练习,并思考此种题目解题程序
变式训练
1 将例3中条件改为若 AM 2MQ , 求M
的轨迹方程.
2 改为:求椭圆关于点(3,4)对称的曲 线方程
总结:相关点法的判别与程序
判别:看题目是否具有下列两个条件 【1】有主动点和从动点两种动点 【2】主动点在已知曲线上运动
求轨迹方程
高二数学组 崔建欣
学习如几何曲线 幸福似小数循环.
教学目标:
1、知识与能力:会求各种曲线的方程 2、过程与方法:会用直接法、相关点法、 定义法求曲线的方程
3、情感态度与价值观:培养合作探讨、 勇于创新的精神,渗透事物之间等价转 化的辩证唯物主义观点
重点:会用相关点法求曲线的轨迹方程
难点:灵活运用各种方法求轨迹方程
变式训练
3. 点P是圆 x 4 y 1 4上的动点,O
2 2
是坐标原点,求线段OP的中点Q的轨迹.
y 解:做简图如图 2 2 圆 x 4 y 1 4 x 4 2cos (θ为参数) 的参数方程为 0 y 1 2sin
定义法求曲线方程
学案例 2 已知圆 C1: (x +3)2+y2=1 和圆 C2: (x -3)2 +y2=9,动圆 M 同时与圆 C1 与圆 C2 相外切,求动圆圆 心 M 的轨迹方程.
• [解析] 如图所示,设动圆 M与圆C1及圆C2分别外切于点 A和B,根据两圆外切的充要条 件,得 • |MC1|=r+1 • |MC2|=r+3
连接QO,可知,QO为 F1 F2 M 的中位线
故 QO 1 MF2 4 ,所以点Q的轨迹是以O为圆心,4为
半径的圆。其方程为 x 2 y 2 16
2
相关点代入法求曲线的方程 2 x 2 例3 已知x轴上一定点A(1,0),Q为椭圆 y 1 上一动点,求线段AQ中点M的轨迹方程 4 解 设M(x,y) Q(x0, y0 )
学后反思 当动点所满足的条件本身就是一些几 何量的等量关系或这些几何条件简单明了易于表 达时,只要将这种关系“翻译”成含x、y的等式 就能得到曲线的轨迹方程,这种求轨迹方程的方 法称之为直接法,也叫直译法.
• [点评] 1.直接法求轨迹方程是常用的基本方法, 大多数题目可以依据文字叙述的条件要求,直接“翻 译”列出等式整理可得. • 2 直接法步骤是:建系设点、列等式、代 换、化简、证明“五步法”.在解题时,根据题意, 正确列出方程是关键,还要注意最后一步,如果有不 符合题意的特殊点要加以说明.一般情况下,求出曲 线方程后的证明可以省去.
[点评] 因为直线PM和直线MQ的斜率都存 在,所以在①中,x≠±2,但在②中却有x= ±2,此时点P(2,2)和Q(-2,0)在方程②的曲线 上,其原因是从①到②是非等价变形,x的范围 扩大了
• 练习2 已知动圆M与圆C1:(x+4)2+y2=2外 切,与圆C2:(x-4)2+y2=2内切,求动圆圆心 M的轨迹方程.
课后作业 1. 已知点Q是曲线 y x2 ,上的动点,点A的坐
标为(1,0),求线段QA的中点P的轨迹方程.
与抛物线相交于A、B两点,求线段AB的中点P的轨迹方程 解析: 由题意知,两直线的斜率都存在. . 设直线OA的斜率为k,则OA:y=kx,OB:y 1 x
y kx 由 2 y 4x
k
4 4 得A 2, k k
1 y x 得 2 同理由 B 4k , 4k k y2 4x
2
所以 点M轨迹方程为 2 1 2 x- 2 4 y 1
点评: 在这个题目中,有两个动点Q,M,其中Q为主 动点,M为从动点;主动点Q在已知曲线上运 y 动。也就是说这种问题的辨别特征是: Q 【1】有主动点和从动点两种动点 M 【2】主动点在已知曲线上运动 A • 这种根据已知动点的轨迹方程,求另外一点 的轨迹方程的方法称为代入法或相关点法. • 一般地,定比分点问题,对称问题或能转化 为这两类的轨迹问题,都可用相关点法 .
QPx来自所以点P的坐标为(4+2cosθ,1+2sinθ) 设Q点的坐标为(x,y)
由中点坐标公式得
x 2 cos 1 y sin 2
化简得 ( x 2)2 ( y 1 )2 1 2
变式训练
4. 过抛物线 y 2 4 x 的顶点O引两条互相垂直的直线分别
• 练习1 点M与已知点P(2,2)连线的斜率是 它与点Q(-2,0)连线的斜率的2倍,求点M的轨 迹方程.
[误解] 设点 M 的坐标为(x ,y), y-2 y 由已知可得 =2× , ① x +2 x -2 化简整理得,点 M 的轨迹方程为 xy+2x -6y+4=0. ②
[正解] 设点 M 的坐标为(x ,y), 当 x =2 时,直线 PM 的斜率不存在; 当 x =-2 时,直线 MQ 的斜率不存在,均不合题意; y-2 y 当 x ≠±2 时,由已知得 =2× , x +2 x -2 化简整理得,点 M 的轨迹方程为 xy+2x -6y+4=0(x ≠±2).
2 2 2
• 练3 过双曲线x2-y2=1上一动点Q引直线x +y=2的垂线,垂足为M,求线段QM的中点P 的轨迹方程.
• • • • [分析] 题目中的Q,M均为动点,因而其 中点P也为动点,由条件中的中点和垂直关 系可得到坐标关系,最后将坐标代入曲线 方程,即得到QM中点P的轨迹方程.
[解析] 设 QM 中点为 P(x ,y),Q(x 1,y1),由中点关系 得: M 点坐标为(2x -x 1,2y-y1). ∴2x -x 1+2y-y1=2. 又 QM 垂直于直线 x +y=2, y-y1 ∴ =1 即 y-y1=x -x 1. x -x 1 ② ①
x2 y2 已知 F1、F2是椭圆 16 9 1 的两个焦点,P是 椭圆上任意一点,从任一焦点引F1 PF2 的外角平分线
的垂线,垂足为Q,求点Q的轨迹方程。 M Q 解:如图
F1
P
y
0
F2
x
延长F1Q 交 F2 P 的延长线于点M,可得 F1 PM 为等腰三 角形,故F1 P PM ,所以F2 M F2 P PM F2 P F1 P 2a 8
4 4 思考:若将例1中 改为 9 9
2 2
结果是什么?
x y 1( x 6) 36 16
结论:平面内的动点到两定点A1 (a,0), A2 (a,0) 的斜率
乘积等于常数的点的轨迹叫做椭圆或双曲线. 其中两定点分别为椭圆或双曲线的顶点.
当常数大于-1小于0时为椭圆;当常数大于0时为双曲线.
• [点评] (1)本题是用定义法求动点的轨迹方 程,当判断出动点的轨迹是双曲线的一支,且 可求出a、b时,直接根据定义写出其标准方 程,而无需用距离公式写出方程,再通过复杂 的运算进行化简. • (2)由于动点M到两定点C2、C1的距离的差 为常数,而不是差的绝对值为常数,因此,其 轨迹只能是双曲线的一支.这一点要特别注 意!
