浙江省湖州四中八年级(上)入学数学试卷
浙江省湖州市第四中学八年级数学上册 第一章《平行线》单元测试(无答案) 浙教版

班级_________学号________姓名________得分________一、选择题(共10题,每小题3分,共30分)1.如图1,直线AB、AC被直线BC所截,则∠1与∠2是()A、对顶角B、同位角C、内错角D、同旁内角2.已知∠1和∠2是同旁内角,∠1=40°,∠2等于()A、160°B、140°C、40°D、无法确定3.如图2,已知AB∥CD,那么()A、∠1=∠2B、∠3=∠4C、∠1+∠3=180°D、∠4+∠2=1804.如图3,∠1与∠2互补,∠3=130°,那么∠4的度数是()A、50°B、60°C、70°D、80°5.如图,直线a、b被直线c所截,现给出下列四个条件:(1)∠1=∠5;(2)∠1=•∠7;(3)∠2+∠3=180°;(4)∠4=∠7,其中能判定a∥b的条件的序号是()A.(1)、(2) B.(1)、(3)C.(1)、(4) D.(3)、(4)6.如图12,FA⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是( )A.由∠CAB=∠NCD,得AB∥CD;B.由∠DCG=∠BAC,得AB∥CDC.由∠MAE=∠ACG,∠DCG=∠BAE,得AB∥CD;D.由∠MAB=∠ACD,得AB∥CD7.如图,R t△ABC中,∠ACB=90°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是()A、65°B、45°C、55°D、35°8.下列语句中,不能判定两直线平行的是( ).A.内错角相等,两直线平行¬B.同位角相等,两直线平行C.同旁内角相等,两直线平行D.同一平面内,垂直于同一直线的两条直线平行9.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将()A、变大B、变小C、不变D、变大变小要看点P向左还是向右移动10.若∠A和∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠B的度数为()A.20° B.75° C.20°或55° D.55°二、填空题(共10题,每题3分,共30分)11.如图T-8,∠1的同位角是,∠1的内错角是,∠2与∠3是12.如图T-9,若∠1= ,则a∥b, 理由是13.如图T-10,a∥b, ∠1=65°则∠3= °14.如图,AB∥CD,∠A=48°,∠C=∠E,则∠C的度数为°15.如图所示,已知AB∥CD,AO与OC交于点O,∠1=110°,∠2=120°,则a的度数为16.面积为4cm2的正方形的两条对边所在的直线之间的距离为.17.若两条平行线被第三条直线所截,则同旁内角的平分线互相________.18.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2= .19.如图,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′上,EC′交AD于点G,已知∠EFG=58°,那么∠BEG= 度.20.如图所示,已知AB∥CD,∠BAE=α,∠AED=β,∠CDE=γ,则α,β,γ之间的关系为四、解答题(共40分)21.如图,已知∠B=∠E, BC∥EF,则AB∥DE,请说明理由.(4分)dabc1432T-9T-1031cbaT-812435AB CDE FG22.如图8,已知A D ∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据(6分)解:∵AD ∥BC(已知),∴∠1=∠3( ), ∵∠1=∠2(已知),∴∠2=∠3( ),∴________∥________( ), ∴∠3+∠4=180°( ).23. 如图,已知∠4=∠B,∠1=∠3,求证:AC 平分∠BAD.(6分)24. 如图,直线AB 、CD 被直线EF 所截,点G 、H 为它们的交点,已知HP 是∠EHD 的平分线,∠AGE 与它的同位角相等,且∠AGH :∠BGH=4:5,试求∠CHG 和∠PHD 的度数. (6分)GA BEP4321(8)DCF AE B25.(8分)如图,长方形纸片EFGH 可以绕着长方形纸片ABCD 上的点O 自由的旋转,当边EH 与AB 相交时,形成了∠1,∠2,求∠1+∠2的度数。
浙江省湖州市第四中学八年级数学测试题1(无答案)

浙江省湖州市第四中学八年级数学测试题1 新人教版姓名 班级一、化简计算(每小题4分) 1.14425081010⨯⨯.. 2.521312321⨯÷;3. 2484554+-+4 、2332326--5. 3)154276485(÷+- 6、 ()1485423313⎛⎫-÷+-+ ⎪⎝⎭7、⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+121580325.12712 8、 ()()()2743743351+---二、选择适当的方法解方程(每小题4分)9、; 10、.11、 12、13、;14、15、; 16、17、18、解关于x 的一元二次方程:()0012422≠=--a ax x a19、02222=-+-n m mx x 20.()()2222222,06b a b a b a +=-+-+求21、用配方法求262+-x x 的最小值; 22、用配方法求1232++-x x 的最大值23、对于任意实数x ,试比较两代数x x x 42323--+1与10433++x x 的值的大小。
24、已知二次三项式2)6(92-++-m x m x 是一个完全平方式,试求m 的值.25、关于x 的一元二次方程()0422=+++k x k kx 有两个不相等的实数根,求k 的取值范围;26、已知()0053222≠=-+y xy y x ,求yx 的值。
27.若142=++y xy x ,282=++x xy y ,则x+y 的值为28.如果012=-+x x ,那么代数式7223-+x x 的值。
29. 已知实数a 、b 满足条件:求ab -的平方根。
30.某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,现在采用提高售价,减少进货量的方法增加利润,已知这种商品每涨价0.5元,其销量就减少10件;要使每天获得利润700元,请你帮忙确定售价。
浙江省湖州市第四中学八年级数学测试题 新人教版

1浙江省湖州市第四中学八年级数学测试题 新人教版一、选择题(24)1. 有四个说法:(1)若两实数之和与积都是奇数,则这两数都是奇数;(2)若两实数之和与积都是偶数,则这两数都是偶数;(3)若两实数之和与积都是有理数,则这两数都是有理数;(4)若这两实数之和与积都是无理数,则这两数都是无理数,其中正确的说法有( )(A )0个 (B )1个 (C )2个 (D )3个2. 已知一次函数y=-x +3,当0≤x ≤3时,函数y 的最大值是( ).A.0B.3C.-3D.无法确定3. 当k >0,b <0时,直线y=kx+b 不经过( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限4. 如图,设b >a ,则位于同一坐标系内的一次函数y=ax+b 和y=bx+a 的图象可能是( ).5. 在π、1.313、20/7、√2、0中,无理数的有( )A.1个B.2个C.3个D.4个6. 把a a 1-根号外的因式移到根号内,得( ) A a B a - C a -- D a -7.已知一次函数32y x m =+和12y x n =-+的图象都经过点A (-2,0)且与y 轴分别交于B 、C 两点,那ABC △的面积是( )A .2 B.3 C.4 D.68. 在同一时刻的阳光下,某同学的身影长时0.6米,而树的影长时4.8米,如果他知道自己的身高为1.4米,那么他应该估算树的高度是( )A. 8米B.9米C.10米D.11米二、填空( 22)1. 322(1)26 10;(2) 6 7;(3) .7π-- 2. 点P (m+3,m+1)在直角坐标系的x 轴上,则P 点的坐标是 。
3. 若反比例函数y=k x的图象在第二、四象限, 则直线y=kx+4不经过第 象限。
4. 已知一次函数y=kx+b 的图象如图所示,则这个一次函数的解析式为 。
.2 4 2 x y 5. 在1:200和1:500的两张城市规划图上,都标有阳光小区的位置,那么这两张规划图的相似比为 ,面积比是 。
浙江省湖州市第四中学八年级数学测试题3 新人教版

1浙江省湖州市第四中学八年级数学测试题3 新人教版姓名 得分 一、选择题(每小题3分,共30分) 1、下列各式中,不是二次根式的是( )A 、B 、C 、D 、2下列计算正确的是( ) A .3333+= B 、3327=÷ C . 235⋅= D .2(2)2-=-3、用配方法将方程x 2+6x-11=0变形为( )A .(x-3)2=20 B .(x+3)2=20 C .(x+3)2=2 D .(x-3)2=2 4、能证明命题“x 是实数,则2(3)0x ->”是假命题的反例是( ) A.x=1B. x=2C.x=3D. x=45、一组数据 -1,3,0,5,a 的极差是7,那么a 的值可能是( ) A 8 B 6 C -2 D 6或-26、已知直角三角形的两条边长分别是方程214480x x -+=的两个根,则此三角形的第三边是( )7 108 27 A B C D 、6或8 、 2、 或、10或7、磐安某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分): 10 、12、15、10、16、18、19、18、20、18、18、20、28、22、25、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( ) A .4组 B .5组 C .6组 D .7组8、关于x 的一元二次方程22(1)10a x x a -++-=的一个根为0,则a 的值为( ) A .-1 B . 1 C .-1或1D .09.某开发公司今年一月份收益达50万元,且一月份、二月份、三月份的收益共为175万元,问二、三月平均每月的增长率是多少?设平均每月的增长率为 x ,根据题意可列方程( ) A. 50(1+x)2=175 B. 50+50(1+x)2=175 C. 50(1+x)+50(1+x)2=175 D. 50+50(1+x)+50(1+x)2=17510. 如图,将图甲表示的正方形纸片剪成四块,恰 好拼成图乙表示的矩形。
八年级数学上学期起始试题 浙教版-浙教版初中八年级全册数学试题

某某省某某市书生中学2016-2017学年八年级数学上学期起始试题(满分:100分考试时间:100分钟)一、选择题(30分)1、一个数的平方根与立方根都是它本身,这个数是()A.1 B.﹣1 C.0 D.±1,02、﹣π的绝对值是()A.﹣πB. +πC.D.﹣﹣π3、要调查下列问题,你认为哪些适合抽样调查()①市场上某种食品的某种添加剂的含量是否符合国家标准②检测某地区空气质量③调查全市中学生一天的学习时间.A.①② B.①③ C.②③ D.①②③4、如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,则∠1+∠2等于()A.30° B.40° C.45° D.60°5、下列推理中,错误的是()A.∵AB=CD,CD=EF,∴AB=EF B.∵∠α=∠β,∠β=∠γ,∴∠α=∠γC.∵a∥b,b∥c,∴a∥c D.∵AB⊥EF,EF⊥CD,∴AB⊥CD6、把不等式组的解集表示在数轴上,下列选项正确的是()A.B.C. D.7、已知是二元一次方程4x+ay=7的一组解,则a的值为()A.﹣5 B.5C.D.﹣8、已知等腰三角形的两边长是5cm 和6cm ,则此三角形的周长是( )A .16cmB .17cmC .11cmD .16cm 或17cm9、如图,把△ABC 沿EF 对折,叠合后的图形如图所示.若∠A =60°,∠1=95°,则∠2的度数为( )A .24° B.25° C .30° D.35°10、若方程的解是非正数,则m 的取值X 围是()A . m≤3B.m≤2 C .m≥3D .m≥2二、填空题(21分)11、如图,将周长为8的△ABC 沿BC 方向向右平移1个单位得到△DEF ,则四边形ABFD 的周长为. 12、不等式组的解集是.13、若点A (a ,3)在y 轴上,则点B (a ﹣3,a+2)在第象限.14、已知是二元一次方程组的解,则m ﹣n 的平方根为.15、一个班级有40人,一次数学考试中,优秀的有18人.在扇形图中表示优秀的人数所占百分比的扇形的圆心角的度数是.16、已知关于x 的不等式组只有四个整数解,则实数a 的取值X 是.17、如图,△ABC 中,∠ABC=96°,延长BC 到点D ,∠ABC 与∠ACD 的平分线相交于点A 1,则A ∠1的大小是,A BC ∠1和A CD ∠1的平分线相交于点A 2,依次类推,A BC ∠2012和A CD ∠2012的平分线交于点A 2013,则A ∠2013的大小是.ABCB'C'EF12三、解答题(49分)18、计算:﹣12+(﹣2)3×﹣×|﹣|+2÷()2.19、解方程组.20、求不等式组的解集,并求它的整数解.21、如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC 的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).(1)直接写出点C1的坐标;(2)在图中画出△A1B1C1;(3)求△AOA1的面积.22、为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:(1)该校对多少名学生进行了抽样调查?(2)①请补全图1并标上数据②图2中x=?.(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?23、如图,已知AB∥EF∥CD,∠ABC=46°,∠CEF=154°,求∠BCE的度数.24、去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)求饮用水和蔬菜各有多少件?(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;25、探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.某某市书生中学起始考初二数学答卷 一、选择题(30分)二、填空题(21分)11. 10.12. x <-3 13.二 .14..± 1.15.162°. 16.﹣3<a ≤﹣2 17.48°,2013962.三、解答题(49分)18(3分)、计算:﹣12+(﹣2)3×﹣×|﹣|+2÷()2.解:原式=﹣1﹣8×+2÷2=﹣2.19(4分)、解方程组.解: ①×2﹣②×3得:﹣5x=﹣15,即x=3, 将x=3代入①得:y=1, 则方程组的解为.20(4分)、求不等式组的解集,并求它的整数解.解:解①得:x≤3, 解②得:x >﹣1.则不等式组的解集是:﹣1<x≤3. 则整数解是:0,1,2,3.题号12345678910答案CCDCDBCDBA21(6分)、如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).(1)直接写出点C1的坐标;(2)在图中画出△A1B1C1;(3)求△AOA1的面积.解:(1)∵点P(a,b)的对应点为P1(a+6,b﹣2),∴平移规律为向右6个单位,向下2个单位,∴C(﹣2,0)的对应点C1的坐标为(4,﹣2);(2)△A1B1C1如图所示;(3)△AOA1的面积6×3﹣×3×3﹣×3×1﹣×6×2=6.22(6分)、为了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的一部分.请根据以上信息解答以下问题:(1)该校对多少名学生进行了抽样调查?(2)①请补全图1并标上数据②图2中x=?.(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?解:(1)抽样调查的总人数是:10÷20%=50(人);(2)x=100﹣20﹣40﹣10=30;(3)该校最喜欢跳绳项目的学生约有900×10%=90(人).23(6分)、如图,已知AB∥EF∥CD,∠ABC=46°,∠CEF=154°,求∠BCE的度数.解:∵AB∥CD,∠ABC=46°,∴∠BCD=∠ABC=46°,∵EF∥CD,∠CEF=154°,∴∠ECD=180°﹣∠CEF=180°﹣154°=26°,∴∠BCE=∠BCD﹣∠ECD=46°﹣26°=20°.24(10分)、去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)求饮用水和蔬菜各有多少件?(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;解:(1)设饮用水有x件,则蔬菜有(x﹣80)件.则x+(x﹣80)=320,解这个方程,得x=200.∴x﹣80=120.答:饮用水和蔬菜分别为200件和120件;(2)设租用甲种货车m辆,则租用乙种货车(8﹣m)辆.得:,解这个不等式组,得2≤m≤4.∵m为正整数,∴m=2或3或4,安排甲、乙两种货车时有3种方案.设计方案分别为:①甲车2辆,乙车6辆;②甲车3辆,乙车5辆;③甲车4辆,乙车4辆;25(10)、探究与发现:如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:①如图2,把一块三角尺XYZ放置在△ABC 上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX=°;②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.解:(1)连接AD并延长至点F,由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD;且∠BDC=∠BDF+∠CDF及∠BAC=∠BAD+∠CAD;相加可得∠BDC=∠A+∠B+∠C;(2)①由(1)的结论易得:∠ABX+∠ACX+∠A=∠BXC,又因为∠A=50°,∠BXC=90°,所以∠ABX+∠ACX=90°-50°=40°;②由(1)的结论易得∠DBE=∠A+∠ADB+∠AEB,易得∠ADB+∠AEB=80°;而∠DCE=(∠ADB+∠AEB)+∠A,代入∠DAE=50°,∠DBE=130°,易得∠DCE=90°;③∠BG1C=(∠ABD+∠ACD)+∠A,∵∠BG1C=77°,∴设∠A为x°,∵∠ABD+∠ACD=140°-x°∴(140-x)+x=77,x=70∴∠A为70°.。
初中八年级(初二)数学上册开学考试3含答案解析

初中八年级(初二)数学上册开学考试卷I一.选择题(共5题)1.已知点在第四象限,且,则点的坐标是()A. B. C. D.2.下列方程组中,属于二元一次方程组的有()A. B. C. D.3.若m>n,a是任意实数,则下列不等式一定成立的是(? )A. a?2m <a?2n B. am>an C. ma 2>na 2 D. m+a <n+b4.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是()A. 16cmB. 18cmC. 20cmD. 21cm5.据网上数据显示,长沙常住人口已达到万人,请问这一近似数是精确到哪一位?( )A.万位B.千位C.百位D.百分位二.填空题(共3题)1.一个n边形的每一个内角都是120°,那么n=_________.2.据科学测算,肥皂泡的泡壁厚度大约为0.0007mm,用科学记数法表示0.0007= .3.方程与方程的解相同,则m的值为_____.1.如图,是等边的边上一点,是延长线上一点,连接交于,过点作于点.证明下列结论:2.计算题:3.解不等式组卷I参考答案一.选择题1.【答案】C【解析】根据点在第四象限的坐标特点解答即可.解:∵|x|=3,|y|=5,∴x=3,y=5,∵点P(x,y)在第四象限,∴x>0,y<0,∴点P的坐标是(3,-5).故选:C.根据二元一次方程组的定义判断逐项分析即可,方程的两边都是整式,含有两个未知数,并且未知数的项的次数都是1次的方程叫做二元一次方程.A. 含有三个未知数,故不是二元一次方程组;B. 是二元一次方程组;C. 中含有2次项,故不是二元一次方程组;D. 中含有2次项,故不是二元一次方程组;故选B.3.【答案】A【解析】试题分析:在不等式的两边同时乘以一个正数,不等式仍然成立;在不等式的两边同时乘以一个负数,不等符号需要改变.4.【答案】C【解析】试题分析:已知,△ABE向右平移2cm得到△DCF,根据平移的性质得到EF=AD=2cm,AE=DF,又因△ABE的周长为16cm,所以AB+BC+AC=16cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16cm+2cm+2cm=20cm.故答案选C.5.【答案】C【解析】根据精确值的确定方法,首先得出原数据,再从原数据找出2所在数据的位置,再确定精确到了多少位.解:764.52万=7645200,精确到百位,故选:C.二.填空题1.【答案】6【解析】试题分析:正多边形的每一个的度数=,根据题意求出n的值.试题分析:科学技术法是指:a×,且,小数点向右移动几位,则n的相反数就是几.3.【答案】-6【解析】解:去分母得:x﹣16=﹣12去括号、合并同类项得:x=4.把x=4代入方程,得:2+=4﹣4,解得m=﹣6.三.解答题1.【答案】(1)见解析;(2)见解析;(3)见解析【解析】(1)由等边△ABC,DG⊥AC,可求得∠AGD=90°,∠ADG=30°,然后根据直角三角形中,30°角所对的直角边等于斜边的一半,即可证得AG=AD;(2)首先过点D作DH∥BC交AC于点H,证得△ADH是等边三角形,又由CE=DA,可利用AAS证得△DHF≌△ECF,继而可得DF=EF;(3)由△ABC是等边三角形,DG⊥AC,可得AG=GH,即可得S△ADG=S△HDG,又由△DHF≌△ECF,即可证得S△DGF=S△ADG+S△ECF.证明:(1)∵△ABC是等边三角形,∴∠A=60°,∵DG⊥AC,∴∠AGD=90°,∠ADG=30°,∴AG=AD;(2)过点D作DH∥BC交AC于点H,∴∠ADH=∠B,∠AHD=∠AC B,∠FDH=∠E,∵△ABC是等边三角形,∴∠B=∠ACB=∠A=60°,∵AD=CE,∴DH=CE,在△DHF和△ECF中,∴△DHF≌△ECF(AAS),∴DF=EF(3)∵△ABC是等边三角形,DG⊥AC,∴AG=GH,∴S△ADG=S△HDG,∵△DHF≌△ECF,∴S△DHF=S△ECF,∴S△DGF=S△DGH+S△DHF=S△ADG+S△ECF.2.【答案】【解析】根据有理数的乘方、立方根、平方根、绝对值进行计算即可.解:3.【答案】-1≤x<2【解析】试题分析:分别求出两个不等式的解集,从而得出不等式组的解. 试题解析:解不等式不等式①得x≥-1解不等式不等式②得x<2不等式组的解集为-1≤x<2。
浙江省湖州市第四中学八年级数学开学检测试题(无答案)

浙江省湖州市第四中学八年级数学开学检测试题浙教版(满分120分时间100分钟)一、选择题(本题共10 小题,每小题3分,共30分)1.小马虎在做下面的计算中只做对了一题,他做对的题目是().A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D. 错误!未找到引用源。
2.如图:撕了一个角后的三角形纸片,其中∠A=30°,∠B=70°,则撕去的角的度数是( )A.100° B.80° C.70° D.90°a ”这一事件是()3.“a是实数, ||0A.必然事件 B.不确定事件 C.不可能事件 D.随机事件4.在平坦的草坪上有A、B、C三个小球,且A球和B球相距3米,A球和C球相距1米,则B球与C球距离()A.BC=2米B.BC=2米或4米 C.2米<BC<4米 D.2米≤BC≤ 4米5.不等式组错误!未找到引用源。
,的解集在数轴上可以表示为( )6.若关于错误!未找到引用源。
、错误!未找到引用源。
的二元一次方程组错误!未找到引的解也是方程错误!未找到引用源。
的解,则错误!未找到引用源。
的值用源。
为() A.-1 B.1 C.5 D.-57.如图,在直角三角形A BC中,∠C为直角,∠A=30°,CD、CE分别是它的高和角平分线,则∠ECD为() A.15° B.25° C.35° C.30°8.多项式4x 2+1加上一个单项式后,使它能成为一个二项整式的完全平方,则满足条件的单项式有( ) A .2个 B .3个 C .4个 D .5个9.仓库有存煤错误!未找到引用源。
吨, 原计划每天烧煤错误!未找到引用源。
吨, 现在每天节约错误!未找到引用源。
吨, 则可多烧的天数为( ) A .错误!未找到引用源。
B .错误!未找到引用源。
C .错误!未找到引用源。
D .错误!未找到引用源。
浙江省湖州市八年级上学期数学开学试卷
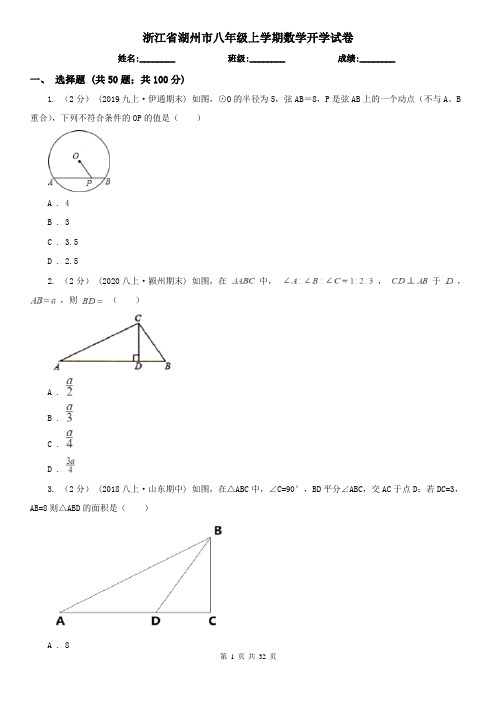
浙江省湖州市八年级上学期数学开学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共50题;共100分)1. (2分) (2019九上·伊通期末) 如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B 重合),下列不符合条件的OP的值是()A . 4B . 3C . 3.5D . 2.52. (2分) (2020八上·颍州期末) 如图,在中,,于,,则()A .B .C .D .3. (2分) (2018八上·山东期中) 如图,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D;若DC=3,AB=8则△ABD的面积是()A . 8B . 12C . 16D . 244. (2分) (2019八上·句容期末) 下列四组数,可作为直角三角形三边长的是()A . 、、B . 、、C . 、、D . 、、5. (2分) (2020八下·抚顺期末) 如图,在矩形中,将矩形沿折叠,点落在点处,与交于则的面积为()A .B . 7C .D .6. (2分) (2019八下·北京期中) 已知直角三角形的两条边长分别是3和5,那么这个三角形的第三条边的长()A . 4B . 16C .D . 4或7. (2分) (2020七下·高新期末) 下列各组数据不是勾股数的是()A . 2,3,4B . 3,4,5C . 5,12,13D . 6,8,108. (2分) (2020八下·延平月考) 如图,正方形ABCD和正方形CGEF的边长分别是2和3,且点B , C ,G在同一直线上,M是线段AE的中点,连接MF ,则MF的长为()A .B .C .D . 29. (2分)(2020·沙河模拟) 嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km (最小圆的半径是1km ),下列关于小艇 A , B 的位置描述,正确的是()A . 小艇 A 在游船的北偏东60°方向上,且与游船的距离是3kmB . 游船在小艇A的南偏西60°方向上,且与小艇 A 的距离是3kmC . 小艇 B 在游船的北偏西30°方向上,且与游船的距离是 2kmD . 游船在小艇 B 的南偏东60°方向上,且与小艇 B 的距离是 2km10. (2分) (2019八下·孝南月考) 图中字母所代表的正方形的面积为144的选项为()A .B .C .D .11. (2分)如图所示,已知在平行四边形ABCD中,AB=6,BC=4,若∠B=45°,则平行四边形ABCD的面积为()A . 8B . 12C . 16D . 2412. (2分) (2019八上·永春月考) 如图,数轴上的点A所表示的数是()A .B .C .D .13. (2分) (2020八上·文水期末) 如图,已知△ ,按以下步骤作图:①分别以、为圆心,大于的长为半径画弧,两弧交于点、;②作直线交于点,连接,若,则下列结论中不一定成立的是()A .B . △ 是等边三角形C . 点D是AB的中点D .14. (2分) (2020九上·嵩县期末) 在△ABC中,tanC=,cosA=,则∠B=()A . 60°B . 90°C . 105°D . 135°15. (2分) (2020八下·崆峒期末) 已知直角三角形的两条直角边的长分别为和,则斜边的长为()A . 3B . 4C . 5D .16. (2分)(2020·苏州模拟) 如图,中,,,则的值为()A .B .C .D .17. (2分)等腰三角形的底边长为6,底边上的中线长为4,它的腰长为()A . 7B . 6C . 5D . 418. (2分) (2020八上·郑州月考) 下面各图中,不能证明勾股定理正确性的是()A .B .C .D .19. (2分) (2019八上·福田期中) 在Rt△ABC中,∠C=90°,若AC+BC=14cm,AB=10cm,则Rt△ABC的面积是()A . 24cm2B . 36cm2C . 48cm2D . 60cm220. (2分)(2020·郑州模拟) 平面直角坐标系中,菱形ABCD如图所示,,点D在线段AB的垂直平分线上,若菱形ABCD绕点O逆时针旋转,旋转速度为每秒,则第70秒时点D的对应坐标为()A .B .C .D .21. (2分)﹣2,0,0.5,﹣这四个数中,属于无理数的是()A . ﹣2B . 0C . 0.5D .22. (2分) (2017七下·东城期中) 如图,数轴上点表示的数可能是().A .B .C .D .23. (2分)(2020·滨湖模拟) 8的立方根为()A . 2B . ±2C . -2D . 424. (2分) (2017八下·路南期末) 等于()A . 4B . ±4C . -4D . ±225. (2分) (2017七下·南通期中) - 的相反数是()A .B . -C .D . -26. (2分) (2019七下·厦门期中) 在下列式子中,正确是()A . =﹣2B . ﹣=﹣0.6C . =﹣13D . =±627. (2分) (2020八下·兴城期末) 下列各二次根式中,为最简二次根式的是()A .B .C .D .28. (2分)(2018·吉林模拟) 的倒数是()A .B .C . ﹣D . ﹣29. (2分) (2020七下·肇庆月考) 下列等式正确的是()A .B .C .D .30. (2分) (2018八下·永康期末) 二次根式中,字母a的取值范围是A .B .C .D .31. (2分)下列各式中,运算正确的是().A .B .C .D .32. (2分)下列说法正确的是()A . 1的相反数是﹣1B . 1的倒数是﹣1C . 1的立方根是±1D . ﹣1是无理数33. (2分)(2017·萍乡模拟) 1不是﹣1的()A . 相反数B . 绝对值C . 平方数D . 倒数34. (2分) (2019八上·太原期中) 下列计算结果正确的是()A .B .C .D .35. (2分) (2020七下·河池期末) 16的平方根是A .B .C . 8D .36. (2分) (2019七下·厦门期末) 下列各点中,在第一象限的是()A . (1,0)B . (1,1)C . (1,﹣1)D . (﹣1,1)37. (2分) (2019七下·钦州期末) 点A(﹣3,4)所在象限为()A . 第一象限B . 第二象限C . 第三象限D . 第四象限38. (2分) (2018九上·椒江月考) 平面直角坐标系中,点P(2,-3)关于原点对称的点的坐标是()A . (2,3)B . (2,-3)C . (-2,3)D . (-2,-3)39. (2分)(2017·咸宁) 已知a、b、c为常数,点P(a,c)在第二象限,则关于x的方程ax2+bx+c=0根的情况是()A . 有两个相等的实数根B . 有两个不相等的实数根C . 没有实数根D . 无法判断40. (2分)(2020·大连) 平面直角坐标系中,点P(3, 1)关于x轴对称的点的坐标是()A . (3,1)B . (3,-1)C . (-3,1)D . (-3,-1)41. (2分) (2019八下·新余期末) 如图,在平面直角坐标系中,点A(2,m)在第一象限,若点A关于x 轴的对称点B在直线y=﹣x+1上,则m的值为()A . ﹣1B . 1C . 2D . 342. (2分) (2017八上·龙泉驿期末) 在平面直角坐标系xOy中,点P(﹣3,5)关于y轴的对称点在第()象限.A . 一B . 二C . 三D . 四43. (2分) (2017八上·潜江期中) 若等腰三角形的周长为16cm,其中一边长为4cm,则该等腰三角形的底边为()A . 4cmB . 6cmC . 4cm或8cmD . 8cm44. (2分) (2020八上·奉化期末) 在平面直角坐标系中,若点P与点Q的横坐标相同,而纵坐标不同,则直线PQ与x轴的关系是()A . 平行B . 垂直C . 重合D . 以上都不对45. (2分) (2017七下·福建期中) 已知点P(a,b),ab>0,a+b<0,则点P在()A . 第一象限B . 第二象限C . 第三象限D . 第四象限46. (2分)现定义运算“★”,对于任意实数a、b,都有a★b=a2-3a+b,如:4★5=42-3×4+5,若x★2=6,则实数x的值是()A . -4或-1B . 4或-1C . 4或-2D . -4或247. (2分)点P(-3,2)在()A . 第一象限B . 第二象限C . 第三象限D . 第四象限48. (2分)(2019·台湾) 如图的坐标平面上有原点O与A,B,C,D四点.若有一直线L通过点(-3,4)且与y轴垂直,则L也会通过下列哪一点?()A . AB . BC . CD . D49. (2分) (2017八上·武城开学考) 若A(2x-5,6-2x)在第四象限,则X的取值范围是()A . x>3B . x>-3C . x<-3D . x<350. (2分) (2019七下·重庆期中) 下列说法中,正确的是()A . 直线外一点到这条直线的垂线段,叫做点到直线的距离;B . 已知线段,轴,若点的坐标为(-1,2),则点的坐标为(-1,-2)或(-1,6);C . 若与互为相反数,则;D . 已知关于的不等式的解集是,则的取值范围为 .参考答案一、选择题 (共50题;共100分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省湖州四中八年级(上)入学数学试卷一、选择题(每小题3分,共30分)1.(3分)下列各式中,不是二次根式的是()A.B.C.D.2.(3分)已知二次根式的值为3,那么x的值是()A.3B.9C.﹣3D.3或﹣33.(3分)估算+2的值是在()A.5和6之间B.6和7之间C.7和8之间D.8和9之间4.(3分)下列计算中正确的是()A.B.C.D.5.(3分)下列方程是一元二次方程()A.x+2y=1B.2x(x﹣1)=2x2+3C.3x+=4D.x2﹣2=06.(3分)关于x的一元二次方程x2﹣k=0有实数根,则()A.k<0B.k>0C.k≥0D.k≤07.(3分)方程x2=3x的解是()A.x=0B.x1=0,x2=﹣3C.x=3D.x1=0,x2=3 8.(3分)下列能断定△ABC为等腰三角形的是()A.∠A=30°,∠B=60°B.AB=AC=2,BC=4C.∠A=50°,∠B=80°D.AB=3、BC=7,周长为139.(3分)设min{x,y}表示x,y两个数中的最小值,例如min{0,2}=0,min{12,8}=8,则关于x的函数y=min{2x,x+2}可以表示为()A.y=B.y=C.y=2x D.y=x+210.(3分)某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为()A.x(x+1)=1056B.x(x﹣1)=1056×2C.x(x﹣1)=1056D.2x(x+1)=1056二、填空题(每小题3分,共18分)11.(3分)如图,AB∥CD,CE平分∠ACD交AB于E,∠A=118°,则∠AEC等于度.12.(3分)在平面直角坐标系中点A(,1)到原点的距离是.13.(3分)若a、b都为实数,且b=2011,a=,a b=.14.(3分)当x=时,代数式x2+4x的值与代数式2x+3的值相等.15.(3分)一元二次方程(m﹣3)x2﹣5mx+7m=2mx﹣6中,二次项系数为;一次项为;常数项为.三、解答题(共40分)16.(16分)计算题(1)(﹣)2﹣(2)(3)(4).17.(8分)用适当方法解一元二次方程(1)16(x+5)2﹣9=0(2)3x2+2x+4=O.18.(6分)已知关于x的一元二次方程x2﹣(k+1)x﹣6=0的一个根是2,求方程的另一根x1=和k=.19.(5分)如图:Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB 边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,则P、Q分别从A、B同时出发,经过多少秒钟,△PBQ的面积等于8cm2?20.(7分)如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1),与y轴的交点为C,与x轴的交点为D.(1)求一次函数解析式;(2)求C点的坐标;(3)求△AOD的面积.21.(10分)随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据某市交通部门统计,2008年底全市汽车拥有量为150万辆,而截止到2010年底,全市的汽车拥有量已达216万辆.(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;(2)为保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过231.96万辆;另据估计,从2011年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%.假定每年新增汽车数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆.22.(3分)当x=﹣1时,二次根式的值是.浙江省湖州四中八年级(上)入学数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)下列各式中,不是二次根式的是()A.B.C.D.【分析】根据二次根式的性质,被开方数应大于或等于0.【解答】解:A、是二次根式;B、3﹣π<0,所以不是二次根式;C、是二次根式;D、是二次根式.故选:B.【点评】主要考查了二次根式的概念.二次根式的概念:式子(a≥0)叫二次根式.(a≥0)是一个非负数.二次根式中的被开方数必须是非负数,否则二次根式无意义.当二次根式在分母上时还要考虑分母不等于零,此时被开方数大于0.2.(3分)已知二次根式的值为3,那么x的值是()A.3B.9C.﹣3D.3或﹣3【分析】根据二次根式的定义和性质可直接解答.【解答】解:∵=3,=3,∴x=±3.故选:D.【点评】概念:式子(a≥0)叫二次根式;性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.3.(3分)估算+2的值是在()A.5和6之间B.6和7之间C.7和8之间D.8和9之间【分析】先估计的近似值,然后即可判断+2的近似值.【解答】解:由于16<19<25,所以4<<5,因此6<+2<7.故选:B.【点评】此题主要考查了估算无理数的大小的能力,现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.4.(3分)下列计算中正确的是()A.B.C.D.【分析】求出每个式子的值,再判断即可.【解答】解:A、结果是5,不是7,故本选项错误;B、结果是,不是1,故本选项错误;C、结果是﹣1,故本选项正确;D、结果是3﹣,故本选项错误;故选:C.【点评】本题考查了二次根式的性质的应用,主要考查学生的计算能力和判断能力.5.(3分)下列方程是一元二次方程()A.x+2y=1B.2x(x﹣1)=2x2+3C.3x+=4D.x2﹣2=0【分析】只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程.一元二次方程有三个特点:(1)只含有一个未知数;(2)未知数的最高次数是2;(3)是整式方程.【解答】解:A、x+2y=1是二元一次方程,故错误;B、方程去括号得:2x2﹣2x=2x2+3,整理得:﹣2x=3,为一元一次方程,故错误;C、3x+=4是分式方程,故错误;D、x2﹣2=0,符合一元二次方程的形式,正确.故选:D.【点评】要判断一个方程是否为一元二次方程,先看它是否为整式方程,若是,再对它进行整理.如果能整理为ax2+bx+c=0(a≠0)的形式,则这个方程就为一元二次方程.6.(3分)关于x的一元二次方程x2﹣k=0有实数根,则()A.k<0B.k>0C.k≥0D.k≤0【分析】根据直接开平方法的步骤得出x2=k,再根据非负数的性质得出k≥0即可.【解答】解:∵x2﹣k=0,∴x2=k,∴一元二次方程x2﹣k=0有实数根,则k≥0,故选:C.【点评】此题考查了直接开平方法解一元二次方程,用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.7.(3分)方程x2=3x的解是()A.x=0B.x1=0,x2=﹣3C.x=3D.x1=0,x2=3【分析】把方程整理后,运用因式分解法求解即可.【解答】解:原方程变形为:x2﹣3x=0,x(x﹣3)=0,∴x1=0,x2=3.故选D.【点评】方程整理后,容易分解因式的,用分解因式法求解一元二次方程较简单.8.(3分)下列能断定△ABC为等腰三角形的是()A.∠A=30°,∠B=60°B.AB=AC=2,BC=4C.∠A=50°,∠B=80°D.AB=3、BC=7,周长为13【分析】求出∠C,即可判断A;根据三角形的三边关系定理即可判断B;求出∠C即可判断C;求出AC,根据三角形三边关系定理即可判断D.【解答】解:A、∵∠A=30°,∠B=60°,∴∠C=180°﹣∠A﹣∠B=90°,即∠A≠∠B≠∠C,∴△ABC不是等腰三角形,故本选项错误;B、∵AB=AC=2,BC=2,∴2+2=4,即三条线段不能组成三角形,故本选项错误;C、∵∠A=50°,∠B=80°,∴∠C=180°﹣∠A﹣∠B=50°,即∠A=∠C,∴△ABC是等腰三角形,故本选项正确;D、∵AB=3,BC=7,周长是13,∴AC=13﹣3﹣7=3,∵3+3<7,∴三条线段不能组成三角形,故本选项错误;故选:C.【点评】本题考查了三角形的三边关系定理和等腰三角形的判定的应用,主要考查学生的理解能力和判断能力.9.(3分)设min{x,y}表示x,y两个数中的最小值,例如min{0,2}=0,min{12,8}=8,则关于x的函数y=min{2x,x+2}可以表示为()A.y=B.y=C.y=2x D.y=x+2【分析】根据题意要求及函数性质,可对每个选项加以论证得出正确选项.【解答】解:根据已知,在没有给出x的取值范围时,不能确定2x和x+2的大小,所以不能直接表示为,C:y=2x,D:y=x+2.当x<2时,可得:x+x<x+2,即2x<x+2,可表示为y=2x.当x≥2时,可得:x+x≥x+2,即2x≥x+2,可表示为y=x+2.故选:A.【点评】此题考查的是一次函数的性质,解题的关键是根据已知和函数性质讨论得出.10.(3分)某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1056张照片,如果全班有x名同学,根据题意,列出方程为()A.x(x+1)=1056B.x(x﹣1)=1056×2C.x(x﹣1)=1056D.2x(x+1)=1056【分析】如果全班有x名同学,那么每名同学要送出(x﹣1)张,共有x名学生,那么总共送的张数应该是x(x﹣1)张,即可列出方程.【解答】解:∵全班有x名同学,∴每名同学要送出(x﹣1)张;又∵是互送照片,∴总共送的张数应该是x(x﹣1)=1056.故选:C.【点评】本题考查一元二次方程在实际生活中的应用.计算全班共送多少张,首先确定一个人送出多少张是解题关键.二、填空题(每小题3分,共18分)11.(3分)如图,AB∥CD,CE平分∠ACD交AB于E,∠A=118°,则∠AEC等于31度.【分析】要求∠AEC的度数,根据平行线的性质,只需求得∠2的度数.显然结合平行线的性质以及角平分线的定义就可解决.【解答】解:∵AB∥CD,CE平分∠ACD交AB于E,∠A=118°,∴∠1=∠2=(180°﹣∠A)=(180°﹣118°)=31°,∴∠AEC=∠2=31°.【点评】本题考查的是角平分线的性质及平行线的性质,比较简单,需同学们熟练掌握.12.(3分)在平面直角坐标系中点A(,1)到原点的距离是2.【分析】求出与1的平方和的算术平方根即可.【解答】解:点A(,1)到原点的距离是=2.故答案为:2.【点评】本题主要考查了点到原点的距离求法:一个点横坐标与纵坐标平方和的算术平方根即为此点到原点的距离.13.(3分)若a、b都为实数,且b=2011,a=2,a b=1.【分析】先根据二次根式的基本性质:有意义,则a≥0求出a的值,进一步求出b 的值,再代入可求a b的值.【解答】解:∵b=2011,∴a﹣2≥0,则有a≥2;2﹣a≥0,则有a≤2,综合得,a=2将a=2代入,得b=2011=0,∴a b=1.故答案为:2;1.【点评】考查了二次根式有意义的条件,解决此题的关键是掌握二次根式的基本性质:有意义,则a≥0.14.(3分)当x=﹣3,1时,代数式x2+4x的值与代数式2x+3的值相等.【分析】先根据题意列出方程,解得方程的解即可.【解答】解:x2+4x=2x+3,整理得,x2+2x﹣3=0,解得,x1=1,x2=﹣3,∴当x=﹣3或1时,代数式x2+4x的值与代数式2x+3的值相等.【点评】本题考查了简单的列一元二次方程和解一元二次方程.15.(3分)一元二次方程(m﹣3)x2﹣5mx+7m=2mx﹣6中,二次项系数为m﹣3;一次项为﹣7m;常数项为7m+6.【分析】一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0).在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.【解答】解:(m﹣3)x2﹣5mx+7m=2mx﹣6,(m﹣3)x2﹣5mx+7m﹣2mx+6=0,(m﹣3)x2﹣7mx+7m+6=0,∴二次项系数为:m﹣3,一次项为:﹣7m,常数项为:7m+6,故答案为:m﹣3,﹣7m,7m+6,【点评】此题主要考查了一元二次方程的一般形式,要确定各项的系数时,一定要注意前面的符号,尤其是负号.三、解答题(共40分)16.(16分)计算题(1)(﹣)2﹣(2)(3)(4).【分析】(1)根据二次根式的性质计算;(2)先把各二次根式化为最简二次根式,然后合并即可;(3)根据二次根式的乘除法则运算;(4)利用完全平方公式和平方差公式计算.【解答】解:(1)原式=10﹣7=3;(2)原式=+3﹣2=2;(3)原式=3×(﹣)×=﹣;(4)原式=3﹣+2+2+3﹣2=6.【点评】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.17.(8分)用适当方法解一元二次方程(1)16(x+5)2﹣9=0(2)3x2+2x+4=O.【分析】(1)先变形为(x+5)2=,然后利用直接开平方法求解;(2)先计算判别式得到△=22﹣4×3×4<0,然后根据判别式的意义判断方程没有实数根.【解答】解:(1)(x+5)2=,x+5=±,所以x1=﹣,x2=﹣;(2)△=22﹣4×3×4<0,所以方程没有实数根.【点评】本题考查了解一元二次方程﹣直接开平方法:如果方程化成x2=p的形式,那么可得x=±p;如果方程能化成(nx+m)2=p(p≥0)的形式,那么nx+m=±p.也考查了根的判别式.18.(6分)已知关于x的一元二次方程x2﹣(k+1)x﹣6=0的一个根是2,求方程的另一根x1=﹣3和k=﹣2.【分析】根据一元二次方程ax2+bx+c=0(a≠0,且a,b,c是常数)的两个实根之积求出另一根,再根据两根之和求出k则可.【解答】解:设方程的另一根为x1,由韦达定理:2x1=﹣6,∴x1=﹣3.由韦达定理:﹣3+2=k+1,∴k=﹣2.当k=﹣2时,△>0,k=﹣2.【点评】本题考查了韦达定理(即根与系数的关系)的应用,注意这个定理的应用条件,在求出k的值以后要检验一下方程是否有解.因为定理应用的条件是原方程有解.19.(5分)如图:Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB 边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,则P、Q分别从A、B同时出发,经过多少秒钟,△PBQ的面积等于8cm2?【分析】设经过x秒钟,△PBQ的面积等于8平方厘米,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解.【解答】解:设经过x秒以后△PBQ面积为8整理得:x2﹣6x+8=0解得:x=2或x=4答:2或4秒后△PBQ的面积等于8cm2【点评】此题主要考查了一元二次方程的应用,找到关键描述语“△PBQ的面积等于8cm2”,得出等量关系是解决问题的关键.20.(7分)如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1),与y轴的交点为C,与x轴的交点为D.(1)求一次函数解析式;(2)求C点的坐标;(3)求△AOD的面积.【分析】(1)首先根据正比例函数解析式求得m的值,再进一步运用待定系数法求得一次函数的解析式;(2)根据(1)中的解析式,令x=0求得点C的坐标;(3)根据(1)中的解析式,令y=0求得点D的坐标,从而求得三角形的面积.【解答】解:(1)∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),∴2m=2,m=1.把(1,2)和(﹣2,﹣1)代入y=kx+b,得,解得:,则一次函数解析式是y=x+1;(2)令x=0,则y=1,即点C(0,1);(3)令y=0,则x=﹣1.则△AOD的面积=×1×2=1.【点评】此题综合考查了待定系数法求函数解析式、直线与坐标轴的交点的求法.21.(10分)随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据某市交通部门统计,2008年底全市汽车拥有量为150万辆,而截止到2010年底,全市的汽车拥有量已达216万辆.(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;(2)为保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过231.96万辆;另据估计,从2011年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%.假定每年新增汽车数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆.【分析】(1)设该市汽车拥有量的年平均增长率为x,根据2008年底全市汽车拥有量为150万辆,而截止到2010年底,全市的汽车拥有量已达216万辆可列方程求解.(2)设全市每年新增汽车数量为y万辆,则2011年底全市的汽车拥有量为216×90%+y 万辆,2012年底全市的汽车拥有量为(216×90%+y)×90%+y万辆根据要求到2012年底全市汽车拥有量不超过231.96万辆可列不等式求解.【解答】解:(1)设该市汽车拥有量的年平均增长率为x(1分)根据题意,得150(1+x)2=216(2分)解得x1=0.2=20%,x2=﹣2.2(不合题意,舍去).答:该市汽车拥有量的年平均增长率为20%;(4分)(2)设全市每年新增汽车数量为y万辆,则2011年底全市的汽车拥有量为216×90%+y 万辆,2012年底全市的汽车拥有量为(216×90%+y)×90%+y万辆.根据题意得(216×90%+y)×90%+y≤231.96,(6分)解得y≤30;(7分)答:该市每年新增汽车数量最多不能超过30万辆.(8分)【点评】本题考查理解题意的能力,根据增长的结果做为等量关系列出方程求解,根据2012车的总量这个不等量关系列出不等式求解.22.(3分)当x=﹣1时,二次根式的值是2.【分析】把x=﹣1代入二次根式即可.【解答】解:当x=﹣1时,==2.故填2.【点评】本题主要考查二次根式的化简求值,比较简单.。
