第五章点的运动学1
合集下载
工程力学之点的运动学
。
简谐振动
点在平衡位置附近作周期性往 复运动，加速度与位移成正比 、方向相反。
抛体运动
点在重力作用下沿抛物线轨迹 的运动，如平抛、斜抛等。
一般平面曲线运动
点在平面内沿任意曲线轨迹的 运动，加速度和速度方向可任
意变化。
05
工程应用实例分析
机械手臂的运动控制
运动学建模
01
通过D-H参数法或旋量理论建立机械手臂的运动学模型，描述
在航空航天工程中，点的运动学可用于分 析飞行器的飞行轨迹和姿态控制，为航空 航天技术的发展提供理论支持。
土木工程
生物医学工程
在土木工程中，点的运动学可用于研究结 构的动力响应和稳定性问题，为工程结构 的设计和施工提供科学依据。
在生物医学工程中，点的运动学可用于分 析人体运动系统的生物力学特性，为医疗 器械的设计和康复治疗提供理论指导。
曲线运动的合成与分解
运动的合成
将点的运动分解为沿不同坐标轴的分运动，通过矢量合成得到点 的实际运动。
运动的分解
根据实际需要，将点的曲线运动分解为多个简单的直线或圆周运动， 便于分析和计算。
运动的叠加原理
多个独立的分运动可以线性叠加，形成复杂的曲线运动。
曲线运动的特殊形式
匀速圆周运动
点绕固定中心以恒定速率作圆 周运动，加速度始终指向圆心
速直线运动。
特点
速度大小随时间均匀变化，加速度 大小和方向保持不变。
公式
s = v0t + 1/2at^2，其中s为位移， v0为初速度，a为加
已知分运动求合运动，其位移、速度、加速度遵 循平行四边形定则。
分解
已知合运动求分运动，可将合运动分解为两个简 单的分运动进行处理。
简谐振动
点在平衡位置附近作周期性往 复运动，加速度与位移成正比 、方向相反。
抛体运动
点在重力作用下沿抛物线轨迹 的运动，如平抛、斜抛等。
一般平面曲线运动
点在平面内沿任意曲线轨迹的 运动，加速度和速度方向可任
意变化。
05
工程应用实例分析
机械手臂的运动控制
运动学建模
01
通过D-H参数法或旋量理论建立机械手臂的运动学模型，描述
在航空航天工程中，点的运动学可用于分 析飞行器的飞行轨迹和姿态控制，为航空 航天技术的发展提供理论支持。
土木工程
生物医学工程
在土木工程中，点的运动学可用于研究结 构的动力响应和稳定性问题，为工程结构 的设计和施工提供科学依据。
在生物医学工程中，点的运动学可用于分 析人体运动系统的生物力学特性，为医疗 器械的设计和康复治疗提供理论指导。
曲线运动的合成与分解
运动的合成
将点的运动分解为沿不同坐标轴的分运动，通过矢量合成得到点 的实际运动。
运动的分解
根据实际需要，将点的曲线运动分解为多个简单的直线或圆周运动， 便于分析和计算。
运动的叠加原理
多个独立的分运动可以线性叠加，形成复杂的曲线运动。
曲线运动的特殊形式
匀速圆周运动
点绕固定中心以恒定速率作圆 周运动，加速度始终指向圆心
速直线运动。
特点
速度大小随时间均匀变化，加速度 大小和方向保持不变。
公式
s = v0t + 1/2at^2，其中s为位移， v0为初速度，a为加
已知分运动求合运动，其位移、速度、加速度遵 循平行四边形定则。
分解
已知合运动求分运动，可将合运动分解为两个简 单的分运动进行处理。
第五章 点的运动学
l
于是B的运动方程为 x r cos l 1 ( r )2 sin 2
l
为使计算方便,令 y
cos 1 ( r )2 sin2 1 1 ( r )2 sin2
l
2l
1 1 ( r )2 1 ( r )2 cos2
4l 4l
A
r
l
φ O
ψ
ωC
x
得x r cos l[1 1 ( r )2 1 ( r )2 cos2 ]
则有
ax
dvx dt
d2x dt 2
ay
dvy dt
d2 y dt 2
az
dvz dt
d2z dt 2
因此，加速度在直角坐标轴上的投影等于动点的各对应坐
标对时间的二阶导数。
[例1] 曲柄连杆机构中,曲柄OA以ω=常数绕O转动,带动杆AB
及滑块B沿直线运动,已知OA=r,AB=l,且 l>r;求块B的运动方
试求动点的轨迹、速度和加速度？ z
解：
由运动方程消去时间t得动点的 轨迹方程为
x2 y2 r2 , y r sin z
u
由此可知动点的轨迹是一条螺旋线 o a
如图所示
t
y
X
5.2点的运动学描述（直角坐标法）
动点的速度在直角坐标轴上的投影：
z
•
x x r sin t
an
v
d
dt
v lim
t0
t
v lim (
t0
S
S t
)
v
2
lim
于是B的运动方程为 x r cos l 1 ( r )2 sin 2
l
为使计算方便,令 y
cos 1 ( r )2 sin2 1 1 ( r )2 sin2
l
2l
1 1 ( r )2 1 ( r )2 cos2
4l 4l
A
r
l
φ O
ψ
ωC
x
得x r cos l[1 1 ( r )2 1 ( r )2 cos2 ]
则有
ax
dvx dt
d2x dt 2
ay
dvy dt
d2 y dt 2
az
dvz dt
d2z dt 2
因此，加速度在直角坐标轴上的投影等于动点的各对应坐
标对时间的二阶导数。
[例1] 曲柄连杆机构中,曲柄OA以ω=常数绕O转动,带动杆AB
及滑块B沿直线运动,已知OA=r,AB=l,且 l>r;求块B的运动方
试求动点的轨迹、速度和加速度？ z
解：
由运动方程消去时间t得动点的 轨迹方程为
x2 y2 r2 , y r sin z
u
由此可知动点的轨迹是一条螺旋线 o a
如图所示
t
y
X
5.2点的运动学描述（直角坐标法）
动点的速度在直角坐标轴上的投影：
z
•
x x r sin t
an
v
d
dt
v lim
t0
t
v lim (
t0
S
S t
)
v
2
lim
理论力学第五章 点的运动
【例5.1】 已知点的运动方程为 x r cost y r sin t 其中：r、ω是常数。求动点的运动轨迹、速度与加速度。
目录
第五章 点的运动\描述点运动的直角坐标表示法
【解】 为求动点的运动轨迹，将运动方程平方后相加，消去t得 x2 y2 r 2
这说明动点的运动轨迹是以O为圆心、r为半径的一个圆。当 ωt=0时，x=r, y=0，动点位于x轴上，当ωt=π/2时，x=0, y=r，动点位 于y轴上。 y v 动点的速度在坐标轴上的投影为 M r v x r sin t t v y r cost x O 因此速度的大小为
z M k O r z
a
v x y
i
j y
上式表明，动点的加速度在各坐标轴上的投影分别等于动点相 应的位置坐标对时间t的二阶导数。 目录
第五章 点的运动\描述点运动的直角坐标表示法 加速度的大小及方向余弦为
2 2 2 d x d y d z 2 2 2 2 2 2 a ax a y az ( 2 ) ( 2 ) ( 2 ) dt dt dt ay ax az cosa , i cosa , j cosa , k a a a
x x(t ) y y (t )
当动点始终沿一直线运动时，如取该直线为坐标轴Ox，则动点 的运动方程为
x x(t )
目录
第五章 点的运动\描述点运动的直角坐标表示法
5.2.2 用直角坐标表示点的速度
如图所示，若以O点为坐标原点建立 Oxyz直角坐标系，则动点的位置矢量r 可表示为
第五章 点的运动\描述点运动的弧坐标表示法
dr τ ds 式中：—沿轨迹切向指向弧坐标正向的单位矢量。此外，
理论力学(第7版)第五章 点的运动学
a 4、匀速运动： v 常数， 0, s s0 vt
运 动 规 律
[例5-1 ] 已知点的运动方程为x=2sin 4t m，y=2cos 4t m， z=4t m。 求：点运动轨迹的曲率半径 。
解：
vx x 8 cos 4t , ax 32 sin 4t x
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
3
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
三.加速度
dv d 2r a r 2 dt dt
dv v2 a a a n a a n n n dt
17
5-3 自然法 曲率(1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
d lim| | t 0 S dS 1
由于a , an均在密切面内，全加速a必在密切面内。 度
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
(动画自然坐标轴的几何性质)
曲线在P点的密切面形成
5-3 自然法
二.点的速度
当t 0时，r MM' S
v y y 8 sin 4t , a y 32 cos 4t y
v z z 4, a z 0 z
2 2 2 2 v v x v 2 v z 80 m s , a a x a 2 a z 32m s 2 y y
运 动 规 律
[例5-1 ] 已知点的运动方程为x=2sin 4t m，y=2cos 4t m， z=4t m。 求：点运动轨迹的曲率半径 。
解：
vx x 8 cos 4t , ax 32 sin 4t x
r r t
—以矢量表示的 点的运动方程
矢端曲线：动点M在运动过程中，矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
3
二.点的速度
dr v r dt
方向：沿着矢径r的矢端曲线的切线 方向，且与此点的运动方向一致。
大小：速度矢的模，表明点运动的快慢。
三.加速度
dv d 2r a r 2 dt dt
dv v2 a a a n a a n n n dt
17
5-3 自然法 曲率(1 / ) ：
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
d lim| | t 0 S dS 1
由于a , an均在密切面内，全加速a必在密切面内。 度
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]：自然坐标系是沿曲 13 线而变动的游动坐标系。
(动画自然坐标轴的几何性质)
曲线在P点的密切面形成
5-3 自然法
二.点的速度
当t 0时，r MM' S
v y y 8 sin 4t , a y 32 cos 4t y
v z z 4, a z 0 z
2 2 2 2 v v x v 2 v z 80 m s , a a x a 2 a z 32m s 2 y y
(完整版)第五章-点的运动学
解： 炸弹的运动方程
x vt cos45
y vt sin 45 gt2 / 2
炸弹的初速度
求炸弹落到地面的时间，由 1800 277.8t sin 45 gt2 / 2
得 t 7.688s
可求出炸弹与目标的水平距离，
40
45 40 5
得： 又： 比较两式得：
速度在各坐标轴上的投影等于动点的各对应坐标对时间的一阶导数。
Part two 运动学
运动学是研究 物体运动的几何性质的学科。
研究一个物体的机械运动，必须选取另一个物体作为 参考，这个参考的物体称为参考体。
运动学研究 点和刚体的运动。
点的运动学 是研究一般物体运动的基础，又 具有独立的应用意义.
研究点的简单运动，研究点相对某一个参考系的 几何位置随时间变动的规律。
(4)求点M速度矢、加速度矢的大小、方向。
x=asin=asinωt 轨迹方程： y=bcos=bcosωt
大小、方向均可求
例：如图，物体M自O点以速度v0 与水平成 角抛出，求M 点的运动规律及轨迹。
解：依题意，建坐标，有：
当t=0时： 得：
所以，有： V0 cos0t C3
V0 sin0t gt2 2 C4
连接各矢量端点构成矢量端点的连续曲线，称为速度
矢端曲线。
见flash
动点的加速度矢a 的方向与速度矢端曲线在相应点的切线相平行。
r1 r2 r3
v1 a
v2 v3
v1
v2
v v3
a
§5-2 直角坐标法
动点M的位置可以用r表示，也可 用坐标x、y、z来表示，如图所示。
矢径原点与坐标原点重合时，有：
当t=0时，有： x 0, y 0 得 C3 C4 0
理论力学第5章(点的运动)
包括几何静力学、分析静力学
(2) 运动学: 研究点与刚体运动的几何性质。
包括位移、轨迹、速度、加速度。 (与力无关、也是变形体运动基础)
A B
F
C
B
刚体运动
C
变形(包含刚体位移和相对位移)
(3) 动力学: 研究物体所受力与运动间的关系。
包括质点系、刚体，变形体的动力效应。
第五章 点的运动学
§5-1 运动学的基本概念
速度
已知： OC AC BC l , MC a , t。 求：运动方程、轨迹、速度和加速度。
x l a cost ax v x 2 a y vy y l a sin t
2
加速度
a a a
F ( x, y) 0
二、点的速度v
又
r = xi + yj + zk
式中 v x 所以得
dr dx dy dz v i j k dt dt dt dt v = vx i + vy j + vz k
、v y
、v z
vx
dx dt
v
表明：“动点的速度在坐标轴上的投影，等于动点对应的位置 坐标对时间 t 的一阶导数”。 则速度的大小和方向余弦为
弧坐标的运动方程sf切向加速度表示速度大小的变化三点的加速度法向加速度表示速度方向的变化匀速运动v常数常数常数匀变速直线运动匀速圆周运动匀速直线运动或静止直线运动匀速运动圆周运动匀速运动直线运动匀速曲线运动匀变速曲线运动点作曲线运动画出下列情况下点的加速度方向
(1) 静力学: 研究物体所受力系的简化、平衡规律及其应用。
△r称为在△t时间内动点M的位移。
间间隔△t内的平均速度。以 v*表示。则： Δr v Δt 平均速度表示动点在△t内平均运动的快慢和运动方向。
(2) 运动学: 研究点与刚体运动的几何性质。
包括位移、轨迹、速度、加速度。 (与力无关、也是变形体运动基础)
A B
F
C
B
刚体运动
C
变形(包含刚体位移和相对位移)
(3) 动力学: 研究物体所受力与运动间的关系。
包括质点系、刚体，变形体的动力效应。
第五章 点的运动学
§5-1 运动学的基本概念
速度
已知： OC AC BC l , MC a , t。 求：运动方程、轨迹、速度和加速度。
x l a cost ax v x 2 a y vy y l a sin t
2
加速度
a a a
F ( x, y) 0
二、点的速度v
又
r = xi + yj + zk
式中 v x 所以得
dr dx dy dz v i j k dt dt dt dt v = vx i + vy j + vz k
、v y
、v z
vx
dx dt
v
表明：“动点的速度在坐标轴上的投影，等于动点对应的位置 坐标对时间 t 的一阶导数”。 则速度的大小和方向余弦为
弧坐标的运动方程sf切向加速度表示速度大小的变化三点的加速度法向加速度表示速度方向的变化匀速运动v常数常数常数匀变速直线运动匀速圆周运动匀速直线运动或静止直线运动匀速运动圆周运动匀速运动直线运动匀速曲线运动匀变速曲线运动点作曲线运动画出下列情况下点的加速度方向
(1) 静力学: 研究物体所受力系的简化、平衡规律及其应用。
△r称为在△t时间内动点M的位移。
间间隔△t内的平均速度。以 v*表示。则： Δr v Δt 平均速度表示动点在△t内平均运动的快慢和运动方向。
第五章 点的运动
HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY ENGINEERING MECHANICS HOHAI UNIVERSITY HOHAI UNIVERSITY
例1：图示机构中A、B两滑块可分别沿互相垂直的两 ：图示机构中A 直槽滑动。 直槽滑动。已知BA=a，AM＝b，＝ωt+α(ω, α为常 y 求点M的运动轨迹、速度和加速度。 量)，求点M的运动轨迹、速度和加速度。 M 解： 运动方程： 运动方程：
HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY ENGINEERING MECHANICS HOHAI UNIVERSITY HOHAI UNIVERSITY
A
vA x
I
vA vAt && x = ax = sin R R 2 vA vAt && = a y = y cos R R 2 vA a= R
( a, x ) =
2
aM
O
π
2
; ( a, y ) =
指向A 即a沿MA，指向 沿 指向
§5-3 点的运动的自然表示法
HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY HOHAI UNIVERSITY ENGINEERING MECHANICS HOHAI UNIVERSITY HOHAI UNIVERSITY
理论力学5__点的运动学
23
第五章 点的运动学
§5-3 自然法
—— 已知运动轨迹 求速度和加速度
24
§5-3 自然法
一、弧坐标与运动方程
如果点沿着已知的轨迹 运动，则点的运动方程， 可用点在已知轨迹上所走 过的弧长随时间变化的规 律来描述。
25
§5-3 自然法
弧坐标具有以下要素：
（1）有坐标原点(一般在轨迹上 任选一参考点作为坐标原点)；
曲率：曲线切线的转角对弧长一阶导数的绝对值。
曲率半径ρ：曲率的倒数称为曲率半径。 1 lim d s0 s ds
31
§5-3 自然法
2、
点的速度
r v
r v
lim
r r
t0 t
r
r dr
dt
dr ds
ds dt
rr
τv vτ
τr vr
r r
rr
rr
速度的大小： v ds s& dt
空间曲线上的任意点都存在且仅存在唯一 的一个密切面。
空间曲线上任意点的无穷小邻域内的一段 弧长，可以看作是位于密切面内的平面曲线。
曲线在密切面内的弯曲程度，称为曲线的 曲率，用 1 表示。
28
§5-3 自然法
2、自然轴系
副法线
法平面－ 过动点M并与切 线垂直的平面；
主法线－ 密切面与法平面的
s+
交线；
加速度 ：
r a
=
r dv
dt
d2rr dt2
= vr&= r&r&
物理意义：表征点速度变化快慢的物理量。
单位：m/s2，方向沿速度矢端曲线的切线。
11
§5-1 矢量法
矢端曲线
第五章 点的运动学
§5-3 自然法
—— 已知运动轨迹 求速度和加速度
24
§5-3 自然法
一、弧坐标与运动方程
如果点沿着已知的轨迹 运动，则点的运动方程， 可用点在已知轨迹上所走 过的弧长随时间变化的规 律来描述。
25
§5-3 自然法
弧坐标具有以下要素：
（1）有坐标原点(一般在轨迹上 任选一参考点作为坐标原点)；
曲率：曲线切线的转角对弧长一阶导数的绝对值。
曲率半径ρ：曲率的倒数称为曲率半径。 1 lim d s0 s ds
31
§5-3 自然法
2、
点的速度
r v
r v
lim
r r
t0 t
r
r dr
dt
dr ds
ds dt
rr
τv vτ
τr vr
r r
rr
rr
速度的大小： v ds s& dt
空间曲线上的任意点都存在且仅存在唯一 的一个密切面。
空间曲线上任意点的无穷小邻域内的一段 弧长，可以看作是位于密切面内的平面曲线。
曲线在密切面内的弯曲程度，称为曲线的 曲率，用 1 表示。
28
§5-3 自然法
2、自然轴系
副法线
法平面－ 过动点M并与切 线垂直的平面；
主法线－ 密切面与法平面的
s+
交线；
加速度 ：
r a
=
r dv
dt
d2rr dt2
= vr&= r&r&
物理意义：表征点速度变化快慢的物理量。
单位：m/s2，方向沿速度矢端曲线的切线。
11
§5-1 矢量法
矢端曲线
第五章点的运动学
第5章
点的运动学
§5-1 矢量法 §5-2 直角坐标法 §5-3 自然法
运动学： 以几何观点(几何公理)研究物体的 运动(轨迹,速度和加速度), 不考虑物体运动的原 因. 固定参考系: 一般采用固连于地球上的坐标系为 参考系,称为固定参考系.
时间: 瞬时和时间间隔
本章将研究点的简单运动，研究点相对某一个 参考系的几何位置随时间变动的规律，包括点的 运动方程、运动轨迹、速度和加速度等。
OC M C r r t
问题：以M点的轨迹为弧坐标（摆线），求M点的运动方程？
M点的速度：
v x r (1 cos t ) v y r sin t
y
x r ( t sin t ) y r (1 cos t )
2
M
M点的速度大小为
2 2
cos( a , j)
ay a
( l a ) sin t l a 2 al cos 2 t
2 2
例 直杆AB两端分别沿两互相垂直的固定直线Ox和Oy运动， 如图所示。试确定杆上任一点M的运动方程和轨迹方程，已 知MA=a，MB=b，角= t。
y
A
x
a M b y
80 m s ,
a
a x a y a z 32 m s
2 2 2
2
而
a
故
dv dt
0,
v
2
a n a 32 m s
2
r
2 .5 m
an
例：半径为r的轮子沿着直线轨道无滑动的滚动，设轮子转角为
ψ=ωt。求用直角坐标和弧坐标表示轮缘上一点M的运动方程， 并求该点的速度、切向加速度和法向加速度。 解： 取点M与直线轨道的接触点O为原点.
点的运动学
§5-1 矢量法 §5-2 直角坐标法 §5-3 自然法
运动学： 以几何观点(几何公理)研究物体的 运动(轨迹,速度和加速度), 不考虑物体运动的原 因. 固定参考系: 一般采用固连于地球上的坐标系为 参考系,称为固定参考系.
时间: 瞬时和时间间隔
本章将研究点的简单运动，研究点相对某一个 参考系的几何位置随时间变动的规律，包括点的 运动方程、运动轨迹、速度和加速度等。
OC M C r r t
问题：以M点的轨迹为弧坐标（摆线），求M点的运动方程？
M点的速度：
v x r (1 cos t ) v y r sin t
y
x r ( t sin t ) y r (1 cos t )
2
M
M点的速度大小为
2 2
cos( a , j)
ay a
( l a ) sin t l a 2 al cos 2 t
2 2
例 直杆AB两端分别沿两互相垂直的固定直线Ox和Oy运动， 如图所示。试确定杆上任一点M的运动方程和轨迹方程，已 知MA=a，MB=b，角= t。
y
A
x
a M b y
80 m s ,
a
a x a y a z 32 m s
2 2 2
2
而
a
故
dv dt
0,
v
2
a n a 32 m s
2
r
2 .5 m
an
例：半径为r的轮子沿着直线轨道无滑动的滚动，设轮子转角为
ψ=ωt。求用直角坐标和弧坐标表示轮缘上一点M的运动方程， 并求该点的速度、切向加速度和法向加速度。 解： 取点M与直线轨道的接触点O为原点.
G第5章点的运动学
• 点的运动学的基本概念：点是几何学中最简单的元素，运动学是研究物体运动 的科学。点的运动学主要研究点在平面或空间中的运动轨迹和规律。
• 点的运动轨迹的描述：点的运动轨迹可以通过参数方程或直角坐标方程进行描 述。参数方程通常包含一个时间变量，用于描述点在平面或空间中的位置和方 向随时间的变化。直角坐标方程则通过一组坐标值描述点的位置。
通过参数t来表示点的位置，通 常用于描述具有特定规律的点的
运动轨迹。
速度与加速度
速度
描述点在运动过程中的位置变化快慢，由位置对时间的一阶导数得到。在二维 平面内，速度是一个矢量，包含大小和方向；在三维空间中，速度是一个矢量 矩阵。
加速度
描述点在运动过程中的速度变化快慢，由速度对时间的一阶导数得到。在二维 平面内，加速度是一个矢量，包含大小和方向；在三维空间中，加速度是一个 矢量矩阵。
学习刚体的运动学
刚体是机械系统中常见的一种理想化模型，其运动学研究对于理解各种机械装置的工作原 理非常重要。可以学习刚体的平移、旋转等基本运动形式，以及刚体的速度和加速度的计 算方法。
THANKS FOR WATCHING
感谢您的观看
运动方程
基础运动方程
描述点在运动过程中位置随时间变化的规律，通常表示为 s=f(t)，其中s表示点的位置，f表示与时间t相关的函数。
微分方程
描述点在运动过程中速度和加速度随时间变化的规律，通 常表示为a=f(t, s, ds/dt)，其中a表示加速度，ds/dt表示 速度对时间的一阶导数。
积分方程
02 点的运动学基础
点的位置描述
直角坐标系
在二维平面内，点的位置可以通 过两个坐标值（x, y）进行描述。 在三维空间中，点的位置需要三 个坐标值（x, y, z）进行描述。
理论力学-点的运动学
详细描述
速度和加速度的矢量表示
04
CHAPTER
点的运动轨迹和运动参数
通过已知的初始位置和速度矢量，利用矢量合成法则确定点的运动轨迹。
直角坐标系
极坐标系
参数方程
利用极坐标表示点的位置，通过已知的初始位置和速度矢量，确定点的运动轨迹。
通过设定参数表示点的位置，根据初始条件和运动规律，确定参数方程，从而确定点的运动轨迹。
加速度与轨迹的关系
根据点的加速度矢量，可以判断点加速或减速的情况，进一步推断出其运动轨迹的变化趋势。
位移与轨迹的关系
根据点的位移矢量，可以确定点在平面或空间中的运动轨迹。
运动参数与轨迹的关系
05
CHAPTER
点的运动学应用
刚体的平动是指刚体在空间中的移动，其上任意两点之间的距离保持不变。
总结词
刚体的平动是刚体运动的一种基本形式，它描述了刚体在空间中的移动。在这种运动中，刚体的所有点都以相同的速度和方向移动，因此刚体上任意两点之间的距离保持不变。平动不会改变刚体的形状和大小。
点的速度和加速度
总结词
速度是描述物体运动快慢的物理量，其大小等于物体在单位时间内通过的位移。
详细描述
速度的大小可以用矢量表示，其大小等于物体在单位时间内通过的位移量，方向与物体运动方向相同。在直角坐标系中，速度矢量可以表示为位置矢量对时间的一阶导数。
速度的定义与计算
总结词
加速度是描述物体速度变化快慢的物理量，其大小等于物体在单位时间内速度的变化量。
详细描述
加速度的大小可以用矢量表示，其大小等于物体在单位时间内速度的变化量，方向与物体速度变化方向相同。在直角坐标系中，加速度矢量可以表示为速度矢量对时间的一阶导数。
速度和加速度的矢量表示
04
CHAPTER
点的运动轨迹和运动参数
通过已知的初始位置和速度矢量，利用矢量合成法则确定点的运动轨迹。
直角坐标系
极坐标系
参数方程
利用极坐标表示点的位置，通过已知的初始位置和速度矢量，确定点的运动轨迹。
通过设定参数表示点的位置，根据初始条件和运动规律，确定参数方程，从而确定点的运动轨迹。
加速度与轨迹的关系
根据点的加速度矢量，可以判断点加速或减速的情况，进一步推断出其运动轨迹的变化趋势。
位移与轨迹的关系
根据点的位移矢量，可以确定点在平面或空间中的运动轨迹。
运动参数与轨迹的关系
05
CHAPTER
点的运动学应用
刚体的平动是指刚体在空间中的移动，其上任意两点之间的距离保持不变。
总结词
刚体的平动是刚体运动的一种基本形式，它描述了刚体在空间中的移动。在这种运动中，刚体的所有点都以相同的速度和方向移动，因此刚体上任意两点之间的距离保持不变。平动不会改变刚体的形状和大小。
点的速度和加速度
总结词
速度是描述物体运动快慢的物理量，其大小等于物体在单位时间内通过的位移。
详细描述
速度的大小可以用矢量表示，其大小等于物体在单位时间内通过的位移量，方向与物体运动方向相同。在直角坐标系中，速度矢量可以表示为位置矢量对时间的一阶导数。
速度的定义与计算
总结词
加速度是描述物体速度变化快慢的物理量，其大小等于物体在单位时间内速度的变化量。
详细描述
加速度的大小可以用矢量表示，其大小等于物体在单位时间内速度的变化量，方向与物体速度变化方向相同。在直角坐标系中，加速度矢量可以表示为速度矢量对时间的一阶导数。
点的运动
第五章点的运动学本章将研究点的运动，包括点的运动方程、运动轨迹、速度、加速度等。
点的运动学也是研究刚体运动的基础。
第一节点的运动方程点在取定的坐标系中位置坐标随时间连续变化的规律称为点的运动方程。
点在空间运动的路径称为轨迹。
在某一参考体上建立不同的参考系，点的运动方程有不同的形式。
一、矢量法设点作空间曲线运动，在某一瞬时t ，动点为M，如图5-1所示。
选取参考体上某固定点O为坐标原点，自点O向动点M作矢量r，称r为点M相对于原点O的矢径。
当动点M运动时，矢径r随时间而变化，并且是时间的单值连续函数，即(5-1)上式称为矢量形式表示的点的运动方程。
显然，矢径r的矢端曲线就是动点的运动轨迹。
图5-1二、直角坐标法过点O建立固定的直角坐标系Oxyz，则动点M在任意瞬时的空间位置也可以用它的三个直角坐标x , y , z表示，如图5-1所示。
由于矢径的原点和直角坐标系的原点重合，矢径r可表为(5-2)式中i , j , k 分别为沿三根坐标轴的单位矢量。
坐标x , y , z也是时间的单值连续函数，即(5-3)式(5-3)称为点的直角坐标形式的运动方程，也是点的轨迹的参数方程。
三、自然法当动点相对于所选的参考系的轨迹已知时，可以沿此轨迹确定动点的位置。
在轨迹上任取固定点O 作为原点，选定沿轨迹量取弧长的正负方向，则动点的位置可用弧坐标s 来确定。
如图5-2所示。
动点沿轨迹运动时，弧长s 是时间的单值连续函数(5-4)上式称为点用自然法描述的运动方程。
图5-2以上三种形式的运动方程在使用上各有所侧重。
矢量形式的运动方程常用于公式推导；直角坐标形式的运动方程常用于轨迹未知或轨迹较复杂的情况；当轨迹已知为圆或圆弧时，用自然法则较为方便。
第二节点的速度和加速度动点运动的快慢和方向用速度表示，速度的变化情况则用加速度表示。
下面给出在各坐标系下，速度、加速度的数学表达式。
一、用矢量法表示点的速度和加速度如动点矢量形式的运动方程为r=r(t) ，则动点的速度定义为（5-5）即动点的速度等于动点的矢径r对时间的一阶导数。
理论力学5—点的运动学
M
t
r
△s
v
△
用矢量表示为： ds v τ vτ dt
r
M' r'
在曲线运动中，点的速度是矢量。它的 大小等于弧坐标对于时间的一阶导数，它 的方向沿轨迹的切线，并指向运动的一方。
5.3 自然法
ds v τ vτ dt
dτ τ j 1 lim lim n n s 0 s s 0 s ds
2 2
x l (1
2
4
) r (cos wt
4
cos 2wt )
由此可得滑块B的速度和加速度： dx v rw (sin wt sin 2wt )
dt 2 dv a rw 2 (cos wt cos 2w ) dt
6.3 自然法
1 弧坐标 动点M在轨迹上的位置可以这样确定：在轨迹 上任选一点O为参考点，并设点O的某一侧为正 向，动点M在轨迹上的位置由弧长s确定，视弧 长s为代数量，称它为动点M在轨迹上的弧坐标。 当动点M运动时，s随着时间变化，它是时间t的 单值连续函数，即 (+)
解: 点的速度和加速度在三个坐标轴上的投影 分别为: 32sin 4t x 8cos 4t x
y 8sin 4t
z4
32cos 4t y
0 z
v x y z 80 m/s
4 点的切向加速度和法向加速度
dv d dv dτ a (vτ ) τ v at an at τ an n dt dt dt dt
dv at dt
dτ dτ ds dτ ds v 由于 n dt ds dt ds dt
t
r
△s
v
△
用矢量表示为： ds v τ vτ dt
r
M' r'
在曲线运动中，点的速度是矢量。它的 大小等于弧坐标对于时间的一阶导数，它 的方向沿轨迹的切线，并指向运动的一方。
5.3 自然法
ds v τ vτ dt
dτ τ j 1 lim lim n n s 0 s s 0 s ds
2 2
x l (1
2
4
) r (cos wt
4
cos 2wt )
由此可得滑块B的速度和加速度： dx v rw (sin wt sin 2wt )
dt 2 dv a rw 2 (cos wt cos 2w ) dt
6.3 自然法
1 弧坐标 动点M在轨迹上的位置可以这样确定：在轨迹 上任选一点O为参考点，并设点O的某一侧为正 向，动点M在轨迹上的位置由弧长s确定，视弧 长s为代数量，称它为动点M在轨迹上的弧坐标。 当动点M运动时，s随着时间变化，它是时间t的 单值连续函数，即 (+)
解: 点的速度和加速度在三个坐标轴上的投影 分别为: 32sin 4t x 8cos 4t x
y 8sin 4t
z4
32cos 4t y
0 z
v x y z 80 m/s
4 点的切向加速度和法向加速度
dv d dv dτ a (vτ ) τ v at an at τ an n dt dt dt dt
dv at dt
dτ dτ ds dτ ds v 由于 n dt ds dt ds dt
点的运动学
(t )
M b
度和加速度。
第五章
点的运动学
取如图所示的直角坐标系，则M点的坐标为
第 二 节 直 角 坐 标 法
x a cos
y A
y b sin
由此得M点的轨迹方程为
x y 2 1 2 a b
x0
2 2
a M O
(t )
b B x
y0
第五章
点的运动学
M点的速度为
第五章
点的运动学 P´
轨迹
第 一 节 矢 量 法
r ( t t ) r r (t )
P
向量端图
矢径 r (t ) OP 运动方程
O
r r (t )
r r (t t ) r (t )
位
速
移
度
加速 度
第五章
点的运动学
第二节 直角坐标法
第 二 节 直 角 坐 标 法
z
k
四分之一圆
O
第五章
点的运动学
• 当 a = b = l 时，M点的速度：
第 二 节 直 角 坐 标 法
abl
y
A l M
r
v r 0
O M点的速度垂直于其矢径！
l
B x
第五章
点的运动学
第 二 节 直 角 坐 标 法
• 当 a = b = l 、且 0 时，M点的加 速度：
abl
第五章
点的运动学
第 三 节 自 然 坐 标 法
第五章
点的运动学
第 三 节 自 然 坐 标 法
+
S=0
n
n
n n
M b
度和加速度。
第五章
点的运动学
取如图所示的直角坐标系，则M点的坐标为
第 二 节 直 角 坐 标 法
x a cos
y A
y b sin
由此得M点的轨迹方程为
x y 2 1 2 a b
x0
2 2
a M O
(t )
b B x
y0
第五章
点的运动学
M点的速度为
第五章
点的运动学 P´
轨迹
第 一 节 矢 量 法
r ( t t ) r r (t )
P
向量端图
矢径 r (t ) OP 运动方程
O
r r (t )
r r (t t ) r (t )
位
速
移
度
加速 度
第五章
点的运动学
第二节 直角坐标法
第 二 节 直 角 坐 标 法
z
k
四分之一圆
O
第五章
点的运动学
• 当 a = b = l 时，M点的速度：
第 二 节 直 角 坐 标 法
abl
y
A l M
r
v r 0
O M点的速度垂直于其矢径！
l
B x
第五章
点的运动学
第 二 节 直 角 坐 标 法
• 当 a = b = l 、且 0 时，M点的加 速度：
abl
第五章
点的运动学
第 三 节 自 然 坐 标 法
第五章
点的运动学
第 三 节 自 然 坐 标 法
+
S=0
n
n
n n
第五章点的运动学
3. 速度和加速度 – 自然坐标系
y
B ds
et
A s(t)
d
en
C
引进单位矢量et 和 en et 和 en 相互垂直, 大小为1。
et 和 en 方向并不固定, 由动点 A的位置确定。
et 是A的切线方向且指向s的 增加方向。
o
x
en 垂直于A的轨迹并指向曲 率中心 C
Part C 速度和加速度
向相反。
an 法向加速度，描述了速度方向的变
化。
a an2 at2
Part C 速度和加速度
3. 速度和加速度 – 自然坐标系
关于 空间自然轴系
3. 速度和加速度 – 自然坐标系
因为 d d d d 1 ds d ds ds
方向同 n
所以 n d
ds
3. 速度和加速度 – 自然坐标系 速度
3.轨迹方程
用以描述动点运动的几何轨迹。 例如，沪宁高速公路上运动的车辆，其运动轨迹即为高速公路
的几何曲线。
Part B 点的运动方程
4.运动方程与轨迹方程
轨迹方程：
f (x,y,z)0
运动方程：
f (x,y,z,t)0 or
x y
f1 (t ) f2 (t)
z f3(t)
Part B 点的运动方程
v dr dr ds ds v
dt ds dt dt
加速度
a dv dv v d
dt dt dt
代入
d d ds v n
dt ds dt
则
a
dv
dt
v2
n
at
ann
n d
ds
Part C 速度和加速度 4. 应用
y
B ds
et
A s(t)
d
en
C
引进单位矢量et 和 en et 和 en 相互垂直, 大小为1。
et 和 en 方向并不固定, 由动点 A的位置确定。
et 是A的切线方向且指向s的 增加方向。
o
x
en 垂直于A的轨迹并指向曲 率中心 C
Part C 速度和加速度
向相反。
an 法向加速度，描述了速度方向的变
化。
a an2 at2
Part C 速度和加速度
3. 速度和加速度 – 自然坐标系
关于 空间自然轴系
3. 速度和加速度 – 自然坐标系
因为 d d d d 1 ds d ds ds
方向同 n
所以 n d
ds
3. 速度和加速度 – 自然坐标系 速度
3.轨迹方程
用以描述动点运动的几何轨迹。 例如，沪宁高速公路上运动的车辆，其运动轨迹即为高速公路
的几何曲线。
Part B 点的运动方程
4.运动方程与轨迹方程
轨迹方程：
f (x,y,z)0
运动方程：
f (x,y,z,t)0 or
x y
f1 (t ) f2 (t)
z f3(t)
Part B 点的运动方程
v dr dr ds ds v
dt ds dt dt
加速度
a dv dv v d
dt dt dt
代入
d d ds v n
dt ds dt
则
a
dv
dt
v2
n
at
ann
n d
ds
Part C 速度和加速度 4. 应用
第5章点的运动学
ds 三、速度： v ，式中， ，方向沿切向。 v v
dt
2 2 d v d s v 2， a 四、加速度： a ，式中，a ，位于密 a a n n n d t d t 切面内。
注：以上诸式不加证明。
密切面
伸直面
5
例1：例5-2(老书例6-2)（直角坐标法与自然坐标法）
3
§5-3 点运动的自然坐标法
先介绍自然坐标系：弧坐标系与自然轴系。
原点O，弧坐标s → 弧坐标系
密切面 密切面
切线：M'→M， MM →τ 密切面： M'→M，′组成 平面的极限位置
伸直面
M(动点)bn → 自然轴系 （随动坐标系）
4
一、运动方程： s f (t)
二、轨迹方程：已知。
刚体 运动 学
第5章 点的运动学
用绝对法研究点的运动：只在一个参考系下研究点的运动规律。 根据所选坐标系不同，有多种方法。此处只简介三种。
§5-1 点运动的矢径法
主要给出定义，常用于公式推导。 一、运动方程：
r r ( t )
二、轨迹方程：同上，为含参数 t 的方程。
dr 三、速度：v ，方向：轨迹上动点切线方向。 dt
考察待求量，均与自然坐标系有关。逐一考虑。
d v ，而 v 通过直角坐标系可求，故 a 可求； dt 2 v b) 法向加速度定义 a n ，因ρ尚未知，故由此不能直接求 a ， n 2 2 但 a 或 a2 a ，而 a 由直角坐标系可求， a a n a n
动点M，O为原点
d v d2r 2 ，方向：密切面内指向凹的一方。 四、加速度：a d t d t
理论力学 第五章 点的运动学(合)
⋅
τ
+v⋅dτ dt
z 切向加速度 at
第一项反映速度大小随时间的变化率，方向沿切线 方向。
at
=
dvτ
dt
=
d2 sτ
dt2
at
=
dv dt
=
d2 s dt2
25
第五章 点的运动学
z 法向加速度 an ——反映速度方向随时间的变化率
an
=
v
dτ
dt
= v lim Δτ
Δt→0 Δt
方向沿主法线正向。
s
O
正方向：坐标原点O的某一侧为正向。
弧坐标 s ：沿轨迹从O到点M的弧长。
M
(+)
B
弧坐标表示的运动方程 s = f (t) = s(t)
21
二、自然轴系
第五章 点的运动学
切线：单位矢量 τ ，指向与弧坐标正向一致。
主法线：单位矢量 n，正向指向凹侧。
副法线：单位矢量 b ，且满足 b = τ × n 。
⑦ at ≡ 0, an = 常数 （匀速曲线运动）
⑧ at = 常数，an = 常数 （匀变速曲线运动）
38
第五章 点的运动学
（4）判断下列运动是否可能出现？若能出现，则判断是 什么运动?
(加速曲线运动) (不可能) (匀速曲线运动) (不可能)
(不可能)
(减速曲线运动) (不可能)
39
第五章 点的运动学
xB = r sin( ωt + θ )
vB = rω cos( ω t + θ )
a B = − rω 2 sin( ω t + θ ) = −ω2xB
运动图线
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
r (t )
O
点所经过的路径称为点的运动轨迹。
5.1 矢量法
二、点的速度
在从t 时刻到t +Δ t 时刻这一段时间间隔内 位移 r MM r ( t t ) r ( t )
平均速度
瞬时速度
r v* t
Δr dr v lim r Δt 0 Δt dt
自然轴系、n、b的方向随动点位置的变动 而变动， 单位矢量、n、b的方向不断变化。
5.3 自然法
四、点的速度
r v lim t 0 t r S lim ( ) t 0 S t S r lim lim t 0 t t 0 S dS dr dS dt dS dt
2 d v an v v 2 lim n t 0 dt S
| || ' | 2 | | sin 2 sin 2 2
当t 0时, S 0, sin 2 2
| |1于是
2 sin 2 sin 2 d 1 lim | | lim lim ( ) t 0 S t 0 t 0 S S dS 2
5.3 自然法
二、运动方程
弧坐标 S 是代数量，是关于时间 t 的连 续函数，称作运动方程，即
S S( t )
5.3 自然法
三、自然轴系
1、密切面的概念
由于动点附近的微小弧段可以可以近似的看 成为一条在密切面内的平面曲线，因此对平面曲 线而言，密切面就是此时该曲线所在的平面。
5.3 自然法
方向沿轨迹的切线。
v
5.3 自然法
五、点的加速度
dv d dv dτ d 2 S dτ a (v τ ) τ v 2 τ v dt dt dt dt dt dt
★ 切向加速度
a
——表示速度大小的变化
dv d 2 S a 2 dt dt
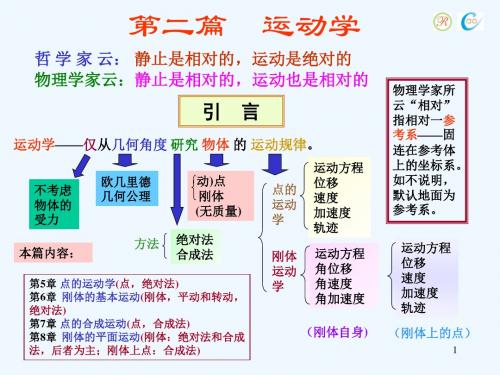
第二篇 运动学
第五章 点的运动学
第五章 点的运动学
•矢量法 •直角坐标法 •自然法
第五章 点的运动学
一、运动学的研究内容
经典力学中的运动学研究物体运动的几何性质， 即宏观物体的空间位置随着时间流逝的变化规律。
★ 建立物体的运动方程 ★ 分析物体运动的速度和加速度、角速度和角加速度
★ 研究物体运动的分解与合成规律
dv v dt
v vxi vy j vz k
速度
vx ,vy ,vz
dx dt dy dt
dz dt
ds v dt
v vx v y vz
加 速 度
2
2
2
dv a dt 2 d r 2 dt
a axi ay j az k
a ax a y az
2、自然轴系的概念
由切线、主法线和副法线组成的直角坐标 系称为自然轴系。、 n、 b分别为切向、主法 向和副法向单位矢量，三个相互垂直矢量的轴 线构成的坐标轴即为自然坐标轴。 的正向指向弧坐标正向，n的正向指向曲线 在M点的曲率中心，b的正向则由右手规则决定， 即
b= ×n
5.3 自然法
2、自然轴系的概念
★ 法向加速度 an ——表示速度方向的变化
d S 2 an v v lim v lim ( ) v lim t 0 t 0 t 0 S dt t S t
5.3 自然法
★ 法向加速度
d 2 an v v lim t 0 S dt
v
v vx i v y j vz k
v v x v y vz
2 2 2
vx cos(v , i ) v vy cos(v , j ) v v cos(v , k ) z v
5.2 直角坐标法
三、点的加速度
dv a axi a y j az k dt dv y dv x dv z i j k dt dt dt d 2x d2y d 2z 2 i 2 j 2 k dt dt dt
a
v
a a a a
2 x 2 y
2 z
ay ax az cos( a ,i ) , cos( a , j ) , cos( a , k ) a a a
5.3 自然法
一、弧坐标与自然法
当点的运动轨迹已知时，可沿点的轨迹曲线 建立一条曲线坐标轴，任选一点O为原点，并规定 原点O的一侧弧长为正，动点M到原点O的弧长S=OM 称为弧坐标，用弧坐标来描述点的运动的方法称 作自然坐标法，也称自然法。
Байду номын сангаас
第五章 点的运动学
三、运动学的建立基础
由于空间、时间与物体运动的无关性，因此整 个运动学的理论体系可建立在欧几里德几何学公理 的基础上。
四、运动学中的两种力学模型：
•质点：不计尺寸大小的物体。 •刚体：形状和大小都不变化的物体。
第五章 点的运动学
五、运动学中与时间相关的两个重要概念
•瞬时：在整个时间流逝过程中的某一时刻。 •时间间隔：两个瞬时之间流逝的时间。
六、运动学中与位置相关的重要概念——参 考体
•参考体：描述物体的运动之前被选作参照物的物体 •参考系：将所取参考体经抽象化处理，以坐标系出现
第五章 点的运动学
1、能选用合适的方法描述点的运动和刚体的基 本运动。能熟练的计算速度和加速度、角速度和角 加速度； 2、能正确的分析刚体的平面运动，能熟练地确 定速度瞬值，计算刚体角速度，熟练的选用不同的 方法求平面图形上各点的速度和角速度; 3、正确地选择动点和动系，应用合成运动的方 法求点的速度和加速度。
方向沿轨迹的切线
5.1 矢量法
曲线运动中速度沿轨迹切线，指向前进的方向。
5.1 矢量法
三、点的加速度
在从t 时刻到t +Δ t 时刻这一段时间间隔内 M 速度变化量
v v ( t t ) v ( t )
v
v
平均加速度
v a* t
M
a
v
v
5.1 矢量法
加速度
Δv dv d r a lim 2 r Δt 0 Δt dt dt
2
M
v
a
加速度方向沿速度矢端 曲线的切线。
速度矢端曲线
5.2 直角坐标法
一、运动方程
r xi yj zk
x x(t ), y y(t ), z z (t )
消去参数 t 后，可得到 F(x,y,z)=0 形式的轨迹方程。
5.2 直角坐标法
二、点的速度
dr dx dy dz v i j k dt dt dt dt
5.3 自然法
★ 加速度
dv v a a an n dt
2
| a | a a a , arctan an
2 2 n
矢径法
直角坐标法
自然法
运动 方程
r r ( t ) x x( t ), y y( t ),z z( t ) s s( t )
2 2 2
dv a dt
v an
2
小结
1、矢量法适用于理论推导； 2、直角坐标法为最常用的方法。
3、自然法适用于点的运动轨迹已知时；
点的运动的两类问题
1、已知运动方程（或某些运动条件，建立运动
方程），然后求其它量。——微分法
2、已知速度方程（或加速度方程），求运动方 程。——积分法
七、基本要求
第五章 点的运动学
运 动 学
点的运动
刚体的运动
曲线运动 平面曲线运动
直线运动 刚体的平动 刚体的定轴运动 刚体的平面运动 刚体的定点运动
空间曲线运动
刚体的基本运动
刚体的一般运动
5.1 矢量法
一、运动方程
选 O 为原点 ， 当动点 运动时，则矢径 r 的大小 及方向均随时间而变，矢 径端点所抽绘的曲线就是 动点的轨迹。矢径的运动 方程为 r OM r ( t ) M