条件概率例题

合集下载

条件概率经典例题条件概率例题

条件概率经典例题条件概率例题条件概率例题山东省莱芜市第一中学刘志例1 一个家庭中有两个小孩，已知其中有一个是女孩，则这时另一个小孩是男孩的概率为(假定一个小孩是男孩还是女孩是等可能的)( ) 一个家庭中有两个小孩只有4种可能:{男，男}，{男，女}，{女，男}，{女，女}(记…二、计算题解.设事件A表示“甲取到的数比乙大”,设事件B表示“甲取到的数是5的倍数”.则显然所要求的概率为P(A|B).1. 从1, 2, 3,…, 15中,甲、乙两人各任取一数(不重复),已知甲取到的数是5的倍数,求甲数大于乙数的概率.根据公式…条件概率专题一、知识点? 只须将无条件概率P(B)替换为条件概率P(BA)，即可类比套用概率满足的三条公理及其它性质 ? 在古典概型中---P(BA) P(AB) (AB)事件AB包括的基本事件(样本点)数事件A包括的基本事件(样本点)数P(A)…1条件概率例题山东省莱芜市第一中学刘志例1 一个家庭中有两个小孩，已知其中有一个是女孩，则这时另一个小孩是男孩的概率为(假定一个小孩是男孩还是女孩是等可能的)( )一个家庭中有两个小孩只有4种可能:{男，男}，{男，女}，{女，男}，{女，女}(记事件A为“其中一个是女孩”，事件B为“另一个是男孩”，则A={(男，女)，(女，男)，(女，女)}，B={(男，女)，(女，男)，(男，男)}，AB={(男，女)，(女，男)}(211131 ，P(AB)= 或P(AB)= C2 442221P(AB)22于是P(B|A)= 33P(A)4解法1:可知P(A)=解法2:事件A包括{(男，女)，(女，男)，(女，女)}，即n(A)=3事件AB包括{(男，女)，(女，男)}(即n(AB)=2所以P(B|A)=n(AB)2 n(A)3例2 一个家庭中有两个小孩，已知其中有一个是男孩，则这时另一个小孩是男孩的概率为(假定一个小孩是男孩还是女孩是等可能的)( )2一个家庭中有两个小孩只有4种可能:{男，男}，{男，女}，{女，男}，{女，女}(记事件A为“其中一个是男孩”，事件B为“另一个也是男孩”，则A={(男，女)，(女，男)，(男，男)}，B={(男，女)，(女，男)，(男，男)}，AB={(男，男)}(解法1:可知P(A)=31111，P(AB)= ，或P(AB)= 4422411P(AB)41P(B|A)= 33P(A)4解法2:事件A包括{(男，男)，(男，女)，(女，男)}，即n(A)=3事件AB包括{(男，男)}(即n(AB)=1所以P(B|A)=n(AB)1n(A)32条件概率例题山东省莱芜市第一中学刘志例1 一个家庭中有两个小孩，已知其中有一个是女孩，则这时另一个小孩是男孩的概率为(假定一个小孩是男孩还是女孩是等可能的)( ) 一个家庭中有两个小孩只有4种可能:{男，男}，{男，女}，{女，男}，{女，女}(记…3条件概率例题山东省莱芜市第一中学刘志例1 一个家庭中有两个小孩，已知其中有一个是女孩，则这时另一个小孩是男孩的概率为(假定一个小孩是男孩还是女孩是等可能的)( ) 一个家庭中有两个小孩只有4种可能:{男，男}，{男，女}，{女，男}，{女，女}(记…条件概率例题山东省莱芜市第一中学刘志例1 一个家庭中有两个小孩，已知其中有一个是女孩，则这时另一个小孩是男孩的概率为(假定一个小孩是男孩还是女孩是等可能的)( ) 一个家庭中有两个小孩只有4种可能:{男，男}，{男，女}，{女，男}，{女，女}(记…百度搜索“就爱阅读”,专业资料,生活学习,尽在就爱阅读网,您的在线图书馆4。

条件概率例题

20 道条件概率例题例题1袋中有 5 个红球和 3 个白球，从中不放回地依次摸出两个球。

已知第一次摸出红球，求第二次摸出红球的概率。

解：第一次摸出红球后，袋中还有 4 个红球和 3 个白球，所以第二次摸出红球的概率为4/7。

例题2一个盒子里有 6 个黑球和 4 个白球，从中随机取出两个球。

若已知第一个球是黑球，求第二个球也是黑球的概率。

解：第一个球是黑球后，盒子里还有 5 个黑球和 4 个白球，所以第二个球是黑球的概率为5/9。

例题3有三张卡片，分别写着数字1、2、3。

从中随机抽取一张，放回后再抽取一张。

已知第一次抽到数字2，求第二次抽到数字 3 的概率。

解：因为是有放回抽取，所以第一次抽到数字 2 后，第二次抽取时每张卡片被抽到的概率仍为1/3，所以第二次抽到数字 3 的概率为1/3。

例题4一批产品中有合格品和次品，合格品率为80%。

从中随机抽取一件产品，已知是合格品，求该产品是一等品的概率（设合格品中一等品率为60%）。

解：由条件概率公式，所求概率为合格品中的一等品率，即60%。

例题5箱子里有红色球和蓝色球，红色球占总数的40%。

从箱子里随机取出一个球，已知是红色球，求这个球上标有数字 5 的概率（设红色球中有30%标有数字5）。

解：根据条件概率公式，所求概率为红色球中标有数字 5 的比例，即30%。

例题6某班级男生占总人数的60%。

在男生中，喜欢数学的占70%。

从班级中随机抽取一名学生，已知是男生，求该学生喜欢数学的概率。

解：所求概率为男生中喜欢数学的比例，即70%。

例题7有两个盒子，盒子 A 中有 3 个红球和 2 个白球，盒子 B 中有 4 个红球和3 个白球。

从盒子 A 中随机取出一个球放入盒子B，然后从盒子 B 中随机取出一个球。

已知从盒子 B 中取出的是红球，求从盒子 A 中取出的也是红球的概率。

解：设从盒子 A 中取出红球为事件A，从盒子 B 中取出红球为事件B。

先求P(A) = 3/5，P(B|A) = (4 + 1)/(7 + 1) = 5/8。

高中试卷-专题7.1 条件概率与全概率公式(含答案)

专题7.1 条件概率与全概率公式姓名：班级：重点条件概率的公式及其应用。

难点全概率公式的应用。

例1-1．同时抛掷一个红骰子和一个蓝骰子，观察向上的点数，记“红骰子向上的点数为奇数”为事件A ，“两个骰子的点数之积为奇数”为事件B ，则=)|(A B P （）。

A 、61B 、41C 、31D 、21【答案】D 【解析】21)(=A P ，若A 、B 同时发生，则蓝色骰子向上点数为偶数，则412121)(=⨯=AB P ，∴21)()()|(==A P AB P A B P ，故选D 。

例1-2．现从4名男医生和3名女医生中抽取两人加入“援鄂医疗队”，用A 表示事件“抽到的两名医生性别相同”，B 表示事件“抽到的两名医生都是女医生”，则=)|(A B P （）。

A 、31B 、74C 、32D 、43【答案】A【解析】由已知得73)(272324=+=C C C A P 、71)(2723==C C AB P ，则31)()()|(==A P AB P A B P ，故选A 。

例1-3．某市气象台统计，2022年3月1日该市市区下雨的概率为154，刮风的概率为152，既刮风又下雨的概率为101，设事件A 为下雨，事件B 为刮风，则=)|(B A P （）。

5B 、83C 、21D 、43【答案】D【解析】由题意可知154)(=A P 、152)(=B P 、101)(=AB P ，利用条件概率的计算公式可得：43)()()|(==B P AB P B A P ，故选D 。

例1-4．甲、乙、丙、丁四名同学分别从篮球、足球、排球、羽毛球四种球类项目中选择一项进行活动，记事件A 为“四名同学所选项目各不相同”，事件B 为“只有甲同学选羽毛球”，则=)|(B A P （）。

A 、92B 、83C 、43D 、98【答案】A【解析】事件AB ：甲选羽毛球且四名同学所选项目各不相同，∴其它3名同学排列在其它3个项目，且互不相同为33A ，事件B ：甲选羽毛球，∴其它3名同学排列在其它3个项目，可以安排在相同项目为33，∴92434)()()|(43433===A B P AB P B A P ，故选A 。

条件概率练习题

条件概率练习题1. 假设事件A和事件B是两个独立的事件，它们各自发生的概率分别是P(A)=0.3和P(B)=0.4。

计算事件A和事件B同时发生的概率。

2. 如果事件A和事件B不是独立的，已知P(A)=0.5，P(B)=0.6，以及P(AB)=0.2，求事件B在事件A发生的条件下发生的概率。

3. 某工厂生产的产品中，有5%的产品是次品。

如果从这批产品中随机抽取10件，计算恰好有2件次品的概率。

4. 已知一个家庭有两个孩子，其中一个是男孩。

求这个家庭有两个男孩的概率。

5. 某城市发生地震的概率是0.01，如果这个城市发生了地震，那么发生海啸的概率是0.8。

求这个城市发生海啸的概率。

6. 假设有三扇门，其中一扇门后有奖品，另外两扇门后是空的。

你选择了一扇门，但主持人知道每扇门后的情况，并打开了另一扇没有奖品的门。

现在主持人问你，是否要改变你的选择。

求改变选择后赢得奖品的概率。

7. 某公司有30%的员工是女性，70%的员工是男性。

如果随机抽取一名员工，发现他是部门经理，已知部门经理中有40%是女性，求这名员工是女性的概率。

8. 假设一个袋子里有5个红球和3个蓝球。

如果从袋子里随机取出一个球，发现是红球，计算袋子里剩下4个红球的概率。

9. 某医院对患者进行两种不同的疾病测试，测试A和测试B。

已知测试A的准确率是90%，测试B的准确率是95%。

如果一个患者同时进行了这两种测试，并且两种测试都显示他患病，求他真正患病的概率。

10. 假设有一对夫妇，他们的第一个孩子是女孩。

求他们第二个孩子也是女孩的概率。

11. 某公司有100名员工，其中10名是经理。

如果随机选择一名员工进行培训，发现他已经是经理，求这名员工是经理的概率。

12. 某彩票的中奖概率是1/1000，如果一个人购买了10张彩票，计算他中奖至少一次的概率。

13. 某城市在一年中有30天下雨，如果今天下雨了，那么明天下雨的概率是0.4。

求明天下雨的概率。

条件概率经典例题

1、一个盒子里有10个红球和5个蓝球，从中随机摸取一个球后不放回，再摸取一个球。

若第一次摸到红球，则第二次摸到蓝球的概率是？A. 1/3B. 1/4C. 5/19（答案）D. 5/182、某城市有60%的家庭拥有汽车，拥有汽车的家庭中80%至少有一辆SUV。

随机选择一个家庭，若该家庭拥有汽车，则它至少拥有一辆SUV的概率是？A. 0.6B. 0.48（答案）C. 0.8D. 0.43、一家医院接收了100名流感患者，其中60人患有A型流感，40人患有B型流感。

已知患有A型流感的患者中，70%需要住院治疗；患有B型流感的患者中，40%需要住院治疗。

若随机选择一名患者且该患者需要住院治疗，则他患有A型流感的概率是？A. 0.6B. 0.7（答案）C. 0.4D. 0.54、一个班级里有20名男生和15名女生，男生中有80%喜欢数学，女生中有60%喜欢数学。

随机选择一名学生，若该学生喜欢数学，则他是男生的概率是？A. 8/19B. 12/19C. 8/13（答案）D. 15/235、一家电子产品商店售出了100台平板电脑，其中60台是安卓系统，40台是苹果系统。

已知安卓系统平板电脑中，有10%出现了故障；苹果系统平板电脑中，有5%出现了故障。

若随机选择一台平板电脑且该平板电脑出现了故障，则它是安卓系统的概率是？A. 0.6B. 0.4（答案，考虑故障率与销量的综合影响）C. 0.1D. 0.56、一个篮子里有12个鸡蛋，其中4个是坏的。

随机取出两个鸡蛋，若第一个取出的是好鸡蛋，则第二个取出的是坏鸡蛋的概率是？A. 4/11（答案）B. 4/12C. 3/11D. 1/37、一家餐厅提供了100份外卖，其中60份是披萨，40份是汉堡。

已知披萨订单中，有80%包含了饮料；汉堡订单中，有50%包含了饮料。

若随机选择一份外卖且该外卖包含了饮料，则它是披萨的概率是？A. 0.6B. 0.48（答案，利用条件概率公式计算）C. 0.5D. 0.88、一个盒子里有5张红牌和3张黑牌，随机抽取两张牌。

条件概率练习题

条件概率练习题问题一某电子商务平台调查了2000名用户对于两种不同颜色的产品的满意度。

结果显示，用户对绿色产品的满意度为80%，对蓝色产品的满意度为75%。

此外，调查还发现，用户中有30%的人购买绿色产品，70%的人购买蓝色产品。

请你回答以下问题：1. 如果一个用户购买了蓝色产品，那么他对产品满意的概率是多少？2. 如果一个用户对产品满意，那么他购买的是蓝色产品的概率是多少？问题二某公司对其销售人员进行了培训，以提高销售业绩。

根据培训后的数据统计，已知一个销售人员达到预定销售目标的概率为80%，未达到预定销售目标的概率为20%。

另外，对于已达到预定销售目标的销售人员，他们接受过培训的概率为90%；对于未达到预定销售目标的销售人员，他们也接受过培训的概率为50%。

请你回答以下问题：1. 已知一个销售人员接受过培训，他达到预定销售目标的概率是多少？2. 已知一个销售人员未达到预定销售目标，他接受过培训的概率是多少？问题三某城市统计数据显示，约有10%的人是患有特定疾病的。

医生发现，在患有该疾病的人中，约有95%的人会出现某种症状。

而在没有患有该疾病的人中，约有5%的人也会出现该症状。

现在有一个人出现了这种症状，请你回答以下问题：1. 这个人患有上述特定疾病的概率是多少？2. 已知这个人患有上述特定疾病，他出现该症状的概率是多少？解答问题一1. 根据题意可得，购买蓝色产品的用户对产品满意的概率为75%。

购买蓝色产品并对产品满意的人数为 70% * 75% = 52.5%购买蓝色产品的总人数为 70%因此，如果一个用户购买了蓝色产品，他对产品满意的概率为52.5% / 70% ≈ 75%2. 已知用户对产品满意，购买蓝色产品的概率为？购买蓝色产品并对产品满意的人数为 52.5%总对产品满意的人数为（购买绿色产品并对产品满意的人数 +购买蓝色产品并对产品满意的人数）总对产品满意的人数为 30% * 80% + 70% * 75% = 67.5%因此，如果一个用户对产品满意，他购买的是蓝色产品的概率为52.5% / 67.5% ≈ 78%问题二1. 已知销售人员接受过培训，他达到预定销售目标的概率为？接受过培训的人达到预定销售目标的人数为 90% * 80% = 72%接受过培训的人总人数为 90%因此，已知一个销售人员接受过培训，他达到预定销售目标的概率为72% / 90% ≈ 80%2. 已知销售人员未达到预定销售目标，他接受过培训的概率为？未达到预定销售目标的人接受过培训的人数为 50% * 20% = 10% 未达到预定销售目标的人总人数为 20%因此，已知一个销售人员未达到预定销售目标，他接受过培训的概率为 10% / 20% = 50%问题三1. 这个人患有上述特定疾病的概率为？患有特定疾病并出现症状的人数为 10% * 95% = 9.5%出现症状的人数为（患有特定疾病并出现症状的人数 + 没有患有特定疾病但出现症状的人数）出现症状的人数为 10% * 95% + 90% * 5% = 9.5% + 4.5% = 14% 因此，这个人患有上述特定疾病的概率为9.5% / 14% ≈ 67.9%2. 已知这个人患有上述特定疾病，他出现该症状的概率为？患有特定疾病并出现症状的人数为 9.5%患有特定疾病的人数为（患有特定疾病并出现症状的人数 + 没有患有特定疾病但出现症状的人数）患有特定疾病的人数为 10%因此，已知这个人患有上述特定疾病，他出现该症状的概率为9.5% / 10% = 95%。

概率统计中的条件概率计算练习题

概率统计中的条件概率计算练习题在概率统计中，条件概率是指在已知事件B发生的情况下，事件A 发生的概率。

通过条件概率的计算，我们可以进一步了解事件之间的关联性，并应用于实际问题的解决中。

以下是一些条件概率计算的练习题，通过解答这些题目，能够帮助我们更好地理解条件概率的概念和计算方法。

练习题1：某学校有500名学生，其中300人喜欢足球，200人喜欢篮球，100人既喜欢足球又喜欢篮球。

现从中随机选取一名学生，求该学生既喜欢足球又喜欢篮球的概率。

解答1：设事件A为选中的学生喜欢足球，事件B为选中的学生喜欢篮球。

根据题目可知，P(A)=300/500=0.6，P(B)=200/500=0.4，P(A∩B)=100/500=0.2。

根据条件概率的计算公式：P(A|B) = P(A∩B) / P(B)= 0.2 / 0.4= 0.5所以，选中的学生既喜欢足球又喜欢篮球的概率为0.5。

练习题2：一批产品有100个，其中有20个次品。

现从中连续取出5个产品进行检验，若发现有次品，则不放回，再取下一个，求连续取出的5个产品中有3个次品的概率。

解答2：设事件A为连续取出的5个产品中有3个次品，事件B为取出的第一个产品是次品。

根据题目可知，P(B)=20/100=0.2，因为已经取出了第一个次品，所以还剩下19个次品和99个正品。

因此，P(A|B)的计算可采用超几何分布的方法：P(A|B) = (C(19,2) * C(99,3)) / C(118, 5)其中C(m,n)表示从m个物体中选取n个物体的组合数，计算得到：P(A|B) ≈ 0.236练习题3：某班级有60%的男生和40%的女生，男生中50%擅长数学，女生中40%擅长数学。

现从班级中随机选取一名学生，求选中的学生擅长数学的概率。

解答3：设事件A为选中的学生擅长数学，事件B为选中的学生为男生。

根据题目可知，P(B)=0.6，P(A|B)=0.5，P(A|B')=0.4，其中B'表示事件B 的补事件，即选中的学生为女生。

条件概率通俗易懂例子

条件概率通俗易懂例子
1. 比如说抽奖，盒子里有 10 个球，5 个红球 5 个蓝球。

你先摸出一个红球，然后在剩下的球里再摸一个还是红球的概率是多少呢？这就是条件概率啊！就好像你已经踏上了一条路，接下来走的方向可就不一样了哟。

2. 想象一下你去考试，第一题答对了，那在这种情况下，后面几道题都答对的概率是多少呢？这和条件概率多像呀！不是单独去看后面题答对的概率，而是有了前面的这个条件呢，很神奇吧！
3. 你去买水果，在一堆苹果里挑了一个好吃的，那再挑到一个好吃的苹果的概率会受到之前挑到好吃苹果这个条件影响呀！这不就是很实际的条件概率嘛，多有意思呀！
4. 玩游戏掷骰子，第一次掷出了个 3 ，那接下来再掷出比 3 大的数字的概率是多少呢？这可就是在特定条件下的概率啦，是不是好像给游戏增添了一些特别的感觉呢？
5. 去公园坐摩天轮，你已经坐过一次了，那下次再来坐同一个摩天轮的概率会因为你之前坐过而不一样哦！这不像条件概率吗，生活中好多这样的例子呀！
6. 你和朋友比赛跑步，你第一场赢了，那接下来几场都赢的概率会和第一场赢了这个条件有关系呀！就如同条件概率一样改变着事情发展的方向呢！
结论：条件概率其实就在我们生活的方方面面呀，只要细心观察就能发现它的奇妙之处呢！。

条件概率趣味例子

条件概率趣味例子1. 你知道吗，比如说抽奖的时候，一共有 10 个球，其中只有 1 个红球能中奖。

你先抽了一个没中，然后主持人在剩下的 9 个球中去掉了 8 个白球，这时候你再抽中红球的概率不就大多了嘛！这就是条件概率在起作用啊！2. 想象一下，你和朋友玩猜硬币正反的游戏。

前三次你都猜错了，你就觉得下一次猜中的概率会很大呢，哈哈，其实这也包含了条件概率呀！就好像一直下雨，你觉得接下来晴天的概率会大一点似的。

比如你说：“哎呀，总不能一直下雨吧，下次肯定是晴天啦！”3. 有一次我参加考试，前面几道题都很难，我做得不太好。

但我就想后面简单题答对的概率会变大吧！这不就是条件概率嘛，就好比走路摔了一跤，总觉得接下来会走得更稳啦！就像我当时对自己说：“前面这么难，后面肯定会容易些呀！”4. 去超市抽奖，前面已经有好多人没抽中大奖，你会不会觉得自己抽中大奖的概率变大了呢？这就是条件概率呀！就好像排队买好吃的，看到前面的人买了好多，你就觉得自己能买到的机会也大了呢。

例如你会说：“前面那么多人都没中，该轮到我啦！”5. 大家打篮球的时候，一个人连续几次投篮都不进，是不是觉得下一次投进的概率会增加呀？嘿嘿，这可不就是条件概率嘛！就跟等公交车似的，等了好久没来，就感觉下一刻车肯定会来啦。

就像球友会喊：“都不进这么多次了，这次肯定能进！”6. 玩猜数字游戏，你猜了几次都不对，然后根据提示再猜，这时候猜对的概率不就变了嘛。

这就是条件概率的魅力呀！好比找东西，找了一会儿没找到，后面再找就更有方向了。

比如你会念叨：“都猜了这么多次了，这次肯定能中！”7. 掷骰子的时候，前几次都没掷出六点，你是不是就觉得接下来掷出六点的可能性大了呢？对呀，这就是条件概率在捣鬼呢！跟买彩票一个道理，买了很多次没中，就觉得下一次有希望呀。

就像玩家会说：“一直没六点，下把肯定是了！”8. 上课回答问题，前面几个同学都答错了，那你答对的概率是不是就相对提高了呢？哈哈，这就是条件概率啦！就像去旅游找景点，别人走错路了，你就觉得自己能找对似的。

条件概率习题

． B ．C ．D ．2.一个工人看管三台机床，在一小时内，这三台机床需要工人照管的概率分别0.90.9、、0.80.8、、0.70.7，则没，则没有一台机床需要工人照管的概率为（有一台机床需要工人照管的概率为（） A ．0.018 B ．0.016C ．0.014D ．0.0063.（5分）同时抛掷两枚质地均匀的硬币，则出现两个正面朝上的概率是（） A．B．C．D．4.某射手有4发子弹，射击一次命中目标的概率为9.0，如果命中就停止射击，否则一直到子弹用尽，用x 表示用的子弹数，则)4(=x P 等于（等于（））（A ） 0009.0 (B) 001.0 (C) 009.0 (D) (D) 以上都不对以上都不对5.若随机变量η的分布列如下：的分布列如下：h 2-1- 0 1 2 3 P0.10.2 0.20.30.10.1则当()0.8P x h <=时，实数x 的取值范围是（的取值范围是（）Ａ．Ａ．x x ≤1 Ｂ．Ｂ．11≤x ≤2 Ｃ．Ｃ．11＜x ≤2 Ｄ．Ｄ．11£x ＜26.将两枚质地均匀的骰子各掷一次将两枚质地均匀的骰子各掷一次,,设事件A={A={两个点数互不相同两个点数互不相同两个点数互不相同},B={},B={},B={出现一个出现一个5点},},则则P(B|A)=( ). A.12 B.13 C.14 D. 157.有错误！未找到引用源。

件产品，其中有错误！未找到引用源。

件次品，每次抽取错误！未找到引用源。

件检验，抽检后不放回，共抽错误！未找到引用源。

次，则第错误！未找到引用源。

次抽到正品，第错误！未找到引用源。

次抽到次品的概率是（次抽到次品的概率是（）） A ．错误！未找到引用源。

B B．．错误！未找到引用源。

C C．．错误！未找到引用源。

D D．．错误！未找到引用源。

8.已知盒中装有大小一样，形状相同的3个白球与7个黑球，每次从中任取一个球并不放回，则在第1次取到的白球条件下，第2次取到的是黑球的概率为次取到的是黑球的概率为 ( ( ) 1.一对夫妇有两个孩子，已知其中一个孩子是女孩，那么另一个孩子也是女孩的一对夫妇有两个孩子，已知其中一个孩子是女孩，那么另一个孩子也是女孩的概率概率为（） AA ．103B B．．92C C．．87D D．．979.从1，2，3，4，5中任取2各不同的数，事件A=“取到的2个数之和为偶数”，事件B=“取到的2个数均为偶数”，则()P B A =（）） A A．．18B ．14C ．25D ．1210.有3A. 827 B. 49C. 23D. 1927 11.某人射击5枪，命中3枪，枪，33枪中恰有2枪连中的概率为（枪连中的概率为（）） A.错误！未找到引用源。

条件概率应用练习

条件概率应用练习简介条件概率是概率论的重要概念之一，用于计算在给定某个条件下，事件发生的概率。

在实际应用中，条件概率可以帮助我们了解和分析事件之间的依赖关系。

本文档将提供一些条件概率的应用练，帮助读者加深对条件概率的理解和应用能力。

练1：扑克牌游戏现有一副标准的扑克牌，其中包括了52张牌，分为4种花色（红桃、黑桃、梅花、方块）和13个点数（A、2、3、4、5、6、7、8、9、10、J、Q、K）。

假设从这副牌中随机抽取一张牌，请回答以下问题：1. 如果已知所抽取的牌是红桃，那么它是红桃A的概率是多少？2. 如果已知所抽取的牌是红桃，那么它是红色的（红桃或方块）概率是多少？3. 如果已知所抽取的牌是红桃，那么它是点数小于等于10的概率是多少？练2：疾病诊断假设有一个疾病测试，已知该测试的准确率是95%，即在真实情况下，该测试能正确诊断为阳性的概率为95%。

又已知某人患有这种疾病的概率是1%。

请回答以下问题：1. 如果某人的测试结果为阳性，那么他实际上患有这种疾病的概率是多少？2. 如果某人的测试结果为阴性，那么他实际上没有患有这种疾病的概率是多少？练3：购买农产品某农场销售苹果和橙子，已知该农场销售的苹果和橙子的比例为3:2。

现有一个顾客购买了农场销售的一种水果，请回答以下问题：1. 如果已知顾客购买的是苹果，那么他购买的是农场销售的橙子的概率是多少？2. 如果已知顾客购买的是苹果，那么他购买的是该农场销售水果的橙子的概率是多少？练4：天气预报根据过去的统计数据，某地区的冬天有80%的天气是寒冷的。

天气预报显示，该地明天是寒冷天气的概率是90%。

请回答以下问题：1. 如果已知明天是寒冷天气，那么当天天气实际上是寒冷的概率是多少？2. 如果已知当天是寒冷天气，那么明天也是寒冷天气的概率是多少？总结通过以上练习，我们可以看到条件概率在各个实际应用中都起到了重要的作用。

掌握好条件概率的概念及其应用方法，对于数据分析、决策制定等领域都非常有帮助。

专题10 条件概率(解析版)

专题10 条件概率例1．小智和电脑连续下两盘棋，已知小智第一盘获胜概率是0.5，小智连续两盘都获胜的概率是0.4，那么小智在第一盘获胜的条件下，第二盘也获胜的概率是( ) A ．0.8B ．0.4C ．0.2D ．0.5【解析】解：设事件A 表示“小智第一盘获胜”，则P （A ）0.5=，设事件B 表示“小智第二盘获胜”，则()0.4P AB =，∴小智在第一盘获胜的条件下，第二盘也获胜的概率是：()0.4(|)0.8()0.5P AB P B A P A ===．故选：A ．例2．某种灯泡的使用寿命为2000小时的概率为0.85，超过2500小时的概率为0.35，若某个灯泡已经使用了2000小时，那么它能使用超过2500小时的概率为( ) A ．1720B ．717C ．720D ．317【解析】解：记灯泡的使用寿命为2000小时为事件A ，超过2500小时为事件B ，则()0.357(|)()0.8517P AB P B A P A ===，故选：B ．例3．甲乙二人争夺一场围棋比赛的冠军，若比赛为“三局两胜”制（无平局），甲在每局比赛中获胜的概率均为23，且各局比赛结果相互独立，则在甲获得冠军的条件下，比赛进行了三局的概率为( ) A ．13B ．25C ．23D ．45【解析】解：由题意，甲获得冠军的概率为22212122203333333327⨯+⨯⨯+⨯⨯=，其中比赛进行了3局的概率为212122833333327⨯⨯+⨯⨯=，∴所求概率为820227275÷=，故选：B ．例4．盒中有10个零件，其中8个是合格品，2个是不合格品，不放回地抽取2次，每次抽1个．已知第一次抽出的是合格品，则第二次抽出的是合格品的概率是( ) A ．15B ．29C ．79D ．710【解析】解：第一次抽出的是合格品，则还有9个零件，其中7个为合格品，故第二次抽出的是合格品的概率是79，故选：C．例5．现从4名男医生和3名女医生中抽取两人加入“援鄂医疗队”，用A表示事件“抽到的两名医生性别相同”，B表示事件“抽到的两名医生都是女医生”，则(|)(P B A=)A．13B．47C．23D．34【解析】解：由题意可得：事件A基本事件数，22439C C+=；事件B的基本事件数，233C=；所以31 (|)93P B A==．故选：A．例6．小赵、小钱、小孙、小李到4个景点旅游，每人只去一个景点，设事件A为“4个人去的景点不完全相同”，事件B为“小赵独自去一个景点”，则(|)(P B A=)A．37B．47C．57D．67【解析】解：小赵独自去一个景点，则有4个景点可选，其余3人只能在小赵剩下的3个景点中选择，可能性为33327⨯⨯=种所以小赵独自去一个景点的可能性为427108⨯=种，因为4个人去的景点不相同的可能性444252-=种，所以1083 (|)2527P B A==．故选：A．例7．口袋中装有大小形状相同的红球2个，白球3个，黄球1个，甲从中不放回的逐一取球，已知在第一次取得红球的条件下，第二次仍取得红球的概率为15．【解析】解：口袋中装有大小形状相同的红球2个，白球3个，黄球1个，甲从中不放回的逐一取球，设事件A表示“第一次取得红球”，事件B表示“第二次取得红球”，P（A）2163==，211()6515P AB=⨯=，∴在第一次取得红球的条件下，第二次仍取得红球的概率为：1()115(|)1()53P AB P B A P A ===．故答案为：15．例8．已知1(|)2P B A =，3()10P AB =，则P （A ）= 35 ．【解析】解：1(|)2P B A =，3()10P AB =， P ∴（A ）3()3101(|)52P AB P B A ===．故答案为：35．例9．篮子里装有2个红球，3个白球和4个黑球．某人从篮子中随机取出两个球，记事件A = “取出的两个球颜色不同”，事件B = “取出一个红球，一个白球”，则(|)P B A =313．【解析】解：P （A ）2222342913118C C C C ++=-=， 1123291()6C C P AB C ==，()3(|)()13P AB P B A P A ∴==．故答案为：313．例10．某种疾病的患病率为0.50，患该种疾病且血检呈阳性的概率为0.49，则已知在患该种疾病的条件下血检呈阳性的概率为 0.98 ．【解析】解：设事件A 表示“患某种疾病”，设事件B 表示“血检呈阳性”，则P （A ）0.5=，()0.49P AB =，∴在患该种疾病的条件下血检呈阳性的概率为：()0.49(|)0.98()0.5P AB P B A P A ===．故答案为：0.98．例11．已知口袋中有2个白球和4个红球，现从中随机抽取两次，每次抽取1个．（1）若采取放回的方法连续抽取两次，求两次都取得白球的概率；（2）若采取不放回的方法连续抽取两次，求在第一次取出红球的条件下，第二次取出的是红球的概率．【解析】解：（1）放回抽取，每次取得白球的概率均为2163=，所以两次都取得白球的概率111339P =⨯=．（2）记“第一次取出的是红球“为事件A ，“第二次取出的是红球”为事件B ，则452()653P A ⨯==⨯，432()655P AB ⨯==⨯，利用条件概率的计算公式，可得()233(|)()525P AB P B A P A ==⨯=．例12．某校从学生文艺部6名成员(4男2女）中，挑选2人参加学校举办的文艺汇演活动．（1）求男生甲被选中的概率；（2）在已知男生甲被选中的条件下，女生乙被选中的概率；（3）在要求被选中的两人中必须一男一女的条件下，求女生乙被选中的概率．【解析】解：（1）从6名成员中挑选2名成员，共有15种情况，记“男生甲被选中”为事件A ，事件A 所包含的基本事件数为5种，故1()3P A =．（2）记“男生甲被选中”为事件A ，“女生乙被选中”为事件B ，则1()15P AB =，由（1）知1()3P A =，故()1(|)()5P AB P B A P A ==．（3）记“挑选的2人一男一女”为事件C ，则8()15P C =，“女生乙被选中”为事件B ，4()15P BC =，故()1(|)()2P BC P B C P C ==．例13．哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查，饮食指数结果用茎叶图表示如图，图中饮食指数低于70的人是饮食以蔬菜为主：饮食指数高于70的人是饮食以肉类为主．（1）完成下列22⨯列联表：能否有99%的把握认为老师的饮食习惯与年龄有关？（2）从群力校区任一名老师设“选到45岁以上老师为事件A ，“饮食指数高于70的老师”为事件B ，用调查的结果估计(|)P B A 及(|)P B A （用最简分数作答）；（3）为了给食堂提供老师的饮食信息，根据（1）（2）的结论，能否有更好的抽样方法来估计老师的饮食习惯，并说明理由．附：2()()()()()n ad bc k a b c d a c b d -=++++【解析】解：（1）由2230(42168)10 6.63520101218K ⨯-⨯==>⨯⨯⨯即有99%的把握认为老师的饮食习惯与年龄有关，故答案为：有99%的把握认为老师的饮食习惯与年龄有关，（2）121181(|)9C P B A C ==，181122(|)3C P B A C ==，故答案为：19，23（3）为了给食堂提供老师的饮食信息，根据（1）（2）的结论， “选到45岁以上老师“与，“选到45岁以下老师“调查差异较大，为了更科学估计老师的饮食习惯，采用分层抽样的抽样方法更好．故答案为：分层抽样例14．某保险公司开设的某险种的基本保费为1万元，今年参加该保险的人来年继续购买该险种的投保人称为续保人，续保人的下一年度的保费与其与本年度的出险次数的关联如下：设今年初次参保该险种的某人准备来年继续参保该险种，且该参保人一年内出险次数的概率分布列如下：（1）求此续保人来年的保费高于基本保费的概率．（2）若现如此续保人来年的保费高于基本保费，求其保费比基本保费高出60%的概率．（3）求该续保人来年的平均保费与基本保费的比值．【解析】解：（1）设出险次数为事件X ，一续保人本年度的保费为事件A ，则续保人本年度保费高于基本保费为事件C ，则P （C ）()P A a =>，P （C ）(2)(3)(4)(5)P x P x P x P x ==+=+=+ 0.200.200.100.050.55=+++=．（2）设保费比基本保费高出60%为事件B ， ()(4)(5)0.10.053(/)()()0.5511P BC P x P x P B C P C P C =+=+====．（3）平均保费0.850.300.15 1.2550.20 1.50.20 1.750.1020.05EX a =⨯+++⨯+⨯+⨯+⨯ 0.2550.150.250.30.1750.1 1.23=+++++=， ∴平均保费与基本保费比值为1.23．例15．某校准备从报名的7位教师（其中男教师4人，女教师3人）中选3人去边区支教．（Ⅰ）设所选 3人中女教师的人数为X ，求X 的分布列及数学期望；（Ⅱ）若选派的三人依次到甲、乙、丙三个地方支教，求甲地是男教师的情况下，乙地为女教师的概率．【解析】解：（Ⅰ）X 的所有可能取值为0，1，2，3，且34374(0)35C P X C ===，12343718(1)35C C P X C ===，21343712(2)35C C P X C ===，33371(3)35C P X C ===，所以X 的分布列为：故4181219()0123353535357E X =⨯+⨯+⨯+⨯=．⋯（6分）（Ⅱ）设事件A 为“甲地是男教师”，事件B 为“乙地是女教师”，则1246374()7C A P A A ==，111435372()7C C C P AB A ==，所以()1(|)()2P AB P B A P A ==．⋯（12分）例16．甲、乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为321,,432，乙队每人答对的概率都是23．设每人回答正确与否相互之间没有影响，用ξ表示甲队总得分．（Ⅰ）求2ξ=概率；（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．【解析】解：（Ⅰ）32112131111(2)43243243224P ξ==⨯⨯+⨯⨯+⨯⨯=；⋯（4分）（Ⅱ）设“甲队和乙队得分之和为4”为事件A ，“甲队比乙队得分高”为事件B 则 3322123331211211211()()()()()4324334333P A C C C =⨯+⨯⨯+⨯⨯=，1231211()()()43318P AB C =⨯⨯=， ∴1()118(|)1()63P AB P B A P A ===⋯（12分）例17．甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为34，23，12，乙队每人答对的概率都是23．设每人回答正确与否相互之间没有影响，用ξ表示甲队总得分．（Ⅰ）求随机变量ξ的分布列及其数学期望()E ξ；（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．【解析】解：（Ⅰ）由题设知ξ的可能取值为0，1，2，3， 3211(0)(1)(1)(1)43224P ξ==---=， 3213213211(1)(1)(1)(1)(1)(1)(1)4324324324P ξ==--+-⨯⨯-+--⨯=，32132132111(2)(1)(1)(1)43243243224P ξ==⨯⨯-+⨯-⨯+-⨯⨯=， 3211(3)4324P ξ==⨯⨯=，∴随机变量ξ的分布列为：数学期望1111123()012324424412E ξ=⨯+⨯+⨯+⨯=．（Ⅱ）设“甲队和乙队得分之和为4”为事件A ，“甲队比乙队得分高”为事件B ，则P （A ）3322123331211221221()()(1)(1)4324334333C C C =⨯⨯+⨯⨯⨯-+⨯⨯⨯-=，1231221()(1)43318P AB C =⨯⨯⨯-=，1()118(|)1()63P AB P B A P A ===．例18．市场上供应的灯泡中，甲厂产品占70%，乙厂产品占30%，甲厂产品的合格率是95%，乙厂产品的合格率是80%，若用事件A 、A 分别表示甲、乙两厂的产品，用B 表示产品为合格品．（1）试写出有关事件的概率；（2）求从市场上买到一个灯泡是甲厂生产的合格灯泡的概率．【解析】解：（1）依题意，P （A ）70%=，()30%P A =， (|)95%P B A =，P (|)80%B A =．进一步可得()(|)5%()p BA P B A P A ==，()(|)20%()P AB P B A P A ==．（2）要计算从市场上买到的灯泡既是甲厂生产的（事件A 发生），又是合格的（事件B 发生）的概率，也就是求A 与B 同时发生的概率，有()P AB P =（A ）(|)0.70.950.665P B A =⨯=．例19．惠州市某校中学生篮球队假期集训，集训前共有6个篮球，其中3个是新球（即没有用过的球），3个是旧球（即至少用过一次的球）．每次训练都从中任意取出2个球，用完后放回．（1）设第一次训练时取到的新球个数为ξ，求ξ的分布列和数学期望；（2）已知第一次训练时用过的球放回后都当作旧球，求第二次训练时恰好取到1个新球的概率．参考公式：互斥事件加法公式：()P A B P =（A ）P +（B ）（事件A 与事件B 互斥）．独立事件乘法公式：()P A B P =（A ）P （B ）（事件A 与事件B 相互独立）．条件概率公式：()(|)()P AB P B A P A =．【解析】解：（1）ξ的所有可能取值为0，1，2设“第一次训练时取到i 个新球（即)i ξ=”为事件(0i A i =，1，2)．因为集训前共有6个篮球，其中3个是新球，3个是旧球，所以230261()(0)5C P A P C ξ====；11331263()(1)5C C P A P C ξ====；232261()(2)5C P A P C ξ====，所以ξ的分布列为ξ的数学期望为1310121555E ξ=⨯+⨯+⨯=．（2）设“从6个球中任意取出2个球，恰好取到一个新球”为事件B ，则“第二次训练时恰好取到一个新球”就是事件012A B A B A B ++，而事件0A B 、1A B 、2A B 互斥，所以111113352401201222266613138()()()()55575C C C C C P A B A B A B P A B P A B P A B C C C ++=++=⨯+⨯+⨯=．所以第二次训练时恰好取到一个新球的概率为3875．。

条件概率练习

7.1.1条件概率一、选择题1．袋中有除颜色外完全相同的5个球，其中3个红球和2个白球.现从袋中不放回地连取两个.已知第一次取得红球，则第二次取得白球的概率为（） A ．0.4 B ．0.5 C ．0.6 D ．0.72．10张奖券中有4张“中奖”奖券，甲乙两人先后参加抽奖活动，每人从中不放回抽取一张奖券，甲先抽，乙后抽，在甲中奖条件下，乙没有中奖的概率为（）A ．35B ．23 C ．34 D ．4153．（多选）设M 、N 是两个随机事件，则下列等式一定成立的是（）A ．()()()P M N P M P N ⋃=+B ．()()1P MN P MN =-C ．()()()|P MN P M P N M =D ．()()()()||P N M P M P M N P N = 二、填空题4．已知甲每次来渝乘坐飞机和高铁的概率分别为0.6和0.4，飞机和高铁正点到达的概率分别为0.8和0.9，若甲已正点抵渝，则甲此次来渝乘坐高铁的概率为____________.5．为积极应对人口老龄化，2021年8月20日，全国人大常委会会议表决通过了关于修改人口与计划生育法的决定，提倡适龄婚育､优生优育，一对夫妻可以生育三个子女.若已知某个家庭有3个小孩，且其中至少有1个男孩的条件下，则第三个孩子是女孩的概率为___________.6．已知1(|)(|)2P A B P B A ==，3(4P A =，则()P B =________. 7．甲､乙两名运动员进行乒乓球比赛，比赛采取5局3胜制，已知每局比赛甲胜的概率为23，乙胜的概率为13，且各局比赛结果互不影响.若第一局乙胜，则本次比赛甲胜的概率为___________.8．已知()()()13P A P B P A B ===∣，则()P A B =∣___________. 9．某医院从3名医生和3名护士中选派4人参加志愿者服务，事件A 表示选派的4人中至少有2名医生，事件B 表示选派的4人中有2名护士，则()P B A =___________.三、解答题10．一个盒子中有6只好晶体管，4只坏晶体管，任取两次，每次取一只，每一次取后不放回.若已知第一只是好的，求第二只也是好的的概率.11．袋中有10个大小、材质都相同的小球，其中红球3个，白球7个.每次从袋中随机摸出1个球，摸出的球不再放回.求：（Ⅰ）第一次摸到红球的概率；（Ⅰ）在第一次摸到红球的条件下，第二次也摸到红球的概率；（Ⅰ）第二次摸到红球的概率.。

条件概率经典练习

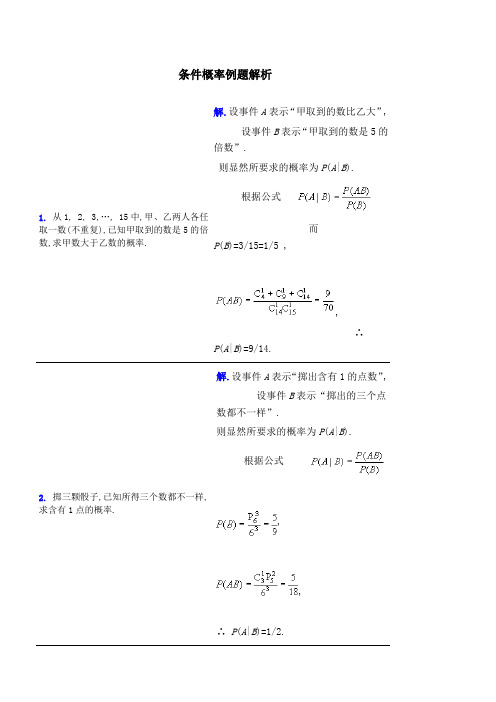
条件概率例题解析1.从1, 2, 3,…, 15中,甲、乙两人各任取一数(不重复),已知甲取到的数是5的倍数,求甲数大于乙数的概率. 解.设事件A表示“甲取到的数比乙大”, 设事件B表示“甲取到的数是5的倍数”.则显然所要求的概率为P(A|B).根据公式而P(B)=3/15=1/5 ,,∴P(A|B)=9/14.2. 掷三颗骰子,已知所得三个数都不一样,求含有1点的概率. 解.设事件A表示“掷出含有1的点数”, 设事件B表示“掷出的三个点数都不一样”.则显然所要求的概率为P(A|B).根据公式,,∴P(A|B)=1/2.3.袋中有一个白球和一个黑球,一次次地从袋中摸球,如果取出白球,则除把白球放回外再加进一个白球,直至取出黑球为止,求取了N次都没有取到黑球的概率. 1解.设事件A i表示“第i次取到白球”. (i=1,2,…,N)则根据题意P(A1)=1/2 , P(A2|A1)=2/3,由乘法公式可知:P(A1A2)=P(A2|A1)P(A1)=1/3.而P(A3|A1A2)=3/4 ,P(A1A2A3)=P(A3|A1A2)P(A1A2)=1/4 .由数学归纳法可以知道P(A1A2…AN)=1/(N+1).4. 甲袋中有5只白球, 7 只红球;乙袋中有4只白球, 2只红球.从两个袋子中任取一袋, 然后从所取到的袋子中任取一球,求取到的球是白球的概率. 解.设事件A 表示“取到的是甲袋”, 则表示“取到的是乙袋”,事件B表示“最后取到的是白球”.根据题意: P(B|A)=5/12 ,,P(A)=1/2.∴.5.有甲、乙两袋,甲袋中有3只白球,2只黑球;乙袋中有4只白球,4只黑球.现从甲袋中任取2个球放入乙袋,然后再从乙袋中任取一球,求此球为白球的概率. 解.设事件A i表示“从甲袋取的2个球中有i个白球”,其中i=0,1,2 .事件B表示“从乙袋中取到的是白球”.显然A0, A1, A2构成一完备事件组,且根据题意P(A)=1/10 , P(A1)=3/5 ,P(A2)=3/10 ;P(B|A)=2/5 , P(B|A1)=1/2 ,P(B|A2)=3/5 ;由全概率公式P(B)=P(B|A)P(A0)+P(B|A1)P(A1)+P(B|A2)P(A2)=2/5×1/10+1/2×3/5+3/5×3/10=13/25.6.袋中装有编号为1, 2,…, N的N个球,先从袋中任取一球,如该球不是1号球就放回袋中,是1号球就不放回,然后再摸一次,求取到2号球的概率. 解.设事件A表示“第一次取到的是1号球”,则表示“第一次取到的是非1号球”;事件B表示“最后取到的是2号球”.显然 P(A)=1/N,,且 P(B|A)=1/(N-1),;∴=1/(N-1)×1/N+1/N×(N-1)/N=(N2-N+1)/N2(N-1) .7. 袋中装有8只红球 , 2只黑球,每次从中任取一球, 不放回地连续取两次, 求下列事件的概率.(1)取出的两只球都是红球;(2)取出的两只球都是黑球;(3)取出的两只球一只是红球,一只是黑球; 解.设事件A1表示“第一次取到的是红球”,设事件A2表示“第二次取到的是红球”.(1)要求的是事件A1A2的概率.根据题意P(A1)=4/5,,P(A2|A1)=7/9,∴P(A1A2)=P(A1)P(A2|A1)=4/5×7/9=28/45.(2)要求的是事件的概率.(4)第二次取出的是红球.根据题意:,,∴.(3)要求的是取出一只红球一只黑球,它包括两种情形,即求事件的概率.,,,, ∴.(4)要求第二次取出红球,即求事件A2的概率.由全概率公式:=7/9×4/5+8/9×1/5=4/5.8. 某射击小组共有20名射手,其中一级射手4人, 二级射手8人, 三级射手7人, 四级射手1人. 一、二、三、四级射手能通过选拔进入比赛的概率分别是0.9、0.7、0.5、0.2 . 求任选一名射手能通过选拔进入比赛的概率. 解.设事件A表示“射手能通过选拔进入比赛”,设事件B i表示“射手是第i级射手”.(i=1,2,3,4)显然, B1、B2、B3、B4构成一完备事件组,且P(B1)=4/20, P(B2)=8/20, P(B3)=7/20, P(B4)=1/20;P(A|B1)=0.9, P(A|B2)=0.7, P(A|B3)=0.5, P(A|B4)=0.2. 由全概率公式得到P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)P(B3)+P(A|B4)P(B4)=0.9×4/20+0.7×8/20+0.5×7/20+0.2×1/20=0.645.9.轰炸机轰炸某目标,它能飞到距目标400、200、100(米)的概率分别是0.5、0.3、0.2,又设它在距目标400、200、100(米)时的命中率分别是0.01、0.02、0.1 .求目标被命中的概率为多少? 解.设事件A1表示“飞机能飞到距目标400米处”,设事件A2表示“飞机能飞到距目标200米处”,设事件A3表示“飞机能飞到距目标100米处”,用事件B表示“目标被击中”.由题意, P(A1)=0.5, P(A2)=0.3, P(A3)=0.2,且A1、A2、A3构成一完备事件组.又已知P(B|A1)=0.01, P(B|A2)=0.02,P(B|A)=0.1.3由全概率公式得到 :P(B)=P(B|A)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A1)3=0.01×0.5+0.02×0.3+0.1×0.2=0.0 31.。

条件概率及答案

条件概率1.甲乙两城市都位于长江下游，根据一百多年的气象记录，知道一年中雨天的比例甲城市占20%,乙城市占18%，两地同时下雨占12%.求（1）已知甲城市下雨，求乙城市下雨的概率；（2）已知乙城市下雨，求甲城市下雨的概率；2.设100件产品中有70件一等品，25件二等品，规定一、二等品为合格品.从中任取1件, 求（1）取得一等品的概率；（2）已知取得的是合格品，求它是一等品的概率.3.把一枚硬币任意抛掷两次，事件A表示“第一次出现正面”，事件B表示“第二次出现正面”，求P （BIA）.4.一批产品中有4%的次品，而合格品中一等品占45%.从这批产品中任取一件，求该产品是一等品的概率.5.抛掷红、蓝两个骰子，事件A表示“红骰子出现4点”，事件B表示“蓝骰子出现的点数是偶数"，求P （AIB）.6.一个盒子中有6只白球、4只黑球，从中不放回地每次任取1只，连取2次，求(1)第一次取得白球的概率；(2)第一、第二次都取得白球的概率；(3)第一次取得黑球而第二次取得白球的概率.7.两台车床加工同一种零件共100个，结果如下8.掷两枚均匀的骰子，已知点数不同，求至少有一个是6点的概率.9.设某种动物活到20岁以上的概率为0.7,活到25岁以上的概率为0.4,求现龄为20的这种动物能活到25 岁以上的概率？10.某彩票的中奖规则为：从1, 2,…，6这六个号码中任意选出三个不同的号码，如果全对（与顺序无关）则中一等奖，求（1）买一注号码中一等奖的概率；（2）假设本期开出的中奖号码为1，2, 3,如果某位彩票预测专家根据历史数据推断本期中奖号码中必有2,那么买一注号码中一等奖的概率是多少？（3）若预测本期不会出现5,且本期开出的中奖号码为1, 2, 3,那么买一注号码中一等奖的概率是多少？11.设A, B 为两事件，已知P（A）=0.5, P（B）=0.6, P（BI A）=0.4,试求（1）P（A B）；（2）P（AB）；12.一个盒子中有6只白球、4只黑球，从中不放回地每次任取1只，连取2次，求第二次取到白球的概率. 解析：A=｛第一次取到白球｝13.盒子中有25个外形相同的球，其中10个白的，5个黄的，10个黑的，从盒子中任意取出一球，已知它不是黑球，试求它是黄球的概率.14.盒中有10个红球及1个黄球.A随意抽出第一个球后不放回盒中，之后B随意抽出第二个球.求下列事件的概率.（1）A和B都抽得红球.（2）A和B都抽得黄球.（3）A抽得黄球和B抽得红球.（4）A和B抽得不同颜色的球.（5）已知B抽得黄球，A抽得红球.15.设某种灯管使用了500 h还能继续使用的概率是0.94,使用到700 h后还能继续使用的概率是0.87,问已经使用了500 h的灯管还能继续使用到700 h的概率是多少？课后导练1 .甲乙两城市都位于长江下游，根据一百多年的气象记录，知道一年中雨天的比例甲城市占20%,乙城市占 18%,两地同时下雨占12%.求(1)已知甲城市下雨，求乙城市下雨的概率；(2)已知乙城市下雨，求甲城市下雨的概率；解析：以事件A 记甲城市出现雨天，事件B 记乙城市出现雨天，事件AB 则为两地同时出现雨天.已知P(A ) =0.20, P (B ) =0.18, P (AB ) =0.12,因此，P (BIA ) =P (AB ) /P (A ) =0.12/0.20=0.60, P (AIB ) =P (AB ) /P (B ) =0.12/0.18= (1) 0.60,(2)0.672 .设100件产品中有70件一等品，25件二等品，规定一、二等品为合格品.从中任取1件，求(1)取得一等品的概率；(2)已知取得的是合格品，求它是一等品的概率.解析：设A 表示取得一等品，B 表示取得合格品，则70(1)因为100件产品中有70件一等品，所以P (A ) = — =0.7(2)方法1：因为95件合格品中有70件一等品，所以70一 =0.736 895方法2：P (AB ) 70/100 = ------- -0.736 8 P (B ) 95/1003 .把一枚硬币任意抛掷两次，事件A 表示“第一次出现正面”，事件B 表示“第二次出现正面”，求P (BIA ). 解析：基本事件空间为：答案：—4 .一批产品中有4%的次品，而合格品中一等品占45%.从这批产品中任取一件，求该产品是一等品的概率. 解析：设A 表示取到的产品是一等品，B 表示取出的产品是合格品，则P (AIB ) =45%, P ( B ) =4% 于是 P (B ) =1-P ( B ) =96%所以 P (A ) =P (AB ) =P (B ) P (AIB ) =96%x45%=43.2%5 .抛掷红、蓝两个骰子，事件A 表示“红骰子出现4点”，事件B 表示“蓝骰子出现的点数是偶数"，求P(AIB ). 解析：设蓝、红骰子出现的点数分别为x,y ,则(x-y)表示“蓝骰子出现x 点，红骰子出现y 点”的试验结果，于是基本事件空间中的事件数为n(Q)=36 (个).n(B)=3x6=18(个)P (AIB ) P (AIB ) Q={ A={ B={ (正 (正 (反正)，正)，正)， 1 (正反)，(反，正)，(反，反)).・・・P(AB)=4，P(A)=4(正，反)}(正，正)} 2 .•・P(BIA)二 1P (AB ) 4n (B) 18 A P (B)= ------- =——=n (Q) 36P (AB)=3136 12P (AB)A P (AIB)= ---------P (B) 12 丁26.一个盒子中有6只白球、4只黑球，从中不放回地每次任取1只，连取2次，求(1)第一次取得白球的概率；(2)第一、第二次都取得白球的概率；(3)第一次取得黑球而第二次取得白球的概率.解析：设A表示第一次取得白球，B表示第二次取得白球，则6(1)P(2)P(3)P 6 5(AB)=P(A)P(BIA)= x§ -0.33- - - 4 6 (A B)=P( A)p(BI A)= x§ -0.2780 解析：P(A)=10030P(AB)=而,35 P(B)=100，30P(AIB)=358.掷两枚均匀的骰子，已知点数不同，求至少有一个是6点的概率.解析1：设两枚骰子出现的点数分别为x,y,事件A：“两枚骰子出现的点数不同，即x，y”，事件B：“x,y中有且只有一个是6点”；事件C："x=y=6"，则P(BIA)二10 P ( AB )P(CIA)=P (A) 30360 P (AC) 36P (A)3036设A=｛从100个零件中任取一个是合格品｝B=｛从100个零件中任取一个是第一台车床加工的｝求：P(A),P(B),P(AB),P(AIB).・•・至少有一个是6点的概率为：1 1P(B U CIA)=P(BIA)+P(CIA)=3 +0=3 .解析2：也可用古典概型来求解D“至少有一个是6点”包含的结果数是10个，故所求的概率为:P(D)=30 = 3(由于两枚骰子点数不同，故基本事件空间中包含30个结果).9.设某种动物活到20岁以上的概率为0.7,活到25岁以上的概率为0.4,求现龄为20的这种动物能活到25 岁以上的概率？解析：设这种动物活到20岁以上的事件为人，活到25岁以上的事件为B,贝U P(A)=0.7,而AB=B，即P(AB)=P(B)=0.4.故事件A发生条件下B发生的条件概率为P (AB) 0.4P(B1A)=E "而诬571 410.某彩票的中奖规则为：从1, 2,…，6这六个号码中任意选出三个不同的号码，如果全对(与顺序无关) 则中一等奖，求(1)买一注号码中一等奖的概率；(2)假设本期开出的中奖号码为1, 2, 3,如果某位彩票预测专家根据历史数据推断本期中奖号码中必有2,那么买一注号码中一等奖的概率是多少？(3)若预测本期不会出现5,且本期开出的中奖号码为1, 2, 3,那么买一注号码中一等奖的概率是多少？C 3 1解析：(1)中一等奖概率为：P=f =:C 3 206(2)所有含有号码 2 的组合有(1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 2, 6), (2, 3, 4), (2, 3, 5),1(2, 3, 6), (2, 4, 5), (2, 4, 6), (2, 5, 6).故中一等奖概率为P= —=0.1.(3)记事件A为“从1, 2, 3, 4, 5, 6中任选3个数字，这3个数字中不含有5”，事件B：“选的号码为1, 2, 3”，于是：n (A ) C 3P(A)= ------ =一n (Q) C 36P(AB)= K3620A P(BIA)= P (AB)120P (A) 1 1021即中一等奖概率为—.11.设A, B为两事件，已知P(A)=0.5, P(B)=0.6, P(B| A )=0.4,试求(2)P(AB)=P(B)-P( A B)=0.6-0.2=0.412.一个盒子中有6只白球、4只黑球，从中不放回地每次任取1只，连取2次，求第二次取到白球的概率. 解析：A=｛第一次取到白球｝B=｛第二次取到白球｝因为B=AB U A B且AB与A B互不相容，所以P (B) =P(AB)+P(A B)=P(A)P(BIA)+P( A )P(BI A)6 5 4 6=x —+ — x— =0.610 9 10 913.盒子中有25个外形相同的球，其中10个白的，5个黄的，10个黑的，从盒子中任意取出一球，已知它不是黑球，试求它是黄球的概率.解析：设事件A为“从盒子中任取一球，它不是黑球”事件B为“取的球是黄球”，则所求事件的概率为：5P( AB) = 25 = 1P (A)—15 — 3.2514.盒中有10个红球及1个黄球.A随意抽出第一个球后不放回盒中，之后B随意抽出第二个球.求下列事件的概率.(1)A和B都抽得红球.(2)A和B都抽得黄球.(3)A抽得黄球和B抽得红球.(4)A和B抽得不同颜色的球.(5)已知B抽得黄球，A抽得红球.A 2 9解析：(1) P=—10=11(2)P=01X A1 1(3)P= 拚=-A 2 1111A 2 11(4)P= ---- 10 ----- 10A2 1111(5)P(AIB)= P (AB) 11P (A) 10 101115.设某种灯管使用了500 h还能继续使用的概率是0.94,使用到700 h后还能继续使用的概率是0.87,问已经使用了500 h的灯管还能继续使用到700 h的概率是多少？解析：P= 0|4 =0.926(1) P(A B)；(2) P(AB)；解析：(1) P(A B)=P(A)P(BI A)= (1-0.5) x0.4=0.2。

条件概率练习题含答案

条件概率练习题含答案条件概率是概率论中的一个重要概念，用于描述事件在给定其他事件发生的条件下发生的概率。

条件概率的计算往往需要运用到贝叶斯定理，是解决实际问题中复杂概率计算的基础。

下面将给出一些条件概率的练习题，并附带答案供读者参考。

练习题一：某城市有两个广播车队，A车队和B车队，各自服务不同的区域。

根据统计数据，A车队在A区域的音质不良时间占总时间的5%，而在B区域的音质不良时间占总时间的10%。

已知听众在该城市80%来自A区域，20%来自B区域。

现在假设一位听众正遇到音质不良的情况，请问这位听众是来自A区域的概率是多少？解答一：设事件A为来自A区域，事件B为遇到音质不良。

根据题意，我们要求的是在遇到音质不良的条件下，该听众来自A区域的概率。

根据条件概率公式，可以得到：P(A|B) = P(A∩B) / P(B)，其中P(A∩B)表示事件A和B同时发生的概率，P(B)表示事件B发生的概率。

根据题目中的信息，我们可以得到P(A∩B) = P(A) * P(B|A) = 0.8 * 0.05 = 0.04，P(B) = P(A) * P(B|A) + P(B') * P(B|B') = 0.8 * 0.05 + 0.2 * 0.1 = 0.06，所以P(A|B) = 0.04 / 0.06 = 2/3。

练习题二：一家剧院即将上演两台戏剧，A戏剧和B戏剧，已知A戏剧的门票占总票数的60%，B戏剧的门票占总票数的40%。

观众对A戏剧感兴趣的概率是70%，对B戏剧感兴趣的概率是50%。

现在假设一位观众购票，且对所购剧目感兴趣，请问该观众购买的是B戏剧门票的概率是多少？解答二：设事件A为购买A戏剧门票，事件B为对所购剧目感兴趣。

求解的是在对所购剧目感兴趣的条件下，购买B戏剧门票的概率。

根据条件概率的定义，可以得到：P(B|A) = P(B∩A) / P(A)，其中P(B∩A)表示事件B和A同时发生的概率，P(A)表示购买A戏剧门票的概率。

条件概率练习题

条件概率练习题一、基本概念题1. 设事件A和事件B相互独立，P(A) = 0.4，P(B) = 0.6，求P(A|B)。

2. 已知P(A) = 0.5，P(B) = 0.7，P(A ∩ B) = 0.3，求P(A|B)和P(B|A)。

3. 在一个袋子里有5个红球和3个蓝球，随机取出一个球，求取出红球的条件下，取出第二个球也是红球的概率。

4. 某班级有50名学生，其中30名喜欢篮球，20名喜欢足球，10名既喜欢篮球又喜欢足球。

随机选取一名学生，求该学生喜欢篮球的条件下，也喜欢足球的概率。

二、应用题1. 一批产品中有10%的次品，现随机抽取10件产品，求恰好有2件次品的概率。

3. 抛掷一枚硬币3次，求恰好出现2次正面的概率。

4. 从一副52张的扑克牌中随机抽取4张，求抽到的都是红桃的概率。

三、综合题1. 甲、乙、丙三人独立解同一道数学题，甲解出的概率为0.4，乙解出的概率为0.5，丙解出的概率为0.3。

求至少有两人解出这道题的概率。

2. 一批产品中有20%的次品，现随机抽取5件产品，求恰好有1件次品且第2件是正品的概率。

3. 抛掷一枚均匀的骰子，求出现偶数点数的条件下，再次抛掷出现奇数点数的概率。

4. 从一副52张的扑克牌中随机抽取5张，求抽到的牌中至少有一张是红桃的概率。

四、拓展题1. 设事件A和事件B互斥，P(A) = 0.3，P(B) = 0.4，求P(A|B)。

2. 已知P(A) = 0.6，P(B|A) = 0.8，P(B|非A) = 0.4，求P(A∩ B)。

3. 某班级有60名学生，其中40名喜欢数学，30名喜欢英语，20名既喜欢数学又喜欢英语。

随机选取一名学生，求该学生喜欢数学的条件下，也喜欢英语的概率。

4. 抛掷一枚硬币和一枚骰子，求硬币出现正面且骰子出现6点的概率。

五、逻辑推理题1. 在一个家庭中，有两个孩子，已知至少有一个是女孩，求两个孩子都是女孩的概率。

2. 有三个箱子，分别装有苹果、橘子和苹果橘子混合。

条件概率专题练习及答案都

条件概率专题练习一、选择题1．下列式子成立的是( )A ．P (A |B )＝P (B |A ) B ．0<P (B |A )<1C ．P (AB )＝P (A )·P (B |A )D ．P (A ∩B |A )＝P (B ) [答案] C [解析] 由P (B |A )＝P (AB )P (A )得P (AB )＝P (B |A )·P (A )． 2．在10个形状大小均相同的球中有6个红球和4个白球，不放回地依次摸出2个球，在第1次摸出红球的条件下，第2次也摸到红球的概率为( )A.35B.25C.110D.59[答案] D [解析] 设第一次摸到的是红球(第二次无限制)为事件A ，则P (A )＝6×910×9＝35，第一次摸得红球，第二次也摸得红球为事件B ，则P (B )＝6×510×9＝13，故在第一次摸得红球的条件下第二次也摸得红球的概率为P ＝P (B )P (A )＝59，选D.3．已知P (B |A )＝13，P (A )＝25，则P (AB )等于( )A.56B.910C.215D.115[答案] C [解析] 本题主要考查由条件概率公式变形得到的乘法公式，P (AB )＝P (B |A )·P (A )＝13×25＝215，故答案选C.4．抛掷红、黄两颗骰子，当红色骰子的点数为4或6时，两颗骰子的点数之积大于20的概率是( ) A.14B.13C.12D.35[答案] B [解析] 抛掷红、黄两颗骰子共有6×6＝36个基本事件，其中红色骰子的点数为4或6的有12个基本事件，两颗骰子点数之积包含4×6,6×4,6×5,6×6共4个基本事件．所以其概率为4361236＝13.5．一个盒子里有20个大小形状相同的小球，其中5个红的，5个黄的，10个绿的，从盒子中任取一球，若它不是红球，则它是绿球的概率是( )A.56B.34C.23D.13[答案] C6．根据历年气象统计资料，某地四月份吹东风的概率为930，下雨的概率为1130，既吹东风又下雨的概率为830.则在吹东风的条件下下雨的概率为( )A.911B.811C.25D.89[答案] D [解析] 设事件A 表示“该地区四月份下雨”，B 表示“四月份吹东风”，则P (A )＝1130，P (B )＝930，P (AB )＝830，从而吹东风的条件下下雨的概率为P (A |B )＝P (AB )P (B )＝830930＝89. 7．一个口袋中装有2个白球和3个黑球，则先摸出一个白球后放回，再摸出一个白球的概率是( ) A.23B.14C.25D.15[答案] C [解析] 设A i 表示第i 次(i ＝1,2)取到白球的事件，因为P (A 1)＝25，P (A 1A 2)＝25×25＝425，在放回取球的情况P (A 2|A 1)＝25×2525＝25.8．把一枚骰子连续掷两次，已知在第一次抛出的是偶数点的情况下，第二次抛出的也是偶数点的概率为( ) A ．1B.12C.13D.14[答案] B [解析] 设A i 表示第i 次(i ＝1,2)抛出偶数点，则P (A 1)＝1836，P (A 1A 2)＝1836×918，故在第一次抛出偶数点的概率为P (A 2|A 1)＝P (A 1A 2)P (A 1)＝1836×9181836＝12，故选B.二、填空题9．某人提出一个问题，甲先答，答对的概率为0.4，如果甲答错，由乙答，答对的概率为0.5，则问题由乙答对的概率为________．[答案] 0.310．100件产品中有5件次品，不放回地抽取两次，每次抽1件，已知第一次抽出的是次品，则第2次抽出正品的概率为________．[答案] 9599[解析] 设“第一次抽到次品”为事件A ，“第二次抽到正品”为事件B ，则P (A )＝5100，P (AB )＝5100×9599，所以P (B |A )＝P (AB )P (A )＝9599.准确区分事件B |A 与事件AB 的意义是关键． 11．一个家庭中有两个小孩．假定生男、生女是等可能的，已知这个家庭有一个是女孩，则这时另一个小孩是男孩的概率是________．[答案] 12 [解析] 一个家庭的两个小孩只有3种可能：{两个都是男孩}，{一个是女孩，另一个是男孩}，{两个都是女孩}，由题目假定可知这3个基本事件的发生是等可能的．12．从1～100这100个整数中，任取一数，已知取出的一数是不大于50的数，则它是2或3的倍数的概率为________．[答案]3350[解析] 根据题意可知取出的一个数是不大于50的数，则这样的数共有50个，其中是2或3的倍数共有33个，故所求概率为3350.三、解答题13．把一枚硬币任意掷两次，事件A ＝“第一次出现正面”，事件B ＝“第二次出现正面”，求P (B |A )． [解析] P (B )＝P (A )＝12，P (AB )＝14， P (B |A )＝P (AB )P (A )＝1412＝12.14．盒中有25个球，其中10个白的、5个黄的、10个黑的，从盒子中任意取出一个球，已知它不是黑球，试求它是黄球的概率．[解析] 解法一：设“取出的是白球”为事件A ，“取出的是黄球”为事件B ，“取出的是黑球”为事件C ，则P (C )＝1025＝25，∴P (C )＝1－25＝35，P (B C )＝P (B )＝525＝15∴P (B |C )＝P (B C )P (C )＝13.解法二：已知取出的球不是黑球，则它是黄球的概率P ＝55＋10＝13.15．1号箱中有2个白球和4个红球，2号箱中有5个白球和3个红球，现随机地从1号箱中取出一球放入2号箱，然后从2号箱随机取出一球，问：(1)从1号箱中取出的是红球的条件下，从2号箱取出红球的概率是多少？ (2)从2号箱取出红球的概率是多少？[解析] 记事件A ：最后从2号箱中取出的是红球；事件B ：从1号箱中取出的是红球．P (B )＝42＋4＝23，P (B －)＝1－P (B )＝13. (1)P (A |B )＝3＋18＋1＝49.(2)∵P (A |B －)＝38＋1＝13， ∴P (A )＝P (A ∩B )＋P (A ∩B －)＝P (A |B )P (B )＋P (A |B －)P (B －)＝49×23＋13×13＝1127.16．某校高三(1)班有学生40人，其中共青团员15人．全班分成4个小组，第一组有学生10人，共青团员4人．从该班任选一个作学生代表．(1)求选到的是第一组的学生的概率； (2)已知选到的是共青团员，求他是第一组学生的概率． [解析] 设事件A 表示“选到第一组学生”，事件B 表示“选到共青团员”． (1)由题意，P (A )＝1040＝14.(2)要求的是在事件B 发生的条件下，事件A 发生的条件概率P (A |B )．不难理解，在事件B 发生的条件下(即以所选到的学生是共青团员为前提)，有15种不同的选择，其中属于第一组的有4种选择．因此，P (A |B )＝415。

条件概率推理练习

条件概率推理练习
本文档将为您提供一些条件概率推理练，帮助您更好地理解和应用条件概率的概念。

练一
假设有一批电子产品，其中有200部手机和300部平板电脑。

这些产品被分为两个仓库，仓库A和仓库B。

根据记录，仓库A 中有150部手机和50部平板电脑，仓库B中有50部手机和250部平板电脑。

现在，请根据以上信息回答以下问题：
1. 如果我们从仓库A中随机选择一部设备，那么它是手机的概率是多少？
2. 如果我们从仓库B中随机选择一部设备，那么它是平板电脑的概率是多少？
练二
假设有一批学生，其中有60%是女生，40%是男生。

我们还知道，在所有女生中，有30%是年龄小于18岁的，而在所有男生中，有20%是年龄小于18岁的。

现在，请根据以上信息回答以下问题：
1. 如果我们随机选择一个学生，那么他/她是女生且年龄小于
18岁的概率是多少？
2. 如果我们随机选择一个学生，那么他/她是男生且年龄小于
18岁的概率是多少？
练三
假设某城市的天气有三种状态：晴朗、多云和雨天。

根据历史
数据，我们知道在一年365天中，晴朗的天数占比40%，多云的天
数占比30%，雨天的天数占比30%。

现在，请根据以上信息回答以下问题：
1. 如果今天是雨天，那么明天是多云天气的概率是多少？
2. 如果今天是晴朗天气，那么明天是雨天的概率是多少？
这些练可以帮助您巩固条件概率的概念和运用，希望能对您有所帮助！。

利用条件概率公式求解条件概率(附word)

利用条件概率公式求解条件概率1．袋中有5个球（3个白球，2个黑球）现每次取一球，无放回抽取2次，则在第一次抽到白球的条件下，第二次抽到白球的概率为（） A ．3/5B ．3/4C ．1/2D ．3/10【分析】先记事件A 为“第一次取到白球”，事件B 为“第二次取到白球”，则事件AB 为“两次都取到白球”，根据题意得到()P A 与()P AB ，再由条件概率，即可求出结果. 【解析】记事件A 为“第一次取到白球”，事件B 为“第二次取到白球”，则事件AB 为“两次都取到白球”，依题意知3()5P A =，3263()542010P AB =⨯==，所以，在第一次取到白球的条件下，第二次取到白球的概率是3110()325P B A ==，选C.【小结】本题主要考查条件概率与独立事件，熟记条件概率的计算公式即可，属于常考题型.2．有歌唱道：“江西是个好地方，山清水秀好风光.”现有甲乙两位游客慕名来到江西旅游，分别准备从庐山、三清山、龙虎山和明月山4个著名旅游景点中随机选择其中一个景点游玩，记事件A ：甲和乙至少一人选择庐山，事件B ：甲和乙选择的景点不同，则条件概率()P B A =（） A ．716B ．78C ．37D ．67【分析】首先根据题意分别算出()n A 和()n AB ，再利用条件概率公式计算即可.【解析】由题知：事件A ：甲和乙至少一人选择庐山共有：1123()17n A C C =⋅+=种情况，事件AB ：甲和乙选择的景点不同，且至少一人选择庐山，共有1123()6n AB C C =⋅=种情况，()()6=()7n AB P B A n A =，选D 【小结】本题主要考查条件概率，理解条件概率及掌握公式为解题的关键，属于中档题.3．长春气象台统计，7月15日净月区下雨的概率为415，刮风的概率为215，既刮风又下雨的概率为110，设事件A 为下雨，事件B 为刮风，那么()|P A B =（） A ．12B ．34C ．25D ．38【分析】确定421(),(),()151510P A P B P AB ===，再利用条件概率的计算公式，即可求解. 【解析】由题意，可知421(),(),()151510P A P B P AB ===，利用条件概率的计算公式，可得1()310(|)2()415P AB P A B P B ===，选B. 【小结】本题主要考查了条件概率的计算，其中解答中认真审题，熟记条件概率的计算公式，准确计算是解答的关键，着重考查了推理与运算能力，属于基础题.4．根据历年气象统计资料，某地四月份吹东风的概率为930，下雨的概率为1130，既吹东风又下雨的概率为830.则在下雨条件下吹东风的概率为（） A ．25 B ．89 C ．811D ．911【分析】在下雨条件下吹东风的概率=既吹东风又下雨的概率÷ 下雨的概率【解析】在下雨条件下吹东风的概率为8830=111130，选C【小结】本题考查条件概率的计算，属于简单题．5．甲、乙、丙、丁四位同学计划去4个景点旅游，每人只去一个景点，设事件A =“四位同学去的景点不相同”，事件B =“甲同学独自去一个景点”，则()P A B =（） A ．29B ．13C ．49D ．59【分析】由题意结合计数原理的知识求出所有基本事件数、B 发生的基本事件数、AB 发生的基本事件数，由古典概型概率公式可得()P B 、()P AB ，再利用条件概率概率公式即可得解.【解析】甲、乙、丙、丁四位同学计划去4个景点旅游，每人只去一个景点共有44256=个基本事件，甲同学独自去一个景点，共有1343108C ⋅=个基本事件，则()1082725664P B ==；事件A 、B 同时发生即事件A ：四位同学去的景点不相同发生，共有4424A =个基本事件，则()24325632P AB ==；所以()()()323227964P AB P A B P B ===，选A. 【小结】本题考查了条件概率的求解，考查了计数原理与古典概型概率公式的应用，熟记公式、合理分步是解题关键，属于中档题.6．袋中有大小完全相同的2个白球和3个黄球，逐个不放回的摸出两球，设“第一次摸得白球”为事件A ，“摸得的两球同色”为事件B ，则()P B A =（） A ．110B ．15C ．14D ．25【解析】()P B A =21()1542()45P AB P A ⨯⨯== ,选C.7．已知6个高尔夫球中有2个不合格，每次任取1个，不放回地取两次．在第一次取到合格高尔夫球的条件下，第二次取到不合格高尔夫球的概率为（） A ．35B ．25C ．23D ．310【分析】记事件{A =第一次取到的是合格高尔夫球}，事件{B =第二次取到不合格高尔夫球}，由题意可得事件B 发生所包含的基本事件数()428n A B ⋂=⨯=，事件A 发生所包含的基本事件数()4520n A =⨯=，然后即可求出答案.【解析】记事件{A =第一次取到的是合格高尔夫球}，事件{B =第二次取到不合格高尔夫球}由题意可得事件B 发生所包含的基本事件数()428n A B ⋂=⨯=事件A 发生所包含的基本事件数()4520n A =⨯=，所以()()()82205n A B P B A n A ⋂===，选B 【小结】本题考查的是条件概率，较简单.8．袋中装有形状和大小完全相同的4个黑球，3个白球，从中不放回地依次随机摸取两球，在第一次摸到了黑球的条件下，第二次摸到白球的概率是( ) A ．47B ．27C ．12D ．13【分析】首先求出第一次摸到黑球概率，再求出第二次摸到白球概率，利用条件概率的求法公式即可求解.【解析】设第一次摸到黑球为事件A ，则()47P A =，第二次摸到白球为事件B ，则()4376P AB =⨯，设第一次摸到黑球的条件下，第二次摸到球的概率为()()()43176427|P AB P B A P A ⨯===，选C. 【小结】本题考查了条件概率的求法，属于基础题.9．已知1()5P AB =，2()5P A =，则()P BA ∣等于（） A ．225B ．12 C ．35D ．14【分析】直接利用条件概率公式求解.【解析】因为1()5P AB =，2()5P A =，所以1()52))512((P AB P BA P A ===∣，选B 【小结】本题主要考查条件概率的求法，属于基础题.10．对标有不同编号的6件正品和4件次品的产品进行检测，不放回地依次摸出2件.在第一次摸出次品的条件下，第二次摸到正品的概率是（） A ．35B ．25C ．59D ．23【分析】分别求出第一次摸出的是次品的概率以及第一次摸出的是次品，第二次摸到的是正品的概率，结合条件概率的计算公式即可求出所求答案.【解析】记A =“第一次摸出的是次品”， B =“第二次摸到的是正品”，由题意知，()42105P A ==,()46410915P AB =⨯=，则()()()4215235P AB P B A P A ===，选D 【小结】本题考查了条件概率的求解，属于基础题.11．一袋中共有10个大小相同的黑球和白球，若从袋中任意摸出2个球，至少有1个白球的概率为1315，现从中不放回地取球，每次取1球，取2次，若已知第2次取得白球的条件下，则第1次取得黑球的概率为（） A ．49B ．59C ．79D ．1318【分析】先计算出黑球和白球的数量，然后根据条件概率计算公式，计算出所求概率.【解析】设黑球有x 个（010,N x x +<<∈），则白球有10x -个. 从袋中任意摸出2个球，至少有1个白球的概率为1315，没有白球的概率为13211515-=.即()221012214515x x x C C -⨯== 由于010,N x x +<<∈，故解得4x =.所以黑球有4个，白球有6个设事件A =｛第2次取得白球｝，事件B =｛第1次取得黑球｝，()11114665210543905C C C C P A A +===，()11462102449015C C P AB A ⨯===. 所以已知第2次取得白球的条件下，则第1次取得黑球的概率为()()()4415|395P AB P B A P A ===，选A 【小结】本小题主要考查条件概率计算，属于基础题.12．“幻方”最早记载于我国公元前500年的春秋时期《大戴礼》中，n 阶幻方（3n ≥，*n N ∈）是由前2n 个正整数组成的一个n 阶方阵，其各行各列及两条对角线所含的n 个数之和（简称幻和）相等，例如“3阶幻方”的幻和为15.现从如图所示的3阶幻方中任取3个不同的数，记“取到的3个数和为15”为事件A ，“取到的3个数可以构成一个等差数列”为事件B ，则()|P B A =（）A ．34B ．23C ．13D ．12【分析】根据题意，先列举出事件A 发生对应的基本事件，再列举出事件AB 同时发生对应的基本事件，基本事件的个数比，即为所求的概率.【解析】根据题意，事件A 包含的基本事件有：()8,1,6，()3,5,7，()4,9,2，()8,3,4，()1,5,9，()6,7,2，()8,5,2，()4,5,6；共8个基本事件；事件AB 同时发生包含的基本事件有：()3,5,7，()1,5,9，()8,5,2，()4,5,6共4个基本事件，所以()()()48|12n AB P B A n A ===，选D【小结】本题主要考查求条件概率，属于基础题型.13．2020年疫情的到来给我们生活学习等各方面带来种种困难.为了顺利迎接高考，省里制定了周密的毕业年级复学计划.为了确保安全开学，全省组织毕业年级学生进行核酸检测的筛查.学生先到医务室进行咽拭子检验，检验呈阳性者需到防疫部门做进一步检测.已知随机抽一人检验呈阳性的概率为0.2%，且每个人检验是否呈阳性相互独立，若该疾病患病率为0.1%，且患病者检验呈阳性的概率为99%.若某人检验呈阳性，则他确实患病的概率（） A ．0.99%B ．99%C ．49.5%.D ．36.5%【分析】利用条件概率可求某人检验呈阳性时他确实患病的概率. 【解析】设A 为“某人检验呈阳性”，B 为“此人患病”. 则“某人检验呈阳性时他确实患病”为|B A ，又()()()99%0.1%|49.5%0.2%P AB P B A P A ⨯===，选C【小结】本题考查条件概率的计算及其应用，此题需将题设的各个条件合理转化为事件的概率或条件概率.14．已知()310P AB =，()35P A =，则()|P B A 等于（）A ．950B ．12 C ．910D ．14【分析】利用条件概率公式计算可得结果.【解析】由条件概率公式得()()()3110|325P A P AB P B A ===，选B 【小结】本题考查利用条件概率公式计算概率值，考查计算能力，属于基础题.15．端午节是我国的传统节日，每逢端午家家户户都要吃粽子，现有5个粽子，其中3个咸蛋黄馅2个豆沙馅，随机取出2个，事件A =“取到2个为同一种馅”，事件B =“取到的2个都是豆沙馅”，则()P B A =（） A ．14B ．34C ．110D ．310【分析】分别计算出取出的两个粽子为同一种馅，以及取到的2个都是豆沙馅的基本事件个数，然后由条件概率公式计算即可.【解析】由已知，有5个粽子，其中3个咸蛋黄馅2个豆沙馅，随机取出2个，则()22328n A A A =+=，()222n AB A ==，所以()()()2184n AB P B A n A ===，选A 【小结】本题考查条件概率的计算公式，以及古典概率的计算方法，属于基础题.16．从1，2，3，4，5，6，7中任取两个不同的数，事件A 为“取到的两个数的和为偶数”，事件B 为“取到的两个数均为偶数”，则()P B A =（） A ．47B ．12C ．37D ．13【分析】分别计算出()P AB 和()P A ，由条件概率公式可计算求得结果.【解析】由题意知：事件AB 有()2,4，()2,6，()4,6，共3个基本事件；事件A 有()1,3，()1,5，()1,7，()3,5，()3,7，()5,7，()2,4，()2,6，()4,6，共9个基本事件；()27317P AB C ∴==，()27937P A C ==，()()()117337P AB P B A P A ∴===，选D【小结】本题考查条件概率的求解问题，属于基础题.17．四边形EFGH 是以O 为圆心，半径为1的圆的内接正方形，将一颗豆子随机地扔到该圆内，用A 表示事件“豆子落在正方形EFGH 内”，用B 表示事件“豆子落在扇形OHE （阴影部分）内”，则()P B A =（）A ．12B ．13C ．14D ．15【分析】由已知关系分别求出,,O EFGH EOH S S S ，由几何概型求概率的计算方式求得()P A 与()P AB ，最后利用条件概率计算公式求得答案.【解析】因为四边形EFGH 是以O 为圆心，半径为1的圆的内接正方形，即1,2r EG ==，则EF =所以2111,2,42O EFGH EOH EFGH S S S S ππ=⋅===== A 表示事件“豆子落在正方形EFGH 内”， ()2EFGH O S P A S π== B 表示事件“豆子落在扇形OHE ”，则AB 表示事件“豆子落在三角形EOH 内”，()1122EOHOS P AB S ππ===所以()()()11224P AB P B A P A ππ===，选C 【小结】本题考查在几何图形中求条件概率，属于简单题.18．某学校高三（5）班要从8名班干部（其中5名男生，3名女生）中选取3人参加学校优秀班干部评选，事件:A 男生甲被选中，事件:B 有两名女生被选中，则()P B A =（） A ．18B ．17C ．38D ．37【分析】计算出事件A 、AB 的概率，利用条件概率公式可求得()P B A 的值.【解析】由题意可得()273838C P A C ==，事件:AB 男生甲与两名女生被选中，则()2338356C P AB C ==，因此，()()()3815637P AB P B A P A ==⨯=，选B. 【小结】本题考查条件概率的计算，考查运算求解能力和推理论证能力，考查数学运算和逻辑推理核心素养，属于中等题.19．从标有数字1，2，3，4，5的五张卡片中，依次抽出2张（取后不放回），则在第一次抽到卡片是偶数的情况下，第二次抽到卡片是奇数的概率为（） A ．14B ．23C ．34D ．12【分析】设事件A 表示“第一张抽到偶数”，事件B 表示“第二张抽取奇数”，分别求出()P A 和()P AB ，利用条件概率计算公式即可求得结果.【解析】从标有1，2，3，4，5五张卡片中，依次抽出2张，设事件A 表示“第一张抽到偶数”，事件B 表示“第二张抽取奇数”，则()25P A =，3()523410P AB =⨯=，在第一次抽到卡片是偶数的情况下，第二次抽到卡片是奇数的概率为3()10(|)()5324P AB P A B P A ===，选C 【小结】本题主要考查的是条件概率的计算，要熟记条件概率的计算公式，属于基础题.事件A 发生的前提下，事件B 发生的概率，用公式可表示为()(|)()P AB P A B P A =.20．某次校园活动中，组织者给到场的前1000名同学分发编号000999的号码纸，每人一张，活动结束时公布获奖规则.获奖规则为：①号码的三位数字之和是7的倍数者可获得纪念品M ；①号码的三位数字全是奇数者可获得纪念品N .已知某同学的号码满足获得纪念品N 的条件，则他同时可以获得纪念品M 的概率是（） A ．0.016B ．0.032C ．0.064D ．0.128【分析】记某同学获得纪念品M ､纪念品N 分別为事件A ､B ，由分步乘法计数原理结合古典概型概率公式可得125()1000P B =；再由分类加法、排列组合的知识结合古典概型概率公式可得16()1000P AB =；最后由条件概率公式即可得解.【解析】记某同学获得纪念品M ､纪念品N 分別为事件A ､B ，则事件B 发生的充要条件是：三位数字均是1，3，5，7，9五个数中的一个，对应的概率555125()10001000P B ⨯⨯==；事件AB 是在三位数字均为奇数的基础上，还需满足三位数字之和为7的倍数，三个09之间的数字之和范围为027，又因为每位数字都是奇数，故其和亦为奇数，故三位数字之和只可能是7或21，所以三位数字从小到大排列只有以下五种可能：①1，1，5，对应的三位数个数为133C =；①1，3，3，对应的三位数个数为133C =；①3，9，9，对应的三位数个数为133C =；①5，7，9，对应的三位数个数为336A =；①7，7，7，对应的三位数有1个；故3336116()10001000P AB ++++==，于是所求概率为16()161000()0.128125()1251000P AB P A B P B ====，选D 【小结】考查计数原理及古典概型概率公式应用，考查了条件概率公式的应用及运算求解能力，中档题.21．假定男女出生率相等，某个家庭有两个小孩，已知该家庭至少有一个女孩，则两个小孩都是女孩的概率是（） A ．12B ．13C ．14D ．16【分析】记事件A 为“至少有一个女孩”，事件B 为“另一个也是女孩”，分别求出A 、B 的结果个数，问题是求在事件A 发生的情况下，事件B 发生的概率，即求(|)P B A ，由条件概率公式求解即可. 【解析】一个家庭中有两个小孩只有4种可能：{男，男}，{男，女}，{女，男}，{女，女}．记事件A 为“至少有一个女孩”，事件B 为“另一个也是女孩”，则{A =（男，女），（女，男），（女，女）}，{B =（男，女），（女，男），（女，女）}，{AB =（女，女）}．于是可知3()4P A =，1()4P AB =．问题是求在事件A 发生的情况下，事件B 发生的概率，即求(|)P B A ，()114334P B A ==，选B ．【小结】本题的考点是条件概率与独立事件，主要考查条件概率的计算公式：()()()P AB P B A P A =，等可能事件的概率的求解公式：()mP M n=（其中n 为试验的所有结果，m 为基本事件的结果）.22．甲、乙两人独立地对同一目标各射击一次，命中率分别为0.6和0.8，在目标被击中的条件下，甲、乙同时击中目标的概率为（） A ．2144B ．1223C ．1225D ．2111【分析】根据题意,记甲击中目标为事件A ,乙击中目标为事件B ,目标被击中为事件C ,由相互独立事件的概率公式,计算可得目标被击中的概率,进而计算在目标被击中的情况下,甲、乙同时击中目标的概率,可得答案. 【解析】根据题意,记甲击中目标为事件A ,乙击中目标为事件B ,目标被击中为事件C , 则()()()()()1110.610.80.92P C P A P B =-=--⨯-=；则在目标被击中的情况下,甲、乙同时击中目标的概率为0.60.80.921223P ⨯==，选B【小结】本题考查条件概率的计算,是基础题,注意认清事件之间的关系,结合条件概率的计算公式正确计算即可.属于基础题.23．如图，在边长为1的正方形OABC 内任取一点P ，用A 表示事件“点P恰好取自曲线y =1x =及x 轴所围成的曲边梯形内”，B 表示事件“点P 恰好取自阴影部分内”，则(|)P B A =（）A ．14B ．15C ．16D ．17【解析】根据题意，正方形OABC 的面积为1×1=1，而y =1x =及x轴所围成的曲边梯形的面积为()312022223|,,3313x P A ==∴==⎰而阴影部分的面积为)312120211|326x dx x x ⎛⎫=-= ⎪⎝⎭⎰,①正方形OABC 中任取一点P ，点P 取自阴影部分的概率为()11616P B ==， ()()()116|243P B P B A P A ∴===，选A24．.三台中学实验学校现有三门选修课，甲、乙、丙三人每人只选修一门，设事件A 为“三人选修的课程都不同”，B 为“甲独自选修一门”，则概率P (A |B )等于（） A ．49B ．12C ．13D ．29【分析】利用条件概率的计算公式即可求解. 【解析】甲独自选修一门，则有3门选修课可选，则乙、丙只能从剩下的2门选修课中选择，可能性为224⨯=，所以甲独自选修一门的可能性为32212⨯⨯=，因为三个人选修的课程都不同的可能性为3216⨯⨯=.()61122P A B ==，选B 【小结】本题考查了条件概率的求法，考查了排列、组合的应用，属于基础题.25．掷骰子2次，每个结果以()11,x y 记之，其中1x ，2x ，分别表示第一颗，第二颗骰子的点数，设(){}1212,6A x x x x =+=，(){}1212,B x x x x =>，则()P B A =（）A ．18B ．13C ．25D ．12【分析】根据古典概型概率计算方法,列举出A 集合的所有情况,即可由条件概率求解. 【解析】根据题意(){}1212,6A x x x x=+=则集合A 所有可能为()()()()()1,5,2,4,3,3,4,2,5,1 ，(){}1212,B x x x x =>,则B 集合为()()4,2,5,1，根据条件概率求法可得()25P B A =，故选:C 【小结】本题考查了列举法求古典概型的概率,条件概率的求法,属于基础题.26．已知某同学在高二期末考试中，A 和B 两道选择题同时答对的概率为23，在A 题答对的情况下，B 题也答对的概率为89，则A 题答对的概率为( ) A ．1 4B ．3 4C ．1 2D ．79【分析】根据条件概率公式计算即可.【解析】设事件A ：答对A 题，事件B①答对B 题①则()()()23P AB P A P B =⋅=① ()()()8|9P AB P B A P A ∴==，()34P A ∴=，选B27．设A ，B 为两个事件，若事件A 和B 同时发生的概率为310，在事件A 发生的条件下，事件B 发生的概率为12，则事件A 发生的概率为（） A ．35 B ．310C ．25D ．710【分析】根据条件概率公式求解即可得答案.【解析】由题意得()310P AB =，()12P B A =，根据条件概率的公式得：()()()()31102P AB P B A P A P A ===，解得()35P A =，所以事件A 发生的概率为()35P A =，选A.28．抛掷一枚质地均匀的骰子两次，记事件A ={两次的点数均为偶数}，B ={两次的点数之和小于8}，则()|P B A =（）A ．12B ．13C ．14D ．15【分析】先求出事件A 包含的基本事件数，以及在A 发生的条件下，事件B 包含的基本事件数，再用条件概率公式求出结果．【解析】由题意，事件A ={两次的点数均为偶数}，包含的基本事件数是()()()()()()()()()2,2,2,4,2,6,4,2,4,4,4,6,6,2,6,4,6,6共9个基本事件；在事件A 发生的条件下，事件B ={两次的点数之和小于8}，包含的基本事件数是()()()2,2,2,4,4,2共3个基本事件，所以()31|93P B A ==，选B ．29．甲箱中有5个红球，2个白球和3个黑球，乙箱中有4个红球，3个白球和3个黑球．先从甲箱中随机取出一球放入乙箱中，分别以1A ，2A ，3A 表示由甲箱中取出的是红球，白球和黑球的事件；再从乙箱中随机取出一球，以B 表示由乙箱中取出的球是红球的事件，则下列结论正确的是（） A ．2()5P B =B ．15()11P B A =C ．事件B 与事件1A 相互独立D ．1A 、2A 、3A 两两互斥【分析】根据每次取一球，易得1A ，2A ，3A 是两两互斥的事件，求得()()()123,,p A p A p A ，然后由条件概率求得1()P B A ，123()()()()P B P BA P BA P BA =++，再逐项判断. 【解析】因为每次取一球，所以1A ，2A ，3A 是两两互斥的事件，故D 正确；因为()()()123523,,101010p A p A p A ===，所以11155()51011()5()1110P BA P B A P A ⨯===，故B 正确；同理3223232434()()4410111011(),()23()11()111010P BA P BA P B A P B A P A P A ⨯⨯======，所以1235524349()()()()10111011101122P B P BA P BA P BA =++=⨯+⨯+⨯=，故AC 错误；选BD 【小结】本题考查互斥事件，相互独立事件，条件概率的求法，还考查了运算求解的能力，属于中档题.30．一袋中有大小相同的4个红球和2个白球，给出下列结论：①从中任取3球，恰有一个白球的概率是35；①从中有放回的取球6次，每次任取一球，恰好有两次白球的概率为80243；①现从中不放回的取球2次，每次任取1球，则在第一次取到红球后，第二次再次取到红球的概率为25；①从中有放回的取球3次，每次任取一球，则至少有一次取到红球的概率为2627. 则其中正确命题的序号是（） A ．①B ．①C ．①D ．①【分析】①利用古典概型的概率求解判断.①利用独立重复实验的概率求解判断.①利用古典概型概率求解判断.①利用独立重复实验的概率求解判断.【解析】一袋中有大小相同的4个红球和2个白球，①从中任取3球，恰有一个白球的概率是21423635C C p C ==故正确； ①从中有放回的取球6次，每次任取一球，每次抽到白球的概率为2163p ==，则恰好有两次白球的概率为4226218033243p C ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，故正确； ①现从中不放回的取球2次，每次任取1球，则在第一次取到红球后，第二次再次取到红球的概率为1143114535C C C C =，故错误；①从中有放回的取球3次，每次任取一球，每次抽到红球的概率为4263p ==：则至少有一次取到红球的概率为3031261327p C ⎛⎫=-=⎪⎝⎭，故正确. 选ABD.【小结】本题主要考查概率的求法，还考查了运算求解的能力，属于中档题.31．下列有关说法正确的是（）A ．5122x y ⎛⎫- ⎪⎝⎭的展开式中含23x y 项的二项式系数为20； B ．事件AB 为必然事件，则事件A 、B 是互为对立事件；C ．设随机变量ξ服从正态分布(),7N μ，若()()24P P ξξ<=>，则μ与D ξ的值分别为3μ=，7D ξ=； D ．甲、乙、丙、丁4个人到4个景点旅游，每人只去一个景点，设事件A =“4个人去的景点各不相同”，事件B =“甲独自去一个景点”，则()2|9P A B =. 【分析】由二项式定理得：51(2)2x y -的展开式中含23x y 项的二项式系数为35C ，即可判断A ；由对立事件与互斥事件的概念，进行判断B ；由正态分布的特点，即可判断C ；由条件概率的公式()(|)()P AB P A B P B =，计算即可判断D .【解析】对于A ，由二项式定理得：51(2)2x y -的展开式中含23x y 项的二项式系数为3510C =，故A 错误；对于B ，事件AB 为必然事件，若A ，B 互斥，则事件A 、B 是互为对立事件；若A ，B 不互斥，则事件A 、B 不是互为对立事件，故B 错误对于C ，设随机变量ξ服从正态分布(,7)N μ，若(2)(4)P P ξξ<=>，则曲线关于3x =对称，则μ与D ξ的值分别为3μ=，7D ξ=．故C 正确．对于D ，设事件A = “4个人去的景点不相同”，事件B = “甲独自去一个景点”，则P （A ）44!4=，P （B ）344327464==，443!3()432P AB ⨯==，则()2(|)()9P AB P A B P B ==，故D 正确；选CD ．【小结】本题考查命题的真假判断和应用，考查事件的关系、条件概率的求法，考查二项式定理的判定方法和正态分布的特点，考查判断和推理能力，是中档题．32．伟大出自平凡，英雄来自人民.在疫情防控一线，北京某大学学生会自发从学生会6名男生和8名女生骨干成员中选出2人作为队长率领他们加入武汉社区服务队，用A 表示事件“抽到的2名队长性别相同”，B 表示事件“抽到的2名队长都是男生”，则()|P B A =______. 【分析】求出(),()P A P AB ,再利用条件概率求解.【解析】由已知得()22682144391C C P A C +==，()262141591C P AB C ==，则()()()151591|434391P AB P B A P A ===. 【小结】求条件概率方法：（1）()()()|P AB P B A P A =；（2）()()()|n AB P B A n A =；（3）转化为古典概型求解.33．袋中有5个大小完全相同的球，其中2个黑球，3个白球.不放回地连续取两次，则已知在第一次取到黑球的条件下，第二次取到白球的概率为__________.【分析】记事件A 为“第一次取得黑球”，事件B 为“第二次白球”，根据题中条件，由条件概率的计算公式，即可得出结果.【解析】记事件A 为“第一次取得黑球”，事件B 为“第二次白球”：则()25P A =，()11231154310C C P AB C C ==所以已知在第一次取到黑球的条件下，第二次取到白球的概率为()()()3310245P AB P B A P A ===. 【小结】本题主要考查求条件概率，属于基础题型.34．从装有3个红球2个白球的袋子中先后取2个球，取后不放回，在第一次取到红球的条件下，第二次取到红球的概率为______.【分析】分别算出“第一次取到红球”的基本事件个数，“两次都取到红球”的个数，然后套用条件概率计算公式求解.【解析】设事件A 为 “第一次取到的是红球”，事件AB 为 “第一、二次都取到红球”，则()113412n A C C =⋅=，()11326n AB C C =⋅=，所以在第一次取到红球的条件下，第二次取到红球的概率为：()()()61122n AB P B A n A ===. 【小结】本题考查条件概率及其计算，较简单，解答时要灵活运用条件概率的运算公式.35．某校组织甲、乙、丙、丁、戊、己等6名学生参加演讲比赛，采用抽签法决定演讲顺序，在“学生甲和乙都不是第一个出场，且甲不是最后一个出场”的前提下，学生丙第一个出场的概率为__________．【分析】由条件概率计算方式，分别计算事件A ：“学生甲和乙都不是第一个出场，且甲不是最后一个出场”的基本事件个数，其中分两类乙在最后与乙不在最后计数，与事件AB 的基本事件个数，最后由公式求解. 【解析】事件A ：“学生甲和乙都不是第一个出场，且甲不是最后一个出场”；事件B ：“学生丙第一个出场”，对事件A ，甲和乙都不是第一个出场，第一类：乙在最后，则优先从中间4个位置中选一个给甲，再将余下的4个人全排列有1444C A ⋅种；第二类：乙没有在最后，则优先从中间4个位置中选两个给甲乙，再将余下的4个人全排列有2444A A ⋅种，故总的有()14244444n A C A A A =⋅+⋅.对事件AB ，此时丙第一个出场，优先从除了甲以外的4人中选一人安排在最后，再将余下的4人全排列有1444C A ⋅种，故()()()14441424444414n AB C A P B A n A C A A A ⋅===⋅+⋅.36．已知()12P B A =，3()10P AB =，则()P A =__________. 【分析】直接根据条件概率公式计算即可得答案. 【解析】根据条件概率公式()()()P AB P B A P A =和已知条件()12P B A =，3()10P AB =，所以()()()3310152P AB P A P B A ===.37．某盒中装有10只乒乓球，其中6只新球，4只旧球，不放回地依次摸出2个球使用，在第一次摸出新球的条件下，第二次也取到新球的概率为_______．【分析】直接利用条件概率公式计算得到答案.【解析】记第一次摸出新球为事件A ，第二次取到新球为事件B ，则()()()2621016110155456910C P AB C P B A C P A C ====. 【小结】本题考查了条件概率的计算，意在考查学生的计算能力和应用能力.38．据统计，连续熬夜48小时诱发心脏病的概率为0.055，连续熬夜72小时诱发心脏病的概率为0.19.现有一人已连续熬夜48小时未诱发心脏病，则他还能继续连续熬夜24小时不诱发心脏病的概率为______. 【分析】由对立设事件的概率分别得到连续熬夜48小时和连续熬夜72小时未诱发心脏病的概率，再利用条件概率公式求解.【解析】设事件A 为48h 发病，事件B 为72h 发病，由题意可知：()0.055P A =，()0.19P B =，则()0.945P A =，()0.81P B =，由条件概率公式可得：()()()()()0.8160.9457P AB P B P B A P A P A ====. 【小结】本题主要考查对立事件和条件概率的求法，属于基础题.39．某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6．已知某天的空气质量为优良，则随后一天的空气质量为优良的概率为______________．【分析】记事件A ：某天的空气质量为优，事件B ：第二天的空气也为优，由题意可得()0.75P A =，()0.6P AB =，再由条件概率公式即可得解.【解析】记事件A ：某天的空气质量为优，事件B ：第二天的空气也为优，由题意()0.75P A =，()0.6P AB =，则()()()0.640.755P AB P B A P A ===. 【小结】本题考查了条件概率的求解，属于基础题.40．为了营造勤奋读书、努力学习、奋发向上的文化氛围，提高学生的阅读兴趣，某校开展了“朗读者”闯关活动，各选手在第一轮要进行诗词朗读的比拼，第二轮进行诗词背诵的比拼.已知某学生通过第一关的概率为0.8，在已经通过第一关的前提下通过第二关的概率为0.5，则该同学两关均通过的概率为______. 【分析】根据条件概率公式，计算求值即可.【解析】设该学生通过第一关为事件A ，通过第二关为事件B ，在通过第一关的前提下通过第二关的概率为()P B A ，因为()()()P AB P B A P A =，所以()()()0.50.80.4P AB P B A P A ==⨯=.【小结】本题考查条件概率的计算，考查逻辑分析，运算求解的能力，属基础题.。