量子力学英文格里菲斯Chapter2PPT课件
合集下载
复旦量子力学讲义qmapter2-
Chapter 2 Many Body Problem
2020/5/29
2020/5/29
§2.1 Second quantization
➢The identical particles cannot be distinguished
2020/5/29
§2.1 Second quantization
2020/5/29
§2.1 Second quantization
➢Bose system
2020/5/29
§2.1 Second quantization
n 1,...,nk,...(r r1,...r rN) N n !i!PPk1(r r1)...
r kN(rN)
2020/5/29
§2.1 Second quantization
Screening Coulomb potential
Positive charge background cancels k=0 part
2020/5/29
§2.2 Hartree-Fork mean field approximation
2020/5/29
§2.2 Hartree-Fork mean field approximation
2020/5/29
§2.1 Second quantization
➢We need to introduce the creation and the annihilation operators to deal with various problem in the many-body system
ni!
A(k1,k2,...,kn,t)
n
N!
C(n1,n2,...,nk,...,t)
2020/5/29
2020/5/29
§2.1 Second quantization
➢The identical particles cannot be distinguished
2020/5/29
§2.1 Second quantization
2020/5/29
§2.1 Second quantization
➢Bose system
2020/5/29
§2.1 Second quantization
n 1,...,nk,...(r r1,...r rN) N n !i!PPk1(r r1)...
r kN(rN)
2020/5/29
§2.1 Second quantization
Screening Coulomb potential
Positive charge background cancels k=0 part
2020/5/29
§2.2 Hartree-Fork mean field approximation
2020/5/29
§2.2 Hartree-Fork mean field approximation
2020/5/29
§2.1 Second quantization
➢We need to introduce the creation and the annihilation operators to deal with various problem in the many-body system
ni!
A(k1,k2,...,kn,t)
n
N!
C(n1,n2,...,nk,...,t)
《量子力学》课件
贝尔不等式实验
总结词
验证量子纠缠的非局域性
详细描述
贝尔不等式实验是用来验证量子纠缠特性的重要实验。通过测量纠缠光子的偏 振状态，实验结果违背了贝尔不等式，证明了量子纠缠的非局域性，即两个纠 缠的粒子之间存在着超光速的相互作用。
原子干涉仪实验
总结词
验证原子波函数的存在
详细描述
原子干涉仪实验通过让原子通过双缝，观察到干涉现象，证明了原子的波函数存在。这个实验进一步 证实了量子力学的预言，也加深了我们对微观世界的理解。
量子力学的意义与价值
推动物理学的发展
量子力学是现代物理学的基础之一，对物理学的发展产生了深远 的影响。
促进科技的创新
量子力学的发展催生了一系列高科技产品，如电子显微镜、晶体 管、激光器等。
拓展人类的认知边界
量子力学揭示了微观世界的奥秘，拓展了人类的认知边界。
量子力学对人类世界观的影响
01 颠覆了经典物理学的观念
量子力学在固体物理中的应用
量子力学解释了固体材料的电子 结构和热学性质，为半导体技术 和超导理论的发现和应用提供了
基础。
量子力学揭示了固体材料的磁性 和光学性质，为磁存储器和光电 子器件的发展提供了理论支持。
量子力学还解释了固体材料的相 变和晶体结构，为材料科学和晶
体学的发展提供了理论基础。
量子力学在光学中的应用
复数与复变函数基础
01
复数
复数是实数的扩展，包含实部和虚部，是量子力 学中描述波函数的必备工具。
02
复变函数
复变函数是定义在复数域上的函数，其性质与实 数域上的函数类似，但更为丰富。
泛函分析基础
函数空间
泛函分析是研究函数空间的数学分支，函数空间中的元素称为函数或算子。
量子力学基础知识PPT讲稿
Plank
The Nobel Prize in Physics 1918
"for their theories, developed independently, concerning the course of chemical reactions"
Max Karl Ernst Ludwig Planck
(3).光子具有一定的动量(p)
P = mc = h /c = h／λ
光子有动量在光压实验中得到了证实。 (4).光的强度取决于单位体积内光子的数目，即光子密度。
将频率为的光照射到金属上，当金属中的一个电子受到一个光子撞击时， 产生光电效应，光子消失，并把它的能量h转移给电子。电子吸收的能量，一 部分用于克服金属对它的束缚力，其余部分则表现为光电子的动能。
Germany Berlin University Berlin, Germany
1858在金属表面上，金属发射出电子的现象。
.1 只有当照射光的频率超过某个最小频率（即临阈频率）时，金属才能发射光电
子，不同金属的临阈频率不同。 2.随着光强的增加，发射的电子数也增加，但不影响光电子的动能。 3.增加光的频率，光电子的动能也随之增加。
“光子说”表明——光不仅有波动性，且有微粒性，这就是光的波粒 二象性思想。
Einstein
The Nobel Prize in Physics 1921
"for their theories, developed independently, concerning the course of chemical reactions"
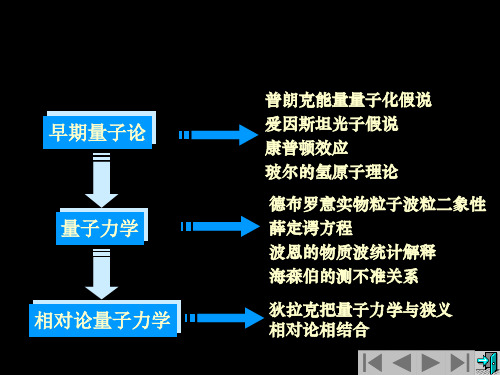
第一节.微观粒子的运动特征
电子、原子、分子和光子等微观粒子，具有波粒二象 性的运动特征。这一特征体现在以下的现象中，而这些现 象均不能用经典物理理论来解释，由此人们提出了量子力 学理论，这一理论就是本课程的一个重要基础。
量子力学课件(完整版)
Light beam
metal
electric current
11
能量量子化的假设
造成以上难题的原因是经典物理学认为 能量永远是连续的。
如果能量是量子化的，即原子吸收或发 射电磁波，只能以“量子”的方式进行， 那末上述问题都能得到很好的解释。
12
能量量子化概念对难题的解释
原子寿命 ①原子中的电子只能处于一系列分立的能级之中。
18
当 kT hc（高频区）
E(, T)
2hc2 5
e hc
kT
Wein公式
当 kT hc（低频区）
E(, T)
2c 4
kT
Rayleigh–Jeans公式
19
能量量子化概念对难题的解释
对光电效应的解释
如果电子处于分立能级且入射光的能 量也是量子化的，那么只有当光子的能 量（E =hυ）大于电子的能级差，即E =hυ > En－Em时，光电子才会产生。如 果入射光的强度足够强，但频率υ足够 小，光电子是无法产生的。
2 , k 2 / ,
得到 d 2 0,所以，t x(t)
dk 2 m
物质波包的观点夸大了波动性的一面，抹杀 了粒子性的一面，与实际不符。
45
（2）第二种解释：认为粒子的衍射行为是大 量粒子相互作用或疏密分布而产生的行为。 然而，电子衍射实验表明，就衍射效果 而言， 弱电子密度＋长时间＝强电子密度＋短时间 由此表明，对实物粒子而言，波动性体 现在粒子在空间的位置是不确定的，它是以 一定的概率存在于空间的某个位置。
2
这面临着两个问题：
1、信号电磁波所覆盖的区域包括大量的 元件，每个元件的工作状态有随机性，但 器件的响应具有统计性；
量子力学(全套) ppt课件
1 n2
人们自然会提出如下三个问题：
1. 原子线状光谱产生的机制是什么？ 2. 光谱线的频率为什么有这样简单的规律？
nm
3. 光谱线公式中能用整数作参数来表示这一事实启发我们 思考： 怎样的发光机制才能认为原子P的PT课状件态可以用包含整数值的量来描写12 。
从前，希腊人有一种思想认为：
•2.电子的能量只是与光的频率有关，与光强无关，光
强只决定电子数目的多少。光电效应的这些规律是经典
理论无法解释的。按照光的电磁理论，光的能量只决定
于光的强度而与频率无关。
PPT课件
24
（3） 光子的动量
光子不仅具有确定的能量 E = hv，
而且具有动量。根据相对论知，速度 为 V 运动的粒子的能量由右式给出：
nm
11
谱系
m
Lyman
1
Balmer
2
Paschen
3
Brackett
4
Pfund
5
氢原子光谱
n 2,3,4,...... 3,4,5,...... 4,5,6,...... 5,6,7,...... 6,7,8,......
区域 远紫外 可见 红外 远红外 超远红外
RH
C
1 m2
自然之美要由整数来表示。例如：
奏出动听音乐的弦的长度应具有波长的整数倍。
这些问题，经典物理学不能给于解释。首先，经典物理学不能 建立一个稳定的原子模型。根据经典电动力学，电子环绕原子 核运动是加速运动，因而不断以辐射方式发射出能量，电子的 能量变得越来越小，因此绕原子核运动的电子，终究会因大量 损失能量而“掉到”原子核中去，原子就“崩溃”了，但是， 现实世界表明，原子稳定的存在着。除此之外，还有一些其它 实验现象在经典理论看来是难以解释的，这里不再累述。
量子力学课件第二章
2 dW ( p, t ) | c( p, t ) | dp t时刻粒子出现在动量 点附近 p dp体积元内的几率。
2.2 态叠加原理
若(r , t )是归一化的，则 p, t 也是归一化的 c
若 ( r , t ) ( r , t )dr 1
率成比例。
量子力学的第一条基本假定（或公设）
强度大 强度小 或为0 粒子出现 的概率大
粒子出现 的概率小
2.1 波函数的统计解释
假设衍射波用 (x) 描述，衍射花样的强度则用振
幅的平方
2 描述。就可以得到粒子在空间任意 ( r ) ( r ) ( r ) *
一点出现的概率。
波函数（概率幅）描写体系的量子状态（态或状态）
动量算符
2 2 i t 2m
2.3 薛定谔方程
三、力场中粒子的波函数方程
P2 力场中E U(r ) 2m P2 E 【 U(r )】 2m
p i，E i t
2 2 i (r , t ) [ U(r , t )] (r , t ) t 2m
波叠加原理称为态叠加原理。
解释电子双缝干涉
S1 Ψ= C1Ψ1 + C2Ψ2 也是电子可能状态。
电子源
Ψ1
P
S2
Ψ2
感 光 屏
空间找到电子的几率则是： |Ψ|2 = |C1Ψ1+ C2Ψ2|2
= (C1*Ψ1*+ C2*Ψ2*) (C1Ψ1+ C2Ψ2)
= |C1 Ψ1|2+ |C2Ψ2|2 + [C1*C2Ψ1*Ψ2 + C1C2*Ψ1Ψ2*]
薛定谔波动方程
2.2 态叠加原理
若(r , t )是归一化的，则 p, t 也是归一化的 c
若 ( r , t ) ( r , t )dr 1
率成比例。
量子力学的第一条基本假定（或公设）
强度大 强度小 或为0 粒子出现 的概率大
粒子出现 的概率小
2.1 波函数的统计解释
假设衍射波用 (x) 描述，衍射花样的强度则用振
幅的平方
2 描述。就可以得到粒子在空间任意 ( r ) ( r ) ( r ) *
一点出现的概率。
波函数（概率幅）描写体系的量子状态（态或状态）
动量算符
2 2 i t 2m
2.3 薛定谔方程
三、力场中粒子的波函数方程
P2 力场中E U(r ) 2m P2 E 【 U(r )】 2m
p i，E i t
2 2 i (r , t ) [ U(r , t )] (r , t ) t 2m
波叠加原理称为态叠加原理。
解释电子双缝干涉
S1 Ψ= C1Ψ1 + C2Ψ2 也是电子可能状态。
电子源
Ψ1
P
S2
Ψ2
感 光 屏
空间找到电子的几率则是： |Ψ|2 = |C1Ψ1+ C2Ψ2|2
= (C1*Ψ1*+ C2*Ψ2*) (C1Ψ1+ C2Ψ2)
= |C1 Ψ1|2+ |C2Ψ2|2 + [C1*C2Ψ1*Ψ2 + C1C2*Ψ1Ψ2*]
薛定谔波动方程
Chapter 2 The Schrodinger Equation 量子力学英文教案课件
The principle of the superposition state back
（1） The principle of the superposition state （2） The wave function in momentum space
ω( r, t )= {dW(r, t )/ dτ}= C |Ψ (r,t)|2
W(t)=∫V dW =∫Vω( r, t )dτ= C∫V|Ψ (r,t)|2 dτ
University of Electronic Science and Technology of China
2005-3-1
Prof. Zhang Xiaoxia©
back
Chapter 2 The Schrodinger Equation
The Interpretation of the Wave Function The principle of the superposition state Average value of dynamics quantity and Differential Operators Schrodinger Equation Time-independent Schrodinger Equation The Heisenberg Uncertainty Relation
p (r ,t)[2 1]3/2e i[p •r E]t p (r )e iEt
where
1
p(r)[2]3/2
i[p•r]
e
University of Electronic Science and Technology of China
2005-3-1
Prof. Zhang Xiaoxia©
量子力学ppt课件
To see a world in a grain of sand and a heaven in a wild flower Hold infinite in the palm of your hand and eternity in an hour.
一粒沙里有一个世界 一朵花里有一个天堂 把无穷无尽握于手掌 永恒宁非是刹那时光 (荷兰，乌仑贝克，1925年电子自旋发现者）
一． 黑体辐射问题
黑体：一个物体能全部吸收辐射在它上面的电磁波而无反 射。 热辐射：任何物体都有热辐射。 当黑体的辐射与周围物体处于平衡状态时的能量分布：
热力学+特殊假设→维恩公式, (长波部分不一致). 经典电动力学+统计物理学→瑞利金斯公式（短波部分完 全不一致） 二．光电效应
光照在金属上有电子从金属上逸出的现象，这种电子叫光 电子。光电效应的规律： （1）存在临界频率 ； （2）光电子的能量只与光的频率有关，与光强无关，光 频率越高，光电子能量越大，光强只影响光电子数目。光 强越大，光电子数目越多。
1921诺贝尔物理学奖
• A.爱因斯坦 • 对现代物理方面的
贡献，特别是阐明 光电效应的定律
二、爱因斯坦光量子理论
爱因斯坦在普朗克能量子论基础上进一步提出光量 子（或光子）的概念。辐射场是由光量子组成的，光 具有粒子特性，既有能量，又有动量。
光是以光速 c 运动的微粒流，称为光量子（光子）
光子的能量 h 说明光具有微粒性
m m0
1
v2 c2
h
n
c
h 0
c
n0
X
mv
0
2h m0c
sin2
2
康普顿散射公式
c
h m0c
一粒沙里有一个世界 一朵花里有一个天堂 把无穷无尽握于手掌 永恒宁非是刹那时光 (荷兰，乌仑贝克，1925年电子自旋发现者）
一． 黑体辐射问题
黑体：一个物体能全部吸收辐射在它上面的电磁波而无反 射。 热辐射：任何物体都有热辐射。 当黑体的辐射与周围物体处于平衡状态时的能量分布：
热力学+特殊假设→维恩公式, (长波部分不一致). 经典电动力学+统计物理学→瑞利金斯公式（短波部分完 全不一致） 二．光电效应
光照在金属上有电子从金属上逸出的现象，这种电子叫光 电子。光电效应的规律： （1）存在临界频率 ； （2）光电子的能量只与光的频率有关，与光强无关，光 频率越高，光电子能量越大，光强只影响光电子数目。光 强越大，光电子数目越多。
1921诺贝尔物理学奖
• A.爱因斯坦 • 对现代物理方面的
贡献，特别是阐明 光电效应的定律
二、爱因斯坦光量子理论
爱因斯坦在普朗克能量子论基础上进一步提出光量 子（或光子）的概念。辐射场是由光量子组成的，光 具有粒子特性，既有能量，又有动量。
光是以光速 c 运动的微粒流，称为光量子（光子）
光子的能量 h 说明光具有微粒性
m m0
1
v2 c2
h
n
c
h 0
c
n0
X
mv
0
2h m0c
sin2
2
康普顿散射公式
c
h m0c
量子力学教程课件
量子力学教程课件1. 简介量子力学是一门研究微观粒子行为的物理学分支，描述了微观世界的基本原理和规律。
本教程课件旨在介绍量子力学的基本概念、数学描述和常见应用，帮助学生深入理解和应用量子力学知识。
2. 量子力学基础2.1 波粒二象性介绍波粒二象性的基本概念，包括波动性和粒子性的相互转化，以及双缝实验等经典实例。
2.2 不确定性原理解释不确定性原理的概念和意义，说明无法同时准确确定粒子的位置和动量的原理。
2.3 波函数和 Schrödinger 方程介绍波函数的概念，以及薛定谔方程的基本形式和求解方法，引导学生理解波函数描述微观粒子的性质和行为。
3. 定态量子力学3.1 定态和定态方程介绍定态的概念，以及定态方程的推导和求解方法，帮助学生理解波函数与能量之间的关系。
3.2 算符和本征值问题解释算符和本征值问题的基本概念，包括算符的作用和本征函数的定义，引导学生掌握本征值问题的求解方法。
3.3 动量和位置算符介绍动量和位置算符的定义和性质，解释它们对应的本征函数和本征值，讨论动量-位置不确定性关系。
4. 哈密顿力学和波函数演化4.1 哈密顿量和状态演化解释哈密顿量的概念和物理意义，讨论波函数演化的基本原理，引导学生理解时间演化和态矢量的变化关系。
4.2 边界条件和量子力学稳定态探讨边界条件对量子力学系统稳定态的影响，以及波函数在无穷深势阱等特定势场中的求解。
4.3 时间演化和量子力学测量介绍时间演化算符的定义和性质，讨论量子力学测量的基本原理和微扰态的提取方法。
5. 特殊系统和量子力学应用5.1 含时量子力学引入含时量子力学的概念，解释含时薛定谔方程的物理意义，介绍准确求解和近似求解的方法。
5.2 简谐振子讨论简谐振子的基本性质和量子化过程，引导学生理解能级和激发态的概念。
5.3 氢原子和多电子系统介绍氢原子的量子力学描述和能级结构，讨论多电子系统的波函数形式和近似求解方法。
5.4 量子力学与量子信息探索量子力学与量子信息科学的联系，简要介绍量子计算、量子通信和量子加密等前沿应用。
量子力学ppt
里德伯 氢原子谱普适公式：
~
R( 1 m2
1)
n2
n m 1,m 2,
Balmer公式与观测结果的惊人符合，引起了光谱学家的注 意。紧接着就有不少人对光谱线波长（数）的规律进行了 大量分析，发现，每一种原子都有它特有的一系列光谱项 T(n)，而原子发出的光谱线的波数，总可以表成两个光谱 项之差
迈克尔逊－莫雷实验 是 物理史上最有名 的 “失败的 实验”
证明了以太不存在， 说明了光速在真空
的不变性。
图1.1 迈克尔逊-莫雷实验
二、固体与气体分子的比热
固体中每个原子在其平衡位置附近作小振动，可以看 成是具有三个自由度的粒子。按照经典统计力学，其平均 动能与势能均为3kT/2。因此，固体的定容比热为
维恩（Wien）由热力学的讨论，加上一些特殊的假设得出 一个分布公式，维恩公式：
d C1 3eC2 /T d
其中，C1, C2通过与实验数据对比得到
即随着温度升高，热辐射峰值向短波高频方向移动。
1700k
T m b
b 2.897103 m K
1500k 1300k
问：1 温度为室温20 ℃的黑体，其单色辐出度的峰值所
世纪之交实验物理学对理论物理学的挑战
1899年开尔文在欧洲科学家新年聚会的贺词中说： 物理学晴朗的天空上， 飘着两朵令人不安的乌云
迈克尔逊 —莫雷实验
光电效应
康普顿效应
黑体辐射
氢原子光谱
以太 相对论
量子力学
一、迈克耳逊—莫雷实验 （以太）
18-19世纪时，人们认为“真空”中存在 着一种无所不在的物体称为“以太”，光波 应该通过以太传播 。
~nm T (n) T (m)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
14
Once we have found the separable solutions, then, we can immediately construct a much more general solution, of the form
It so happens that every solution to the (time dependent) Schrödinger equation can be written in this form — it is simply a matter of finding the right constants (c1, c2, c3, c4, …）so as to fit the initial conditions for the problem at hand.
4
Now the left side is a function of t alone, and the right side is a function of x alone.
5
The only way this can be possibly be true is if both sides are in fact constant, we shall call the separation constant E. Then
But before we get to that we would like to consider further the question:
7
What’s so great about separable solution ?
可分离的解（即 (x,t)=(x) f(t) ）为何如此重要？
After all, most solutions to the (time-dependent)
The second equation [2.4] is called the time independent Schrödinger equation, we can go on further with it until the potential V(x) is specified.
The rest of this chapter will be devoted to solving the time-independent Schrödinger equation [2.4], for a variety of simple potentials.
Schrödinger equation do not take the form (x)f(t). We
will offer three answers — two of them physical and one mathematical:
8
NOTE: for normalizable solutions, E must be real (see Problem ).
15
You’ll see in the following sections how all this works out in practice, and in Chapter 3 we’ll put it into more elegant language, but the main point is this:
Question: How do you get (x,t) in the first place ? How do you go about solving the Schrödinger equation ?
3
In this Chapter，we assume that the potential (or potential energy function), V(x,t)=V(x), of the system, is independent of time t !!!
9
Nothing ever happens in the Stationary State (x,t) !10
11
Please distinguish the operator with “hat” (^) to its dynamical variable in Eq.[2.12].
12
Conclusion: A separable solution has the property that every measurement of the total energy is certain to return the value E.
(That’s why we chose that letter E for the separation constant.)
3. The general solution is a linear combination of separable solutions
13
Now the (time-dependent) Schrödinger equation (Eq. 1.1) has the property that any linear combination5 of solutions is itself a solution.
Outline
1
整体概况
+ 概况1
您的内容打在这里，或者通过复制您的文本后。
概况2
+ 您的内容打在这里，或者通过复制您的文本后。
概况3
+ 您的内容打在这里，或者通过复制您的文本后。 2
In Chapter 1, we have studied a lot about the wave function and how you use it to calculate various quantities of interest.
Separation of variables has turned a partial differential
equation into two ordinary differential equations (Eq.
[2.3] and [2.4]).
6
The first equation [2.3] is easy to solve, the general solution of Eq.[2.3] is
Once we have found the separable solutions, then, we can immediately construct a much more general solution, of the form
It so happens that every solution to the (time dependent) Schrödinger equation can be written in this form — it is simply a matter of finding the right constants (c1, c2, c3, c4, …）so as to fit the initial conditions for the problem at hand.
4
Now the left side is a function of t alone, and the right side is a function of x alone.
5
The only way this can be possibly be true is if both sides are in fact constant, we shall call the separation constant E. Then
But before we get to that we would like to consider further the question:
7
What’s so great about separable solution ?
可分离的解（即 (x,t)=(x) f(t) ）为何如此重要？
After all, most solutions to the (time-dependent)
The second equation [2.4] is called the time independent Schrödinger equation, we can go on further with it until the potential V(x) is specified.
The rest of this chapter will be devoted to solving the time-independent Schrödinger equation [2.4], for a variety of simple potentials.
Schrödinger equation do not take the form (x)f(t). We
will offer three answers — two of them physical and one mathematical:
8
NOTE: for normalizable solutions, E must be real (see Problem ).
15
You’ll see in the following sections how all this works out in practice, and in Chapter 3 we’ll put it into more elegant language, but the main point is this:
Question: How do you get (x,t) in the first place ? How do you go about solving the Schrödinger equation ?
3
In this Chapter，we assume that the potential (or potential energy function), V(x,t)=V(x), of the system, is independent of time t !!!
9
Nothing ever happens in the Stationary State (x,t) !10
11
Please distinguish the operator with “hat” (^) to its dynamical variable in Eq.[2.12].
12
Conclusion: A separable solution has the property that every measurement of the total energy is certain to return the value E.
(That’s why we chose that letter E for the separation constant.)
3. The general solution is a linear combination of separable solutions
13
Now the (time-dependent) Schrödinger equation (Eq. 1.1) has the property that any linear combination5 of solutions is itself a solution.
Outline
1
整体概况
+ 概况1
您的内容打在这里，或者通过复制您的文本后。
概况2
+ 您的内容打在这里，或者通过复制您的文本后。
概况3
+ 您的内容打在这里，或者通过复制您的文本后。 2
In Chapter 1, we have studied a lot about the wave function and how you use it to calculate various quantities of interest.
Separation of variables has turned a partial differential
equation into two ordinary differential equations (Eq.
[2.3] and [2.4]).
6
The first equation [2.3] is easy to solve, the general solution of Eq.[2.3] is