第三届学院杯大学生数学竞赛
全国大学生数学建模竞赛级一等奖队长

荣誉称号社会工作其他加分学术科研学术竞赛社会实践经济统计15220142201649顾玲云经济统计班团支书/2017.2至今(半年) 0.10.51.全国大学生数学建模竞赛省级一等奖(队长)0.6 2.美国大学生数学建模竞赛M奖,按省级二等奖计算(队长)0.361.56经济统计15220142201577曹梦宇厦门大学2014级本科生经济统计班班长/2015.9至今0.40.52016全国大中专学生暑期“三下乡”社会实践优秀团队,(国家级,队员)0.31.2经济统计15220142201743李泽为0.5全国大学生福建省数学建模竞赛(队长)0.61.1经济统计15220142202099朱芸0.5第三届“大智慧杯”全国大学生金融精英挑战赛三等奖(队员) 0.81.3经济统计15220142201686黄砾览0.51.美国大学生数学建模大赛H奖,按省级三等奖计算 (队长)0.242.全国大学生数学建模大赛省级一等奖(队长)0.63.大学生创新创业训练项目,团体项目未结项,按国家级二等奖减半两次,队员 0.251.59总分德育加分(满分2分)学术科研、竞赛级社会实践加分(满分3分)专业学号姓名经济统计15220142201767林伟杰统计系团学联学术部部长/2016.9-2017.7 0.20.52016年大学生创新创业训练项目国家级立项,团体项目已结项,按国家级二等奖减半一次,队员 0.51.2经济统计 15220142201642高超平经济学院就业促进中心求职培训部部长/2016.6-2017.6 0.20.50.7经济统计15220142201791刘欣然统计系团学联文体部部长/2016.9-2017.7 0.20.50.7经济统计15220142202122张蕴涵1.统计系团学联青工部部长/2016.7至今 0.20.50.7经济统计15220142201829潘宇阳0.52016年全国大学生数学建模竞赛省级二等奖(队长) 0.360.86经济统计15220142201630邓美玲经济学院青年志愿者协会管理长服务部部长/2016.90.20.5全国大学生数学建模竞赛省级一等奖(队长)0.61.3经济统计15220142201619成安琪0.5大学生创新创业训练项目国家级立项,团体项目未结项,按国家级二等奖减半两次,队员 0.250.75经济统计15220142201703姜佳佳0.51.2016年全国大学生数学建模竞赛省级一等奖(队长) 0.62.2017年美国大学生数学建模大赛H等奖,按省级三等奖计算(队员)0.2; 3.2017年大学生创新创业训练项目省级立项,团体项目未结项,按省级二等奖减半两2016年“调研中国——大学生社会调查奖学金”三等奖,按省级三等奖计算,团队队员0.061.51经济统计15220142201700贾若凡0.51.2016年全国大学生数学建模竞赛省级一等奖 0.52.2017年美国大学生数学建模大赛H奖,按省级三等奖计算(队员) 0.21.2经济统计15220142201793刘雪莹0.50.5数理统计15220142201765林诗雅0.51.2016年全国大学生数学建模竞赛省级一等奖 0.62.2017年美国大学生数学建模大赛H奖,按省级三等奖计算(队员) 0.22016年“调研中国——大学生社会调查奖学金”三等奖,按省级三等奖计算,团队队员1.36数理统计15220142201862宋戈0.52016年全国大学生数学建模竞赛省级一等奖 0.61.1数理统计15220142201809罗含笑2016-2017学年统计系团学联记者团部长 0.20.5美国大学生数学建模大赛M奖,按省级二等奖计算(队员) 0.31数理统计15220142201756林嘉文0.5数理统计15220142201770林昕宜0.51.2016年全国大学生数学建模竞赛省级一等奖 0.62.大学生创新创业训练项目国家级立项,团体项目已结项,按国家级二等奖减半一次,队员 0.51.6数理统计15220142201719李翀宇0.51.第七届全国大学生数学竞赛国家级三等奖 0.82.2016年高教社杯全国大学生数学建模竞赛国家级一等奖 0.92.2数理统计15220142201931王智博0.51.2016年高教社杯全国大学生数学建模竞赛国家级一等奖 0.91.4数理统计15220142201909王姜0.52016年高教社杯全国大学生数学建模竞赛国家级二等奖(队长) 0.61.1数理统计15220142202101朱正天0.51.论文《车道占用状态下城市道路通行能力的研究》(一般CN)0.032.论文《中国户籍人口城镇化空间分异和机制研究》(一般CN)0.032016-2017学年大学生创新创业训练项目国家级立项,团体项目未结项,(队长) 0.30.86数理统计15220142201758林金镇0.51.2016年全国大学生数学建模竞赛省级一等奖(队长) 0.6;2. 2015-2016学年大学生创新创业训练项目国家级立项,团体项目已结项,按国家级二等奖减半一次,队长 0.6 ;3.2016-2017学年大学生创新创业训练项目省级立项,团体项目未结项,按省级二等奖减半两次,队长 0.181.2016年南风窗调研中国项目三等奖,按省级三等奖计算(队长)0.362.24数理统计15220142201828潘柯羽1.经济学院2014级5班班长/2014.9-2015.7 0.22.统计系2014级本科生党支部/2015.7至今 0.40.5 1.1。
全国大学生数学竞赛上海赛区获奖名单

全国大学生数学竞赛上海赛区获奖名单近日,第15届全国大学生数学竞赛上海赛区比赛结束。
本次比赛由上海市教育委员会主办,上海市教育发展基金会、上海市市场监督管理局、上海师范大学数学科学学院和上海市科学技术协会共同承办。
全国大学生数学竞赛是国家教育部高等教育司、教育部高等学校数学与统计学科教学指导委员会组织的一项大型综合性教学竞赛活动,旨在激发学生数学科学研究热情、培养学生数学分析解题能力,增强学生创新意识和实践能力,以及促进全国大学生数学科学教育的发展。
本次比赛共招募上海市全部大学393所,参赛选手达2.7万余人,参赛队伍达1.5万支。
本次比赛考察了数学共性知识和数学基本运算能力,以及初等函数、初等数论、线性代数、概率论、微积分初级、数据结构、计算机科学等方面的数学科学素养。
比赛结果非常平均,参赛者高水平表现得到了表彰。
此次评选活动,上海赛区共推荐400余人,获奖名单如下:一等奖:胡佳(上海外国语大学)、林颖(华东理工大学)、钟航(上海大学)二等奖:张嘉怡(上海理工大学)、吴钥(上海财经大学)、卫妍(华东师范大学)三等奖:李杰(上海师范大学)、黄韵(华东政法大学)、陈云(上海交通大学)优胜奖:刘昊(上海外国语大学)、苏柯泽(同济大学)、陈弈(上海大学)参赛者获奖名单中,不仅有来自上海各大学的学子,还有一些来自全国各个城市的参赛者。
他们在精心准备、认真训练的基础上,都以极高的水平参赛,出色地完成了比赛,获得了各自的成绩,受到了广泛的肯定与关注。
从本次比赛中可以看到,大学生们在探索与学习数学的道路上,拥有良好的心态、高度的热情与进取的气概,并取得了突出的成绩,这鼓舞着我们更加致力于深入探索数学之美,努力提高数学水平。
随着社会对科技创新和创业能力的日益需求,数学作为基础科学,其研究与发展所带来的重要性和意义有增无减,未来科技创新的成功必将离不开数学的支撑。
期望本次比赛为学生架起一座桥梁,让他们在比赛的过程中深入探究和发现数学之美,不断提升技能,实现潜能发挥,以及团结协作的品质,为今后的科技创新打下更加坚实的基础。
大学数学的比赛策划书3篇

大学数学的比赛策划书3篇篇一《大学数学的比赛策划书》一、活动背景随着大学教育的不断发展,数学作为一门基础学科,对于培养学生的逻辑思维、创新能力和解决问题的能力具有重要意义。
为了激发学生对数学的兴趣,提高学生的数学素养,特举办此次大学数学比赛。
二、活动目的1. 激发学生对数学的兴趣,提高学生的学习积极性。
2. 增强学生的数学思维能力和创新能力。
4. 选拔优秀学生,为学校参加更高级别的数学竞赛储备人才。
三、活动主体全体在校大学生四、比赛时间及地点[具体比赛时间][具体比赛地点]五、比赛内容1. 高等数学:极限、导数、积分等。
2. 线性代数:矩阵、行列式、线性方程组等。
3. 概率论与数理统计:概率、随机变量、统计推断等。
六、比赛形式1. 初赛:采用笔试形式,主要考查学生对基础知识的掌握程度。
2. 决赛:采用现场答题形式,包括必答题、抢答题、风险题等,综合考查学生的数学素养和应变能力。
七、活动流程1. 宣传阶段通过学校官网、公众号、班级群等渠道进行广泛宣传,吸引更多学生参加比赛。
2. 报名阶段学生在规定时间内填写报名表格,提交至指定地点或。
3. 初赛阶段组织参赛学生进行笔试,根据成绩选拔出进入决赛的选手。
4. 决赛阶段(1)组织进入决赛的选手进行现场比赛。
(2)邀请专业教师担任评委,对选手的表现进行评分。
(3)根据评分结果,评选出一等奖、二等奖、三等奖和优秀奖。
5. 颁奖阶段举行颁奖典礼,对获奖选手进行表彰和奖励。
八、奖项设置1. 一等奖:[X]名,奖金[X]元,荣誉证书。
2. 二等奖:[X]名,奖金[X]元,荣誉证书。
3. 三等奖:[X]名,奖金[X]元,荣誉证书。
4. 优秀奖:[X]名,荣誉证书。
九、活动预算1. 奖金:[具体金额]元。
2. 证书制作费:[具体金额]元。
3. 宣传费:[具体金额]元。
4. 其他费用:[具体金额]元。
十、注意事项1. 比赛过程中,要确保公平、公正、公开。
2. 工作人员要认真负责,做好各项组织工作。
北京工业大学教务处
北京工业大学教务处
工大教发[2007] 007号关于发布《北京工业大学认定的本科生科技竞赛项目名单》的通知
为配合《北京工业大学本科生科技竞赛管理办法》(工大发…2007‟11号)、《北京工业大学本科生创新学分实施办法》(工大教发 [2007] 005号)、《北京工业大学推荐优秀应届本科毕业生免试攻读硕士学位研究生的实施办法》(工大教发 [2007] 006号)等文件的实施,现发布北京工业大学认定的本科生科技竞赛项目名单。
北京工业大学认定的本科生科技竞赛项目名单
本文解释权在教务处。
教务处、校团委、学生处、研究生部、党委研究生工作部
2007年5月25日。
大学生可以参加地竞赛汇总情况
大学生可以参加的竞赛文案大全文案大全文案大全注:加黑赛事为教育部资助的九大赛事,上面共有八个,还有一个是全国大学生英语竞赛。
文案大全文案大全重庆大学大学生课外科技创新实践活动一览表文案大全文案大全注:1 含(*)赛事为教育部资助的九大赛事,上面共有 6个,还有“挑战杯”大学生课外学术科技作品竞赛、中国MEMS传感器应用大赛、全国大学生物流设计大赛。
2 加黑赛事为在机械学子关注较多、有广泛参与度的比赛。
重点项目竞赛的介绍及获奖情况主要分为三类,一.实践类1.国家大学生创新训练项目该项目隶属于国家大学生创新创业训练计划(原名“国家大学生创新性实验计划”)。
国家大学生创新训练项目是教育部为推动创新性人才培养工作的一项重要举措,是国家直接面向大学生组织开展的自主性、探索性、过程性、协作性和学科性的创新训练项目。
该计划项目的开展旨在探索并建立以问题和课题为核心的教学模式,倡导以本科学生为主体的创新性实验教学改革,调动学生的主动性、积极性和创造性,激发学生的创新思维和创新意识,掌握分析问题、解决问题的方法,培养学生从事科学研究和创造发明的素质,提高其创新实践的能力。
文案大全学生以个人或团队形式开展项目申请,每队人数最多不超过3人。
项目申报对象主要为学习成绩优良(或个别有特长)、学有余力、项目开展期间为2、3年级(五年制本科为2-4年级)的在校本科学生,申报项目的学生必须符合以下条件之一:(1)、弘深学院学生;(2)、课程成绩平均分值≥ 70 ,平均学年重修课程数不得多于 1 门,学有余力的学生;(3)、不满足1、2条中任何一条,但个别有特长的学生,经审查批准后可参加申报。
目前我校已连续开展六届,立项项目近400项,参与学生1100余人。
2.大学生科研训练计划“重庆大学大学生科研训练计划”( students research training program ,简称 SRTP ),是学校面向全校本科生开展的一项创新教育计划,是学校创新体系的重要组成部分。
2013年全国大学生数学建模竞赛国家奖获奖名单

天津
天津职业技术师范大学
苏静
刘梦楠
宋垚
曲克杰
22
天津
天津商业大学
王彦清
常丹丹
张剑
李景焕
23
天津
军事交通学院
王学全
王作夫
刘金鹏
李梅英
24
天津
军事交通学院
邹梦
张龙
丁帅毅
郭彦
25
天津
南开大学
郑皓珺
周玉
马磊
王奎
26
天津
南开大学
李栩
李紫珅
刘炜男
27
河北
华北电力大学
汤潘
邓睿
臧晓玲
孔倩
28
2013高教社杯全国大学生数学建模竞赛获奖名单(本科组)
全国大学生数学建模竞赛组委会
2013年11月23日
本科组高教社杯获得者:刘世尧、王钰聪、李文然(厦门大学)
本科组MATLAB创新奖获得者:向航、王帆、郭树璇(国防科技大学)
本科组IBM SPSS创新奖获得者:周晨阳、周登岳、孔垂烨(北京理工大学)
冯艳
万建
贺衎
36
山西
中北大学
薛志强
王立超
廖金明
肖亚峰
37
山西
运城学院
郑路通
杨雯雯
陶佳琪
买阿丽
38
内蒙古
内蒙古大学
李美玲
张楠
李小平
何斯日古楞
39
内蒙古
河套学院
关美玲
李伟
王泽奇
成乐
40
辽宁
大连海事大学
黄春龙
贾晓岩
王义
教师组
41
辽宁
指导学生获得的成果数奖项

王飞
王福娟、 雷宏香
王自鑫
曾剑
LabVIEW虚拟仪器测量远程管理共享 系统
黄家政
光偏振态实时检测系统
蔡文睿
无线电灯的设计与制作 电动摆钟
朱允中 蒲岭 曾海强 黎英龙
徐前 杨康明 曾万 祺
2009 2008 2008 2008 2008
2009年国家专利
国家专利局
NI2008年毕业设计竟赛鼓励奖 美国国家仪器公司院校市场部 蔡志岗
肖俊.黄瑞祺.李恭檀
无线电灯的设计与制作
张煜彬
2009年世界大学生数学建模竞赛
吴聪、许弘毅、朱晨 卉
第七届广东省大学生程序设计竞赛
刘雪涛、邓智平、邓 伟明
第七届广东省大学生程序设计竞赛 李鹏程
全国大学生电子设计大赛广东省赛区
洪梅华.李佳明.蔡晓 绪
广东省大学生课外学术科技作品竞赛
方耀铭.邓海标.林庆 港.徐铎雄等
广东省物理学会
周建英
基础性实验项目
刘美壮
2012年12月
2012年全国大学生物理实验竞赛 三等奖
高等学校国家级实验教学示范 中心联席会,第二届全国大学 沈 生物理实验竞赛组委会
韩
地下自来水管爆裂处的定位
杨斯媚、苏晓君、李 娟
2012年11月
广东省第十三届大学生物理实验 设计大赛一等奖
广东省物理学会
谢向生、 周张凯
雷东玮 范锡添 江 嘉文
基于LabVIEW的多路光信号测量系统 刘玉县、刘关玉、雷
设计
卉、刘建业、蔡志岗
利用开关电路驱动的小功率高效无线 朱允中、蒲岭、曾海
能量传输系统
强、黎英龙、沈韩
基于激光多普勒效应的激光测速装置 孙双鹏、李菲、吴万
09-13全国大学生高等数学竞赛真题及答案(非数学类)-无答案

一、填空题(每小题 5 分,共 20分)
(x y) ln(1 y )
1.计算 D
x dxdy ____________,其中区域 D 由直线 x y 1 与 1x y
两坐标轴所围成三角形区域.
2.设 f (x) 是连续函数,且满足 f (x) 3x2 2 f (x)dx 2 , 则 f (x) ____________. 0
3.曲面 z x22 y 2 2 平行平面 2x 2 y z 0 的切平面方程是__________.
4.设函数 y y(x) 由方程 xe f ( y) d2 y ________________. dx 2
ey ln 29确定,其中 f 具有二阶导数,且 f
1 ,则
二、(5 分)求极限 lim( ex e2x
2.证明广义积分
0
sin x
x
dx
不是绝对收敛的
3.设函数 y y x 由 x3 3x2 y 2 y3 2 确定,求 y x 的极值。
4.过曲线 y 3 x x 0 上的点 A 作切线,使该切线与曲线及 x 轴所围成的平面图形 3
的面积为 4 ,求点 A 的坐标。
二、(满分 12)计算定积分 I
x sin x arctan ex dx 1 cos2 x
三 、( 满 分 12 分 ) 设 f x 在 x 0 处 存 在 二 阶 导 数 f 0 , 且
lim f x x0 x
0 。证明 :级数 f 1 收敛。
n1
n
四 、( 满 分 12 分 ) 设 f x
b
sin f x dx
2
a
m
,f x
0a x b,证 明
第三届全国大学生数学竞赛非数学类预赛试卷评分标准

2
……………………………2 分 ………………………4 分
sgn( xy 1)dxdy dxdy
D D3
dxdy 2 4 ln 2 .
………………………6 分
D2 D3
4. 求幂级数
2n 1 2 n 2 2n 1 的和函数,并求级数 的和. x 2 n 1 n 2 n 1 2 n 1
…………………2 分
|d | a2 b2 c2
设平面 Pu : u .Βιβλιοθήκη …………………………5 分
ax by cz a2 b2 c2
第三届全国大学生数学竞赛预赛试卷 参考答案及评分标准 (非数学类,2011)
一、 (本题共 4 小题,每题 6 分,共 24 分)计算题
(1 x) x e 2 (1 ln(1 x)) 1. lim . x 0 x
解:因为
2
(1 x) e (1 ln(1 x)) e = x
n
2. 如果存在正整数 p,使得 lim( an p an ) ,则 lim
an . n n p
证明:1. 由 lim an a , M 0 使得 | an | M ,且 0, N1 ,当 n > N1 时,
n
2 N ( M | a |) 因为 N 2 N1 ,当 n > N2 时, 1 . n 2
2 2 2
I f ( ax by cz ) dS . 求证: I 2 f ( a 2 b 2 c 2 u )du
1
1
解:由 的面积为 4 可见:当 a, b, c 都为零时,等式成立. 当它们不全为零时, 可知:原点到平面 ax by cz d 0 的距离是
第三届丘成桐大学生数学竞赛试题-概率统计及应用数学

3. Suppose that {p(i, j) : i = 1, 2, · · · , m; j = 1, 2, · · · , n} is a finite bivariate joint probability distribution, that is,
mn
p(i, j) > 0,
p(i, j) = 1.
i=1 j=1
(i) Can {p(i, j)} be always expressed as
p(i, j) = λkak(i)bk(j)
k
for some finite λk ≥ 0,
0,
n j=1
bk(j)
=
1?
k λk = 1, ak(i) ≥ 0,
1
m i=1
ak(i)
=
1,
bk(j) ≥
2
function f (x) near a point x given K points xk around x in R, k ∈ [1, · · · , K].
K
(2)
min
Px∈Πm
k=1
|Px(xk)
−
fk |2
where fk = f (xk), Πm is the space of polynomials of degree less or equal to m, i.e.
第三届丘成桐大学生数学竞赛试题概率统计及应用数学
INDIVIDUAL TEST S.-T YAU COLLEGE MATH CONTESTS 2012
Probability and Statistics
Please solve 5 out of the following 6 problems, or highest scores of 5 problems will be counted.
第三届全国大学生数学竞赛决赛解答

第三届全国大学生数学竞赛决赛试卷 (非数学类,2012)时间150分钟,满分100分一、(本大题共5小题,每小题6分,共30分)计算下列各题(要求写出重要步骤)(1)xx xx x x 222220sin cos sin lim -→ 解:422222330222220)](21[)](6[lim sin cos sin lim x x o x x x o x x x x x x x x x +--+-=-→→ 32)(32l i m 4440=+=→x x o x x (2)]1)1tan 2[(lim 613x e xx x x x +--++∞→解:原式]1)2[(lim 613x e xx x x +-+=+∞→366332203620)](21[)](621)[211(lim 1)211(lim tt o t e t o t t t t t te t t t t t ++-+++++=+-+=++→→ +∞=。
或+∞=+-++=+-+=++→→36520362013)211(lim 1)211(lim tt t e t t t t e t t t tt (3)设函数),(y x f 有二阶连续偏导数,满足0222=+-xx y xy y x yy x f f f f f f f ,且0≠y f ,),(z x y y =是由方程),(y x f z =所确定的函数,求22xy∂∂。
解:yx f f x y-=∂∂ 222)]([)]([y yx yy yx x y x xy xx y f f f f f f f f f f f x y -+--+-=∂∂02322=+--=yxxy xy y x yy x ff f f f f f f(4)求不定积分⎰+-+=dx e xx I x x 1)11(。
解:⎰⎰⎰++++=-+=x x xx xx xde dx e dx e xx I 111)11(C xedx exedx exx xx xx xx +=-+=++++⎰⎰1111(5)求曲面az y x =+22和)0(222>+-=a y x a z 所围立体的表面积。
2011年第三届全国大学生数学竞赛(浙江赛区)各类奖项公布

2011年第三届全国大学生数学竞赛(浙江赛区)各类奖项公布各高等院校:2011年第三届全国大学生数学竞赛的考试、阅卷、遴选等工作已经顺利结束。
经第三届全国大学生数学竞赛委员会评定,我省共906名同学分获由中国数学会普及工作委员会颁发的第三届全国大学生数学竞赛(浙江赛区)一等奖、二等奖及三等奖。
经浙江省数学会高等学校竞赛工作小组评定,我省共954名学生获由浙江省数学会颁发的第三届全国大学生数学竞赛(浙江赛区)优胜奖,共21个竞赛指导(辅导)小组获优秀指导小组奖。
现将获奖名单公布如下(学校名称按拼音排序,姓名排序不分先后):数学专业获奖名单一等奖(共22人)序号 姓名 学校名称 序号姓名 学校名称1陈祥升宁波大学12周远浙江理工大学2刘新亮宁波大学13冯汉浙江师范大学3章宏睿宁波大学14顾雪花浙江师范大学4李瑜苗宁波工程学院15康晓强浙江师范大学5吕吴俊温州大学瓯江学院16李卫星浙江师范大学6刘剑波浙江工商大学17郦莎莎浙江师范大学7赵亮浙江工商大学18钟杰浙江师范大学8赵荣杰浙江工商大学19周洁浙江师范大学9张克克浙江工业大学20伊燕瑛中国计量学院10张铭杰浙江工业大学21张颖浙江大学11赵琦浙江工业大学22王六权浙江大学二等奖(共41人)序号 姓名 学校名称 序号姓名 学校名称1何波禄杭州师范大学11孟海红绍兴文理学院2吴应富杭州师范大学12宋一威绍兴文理学院3张斌敏杭州师范大学13吴阳洋绍兴文理学院4张海燕杭州师范大学14卢周扬温州大学5雷成宝湖州师范学院15宓清洁温州大学6郭晋瑞宁波大学16王崇潮温州大学7徐森荣宁波大学17於家海温州大学8丁钰宁波工程学院18陈建海浙江工业大学9陈洁绍兴文理学院19陈伟浙江工业大学10陈达宝绍兴文理学院20何秀秀浙江工业大学21楼雄鹏浙江工业大学32吴雯浙江师范大学22王福东浙江工业大学33徐夙莹浙江师范大学23严杭统浙江工业大学34赵旖旎浙江师范大学24季伟平浙江海洋学院35张文杰中国计量学院25许平浙江海洋学院36侯俊哲浙江大学26杨超浙江海洋学院37郭政扬浙江大学27王学士浙江理工大学38钱炜浙江大学28邢伟超浙江理工大学39咸晓晨浙江大学29方倩倩浙江师范大学40肖其昌浙江大学30钱芳浙江师范大学41张寒煜浙江大学31吴芬芬浙江师范大学三等奖(共70人)序号 姓名 学校名称 序号姓名 学校名称 1蔡莎莎杭州师范大学29孙勘洲温州大学2冯姗姗杭州师范大学30徐晶温州大学3张康康杭州师范大学31林敬航浙江工商大学4朱卉杭州师范大学32孙正杰浙江工商大学5黄杰湖州师范学院33汪婉浙江工商大学6金志彬湖州师范学院34常帅浙江工业大学7朱秀珠湖州师范学院35丁佳丽浙江工业大学8刘君楼宁波大学36丁凌云浙江工业大学9刘丽君宁波大学37龚德伟浙江工业大学10浦东宁波大学38何艳超浙江工业大学11唐琪宁波大学39李浩浙江工业大学12徐其林宁波大学40罗雨欣浙江工业大学13余海松宁波大学41倪惠宏浙江工业大学14张海红宁波大学42任佳萍浙江工业大学15张庭兔宁波大学43余伟栋浙江工业大学16陈辉绍兴文理学院44虞焚博浙江工业大学17陈科成绍兴文理学院45张敏凯浙江工业大学18陈茂亮绍兴文理学院46周婷婷浙江工业大学19胡恺峥绍兴文理学院47胡坚强浙江海洋学院20胡永刚绍兴文理学院48代成雷浙江科技学院21厉洁绍兴文理学院49杜丽晴浙江科技学院22刘琦绍兴文理学院50林崇崇浙江科技学院23袁海明绍兴文理学院51邢浙斌浙江科技学院24臧如玉绍兴文理学院52李帅芳浙江理工大学25陈增儿温州大学53连丽花浙江理工大学26戴康顺温州大学54王明杰浙江理工大学27黄明海温州大学55伍凤华浙江理工大学28厉莉蔓温州大学56周楠浙江理工大学57何呈斌浙江师范大学64唐秦飞中国计量学院58黄城辉浙江师范大学65姚云锋中国计量学院59黄贤录浙江师范大学66薄乐阳浙江大学60潘驰宇浙江师范大学67雷琦浙江大学61王小英浙江师范大学68潘人可浙江大学62张智慧浙江师范大学69郦言浙江大学63曹虎中国计量学院70梁宇晨浙江大学省优胜奖(共179人)序号 姓名 学校名称 序号姓名 学校名称 1曹仁凤杭州师范大学32周阳杭州师范大学2陈红燕杭州师范大学33管丹凤湖州师范学院3陈慧娟杭州师范大学34周静湖州师范学院4陈小翠杭州师范大学35彭绍林嘉兴学院5陈燕玲杭州师范大学36温春玲嘉兴学院6杜姗姗杭州师范大学37戴承惠丽水学院7方辉芳杭州师范大学38何标丽水学院8何露叶杭州师范大学39唐增艳丽水学院9何舒婷杭州师范大学40徐春杰丽水学院10蒋金妙杭州师范大学41陈见娃宁波大学11景玲雪杭州师范大学42董嵩柏宁波大学12李涛杭州师范大学43胡慧宁波大学13骆明旭杭州师范大学44李丹宁波大学14马安庆杭州师范大学45李婷宁波大学15毛妍杭州师范大学46林助花宁波大学16茅雪纯杭州师范大学47马科杰宁波大学17邱炀燕杭州师范大学48施燕芬宁波大学18阮雪琦杭州师范大学49唐岱宁波大学19沈佳骊杭州师范大学50王春宇宁波大学20施莹莹杭州师范大学51王根男宁波大学21孙毛瑾杭州师范大学52王晖宁波大学22汪玲杭州师范大学53王微微宁波大学23王红艳杭州师范大学54武新宇宁波大学24王文玲杭州师范大学55姚凯飞宁波大学25王燕玲杭州师范大学56俞丹盛宁波大学26王颖杭州师范大学57张文宁波大学27吴思宜杭州师范大学58赵炜婧宁波大学28吴越舟杭州师范大学59吴继鹏宁波工程学院29严玲俏杭州师范大学60吴玉明宁波工程学院30张丹玲杭州师范大学61张冰清宁波工程学院31张忆颖杭州师范大学62何阿红温州大学瓯江学院序号 姓名 学校名称 序号序号 姓名 63叶琼琼温州大学瓯江学院105桑茂原浙江工业大学64袁苗温州大学瓯江学院106施林坚浙江工业大学65包志鹏绍兴文理学院107杨洋浙江工业大学66池海啸绍兴文理学院108张里博浙江工业大学67胡静绍兴文理学院109张巧浙江工业大学68李望绍兴文理学院110张雄江浙江工业大学69骆介斌绍兴文理学院111章琦浙江工业大学70毛露露绍兴文理学院112周烨浙江工业大学71梅茜茜绍兴文理学院113朱琴浙江工业大学72孙厦绍兴文理学院114钱琳瑞浙江海洋学院73王晓燕绍兴文理学院115应超浙江海洋学院74王依盈绍兴文理学院116周利浙江海洋学院75朱月明绍兴文理学院117单夏军浙江科技学院76方伟温州大学118宋晨翔浙江科技学院77侯晓蒙温州大学119孙盼浙江科技学院78黄锦温州大学120吴昌烽浙江科技学院79金佩蒙温州大学121应金申浙江科技学院80施珊龙温州大学122凤萍浙江师范大学81郑太丽温州大学123甘珍珍浙江师范大学82金梦琦浙江工商大学124胡江泽浙江师范大学83梁云峰浙江工商大学125胡丽微浙江师范大学84刘帅浙江工商大学126金治豪浙江师范大学85倪正华浙江工商大学127郎杰浙江师范大学86危璐燕浙江工商大学128李特浙江师范大学87许玉完浙江工商大学129李以孝浙江师范大学88杨爱丽浙江工商大学130刘立群浙江师范大学89易青山浙江工商大学131陆磊波浙江师范大学90张乐孝浙江工商大学132陆秧浙江师范大学91蔡建光浙江工业大学133罗意娜浙江师范大学92陈冲浙江工业大学134马金艳浙江师范大学93陈颖浙江工业大学135潘志浙江师范大学94程路尹浙江工业大学136钱灵芝浙江师范大学95董建狄浙江工业大学137邱佳辉浙江师范大学96杜飞航浙江工业大学138邵媛媛浙江师范大学97杜镇辉浙江工业大学139施晓明浙江师范大学98冯健俊浙江工业大学140史宽宽浙江师范大学99何玉婷浙江工业大学141王洁浙江师范大学100黄越翱浙江工业大学142王启蒙浙江师范大学101罗骏辉浙江工业大学143王智宇浙江师范大学102钱航永浙江工业大学144吴旻诚浙江师范大学103钱丽庆浙江工业大学145徐丽峰浙江师范大学104任海燕浙江工业大学146徐晓鹏浙江师范大学序号 姓名 学校名称 序号姓名 学校名称147许桑桑浙江师范大学164李斌中国计量学院148严瑾浙江师范大学165戚天兰中国计量学院149叶勤军浙江师范大学166陈婷婷浙江大学150叶鑫安浙江师范大学167关任浙江大学151应洁浙江师范大学168王俊浙江大学152应晓笑浙江师范大学169周轶柯浙江大学153张佳莲浙江师范大学170王昌翰浙江大学154张林晨浙江师范大学171孔艳阳浙江大学155章卫星浙江师范大学172任之乐浙江大学156赵燕波浙江师范大学173童赫扬浙江大学157郑利达浙江师范大学174夏羽浙江大学158郑娜浙江师范大学175杨文青浙江大学159周亚君浙江师范大学176杨程然浙江大学160祝曦俊浙江师范大学177陈曦浙江大学161方赢海中国计量学院178楼子璐浙江大学162国金宇中国计量学院179罗俊杰浙江大学163胡荷萍中国计量学院非数学专业获奖名单一等奖(共155人)序号 姓名 学校名称 序号姓名 学校名称1褚宏锋杭州师范大学21张佳斌宁波大学2李冰杭州师范大学22朱俊翔宁波大学3马梅娇杭州师范大学23朱林圆宁波大学4倪挺杭州师范大学24孙强宁波大学科学技术学院5田蕾杭州师范大学25廖靖斌宁波工程学院6冯志军嘉兴学院26王杭成宁波工程学院7黄凯嘉兴学院27郑润宁波工程学院8林文武丽水学院28刘万波绍兴文理学院9陈蕾宁波大学29郑扬台州学院10高飞宁波大学30邱忠洋温州大学11韩泽文宁波大学31魏杰温州大学12黄国勋宁波大学32吴建温州大学13李敏钰宁波大学33周浩温州大学14刘峥强宁波大学34曹文文浙江传媒学院15钱凯宁波大学35戚宏健浙江传媒学院16宋克兰宁波大学36曹蔚浙江工商大学17王江良宁波大学37顿倩浙江工商大学18王琪宁波大学38蒋梦琪浙江工商大学19吴国林宁波大学39蒋汝婷浙江工商大学20于升杰宁波大学40林智同浙江工商大学41刘丽君浙江工商大学84朱治亮浙江工业大学42刘余钱浙江工商大学85段超浙江海洋学院43陆春君浙江工商大学86苏腾云浙江海洋学院44马丽亚浙江工商大学87陶灵江浙江海洋学院45莫敏珍浙江工商大学88吴铃蔚浙江海洋学院46苏文成浙江工商大学89陈凯浙江科技学院47汪济民浙江工商大学90陈中师浙江科技学院48王江峰浙江工商大学91傅宣琪浙江科技学院49王文燕浙江工商大学92蒋秀忠浙江科技学院50张靖浙江工商大学93吕梦姣浙江科技学院51张扬进浙江工商大学94苏海翔浙江科技学院52何健伟浙江工商大学杭州商学院95汪江平浙江科技学院53陈礼诚浙江工业大学96王静浙江科技学院54陈敏骏浙江工业大学97徐培麒浙江科技学院55陈年增浙江工业大学98许臻泽浙江科技学院56何锦灜浙江工业大学99张坚浙江科技学院57洪涛浙江工业大学100周凯浙江科技学院58胡胜军浙江工业大学101朱庆贺浙江科技学院59黄炳川龙 浙江工业大学102陈冬冬浙江理工大学60李林鹏浙江工业大学103陈俊健浙江理工大学61李琪玮浙江工业大学104单美晨浙江理工大学62李帅浙江工业大学105丁奇浙江理工大学63林春儿浙江工业大学106丁瑞翔浙江理工大学64鲁晨阳浙江工业大学107何国权浙江理工大学65陆彬浙江工业大学108黄锡波浙江理工大学66马宇飞浙江工业大学109李源浙江理工大学67缪克俊浙江工业大学110沈娟浙江理工大学68倪彬鑫浙江工业大学111王益恩浙江理工大学69倪嘉斌浙江工业大学112文绪亮浙江理工大学70潘力策浙江工业大学113吴文军浙江理工大学71钱志欢浙江工业大学114俞庆泽浙江理工大学72沈渊浙江工业大学115袁景华浙江理工大学73史文龙浙江工业大学116董皇帅浙江农林大学74王鸣山浙江工业大学117刘亮亮浙江农林大学75王叶峰浙江工业大学118邬双兵浙江农林大学76吴雄增浙江工业大学119徐龙龙浙江农林大学77谢志诚浙江工业大学120陈微微浙江师范大学78许新望浙江工业大学121吴哲明浙江师范大学79姚翔浙江工业大学122张楠浙江师范大学80郑超浙江工业大学123戴剑迪中国计量学院81郑林俊浙江工业大学124樊剑中国计量学院82郑骁能浙江工业大学125金仁波中国计量学院83朱超逸浙江工业大学126李来利中国计量学院127李鑫中国计量学院142冯继雄浙江大学128梁璇中国计量学院143葛帅浙江大学129吕佩佩中国计量学院144谷坤奇浙江大学130马驰飞中国计量学院145金松浙江大学131戚红芳中国计量学院146金伟浙江大学132邱型泽中国计量学院147刘畅浙江大学133谭量量中国计量学院148刘海鹏浙江大学134王福民中国计量学院149陶东亮浙江大学135王新淮中国计量学院150滕超浙江大学136王新亮中国计量学院151童童浙江大学137谢正超中国计量学院152王凯浙江大学138徐杰中国计量学院153王帅浙江大学139杨陈中国计量学院154谢炜浙江大学140杨晓东中国计量学院155周小楠浙江大学141张权耀中国计量学院二等奖(共231人)序号 姓名 学校名称 序号姓名 学校名称 1包董叶杭州师范大学25潘莹宁波工程学院2刘艺杭州师范大学26戚肖川宁波工程学院3郑伟湖州师范学院27吴凯强宁波工程学院4徐超超嘉兴学院28吴文敬宁波工程学院5闫霞嘉兴学院29祝学文宁波工程学院6陈永福丽水学院30黄晓春绍兴文理学院7李文尚丽水学院31孙兵绍兴文理学院8张燕琼丽水学院32严剑芳绍兴文理学院9陈喻宁波大学33余蓉绍兴文理学院10戴享宇宁波大学34宋马奎同济大学浙江学院11龚健宁波大学35范启弘温州大学12龚鑫宁波大学36刘雪松温州大学13郭赟宁波大学37饶俊波温州大学14李凯伟宁波大学38张昌宪温州大学15秦百夫宁波大学39童心萌浙大宁波理工16石安其琛宁波大学40何玲燕浙江传媒学院17杨忠宁波大学41陈彬彬浙江工商大学18詹侃宁波大学42程兴斌浙江工商大学19张柠溪宁波大学43冯倩倩浙江工商大学20赵艳平宁波大学44韩懿榕浙江工商大学21陈峰宁波大学科学技术学院45金清良浙江工商大学22陈尧宁波工程学院46李凯锐浙江工商大学23陈以军宁波工程学院47李昀浙江工商大学24何江鸿宁波工程学院48林细亚浙江工商大学49凌燕浙江工商大学92林辉浙江工业大学50刘垚浙江工商大学93林立浙江工业大学51马吉跃浙江工商大学94刘帅浙江工业大学52梅俊腾浙江工商大学95卢慧剑浙江工业大学53沈泉英浙江工商大学96吕建峰浙江工业大学54涂宏志浙江工商大学97茅立勋浙江工业大学55屠超杰浙江工商大学98缪烽民浙江工业大学56王栋浙江工商大学99任国栋浙江工业大学57王田浙江工商大学100沈婷浙江工业大学58吴佳佳浙江工商大学101唐亮亮浙江工业大学59吴婷浙江工商大学102屠成杰浙江工业大学60徐海红浙江工商大学103屠晓明浙江工业大学61章安然浙江工商大学104汪华锋浙江工业大学62郑群龙浙江工商大学105王鹏浙江工业大学63周攀浙江工商大学106王鹏飞浙江工业大学64蔡礼年浙江工业大学107王申浙江工业大学65曹诚斌浙江工业大学108王炜槐浙江工业大学66曹杰浙江工业大学109王媛媛浙江工业大学67曾庆贵浙江工业大学110委佩涛浙江工业大学68曾宪宇浙江工业大学111谢佩佩浙江工业大学69陈诚浙江工业大学112谢逸坤浙江工业大学70陈晟恺浙江工业大学113谢振达浙江工业大学71陈威子浙江工业大学114徐晨烨浙江工业大学72陈夏琦浙江工业大学115徐栋浙江工业大学73陈元正浙江工业大学116许晨祥浙江工业大学74单挺挺浙江工业大学117许华杰浙江工业大学75符聪浙江工业大学118宣建楠浙江工业大学76付铭浙江工业大学119姚盛宇浙江工业大学77傅君浙江工业大学120易永坤浙江工业大学78高维浙江工业大学121应豪超浙江工业大学79龚余峰浙江工业大学122余承涛浙江工业大学80顾锐锐浙江工业大学123俞骋超浙江工业大学81郭琪浙江工业大学124詹斌浙江工业大学82韩利杰浙江工业大学125张丹阳浙江工业大学83何彬浙江工业大学126张恺浙江工业大学84何煜浙江工业大学127张梦夕浙江工业大学85华俊豪浙江工业大学128章博浙江工业大学86黄翀浙江工业大学129章中宏浙江工业大学87金浩浙江工业大学130赵佳飞浙江工业大学88李光明浙江工业大学131钟婧如浙江工业大学89李洪飞浙江工业大学132钟麒浙江工业大学90李秀超浙江工业大学133周菲浙江工业大学91厉万富浙江工业大学134周文韬浙江工业大学135朱俊杰浙江工业大学178何慧敏浙江农林大学136朱李核浙江工业大学179季永权浙江农林大学137诸亮浙江工业大学180缪小佩浙江农林大学138祝庆军浙江工业大学181钱辰雯浙江农林大学139刘洋浙江工业大学之江学院182吴世联浙江农林大学140屈平浙江海洋学院183吴世全浙江农林大学141许灵静浙江海洋学院184俞沈晶浙江农林大学142张光明浙江海洋学院185项嘉旎浙江农林大学天目学院143陈强强浙江科技学院186陈孝章浙江师范大学144陈振华浙江科技学院187顾静琰浙江师范大学145冯尧浙江科技学院188黄媛媛浙江师范大学146洪西洋浙江科技学院189阮柳晖浙江师范大学147花广兵浙江科技学院190许建明浙江师范大学148黄利华浙江科技学院191叶晔浙江师范大学149黄晓进浙江科技学院192徐文斌浙江树人大学150金承浙江科技学院193张鹏浙江树人大学151李特浙江科技学院194朱月霞浙江树人大学152罗项欢浙江科技学院195郭杜斌浙江万里学院153吴云杰浙江科技学院196郭晨中国计量学院154邢涛浙江科技学院197黑珊珊中国计量学院155徐瀚辉浙江科技学院198洪文娟中国计量学院156周文来浙江科技学院199李彩琴中国计量学院157周秀泽浙江科技学院200潘琳中国计量学院158陈豪浙江理工大学201唐薇中国计量学院159韩琳琳浙江理工大学202汪洁中国计量学院160贾王欢浙江理工大学203王蕾中国计量学院161金雷过浙江理工大学204王赛波中国计量学院162李铖瀚浙江理工大学205文一章中国计量学院163李高军浙江理工大学206吴月婷中国计量学院164李杰民浙江理工大学207薛君义中国计量学院165刘季华浙江理工大学208于冰洋中国计量学院166苏怡雪浙江理工大学209余波中国计量学院167孙钢杰浙江理工大学210袁海波中国计量学院168王中华浙江理工大学211陈焯颢浙江大学169宣海枫浙江理工大学212陈杰浙江大学170薛重飞浙江理工大学213葛清惠浙江大学171颜慧慧浙江理工大学214胡道宇浙江大学172杨敏浙江理工大学215胡辉勇浙江大学173杨威浙江理工大学216李佳勇浙江大学174张琳浙江理工大学217李浙鲁浙江大学175曾丹浙江农林大学218刘卉芸浙江大学176陈俊仪浙江农林大学219王斌斌浙江大学177单武斌浙江农林大学220王泓浙江大学221王治飞浙江大学227郑天一浙江大学222胥秉钧浙江大学228郑璇浙江大学223严霄玮浙江大学229周嘉文浙江大学224俞杰草浙江大学230周鑫浙江大学225张旭东浙江大学231周游浙江大学226赵康浙江大学三等奖(共387人)序号 姓名 学校名称 序号 姓名 学校名称1高黎英杭州师范大学34南柏惠宁波大学2姜科杭州师范大学35潘云峰宁波大学3李存友杭州师范大学36饶尚坤宁波大学4聂聪杭州师范大学37阮超宁波大学5史美芳杭州师范大学38寿亚锋宁波大学6吴云河杭州师范大学39王润龙宁波大学7徐陈超杭州师范大学40王翔宁波大学8宣晟杰杭州师范大学41吴俊敏宁波大学9郑蔚玮杭州师范大学42闫丽宁波大学10杨平湖州师范学院43杨春晖宁波大学11周薇湖州师范学院44尹杰茜宁波大学12蔡珍珍嘉兴学院45张乐宁波大学13黄正取丽水学院46张兴旺宁波大学14张金军丽水学院47张自龙宁波大学15周慧杰丽水学院48郑丽文宁波大学16柏定波宁波大学49王浩宁波大学科学技术学院17陈岙宁波大学50徐欣慰宁波大学科学技术学院18陈建武宁波大学51陈晓龙宁波工程学院19崔力宁波大学52陈兴旺宁波工程学院20董少奇宁波大学53黄云宁波工程学院21杜眯宁波大学54黄云飞宁波工程学院22冯渊宁波大学55姜晨如宁波工程学院23甘瑜瑜宁波大学56吕超镇宁波工程学院24胡洒帅宁波大学57王军伟宁波工程学院25靳泽中宁波大学58张家瑜宁波工程学院26李少博宁波大学59陈君琳绍兴文理学院27李祖团宁波大学60季康康绍兴文理学院28林学彬宁波大学61李小千绍兴文理学院29刘超宁波大学62潘春辉绍兴文理学院30鲁斌宁波大学63沈孔超绍兴文理学院31鲁璐宁波大学64沈涛绍兴文理学院32陆奕萍宁波大学65王佐奉绍兴文理学院33罗晓燕宁波大学66吴继宝绍兴文理学院序号 姓名 学校名称 序号姓名 学校名称67章姣姣绍兴文理学院110张凌浙江工商大学68李程翔绍兴文理学院元培学院111张晓旭浙江工商大学69蒋汉阳台州学院112章天平浙江工商大学70周徐聪台州学院113林晶晶浙江工商大学杭州商学院71朱理晃同济大学浙江学院114庞林芳浙江工商大学杭州商学院72杜文洁温州大学115姚旭丽浙江工商大学杭州商学院73高建栋温州大学116包瑞鹏浙江工业大学74黄书杭温州大学117包勋浙江工业大学75潘益斌温州大学118鲍帮龙浙江工业大学76伍飞飞温州大学119曹国栋浙江工业大学77朱帅军温州大学120陈晗浙江工业大学78宗凯温州大学121陈辉浙江工业大学79董任姣温州大学城市学院122陈可慰浙江工业大学80戴骏温州大学瓯江学院123陈璐浙江工业大学81薛一强温州大学瓯江学院124陈鹏浙江工业大学82罗康佳浙江传媒学院125陈琦浙江工业大学83徐遥浙江传媒学院126陈武斌浙江工业大学84岑梦璐浙江工商大学127陈晓庆浙江工业大学85陈海辉浙江工商大学128陈新峰浙江工业大学86陈弘挺浙江工商大学129陈泽安浙江工业大学87池若楠浙江工商大学130戴明敏浙江工业大学88郭晓钰浙江工商大学131邓代琪浙江工业大学89洪志勇浙江工商大学132狄晓霞浙江工业大学90胡珍珍浙江工商大学133董炜浙江工业大学91黄章鹏浙江工商大学134方圣浙江工业大学92李坚村浙江工商大学135方祝敏浙江工业大学93李敏浙江工商大学136付金武浙江工业大学94李修竹浙江工商大学137葛柳钦浙江工业大学95李艳茹浙江工商大学138宫紫辉浙江工业大学96林家易浙江工商大学139官秋林浙江工业大学97刘意浙江工商大学140韩帅非浙江工业大学98刘莹浙江工商大学141何俊浙江工业大学99吕安佳浙江工商大学142贺磊浙江工业大学100潘丽娜浙江工商大学143贺秧秧浙江工业大学101潘雨亭浙江工商大学144洪斌勋浙江工业大学102邵东浙江工商大学145胡碧涛浙江工业大学103沈楚遥浙江工商大学146胡宏笋浙江工业大学104沈洁心浙江工商大学147胡丽波浙江工业大学105施正政浙江工商大学148华昀峰浙江工业大学106陶政旭浙江工商大学149黄居华浙江工业大学107杨峰浙江工商大学150黄鲁斌浙江工业大学108杨志妮浙江工商大学151黄雪峰浙江工业大学109余丹浙江工商大学152姜慧强浙江工业大学。
2023年历届全国大学生数学竞赛预赛试卷

全国大学生数学竞赛预赛试卷(非数学类)2023年 第一届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题5分,共20分)1.计算()ln(1)d yx y x y ++=⎰⎰____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.2.设)(x f 是连续函数,且满足220()3()d 2f x x f x x =--⎰,则()f x =____________.3.曲面2222x z y =+-平行平面022=-+z y x 的切平面方程是__________.4.设函数)(x y y =由方程29ln )(y y f e xe =拟定,其中f 具有二阶导数,且1≠'f ,则=22d d x y________________. 二、(5分)求极限xenx x x x ne e e )(lim 20+++→ ,其中n 是给定的正整数. 三、(15分)设函数)(x f 连续,10()()g x f xt dt =⎰,且A xx f x =→)(lim,A 为常数,求()g x '并讨论)(x g '在0=x 处的连续性.四、(15分)已知平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:(1)⎰⎰-=---Lx y Lx yx ye y xe x ye y xed d d d sin sin sin sin ;(2)2sin sin 25d d π⎰≥--Ly yx ye y xe.五、(10分)已知xxe xe y 21+=,xxexe y -+=2,xx x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.六、(10分)设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又已知该抛物线与x 轴及直线1=x 所围图形的面积为31.试拟定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积V 最小.七、(15分)已知)(x u n 满足1()()1,2,n x nn u x u x x e n -'=+=,且neu n =)1(,求函数项级数∑∞=1)(n nx u之和.八、(10分)求-→1x 时,与∑∞=02n n x 等价的无穷大量.2023年 第二届全国大学生数学竞赛预赛试卷(非数学类)一、(25分,每小题5分) (1)设22(1)(1)(1)nn x a a a =+++,其中||1,a <求lim .n n x →∞(2)求21lim 1x xx ex -→∞⎛⎫+ ⎪⎝⎭. (3)设0s >,求0(1,2,)sx n n I e x dx n ∞-==⎰.(4)设函数()f t 有二阶连续导数,1(,)r g x y f r ⎛⎫== ⎪⎝⎭,求2222g g x y ∂∂+∂∂.(5)求直线10:0x y l z -=⎧⎨=⎩与直线2213:421x y z l ---==--的距离. 二、(15分)设函数()f x 在(,)-∞+∞上具有二阶导数,并且()0f x ''>,lim ()0x f x α→+∞'=>,lim ()0x f x β→-∞'=<,且存在一点0x ,使得0()0f x <. 证明:方程()0f x =在(,)-∞+∞恰有两个实根.三、(15分)设函数()y f x =由参数方程22(1)()x t t t y t ψ⎧=+>-⎨=⎩所拟定,且22d 3d 4(1)y x t =+,其中()t ψ具有二阶导数,曲线()y t ψ=与22132t u y e du e-=+⎰在1t =出相切,求函数()t ψ. 四、(15分)设10,nn n kk a S a=>=∑,证明:(1)当1α>时,级数1nn na S α+∞=∑收敛; (2)当1α≤且()n s n →∞→∞时,级数1nn na S α+∞=∑发散. 五、(15分)设l 是过原点、方向为(,,)αβγ,(其中2221)αβγ++=的直线,均匀椭球2222221x y z a b c ++≤(其中0c b a <<<,密度为1)绕l 旋转. (1)求其转动惯量;(2)求其转动惯量关于方向(,,)αβγ的最大值和最小值.六、(15分)设函数()x ϕ具有连续的导数,在围绕原点的任意光滑的简朴闭曲线C 上,曲线积分422d ()d 0L xy x x yx y ϕ+=+⎰的值为常数.(1)设L 为正向闭曲线22(2)1x y -+=,证明422d ()d 0L xy x x yx y ϕ+=+⎰;(2)求函数()x ϕ;(3)设C 是围绕原点的光滑简朴正向闭曲线,求422d ()d C xy x x y x y ϕ++⎰.2023年 第三届全国大学生数学竞赛预赛试卷(非数学类)一、计算下列各题(本题共3小题,每小题各5分,共15分)(1)求11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭;(2).求111lim ...12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭; (3)已知()2ln 1arctan tt x e y t e⎧=+⎪⎨=-⎪⎩,求22d d y x .二、(本题10分)求方程()()24d 1d 0x y x x y y +-++-=的通解.三、(本题15分)设函数()f x 在0x =的某邻域内具有二阶连续导数,且()()()0,0,0f f f '''均不为0,证明:存在唯一一组实数123,,k k k ,使得()()()()12320230lim0h k f h k f h k f h f h→++-=. 四、(本题17分)设2221222:1x y z a b c ∑++=,其中0a b c >>>,2222:z x y ∑=+,Γ为1∑与2∑的交线,求椭球面1∑在Γ上各点的切平面到原点距离的最大值和最小值.五、(本题16分)已知S 是空间曲线22310x y z ⎧+=⎨=⎩绕y 轴旋转形成的椭球面的上半部分(0z ≥)(取上侧),∏是S 在(,,)P x y z 点处的切平面,(,,)x y z ρ是原点到切平面∏的距离,,,λμν表达S 的正法向的方向余弦. 计算:(1)()d ,,SzS x y z ρ⎰⎰;(2)()3d Sz x y z S λμν++⎰⎰ 六、(本题12分)设()f x 是在(,)-∞+∞内的可微函数,且()()f x mf x '<,其中01m <<,任取实数0a ,定义1ln (),1,2,...n n a f a n -==,证明:11()n n n a a ∞-=-∑绝对收敛.七、(本题15分)是否存在区间[]0,2上的连续可微函数()f x ,满足(0)(2)1f f ==,()1f x '≤,2()d 1f x x ≤⎰?请说明理由.2023年 第四届全国大学生数学竞赛预赛试卷(非数学类)一、(本大题共5小题,每小题6分,共30分)解答下列各题(规定写出重要环节). (1)求极限21lim(!)n n n →∞.(2)求通过直线2320:55430x y z l x y z +-+=⎧⎨+-+=⎩的两个互相垂直的平面1π和2π,使其中一个平面过点(4,3,1)-.(3)已知函数(,)ax byz u x y e+=,且20ux y∂=∂∂. 拟定常数a 和b ,使函数(,)z z x y =满足方程20z z zz x y x y∂∂∂--+=∂∂∂∂. (4)设函数()u u x =连续可微,(2)1u =,且3(2)d ()d Lx y u x x u u y +++⎰在右半平面与途径无关,求(,)u x y . (5)求极限1lim x xx t +.二、(本题10分)计算20sin d x e x x +∞-⎰.三、(本题10分)求方程21sin 2501x x x=-的近似解,精确到0.001.四、(本题12分)设函数()y f x =二阶可导,且()0f x ''>,(0)0f =,(0)0f '=,求330()lim ()sin x x f u f x u→,其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距. 五、(本题12分)求最小实数C ,使得满足10()d 1f x x =⎰的连续函数()f x 都有10f dx C ≤⎰.六、(本题12分)设()f x 为连续函数,0t >. 区域Ω是由抛物面22z x y =+和球面 2222x y z t ++=(0)z >所围起来的部分. 定义三重积分222()()d F t f x y z v Ω=++⎰⎰⎰,求()F t 的导数()F t ''.七、(本题14分)设1n n a ∞=∑与1n n b ∞=∑为正项级数,证明:(1)若()111lim 0n n n n n a a b b →∞++->,则级数1n n a ∞=∑收敛;(2)若()111lim 0n n n n n a a b b →∞++-<,且级数1n n b ∞=∑发散,则级数1n n a ∞=∑发散.2023年 第五届全国大学生数学竞赛预赛试卷(非数学类)一、解答下列各题(每小题6分,共24分,规定写出重要环节) 1.求极限(lim 1sin nn →∞+.2.证明广义积分0sin d xx x+∞⎰不是绝对收敛的. 3.设函数()y y x =由323322x x y y +-=拟定,求()y x 的极值.4.过曲线0)y x =≥上的点A 作切线,使该切线与曲线及x 轴所围成的平面图形的面积为34,求点A 的坐标. 二、(满分12分)计算定积分2sin arctan d 1cos xx x e I x xππ-⋅=+⎰.三、(满分12分)设()f x 在0x =处存在二阶导数(0)f '',且()lim0x f x x→=.证明:级数11n f n ∞=⎛⎫⎪⎝⎭∑收敛.四、(满分12分)设(),()0()f x f x m a x b π'≤≥>≤≤,证明2sin ()d baf x x m≤⎰. 五、(满分14分)设∑是一个光滑封闭曲面,方向朝外.给定第二型的曲面积分()()()333d d 2d d 3d d I x x y z y y z x z z x y ∑=-+-+-⎰⎰.试拟定曲面∑,使积分I 的值最小,并求该最小值.六、(满分14分)设22d d ()()a a C y x x yI r x y -=+⎰,其中a 为常数,曲线C 为椭圆222x xy y r ++=,取正向.求极限lim ()a r I r →+∞.七、(满分14分)判断级数()()1111212n n n n ∞=+++++∑的敛散性,若收敛,求其和.2023年 第六届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(共有5小题,每题6分,共30分)1.已知1x y e =和1x y xe =是齐次二阶常系数线性微分方程的解,则该方程是 .2.设有曲面22:2S z x y =+和平面022:=++z y x L . 则与L 平行的S 的切平面方程是 .3.设函数()y y x =由方程21sin d 4y xt x t π-⎛⎫= ⎪⎝⎭⎰所拟定.求d d x y x == .4.设1(1)!nn k kx k ==+∑,则=∞→n n x lim .5.已知130()lim 1xx f x x e x →⎛⎫++= ⎪⎝⎭,则=→20)(lim x x f x .二、(本题12分)设n 为正整数,计算21d 1cos ln d d n eI x x x π-⎛⎫= ⎪⎝⎭⎰. 三、(本题14分)设函数()f x 在]1,0[上有二阶导数,且有正常数,A B 使得()f x A ≤,|"()|f x B ≤. 证明:对任意]1,0[∈x ,有22|)('|BA x f +≤. 四、(本题14分)(1)设一球缺高为h ,所在球半径为R . 证明该球缺体积为2)3(3h h R -π,球冠面积为Rh π2;(2)设球体12)1()1()1(222≤-+-+-z y x 被平面6:=++z y x P 所截的小球缺为Ω,记球缺上的球冠为∑,方向指向球外,求第二型曲面积分d d d d d d I x y z y z x z x y ∑=++⎰⎰.五、(本题15分)设f 在],[b a 上非负连续,严格单增,且存在],[b a x n ∈,使得⎰-=b a nn n dx x f ab x f )]([1)]([.求n n x ∞→lim . 六、(本题15分)设2222212n n nnA n n n n =++++++,求⎪⎭⎫ ⎝⎛-∞→n n A n 4lim π.2023年 第七届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题6分,共5小题,满分30分)(1)极限2222sin sin sin lim 12n n n n n n n n πππ→∞⎛⎫⎪+++= ⎪+++ ⎪⎝⎭. (2)设函数(),z z x y =由方程,0z z F x y y x ⎛⎫++= ⎪⎝⎭所决定,其中(),F u v 具有连续偏导数,且0u v xF yF +≠则z zxy x y∂∂+=∂∂ .(3)曲面221z x y =++在点()1,1,3M -的切平面与曲面所围区域的体积是 .(4)函数()[)[)3,5,00,0,5x f x x ⎧∈-⎪=⎨∈⎪⎩在(]5,5-的傅立叶级数在0x =收敛的是 . (5)设区间()0,+∞上的函数()u x 定义域为()2xt u x e dt +∞-=⎰,则()u x 的初等函数表达式是 .二、(12分)设M 是以三个正半轴为母线的半圆锥面,求其方程.三、(12分)设()f x 在(),a b 内二次可导,且存在常数,αβ,使得对于(),x a b ∀∈,有()()()f x f x f x αβ'=+,则()f x 在(),a b 内无穷次可导.四、(14分)求幂级数()()30211!nn n x n ∞=+-+∑的收敛域及其和函数.五、(16分)设函数()f x 在[]0,1上连续,且()()110,1f x dx xf x dx ==⎰⎰. 试证:(1)[]00,1x ∃∈使()04f x >; (2)[]10,1x ∃∈使()14f x =.五、(16分)设(),f x y 在221x y +≤上有连续的二阶偏导数,且2222xx xy yy f f f M ++≤. 若()()()0,00,0,00,00x y f f f ===,证明:()221,4x y f x y dxdy +≤≤⎰⎰.2023年 第八届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题5分,满分30分) 1、若()f x 在点x a =可导,且()0f a ≠,则()1lim nn f a n f a →∞⎛⎫⎛⎫+ ⎪⎪⎝⎭⎪= ⎪⎪⎝⎭__________. 2、若()10f =,()1f '存在,求极限()()220sin cos tan3lim1sin x x f x x xI ex→+=-.3、设()f x 有连续导数,且()12f =,记()2x z f e y =,若zz x∂=∂,求()f x 在0x >的表达式.4、设()sin 2x f x e x =,求02n a π<<,()()40f .5、求曲面22 2x z y =+平行于平面220x y z +-=的切平面方程.二、(14分)设()f x 在[]0,1上可导,()00f =,且当()0,1x ∈,()01f x '<<,试证当()0,1a ∈,()()()230d d aaf x xf x x >⎰⎰.三、(14分)某物体所在的空间区域为222:22x y z x y z Ω++≤++,密度函数为222x y z ++,求质量()222d d d M x y z x y z Ω=++⎰⎰⎰.四、(14分)设函数()f x 在闭区间[]0,1上具有连续导数,()00f =,()11f =, 证明:()10111lim 2n n k k n f x dx fn n →∞=⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭∑⎰.五、(14分)设函数()f x 在闭区间[]0,1上连续,且()1d 0I f x x =≠⎰,证明:在()0,1内存在不同的两点12,x x ,使得()()12112f x f x I+=. 六、(14分)设()f x 在(),-∞+∞可导,且()()()23f x f x f x =+=+.用Fourier 级数理论证明()f x 为常数.2023年 第九届全国大学生数学竞赛预赛试卷(非数学类)一、1. 已知可导函数满足⎰+=+xx tdt t f x xf 01sin )(2)(cos ,则()f x =_________.2. 求⎪⎭⎫ ⎝⎛+∞→n n n 22sin lim π.3. 设(,)w f u v =具有二阶连续偏导数,且==+u x cy v x cy -,,其中c 为非零常数. 则21xx yy w w c-=_________. 4. 设()f x 有二阶导数连续,且(0)'(0)0,"(0)6f f f ===,则240(sin )lim x f x x→=____. 5. 不定积分sin 2sin 2(1sin )x e x I dx x -=-⎰=________. 6. 记曲面222z x y =+和z =围成空间区域为V ,则三重积分Vzdxdydz ⎰⎰⎰=___________.二、(本题满分14分) 设二元函数(,)f x y 在平面上有连续的二阶偏导数. 对任何角度α,定义一元函数()(cos ,sin )g t f t t =ααα.若对任何α都有(0)0dg dtα=且22(0)0d g dt α>. 证明)0,0(f 是(,)f x y 的极小值. 三、(本题满分14分) 设曲线Γ为在2221x y z ++=,1x z +=,0,0,0x y z ≥≥≥上从(1,0,0)A 到(0,0,1)B 的一段. 求曲线积分⎰Γ++=xdz zdy ydx I .四、(本题满分15分) 设函数()0f x >且在实轴上连续,若对任意实数t ,有||()1t x e f x dx +∞---∞≤⎰,则,()a b a b ∀<,2()2b a b a f x dx -+≤⎰. 五、(本题满分15分) 设{}n a 为一个数列,p 为固定的正整数。
2011年广东工业大学第三届大学生数学建模竞赛(最终版)

2011年广东工业大学第三届大学生数学建模竞赛承诺书我们仔细阅读了2011年广东工业大学数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛的题目是:CPI中的数学模型我们的参赛报名号为:16参赛队员(打印并签名) :姓名陈千文学号3110008367___参赛院系应用数学学院姓名陈静旋学号_3210008502___参赛院系应用数学学院姓名杜泽霖学号_3110008369___参赛院系应用数学学院日期:2011年4月24日CPI中的数学模型陈千文陈静旋杜泽霖一、摘要本文针对不同问题分别利用统计回归模型、线性相关系数方法、ARMA模型等,以我国2008年7月到2010年12月的居民消费指数为例建立合理的数学模型进行预测分析。
针对问题一,通过建立统计回归模型和以主成分分析法相结合分析各个指标的相关性,来说明影响CPI的主要三大因素及原因。
针对问题二,通过以线性相关系数方法来分析新增的五个因素(即房屋销售价格指数、固定资产购买价格指数、土地交易价格指数、国房景气指数和物业管理价格指数)的线性相关性,以及是否把居民住房消费指数纳入CPI的前后数据对比进行分析,找出充分有说服力的论据,从而说明不把居民住房消费指数纳入CPI 的重要原因。
针对问题三,通过分析08年1月—11年3月CPI指数的统计数据,建立时间序列模型,对今年即2011年CPI指数的走势进行数据上的验证,并进行短期预测;并且建立ARMA模型对数据序列进行平稳性检验,看起是否具有季节性,来说明今年的通货膨胀及波动高度。
大学生可以参加的竞赛项目
(共91项)
序号
竞赛名称
主办单位
1
第八届“挑战杯”全国大学生创业计划竞赛
共青团中央、中国科协、教育部、全国学联
2
第三届“北斗杯”全国青少年科技创新大赛
教育部科技司、团中央学校部、中国科协青少年科技中心、中国卫星导航系统管理办公室
3
第二届全国高等学校采矿工程专业学生实践作品大赛
12
山东省高校大学生测量技能大赛
山东测量学会
13
全国第二届地质技能大赛
中国地质调查局、中国地质学会地质教育研究分会
14
第五届山东省高校结构设计大赛
山东省土木工程学会建筑结构专业委员会、山东大学
15
2012年山东省大学生建筑设计竞赛
山东省住房和城乡建设厅、山东省科学技术协会
16
2012全国高等学校城市规划专业社会综合实践调研报告课程作业评优
38
第三届“蓝桥杯”全国软件专业人才设计与创业大赛
工业与信息化部人才交流中心
39
建行“e路通”杯第五届全国大学生网络商务创新应用大赛
中国建设银行、中国互联网协会
40
“金蝶杯”全国大学生创业设计大赛
教育部全国高等学校学生信息咨询与就业指导中心
41
第四届全国大学生“创新创意创业”电子商务挑战赛
中国信息经济学学会信息管理专业委员会
8
supermap杯全国高校GIS大赛
中国地理学会、北京超图软件股份有限公司
9
全国高校GIS技能大赛
中国测绘学会、工业和信息化部人才交流中心、教育部地理信息系统软件及其应用工程研究中心
10
全国高校GIS论坛
GIS论坛组委会
第三届全国大学生数学竞赛决赛获奖名单(数学类)
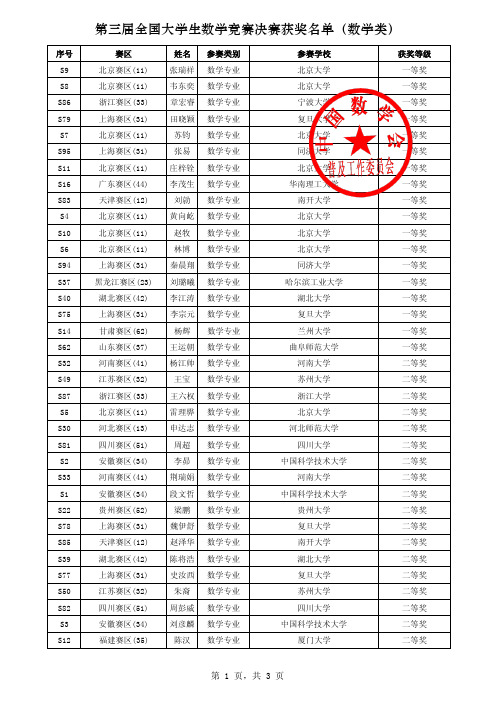
S9北京赛区(11)张瑞祥数学专业北京大学一等奖S8北京赛区(11)韦东奕数学专业北京大学一等奖S86浙江赛区(33)章宏睿数学专业宁波大学一等奖S79上海赛区(31)田晓颖数学专业复旦大学一等奖S7北京赛区(11)苏钧数学专业北京大学一等奖S95上海赛区(31)张易数学专业同济大学一等奖S11北京赛区(11)庄梓铨数学专业北京大学一等奖S16广东赛区(44)李茂生数学专业华南理工大学一等奖S83天津赛区(12)刘勍数学专业南开大学一等奖S4北京赛区(11)黄向屹数学专业北京大学一等奖S10北京赛区(11)赵牧数学专业北京大学一等奖S6北京赛区(11)林博数学专业北京大学一等奖S94上海赛区(31)秦晨翔数学专业同济大学一等奖S37黑龙江赛区(23)刘璐曦数学专业哈尔滨工业大学一等奖S40湖北赛区(42)李江涛数学专业湖北大学一等奖S75上海赛区(31)李宗元数学专业复旦大学一等奖S14甘肃赛区(62)杨辉数学专业兰州大学一等奖S62山东赛区(37)王运朝数学专业曲阜师范大学一等奖S32河南赛区(41)杨江帅数学专业河南大学二等奖S49江苏赛区(32)王宝数学专业苏州大学二等奖S87浙江赛区(33)王六权数学专业浙江大学二等奖S5北京赛区(11)雷理骅数学专业北京大学二等奖S30河北赛区(13)申达志数学专业河北师范大学二等奖S81四川赛区(51)周超数学专业四川大学二等奖S2安徽赛区(34)李昴数学专业中国科学技术大学二等奖S33河南赛区(41)荆瑞娟数学专业河南大学二等奖S1安徽赛区(34)段文哲数学专业中国科学技术大学二等奖S22贵州赛区(52)梁鹏数学专业贵州大学二等奖S78上海赛区(31)魏伊舒数学专业复旦大学二等奖S85天津赛区(12)赵泽华数学专业南开大学二等奖S39湖北赛区(42)陈将浩数学专业湖北大学二等奖S77上海赛区(31)史汝西数学专业复旦大学二等奖S50江苏赛区(32)朱裔数学专业苏州大学二等奖S82四川赛区(51)周彭威数学专业四川大学二等奖S3安徽赛区(34)刘彦麟数学专业中国科学技术大学二等奖S12福建赛区(35)陈汉数学专业厦门大学二等奖S46吉林赛区(22)王斌数学专业东北师范大学二等奖S66山东赛区(37)孟凡钦数学专业山东科技大学二等奖S93重庆赛区(50)宋海娟数学专业重庆师范大学二等奖S55辽宁赛区(21)刘思序数学专业大连理工大学二等奖S84天津赛区(12)王志超数学专业南开大学二等奖S21贵州赛区(52)黄荣锋数学专业贵州大学二等奖S41湖北赛区(42)余红杰数学专业武汉大学二等奖S88浙江赛区(33)张颖数学专业浙江大学二等奖S90浙江赛区(33)周远数学专业浙江理工大学二等奖S17广东赛区(44)梅河数学专业中山大学三等奖S18广东赛区(44)朱伟鹏数学专业中山大学三等奖S36黑龙江赛区(23)王丽娜数学专业哈尔滨师范大学三等奖S43湖南赛区(43)杨苗数学专业长沙学院三等奖S80四川赛区(51)傅费思数学专业四川大学三等奖S54辽宁赛区(21)蒋瑶数学专业大连理工大学三等奖S70陕西赛区(61)张纯数学专业西安交通大学三等奖S24国防科大赛区(66)陈玺数学专业国防科学技术大学三等奖S52江西赛区(36)周颖颖数学专业赣南师范学院三等奖S64山东赛区(37)屈宝友数学专业山东大学三等奖S76上海赛区(31)倪晨頔数学专业复旦大学三等奖S53江西赛区(36)王利军数学专业江西理工大学三等奖S92重庆赛区(50)张军强数学专业重庆师范大学三等奖S51江苏赛区(32)钱欣洁数学专业徐州师范大学三等奖S26国防科大赛区(66)徐立平数学专业信息工程大学三等奖S31河北赛区(13)李泊宁数学专业河北师范大学三等奖S42湖北赛区(42)曾桢数学专业武汉大学三等奖S44湖南赛区(43)肖惠数学专业湖南师范大学三等奖S45湖南赛区(43)庄晓数学专业湘潭大学三等奖S71陕西赛区(61)薛向宏数学专业西安理工大学三等奖S89浙江赛区(33)赵亮数学专业浙江工商大学三等奖S91重庆赛区(50)陈庚生数学专业西南大学三等奖S15甘肃赛区(62)廖丽丹数学专业河西学院三等奖S27海南赛区(46)王健数学专业海南大学三等奖S68山西赛区(14)郭艳艳数学专业太原理工大学三等奖S69陕西赛区(61)陈阳数学专业陕西师范大学三等奖S25国防科大赛区(66)许晓川数学专业海军工程大学三等奖S34河南赛区(41)杨会波数学专业商丘师范学院三等奖S48江苏赛区(32)李桂林数学专业淮阴师范学院三等奖S60宁夏赛区(64)田丽茹数学专业北方民族大学三等奖S13福建赛区(35)徐赛国数学专业厦门大学三等奖S28海南赛区(46)乔春雨数学专业海南大学三等奖S59内蒙古赛区(15)杨康数学专业内蒙古大学三等奖S61宁夏赛区(64)岳振芳数学专业宁夏大学三等奖S65山东赛区(37)翟汉征数学专业山东大学三等奖S67山西赛区(14)曹新宇数学专业大同大学三等奖S56辽宁赛区(21)张阳数学专业沈阳航空航天大学三等奖S57辽宁赛区(21)周辰红数学专业沈阳师范大学三等奖S63山东赛区(37)张兴宽数学专业曲阜师范大学三等奖S38黑龙江赛区(23)王姝宇数学专业哈尔滨工业大学三等奖S19广西赛区(45)杨天山数学专业广西师范学院三等奖S20广西赛区(45)李徘菱数学专业广西师范学院三等奖。
大学数学知识竞赛活动策划书

大学数学知识竞赛活动策划书(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作总结、工作方案、职业规划、合同协议、条据文书、演讲致辞、规章制度、心得体会、教学资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as work summaries, work plans, career plans, contract agreements, document documents, speeches, rules and regulations, insights, teaching materials, other sample essays, etc. If you want to learn about different sample formats and writing methods, please pay attention!大学数学知识竞赛活动策划书大学数学知识竞赛活动策划书(精选5篇)时间过得太快,让人不知所措,工作已经告一段落了,我们又迎来一个新的工作阶段,要定下新的目标了,何不赶紧趁现在写写策划书。
大学生科技竞赛基本赛事汇总及简介

大学生科技竞赛基本赛事汇总及简介1.全国大学生机械创新大赛2.全国大学生焊接创新大赛3.江西省模具设计制作团体大赛和个人比赛4.永冠杯中国大学生铸造工艺大赛5.瑞萨超级MCU模型车大赛6.未来合作杯智能机器人竞赛7.全国大学生电子设计大赛8.数控技能大师赛9.中国大学生LED大师赛10.校级电子制作大赛11.三维建模设计大赛12.中国3C网络设计大赛13.三维数字化创新大赛14.高校杯全国大学生先进图形技能与创新大赛15.全国大学生节能减排科技大赛16.江西省挑战杯大赛17.三小竞赛18.全国大学生英语竞赛19.全国大学生周培源力学竞赛20.全国大学生数学竞赛一、“挑战杯”大学生课外学术科技作品竞赛活动背景:由共青团中央、教育部、工业和信息化部、中国科协、全国学联主办的“挑战杯”大学生课外学术科技作品竞赛(以下简称“‘挑战杯’竞赛”)是一项具有导向性、示范性和权威性的全国科技竞赛活动,自1989年首届竞赛举办以来,“挑战杯”竞赛始终坚持“崇尚科学、追求真知、勤奋学习、锐意创新、迎接挑战”的宗旨,在促进青年创新人才成长、深化高校素质教育、推动经济社会发展等方面发挥了积极作用,在广大高校乃至社会上产生了广泛而良好的影响,被誉为当代大学生科技创新的“奥林匹克”盛会。
我校学生曾在该项赛事中取得过全国二等奖的好成绩。
第十二届“挑战杯”全国大学生课外学术科技作品竞赛终审决赛将于2011年10月在西北工业大学举行。
为引导和激励我校大学生刻苦钻研、勇于创新的精神,进一步推动我校大学生课外科技活动的蓬勃开展,选拔出能充分展现我校学生学术实力和创新风采的优秀学术科技创新成果,校团委决定在全校范围内开展第十二届“挑战杯”大学生课外学术科技作品竞赛校内选拔赛。
活动内容:1、参赛对象凡在2011年7月以前正式注册的全日制非成人教育的中国籍在校专科生、本科生、研究生都可以申报作品参赛。
2、竞赛章程及评审办法本届竞赛遵从《“挑战杯”全国大学生课外学术科技作品竞赛章程》,作品资格审查遵从《“挑战杯”全国大学生课外学术科技作品竞赛资格及形式审查实施细则》,作品评审遵从《“挑战杯”全国大学生课外学术科技作品竞赛评审规则》。
