立体几何证明题

合集下载

高中数学立体几何10道大题

高中数学立体几何10道大题1.在四棱锥S-ABCD中，底面ABCD为平行四边形，侧面SBC垂直于面ABCD，已知∠ABC=45°，AB=2，BC=22，SB=SC=3.1) 证明平面SCD与平面SAB的交线l平行于AB；2) 证明SA垂直于BC；3) 求直线SD与面SAB所成角的正弦值。

2.在四棱锥P-ABCD中，底面ABCD是平行四边形，P为其顶点，O为其中心，PO平行于AB且PO=2，M为PD的中点，AD=AC=1，O为AC的中点。

1) 证明PB平行于平面ACM；2) 证明AD在平面PAC上；3) 求直线AM与平面ABCD所成角的正切值。

3.在四棱锥P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD均为等边三角形。

1) 证明CD垂直于平面PBD；2) 求二面角CPBD的平面角的余弦值。

4.在四棱锥P-ABCD中，PA垂直于底面ABCD，AC垂直于AD，ABCD为梯形，AB平行于DC，AB垂直于BC，PA=AB=BC=3，点E在棱PB上，且PE=2EB。

Ⅰ) 证明平面PAB垂直于平面PCB；Ⅱ) 证明PD平行于平面EAC；Ⅲ) 求平面AEC和平面PBC所成锐二面角的余弦值。

5.在图中，矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB，平面ABCD与平面ABPE的交线为AB，且AB=BP=2，AD=AE=1，AE垂直于AB，且AE平行于BP。

1) 在面ABCD内是否存在点N，使得MN垂直于平面ABCD？若存在，请证明；若不存在，请说明理由；2) 求二面角D-PE-A的余弦值。

6.在直三棱柱ABC-A1B1C1中，平面A1BC垂直于侧面A1BB1，且AA1=AB=2.1) 证明AB垂直于BC；2) 若直线AC与平面A1BC所成角为α，求锐二面角AAC1B的大小。

7.在四棱锥V-ABCD中，底面ABCD为正方形，侧面VAD 为正三角形，平面VAD垂直于底面ABCD。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

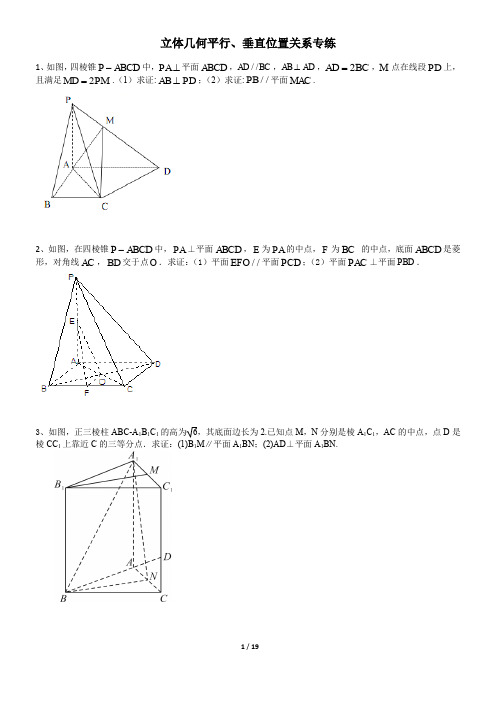
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ，又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点，所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ，所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

高中数学立体几何证明题汇总

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形，E,F,G,H分别是边AB,BC,CD,DA的中点。

1）证明EFGH是平行四边形。

2）已知BD=23，AC=2，EG=2，求异面直线AC、BD所成的角和EG、BD所成的角。

2.如图，已知空间四边形ABCD中，BC=AC,AD=BD，E 是AB的中点。

1）证明AB垂直于平面CDE。

2）证明平面CDE垂直于平面ABC。

3.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。

证明A1C平行于平面BDE。

4.已知三角形ABC中∠ACB=90，SA垂直于面ABC，AD垂直于SC。

证明AD垂直于面SBC。

5.已知正方体ABCD-A1B1C1D1，O是底面ABCD对角线的交点。

1）证明C1O平行于面AB1D1.2）证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。

1）证明AC垂直于平面B1D1D。

2）证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。

1）证明平面A1BD平行于平面B1DC。

2）已知E、F分别是AA1、CC1的中点，证明平面EB1D1平行于平面FBD。

8.四面体ABCD中，AC=BD，E、F分别为AD、BC的中点，且EF=AC/2，∠XXX。

证明BD垂直于平面ACD。

9.如图P是△ABC所在平面外一点，PA=PB，CB垂直于平面PAB，M是PC的中点，N是AB上的点，AN=3NB。

1）证明XXX垂直于AB。

2）当∠APB=90，AB=2BC=4时，求MN的长度。

10.如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点。

证明平面D1EF平行于平面BDG。

11.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。

1）证明A1C平行于平面BDE。

2）证明平面A1AC垂直于平面BDE。

12、已知矩形ABCD，PA垂直于平面ABCD，AB=2，PA=AD=4，E为BC的中点。

立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

立体几何立体几何是高考数学的必考内容，在大题中一般分两问，第一问考查空间直线与平面的位置关系证明；第二问考查空间角、空间距离等的求解。

考题难度中等，常结合空间向量知识进行考查。

2024年高考有很大可能延续往年的出题方式。

题型一：空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图，在三棱锥A-BCD中，平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证：AO⊥CD；(2)若BD⊥DC,BD=DC,AO=BO，求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N，利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中，由AB=AD,O为BD的中点，得AO⊥BD，而平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，AO⊂平面ABD，因此AO⊥平面BCD，又CD⊂平面BCD，所以AO⊥CD.(2)分别取AB,AC的中点M,N，连接OM,ON,MN，于是MN⎳BC,OM⎳AD，则∠OMN是异面直线BC与AD所成的角或其补角，由(1)知，AO ⊥BD ，又AO =BO ，AB =AD ，则∠ADB =∠ABD =π4，于是∠BAD =π2，令AB =AD =2，则DC =BD =22，又BD ⊥DC ，则有BC =BD 2+DC 2=4，OC =DC 2+OD 2=10，又AO ⊥平面BCD ，OC ⊂平面BCD ，则AO ⊥OC ，AO =2，AC =AO 2+OC 2=23，由M ,N 分别为AB ,AC 的中点，得MN =12BC =2,OM =12AD =1,ON =12AC =3，显然MN 2=4=OM 2+ON 2，即有∠MON =π2，cos ∠OMN =OM MN =12，则∠OMN =π3，所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤：(1)平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线．(2)证明：证明所作的角是异面直线所成的角．(3)寻找：在立体图形中，寻找或作出含有此角的三角形，并解之．(4)取舍：因为异面直线所成角θ的取值范围是0,π2，所以所作的角为钝角时，应取它的补角作为异面直线所成的角．2、可通过多种方法平移产生，主要有三种方法：(1)直接平移法(可利用图中已有的平行线)；(2)中位线平移法；(3)补形平移法(在已知图形中，补作一个相同的几何体，以便找到平行线)．3、异面直线所成角：若n 1 ,n 2分别为直线l 1,l 2的方向向量，θ为直线l 1,l 2的夹角，则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图，在正四棱台ABCD -A 1B 1C 1D 1中，E ,F 分别是BB 1,CD 的中点.(1)证明：EF ⎳平面AB1C 1D ；(2)若AB =2A 1B 1，且正四棱台的侧面积为9，其内切球半径为22，O 为ABCD 的中心，求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析；(2)45【分析】(1)根据中位线定理，结合线面平行判定定理以及面面平行判定定理，利用面面平行的性质，可得答案；(2)根据题意，结合正四棱台的几何性质，求得各棱长，利用线线角的定义，可得答案.【解析】(1)取CC 1中点G ，连接GE ,GF ，如下图：在梯形BB 1C 1C 中，E ,G 分别为BB 1,CC 1的中点，则EG ⎳B 1C 1，同理可得FG ⎳C 1D ，因为EG ⊄平面AB 1C 1D ，B 1C 1⊂平面AB 1C 1D ，所以EG ⎳平面AB 1C 1D ，同理可得GF ⎳平面AB 1C 1D ，因为EG ∩FG =G ，EG ,FG ⊆平面EFG ，所以平面EFG ⎳平面AB 1C 1D ，又因为EF ⊆平面EFG ，所以EF ⎳平面AB 1C 1D ；(2)连接AC ,BD ，则AC ∩BD =O ，连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中，作B 1N ⊥BC 交BC 于N ，在平面BB 1D 1D 中，作B 1M ⊥BD 交BD 于M ，连接MN ，如下图：因为AB =2A 1B 1，则OC =A 1C 1，且OC ⎳A 1C 1，所以A 1C 1CO 为平行四边形，则A 1O ⎳CC 1，且A 1O =CC 1，所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角，同理可得：B 1D 1DO 为平行四边形，则B 1O =D 1D ，在正四棱台ABCD -A 1B 1C 1D 1中，易知对角面BB 1D 1D ⊥底面ABCD ，因为平面ABCD ∩平面BB 1D 1D =BD ，且B 1M ⊥BD ，B 1M ⊂平面BB 1D 1D ，所以B 1M ⊥平面ABCD ，由内切球的半径为22，则B 1M =2，在等腰梯形BB 1C 1C 中，BC =2B 1C 1且B 1N ⊥BC ，易知BN =14BC ，同理可得BM =14BD ，在△BCD 中，BN BC=BM BD =14，则MN =14CD ，设正方形ABCD 的边长为4x x >0 ，则正方形A 1B 1C 1D 1的边长为2x ，MN =x ，由正四棱台的侧面积为9，则等腰梯形BB 1C 1C 的面积S =94，因为B 1M ⊥平面ABCD ，MN ⊂平面ABCD ，所以B 1M ⊥MN ，在Rt △B 1MN ，B 1N =B 1M 2+MN 2=2+x 2，可得S =12⋅B 1N ⋅B 1C 1+BC ，则94=12×2+x 2×4x +2x ，解得x =12，所以BC =2，B 1C 1=1，BN =14BC =12，B 1N =32，则A 1B 1=1，在Rt △BB 1N 中，BB 1=B 1N 2+BN 2=102，则CC 1=DD 1=102，所以在△A 1OB 1中，则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45，所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图，平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等，平面CDD 1C 1⊥平面ABCD ，AD ⊥DC ，二面角D 1-AD -C 的大小为120°，E 为棱C 1D 1的中点．(1)证明：CD ⊥AE ；(2)点F 在棱CC 1上，AE ⎳平面BDF ，求直线AE 与DF 所成角的余弦值．【答案】(1)证明见解析；(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直，由二面角定义可得∠D 1DC =120°，进而根据中点得线线垂直即可求；(2)由线面平行的性质可得线线平行，由线线角的几何法可利用三角形的边角关系求解，或者建立空间直角坐标系，利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ，且两平面交线为DC ,AD ⊥DC ，AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1，所以AD ⊥D 1D ,AD ⊥DC ，∠D 1DC 是二面角D 1-AD -C 的平面角，故∠D 1DC =120°．连接DE ，E 为棱C 1D 1的中点，则DE ⊥C 1D 1,C 1D 1⎳CD ，从而DE ⊥CD ．又AD ⊥CD ，DE ∩AD =D ，DE ,AD ⊂平面AED ，所以CD ⊥平面AED ，ED ⊂平面AED ,因此CD ⊥AE ．(2)解法1：设AB =2，则DE =D 1D 2-12D 1C 1 2=3，所以CE =AE =AD 2+DE 2=7．连AC 交BD 于点O ，连接CE 交DF 于点G ，连OG ．因为AE ⎳平面BDF ，AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ，所以AE ∥OG ，因为O 为AC 中点，所以G 为CE 中点，故OG =12AE =72．且直线OG 与DF 所成角等于直线AE 与DF 所成角．在Rt △EDC 中，DG =12CE =72，因为OD =2，所以cos ∠OGD =722+72 2-(2)22×72×72=37．因此直线AE 与DF 所成角的余弦值为37．解法2；设AB =2，则DE =D 1D 2-12D 1C 1 2=3，所以CE =AE =AD 2+DE 2=7．取DC 中点为G ，连接EG 交DF 于点H ，则EG =DD 1=2．连接AG 交BD 于点I ，连HI ，因为AE ⎳平面BDF ，AE ⊂平面AGE ，平面AGE ∩平面BDF =IH ，所以AE ∥IH ．HI 与DH 所成角等于直线AE 与DF 所成角．正方形ABCD 中，GI =13AG ，DI =13DB =223，所以GH =13EG ，故HI =13AE =73．在△DHG 中，GH =13EG =23，GD =1，∠EGD =60°，由余弦定理DH =1+49-1×23=73．在△DHI 中，cos ∠DHI =732+73 2-223 22×73×73=37．因此直线AE 与DF 所成角的余弦值为37．解法3:由(1)知DE ⊥平面ABCD ，以D 为坐标原点，DA为x 轴正方向，DA为2个单位长，建立如图所示的空间直角坐标系D -xyz ．由(1)知DE =3，得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3)，C 1(0,1,3)．则CC 1=(0,-1,3)，DC =(0,2,0)，AE =(-2,0,3)，DB =(2,2,0)．由CF =tCC 1 0≤t ≤1 ，得DF =DC +CF =(0,2-t ,3t )．因为AE ⎳平面BDF ，所以存在唯一的λ，μ∈R ，使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ，故2λ=-2,2λ+2μ-tμ=0,3μt =3，解得t =23，从而DF =0,43,233 ．所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37．题型二：空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图，三棱柱ABC -A 1B 1C 1中，四边形ACC 1A 1,BCC 1B 1均为正方形，D ,E 分别是棱AB ,A 1B 1的中点，N 为C 1E 上一点.(1)证明：BN ⎳平面A 1DC ；(2)若AB =AC ,C 1E =3C 1N，求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ，可得BN ⎳平面A 1DC ；(2)建立空间直角坐标系，利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1，且AB =A 1B 1，又D ,E 分别是棱AB ,A 1B 1的中点，所以BD ⎳A 1E ，且BD =A 1E ，所以四边形BDA 1E 为平行四边形，所以A 1D ⎳EB ，又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ，所以EB ⎳平面A 1DC ，因为DE ⎳BB 1⎳CC 1，且DE =BB 1=CC 1，所以四边形DCC 1E 为平行四边形，所以C 1E ⎳CD ，又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ，所以C 1E ⎳平面A 1DC ，因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1，所以平面BEC 1⎳平面A 1DC ，因为BN ⊂平面BEC 1，所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形，所以CC 1⊥AC ,CC 1⊥BC ，所以CC 1⊥平面ABC .因为DE ⎳CC 1，所以DE ⊥平面ABC ，从而DE ⊥DB ,DE ⊥DC .又AB =AC ，所以△ABC 为等边三角形.因为D 是棱AB 的中点，所以CD ⊥DB ，即DB ,DC ,DE 两两垂直.以D 为原点，DB ,DC ,DE 所在直线为x ,y ,z 轴，建立如图所示的空间直角坐标系D -xyz .设AB =23，则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ，所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量，则n ⋅DC=0n ⋅DA 1 =0，即3y =0-3x +23z =0 ，可取n=2,0,1 .因为C 1E =3C 1N ，所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ，则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510，即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法)：(1)先确定斜线与平面，找到线面的交点B 为斜足；找线在面外的一点A ，过点A 向平面α做垂线，确定垂足O ；(2)连结斜足与垂足为斜线AB 在面α上的投影；投影BO 与斜线AB 之间的夹角为线面角；(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。

高中立体几何证明题

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1}，E，F分别是AB，BC的中点，求证：EF∥平面A_{1}C_{1}D。

解析1. 连接AC。

- 在 ABC中，因为E，F分别是AB，BC的中点，所以EF∥ AC。

2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中：- AC∥ A_{1}C_{1}。

- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。

- 又A_{1}C_{1}⊂平面A_{1}C_{1}D，EFnot⊂平面A_{1}C_{1}D。

- 根据线面平行的判定定理，所以EF∥平面A_{1}C_{1}D。

题2在三棱柱ABC - A_{1}B_{1}C_{1}中，D是AB的中点，求证：AC_{1}∥平面CDB_{1}。

解析1. 连接BC_{1}，交B_{1}C于点E。

- 在三棱柱ABC - A_{1}B_{1}C_{1}中，E为BC_{1}的中点。

2. 因为D是AB的中点：- 所以在 ABC_{1}中，DE∥ AC_{1}。

- 又DE⊂平面CDB_{1}，AC_{1}not⊂平面CDB_{1}。

- 根据线面平行的判定定理，可得AC_{1}∥平面CDB_{1}。

二、线面垂直的证明题3在四棱锥P - ABCD中，底面ABCD是正方形，PA = PB = PC = PD，求证：PA⊥平面ABCD。

解析1. 连接AC，BD交于点O，连接PO。

- 因为底面ABCD是正方形，所以O为AC，BD中点。

- 又PA = PC，PB = PD，根据等腰三角形三线合一的性质：- 可得PO⊥ AC，PO⊥ BD。

- 而AC∩ BD = O，AC⊂平面ABCD，BD⊂平面ABCD。

- 根据直线与平面垂直的判定定理，所以PO⊥平面ABCD。

- 又PA = PB = PC = PD，AO = BO = CO = DO，所以 PAO≅ PBO≅ PCO ≅ PDO。

第八讲立体几何(基础大题)

立体几何大题一证明方法汇总二同步练习汇总：1、已知四边形ABCD 是空间四边形，,,,E F G H 分别是边,,,AB BC CD DA 的中点（1）求证：EFGH 是平行四边形（2）若BD=23，AC=2，EG=2。

求异面直线AC 、BD 所成的角和EG 、BD 所成的角。

AHGFEDCB22．如图，四面体ABCD 中，BCD AD 平面⊥，E 、F 分别为AD 、AC 的中点，CD BC ⊥．求证：（1）BCD EF 平面// （2）ACD BC 平面⊥．（简单题），以线面平行的性质定理去找平行线，用判定定理证明！！！！3. 如图，P 为ABC ∆所在平面外一点，⊥PA 平面ABC ，︒=∠90ABC ，PB AE ⊥于E ，PC AF ⊥于F求证：（1）⊥BC 平面PAB ；（2）⊥AE 平面PBC ；（3）⊥PC 平面AEF ．线面垂直的经典例题！！！！！！！！4、如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，FEPCBA（1）求证：AC ⊥平面B 1D 1DB; （2）求证：BD 1⊥平面ACB 1 （3）求三棱锥B-ACB 1体积．5、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点. 求证：（１） C 1O ∥面11AB D（2 ）1AC ⊥面11AB D ． D 1ODB AC 1B 1A 1C6、如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点求证：（1）PA ∥平面BDE D 1C 1B 1A CDBA4（2）平面PAC ⊥平面BDE（3）若棱锥的棱长都为2，求棱锥的体积。

7.如图，PA ⊥平面ABC ，平面PAB ⊥平面PBC 求证：AB ⊥BC8.如图，在三棱锥S-ABC 中，,90︒=∠=∠=∠ACB SAC SAB , （Ⅰ）证明SC ⊥BC ；PA B CS（Ⅱ）,29,13,2===SB BC AC 若已知求侧面SBC 与底面ABC 所成二面角的大小。

立体几何练习题

立体几何题型一、平行与垂直的证明例1．如图，在四棱锥P —ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD =DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F . （1）证明PA //平面EDB ；（2）证明PB ⊥平面EFD例2．四棱锥S A B C D -中，底面ABCD 为平行四边形，侧面SB C ⊥底面ABCD ，已知45A B C ∠=︒，2A B =，BC =SA SB ==（Ⅰ）证明：SA B C ⊥；（Ⅱ）求直线SD 与平面SBC 所成角的大小．变式：已知四棱锥P -ABCD 的底面为直角梯形，AB ∥DC ，⊥=∠PA DAB ,90底面ABCD ，且PA =AD =DC =21AB =1，M 是PB 的中点.（Ⅰ）证明：面PAD ⊥面PCD ；（Ⅱ）求AC 与PB 所成的角；（Ⅲ）求面AMC 与面BMC 所成二面角的大小.ACDBCASOE A DCBNM EP题型二、空间角与距离例3．如图，在四棱锥O A B C D -中，底面A B C D 四边长为1的菱形，4A B C π∠=， OA ABCD ⊥底面， 2O A =，M 为O A 的中点。

（Ⅰ）求异面直线AB 与MD 所成角的大小；（Ⅱ）求点B 到平面OCD 的距离。

例4. 如图，四面体ABCD 中，O 、E 分别BD 、BC 的中点，CA =CB =CD =BD =2 （Ⅰ）求证：AO ⊥平面BCD ；（Ⅱ）求异面直线AB 与CD 所成角的大小；（Ⅲ）求点E 到平面的距离. 变式：如图，正三棱锥O A B C -的三条侧棱O A 、O B 、O C 两两垂直，且长度均为2．E 、F 分别是A B 、A C 的中点，H 是E F 的中点，过E F 的平面与侧棱O A 、O B 、O C 或其延长线分别相交于1A 、1B 、1C ，已知132O A =．（1）求证：11B C ⊥面O A H ；（2）求二面角111O A BC --的大小．1C 1A题型三、探索性问题例5.在四棱锥P-ABCD 中，底面ABCD 是矩形，侧棱PA 垂直于底面，E 、F 分别是AB 、PC 的中点．（1）求证：//EF 平面PAD ；（2）当平面PCD 与平面ABCD 成多大二面角时，⊥EF 平面PCD ？变式：如图，在三棱锥A －BCD 中，侧面ABD 、ACD 是全等的直角三角形，AD 是公共的斜边，且AD ，BD ＝CD ＝1，另一个侧面是正三角形 (1)求证：AD ⊥BC(2)求二面角B －AC －D 的大小(3)在直线AC 上是否存在一点E ，使ED 与面BCD 成30︒角？若存在，确定E 的位置；若不存在，说明理由.DC题型四、折叠、展开问题例6．已知正方形A B C D E 、F 分别是A B 、C D 的中点，将AD E 沿D E 折起，如图所示，记二面角A D E C --的大小为(0)θθπ<< (1) 证明//B F 平面ADE ；(2)若A C D 为正三角形，试判断点A 在平面B C D E 内的射影G 是否在直线E F 上，证明你的结论，并求角θ的余弦值。

立体几何平行证明题

立体证明题(2)1•如图，直二面角D- AB- E中，四边形ABCD是正方形，AE=EB F为CE上的点，且BF丄平面ACE(1) 求证：AE丄平面BCE(2) 求二面角B-AC- E的余弦值.2•等腰△ ABC中, AC=BC= AB=2, E、F分别为AC BC的中点，将△ EFC沿EF折起，使得C 至U P,得至U四棱锥P— ABFE 且AP=BP=(1) 求证：平面EFP!平面ABFE(2) 求二面角B-AP- E的大小.3•如图，在四棱锥P- ABCD中，底面是正方形，侧面PADL底面ABCD且PA=PD= AD,若E、F分别为PC BD的中点.(I)求证：EF//平面PAD(n)求证：EF丄平面PDC4•如图：正△ ABC与Rt△ BCD所在平面互相垂直，且/ BCD=90°,/ CBD=30°(1)求证：AB丄CD(2)求二面角D- AB- C的正切值.5•如图，在四棱锥P- ABCD中，平面PADL平面ABCD^ PAD是等边三角形，四边形ABCD 是平行四边形，/ ADC=120 , AB=2AD(1)求证：平面PADL平面PBD(2)求二面角A- PB- C的余弦值.6•如图，在直三棱柱ABC- A1B1C1 中，/ ACB=90°, AC=CB=CC2, E是AB中点.(I)求证：AB丄平面ACE(H)求直线AG与平面ACE所成角的正弦值.7•如图，在四棱锥P- ABCD中, PA丄平面ABCD / DAB为直角，AB// CD, AD=CD=2AB=2E, F分别为PC, CD的中点.(I)证明：AB丄平面BEF;(H)若PA=求二面角E- BD- C.8•如图，在四棱锥P-ABCD 中，PA丄平面ABCD , PA=AB=AD=2，四边形ABCD 满足AB 丄AD , BC // AD 且BC=4，点M 为PC 中点.(I)求证：DM丄平面PBC;BE(2)若点E为BC边上的动点，且一一，是否存在实数人使得二面角P- DE - B的EC2余弦值为-？若存在，求出实数入的值；若不存在，请说明理由.39•如图，ABED是长方形，平面ABEDL平面ABC AB=AC=5 BC=BE=6且M是BC的中点(I) 求证：AM L平面BEC(H) 求三棱锥B- ACE的体积；(川)若点Q是线段AD上的一点，且平面QECL平面BEC求线段AQ的长.10. 如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直，AB// CD AB丄BC, AB=2CD=2BC EA L EB(1)求证：EA丄平面EBC(2)求二面角C- BE- D的余弦值.11. 如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD// BC, / ADC=90°,平面PADL 底面ABCD O为AD中点，M是棱PC上的点，AD=2BC(1)求证：平面POBL平面PAD12. 如图，三棱柱ABC- A1B1C中，侧棱AA丄平面ABC △ ABC为等腰直角三角形，/BAC=90，且AB=AA, E、F 分别是CC, BC的中点.(1)求证：平面ABF丄平面AEF;(2)求二面角B1- AE- F 的余弦值.13. 如图，在菱形ABCD中，/ ABC=60°, AC与BD相交于点Q AE丄平面ABCD CF/ AE, AB=AE=2．(I )求证：BD丄平面ACFE(II )当直线FO与平面BDE所成的角为45。

立体几何证明题常见题型01

A B CDP EF立体几何证明题常见题型1、如图，在四棱锥ABCD P -中，底面ABCD 是正方形，侧棱⊥PD 底面ABCD ，1==DC PD ，E 是PC 的中点，作PB EF ⊥交PB 于点F ．(I) 证明： PA ∥平面EDB ；(II) 证明：PB ⊥平面EFD ；(III) 求三棱锥DEF P -的体积．2、如图，已知四棱锥P ABCD -的底面为等腰梯形，AB ∥CD ,AC BD ⊥,垂足为H ，PH 是四棱锥的高。

（Ⅰ）证明：平面PAC ⊥ 平面PBD ; （Ⅱ）若6AB =,APB ADB ∠=∠=60°,求四棱锥P ABCD -的体积。

3、如图，矩形ABCD 中，ABE AD 平面⊥，2===BC EB AE ，F 为CE 上的点，且ACE BF 平面⊥. （Ⅰ）求证：BCE AE 平面⊥；（Ⅱ）求证；BFD AE 平面//；（Ⅲ）求三棱锥BGF C -的体积.4、如图，正方形ABCD 和四边形ACEF 所在的平面互相垂直。

EF//AC ，AB=2,CE=EF=1 （Ⅰ）求证：AF//平面BDE ；（Ⅱ）求证：CF ⊥平面BDF;5、在如图所示的几何体中，四边形ABCD 是正方形，BCD A MA 平面⊥,PD ∥MA ,E G F 、、分别为MB 、PC PB 、的中点，且2MA PD AD ==.(Ⅰ) 求证：平面PDC EFG 平面⊥;ABCDHPABCDEFA BCDEFG(Ⅱ)求三棱锥的体积之比与四棱锥ABCD P MAB P --.6、如图所示，矩形ABCD 中，AD ⊥平面ABE ，AE=EB=BC=2，F 为CE 上的点，且BF ⊥平面ACE （1）求证：AE ⊥平面BCE ；（2）求证：AE ∥平面BFD ；（3）求三棱锥C-BGF 的体积。

7、在三棱锥S —ABC 中，∠SAB =∠SAC =∠ACB =90°，且AC =BC =5，SB =55。

立体几何100题

立体几何100题1.如图，三角形中，，是边长为l 的正方形，平面底面，若分别是的中点.（1）求证：底面；（2）求几何体的体积.2．在三棱锥P ABC -中， PAC ∆和PBC ∆ 2AB =， ,O D分别是,AB PB 的中点.（1）求证： //OD 平面PAC ；（2）求证: OP ⊥平面ABC ；（3）求三棱锥D ABC -的体积.3．如图，在直三棱柱111ABC A B C -中， 090BAC ∠=，2AB AC ==，点,M N 分别为111,AC AB 的中点.（1）证明： //MN 平面11BB C C ；（2）若CM MN ⊥，求三棱锥M NAC -的体积.. 4．如图，在三棱柱中，平面，点是与的交点，点在线段上，平面.（1）求证：；（2）若,求点到平面的距离.5．如图，四棱锥P A B C -中，底面ABCD 是直角梯形，1,//,2AB BC AD BC AB BC AD ⊥==， PAD ∆是正三角形， E 是PD 的中点．（1）求证： AD PC ⊥；（2）判定CE 是否平行于平面PAB ，请说明理由．6．如图，在四棱锥S ABCD -中，侧面SAD ⊥底面ABCD ， SA SD =， //AD BC ， 22AD BC CD ==， M ， N 分别为AD ， SD 的中点．（1）求证： //SB 平面CMN ；（2）求证： BD ⊥平面SCM ．7．如图，在矩形中，，平面，分别为的中点，点是上一个动点．(1) 当是中点时，求证:平面平面；(2) 当时，求的值．8．如图，在正三棱柱111A B C ABC -中，点,D E 分别是1,AC AB 的中点．求证： ED ∥平面11BB C C若1AB =求证：A 1B ⊥平面B 1CE.9．如图，在长方体1111ABCD A BC D -中， 12,1,1AB AD A A ===.（1）证明直线1BC 平行于平面1D AC ；（2）求直线1BC 到平面1D AC 的距离.10．如图所示，菱形ABCD 与正三角形BCE 所在平面互相垂直， FD ⊥平面ABCD ，且2AB =， FD（1）求证： //EF 平面ABCD ；（2）若3CBA π∠=，求几何体EFABCD 的体积.11．在直三棱柱ABC －A 1B 1C 1中，AB ＝AC ，E 是BC 的中点，求证：（Ⅰ）平面AB 1E ⊥平面B 1BCC 1；（Ⅱ）A 1C //平面AB 1E ．12．如图，在三棱柱中，平面，，，点为的中点. （1）证明：平面；（2）求三棱锥的体积.13．如图，在多面体中，四边形是正方形，在等腰梯形中，，，，为中点，平面平面.(1)证明：；(2)求三棱锥的体积.14．已知三棱锥，，，为的中点，平面，，，是中点，与所成的角为，且.（1）求证：；（2）求三棱锥的体积.15．在四棱锥中，平面平面，，是等边三角形，已知，，.（1）设是上一点，求证：平面平面.（2）求四棱锥的体积.-中，PA⊥底面A B C D，底面A B C D为菱形，16．如图，在四棱锥P ABCD60∠=，1,ABC==为PC的中点PA PB E.（1）求证： //PA 平面BDE ；（2）求三棱锥P BDE -的体积.17．如图，在直三棱柱（侧棱与底面垂直的棱柱）111ABC A B C -中，点G 是AC 的中点．（1）求证： 1//B C 平面1A BG ；（2）若A B B C =， 1AC ，求证： 11AC A B ⊥． 18．如图所示，四棱锥S ABCD -中，平面SAD ⊥平面ABCD ， SA AD ⊥， //AD BC ，43SA BC AB ==24AD ==．（1）证明：在线段SC 上存在一点E ，使得//ED 平面SAB ；（2）若AB AC =，在（1）的条件下，求三棱锥S AED -的体积． 19．（本小题共12分）如图，边长为3的正方形ABCD 所在平面与等腰直角三角形ABE 所在平面互相垂直，AE AB ⊥，且2EM MD =， 3AB AN =.（Ⅰ）求证： //MN 平面BEC ；（Ⅱ）求三棱锥E BMC -的体积.20．如图，在四棱锥中，底面是边长为2的正方形，分别为的中点，平面底面.（1）求证:平面；（2）若，求三棱锥的体积.21．在直三棱柱ABC －A 1B 1C 1中，AB ＝AC ，E 是BC 的中点，求证：（Ⅰ）平面AB 1E ⊥平面B 1BCC 1；（Ⅱ）A 1C //平面AB 1E ．22．如图1，四边形ABCD 为等腰梯形， 2,1AB AD DC CB ====，将ADC ∆沿AC 折起，使得平面ADC ⊥平面ABC ， E 为AB 的中点，连接,DE DB .（1）求证： BC AD ⊥；（2）求E 到平面BCD 的距离. 23．如图，四棱锥中，底面为菱形，平面，为的中点．（Ⅰ）证明：平面；（Ⅱ）设，求三棱锥的体积．24．如图，在多面体中，四边形是正方形，在等腰梯形中，，，，为中点，平面平面.(1)证明：；(2)求三棱锥的体积.25．如图1，在矩形中，，，是的中点，将沿折起，得到如图2所示的四棱锥，其中平面平面.（1）证明：平面；（2）设为的中点，在线段上是否存在一点，使得平面，若存在，求出的值；若不存在，请说明理由.26．如图，在四棱锥P ABCD -中， 90ABC ACD ∠=∠=， BAC ∠ 60CAD =∠=，PA ⊥平面ABCD ， 2,1PA AB ==.设,M N 分别为,PD AD 的中点.（1）求证：平面CMN ∥平面PAB ；（2）求三棱锥P ABM -的体积.27．如图所示，在长方体1111ABCD A BC D -中，底面ABCD 是边长为1的正方形， 12AA =，P 为棱1BB 上的一个动点.（1）求三棱锥1C PAA -的体积；（2）当1A P PC +取得最小值时，求证： 1PD ⊥平面PAC . 28．在三棱柱111ABC A B C -中，已知侧棱1CC ⊥底面,ABCM 为BC 的中点，13,2,AC AB BC CC ===（1）证明: 1B C ⊥平面1AMC ；（2）求点1A 到平面1AMC 的距离.29．五边形11ANB C C 是由一个梯形1ANB B 与一个矩形11BB C C 组成的，如图甲所示，B 为AC 的中点， 128AC CC AN ===．先沿着虚线1BB 将五边形11ANB C C 折成直二面角1A BB C --，如图乙所示．（Ⅰ）求证：平面BNC ⊥平面11C B N ；（Ⅱ）求图乙中的多面体的体积．30．如图1， 1AFA ∆中， 11,82FA FA AA CF ===，，点,,B C D 为线段1AA 的四等分点，线段,,BE CF DG 互相平行，现沿,,BE CF DG 折叠得到图2所示的几何体，此几何体的底面ABCD 为正方形.（1）证明： ,,,A E F G 四点共面；（2）求四棱锥B AEFG -的体积.31．如图，三棱锥P ABC -中， PC ⊥平面ABC ， ,,F G H 分别是,,PC AC BC 的中点，I 是线段FG 上的任意一点， 22PC AB BC ===，过点F 作平行于底面ABC 的平面DEF 交AP 于点D ，交BP 于点E . （1）求证： //HI 平面ABD ；（2）若AC BC ⊥，求点E 到平面FGH 的距离.32．如图，已知正方体的棱长为3，分别是棱、上的点，且.（1）证明：四点共面；（2）求几何体的体积.33．如图，在四棱柱1111ABCD A BC D -中，已知平面11AAC C ⊥平面A B C D ，且AB BC == 1AD CD ==．（1）求证： 1BD AA ⊥；（2）若E 为棱BC 的中点，求证： //AE 平面11DCC D ． 34．如图，在三棱柱111ABC A B C -中，底面ABC ∆是等边三角形，且1AA ⊥平面ABC , D 为AB 的中点，(Ⅰ) 求证：直线1//BC 平面1ACD ； (Ⅱ) 若12,AB BB E ==是1BB 的中点，求三棱锥1A CDE -的体积；35．如图，将菱形沿对角线折叠，分别过，作所在平面的垂线，，垂足分别为，，四边形为菱形，且.（1）求证：平面；（2）若，求该几何体的体积.36．如图，在四棱锥P ABCD -中， 122PC AD CD AB ====， //AB DC ， AD CD ⊥， PC ⊥平面ABCD .（1）求证： BC ⊥平面PAC ；（2）若M 为线段PA 的中点，且过,,C D M 三点的平面与线段PB 交于点N ，确定点N 的位置，说明理由；并求三棱锥A CMN -的高.37．如图，在四棱锥O ABCD -中，底面ABCD 是边长为2的正方形，侧棱OB ⊥底面ABCD ，且侧棱OB 的长是2，点,,E F G 分别是,,AB OD BC 的中点.（Ⅰ）证明： OD ⊥平面EFG ；（Ⅱ）求三棱锥O EFG -的体积.38．如图，多面体ABCDEF 中， //,AD BC AB AD ⊥, FA ⊥平面,//ABCD FA DE ，且222AB AD AF BC DE =====.（Ⅰ）M 为线段EF 中点，求证： //CM 平面ABF ；（Ⅱ）求多面体ABCDEF 的体积.39．在如图所示的几何体中，四边形11BB C C 是矩形， 1BB ⊥平面ABC ，1111//,2,A B AB AB A B E =是AC 的中点.（1）求证： 1//A E 平面11BB C C ；（2）若AC BC =， 12AB BB =，求证平面1BEA ⊥平面11AAC .40．如图，四边形ABCD 为梯形， AB CD ， PD ⊥平面A B C D ，90BAD ADC ∠∠==︒， 22DC AB a ==， DA =， E 为BC 中点.（1）求证：平面PBC ⊥平面PDE ；（2）线段PC 上是否存在一点F ，使PA 平面BDF ？若有，请找出具体位置，并进行证明：若无，请分析说明理由.41．已知四棱锥S ABCD -中，底面ABCD 是边长为2的菱形， 60BAD ∠=︒，SA SD SB =E 是棱AD 的中点，点F 在棱SC 上，且SFSCλ=， SA //平面BEF ．（Ⅰ）求实数λ的值；（Ⅱ）求三棱锥F EBC -的体积．42．在三棱柱ABC-A 1B 1C 1中，AB=BC=CA=AA 1=2，侧棱AA 1⊥平面ABC ，且D ，E 分别是棱A 1B 1，AA 1的中点，点F 在棱AB 上，且AF=14AB 。

立体几何平行证明题

立体证明题（2）1.如图，直二面角D﹣AB﹣E中，四边形ABCD是正方形，AE=EB，F为CE上的点，且BF⊥平面ACE．（1）求证：AE⊥平面BCE；（2）求二面角B﹣AC﹣E的余弦值．2.等腰△ABC中，AC=BC=，AB=2，E、F分别为AC、BC的中点，将△EFC沿EF折起，使得C到P，得到四棱锥P﹣ABFE，且AP=BP=．（1）求证：平面EFP⊥平面ABFE；（2）求二面角B﹣AP﹣E的大小．3.如图，在四棱锥P﹣ABCD中，底面是正方形，侧面PAD⊥底面ABCD，且PA=PD=AD，若E、F分别为PC、BD的中点．（Ⅰ）求证：EF∥平面PAD；（Ⅱ）求证：EF⊥平面PDC．4.如图：正△ABC与Rt△BCD所在平面互相垂直，且∠BCD=90°，∠CBD=30°．（1）求证：AB⊥CD；（2）求二面角D﹣AB﹣C的正切值．5.如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，△PAD是等边三角形，四边形ABCD 是平行四边形，∠ADC=120°，AB=2AD．（1）求证：平面PAD⊥平面PBD；（2）求二面角A﹣PB﹣C的余弦值．6.如图，在直三棱柱ABC ﹣A 1B 1C 1中，∠ACB=90°，AC=CB=CC 1=2，E 是AB 中点．（Ⅰ）求证：AB 1⊥平面A 1CE ；（Ⅱ）求直线A 1C 1与平面A 1CE 所成角的正弦值．7.如图，在四棱锥P ﹣ABCD 中，PA ⊥平面ABCD ，∠DAB 为直角，AB ∥CD ，AD=CD=2AB=2，E ，F 分别为PC ，CD 的中点．（Ⅰ）证明：AB ⊥平面BEF ；（Ⅱ）若PA=，求二面角E ﹣BD ﹣C ．8.如图，在四棱锥P ﹣ABCD 中，PA ⊥平面ABCD ，PA=AB=AD=2，四边形ABCD 满足AB ⊥AD ，BC ∥AD 且BC=4，点M 为PC 中点．（1）求证：DM ⊥平面PBC ；（2）若点E 为BC 边上的动点，且λ=EC BE ，是否存在实数λ，使得二面角P ﹣DE ﹣B 的余弦值为32？若存在，求出实数λ的值；若不存在，请说明理由．9.如图，ABED是长方形，平面ABED⊥平面ABC，AB=AC=5，BC=BE=6，且M是BC的中点（Ⅰ）求证：AM⊥平面BEC；（Ⅱ）求三棱锥B﹣ACE的体积；（Ⅲ）若点Q是线段AD上的一点，且平面QEC⊥平面BEC，求线段AQ的长．10.如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直，AB∥CD，AB⊥BC，AB=2CD=2BC，EA⊥EB（1）求证：EA⊥平面EBC（2）求二面角C﹣BE﹣D的余弦值．11.如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，O为AD中点，M是棱PC上的点，AD=2BC．（1）求证：平面POB⊥平面PAD；12.如图，三棱柱ABC﹣A1B1C1中，侧棱AA1⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，E、F分别是CC1，BC的中点．（1）求证：平面AB1F⊥平面AEF；（2）求二面角B1﹣AE﹣F的余弦值．13.如图，在菱形ABCD中，∠ABC=60°，AC与BD相交于点O，AE⊥平面ABCD，CF∥AE，AB=AE=2．（ I）求证：BD⊥平面ACFE；（ II）当直线FO与平面BDE所成的角为45°时，求二面角B﹣EF﹣D的余弦角．14.如图所示，该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成，AD⊥AF，AE=AD=2．（1）证明：平面PAD⊥平面ABFE；（2）求正四棱锥P﹣ABCD的高h，使得二面角C﹣AF﹣P的余弦值是．15.如图，已知斜三棱柱ABC一A1B1C1，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，且BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求二面角A﹣A1B﹣C的平面角的余弦值．试卷答案1.【考点】与二面角有关的立体几何综合题；直线与平面垂直的判定．【分析】（1）由已知中直二面角D﹣AB﹣E中，四边形ABCD是正方形，且BF⊥平面ACE，我们可以证得BF⊥AE，CB⊥AE，进而由线面垂直的判定定理可得AE⊥平面BCE．（2）连接BD与AC交于G，连接FG，设正方形ABCD的边长为2，由三垂线定理及二面角的平面角的定义，可得∠BGF是二面角B﹣AC﹣E的平面角，解Rt△BFG即可得到答案．【解答】证明：（1）∵BF⊥平面ACE∴BF⊥AE…∵二面角D﹣AB﹣E为直二面角，且CB⊥AB，∴CB⊥平面ABE∴CB⊥AE…∴AE⊥平面BCE．…解：（2）连接BD与AC交于G，连接FG，设正方形ABCD的边长为2，∴BG⊥AC，BG=，…∵BF垂直于平面ACE，由三垂线定理逆定理得FG⊥AC∴∠BGF是二面角B﹣AC﹣E的平面角…由（1）AE⊥平面BCE，得AE⊥EB，∵AE=EB，BE=．∴在Rt△BCE中，EC==，…由等面积法求得，则∴在Rt△BFG中，故二面角B﹣AC﹣E的余弦值为．…2.【考点】二面角的平面角及求法；平面与平面垂直的判定．【分析】（1）用分析法找思路，用综合法证明．取EF中点O，连接OP、OC．等腰三角形CEF中有CO⊥EF，即OP⊥EF．根据两平面垂直的性质定理，平面PEF和平面ABFE的交线是EF，且PO⊥EF，分析得PO⊥平面ABFE．故只需根据题中条件证出PO⊥平面ABFE，即可利用面面垂直的判定定理证得平面EFP⊥平面ABFE．（2）根据第一问分析空间位置关系，可建立空间直角坐标线求得平面ABP和平面AEP的法向量的所成角，利用向量角和二面角关系，确定二面角大小．【解答】解：（1）证明：在△ABC中，D为AB中点，O为EF中点．由AC=BC=，AB=2．∵E、F分别为AC、BC的中点，∴EF为中位线，得CO=OD=1，CO⊥EF∴四棱锥P﹣ABFE中，PO⊥EF，…2分∵OD⊥AB，AD=OD=1，∴AO=，又AP=，OP=1，∴四棱锥P﹣ABFE中，有AP2=AO2+OP2，即OP⊥AO，…4分又AO∩EF=O，EF、AO⊂平面ABFE，∴OP⊥平面ABFE，…5分又OP⊂平面EFP，∴平面EFP⊥平面ABFE．…6分（2）由（1）知OD，OF，OP两两垂直，以O为原点，建立空间直角坐标系（如图）：则A（1，﹣1，0），B（1，1，0），E（0，，0），P（0，0，1）…7分∴，，设，分别为平面AEP、平面ABP的一个法向量，则⇒取x=1，得y=2，z=﹣1∴．…9分同理可得，…11分由于=0，所以二面角B﹣AP﹣E为90°．…12分3.【考点】空间中直线与平面之间的位置关系．【专题】证明题．【分析】对于（Ⅰ），要证EF∥平面PAD，只需证明EF平行于平面PAD内的一条直线即可，而E、F分别为PC、BD的中点，所以连接AC，EF为中位线，从而得证；对于（Ⅱ）要证明EF⊥平面PDC，由第一问的结论，EF∥PA，只需证PA⊥平面PDC即可，已知PA=PD=AD，可得PA⊥PD，只需再证明PA⊥CD，而这需要再证明CD⊥平面PAD，由于ABCD是正方形，面PAD⊥底面ABCD，由面面垂直的性质可以证明，从而得证．【解答】证明：（Ⅰ）连接AC，则F是AC的中点，在△CPA中，EF∥PA（3分）且PA⊂平面PAD，EF⊊平面PAD，∴EF∥平面PAD（6分）（Ⅱ）因为平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，又CD⊥AD，所以CD⊥平面PAD，∴CD⊥PA（9分）又PA=PD=AD，所以△PAD是等腰直角三角形，且∠APD=，即PA⊥PD（12分）而CD∩PD=D，∴PA⊥平面PDC，又EF∥PA，所以EF⊥平面PDC（14分）【点评】本题考查线面平行的判定及线面垂直的判定，而其中的转化思想的应用值得注意，将线面平行转化为线线平行；证明线面垂直，转化为线线垂直，在证明线线垂直时，往往还要通过线面垂直来进行．4.【考点】与二面角有关的立体几何综合题；空间中直线与直线之间的位置关系．【分析】（1）利用平面ABC⊥平面BCD，平面ABC∩平面BCD=BC，可得DC⊥平面ABC，利用线面垂直的性质，可得DC⊥AB；（2）过C作CE⊥AB于E，连接ED，可证∠CED是二面角D﹣AB﹣C的平面角．设CD=a，则BC==，从而EC=BCsin60°=，在Rt△DEC中，可求tan∠DEC．【解答】（1）证明：∵DC⊥BC，且平面ABC⊥平面BCD，平面ABC∩平面BCD=BC，∴DC⊥平面ABC，又AB⊂平面ABC，∴DC⊥AB．…（2）解：过C作CE⊥AB于E，连接ED，∵AB⊥CD，AB⊥EC，CD∩EC=C，∴AB⊥平面ECD，又DE⊂平面ECD，∴AB⊥ED，∴∠CED是二面角D﹣AB﹣C的平面角，…设CD=a，则BC==，∵△ABC是正三角形，∴EC=BCsin60°=，在Rt△DEC中，tan∠DEC=．…5.【考点】MT：二面角的平面角及求法；LY：平面与平面垂直的判定．【分析】（1）令AD=1，求出BD=，从而AD⊥BD，进而BD⊥平面PAD，由此能证明平面PAD⊥平面PBD．（2）以D为坐标原点，DA为x轴，DC为y轴，过D作垂直于平面ABCD的直线为z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣PB﹣C的余弦值．【解答】证明：（1）在平行四边形ABCD中，令AD=1，则BD==，在△ABD中，AD2+BD2=AB2，∴AD⊥BD，又平面PAD⊥平面ABCD，∴BD⊥平面PAD，BD⊂平面PBD，∴平面PAD⊥平面PBD．解：（2）由（1）得AD⊥BD，以D为坐标原点，DA为x轴，DC为y轴，过D作垂直于平面ABCD的直线为z轴，建立空间直角坐标系，令AD=1，则A（1，0，0），B（0，，0），C（﹣1，，0），P（，0，），=（﹣1，，0），=（﹣），=（﹣1，0，0），设平面PAB的法向量为=（x，y，z），则，取y=1，得=（），设平面PBC的法向量=（a，b，c），，取b=1，得=（0，1，2），∴cos＜＞===，由图形知二面角A﹣PB﹣C的平面角为钝角，∴二面角A﹣PB﹣C的余弦值为﹣．6.【考点】直线与平面垂直的判定；直线与平面所成的角．【分析】（Ⅰ）由ABC﹣A1B1C1是直三棱柱，可知CC1⊥AC，CC1⊥BC，∠ACB=90°，AC⊥BC．建立空间直角坐标系C﹣xyz．则A，B1，E，A1，可得，，，可知，根据，，推断出AB1⊥CE，AB1⊥CA1，根据线面垂直的判定定理可知AB1⊥平面A1CE．（Ⅱ）由（Ⅰ）知是平面A1CE的法向量，，进而利用向量数量积求得直线A1C1与平面A1CE所成角的正弦值【解答】（Ⅰ）证明：∵ABC﹣A1B1C1是直三棱柱，∴CC1⊥AC，CC1⊥BC，又∠ACB=90°，即AC⊥BC．如图所示，建立空间直角坐标系C﹣xyz．A（2，0，0），B1（0，2，2），E（1，1，0），A1（2，0，2），∴，，．又因为，，∴AB1⊥CE，AB1⊥CA1，AB1⊥平面A1CE．（Ⅱ）解：由（Ⅰ）知，是平面A1CE的法向量，，∴|cos＜，＞|==．设直线A1C1与平面A1CE所成的角为θ，则sinθ=|cos＜，＞|=．所以直线A1C1与平面A1CE所成角的正弦值为．7.【考点】二面角的平面角及求法；直线与平面垂直的判定．【分析】（Ⅰ）只需证明AB⊥BF．AB⊥EF即可．（Ⅱ）以A为原点，以AB，AD，AP为x轴，y轴，z轴正向建立空间直角坐标系，求出平面CDB的法向量为，平面EDB的法向量为，设二面角E﹣BD﹣C的大小为θ，则=，【解答】解：（Ⅰ）证：由已知DF∥AB且∠DAB为直角，故ABFD是矩形，从而AB⊥BF．又PA⊥底面ABCD，∴平面PAD⊥平面ABCD，∵AB⊥AD，故AB⊥平面PAD，∴AB⊥PD，在△PCD内，E、F分别是PC、CD的中点，EF∥PD，∴AB⊥EF．由此得AB⊥平面BEF…（Ⅱ）以A为原点，以AB，AD，AP为x轴，y轴，z轴正向建立空间直角坐标系，则设平面CDB的法向量为，平面EDB的法向量为，则可取设二面角E﹣BD﹣C的大小为θ，则=，所以，…8.【考点】二面角的平面角及求法；直线与平面垂直的判定．【分析】（1）取PB中点N，连结MN，AN．由三角形中位线定理可得四边形ADMN为平行四边形．由AP⊥AD，AB⊥AD，由线面垂直的判定可得AD⊥平面PAB．进一步得到AN⊥MN．再由AP=AB，得AN⊥PB，则AN⊥平面PBC．又AN∥DM，得DM⊥平面PBC；（2）以A为原点，方向为x轴的正方向，方向为y轴的正方向，方向为z轴的正方向，建立如图所示的空间直角坐标系．设E（2，t，0）（0≤t≤4），再求得P，D，B的坐标，得到的坐标，求出平面PDE的法向量，再由题意得到平面DEB的一个法向量，由两法向量夹角的余弦值得到实数λ的值．【解答】（1）证明：如图，取PB中点N，连结MN，AN．∵M是PC中点，∴MN∥BC，MN=BC=2．又∵BC∥AD，AD=2，∴MN∥AD，MN=AD，∴四边形ADMN为平行四边形．∵AP⊥AD，AB⊥AD，AP∩AB=A，∴AD⊥平面PAB．∵AN⊂平面PAB，∴AD⊥AN，则AN⊥MN．∵AP=AB，∴AN⊥PB，又MN∩PB=N，∴AN⊥平面PBC．∵AN∥DM，∴DM⊥平面PBC；（2）解：存在符合条件的λ．以A为原点，方向为x轴的正方向，方向为y轴的正方向，方向为z轴的正方向，建立如图所示的空间直角坐标系．设E（2，t，0）（0≤t≤4），P（0，0，2），D（0，2，0），B（2，0，0），则，．设平面PDE的法向量=（x，y，z），则，令y=2，则z=2，x=t﹣2，取平面PDE的一个法向量为=（2﹣t，2，2）．又平面DEB即为xAy平面，故其一个法向量为=（0，0，1），∴cos＜＞==．解得t=3或t=1，∴λ=3或．9.【考点】棱柱、棱锥、棱台的体积；平面与平面垂直的判定．【分析】（Ⅰ）推导出BE⊥AM，BC⊥AM，由此能证明AM⊥平面BEC．（Ⅱ）由V B﹣ACE=V E﹣ABC，能求出三棱锥B﹣ACE的体积．（Ⅲ）在平面QEC内作QN⊥EC，QN交CE于点N．QN与AM共面，设该平面为a，推导出四边形AMNQ是平行四方形，由此能求出AQ．【解答】证明：（Ⅰ）∵平面ABED⊥平面ABC，平面ABED∩平面ABC=AB，BE⊥AB，BE⊂平面ABED，∴BE⊥平面ABC，又AM⊂平面ABC，∴BE⊥AM．又AB=AC，M是BC的中点，∴BC⊥AM，又BC∩BE=B，BC⊂平面BEC，BE⊂平面BEC，∴AM⊥平面BEC．解：（Ⅱ）由（Ⅰ）知，BE⊥平面ABC，∴h=BE=6．在Rt△ABM中，，又，∴．（Ⅲ）在平面QEC内作QN⊥EC，QN交CE于点N．∵平面QEC⊥平面BEC，平面QEC∩平面BEC﹣EC，∴QN⊥平面BEC，又AM⊥平面BEC．∴QN∥AM．∴QN与AM共面，设该平面为a，∵ABED是长方形，∴AQ∥BE，又Q⊄平面BEC，BE⊂平面BEC，∴AQ∥平面BEC，又AQ⊂α，α∩平面BEC=MN，∴AQ∥MN，又QN∥AM，∴四边形AMNQ是平行四方形．∴AQ=MN．∵AQ∥BE，AQ∥MN，∴MN∥BE，又M是BC的中点．∴，∴AQ=MN=3．10.【考点】二面角的平面角及求法；直线与平面垂直的判定．【分析】（1）根据线面垂直的判定定理即可证明EA⊥平面EBC；（2）求出平面的法向量，利用向量法进行求解即可．【解答】（1）∵平面ABE⊥平面ABCD，且AB⊥BC，∴BC⊥平面ABE∵EA⊂平面ABE，∴EA⊥BC，∵EA⊥EB，EB∩BC=B，∴EA⊥平面EBC（2）取AB中O，连接EO，DO．∵EB=EA，∴EO⊥AB．∵平面ABE⊥平面ABCD，∴EO⊥平面ABCD∵AB=2CD，AB∥CD，AB⊥BC，∴DO⊥AB，建立如图的空间直角坐标系O﹣xyz如图：设CD=1，则A（0，1，0），B（0，﹣1，0），C（1，﹣1，0），D（1，0，0），E（0，0，1），由（1）得平面EBC的法向量为=（0，1，﹣1），设平面BED的法向量为=（x，y，z），则，即，设x=1，则y=﹣1，z=1，则=（1，﹣1，1），则|cos＜，＞|===，故二面角C﹣BE﹣D的余弦值是．11.【考点】平面与平面垂直的判定；直线与平面平行的判定．【分析】（1）证明四边形BCDO是平行四边形，得出OB⊥AD；再证明BO⊥平面PAD，从而证明平面POB⊥平面PAD；（2）解法一：由，M为PC中点，证明N是AC的中点，MN∥PA，PA∥平面BMO．解法二：由PA∥平面BMO，证明N是AC的中点，M是PC的中点，得．【解答】解：（1）证明：∵AD∥BC，，O为AD的中点，∴四边形BCDO为平行四边形，∴CD∥BO；又∵∠ADC=90°，∴∠AOB=90°，即OB⊥AD；又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，∴BO⊥平面PAD；又∵BO⊂平面POB，∴平面POB⊥平面PAD；（2）解法一：，即M为PC中点，以下证明：连结AC，交BO于N，连结MN，∵AD∥BC，O为AD中点，AD=2BC，∴N是AC的中点，又点M是棱PC的中点，∴MN∥PA，∵PA⊄平面BMO，MN⊂平面BMO，∴PA∥平面BMO．解法二：连接AC，交BO于N，连结MN，∵PA∥平面BMO，平面BMO∩平面PAC=MN，∴PA∥MN；又∵AD∥BC，O为AD中点，AD=2BC，∴N是AC的中点，∴M是PC的中点，则．12.【考点】与二面角有关的立体几何综合题；平面与平面垂直的判定．【分析】（1）连结AF，由已知条件推导出面ABC⊥面BB1C1C，从而AF⊥B1F，由勾股定理得B1F⊥EF．由此能证明平面AB1F⊥平面AEF．（2）以F为坐标原点，FA，FB分别为x，y轴建立直角坐标系，利用向量法能求出二面角B1﹣AE﹣F的余弦值．【解答】（1）证明：连结AF，∵F是等腰直角三角形△ABC斜边BC的中点，∴AF⊥BC．又∵三棱柱ABC﹣A1B1C1为直三棱柱，∴面ABC⊥面BB1C1C，∴AF⊥面BB1C1C，AF⊥B1F．…设AB=AA 1=1，则，EF=，．∴=，∴B 1F ⊥EF ．又AF ∩EF=F ，∴B 1F ⊥平面AEF ．…而B 1F ⊂面AB 1F ，故：平面AB 1F ⊥平面AEF ．…（2）解：以F 为坐标原点，FA ，FB 分别为x ，y 轴建立直角坐标系如图，设AB=AA 1=1，则F （0，0，0），A （），B 1（0，﹣，1），E （0，﹣，），，=（﹣，，1）．…由（1）知，B 1F ⊥平面AEF ，取平面AEF 的法向量：=（0，，1）．…设平面B 1AE 的法向量为，由，取x=3，得．…设二面角B 1﹣AE ﹣F 的大小为θ，则cos θ=|cos ＜＞|=||=．由图可知θ为锐角，∴所求二面角B 1﹣AE ﹣F 的余弦值为．…13.【考点】MT：二面角的平面角及求法；LW：直线与平面垂直的判定．【分析】（ I）只需证明DB⊥AC，BD⊥AE，即可得BD⊥平面ACFE；（ II）取EF的中点为M，以O为坐标原点，以OA为x轴，以OB为y轴，以OM为z轴，建立空间直角坐标系，则，D（0，﹣，0），F（﹣1，0，h），E（1，0，2），则，，利用向量法求解【解答】（ I）证明：在菱形ABCD中，可得DB⊥AC，又因为AE⊥平面ABCD，∴BD⊥AE，且AE∩AC=A，BD⊥平面ACFE；（ II）解：取EF的中点为M，以O为坐标原点，以OA为x轴，以OB为y轴，以OM为z 轴，建立空间直角坐标系，则，D（0，﹣，0），F（﹣1，0，h），E（1，0，2），则，，设平面BDE的法向量，由，可取，|cos|=，⇒h=3，故F（﹣1，0，3），，，设平面BFE的法向量为，由，可取，，设平面DFE的法向量为，由，可取，cos=，二面角B﹣EF﹣D的余弦值为．14.【考点】MT：二面角的平面角及求法；LY：平面与平面垂直的判定．【分析】（Ⅰ）证明：AD⊥平面ABFE，即可证明平面PAD⊥平面ABFE；（Ⅱ）建立空间坐标系，求出平面的法向量，利用向量法建立方程关系即可求正四棱锥P ﹣ABCD的高．【解答】（Ⅰ）证明：直三棱柱ADE﹣BCF中，AB⊥平面ADE，所以：AB⊥AD，又AD⊥AF，所以：AD⊥平面ABFE，AD⊂平面PAD，所以：平面PAD⊥平面ABFE…．（Ⅱ）∵AD⊥平面ABFE，∴建立以A为坐标原点，AB，AE，AD分别为x，y，z轴的空间直角坐标系如图：设正四棱锥P﹣ABCD的高为h，AE=AD=2，则A（0，0，0），F（2，2，0），C（2，0，2），=（2，2，0），=（2，0，2），=（1，﹣h，1），=（x，y，z）是平面AFC的法向量，则，令x=1，则y=z=﹣1，即=（1，﹣1，﹣1），设=（x，y，z）是平面ACP的法向量，则，令x=1，则y=﹣1，z=﹣1﹣h，即=（1，﹣1，﹣1﹣h），∵二面角C﹣AF﹣P的余弦值是．∴cos＜，＞===．得h=1或h=﹣（舍）则正四棱锥P﹣ABCD的高h=1．15.【考点】二面角的平面角及求法；直线与平面垂直的判定．【专题】证明题；数形结合；综合法；空间位置关系与距离．【分析】（1）推导出BC⊥AC，BC⊥AC1，BA1⊥AC1，由此能证明AC1⊥平面A1BC．（2）推导出平面A1AB⊥平面BCF，过C作CH⊥BF于H，则CH⊥面A1AB，求出CH=，过H作HG⊥A1B于G，连CG，则CG⊥A1B，从而∠CGH为二面角A﹣A1B﹣C的平面角，由此能求出二面角A﹣A1B﹣C的平面角的余弦值．【解答】证明：（1）因为A1D⊥平面ABC，所以，平面AA1C1C⊥平面ABC，又BC⊥AC，所以，BC⊥平面AA1C1C，得BC⊥AC1，又BA1⊥AC1，所以，AC1⊥平面A1BC．解：（2）因为AC1⊥A1C，所以四边形AA1C1C为菱形，故AA1=AC=2，又D为AC中点，知∠A1AC=60°，取AA1的中点F，则AA1⊥平面BCF，从而，平面A1AB⊥平面BCF，过C作CH⊥BF于H，则CH⊥面A1AB，在Rt△BCF，BC=2，CF=，故CH=，过H作HG⊥A1B于G，连CG，则CG⊥A1B，从而∠CGH为二面角A﹣A1B﹣C的平面角，在Rt△A1BC中，A1C=BC=2，所以，CG=，在Rt△CGH中，sin∠CGH=，cosCGH==．故二面角A﹣A1B﹣C的平面角的余弦值为．【点评】本题考查线面垂直的证明，考查二面角的余弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．。

立体几何证明题专题(教师版)

立体几何证明题考点1：点线面的位置关系及平面的性质例1.下列命题：①空间不同三点确定一个平面；②有三个公共点的两个平面必重合；③空间两两相交的三条直线确定一个平面；④三角形是平面图形；⑤平行四边形、梯形、四边形都是平面图形；⑥垂直于同一直线的两直线平行；⑦一条直线和两平行线中的一条相交，也必和另一条相交；⑧两组对边相等的四边形是平行四边形．其中正确的命题是________．【解析】由公理3知，不共线的三点才能确定一个平面，所以知命题①错，②中有可能出现两平面只有一条公共线(当这三个公共点共线时)，②错．③空间两两相交的三条直线有三个交点或一个交点，若为三个交点，则这三线共面，若只有一个交点，则可能确定一个平面或三个平面．⑤中平行四边形及梯形由公理2可得必为平面图形，而四边形有可能是空间四边形，如图(1)所示．在正方体ABCD—A′B′C′D′中，直线BB′⊥AB，BB′⊥CB，但AB与CB不平行，∴⑥错．AB∥CD，BB′∩AB＝B，但BB′与CD不相交，∴⑦错．如图(2)所示，AB＝CD，BC＝AD，四边形ABCD不是平行四边形，故⑧也错．【答案】④2.若P是两条异面直线l、m外的任意一点，则()A．过点P有且仅有一条直线与l、m都平行B．过点P有且仅有一条直线与l、m都垂直C．过点P有且仅有一条直线与l、m都相交D．过点P有且仅有一条直线与l、m都异面答案B解析对于选项A，若过点P有直线n与l，m都平行，则l∥m，这与l，m异面矛盾．对于选项B，过点P与l、m都垂直的直线，即过P且与l、m的公垂线段平行的那一条直线．对于选项C，过点P与l、m都相交的直线有一条或零条．对于选项D，过点P与l、m都异面的直线可能有无数条．3.已知异面直线a，b分别在平面α，β内，且α∩β＝c，那么直线c一定A．与a，b都相交B．只能与a，b中的一条相交C．至少与a，b中的一条相交D．与a，b都平行答案C解析若c与a，b都不相交，则c与a，b都平行，根据公理4，则a∥b，与a，b异面矛盾．考点2：共点、共线、共面问题例1.下列各图是正方体和正四面体，P、Q、R、S分别是所在棱的中点，这四个点不共面的图形是【解析】①在A中易证PS∥QR，∴P、Q、R、S四点共面．②在C中易证PQ∥SR，∴P、Q、R、S四点共面．③在D中，∵QR⊂平面ABC，PS∩面ABC＝P且P∉QR，∴直线PS与QR为异面直线．∴P、Q、R、S四点不共面．④在B中P、Q、R、S四点共面，证明如下：取BC中点N，可证PS、NR交于直线B1C1上一点，∴P、N、R、S四点共面，设为α.可证PS∥QN，∴P、Q、N、S四点共面，设为β.∵α、β都经过P、N、S三点，∴α与β重合，∴P、Q、R、S四点共面．【答案】D2.空间四点中，三点共线是这四点共面的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件答案A3.下面三条直线一定共面的是()A ．a 、b 、c 两两平行B ．a 、b 、c 两两相交C ．a ∥b ，c 与a 、b 均相交D ．a 、b 、c 两两垂直答案 C4.已知三个平面两两相交且有三条交线，试证三条交线互相平行或者相交于一点．【解析】设α∩β＝a ，β∩γ＝b ，γ∩α＝c ，由a ⊂β，b ⊂β，则a ∩b ＝O ，如图(1)，或a ∥b ，如图(2)，若a ∩b ＝O ，O ∈a ，a ⊂α，则O ∈α，O ∈b ，b ⊂γ，则O ∈γ，又γ∩α＝c ，因此O ∈c ；若a ∥b ，a ⊄γ，b ⊂γ，则a ∥γ，又a ⊂α，α∩γ＝c ，则a ∥c . 因此三条交线相交于一点或互相平行．5.如图所示，已知空间四边形ABCD 中，E 、H 分别是边AB ，AD 的中点，F ，G 分别是边BC ，CD 上的点，且CF CB ＝CG CD ＝23.(1)求证：三条直线EF ，GH ，AC 交于一点．(2)若在本题中，AE EB ＝CF FB ＝2，AH HD ＝CGGD ＝3，其他条件不变．求证：EH 、FG 、BD 三线共点．【解析】 (1)∵E ，H 分别是AB ，AD 的中点， ∴由中位线定理可知，EH 綊12BD . 又∵CF CB ＝CG CD ＝23，∴在△CBD 中，FG ∥BD ，且FG ＝23BD . ∴由公理4知，EH ∥FG ，且EH <FG .∴四边形EFGH 是梯形，EH 、FG 为上、下两底． ∴两腰EF 、GH 所在直线必相交于一点P . ∵P ∈直线EF ，EF ⊂平面ABC ， ∴P ∈平面ABC .同理可得P ∈平面ADC . ∴P 在平面ABC 和平面ADC 的交线上．又∵面ABC ∩面ADC ＝AC ， ∴P ∈直线AC .故EF 、GH 、AC 三直线交于一点． (2)∵AE EB ＝CFFB ＝2， ∴EF ∥AC .又AH HD ＝CGGD ＝3，∴HG ∥AC ，∴EF ∥HG ，且EF >HG . ∴四边形EFGH 为梯形．设EH 与FG 交于点P ，则P ∈平面ABD ，P ∈平面BCD . ∴P 在两平面的交线BD 上． ∴EH 、FG 、BD 三线共点．考点3：异面直线的夹角1.在正方体ABCD －A 1B 1C 1D 1中，E 为AB 的中点．求BD 1与CE 所成角的余弦值．【解析】连接AD 1，A 1D 交点为M ，连接ME ，MC ，则∠MEC (或其补角)即为异面直线BD 1与CE 所成的角，设AB ＝1，CE ＝52，ME ＝12BD 1＝32，CM 2＝CD 2＋DM 2＝32.在△MEC 中，cos ∠MEC＝CE 2＋ME 2－CM 22CE ·ME＝1515，因此异面直线BD 1与CE 所成角的余弦值为1515.2.如图，若正四棱柱ABCD －A 1B 1C 1D 1的底面边长为2，高为4，则异面直线BD 1与AD 所成角的正切值是______．答案 53.已知正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ，E 为AA 1中点，则异面直线BE 与CD 1所成角的余弦值为()答案C解析连接BA1，则CD1∥BA1，于是∠A1BE就是异面直线BE与CD1所成的角(或补角)，设AB＝1，则BE＝2，BA1＝5，A1E＝1，在△A1BE中，cos∠A1BE＝5＋2－125·2＝31010，选C.4.已知正方体ABCD－A1B1C1D1中，E为C1D1的中点，则异面直线AE与BC所成角的余弦值为________．【解析】取A1B1的中点F，连接EF，FA，则有EF∥B1C1∥BC，∠AEF即是直线AE与BC所成的角或其补角．设正方体ABCD—A1B1C1D1的棱长为2a，则有EF＝2a，AF＝2a2＋a2＝5a，AE＝2a2＋2a2＋a2＝3a.在△AEF中，cos∠AEF＝AE2＋EF2－AF22AE·EF＝9a2＋4a2－5a22×3a×2a＝23.因此，异面直线AE与BC所成的角的余弦值是23.【答案】2 3考点4：直线与平面平行的判定与性质1.下列命题中正确的是________．①若直线a不在α内，则a∥α；②若直线l上有无数个点不在平面α内，则l∥α；③若直线l与平面α平行，则l与α内的任意一条直线都平行；④如果两条平行线中的一条与一个平面平行，那么另一条也与这个平面平行；⑤若l与平面α平行，则l与α内任何一条直线都没有公共点；⑥平行于同一平面的两直线可以相交．答案⑤⑥解析a∩α＝A时，a不在α内，∴①错；直线l与α相交时，l上有无数个点不在α内，故②错；l ∥α时，α内的直线与l平行或异面，故③错；a∥b，b∥α时，a∥α或a⊂α，故④错；l∥α，则l与α无公共点，∴l与α内任何一条直线都无公共点，⑤正确；如图，长方体中，A1C1与B1D1都与平面ABCD 平行，∴⑥正确．2.给出下列四个命题：①若一条直线与一个平面内的一条直线平行，则这条直线与这个平面平行；②若一条直线与一个平面内的两条直线平行，则这条直线与这个平面平行；③若平面外的一条直线和这个平面内的一条直线平行，则这条直线和这个平面平行；④若两条平行直线中的一条与一个平面平行，则另一条也与这个平面平行．其中正确命题的个数是________个．答案 1解析命题①错，需说明这条直线在平面外．命题②错，需说明这条直线在平面外．命题③正确，由线面平行的判定定理可知．命题④错，需说明另一条直线在平面外． 3.已知不重合的直线a ，b 和平面α， ①若a ∥α，b ⊂α，则a ∥b ； ②若a ∥α，b ∥α，则a ∥b ； ③若a ∥b ，b ⊂α，则a ∥α； ④若a ∥b ，a ⊂α，则b ∥α或b ⊂α，上面命题中正确的是________(填序号)．答案 ④解析 ①若a ∥α，b ⊂α，则a ，b 平行或异面；②若a ∥α，b ∥α，则a ，b平行、相交、异面都有可能；③若a ∥b ，b ⊂α，a ∥α或a ⊂α.4.正方形ABCD 与正方形ABEF 所在平面相交于AB ，在AE 、BD 上各有一点P 、Q ，且AP ＝DQ .求证：PQ ∥平面BCE .【证明】方法一如图所示．作PM ∥AB 交BE 于M ，作QN ∥AB 交BC 于N ，连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ，∴AE ＝BD . 又AP ＝DQ ，∴PE ＝QB .又PM ∥AB ∥QN ，∴PM AB ＝PE AE ＝QB BD ，QN DC ＝BQ BD . ∴PM AB ＝QN DC .∴PM 綊QN ，即四边形PMNQ 为平行四边形． ∴PQ ∥MN .又MN ⊂平面BCE ，PQ ⊄平面BCE ， ∴PQ ∥平面BCE .方法二如图，连接AQ ，并延长交BC 延长线于K ，连接EK . ∵AE ＝BD ，AP ＝DQ ， ∴PE ＝BQ ，∴AP PE ＝DQBQ .又AD ∥BK ，∴DQ BQ ＝AQ QK ，∴AP PE ＝AQQK ，∴PQ ∥EK . 又PQ ⊄平面BCE ，EK ⊂平面BCE ， ∴PQ ∥平面BCE .方法三如图，在平面ABEF 内，过点P 作PM ∥BE ，交AB 于点M ，连接QM .∴PM ∥平面BCE .又∵平面ABEF ∩平面BCE ＝BE ， ∴PM ∥BE ，∴AP PE ＝AMMB .又AE ＝BD ，AP ＝DQ ，∴PE ＝BQ . ∴AP PE ＝DQ BQ ，∴AM MB ＝DQ QB . ∴MQ ∥AD .又AD ∥BC ，∴MQ ∥BC ，∴MQ ∥平面BCE .又PM ∩MQ ＝M ， ∴平面PMQ ∥平面BCE .又PQ ⊂平面PMQ ， ∴PQ ∥平面BCE .5.一个多面体的直观图和三视图如图所示(其中M ，N 分别是AF ，BC 中点)．<1>求证：MN ∥平面CDEF ； <2>求多面体A —CDEF 的体积．解析 (1)证明由三视图知，该多面体是底面为直角三角形的直三棱柱，且AB ＝BC ＝BF ＝2， DE ＝CF ＝22，∴∠CBF ＝90°.取BF 中点G ，连接MG ，NG ，由M ，N 分别是AF ，BC 中点，可知：NG ∥CF ，MG ∥EF .又MG ∩NG ＝G ，CF ∩EF ＝F ，∴平面MNG ∥平面CDEF ，∴MN ∥平面CDEF .(2)作AH ⊥DE 于H ，由于三棱柱ADE —BCF 为直三棱柱，∴AH ⊥平面CDEF ，且AH ＝2.∴V A －CDEF ＝13S 四边形CDEF ·AH ＝13×2×22×2＝83.6.若P 为异面直线a ，b 外一点，则过P 且与a ，b 均平行的平面A．不存在B．有且只有一个C．可以有两个D．有无数多个答案B7.如图，在正方体ABCD—A1B1C1D1中，点N在BD上，点M在B1C上，且CM＝DN，求证：MN∥平面AA1B1B.【证明】方法一如右图，作ME∥BC，交BB1于E；作NF∥AD，交AB于F，连接EF，则EF⊂平面AA1B1B.∵BD＝B1C，DN＝CM，∴B1M＝BN.∵MEBC＝B1MB1C，NFAD＝BNBD，∴MEBC＝BNBD＝NFAD，∴ME＝NF.又ME∥BC∥AD∥NF，∴MEFN为平行四边形．∴NM∥EF.又∵MN⊄面AA1B1B，∴MN∥平面AA1B1B.方法二如图，连接CN并延长交BA的延长线于点P，连接B1P，则B1P⊂平面AA1B1B.∵△NDC∽△NBP，∴DNNB＝CNNP.又CM＝DN，B1C＝BD，CMMB1＝DNNB＝CNNP，∴MN∥B1P.∵B1P⊂平面AA1B1B，∴MN∥平面AA1B1B.方法三如右图，作MP∥BB1，交BC于点P，连接NP.∵MP∥BB1，∴CMMB1＝CPPB.∵BD＝B1C，DN＝CM，∴B1M＝BN.∵CMMB1＝DNNB，∴CPPB＝DNNB，∴NP∥DC∥AB.∴平面MNP∥平面AA1B1B.∴MN∥平面AA1B1B.8.如图所示，四棱锥P—ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD＝AB＝2，E，F，G分别为PC、PD、BC的中点．(1)求证：PA∥平面EFG；(2)求三棱锥P—EFG的体积．解析(1)证明如图，取AD的中点H，连接GH，FH.∵E，F分别为PC，PD的中点，∴EF∥CD.∵G，H分别是BC，AD的中点，∴GH∥CD.∴EF∥GH，∴E，F，H，G四点共面．∵F，H分别为DP，DA的中点，∴PA∥FH.∵PA⊄平面EFG，FH⊂平面EFG，∴PA∥平面EFG.(2)∵PD⊥平面ABCD，CG⊂平面ABCD，∴PD⊥CG.又∵CG⊥CD，CD∩PD＝D，∴GC⊥平面PCD.∵PF ＝12PD ＝1，EF ＝12CD ＝1，∴S △PEF ＝12EF ·PF ＝12. 又GC ＝12BC ＝1，∴V P —EFG ＝V G —PEF ＝13×12×1＝16.9.如图所示，a ，b 是异面直线，A 、C 与B 、D 分别是a ，b 上的两点，直线a ∥平面α，直线b ∥平面α，AB ∩α＝M ，CD ∩α＝N ，求证：若AM ＝BM ，则CN ＝DN .【证明】连接AD 交平面α于E 点，并连接ME ，NE . ∵b ∥α，ME ⊂平面ABD ，平面α∩面ABD ＝ME ， ∴ME ∥BD .又在△ABD 中AM ＝MB ， ∴AE ＝ED .即E 是AD 的中点．又a ∥α，EN ⊂平面ACD ，平面α∩面ADC ＝EN ， ∴EN ∥AC ，而E 是AD 的中点． ∴N 必是CD 的中点，∴CN ＝DN .10.如图，在三棱柱ABC －A 1B 1C 1中，E 为AC 上一点，若AB 1∥平面C 1EB ，求：AE ∶EC .【解析】连接B 1C 交BC 1于点F ，则F 为B 1C 中点． ∵AB 1∥平面C 1EB ，AB 1⊂平面AB 1C ，且平面C 1EB ∩平面AB 1C ＝EF . ∴AB 1∥EF ，∴E 为AC 中点． ∴AE ∶EC ＝1∶1. 【答案】 1∶1考点5：面面平行的判定及性质1.设m ，n 是平面α内的两条不同直线；l 1，l 2是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是( )A ．m ∥β且l 1∥αB ．m ∥l 1且n ∥l 2C ．m ∥β且n ∥β 答案 B解析因m ⊂α，l 1⊂β，若α∥β，则有m ∥β且l 1∥α，故α∥β的一个必要条件是m ∥β且l 1∥α，排除A.因m ，n ⊂α，l 1，l 2⊂β且l 1与l 2相交，若m ∥l 1且n ∥l 2，因l 1与l 2相交，故m 与n 也相交，∴α∥β；若α∥β，则直线m 与直线l 1可能为异面直线，故α∥β的一个充分而不必要条件是m ∥l 1且n ∥l 2，应选B.2.棱长为1的正方体ABCD —A 1B 1C 1D 1中，点P ，Q ，R 分别是面A 1B 1C 1D 1，BCC 1B 1，ABB 1A 1的中心，给出下列结论：①PR 与BQ 是异面直线；②RQ ⊥平面BCC 1B 1；③平面PQR ∥平面D 1AC ；④过P ，Q ，R 的平面截该正方体所得截面是边长为2的等边三角形．以上结论正确的是________．(写出所有正确结论的序号)答案 ③④解析由于PR 是△A 1BC 1的中位线，所以PR ∥BQ ，故①不正确；由于RQ ∥A 1C 1，而A 1C 1不垂直于面BCC 1B 1，所以②不正确；由于PR ∥BC 1∥D 1A ，PQ ∥A 1B ∥D 1C ，所以③正确；由于△A 1BC 1是边长为2的正三角形，所以④正确．故填③④.3.已知P 为△ABC 所在平面外一点，G 1、G 2、G 3分别是△PAB 、△PCB 、△PAC的重心．<1>求证：平面G 1G 2G 3∥平面ABC ；<2>求S △G 1G 2G 3∶S △ABC .【解析】 (1)如图，连接PG 1、PG 2、PG 3并延长分别与边AB 、BC 、AC 交于点D 、E 、F .连接DE 、EF 、FD .则有PG 1∶PD ＝2∶3，PG 2∶PE ＝2∶3.∴G 1G 2∥DE .又G 1G 2不在平面ABC 内，∴G 1G 2∥平面ABC .同理G 2G 3∥平面ABC .又因为G 1G 2∩G 2G 3＝G 2，∴平面G 1G 2G 3∥平面ABC .(2)由(1)知PG 1PD ＝PG 2PE ＝23，∴G 1G 2＝23DE .又DE ＝12AC ，∴G 1G 2＝13AC .同理G 2G 3＝13AB ，G 1G 3＝13BC .∴△G 1G 2G 3∽△CAB ，其相似比为1∶3.∴S △G 1G 2G 3∶S △ABC ＝1∶9.4.给出下列关于互不相同的直线l 、m 、n 和平面α、β、γ的三个命题：①若l 与m 为异面直线，l ⊂α，m ⊂β，则α∥β；②若α∥β，l ⊂α，m ⊂β，则l ∥m ；③若α∩β＝l ，β∩γ＝m ，γ∩α＝n ，l ∥γ，则m ∥n .其中真命题为________．答案 ③解析 ①中当α与β不平行时，也能存在符合题意的l 、m .②中l 与m 也可能异面．③中⎭⎪⎬⎪⎫l ∥γl ⊂ββ∩γ＝m ⇒l ∥m ，同理l ∥n ，则m ∥n ，正确．5.如图所示，正方体ABCD —A 1B 1C 1D 1中，M 、N 、E 、F 分别是棱A 1B 1，A 1D 1，B 1C 1，C 1D 1的中点．求证：平面AMN ∥平面EFDB .【证明】连接MF ，∵M 、F 是A 1B 1、C 1D 1的中点，四边形A 1B 1C 1D 1为正方形，∴MF A 1D 1.又A 1D 1 AD ，∴MF AD .∴四边形AMFD 是平行四边形．∴AM ∥DF .∵DF ⊂平面EFDB ，AM ⊄平面EFDB ，∴AM ∥平面EFDB ，同理AN ∥平面EFDB .又AM 、AN ⊂平面ANM ，AM ∩AN ＝A ，∴平面AMN ∥平面EFDB .6.在正方体ABCD －A 1B 1C 1D 1中，M ，N ，P 分别是C 1C ，B 1C 1，C 1D 1的中点，求证：平面MNP ∥平面A 1BD . 证明方法一如图(1)所示，连接B 1D 1.∵P ，N 分别是D 1C 1，B 1C 1的中点，∴PN ∥B 1D 1.又B1D1∥BD，∴PN∥BD.又PN⊄平面A1BD，∴PN∥平面A1BD.同理：MN∥平面A1BD.又PN∩MN＝N，∴平面PMN∥平面A1BD.方法二如图(2)所示，连接AC1，AC，∵ABCD－A1B1C1D1为正方体，∴AC⊥BD.又CC1⊥平面ABCD，∴AC为AC1在平面ABCD上的射影，∴AC1⊥BD.同理可证AC1⊥A1B，∴AC1⊥平面A1BD.同理可证AC1⊥平面PMN.∴平面PMN∥平面A1BD.7.如图所示，平面α∥平面β，点A∈α，C∈α，点B∈β，D∈β，点E、F分别在线段AB，CD上，且AE∶EB＝CF∶FD.求证：EF∥β.【证明】①当AB，CD在同一平面内时，由α∥β，α∩平面ABDC＝AC，β∩平面ABDC＝BD，∴AC∥BD.∵AE∶EB＝CF∶FD，∴EF∥BD.又EF⊄β，BD⊂β，∴EF∥β.②当AB与CD异面时，设平面ACD∩β＝DH，且DH＝AC，∵α∥β，α∩平面ACDH＝AC，∴AC∥DH.∴四边形ACDH是平行四边形．在AH上取一点G，使AG∶GH＝CF∶FD，又∵AE∶EB＝CF∶FD，∴GF∥HD，EG∥BH.又EG ∩GF ＝G ，∴平面EFG ∥平面β.∵EF ⊂平面EFG ，∴EF ∥β.综上，EF ∥β.8.已知：如图，斜三棱柱ABC —A 1B 1C 1中，点D 、D 1分别为AC 、A 1C 1上的点．(1)当A 1D 1D 1C 1的值等于何值时，BC 1∥平面AB 1D 1； (2)若平面BC 1D ∥平面AB 1D 1，求AD DC 的值．【解析】 (1)如图，取D 1为线段A 1C 1的中点，此时A 1D 1D 1C 1＝1，连接A 1B 交AB 1于点O ，连接OD 1.由棱柱的性质，知四边形A 1ABB 1为平行四边形，所以点O 为A 1B的中点．在△A 1BC 1中，点O 、D 1分别为A 1B 、A 1C 1的中点，∴OD 1∥BC 1.又∵OD 1⊂平面AB 1D 1，BC 1⊄平面AB 1D 1，∴BC 1∥平面AB 1D 1.∴A 1D 1D 1C 1＝1时，BC 1∥平面AB 1D 1. (2)由已知，平面BC 1D ∥平面AB 1D 1，且平面A 1BC 1∩平面BDC 1＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ，因此BC 1∥D 1O ，同理AD 1∥DC 1.∴A 1D 1D 1C 1＝A 1O OB ，A 1D 1D 1C 1＝DC AD . 又∵A 1O OB ＝1，∴DC AD ＝1，即AD DC ＝1.考点6：线线、线面垂直1.设α、β是两个不同的平面，a 、b 是两条不同的直线，给出下列四个命题，其中真命题是A ．若a ∥α，b ∥α，则a ∥bB ．若a ∥α，b ∥β，a ∥b ，则α∥βC ．若a ⊥α，b ⊥β，a ⊥b ，则α⊥βD ．若a 、b 在平面α内的射影互相垂直，则a ⊥b答案 C解析与同一平面平行的两条直线不一定平行，所以A 错误；与两条平行直线分别平行的两个平面未必平行，所以B 错误；如图(1)，设OA ∥a ，OB ∥b ，直线OA 、OB 确定的平面分别交α、β于AC 、BC ，则OA ⊥AC ，OB ⊥BC ，所以四边形OACB 为矩形，∠ACB 为二面角α－l －β的平面角，所以α⊥β，C 正确；如图(2)，直线a 、b 在平面α内的射影分别为m 、n ，显然m ⊥n ，但a 、b 不垂直，所以D 错误，故选C.2.“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件答案 B3.若m ，n 表示直线，α表示平面，则下列命题中，正确命题的个数为① ⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α ② ⎭⎪⎬⎪⎫n ⊥αm ⊥α⇒m ∥n③ ⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n ④ ⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥αA ．1B ．2C ．3D ．4答案 C解析 ①②③正确，④错误．4.如图，四棱锥P －ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，AC ⊥CD ，∠ABC＝60°，PA ＝AB ＝BC ，E 是PC 的中点．求证：(1)CD ⊥AE ；(2)PD ⊥平面ABE .【证明】 (1)∵PA ⊥底面ABCD ，∴CD ⊥PA .又CD ⊥AC ，PA ∩AC ＝A ，故CD ⊥平面PAC ，AE ⊂平面PAC .故CD ⊥AE .(2)∵PA ＝AB ＝BC ，∠ABC ＝60°，故PA ＝AC .∵E 是PC 的中点，故AE ⊥PC .由(1)知CD ⊥AE ，从而AE ⊥平面PCD ，故AE ⊥PD .易知BA ⊥PD ，故PD ⊥平面ABE .5.设l 是直线，α，β是两个不同的平面( )A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若l⊥α，α⊥β，则l⊥βD．若α⊥β，l∥α，则l⊥β答案B解析A项中由l∥α，l∥β不能确定α与β的位置关系，C项中由α⊥β，l⊥α可推出l∥β或l⊂β，D项由α⊥β，l∥α不能确定l与β的位置关系．6.设b，c表示两条直线，α，β表示两个平面，下列命题中真命题是A．若b⊂α，c∥α，则b∥cB．若b⊂α，b∥c，则c∥αC．若c∥α，c⊥β，则α⊥βD．若c∥α，α⊥β，则c⊥β答案C解析如果一条直线平行于一个平面，它不是与平面内的所有直线平行，只有部分平行，故A错；若一条直线与平面内的直线平行，该直线不一定与该平面平行，该直线可能是该平面内的直线，故B 错；如果一个平面与另一个平面的一条垂线平行，那么这两个平面垂直，这是一个真命题，故C对；对D来讲若c∥α，α⊥β，则c与β的位置关系不定，故选C.7. 在三棱柱ABC—A1B1C1中，AA1⊥平面ABC，AC＝BC＝AA1＝2，∠ACB＝90°，E为BB1的中点，∠A1DE＝90°，求证：CD⊥平面A1ABB1.证明连接A1E，EC，∵AC＝BC＝2，∠ACB＝90°，∴AB＝2 2.设AD＝x，则BD＝22－x.∴A1D2＝4＋x2，DE2＝1＋(22－x)2，A1E2＝(22)2＋1.∵∠A1DE＝90°，∴A1D2＋DE2＝A1E2.∴x＝ 2.∴D为AB的中点．∴CD⊥AB.又AA1⊥CD，且AA1∩AB＝A，∴CD⊥平面A1ABB1.8.如图，长方体ABCD—A1B1C1D1中，底面A1B1C1D1是正方形，O是BD的中点，E是棱AA1上任意一点．<1>证明：BD⊥EC1；<2>如果AB＝2，AE＝2，OE⊥EC1，求AA1的长．【解析】 (1)如图，连接AC ，A 1C 1，AC 与BD 相交于点O .由底面是正方形知，BD ⊥AC .因为AA 1⊥平面ABCD ，BD ⊂平面ABCD ，所以AA 1⊥BD .又由AA 1∩AC ＝A ，所以BD ⊥平面AA 1C 1C .再由EC 1⊂平面AA 1C 1C 知，BD ⊥EC 1.(2)设AA 1的长为h ，连接OC 1.在Rt △OAE 中，AE ＝2，AO ＝2，故OE 2＝(2)2＋(2)2＝4.在Rt △EA 1C 1中，A 1E ＝h －2，A 1C 1＝2 2.故EC 21＝(h －2)2＋(22)2.在Rt △OCC 1中，OC ＝2，CC 1＝h ，OC 21＝h 2＋(2)2.因为OE ⊥EC 1，所以OE 2＋EC 21＝OC 21.即4＋(h －2)2＋(22)2＝h 2＋(2)2，解得h ＝3 2.所以AA 1的长为3 2.考点7：面面垂直1.△ABC 为正三角形，EC ⊥平面ABC ，BD ∥CE ，且CE ＝CA ＝2BD ，M 是EA 的中点，求证： ①DE ＝DA ；②平面BDM ⊥平面ECA ；③平面DEA ⊥平面ECA .【证明】 ①取EC 的中点F ，连接DF .∵BD ∥CE ，∴DB ⊥BA .又EC ⊥BC ，在Rt △EFD 和Rt △DBA 中，∵EF ＝12EC ＝BD ，FD ＝BC ＝AB ，∴Rt △EFD ≌Rt △DBA ，∴DE ＝DA .②取CA 的中点N ，连接MN 、BN ，则MN 綊12EC .∴MN ∥BD ，∴N 点在平面BDM 内．∵EC ⊥平面ABC ，∴EC ⊥BN .又CA ⊥BN ，∴BN ⊥平面ECA .∵BN ⊂平面BDM ，∴平面BDM ⊥平面ECA .③∵DM ∥BN ，BN ⊥平面ECA ，∴DM ⊥平面ECA ，又DM ⊂平面DEA ，∴平面DEA ⊥平面ECA .2.已知平面PAB ⊥平面ABC ，平面PAC ⊥平面⊥平面PBC ，E 为垂足．①求证：PA ⊥平面ABC ；②当E 为△PBC 的垂心时，求证：△ABC 是直角三角形．【证明】 ①在平面ABC 内取一点D ，作DF ⊥AC 于F .平面PAC ⊥平面ABC ，且交线为AC ，∴DF ⊥平面PAC .又PA ⊂平面PAC ，∴DF ⊥PA .作DG ⊥AB 于G ，同理可证：DG ⊥PA .DG 、DF 都在平面ABC 内，∴PA ⊥平面ABC .②连接BE 并延长交PC 于H ，∵E 是△PBC 的垂心，∴PC ⊥BH .又已知AE 是平面PBC 的垂线，PC ⊂平面PBC ，∴PC ⊥AE .又BH ∩AE ＝E ，∴PC ⊥平面ABE .又AB ⊂平面ABE ，∴PC ⊥AB .∵PA ⊥平面ABC ，∴PA ⊥AB .又PC ∩PA ＝P ，∴AB ⊥平面PAC .又AC ⊂平面PAC ，∴AB ⊥AC .即△ABC 是直角三角形．3.如图所示，在斜三棱柱A 1B 1C 1－ABC 中，底面是等腰三角形，AB ＝AC ，侧面BB 1C 1C ⊥底面ABC .(1)若D 是BC 的中点，求证：AD ⊥CC 1；(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ，若AM ＝MA 1，求证：截面MBC 1⊥侧面BB 1C 1C ；(3)AM ＝MA 1是截面MBC 1⊥侧面BB 1C 1C 的充要条件吗请你叙述判断理由．【证明】 (1)∵AB ＝AC ，D 是BC 的中点，∴AD ⊥BC .∵底面ABC ⊥侧面BB 1C 1C ，且交线为BC ，∴由面面垂直的性质定理可知AD ⊥侧面BB 1C 1C .又∵CC 1⊂侧面BB 1C 1C ，∴AD ⊥CC 1.(2)方法一取BC 1的中点E ，连接DE 、ME .在△BCC 1中，D 、E 分别是BC 、BC 1的中点．∴DE 綊12CC 1.又AA 1綊CC 1，∴DE 綊12AA 1.∵M 是AA 1的中点(由AM ＝MA 1知)，∴DE 綊AM .∴AMED 是平行四边形，∴AD 綊ME .由(1)知AD ⊥面BB 1C 1C ，∴ME ⊥侧面BB 1C 1C .又∵ME ⊂面BMC 1，∴面BMC 1⊥侧面BB 1C 1C .方法二延长B 1A 1与BM 交于N (在侧面AA 1B 1B 中)，连接C 1N .∵AM ＝MA 1，∴NA 1＝A 1B 1.又∵AB ＝AC ，由棱柱定义知△ABC ≌△A 1B 1C 1.∴AB ＝A 1B 1，AC ＝A 1C 1.∴A 1C 1＝A 1N ＝A 1B 1.在△B 1C 1N 中，由平面几何定理知：∠NC 1B 1＝90°，即C 1N ⊥B 1C 1.又∵侧面BB 1C 1C ⊥底面A 1B 1C 1，交线为B 1C 1，∴NC 1⊥侧面BB 1C 1C .又∵NC 1⊂面BNC 1，∴截面C 1NB ⊥侧面BB 1C 1C ，即截面MBC 1⊥侧面BB 1C 1C .(3)结论是肯定的，充分性已由(2)证明．下面仅证明必要性(即由截面BMC 1⊥侧面BB 1C 1C 推出AM ＝MA 1，实质是证明M 是AA 1的中点)，过M 作ME 1⊥BC 1于E 1.∵截面MBC 1⊥侧面BB 1C 1C ，交线为BC 1.∴ME 1⊥面BB 1C 1C .又由(1)知AD ⊥侧面BB 1C 1C ，∵垂直于同一个平面的两条直线平行，∴AD ∥ME 1，∴M 、E 1、D 、A 四点共面．又∵AM ∥侧面BB 1C 1C ，面AME 1D ∩面BB 1C 1C ＝DE 1，∴由线面平行的性质定理可知AM ∥DE 1.又AD ∥ME 1，∴四边形AME 1D 是平行四边形．∴AD ＝ME 1，DE 1綊AM .又∵AM ∥CC 1，∴DE 1∥CC 1.又∵D 是BC 的中点，∴E 1是BC 1的中点．∴DE 1＝12CC 1＝12AA 1.∴AM ＝12AA 1，∴MA ＝MA 1.∴AM ＝MA 1是截面MBC 1⊥侧面BB 1CC 1的充要条件．考点8：平行与垂直的综合问题1.如图所示，在直角梯形ABEF 中，将DCEF 沿CD 折起使∠FDA ＝60°，得到一个空间几何体．(1)求证：BE ∥平面ADF ；(2)求证：AF ⊥平面ABCD ；(3)求三棱锥E —BCD 的体积．【解析】 (1)由已知条件，可知BC ∥AD ，CE ∥DF ，折叠之后平行关系不变．又因为BC ⊄平面ADF ，AD ⊂平面ADF ，所以BC ∥平面ADF .同理CE ∥平面ADF .又因为BC ∩CE ＝C ，BC ，CE ⊂平面BCE ，所以平面BCE ∥平面ADF .所以BE ∥平面ADF .(2)由于∠FDA ＝60°，FD ＝2，AD ＝1，所以AF 2＝FD 2＋AD 2－2×FD ×AD ×cos FDA ＝4＋1－2×2×1×12＝3.即AF ＝ 3.所以AF 2＋AD 2＝FD 2.所以AF ⊥AD .又因为DC ⊥FD ，DC ⊥AD ，AD ∩FD ＝D ，所以DC ⊥平面ADF .又因为AF ⊂平面ADF ，所以DC ⊥AF .因为AD ∩DC ＝D ，AD ，DC ⊂平面ABCD ，所以AF ⊥平面ABCD .(3)因为DC ⊥EC ，DC ⊥BC ，EC ，BC ⊂平面EBC ，EC ∩BC ＝C ，所以DC ⊥平面EBC .又因为DF ∥EC ，AD ∥BC ，∠FDA ＝60°，所以∠ECB ＝60°.又因为EC ＝1，BC ＝1，所以S △ECB ＝12×1×1×32＝34.所以V E －BCD ＝V D －EBC ＝13×DC ×S △ECB ＝13×1×34＝312.2.如图1，在Rt △ABC 中，∠C ＝90°，D ，E 分别为AC ，AB 的中点，点F 为线段CD 上的一点．将△ADE 沿DE 折起到△A 1DE 的位置，使A 1F ⊥CD ，如图2.<1>求证：DE ∥平面A 1CB ；<2>求证：A 1F ⊥BE ；<3>线段A 1B 上是否存在点Q ，使A 1C ⊥平面DEQ 说明理由．【解析】 (1)因为D ，E 分别为AC ，AB 的中点，所以DE ∥BC .又因为DE ⊄平面A 1CB ，所以DE ∥平面A 1CB .(2)由已知得AC ⊥BC 且DE ∥BC ，所以DE ⊥AC .所以DE ⊥A 1D ，DE ⊥CD ，所以DE ⊥平面A 1DC .而A 1F ⊂平面A 1DC ，所以DE ⊥A 1F .又因为A 1F ⊥CD ，所以A 1F ⊥平面BCDE .所以A 1F ⊥BE .(3)线段A 1B 上存在点Q ，使A 1C ⊥平面DEQ .理由如下：如图，分别取A 1C ，A 1B 的中点P ，Q ，连接PQ ，QE ，PD ，则PQ ∥BC .因为DE ∥BC ，所以DE ∥PQ .所以平面DEQ 即为平面DEP .由(2)知，DE ⊥平面A 1DC ，所以DE ⊥A 1C .又因为P 是等腰三角形DA 1C 底边A 1C 的中点，所以A 1C ⊥DP .所以A 1C ⊥平面DEP .从而A 1C ⊥平面DEQ .故线段A 1B 上存在点Q ，使得A 1C ⊥平面DEQ .3.如图，四棱锥P －ABCD 中，四边形ABCD 为矩形，△PAD 为等腰三角形，∠APD ＝90°，平面PAD ⊥平面ABCD ，且AB ＝1，AD ＝2，E 、F 分别为PC 、BD 的中点．<1>证明：EF ∥平面PAD ；<2>证明：平面PDC ⊥平面PAD ；<3>求四棱锥P —ABCD 的体积．解析 (1)证明：如图，连接AC .∵四边形ABCD 为矩形且F 是BD 的中点，∴F 也是AC 的中点．又E 是PC 的中点，EF ∥AP ，∵EF ⊄平面PAD ，PA ⊂平面PAD ，∴EF ∥平面PAD .(2)证明：∵面PAD ⊥平面ABCD ，CD ⊥AD ，平面PAD ∩平面ABCD ＝AD ，∴CD ⊥平面PAD .∵CD ⊂平面PDC ，∴平面PDC ⊥平面PAD .(3)取AD 的中点为O .连接PO .∵平面PAD ⊥平面ABCD ，△PAD 为等腰直角三角形，∴PO ⊥平面ABCD ，即PO 为四棱锥P —ABCD 的高．∵AD ＝2，∴PO ＝1.又AB ＝1，∴四棱锥P —ABCD 的体积V ＝13PO ·AB ·AD ＝23.。

立体几何证明(教师版)

立体几何证明1．（2021·北京师大附中高一期末）已知四棱锥P ABCD -的底面为直角梯形，//,90,AB DC DAB PA ∠=⊥平面ABCD ，且112PA AD DC AB ====，M 是棱PB 上的动点.（1）求证：平面PAD ⊥平面PCD ；（2）若//PD 平面ACM ，求PM MB的值；（3）当M 是PB 中点时，设平面ADM 与棱PC 交于点N ，求截面ADNM 的面积.2．（2021·北京·人大附中高一期末）如图，已知正方体1111ABCD A B C D -，点E 为棱1CC 的中点．（1）证明：1AC ∥平面BDE ．（2）证明1AC BD ⊥．3．（2021·北京·汇文中学高一期末）如图1，已知菱形AECD 的对角线AC ，DE 交于点F ，点E 为AB 的中点．将三角形ADE 沿线段DE 折起到PDE 的位置，如图2所示．（1）求证：DE PC ⊥；（2）试问平面PFC 与平面PBC 所成的二面角是否为90︒，如果是，请证明；如果不是，请说明理由；（3）在线段PD ，BC 上是否分别存在点M ，N ，使得平面//CFM 平面PEN ？若存在，请指出点M ，N 的位置，并证明；若不存在，请说明理由．4．（2021·北京·首都师范大学附属中学高一期末）如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，O ，M 分别为BD ，PC 的中点.设平面PAD 与平面PBC 的交线为l .（1）求证：//OM 平面PAD ；（2）求证：//BC l ；（3）在棱PC 上是否存在点N （异于点C ），使得//BN 平面PAD ？若存在，求出PN PC的值；若不存在，说明理由.5．（2021·北京·101中学高一期末）已知正四棱柱1111ABCD A B C D -中，M 是1DD 的中点．（1）求证：1//BD 平面AMC ；（2）求证：1AC BD ⊥；（3）在线段1BB 上是否存在点P ，当1BP BB λ=时，平面11//A PC 面AMC ？若存在，求出λ的值并证明；若不存在，请说明理由．6．（2021·北京师大附中高一期末）在正方体1111ABCD A B C D -中，E 为1CC 中点.（1）求证：1//BC 平面1AD E ；（2）求证：1A D ⊥平面11ABC D .7．（2021·北京·汇文中学高一期末）如图所示，在三棱锥A BCD -中，点M ､N 分别在棱BC ､AC 上，且//MN AB .（1）求证：//MN 平面ABD ；（2）若MN CD ⊥，BD CD ⊥，求证：平面CBD ⊥平面ABD .8．（2019·北京师大附中高一期末）如图，在三棱柱111ABC A B C -中，1AA ⊥底面ABC ，90BAC ∠=，2AB AC ==，1AA ,M N 分别为1,BC CC 的中点，P 为侧棱1BB 上的动点（Ⅰ）求证：平面APM ⊥平面11BB C C ；（Ⅱ）若P 为线段1BB 的中点，求证：1//A N 平面APM ；（Ⅲ）试判断直线1BC 与平面APM 是否能够垂直．若能垂直，求PB 的值；若不能垂直，请说明理由9．（2019·北京师大附中高一期末）如图，已知四棱锥S ABCD-，底面ABCD是边长为2的菱形，60∠=，侧面SAD为正三角形，侧面SAD⊥底面ABCD，M为侧棱SB的中点，ABCE为线段AD的中点SD平面MAC；（Ⅰ）求证：//⊥；（Ⅱ）求证：SE AC-的体积（Ⅲ）求三棱锥M ABC-中，PA⊥平面ABCD，底10．（2019·北京·101中学高一期末）如图，在四棱锥P ABCD部ABCD为菱形，E为CD的中点.（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若∠ABC=60°，求证：平面PAB⊥平面PAE；（Ⅲ）棱PB上是否存在点F，使得CF∥平面PAE？说明理由.11．（2019·北京·中央民族大学附属中学高一期末）在四面体ABCD 中，CB =CD ，AD BD ⊥，且E ，F 分别是AB ，BD 的中点，求证：（I ）直线EF ACD 面；（II ）EFC BCD ⊥面面．12．（2020·北京师大附中高一期末）如图，四棱锥P ABCD -的底面是正方形，侧棱PA ⊥底面ABCD ，E 是PA 的中点.（1）求证：//CD 平面PAB ；（2）求证：//PC 平面BDE ；（3）证明：BD CE ⊥.13．（2021·北京·人大附中高一期末）如图1，已知△ABD 和△BCD 是两个直角三角形，∠BAD ＝∠BDC ＝2π.现将△ABD 沿BD 边折起到1A BD 的位置，如图2所示，使平面1A BD ⊥平面BCD .（1）求证：平面1A BC ⊥平面1A CD ；（2）1A C 与BD 是否有可能垂直，做出判断并写明理由.14．（2020·北京·101中学高一期末）如图1，在△ABC 中，D ，E 分别为AB ，AC 的中点，O 为DE 的中点，AB AC ==4BC =．将△ADE 沿DE 折起到△1A DE 的位置，使得平面1A DE ⊥平面BCED ，F 为1A C 的中点，如图2．（1）求证：//EF 平面1A BD ；（2）求证：平面1A OB ⊥平面1A OC ；（3）线段OC 上是否存在点G ，使得OC ⊥平面EFG ？说明理由．15．（2020·北京师大附中高一期末）如图，在多面体ABCDEF 中，底面ABCD 为矩形，侧面ADEF 为梯形，//AF DE ，DE AD ⊥，DC DE =.⊥；（Ⅰ）求证：AD CEBF平面CDE；（Ⅱ）求证：//（Ⅲ）判断线段BE上是否存在点Q，使得平面ADQ⊥平面BCE？并说明理由．-中，平面16．（2020·北京·中国人民大学附属中学朝阳学校高一期末）在三棱锥P ABC⊥．设D，E分别为PA，AC中点．PAC⊥平面ABC，PA AC⊥，AB BCDE平面PBC；（Ⅰ）求证：//（Ⅱ）求证：BC⊥平面PAB；（Ⅲ）试问在线段AB上是否存在点F，使得过三点D，E，F的平面内的任一条直线都与平面PBC平行？若存在，指出点F的位置并证明；若不存在，请说明理由．答案：1．(1)证明见解析；(2)12；【分析】 (1) 要证平面PAD ⊥平面PCD ，只需证明DC ⊥平面PAD ，利用线面垂直的判定可证DC ⊥平面PAD .(2) 根据题意，作出点M ，再利用相似三角形求PM MB的值 (3) 从四点共面角度出发，利用平面向量基本定理确定点N 的位置，再求截面面积.【详解】(1)证明：因为90DAB ∠=，所以AB AD ⊥，又//AB DC ，所以DC AD ⊥.因为PA ⊥平面ABCD ，DC ⊂平面ABCD ，所以PA DC ⊥.又AD ，PA 在平面PAD 内，且相交于点A ，所以DC ⊥平面PAD . 又DC ⊂平面PCD ，所以平面PAD ⊥平面PCD .(2)如图，连接AC ，BD 相交于点E ，过点E 作//EM PD ，交PB 于点M . 因为//EM PD ，PD ⊄平面ACM ，EM ⊂平面ACM ，所以//PD 平面ACM . 故上述所作点M 为使得//PD 平面ACM 的点M .如图在梯形ABCD 中，有//AB DC ，112AD DC AB === 令()22DE DB DA DC DA DC λλλλ==+=+，因为A ，E ，C 三点共线，所以21λλ+=，13λ=.即13DE DB =，所以23BE DB =，12DE BE =. 因为//EM PD ，所以BME BPD ，12DE P MB BE M ==. (3)设PN PC μ=，因为,,,A D N M 四点共面，所以存在实数m ，n ，使得AN mAD nAM =+. 因为()12AN AP PN AP PC AD AB AP μμμμ=+=+=++-，22n n mAD nAM mAD AB AP +=++，又AD ，AB ，AP 为一组基底，所以,,2212m n n μμμ⎧⎪=⎪⎪=⎨⎪⎪-=⎪⎩解得23m n ==. 所以2233AN AD AM =+.因为PA ⊥平面ABCD ，AD ⊂平面ABCD ，所以PA AD ⊥. 又AD AB ⊥，PA ，AB 在平面PAB 内，且相交于点A ，所以AD ⊥平面PAB ，又AM ⊂平面PAB ，所以AD AM ⊥. 在四边形AMND 中，AD AM ⊥，1AD =，AM = 因为2233AN AD AM =+，点N 到AM 的距离为2233AD =，点N 到AD的距离为23AM . 所以截面ADNM的面积1121223ADN AMNS S S =+=⨯+2．（1）见解析；（2）见解析【详解】试题分析：（1）连结AC 交BD 于F ，连结EF ，通过正方形对角线的性质以及三角形中位线可得112EF AC ，根据线面平行判定定理可得结果；（2）通过证明BD ⊥平面1ACC 可得结论.试题解析：（1）证明：连结AC 交BD 于F ，连结EF ，正方形ABCD 中，AC 与BD 互相平分，∴F 为AC 中点，在1ACC 中，∵E ，F 分别为1CC 与AC 中点，∴112EF AC ，∵EF ⊂平面BDE ，1AC ⊄平面BDE ，∴EF 平面BDE ．（2）证明：在正方形ABCD 中，AC BD ⊥，在正方体1111ABCD A B C D -中， 1CC ⊥平面ABCD ，∵BD ⊂平面ABCD ，∴1CC BD ⊥，∵1AC CC C ⋂=，∴BD ⊥平面1ACC ，∵1AC ⊂平面1ACC ，∴1AC BD ⊥．3．（1）证明见解析；（2）平面PFC 与平面PBC 所成的二面角为90︒，证明见解析；（3）存在满足条件的,M N ，,M N 分别为,PD BC 中点，证明见解析. 【分析】（1）根据线面垂直的判定可证得DE ⊥平面PCF ，由线面垂直性质可证得结论；（2）根据平行关系可证得BC ⊥平面PCF ，由面面垂直的判定可证得两平面垂直，由此得到所成角为90︒；（3）利用平行四边形和三角形中位线性质可证得线线平行关系，由此证得线面平行和面面平行，从而确定存在满足条件的,M N . 【详解】（1）四边形AECD 为菱形，AC DE ∴⊥，即DE PF ⊥，DE CF ⊥，又,PF CF ⊂平面PCF ，PFCF F =，DE ∴⊥平面PCF ，PC ⊂平面PCF ，DE PC ∴⊥.（2）平面PFC 与平面PBC 所成的二面角为90︒，证明如下：E 为AB 中点且四边形AECD 为菱形，//BE CD ∴，∴四边形BCDE 为平行四边形，//BC DE ∴，由（1）知：DE ⊥平面PCF ，BC ∴⊥平面PCF ，又BC ⊂平面PBC ，∴平面PCF ⊥平面PBC ，即平面PFC 与平面PBC 所成的二面角为90︒.（3）存在满足条件的,M N ，,M N 分别为,PD BC 中点，证明如下：由（2）知：四边形BCDE 为平行四边形，又,F N 分别为,DE BC 中点，//EF CN ∴，∴四边形EFCN 为平行四边形，//CF EN ∴，又EN ⊂平面PEN ，CF ⊄平面PEN ，//CF ∴平面PEN ；,M F 分别为,PD DE 中点，MF ∴为PDE △中位线，//MF PE ∴，又PE ⊂平面PEN ，MF ⊄平面PEN ，//MF ∴平面PEN ，又MFCF F =，,MF CF ⊂平面FCM ，∴平面//CFM 平面PEN .【点睛】本题考查立体几何中线线垂直关系、面面垂直与平行关系的证明问题，涉及到线面垂直的判定与性质、面面垂直的判定、线面平行与面面平行的判定等定理的应用，属于常考题型.4．（1）证明见解析；（2）证明见解析；（3）不存在，理由见解析. 【分析】（1）连接AC ，易知O 为AC 的中点，进而得//AP OM ，再结合线面平行的判定定理即可证明；（2）由题知//BC 平面PAD ，进而根据线面平行的性质定理即可证明//BC l ；（3））假设在棱PC 上存在点N （异于点C ），使得//BN 平面PAD ，进而在平面PDC 中，过点N 作PD 的平行线EN ，交DC 于E ，故平面//BEN 平面PAD ，进而得//BE AD ，另一方面，在平行四边形ABCD 中，BE 与AD 不平行，矛盾，故不存在. 【详解】解：（1）证明：连接AC ，因为底面ABCD 为平行四边形，O 为BD 的中点，所以O 为AC 的中点，因为M 为PC 的中点，所以在APC △中，//AP OM ，因为OM ⊄平面PAD ，AP ⊂平面PAD ，所以//OM 平面PAD（2）因为底面ABCD 为平行四边形，所以//AD BC ，因为AD ⊂平面PAD ，BC ⊄平面PAD ，所以//BC 平面PAD ，因为平面PAD 与平面PBC 的交线为l ，BC ⊂平面PBC ，所以//BC l（3）假设在棱PC 上存在点N （异于点C ），使得//BN 平面PAD ，在平面PDC 中，过点N 作PD 的平行线EN ，交DC 于E ，因为EN ⊄平面PAD ，PD ⊂平面PAD ，所以//EN 平面PAD ，因为EN BN N ⋂=，所以平面//BEN 平面PAD ，因为BE ⊂平面BEN ，所以//BE 平面PAD ，又因为BE ⊂平面ABCD ，平面ABCD 平面PAD AD =，所以//BE AD 另一方面，在平行四边形ABCD 中，BE 与AD 不平行，矛盾，所以在棱PC 上不存在点N （异于点C ），使得//BN 平面PAD .5．(1)证明见解析；(2) 证明见解析；(3)在线段1BB 上存在点P ，当12λ=时，平面11//A PC 平面AMC . 【分析】(1) 利用线面平行的判定定理证明1//BD 平面AMC ；(2) 利用线面垂直的判定定理证明AC ⊥平面11BB D D ，则有1AC BD ⊥； (3) 先确定λ的值，再根据面面平行的判定定理证明两平面平行. 【详解】因为四棱柱1111ABCD A B C D -是正四棱柱，所以底面ABCD 为正方形，侧棱垂直底面，侧面均为矩形.(1)证明：记AC 和BD 相交于点N ，因为ABCD 为正方形，所以N 为BD 的中点.又M 是1DD 的中点，所以1//MN BD .又1BD ⊄平面AMC ，MN ⊂平面AMC ，所以1//BD 平面AMC .(2)证明：因为ABCD 为正方形，所以AC BD ⊥.因为1D D ⊥平面ABCD ，AC ⊂平面ABCD ，所以1D D AC ⊥. 又BD ，1D D 在平面11BB D D 内，且相交于点D ，所以AC ⊥平面11BB D D .又1BD ⊂平面11BB D D ，所以1AC BD ⊥.(3) 在线段1BB 上存在点P ，当12λ=，即112BP BB =时，平面11//A PC 面AMC . 理由如下：当112BP BB =时，P 为1BB 的中点. 取1CC 的中点G ，连接1PC ，GB ，则有1//PC GB .连接MG ，因为四边形11CC D D 是矩形，M 是1DD 的中点，G 是1CC 的中点，所以//MG CD ，MG CD =.在正方形ABCD 中，有，//CD AB ，CD AB =.所以//MG AB ，MG AB =，四边形ABGM 为平行四边形. 有//BG AM ，又1//PC GB ，所以1//PC AM ，又1PC ⊄平面AMC ，AM ⊂平面AMC ，所以1PC //平面AMC . 同理可证：1//PA 平面AMC .又1PC ，1PA 在平面11A PC 内，且相交于点P ，所以平面11//A PC 平面AMC . 6．(1)证明见解析；(2) 证明见解析. 【分析】(1)先证明四边形11ABC D 为平行四边形，得到11//BC AD ，再利用线面平行的判定定理证明1//BC 平面1AD E ；(2)先证明11A D AD ⊥，再由线面垂直的性质得到1AB A D ⊥，最后由线面垂直的判定定理证明1A D ⊥平面11ABC D.(1)证明：在正方体1111ABCD A B C D -中，有//AB CD ，11//CD C D ，所以11//AB C D .又11AB C D =，所以四边形11ABC D 为平行四边形，有11//BC AD . 又1BC ⊄平面1AD E ，1AD ⊂平面1AD E ，所以1//BC 平面1AD E(2)证明：因为1A D ，1AD 为正方形的对角线，所以11A D AD ⊥. 因为AB ⊥平面11AA D D ，1A D ⊂平面11AA D D ，所以1AB A D ⊥. 又1AD ，AB 在平面11ABC D 内，且相交于点A ，所以1A D ⊥平面11ABC D .7．（1）证明见解析；（2）证明见解析. 【分析】（1）由//MN AB ，利用直线与平面平行的判断定理，证明//MN 平面ABD .（2）推导出BA DC ⊥，DC BD ⊥，从而CD ⊥平面ABD ，由此能证明平面ABD ⊥平面BCD . 【详解】（1）∵在三棱锥A BCD -中，点M ､N 分别在棱BC ､AC 上，且//MN AB .MN ⊄平面ABD ，AB 平面ABD ，∴//MN 平面ABD（2）∵MN CD ⊥，//MN AB ，∴AB CD ⊥， ∵BD CD ⊥，ABBD B =∴CD ⊥平面ABD ， ∵CD ⊂平面BCD ∴平面ABD ⊥平面BCD . 【点睛】本题考查的是空间中平行与垂直的证明，较简单.8．（Ⅰ）见解析（Ⅱ）见解析（Ⅲ）直线BC 1与平面APM 不能垂直，详见解析【分析】（Ⅰ）由等腰三角形三线合一得AM BC ⊥；由线面垂直性质可得1AM BB ⊥；根据线面垂直的判定定理知AM ⊥平面11BB C C ；由面面垂直判定定理证得结论；（Ⅱ）取11C B 中点D ，可证得1//A D AM ，//DN MP ；利用线面平行判定定理和面面平行判定定理可证得平面1//A DN 平面APM ；根据面面平行性质可证得结论；（Ⅲ）假设1BC ⊥平面APM ，由线面垂直性质可知1BC PM ⊥，利用相似三角形得到111C B PB MB BB =，从而解得BP 长度，可知满足垂直关系时，P 不在棱1BB 上，则假设错误，可得到结论.（Ⅰ）AB AC =，M 为BC 中点 AM BC ∴⊥1AA ⊥平面ABC ，11//AA BB 1BB ∴⊥平面ABC又AM ⊂平面ABC 1AM BB ∴⊥ 1,BB BC ⊂平面11BB C C ，1BB BC B = AM ∴⊥平面11BB C C又AM ⊂平面APM ∴平面APM ⊥平面11BB C C （Ⅱ）取11C B 中点D ，连接11,,,A D DN DM B C,D M 分别为11,C B CB 的中点 1//DM AA ∴且1DM AA = ∴四边形1A AMD 为平行四边形 1//A D AM ∴又1A D ⊄平面APM ，AM ⊂平面APM 1//A D ∴平面APM,D N 分别为111,C B CC 的中点 1//DN B C ∴又,P M 分别为1,BB CB 的中点 1//MP B C ∴ //DN MP ∴ 又DN ⊄平面APM ，MP ⊂平面APM //DN ∴平面APM 1,A D DN ⊂平面1A DN ，1A DDN D = ∴平面1//A DN 平面APM又1A N ⊂平面1A DN 1//A N ∴平面APM（Ⅲ）假设1BC ⊥平面APM ，由PM ⊂平面APM 得：1BC PM ⊥设PB x =，x ⎡∈⎣当1BC PM ⊥时，11BPM B C B ∠=∠ Rt PBM ∴∆∽11Rt B C B ∆ 111C B PB MB BB =∴由已知得：MB11C B =1BB=，解得：x ⎡=⎣ ∴假设错误 ∴直线1BC 与平面APM 不能垂直【点睛】本题考查立体几何中面面垂直、线面平行关系的证明、存在性问题的求解；涉及到线面垂直的判定与性质、线面平行的判定、面面平行的判定与性质定理的应用；处理存在性问题时，常采用假设法，通过假设成立构造方程，判断是否满足已知要求，从而得到结论. 9．（Ⅰ）见解析（Ⅱ）见解析（Ⅲ）12【分析】（Ⅰ）连接BD ，交AC 于点O ；根据三角形中位线可证得//MO SD ；由线面平行判定定理可证得结论；（Ⅱ）由等腰三角形三线合一可知SE AD ⊥；由面面垂直的性质可知SE ⊥平面ABCD ；根据线面垂直性质可证得结论；（Ⅲ）利用体积桥的方式将所求三棱锥体积转化为14S ABCD V -；根据已知长度和角度关系分别求得四边形面积和高，代入得到结果. 【详解】（Ⅰ）证明：连接BD ，交AC 于点O四边形ABCD 为菱形 O ∴为BD 中点又M 为SB 中点 //MO SD ∴MO ⊂平面MAC ，SD ⊄平面MAC //SD ∴平面MAC （Ⅱ）SAD ∆为正三角形，E 为AD 中点 SE AD ∴⊥平面SAD ⊥平面ABCD ，平面SAD ⋂平面ABCD AD =，SE ⊂平面SADSE ∴⊥平面ABCD ，又AC ⊂平面ABCD SE AC ∴⊥ （Ⅲ）M 为SB 中点 11112443M ABC M ABCD S ABCD ABCDV V V SSE ---∴===⨯⋅又2AB BC AD CD SA SD ======，60ABC ∠= 2AC ∴=，12222sin 60232ABCDABC SS ∆==⨯⨯⨯=由（Ⅱ）知，SE AD ⊥ SE ∴=11122M ABC V -=⨯∴ 【点睛】本题考查立体几何中线面平行、线线垂直关系的证明、三棱锥体积的求解问题；涉及到线面平行判定定理、面面垂直性质定理和判定定理的应用、体积桥的方式求解三棱锥体积等知识，属于常考题型. 10．（Ⅰ）见解析；（Ⅱ）见解析；（Ⅲ）见解析. 【分析】(Ⅰ)由题意利用线面垂直的判定定理即可证得题中的结论；(Ⅱ)由几何体的空间结构特征首先证得线面垂直，然后利用面面垂直的判断定理可得面面垂直；(Ⅲ)由题意，利用平行四边形的性质和线面平行的判定定理即可找到满足题意的点. 【详解】（Ⅰ）证明：因为PA ⊥平面ABCD ,所以PA BD ⊥；因为底面ABCD 是菱形，所以AC BD ⊥; 因为PAAC A =,,PA AC ⊂平面PAC ,所以BD ⊥平面PAC .（Ⅱ）证明：因为底面ABCD 是菱形且60ABC ∠=︒，所以ACD ∆为正三角形，所以AE CD ⊥, 因为//AB CD ,所以AE AB ⊥；因为PA ⊥平面ABCD ，AE ⊂平面ABCD , 所以AE PA ⊥；因为PA AB A = 所以AE ⊥平面PAB ，AE ⊂平面PAE ,所以平面PAB ⊥平面PAE .（Ⅲ）存在点F 为PB 中点时，满足//CF 平面PAE ；理由如下:分别取,PB PA 的中点,F G ，连接,,CF FG EG , 在三角形PAB 中，//FG AB 且12FG AB =；在菱形ABCD 中，E 为CD 中点，所以//CE AB 且12CE AB =，所以//CE FG 且CE FG =，即四边形CEGF 为平行四边形，所以//CF EG ; 又CF⊄平面PAE ，EG ⊂平面PAE ，所以//CF 平面PAE .【点睛】本题主要考查线面垂直的判定定理，面面垂直的判定定理，立体几何中的探索问题等知识，意在考查学生的转化能力和计算求解能力. 11．（I ）证明见解析．（II ）证明见解析．【详解】证明：（I ）E ，F 分别为AB ，BD 的中点EF AD ⇒}EF ADAD ACD EF ACD EF ACD⇒⊂⇒⊄面面面．（II ）}}}EF ADEF BDAD BD CD CB CF BD BD EFCF BD EF CF F⇒⊥⊥=⇒⊥⇒⊥⋂=面为的中点，又BD BCD ⊂面，所以EFC BCD ⊥面面．12．（1）证明见解析；（2）证明见解析；（3）证明见解析. 【分析】（1）根据底面是正方形，得到CDAB ，再利用线面平行判定定理证明.（2）连结AC ，BD ，交于点O ，连结OE ，由中位线定理得到OE PC ∥，再利用线面平行判定定理证明.（3）根据底面是正方形，得到BD AC ⊥，由侧棱PA ⊥底面ABCD ，得到BD PA ⊥，从而BD ⊥平面ACE ，由此能证明BD CE ⊥. 【详解】（1）∵四棱锥P ABCD -的底面是正方形， ∴CDAB ，∵CD CD ⊄平面PAB ，AB 平面PAB ，∴CD ∥平面PAB . （2）如图所示：连结AC ，BD ，交于点O ，连结OE ，∵四棱锥P ABCD -的底面是正方形，∴O 是AC 中点，∵E 是PA 的中点.∴OE PC ∥，∵PC ⊄平面BDE ，OE ⊂平面BDE ，∴PC 平面BDE .（3）∵四棱锥P ABCD -的底面是正方形，侧棱PA ⊥底面ABCD ，∴BD AC ⊥，BD PA ⊥，∵AC PA A ⋂=，∴BD ⊥平面ACE ，∵CE ⊂平面ACE ，∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理，线面垂直的判定定理，还考查了转化化归的思想和逻辑推理的能力，属于中档题.13.（1）证明见解析；（2）1A C 与BD 不可能垂直，证明见解析.【分析】（1）证得1A B ⊥平面1A CD ，结合面面垂直的判定定理即可得出结论；（2）假设1A C 与BD 垂直，然后推出与已知条件11A B A D ⊥矛盾，即可得出1A C 与BD 不可能垂直.【详解】（1）因为平面1A BD ⊥平面BCD ，平面1A BD 平面BCD =BD ，CD ⊂平面BCD ，CD ⊥BD ，所以CD ⊥平面1A BD ，又因为1A B ⊂平面1A BD ，所以CD ⊥1A B ，又因为11A B A D ⊥,1A D CD D =，所以1A B ⊥平面1A CD ，且1A B ⊂平面1A BC ，所以平面1A BC ⊥平面1A CD ；（2）假设1A C 与BD 垂直，又因为CD ⊥BD ，且1AC CD C ⋂=，所以DB ⊥平面1A CD ，又因为1A D ⊂平面1A CD ，所以1DB A D ⊥，这与11A B A D ⊥矛盾，故假设不成立，即1A C 与BD 不可能垂直.23．（1）见解析；（2）见解析；（3）见解析【解析】试题分析：（1）取线段1A B 的中点H ，由三角形中位线性质以及平行四边形性质得四边形DEFH 为平行四边形，即得//EF HD ．再根据线面平行判定定理得结论，（2）先根据等腰三角形性质得1A O DE ⊥．再根据面面垂直性质定理得1A O ⊥平面BCED ，即得1CO A O ⊥，根据勾股定理得CO BO ⊥，所以由线面垂直判定定理得 CO ⊥平面1A OB ，最后根据面面垂直判定定理得结论，（3）假设线段OC 上存在点G ，使得OC ⊥平面EFG ，则EO EC =，与条件矛盾.试题解析：解：（1）取线段1A B 的中点H ，连接HD ，HF ．因为在△ABC 中，D ，E 分别为AB ，AC 的中点，所以 //DE BC ，12DE BC =．因为 H ，F 分别为1A B ，1A C 的中点，所以 //HF BC ，12HF BC =，所以 //HF DE ，HF DE =，所以四边形DEFH 为平行四边形，所以 //EF HD ．因为 EF ⊄平面1A BD ， HD ⊂平面1A BD ，所以 //EF 平面1A BD ．（2）因为在△ABC 中，D ，E 分别为AB ，AC 的中点，所以 AD AE =．所以11A D A E =，又O 为DE 的中点，所以 1A O DE ⊥．因为平面1A DE ⊥平面BCED ，且1AO ⊂平面1A DE ，所以 1A O ⊥平面BCED ，所以 1CO A O ⊥．在△OBC 中，4BC =，易知 OB OC ==所以 CO BO ⊥，所以 CO ⊥平面1A OB ，所以平面1A OB ⊥平面1A OC ．（3）线段OC 上不存在点G ，使得OC ⊥平面EFG ．否则，假设线段OC 上存在点G ，使得OC ⊥平面EFG ，连接 GE ，GF ，则必有 OC GF ⊥，且OC GE ⊥．在Rt △1A OC 中，由F 为1A C 的中点，OC GF ⊥，得G 为OC 的中点．在△EOC 中，因为OC GE ⊥，所以EO EC =，这显然与1EO =，EC =所以线段OC 上不存在点G ，使得OC ⊥平面EFG ．14．（Ⅰ）见证明；（Ⅱ）见证明；（Ⅲ）见解析【分析】（I ）由AD ⊥DE ，AD ⊥CD 可得AD ⊥平面CDE ，故而AD ⊥CE ；（II ）证明平面ABF ∥平面CDE ，故而BF ∥平面CDE ；（III ）取CE 的中点P ，BE 的中点Q ，证明CE ⊥平面ADPQ 即可得出平面ADQ ⊥平面BCE ．【详解】（Ⅰ）由底面ABCD 为矩形，知AD CD ⊥.又因为DE AD ⊥，DE CD D ⋂=，所以AD ⊥平面CDE .又因为CE ⊂平面CDE ，所以AD CE ⊥.（Ⅱ）由底面ABCD 为矩形，知//AB CD ，又因为AB ⊄平面CDE ，CD ⊂平面CDE ，所以//AB 平面CDE .同理//AF 平面CDE ，又因为AB AF A ⋂=，所以平面//ABF 平面CDE .又因为BF ⊂平面ABF ，所以//BF 平面CDE .（Ⅲ）结论：线段BE 上存在点Q （即BE 的中点），使得平面ADQ ⊥平面BCE . 证明如下：取CE 的中点P ，BE 的中点Q ，连接,,AQ DP PQ ，则//PQ BC .由//AD BC ，得//PQ AD .所以,,,A D P Q 四点共面.由（Ⅰ），知AD ⊥平面CDE ，所以AD DP ⊥，故BC DP ⊥.在△CDE 中，由DC DE =，可得DP CE ⊥.又因为BC CE C ⋂=，所以DP ⊥平面BCE .又因为DP ⊂平面ADPQ所以平面ADPQ ⊥平面BCE （即平面ADQ ⊥平面BCE ）.即线段BE 上存在点Q （即BE 中点），使得平面ADQ ⊥平面BCE【点睛】本题考查了线面垂直、面面垂直的判定与性质定理的应用，线面平行的判定，熟练运用定理是解题的关键，属于中档题．15．（Ⅰ）见证明；（Ⅱ）见证明；（Ⅲ）见解析.【分析】（Ⅰ）证明以DE ∥平面PBC ，只需证明DE ∥PC ；（Ⅱ）证明BC ⊥平面PAB ，根据线面垂直的判定定理，只需证明PA ⊥BC ，AB ⊥BC ；（Ⅲ）当点F 是线段AB 中点时，证明平面DEF ∥平面PBC ，可得平面DEF 内的任一条直线都与平面PBC 平行．【详解】（Ⅰ）证明：因为点E 是AC 中点，点D 为PA 的中点，所以//DE PC ．又因为DE ⊄面PBC ，PC ⊂面PBC ，所以DE ∥平面PBC ．（Ⅱ）证明：因为平面PAC ⊥面ABC ，平面PAC ∩平面ABC =AC ，又PA ⊂平面PAC ，PA ⊥AC ，所以PA ⊥面ABC ，因为BC ⊂平面ABC ，所以PA ⊥BC ．又因为AB ⊥BC ，且PA ∩AB =A ，所以BC ⊥面PAB ．（Ⅲ）当点F 是线段AB 中点时，过点D ，E ，F 的平面内的任一条直线都与平面PBC 平行．取AB 中点F ，连EF ，连DF ．由（Ⅰ）可知DE ∥平面PBC ．因为点E 是AC 中点，点F 为AB 的中点，所以EF ∥BC ．又因为EF ⊄平面PBC ，BC ⊂平面PBC ，所以EF ∥平面PBC ．又因为DE ∩EF =E ，所以平面DEF ∥平面PBC ，所以平面DEF 内的任一条直线都与平面PBC 平行．故当点F 是线段AB 中点时，过点D ，E ，F 所在平面内的任一条直线都与平面PBC 平行．【点睛】本题考查线面平行，考查线面垂直，考查面面平行，考查学生分析解决问题的能力，掌握线面平行、线面垂直、面面垂直的判定定理是关键．16．（1）证明见解析；（2）证明见解析；（3）证明见解析.【分析】（1）根据底面是正方形，得到CD AB ，再利用线面平行判定定理证明.（2）连结AC ，BD ，交于点O ，连结OE ，由中位线定理得到OE PC ∥，再利用线面平行判定定理证明.（3）根据底面是正方形，得到BD AC ⊥，由侧棱PA ⊥底面ABCD ，得到BD PA ⊥，从而BD ⊥平面ACE ，由此能证明BD CE ⊥.【详解】（1）∵四棱锥P ABCD -的底面是正方形，∴CD AB ，∵CD ⊄平面PAB ，AB平面PAB ， ∴CD ∥平面PAB .（2）如图所示：连结AC ，BD ，交于点O ，连结OE ，∵四棱锥P ABCD -的底面是正方形，∴O 是AC 中点，∵E 是PA 的中点.∴OE PC ∥，∵PC ⊄平面BDE ，OE ⊂平面BDE ，∴PC 平面BDE .（3）∵四棱锥P ABCD -的底面是正方形，侧棱PA ⊥底面ABCD ，∴BD AC ⊥，BD PA ⊥，∵AC PA A ⋂=，∴BD ⊥平面ACE ，∵CE ⊂平面ACE ，∴BD CE ⊥.【点睛】本题主要考查线面平行的判定定理，线面垂直的判定定理，还考查了转化化归的思想和逻辑推理的能力，属于中档题.。

立体几何经典试题（含答案）

1. 如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比. 【解析】（Ⅰ）由题设知BC BC⊥⊥1CC ,BC ,BC⊥⊥AC AC，，1CC AC C Ç=,∴BC ^面11ACC A , , 又又∵1DC Ì面11ACC A ，∴1DC BC ^,由题设知01145A DC ADC Ð=Ð=,∴1CDC Ð=090,即1DC DC ^, 又∵DC BC C Ç=, , ∴∴1DC ⊥面BDC , , ∵∵1DC Ì面1BDC ， ∴面BDC ⊥面1BDC ；（Ⅱ）设棱锥1B DACC -的体积为1V ，AC =1，由题意得，1V =1121132+´´´=12，由三棱柱111ABC A B C -的体积V =1，∴11():V V V -=1:1， ∴平面1BDC 分此棱柱为两部分体积之比为1:1. 2. 如图5所示，在四棱锥P ABCD -中，AB ^平面PAD ，//AB CD ，PD AD =，E 是PB 的中点，F 是CD 上的点且12DF AB =，PH 为△PAD 中AD 边上的高. （1）证明：PH ^平面ABCD ；（2）若1PH =，2AD =，1FC =，求三棱锥E BCF -的体积；的体积；（3）证明：EF ^平面PAB . B 1C B A D C 1A 1【解析】（1）证明：因为AB ^平面PAD ，所以PH AB ^。

因为PH 为△PAD 中AD 边上的高，边上的高，所以PH AD ^。

因为AB AD A = ，所以PH ^平面ABCD 。

（2）连结BH ，取BH 中点G ，连结EG 。

高中立体几何证明题精选

1、已知正方体1111ABCD A B C D-，O是底ABCD对角线的交点.求证：(１) C1O∥面11AB D；(2)1AC⊥面11AB D．2、正方体''''ABCD A B C D-中，求证：（1）''AC B D DB⊥平面；（2）''BD ACB⊥平面.3、正方体ABCD—A1B1C1D1中．(1)求证：平面A1BD∥平面B1D1C；(2)若E、F分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD．D1ODBAC1B1A1CA1AB1C1D1DGEFN MPC BA4、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =， 90BDC ∠=o ，求证：BD ⊥平面ACD5、如图P 是ABC ∆所在平面外一点，,PA PB CB =⊥平面PAB ，M 是PC 的中点，N 是AB 上的点，3AN NB =（1）求证：MN AB ⊥；6、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .7、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. （1）求证：1//A C 平面BDE ；（2）求证：平面1A AC ⊥平面BDE .8、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．求证：DE ⊥平面PAE ；9、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG ⊥平面PAD ；（2）求证：AD PB ⊥；10、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD ．D 1 C 1 A 1 B 1D CA B11、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．证明：取AB 的中点Ｆ，连结CF ，DF ． ∵AC BC =，∴CF AB ⊥．∵AD BD =，∴DF AB ⊥．又CF DF F =I ，∴AB ⊥平面CDF ． ∵CD ⊂平面CDF ，∴CD AB ⊥．又CD BE ⊥，BE AB B ⋂=， ∴CD ⊥平面ABE ，CD AH ⊥．∵AH CD ⊥，AH BE ⊥，CD BE E ⋂=，∴ AH ⊥平面BCD ．考点：线面垂直的判定12、证明：在正方体ABCD －A 1B 1C 1D 1中，A 1C ⊥平面BC 1D证明：连结ACBD AC ∵⊥∴ AC 为A 1C 在平面AC 上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面考点：线面垂直的判定，三垂线定理13、如图，过S 引三条长度相等但不共面的线段SA 、SB 、SC ，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC ⊥平面BSC ．证明∵SB=SA=SC ，∠ASB=∠ASC=60°∴AB=SA=AC 取BC 的中点O ，连AO 、SO ，则AO ⊥BC ，SO ⊥BC ，∴∠AOS 为二面角的平面角，设SA=SB=SC=a ，又∠BSC=90°，∴BC=2a ，SO=22a ，AO 2=AC 2－OC 2=a 2－21a 2=21a 2，∴SA 2=AO 2+OS 2，∴∠AOS=90°，从而平面ABC ⊥平面BSC ．考点：面面垂直的判定（证二面角是直二面角）高三数学立体几何证明题训练1、如图，在长方体1111D C B A ABCD -中，a AD AA ==1，a AB 2=，E 、F 分别为11C D 、11D A 的中点．（Ⅰ）求证：⊥DE 平面BCE ；（Ⅱ）求证：//AF 平面BDE ．2、如图，已知棱柱1111D C B A ABCD -的底面是菱形，且⊥1AA 面ABCD ，ο60=∠DAB ，1AA AD =，F 为棱1AA 的中点，M 为线段1BD 的中点，（1）求证：//MF 面ABCD ；（2）求证：⊥MF 面11B BDD ；3、如图，四棱锥P —ABCD 中，PA ⊥底面ABCD ，AC ⊥CD ，∠DAC=60°，AB=BC=AC ，E 是PD 的中点，F 为ED 的中点。

高中数学立体几何证明题汇总

立体几何常考证明题1、已知四边形ABCD 是空间四边形，E, F,G, H 分别是边AB,BC,CD , DA 的中点（1）求证：EFGH是平行四边形（2）若BD=2 3 ，AC=2，EG=2。

求异面直线AC、BD所成的角和EG、BD所成的角。

AEHB DF GC2、如图，已知空间四边形ABCD 中，BC AC, AD BD ，E 是AB 的中点。

求证：（1）AB 平面CDE;（2）平面CDE 平面ABC 。

AEB CD3、如图，在正方体A BCD ABC D 中，E 是AA1 的中点，1 1 1 1求证：A1C // 平面BDE 。

A D1B1 CEADBC 14、已知ABC 中ACB 90 , SA 面ABC , AD SC ,求证：AD 面SBC ．SDBAC5、已知正方体ABCD A1B1C1D1，O是底ABCD 对角线的交点. D1C1B1求证：(１) C1O∥面AB1D1 ；(2) A1C 面AB1D1 ．A1DCOA B6、正方体ABCD A'B'C 'D'中，求证：（1）AC 平面B'D 'DB ；（2）BD ' 平面ACB '.27、正方体ABCD —A1B1C1D1 中．(1)求证：平面A1BD∥平面B1D1C；D 1C1 (2)若E、F 分别是AA1，CC1 的中点，求证：平面EB1D1∥平面FBD ．A1B1FEGCDAB8、四面体ABCD 中，AC BD,E, F 分别为AD, BC 的中点，且BDC 90 ，求证：BD 平面ACD2EF AC ，29、如图P 是ABC 所在平面外一点，PA PB, CB 平面PAB ，M 是PC 的中点，N 是AB 上的点，AN 3NBP（1）求证：MN AB ；（2）当APB 90 ，AB 2BC 4 时，求MN 的长。

MCANB310、如图，在正方体ABCD A1B1C1D1 中，E 、F 、G 分别是AB 、AD 、C1D1 的中点. 求证：平面D1EF ∥平面BDG .11、如图，在正方体A BCD ABC D 中，E 是1 1 1 1 AA 的中点.1（1）求证：A1C // 平面BDE ；（2）求证：平面A AC 平面BDE .112、已知ABCD 是矩形，PA 平面ABCD ，AB 2 ，PA AD 4 ，E 为BC 的中点．（1）求证：DE 平面PAE ；（2）求直线DP 与平面PAE 所成的角．413 、如图，在四棱锥P ABCD 中，底面ABCD 是DAB 600 且边长为a的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG 平面PAD ；（2）求证：AD PB ；（3）求二面角 A BC P 的大小．14、如图1,在正方体ABCD A1B1C1D1 中，M 为CC1 的中点，AC 交BD 于点O，求证：A1O 平面MBD ．15、如图２，在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，作BE⊥CD，Ｅ为垂足，作AH⊥BE于Ｈ．求证：AH⊥平面BCD．516、证明：在正方体ABCD －A1B1C1D1 中，A 1C⊥平面BC1DD1 C1A 1B 1D CA B17、如图，过S 引三条长度相等但不共面的线段SA、SB、SC，且∠ASB= ∠ASC=60 °，∠BSC=90°，求证：平面ABC ⊥平面BSC．WORD文档6专业资料。

(完整)立体几何证明基础题

立体几何证明基础题一．解答题（共28小题)1．如图,在三棱锥P﹣ABC中，PB⊥BC，AC⊥BC,点E，F，G分别为AB，BC，PC，的中点（1）求证:PB∥平面EFG；（2）求证：BC⊥EG．2．如图，在三棱锥P﹣ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．（1)求证DE∥PA(2）求证：DE∥平面PAC;（3)求证：AB⊥PB．3．如图所示，△ABC为正三角形，CE⊥平面ABC，BD∥CE且CE=AC=2BD,试在AE上确定一点M，使得DM∥平面ABC．4．如图:在四棱锥P﹣ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD,点M，N分别为BC，PA的中点，且PA=AB=2．（Ⅰ）证明：BC⊥平面AMN；(Ⅱ)求三棱锥N﹣AMC的体积；(Ⅲ）在线段PD上是否存在一点E,使得NM∥平面ACE；若存在,求出PE的长；若不存在，说明理由．5．如图,四棱锥P﹣ABCD的底面是边长为1的正方形，侧棱PA⊥底面ABCD,且PA=2，E是侧棱PA上的动点．（1）求四棱锥P﹣ABCD的体积；(2）如果E是PA的中点，求证：PC∥平面BDE；（3）是否不论点E在侧棱PA的任何位置，都有BD⊥CE？证明你的结论．6．已知四棱锥A ﹣BCDE ，其中AB=BC=AC=BE=1，CD=2,CD ⊥面ABC,BE ∥CD,F 为AD 的中点．（Ⅰ）求证：EF ∥面ABC ； (Ⅱ)求证：平面ADE ⊥平面ACD ；（Ⅲ)求四棱锥A ﹣BCDE 的体积．7．如图，四棱柱ABCD ﹣A 1B 1C 1D 1中，平面A 1ABB 1⊥平面ABCD ，且∠ABC=．（1）求证：BC ∥平面AB 1C 1；（2）求证:平面A 1ABB 1⊥平面AB 1C 1．8．如图，三角形ABC中,AC=BC=，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．（Ⅰ)求证：GF∥底面ABC;（Ⅱ)求证：AC⊥平面EBC；(Ⅲ）求几何体ADEBC的体积V．9．如图,在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD|｜BC,PD⊥底面ABCD，∠ADC=90°，AD=2BC,Q为AD的中点,M为棱PC的中点．（Ⅰ)证明：PA∥平面BMQ;(Ⅱ）已知PD=DC=AD=2，求点P到平面BMQ的距离．10．已知直三棱柱ABC ﹣A 1B 1C 1的底面△ABC 中，∠C=90°，BC=，BB 1=2，O 是AB 1的中点，D是AC 的中点，M 是CC 1的中点， (1)证明：OD ∥平面BB 1C 1C ；（2)试证:BM ⊥AB 1．11．如图，在四棱锥P ﹣ABCD 中，四边形ABCD 是平行四边形，E 、F 分别是AB 、PC 中点,求证：EF ∥面PAD ．12．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，E 是AA 1的中点，求证：（Ⅰ）A 1C ∥平面BDE ；（Ⅱ）平面A 1AC ⊥平面BDE ．13．如图，四棱锥P ﹣ABCD 中，底面ABCD 为矩形，E 为PD 的中点． (1）求证：PB ∥平面AEC ；（2)若PA ⊥平面ABCD ，PA=AD ，求证：平面AEC ⊥平面PCD ．14．如图,ABCD 是正方形,O 是正方形的中心，PO ⊥底面ABCD ，E 是PC 的中点．求证：（1）PA ∥平面BDE ；（2）BD ⊥平面PAC ．15．如图，正四棱柱ABCD ﹣A 1B 1C 1D 1，底面边长AB=1,侧棱长AA 1=2．（Ⅰ）求正四棱柱ABCD ﹣A 1B 1C 1D 1的表面积; （Ⅱ）证明：AC ⊥平面BDD 1B 1．16．已知正方体ABCD ﹣A 1B 1C 1D 1，O 是底ABCD 对角线的交点．求证： (1)C 1O ∥面AB 1D 1；（2）A 1C ⊥面AB 1D 1．17．如图所示,在正方体ABCD ﹣A 1B 1C 1D 1中，M ，E,F,N 分别为A 1B 1,B 1C 1,C 1D 1，D 1A 1的中点，求证：（1）E ，F ，D ，B 四点共面； (2）面AMN ∥平面EFDB ．18．如图，长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1,AA 1=2,点P 是DD 1的中点．求证：（1）直线BD 1∥平面PAC(2）①求异面直线PC 与AA 1所成的角． ②平面PAC ⊥平面BDD 1．19．如图,在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AC=CB=CC1=2，E是AB中点．（Ⅰ）求证：AB1⊥平面A1CE；（Ⅱ）求直线A1C1与平面A1CE所成角的正弦值．20．如图，在正方体ABCD﹣A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点．求证：平面D1EF∥平面BDG．21．（文科）如图，正方体ABCD﹣A1B1C1D1中,M,N，E，F分别是棱A1B1，A1D1，B1C1，C1D1的中点，求证：平面AMN∥平面EFDB．22．如图，在四棱锥P﹣ABCD中，侧面PAD是正三角形,且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点,求证：（1）EN∥平面PDC；（2）BC⊥平面PEB；(3)平面PBC⊥平面ADMN．23．如图，在正三棱锥P﹣ABC中，D,E分别是AB，BC的中点．（1）求证:DE∥平面PAC；（2）求证：AB⊥PC．24．如图所示,在四棱锥P﹣ABCD中，底面是边长为1的正方形，侧棱PD=1，PA=PC=．(1)求证：PD⊥平面ABCD；（2）求证：平面PAC⊥平面PBD．25．如图，在三棱柱ABC ﹣A 1B 1C 1中，侧棱AA 1⊥底面ABC ，AB ⊥BC,D 为AC 的中点，A 1A=AB=2．（1）求证：AB 1∥平面BC 1D ；（2)过点B 作BE ⊥AC 于点E,求证：直线BE ⊥平面AA 1C 1C (3）若四棱锥B ﹣AA 1C 1D 的体积为3，求BC 的长度．26．如图,已知四棱锥P ﹣ABCD 的底面ABCD 是菱形，PA ⊥平面ABCD ，点F 为PC 的中点．（1）求证：PA ∥平面BDF ； (2）求证:PC ⊥BD ．27．如图，在正方体ABCD ﹣A 1B 1C 1D 1中,E 是CC 1的中点．（1）求证：AC 1⊥BD ． (2）求证：AC 1∥平面BDE ．28．已知空间四边形ABCD （如图所示），E 、F 分别是AB 、AD 的中点，G 、H 分别是BC 、CD 上的(完整)立体几何证明基础题点，且CG=BC，CH=DC．求证：①E、F、G、H四点共面；②三直线FH、EG、AC共点．立体几何证明基础题参考答案与试题解析一．解答题（共28小题）1．如图,在三棱锥P﹣ABC中，PB⊥BC，AC⊥BC，点E，F，G分别为AB，BC，PC，的中点(1）求证：PB∥平面EFG；（2）求证：BC⊥EG．【分析】（1）推导出GF∥PB,由此能证明PB∥平面EFG．（2）推导出EF⊥BC,GF⊥BC，从而BC⊥平面EFG，由此能证明BC⊥EG．【解答】证明：（1）∵点F，G分别为BC，PC，的中点，∴GF∥PB,∵PB⊄平面EFG，FG⊂平面EFG，∴PB∥平面EFG．(2）∵在三棱锥P﹣ABC中，PB⊥BC，AC⊥BC，点E,F，G分别为AB,BC，PC，的中点,∴EF∥AC，GF∥PB，∴EF⊥BC，GF⊥BC,∵EF∩FG=F，∴BC⊥平面EFG，∵EG⊂平面EFG，∴BC⊥EG．【点评】本题考查线面平行、线线垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．2．如图，在三棱锥P﹣ABC中，PC⊥底面ABC,AB⊥BC，D，E分别是AB,PB的中点．(1)求证DE∥PA（2)求证：DE∥平面PAC；(3）求证：AB⊥PB．【分析】（1）由D，E分别是AB，PB的中点，能证明DE∥PA．(2）由PA⊂平面PAC，DE∥PA，且DE⊄平面PAC，能证明DE∥平面PAC．(3）推导出AB⊥PC，AB⊥BC，得AB⊥平面PBC,由此能证明AB⊥PB．【解答】证明：（1）因为D，E分别是AB，PB的中点，所以DE∥PA．（2）因为PA⊂平面PAC，DE∥PA，且DE⊄平面PAC，所以DE∥平面PAC．(3）因为PC⊥平面ABC，且AB⊂平面ABC，所以AB⊥PC．又因为AB⊥BC，且PC∩BC=C．所以AB⊥平面PBC．又因为PB⊂平面PBC，所以AB⊥PB．【点评】本题考查线线平行、线面平行、线线垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．3．如图所示，△ABC为正三角形,CE⊥平面ABC，BD∥CE且CE=AC=2BD,试在AE上确定一点M，使得DM∥平面ABC．【分析】AE中点为M，取AC中点为N,通过证明四边形MNBD是平行四边形得出DM∥BN，从而可得DM∥平面ABC．【解答】解:取AE中点为M，取AC中点为N，连结MD，MN，NB，在△ABC中，∵M，N分别是边AC，AE的中点,∴CE=2MN且MN∥CE，又∵CE=2BD且BD∥CE，∴MN∥BD且MN=BD,∴四边形BDMN是平行四边形．∴DM∥BN，又∵BN⊂平面ABC，DM⊄平面ABC,∴DM∥平面ABC．故M为AE的中点时，DM∥平面ABC．【点评】本题考查了线面平行的判定，属于基础题．4．如图：在四棱锥P﹣ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，点M，N分别为BC，PA的中点，且PA=AB=2．（Ⅰ)证明:BC⊥平面AMN;（Ⅱ）求三棱锥N﹣AMC的体积；（Ⅲ）在线段PD上是否存在一点E，使得NM∥平面ACE；若存在，求出PE的长；若不存在，说明理由．【分析】(I）要证线与面垂直，只要证明线与面上的两条相交线垂直，找面上的两条线，根据四边形是一个菱形,从菱形出发找到一条,再从PA⊥平面ABCD，得到结论．(II）要求三棱锥的体积，首先根据所给的体积确定用哪一个面做底面，会使得计算简单一些，选择三角形AMC,做出底面面积，利用体积公式得到结果．（III）对于这种是否存在的问题，首先要观察出结论，再进行证明,根据线面平行的判定定理,利用中位线确定线与线平行，得到结论．【解答】解：（Ⅰ）证明：∵ABCD为菱形，∴AB=BC又∠ABC=60°，∴AB=BC=AC，又M为BC中点，∴BC⊥AM而PA⊥平面ABCD,BC⊂平面ABCD，∴PA⊥BC 又PA∩AM=A,∴BC⊥平面AMN（II）∵又PA⊥底面ABCD，PA=2，∴AN=1•AN∴三棱锥N﹣AMC的体积S△AMC=（III）存在点E，取PD中点E，连接NE，EC，AE，∵N，E分别为PA，PD中点，∴又在菱形ABCD中,∴，即MCEN是平行四边形∴NM∥EC，又EC⊂平面ACE，NM⊄平面ACE∴MN∥平面ACE，即在PD上存在一点E,使得NM∥平面ACE，此时．【点评】本题考查空间中直线与平面之间的位置关系，是一个非常适合作为高考题目出现的问题，题目包含的知识点比较全面，重点突出,是一个好题．5．如图，四棱锥P﹣ABCD的底面是边长为1的正方形，侧棱PA⊥底面ABCD，且PA=2,E是侧棱PA上的动点．（1）求四棱锥P﹣ABCD的体积；(2）如果E是PA的中点,求证：PC∥平面BDE；（3）是否不论点E在侧棱PA的任何位置,都有BD⊥CE？证明你的结论．【分析】（1)利用四棱锥的体积计算公式即可；(2）利用三角形的中位线定理和线面平行的判定定理即可证明;（3)利用线面垂直的判定和性质即可证明．【解答】解:（1）∵PA⊥底面ABCD,∴PA为此四棱锥底面上的高．∴V==．四棱锥P﹣ABCD（2）连接AC交BD于O,连接OE．∵四边形ABCD是正方形，∴AO=OC,又∵AE=EP，∴OE∥PC．又∵PC⊄平面BDE，OE⊂平面BDE．∴PC∥平面BDE．（3）不论点E在侧棱PA的任何位置，都有BD⊥CE．证明：∵四边形ABCD是正方形,∴BD⊥AC．∵PA⊥底面ABCD,∴PA⊥BD．又∵PA∩AC=A，∴BD⊥平面PAC．∵CE⊂平面PAC．∴BD⊥CE．【点评】熟练掌握线面平行、垂直的判定和性质定理及四棱锥的体积计算公式是解题的关键．6．已知四棱锥A﹣BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥面ABC，BE∥CD,F为AD的中点．(Ⅰ）求证:EF∥面ABC；（Ⅱ）求证：平面ADE⊥平面ACD；（Ⅲ)求四棱锥A﹣BCDE的体积．【分析】（Ⅰ)取AC中点G，连接FG、BG，根据三角形中位线定理，得到四边形FGBE为平行四边形，进而得到EF∥BG，再结合线面平行的判定定理得到EF∥面ABC；(Ⅱ)根据已知中△ABC为等边三角形，G为AC的中点，DC⊥面ABC得到BG⊥AC，DC⊥BG,根据线面垂直的判定定理得到BG⊥面ADC，则EF⊥面ADC，再由面面垂直的判定定理，可得面ADE⊥面ACD；(Ⅲ）方法一：四棱锥四棱锥A﹣BCDE分为两个三棱锥E﹣ABC和E﹣ADC，分别求出三棱锥E﹣ABC和E﹣ADC的体积，即可得到四棱锥A﹣BCDE的体积．的高,求出底面面积和方法二：取BC的中点为O，连接AO，可证AO⊥平面BCDE,即AO为VA﹣BCDE高代入棱锥体积公式即可求出四棱锥A﹣BCDE的体积．【解答】证明：（Ⅰ)取AC中点G,连接FG、BG，∵F，G分别是AD，AC的中点∴FG∥CD,且FG=DC=1．∵BE∥CD∴FG与BE平行且相等∴EF∥BG．EF⊄面ABC，BG⊂面ABC∴EF∥面ABC…（4分）(Ⅱ)∵△ABC为等边三角形∴BG⊥AC又∵DC ⊥面ABC ，BG ⊂面ABC ∴DC ⊥BG ∴BG 垂直于面ADC 的两条相交直线AC,DC ，∴BG ⊥面ADC ． …(6分) ∵EF ∥BG ∴EF ⊥面ADC∵EF ⊂面ADE ，∴面ADE ⊥面ADC ． …(8分) 解：(Ⅲ)方法一:连接EC ，该四棱锥分为两个三棱锥E ﹣ABC 和E ﹣ADC ．．…（12分）方法二：取BC 的中点为O ，连接AO,则AO ⊥BC ，又CD ⊥平面ABC ， ∴CD ⊥AO ，BC ∩CD=C ，∴AO ⊥平面BCDE ， ∴AO 为V A ﹣BCDE 的高，，∴．【点评】本题考查的知识点是直线与平面平行的判定，平面与平面垂直的判定，棱锥的体积，其中熟练掌握空间线面平行或垂直的判定、性质、定义、几何特征是解答此类问题的关键．7．如图，四棱柱ABCD ﹣A 1B 1C 1D 1中,平面A 1ABB 1⊥平面ABCD,且∠ABC=．（1）求证：BC ∥平面AB 1C 1;（2)求证：平面A 1ABB 1⊥平面AB 1C 1．【分析】（1）根据BC ∥B 1C 1，且B 1C 1⊂平面AB 1C 1，BC ⊄平面AB 1C 1，依据线面平行的判定定理推断出BC ∥平面AB 1C 1．（2）平面A 1ABB 1⊥平面ABCD ，平面ABCD ∥平面A 1B 1C 1D 1，推断出平面A 1ABB 1⊥平面A 1B 1C 1D 1，又平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1，A 1B 1⊥C 1B 1，C 1B 1⊂平面AB 1C 1，根据面面垂直的性质推断出平面A 1ABB 1⊥平面AB 1C 1．【解答】证明：（1）∵BC ∥B 1C 1，且B 1C 1⊂平面AB 1C 1，BC ⊄平面AB 1C 1， ∴BC ∥平面AB 1C 1．（2）∵平面A 1ABB 1⊥平面ABCD ，平面ABCD ∥平面A 1B 1C 1D 1, ∴平面A 1ABB 1⊥平面A 1B 1C 1D 1，∵平面A 1ABB 1∩平面A 1B 1C 1D 1=A 1B 1,A 1B 1⊥C 1B 1, ∴C 1B 1⊂平面AB 1C 1，∴平面A 1ABB 1⊥平面AB 1C 1．【点评】本题主要考查了线面平行和面面垂直的判定定理．注重了对基础知识的考查．8．如图，三角形ABC 中，AC=BC=，ABED 是边长为1的正方形，平面ABED ⊥底面ABC ，若G 、F 分别是EC 、BD 的中点．（Ⅰ)求证:GF ∥底面ABC ；（Ⅱ）求证：AC⊥平面EBC；（Ⅲ）求几何体ADEBC的体积V．【分析】（1）证法一:证明一条直线与一个平面平行,除了可以根据直线与平面平行的判定定理以外,通常还可以通过平面与平面平行进行转化,比如取BE的中点H，连接HF、GH，根据中位线定理易证得：平面HGF∥平面ABC，进一步可得:GF∥平面ABC．证法二：根据直线与平面平行的判定定理可知：如果不在一个平面内的一条直线和平面内的一条直线平行，那么直线和这个平面平行．故只需在平面ABC中找到与GF平行的直线即可．因为G、F分别是EC、BD的中点，故平移是可以通过构造特殊的四边形、三角形来实现．证法三:根据直线与平面平行的判定定理可知:如果不在一个平面内的一条直线和平面内的一条直线平行，那么直线和这个平面平行．故只需在平面ABC中找到与GF平行的直线即可．因为G、F分别是EC、BD的中点，所以构造中位线是常用的找到平行直线的方法．（2）证明直线与平面垂直,关键要找到两条相交直线与之都垂直．有时候题目中没有现成的直线与直线垂直，需要我们先通过直线与平面垂直或者平面与平面垂直去转化一下．由第一问可知：GF∥平面ABC，而平面ABED⊥平面ABC，所以BE⊥平面ABC，所以BE⊥AC；又由勾股定理可以证明：AC⊥BC．（3）解决棱锥、棱柱求体积的问题，关键在于找到合适的高与对应的底面，切忌不审图形，盲目求解;根据平面与平面垂直的性质定理可知:CN⊥平面ABED，而ABED是边长为1的正方形,进一步即可以求得体积．【解答】解：（I）证法一：取BE的中点H，连接HF、GH,（如图）∵G、F分别是EC和BD的中点∴HG∥BC，HF∥DE,(2分）又∵ADEB为正方形∴DE∥AB，从而HF∥AB∴HF∥平面ABC,HG∥平面ABC,HF∩HG=H，∴平面HGF∥平面ABC∴GF∥平面ABC（5分）证法二:取BC的中点M,AB的中点N连接GM、FN、MN（如图）∵G、F分别是EC和BD的中点∴（2分）又∵ADEB为正方形∴BE∥AD，BE=AD∴GM∥NF且GM=NF∴MNFG为平行四边形∴GF∥MN，又MN⊂平面ABC，∴GF∥平面ABC（5分）证法三：连接AE，∵ADEB为正方形，∴AE∩BD=F，且F是AE中点，（2分）∴GF∥AC，又AC⊂平面ABC，∴GF∥平面ABC(5分）（Ⅱ）∵ADEB为正方形，∴EB⊥AB,∴GF∥平面ABC（5分）又∵平面ABED⊥平面ABC,∴BE⊥平面ABC(7分)∴BE⊥AC又∵CA2+CB2=AB2∴AC⊥BC，∵BC∩BE=B，∴AC⊥平面BCE（9分）（Ⅲ)连接CN，因为AC=BC,∴CN⊥AB，(10分）又平面ABED⊥平面ABC，CN⊂平面ABC，∴CN⊥平面ABED．（11分）∵三角形ABC是等腰直角三角形,∴,（12分）∵C﹣ABED是四棱锥，==（14分）∴VC﹣ABED【点评】本小题主要考查空间线面关系、面面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．9．如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD||BC，PD⊥底面ABCD，∠ADC=90°,AD=2BC,Q为AD的中点，M为棱PC的中点．（Ⅰ）证明：PA∥平面BMQ；（Ⅱ)已知PD=DC=AD=2,求点P到平面BMQ的距离．【分析】（1)连结AC交BQ于N，连结MN，只要证明MN∥PA,利用线面平行的判定定理可证；（2)由（1）可知，PA∥平面BMQ，所以点P到平面BMQ的距离等于点A到平面BMQ的距离．【解答】解：（1）连结AC交BQ于N,连结MN,因为∠ADC=90°，Q为AD的中点，所以N为AC的中点．…（2分）当M为PC的中点，即PM=MC时，MN为△PAC的中位线，故MN∥PA，又MN⊂平面BMQ，所以PA∥平面BMQ．…（5分)（2）由（1)可知，PA∥平面BMQ，所以点P到平面BMQ的距离等于点A到平面BMQ的距离，所以VP﹣BMQ =VA﹣BMQ=VM﹣ABQ,取CD的中点K,连结MK，所以MK∥PD，，…(7分）又PD⊥底面ABCD，所以MK⊥底面ABCD．又，PD=CD=2，所以AQ=1，BQ=2，,…（10分）所以VP﹣BMQ =VA﹣BMQ=VM﹣ABQ=.,…(11分）则点P到平面BMQ的距离d=…（12分）【点评】本题考查了线面平行的判定定理的运用以及利用三棱锥的体积求点到直线的距离．10．已知直三棱柱ABC ﹣A 1B 1C 1的底面△ABC 中，∠C=90°，BC=，BB 1=2，O 是AB 1的中点,D 是AC 的中点，M 是CC 1的中点，（1）证明：OD ∥平面BB 1C 1C ；（2)试证:BM ⊥AB 1．【分析】（1)连B 1C 利用中位线的性质推断出OD ∥B 1C ，进而根据线面平行的判定定理证明出OD ∥平面BB 1C 1C ．（2)先利用线面垂直的性质判断出CC 1⊥AC ，进而根据线面垂直的判定定理证明出AC ⊥平面BB 1C 1C ，进而可知AC ⊥MB ．利用证明△BCD ∽△B 1BC,推断出∠CBM=∠BB 1C ，推断出BM ⊥B 1C ，最后利用线面垂直的判定定理证明出BM ⊥平面AB 1C ，进而可知BM ⊥AB 1．【解答】证明：（1)连B 1C ，∵O 为AB 1中点，D 为AC 中点， ∴OD ∥B 1C ，又B 1C ⊂平面BB 1C 1C,OD ⊄平面BB 1C 1C,∴OD ∥平面BB 1C 1C ．（2)连接B 1C ，∵直三棱柱ABC ﹣A 1B 1C 1，∴CC 1⊥平面ABC AC ⊂平面ABC, ∴CC 1⊥AC,又AC ⊥BC ，CC 1，BC ⊂平面BB 1C 1C ， ∴AC ⊥平面BB 1C 1C ，BM ⊂平面BB 1C 1C ， ∴AC ⊥MB ．在Rt △BCM 与Rt △B 1BC 中，==，∴△BMC ∽△B 1BC, ∴∠CBM=∠BB 1C,∴∠BB 1C+∠B 1BM=∠CBM+∠B 1BM=90°， ∴BM ⊥B 1C ，AC ，B 1C ⊂平面AB 1C ， ∴BM ⊥AB 1C ， ∵AB 1⊂平面AB 1C ， ∴BM ⊥AB 1．【点评】本题主要考查了线面平行和线面垂直的判定定理的应用．证明线线平行和线线垂直是解题的关键．11．如图,在四棱锥P ﹣ABCD 中，四边形ABCD 是平行四边形，E 、F 分别是AB 、PC 中点，求证:EF ∥面PAD ．【分析】取PD的中点G,连接FG、AG，由PF=CF，PG=DG,所以FG∥CD,且FG=CD．又因为四边形ABCD是平行四边形，且E是AB的中点．所以AE∥CD，且AE=CD．证得四边形EFGA是平行四边形,所以EF∥AG，由线面平行的判定定理即可得证．【解答】证明：取PD的中点G，连接FG、AG．因为PF=CF，PG=DG,所以FG∥CD,且FG=CD．又因为四边形ABCD是平行四边形，且E是AB的中点．所以AE∥CD，且AE=CD．所以FG∥AE，且FG=AE,所以四边形EFGA是平行四边形，所以EF∥AG．又因为EF⊄平面PAD,AG⊂平面PAD，所以EF∥平面PAD．【点评】本题考查直线与平面平行的证明，解题时要认真审题,仔细解答，注意等价转化思想的合理运用．12．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，E 是AA 1的中点，求证：（Ⅰ）A 1C ∥平面BDE ；（Ⅱ）平面A 1AC ⊥平面BDE ．【分析】（Ⅰ）连接AC 交BD 于O,连接EO ，△A 1AC 中利用中位线，得EO ∥A 1C ．再结合线面平行的判定定理，可得A 1C ∥平面BDE;（II ）根据正方体的侧棱垂直于底面，结合线面垂直的定义,得到AA 1⊥BD ．再结合正方形的对角线互相垂直，得到AC ⊥BD ，从而得到BD ⊥平面A 1AC,最后利用面面垂直的判定定理，可以证出平面A 1AC ⊥平面BDE ．【解答】证明:（Ⅰ）连接AC 交BD 于O ，连接EO ， ∵E 为AA 1的中点，O 为AC 的中点 ∴EO 为△A 1AC 的中位线 ∴EO ∥A 1C又∵EO ⊂平面BDE ，A 1C ⊄平面BDE ∴A 1C ∥平面BDE ；…(6分）（Ⅱ)∵AA 1⊥平面ABCD,BD ⊂平面ABCD ∴AA 1⊥BD又∵四边形ABCD 是正方形 ∴AC ⊥BD ，∵AA1∩AC=A，AA1、AC⊂平面A1AC∴BD⊥平面A1AC又∵BD⊂平面BDE∴平面A1AC⊥平面BDE．…（12分）【点评】本题以正方体为例，要求我们证明线面平行和面面垂直,着重考查了空间直线与平面的位置关系和平面与平面位置关系等知识点,属于基础题．13．如图,四棱锥P﹣ABCD中,底面ABCD为矩形，E为PD的中点．（1)求证：PB∥平面AEC；（2）若PA⊥平面ABCD,PA=AD,求证:平面AEC⊥平面PCD．【分析】（1）连接BD交AC于O点，连接EO，只要证明EO∥PB，即可证明PB∥平面AEC;（2）要证平面PDC⊥平面AEC，需要证明CD⊥AE,AE⊥PD，即垂直平面AEC内的两条相交直线．【解答】证明：(1）连接BD交AC于O点，连接EO，∵O为BD中点，E为PD中点，∴EO∥PB，又EO⊂平面AEC，PB⊄平面AEC,∴PB∥平面AEC．（2）∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD，又AD⊥CD，且AD∩PA=A，∴CD⊥平面PAD，又AE⊂平面PAD，∴CD⊥AE．∵PA=AD，E为PD中点,∴AE⊥PD．又CD∩PD=D，∴AE⊥平面PDC,又AE⊂平面PAD，∴平面PDC⊥平面AEC．【点评】本题考查了线面平行，面面垂直的判定定理，属于基础题．14．如图，ABCD是正方形，O是正方形的中心,PO⊥底面ABCD，E是PC的中点．求证:（1）PA∥平面BDE；（2）BD⊥平面PAC．【分析】（1）连接OE，根据三角形中位线定理，可得PA∥EO,进而根据线面平行的判定定理，得到PA∥平面BDE．（2）根据线面垂直的定义，可由PO⊥底面ABCD得到BD⊥PO，结合四边形ABCD是正方形及线面垂直的判定定理可得BD⊥平面PAC【解答】证明(1)连接OE，在△CAP中，CO=OA，CE=EP,∴PA∥EO，又∵PA⊄平面BDE，EO⊂平面BDE，∴PA∥平面BDE．（2）∵PO⊥底面ABCD，BD⊂平面ABCD，∴BD⊥PO又∵四边形ABCD是正方形，∴BD⊥AC∵AC∩PO=O，AC，PO⊂平面PAC∴BD⊥平面PAC【点评】本题考查的知识点是直线与平面平行的判定，直线与平面垂直的判定，熟练掌握空间线面关系的判定定理是解答的关键．15．如图，正四棱柱ABCD ﹣A 1B 1C 1D 1，底面边长AB=1，侧棱长AA 1=2． (Ⅰ）求正四棱柱ABCD ﹣A 1B 1C 1D 1的表面积； (Ⅱ）证明：AC ⊥平面BDD 1B 1．【分析】（I)求出各面的面积即可得出表面积；（II ）根据BB 1⊥平面ABCD 可得AC ⊥BB 1，根据正方形ABCD 的性质可得AC ⊥BD ，从而有AC ⊥平面BDD 1B 1．【解答】解：(I)正四棱柱的表面积为1×1×2+1×2×4=10．（II ）连接AC,BD,B 1D 1,∵BB 1⊥平面ABCD ，AC ⊂平面ABCD ， ∴AC ⊥BB 1，∵四边形ABCD 是正方形, ∴AC ⊥BD,又BD ⊂平面BDD 1B 1，BB 1⊂平面BDD 1B 1，BD ∩BB 1=B ， ∴AC ⊥平面BDD 1B 1．【点评】本题考查了直棱柱的结构特征，线面垂直的判定，属于基础题．16．已知正方体ABCD ﹣A 1B 1C 1D 1，O 是底ABCD 对角线的交点．求证：（1）C 1O ∥面AB 1D 1; (2)A 1C ⊥面AB 1D 1．【分析】(1)欲证C 1O ∥面AB 1D 1,根据直线与平面平行的判定定理可知只需证C 1O 与面AB 1D 1内一直线平行，连接A 1C 1，设A 1C 1∩B 1D 1=O 1，连接AO 1，易得C 1O ∥AO 1，AO 1⊂面AB 1D 1，C 1O ⊄面AB 1D 1，满足定理所需条件；（2）欲证A 1C ⊥面AB 1D 1,根据直线与平面垂直的判定定理可知只需证A 1C 与面AB 1D 1内两相交直线垂直根据线面垂直的性质可知A 1C ⊥B 1D 1，同理可证A 1C ⊥AB 1，又D 1B 1∩AB 1=B 1，满足定理所需条件．【解答】证明:（1)连接A 1C 1，设A 1C 1∩B 1D 1=O 1，连接AO 1, ∵ABCD ﹣A 1B 1C 1D 1是正方体, ∴A 1ACC 1是平行四边形，∴A1C1∥AC且A1C1=AC，又O1，O分别是A1C1，AC的中点，∴O1C1∥AO且O1C1=AO,∴AOC1O1是平行四边形，∴C1O∥AO1,AO1⊂面AB1D1，C1O⊄面AB1D1,∴C1O∥面AB1D1；(2)∵CC1⊥面A1B1C1D1∴CC1⊥B1D!，又∵A1C1⊥B1D1，∴B1D1⊥面A1C1C，即A1C⊥B1D1，∵A1B⊥AB1,BC⊥AB1，又A1B∩BC=B,AB1⊥平面A1BC，又A1C⊂平面A1BC,∴A1C⊥AB1，又D1B1∩AB1=B1，∴A1C⊥面AB1D1【点评】本题主要考查了线面平行、线面垂直的判定定理，考查对基础知识的综合应用能力和基本定理的掌握能力．17．如图所示，在正方体ABCD﹣A1B1C1D1中，M,E,F，N分别为A1B1，B1C1，C1D1，D1A1的中点，求证:(1）E，F，D，B四点共面；（2）面AMN∥平面EFDB．【分析】（1)由E,E分别是B1C1,C1D1的中点，知EF∥B1D1，从而得到EF∥BD，由此能证明E，F，B，D，四点共面．（2）由题设条件推导出MN∥EF，AN∥CF，由此能够证明面MAN∥面EFDB．【解答】证明:（1）∵E，E分别是B1C1，C1D1的中点,∴EF∥B1D1 ,∵B1D1∥BD,∴EF∥BD，∴E，F，B，D，四点共面．（2）∵M,N分别是A1B1，D1A1的中点，∴MN∥B1D1，∵EF∥B1D1，∴MN∥EF，∵F，N分别是D1C1、A1B1的中点，∴NF A1D1，∵，∴NF AC,∴四边形NFCA是平行四边形，∴AN∥CF，∵MN∩AN=N，EF∩DF=F，∴面MAN∥面EFDB．【点评】本题考查四点共面的证明,考查两个平面平行的证明．解题时要认真审题，注意中位线定理和平行公理的合理运用．18．如图，长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=1，AA 1=2，点P 是DD 1的中点．求证:(1）直线BD 1∥平面PAC（2）①求异面直线PC 与AA 1所成的角． ②平面PAC ⊥平面BDD 1．【分析】(1)连接BD ，交AC 于O,连接PO ，由三角形的中位线定理和线面平行的判定定理，即可得证；（2）①连接PC 1，AA 1∥CC 1，∠C 1CP 即为异面直线PC 与AA 1所成的角，分别求出△C 1CP 的三边，由解三角形即可得到所求角;②运用正方形的对角线垂直和线面垂直的性质定理，可得AC ⊥平面BDD 1B 1，再由面面垂直的判定定理，即可得证．【解答】（1）证明:连接BD ，交AC 于O ，连接PO ，在△BDD1中，OP 为中位线,可得OP∥BD1，又OP⊂平面PAC，BD1⊄平面PAC，则直线BD1∥平面PAC；（2）①连接PC1，AA1∥CC1，∠C1CP即为异面直线PC与AA1所成的角，在△C1CP中，C1C=2，PC===，PC1===,由PC2+PC12=CC12，可得△C1CP为等腰直角三角形，则异面直线PC与AA1所成的角为45°；②证明：在底面ABCD中，AB=AD，即有四边形ABCD为正方形，可得AC⊥BD，D1D⊥平面ABCD，AC⊂平面ABCD,即有D1D⊥AC,D1D∩BD=D,可得AC⊥平面BDD1B1，AC⊂平面PAC，则平面PAC⊥平面BDD1．【点评】本题考查线面平行的判定，注意运用中位线定理和线面平行的判定定理,考查异面直线所成角的求法,注意运用平移法，考查面面垂直的判定，注意运用线面垂直的判定和性质，考查空间想象能力和推理能力，属于基础题．19．如图，在直三棱柱ABC ﹣A 1B 1C 1中，∠ACB=90°，AC=CB=CC 1=2，E 是AB 中点． (Ⅰ)求证:AB 1⊥平面A 1CE ；（Ⅱ）求直线A 1C 1与平面A 1CE 所成角的正弦值．【分析】（Ⅰ）由ABC ﹣A 1B 1C 1是直三棱柱，可知CC 1⊥AC ，CC 1⊥BC ，∠ACB=90°,AC⊥BC ．建立空间直角坐标系C ﹣xyz ．则A ，B 1，E ，A 1，可得，，，可知，根据，，推断出AB 1⊥CE ，AB 1⊥CA 1，根据线面垂直的判定定理可知AB 1⊥平面A 1CE ． (Ⅱ）由（Ⅰ)知是平面A 1CE 的法向量，，进而利用向量数量积求得直线A 1C 1与平面A 1CE 所成角的正弦值【解答】（Ⅰ）证明：∵ABC ﹣A 1B 1C 1是直三棱柱， ∴CC 1⊥AC,CC 1⊥BC, 又∠ACB=90°，即AC ⊥BC ．如图所示，建立空间直角坐标系C ﹣xyz ．A （2，0,0)，B 1（0,2,2)，E(1，1，0），A 1(2，0，2）， ∴,,．又因为 ,，∴AB 1⊥CE ，AB 1⊥CA 1，AB 1⊥平面A 1CE ．（Ⅱ)解:由（Ⅰ)知，是平面A 1CE 的法向量，，∴｜cos ＜，＞｜==．设直线A 1C 1与平面A 1CE 所成的角为θ，则sinθ=｜cos ＜，＞｜=．所以直线A 1C 1与平面A 1CE 所成角的正弦值为．【点评】本题主要考查了线面垂直的判定定理，向量的数量积的运用，法向量的运用．综合考查了学生所学知识的灵活运用．20．如图,在正方体ABCD ﹣A 1B 1C 1D 1中，E 、F 、G 分别是AB 、AD 、C 1D 1的中点．求证：平面D 1EF ∥平面BDG ．【分析】欲证平面D 1EF ∥平面BDG,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行，EF ∥BD 又EF ⊄平面BDG ，BD ⊂平面BDG 根据线面平行的性质可知EF ∥平面BDG ，同理可证D 1E ∥平面BDG ，EF ∩D 1E=E ，满足定理条件．【解答】证明:∵E 、F 分别是AB 、AD 的中点，∴EF ∥BD 又EF ⊄平面BDG ，BD ⊂平面BDG ∴EF ∥平面BDG ∵D 1G EB ∴四边形D 1GBE 为平行四边形，D 1E ∥GB 又D 1E ⊄平面BDG,GB ⊂平面BDG∴D 1E ∥平面BDG,EF ∩D 1E=E ， ∴平面D 1EF ∥平面BDG【点评】本小题主要考查空间中的线面关系，考查线面平行的判定，考查识图能力和逻辑思维能力与推理论证能力，考查转化思想，属于基础题．21．（文科)如图，正方体ABCD ﹣A 1B 1C 1D 1中，M ，N,E ，F 分别是棱A 1B 1，A 1D 1，B 1C 1，C 1D 1的中点, 求证：平面AMN ∥平面EFDB ．【分析】连接B 1D 1，NE ，分别在△A 1B 1D 1中和△B 1C 1D 1中利用中位线定理，得到MN ∥B 1D 1，EF ∥B 1D 1，从而MN ∥EF,然后用直线与平面平行的判定定理得到MN ∥面BDEF ．接下来利用正方形的性质和平行线的传递性，得到四边形ABEN 是平行四边形，得到AN ∥BE ，直线与平面平行的判定定理得到AN ∥面BDEF,最后可用平面与平面平行的判定定理，得到平面AMN ∥平面EFDB ，问题得到解决．【解答】证明:如图所示,连接B 1D 1，NE∵M,N ，E ，F 分别是棱A 1B 1,A 1D 1，B 1C 1，C 1D 1的中点 ∴MN ∥B 1D 1，EF ∥B 1D 1 ∴MN ∥EF又∵MN ⊄面BDEF ，EF ⊂面BDEF ∴MN ∥面BDEF∵在正方形A 1B 1C 1D 1中,M ，E ，分别是棱 A 1B 1，B 1C 1的中点∴NE∥A1B1且NE=A1B1又∵A1B1∥AB且A1B1=AB∴NE∥AB且NE=AB∴四边形ABEN是平行四边形∴AN∥BE又∵AN⊄面BDEF，BE⊂面BDEF∴AN∥面BDEF∵AN⊂面AMN，MN⊂面AMN，且AN∩MN=N∴平面AMN∥平面EFDB【点评】本题借助于正方体模型中的一个面面平行位置关系的证明，着重考查了三角形的中位线定理、线面平行的判定定理和面面平行的判定定理等知识点，属于基础题．22．如图，在四棱锥P﹣ABCD中，侧面PAD是正三角形，且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M，E为AD的中点，求证：（1)EN∥平面PDC;(2）BC⊥平面PEB；（3）平面PBC⊥平面ADMN．【分析】（1）先证明AD∥MN由N是PB的中点，E为AD的中点，底面ABCD是边长为2的菱形得EN∥DM，DM⊂平面PDC，可得EN∥平面PDC；（2）由侧面PAD是正三角形,且与底面ABCD垂直，E为AD的中点，得PE⊥AD，PE⊥EB,PE⊥BC，由∠BAD=60°，AB=2,AE=1,由余弦定理可得BE=,由正弦定理可得：BE⊥AD，有由AD∥BC可得BE⊥BC,可得BC⊥平面PEB；（3）由（2）知BC⊥平面PEB，EN⊂平面PEB可得PB⊥MN，由AP=AB=2,N是PB的中点，得PB ⊥AN，有MN∩AN=N．PB⊥平面ADMN，可证平面PBC⊥平面ADMN．【解答】解：（1）∵AD∥BC,AD⊂平面ADMN，BC⊄平面ADMN，∴BC∥平面ADMN，∵MN=平面ADMN∩平面PBC,BC⊂平面PBC，∴BC∥MN．又∵AD∥BC，∴AD∥MN．∴ED∥MN∵N是PB的中点，E为AD的中点，底面ABCD是边长为2的菱形，∴ED=MN=1∴四边形ADMN是平行四边形．∴EN∥DM，DM⊂平面PDC，∴EN∥平面PDC；（2）∵侧面PAD是正三角形，且与底面ABCD垂直，E为AD的中点，∴PE⊥AD，PE⊥EB,PE⊥BC∵∠BAD=60°，AB=2，AE=1，由余弦定理可得BE=，由正弦定理可得：BE⊥AD∴由AD∥BC可得BE⊥BC，∵BE∩PE=E∴BC⊥平面PEB；（3）∵由(2)知BC⊥平面PEB,EN⊂平面PEB∴BC⊥EN∵PB⊥BC，PB⊥AD∴PB⊥MN∵AP=AB=2，N是PB的中点，∴PB⊥AN,∴MN∩AN=N．PB⊥平面ADMN，∵PB⊂平面PBC∴平面PBC⊥平面ADMN．【点评】本题主要考察了平面与平面垂直的判定,直线与平面平行的判定，直线与平面垂直的判定，属于基本知识的考查．23．如图，在正三棱锥P﹣ABC中，D,E分别是AB,BC的中点．(1）求证:DE∥平面PAC；(2)求证：AB⊥PC．【分析】（1）推导出DE∥AC，由此能证明DE∥平面PAC．（2）连结PD，CD，则PD⊥AB，CD⊥AB，从而AB⊥平面PDC,由此能证明AB⊥PC．【解答】证明：（1）∵在正三棱锥P﹣ABC中，D，E分别是AB，BC的中点．∴DE∥AC，∵DE⊄平面PAC，AC⊂平面PAC，∴DE∥平面PAC．（2）连结PD,CD，∵正三棱锥P﹣ABC中，D是AB的中点,∴PD⊥AB，CD⊥AB,∵PD∩CD=D,∴AB⊥平面PDC，∵PC⊂平面PDC,∴AB⊥PC．【点评】本题考查线面平行的证明，考查线线垂直的证明，是中档题，解题时要认真审题,注意空间思维能力的培养．24．如图所示，在四棱锥P﹣ABCD中，底面是边长为1的正方形，侧棱PD=1,PA=PC=．(1)求证:PD⊥平面ABCD；（2）求证：平面PAC⊥平面PBD．【分析】(1）由勾股定理逆定理可证明AD⊥PD,PD⊥CD即可得出PD⊥平面ABCD；(2）由（1）可得PD⊥AC，结合AC⊥BD,得出AC⊥平面PBD,从而平面PAC⊥平面PBD．。

立体几何题

1．已知:直三棱柱ABC-A1B1C1中,AC垂直于BC,D为AB中点,AC=BC=BB1=2.求证:(1)BC1平行于面CA1D 。

(2)求B1到面CA1D的距离。

2．正方体ABCD-A1B1C1D1中,O是底面中心,B1H垂直于D1O,H为垂足.求证:B1H垂直于面AD1C。

3．四面体ABCD中,AB,AC,AD两两垂直,若△BCD的垂心为O,求证:AO⊥平面BCD.4．α∩β=CD,A、B是直线l上的两点，A、B在β内的射影分别为A1，B1两点，当直线l满足条件______时,CD⊥A1B1。

注:此题有多种答案,所填答案正确即可,不必考虑所有情况。

5．AB为⊙O的直径,MB⊥⊙O所在的平面于点B,C为⊙O上一点,且MB=4,AC=BC=2.⑴证明:平面MAC⊥平面MBC。

⑵求MA与BC所成角的大小。

⑶设P为MA的中点,求点M到平面PBC的距离。

6．在矩性ABCD中,AB=a,AD=2b,a<b,E,F分别是AD,BC的中点,以EF为折痕把四边形EFCD 折起,当角CEB=90度时,二面角C-EF-B的平面角的余弦值=_____ 。

7．正方体中ABCD-A1B1C1D1，E为BC的中点，则二面角D1-B1E-C1的正切值是（）。

[答案2分之根5]8．把边长为a的正三角形沿高线折成60度的二面角，求A到BC的距离。

9．ABCD是矩形，AB=4 ，BC=3，E是CD中点。

沿AE将三角形AED折起，二面角D-AE-B为60度。

求二面角D-EC-B大小。

10．在四面体P-ABC中，已知PA=BC=6,PC=AB=10,AC=8,PB=2√34，F是线段PB上一点，CF=15/17√34，点E在线段AB上，且EF⊥PB.(1)证明：PB⊥平面CEF;(2)求二面角B-CE-F的正切值。

11．平行四边形ABCD中,∠DAB=60度,AD= 1∕2 AB=a , E,F分别是AB,CD的中点,以EF 为二面角的棱,转动平行四边形AEFD,当转成二面角A-EF-B为60度时,求三棱柱ABE-DCF 的侧面积。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

立体几何1. 如图：梯形ABCD 和正△PAB 所在平面互相垂直，其中//,AB DC12AD CD AB ==，且O 为AB 中点. ( I ) 求证：//BC 平面POD ； ( II ) 求证：AC ⊥PD .2.如图，菱形ABCD 的边长为6，60BAD ∠=o ,AC BD O =I .将菱形ABCD 沿对角线AC 折起，得到三棱锥B ACD -,点M 是棱BC的中点，DM =（Ⅰ）求证：//OM 平面ABD ；（Ⅱ）求证：平面ABC ⊥平面MDO ；（Ⅲ）求三棱锥M-的体积.BACDOPA ABCMOD3. 如图，在四棱锥中，底面为直角梯形，AD 12已知四棱锥的底面是菱形．PB PD =，为的中点．（Ⅰ）求证：PC ∥平面；（Ⅱ）求证：平面PAC ⊥平面BDE ．5. 已知直三棱柱111C B A ABC -的所有棱长都相等，且F E D ,,分别为11,,AA BB BC 的中点. (I) 求证：平面//1FC B 平面EAD ；（II ）求证：⊥1BC 平面EAD .PABCDQ M6. 如图所示，正方形ABCD 与直角梯形ADEF 所在平面互相垂直，90ADE ∠=o ，DE AF //，22===AF DA DE .(Ⅰ)求证：AC ⊥平面BDE ； (Ⅱ)求证：//AC 平面BEF ；（Ⅲ）求四面体BDEF 的体积.7. 如图，在四棱锥ABCD P -中，平面PAD ⊥平面ABCD ， AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点求证：（1）直线EF8.如图，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD ∥QA ，QA =AB =12PD ．（I ）证明：PQ ⊥平面DCQ ；（II ）求棱锥Q —ABCD 的的体积与棱锥P —DCQ 的体积的比值．ABCDFE(16)第题图9. 如图，在△ABC中，∠ABC=45°，∠BAC=90°，AD是BC上的高，沿AD把△ABD折起，使∠BDC=90°。

（1）证明：平面ＡＤＢ⊥平面ＢＤＣ；（2 ）设BD=1，求三棱锥D—ＡＢＣ的表面积。

参考答案：1. 证明: (I) 因为O 为AB 中点，所以1,2BO AB =…………………1分又//,AB CD 12CD AB =，所以有,//,CD BO CD BO = …………………2分所以ODCB 为平行四边形,所以//,BC OD …………………3分又DO ⊂平面,POD BC ⊄平面,POD 所以//BC 平面POD . …………………5分(II)连接OC .因为,//,CD BO AO CD AO ==所以ADCO 为平行四边形， …………………6分又AD CD =,所以ADCO 为菱形，BACDOP所以 AC DO ⊥， …………………7分因为正三角形PAB ,O 为AB 中点，所以PO AB ⊥ ， …………………8 分又因为平面ABCD ⊥平面PAB ,平面ABCD I 平面PAB AB = ，所以PO ⊥平面ABCD ， …………………10分而AC ⊂平面ABCD ，所以 PO AC ⊥，又PO DO O =I ，所以AC ⊥平面POD . …………………12分又PD ⊂平面POD ，所以AC ⊥PD . …………………13分2. （Ⅰ）证明：因为点是菱形ABCD 的对角线的交点，所以是的中点.又点M 是棱BC 的中点，所以是的中位线，. ……………2分因为平面ABD ,平面ABD ，所以//OM 平面ABD . ……………4分（Ⅱ）证明：由题意，,因为DM =所以，. ……………6分又因为菱形ABCD ，所以. …………7分因为OM AC O =I ,所以平面ABC ， ……………8分因为平面MDO ，ABCMOD所以平面ABC ⊥平面MDO . ……………9分（Ⅲ）解：三棱锥M ABD -的体积等于三棱锥的体积. ……………10分由（Ⅱ）知，平面，所以3OD =为三棱锥的高. ……………11分的面积为， ……………12分所求体积等于13ABM S OD ∆⨯⨯=. ……………13分3. 证明：（Ⅰ）AD121t =//12⊂⊄（Ⅰ）证明：因为E ，O 分别为PA ，AC 的中点，所以EO ∥PC ．因为EO ⊂平面BDE PC ⊄平面BDE所以PC ∥平面BDE ．……………………6分（Ⅱ）证明：连结OP 因为PB PD =，所以OP BD ⊥．在菱形ABCD 中，BD AC ⊥ 因为OP AC O =I 所以BD ⊥平面PAC 因为BD ⊂平面BDE所以平面PAC ⊥平面BDE ． ……………………13分PABCD Q MN5. （Ⅰ）由已知可得1//AF B E ，1AF B E =， ∴四边形E AFB 1是平行四边形，∴1//FB AE ， ……………1分AE ⊄Q 平面FC B 1，1FB ⊂平面FC B 1， //AE ∴平面FC B 1； ……………2分又 E D ,分别是1,BB BC 的中点，∴C B DE 1//， ……………3分 ED ⊄Q 平面FC B 1，1B C ⊂平面FC B 1，//ED ∴平面FC B 1； ……………4分,AE DE E AE =⊂Q I 平面EAD ，ED ⊂平面EAD ， ……………5分∴平面FC B 1∥平面EAD . ……………6分 (Ⅱ) Θ三棱柱111C B A ABC -是直三棱柱， ∴⊥C C 1面ABC ，又Q ⊂AD 面ABC ，∴⊥C C 1AD . ……………7分又Q 直三棱柱111C B A ABC -的所有棱长都相等，D 是BC 边中点， ∴ABC ∆是正三角形，∴BC AD ⊥， ……………8分而1C C BC C =I ， 1CC ⊂面11B BCC ，BC ⊂面11B BCC ，⊥∴AD 面11B BCC ， ……………9分故 1AD BC ⊥ . ……………10分Q 四边形11BCC B 是菱形，∴C B BC 11⊥， ……………11分而C B DE 1//，故 1DE BC ⊥ , ……………12分由D DE AD =I AD ⊂，面EAD ，ED ⊂面EAD ，得 ⊥1BC 面EAD . ……………13分6. (Ⅰ)证明：因为平面ABCD ⊥平面ADEF ，90ADE ∠=o ，所以DE ⊥平面ABCD ， …………………2分所以AC DE ⊥. …………………3分因为ABCD 是正方形，所以BD AC ⊥，所以AC ⊥平面BDE . …………………4分 (Ⅱ)证明：设AC BD O =I ，取BE 中点G ，连结OG FG ,，所以，OG //=12DE . ……………………5分因为DE AF //，AF DE 2=，所以AF //=OG ， ……………………6分从而四边形AFGO 是平行四边形，AO FG //. ……………………7分因为FG ⊂平面BEF ,AO ⊄平面BEF , ……………………8分所以//AO 平面BEF ，即//AC 平面BEF . ……………………9分（Ⅲ）解：因为平面ABCD ⊥平面ADEF ，AB AD ⊥,所以AB ⊥平面ADEF . ……………………11分因为DE AF //,90ADE ∠=o ,22===AF DA DE ，所以DEF ∆的面积为122ED AD ⨯⨯=， ……………………12分所以四面体BDEF 的体积=⨯=∆AB S DEF 3143. ……………………13分 7. 答案：（1）因为E 、F 分别是AP 、AD 的中点，,EF PD ∴P 又,PD PCD EF PCD ⊂⊄Q 面面∴直线EF AB=AD,BAD=60,∠o Q ABD ∆,BF AD ∴⊥PAD ABCD AD,⋂面面＝,BF PAD BF BEF ∴⊥⊂面面8. 解：（I ）由条件知PDAQ 为直角梯形因为QA ⊥平面ABCD ，所以平面PDAQ ⊥平面ABCD ，交线为AD. 又四边形ABCD 为正方形，DC ⊥AD ，所以DC ⊥平面PDAQ ，可得PQ ⊥DC.在直角梯形PDAQ 中可得DQ=PQ=2PD ，则PQ ⊥QD 所以PQ ⊥平面DCQ. ………………6分（II ）设AB=a .由题设知AQ 为棱锥Q —ABCD 的高，所以棱锥Q —ABCD 的体积311.3V a =由（I ）知PQ 为棱锥P —DCQ 的高，而，△DCQ 2，所以棱锥P —DCQ 的体积为321.3V a =故棱锥Q —ABCD 的体积与棱锥P —DCQ 的体积的比值为1.…………12分 9. 1）∵折起前ＡＤ是ＢＣ边上的高，∴ 当Δ ＡＢＤ折起后，AD ⊥ＤＣ，AD ⊥ＤＢ，又DB ⋂ＤＣ＝Ｄ，∴ＡＤ⊥平面ＢＤＣ，又∵AD 平面BDC. ∴平面ABD ⊥平面BDC ．（2）由（1）知，DA DB ⊥,DB DC ⊥,DC DA ⊥,Q DB=DA=DC=1，∴,1111,22DAM DBC DCA S S S ===⨯⨯=V V V 1sin 6022ABC S =︒=V∴三棱锥D —ＡＢＣ的表面积是133222S =⨯+=。

立体几何证明题

高中数学立体几何10道大题

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

高中数学立体几何证明题汇总

立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

高中立体几何证明题

第八讲 立体几何(基础大题)

立体几何练习题

立体几何平行证明题

立体几何证明题常见题型01

立体几何100题

立体几何平行证明题

立体几何证明题专题(教师版)

立体几何证明(教师版)

立体几何经典试题（含答案）

高中立体几何证明题精选

高中数学立体几何证明题汇总

(完整)立体几何证明基础题

立体几何题

第八讲立体几何(基础大题)