对浙江省高考立体几何翻折问题的剖析
立体几何中的翻折问题

C Q O P D
B
2 2 2 2 ) x2 2 x cos 45 ( )2 (2 x) 2 . 2 2 2
解得 x 1 . 由(1)知 AB 面 ACQ .
直线 AP 与平面 ACQ 所成的角的正弦值 sin 就是直线 AP 与直线 AB 所成角的
余弦值 cos BAP ,即 sin cos BAP = 即直线 AP 与平面 ACQ 所成的角为
绍兴市稽山中学 骆永明2来自展成平面, 逆向探究求最小值例5(06年江西卷文)
绍兴市稽山中学 骆永明
3.探寻轨迹, 点动成圆用两性质
例 6 已知矩形 ABCD,AB = 1,BC = 2 . 将△ABD 沿矩形 的对角线 BD 所在的直线进行翻折,在翻折过程中 ( ) A. 存在某个位置,使得直线 AC 与直线 BD 垂直 B. 存在某个位置,使得直线 AB 与直线 CD 垂直 C. 存在某个位置,使得直线 AD 与直线 BC 垂直 D. 对任意位置,直线 AC 与 BD,AB 与 CD,AD 与 BC 均 不垂直 ( 2012 年浙江省数学高考理科试题)
立体几何中的翻折问题
绍兴市稽山中学 骆永明
随着自主命题的深入,浙江省数学高 考立体几何试题对翻折问题似乎情有独 钟,且常考常新. 这类试题背景简单, 立意深远,对考生的空间想象能力要求很 高,能较好地改善学生对立体几何的思维 定势.
绍兴市稽山中学 骆永明
研究翻折问题应注意折前折后各元素相对位置的 变化. 要理清哪些位置关系和度量关系发生了变 化,哪些没有改变. 解决翻折问题的关键可以归纳 如下: ( 1) 找准“基准图”折叠; ( 2) 画好“2 个图”———折叠前的平面图和折 叠后的立体图; ( 3) 寻找“2 个量”———哪些量( 或关系) 发 生了变化,哪些量( 或关系) 没有发生变化.
立体几何中的翻折问题

AE = CFꎬ EF 交 BD 于 点 Hꎬ
将△DEF 沿 EF 折到△D′EF
的位置.
(1) 证明:AC⊥HD′ꎻ
(2) 若 AB
= 5ꎬAC
= 6ꎬAE
=
5 4
ꎬ OD′
=2
2 ꎬ求五棱锥
D′—ABCFE 的体积.
解析 (1) 由已知得 AC⊥BDꎬAD = CDꎬ又由 AE = CF
得AADE = CCDFꎬ故 AC∥EF.
参考文献:
[1]柴勤. 高中数学教学中学生解题能力的培养策略 [ J] . 考试周刊ꎬ208(45) :71.
[2]陈志全. 如何在高中数学教学中培养学生的数学 思维能力[ J] . 考试周刊ꎬ2018(43) :69.
[ 责任编辑:杨惠民]
立体几何中的翻折问题
莫碧华
( 重庆市第三十七中学校 400084)
由此得 EF⊥HDꎬEF⊥HD′ꎬ所以 AC⊥HD′.
— 32 —
为折痕ꎬ把△ABD 和△ACD 翻折成互相垂直的两个平面 后ꎬ某学生得出下列四个结论:
①AB⊥CDꎻ ②△BAC 是等边三角形ꎻ ③三棱锥 D—ABC 是正三棱锥ꎻ ④平面 ABD⊥平面 ABCꎻ 其中正确的是 . (写出所有正确命题的序号) 解析 由题知ꎬCD⊥平面 ABDꎬ故 CD⊥ABꎬ①正确ꎻ AD 为等腰直角△ABC 的斜边 BC 上的高ꎬ平面 ABD⊥平 面 ACDꎬ则 AB = AC = BCꎬ△BAC 是等边三角形ꎬ②正确ꎻ 易知 DA = DB = DCꎬ又由②知③正确ꎻ由①知④错. 故填: ①②③. 点评 涉及翻折中的线面位置关系的判定ꎬ根据翻 折前后所对应的平面图形与空间图形的位置关系ꎬ判定 线线、线面、面面的平行、垂直等位置关系.
立体几何中的折叠问题

链接高考:
(09 浙江)17.如图,在长方形 ABCD 中,AB 2 ,BC 1,E 为 DC 的
中点, F 为线段 EC (端点除外)上一动点.现将AFD 沿 AF 折起,
使平面 ABD 平面 ABC .在平面 ABD 内过点 D 作 DK AB , K 为垂
足.设 AK t ,则 t 的取值范围是
(3)AD与面BDM所成的角固定吗?(M为AC中点)
(4)二面角A-DB-C固定吗?
你能不用求解看出它的范围吗?
考向二:通过翻折得到一个不确定的几何体, 研究其点线面的位置关系
策略:明确不变量、紧抓关键量
C B
课本中翻折:
如图:边长为2的正方形ABCD中, (1)点E、F分别是边BC和CD的中点,将△ABE, △AFD分别沿AE,AF折起,使两点重合于P点,
归结为一个条件与结论明朗化的立几问题。 (3)将不变的条件集中到几何体图形中,将问题归结为一个条件与结论明朗化的立几问题。
研究其点线面的位置关系 求解翻折问题的基本方法: (4)二面角A-DB-C固定吗? 问题2、AD与BC会垂直吗? 温一模(16题) 图形的翻折问题在历年高考中时常出现,浙江省近几年就出现了四次,因为它是一个由直观到抽象的过程,所以每次的出现的题号都 偏后,同学们的答题情况也不太理想。
(1)AD与BC所成的角固定吗? 如图:边长为2的正方形ABCD中,
【总结规律】 你能不用求解看出它的范围吗?
问题6、二面角D-AC-B固定吗?范围为? 研究其点线面的位置关系。 如图:边长为2的正方形ABCD中,将△ACD沿对角线AC折起,连接BD,得到一个新的三棱锥D-ABC 问题5、AD与面BDM所成的角固定吗?(M为AC中点)
(2)求AD与面DBC所成角的正弦值 如图:边长为2的正方形ABCD中,将△ACD沿对角线AC折起,连接BD,得到一个新的三棱锥D-ABC (1)根据题中条件画出立体图形
立体几何中的翻折问题

规律小结:
分析求解折叠问题的关键是分辨折叠前后的不变量和不 变关系,在求解过程中充分利用不变量和不变关系.
如图,已知四边形ABCD是上、下底边长分别为2和6,高为 3 的等
腰梯形(如图①).将它沿对称轴OO1折成直二面角(如图②).
(1)证明:AC⊥BO1; (2)求二面角O—AC—O1的正弦值.
H
又因为BC⊂平面β,所以BC⊥D′E, 所以BC⊥α. 而D′C ⊂ α,所以BC⊥D′C, 所以∠D′CA为二面角β-BC-γ的平面角. 由于∠D′CA=45°, 所以二面角β-BC-γ的大小为45°.
VD'-ABC
=13SDABC
•D'O=1•1AC•BC•D'O 32
=13a2 46a=126a3
求解翻折问题的基本方法:
(1)先比较翻折前后的图形,弄清哪些量和位置关系在翻 折过程中不变,哪些已发生变化; (2)将不变的条件集中到立方体图形中,将问题归结为一 个条件与结论明朗化的立几问题.
(1)若二面角α-AC-β为直二面角,求二面角β-BC-γ的大小; (2)若二面角α-AC-β为60°,求三棱锥D′-ABC的体积.
立体几何中的翻折问题
如有一只小虫要从A爬到点M,
N
所走的最短路径是什么?
E
N
M
Hale Waihona Puke EFDC
A
B
N
MN
M
E
E F
F
D
C
D
C
A
BA
B
D
A
M
F
C
B
把一个平面图形按某种要求折起,转化为空间图 形,进而研究图形在位置关系和数量关系上的变 化,这就是翻折问题.
立体几何中的翻转与折叠问题

∵ AP=2,MP= √2 AP ⊥MP, ∴ tan ∠AMP=2√2
2
∴二面角A-EF-P大小为arctan ∠ AMP=2√2
(2) ∵ AP⊥PE,PE⊥PF,PF⊥AP,
∴VP-ABC=
1 3
×1×1×2=
2 3
(3)利用体积桥,
设P到平面AEF的距离为h,则S△AEF · h=3 VP-ABC
学生课前通过网络搜集资料,课上通 过学生动手操作、多媒体展示、师生互 动的讨论等环节,让学生在亲历探究的 过程中获得知识,从而达到培养能力的 目的,使学生情感、意志和能力都得到 充分的发展。
一.教学内容分析 二.教学对象分析 三.教学目标 四.教学方法 五.课堂结构和教学过程 六.教学评价 七.多媒体的应用
课堂小结 课后纸笔评价(分层作业)
五、课堂结构和教学过程
【课堂小结】
平面图形
翻 折 、展 剪开 拼 平面图形
不变量
位置关系 数量关系
解题关键
变量
位置关系 数量关系
五、课堂结构和教学过程
课后纸笔评价(分层作业)
变式训练:如图,已知ABCD是上下底边长分 D O 1
必 别为2和6,高为3 的等腰梯形,将它沿对称轴
一.教学内容分析 二.教学对象分析 三.教学目标 四.教学方法 五.课堂结构和教学过程 六.教学评价 七.多媒体的应用
三、教学目标
◆知识与技能目标: 1.使学生掌握翻折问题的解题方法,并会初步应用。 2.通过立体几何中翻折问题的学习,进一步掌握立体几何中
距离与成角的求法。
◆能力与方法目标: 1.培养学生的动手实践能力。 2.在实践过程中,使学生提高对立体图形的分析能力,进一
求解翻折问题的基本方法:
立体几何中的折叠问题含解析

高考热点问题:立体几何中折叠问题一、考情分析立体几何中的折叠问题是历年高考命题的一大热点与难点,主要包括两个方面:一是平面图形的折叠问题,多涉及到空间中的线面关系、体积的求解以及空间角、距离的求解等问题;二是几何体的表面展开问题,主要涉及到几何体的表面积以及几何体表面上的最短距离等.二、经验分享(1)立体几何中的折叠问题主要包含两大问题:平面图形的折叠与几何体的表面展开.把一个平面图形按照某种要求折起,转化为空间图形,进而研究图形在位置关系和数量关系上的变化,这就是折叠问题.把一个几何体的表面伸展为一个平面图形从而研究几何体表面上的距离问题,这就是几何体的表面展开问题.折叠与展开问题是立体几何的两个重要问题,这两种方式的转变正是空间几何与平面几何问题转化的集中体现,展开与折叠问题就是一个由抽象到直观,由直观到抽象的过程.此类问题也是历年高考命题的一大热点. (2) 平面图形通过折叠变为立体图形,就在图形发生变化的过程中,折叠前后有些量(长度、角度等)没有发生变化,我们称其为“不变量”.求解立体几何中的折叠问题,抓住“不变量”是关键.(3)把曲面上的最短路线问题利用展开图转化为平面上两点间距离的问题,从而使问题得到解决,这是求曲面上最短路线的一种常用方法.三、题型分析(一) 平面图形的折叠解答折叠问题的关键在于画好折叠前后的平面图形与立体图形,抓住两个关键点:不变的线线关系、不变的数量关系.不变的线线关系,尤其是平面图形中的线线平行、线线垂直关系是证明空间平行、垂直关系的起点和重要依据;不变的数量关系是求解几何体的数字特征,如几何体的表面积、体积、空间中的角与距离等的重要依据.1. 折叠后的形状判断【例1】如下图,在下列六个图形中,每个小四边形皆为全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的是_____________(要求:把你认为正确图形的序号都填上)①②③④⑤⑥【分析】根据平面图形的特征,想象平面图形折叠后的图形进行判断.也可利用手中的纸片画出相应的图形进行折叠.【答案】①③⑥【解析】①③⑥可以.②把横着的小方形折起后,再折竖着的小方形,则最上方的小方形与正方体的一个侧面重合,导致正方体缺少一个侧面;④把下方的小方形折起后,则上方的小方形中的第1,2个重合,导致正方体的底面缺少,不能折成正方体;⑤把中间的小方形当成正方体的底面,则右下方的小方形折叠不起来,构不成正方体.【小试牛刀】下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后的图形是()A. B. C. D.【例2】将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四边形ABCD(如图2),则在空间四边形ABCD中,AD与BC的位置关系是( )图1 图2A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直【答案】C【解析】在图1中的等腰直角三角形ABC 中,斜边上的中线AD 就是斜边上的高,则AD ⊥BC ,折叠后如图2,AD 与BC 变成异面直线,而原线段BC 变成两条线段BD 、CD ,这两条线段与AD 垂直,即AD ⊥BD ,AD ⊥CD ,故AD ⊥平面BCD ,所以AD ⊥BC .【小试牛刀】如图,在正方形ABCD 中,点E,F 分别为边BC,AD 的中点,将沿BF 所在直线进行翻折,将沿DE 所在直线进行翻折,在翻折过程中( )A. 点A 与点C 在某一位置可能重合B. 点A 与点C 的最大距离为C. 直线AB 与直线CD 可能垂直D. 直线AF 与直线CE 可能垂直 3.折叠后几何体的数字特征折叠后几何体的数字特征包括线段长度、几何体的表面积与体积、空间角与距离等,设计问题综合、全面,也是高考命题的重点.解决此类问题的关键是准确确定折叠后几何体的结构特征以及平面图形折叠前后的数量关系之间的对应.【例3】(体积问题)如图所示,等腰ABC △的底边66AB =,高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF △的位置,使PE AE ⊥,记BE x =,()V x 表示四棱锥P ACFE -的体积.(1)求()V x 的表达式;(2)当x 为何值时,()V x 取得最大值?PED F B CA【解析】(1)由折起的过程可知,PE ⊥平面ABC,96ABC S ∆=,V(x)= (036x <<)(2),所以(0,6)x ∈时,'()0v x > ,V(x)单调递增;636x <<时'()0v x < ,V(x)单调递减;因此x=6时,V(x)取得最大值126.【小试牛刀】【河北省五个一名校联盟2019届高三下学期一诊】在平面四边形 中,AB=BC=2,AC=AD=2,现沿对角线AC 折起,使得平面DAC平面ABC ,则此时得到的三棱锥D-ABC外接球的表面积为( ) A .B .C .D .【例4】(空间角问题)如左图,矩形ABCD 中,12AB =,6AD =,E 、F 分别为CD 、AB 边上的点,且3DE =,4BF =,将BCE ∆沿BE 折起至PBE ∆位置(如右图所示),连结AP 、EF 、PF ,其中25PF =.(Ⅰ)求证:PF ⊥平面ABED ; (Ⅱ)求直线AP 与平面PEF 所成角的正弦值.【解析】(Ⅰ)由翻折不变性可知, , ,在PBF ∆中, ,所以PF BF ⊥ 在图1中,易得,在PEF ∆中, ,所以PF EF ⊥又,BF ⊂平面ABED ,EF ⊂平面ABED ,所以PF ⊥平面ABED .. .ACDBEF图图ABCD PEF(Ⅱ)方法一:以D 为原点,建立空间直角坐标系D xyz -如图所示,则()6,0,0A ,,()0,3,0E ,()6,8,0F ,所以, ,,设平面PEF 的法向量为(),,x y z =n ,则0FP EF ⎧⋅=⎪⎨⋅=⎪⎩n n ,即,解得560x y z ⎧=-⎪⎨⎪=⎩令6y =-,得,设直线AP 与平面PEF 所成角为θ,则81281427. 所以直线AP 与平面PEF 所成角的正弦值为81281427. 方法二:过点A 作AH EF ⊥于H ,由(Ⅰ)知PF ⊥平面ABED ,而AH ⊂平面ABED 所以PF AH ⊥,又,EF ⊂平面PEF ,PF ⊂平面PEF ,所以AH ⊥平面PEF ,所以APH ∠为直线AP 与平面PEF 所成的角. 在Rt APF ∆中,在AEF ∆中,由等面积公式得4861在Rt APH ∆中,所以直线AP 与平面PEF 所成角的正弦值为81281427. 【点评】折叠问题分析求解两原则:解法二图ABCD PEFHxy z 解法一图A BC D PEF(1)折叠问题的探究须充分利用不变量和不变关系;(2)折叠前后始终位于折线的同侧的几何量和位置关系保持不变.【小试牛刀】【广东省汕头市2019届高三上学期期末】如图,已知是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足,如图,将沿DE折成四棱锥,且有平面平面BCED.求证:平面BCED;记的中点为M,求二面角的余弦值.(二) 几何体的展开几何体表面展开问题是折叠问题的逆向思维、逆过程,一般地,涉及到多面体表面距离的问题,解题时不妨将它展开成平面图形试一试.1.展开后形状的判断【例5】把正方体的表面沿某些棱剪开展成一个平面图形(如右下图),请根据各面上的图案判断这个正方体是()解析:这是图③模型,在右图中,把中间的四个正方形围起来做“前后左右”四个面,有“空心圆”的正方形做“上面”,显然是正方体C的展形图,故选(C).【小试牛刀】水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图,是一个正方体的平面展开图,若图中的“似”表示正方体的前面, “锦”表示右面, “程”表示下面.则“祝”、“你”、“前”分别表示正方体的______________________.2.展开后的数字特征——表面上的最短距离问题【例6】如图,已知圆柱体底面圆的半径为2π,高为2,AB CD,分别是两底面的直径,AD BC,是母线.若一只小虫从A点出发,从侧面爬行到C点,求小虫爬行的最短路线的长度.【解析】如图,将圆柱的侧面展开,其中AB为底面周长的一半,即,2AD=.则小虫爬行的最短路线为线段AC.在矩形ABCD中,.所以小虫爬行的最短路线长度为22.【点评】几何体表面上的最短距离需要将几何体的表面展开,将其转化为平面内的最短距离,利用平面内两点之间的距离最短求解.但要注意棱柱的侧面展开图可能有多种展开图,如长方体的表面展开图等,要把不同展开图中的最短距离进行比较,找出其中的最小值.【小试牛刀】如图,在长方体中, ,求沿着长方体表面从A到1C的最短路线长.四、迁移运用1.【浙江省2019年高考模拟训练】已知四边形中,,,在将沿着翻折成三棱锥的过程中,直线与平面所成角的角均小于直线与平面所成的角,设二面角,的大小分别为,则()A. B. C.存在 D.的大小关系无法确定【答案】B【解析】如图,在三棱锥中,作平面于,连,则分别为与平面所成的角.∵直线与平面所成角的角均小于直线与平面所成的角,∴.过作,垂足分别为,连,则有,∴分别为二面角,的平面角,∴.在中,,设BD的中点为O,则为边上的中线,由可得点H在CO的左侧(如图所示),∴.又,∴.又为锐角, ∴.故选B .2.【四川省德阳市2018届高三二诊】以等腰直角三角形ABC 的斜边BC 上的中线AD 为折痕,将ABD ∆与ACD ∆折成互相垂直的两个平面,得到以下四个结论:①BD ⊥平面ACD ;②ABC ∆为等边三角形;③平面ADC ⊥平面ABC ;④点D 在平面ABC 内的射影为ABC ∆的外接圆圆心.其中正确的有( ) A. ①②③ B. ②③④ C. ①②④ D. ①③④ 【答案】C【解析】由于三角形ABC 为等腰直角三角形,故,所以BD ⊥平面ACD ,故①正确,排除B 选项.由于AD BD ⊥,且平面ABD ⊥平面ACD ,故AD ⊥平面BCD ,所以AD CD ⊥,由此可知,三角形为等比三角形,故②正确,排除D 选项.由于,且ABC ∆为等边三角形,故点D 在平面ABC 内的射影为ABC ∆的外接圆圆心, ④正确,故选C .3.已知梯形如下图所示,其中,,为线段的中点,四边形为正方形,现沿进行折叠,使得平面平面,得到如图所示的几何体.已知当点满足时,平面平面,则的值为( )A. B. C. D.【答案】C 【解析】因为四边形为正方形,且平面平面,所以两两垂直,且,所以建立空间直角坐标系(如图所示),又因为,,所以,则,,设平面的法向量为,则由得,取,平面的法向量为,则由得,取,因为平面平面,所以,解得.故选C.4.如图是棱长为1的正方体的平面展开图,则在这个正方体中,以下结论错误的是( )A .点M 到AB 的距离为22B .AB 与EF 所成角是90︒C .三棱锥C DNE -的体积是16D .EF 与MC 是异面直线 【答案】D【解析】根据正方体的平面展开图,画出它的立体图形如图所示,A 中M 到AB 的距离为222MC =,A 正确;AB 与EF 所成角是90︒,B 正确;三棱锥C DNE -的体积是,C 正确;//EF MC ,D 错误.5.把正方形ABCD 沿对角线AC 折起,当以四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为( )度A .90B .60C .45D .30 【答案】C【解析】折叠后所得的三棱锥中易知当平面ACD 垂直平面ABC 时三棱锥的体积最大.设AC 的中点为O ,则DBO ∠即为所求,而DOB ∆是等腰直角三角形,所以,故选C .6.【辽宁省辽阳市2018学届高三第一次模拟】如图,圆形纸片的圆心为O ,半径为6cm ,该纸片上的正方形ABCD 的中心为O , E , F , G , H 为圆O 上的点, ABE , BCF , CDG , ADH 分别以AB , BC , CD , DA 为底边的等腰三角形,沿虚线剪开后,分别以AB , BC , CD , DA 为折痕折起ABE , BCF , CDG , ADH ,使得E , F , G , H 重合,得到一个四棱锥,当该四棱锥的侧面积是底面积的2倍时,该四棱锥的外接球的体积为__________.【答案】500327π3cm【解析】如图:连接OE 交AB 于点I ,设E ,F ,G ,H 重合于点P ,正方形的边长为x ()0x >,则OI=2x , IE 62x =-. 因为该四棱锥的侧面积是底面积的2倍,所以,解得4x =,设该四棱锥的外接球的球心为Q ,半径为R ,则,,解得5R 3=,外接球的体积3cm7.【山东省济南市2019届高三上学期期末】在正方形中,点,分别为,的中点,将四边形沿翻折,使得平面平面,则异面直线与所成角的余弦值为__________.【答案】【解析】连接FC ,与DE 交于O 点,取BE 中点为N , 连接ON ,CN ,易得ON ∥BD ∴∠CON 就是异面直线与所成角设正方形的边长为2, OC=,ON=,CN=∴cos ∠CON==故答案为:8.如图所示,在四边形ABCD 中,,将四边形ABCD 沿对角线BD 折成四面体BCD A -',使平面⊥BD A /平面BCD ,则下列结论正确的是 .(1)BD C A ⊥'; (2);(3)A C '与平面BD A '所成的角为︒30; (4)四面体BCD A -'的体积为61. 【答案】(2)(4)【解析】平面⊥BD A /平面BCD CD ∴⊥平面'A BD ,/CA 与平面BD A /所成的角为'CA D ∠,四面体BCDA -/的体积为,,综上(2)(4)成立.9.如图,矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1AC 的中点,则在ADE ∆翻折过程中,下面四个选项中正确的是 (填写所有的正确选项)(1)||BM 是定值 (2)点M 在某个球面上运动(3)存在某个位置,使1DE A C ⊥ (4)存在某个位置,使//MB 平面1A DE 【答案】(1)(2)(4).【解析】取CD 中点F ,连接MF ,BF ,则1//MF DA ,//BF DE ,∴平面//MBF 平面1A DE , ∴//MB 平面1A DE ,故(4)正确;由,为定值,FB DE =为定值,由余弦定理可得,∴MB 是定值,故(1)正确;∵B 是定点,∴M 是在以B 为圆心,MB 为半径的圆上,故(2)正确;∵1AC 在平面ABCD 中的射影为AC ,AC 与DE 不垂直,∴存在某个位置,使1DE A C ⊥错误,故(3)错误.10.【四川省广元市高2018届第二次高考适应性统考】如图,在矩形ABCD 中, 4AB =, 2AD =, E 是CD 的中点,以AE 为折痕将DAE ∆向上折起, D 变为'D ,且平面'D AE ⊥平面ABCE .(Ⅰ)求证: 'AD EB ⊥; (Ⅱ)求二面角'A BD E --的大小. 【答案】(Ⅰ)证明见解析;(Ⅱ) 90. 【解析】(Ⅰ)证明:∵, AB 4=,∴,∴AE EB ⊥,取AE 的中点M ,连结MD ',则,∵ 平面D AE '⊥平面ABCE ,∴MD '⊥平面ABCE ,∴MD '⊥ BE , 从而EB ⊥平面AD E ',∴AD EB '⊥ (Ⅱ)如图建立空间直角坐标系,则()A 4,2,0、()C 0,0,0、()B 0,2,0、()D 3,1,2',()E 2,0,0,从而BA =(4,0,0),,.设为平面ABD '的法向量,则可以取设为平面BD E '的法向量,则可以取因此, 12n n 0⋅=,有12n n ⊥,即平面ABD ' ⊥平面BD E ', 故二面角的大小为90.11.【福建省龙岩市2019届高三下学期教学质量检查】如图1,已知菱形的对角线交于点,点为线段的中点,,,将三角形沿线段折起到的位置,,如图2所示.(Ⅰ)证明:平面平面;(Ⅱ)求三棱锥的体积.【解析】(Ⅰ)折叠前,因为四边形为菱形,所以;所以折叠后,,, 又,平面,所以平面因为四边形为菱形,所以.又点为线段的中点,所以.所以四边形为平行四边形.所以.又平面,所以平面.因为平面,所以平面平面.(Ⅱ)图1中,由已知得,,所以图2中,,又所以,所以又平面,所以又,平面,所以平面,所以.所以三棱锥的体积为.12.【湖南省长沙市长郡中学2019届高三上学期第一次适应性考试(一模】如图,在多边形中(图1),为长方形,为正三角形,现以为折痕将折起,使点在平面内的射影恰好在上(图2).(Ⅰ)证明:平面;(Ⅱ)若点在线段上,且,当点在线段上运动时,求三棱锥的体积. 【解析】(Ⅰ)过点作,垂足为.由于点在平面内的射影恰好在上,∴平面.∴.∵四边形为矩形,∴.又,∴平面,∴.又由,,可得,同理.又,∴,∴,且,∴平面.(Ⅱ)设点到底面的距离为,则.由,可知,∴.又,∴.13.【江西省上饶市重点中学2019届高三六校第一次联考】如图所示,在边长为2的菱形中,,现将沿边折到的位置.(1)求证:;(2)求三棱锥体积的最大值.【解析】(1)如图所示,取的中点为,连接,易得,,又面(2)由(1)知,= ,当时,的最大值为1.14.【云南师范大学附属中学2019届高三上学期第一次月考】如图所示甲,在四边形ABCD中,,,是边长为8的正三角形,把沿AC折起到的位置,使得平面平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.求证:平面PON;求三棱锥的体积.【解析】如图所示,为正三角形,O为AC的中点,,平面平面ACD,平面平面,平面ACD,平面ACD,.,,,,即.,N分别为棱AC,AD的中点,,,又,平面PON;解:由,,,可得,点O、N分别是AC、AD的中点,,是边长为8的等边三角形,,又为PA的中点,点M到平面ANO的距离,.又,.15.【湖北省荆门市2019届高三元月调研】如图,梯形中,,过分别作,,垂足分别,,已知,将梯形沿同侧折起,得空间几何体,如图.1若,证明:平面;2若,,线段上存在一点,满足与平面所成角的正弦值为,求的长.【解析】1由已知得四边形ABFE是正方形,且边长为2,在图2中,,由已知得,,平面又平面BDE,,又,,平面2在图2中,,,,即面DEFC,在梯形DEFC中,过点D作交CF于点M,连接CE,由题意得,,由勾股定理可得,则,,过E作交DC于点G,可知GE,EA,EF两两垂直,以E为坐标原点,以分别为x轴,y轴,z轴的正方向建立空间直角坐标系,则,.设平面ACD的一个法向量为,由得,取得,设,则m,,,得设CP与平面ACD所成的角为,.所以16.【山西省吕梁市2019届高三上学期第一次模拟】已知如图(1)直角梯形,,,,,为的中点,沿将梯形折起(如图2),使.(1)证明:平面;(2)求点到平面的距离.【解析】(1)由已知可得为直角三角形,所以.又,所以,所以平面.(2)因为平面,平面,所以,又因为,平面,平面,,所以,平面,又因为,所以平面,又因为平面,所以.在直角中,,设点到平面的距离为,由,则,所以.16.正△ABC的边长为4,CD是AB边上的高,,E F分别是AC和BC边的中点,现将△ABC沿CD翻折--.成直二面角A DC B(1)试判断直线AB与平面DEF的位置关系,并说明理由;--的余弦值;(2)求二面角E DF C(3)在线段BC 上是否存在一点P ,使AP DE ⊥?证明你的结论.【分析】(1)问可利用翻折之后的几何体侧面ABC ∆的中位线得到//AB EF ,便可由线面平行的判定定理证得;(2)先根据直二面角A DC B --将条件转化为AD ⊥面BCD ,然后做出过点E 且与面BCD 垂直的直线EM ,再在平面BCD 内过M 作DF 的垂线即可得所求二面角的平面角;(3)把AP DE ⊥作为已知条件利用,利用ADC ∆中过A 与DE 垂直的直线确定点P 的位置.【解析】(1)如图:在△ABC 中,由E 、F 分别是AC 、BC 中点,得EF//AB,又AB ⊄平面DEF,EF ⊂平面DEF .∴AB ∥平面DEF .(2)∵AD ⊥CD,BD ⊥CD∴∠ADB 是二面角A —CD —B 的平面角∴AD ⊥BD ∴AD ⊥平面BCD取CD 的中点M,这时EM ∥AD ∴EM ⊥平面BCD过M 作MN ⊥DF 于点N,连结EN,则EN ⊥DF∴∠MNE 是二面角E —DF —C 的平面角,在Rt △EMN 中,EM=1,MN=23 ∴tan ∠MNE=233,cos ∠MNE=721(3)在线段BC 上存在点P,使AP ⊥DE. 证明如下:在线段BC 上取点P,使BC BP 31 ,过P 作PQ ⊥CD 与点Q, ∴PQ ⊥平面ACD∵, 在等边△ADE 中,∠DAQ=30°,∴AQ ⊥DE ∴AP ⊥DE.。
【高考数学专题】立体几何中的翻折问题与最值问题 专题 高三一轮复习备考

立体几何中的翻折问题与最值问题一知识点导学1.解决折叠问题注意什么?折叠问题是立体几何的一个重要内容,是空间几何问题与平面几何问题相互转化的集中体现,处理这类问题的关键就是抓住折叠前后图形的特征关系。
解答折叠问题在于画好折叠前后的平面图形和立体图形,并弄清折叠前后哪些量和位置关系发生了变化,哪些量和位置关系没有发生变化,这些未发生变化的已知条件就是我们分析问题和解决问题的依据。
2立体几何常见的最值问题有哪些?如何解决?空间图形最值问题有线段、角、距离、面积、体积等最值问题,通常应注意分析题目中所有的条件,首先应该在充分理解题意的基础上,分析是否能用公理与定义直接解决题中问题;如果不能,再看是否可将问题条件转化为函数,若能写出确定的表意函数,则可用建立函数法求解;再不能,则要考虑其中是否存在不等关系,看是否能运用解等不式法求解;还不行则应考虑是否可将其体图展开成平面,这样依次顺序思考,基本可以找到解题的途径.3如何解决涉及几何体切接问题最值计算?求解与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径等.通过作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.这样才能进一步将空间问题转化为平面内的问题;4解决折叠问题的步骤有哪些?二.考点典例考点一:面积、体积最值问题空间几何体的侧面积、表面积、截面面积、体积等最值问题,往往是几何体中有关几何元素如顶点、侧棱、侧面、截面等在运动变化过程中,达到某个特殊位置时所具有的度量性质。
因此,在解决此类问题时,要注意分析这些几何元素运动变化与所求量的联系,建立两者之间的数量关系。
实例演练1(2021•湖南模拟)如图所示,圆形纸片的圆心为O,半径为6cm,该纸片上的等边三角形ABC的中心为O,D,E,F为圆O上的点,DBC∆分别是∆,FAB∆,ECA以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起DBC ∆,ECA ∆,FAB ∆,使得D ,E ,F 重合,得到三棱锥.则当ABC ∆的边长变化时,三棱锥的表面积S 的取值范围是( )A .(0,36)πB .(0,C .(0,45-D .(0,解:设三棱锥的底面边长为a ,则0a <<连接OD ,交BC 于点G ,则6OD =,OG ,6DG =,∴2,侧面积为213(6)92S a a =⨯⨯=,∴三棱锥的表面积9S a =,0a <<9(0S a ∴=∈,,∴当ABC ∆的边长变化时,三棱锥的表面积S 的取值范围是(0,.故选:D .实例演练2(2021•宜宾模拟)已知三棱锥A BCD -的各个顶点都在球O 的表面上,AD ⊥平面BCD ,BD CD ⊥,3BD =,CD =E 是线段CD 上一点,且3CD CE =.若球O 的表面积为40π,则过点E 作球O 的截面,所得截面圆面积的最小值为( )A .4πB .6πC .8πD .10π解:依题意,AD ,BD ,CD 两两互相垂直,取BC 中点M ,连接MD ,由对称性可知,球心O 在M 点正上方,且OM ⊥平面BCD ,OA OB OC OD R ====,3BD =,CD =6BC ∴=,则3BM CM DM ===,设球O 的半径为R ,则2440R ππ=,解得R由22222222()OM BM R OB AD OM DM R OA⎧+==⎨-+==⎩,解得12OM AD =⎧⎨=⎩,OM ⊥平面BCD ,OM ME ∴⊥,又13CE CD =cos CD BCD BC ∠==,∴在CEM ∆中,由余弦定理有2222cos 3ME CE MC CE MC BCD =+-⋅⋅∠=,故ME =,在OME ∆中,2OE =,要使过E 作圆O 的截面面积最小,则此时截面与OE垂直,设此时截面圆半径为r ,则r ==∴26min S r ππ==.故选:B .实例演练3.(2021•河南模拟)现有一批大小不同的球体原材料,某工厂要加工出一个四棱锥零件,要求零件底面ABCD 为正方形,2AB =,侧面PAD ∆为等边三角形,线段BC 的中点为E ,若1PE =,则所需球体原材料的最小体积为( )A B .283π C .9π D 解:所需原材料体积最小的球体即为四棱锥P ABCD -的外接球,如图,设F 为AD 中点,G 为正方形ABCD 中心,PAD ∆为边长为2的等边三角形,PF ∴,又1PE =,2EF =,60PEF ∴∠=︒1PE EB EC ===,E ∴是PBC ∆的外心,过E 作面PBC 的垂线与过G 与面ABCD 的垂线交于O ,则O 为四棱锥P ABCD -外接球的球心.906030OEG OEP FEP ∠=∠-∠=︒-︒=︒,又1GE =,∴在直角三角形OGE 中求出OG =,又直角OAG ∆中,AG ,OA ∴=,即球半径R =,得343V R π==球.由于此时四棱锥P ABCD -在球心同侧,不是最小球,可让四棱锥下移到面ABCD 过球心时,即球半径12R AC =时,原材料最省,此时343V π=⨯=球.故选:A .实例演练4(20211,O 为底面圆心,OA ,OB 为底面半径,且23AOB π∠=,M 是母线PA 的中点.则在此圆锥侧面上,从M 到B 的路径中,最短路径的长度为( )A B 1 C D 1解:由题意,在底面半径为1O 是底面圆心,P 为圆锥顶点,圆锥的侧面展开图是半圆,如图,A ,B 是底面圆周上的两点,23AOB π∠=,所以在展开图中,3APB π∠=2=,M 为母线PA 的中点,所以1PM =,所以从B 到M 的最短路径的长是BM A .考点2:角的最值问题立体几何中的角有异面直线所成角、线面角和二面角的平面角三种。
高考数学难点突破八立体几何中的翻折问题答案
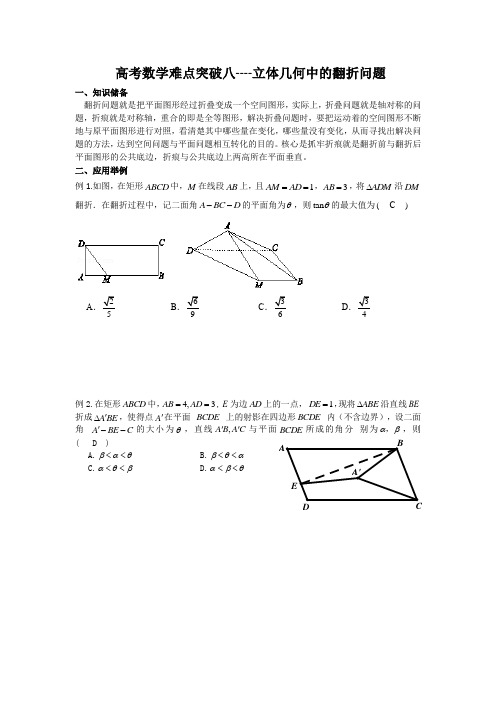
高考数学难点突破八----立体几何中的翻折问题一、知识储备翻折问题就是把平面图形经过折叠变成一个空间图形,实际上,折叠问题就是轴对称的问题,折痕就是对称轴,重合的即是全等图形,解决折叠问题时,要把运动着的空间图形不断地与原平面图形进行对照,看清楚其中哪些量在变化,哪些量没有变化,从而寻找出解决问题的方法,达到空间问题与平面问题相互转化的目的。
核心是抓牢折痕就是翻折前与翻折后平面图形的公共底边,折痕与公共底边上两高所在平面垂直。
二、应用举例例1.如图,在矩形ABCD 中,M 在线段AB 上,且1AM AD ==,3AB =,将ADM ∆沿DM 翻折.在翻折过程中,记二面角A BC D --的平面角为θ,则tan θ的最大值为(C )ABCD例2.在矩形ABCD 中,4,3AB AD ==,E 为边AD 上的一点,1DE =,现将ABE ∆沿直线BE 折成A BE '∆,使得点A '在平面 BCDE 上的射影在四边形BCDE 内(不含边界),设二面角 A BE C '--的大小为θ,直线,A B A C ''与平面BCDE 所成的角分 别为αβ,,则( D ) A.βαθ<< B.βθα<< C.αθβ<< D.αβθ<<例3.如图,矩形ABCD 中心为, O BC AB >,现将DAC 沿着对角线AC 翻折成EAC ,记BOE a ∠=,二面角B AC E --的平面角为β,直线DE 和BC 所成角为γ,则( D )A. ,2a ββγ>>B. ,2a ββγ><C. ,2a ββγ<>D. ,2a ββγ<<例4.如图,在ABC △中,1AB =,22BC =,4B π=,将ABC △绕边AB 翻转至ABP △,使面ABP ⊥面ABC ,D 是BC 中点,设Q 是线段PA 上的动点,则当PC 与DQ 所成角取得最小值时,线段AQ 的长度为( B ) A .5 B .25C .35D .25例5.已知在矩形ABCD 中,2AD AB =,沿直线BD 将ABD ∆ 折成'A BD ∆,使得点'A 在平面BCD 上的射影在BCD ∆内(不含边界),设二面角'A BD C --的大小为θ,直线','A D A C 与平面BCD 所成的角分别为,αβ,则( )A. αθβ<<B. βθα<<C. βαθ<<D. αβθ<< 【答案】DQ DPCBA【解析】分析:由题意画出图形,由两种特殊位置得到点A′在平面BCD上的射影的情况,由线段的长度关系可得三个角的正弦的大小,则答案可求.详解:如图,∵四边形ABCD为矩形,∴BA′⊥A′D,当A′点在底面上的射影O落在BC上时,有平面A′BC⊥底面BCD,又DC⊥BC,可得DC⊥平面A′BC,则DC⊥BA′,∴BA′⊥平面A′DC,在Rt△BA′C中,设BA′=1,则,∴A′C=1,说明O为当A′点在底面上的射影E落在BD上时,可知A′E⊥BD,设BA′=1,则A D'=,要使点A′在平面BCD上的射影F在△BCD内(不含边界),则点A′的射影F落在线段OE上(不含端点).可知∠A′EF为二面角A′﹣BD﹣C的平面角θ,直线A′D与平面BCD所成的角为∠A′DF=α,直线A′C与平面BCD所成的角为∠A′CF=β,<,而A′C的最小值为1,可求得DF>CF,∴A′C<A′D,且A′E=13∴sin∠A′DF<sin∠A′CF<sin∠A′EO,则α<β<θ.故答案为:D点睛:本题主要考查二面角的平面角和直线与平面所成的角,考查正弦函数的单调性,意在考查学生对这些基础知识的掌握能力和空间想象能力分析推理能力.例6、(嘉兴市2020年1月期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .22π分析:设 AC ,FC 的中点为 M , N ,CP 的中点G 的轨迹是以 MN 为直径的半圆.例7、(宁波市2020年1月期终)已知平面四边形ABCD 中,90A C ∠=∠=︒,BC CD =,AB AD >,现将ABD △沿对角线BD 翻折得到三棱锥A BCD '-,在此过程中,二面角A BC D '--、A CDB '--的大小分别为α,β,直线A B '与平面BCD 所成角为γ,直线A D '与平面BCD 所成角为δ,则( )A .γδβ<<B .γαβ<<C .αδβ<<D .γαδ<<例8、(柯桥一中2020年1月期终)已知在矩形ABCD 中,2AB =,4AD =,E ,F 分别在边AD ,BC 上,且1AE =,3BF =,如图所示, 沿EF 将四边形AEFB 翻折成A EFB '',则在翻折过程中,二面角B CD E '--的大小为θ,则tan θ的最大值为( C ) A.5B.5C.4例9、(名校合作体2020年3月)已知C 为ABD Rt ∆斜边BD 上一点,且ACD ∆为等边三角形,现将ABC ∆沿AC 翻折至C B A '∆,若在三棱锥ACD B -'中,直线B C '和直线B A '与平面ACD 所成角分别为βα,,则( )A. βα<<0B.βαβ2≤<C.βαβ32≤≤例10、(2020年1月嘉兴期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .分析:取DE 中点O ,连CO PO ,,则点G 的轨迹是以CO 的中点为圆心,2221=PO 为半径的半圆,轨迹长为22ππ=r例11、(2020年4月温州模拟)如图,在ABC ∆中,点M 是边BC 的中点,将ABN ∆沿着AM 翻折成M B A '∆,且点B '不在平面AMC 内,点P 是线段C B '上一点,若二面角B AM P '--与二面角C AM P --的平面角相等,则直线AP 经过C B A '∆的( A ) A. 重心 B. 垂心 C. 内心 D.外心G PFD B A例12、(2020年嘉兴一模)将边长为1的正方形ABCD 沿对角线BD 翻折,使得二面角A BD C --的平面角的大小为π3,若点E ,F 分别是线段AC 和BD 上的动点,则BE CF 的取值范围为 ( )A .[1,0]-B .1[1,]4-C .1[,0]2-D . 11[,]24-例13、(2020年5月暨阳联考)如图:ABC ∆中,︒=∠⊥90,ACB BC AB ,D 为AC 的中点,ABD ∆沿BD 边翻折过程中,直线AB 与BC 直线所成的最大角,最小角分别记为11βα,,直线AD 与直线BC 所成的最大角,最小角分别记为22βα,,则有( D )A. ββαα≤<121,B. 2121ββαα><,C. 2121ββαα≤≥,D.2121ββαα>≥,分析一:翻折到180时,,AB BC 所成角最小,可知130β=,,AD BC 所成角最小,20β=,翻折0时,,AB BC 所成角最大,可知190α=,翻折过程中,可知AD 的投影可与BC 垂直,所以,AD BC 所成最大角290α=,所以 1190,30αβ︒︒==,2290,0αβ︒︒==分析二:对角线向量定理例14、(2020年4月台州二模)如下图①,在直角梯形ABCD 中,90=∠=∠=∠DAB CDB ABC , 30=∠BCD ,4=BC ,点E 在线段CD 上运动,如下图②,沿BE 将BEC ∆折至C BE '∆,使得平面⊥'C BE 平面ABED ,则C A '的最小值为 .⇒例15、(2020年嘉兴市基础知识测试)如图,矩形ABCD 中,2,1==BC AB ,点E 为AD 中点,将ABE ∆沿BE 折起,在翻折过程中,记二面角B DC A --的平面角大小为α,则当α最大时,=αtan ( ) A. 22 B. 32 C. 31 D.21。
高考数学复习考点题型专题讲解16 立体几何中的折叠、探究问题

高考数学复习考点题型专题讲解专题16 立体几何中的折叠、探究问题高考定位 1.立体几何中的折叠问题是历年高考命题的一大热点与难点,主要包括两个方面:一是平面图形的折叠问题,多涉及到空间中的线面关系、体积的求解以及空间角、距离的求解等问题;二是几何体的表面展开问题,主要涉及到几何体的表面积以及几何体表面上的最短距离等;2.以空间向量为工具,探究空间几何体中线面关系或空间角存在的条件,计算量较大,一般以解答题的形式考查,难度中等偏上.1.(2019·全国Ⅲ卷)图①是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图②.(1)证明:图②中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图②中的平面BCG与平面CGA夹角的大小.(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,所以AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,且BE∩BC=B,BE,BC⊂平面BCGE,所以AB⊥平面BCGE.又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE . (2)解 作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,平面BCGE ∩平面ABC =BC , 所以EH ⊥平面ABC .由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EH = 3.以H 为坐标原点,HC →的方向为x 轴的正方向,建立如图所示的空间直角坐标系H -xyz ,则A (-1,1,0),C (1,0,0),G (2,0,3),CG →=(1,0,3),AC →=(2,-1,0). 设平面ACGD 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧CG →·n =0,AC →·n =0,即⎩⎨⎧x +3z =0,2x -y =0. 所以可取n =(3,6,-3).又平面BCGE 的法向量可取m =(0,1,0), 设平面BCG 与平面CGA 夹角的大小为θ, 所以cos θ=|cos 〈n ,m 〉|=|n ·m ||n ||m |=32.因此平面BCG 与平面CGA 夹角的大小为30°.2.(2021·全国甲卷)已知直三棱柱ABC -A 1B 1C 1中,侧面AA 1B 1B 为正方形,AB =BC =2,E ,F 分别为AC 和CC 1的中点,D 为棱A 1B 1上的点,BF ⊥A 1B 1.(1)证明:BF⊥DE;(2)当B1D为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?(1)证明因为E,F分别是AC和CC1的中点,且AB=BC=2,侧面AA1B1B为正方形,所以CF=1,BF= 5.如图,连接AF,由BF⊥A1B1,AB∥A1B1,得BF⊥AB,于是AF=BF2+AB2=3,所以AC =AF2-CF2=2 2.由AB2+BC2=AC2,得BA⊥BC.∵三棱柱ABC-A1B1C1为直三棱柱,∴BB1⊥AB且BB1⊥BC,则BA,BC,BB1两两互相垂直,故以B为坐标原点,以BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系B -xyz,则B(0,0,0),E(1,1,0),F(0,2,1),BF→=(0,2,1).设B1D=m(0≤m≤2),则D(m,0,2),于是DE→=(1-m,1,-2).所以BF →·DE →=0,所以BF ⊥DE .(2)解 易知平面BB 1C 1C 的一个法向量为n 1=(1,0,0). 设平面DFE 的法向量为n 2=(x ,y ,z ), 则⎩⎪⎨⎪⎧DE →·n 2=0,EF →·n 2=0,又由(1)得DE →=(1-m ,1,-2),EF →=(-1,1,1), 所以⎩⎨⎧(1-m )x +y -2z =0,-x +y +z =0,令x =3,得y =m +1,z =2-m ,于是,平面DFE 的一个法向量为n 2=(3,m +1,2-m ), 所以cos 〈n 1,n 2〉=32⎝⎛⎭⎪⎫m -122+272.设平面BB 1C 1C 与平面DFE 所成的二面角为θ, 则sin θ=1-cos 2〈n 1,n 2〉=1-92⎝ ⎛⎭⎪⎫m -122+272,故当m =12时,平面BB 1C 1C 与平面DFE 所成的二面角的正弦值最小为33,即当B 1D =12时,平面BB 1C 1C 与平面DFE 所成的二面角的正弦值最小.热点一 折叠问题解答折叠问题的关键是分清翻折前后图形的位置和数量关系的变与不变,一般地,位于“折痕”同侧的点、线、面之间的位置和数量关系不变,而位于“折痕”两侧的点、线、面之间的位置关系会发生变化;对于不变的关系应在平面图形中处理,而对于变化的关系则要在立体图形中解决.考向1 折叠后的位置关系及空间角例1(2022·青岛模拟)在直角梯形ABCD 中,AB ∥CD ,AB ⊥AD ,AB =2CD =4,E ,F 分别为AD ,BC 的中点,沿EF 将四边形EFCD 折起,使得DE ⊥BF (如图2).(1)求证:平面ABFE ⊥平面EFCD ;(2)若直线AC 与平面ABFE 所成角的正切值为63,求平面CEB 与平面EBF 夹角的余弦值.(1)证明 由题设条件,得EF ∥AB ∥CD ,AB ⊥AD , 则DE ⊥EF ,又DE ⊥BF 且BF ∩EF =F ,BF ,EF ⊂平面ABFE , 则DE ⊥平面ABFE , 又DE ⊂平面EFCD , 故平面ABFE ⊥平面EFCD .(2)解 如图过点C 作CG ⊥EF ,交EF 于点G ,连接AG ,因为平面ABFE ⊥平面 EFCD ,且平面ABFE ∩平面EFCD =EF , 所以CG ⊥平面ABFE ,故直线AC 与平面ABFE 所成的角为∠CAG , 设DE =h ,则在Rt△CAG 中 ,CG =DE =h ,AG =EG 2+EA 2=h 2+4,所以tan∠CAG =CG AG =h h 2+4=63,解得h =22,如图,建立空间直角坐标系E -xyz ,则E (0,0,0),B (22,4,0),C (0,2,22), 所以EC →=(0,2,22),EB →=(22,4,0), 则平面EBF 的法向量为m =(0,0,1), 设平面CEB 的法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·EC →=2y +22z =0,n ·EB →=22x +4y =0,令y =-2,则n =(2,-2,1),则平面CEB 与平面EBF 夹角的余弦值为 |cos 〈m·n 〉|=|m·n ||m |·|n |=77.所以平面CEB 与平面EBF 夹角的余弦值为77. 易错提醒 注意图形翻折前后变与不变的量以及位置关系.对照前后图形,弄清楚变与不变的元素后,再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.考向2 展开后的数字特征例2 (1)(2022·青岛质检)如图所示,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=6,BC=CC1=2,P是BC1上一动点,则CP+PA1的最小值是________.(2)如图,一立在水平地面上的圆锥形物体的母线长为4 m,一只小虫从圆锥的底面圆上的点P出发,绕圆锥表面爬行一周后回到点P处.若该小虫爬行的最短路程为4 3 m,则圆锥底面圆的半径等于________m.答案(1)5 2 (2)4 3解析(1)如图,以BC1为轴,把平面BCC1翻折到与平面A1BC1共面,则A1BCC1在同一个平面内,图中A1C就是所求最小值.通过计算可得∠A1C1B=90°,∠BC1C=45°,所以∠A1C1C=135°,由余弦定理可得A1C=5 2.(2)圆锥顶点记为O,把圆锥侧面沿母线OP展开成如图所示的扇形,由题意OP=4,PP′=43,则cos∠POP′=42+42-(43)22×4×4=-12,又∠POP′为△POP′一内角,所以∠POP′=2π3.设底面圆的半径为r,则2πr=2π3×4,所以r=4 3 .易错提醒几何体表面上的最短距离要注意棱柱的侧面展开图可能有多种,如长方体的表面展开图等,要把不同展开图中的最短距离进行比较,找出其中的最小值.训练1 如图1,在直角梯形ABCD中,AB∥DC,∠D=90°,AB=2,DC=3,AD=3,CE=2ED.沿BE将△BCE折起,使点C到达点C1的位置,且AC1=6,如图2.(1)求证:平面BC1E⊥平面ABED;(2)求直线BC1与平面AC1D所成角的正弦值.(1)证明在图①中,连接AE,由已知得AE=2.图①∵CE∥AB,CE=AB=AE=2,∴四边形ABCE为菱形.连接AC交BE于点F,则CF⊥BE.在Rt△ACD中,AC=32+(3)2=23,所以AF=CF= 3.图②如图②中,由翻折,可知C1F=3,C1F⊥BE.∵AC1=6,AF=C1F=3,∴AF2+C1F2=AC21,∴C1F⊥AF,又BE∩AF=F,BE⊂平面ABED,AF⊂平面ABED,∴C1F⊥平面ABED.又C1F⊂平面BC1E,所以平面BC1E⊥平面ABED.(2)解如图②,建立空间直角坐标系,则D(0,0,0),A(3,0,0),B(3,2,0),C 1⎝⎛⎭⎪⎫32,32,3, 所以BC 1→=⎝ ⎛⎭⎪⎫-32,-12,3,DA →=(3,0,0),DC 1→=⎝ ⎛⎭⎪⎫32,32,3,设平面AC 1D 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧DA →·n =0,DC 1→·n =0,即⎩⎨⎧3x =0,32x +32y +3z =0, 令z =3,则x =0,y =-2,所以n =(0,-2,3)为平面AC 1D 的一个法向量. 设直线BC 1与平面AC 1D 所成的角为θ,则sin θ=|cos 〈BC 1→,n 〉|=|BC 1→·n ||BC 1→||n |=42×7=277.所以直线BC 1与平面AC 1D 所成角的正弦值为277. 热点二 探究问题与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或平面与平面的夹角满足特定要求时的存在性问题.解题思路:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断. 考向1 探究线面位置关系例3(2022·济南质检)如图,在正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2AB =2,E ,F 分别为棱AA 1,CC 1的中点,G 为棱DD 1上的动点.(1)求证:B,E,D1,F四点共面;(2)是否存在点G,使得平面GEF⊥平面BEF?若存在,求出DG的长;若不存在,说明理由.(1)证明如图,连接D1E,D1F,取BB1的中点为M,连接MC1,ME,因为E为AA1的中点,所以EM∥A1B1∥C1D1,且EM=A1B1=C1D1,所以四边形EMC1D1为平行四边形,所以D1E∥MC1,又F为CC1的中点,所以BM∥C1F,且BM=C1F,所以四边形BMC1F为平行四边形,所以BF∥MC1.所以BF∥D1E,所以B,E,D1,F四点共面.(2)解以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,假设存在满足题意的点G (0,0,t ), 由已知B (1,1,0),E (1,0,1),F (0,1,1),则EF →=(-1,1,0),EB →=(0,1,-1),EG →=(-1,0,t -1), 设平面BEF 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n 1·EF →=0,n 1·EB →=0,即⎩⎨⎧-x 1+y 1=0,y 1-z 1=0,取x 1=1,则y 1=1,z 1=1,n 1=(1,1,1).设平面GEF 的法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧n 2·EF →=0,n 2·EG →=0,即⎩⎨⎧-x 2+y 2=0,-x 2+(t -1)z 2=0, 取x 2=t -1,则y2=t-1,z2=1,n2=(t-1,t-1,1). 因为平面GEF⊥平面BEF,所以n1·n2=0所以t-1+t-1+1=0,所以t=1 2,所以存在满足题意的点G,使得平面GEF⊥平面BEF,且DG的长为1 2 .考向2 与空间角有关的探究性问题例4 如图,四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,BC=CD=1,AB=2.△PBC 是等边三角形,平面PBC⊥平面ABCD,点M在棱PC上.(1)当M为棱PC的中点时,求证:AP⊥BM;(2)是否存在点M,使得平面DMB与平面MBC夹角的余弦值为34?若存在,求CM的长;若不存在,请说明理由.(1)证明连接AC,由底面ABCD是等腰梯形且AB=2,BC=CD=1,得∠ABC=π3,在△ABC中,由余弦定理得AC=3,∴AC2+BC2=AB2,∴∠ACB=π2,∴AC⊥BC.又∵平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AC⊂平面ABCD,∴AC ⊥平面PBC , ∵BM ⊂平面PBC ,∴AC ⊥BM ,又M 为棱PC 的中点,且△PBC 是等边三角形, ∴BM ⊥PC ,又∵PC ∩AC =C ,PC ⊂平面APC ,AC ⊂平面APC , ∴BM ⊥平面APC , ∵AP ⊂平面APC , ∴AP ⊥BM .(2)解 假设存在点M ,使得平面DMB 与平面MBC 夹角的余弦值为34.过点P 作PO ⊥BC 交BC 于点O ,∵平面PBC ⊥平面ABCD ,平面PBC ∩平面ABCD =BC ,PO ⊂平面PBC ,∴PO ⊥平面ABCD ,取AB 的中点E ,连接OE ,则OE ∥CA ,由(1)知OE ⊥平面PBC ,因此以O 为原点,以OC ,OE ,OP 所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系O -xyz .∴O (0,0,0),P ⎝ ⎛⎭⎪⎫0,0,32,C ⎝ ⎛⎭⎪⎫12,0,0,B ⎝ ⎛⎭⎪⎫-12,0,0,D ⎝ ⎛⎭⎪⎫1,32,0,则DB →=⎝ ⎛⎭⎪⎫-32,-32,0,CP →=⎝ ⎛⎭⎪⎫-12,0,32.设CM →=tCP→(0<t ≤1),则M ⎝⎛⎭⎪⎫1-t 2,0,32t .则DM →=⎝ ⎛⎭⎪⎫-t -12,-32,32t ,设平面DMB 的法向量为a =(x ,y ,z ), 则⎩⎪⎨⎪⎧a ·DM →=-1+t 2x -32y +32tz =0,a ·DB →=-32x -32y =0,令x =3,则y =-3,z =t -2t,∴a =⎝⎛⎭⎪⎫3,-3,t -2t 为平面DMB 的一个法向量, 易知平面MBC 的一个法向量为b =(0,1,0), 则|cos 〈a ,b 〉|=|a·b||a||b|=33+9+⎝⎛⎭⎪⎫t -2t 2=312+⎝⎛⎭⎪⎫t -2t 2=34, 则⎝ ⎛⎭⎪⎫t -2t 2=4,即t -2t =-2,解得t =23,故CM =|CM →|=23|CP →|=23.所以存在点M ,使得平面DMB 与平面MBC 夹角的余弦值为34,且CM 的长为23.规律方法 解决立体几何中探索性问题的基本方法(1)通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明,否则假设不成立.(2)探索线段上是否存在满足条件的点时,一定注意三点共线的应用.训练2(2022·盐城模拟)如图,三棱柱ABC -A 1B 1C 1的所有棱长都为2,B 1C =6,AB ⊥B 1C .(1)求证:平面ABB 1A 1⊥平面ABC ;(2)在棱BB 1上是否存在点P ,使直线CP 与平面ACC 1A 1所成角的正弦值为45,若不存在,请说明理由,若存在, 求BP 的长.(1)证明 如图,取AB 的中点D ,连接CD ,B 1D ,因为三棱柱ABC -A 1B 1C 1的所有棱长都为2, 所以AB ⊥CD ,CD =3,BD =1. 又因为AB ⊥B 1C ,且CD ∩B 1C =C ,CD ,B 1C ⊂平面B 1CD , 所以AB ⊥平面B 1CD . 又因为B 1D ⊂平面B 1CD , 所以AB ⊥B 1D .在Rt△B 1BD 中,BD =1,B 1B =2, 所以B 1D = 3.在△B 1CD 中,CD =3,B 1D =3,B 1C =6,所以CD 2+B 1D 2=B 1C 2, 所以CD ⊥B 1D ,又因为AB ⊥B 1D ,AB ∩CD =D ,AB ,CD ⊂平面ABC , 所以B 1D ⊥平面ABC . 又因为B 1D ⊂平面ABB 1A 1, 所以平面ABB 1A 1⊥平面ABC .(2)解 假设存在,以DC ,DA ,DB 1所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,则A (0,1,0),B (0,-1,0),C (3,0,0),B 1(0,0,3), 因此BB 1→=(0,1,3),AC →=(3,-1,0),AA 1→=BB 1→=(0,1,3), CB →=(-3,-1,0). 因为点P 在棱BB 1上, 设BP →=λBB 1→=λ(0,1,3),其中0≤λ≤1.则CP →=CB →+BP →=CB →+λBB 1→=(-3,-1+λ,3λ). 设平面ACC 1A 1的法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·AC →=0,n ·AA 1→=0,得⎩⎪⎨⎪⎧3x -y =0,y +3z =0,取x =1,则y =3,z =-1,所以平面ACC 1A 1的一个法向量为n =(1,3,-1). 因为直线CP 与平面ACC 1A 1所成角的正弦值为45,所以|cos 〈n ,CP →〉|=|n ·CP →||n ||CP →|=⎪⎪⎪⎪⎪⎪-235×3+(λ-1)2+3λ2=45, 化简得16λ2-8λ+1=0,解得λ=14,所以|BP →|=14|BB 1→|=12, 故BP 的长为12.一、基本技能练1.(2022·丽水质检)如图1,矩形ABCD 中,点E ,F 分别是线段AB ,CD 的中点,AB =4,AD =2,将矩形ABCD 沿EF 翻折.(1)若所成二面角的大小为π2(如图2),求证:直线CE ⊥平面DBF ; (2)若所成二面角的大小为π3(如图3),点M 在线段AD 上,当直线BE 与平面EMC 所成角为π4时,求平面DEM 和平面EMC 夹角的余弦值. (1)证明 由题设易知:四边形BEFC 是边长为2的正方形,BF ,EC 是其对角线, 所以BF ⊥EC ,又平面BEFC ⊥平面AEFD ,平面BEFC ∩平面AEFD =EF ,DF ⊥EF ,DF ⊂平面AEFD , 所以DF ⊥平面BEFC , 又EC ⊂平面BEFC ,则DF ⊥EC ,又DF ∩BF =F ,BF ,DF ⊂平面BDF ,则EC ⊥平面BDF .(2)解 过E 作Ez ⊥平面AEFD ,而AE ,EF ⊂平面AEFD ,则Ez ⊥AE ,Ez ⊥EF ,而AE ⊥EF , 可建立如图所示的空间直角坐标系,由题设知:∠BEA =∠CFD =π3,所以E (0,0,0),B (1,0,3),C (1,2,3),M (2,m ,0)且0≤m ≤2, 则EB →=(1,0,3),EC →=(1,2,3),EM →=(2,m ,0),若n =(x ,y ,z )是平面EMC 的法向量,则⎩⎪⎨⎪⎧EC →·n =x +2y +3z =0,EM →·n =2x +my =0,令x =m ,则n =(m ,-2,4-m3), |cos 〈EB →,n 〉|=|EB →·n ||EB →||n |=1m 2-2m +73=12,可得m=1,则n =(1,-2,3),又l =(0,0,1)是平面EMD 的一个法向量, 所以|cos 〈l ,n 〉|=|l ·n ||l ||n |=322=64,所以平面DEM 和平面EMC 夹角的余弦值为64.2.如图,四棱锥S -ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点.(1)求证:AC ⊥SD ;(2)若SD ⊥平面PAC ,求平面PAC 与平面ACS 夹角的大小;(3)在(2)的条件下,侧棱SC 上是否存在一点E ,使得BE ∥平面PAC ?若存在,求SC ∶SE 的值;若不存在,试说明理由.(1)证明 连接BD 交AC 于点O ,连接SO ,由题意知SO ⊥AC . 在正方形ABCD 中,AC ⊥BD .因为BD ∩SO =O ,BD ,SO ⊂平面SBD ,所以AC ⊥平面SBD ,又SD ⊂平面SBD ,所以AC ⊥SD .(2)解 由题设知,SO ⊥平面ABCD .以O 为坐标原点,OB →,OC →,OS →的方向分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O -xyz ,如图.设底面边长为a ,则高SO =62a , 则B ⎝ ⎛⎭⎪⎫22a ,0,0,S ⎝ ⎛⎭⎪⎫0,0,62a ,D ⎝ ⎛⎭⎪⎫-22a ,0,0,C ⎝ ⎛⎭⎪⎫0,22a ,0, 又SD ⊥平面PAC ,则平面PAC 的一个法向量为DS →=⎝ ⎛⎭⎪⎫22a ,0,62a , 平面SAC 的一个法向量为OD →=⎝ ⎛⎭⎪⎫-22a ,0,0, 设平面PAC 与平面ACS 夹角的大小为θ.则cos θ=|cos 〈DS →,OD →〉|=|DS →·OD →||DS →||OD →|=12, 所以平面PAC 与平面ACS 夹角的大小为π3. (3)解 在棱SC 上存在一点E 使BE ∥平面PAC .理由如下:由(2)知DS →是平面PAC 的一个法向量,且DS →=⎝ ⎛⎭⎪⎫22a ,0,62a ,CS →=⎝ ⎛⎭⎪⎫0,-22a ,62a ,BC →=⎝ ⎛⎭⎪⎫-22a ,22a ,0. 设CE →=tCS→,t ∈[0,1], 则BE →=BC →+CE →=BC →+tCS →=⎝ ⎛⎭⎪⎫-22a ,22a (1-t ),62at .因为BE ∥平面PAC ,所以BE →·DS →=0,所以-12a 2+32a 2t =0,解得t =13. 故侧棱SC 上存在一点E ,使得BE ∥平面PAC ,此时SC ∶SE =3∶2.3.(2022·全国名校大联考)如图1,直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,E 为AD 边上的点,且AD =2AE =2AB =2BC =2.将△ABE 沿BE 向上折起,使得异面直线AB 与ED 所成的角为60°,F 为线段AD 上一点,如图2.(1)若DE ⊥CF ,求AF FD的值; (2)求平面ABC 与平面AED 所成锐二面角的余弦值.解 (1)如图①中,连接CE .图①由题意可知,△ABE ,△CED ,△BCE 均为等腰直角三角形,因为BC ∥ED ,所以∠ABC 即为异面直线AB 与ED 所成的角,所以∠ABC =60°,所以AC =1.取BE 的中点O ,连接OC ,OA ,OD ,则OA ⊥BE ,OC ⊥BE ,且OA =OC =22,因为OA 2+OC 2=AC 2,所以OA ⊥OC ,因为BE ∩OC =O ,BE ,OC ⊂平面BCDE .所以OA ⊥平面BCDE .连接EF ,因为DE ⊥EC ,DE ⊥CF ,CE ∩CF =C ,CE ,CF ⊂平面ECF ,所以DE ⊥平面ECF , 又DE ⊂平面BCDE ,所以平面ECF ⊥平面BCDE ,故OA ∥平面ECF .连接OD 交CE 于点G ,连接FG ,因为平面AOD ∩平面ECF =FG ,所以OA ∥GF ,故AF FD =OG GD =OE CD =12.图②(2)如图②,以O 为坐标原点,OB ,OC ,OA 所在直线分别为x ,y ,z 轴,建立空间直角坐标系O -xyz .则A ⎝ ⎛⎭⎪⎫0,0,22,C ⎝ ⎛⎭⎪⎫0,22,0,B ⎝ ⎛⎭⎪⎫22,0,0, E ⎝ ⎛⎭⎪⎫-22,0,0,D ⎝ ⎛⎭⎪⎫-2,22,0. 所以AB →=⎝ ⎛⎭⎪⎫22,0,-22, BC →=⎝ ⎛⎭⎪⎫-22,22,0,AE →=⎝ ⎛⎭⎪⎫-22,0,-22,ED →=⎝ ⎛⎭⎪⎫-22,22,0. 设平面ABC 的法向量为n 1=(x 1,y 1,z 1),则⎩⎪⎨⎪⎧n 1·AB →=0,n 1·BC →=0,即⎩⎪⎨⎪⎧22x 1-22z 1=0,-22x 1+22y 1=0, 令x 1=2,则y 1=2,z 1=2,所以平面ABC 的一个法向量为n 1=(2,2,2),设平面AED 的法向量为n 2=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧n 2·AE →=0,n 2·ED →=0,即⎩⎪⎨⎪⎧-22x 2-22z 2=0,-22x 2+22y 2=0, 令x 2=2,则y 2=2,z 2=-2,所以平面AED 的一个法向量为n 2=(2,2,-2),所以|cos 〈n 1,n 2〉|=|n 1·n 2||n 1|·|n 2|=|2×2+2×2-2×2|22+22+22·22+22+(-2)2=13, 故平面ABC 与平面AED 所成锐二面角的余弦值为13. 二、创新拓展练4.如图1,四边形ABCD 为梯形,AD ∥BC ,BM ⊥AD 于点M ,CN ⊥AD 于点N ,∠A =45°,AD =4BC =4,AB =2,现沿CN 将△CDN 折起,使△ADN 为正三角形,且平面ADN ⊥平面ABCN ,过BM 的平面与线段DN ,DC 分别交于点E ,F ,如图2.(1)求证:EF⊥DA;(2)在棱DN上(不含端点)是否存在点E,使得直线DB与平面BMEF所成角的正弦值为3 4,若存在,请确定E点的位置;若不存在,说明理由.(1)证明因为BM⊥AD,CN⊥AD,所以BM∥CN.在四棱锥D-ABCN中,CN⊂平面CDN,BM⊄平面CDN,所以BM∥平面CDN.又平面BMEF∩平面CDN=EF,所以BM∥EF.因为平面ADN⊥平面ABCN且交于AN,BM⊥AN,所以BM⊥平面ADN,即EF⊥平面ADN.又DA⊂平面ADN,所以EF⊥DA.(2)解存在,E为棱DN上靠近N点的四等分点.因为∠A=45°,AD=4BC=4,AB=2,所以AM=MN=BM=CN=1,DN=2,因为DA=DN,连接DM ,所以DM ⊥AN .又平面ADN ⊥平面ABCN 且交于AN ,故DM ⊥平面ABCN .如图,以M 为坐标原点,分别以MA ,MB ,MD 所在直线为x ,y ,z 轴建立空间直角坐标系,则D (0,0,3),B (0,1,0),M (0,0,0),N (-1,0,0),DB →=(0,1,-3),BM →=(0,-1,0),ND →=(1,0,3). 设NE →=λND →(0<λ<1),则E (λ-1,0,3λ),ME →=(λ-1,0,3λ).设平面BMEF 的法向量n =(x ,y ,z ),则⎩⎪⎨⎪⎧BM →·n =0,ME →·n =0,即⎩⎨⎧-y =0,(λ-1)x +3λz =0,不妨令x =3λ,则z =1-λ,n =(3λ,0,1-λ).设直线DB与平面BMEF所成的角为α,则有sin α=|cos〈n,DB→〉|=|n·DB→||n||DB→|=|3(λ-1)|23λ2+(1-λ)2=34.解得λ=14或λ=-12(舍去),所以NE→=14ND→,即在棱DN上存在点E,使得直线DB与平面BMEF所成角的正弦值为3 4,此时E为棱DN上靠近N点的四等分点.。
2023年高考数学----立体几何折叠问题规律方法与典型例题讲解

2023年高考数学----立体几何折叠问题规律方法与典型例题讲解【规律方法】1、处理图形翻折问题的关键是理清翻折前后长度和角度哪些发生改变,哪些保持不变.2、把空间几何问题转化为平面几何问题,把握图形之间的关系,感悟数学本质. 【典型例题】例1.(2022春·江苏南通·高三期中)已知梯形ABCD 中,//AD BC ,π2∠=∠=ABC BAD ,24AB BC AD ===,E ,F 分别是AB ,CD 上的点,//EF BC ,AE x =,G 是BC 的中点,沿EF 将梯形ABCD 翻折,使平面AEFD ⊥平面EBCF . (1)当2x =时①求证:BD EG ⊥;②求二面角D BF C −−的余弦值;(2)三棱锥D FBC −的体积是否可能等于几何体ABE FDC −体积的一半?并说明理由. 【解析】(1)证明:过D 点作EF 的垂线交EF 于H ,连接BH .如图.2AE AD == 且//AE DH ,//AD EF ,π2EAD ∠=. ∴四边形ADHE 是正方形.2EH =,∴四边形EHGB 是正方形.所以BH EG ⊥(正方形对角线互相垂直).因为平面AEFD ⊥平面EBCF ,平面AEFD ⋂平面EBCF EF =,,AE EF AE ⊥⊂平面AEFD , 所以⊥AE 平面EBCF , 所以DH ⊥平面EBCF , 又因为EG ⊂平面EBCF ,所以EG DH ⊥. 又,,BHDH H BH DH =⊂平面BDH ,所以EG ⊥平面BDH ,又BD ⊂平面BDH , 所以EG BD ⊥.②以E 为原点,EB 为x 轴,EF 为y 轴,EA 为z 轴,建立空间直角坐标系,(2B ,0,0),(0F ,3,0),(0D ,2,2),(2C ,4,0),(2BF =−,3,0),(2BD =−,2,2),设平面BDF 的法向量(n x =,y ,)z ,则·2220·230n BD x y z n BF x y ⎧=−++=⎪⎨=−+=⎪⎩,取3x =,得(3n =,2,1),又平面BCF 的法向量(0m =,0,1),1cos ,||||14m n m n m n <>==∴钝二面角D BF C −−的余弦值为.(2)AE EF ⊥Q ,平面AEFD ⊥平面EBCF , 平面AEFD ⋂平面EBCF EF =,AE ⊂平面AEFD . AE ∴⊥平面EBCF .结合DH ⊥平面EBCF ,得//AE DH ,∴四边形AEHD 是矩形,得DH AE =,故以F 、B 、C 、D 为顶点的三棱锥D BCF −的高DH AE x ==, 又114(4)8222BCFSBC BE x x ==⨯⨯−=−. ∴三棱锥D BCF −的体积为()2=11822(82)433333BFCV SDH x x x x x x ==−=−−,ABE FDC ABE DGH D HGCF V V V −−−=+13ABEHGCF SAD S DH =+111111(4)2(2)(4)=(4)1+(2)232262x x x x x x x x ⎡⎤=−⨯+⨯+−−+⎢⎥⎣⎦, 令()112(4)1+(2)=24623x x x x x ⎡⎤−+⨯−⎢⎥⎣⎦,解得0x =或4x =,不合题意;∴棱锥D FBC −的体积不可能等于几何体ABE FDC −体积的一半.例2.(2022春·辽宁·高三辽宁实验中学校考期中)如图1,在平面四边形ABCD 中,已知ABDC ,AB DC ∥,142AD DC CB AB ====,E 是AB 的中点.将△BCE 沿CE 翻折至△PCE ,使得2DP =,如图2所示.(1)证明:DP CE ⊥;(2)求直线DE 与平面P AD 所成角的正弦值. 【解析】(1)如图取CE 的中点F ,连接PF ,DF ,由题易知△PCE ,△DCE 都是等边三角形, ⸫DF ⊥CE ,PF ⊥CE , ⸫DFPF F =,DF ⊂平面DPF ,PF ⊂平面DPF⸫CE ⊥平面DPF . ⸫DP ⊂平面DPF ⸫DP ⊥CE . (2)解法一:由题易知四边形AECD 是平行四边形, 所以AD ∥CE ,又AD ⊂平面P AD ,所以CE ⊂平面P AD , 所以点E 与点F 到平面P AD 的距离相等. 由(1)知CE ⊥平面DPF ,所以AD ⊥平面DPF . 又AD ⊂平面P AD , 所以平面P AD ⊥平面DPF .过F 作FH ⊥PD 交PD 于H ,则FH ⊥平面P AD .DF PF ==2DP =,故点F 到平面P AD 的距离FH =设直线DE 与平面P AD 所成的角为θ,则sin FH DE θ==, 所以直线DE 与平面P AD 所成角的正弦值为4. 解法二:由题易知四边形AECD 是平行四边形,所以AD ∥CE ,由(1)知CE ⊥平面DPF ,所以AD ⊥平面DPF . 如图,以D 为坐标原点,DA ,DF 所在直线分别为x ,y 轴,过D 且垂直于平面AECD 的直线为z 轴建立空间直角坐标系, 则()0,0,0D ,()4,0,0A ,()E , 设()0,,P a b ,0a >,0b >. 易知DF PF ==2DP =,故(2222124a b a b ⎧−+=⎪⎨⎪+=⎩,P ⎛ ⎝⎭, 所以()4,0,0DA =,DP ⎛= ⎝⎭,()DE =,设平面P AD 的法向量为(),,n x y z =, 则00n DA n DP ⎧⋅=⎪⎨⋅=⎪⎩,得00x y =⎧⎪⎨+=⎪⎩,令y =1z =−,所以()0,11,1n =−.设直线DE 与平面P AD 所成的角为θ,则11sin |cos ,|4DE nDE n DE nθ⋅=〈〉==, 故直线DE 与平面P AD 例3.(2022春·湖南长沙·高三宁乡一中校考期中)如图,平面五边形P ABCD 中,PAD 是边长为2的等边三角形,//AD BC ,AB =2BC =2,AB BC ⊥,将PAD沿AD 翻折成四棱锥P -ABCD ,E 是棱PD 上的动点(端点除外),F ,M 分别是AB ,CE 的中点,且PC(1)证明:AB FM ⊥;(2)当直线EF 与平面P AD 所成的角最大时,求平面ACE 与平面PAD 夹角的余弦值. 【解析】(1)设O 是AD 的中点,连接,OP OC , 三角形PAD 是等边三角形,所以OP AD ⊥,OP =四边形ABCD 是直角梯形,//,OA BC OA BC =,所以四边形ABCO 是平行四边形,也即是矩形,所以OC AD ⊥,2==OC AB .折叠后,PC =222OP OC PC +=,所以OP OC ⊥, 由于,,AD OC O AD OC ⋂=⊂平面ABCD , 所以OP ⊥平面ABCD ,则,,OC OD OP 两两相互垂直,由此建立如图所示的空间直角坐标系, ()2,0,0,AB OC ==()1,1,0F −,设)()0,1,01E t t t −<<,()2,0,0C,所以)11,,22t t M ⎛⎫− ⎪ ⎪⎝⎭,则)120,,22t t FM ⎛⎫−+= ⎪ ⎪⎝⎭,所以0AB FM ⋅=, 所以AB FM ⊥.(2)由于OP ⊥平面ABCD ,AB ⊂平面ABCD ,所以OP AB ⊥, 由于,,,AB AD AD OP O AD OP ⊥⋂=⊂平面PAD ,所以AB ⊥平面PAD ,由于AE ⊂平面PAD ,所以AB AE ⊥, 所以FEA ∠是直线EF 与平面PAD 所成角, 在直角三角形AEF 中,tan AFFEA AE∠=, 由于1AF =,所以当AE 最小时,tan FEA ∠最大,也即FEA ∠最大,由于三角形PAD 是等边三角形,所以当E 为PD 的中点时,AE PD ⊥,AE 取得最小值.由于(P ,()0,1,0D,故此时10,2E ⎛ ⎝⎭,平面PAD 的法向量为()1,0,0m =,()()()30,1,0,2,0,0,2,1,0,0,2A C AC AE ⎛−== ⎝⎭,设平面ACE 的法向量为(),,n x y z =,则20302n ACx y n AE y ⎧⋅=+=⎪⎨⋅==⎪⎩,故可设(1,n =−, 设平面ACE 与平面PAD 的夹角为θ, 则1cos 17m n m nθ⋅===⋅例4.(2022·四川雅安·统考模拟预测)如图①,ABC 为边长为6的等边三角形,E ,F 分别为AB ,AC 上靠近A 的三等分点,现将AEF △沿EF 折起,使点A 翻折至点P 的位置,且二面角P EF C −−的大小为120°(如图②).(1)在PC 上是否存在点H ,使得直线//FH 平面PBE ?若存在,确定点H 的位置;若不存在,说明理由.(2)求直线PC 与平面PBE 所成角的正弦值.【解析】(1)满足条件的点H 存在,且为PC 上靠近P 的三等分点.在PC 上取靠近P 的三等分点H ,连接AP ,FH ,如图,则AP 是平面P AB 与平面P AC 的交线,依题意,12PH AF HC FC ==,则有//FH AP ,又AP ⊂平面PBE ,FH ⊄平面PBE ,因此直线//FH平面PBE ,所以在PC 上是存在点H ,为PC 上靠近P 的三等分点,使得直线//FH 平面PBE . (2)取BC 中点G ,连接AG ,交EF 于点D ,连接PD ,因//EF BC ,依题意,EF DG ⊥,EF PD ⊥,则PDG ∠为二面角P EF C −−的平面角,即120PDG ∠=︒,且EF ⊥平面PAD , 而EF ⊂平面BCFE ,则平面PAD ⊥平面BCFE ,在平面PAD 内过P 作PO AD ⊥于O , 又平面PAD ⋂平面BCFE AD =,因此PO ⊥平面BCFE ,在平面BCFE 内过O 作Ox AD ⊥, 显然Ox ,AD ,OP 两两垂直,分别以向量Ox ,OD ,OP 的方向为x ,y ,z 轴正方向,建立空间直角坐标系O xyz −,如图,则B ⎛⎫ ⎪ ⎪⎝⎭,C ⎛⎫− ⎪ ⎪⎝⎭,E ⎛⎫ ⎪ ⎪⎝⎭,30,0,2P ⎛⎫ ⎪⎝⎭,所以,32PC ⎛⎫=−− ⎪ ⎪⎝⎭,()EB =,31,2EP ⎛⎫=− ⎪ ⎪⎝⎭, 设平面PBE 的一个法向量为(),,n x y z =r,由20302n EB x n EP x y z ⎧⋅=+=⎪⎨⋅=−+=⎪⎩,令y =()3,3,1n =−,设直线PC 与平面PBE 所成角为α,则||18sin |cos ,|||||30PC n PC n PC n α⋅=〈〉===⋅所以直线PC 与平面PBE .。
2021届高考数学一轮复习第八章立体几何与空间向量补上一课立体几何中的翻折轨迹及最值范围问题含解析

立体几何中的翻折、轨迹及最值(范围)问题知识拓展1.翻折问题是立体几何的一类典型问题,是考查实践能力与创新能力的好素材.解答翻折问题的关键在于画好折叠前后的平面图形与立体图形,并弄清折叠前后哪些发生了变化,哪些没有发生变化。
解题时我们要依据这些变化的与未变化的量来分析问题和解决问题.而表面展开问题是折叠问题的逆向思维、逆向过程,一般地,涉及多面体表面的距离问题不妨将它展开成平面图形试一试。
2.在立体几何中,某些点、线、面依一定的规则运动,构成各式各样的轨迹,探求空间轨迹与求平面轨迹类似,应注意几何条件,善于基本轨迹转化.对于较为复杂的轨迹,常常要分段考虑,注意特定情况下的动点的位置,然后对任意情形加以分析判定,也可转化为平面问题。
对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性.3.立体几何中的体积最值问题一般是指有关距离的最值、角的最值(上节)或(面积)体积的最值的问题。
其一般方法有:(1)几何法:通过证明或几何作图,确定图形中取得最值的特殊位置,再计算它的值;(2)代数方法:分析给定图形中的数量关系,选取适当的自变量及目标函数,确定函数解析式,利用函数的单调性、有界性,以及不等式的均值定理等,求出最值.题型突破题型一立体几何中的翻折问题【例1】(2019·全国Ⅲ卷)图①是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC =60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图②。
(1)证明:图②中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图②中的二面角B-CG-A的大小.(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,所以AD,CG确定一个平面,从而A,C,G,D四点共面。
由已知得AB⊥BE,AB⊥BC,且BE∩BC=B,BE,BC⊂平面BCGE,所以AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE。
高考数学难点突破八立体几何中的翻折问题
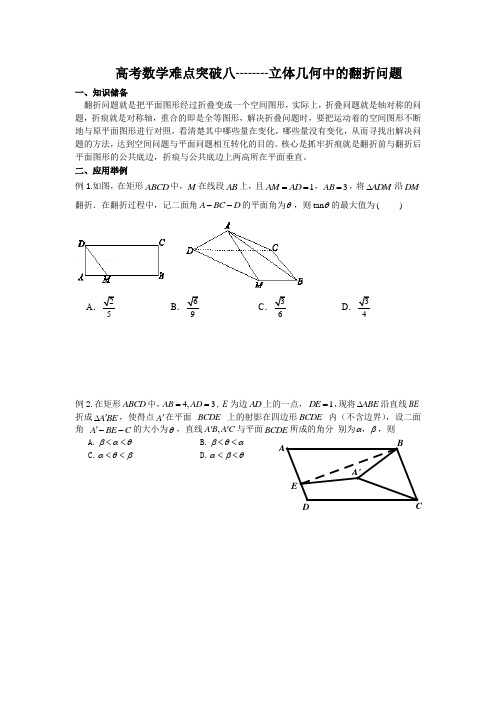
高考数学难点突破八--------立体几何中的翻折问题一、知识储备翻折问题就是把平面图形经过折叠变成一个空间图形,实际上,折叠问题就是轴对称的问题,折痕就是对称轴,重合的即是全等图形,解决折叠问题时,要把运动着的空间图形不断地与原平面图形进行对照,看清楚其中哪些量在变化,哪些量没有变化,从而寻找出解决问题的方法,达到空间问题与平面问题相互转化的目的。
核心是抓牢折痕就是翻折前与翻折后平面图形的公共底边,折痕与公共底边上两高所在平面垂直。
二、应用举例例1.如图,在矩形ABCD 中,M 在线段AB 上,且1AM AD ==,3AB =,将ADM ∆沿DM 翻折.在翻折过程中,记二面角A BC D --的平面角为θ,则tan θ的最大值为( )ABCD例2.在矩形ABCD 中,4,3AB AD ==,E 为边AD 上的一点,1DE =,现将ABE ∆沿直线BE 折成A BE '∆,使得点A '在平面 BCDE 上的射影在四边形BCDE 内(不含边界),设二面角 A BE C '--的大小为θ,直线,A B A C ''与平面BCDE 所成的角分 别为αβ,,则 A.βαθ<< B.βθα<< C.αθβ<< D.αβθ<<例3.如图,矩形ABCD 中心为, O BC AB >,现将DAC 沿着对角线AC 翻折成EAC ,记BOE a ∠=,二面角B AC E --的平面角为β,直线DE 和BC 所成角为γ,则( )A. ,2a ββγ>>B. ,2a ββγ><C. ,2a ββγ<>D. ,2a ββγ<<例4.如图,在ABC △中,1AB =,22BC =,4B π=,将ABC △绕边AB 翻转至ABP △,使面ABP ⊥面ABC ,D 是BC 中点,设Q 是线段PA 上的动点,则当PC 与DQ 所成角取得最小值时,线段AQ 的长度为( ) A .5 B .25C .35D .25例5.已知在矩形ABCD 中,2AD AB =,沿直线BD 将ABD ∆ 折成'A BD ∆,使得点'A 在平面BCD 上的射影在BCD ∆内(不含边界),设二面角'A BD C --的大小为θ,直线','A D A C 与平面BCD 所成的角分别为,αβ,则( )A. αθβ<<B. βθα<<C. βαθ<<D. αβθ<<Q DPCBA例6、(嘉兴市2020年1月期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .例7、(宁波市2020年1月期终)已知平面四边形ABCD 中,90A C ∠=∠=︒,BC CD =,AB AD >,现将ABD △沿对角线BD 翻折得到三棱锥A BCD '-,在此过程中,二面角A BC D '--、A CDB '--的大小分别为α,β,直线A B '与平面BCD 所成角为γ,直线A D '与平面BCD 所成角为δ,则( )A .γδβ<<B .γαβ<<C .αδβ<<D .γαδ<<例8、(柯桥一中2020年1月期终)已知在矩形ABCD 中,2AB =,4AD =,E ,F 分别在边AD ,BC 上,且1AE =,3BF =,如图所示, 沿EF 将四边形AEFB 翻折成A EFB '',则在翻折过程中,二面角B CD E '--的大小为θ,则tan θ的最大值为( ) A.5C.4例9、(2020年3月名校合作体)已知C 为ABD Rt ∆斜边BD 上一点,且ACD ∆为等边三角形,现将ABC ∆沿AC 翻折至C B A '∆,若在三棱锥ACD B -'中,直线B C '和直线B A '与平面ACD 所成角分别为βα,,则( )A. βα<<0B.βαβ2≤<C.βαβ32≤≤D.βα3≥例10、(2020年1月嘉兴期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .例11、(2020年4月温州模拟)如图,在ABC ∆中,点M 是边BC 的中点,将ABN ∆沿着AM 翻折成M B A '∆,且点B '不在平面AMC 内,点P 是线段C B '上一点,若二面角B AM P '--与二面角C AM P --的平面角相等,则直线AP 经过C B A '∆的( ) A. 重心 B. 垂心 C. 内心 D.外心B DACG PFD C B A例12、(2020年嘉兴一模)将边长为1的正方形ABCD 沿对角线BD 翻折,使得二面角A BD C --的平面角的大小为π3,若点E ,F 分别是线段AC 和BD 上的动点,则BE CF 的取值范围为 ( )A .[1,0]-B .1[1,]4-C .1[,0]2-D . 11[,]24-例13、(2020年5月暨阳联考)如图:ABC ∆中,︒=∠⊥90,ACB BC AB ,D 为AC 的中点,ABD ∆沿BD 边翻折过程中,直线AB 与BC 直线所成的最大角,最小角分别记为11βα,,直线AD 与直线BC 所成的最大角,最小角分别记为22βα,,则有( )A. ββαα≤<121,B. 2121ββαα><,C. 2121ββαα≤≥,D.2121ββαα>≥,例14、(2020年4月台州二模)如下图①,在直角梯形ABCD 中,90=∠=∠=∠DAB CDB ABC , 30=∠BCD ,4=BC ,点E 在线段CD 上运动,如下图②,沿BE 将BEC ∆折至C BE '∆,使得平面⊥'C BE 平面ABED ,则C A '的最小值为 .⇒例15、(2020年9月嘉兴基础知识测试)如图,矩形ABCD 中,2,1==BC AB ,点E 为AD 中点,将ABE ∆沿BE 折起,在翻折过程中,记二面角B DC A --的平面角大小为α,则当α最大时,=αtan ( ) A. 22 B. 32 C. 31 D.21。
立体几何中的翻折问题和探索性问题

(3)连接 AC,过 M 作 MP⊥AC 于 P.在正方体 ABCD- EFGH 中,AC∥EG,所以 MP⊥EG.过 P 作 PK⊥EG 于 K, 连接 KM,所以 EG⊥平面 PKM,从而 KM⊥EG.所以∠PKM 是二面角 A-EG-M 的平面角.设 AD=2,则 CM=1,PK =2,
在 Rt△CMP 中,PM=CMsin45°= 22.在 Rt△MPK 中,
解 (1)证明:按题意作出三棱锥,如图.
由题知 AD=AE,DG=GE,∴DE⊥AG,又 DF=EF, DG=GE,∴DE⊥FG.又 AG∩FG=G,∴DE⊥平面 AGF.
(2)由(1)得 DE⊥AG,DE⊥FG,所以∠AGF 为二面角 A
-DE-F 的平面角.
在△AGF 中,AF=3,AG=323,FG= 23, 所以 cos∠AGF=AG22+·AFGG·F2-GAF2
又 CE⊂平面 ABCD,以平面 PCE⊥平面 PAH.
过 A 作 AQ⊥PH 于 Q,则 AQ⊥平面 PCE.
所以∠APH 是 PA 与平面 PCE 所成的角.
在
Rt△AEH
中,∠AEH=45°,AE=1,所以
AH=
2 2.
在 Rt△PAH 中,PH= PA2+AH2=322,
【针对训练】 (2016·四川高考)如图,在四棱锥 P-ABCD 中,AD∥BC, ∠ADC=∠PAB=90°,BC=CD=12AD,E 为棱 AD 的中点, 异面直线 PA 与 CD 所成的角为 90°.
(1)在平面 PAB 内找一点 M,使得直线 CM∥平面 PBE, 并说明理由;
(2)若二面角 P-CD-A 的大小为 45°,求直线 PA 与平 面 PCE 所成角的正弦值.
高中 立体几何中折叠问题的求解策略

立体几何中折叠问题的求解策略折叠问题,是立体几何中的热点、同时也是难点问题.该类问题难的根源在于所研究的是“动态”空间图形,折叠后的图形中点、线、面的位置关系难以确定,需要联系折叠前后图形之间的关系,因此对空间想象、识图及分析能力都提出了较高要求.在考试中此类问题得分率普遍不高,分析其原因,首先是空间想象力不足,其次是对这类问题没有形成解题的模型和方法.解决折叠问题的关键在于抓住折叠前后图形的特征关系,弄清折叠前后哪些量发生了变化、哪些量没有发生变化,以及确定动点在底面上的投影位置,这是分析和解决问题的依据,也是求解此类问题的钥匙.首先要弄清楚空间中折叠的本质含义是什么?教材中并没有明确给出空间中折叠的定义,但是不难看出空间中的折叠是平面中的翻折的推广,所以不妨从平面翻折的定义来揣测空间中折叠的含义.翻折的定义:将一个图形沿着某一条直线翻折180︒,直线两旁的部分能够相互重合.其中这条直线就是它的对称轴,翻折前图形中的任意一点与翻折后的对应点关于对称轴对称.于是可以类似的给空间中折叠下一个定义:将一个平面图形沿着一条直线翻折某个角度θ(其中0180θ︒<<︒),直线两侧的部分能够相互重合.其中这条直线就是它的折线,过翻折前图形中的任意一点及翻折后的对应点分别向折线做垂线,所构成的图形就是翻折前后所成二面角的平面角,即为θ.由上述对空间中折叠的定义,可以得到以下几个结论.如图1,将ADE ∆沿AE 折起.结论1折起的面上任意一点在底面的投影在过该点折起前的对应点垂直于折线的射线上.例如,点'D 在底面ABCE 上的投影O 一定在射线DF 上;结论2折叠前后折线同侧的量不变.如'D A DA =,'D E DE =.对于折叠问题的求解难度在于确定折起后图形中动点的位置,该类问题在具体出题时并不会直接给出动点的位置,而往往是借助动点在底面的投影大概位置、线段长度、相应的角度等来刻画.这就需要通过给出的关系来确定动点在底面中投影的具体位置来确定动点的位置,然后再进一步求解.1已知动点在底面的投影在某线段上例1如图2,四边形ABCD 是矩形,沿对角线AC 将ACD ∆折起,使得点D 在平面ABC 内的投影恰好落在边AB 上.(1)求证:平面ACD ⊥平面BCD ;(2)当2AB AD =时,求二面角D AC B --的余弦值.ABCDEFH 图1ABCD'D H OF EABCDA BCD分析第一问由结论2,折线同侧的量不变,则AD DC ⊥,BC AB ⊥.又D 与它在底面的投影的连线垂直底面,则垂直BC ,从而BC ⊥平面ABD ,得BC AD ⊥,所以AD ⊥平面BCD ,于是得证.第二问关键是确定D 在底面的投影的位置,由结论1,可知D 在底面的投影为过D 垂直于折线AC 的垂线与AB 的交点,于是利用平面几何知识求解即可.解(1)略;(2)如图3,过点D 作AC 的垂线交AB 于H ,由结论1知H 即是折起后D 在底面的投影.设1AD =,由DAH CDA ∆∆ ,所以12AH =,折叠后32DH =.方法一:如图4,以B 为原点建立空间直角坐标系.那么(0,2,0)A ,(1,0,0)C,3(0,,22D,则1(0,,)22AD =- ,(1,2,0)AC =- .设平面ACD 的法向量为(,,)n x y z =,则00n AD n AC ⎧=⎪⎨=⎪⎩ ,即1302220y z x y ⎧-+=⎪⎨⎪-=⎩,令1z =,则y =,x =n =.易得平面ABC 的一个法向量为(0,0,1)m =.1cos ,4n m n m n m <>==,所以二面角D AC B --的余弦值为14.方法二:如图3,记DH 与AC 的交点为E ,有AHE CDE ∆∆ ,则14EH AH ED CD ==.由折叠的定义知,沿对角线AC 将ACD ∆折起之后,DEH ∠为二面角D AC B --的图2ABCD HE 图3ABC Dxy z图4平面角.在Rt DHE ∆中,1cos 4EH DEH ED ∠==,即二面角D AC B --的余弦值为14.评注已知动点在底面的投影在某条线段上,由结论1可得该动点在底面的投影就是折叠前过此点垂直于折线的射线与这条线段的交点,只需在平面图形中利用平面几何知识即可确定动点在底面投影的位置.例2如图5,设正方形ABCD 的边长为3,点E ,F 分别在AB ,CD 上,且满足2AE EB =,2CF FD =.将直角梯形AFED 沿EF 折起,使得点A 在平面BEFC 的投影G 恰好在BC 上,H 为EA 的中点.(1)证明:平面ABE ∥平面CDF ;(2)求二面角H BF C --的正弦值.图5ABCD E FA BC DEFGH分析由结论1,可知A 在底面的投影在过点A 垂直于折线EF 的垂线上.又由题意,点A 在平面BEFC 的投影G 恰好在BC 上,所以A 在底面的投影是过点A 垂直于折线EF 的垂线与BC 的交点,于是利用平面几何知识求解就可以确定G 在BC 上的位置,然后建系求解即可.解(1)略.(2)由题意将直角梯形AFED 沿EF 折起,使得点A 在平面BEFC 的投影G 恰好在BC 上,如图6,过A 作EF 的垂线,与BC 的交点即为G .作MF ∥BC ,且交AB 与M ,由平面几何知识易得ABG FME ∆≅∆,所以113BG AB ==,则AG ==.如图7,以G 为原点建立空间直角坐标系,则A ,(1,1,0)E -,则11(,,)222H -,(1,0,0)B -,(2,2,0)F ,所以(3,2,0)BF = ,112(,,)222BH = .设平面BFH 的法向量为(,,)n x y z =,A BCD E FGM 图6AB CD EFGH xyz 图7由由00n BF n BH ⎧=⎪⎨=⎪⎩,即320110222x y x y z +=⎧⎪⎨++=⎪⎩,令2x =,则3y =-,22z =,所以2(2,3,)2n =- ,易得平面BCF 的一个法向量为(0,0,1)m =,所以3cos ,9n m n m n m<>==,所以二面角H BF C --的余弦值39.例3如图8,在矩形ABCD 中,已知2AB =,4AD =,点E ,F 分别在AD ,BC上,且1AE =,3BF =,将四边形AEFB 沿EF 折起,使点B 在平面CDEF 上的射影H 在直线DE 上.(1)求证:CD ⊥BE ;(2)求直线AF 与平面EFCD 所成角的正弦值.分析由结论1,可知B 在底面的投影在过点B 垂直于折线EF 的垂线上.又由题意,点B 在平面CDEF 的投影H 恰好在DE 上,所以B 在底面的投影是过点B 垂直于折线EF 的垂线与DE 的交点,于是利用平面几何知识求解就可以确定H 在DE 上的位置,然后建系求解即可.解(1)略.(2)如图9,作BC 的中点M ,AD 的中点'H ,则四边形'ABMH 为正方形,所以'BH AM ⊥.又AM ∥EF ,则'BH EF ⊥,由题意有BH EF ⊥,所以H 与'H 为同一点,故1EH =,则2BH ==.如图10,以H 为原点建立空间直角坐标系,则(0,1,0)E -,(2,1,0)F ,(0,0,2)B ,所以(2,1,2)BF =-,由13AE BF =,得252(,,)333A --,则872(,,)333AF =- .ABCDEFA BCDEFH图8A BCDE F M'H 图9A BCDEFHxyz图10易得平面EFCD 的一个法向量为(0,0,1)n =,设直线AF 与平面EFCD 所成的角为θ,则sin cos ,39AF n AF n AF nθ=<>==.2已知线段长度例4如图11,平面多边形PABCD 中,PA PD =,224AD DC BC ===,AD ∥BC ,AP ⊥PD ,AD ⊥DC ,E 为PD 的中点,现将APD ∆沿AD 折起,使得PC =(1)证明:CE ∥平面ABP ;(2)求直线AE 与平面ABP 所成角的正弦值.ABCDPEABCDEP分析此题是通过线段PC 的长度来刻画APD ∆沿AD 折起的程度的,也就是折起后折面的位置,该题求解的突破口是如何利用线段PC 的长度来确定P 在底面投影的位置.由结论1知P 在底面投影在过P 垂直于折线AD 的射线PB 上,于是有两个思路来确定投影的位置:一是利用已知条件和线段PC 的长度确定PBO ∆的边长,利用解三角形确定投影位置;二是注意到PC PD =,于是P 在底面投影一定在平面ABCD 内CD 的中垂线上,那么就是OB 与CD 中垂线的交点.解(1)略;(2)方法一:如图12,作AD 的中点O ,连接BO 、PO ,易知2BO PO ==,由结论1,P 在底面ABCD 的投影在射线OB 上.设该投影为H ,连接PH ,则PH ⊥平面ABCD ,从而PH BC ⊥,又BC BO ⊥,所以BC ⊥平面PBO ,则BC PB ⊥.所以,2PB ===,故PBO ∆是等边三角形,则H 为BO的中点.以H 为坐标原点建立空间直角坐标系.那么,(1,2,0)A --,(1,0,0)B,P ,图11ABCD EPx yz HO图12(1,2,0)D -,则13(,1,)22E -,13(,3,)22AE = ,(2,2,0)AB =,(1,AP = .设平面ABP 的法向量为(,,)n x y z = ,则0n AB n AP ⎧=⎪⎨=⎪⎩,即22020x y x y +=⎧⎪⎨++=⎪⎩,令1x =,则1y =-,33z =,则3(1,1,)3n =- .设AE 与平面ABP 所成角为θ,则210sin cos ,35n AE n AE n AEθ=<>==.方法二:注意到PC PD =,于是P 在底面投影一定在平面ABCD 内CD 的中垂线上,那么P 在底面投影就是OB 与CD 中垂线的交点,即为BO 的中点,下同方法一.评注通过线段长度刻画折起后折面的位置的题型,可以通过将该线段长度转化到要确定动点和动点在底面投影所在线段构成的三角形,利用解三角形工具确定投影的位置;也可以利用线段相等,通过中垂线与动点在底面投影所在射线的交点来确定投影的位置.3已知相应角度例4(2018全国1理)如图13,四边形ABCD 为正方形,,E F 分别为,AD BC 的中点,以DF 为折痕把DFC ∆折起,使点C 到达点P 的位置,且PF BF ⊥.(1)证明:平面PEF ⊥平面ABFD ;(2)求DP 与平面ABFD 所成角的正弦值.分析:此题是利用PF BF ⊥刻画折起面的位置,可以考虑利用PF BF ⊥找到过P 且垂直于底面ABFD 的平面,则点P 在底面的投影就在这两个平面的交线上,然后再借助结论1即可确定点P 在底面投影的位置.解(1)因为PF BF ⊥,又BF EF ⊥,且PF EF F = ,,PF EF ⊂平面PEF ,所以BF ⊥平面PEF ,又因为BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD .(2)由(1)知平面PEF ⊥平面ABFD ,且平面PEF 平面ABFD EF =,则点P 在底面ABFD 的投影在直线EF 上.如图14,过C 作折线DF 的垂线交EF 于点H ,由结论1知,点H 即为点P 在底面ABFD 的投影.由CFH DCF ∆∆ ,则ABC D E F P图13ABCD E F H图1412HF CF CF CD ==,设AB a =,则12HF a =.那么32PH a ==.因为PH ⊥底面ABFD ,如图15,连接DH ,则PDH ∠为DP 与平面ABFD 所成角,所以32sin 24a PH PDH PD a ∠===.评注已知相应角度刻画折起面的位置,需将这个角度条件进行适当转化,最好是能够找到过动点且与底面垂直的平面,然后结合结论1,即可确定P 在底面投影的位置.对刻画折起面位置的角度条件的转化是解题的突破口.总结立体几何折叠问题的难点突破关键在于利用好结论1和结论2,搞清楚在折叠过程中哪些量是不变的以及动点在底面的投影在那条射线上运动,再结合已知条件,更多的时候需要对已知条件进行适当的转化,便可以确定动点在底面中的投影的位置,顺藤摸瓜就能确定动点在空间中的位置,从而使得问题迎刃而解.参考文献【1】周建平.变化中的不变量——谈立体几何中的折叠问题【J 】.中学教研(数学),2018.7.ABC D EFPH图15。
高中数学复习 立体几何中的翻折问题典例分析

设平面 ABF 的一个法向量为 n x, y, z ,则由
FAn
0,
得
x
3z 0,
令 z 1,则 n
3,3,1 .
F Bn 0, 3x 3y 0,
平面
AEF
的一个法向量为
p
0,1, 0
(1)求证: BF / / 面 A1DE ; (2)求证:面 A1DE 面 DEBC ; (3)求四棱锥 A1 DEBC 的体积.
分析(1)取 DA1 的中点 G ,连接 FG 、 GE ,通过证明 BF // EG ,利用直线与平面平行 的判定定理证明 BF / / 面 A1DE ;(2)取 DE 的中点 H ,连接 A1H 、 CH ,通过证明 A1H 面 DEBC ,然后通过平面与平面垂直的判定定理证明面 A1DE 面 DEBC ;(3)
(Ⅰ)求证: BD PA ; (Ⅱ)求四棱锥 P BFED 的体积.
分析(Ⅰ)由题证明 EF AO, EF PO ,则 EF 平面 POA ,可得 BD PA ;(Ⅱ)
由勾股定理可得 PO BO ,又 PO EF ,可知 PO 为四棱锥 P BFED 的高,则四棱锥
,所以 cos
n, p
pn
3
13
,
p n 13
显然二面角 E AF B 是锐角,所以ຫໍສະໝຸດ 面角 E AF B 的余弦值为 3
13
.
13
例 2 如图,在边长为 4 的菱形 ABCD 中, DAB 60 ,点 E, F 分别是边 CD , CB 的中 点, AC EF O ,沿 EF 将 CEF 翻折到 PEF ,连接 PA, PB, PD ,得到如图的五棱 锥 P ABFED ,且 PB 10 .
立体几何翻折问题——浅析高考新热点

想象 空间 , 成为高考 题 中的新宠 , 因为这
B E= 9 0 0.
AA1 D E的位置 , 使 Ai F 上C D, 如图 2 .
折叠后 ,这 四个垂直仍保持不 变 , 即
P 8 LP D。 BD _ LDC, P E LB D, EF LB C。
B
C
图1
( 2) 求证 : A】 F_ L B E;
择题、 填空题仍 旧是考查本章 的基本性质 A1 D P与平面 Al B E垂直?说 明理 由.
A
△AB D沿对角线 B D折起 , 记折 起后点 A
的位置为 P , 且使平面 P B D上平面 B C D. ( 1) 求证 : 平面 P B CJ - 平面 P DC;
( 2 ) 在 折 叠前 的 四边 形 A B C D中, 作
所成 角的大小: ( 2) 设 点 P的坐标 为( 0 , a , 0) ( 0 ≤口 ≤ 3 ) ,用向量法 求平面 A1 D P与平 面 A1 B E 的法向量 , 若存在使两个法 向量 的内积 为 解析 : ( 1 )折叠前 ,在 四边 形 AB C D 中, 有 4个直 角 : /B AD =/ - B DC =/ _ A E D =
位线得到 D E #B c , 再由线面平行的判定 定理得到 D E ∥平面A 1 C B:
立体 几何
高考 删 上A1 C, 即可证明 A1 C上平面 D E Q.
立体几何中翻折问题(微专题)(解析版)

立体几何中翻折问题(微专题)一、题型选讲题型一、展开问题1(2022·广东佛山·高三期末)长方体ABCD-A1B1C1D1中,AB=1,AD=AA1=2,E为棱AA1上的动点,平面BED1交棱CC1于F,则四边形BED1F的周长的最小值为()A.43B.213C.2(2+5)D.2+42【答案】B【分析】将几何体展开,利用两点之间直线段最短即可求得截面最短周长.【详解】解:将长方体展开,如图所示:当点E为BD1与AA1的交点,F为BD1与CC1的交点时,截面四边形BED1F的周长最小,最小值为2BD1=222+(1+2)2=213.故选:B.1.(2022·湖北武昌·高三期末)已知四面体ABCD的一个平面展开图如图所示,其中四边形AEFD是边长为22的菱形,B,C分别为AE,FD的中点,BD=22,则在该四面体中()A.BE⊥CDB.BE与平面DCE所成角的余弦值为21015D.四面体ABCD的外接球表面积为9πC.四面体ABCD的内切球半径为10530【答案】ACD【分析】几何体内各相关线段的计算即可.【解析】由题意得,展开图拼成的几何体如下图所示,AB=CD=2,AD=BD=BC=AC=22,取AB中点M,CD中点N,MN中点O,连MN、OA,过O作OH⊥CM于H,则OH是内切球的半径,OA是外接球的半径.所以AM=CN=12AB=22,CM=AN=AC2-CN2=222-222=302MN=CM2-CN2=3022-22 2=7对于A:AN⊥CD,BN⊥CD,AN∩BN=N,故CD⊥平面ABN,而BE⊂平面ABN,所以BE⊥CD,故A正确;对于B:由于CD⊂平面ACD,故平面ABN⊥平面ACD,故∠BAN是BE与平面DCE所成角,故cos∠BAN=AMAN=22×230=1515,故B错误;对于C:OH=CNCM12MN=22×230×12×7=10530,故C正确;对于D:OA2=AM2+12MN2=22 2+72 2=94所以外接球的表面积为9π,故D正确.故选:ACD2.【2020年高考全国Ⅰ卷理数】如图,在三棱锥P-ABC的平面展开图中,AC=1,AB=AD= 3,AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=.【答案】-14【解析】∵AB ⊥AC ,AB =3,AC =1,由勾股定理得BC =AB 2+AC 2=2,同理得BD =6,∴BF =BD =6,在△ACE 中,AC =1,AE =AD =3,∠CAE =30°,由余弦定理得CE 2=AC 2+AE 2-2AC ⋅AE cos30°=1+3-2×1×3×32=1,∴CF =CE =1,在△BCF 中,BC =2,BF =6,CF =1,由余弦定理得cos ∠FCB =CF 2+BC 2-BF 22CF ⋅BC=1+4-62×1×2=-14.故答案为:-14.题型二、折叠问题2(2022·河北唐山·高三期末)如图,四边形ABCD 是边长为2的正方形,E 为AB 的中点,将△AED 沿DE 所在的直线翻折,使A 与A 重合,得到四棱锥A -BCDE ,则在翻折的过程中()A.DE ⊥AAB.存在某个位置,使得A E ⊥CDC.存在某个位置,使得A B ∥DED.存在某个位置,使四棱锥A -BCDE 的体积为1【答案】AB 【分析】过A 作A O ⊥DE ,垂足为O ,证得DE ⊥平面A AO ,可判定A 正确;取DC 的中点G ,连接EG ,A G ,当A 在平面ABCD 上的投影在FG 上时,可判定B 正确;连接A B ,由直线A B 与DE 是异面直线,可判定C错误;求得A O=25,结合体积公式求可判定D错误.【详解】对于A中,如图所示,过A 作A O⊥DE,垂足为O,延长AO交BC于点F,因为DE⊥AO,且AO∩A O=O,所以DE⊥平面A AO,又因为A A⊂平面A AO,所以DE⊥AA ,所以A正确;对于B中,取DC的中点G,连接EG,A G,当A 在平面ABCD上的投影在FG上时,此时DC⊥平面A EG,从而得到A E⊥CD,所以B正确;对于C中,连接A B,因为E⊂平面A BE,D⊄平面A BE,所以直线A B与DE是异面直线,所以不存在某个位置,使得A B∥DE,所以C错误;对于D中,由V A -BCDE=13×12×(1+2)×2×h=1,解得h=1,由A 作A O⊥DE,可得A O=A E⋅A DDE=1×25=25,即此时四棱锥的高h∈0,25 5,此时25<1,所以不存在某个位置,使四棱锥A -BCDE的体积为1,所以D错误.故选:AB.1.(2022·江苏宿迁·高三期末)如图,一张长、宽分别为2,1的矩形纸,A,B,C,D分别是其四条边的中点.现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,则()A.在该多面体中,BD=2B.该多面体是三棱锥C.在该多面体中,平面BAD⊥平面BCDD.该多面体的体积为112【答案】BCD利用图形翻折,结合勾股定理,确定该多面体是以A ,B ,C ,D 为顶点的三棱锥,利用线面垂直,判定面面垂直,以及棱锥的体积公式即可得出结论.【解析】由于长、宽分别为2,1,A ,B ,C ,D 分别是其四条边的中点,现将其沿图中虚线折起,使得P 1,P 2,P 3,P 4四点重合为一点P ,且P 为BD 的中点,从而得到一个多面体ABCD ,所以该多面体是以A ,B ,C ,D 为顶点的三棱锥,故B 正确;AB =BC =CD =DA =32,AC =BD =1,AP =CP =22,故A 不正确;由于22 2+22 2=1,所以AP ⊥CP ,BP ⊥CP ,可得BD ⊥平面ACP ,则三棱锥A -BCD 的体积为13×BD ×S △ACP =13×1×12×22×22=112,故D 正确;因为AP ⊥BP ,AP ⊥CP ,所以AP ⊥平面BCD ,又AP ⊂平面BAD ,可得平面BAD ⊥平面BCD ,故C 正确.故选:BCD2.(2022·江苏海安·高三期末)如图,ABCD 是一块直角梯形加热片,AB ∥CD ,∠DAB =60°,AB =AD =4dm .现将△BCD 沿BD 折起,成为二面角A -BD -C 是90°的加热零件,则AC 间的距离是dm ;为了安全,把该零件放进一个球形防护罩,则球形防护罩的表面积的最小值是dm 2.(所有器件厚度忽略不计)【答案】4设E 为BD 的中点,由题可得AE ⊥平面BCD ,进而可求AC ,再结合条件可得△DAB 的中心为棱锥C -ABD 的外接球的球心,即求.【解析】∵ABCD 是一块直角梯形加热片,AB ∥CD ,∠DAB =60°,AB =AD =4dm .∴△DAB 为等边三角形,BC =23dm ,DC =2dm ,设E 为BD 的中点,连接AE ,CE ,则AE ⊥BD ,又二面角A -BD -C 是90°,∴AE ⊥平面BCD ,CE ⊂平面BCD ,∴AE ⊥CE ,又CE =2dm ,AE =23dm ,∴AC =AE 2+CE 2=4dm ,设△DAB 的中心为O ,则OE ⊥平面BCD ,又E 为BD 的中点,△BCD 为直角三角形,∴OB =OC =OD =OA ,即O 为三棱锥C -ABD 的外接球的球心,又OA =23×23=433dm ,故球形防护罩的表面积的最小值为4π⋅OA 2=64π3dm 2.故答案为:4,64π3.3.(2022·河北保定·高三期末)如图,DE 是边长为4的等边三角形ABC 的中位线,将△ADE 沿DE 折起,使得点A 与P 重合,平面PDE ⊥平面BCDE ,则四棱雉P -BCDE 外接球的表面积是.【答案】52π3求出四边形BCDE 外接圆的圆半径,再设四棱锥P -BCDE 外接球的球心为O ,由R 2=OO 2+O B 2求出半径,代入球的表面积公式即可.【解析】如图,分别取BC ,DE 的中点O ,F ,连接PF ,O F .因为△ABC 是边长为4的等边三角形,所以PF =O F =3,所以O B =O C =O D =O E =2,则四边形BCDE 外接圆的圆心为O ,半径r =2.设四棱锥P -BCDE 外接球的球心为O ,连接OO ,过点O 作OH ⊥PF ,垂足为H .易证四边形HFO O 是矩形,则HF =OO ,OH =O F =3.设四棱锥P -BCDE 外接球的半径为R ,则R 2=OO 2+O B 2=OH 2+PH 2=O F 2+PF -OO 2,即R 2=OO 2+22=3 2+3-OO 2,解得R 2=133,故四棱锥P -BCDE 外接球的表面积是4πR 2=52π3.故答案为:52π3题型三、折叠的综合性问题3(2022·江苏扬州·高三期末)在边长为6的正三角形ABC 中M ,N 分别为边AB ,AC 上的点,且满足AM AB =ANAC=λ,把△AMN 沿着MN 翻折至A ′MN 位置,则下列说法中正确的有()A.在翻折过程中,在边A ′N 上存在点P ,满足CP ∥平面A ′BMB.若12<λ<1,则在翻折过程中的某个位置,满足平面A ′BC ⊥平面BCNMC.若λ=12且二面角A ′-MN -B 的大小为120°,则四棱锥A ′-BCNM 的外接球的表面积为61πD.在翻折过程中,四棱锥A ′-BCNM 体积的最大值为63【答案】BCD 【分析】通过直线相交来判断A 选项的正确性;通过面面垂直的判定定理判断B 选项的正确性;通过求四棱锥A -BCNM 外接球的表面积来判断C 选项的正确性;利用导数来求得四棱锥A -BCNM 体积的最大值.【详解】对于选项A,过P作PQ⎳MN⎳BC,交AM于Q,则无论点P在A′N上什么位置,都存在CP与BQ相交,折叠后为梯形BCQP,则CP不与平面A′BM平行,故选项A错误;对于选项B,设D,E分别是BC,MN的中点,若12<λ<1,则AE>DE,所以存在某一位置使得A′D⊥DE,又因为MN⊥A′E,MN⊥DE,且A′E∩DE=E,所以MN⊥平面A′DE,所以MN⊥A′D,DE∩MN=E,所以A′D⊥平面BCNM,所以A′BC⊥平面BCNM,故选项B正确;对于选项C,设D,E分别是BC,MN的中点,若λ=12且二面角A′-MN-B的大小为120°,则△AMN为正三角形,∠BMN=120°,∠C=60°,则BCNM四点共圆,圆心可设为点G,其半径设为r,DB=DC=DM=DN=3,所以点G即为点D,所以r=3,二面角A′-MN-B的平面角即为∠A′ED=120°,过点A′作A′H⊥DE,垂足为点H,EH=334,DH=934,A′H=94,DH2=24316,设外接球球心为O,由OD2+32=R294-OD2+24316=R2,解得R2=614,所以外接球的表面积为S=4πR2=61π,故选项C正确;对于选项D,设D,E分别是BC,MN的中点,设h是四棱锥A -BCNM的高.S△AMN=12×6λ×6λ×32=93λ2,S△ABC=12×6×6×32=93,所以S四边形BCNM=93(1-λ2),则V A′-BCNM=13×93(1-λ2)×h≤33(1-λ2)×A′E=33(1-λ2)×33λ=27(-λ3+λ),λ∈(0,1),可设f(λ)=27(-λ3+λ),λ∈(0,1),则f λ =27(-3λ2+1),令f λ =0,解得λ=33,则函数f(λ)在0,33上单调递增,在33,1上单调递减,所以f(λ)max=f33=63,则四棱锥A′-BCN体积的最大值为63,故选项D正确.故选:BCD1.(2021·山东滨州市·高三二模)已知正方形ABCD的边长为2,将△ACD沿AC翻折到△ACD 的位置,得到四面体D -ABC,在翻折过程中,点D 始终位于△ACD所在平面的同一侧,且BD 的最小值为2,则下列结论正确的是()A.四面体D -ABC的外接球的表面积为8πB.四面体D -ABC体积的最大值为63C.点D的运动轨迹的长度为22π3D.边AD旋转所形成的曲面的面积为22π3【答案】ACD【解析】对ABCD各选项逐一分析即可求解.【详解】解:对A:∵∠ABC=90o,∠AD C=90o,∴AC中点即为四面体D -ABC的外接球的球心,AC为球的直径,∴R=2,∴SD -ABC =4πR2=4π22=8π,故选项A正确;对B:当平面AD C⏊平面ABC时,四面体D -ABC体积的最大,此时高为2,∴V D -ABCmax=13×12×2×2×2=223,故选项B错误;对C :设方形ABCD 对角线AC 与BD 交于O ,由题意,翻折后当BD 的最小值为2时,△OD B 为边长为2的等边三角形,此时∠D OB =π3,所以点D 的运动轨迹是以O 为圆心2为半径的圆心角为2π3的圆弧,所以点D 的运动轨迹的长度为2π3×2=22π3,故选项C 正确;对D :结合C 的分析知,边AD 旋转所形成的曲面的面积为以A 为顶点,底面圆为以O 为圆心OD =2为半径的圆锥的侧面积的13,即所求曲面的面积为13πrl =13π×2×2=22π3,故选项D 正确.故选:ACD .2.【2022·广东省深圳市宝安区第一次调研10月】如图甲是由正方形ABCD ,等边△ABE 和等边△BCF 组成的一个平面图形,其中AB =6,将其沿AB ,BC ,AC 折起得三棱锥P -ABC ,如图乙.(1)求证:平面PAC ⊥平面ABC ;(2)过棱AC 作平面ACM 交棱PB 于点M ,且三棱锥P -ACM 和B -ACM 的体积比为1:2,求直线AM 与平面PBC 所成角的正弦值.【答案】(1)证明见解析;(2)427.【分析】(1)取AC 的中点为O ,连接BO ,PO ,证明PO ⊥AC ,PO ⊥OB ,即证PO ⊥平面ABC ,即证得面面垂直;(2)建立如图空间直角坐标系,写出对应点的坐标和向量AM 的坐标,再计算平面PBC 法向量n,利用所求角的正弦为cos AM ,n即得结果.【解析】(1)证明:如图,取AC 的中点为O ,连接BO ,PO .∵PA =PC ,∴PO ⊥AC .∵PA =PC =6,∠APC =90°,∴PO =12AC =32,同理BO =32.又PB =6,∴PO 2+OB 2=PB 2,∴PO ⊥OB .∵AC ∩OB =O ,AC ,OB ⊂平面ABC ,11∴PO ⊥平面ABC .又PO ⊂平面PAC ,∴平面PAC ⊥平面ABC ;(2)解:如图建立空间直角坐标系,根据边长关系可知,A 32,0,0 ,C -32,0,0 ,B 0,32,0 ,P 0,0,32 ,∴CB =32,32,0 ,CP =32,0,32.∵三棱锥P -ACM 和B -ACM 的体积比为1:2,∴PM :BM =1:2,∴M 0,2,22 ,∴AM =-32,2,22 .设平面PBC 的法向量为n =x ,y ,z ,则32x +32y =032x +32z =0 ,令x =1,得n =1,-1,-1 .设直线AM 与平面PBC 所成角为θ,则sin θ=cos AM ,n =-6227⋅3 =427.∴直线AM 与平面PBC 所成角的正弦值为427.。
探析平面翻折问题的背景与相关性质

题 中与上述事 实相对应的如下 5 个性质 .
证 明: 类 似 性 质 1 的 证 明,过 点 A作 AO_ L BC, 垂 足 为 点 0, 连 结 A2 0,则 A2 O - l _ B ( 因为 A 2 0是 A ‘ 二 ) 经平面翻折 后的线段) , 所以A 2 、D、A三点共线, 即 2 AL B . 性质4 如图2 , 设 AA 2 BC、△A1 BC分 别 是 △A B 沿直 线 B 折起 1 8 0 。 及 动态折起 过 程 中 的平 面 图形 , 点A 1 在 底 面 B 2 上 的射 影 为 点 日,则 在 折 起 的 过 程 ( 即二 面 角 A 】 一B — 由0 。 至1 8 0 。 的渐变 过程) 中, 动 点 日 的轨迹 为线段 Af 4 2 . 证 明: 由性 质 2 、3知 ,平 面 AA1 2 上底 面A BA 2 C, 交线为A A 2 ,故 由面 面垂 直 的性
动态 折 起 过 程 中的 某个 平 面 图形,点 P是 直 线 上任意一 点, 则 PA 1 =P A. 证 明: 因为 P 1 是 PA经平 面 翻折 之 后
实现 ( 因为BP_ L CD) , 故选项 ( B ) 正确 ( 即选
项( D) 错误) ; 最后看 选项 ( C ) , 欲使 A D_ L BC, 只要 D日- l - B , 而 D 上 J E ; , 故 H ∈直线 D , 而 这 是 不 可 能 的f 因 为 点 日 在 有 限 的 线 段 】 A 0 上运 动) . 综 上 可知 , 只有选项 ( B ) 正
而 B 上 1 .
可 看 作 是 △A日 的 折 起 平 面( 翻 折“ 后” 面) , 而 △ 2 C即为其折起 1 8 0 。 后所 得 到的平 面.
浅析立体几何中的翻折问题

浅析立体几何中的翻折问题
秦学祯
【期刊名称】《数理化解题研究:高中版》
【年(卷),期】2015(000)002
【摘要】将平面图形翻折成空间图形,空间图形翻折成平面图形是立体几何中的一类重要题型.图形翻折前是不变的,翻折使图形处于运动和变化过程中,这个过程体现了运动和静止的两个方面,是培养学生的辩证思维,提高学生分析问题和解决问题的能力的极好素材.本文就如何解决这类问题做以探讨.
【总页数】1页(P21-21)
【作者】秦学祯
【作者单位】甘肃省高台县一中,734300
【正文语种】中文
【中图分类】G633.63
【相关文献】
1.立体几何翻折问题——浅析高考新热点 [J], 肖春梅;
2.平面翻折寻常事一问一变巧传情——一道立体几何翻折问题的教学案例 [J], 张美娟;
3.立体几何中的翻折探究问题 [J], 蔡正伟
4.立体几何中翻折问题的处理策略 [J], 肜彬
5.基于GeoGebra的立体几何问题的探究——以一道翻折问题为例 [J], 李雷;程泽兵
因版权原因,仅展示原文概要,查看原文内容请购买。
