《时间序列分析及应用:R语言》读书笔记
时间序列分析笔记

时间序列分析笔记总结一、主要概念经典的T 检验、f 检验隐含假定了所依据的时间序列是平稳的,若时间序列不平稳,我们做的T 值、F 值、R ²等是失效的。
弱平稳:如果一个随机过程的均值、方差和协方差在时间上是恒定的(不随时间的变化变化)。
平稳性检验可以通过图示简单判断,平稳时间序列的相关图会很快变平,非平稳时间序列消失缓慢;平稳性可以通过时间序列是否含有单位根来检查,如DF ,ADF 检验。
伪回归: 回归分析结果中,R ²>DW 就可能存在伪回归问题。
随机游走:如股票、汇率等价格为随机游走,是非平稳的。
随机游走分为带漂移的随机游走(不存在常数项或截距项)和不带漂移的随机游走(出现常数项)。
单整(单积随机过程):差分后平稳。
不带漂移的随机游走模型为一阶单整序列,记为I(1),如果进行两次差分后为平稳序列,为二阶单整, I (0),I (1),I (2)以此类推。
单位根过程:对于Y t= Y t-1+μt (-1≤ρ≤0),当ρ=1时是一个单位根过程。
两边同时减去一个Y t-1,式子变形为△Y=(ρ-1)Y t-1+μt ,然后看ρ-1的值。
当ρ <1时,我们说Y t 是一个平稳序列;而当ρ >1时, Y t 是非平稳的。
DF 检验:如果ρ=1或者δ=0, xt 就是最基本的单位根过程(随机游走),是非平稳的,然后用最小二乘法估计δ,但是得到的t 统计量不服从t 分布,所以DF 两人构造了专门的临界值分布表。
参数ρ或δ所对应的t 统计量服从DF 分布,若计算值小于临界值,拒绝原假设。
ADF 检验(增广DF ):在DF 基础上通过在三个方程中增加因变量△Yt 的滞后值控制εt 的自相关(差分)。
协整:把两个非平稳的波动相减或相加抵消掉,剩余的部分是平稳的,变成了有效的回归分析。
残差序列做平稳性检验。
二、主要模型ARMA 模型(Auto-Regressive and Moving Average Model )是研究时间序列的重要方法,由自回归模型(简称AR 模型)与滑动平均模型(简称MA 模型)相加构成。
R语言常用上机命令分功能整理 时间序列分析为主

第一讲 应用实例 • R 的基本界面是一个交互式命令窗口,命令提示符是一个大于号,命令的结果马上 显示在命令下面。 • S 命令主要有两种形式:表达式或赋值运算(用’<-’或者’=’表示) 。在命令提示符后 键入一个表达式表示计算此表达式并显示结果。赋值运算把赋值号右边的值计算出 来赋给左边的变量。 • 可以用向上光标键来找回以前运行的命令再次运行或修改后再运行。 • S 是区分大小写的,所以 x 和 X 是不同的名字。 我们用一些例子来看 R 软件的特点。假设我们已经进入了 R 的交互式窗口。如果没有打开 的图形窗口,在 R 中,用:> x11() 可以打开一个作图窗口。然后,输入以下语句: x1 = 0:100 x2 = x1*2*pi/100 y = sin(x2) plot(x2,y,type="l") 这些语句可以绘制正弦曲线图。其中,“=”是赋值运算符。0:100 表示一个从 0 到 100 的等 差数列向量。第二个语句可以看出,我们可以对向量直接进行四则运算,计算得到的 x2 是 向量 x1 的所有元素乘以常数 2*pi/100 的结果。 从第三个语句可看到函数可以以向量为输入, 并可以输出一个向量,结果向量 y 的每一个分量是自变量 x2 的每一个分量的正弦函数值。
#将未来 5 期预测值保存在 prop.fore 变量中 U = prop.fore$pred + 1.96* prop.fore$se L = prop.fore$pred – 1.96* prop.fore$se#算出 95%置信区间 ts.plot(prop, prop.fore$pred,col=1:2)#作时序图,含预测。 lines(U, col="blue", lty="dashed") lines(L, col="blue", lty="dashed")#在时序图中作出 95%置信区间 例题 3.9 d=scan("a1.22.txt") x=diff(d) arima(x, order = c(1,0,1),method="CSS") tsdiag(arima(x, order = c(1,0,1),method="CSS")) 第一点: 对于第三讲中的例 2.5,运行命令 arima(prop, order = c(1,0,0),method="ML")之后,显示: Call: arima(x = prop, order = c(1, 0, 0), method = "ML") Coefficients: ar1 intercept 0.6914 81.5509 s.e. 0.0989 1.7453 sigma^2 estimated as 15.51: log likelihood = -137.02, aic = 280.05 注意:intercept 下面的 81.5509 是均值,而不是截距!虽然 intercept 是截距的意思,这里如 果用 mean 会更好。 (the mean and the intercept are the same only when there is no AR term, 均值和截距是相同的,只有在没有 AR 项的时候) 如果想得到截距,利用公式计算。int=(1-0.6914)*81.5509= 25.16661。课本 P81 的例 2.5 续中 的截距 25.17 是正确的。
R语言与时间序列学习笔记

R语言与时间序列学习笔记(1)继续上一次的参数估计话题。
今天分享的是R语言中时间序列的模型初步估计有关内容。
主要有:时间序列的创建,ARMA模型的建立与模型的参数估计。
一、时间序列的创建时间序列的创建函数为:ts().函数的参数列表如下:ts(data = NA, start = 1, end = numeric(), frequency = 1,deltat = 1, ts.eps = getOption("ts.eps"), class = , names = )参数说明:data:这个必须是一个矩阵,或者向量,再或者数据框frame Frequency:这个是时间观测频率数,也就是每个时间单位的数据数目Start:时间序列开始值,允许第一个个时间单位出现数据缺失举例:ts(matrix(c(NA,NA,NA,1:31,NA),byrow=T,5,7),frequency=7,names=c("Sun"," Mon ","Tue", "Wen" ,"Thu"," Fri"," Sat"))运行上面的代码就可以得到一个日历:Sun Mon Tue Wen Thu Fri SatNA NA NA 1 2 3 45 6 7 8 9 10 1112 13 14 15 16 17 1819 20 21 22 23 24 2526 27 28 29 30 31 NA在R语言中本身也有不少数据集,比如统计包中的sunspots,你可以通过函数data(sunspots)来调用它们。
二、一些时间序列模型这里主要介绍AR,MA,随机游走,余弦曲线趋势,季节趋势等首先介绍一下AR模型:AR模型,即自回归(AutoRegressive, AR)模型,数学表达式为:AR : y(t)=a1y(t-1)+...any(t-n)+e(t)其中,e(t)为均值为0,方差为某值的白噪声信号。
R语言中时间序列分析浅析

R语⾔中时间序列分析浅析时间序列是将统⼀统计值按照时间发⽣的先后顺序来进⾏排列,时间序列分析的主要⽬的是根据已有数据对未来进⾏预测。
⼀个稳定的时间序列中常常包含两个部分,那么就是:有规律的时间序列+噪声。
所以,在以下的⽅法中,主要的⽬的就是去过滤噪声值,让我们的时间序列更加的有分析意义。
语法时间序列分析中ts()函数的基本语法是 <- ts(data, start, end, frequency)以下是所使⽤的参数的描述data是包含在时间序列中使⽤的值的向量或矩阵。
start以时间序列指定第⼀次观察的开始时间。
end指定时间序列中最后⼀次观测的结束时间。
frequency指定每单位时间的观测数。
除了参数“data”,所有其他参数是可选的。
时间序列的预处理:1. 平稳性检验:拿到⼀个时间序列之后,我们⾸先要对其稳定性进⾏判断,只有⾮⽩噪声的稳定性时间序列才有分析的意义以及预测未来数据的价值。
所谓平稳,是指统计值在⼀个常数上下波动并且波动范围是有界限的。
如果有明显的趋势或者周期性,那么就是不稳定的。
⼀般判断有三种⽅法:画出时间序列的趋势图,看趋势判断画⾃相关图和偏相关图,平稳时间序列的⾃相关图和偏相关图,要么拖尾,要么截尾。
检验序列中是否存在单位根,如果存在单位根,就是⾮平稳时间序列。
在R语⾔中,DF检测是⼀种检测稳定性的⽅法,如果得出的P值⼩于临界值,则认为是序列是稳定的。
2. ⽩噪声检验⽩噪声序列,⼜称为纯随机性序列,序列的各个值之间没有任何的相关关系,序列在进⾏⽆序的随机波动,可以终⽌对该序列的分析,因为从⽩噪声序列中是提取不到任何有价值的信息的。
3. 平稳时间序列的参数特点均值和⽅差为常数,并且具有与时间⽆关的⾃协⽅差。
时间序列建模步骤:拿到被分析的时间序列数据集。
对数据绘图,观测其平稳性。
若为⾮平稳时间序列要先进⾏ d 阶差分运算后化为平稳时间序列,此处的 d 即为ARIMA(p,d,q) 模型中的 d ;若为平稳序列,则⽤ ARMA(p,q) 模型。
R语言之数据分析高级方法「时间序列」

R语言之数据分析高级方法「时间序列」作者简介Introduction姚某某本节主要总结「数据分析」的「时间序列」相关模型的思路。
「时间序列」是一个变量在连续时点或连续时期上测量的观测值的序列,它与我们以前见过的数据有本质上的区别,这个区别在于之前的数据都在一个时间的横截面上去测量、计算数据,而「时间序列」给出了一种时间轴线上纵向的视角,将时间作为自变量,测量出一系列纵向数据。
关于「时间序列」的预测模型,我所了解的常用模型有三种:1. 移动平均 2. 指数预测模型 3. ARIMA 预测模型0. 时序的分解要研究时序如何预测,首先需要将复杂的时序数据进行分解,将复杂的时序数据分解为单一的分解成分,这样能利用统计方法进行拟合,然后个个击破,最后再合成为我们需要预测的未来时序数据。
前人在这一问题上已经得到很好的结论,通过对时序数据现实意义的理解,一般将时序数据分解为四个成分:1. 水平项2. 趋势项3. 季节效应(衍生出去为周期项)4. 随机波动•水平项,即剔除时序数据的趋势影响和季节影响后,时序数据所剩的成分,它代表着时序数据在时间轴上相对稳定的一个基础值。
就像一个原点一样,在这个原点上去考虑时间所带来的趋势影响和季节影响。
•趋势项,它用于捕捉时序数据的长期变化,是逐步增长还是逐步下降。
就像在二元空间中的一个单调函数。
•季节效应,衍生出去就是周期型,在一定时间内,时序数据所包含的周期型变化。
就像在二元空间中的三角函数,如y=sinx,其数值是周而复始的。
通常在分解以上各个成分时,有两种模式,一个是乘法模型,一个是加法模型。
其中,加法模型的季节效应被认为不依赖于时间序列,二乘法模型认为季节影响随着时间会发生改变。
不过两种模型在计算时可以相通,对乘法模型作对数处理即可。
1. 移动平均这一方法很简单,只做简单讲解•所谓移动平均,就是使用时间序列中最接近的 k 期数据值的平均值作为下一个时期的预测值。
即:较小的 k 值将更快速追踪时间序列的移动,而较大的 k 值将随着时间的推移更有效地消除随机波动。
《时间序列分析——基于R》王燕,读书笔记

《时间序列分析——基于R》王燕,读书笔记笔记:⼀、检验:1、平稳性检验:图检验⽅法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列⾃相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的⾃相关系数ρ会很快地衰减向0(指数级指数级衰减),反之⾮平稳序列衰减速度会⽐较慢衰减构造检验统计量进⾏假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、⽩噪声检验(Box.test(data,type,lag=n)——lag表⽰输出滞后n阶的⽩噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”⼆、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()⾃动定阶1.3建模arima()1.4模型显著性检验:残差的⽩噪声检验Box.test();参数显著性检验t分布2、⾮平稳确定性分析2.1趋势拟合:直线、曲线(⼀般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、⾮平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3⽩噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差⾃回归模型:4.1建⽴线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差⾃相关DW检验。
dwtest()——lmtest包,增加选项order.by指定延迟因变量4.3对残差建⽴ARIMA模型5、条件异⽅差模型:异⽅差检验:LM检验ArchTest()——FinTS包,⽤ARCH、GARCH模型建模第⼀章简介统计时序分析⽅法:1、频域分析⽅法2、时域分析⽅法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的⼝径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展⽅向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异⽅差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、⾮线性场合:门限⾃回归模型,马尔科夫转移模型第⼆章时间序列的预处理预处理内容:对它的平稳性和纯随机性进⾏检验,最好是平稳⾮⽩噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述⼀个随机变量的统计特征,同样⼀个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
课后习题答案-时间序列分析及应用(R语言原书第2版)

stationary.
(b) Find the autocovariance function for {Yt}. Cov(Yt,Yt − k) = Cov(X,X) = σ2 for all t and k, free of t (and k). (c) Sketch a “typical” time plot of Yt. The plot will be a horizontal “line” (really a discrete-time horizontal line)
relation functions are the same for θ = 3 and θ = 1/3. For simplicity, suppose that the process mean is known
to be zero and the variance of Yt is known to be 1. You observe the series {Yt} for t = 1, 2,..., n and suppose that you can produce good estimates of the autocorrelations ρk. Do you think that you could determine which value of θ is correct (3 or 1/3) based on the estimate of ρk? Why or why not?
R语言读书报告心得

统计软件R语言:期末报告1、R语言特点,学习心得及学习技巧相对于其他统计软件,R语言具有以下特点,或者说是优点:其一,免费免费免费,重要内容说三次!R语言是一个免费的自由软件,它有UNIX、LINUX、MacOS和WINDOWS版本,都是可以免费下载和使用的。
可以这样说,不管你用的电脑操作系统如何,对于R语言来说都是没有影响,也就是说,R语言可以说是所有统计软件中最容易获取的;其二,各式安装包任君选择!R语言的使用,很大程度上是借助各种各样的R包的辅助,从某种程度上讲,R包就是针对于R的插件,不同的插件满足不同的需求,截至2013年3月6日,CRAN已经收录了各类包4338个。
例如用于经济计量、财经分析、人文科学研究以及人工智能。
也就是说,基本你所需要的操作都有对应的安装包来实现,在需要的时候下载即可,极大的减轻了电脑内存负担;其三,R的互动性很强。
图形输出是在另外的窗口处输出,它的输入输出窗口可以在同一个窗口进行的,输入语法中如果出现错误会马上在窗口口中得到提示,对以前输入过的命令有记忆功能,可以随时再现、编辑修改以满足用户的需要;最后也最重要的,数据可视化的功能及其强大,即使是非常复杂的数据,也有图形来实现可视化,比如lattice图像,输出的图形可以直接保存为JPG,BMP,PNG等图片格式,还可以直接保存为PDF文件。
而经过半个学期的学习,特别是老师后期着重强调的R语言的核心,函数编写功能,在R语言的学习路上,终于可以窥见冰山一角。
R语言是一个很强大的软件,它提供各种用于分析和理解数据的方法,从最基础到最前沿的,无所不包,遗憾的是我们的课程没有课本,只有课件,限制了学习的程度。
在接触了R语言之后,我购买了人民邮电出版社出版的《R 语言实战》一书,希望能系统提高自己在R语言上的运用技巧。
最后,感谢老师这一学期的辛苦教导啦!2、导入“概率统计期末成绩”数据,编写代码完成以下任务:> tsy01=read.csv(file.choose(),header=T) #读取数据,输入相应名称可以显示数据(1)计算各班平均分,标准差,中位点,极差,偏度,峰度,并做比较。
时间序列分析R语言分析

时间序列分析R语言分析R语言是一个功能强大的统计分析软件,提供了丰富的包和函数用于时间序列分析。
本文将介绍R语言的时间序列分析方法,并以一个具体的案例来说明。
首先,我们需要导入与时间序列分析相关的包,其中最常用的包是`stats`和`forecast`。
我们可以使用`library(`函数导入这两个包:```Rlibrary(stats)library(forecast)```接下来,我们需要读取时间序列数据。
在R语言中,时间序列数据可以用`ts(`函数来创建。
`ts(`函数的参数包括数据向量、开始时间和时间间隔。
例如,以下代码将创建一个时间序列数据对象`tsdata`:```R```在创建时间序列对象后,我们可以使用`plot(`函数来可视化时间序列数据。
例如,以下代码将绘制时间序列数据的折线图:```Rplot(tsdata)```接下来,我们可以使用时间序列数据进行分析和建模。
一种常用的方法是拟合ARIMA模型。
ARIMA模型是一种常用的时间序列模型,可以用于预测未来的值。
我们可以使用`auto.arima(`函数自动选择ARIMA模型的参数。
例如,以下代码将拟合时间序列数据的ARIMA模型:```Rarima_model <- auto.arima(tsdata)````auto.arima(`函数将返回一个ARIMA模型对象`arima_model`。
我们可以使用`summary(`函数查看ARIMA模型的摘要信息。
例如,以下代码将输出ARIMA模型的参数估计值和统计检验结果:```Rsummary(arima_model)```对于已经拟合好的ARIMA模型,我们可以使用`forecast(`函数来进行预测。
例如,以下代码将使用拟合好的ARIMA模型对未来10个时间点的值进行预测并返回预测结果:```Rforecast_result <- forecast(arima_model, h = 10)````forecast(`函数将返回一个预测结果对象`forecast_result`。
R语言在时间序列中的应用要点

t
1 t1
2 , E( t s ) 0, s t
qtq
若 0 0 ,该模型称为中心化 ARMA(p,q) 模型。
2. 非平稳序列分析 事实上在自然界中绝大部分序列都是非平稳的,因而对非平稳序列的分析更
普遍更重要。 对非平稳时间序列的分析法通常分为确定性时序分析和随机时序分析。这里
简要介绍常用确定性时序分析方法。 (1) 断一个序列是否平稳, 我们主要通过时序图以及自相关图进行检验。 因
为用到 ARIMA 模型的拟合和检验,所以在程序的开头会载入 tseries。 首先绘出时序图、自相关图、偏自相关图(如下) :
-7-
0 3 20 1 V0 1 0
0 10 20 30 40 50 Time
-5-
a. xt Tt St It
b. xt Tt ( St I t )
式中, Tt 代表序列的长期趋势波动; St 代表序列的季节性(周期性)变化; I t 代
表随机波动。
3. 非平稳序列的模型 事实上,许多非平稳序列差分后会显示出平稳序列的性质,称之为差分平稳
序列。对差分平稳序列可以用 ARIMA 模型拟合。 具有如下结构的模型称为求和自回归移动平均 (autoregressive integrated moving
xt
0
1 xt 1
p0
E( t ) 0,Var ( t ) Exs t 0, s t
p xt p
t
2, E( t s ) 0, s t
(2) MA 模型 (moving average)
-4-
具有如下结构的模型称为 q 阶移动平均模型,记为 MA(q) :
xt
t
1 t1
2t2
R语言时间序列分析

R语言时间序列中文教程2012特别声明:R语言是免费语言,其代码不带任何质量保证,使用R语言所产生的后果由使用者负全责。
前言R语言是一种数据分析语言,它是科学的免费的数据分析语言,是凝聚了众多研究人员心血的成熟的使用范围广泛全面的语言,也是学习者能较快受益的语言。
在R语言出现之前,数据分析的编程语言是SAS。
当时SAS的功能比较有限。
在贝尔实验室里,有一群科学家讨论提到,他们研究过程中需要用到数据分析软件。
SAS的局限也限制了他们的研究。
于是他们想,我们贝尔实验室的研究历史要比SAS长好几倍,技术力量也比SAS强好几倍,且贝尔实验室里并不缺乏训练有素的专业编程人员,那么,我们贝尔实验室为什么不自己编写数据分析语言,来满足我们应用中所需要的特殊要求呢于是,贝尔实验室研究出了S-PLUS语言。
后来,新西兰奥克兰大学的两位教授非常青睐S-PLUS的广泛性能。
他们决定重新编写与S-PLUS相似的语言,并且使之免费,提供给全世界所有相关研究人员使用。
于是,在这两位教授努力下,一种叫做R的语言在奥克兰大学诞生了。
R基本上是S-PLUS的翻版,但R是免费的语言,所有编程研究人员都可以对R语言做出贡献,且他们已经将大量研究成果写成了R命令或脚本,因而R语言的功能比较强大,比较全面。
研究人员可免费使用R语言,可通过阅读R语言脚本源代码,学习其他人的研究成果。
笔者曾有幸在奥克兰大学受过几年熏陶,曾经向一位统计系的老师提请教过一个数据模拟方面的问题。
那位老师只用一行R语句就解答了。
R语言的强大功能非常令人惊讶。
为了进一步推广R语言,为了方便更多研究人员学习使用R语言,我们收集了R 语言时间序列分析实例,以供大家了解和学习使用。
当然,这是非常简单的模仿练习,具体操作是,用复制粘贴把本材料中R代码放入R的编程环境;材料中蓝色背景的内容是相关代码和相应输出结果。
经过反复模仿,学习者便能熟悉和学会。
需要提醒学习者的是:建议学习者安装了R语言编程,再继续阅读本材料;执行R 命令时,请删除命令的中文注解,没使用过在命令中加入中文;如果学习者是初次接触R或者Splus,建议先阅读<<R语言样品比较应用举例>>,如果学习者比较熟悉R语言,还可以阅读优秀时间序列读物Ecomometrics in R,也可以上QuickR 网站。
时间序列分析-读书笔记
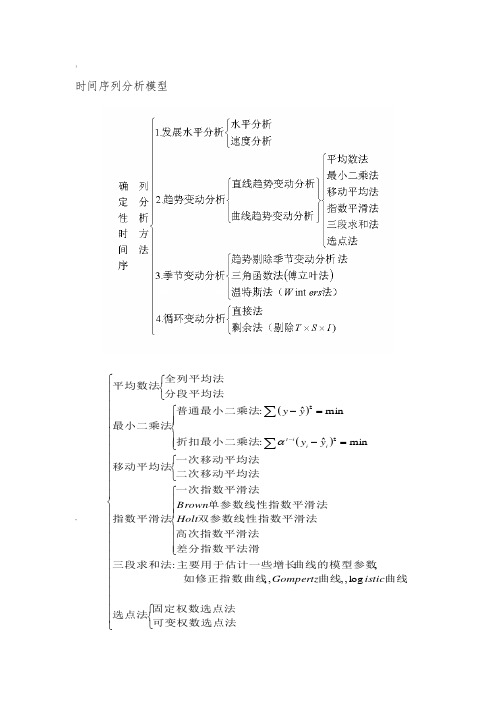
)时间序列分析模型~()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧=-=-⎩⎨⎧∑∑-可变权数选点法固定权数选点法选点法曲线曲线如修正指数曲线曲线的模型参数主要用于估计一些增长三段求和法差分指数平法滑高次指数平滑法双参数线性指数平滑法单参数线性指数平滑法一次指数平滑法指数平滑法二次移动平均法一次移动平均法移动平均法折扣最小二乘法普通最小二乘法最小二乘法分段平均法全列平均法平均数法isticGompertzHoltBrownyyyyiiitlog,,,,,:minˆ:minˆ:22α1. 时间序列作用:描述系统运行规律预测对特殊政策或事件的影响加以估计2. ~3. 时间序列分类:确定时间序列,随机时间序列4. 确定时间序列的分析方法:它不计算时间序列的随机变动值,建模的目的是要消除随机变动的影响,揭示预测对象随时间变动的规律性用于预测,这是确定性时间序列和随机时间序列分析的区别。
趋势外推法:有明显上升或下降趋势,没有明显季节变动,能用函数表示移动平均法:一次移动平均:大体成水平变动,平滑公式,预测公式两次移动平均:线性上升或下降,预测公式指数平滑法:一次指数平滑法:水平变动,平滑公式,预测公式Brown 单参数线性指数平滑法:线性上升或下降,平滑公式,预测公式 ?Holt 双参数线性指数平滑法: 线性上升或下降,平滑公式,预测公式 参数选择主观性较强,不能提供置信区间信息季节调整术:试图度量序列中的季节变动,并利用这些指数剔除序列中的季节变动。
4.随机时间序列分析:平稳时间序列分析严平稳的概率分布与时间的平移无关。
宽平稳序列的均值随时间的平移而不变,自协方差仅与时间间隔有关自回归模型、滑动平均模型和自回归滑动平均模型分析平稳的时间序列的规律。
%自回归模型:如果时间序列() ,2,1=t X t 是平稳的且数据之间前后有一定的依存关系,即t X 与前面p t t t X X X --- ,,21有关与其以前时刻进入系统的扰动(白噪声)无关,具有p 阶的记忆,描述这种关系的数学模型就是p 阶自回归模型可用来预测:t p t p t t t a X X X X ++++=---ϕϕϕ 2211滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21无关与其以前时刻进入系统的扰动(白噪声)有关,具有q 阶的记忆,描述这种关系的数学模型就是q 阶滑动平均模型可用来预测:q t q t t t t a a a a X ---+++-=θθθ 2211回归滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21有关且与其以前时刻进入系统的扰动(白噪声)也有关,则此系统为自回归移动平均系统,预测模型为:=+++----p t p t t t X X X X ϕϕϕ 2211q t q t t t a a a a ---+++-θθθ 2211非平稳时间序列分析!用模型来预测应是要把趋势和波动综合考虑进来,是它们的叠加。
R语言时间序列分析

R语言时间序列分析
时间序列分析是R语言中一种常用的数据分析方法,它用于分析随着时间的变化而变化的值。
它可以用来跟踪历史事件,识别趋势,预测未来发展,以及进行更多的数据分析工作。
R语言提供了一系列的时间序列分析工具,可以用于非常多领域,如金融、工程、统计分析等。
这篇文章将介绍时间序列分析的基本概念,以及如何使用R语言进行时间序列分析的相关知识和技巧。
首先,让我们介绍时间序列数据。
时间序列数据是随着时间的变化而变化的数据,它们可以是连续的(如每隔一分钟)或离散的(如每年)。
时间序列数据可以用来描述不同的理论模型,如线性模型、指数模型和指数平滑模型等。
接下来,让我们来看看R语言有哪些时间序列分析的工具。
R语言提供了一系列的时间序列分析工具,包括ts(函数,它可以创建时间序列对象;stl(函数,它可以分解不同的时间序列;forecast(函数,可以用来预测时间序列;plot(函数,可以将时间序列可视化,以便进行分析等。
时间序列分析学习心得体会

时间序列分析学习心得体会时间序列分析是一门涉及到时间序列的预测和分析的学科。
它涉及到一系列数据,按照时间顺序排列,我们可以通过这些数据来推测未来的走向以及过去的变化。
时间序列分析具有广泛的应用领域,比如股票的走势、天气的预报和经济的波动等等。
在我学习时间序列分析的过程中,我深深地感受到了它的优雅之处,并从中获得了许多经验和体会。
首先,时间序列分析需要对数据进行仔细检查。
对时间序列数据进行检查,可以发现一些异常和错误,比如重复的数据、异常的数据点或者缺失的数据点等等。
我们需要通过做出异常检验、趋势检验等来确定数据质量,以保证最终得到的结果是准确的。
其次,时间序列分析需要对数据进行变换。
对数据进行转化和变换可以使数据与所需的分析方法相适应,方便我们进行后续的处理。
可以采用加法模型或乘法模型,根据数据的性质的不同做出适当的选择。
通过对数据的变换,我们可以在保证数据的准确性的同时,更好地解读它们。
然后,时间序列分析需要选择恰当的模型。
时间序列分析涉及到的模型有很多种,比如滑动平均模型、指数平滑模型、ARIMA模型等等。
在选择模型的过程中,我们需要考虑数据的性质,比如是否有趋势和季节性。
同时,我们需要对各种模型进行比较,选出最适合的模型,以得到准确的预测结果。
最后,时间序列分析需要对模型进行评估和预测。
我们需要对模型进行验证,即检验模型在历史数据上的拟合情况。
同时,我们还需要对模型的预测结果进行评估,以确定模型的准确性和预测能力。
我们需要使用各种检验方法,比如平均绝对误差、平均绝对百分比误差等等,进行评估和比较。
在我学习时间序列分析的过程中,我深深地感受到了这门学科的复杂性和精妙性。
时间序列分析需要对数据进行仔细检查和变换,选择恰当的模型,进行预测和评估。
只有在这个过程中,我们才能够得到准确的预测结果,为我们的决策提供依据。
尽管这个过程可能会较为耗费时间和精力,但是当我们得到准确的结果时,我们会感到收获颇丰,也将带来实际应用领域的实际价值。
时间序列分析-读书笔记

时间序列分析模型~()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧=-=-⎩⎨⎧∑∑-可变权数选点法固定权数选点法选点法曲线曲线如修正指数曲线曲线的模型参数主要用于估计一些增长三段求和法差分指数平法滑高次指数平滑法双参数线性指数平滑法单参数线性指数平滑法一次指数平滑法指数平滑法二次移动平均法一次移动平均法移动平均法折扣最小二乘法普通最小二乘法最小二乘法分段平均法全列平均法平均数法isticGompertzHoltBrownyyyyiiitlog,,,,,:minˆ:minˆ:22α1. 时间序列作用:描述系统运行规律预测对特殊政策或事件的影响加以估计2. 时间序列分类:确定时间序列,随机时间序列3. 确定时间序列的分析方法:它不计算时间序列的随机变动值,建模的目的是要消除随机变动的影响,揭示预测对象随时间变动的规律性用于预测,这是确定性时间序列和随机时间序列分析的区别。
趋势外推法:有明显上升或下降趋势,没有明显季节变动,能用函数表示%移动平均法:一次移动平均:大体成水平变动,平滑公式,预测公式两次移动平均:线性上升或下降,预测公式指数平滑法:一次指数平滑法:水平变动,平滑公式,预测公式Brown 单参数线性指数平滑法:线性上升或下降,平滑公式,预测公式Holt 双参数线性指数平滑法: 线性上升或下降,平滑公式,预测公式 参数选择主观性较强,不能提供置信区间信息季节调整术:试图度量序列中的季节变动,并利用这些指数剔除序列中的季节变动。
4.随机时间序列分析:平稳时间序列分析严平稳的概率分布与时间的平移无关。
宽平稳序列的均值随时间的平移而不变,自协方差仅与时间间隔有关*自回归模型、滑动平均模型和自回归滑动平均模型分析平稳的时间序列的规律。
自回归模型:如果时间序列() ,2,1=t X t 是平稳的且数据之间前后有一定的依存关系,即t X 与前面p t t t X X X --- ,,21有关与其以前时刻进入系统的扰动(白噪声)无关,具有p 阶的记忆,描述这种关系的数学模型就是p 阶自回归模型可用来预测:t p t p t t t a X X X X ++++=---ϕϕϕ 2211滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21无关与其以前时刻进入系统的扰动(白噪声)有关,具有q 阶的记忆,描述这种关系的数学模型就是q 阶滑动平均模型可用来预测:q t q t t t t a a a a X ---+++-=θθθ 2211回归滑动平均模型:如果时间序列() ,2,1=t X t 是平稳的与前面p t t t X X X --- ,,21有关且与其以前时刻进入系统的扰动(白噪声)也有关,则此系统为自回归移动平均系统,预测模型为:=+++----p t p t t t X X X X ϕϕϕ 2211q t q t t t a a a a ---+++-θθθ 2211非平稳时间序列分析用模型来预测应是要把趋势和波动综合考虑进来,是它们的叠加。
R学习日记——分解时间序列(非季节性数据)
R学习⽇记——分解时间序列(⾮季节性数据)分解时间序列,就是将⼀个时间序列拆分成不同的构成元件。
⼀般序列(⾮季节性序列)包含⼀个趋势部分和⼀个不规则部分(也就是随机部分),⽽如果是⼀个季节性序列,除以上两个外,还有季节性部分。
在此,我们先讲——⾮季节性数据的分解。
⼀个⾮季节性时间序列包含⼀个趋势部分和⼀个不规则部分。
分解时间序列即为试图把时间序列拆分成这些成分,也就是说,需要估计趋势的和不规则的这两个部分。
为了估计出⼀个⾮季节性时间序列的趋势部分,使之能够⽤相加模型进⾏描述,最常⽤的⽅法便是平滑法,⽐如计算时间序列的简单移动平均。
这时,我们需要使⽤“TTR”程序包中的SMA()函数。
使⽤ SMA()函数时,你需要通过参数“n” 指定来简单移动平均的跨度。
例如,计算跨度为 5 的简单易懂平均,我们在 SMA()函数中设定n=5。
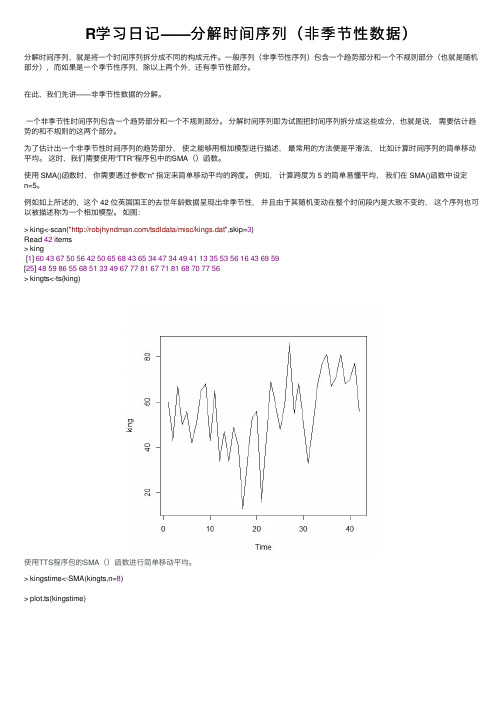
例如如上所述的,这个 42 位英国国王的去世年龄数据呈现出⾮季节性,并且由于其随机变动在整个时间段内是⼤致不变的,这个序列也可以被描述称为⼀个相加模型。
如图:> king<-scan("/tsdldata/misc/kings.dat",skip=3)Read 42 items> king[1] 604367505642506568436534473449411335535616436959[25] 485986556851334967778167718168707756> kingts<-ts(king)使⽤TTS程序包的SMA()函数进⾏简单移动平均。
> kingstime<-SMA(kingts,n=8)> plot.ts(kingstime)。
时间序列分析及应用 R语言原书第二版,潘红宇 等译第二章 时间序列的基本概念汇编

延迟k自协方差函数的估计
可进一步推导出方差、延迟k自相关系数的估 计值。
nk
γˆ(k)
t 1(xt
x)(xt k nk
x) 0
k
n为整数
纯随机序列的定义
n 纯随机序列{Xt}也称为白噪声序列,它满 足如下两条性质
(1)EX t , t T
(2)
(t,
s)
2,t s
第二章
时间序列的基本概念
概率分布
n 概率分布的意义
n 随机变量族的统计特性完全由它们的联合分布 函数或联合密度函数决定
n 时间序列{Xt} 的概率分布族的定义 {Ft1,t2,,tm (x1, x2,, xm) 正整数 m(1,2,,),t1,t2,,tm T}
n 实际应用的局限性 序列的联合分布几乎不
决定时间序列特性的统计规律不随着时 间的变化而改变.
平稳时间序列的统计定义
n 满足如下条件的序列称为严平稳序列
正整数m, t1,t2,,tm T,正整数,有 Ft1 ,t2 tm ( x1 , x 2 , , x m ) Ft1 ,t2 tm ( x1 , x 2 , , x m )
同.
随机游走的方差随着时间线性地增长.
计算该模型的均值, 方差, 自协方差函数, 自相关函数 !
自协方差函数为: 自相关函数为:
0, t
s
,
t,
s
T
简记为 Xt WN (, 2 )
当白噪声{Xt }是独立序列时,称{Xt } 为独立白噪声;
当 =0时,称{Xt }为零均值白噪声; 当=0, 2 =1时,称{Xt}为标准白噪声;
对独立白噪声,当Xt 服从正态分布时,称{Xt}为 正态白噪声。
R语言在时间序列分析中的应用4.19

R语言在时间序列中的应用2013.04.19 未完成written by MiltonDeng,from department of Statistics, XMU一、数据的读入与时间序列化时间序列数据是R语言中一种特定形式的数据类型。
R语言中有许多专门针对时间序列数据编制的函数。
但在运用这些函数前,首先需要对序列进行时间序列化,即运用将一组数据转化为时间序列数据这种数据形式。
ts(data = NA, start = 1, end = numeric(), frequency = 1 )-data :要进行时间序列化的向量。
如果是矩阵,会按列分别处理。
-start :起始时点。
-end :结束时点。
-frequency :频度。
取12时自动识别为月,4时自动识别为季度。
首先,应该注意,与多元统计等统计分析不同,单变量时间序列根本上是一个向量,而不是一个矩阵,或者一个表。
因此,在读入时间序列数据时,常常会有一些不必要的麻烦。
由于数据整理时,数据编排往往不一致,所以应该注意以何种方式读入时间序列数据。
以txt文件为例,假设这组时间序列为“5,4,2,3,6,1”,在文件中以如下方式出现(人大出版社,王燕老师的《应用时间序列分析》中的数据均以这种形式出现):5 4 23 6 1如果以read.table() 读入,读入的是一个2*3的矩阵,如果直接以ts() 时间序列化,R会认为这是3列数据,将对它们分别生成3组时间序列数据。
下面提供两种方法:(1)以scan()直接读入为向量。
(2)以read.table()读入这个矩阵为D,然后D=t(D) #因为是以行录入,所以要先转置D=as.vector(D) #将矩阵线性化为向量D二、描述时间序列对于单组时间序列:(1)ts.plot(D) #可以直接对未ts的向量绘图(2)ts(D); plot(D)如果D是一个矩阵或frame,可以对多个序列画在同一张图里。
时间序列心得体会

时间序列心得体会时间序列我记得再学习时间序列时,花了整整一个星期,每天只看这个,终于在一天的下午给弄明白了,这是本人学习的时候的心得,只要开窍了比就会觉得很简单,事实上却是如此,我的好多同学,在考玩以后,都有这个体会,看样子估计你时大学生,不是研究生吧(弱弱的估计一下)。
本科生学习时间序列的时候我记得好像用不找SAS,不知道你们怎么样,现把我考试时的情况说一下,因为时间序列对于本科生有点吃力,这门科时在大四开,好多学生为了找工作,没有更多的时间学习,有的学校就是开卷考试,当然闭卷的话就相对简单了,老师都会画出范围的。
AMIAR不知道写没写对,值考一员的二元估计不可能,多元的估计时研究生要学的,所以别担心只要在考试前画上一个星期,我保障没有问题。
时间序列分析预测法优缺点时间序列分析预测法有两个特点:①时间序列分析预测法是根据市场过去的变化趋势预测未来的发展,它的前提是假定事物的过去会同样延续到未来。
事物的现实是历史发展的结果,而事物的未来又是现实的延伸,事物的过去和未来是有联系的。
市场预测的时间序列分析法,正是根据客观事物发展的这种连续规律性,运用过去的历史数据,通过统计分析,进一步推测市场未来的发展趋势。
市场预测中,事物的过去会同样延续到未来,其意思是说,市场未来不会发生突然跳跃式变化,而是渐进变化的。
时间序列分析预测法的哲学依据,是唯物辩证法中的基本观点,即认为一切事物都是发展变化的,事物的发展变化在时间上具有连续性,市场现象也是这样。
市场现象过去和现在的发展变化规律和发展水平,会影响到市场现象未来的发展变化规律和规模水平;市场现象未来的变化规律和水平,是市场现象过去和现在变化规律和发展水平的结果。
需要指出,由于事物的发展不仅有连续性的特点,而且又是复杂多样的。
因此,在应用时间序列分析法进行市场预测时应注意市场现象未来发展变化规律和发展水平,不一定与其历史和现在的发展变化规律完全一致。
随着市场现象的发展,它还会出现一些新的特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《时间序列分析及应用:R语言》读书笔记姓名:石晓雨学号:1613152019(一)、时间序列研究目的主要有两个:认识产生观测序列的随机机制,即建立数据生成模型;基于序列的历史数据,也许还要考虑其他相关序列或者因素,对序列未来的可能取值给出预测或者预报。
通常我们不能假定观测值独立取自同一总体,时间序列分析的要点是研究具有相关性质的模型。
(二)、下面是书上的几个例子1、洛杉矶年降水量问题:用前一年的降水量预测下一年的降水量。
第一幅图是降水量随时间的变化图;第二幅图是当年降水量与去年降水量散点图。
win.graph(width=4.875, height=2.5,pointsize=8) #这里可以独立弹出窗口data(larain) #TSA包中的数据集,洛杉矶年降水量plot(larain,ylab='Inches',xlab='Year',type = 'o') #type规定了在每个点处标记一下win.graph(width = 3,height = 3,pointsize = 8)plot(y = larain,x = zlag(larain),ylab = 'Inches',xlab = 'Previous Year Inches')#zlag 函数(TSA包)用来计算一个向量的延迟,默认为1,首项为NA从第二幅图看出,前一年的降水量与下一年并没有什么特殊关系。
2、化工过程win.graph(width = 4.875,height = 2.5,pointsize = 8)data(color)plot(color,ylab = 'Color Property',xlab = 'Batch',type = 'o')win.graph(width = 3,height = 3,pointsize = 8)plot(y = color,x = zlag(color),ylab = 'Color Property',xlab = 'Previous Batch Color Property')len <- length(color)cor(color[2:len],zlag(color)[2:len])#相关系数>0.5549第一幅图是颜色属性随着批次的变化情况。
第二幅图画一下前一批次与本批次是散点图。
上面的图显示了稍微向上的趋势,即数值较大的后一批次也趋向于更大的数值。
但是并不明显,相挂系数只有0.5549.3、加拿大野兔年丰度win.graph(width=4.875, height=2.5,pointsize=8)data(hare)plot(hare,ylab='Abundance',xlab='Year',type='o')win.graph(width=3, height=3,pointsize=8)plot(y=hare,x=zlag(hare),ylab='Abundance',xlab='Previous Year Abundance') len <- length(hare)cor(hare[2:len],zlag(hare)[2:len])>0.7026看一下下面的图,明显有周期性质。
上面的图看出前一年的数值跟本年度数值相关关系较大。
相关系数为0.7026.4、艾奥瓦州迪比克市月平均气温非常明显的周期性。
季节性模式。
5、滤油器月销售量win.graph(width=4.875, height=2.5,pointsize=8)data(oilfilters)plot(oilfilters,type='o',ylab='Sales')win.graph(width=4.875, height=2.5,pointsize=8)plot(oilfilters,type='l',ylab='Sales')Month=c("J","A","S","O","N","D","J","F","M","A","M","J")#注意这里是从1983年7月到1987年6月points(oilfilters,pch=Month)plot(oilfilters,type='l',ylab='Sales')points(y=oilfilters,x=time(oilfilters),pch=as.vector(season(oilfilters)))#这里的season函数的返回值取决于传入数值“向作者提供数据时,经理说没有理由认为销售量存在季节性。
”“假如各年1月与1月的数据之间存在关联趋势,2月与2月的数据之间存在关联趋势,那么就有季节性。
”上面的图作者说没有显示明显的季节性。
其实……还好,季节性比较明显了已经。
在加上月份的标识之后,确实比原来更能显示出季节性规律。
总之,恰当和有益于发现特定模式的绘图方法,有利于找到符合时间序列数据的合适模型。
(三)、建模策略给时间序列寻找合适的模型并非易事,多步建模策略很有用,包括三个可反复使用的主要步骤:1、模型识别2、模型拟合3、模型诊断模型识别就是在时间序列模型类中选择适合观测值的模型。
进一步可以观察时间序列图,计算一些统计量。
选取的模型是有待考证的,选取原则是能表示模型的前提下选取参数少的。
第二步就是用数据将将选取模型中的参数估计出来,估计方法是最小二乘挥着极大似然。
最后就是对模型进行质量评估。
针对一些问题对模型进行估计,看模型是否合理:比如模型对数据的拟合程度有多好,模型前提是否满足等。
如果没有不足之处,就可以进行预测等任务,如果有不足之处,针对不足之处寻找其他模型,再进行上面三个步骤。
(四)、历史上的时间序列图名言:“时间序列图是图形设计最常用的形式,其一个维度沿着秒、分、时、日、周、月、年、乃至千年等规则的时间节律延伸,时间标度的自然顺序赋予了这种设计以解释的力量和效率,这一点在其他图形设计上了无痕迹。
”(五)、笔记:第一章简介统计时序分析方法:1、频域分析方法2、时域分析方法步骤:1、观察序列特征2、根据序列特征选择模型3、确定模型的口径4、检验模型,优化模型5、推断序列其它统计性质或预测序列将来的发展时域分析研究的发展方向:1、AR,MA,ARMA,ARIMA(Box-Jenkins模型)2、异方差场合:ARCH,GARCH等(计量经济学)3、多变量场合:“变量是平稳”不再是必需条件,协整理论3、非线性场合:门限自回归模型,马尔科夫转移模型第二章时间序列的预处理预处理内容:对它的平稳性和纯随机性进行检验,最好是平稳非白噪声的序列1、特征统计量1.1概率分布分布函数或密度函数能够完整地描述一个随机变量的统计特征,同样一个随机变量族{Xt}的统计特性也完全由它们的联合分布函数或联合密度函数决定。
1.2特征统计量:均值Ex方差σ2自协方差函数(γ)和自相关系数(ρ):比较的是1个事件不同时期之间的相互影响程度2、平稳的时间序列2.1定义严平稳:随机变量族的统计性质完全有它们的联合概率分布族决定,若任意的t下的联合概率分布族相等,则认为该序列是严平稳的宽平稳:统计性质主要由它的低阶矩决定:1)Ex2<无穷2)均值为常数:Ex=μ(μ为常数)3)自协方差和自相关系数只依赖于时间的平移长度而与时间的起止点无关满足以上3点则称为宽平稳时间序列(弱平稳或者二阶平稳)一、检验:1、平稳性检验:图检验方法:时序图检验:该序列有明显的趋势性或周期性,则不是平稳序列自相关图检验:(acf函数)平稳序列具有短期相关性,即随着延迟期数k的增加,平稳序列的自相关系数ρ会很快地衰减向0(指数级衰减),反之非平稳序列衰减速度会比较慢构造检验统计量进行假设检验:单位根检验adfTest()——fUnitRoots包2、纯随机性检验、白噪声检验(Box.test(data,type,lag=n)——lag表示输出滞后n阶的白噪声检验统计量,默认为滞后1阶的检验统计量结果)1、Q统计量:type=“Box-Pierce”2、LB统计量:type=“Ljung-Box”二、模型1、ARMA平稳序列模型1.1平稳性检验1.2ARMA的p、q定阶——acf(),pacf(),auto.arima()自动定阶1.3建模arima()1.4模型显著性检验:残差的白噪声检验Box.test();参数显著性检验t分布2、非平稳确定性分析2.1趋势拟合:直线、曲线(一般是多项式,还有其它函数)2.2平滑法移动平均法:SMA()——TTR包指数平滑法:HoltWinters()3、非平稳随机性分析3.1ARIMA1平稳性检验,差分运算2拟合ARMA3白噪声检验3.2疏系数模型arima(p,d,f)3.3季节模型可以叠加的模型4、残差自回归模型:4.1建立线性模型4.2对滞后的因变量间拟合线性模型,对模型做残差自相关DW检验。
dwtest()——lmtest 包,增加选项order.by指定延迟因变量4.3对残差建立ARIMA模型5、条件异方差模型:异方差检验:LM检验ArchTest()——FinTS包,用ARCH、GARCH 模型建模。
