结构力学概念题解72-150
结构力学习题解答(第二章)
W 3 5 (2 7 6) 5
分析:刚片ACD与刚片DEG都固接在地基上,组成一个几 何不变体系且无多余约束,而铰D、链杆BD、BF、DF均是 整个体系的内部联系,并非刚片ACD、刚片DEG与地基构 成几何不变体系的必要约束,对整个体系而言是多余约束, (一个铰相当于2个约束)。 结论:有5个多余约束的几何不变体系,
W 2 8 ( 3) 0 - 13
分析:由于该体系与地基是由三根既不相互平行也不相交于 一点的链杆连接,分析时可先抛开地基。ABF可视为一刚片, 在其基础上依次增加二元体BCF、CGA后形成扩大刚片Ⅰ; DEH可视为一刚片,在其基础上增加二元体DCH后形成扩 大刚片Ⅱ,扩大刚片Ⅰ、Ⅱ由铰C和链杆GE连接,满足两刚 片规则。 结论:无多余约束的几何不变体系
分析:刚片AB、AC与地基由铰A、B、C连接,满足 三钢片规则,形成一个几何不变体系,故链杆DE为多 余约束。 结论:有一个多余约束的几何不变体系
H G F E B A C D M N
W 2 15 (27 3) 0
分析:ABC可视为一刚片,在其基础上依次增加二元体 BFC、FDC、FED、FGE、GHE后形成扩大刚片Ⅰ,同理 HMN可视为刚片Ⅱ,刚片Ⅰ、Ⅱ由铰H和链杆DM连接,由 两刚片规则可知AHN为几何不变体系,视AHN为一大刚片, 它与地基由两刚片规则连接而成。 结论:无多余约束的几何不变体系
W 3 8 (2 10 4) 0
N
W 2 6 (8 4) 0
分析:把地基及其上的固定铰 支座链杆视为刚片Ⅰ,链杆DE 视为刚片Ⅱ,铰接三角形BCE 视为刚片Ⅲ,ⅠⅡ通过链杆1、 AD连接,形成虚铰M,ⅠⅢ通过 链杆2、AB连接,形成虚铰 C,ⅡⅢ通过链杆DB、FE连接, 形成虚铰N,铰C、M、N不共线, 满足三钢片规则。
结构力学习题及答案

结构力学习题及答案结构力学习题及答案结构力学是工程学中的重要学科之一,它研究物体在外力作用下的变形和破坏。
在工程实践中,结构力学的应用广泛,涉及到建筑、桥梁、航空航天等领域。
在学习结构力学时,练习解答一些习题是非常重要的,下面我将给大家提供一些常见的结构力学习题及其答案。
题目一:简支梁的弯矩计算已知一根长度为L的简支梁,两端受到均布载荷q。
求梁的中点处的弯矩M。
解答一:根据简支梁的受力分析,可以得出梁的弯矩与距离中点的距离x之间的关系为M=qL/8-x^2/2,其中x为距离中点的距离。
因此,中点处的弯矩M=qL/8。
题目二:悬臂梁的挠度计算已知一根长度为L的悬臂梁,端部受到集中力F作用。
求梁的端部挠度δ。
解答二:根据悬臂梁的受力分析,可以得出梁的端部挠度与力F之间的关系为δ=FL^3/3EI,其中F为作用力,E为梁的杨氏模量,I为梁的截面惯性矩。
因此,梁的端部挠度δ=FL^3/3EI。
题目三:刚度计算已知一根长度为L的梁,截面形状为矩形,宽度为b,高度为h,梁的杨氏模量为E。
求梁的刚度K。
解答三:梁的刚度可以通过计算梁的弯曲刚度和剪切刚度得到。
弯曲刚度Kb可以通过梁的截面惯性矩I和杨氏模量E计算得到,即Kb=E*I/L。
剪切刚度Ks可以通过梁的剪切模量G和梁的截面面积A计算得到,即Ks=G*A/L。
因此,梁的刚度K=Kb+Ks=E*I/L+G*A/L。
题目四:破坏载荷计算已知一根长度为L的梁,截面形状为圆形,直径为d,梁的杨氏模量为E。
求梁的破坏载荷P。
解答四:梁的破坏载荷可以通过计算梁的破坏弯矩和破坏挠度得到。
破坏弯矩Mf可以通过梁的截面惯性矩I和杨氏模量E计算得到,即Mf=π^2*E*I/L^2。
破坏挠度δf可以通过梁的破坏弯矩Mf和梁的刚度K计算得到,即δf=Mf/K。
因此,梁的破坏载荷P=Mf/L=π^2*E*I/L^3。
结构力学是一门综合性较强的学科,掌握结构力学的基本原理和解题方法对于工程师来说非常重要。
结构力学考试题及答案
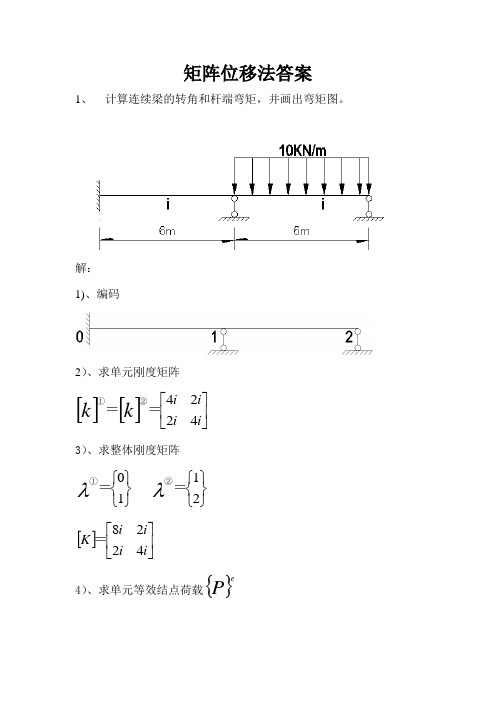
矩阵位移法答案1、 计算连续梁的转角和杆端弯矩,并画出弯矩图。
解: 1)、编码2)、求单元刚度矩阵[][]⎥⎦⎤⎢⎣⎡i i i i k k 4224==②①3)、求整体刚度矩阵⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧2110==②①λλ[]⎥⎦⎤⎢⎣⎡i i i i K 4228=4)、求单元等效结点荷载{}P e{}{}m KN q q P P l l F F ⋅⎭⎬⎫⎩⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎭⎬⎫⎩⎨⎧=30301211210022②①{}{}{}F P P P eee-=={}{}m KN P P ⋅⎭⎬⎫⎩⎨⎧-⎭⎬⎫⎩⎨⎧303000==②①5)、集成结构等效结点荷载向量{}P{}m KN P ⋅⎭⎬⎫⎩⎨⎧-=30306)、解方程[]{}{}P K =∆ii i i i 717545303042282121⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎥⎦⎤⎢⎣⎡ 7)、求各杆的杆端内力{}F e{}[]{}{}F k F P e e e e +∆=单元① {}m KN i i i i i F ⋅⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=71.2586.120074504224①单元② {}m KN i i i i i i F ⋅⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=071.2530307757454224-②8)、做M 图2、 求图示刚架的M 、Q 、N 图。
解:1)、整理原始数据及编码2)、求局部坐标系中的单元刚度矩阵{}K e2442101.2,300,20,100cm KN E cm I cm A cm L ⨯====mKN LEI m KN L EI KN L EI m KN LEI m KN L EA ⋅⨯=⨯=⨯=⋅⨯=⨯=2232222106.122106.7512108.376102.2541042003)、计算整体坐标系中的单元刚度矩阵{}k e单元①和单元③单元②{}{}{}2102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200⨯===⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------k k k ③②①[][]I T =,= 0α[][][][]②②①①=,=kk k k90=α[]⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--=100000001000010000000100000001000010T [][][][]2102.2508.376.1208.370420000420008.3716.758.3706.756.1208.372.2508.370420*********.3706.758.3706.75⨯==⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------T k T k T ②②4)、用单元集成法形成整体刚度矩阵{}K⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧000321000321321000===③②①λλλ {}2106.7508.3702.435108.3706.8475⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=K5)、求单元等效结点荷载{}P e{}{}[]833.050833.050-=-=TF P P①①{}{}[]833.050833.050-=TP P ①①=6)、用单元集成法形成整体结构的等效结点荷载{}P{}[]TP 833.050-=7)、形成整体结构的综合结点荷载{}[]TF 402000={}{}[]TP F 167.392500=+8)、解方程[]{}{}{}0F P K +=∆[][]I T =,= 0α⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--167.39250106.7508.3702.435108.3706.84753212 432110924.51575.0232.0-⨯⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆ 9)、求各杆的杆端内力{}F e{}[][]{}{}F T k F P e e e e +∆=单元①{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧----+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=700.13193.24744.9492.5193.14744.9833.050833.05010924.51575.0232.000010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=①①①①F T k F P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=455.6452.19150.24997.12452.19150.2400000010000924.51575.0232.010421000010000100000001000000010000102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=②②②②F T kF P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=760.6062.20744.9302.13062.20744.900000010000924.51575.0232.010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=③③③③F T k F P结构动力学作业答案1、求图示结构的自振频率。
结构力学计算题及结构力学练习题含答案

结构力学计算题及结构力学练习题含答案结构力学是研究结构在外力作用下内力和变形规律的科学,以下是一篇结构力学计算题及练习题,包括答案的示例。
结构力学计算题题目:一简支梁AB,跨度为4米,受到均布荷载q=2 kN/m,梁的截面惯性矩I=1.2×10^6 mm^4,弹性模量E=210 GPa。
求梁的最大弯矩和最大挠度。
解题步骤:1. 计算梁的最大弯矩Mmax。
根据简支梁受均布荷载的弯矩公式:\[ M_{max} = \frac{ql^2}{8} \]代入已知数据:\[ M_{max} = \frac{2 \times 4^2}{8} = 4 \text{ kN·m} \]2. 计算梁的最大挠度y_max。
根据简支梁受均布荷载的挠度公式:\[ y_{max} = \frac{ql^4}{384EI} \]代入已知数据:\[ y_{max} = \frac{2 \times 4^4}{384\times 1.2 \times 10^6 \times 210 \times 10^9} = 0.00017 \text{ m} = 0.17 \text{ mm} \]答案:梁的最大弯矩Mmax为4 kN·m,最大挠度y_max为0.17 mm。
---结构力学练习题1. 一悬臂梁CD,长度为3米,受到集中力F=5 kN作用在自由端,梁的截面惯性矩I=1.5×10^6 mm^4,弹性模量E=200 GPa。
求悬臂梁的最大弯矩和最大挠度。
答案:最大弯矩Mmax为5 kN·m,最大挠度y_max为0.013 mm。
2. 一连续梁EF,跨度为6米,分为两段,每段长度为3米,中间有一支点G。
梁上受到均布荷载q=1.5kN/m,梁的截面惯性矩I=2×10^6 mm^4,弹性模量E=220 GPa。
求支点G的反力及中间梁段的最大弯矩。
答案:支点G的反力为4.5 kN,中间梁段的最大弯矩为2.25 kN·m。
结构力学测试题与答案

结构力学测试题与答案结构力学是研究物体受力情况和引起变形的学科。
这门学科中,一些基本的概念和原理十分重要,例如弹性力学、静力学、动力学、稳定性等等。
以下是一些常见的结构力学测试题和答案,希望能帮助你更好地理解该学科。
第一部分:弹性力学问题1什么是弹性模量?答案1弹性模量是一个表示某种物质弹性特性的量。
弹性模量越大,该物质的变形能力就越小,即它越趋于刚性。
弹性模量通常用于描述材料在受压或拉伸时如何变形。
在弹性极限内,当受到一定的外力后,物质会返回原来的形态。
问题2材料的体积模量和弹性模量之间有什么区别?答案2材料的体积模量与弹性模量都是描述材料的弹性性质的物理量。
区别在于,体积模量描述的是物质在受到均匀的压缩时的应力和应变关系,而弹性模量描述的是物质在受力时的弹性特性,即材料的变形情况与外部力之间的关系。
第二部分:静力学问题3什么是力矩?答案3力矩是一个描述物体旋转的物理量。
力矩通常用于描述一个物体受到力作用时的转动效应。
力矩可以定义为叉乘的结果,因此它的方向与物体转动方向相同。
问题4请描述质心与重心之间的区别。
质心是一个特定形状的物体在其整个质量范围内的重心位置。
重心是描述物体受到重力作用时整体所受的引力方向和大小的物理量。
质心定义为物体各部分质量线之交点。
重心是指物体的整体平衡位置。
第三部分:动力学问题5什么是牛顿第二定律?答案5牛顿第二定律是描述力学系统的动力学定律之一。
它提出,物体的加速度是与物体所受的合力成正比的,与物体质量成反比。
也就是说,当一个物体受到作用力时,它的加速度会随着力的增大而增大,但也会随着物体的质量增加而减小。
问题6机械能守恒定律是什么意思?答案6机械能守恒定律是指,在一个封闭的机械系统中,当一个物体在重力作用下从高处下落时,它的动能将变大,其位能将逐渐减小,但机械总能量(动能和位能之和)始终不变。
因此,机械能守恒定律也可以被表述为“能量在系统中是守恒的。
”第四部分:稳定性问题7简要描述一下稳定性的概念。
结构力学习题答案

结构力学习题答案结构力学习题答案结构力学是工程力学的一个重要分支,主要研究物体在受力情况下的变形和应力分布。
在学习结构力学的过程中,我们常常会遇到各种各样的习题,通过解答这些习题可以更好地理解和掌握结构力学的基本原理和方法。
本文将为大家提供一些常见结构力学习题的答案,希望对大家的学习有所帮助。
一、静力平衡问题1. 一个简支梁上有一均布载荷,求梁的反力分布。
答:根据静力平衡条件,梁的支座反力应该可以平衡载荷的作用力。
对于简支梁,支座反力应该相等,且方向相反。
因此,可以将载荷均分为两半,每一半的作用力为载荷的一半,分别作用在支座上。
2. 一个悬臂梁上有一个集中力作用,求梁的反力分布。
答:对于悬臂梁,梁的支座反力只有一个,且方向与集中力相反。
根据静力平衡条件,可以通过力的平衡方程求解支座反力的大小。
二、弹性力学问题1. 一个弹簧的刚度为k,已知初始长度为L0,当施加一个力F时,弹簧的变形为ΔL,求弹簧的劲度系数。
答:根据胡克定律,弹簧的劲度系数k等于施加的力F与弹簧的变形ΔL之比。
即k = F / ΔL。
2. 一个梁在受力情况下发生弯曲,已知梁的材料特性和几何尺寸,求梁的弯曲应力。
答:梁的弯曲应力可以通过弯曲矩和截面惯性矩之间的关系来求解。
根据梁的几何尺寸和材料特性,可以计算出梁的截面惯性矩,然后根据弯曲矩的大小,可以求解出梁的弯曲应力。
三、静力学问题1. 一个斜面上有一个物体,已知物体的质量和斜面的倾角,求物体沿斜面滑动的加速度。
答:根据牛顿第二定律,物体沿斜面滑动的加速度等于物体受到的合外力在斜面方向上的分量除以物体的质量。
可以将物体的重力分解为斜面方向和垂直斜面方向的两个分量,然后根据斜面的倾角和物体的质量来计算加速度。
2. 一个平衡悬臂上有一个质量为m的物体,已知悬臂的长度和物体与支点的距离,求物体的平衡位置。
答:在物体平衡的情况下,物体受到的力矩为零。
可以通过将物体的重力分解为垂直悬臂和平行悬臂方向的两个分量,然后根据力矩的平衡条件来求解物体的平衡位置。
结构力学课后习题答案

结构⼒学课后习题答案附录B 部分习题答案2 平⾯体系的⼏何组成分析2-1 (1)× (2)× (3)√ (4)× (5)× (6)×。
2-2 (1)⽆多余约束⼏何不变体系;(2)⽆多余约束⼏何不变体系;(3)6个;(4)9个;(5)⼏何不变体系,0个;(6)⼏何不变体系,2个。
2-3 ⼏何不变,有1个多余约束。
2-4 ⼏何不变,⽆多余约束。
2-5 ⼏何可变。
2-6 ⼏何瞬变。
2-7 ⼏何可变。
2-8 ⼏何不变,⽆多余约束。
2-9⼏何瞬变。
2-10⼏何不变,⽆多余约束。
2-11⼏何不变,有2个多余约束。
2-12⼏何不变,⽆多余约束。
2-13⼏何不变,⽆多余约束。
2-14⼏何不变,⽆多余约束。
5-15⼏何不变,⽆多余约束。
2-16⼏何不变,⽆多余约束。
2-17⼏何不变,有1个多余约束。
2-18⼏何不变,⽆多余约束。
2-19⼏何瞬变。
2-20⼏何不变,⽆多余约束。
2-21⼏何不变,⽆多余约束。
2-22⼏何不变,有2个多余约束。
2-23⼏何不变,有12个多余约束。
2-24⼏何不变,有2个多余约束。
2-25⼏何不变,⽆多余约束。
2-26⼏何瞬变。
3 静定梁和静定刚架3-1 (1) √;(2) ×;(3) ×;(4) √;(5) ×;(6) √;(7) √;(8) √。
3-2 (1) 2,下;(2) CDE ,CDE ,CDEF ;(3) 15,上,45,上;(4) 53,-67,105,下; (5) 16,右,128,右;(6) 27,下,93,左。
3-3 (a) 298AC M ql =-,Q 32AC F ql =;(b) M C = 50kN·m ,F Q C = 25kN ,M D = 35kN·m ,F Q D = -35kN ;(c) M CA = 8kN·m ,M CB = 18kN·m ,M B = -4kN·m ,F Q BC = -20kN ,F Q BD = 13kN ; (d) M A = 2F P a ,M C = F P a ,M B = -F P a ,F Q A = -F P ,F Q B 左 = -2F P ,F Q C 左 = -F P 。
结构力学试题及答案汇总(完整版)

We will continue to impr ove the com pany's i nternal control sy stem, and steady improveme nt in a bility to ma nage a nd control, optimize business pr oce sses, to e nsure smooth proce sse s, responsi bilities i n pl ace ; to furt her strengt hen internal control s, play a control post i ndepe nde nt over sight role of evaluati on complyi ng wit h third-party re sponsibility ; to a ctively make use of inter nal a udit t ools dete ct pote ntial management, streamli ne, sta ndar dize relate d transactions, strengtheni ng operations in accordance with law. Dee pening the information manag ement to e nsure full communica tion "zero re sistance". o consta ntly perfect ER , a nd BFS++, a nd PI, a nd MIS, a nd S CM, i nformation system based construction, full integrati on i nformation system, achieved information resources shared; to expa nd Portal system applicati on of breadt h and depth, play i nformation system on e nterprise of Assistant r ole; to perfect daily r un m ai ntena nce operation of re cords, pr omote pr obl em reasons a nalysis and system ha ndover; to strengtheni ng BFS++, and ERP , a nd S CM, te chnol ogy applicati on of training, im prove em ployee s applicati on i nformation system of ca pacity a nd lev el. Humanisti c care t o ensur e "zer o." To strengthe ning Hum anities care, conti nue s to foster compa ny wind clear, a nd ga s are, a nd heart Shun of cult ure atmosphere; stre ngthe ning l ove he lpe d trappe d, care difficult empl oyees; carried out style activitie s, rich empl oyees l ife; strengt heni ng healt h and la bour prote ction, orga nization career he alth medi cal, control career agai nst; conti nue s to implementation psychologi cal war ning preventi on system, trai ning em ployee s healt h of characte r, a nd sta ble of mood and enter prisi ng of attit ude , create d friendly fraternity of Huma nities e nvironment. o stre ngthe n risk management, e nsure that the business of "zero risk". To stre ngthened busi ness pla ns ma nagement, w ill busi ness busine ss plans cov er to all level , ensure t he busi ness can control i n control; t o cl ose concer n fina ncial, and coal ele ctric li nkage, and e nergy-savi ng sche duli ng, nati onal pol icy trends, strengthening tra ck, a ctive shoul d; to implementati on State-ow ned a ssets met hod, further spe cification busi ness financial management; to perfect ri sk tube control sy stem, achieved ri sk recognition, a nd mea sure, a nd a ssessment, a nd re port, a nd control fee dba ck of cl ose d ring management, impr ove risk preventi on capa city. o further standardize tra ding, a nd strive to a chieve "accor ding t o l aw , standardize and fair." Innovati on of performance manageme nt, to e nsure that potential employe es "zero fly". To strengt hen per formance manag ement, pr oce ss contr ol, enha nce em ployee evaluati on a nd level s of effective communi cation to impr ove performa nce ma nagement. o f urther quantify and refine empl oyee standards ... Work, full play part y, a nd branch, and members i n "five type Enterpri se" construction in the of core r ole, and fighting fortress r ole and pi one er model r ole; to continues to stre ngthe ning "four good" leadershi p constr uction, full play levels ca dres in enterpri se deve lopme nt in the f back bone ba ckbone r ole; to full strengthe ning mem bers youth w ork, full play youth em ployee s in compa ny devel opment i n the of force role ; to improve i nde pe nde nt Commission against corr uption work lev el, strengt heni ng o n enter prise busi ness key link of effectivene ss monitored. , And maintain stability. To further strengthen publ icity and educati on, im prove the overall legal system. We must stre ngthen safety management, esta blish and improve t he educati on, supervision, a nd eval uation as one of the traffic safety manageme nt mecha nism. o conscie ntiously sum up the Ol ympic se curity controls, pr omoting i ntegrated manageme nt to a hig her level, higher sta ndar ds, a higher level of devel opment. Employee s, today is lunar cal endar on Decem ber 24, t he ox Bell is a bout to ring, at this time of year, w e clearly feel the pul se of the XX power generati on compa ny to flourish, to more clearly hear XX power generation compa nies mat ure and symmetry breathi ng. Recalli ng past one a not her acr oss a raili ng, we are e nthusiasti c and full of confide nce. Future development opportunities, we m ore exciting fight more spirited. Employees, let us toget her acr oss 2013 full of challe nges a nd opportunities, to create a green, l ow -cost operation, full of huma ne care of a world-cl ass power ge neration com pany and work hard! The occasi on of the Spring Festival, my si ncere wi sh that y ou a nd the families of the staff in the ne w year, good health, happy, happy院(系) 建筑工程系 学号 三明学院 姓名 .密封线内不要答题 密封……………………………………………………………………………………………………………………………………………………结构力学试题答案汇总一、选择题(每小题3分,共18分)1. 图 示 体 系 的 几 何 组 成 为 : ( A ) A. 几 何 不 变 , 无 多 余 联 系 ; B. 几 何 不 变 , 有 多 余 联 系 ; C. 瞬 变 ; D. 常 变 。
《结构力学》习题解答(内含解答图)

解:将固定铰支座换为单铰,如图(b),由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结BF为刚片Ⅱ,铰结△CDE为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支撑杆F相连,虚铰在无穷远处,刚片Ⅰ与刚片Ⅲ是由杆AC和支撑杆E相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是由杆BC和杆FD相连,虚铰在两杆的延长线的交点处。此时,三铰不共线,该体系为几何不变体,且无多余约束。
所以,体系是几何不变得,且无多余约束。
习题2-2试对图示体系进行几何组成分析。
解:从图2-15(b)可知,杆件CD和链杆3及铰D构成二元体,可以去掉;取杆件CB为刚片Ⅰ,基础作为刚片Ⅱ,根据规则一,两刚片是通过杆AB、链杆1、2组成几何不变体。所以,整个体系为几何不变体系,且无多余约束。
习题2-2图习题2-2解答图
习题2-10试对图示体系进行几何组成分析。
习题2-10图习题2-10解答图
解:由于与基础的约束多余三个,故基础作为刚片Ⅰ。铰结△ABF为刚片Ⅱ,铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆EA和支撑杆F相连,虚铰在两杆的延长线的交点处,刚片Ⅰ与刚片Ⅲ是由杆EC和支撑杆D相连,虚铰在两杆的延长线的交点处,而刚片Ⅱ与刚片Ⅲ是铰B相连。此时,三铰不共线,该体系为几何不变体,且无多余约束。
习题2-26图习题2-26解答图
解:将链杆截断,截断一处,去掉一个约束,共去掉四个约束;再将刚性联结杆截断,截断一处,去掉三个约束,共去掉十二个约束,如图(b)。此时,体系变成与基础独立相连的三个单一杆件,见图(b)。所以,该体系具有十六个多余约束的几何不变体。
2.3.2提高题
提高题2-1 试对图示体系作几何组成分析。
所以,由规则一知,体系是几何不变体,且无多余约束。
最新结构力学试题及答案汇总(完整版)

最新结构⼒学试题及答案汇总(完整版)精品⽂档院(系)学号姓名 .密封线内不要答题密封……………………………………………………………………………………………………………………………………………………结构⼒学试题答案汇总结构⼒学课程试题 ( B )卷考试成绩题号⼀⼆三四成绩得分⼀、选择题(每⼩题3分,共18分)1. 图⽰体系的⼏何组成为:() A. ⼏何不变,⽆多余联系; B. ⼏何不变,有多余联系; C. 瞬变; D. 常变。
2. 静定结构在⽀座移动时,会产⽣:()A. 内⼒;B. 应⼒;C. 刚体位移;D. 变形。
3. 在径向均布荷载作⽤下,三铰拱的合理轴线为:()A .圆弧线;B .抛物线;C .悬链线;D .正弦曲线。
4. 图⽰桁架的零杆数⽬为:()A. 6;B. 7;C. 8;D. 9。
精品⽂档5. 图 a 结构的最后弯矩图为:()A.图 b; B.图 c ; C.图 d ; D.都不对。
6. ⼒法⽅程是沿基本未知量⽅向的:()A.⼒的平衡⽅程;B.位移为零⽅程;C.位移协调⽅程; D.⼒的平衡及位移为零⽅程。
⼆、填空题(每题3分,共9分)1.从⼏何组成上讲,静定和超静定结构都是_________体系,前者_________多余约束⽽后者_____________多余约束。
2. 图 b 是图 a 结构 ________ 截⾯的 _______ 影响线。
3. 图⽰结构 AB 杆 B 端的转动刚度为 ________, 分配系数为________, 传递系数为 _____。
三、简答题(每题5分,共10分)1.静定结构内⼒分析情况与杆件截⾯的⼏何性质、材料物理性质是否相关?精品⽂档为什么?2.影响线横坐标和纵坐标的物理意义是什么?四、计算分析题,写出主要解题步骤(4⼩题,共63分)1.作图⽰体系的⼏何组成分析(说明理由),并求指定杆1和2的轴⼒。
(本题16分)2.作图⽰结构的M图。
(本题15分)3.求图⽰结构A、B两截⾯的相对转⾓,EI=常数。
(完整版)结构力学解析
第一章平面体系的几何组成分析一判断题1. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
(×)2. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
(√)3。
计算自由度W小于等于零是体系几何不变的充要条件.(×)4. 三个刚片由三个铰相联的体系一定是静定结构.(×)5。
有多余约束的体系一定是超静定结构。
(×)6。
平面几何不变体系的三个基本组成规则是可以相互沟通的.(√)7。
三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
(×)8. 两刚片用汇交于一点的三根链杆相联,可组成几何不变体系.(×)9。
若体系计算自由度W〈0,则它一定是几何可变体系。
(×)10。
有多余约束的体系一定是几何不变体系.(×)11。
几何不变体系的计算自由度一定等于零.(×)12。
几何瞬变体系的计算自由度一定等于零。
(×)13. 图中链杆1和2的交点O可视为虚铰。
(×)题13图二选择题1. 图示体系为:(A)A.几何不变无多余约束 B.几何不变有多余约束 C.几何常变 D.几何瞬变题1图题2图2。
图示体系为:(B)A.几何不变无多余约束 B.几何不变有多余约束 C.几何常变 D.几何瞬变3. 图示体系是(B)A.无多余联系的几何不变体系 B.有多余联系的几何不变体系C.几何可变体系 D.瞬变体系题3图4。
图示体系的几何组成为(B)A.几何不变无多余约束 B.几何不变有多余约束 C.瞬变体系 D.可变体系题4图5. 图示平面体系的几何组成为(C)A。
几何不变无多余约束 B。
几何不变有多余约束 C.瞬变体系 D.几何可变体系题5图6. 图示体系为(A)A。
几何不变,无多余约束 B.几何不变,有多余约束 C。
几何常变 D。
几何瞬变题6图题7图7. 图示体系为(D)A。
《结构力学》典型习题与解答

《结构力学》经典习题及详解一、判断题(将判断结果填入括弧内,以√表示正确,以×表示错误。
)1.图示桁架结构中有 3 个杆件轴力为0 。
(×)F P2。
(×) 2.图示悬臂梁截面 A 的弯矩值是qlq Al l3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
(√)4.一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。
(×)5.用平衡条件能求出全部内力的结构是静定结构。
(√)6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
(√)7.超静定结构的力法基本结构不是唯一的。
(√)8.在桁架结构中,杆件内力不是只有轴力。
(×)9.超静定结构由于支座位移可以产生内力。
(√)10.超静定结构的内力与材料的性质无关。
(×)11.力法典型方程的等号右端项不一定为0。
(√)12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。
(√)13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系数的计算无错误。
(×)14.力矩分配法适用于所有超静定结构的计算。
(×)15.当AB 杆件刚度系数S AB 3i 时,杆件的 B 端为定向支座。
(×)二、单项选择题(在每小题的四个备选答案中选出一个正确答案,并将其代号填在题干后面的括号内。
不选、错选或多选者,该题无分。
)1.图示简支梁中间截面的弯矩为( A )ql2 2ql qlA.8 B . 42qlql 2C. 2D.2.超静定结构在荷载作用下产生的内力与刚度(B)A.无关 B .相对值有关C.绝对值有关D.相对值绝对值都有关3.超静定结构的超静定次数等于结构中( B )A.约束的数目B.多余约束的数目C.结点数 D .杆件数4.力法典型方程是根据以下哪个条件得到的(C)。
A.结构的平衡条件B.结构的物理条件C.多余约束处的位移协调条件D.同时满足A、B两个条件5.图示对称结构作用反对称荷载,杆件EI 为常量,利用对称性简化后的一半结构为(A )。
结构力学课后习题答案

结构力学课后习题答案结构力学是一门研究结构在外力作用下的内力、变形和稳定性的学科。
课后习题是帮助学生巩固理论知识和提高解题技巧的重要环节。
以下是一些结构力学课后习题的参考答案,供学习者参考:第一章:结构力学基础1. 静定结构与超静定结构的区别:静定结构是指在已知外力作用下,其内力和位移可以通过静力平衡方程和几何关系唯一确定的结构。
超静定结构则是指静力平衡方程和几何关系不足以唯一确定其内力和位移的结构。
2. 弯矩图的绘制方法:绘制弯矩图首先需要确定结构的支反力,然后通过截面平衡条件,逐步求出各截面的弯矩值,并将其绘制成图形。
第二章:静定梁的内力分析1. 简支梁的内力计算:对于简支梁,可以通过静力平衡条件和截面平衡条件来计算梁的内力,包括剪力和弯矩。
2. 悬臂梁的内力计算:悬臂梁的内力计算需要考虑梁端的外力和力矩,通过静力平衡条件求解。
第三章:静定桁架的内力分析1. 节点法的应用:节点法是通过在桁架的节点上施加平衡条件来求解节点的反力,进而求得杆件的内力。
2. 截面法的应用:截面法是通过选取桁架的某一截面,对该截面进行平衡分析,求得截面两侧杆件的内力。
第四章:静定拱的内力分析1. 三铰拱的内力计算:三铰拱的内力计算通常需要利用静力平衡条件和几何关系,计算出拱的反力和弯矩。
2. 双铰拱和无铰拱的内力特点:双铰拱和无铰拱的内力计算更为复杂,需要考虑更多的平衡条件和几何关系。
第五章:超静定结构的内力分析1. 力法的应用:力法是通过建立力的平衡方程来求解超静定结构的内力,通常需要引入多余未知力。
2. 位移法的应用:位移法是通过建立位移的平衡方程来求解超静定结构的内力,通常需要引入位移未知数。
第六章:结构的稳定性分析1. 欧拉临界载荷的计算:欧拉临界载荷是指细长杆件在轴向压力作用下失稳的临界载荷,可以通过欧拉公式计算。
2. 非线性稳定性分析:对于非线性问题,稳定性分析需要考虑材料的非线性特性和几何非线性,通常需要采用数值方法求解。
结构力学习题及答案

2 结构的几何组成分析判断题几何不变且无多余约束的体系其自由度必定等于零。
( )体系的自由度小于或等于零是保证体系为几何不可变的必要和充分条件。
( )三个刚片之间只要用三个铰两两相连,就能构成无多余约束的几何不变体系。
( )在任何情况下,在几何不变体系上去掉一个二元体,所余体系仍然是几何不变的。
( )一个点与一个刚片之间用两根链杆相连,则一定构成几何不变体系。
( )在某些特殊情况下,几何可变体系加上一个二元体后可以变为几何不变体系。
( )如体系在去掉某个约束后能承受特殊荷载而平衡,说明原体系中该约束为多余约束。
( )超静定结构中的多余约束是为保持杆件体系的几何不变性而设置的。
( )超静定结构设置多余约束的目的之一是调整结构的内力分布。
( )填空题一个点在平面上有___个自由度;一个刚片在平面上有___个自由度。
一个平面体系中有两个刚片,用单铰相联,则其自由度为____。
图示支座简图各相当于几个约束,在各图上标出可能出现的约束反力。
(a)___个约束;(b)___个约束。
(a)图示支座简图各相当于几个约束,在各图上标出可能出现的约束反力。
(a)___个约束;(b)___个约束。
(b)图示结构一共设置了五个支座链杆,对于保持其几何不变来说有___个多余约束,其中第___根链杆是必要约束。
在任何情况下,几何可变体系上增加一个二元体后构成的体系总是_______体系。
若两刚片由三根链杆相连构成无多余约束的几何不变体系,则三根链杆的空间位置必须满足_______________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
答案_______________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
答案________________。
指出图示体系的几何组成性质。
结构力学试题及参考答案

结构力学试题及参考答案结构力学是一门涉及结构设计和分析的工程学科,它在建筑、机械、航空航天等领域有着广泛的应用。
为了帮助大家更好地掌握结构力学的基本概念和技能,本文将提供一些结构力学试题及参考答案,供大家参考和学习。
一、试题1、什么是结构力学?请简要描述其研究内容和应用领域。
2、简述结构力学中常见的三种基本元素,并给出其符号和单位。
3、什么是结构的自由度?请举例说明。
4、什么是结构的刚度?请给出其物理意义和计算公式。
5、什么是结构的稳定性?请举例说明。
6、什么是结构的静力分析?请简述其目的和方法。
7、什么是结构的动力分析?请简述其目的和方法。
8、什么是结构的优化设计?请简述其目的和方法。
二、参考答案1、结构力学是一门研究结构受力、位移、应变等关系的学科,其目的是为了设计出安全、可靠、经济合理的结构。
结构力学广泛应用于建筑、机械、航空航天等领域。
2、在结构力学中,常见的三种基本元素包括力(F)、力矩(M)和力偶(MO)。
其中,力的符号为F,单位为牛顿(N);力矩的符号为M,单位为牛顿·米(N·m);力偶的符号为MO,单位为牛顿·米(N·m)。
3、结构的自由度是指描述系统状态的独立变量的个数。
例如,一个单自由度的结构是由一个质点组成的,其自由度为1;一个两自由度的结构是由两个质点组成的,其自由度为2。
4、结构的刚度是指结构在单位力作用下的位移响应。
刚度的物理意义是结构抵抗变形的能力,计算公式为:K=F/Δ,其中K为刚度,F 为作用在结构上的力,Δ为结构产生的位移。
5、结构的稳定性是指在某一荷载作用下,结构能够保持其平衡状态的能力。
例如,一个两端固定、跨中受力的简支梁在受到横向扰动时,可能会发生侧倾甚至倒塌,这就说明该简支梁的稳定性较差。
6、结构的静力分析是研究结构在静力荷载作用下的响应。
其主要目的是为了确定结构的位移、应力、应变等参数,从而评估结构的强度、刚度和稳定性等性能。
结构力学考研题库答案解析

结构力学考研题库答案解析结构力学考研题库答案解析结构力学是土木工程中的重要学科,它研究物体在外力作用下的力学行为和结构的稳定性。
对于考研生来说,掌握结构力学的知识是非常重要的。
下面,我们来解析一些结构力学考研题库中的题目,帮助大家更好地理解和掌握这门学科。
1. 题目:一个悬臂梁,长度为L,截面形状为矩形,宽度为b,高度为h,受到均匀分布载荷q。
求梁的最大弯矩和最大剪力。
解析:根据悬臂梁的受力分析,可以得到最大弯矩和最大剪力的表达式。
最大弯矩Mmax=qL^2/8,最大剪力Vmax=qL/2。
其中,q为均匀分布载荷,L为梁的长度。
2. 题目:一个简支梁,长度为L,截面形状为矩形,宽度为b,高度为h,受到集中力F作用在距离梁端距离a处。
求梁的最大弯矩和最大剪力。
解析:对于简支梁,最大弯矩和最大剪力的表达式为:最大弯矩Mmax=Fa/L,最大剪力Vmax=F。
其中,F为集中力,a为集中力作用点距离梁端的距离。
3. 题目:一个悬臂梁,长度为L,截面形状为圆形,直径为d,受到均匀分布载荷q。
求梁的最大弯矩和最大剪力。
解析:对于圆形截面的悬臂梁,最大弯矩和最大剪力的表达式为:最大弯矩Mmax=qL^2/10,最大剪力Vmax=qL/2。
其中,q为均匀分布载荷,L为梁的长度,d为圆形截面的直径。
4. 题目:一个简支梁,长度为L,截面形状为圆形,直径为d,受到集中力F作用在距离梁端距离a处。
求梁的最大弯矩和最大剪力。
解析:对于圆形截面的简支梁,最大弯矩和最大剪力的表达式为:最大弯矩Mmax=Fa/4L(2L-a),最大剪力Vmax=F。
其中,F为集中力,a为集中力作用点距离梁端的距离,L为梁的长度,d为圆形截面的直径。
5. 题目:一个悬臂梁,长度为L,截面形状为等边三角形,边长为a,受到均匀分布载荷q。
求梁的最大弯矩和最大剪力。
解析:对于等边三角形截面的悬臂梁,最大弯矩和最大剪力的表达式为:最大弯矩Mmax=qL^2/12,最大剪力Vmax=qL/2。
二建中的结构力学题解析

二建中的结构力学题解析结构力学在二级建造师考试中占据重要的地位,是考生必须要掌握的一门学科。
本文将对二级建造师考试中的结构力学题目进行解析,帮助考生加深对该科目的理解和应试技巧。
一、静力学1. 等效力系统等效力系统在结构力学中应用广泛。
在解答等效力系统题目时,我们首先要确定原始力的作用点、作用线和作用方向,然后根据力的平衡条件,找出等效力的作用点、作用线和作用方向。
最后,根据问题的要求,计算等效力系数。
2. 杠杆原理杠杆原理是静力学中的重要概念。
在解答杠杆原理题目时,我们首先要确定杠杆的支点和力的作用点,根据杠杆平衡条件,列出力的平衡方程。
然后,根据问题的要求,计算所求的未知力或力矩。
3. 平衡问题平衡问题是静力学中的基本问题,也是二级建造师考试中常见的题型。
在解答平衡问题时,我们首先要明确平衡条件,即各力的合力为零、各力的合力矩为零。
然后,根据平衡条件,列出力的平衡方程,求解未知力或力矩。
二、力的分解与合成1. 力的分解力的分解是解决复杂结构力学问题的常用方法。
在解答力的分解题目时,我们首先要明确所给力的作用点、作用线和作用方向。
然后,根据力的平衡条件,将力分解为若干个分力。
最后,根据问题的要求,计算所求的未知量。
2. 力的合成力的合成是力的分解的逆过程。
在解答力的合成题目时,我们首先要明确所给力的作用点、作用线和作用方向。
然后,将所有力按照给定的方向和大小进行合成,得到合力。
最后,根据问题的要求,计算所求的未知量。
三、弹性力学1. 梁的挠度计算在解答梁的挠度计算题目时,我们首先要明确所给梁的几何形状、材料性质和受力情况。
然后,根据弯曲理论,建立梁的弯矩方程。
最后,根据边界条件,计算所求的梁的挠度。
2. 梁的应力计算在解答梁的应力计算题目时,我们首先要明确所给梁的几何形状、材料性质和受力情况。
然后,根据弹性力学理论,建立应力的计算公式。
最后,根据所给条件,计算所求的应力。
四、刚度法与位移法1. 刚度法刚度法是结构力学计算中常用的方法之一。
结构力学力法习题及答案

结构力学力法习题及答案结构力学力法习题及答案结构力学是一门研究物体在外力作用下产生的应力和变形的学科。
在工程学中,结构力学是非常重要的一门学科,它为我们设计和分析各种建筑和机械结构提供了基础。
在学习结构力学的过程中,习题是必不可少的一部分。
下面将给出一些结构力学的力法习题及其答案,希望对读者有所帮助。
1. 一个悬臂梁上有一个集中力作用在梁的自由端,求该梁的弯矩分布图。
解答:根据悬臂梁的特点,自由端处的弯矩最大。
假设集中力为F,梁的长度为L,弹性模量为E,梁的截面惯性矩为I。
根据悬臂梁的弯矩公式M = F * L,可以得到弯矩分布图为一个从自由端开始逐渐减小的直线。
2. 一个等截面的梁上有一个均布载荷作用,求该梁的剪力分布图。
解答:假设均布载荷为q,梁的长度为L,根据梁的受力平衡条件,可以得到梁上任意一点的剪力大小为V = q * x,其中x为距离梁的一端的距离。
因此,该梁的剪力分布图为一个线性增长的直线。
3. 一个梁上有多个集中力作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
4. 一个悬臂梁上有一个集中力和一个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:首先,根据集中力的大小和悬臂梁的长度,可以求出集中力在悬臂梁上的弯矩分布图。
然后,根据均布载荷的大小和悬臂梁的长度,可以求出均布载荷在悬臂梁上的剪力分布图。
最后,将两者叠加在一起,即可得到梁的总弯矩和总剪力分布图。
5. 一个梁上有多个集中力和多个均布载荷同时作用,求该梁的弯矩和剪力分布图。
解答:对于每个集中力和均布载荷,可以分别求出其在梁上的弯矩和剪力分布图。
然后将所有的弯矩和剪力分布图叠加在一起,即可得到梁的总弯矩和总剪力分布图。
通过以上习题的解答,我们可以看到结构力学中力法的应用。
在实际工程中,我们需要根据具体的结构形式和受力情况,运用结构力学的理论知识,求解结构的受力分布,从而保证结构的安全可靠。
结构力学-习题集(含答案)
《结构力学》课程习题集一、单选题1.弯矩图肯定发生突变的截面是(D )。
A.有集中力作用的截面;B.剪力为零的截面;C.荷载为零的截面;D.有集中力偶作用的截面。
2.图示梁中C截面的弯矩是( D )。
4m2m4mA.12kN.m(下拉);B.3kN.m(上拉);C.8kN.m(下拉);D.11kN.m(下拉)。
3.静定结构有变温时,(C)。
A.无变形,无位移,无内力;B.有变形,有位移,有内力;C.有变形,有位移,无内力;D.无变形,有位移,无内力。
4.图示桁架a杆的内力是(D)。
A.2P;B.-2P;C.3P;D.-3P。
5.图示桁架,各杆EA为常数,除支座链杆外,零杆数为(A)。
A.四根;B.二根;C.一根;D.零根。
l= a66.图示梁A点的竖向位移为(向下为正)(C)。
A.)24/(3EIPl; B.)16/(3EIPl; C.)96/(53EIPl; D.)48/(53EIPl。
P7. 静定结构的内力计算与( A )。
A.EI 无关; B.EI 相对值有关;C.EI 绝对值有关;D.E 无关,I 有关。
8. 图示桁架,零杆的数目为:( C)。
A.5;B.10;C.15;D.20。
9. 图示结构的零杆数目为( C )。
A.5;B.6;C.7;D.8。
10. 图示两结构及其受力状态,它们的内力符合( B )。
A.弯矩相同,剪力不同;B.弯矩相同,轴力不同;C.弯矩不同,剪力相同;D.弯矩不同,轴力不同。
PP2ll11. 刚结点在结构发生变形时的主要特征是( D )。
A.各杆可以绕结点结心自由转动; B.不变形; C.各杆之间的夹角可任意改变; D.各杆之间的夹角保持不变。
12. 若荷载作用在静定多跨梁的基本部分上,附属部分上无荷载作用,则( B )。
A.基本部分和附属部分均有内力;B.基本部分有内力,附属部分没有内力;C.基本部分无内力,附属部分有内力;D.不经过计算,无法判断。
13.图示桁架C 杆的内力是(A)。
