PPK-计算表格
如何编写合格的CPK、PPK数据

如何编写合格的CPK、PPK数据如何制作合格的“过程能力分析”PPK数据利用MINITAB软件(Minitab 16)生成假的合适的PPK数据源—25组(每组5个)测量值。
要求计算得到的PPK值≥1.67。
以117.64±0.2为例。
一、打开Minitab软件,选择“计算”-“随机数据”-“正态”(图1)二、在产生的(图2)对话框中填入数据。
“均值”为117.64;PPK为1.67时“标准差”等于单边公差0.2除于5 得到值0.04;“数据行数”填125(25组/每组5个数据);计划在表格中生成9组数据供挑选,表格每列的头部分别标记为1-9;在对话框左边选择全部列号码,点击选择后存入右边的框内。
点击确定后,得到数据如图3三、检验每列数据的PPK是否大于或等于1.67。
选择按钮“改善”-“评估能力”-“变量数据”-“正态能力”,见图4在出现的对话框中分别从左边选择一个列号码,如1;“子组大小”填5;“规格下限”和“规格上限”分别填下公差和上公差的数据。
见图5四、点确定后,出现一个图表(见图6),如果PPK≥1.67,则这组数据可用;如果PPK<1.67,这组数据就放弃。
然后依次用“第三步”的方法检验1-9组数据哪几组可用。
五、在表格第一列前插入一列,循环往下填写1-5数字,一直到125行。
(见图7)六、拆分每列数据为5列。
选“数据”-“拆分列”(图8)在跳出的对话框内选择左边的列号码1到右边,“使用的下标”从左边选择C1列,在新的工作表中生成,点确定。
(图9)在新的工作表中生成5列数据,每列25行。
七、列转置成行。
(图10)选择“数据”-“转置列”,在跳出的对话框选中左边这5列,选择到右边,转置到新的表格中,点确定后生成新表格,5行各行25个数据。
(图11)(图12)。
表格1中,其它可采用的各列数据(2-9列)也可以通过第六、七步骤,产生横置的数据。
八、可以把横置的数据复制,粘贴到各种PPK计算表格中。
CPK、PPK计算

製程特性依不同的工程規格其定義如下:。
等級處理原則無規格界限時Cp(Pp)=***Cpk(Ppk)=***Ca =***單邊上限(USL) Cp(Pp)=CPUCpk(Ppk)=CPUCa =***單邊下限(LSL) Cp(Pp)=CPLCpk(Ppk)=CPLCa =***雙邊規格(USL, LSL) Cp(Pp)=(USL-LSL)/6σCpk(Ppk)=MIN(CPU,CPL)Ca =|平均值-規格中心|/(公差/2)谈到过程能力,首先得解释变异(或者叫波动),正是因为有了变异的存在,才出现了能力大小。
产生变异的原因可以归结为两种,一种是普通原因,一种是特殊的原因。
所谓的普通原因就是平时一直客观存在,对过程有一定的影响但不明显,而特殊因素则是偶然出现,对过程影响很大。
举例说明:在一个有空调的房间进行培训时,虽然空调可能是设定在25度,但由于房间内外温度存在差异,所以每时每刻都会有能量在和房间外进行交换,所以如果用足够精确的温度计测量房间的温度就会发现房间里的温度其实并不是恒定在25.000度,而是24.99,24.98,25.00,25.01…..在微小的在一定范围内进行变化,这时我们就说受到的是普通因素的影响,而如果有人推门进来,那么在这瞬间,房间内的温度会出现较大变化,此时我们说受到了普通因素和特殊因素两种影响。
过程只受普通因素影响的时候在控制图上表现为过程是受控的,如果有特殊原因的影响在控制图上会有异常点的出现。
所以我们如果用Cp和Cpk来衡量过程能力,前提是要过程稳定且数据是正态分布,而且数据应该在25组以上(建议最少不要低于20组,数据组越少采信结果的风险越大),也就是说计算Cp,Cpk只考虑过程受普通因素的影响。
计算公式为:Cp=(usl-lsl)/6σ;1、Cpk=(1-k)Cp;k=|u-M|/(usl-lsl)/2;2、Cpk=min{(usl-u)/3σ ,(u-lsl)/3σ };注释:usl为上规格线,lsl 为下规格线,u为实际测得的平均值,M为上下规格的中心点,K值表示的意思是实际平均值偏离中心值的程度,此时的即为只考虑普通因素产生的变异,通常根据控制图的不同采用Rbar/d2,或者Sbar/C4,在minitab里有三种不同的估算方法。
CPKPPK计算

CPKPPK计算CPK and PPK CalculationCPK (Process Capability Index) and PPK (Process Performance Index) are statistical measures used to assess the capability of a manufacturing or production process. These indices provide information about how well a process is performing in terms of meeting specified tolerance limits and producing quality products consistently. In this article, we will discuss the formulas and calculations for CPK and PPK and their significance in process improvement.CPK Calculation:The CPK index is a measure of how the process is centered (mean) within the specification limits, as well as its ability to produce products within those limits. The formula tocalculate CPK is as follows:CPK = min(CPU, CPL)Where,CPU = (USL - Mean) / (3 * Standard Deviation)CPL = (Mean - LSL) / (3 * Standard Deviation)USL - Upper Specification LimitLSL - Lower Specification LimitThe CPK value can range from 0 to 1. A CPK value less than 1 indicates that the process is not capable of producing products within the specified limits. A value greater than 1 indicates that the process is capable, with higher values indicatingbetter capability.PPK Calculation:PPK is similar to CPK, but it takes into account the overall distribution of data, not just the mean and standard deviation. The formula to calculate PPK is as follows:PPK = min(PPU, PPL)Where,PPU = (USL - Median) / (3 * MAD)PPL = (Median - LSL) / (3 * MAD)USL - Upper Specification LimitLSL - Lower Specification LimitMedian - Median of the dataMAD - Median Absolute Deviation (a measure of data variability)Like CPK, PPK values can range from 0 to 1, with higher values indicating a more capable process.Interpreting CPK and PPK Values:- CPK/PPK < 1: The process is not capable of meeting the specifications, and immediate action is required to improve it.- 1 < CPK/PPK < 1.33: The process is marginally capable, and improvements are needed.- 1.33 < CPK/PPK < 2: The process is moderately capable, but further improvements are desirable.- CPK/PPK > 2: The process is highly capable and meets the specifications consistently.It is important to note that these interpretations are not fixed standards but serve as general guidelines. The acceptability of CPK and PPK values can vary based on the industry, customer requirements, and the criticality of the process.Improving CPK and PPK values:If the calculated CPK or PPK value is below the desired threshold, process improvement efforts should be undertaken to bring them within range. Here are some potential steps for improving these values:1. Identify and eliminate process variations: Analyze the sources of variability in the process and take corrective actions to reduce or eliminate them. These variations can be due to improper machine settings, inconsistent raw materials, or inadequate training of operators.2. Increase process capability: Modify the process parameters to enhance its capability. This can include adjusting machine settings, optimizing process conditions, or implementing advanced control strategies.3. Conduct measurement system analysis (MSA): Ensure the accuracy and repeatability of the measurement system used to collect process data. An unreliable measurement system can introduce errors in the calculations and affect the CPK and PPK values.5. Enhance operator skills and training: Provide adequate training to the operators to increase their knowledge and skills related to the process. Well-trained operators can make better decisions and minimize errors, leading to improved process capability.Conclusion:CPK and PPK indices are valuable tools in assessing process capability and performance. They help identify areas of improvement and guide process improvement efforts. Bycalculating these indices and taking appropriate actions, organizations can enhance process capability, reduce defects, and produce high-quality products consistently.。
SPC(CpkPpk等)工程能力计算公式和Excel制图

SPC(CpkPpk等)工程能力计算公式和Excel制图均值X图均值X图nA2d2D3D4A3c4B3B421.8801.128-3.2672.6590.7979-3.27631.0231.693-2.5711.9540.8862-2.56840.7292.059-2.2821.6280.9213-2.26650.5772.326-2.1141.4270.9400-2.08960.4832.543-2.0041.2870.95150.0301.97070.4192.7040.0761.9241.1820.95940.1181 .88280.3732.8470.1361.8641.0990.96500.1851.81590.3372.9700.1841. 8161.0320.96930.2391.761100.3083.0780.2231.7770.9750.97270.2841. 716110.2853.1730.2561.7440.9270.97540.3211.679120.2663.2580.2831 .7170.8860.97760.3541.640130.2493.3360.3071.6930.8500.97940.3821 .618140.2353.4070.3281.6720.8170.98100.4061.594150.2233.4720.347 1.6530.7890.98230.4281.572160.2123.5320.3631.6370.7630.98350.448 1.552170.2033.5880.3781.6220.7390.98450.4461.534180.1943.6400.39 11.6080.7180.98540.4821.518190.1873.6890.4031.5970.6980.98620.49 71.503200.1803.7350.4151.5850.6800.98690.5101.490210.1733.7780.4 251.5750.6630.98760.5231.477220.1673.8190.4341.5660.6470.98820.5 341.466230.1623.8580.4431.5570.6330.98870.5451.455240.1573.8950. 4511.5480.6190.98920.5551.445250.1533.9310.4591.5410.6060.98960. 5651.435某±A2R某±A2R中位数X图单值X图nA2d2D3D4E2d2D3D421.8801.128-3.2672.6601.128-3.26731.1871.693-2.5741.7721.693-2.57440.7962.059-2.2821.4572.059-2.282标准差估计值的除数UCL某,LCL某=全距R图全距R图中位数图计算控制限用的系数单值图LCLS=B3标准差估计值的除数计算控制限用的系数全距R图子组容量计算控制限用的系数标准差估计值的除数计算控制限用的系数X-R图标准差S图X-图计算控制限用的系数计算控制限用的系数UCLS=B4控制图的常数和公式表δ=R/D2δ=/c4子组容量计算控制限用的系数标准差估计值的除数计算控制限用的系数UCL某,LCL某=UCLR=D4RLCLR=D3R50.6912.326-2.1141.2902.326-2.11460.5482.534-2.0041.1842.534-2.00470.5082.7040.0761.9241.1092.7040.0761.92480.4332.8470.1361. 8641.0542.8470.1361.86490.4122.9700.1841.8161.0102.9700.1841.816 100.3623.0780.2231.7770.9753.0780.2231.777某±A2R某±E2Rδ=R/d2δ=R/d2UCLR=D4RUCLMR=D4RLCLR=D3RLCLMR=D3RUCL,LCL=UCL某,LCL某=UCLP,LCLP==UCLnp,LCLnp=UCLC,LCLC=UCLU,LCLU=Cpk=(1-k)xCp 或MIN{CPU,CPL}Ppk=(1-k)xPp或MIN{PPU,PPL}单边规格(设计规格)因没有规格上限或下限,没有规格下限Cp=CPU =Cpk,没有规格上限Cp=()nPPP/13-±=()nPPP-±=13()PPnPn-±=13nUU3±=CC3±=。
cpk、ppk计算

製程特性依不同的工程規格其定義如下:。
等級處理原則無規格界限時Cp(Pp)=***Cpk(Ppk)=***Ca =***單邊上限(USL) Cp(Pp)=CPUCpk(Ppk)=CPUCa =***單邊下限(LSL) Cp(Pp)=CPLCpk(Ppk)=CPLCa =***雙邊規格(USL, LSL) Cp(Pp)=(USL-LSL)/6σCpk(Ppk)=MIN(CPU,CPL)Ca =|平均值-規格中心|/(公差/2)谈到过程能力,首先得解释变异(或者叫波动),正是因为有了变异的存在,才出现了能力大小。
产生变异的原因可以归结为两种,一种是普通原因,一种是特殊的原因。
所谓的普通原因就是平时一直客观存在,对过程有一定的影响但不明显,而特殊因素则是偶然出现,对过程影响很大。
举例说明:在一个有空调的房间进行培训时,虽然空调可能是设定在25度,但由于房间内外温度存在差异,所以每时每刻都会有能量在和房间外进行交换,所以如果用足够精确的温度计测量房间的温度就会发现房间里的温度其实并不是恒定在25.000度,而是24.99,24.98,25.00,25.01…..在微小的在一定范围内进行变化,这时我们就说受到的是普通因素的影响,而如果有人推门进来,那么在这瞬间,房间内的温度会出现较大变化,此时我们说受到了普通因素和特殊因素两种影响。
过程只受普通因素影响的时候在控制图上表现为过程是受控的,如果有特殊原因的影响在控制图上会有异常点的出现。
所以我们如果用Cp和Cpk来衡量过程能力,前提是要过程稳定且数据是正态分布,而且数据应该在25组以上(建议最少不要低于20组,数据组越少采信结果的风险越大),也就是说计算Cp,Cpk只考虑过程受普通因素的影响。
计算公式为:Cp=(usl-lsl)/6σ;1、Cpk=(1-k)Cp;k=|u-M|/(usl-lsl)/2;2、Cpk=min{(usl-u)/3σ ,(u-lsl)/3σ };注释:usl为上规格线,lsl 为下规格线,u为实际测得的平均值,M为上下规格的中心点,K值表示的意思是实际平均值偏离中心值的程度,此时的即为只考虑普通因素产生的变异,通常根据控制图的不同采用Rbar/d2,或者Sbar/C4,在minitab里有三种不同的估算方法。
Cpk及Ppk计算Excel模板
107
157
8
1.209 58
108
158
9
1.209 59
109
159
10
1.208 60
110
160
11
1.207 61
111
161
12
1.206 62
112
162
13
1.210 63
113
163
14
1.207 64
114
164
15
1.205 65
115
165
16
1.204 66
116
166
17
3
1.20
1.20
1.197
4
1.20
1.20
1.199
5
1.20
1.20
1.201
6
1.20
1.20
1.203
7
1.20
1.21
1.205
8
1.21
1.21
1.207
9
1.21
1.21
1.209
10
1.21
1.21
1.211
11
1.21
1.21
1.213
12
1.21
1.22
1.215
13
1.22
1.22
126
176
27
1.205 77
127
177
28
1.208 78
128
178
29
1.211 79
129
179
30
1.207 80
130
180
31
81
PPK表格

组容/频率 图号
362.47
AVERAGE
UCLR=D4R=
12.40
LCLR=D3R=
0.00
MAX-MIN
01-7 368.00 367.00 363.00 365.00 368.00 1831.0 366.20
5.00
01-8 367.00 367.00 364.00 369.00 365.00 1832.0 366.40
366.00 366.40 367.20 367.60 367.00
5.00 5.00 4.00 5.00 5.00
d2
)≥1.67 2.09
01-25 365.00 364.00 368.00 369.00 367.00 1833.0 366.60
5.00
制表/
审核/
5.00
01-3 360.00 362.00 364.00 368.00 369.00 1823.0 364.60
9.00
01-4 362.00 365.00 368.00 366.00 367.00 1828.0 365.60
6.00
工序名称 机器编号
01-5 365.00 369.00 368.00 364.00 366.00 1832.0 366.40
6.00
01-12 365.00 362.00 368.00 365.00 366.00 1826.0 365.20
6.00
01-13 362.00 365.00 367.00 365.00 365.00 1824.0 364.80
5.00
01-14 368.00 367.00 366.00 365.00 362.00 1828.0 365.60
ppk,计算表格

竭诚为您提供优质文档/双击可除ppk,计算表格篇一:如何编写合格的cpk、ppk数据如何制作合格的“过程能力分析”ppk数据利用minitab软件(minitab16)生成假的合适的ppk 数据源—25组(每组5个)测量值。
要求计算得到的ppk值≥1.67。
以117.64±0.2为例。
一、打开minitab软件,选择“计算”-“随机数据”-“正态”(图1)二、在产生的(图2)对话框中填入数据。
“均值”为117.64;ppk为1.67时“标准差”等于单边公差0.2除于5得到值0.04;“数据行数”填125(25组/每组5个数据);计划在表格中生成9组数据供挑选,表格每列的头部分别标记为1-9;在对话框左边选择全部列号码,点击选择后存入右边的框内。
点击确定后,得到数据如图3三、检验每列数据的ppk是否大于或等于 1.67。
选择按钮“改善”-“评估能力”-“变量数据”-“正态能力”,见图4在出现的对话框中分别从左边选择一个列号码,如1;“子组大小”填5;“规格下限”和“规格上限”分别填下公差和上公差的数据。
见图5四、点确定后,出现一个图表(见图6),如果ppk≥1.67,则这组数据可用;如果ppk<1.67,这组数据就放弃。
然后依次用“第三步”的方法检验1-9组数据哪几组可用。
五、在表格第一列前插入一列,循环往下填写1-5数字,一直到125行。
(见图7)六、拆分每列数据为5列。
选“数据”-“拆分列”(图8)在跳出的对话框内选择左边的列号码1到右边,“使用的下标”从左边选择c1列,在新的工作表中生成,点确定。
(图9)篇二:cpk与ppk的计算和评价等级过程能力计算及评价方法1.过程能力等级说明1.1cp评价等级——《质量专业理论与实务》(中级)1.2无偏时cp与合格(不合格)率的对应关系由上表可知,在无偏时cp与合格(不合格)率的对应关系是非线性的一一对应的关系,过程能力指数越大,合格率越高(反之亦然)。
PPK(CPK)计算及条形分布图

Blank Blank
Blank
Blank Blank Blank Blank Blank Blank Blank Blank Blank Blank Blank
1.786 Blank 1.79 Blank
1.801 Blank 1.814 Blank 1.836 Blank 1.827 Blank
1.75 Blank 1.757 Blank 1.772 Blank 1.726 Blank
1.72 Blank
Blank Blank Blank Blank Blank Blank Blank Blank Blank Blank Blank
F12
1.801 F32
F13
1.814 F33
F14
1.836 F34
F15
1.827 F35
F16
1.750 F36
F17
1.757 37
F18
1.772 38
F19
1.726 39
F20
1.720 40
数量: 12
規格:
1.74
取樣數:
± 30
PCB:
0.1
上限 規格:
下限
規格:
XXXX 1.840 1.64
1.77 8
56.7% 18 8
1.80 8
83.3% 10 8
1.82 2
90.0% 2 2
1.84 0
90.0% 0 0
NO Need to copy the above XAxis number into below yellow block.
Rev. 1.3
Data Data
Data Data Data Data Data Data Data Data Data
ppk怎么计算

ppk怎么计算
ppk(Performance Index of Process)是过程性能指数的缩写,通常用于描述过程性能的指标。
ppk的计算公式如下:
ppk=(过程均值-目标值)/(3*标准偏差)
其中,过程均值是实际生产过程中测量得到的数据的平均值,而目标值是规格限中的中间值。
标准偏差表示数据分布的离散程度,即数据波动的大小。
在实际生产中,ppk值越高表示过程性能越稳定,产品合格率越高。
通常ppk值在1.67以上被认为是优秀的,而在1.33以下则被认为是不合格的。
因此,ppk被广泛应用于生产制造领域中,用于评估和改进生产过程的性能。
要计算ppk,需要收集足够多的实际生产数据,并计算出过程均值和标准偏差。
然后代入公式进行计算即可得到ppk值。
PPK_计算表格
=
需 改 善 不 足
Pp < 1.33
※ 分析意见 ※
σ 能力= Pp ×3 σ 水准= Ppk ×3
判定
○ 格 24.993 测 定 工 具
千分尺 测 量 单 位
㎜
调 审 批 判定基准 及 分析 工 程 特 性 充 分 查 者 核 准
需 改 善 不 足
※ 分析意见 ※
1.67 >Pp ≥1.33
工 程 特 性 充 分
○ △ ×
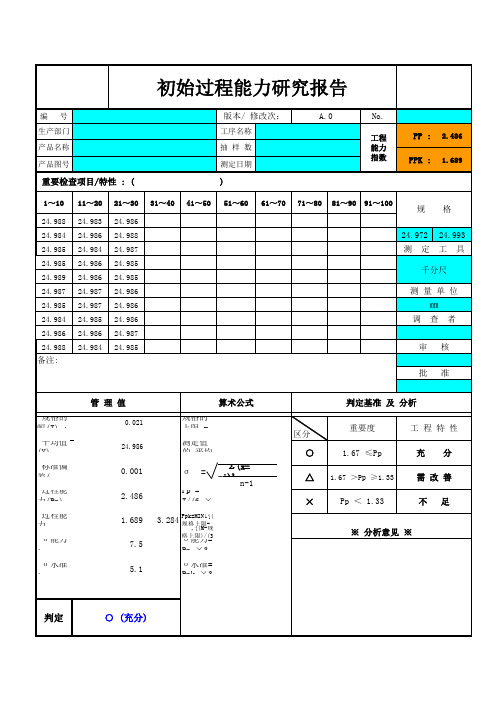
标准偏差( σ ): 过程能力(Pp) : 过程能力(Ppk): σ 能力 : σ 水准 :
0.001 2.486 1.689 7.5 5.1 3.284
σ
Σ (x-xi)² n-1 Pp = T/(6 ×σ )
Ppk=MIN[{(规格上限-M)/(3 ×σ )} ,{(M-规格上限)/(3 ×σ )}]
)
51~60 61~70 71~80 81~90 91~100
规 24.972 测 定
格
工
具
千分尺 测 量 单 位
㎜
调 审 批 查 者 核 准
备注:
管 理 值 规格的 幅(T) : 平均值(X) :
0.021 24.986
算术公式 规格的上限 - 下限值 区分 测定值的 平均
判定基准 及 分析 重要度 1.67 ≤Pp
初始过程能力研究报告
编 号
版本/ 修改次:
工序名称 抽 样 数 测定日期
A.0
No.
工程 能力 指数
生产部门 产品名称 产品图号
PP : PPK :
重要检查项目/特性 : (
1~10 24.988 24.984 24.985 24.985 24.989 24.987 24.985 24.984 24.986 24.988 11~20 24.983 24.986 24.984 24.986 24.986 24.987 24.987 24.985 24.986 24.984 21~30 24.986 24.988 24.987 24.985 24.985 24.986 24.986 24.986 24.987 24.985 31~40 41~50
