三角形旋转
全等三角形旋转模型知识点总结附解析

全等三角形旋转模型知识点总结附解析一、全等三角形旋转模型1.(课题研究)旋转图形中对应线段所在直线的夹角(小于等于90°的角)与旋转角的关系.(问题初探)线段AB 绕点O 顺时针旋转得到线段CD ,其中点A 与点C 对应,点B 与点D 对应,旋转角的度数为α,且0°<α<180°.(1)如图①,当α=60°时,线段AB 、CD 所在直线夹角(锐角)为 ;(2)如图②,当90°<α<180°时,直线AB 与直线CD 所夹锐角与旋转角α存在怎样的数量关系?请说明理由;(形成结论)旋转图形中,当旋转角小于平角时,对应线段所在直线的夹角与旋转角 .(运用拓广)运用所形成的结论解决问题:(3)如图③,四边形ABCD 中,∠ABC =60°,∠ADC =30°,AB =BC ,CD =3,BD =19,求AD 的长.解析:(1)60°;(2)互补,理由见解析;【形成结论】相等或互补;(310【分析】(1)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOB COD SSS ,可得B D ∠=∠,由三角形内角和定理可求解;(2)由旋转的性质可得AB CD =,OA OC =,BO DO =,可证()AOBCOD SSS ,可得B D ∠=∠,由平角的定义和四边形内角和定理可求解; 【形成结论】由(1)(2)可知对应线段所在直线的所夹锐角角与旋转角:相等或互补;【运用拓广】(3)将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,由旋转的性质可得BF BD =,3AF CD ==,由三角形内角和定理可求90FAD ∠=︒,由勾股定理可求解.【详解】解:(1)如图1,延长DC 交AB 于F ,交BO 于E ,α=︒,60∴∠=︒,60BOD线段AB绕点O顺时针旋转得线段CD,=,AB CD=,BO DO∴=,OA OCAOB COD SSS,()B D∴∠=∠,∠=∠,OED BEF,B DBFE EOD,60故答案为:60︒;(2)直线AB与直线CD所夹锐角角与旋转角α互补,理由如下:如图2,延长AB,DC交于点E,线段AB绕点O顺时针旋转得线段CD,=,=,BO DO∴=,OA OCAB CDAOB COD SSS,()ABO D,ABO EBO,180D EBO,180360EBO E D BOD,E BOD,180∴直线AB与直线CD所夹锐角角与旋转角α互补.形成结论由(1)(2)(3)可知:旋转图形中,当旋转角小于平角时,对应线段所在直线的所夹锐角角与旋转角:相等或互补.故答案为:相等或互补.运用拓广(3)如图3,将BCD ∆绕点B 顺时针旋转60︒,得到BAF ∆,连接FD ,延长FA ,DC 交于点E ,∴旋转角60ABC ∠=︒,BCD BAF ,60AED ABC ∴∠=∠=︒,3AF CD ==,BD BF =,30ADC ∠=︒,90FAD AED ADC ,又60FBD ABC ,BF BD =, BFD ∴∆是等边三角形,BF BD DF ,∴在Rt DAF 中,2219910ADDF AF . 【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的判定和性质,等边三角形的判定和性质等知识,添加辅助线构造全等三角形是本题的关键.2.发现规律:(1)如图①,ABC 与ADE 都是等边三角形,直线,BD CE 交于点F .直线BD ,AC 交于点H .求BFC ∠的度数(2)已知:ABC 与ADE 的位置如图②所示,直线,BD CE 交于点F .直线BD ,AC 交于点H .若ABC ADE α∠=∠=,ACB AED β∠=∠=,求BFC ∠的度数 应用结论:(3)如图③,在平面直角坐标系中,点O 的坐标为(0,0),点M 的坐标为(3,0),N 为y 轴上一动点,连接MN .将线段MN 绕点M 逆时针旋转60得到线段MK ,连接NK ,OK ,求线段OK 长度的最小值答案:A解析:(1)BFC ∠的度数为60︒;(2)BFC ∠的度数为180αβ︒--;(3)线段OK 长度的最小值为32 【分析】(1)通过证明BAD CAE ≅△△可得ABD ACE ∠=∠,再由三角形内角和定理进行求解即可;(2)通过证明ABC ADE 可得BAC DAE ∠=∠,AB AC AD AE=,可证ABD ACE ,可得ABD ACE ∠=∠,由外角性质可得BFC BAC ∠=∠,再有三角形内角和定理进行求解即可;(3)由旋转的性质可得MNK △是等边三角形,可得MK MN NK ==,60NMK NKM KNM ∠=∠=∠=︒,如图③将MOK 绕点M 顺时针旋转60︒,得到MQN △,连接OQ ,可得60OMQ ∠=︒,OK =NQ ,MO =MQ ,则当NQ 为最小值时,OK 有最小值,由垂线段最短可得当QN y ⊥轴时,NQ 有最小值,由直角三角形的性质即可求解.【详解】 (1)∵ABC 与ADE 是等边三角形∴AB=AC ,AD=AE ,60BAC DAE ABC ACB ∠=∠=∠=∠=︒∴BAD CAE ∠=∠∴()BAD CAE SAS ≅ ∴ABD ACE ∠=∠∵60ABD DBC ABC ∠+∠=∠=︒∴60ACE DBC ∠+∠=︒∴18060BFC DBC ACE ACB ∠=︒-∠-∠-∠=︒;(2)∵ABC ADE α∠=∠=,ACB AED β∠=∠=∴ABC ADE∴BAC DAE ∠=∠,AB AC AD AE= ∴BAD CAE ∠=∠,AB AD AC AE = ∴ABD ACE ∴ABD ACE ∠=∠ ∵BHC ABD BAC BFC ACE ∠=∠+∠=∠+∠ ∴BFC BAC ∠=∠ ∵180BAC ABC ACB ∠+∠+∠=︒ ∴180BFC αβ∠++=︒∴180BFC αβ∠=︒--;(3)∵将线段MN 绕点M 逆时针旋转60︒得到线段MK∴MN MK =,60NMK ∠=︒∴MNK △是等边三角形∴MK MN NK ==,60NMK NKM KNM ∠=∠=∠=︒如下图,将MOK 绕点M 顺时针旋转60︒,得到MQN △,连接OQ∴MOK MQN ≅,60OMQ ∠=︒∴OK =NQ ,MO =MQ∴MOQ △是等边三角形∴60QOM ∠=︒∴30NOQ ∠=︒∵OK =NQ∴当NQ 为最小值时,OK 有最小值,由垂线段最短可得当QN y ⊥轴时,NQ 有最小值 ∵点M 的坐标为(3,0)∴3OM OQ ==∵QN y ⊥轴,30NOQ ∠=︒∴1322NQ OQ == ∴线段OK 长度的最小值为32. 【点睛】本题属于几何变换综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质,旋转的性质,三角形内角和定理等知识,灵活运用这些性质进行推理是解决本题的关键.3.如图1,在等腰Rt △ABC 中,∠ABC =90°,AB =BC =6,过点B 作BD ⊥AC 交AC 于点D ,点E 、F 分别是线段AB 、BC 上两点,且BE =BF ,连接AF 交BD 于点Q ,过点E 作EH ⊥AF 交AF 于点P ,交AC 于点H .(1)若BF =4,求△ADQ 的面积;(2)求证:CH =2BQ ;(3)如图2,BE =3,连接EF ,将△EBF 绕点B 在平面内任意旋转,取EF 的中点M ,连接AM ,CM ,将线段AM 绕点A 逆时针旋转90°得线段AN ,连接MN 、CN ,过点N 作NR ⊥AC 交AC 于点R .当线段NR 的长最小时,直接写出△CMN 的周长.答案:A解析:(1)1.8;(2)证明见解析;(3)3263351022+. 【分析】(1)利用等腰直角三角形的性质求出1322BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ,最后利用三角形面积公式即可求解;(2)如图,先作辅助线构造()AEH CFG ASA ∆∆≌,得到AH CG =,再通过转化得到2AH DQ =,最后利用AC ,得到一个相等关系,即()2AH HC BQ QD +=+,利用等式性质即可得到所求;(3)如图,通过做辅助线构造全等三角形确定出当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,接着利用勾股定理和等腰直角三角形的性质,分别求出CM 、MN 、CN 的长,相加即可.【详解】解:6AB BC ==,°90ABC =∠,AC ==∴又∵AC BD ⊥∴BD 平分AC ,且BD 是∠ABC 的角平分线∴12BD AD CD AC ====Q 点到BA 和BC 边的距离相等; ∵4BF =, ∴6342ABQBFQ S S ∆∆==, ∴32AQ FQ =,∵AF ===∴35AQ AF ==∴5QD ===,∴1 1.825ADQ S ∆=⨯⨯=, ∴△ADQ 的面积为1.8.(2)如图,作CG ⊥AC ,垂足为C ,交AF 的延长线于点G ,∴°90ACG =∠∵°45ACB CAB ==∠∠,∴°45GCB CAB ==∠∠,∵EH ⊥AF ,∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠,∴AEP CFG =∠∠∵BE BF =,BA BC =∴AE CF =,在AEH ∆和CFG ∆中,AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =;∵BD ⊥AC ,CG ⊥AC ,∴BD ∥CG ,∵D 点是AC 的中点,且BD ∥CG ,∴DQ 是ACG ∆的中位线, ∴12DQ CG =, ∴2DQ CG AH ==; ∵AC =2BD ,∴()2AH HC BQ QD +=+,∵2AH DQ =,∴CH =2BQ .(3)如图①,作AH ⊥AB ,且AH =AB ,∴∠NAH +∠HAM =∠HAM +∠BAM =90°,∴∠BAM =∠NAH ,∵AB =AH ,AM =AN ,∴()ABM AHN SAS ∆∆≌, ∴HN =BM ,∵BE =BF =3,∠EBF =90°, ∴232EF BE ==∴由M 点是EF 的中点,可得1322BM EF == ∴322NH =, ∴N 点在以H 点为圆心,322为半径的圆上,如图②,当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,为NR HR HN HR =-=-∵∠BAC =45°,∴∠HAC =45°,∴∠AHN =45°,HR =AR ,∵222HR AR AH +=,∴HR AR ===,∴22NR HR =-=, ∵AC == ∴CR AC AR =-=∴CN AN === ∵∠MAN =90°,AM =AN ,∴MN ==∴∠ABM =45°,∴∠EBM =45°,∴F 点在BA 上,E 点在CB 延长线上,如图,作MP ⊥EC ,垂足为P ,∴1322BP MP EB ===, ∴315622PC PB BC =+=+=,∴2MC ==∴MC MN CN ++=∴△CMN+.【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识,要求学生熟练掌握相关概念并能灵活应用它们,本题的综合性较强,难点在于作辅助线构造全等三角形以及线段之间的关系转化等,考查了学生综合分析和推理论证以及计算的能力,本题属于压轴题,蕴含了数形结合和转化的思想方法等. 4.如图,已知ABC 和ADE 均为等腰三角形,AC =BC ,DE =AE ,将这两个三角形放置在一起.(1)问题发现:如图①,当60ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,则CEB ∠= °,线段BD 、CE 之间的数量关系是 ;(2)拓展探究:如图②,当90ACB AED ∠∠︒==时,点B 、D 、E 在同一直线上,连接CE ,请判断CEB ∠的度数及线段BD 、CE 之间的数量关系,并说明理由;(3)解决问题:如图③,90ACB AED ∠∠︒==,25AC =,AE =2,连接CE 、BD ,在AED 绕点A 旋转的过程中,当DE BD ⊥时,请直接写出EC 的长.答案:C解析:(1)60BD CE ,=;(2)452CEB BD CE ∠︒=,=,理由见解析;(3)CE 的长为2或2【分析】(1)证明ACE ABD ≌,得出CE =BD ,AEC ADB ∠=∠,即可得出结论; (2)证明ACE ABD ∽,得出AEC ADB ∠=∠,BD =,即可得出结论; (3)先判断出BD =,再求出AB =:①当点E 在点D 上方时,先判断出四边形APDE 是矩形,求出AP =DP =AE =2,再根据勾股定理求出,BP =6,得出BD =4;②当点E 在点D 下方时,同①的方法得,AP =DP =AE =1,BP =6,进而得出BD =BP +DP =8,即可得出结论.【详解】解:(1)ABC 为等腰三角形,60AC BC ACB ∠︒=,=,∴ABC 是等边三角形,同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAE AD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒=≌()故答案为:60CEB BD CE ∠=︒=;.(2)45CEB BD ∠︒=,,理由如下:在等腰三角形ABC 中,AC =BC ,90ACB ∠︒=,45AB CAB ∴∠︒,= ,同理,45AD ADE DAE ∠∠︒,==, ∴AE AC AD AB =,DAE CAB ∠∠=, EAC DAB ∴∠∠=,ACE ABD ∴∽ ,∴BD AD CE AE==∴AEC ADB BD ∠∠=,,点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒==135AEC ∴∠︒=45CEB AEC AED ∴∠∠-∠︒==;(3)由(2)知,ACE ABD ∽, 2BD CE ∴=, 在Rt ABC 中,25AC =,2210AB AC ∴== ,①当点E 在点D 上方时,如图③,过点A 作AP BD ⊥交BD 的延长线于P ,DE BD ⊥,PDE AED APD ∴∠∠∠==,∴四边形APDE 是矩形,AE DE = ,∴矩形APDE 是正方形,2AP DP AE ∴===,在Rt APB △中,根据勾股定理得,226BP AB AP -==,4BD BP AP ∴-==,1222CE BD ∴==; ②当点E 在点D 下方时,如图④同①的方法得,AP =DP =AE =2,BP =6,∴BD =BP +DP =8,122CE BD ∴==4, 综上CE 的长为22或42.【点睛】本题是几何变换的综合题,主要考查了旋转的性质,全等三角形的判定和定理,相似三角形的判定和性质,勾股定理,等边三角形的性质,判断出三角形ACE 和三角形ABD 相似是关键.5.如图,ABD △和ACE △都是等边三角形.(1)连接CD 、BE 交于点P ,求∠BPD ;(2)连接PA ,判断线段PA 、PB 、PD 之间的数量关系并证明;(3)如图,等腰ABC 中AB =AC ,∠BAC =α(0<α<90),在ABC 内有一点M ,连接MA 、MB 、MC .当MA +MB +MC 最小时,∠ABM = (用含α的式子表示)答案:D解析:(1)60BPD ∠=︒(2)PD PB PA =+,证明见详解(3)1602α︒-【分析】(1)证明()DAC BAE SAS ≅,得ADC ABE ∠=∠,就可以证明60BPD DAB ∠=∠=︒;(2)在DP 上截取PF=PB ,连接BF ,证明()DBF ABP SAS ≅,得DF PA =,即可证明PD PB PA =+;(3)分别以AB 和AC 为边,向两边作等边三角形ABD 和等边三角形ACE ,连接BE 和CD ,交于点M ,连接AM ,此时MA MB MC ++最小,然后利用等腰三角形ADC ,求出ADC ∠的度数,即可得到ABM ∠的度数.【详解】解:(1)∵ABD △和ACE △是等边三角形,∴AD AB =,AC AE =,60DAB CAE ∠=∠=︒,∵DAB BAC CAE BAC ∠+∠=∠+∠,∴DAC BAE ∠=∠,在DAC △和BAE △中,AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩,∴()DAC BAE SAS ≅,∴ADC ABE ∠=∠,∵ADC DAB ABE BPD ∠+∠=∠+∠,∴60BPD DAB ∠=∠=︒;(2)如图,在DP 上截取PF=PB ,连接BF ,∵60BPD ∠=︒,PF PB =,∴PFB △是等边三角形,∴BF BP =,60FBP ∠=︒,∴DBA FBP ∠=∠,∵DBA FBA FBP FBA ∠-∠=∠-∠,∴DBF ABP ∠=∠,在DBF 和ABP △中,DB AB DBF ABP BF BP =⎧⎪∠=∠⎨⎪=⎩,∴()DBF ABP SAS ≅,∴DF PA =,∵PD PF FD =+,∴PD PB PA =+;(3)如图,分别以AB 和AC 为边,作等边三角形ABD 和等边三角形ACE ,连接BE 和CD ,交于点M ,连接AM ,此时MA MB MC ++最小,由(2)中的结论可得MD MA MB =+,则当D 、M 、C 三点共线时MA MB MC ++最小,即CD 的长,由(1)得ADC ABM ∠=∠,∵AD AB AC ==,60DAC α∠=︒+,∴()1806016022ADC αα︒-︒+∠==︒-, ∴1602ABM α∠=︒-,故答案是:1602α︒-.【点睛】本题考查全等三角形的性质和判定,等边三角形的性质,解题的关键是做辅助线构造全等三角形来进行证明求解.6.探究:(1)如图①,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠B=28°,则∠ACD的度数是.拓展:(2)如图②,∠MCN=90°,射线CP在∠MCN的内部,点A、B分别存CM、CN 上,分别过点A、B作AD⊥CP、BE⊥CP于点D、E,若AC=CB,则AD、DE、BE三者间的数量关系为.请说明理由;应用:(3)如图③,点A、B分别在∠MCN的边CM、CN上,射线CP在∠MCN的内部,点D、E在射线CP上,连结AD、BE、AE,且使∠MCN=∠ADP=∠BEP.当AC=BC 时,△≌△;此时如果CD=2DE,且S△CBE=6,则△ACE的面积是.答案:D解析:(1)28°(2)DE=AD﹣BE;理由见解析(3)ACD;CBE;9【分析】(1)利用直角三角形的两锐角互余,即可得出结论;(2)利用同角的余角相等判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;(3)利用等式的性质判断出∠ADC=∠CEB,进而判断出△ACD≌△CBE,得出S△ACD=S△CBE,再求出S△ADE=3,即可得出结论.【详解】解:探究:∵CD⊥AB,∴∠CDB=90°,∵∠B=28°,∴∠BCD=90°﹣∠B=68°,∵∠ACB=90°,∴∠ACD=90°﹣∠BCD=28°,故答案为:28°;拓展:(2)∵∠MCN=90°,∴∠ACD+∠BCE=90°,∵AD⊥CP,BE⊥CP,∴∠ADC =∠BEC =90°,∴∠ACD+∠CAD =90°,∴∠CAD =∠BCE ,在△ACD 和△CBE 中,ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴CD =BE ,AD =CE ,∴DE =CE ﹣CD =AD ﹣BE ,故答案为:DE =AD ﹣BE ;应用:(3)∵∠MCN =∠ACD+∠BCD ,∠MCN =∠ADP ,∴∠ADP =∠ACD+∠BCD ,∵∠ADP =∠ACD+∠CAD ,∴∠CAD =∠BCE ,∵∠ADP =∠BEP ,∴∠ADC =∠CEB ,在△ACD 和△CBE 中,ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴S △ACD =S △CBE ,∵S △CBE =6,∴S △ACD =6,∵CD =2DE ,∴S △ACD =2S △ADE ,∴S △ADE =12S △ACD =3, ∴S △ACE =S △ACD +S △ADE =9,故答案为:ACD ,CBE ,9.【点睛】此题是三角形综合题,主要考查了直角三角形的性质,同角的余角相等,等式的性质,全等三角形的判定和性质,判断出△ACD ≌△CBE 是解本题的关键.7.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗? 小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决.(1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABC S = ______________.(2)类比探究 Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒,722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积;【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚,如图1,过B 作BD ⊥AP 于点D∵APB ∠=150°∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8∴BD=4,PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483∴ABC S =234AB =25336+ (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3,在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=22,∵AP=1,∴AP 2+PP'2=1+8=9,∵AP'2=32=9,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E ,∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11,在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2,∵AP=3,∴AP 2+PP'2=9+2=11,∵AP'2=(11)2=11,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F∵∠APB=45°∴△BPF 为等腰直角三角形∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键.8.在等腰Rt ABC △中,AB AC =、90BAC ∠=︒.(1)如图1,D ,E 是等腰Rt ABC △斜边BC 上两动点,且45DAE ∠=︒,将ABE △绕点A 逆时针旋转90后,得到AFC △,连接DF .①求证:AED AFD ≌.②当3BE =,9CE =时,求DE 的长.(2)如图2,点D 是等腰Rt ABC △斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt ADE △(E 点在直线BC 的上方),当3BD =,9BC =时,求DE 的长.答案:D解析:(1)①证明见解析;②5;(2)35或317【分析】(1)①证明∠DAE=∠DAF=45°即可利用SAS 证明全等;②由①中全等可得DE=DF ,再在Rt △FDC 中利用勾股定理计算即可;(2)连接BE ,根据共顶点等腰直角三角形证明全等,再利用勾股定理计算即可。
三角形的旋转体

三角形的旋转体三角形是几何学中最基本的形状之一,它由三条线段组成,这三条线段相互连接起来形成一个封闭的图形。
但当我们将三角形在平面上旋转时,会得到一个全新的形状——三角形的旋转体。
三角形的旋转体是指将一个三角形绕着某一条边作为旋转轴进行旋转,从而形成的由曲面构成的立体图形。
根据旋转轴的不同位置,三角形的旋转体可以分为三种不同的情况:绕底边旋转、绕高旋转和绕斜边旋转。
首先,我们来看绕底边旋转的情况。
假设我们有一个底边为AB,两个顶点分别为C和D的三角形。
当我们将这个三角形以AB为旋转轴进行旋转时,我们可以得到一个旋转体,它的形状类似于一个圆锥。
圆锥的底面是一个与底边平行的圆,而侧面是由直线CD沿着旋转轴旋转形成的曲线。
接下来,我们来看绕高旋转的情况。
假设我们有一个底边为AB,高为h的三角形。
当我们以高AB为旋转轴进行旋转时,我们可以得到一个旋转体,它的形状类似于一个圆柱。
圆柱的底面是一个与底边平行的圆,而侧面是由直线AB沿着旋转轴旋转形成的曲线。
最后,我们来看绕斜边旋转的情况。
假设我们有一个斜边为AB,底边为CD的三角形。
当我们以斜边AB为旋转轴进行旋转时,我们可以得到一个旋转体,它的形状类似于一个旋转椎体。
旋转椎体的底面是一个与底边平行的椭圆,而侧面则是由直线CD沿着旋转轴旋转形成的曲线。
通过以上的描述,我们可以看出,三角形的旋转体具有多种形状,这取决于旋转轴的位置和旋转角度的大小。
不同的旋转方式会带来不同的立体效果,使得三角形的旋转体成为几何学中一个极具美感和变化性的研究对象。
总结起来,三角形的旋转体是指将三角形绕某一条边或者高进行旋转而得到的立体图形。
它的形状可以是圆锥、圆柱或者旋转椎体,具体取决于旋转轴的位置和旋转角度的大小。
这种立体图形丰富了几何学的研究内容,拓宽了我们对三角形的理解和应用。
三角形旋转全等常见模型
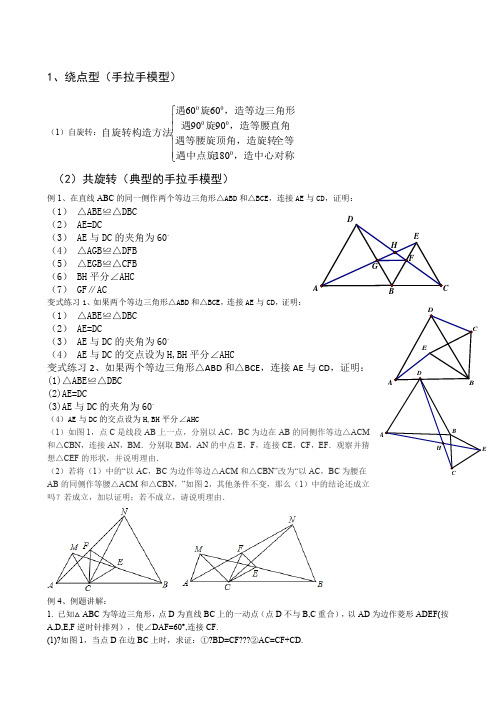
1、绕点型(手拉手模型)(1)自旋转:⎪⎪⎩⎪⎪⎨⎧,造中心对称遇中点旋全等遇等腰旋顶角,造旋转,造等腰直角旋遇,造等边三角形旋遇自旋转构造方法0000018090906060(2)共旋转(典型的手拉手模型)例1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明:(1) △ABE ≌△DBC(2) AE=DC(3) AE 与DC 的夹角为60。
(4) △AGB ≌△DFB (5) △EGB ≌△CFB (6) BH 平分∠AHC (7) GF ∥AC变式练习1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明:(1) △ABE ≌△DBC (2) AE=DC(3) AE 与DC 的夹角为60。
(4) AE 与DC 的交点设为H,BH 平分∠AHC变式练习2、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1)△ABE ≌△DBC (2)AE=DC(3)AE 与DC 的夹角为60。
(4)AE 与DC 的交点设为H,BH 平分∠AHC(1)如图1,点C 是线段AB 上一点,分别以AC ,BC 为边在AB 的同侧作等边△ACM 和△CBN ,连接AN ,BM .分别取BM ,AN 的中点E ,F ,连接CE ,CF ,EF .观察并猜想△CEF的形状,并说明理由.(2)若将(1)中的“以AC ,BC 为边作等边△ACM 和△CBN”改为“以AC ,BC 为腰在AB 的同侧作等腰△ACM 和△CBN ,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由.例4、例题讲解:1. 已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B,C 重合),以AD 为边作菱形ADEF(按A,D,E,F 逆时针排列),使∠DAF=60°,连接CF.(1)?如图1,当点D 在边BC 上时,求证:①?BD=CF???②AC=CF+CD.(2)如图2,当点D 在边BC 的延长线上且其他条件不变时,结论AC=CF+CD 是否成立?若不成立,请写出AC 、CF 、CD 之间存在的数量关系,并说明理由; ?(3)如图3,当点D 在边BC 的延长线上且其他条件不变时,补全图形,并直接写出AC 、CF 、CD 之间存在的数量关系。
三角形旋转最值问题

三角形旋转最值问题三角形旋转最值问题也称为绕心路速或三角形旋转最优化问题,是一种考虑物体旋转以达到最优化的问题。
三角形旋转最值问题可以被用于工业流程的设计,如机械加工、电路板制造等。
在这些工业流程中,物体旋转是达到最佳成果的关键,因此三角形旋转最值问题也就变得非常重要。
三角形旋转最值问题的主要目的是求得三角形旋转的最优路径,以便可以最大程度地减少旋转的距离,达到最佳的旋转效果。
为了解决三角形旋转最值问题,可以使用搜索算法、局部搜索和统计方法等,这些算法均可以被用于求解三角形旋转最值问题。
首先,搜索算法可以用于解决三角形旋转最值问题。
搜索算法是一种用于优化某种特定目标函数的算法,它首先通过在特定空间中搜索一系列可行的解来求解三角形旋转最值问题,搜索算法可以用于求解三角形的最优路径。
此外,搜索算法还可以用于求解三角形的最优旋转角度。
其次,局部搜索也可以用于三角形旋转最值问题。
局部搜索是一种用于优化目标函数的算法,它可以从当前值出发,通过对目标函数的一些微小改变来求解三角形旋转最值问题。
局部搜索可以用来求解三角形最终转弯路径,也可以用于求解三角形最优旋转角度。
另外,统计方法也可以用于三角形旋转最值问题,统计方法的主要目的在于估计物体旋转的最优路径。
统计方法可以根据实际情况来模拟物体旋转的过程,根据模拟的结果来估计出最优的旋转路径。
综上所述,三角形旋转最值问题可以通过搜索算法、局部搜索和统计方法来求解。
三角形旋转最值问题的求解可以视为一个物体从一个地点移动到另一个地点的过程,它可以用来求解三角形最终转弯路径,也可以求解三角形最优旋转角度。
三角形旋转最值问题一直是工业流程设计中重要的问题,可以帮助企业在有限的时间内,达到最佳的旋转效果。
三角形的旋转与角度计算

三角形的旋转与角度计算三角形是几何学中的基本图形之一,它由三个边和三个角组成。
在实际应用中,我们经常需要进行三角形的旋转和角度计算,以满足不同的需求。
本文将探讨三角形旋转的概念和方法,并介绍如何计算旋转后的角度。
一、三角形的旋转概念三角形的旋转是指将整个三角形绕一个旋转中心按一定角度旋转,从而得到新的三角形位置和形状的过程。
旋转可以是顺时针或逆时针方向的,旋转中心可以是三角形的顶点、质心或其他点。
二、三角形的旋转方法1. 绕顶点旋转当我们以三角形的某个顶点为中心进行旋转时,可以通过以下步骤来完成:(1)确定旋转中心,即选择一个顶点作为旋转中心;(2)确定旋转角度,即要把三角形旋转多少度;(3)按照选择的顶点为中心和确定的旋转角度,计算出旋转后的每个顶点的坐标。
2. 绕质心旋转三角形的质心是三条中线的交点,将质心作为旋转中心进行旋转,可以通过以下步骤来完成:(1)计算出三角形的质心坐标;(2)确定旋转角度,即要把三角形旋转多少度;(3)按照质心为中心和确定的旋转角度,计算出旋转后的每个顶点的坐标。
3. 绕其他点旋转除了顶点和质心外,我们还可以选择其他点作为旋转中心。
具体的旋转方法如下:(1)确定旋转中心,即选择一个非顶点、非质心的点作为旋转中心;(2)确定旋转角度,即要把三角形旋转多少度;(3)按照选择的旋转中心和确定的旋转角度,计算出旋转后的每个顶点的坐标。
三、角度计算在进行三角形旋转的过程中,我们还需要计算旋转后的角度。
角度计算可以通过以下步骤来进行:(1)确定顶点的坐标变化;(2)利用向量叉积的性质来计算旋转角度。
四、实例演示假设有一个三角形ABC,其中顶点坐标分别为A(2,4),B(5,6),C(7,8)。
现在要将该三角形绕点A逆时针旋转30度,计算旋转后的三角形的坐标和旋转角度。
首先,我们需要确定旋转后的每个顶点的坐标。
以点A为中心逆时针旋转30度后,顶点B的坐标变为(3.39, 5.10),顶点C的坐标变为(3.23, 8.46)。
旋转中的最值问题方法

旋转中的最值问题方法一、三角形旋转中的最值问题。
题目1:在等腰直角三角形ABC中,∠ ACB = 90^∘,AC = BC=√(2),将ABC绕点C逆时针旋转角α(0^∘<α<90^∘)得到A'B'C,连接A'B。
求A'B的最小值。
解析:1. 因为ABC绕点C旋转得到A'B'C,所以CA = CA'=√(2)。
2. 在A'CB中,根据余弦定理:A'B^2=A'C^2+BC^2- 2A'C· BC·cos(∠ A'CB)。
3. 由于∠ A'CB=∠ ACB+α = 90^∘+α,A'C = AC=√(2),BC=√(2)。
4. 则A'B^2=2 + 2-2×√(2)×√(2)cos(90^∘+α)=4 + 4sinα。
5. 因为0^∘<α<90^∘,当sinα = 0(即α = 0^∘)时,A'B^2取得最小值4,所以A'B的最小值为2。
题目2:已知等边三角形ABC的边长为2,点D是边BC的中点,将ABD绕点A逆时针旋转得到ACE。
求线段DE的最大值。
解析:1. 因为ABD绕点A逆时针旋转得到ACE,所以AD = AE,∠ DAE=∠ BAC = 60^∘,所以ADE是等边三角形。
2. 点D是边BC的中点,在等边三角形ABC中,AD⊥ BC,根据勾股定理可得AD=√(3)。
3. 因为ADE是等边三角形,所以DE = AD=√(3),DE的最大值就是√(3)。
题目3:在ABC中,AB = 3,AC = 4,∠ BAC = 60^∘,将ABC绕点A旋转,得到AB'C'。
求BC'的最大值。
解析:1. 由余弦定理可得BC=√(AB^2)+AC^{2-2AB· AC·cos∠ BAC}- 把AB = 3,AC = 4,∠ BAC = 60^∘代入可得:BC=√(9 + 16-2×3×4×frac{1){2}}=√(13)。
三角形旋转全等常见模型

1、绕点型(手拉手模型)(1)自旋转:自旋转构造放方法:①遇60°旋60°,构造等边三角形;②遇90°旋90°,构造等腰直角三角形;③遇等腰旋转顶角,构造旋转全等;④遇中点180°,构造中心对称。
(2)共旋转(典型的手拉手模型)例1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) AE=DC(3) AE 与DC 的夹角为60。
(4) △AGB ≌△DFB (5) △EGB ≌△CFB (6) BH 平分∠AHC (7) GF ∥AC变式练习1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC(2) AE=DC(3) AE 与DC 的夹角为60。
(4) AE 与DC 的交点设为H,BH 平分∠AHC变式练习2、如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:Array(1)△ABE≌△DBC(2)AE=DC(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分∠AHC(1)如图1,点C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边△ACM和△CBN,连接AN,BM.分别取BM,AN的中点E,F,连接CE,CF,EF.观察并猜想△CEF的形状,并说明理由.(2)若将(1)中的“以AC,BC为边作等边△ACM和△CBN”改为“以AC,BC为腰在AB的同侧作等腰△ACM和△CBN,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由.例4、例题讲解:1. 已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F逆时针排列),使∠DAF=60°,连接CF.(1) 如图1,当点D在边BC上时,求证:① BD=CF ‚②AC=CF+CD.(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系。
三角形旋转最值问题

三角形旋转最值问题三角形旋转最值问题是一个以三角形旋转行为为基本操作的复杂算法问题。
它可以简单地描述为:在三角形的内部极点处假定存在一个可以旋转的物体,给定一组边长,寻找以此边长构造的三角形,并使用此三角形内部的极点旋转,使得物体可以达到最大值的算法。
目前,三角形旋转最值问题已经成为图形学经典问题之一,这个问题在许多领域有很重要的应用,这也是它深受人们关注的原因。
三角形旋转最值问题有多种传统的解决方案,但是这些方法往往比较复杂。
为了解决这个问题,许多研究人员专注于提出更加简单的算法,以及更高的效率的算法。
自1980年以来,许多研究者已经开展了大量的研究,在这些研究中,多种解决方案已经被提出,但大多数算法以牺牲时间效率或空间效率为代价。
针对这样的问题,有一种基于折线搜索的最优解算法,也被称作折线法,它能够有效解决三角形旋转最值问题。
折线法的基本思想是:根据给定的三角形边长,建立一个搜索空间,并在搜索空间中定义一条最优的(或最小的)折线,我们称之为“最优折线”,利用这条最优折线,该算法将从而得到三角形的旋转最值。
具体来说,折线法是通过把三角形内部极点的每一种可能位置看成一个点,将所有极点组成的点集形成一个多边形,然后求解多边形中的最小折线。
折线法得到的结果是可以接受的,它能够快速得到三角形旋转最值。
在实际应用中,该算法能够解决许多复杂的问题,如视觉图形处理、机器视觉、电子器件布局等,已经发挥了重要的作用。
同时,它还具有解决复杂问题的潜力,未来可以继续探索一些新的解决方式。
总之,三角形旋转最值问题是一个复杂且受关注的研究课题,并且具有重要的应用价值。
折线法是解决这一问题的最优算法,它具有解决复杂问题的优势,对于许多领域具有重要的作用。
虽然折线法的效率略低于部分其他算法,但相较于其他算法,它更加容易理解并实现,因此,今后关于三角形旋转最值问题的研究有可能会越来越多,折线法也会得到更多的应用。
三角形旋转一周体积公式

三角形旋转一周体积公式在我们的数学世界里,三角形可是个神奇的存在。
当它旋转起来,形成的立体图形体积计算可是有讲究的。
先来说说三角形旋转一周会得到什么样的立体图形。
如果是一个直角三角形,以其中一条直角边为轴旋转一周,就会得到一个圆锥。
那这圆锥的体积公式是啥呢?这可得好好讲讲。
圆锥体积公式是:V = 1/3 × S × h (其中 V 表示体积,S 表示底面积,h 表示高)。
底面积S = π × r² (r 是底面半径)。
举个例子来说吧,还记得我之前教过的一个学生小明。
有一次上课,我正讲到三角形旋转一周的体积问题,小明听得一脸迷茫。
我就问他:“小明,哪里不懂呀?”他挠挠头说:“老师,这圆锥体积公式我不太明白,为啥要乘以 1/3 呢?”我笑了笑,拿起一个圆锥形的杯子和一个圆柱形的杯子,圆柱形杯子的底面和高都跟圆锥形杯子一样。
然后我把圆锥形杯子装满水,倒进圆柱形杯子里,倒了三次才把圆柱形杯子装满。
我对小明说:“你看,圆锥的体积是不是正好是圆柱体积的三分之一呀?”小明恍然大悟,眼睛一下子亮了起来。
在实际生活中,三角形旋转形成的圆锥体也有很多应用呢。
比如说,工地上的沙堆,很多时候就是圆锥形的。
要计算这沙堆有多少沙子,就得用到我们的圆锥体积公式。
再比如,有些冰淇淋的形状也是圆锥形。
卖冰淇淋的老板要是不知道这个体积公式,都不好估计能做多少个冰淇淋出来卖。
回到学习上来,同学们在计算三角形旋转一周形成的圆锥体积时,一定要找准底面积和高。
底面积得根据底面半径来算,高也要量准确。
可别马虎,一马虎就容易出错。
有时候,题目还会故意给大家设置点小障碍。
比如说,只告诉你圆锥的母线长度,这时候就得先通过勾股定理求出高,然后再计算体积。
这就需要大家灵活运用所学的知识啦。
总之,三角形旋转一周的体积公式虽然看起来简单,但要真正掌握,还得多多练习,多联系实际生活中的例子去理解。
这样,在遇到相关问题时,才能轻松应对,不会被难倒。
三角形角度旋转问题数学七年级下册

三角形角度旋转问题数学七年级下册三角形是几何学中的基本形状之一,它具有许多有趣的性质和定理。
在数学七年级下册的学习中,我们将接触到三角形的角度旋转问题,这是一个非常重要的内容,也是我们对三角形理解的深入之处。
让我们来了解一些基本概念。
三角形是由三条边和三个角组成的图形。
其中,三角形的内角和总是等于180度,这是一个非常重要的性质。
而在角度旋转问题中,我们主要涉及到三角形围绕某一点进行旋转的情况。
这种旋转会改变三角形的位置和朝向,但并不会改变三角形的大小和形状。
接下来,我们可以从简单的情况开始,逐步深入理解角度旋转问题。
让我们考虑围绕顶点旋转的情况。
假设我们有一个三角形ABC,我们围绕顶点A进行逆时针旋转一个角度α,那么三角形的顺序就变成了ABC'。
在这种情况下,我们可以利用三角形的性质和角度的加法性质来解决问题。
如果我们知道了三角形ABC的三个角的大小,我们就可以通过加上或减去α来得到三角形ABC'的三个角的大小。
这是一个相对简单的角度旋转问题,但它为我们理解更复杂的情况打下了基础。
让我们考虑围绕一个点旋转的情况。
假设我们有一个三角形ABC,我们围绕点O进行逆时针旋转一个角度α,那么三角形的位置和朝向就会发生改变。
在这种情况下,我们需要考虑三角形的每个顶点的坐标变化。
通过坐标变化的计算,我们可以得到旋转后三角形的新坐标,从而确定旋转后的位置和朝向。
这是一个相对复杂的角度旋转问题,但它是我们理解角度旋转问题的重要步骤。
在理解了以上两种情况后,我们可以进一步考虑更复杂的情况,例如围绕一条直线旋转或者围绕一个中心进行旋转。
通过逐步深入的学习和实践,我们可以逐渐掌握三角形的角度旋转问题,并将其运用到更广泛的数学和实际问题中。
总结回顾一下,通过本文的学习,我们对三角形角度旋转问题有了更全面、深刻和灵活的理解。
我们从简到繁地探讨了围绕顶点和围绕点旋转的情况,并逐步引入了更复杂的情况。
在学习的过程中,我们不仅掌握了解决问题的方法,也提高了数学建模和问题解决的能力。
三角形在坐标系中旋转问题

三角形在坐标系中旋转问题在坐标系中,三角形旋转的问题,嘿,听起来有点儿高深,但其实嘛,咱们可以轻松搞定。
想象一下,你的三角形就像是一位舞者,站在坐标系的舞台上,准备好好转一圈。
哎呀,想象一下那优雅的旋转,真是让人目不转睛。
你瞧,三角形有三个角,三个边,每个边都像是舞者的手臂,旋转起来那是相当迷人。
先说说怎么旋转吧。
咱们用个简单的例子。
假设这位舞者的顶点在(1,1),(3,1)和(2,4)这三个地方。
要让这位舞者顺时针旋转,咱们可以用一个旋转矩阵。
这就像是给舞者穿上了特殊的舞鞋,能够让她在舞台上轻松自如地旋转。
不管是转个小圈儿还是大圈儿,舞鞋都会把她的每一步都计算得明明白白。
好啦,咱们把焦点放在这个旋转矩阵上。
简单来说,旋转矩阵就像是一个魔法公式,让我们的三角形能够在坐标系中跳起优雅的华尔兹。
你想让她转动多少度?45度?90度?甚至360度?随你便,反正最终的效果都是闪闪发光,别提有多迷人。
比如,咱们要转90度,只需要把每个点的坐标稍微调整一下,像是给她的舞步换了个花样,结果就会变成(1,1),(1,3),(4,2)。
是不是很酷?在这里,三角形的每一个点都是它舞动的灵魂。
随着旋转,原来的坐标就变成了新的坐标。
这就像是人生的旅途,经过一番波折,总能找到新的方向。
我们在坐标系上,不就是在寻找最优的路径吗?就像在迷宫中游走,总会找到出口,嘿,这个比喻太合适了!现在,咱们再来聊聊逆时针旋转。
这个就像是换个舞伴,气氛依旧火热。
逆时针和顺时针的感觉完全不同,就像是喝咖啡和喝茶,各有各的风味。
要逆时针旋转,我们只需要在旋转矩阵中稍作修改,坐标就会变成新的姿态。
想想这过程,真是充满了惊喜。
你看,这个旋转的过程让人想起了那些老掉牙的哲学问题,比如“我是谁,我从哪里来,我要到哪里去”。
每一次旋转,都是一次重新定义自我的过程。
三角形在坐标系中的舞动,仿佛在诉说着生命的哲学。
我们每个人都有自己的舞步,有时候需要旋转,有时候需要停下脚步,审视一下自己。
三角形中心和旋转的关系

三角形中心和旋转的关系三角形中心和旋转的关系在数学中,三角形是一种基本的几何图形,有着丰富的性质和特点。
在三角形的研究中,三角形的中心是一个重要的概念,它可以帮助我们理解三角形的不同性质和特征。
同时,旋转也是三角形研究中一个重要的操作,它可以改变三角形的位置和形状。
本文将探讨三角形的中心和旋转的关系。
三角形的中心是指在三角形内部某个特殊点,它与三角形的三个顶点相关联。
在三角形的研究中,经常讨论的中心有重心、外心、内心和垂心等。
这些中心点各自有着不同的定义和特点,它们能够提供有关三角形内部和外部结构的重要信息。
在三角形中,中心点可以看作是三条边的交点或边的延长线的交点,它们之间的相对位置和距离可以反映出三角形的形状和大小。
与三角形的中心相对应的是旋转,它是指在平面上围绕某个点旋转一定角度的操作。
旋转可以改变物体的位置和形状,从而产生出不同的几何图形。
在三角形中,旋转可以将一个三角形转移到另一个位置,也可以将一个三角形变为同一个三角形的副本。
旋转可以改变三角形的朝向和方向,使其具有对称性和周期性的特征。
在研究三角形的中心和旋转之间的关系时,我们可以发现一些有趣的现象。
首先,三角形的中心点可以是旋转中心点,即三角形绕其中心点旋转的时候保持不变。
例如,三角形的重心就是一个可以作为旋转中心的点,因为三条中线交于重心,绕重心旋转可使三角形保持原状。
其次,三角形的中心点还可以是旋转中心的轨迹点,即三角形绕其中心点旋转的时候形成的轨迹。
例如,外心是三角形的外接圆心,当三角形绕外心旋转时,它会形成一个围绕外心运动的轨迹。
另外,三角形的中心点还与旋转的角度和方向相关。
当旋转角度为90度时,三角形的中心点可以在旋转后固定不变,如果三角形的重心和外心重合,那么它们也可以在旋转后固定不变。
这种情况下,三角形在旋转后具有对称性和周期性。
但是当旋转角度不是90度时,三角形的中心点通常会发生变化,旋转后的三角形也会呈现出不同的形状和位置。
三角形旋转全等常见模型
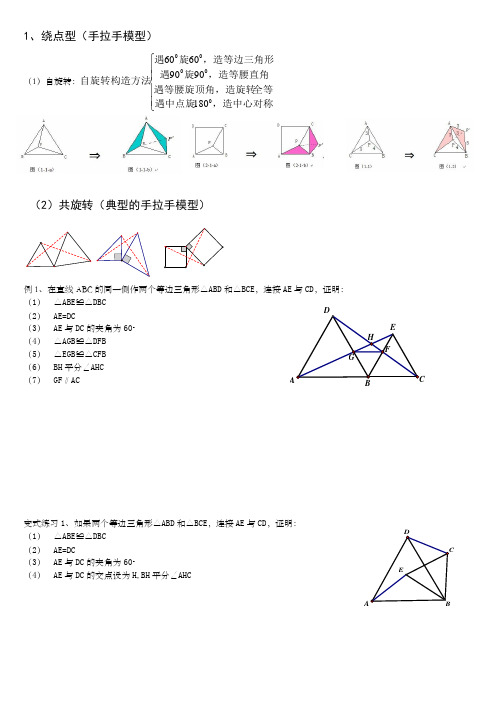
1、绕点型(手拉手模型)(1)自旋转:⎪⎪⎩⎪⎪⎨⎧,造中心对称遇中点旋全等遇等腰旋顶角,造旋转,造等腰直角旋遇,造等边三角形旋遇自旋转构造方法0000018090906060(2)共旋转(典型的手拉手模型)例1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) AE=DC(3) AE 与DC 的夹角为60。
(4) △AGB ≌△DFB (5) △EGB ≌△CFB (6) BH 平分∠AHC (7)GF ∥AC变式练习1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC(2) AE=DC(3) AE 与DC 的夹角为60。
(4) AE 与DC 的交点设为H,BH 平分∠AHCH FGE DEBD变式练习2、如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:(1)△ABE≌△DBC(2)AE=DC(3)AE与DC的夹角为60。
(4)AE与DC的交点设为H,BH平分∠AHC(1)如图1,点C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边△ACM和△CBN,连接AN,BM.分别取BM,AN的中点E,F,连接CE,CF,EF.观察并猜想△CEF的形状,并说明理由.(2)若将(1)中的“以AC,BC为边作等边△ACM和△CBN”改为“以AC,BC为腰在AB的同侧作等腰△ACM 和△CBN,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由.例4、例题讲解:1. 已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F 逆时针排列),使∠DAF=60°,连接CF.(1) 如图1,当点D在边BC上时,求证:① BD=CF ‚②AC=CF+CD.(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系。
三角形旋转解题技巧

在解决三角形的旋转问题时,需要注意以下几点技巧:
寻找旋转的关键点,确定连接对应点的方法。
根据旋转的基本性质,如线段长度不变、角度不变等,进行解答。
掌握任意多边形可分割成几个三角形的原则,以及等边多边形分割后可还原的方法。
理解并运用旋转前后线段、角度等性质的变化规律。
运用旋转的性质解决实际问题,如设计图案、构建建筑结构等。
在具体解题时,需要结合题目要求和条件,选择合适的解题方法,灵活运用旋转的性质和口诀,以得出正确答案。
同时,需要注意细节和计算准确度,避免因粗心或计算错误导致不必要的失分。
三角形旋转解题技巧初中

三角形旋转解题技巧初中引言三角形是初中数学中重要的几何图形之一,而旋转是一种常见的几何变换。
本文将介绍如何运用旋转解决与三角形相关的问题。
我们将从基本概念开始,逐步深入探讨旋转解题技巧,并通过实例演示其应用。
1. 旋转的基本概念1.1 什么是旋转?旋转是指以某个固定点为中心,按照一定的角度和方向,将图形或物体绕着该点进行移动的操作。
在数学中,我们通常以坐标平面上的原点为中心进行旋转操作。
1.2 旋转角度在二维平面上,我们使用弧度或度数来表示旋转角度。
一个完整的圆周对应360°或2π弧度。
在初中数学中,我们通常使用度数来表示旋转角度。
1.3 顺时针和逆时针顺时针方向是指按照钟表走时方向进行旋转;逆时针方向则是相反方向。
在解题过程中,需要根据具体情况确定顺时针或逆时针方向。
2. 三角形的旋转性质2.1 三角形的旋转不改变其形状和大小在二维平面上,三角形绕着一个点进行旋转后,仍然是一个三角形,并且其形状和大小保持不变。
这一性质是我们运用旋转解决三角形问题的基础。
2.2 顶点旋转当我们将一个三角形绕着顶点进行旋转时,可以通过观察发现以下性质:•旋转前后的两条边长度不变;•旋转前后的两条边夹角度数不变。
这些性质对于解题非常有用,可以帮助我们确定未知边长或夹角度数。
2.3 边中点旋转当我们将一个三角形绕着边的中点进行旋转时,可以通过观察发现以下性质:•旋转前后的两条边长度不变;•旋转前后的两条边夹角度数相等;•边中点连线在旋转前后保持不变。
这些性质同样对于解题非常有用,可以帮助我们确定未知边长或夹角度数,并且可以构造出一些特殊图形来简化问题。
3. 旋转解题技巧3.1 求未知边长当我们已知一个三角形的两条边和它们的夹角度数,需要求解第三条边长时,旋转可以帮助我们简化问题。
以顶点旋转为例,假设三角形ABC中,已知边AB和AC的长度分别为a和b,夹角BAC的度数为θ°。
我们需要求解BC的长度。
三角形的旋转

三角形的旋转三角形的旋转是指将一个三角形绕着某个点或某条边旋转一定角度,使其呈现出不同的位置和形状。
三角形的旋转是几何学中的一个重要概念,它在数学、物理和工程学等领域都有广泛的应用。
首先,我们来看一个简单的例子。
假设有一个等边三角形ABC,边长为a。
我们将它绕着顶点A逆时针旋转一定角度θ,得到新的三角形A'B'C'。
那么,如何确定新的顶点A'的坐标呢?对于顶点A的旋转,我们首先需要找到A到A'的向量。
这个向量的长度等于旋转半径,即顶点A到旋转中心的距离。
那么,如何确定旋转中心呢?一种常用的方法是通过计算三角形的重心,将重心作为旋转中心。
重心是三角形三个顶点的平均值,即(xg, yg) =((x1+x2+x3)/3, (y1+y2+y3)/3)。
然后,我们可以使用向量的加法和旋转矩阵来计算顶点A到A'的向量。
旋转矩阵用来描述旋转操作对坐标的影响。
对于逆时针旋转θ度,旋转矩阵可以表示为:R = cos(θ) -sin(θ)sin(θ) cos(θ)那么顶点A'的坐标x'和y'可以通过矩阵运算得到:x' = (x - xg) * cos(θ) - (y - yg) * sin(θ) + xgy' = (x - xg) * sin(θ) + (y - yg) * cos(θ) + yg通过上述公式,我们就可以计算出所有顶点的坐标,从而得到旋转后的三角形。
三角形的旋转不仅可以围绕一个点进行,还可以围绕一条边进行。
当我们绕着一条边旋转时,只需将旋转中心设置在这条边上即可。
例如,如果我们要将三角形ABC绕着边AB逆时针旋转,那么旋转中心就是边AB的中点。
除了上述的等边三角形外,三角形的旋转对于任意形状的三角形同样适用。
只需按照上述方法计算每个顶点的坐标即可。
三角形的旋转在实际应用中有很多重要的场景。
例如,在计算机图形学中,三角形的旋转是实现3D模型的基本操作之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形旋转三角形旋转问题考察旋转变换,三角形全等,三角形相似,三角形面积,线段长度的最值,综合性非常强。
(2011浙江宁波3分)如图,⊙O1 的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,O1O2 =8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现(A)3次(B)5次(C)6次(D)7次【答案】B。
【考点】直线与圆的位置关系,正方形的性质【分析】∵⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于P点,设O1O2交圆O1于M,∴PM=8-3-1=4。
∴圆O1与以P为圆心,以4为半径的圆相外切。
∴在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现5次。
故选B。
问题:证明边相等思路:三角形全等问题:求周长最值思路:和存在性问题结合。
列出周长函数解析式,配方法求出最值(2012四川省南充市,21,8分) 在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.(1)求证:MA=MB;(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值.若存在,求出最小值;若不存在,请说明理由.解析:(1)连接OM.证明⊿AMO ≌⊿AMO即可.(2)在Rt⊿AOB中,运用勾股定理得到求AB长的式子,转化成二次函数的问题,运用二次函数的最值求解.答案:(1)证明:连接OM.∵⊿PQR是等腰之间三角形且M是斜边PQ的中点,∴MO=MQ,∠MOA=∠MOAMQB=450.∵∠AMO+∠OMB=900,∠OMB+∠AMO =900.∴∠AMO =∠AMO.∴⊿AMO ≌⊿AMO.∴MA=MB.(2)解:由(1)中⊿AMO ≌⊿AMO得AO=BQ.设AO=x,则OB=4-x.在Rt⊿OAB中,22222+(4-)=2(-2)+8 AB OA OB x x x=+=.∴当x=2时,AB的最小值为22,∴⊿AOB的周长的最小值为22+4.点评:本题以直角三角形为基本图形,综合考查了全等三角形的性质与判定、等腰直角三角形的性质、勾股定理和二次函数的性质等知识点.考查了学生综合运用数学知识以及转化的数学思想解决问题的能力.对于几何知识与二次函数的综合,是学生解题的难点之一.难度较大例1.【2012义乌市23题】在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.考点:相似三角形的判定与性质;全等三角形的判定与性质;旋转的性质。
解答:解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,∴∠CC1B=∠C1CB=45°,∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.(2)∵△ABC≌△A1BC1,∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,∴∠ABA1=∠CBC1,∴△ABA1∽△CBC1.∴,∵S△ABA1=4,∴S△CBC1=;(3)过点B作BD⊥AC,D为垂足,∵△ABC为锐角三角形,∴点D在线段AC上,在Rt△BCD中,BD=BC×sin45°=,①如图,当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=﹣2;②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+AE=2+5=7.例2.【2012•益阳】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.(1)求出△ABE和△BCF重叠部分(即△BEG)的面积;(2)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.考点:相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;解直角三角形。
专题:几何综合题。
分析:(1)由正方形ABCD的面积等于3,即可求得此正方形的边长,由在△BGE与△ABE 中,∠GBE=∠BAE,∠EGB=∠EBA=90°,可证得△BGE∽△ABE,由相似三角形的面积比等于相似比的平方,即可求得答案;(2)首先由正切函数,求得∠BAE=30°,易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,可得AB′与AE在同一直线上,即BF与AB′的交点是G,然后设BF与AE′的交点为H,可证得△BAG≌△HAG,继而证得结论.解答:(1)解:∵正方形面积为3,∴AB=,在△BGE与△ABE中,∵∠GBE=∠BAE,∠EGB=∠EBA=90°,∴△BGE∽△ABE,∴,又∵BE=1,∴AE2=AB2+BE2=3+1=4,∴S△BGE=×S△ABE==.(2)解:没有变化.理由:∵AB=,BE=1,∴tan∠BAE==,∠BAE=30°,∵AB′=AD,∠AB′E′=∠ADE'=90°,AE′公共,∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,∴∠DAE′=∠B′AE′=∠BAE=30°,∴AB′与AE在同一直线上,即BF与AB′的交点是G,设BF与AE′的交点为H,则∠BAG=∠HAG=30°,而∠AGB=∠AGH=90°,AG公共,∴△BAG≌△HAG,∴S四边形GHE′B′=S△AB′E′﹣S△AGH=S△ABE﹣S△ABG=S△BGE.∴△ABE在旋转前后与△BCF重叠部分的面积没有变化点评:此题考查了相似三角形的判定与性质、正方形的性质、全等三角形的判定与性质以及三角函数等知识.此题综合性较强,难度较大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.求角度:旋转变换产生全等三角形,产生相等的角和相等的边,相等的边构成等腰三角形又产生相等的角,对应边的夹角都等于旋转角,利用这些角度的知识来求一些角度。
求面积:已知(或者没有)一个三角形的面积,求另一个三角形的面积。
因为三角形旋转产生很多相等的角,所以很大可能产生相似三角形。
求出相似三角形的相似比,面积比等于相似比的平方。
如果是直角三角形,可以直接求。
重叠面积是否变化:首先转化为剩下部分的面积是否变化的问题,注意点的特殊位置。
找到全等三角形或相同面积的三角形,从而把三角形面积转化为三角形的面积。
求线段最值:线段的一端固定,另一端是动点而且随着三角形旋转起来,线段的长度会变化。
当线段两端点和旋转中心共线时,出现最值。
证明三角形全等:旋转过程中的边相等,角相等,相等的角加上(或减去)公共角(或相等的角)构成新的相等角,相交线想到对顶角相等,直角三角形想到等角(同角)的余角相等。
证明三角形相似:找到两组相等角,或者夹角相等,两边成比例,这两种方法居多。
求两点距离:构造直角三角形,这两点的线段通常是斜边。
分别求出两条直角边的长度,利用勾股定理求出两点距离。
例3.【2012成都20题】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=92a时,P、Q两点间的距离(用含a的代数式表示).考点:相似三角形的判定与性质;全等三角形的判定与性质;等腰直角三角形;旋转的性质。
解答:(1)证明:∵△ABC是等腰直角三角形,∴∠B=∠C=45°,AB=AC,∵AP=AQ,∴BP=CQ,∵E是BC的中点,∴BE=CE,在△BPE和△CQE中,∵,∴△BPE≌△CQE(SAS);(2)解:∵△ABC和△DEF是两个全等的等腰直角三角形,∴∠B=∠C=∠DEF=45°,∵∠BEQ=∠EQC+∠C,即∠BEP+∠DEF=∠EQC+∠C,∴∠BEP+45°=∠EQC+45°,∴∠BEP=∠EQC,∴△BPE∽△CEQ,∴,∵BP=a,CQ=a,BE=CE,∴BE=CE=a,∴BC=3a,∴AB=AC=BC•sin45°=3a,∴AQ=CQ﹣AC=a,P A=AB﹣BP=2a,连接PQ,在Rt△APQ中,PQ==a.。
