初二数学专题练习三角形旋转

合集下载

八年级数学旋转经典练习题

1、如图△ABD和△BCD均为等边三角形,E为AD上的一个动点,F是CD上的一个动点，且∠EBF=60°。

（1）判断△EBF的形状并说明理由。

（2）若AB=4，求△EBF面积的最小值。

2、如图，在等腰直角三角形MNC中．CN=MN= ，将△MNC绕点C顺时针旋转60°，得到△ABC，连接AM，BM，BM交AC于点O．（1）求证：△CAM为等边三角形；（2）连接AN，求线段AN的长．3、如图，等腰直角△ABC中，∠ABC=90°，点D在AC上，将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE．（1）求∠DCE的度数；（2）当AB=4，AD：DC=1：3时，求DE的长．4、如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．（1）求证：AD=AF；（2）求证：BD=EF；5、如图，AD∥BC，∠D=90°．（1）如图1，若∠DAB的平分线与∠CBA的平分线交于点P，试问：点P是线段CD的中点吗？为什么？（2）如图2，如果P是DC的中点，BP平分∠ABC，∠CPB=35°，求∠PAD的度数为多少？6、已知：如图，△ABC中，AD⊥BC，BD=DE，点E在AC的垂直平分线上．（1）请问：AB、BD、DC有何数量关系？并说明理由．（2）如果∠B=60°，请问BD和DC有何数量关系？并说明理由．7、如图，已知△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，它的两边分别交AB于M，交AC于N，连接MN，求证：MN=BM+CN．8、如图，已知D是等边△ABC内一点，P是△ABC外一点，DB=DA，BP=AB，∠DBP=∠DBC．求∠BPD的度数．9、如图①已知△ACB和△DCB为等腰直角三角形，按如图的位置摆放，直角顶点C重合．（1）求证：AD=BE；（2）将△DCE绕点C旋转得到图②，点A、D、E在同一直线上时，若CD=√2，BE=3，求AB的长；（3）将△DCE绕点C顺时针旋转得到图③，若∠CBD=45°，AC=6，BD=3，求BE的长．10、（1）问题发现如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．填空：①∠AEB的度数为______；②线段AD，BE之间的数量关系为______．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．1、如图，∠AOB=90°，∠B=30°，△COD可以看作是由△AOB绕点O顺时针旋转α角度得到的．若点C在AB上，则α的大小为______．2、如图，P是正等边△ABC内一点，且PA=6，PB=8，PC=10，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与P′之间的距离的PP与∠APB的度数3、给出定义，若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，连接AD，DC，CE，已知∠DCB=30°．（1）求证：△BCE是等边三角形；（2）求证DC2+BC2=AC2，即四边形ABCD是勾股4、两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C逆时针旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F，已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，求CF的长5、如图（1），等边△ABC中，D是AB边上的动点，以CD为一边，向上作等边△EDC，连接AE．（1）△DBC和△EAC会全等吗？请说说你的理由；（2）试说明AE∥BC的理由；（3）如图（2），将（1）动点D运动到边BA的延长线上，所作仍为等边三角形，请问是否仍有AE∥BC？证明你的猜想．6、如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与EN相交于点F．（1）若△CMN的周长为15cm，求AB的长；（2）若∠MFN=70°，求∠MCN的度．7、如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF．（1）求证：AD平分∠BAC；（2）直接写出AB+AC与AE之间的等量关系．如图，等边三角形ABC中，D、E分别为AB、BC边上的两动点，且总使AD=BE，AE与CD交于点F，AG⊥CD于点G ，求的值。

初二数学专题练习三角形旋转

初二数学专题练习三角形旋转1.D为等腰Rt△ABC斜边AB的中点，DM⊥DN，DM，DN分别交BC，CA于点E，F．（1）当∠MDN绕点D转动时，求证：DE=DF．（2）若AB=2，求四边形DECF的面积．2.如图，在等腰Rt△ABC中，∠CAB=90°，P是△ABC内一点，且PA=1，PB=3，PC=．请利用旋转的方法求：∠CPA的大小．3.已知△ABC中，∠ACB=135°，将△ABC绕点A顺时针旋转90°，得到△AED，连接CD，CE．（1）求证：△ACD为等腰直角三角形；（2）若BC=1，AC=2，求四边形ACED的面积．4.如图所示，△ABC为等边三角形，以AB为边向外作△ABD，使∠ADB=120°，然后把△BCD绕着点C按顺时针方向旋转60°得到△ACE，如图所示，已知BD=5，AD=3．（1）由旋转可知线段BC，CD，BD的对应线段分别是什么？（2）求∠DAE的度数；（3）求∠BDC的度数；（4）求CE的长．5.如下图是两个等边△ABC、等边△CDE的纸片叠放在一起的图形．（1）固定△ABC，将△CDE绕点C按顺时针方向旋转30°，连AD，BE，线段BE、AD之间的大小关系如何？证明你的结论；（2）若将△CDE绕点C按顺时针方向任意旋转一个角度，连AD、BE，线段BE、AD之间大小关系如何？证明你的结论．6.将两块斜边长相等的等腰直角三角形按如图A摆放，斜边AB分别交CD、CE 于M、N点，（1）如果把图A中的△BCN绕点C逆时针旋转90°得到△ACF，连接FM，如图B，求证：△CMF≌△CMN：（2）将△CED绕点C旋转：①当点M、N在AB上（不与A、B重合）时，线段AM、MN、NB之间有一个不变的关系式，请你写出这个关系式，并说明理由；②当点M在AB上，点N在AB的延长线上（如图C）时，①中的关系式是否仍然成立？请说明理由．7.在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，①求证：△ADC≌△CEB；②若AD=3，BE=2，求DE长．（2）当直线MN绕点C旋转到图2的位置时，AD=3，BE=1.5，求DE长；（3）当直线MN绕点C旋转到图3的位置时，AD=1.5，BE=3，求DE长．8.小阳遇到这样一个问题：如图（1），O为等边△ABC内部一点，且OA：OB：OC=2，求∠AOB的度数．小阳是这样思考的：图（1）中有一个等边三角形，若将图形中一部分绕着等边三角形的某个顶点旋转60°，会得到新的等边三角形，且能达到转移线段的目的．他的作法是：如图（2），把△ACO绕点A逆时针旋转60°，使点C与点B 重合，得到△ABO′，连接OO′．则△AOO′是等边三角形，故OO′=OA，至此，通过旋转将线段OA、OB、OC转移到同一个三角形OO′B中．（1）请你回答：∠AOB=______°．（2）参考小阳思考问题的方法，解决下列问题：已知：如图（3），四边形ABCD中，AB=AD，∠DAB=60°，∠DCB=30°，AC=5，CD=4．求四边形ABCD的面积．。

初中数学《旋转》专题100题含答案

（1）试猜想四边形AB‸′是什么特殊四边形，并说明理由；
（2）连接h′，C‸，如图③，求证：四边形C‸′h是平行四边形．
24.如图，将OABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，将线段
AB绕点B顺时针旋转9to．得线段A'B，点A的对应点为A'，连接AA'交线段BC于点‸．
（1）写出点B的坐标；
（2）画出O ABC绕点0旋转1‸to后得到的图形O A1B1C1，并写出点B1的坐标?
33. 如图，在建立了平面直角坐标系的正方形网格中，A2t2，B1tt，C3t1．
（1）画出O ABC关于x轴对称的O A1B1C1．
（1）作出旋转后的图形．
（2）C‸=．
‸B
25.如图，已知正方形ABC‸中，Bh平分²‸BC且交C‸边于点h，将OBCh绕点C顺时针旋转到
O‸C′的位置，并延长Bh交‸′于点G．
（1）求证：O B‸G∽O ‸hG；
（2）若hG · BG = t，求Bh的长．
26.如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个OABC和一点0，OABC
（3）求出在O ABC旋转的过程中，点C经过的路径长．
7.正方形ABC‸的边长为3，h，′分别是AB，BC边上的点，且²h‸′=t5o．将O‸Ah绕点‸
逆时针旋转9to，得到O ‸Ch．
（1）求证：h′=′h
（2）当Ah=1时，求h′的长．
8. 如图，将OABC放于平面直角坐标系中，得到顶点坐标为A—3tt，B—3tt，Ctt3，以B为旋转中心，在平面直角坐标系内将O ABC顺时针旋转9to．
（2）将O ABC绕点0顺时针旋转9to，画出旋转后得到的O A2B2C2，并直接写出点A旋转到点A2所经过的路径长．

八年级数学旋转练习题

图形的旋转1、如图，将△ABC绕点A旋转50°后成为△AB′C′，那么点B 的对应点是_____，点C的对应点是_________，线段AB的对应线段是线段________，线段BC的对应线段是线段_________；∠B的对应角是_________，∠C的对应角是__________，旋转中心是点_______，旋转的角度是_____________；2、如图，△ABC是等腰三角形，∠BAC=36°，D是BC上一点，△ABD经过旋转后到达△ACE的位置，⑴旋转中心是哪一点？⑵旋转了多少度？⑶如果M是AB的中点，那么经过上述旋转后，点M转到了什么位置？3、如图，△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，点E在AB上，如果△ABC经旋转后能与△ADE重合，那么哪一点是旋转中心？旋转了多少度？4、如图，四边形ABCD是正方形，△DAE旋转后能与△DCF重合。

⑴旋转中心是哪一点？⑵旋转了多少度？⑶如果连接EF，那么△DEF是怎样的三角形？E ABCDEA BCDEF旋转的特征 1、如图，△ABC 按逆时针方向转动一个角后到△AB ′C ′，则线段AB=_______，AC=_______，BC=________；∠BAC=_________，∠B=_________，∠C=___________；2、画出△ABC 绕点A 逆时针90°后的图形。

3、画出所绘图形绕点D 顺时针旋转90°后的图形，再经几次90°旋转可以与原图重合？4、如图，△ACD 、△ECB 都是等边三角形，画出△ACE 以点C 为旋转中心顺时针方向旋转60°后的三角形。

A B CC′B′A B C AB C DB DE旋转对称图形1、请画出两个日常生活中旋转对称图形的实例。

2、如图所示的图形，绕哪一点旋转多少度方能与自身重合？⑴ ⑵3、在纸上任意画一个△ABC ，再任意画一个点P ，然后画出△ABC 绕点P 逆时针方向旋转45°后的三角形。

初二数学全等三角形角6090旋转知识点-+典型题含答案

初二数学全等三角形角6090旋转知识点-+典型题含答案一、全等三角形角6090旋转1．如图，在四边形ABCD 中，∠ABC ＝30°，将△DCB 绕点C 顺时针旋转60°后，点D 的对应点恰好与点A 重合，得到△ACE ，若AB ＝3，BC ＝4，求BD 的长？2．在△ABC 中90AOB ∠=︒，AO=BO ，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D(1) 当直线MN 绕点O 旋转到图①的位置时，求证：CD=AC+BD ；(2) 当直线MN 绕点O 旋转到图②的位置时，求证：CD=AC-BD ；(3) 当直线MN 绕点O 旋转到图③的位置时，试问：CD 、AC 、BD 有怎样的等量关系？请写出这个等量关系，并加以证明．3．如图，在等腰ABC 中，AC ＝AB ，∠CAB ＝90°，E 是BC 上一点，将E 点绕A 点逆时针旋转90°到AD ，连接DE 、CD ．（1）求证：ABE ACD △≌△；（2）当BC ＝6，CE ＝2时，求DE 的长．4．如图，点A 的坐标是（-2，0），点B 的坐标是（0，6），C 为OB 的中点，将△ABC 绕点B 逆时针旋转90°后得到△A′BC′，若反比例函数k y x=的图像恰好经过A′B 的中点D ，求这个反比例函数的解析式．5．如图1，ABC 与CDE △都是等腰直角三角形，直角边AC ，CD 在同一条直线上，点M 、N 分别是斜边AB 、DE 的中点，点P 为AD 的中点，连接AE ，BD ，PM ，PN ，MN ．（1）观察猜想：图1中，PM 与PN 的数量关系是______，位置关系是______．（2）探究证明：将图1中的CDE △绕着点C 顺时针旋转()090αα︒<<︒，得到图2，AE 与MP 、BD 分别交于点G 、H ，判断PMN 的形状，并说明理由；（3）拓展延伸：把CDE △绕点C 任意旋转，若4AC =，2CD =，请直接写出PMN 面积的最大值． 6．（探索发现）如图①，已知在△ABC 中，∠BAC= 45°，AD ⊥BC ，垂足为D ，BE ⊥AC ，垂足为E ，AD 与BE 相交于F ．（1）线段AF 与BC 的数量关系是：AF BC ，（用>，<，=填空）；（2）若∠ABC=67.5°，试猜想线段AF 与BD 有何数量关系，并说明理由．（拓展应用）（3）如图②，在△ABC 中，AD ⊥BC ，垂足为D ，已知∠BAC=45°，∠C=22.5°，AD=22，求△ABC的面积．7．如图1和图2，四边形ABCD中，已知AB=AD，∠BAD=90°，点E、F分别在BC、CD 上，∠EAF=45°．（1）①如图1，若∠B、∠ADC都是直角，把ABE绕点A逆时针旋转90°至ADG，使AB与AD重合，直接写出线段BE、DF和EF之间的数量关系；②如图2，若∠B、∠D都不是直角，则当∠B+∠D=180°，重复①的操作，线段BE、DF和EF之间的结论是否仍然成立，若成立，请写出证明过程，若不成立，请说明理由．（2）如图3，在ABC中，∠BAC=90°，AB=AC=22，点D、E均在边BC上，且∠DAE=45°，若BD=1，求DE的长．8．如图，点O是正△ABC内一点，∠AOB=90°，∠BOC=α，将△BOC绕点C顺时针旋转60°得到△AEC，连结OE．（1）求证，△COE是正三角形；（2）当α为何值时，AC⊥OE，并说明理由；（3）探究是否存在α的值使得点O到正△ABC三个顶点的距离之比为1:3:2，若存在请直接写出α的值，若不存在请说明理由．∠=45°，正方9．如图，在正方形ABCD中，E、F分别是边BC、CD上的点，BAF△的周长为_______．形ABCD的边长为5，则ECF10．（1）如图，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．求证：AD=BE．（2）如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE边DE上的高，连接BE．①求证：2CM+BE=AE；②若将图2中的△DCE绕点C旋转至图3所示位置，①中的结论还成立吗？若不成立，写出它们之间的数量关系．【参考答案】***试卷处理标记，请不要删除一、全等三角形角6090旋转1．5【分析】连接BE，如图，根据旋转的性质得∠BCE=60°，CB=CE，BD=AE，再判断△BCE为等边三角形得到BE=BC=4，∠CBE=60°，从而有∠ABE=90°，然后利用勾股定理计算出AE即可．【详解】解：连接BE，如图，∵△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，∠BCE=60°，CB=CE，BD=AE，∴△BCE为等边三角形，∴BE=BC=4，∠CBE=60°，∵∠ABC=30°，∴∠ABE=90°，在Rt △ABE 中，AE=223+4=5，∴BD=5．故答案为：5．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．2．（1）证明见解析；（2）证明见解析；（3）CD=BD-AC ，证明见解析.【分析】（1）通过证明△ACO ≌△ODB 得到OC=BD ，AC=OD ，则CD=AC+BD ；（2）通过证明△ACO ≌△ODB 得到OC=BD ，AC=OD ，则CD=AC-BD ；（3）通过证明△ACO ≌△ODB 得到OC=BD ，AC=OD ，则CD=BD-AC ．【详解】解：（1）如图1，∵△AOB 中，∠AOB=90°，∴∠AOC+∠BOD=90°，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D ，∴∠ACO=∠BDO=90°∴∠AOC+∠OAC=90°，∴∠OAC=∠BOD ，在△ACO 和△ODB 中，90ACO ODB OAC BOD AO OB ⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△ACO ≌△ODB （AAS ），∴OC=BD ，AC=OD ，∴CD=AC+BD ；（2）如图2，∵△AOB 中，∠AOB=90°，∴∠AOC+∠BOD=90°，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D ，∴∠ACO=∠BDO=90°∴∠AOC+∠OAC=90°，∴∠OAC=∠BOD ，在△ACO 和△ODB 中，90ACO ODB OAC BOD AO OB ⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△ACO ≌△ODB （AAS ），∴OC=BD ，AC=OD ，∴CD=OD ﹣OC=AC ﹣BD ，即CD=AC ﹣BD ．（3）如图3，∵△AOB 中，∠AOB=90°，∴∠AOC+∠BOD=90°，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D ，∴∠ACO=∠BDO=90°∴∠AOC+∠OAC=90°，∴∠OAC=∠BOD ，在△ACO 和△ODB 中，90ACO ODB OAC BOD AO OB ⎧∠=∠=⎪∠=∠⎨⎪=⎩,∴△ACO≌△ODB（AAS），∴OC=BD，AC=OD，∴CD=OC﹣OD=BD﹣AC，即CD=BD﹣AC．【点睛】此题是一道几何变换综合题，需要掌握全等三角形的判定和性质，直角三角形的性质，是一个探究题目，对于学生的能力要求比较高.3．（1）见解析；（2）【分析】（1）根据E点绕A点逆时针旋转90°到AD，可得AD＝AE，∠DAE＝90°，进而可以证明△ABE≌△ACD；（2）结合（1）△ABE≌△ACD，和等腰三角形的性质，可得∠DCE＝90°，再根据勾股定理即可求出DE的长．【详解】（1）证明：∵E点绕A点逆时针旋转90°到AD，∴AD＝AE，∠DAE＝90°，∵∠CAB＝90°，∴∠DAC＝∠EAB，∵AC＝AB，∴△ABE≌△ACD（SAS）；（2）∵等腰△ABC中，AC＝AB，∠CAB＝90°，∴∠ACB＝∠ABC＝45°，∵△ABE≌△ACD，∴BE＝CD，∠DCA＝∠ABE＝45°，∴∠DCE＝90°，∵BC＝6，CE＝2，∴BE＝4＝CD，∴DE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、等腰直角三角形的性质，解决本题的关键是综合运用以上知识．4．15yx =．【分析】作A′H⊥y轴于H．证明△AOB≌△BHA′（AAS），推出OA=BH，OB=A′H，求出点A′坐标，再利用中点坐标公式求出点D坐标即可解决问题．【详解】作A′H⊥y轴于H.∵∠AOB =∠A ′HB =∠ABA ′=90°，∴∠ABO +∠A ′BH =90°，∠ABO +∠BAO =90°，∴∠BAO =∠A ′BH ，∵BA =BA ′，∴△AOB ≌△BHA ′(AAS )，∴OA =BH ，OB =A ′H ，∵点A 的坐标是(−2,0)，点B 的坐标是(0,6)，∴OA =2，OB =6，∴BH =OA =2，A ′H =OB =6，∴OH =4，∴A ′(6,4)，∵BD =A ′D ，∴D (3,5)，∵反比例函数的图象经过点D ，∴这个反比例函数的解析式15y x =【点睛】本题考查反比例函数图形上的点的坐标特征，坐标与图形的变化-旋转等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．5．（1）PM PN =，PM PN ⊥；（2）PMN 的形状为等腰直角三角形，理由见解析；（3）PMN 的面积的最大值为92．【分析】（1）延长AE 交BD 于点H ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（2）设AE 交BC 于⊙O ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（3）易证ΔPMN 是等腰直角三角形，PM=12BD ，当B 、C 、D 共线时，BD 的值最大，进而求解．【详解】解：（1）如图1，延长AE 交BD 于点H ，∵ΔACB 和ΔECD 是等腰直角三角形，∴AC=BC ，EC=CD ，∠ACB=∠ECD=90°，∴∠ACB+∠BCE=∠ECD+∠BCE ，∴∠ACE=∠BCD ，∴ΔACE ≌ΔBCD （SAS ），∴AE=BD ，∠CAE=∠CBD ，又∵∠AEC=∠BEH ，∴∠BHA=∠ACE=90°，∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴PM=12BD ，PM//BD ，PN=12AE ，PN//AE ， ∴PM=PN ，∴PM ⊥AH ，∴PM ⊥PN ．（2）如图中，设AE 交BC 于O ．∵ACB △和ECD 是等腰直角三角形，∴AC BC =，EC CD =，90ACB ECD ∠=∠=︒∴ACB BCE ECD BCE ∠+∠=∠+∠∴ACE BCD ∠=∠.∴ACE BCD ≅∴AE BD =，CAE CBD ∠=∠又∵AOC BOE ∠=∠，CAE CBD ∠=∠，∴90BHO ACO ∠=∠=︒∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴12PM BD =，//PM BD ； PN AE =，//PN AE .∴PM PN =∴180MGE BHA ∠+∠=︒∴90MGE ∠=︒∴90MPN ∠=︒∴PM PN ⊥（3）PMN 的面积的最大值为92．由（2）可知PMN 是等腰直角三角形，12PM BD =， ∴当BD 的值最大时，PM 的值最大，PMN 的面积最大，∴当B 、C 、D 共线时，BD 的最大值6BC CD =+=，∴3PM PN ==，∴PMN 的面积的最大值193322=⨯⨯=．【点睛】本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质和判定定理，掌握旋转全等三角形模型，是解题的关键．6．（1）=；（2）AF=2BD ，见解析；（3）8【分析】（1）证出△ABE 是等腰直角三角形，得出BE=AE ，证明△CBE ≌△FAE （ASA ），即可得出结论；（2）结论：AF=2BD ．只要证明△ABC 是等腰三角形，利用等腰三角形的三线合一的性质以及（1）得到的结论即可解决问题；（3）如图中，作CH ⊥AB 交AB 的延长线于H ，延长CH 交AD 的延长线于G ．只要证明BC=2AD ，利用三角形面积公式12BC AD ⨯，即可解决问题．【详解】（1）∵∠BAC=45°，BE ⊥AC ，∴△ABE 是等腰直角三角形，∴BE=AE ，∵AD ⊥BC ，∴∠C+∠CBE=∠C+∠FAE=90°，∴∠CBE =∠FAE ，在△CBE 和△FAE 中，90 CEB FEA BE AE CBE FAE ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴△CBE ≌△FAE （ASA ），∴AF=BC ；（2）结论AF=2BD ．理由：∵∠BAC=45°，∠ABC=67.5°，∴∠C=180︒-∠BAC-∠ABC=67.5°，∴∠C=∠ABC ，∴△ABC 是等腰三角形，且AB=AC ，∵AD ⊥BC ，∴BD=CD=12BC ，由（1）得：AF=BC=2BD ；（3）如图，作CH ⊥AB 交AB 的延长线于H ，延长CH 交AD 的延长线于G ．∵∠AHC=90°，∠HAC=∠HCA=45°，∴AH=HC ，∵AD ⊥CD ，∴∠ADB=∠BHC=90°，∵∠ABD=∠CBH ，∴∠GAH=∠BCH ，∵∠AHG=∠CHB=90°，∴△AHG ≌△CHB ，∴BC=AG ，∵∠ACB=22.5°，∠HCA=45°，∴∠ACD=∠GCD=22.5°，又∵CD ⊥AG ，∴△AGC 是等腰三角形，且GC=AC ，∴2，∴2，∴△ABC 的面积为：114222822BC AD ⨯=⨯⨯=．【点睛】本题考查了全等三角形的判定和性质、等腰三角形的判定、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．7．（1）①EF=B E+DF ，②成立，见解析；（2）53【分析】（1）①根据旋转的性质得出AE=AG ，∠BAE=∠DAG ，BE=DG ，求出∠EAF=∠GAF=45°，根据SAS 推出△EAF ≌△GAF ，根据全等三角形的性质得出EF=GF ，即可求出答案； ②根据旋转的性质作辅助线，得出AE=AG ，∠B=∠ADG ，∠BAE=∠DAG ，求出C 、D 、G 在一条直线上，根据SAS 推出△EAF ≌△GAF ，根据全等三角形的性质得出EF=GF ，即可求出答案；（2）如图3，同理作旋转三角形，根据等腰直角三角形性质和勾股定理求出∠ABC=∠C=45°，BC=4，根据旋转的性质得出AF=AE ，∠FBA=∠C=45°，∠BAF=∠CAE ，求出∠FAD=∠DAE=45°，证△FAD ≌△EAD ，根据全等得出DF=DE ，设DE=x ，则DF=x ，BF=CE=3-x ，根据勾股定理得出方程，求出x 即可．【详解】（1）①如图1，∵把△ABE 绕点A 逆时针旋转90°至△ADG ，使AB 与AD 重合，AE=AG ，∠BAE=∠DAG ，BE=DG ，∠B=∠ADG=90°，∵∠ADC=90°，∴∠ADC+∠ADG=180°，∴C 、D 、G 共线，∵∠BAD=90°，∠EAF=45°，∴∠BAE+∠DAF=45°，∴∠DAG+∠DAF=45°，即∠EAF=∠GAF=45°，在△EAF 和△GAF 中，AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩，∴△EAF ≌△GAF （SAS ），∴EF=GF ，∵BE=DG ，∴EF=GF=DF+DG=BE+DF ，故答案为：EF=BE+DF ；②成立，理由：如图2，把△ABE 绕A 点旋转到△ADG ，使AB 和AD 重合，则AE=AG ，∠B=∠ADG ，∠BAE=∠DAG ，∠B+∠ADC=180°，∴∠ADC+∠ADG=180°，∴C 、D 、G 在一条直线上，与①同理得，∠EAF=∠GAF=45°，在△EAF 和△GAF 中，AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩，∴△EAF ≌△GAF （SAS ），∴EF=GF ，∵BE=DG ，∴EF=GF=BE+DF ；（2）解：∵△ABC 中，AB=AC=2，，∠BAC=90°，∴∠ABC=∠C=45°，由勾股定理得：()()222222224AB AC +=+=，如图3，把△AEC 绕A 点旋转到△AFB ，使AB 和AC 重合，连接DF ．则AF=AE ，∠FBA=∠C=45°，∠BAF=∠CAE ，∠DAE=45°，∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC-∠DAE=90°-45°=45°，∴∠FAD=∠DAE=45°，在△FAD 和△EAD 中，AD AD FAD EAD AF AE =⎧⎪∠=∠⎨⎪=⎩，∴△FAD ≌△EAD （SAS ），∴DF=DE ，设DE=x ，则DF=x ，∵BC=4，∴BF=CE=413x x --=-，∵∠FBA=45°，∠ABC=45°，∴∠FBD=90°，由勾股定理得：222DF BF BD =+，即()22231x x =-+，解得：53x =，即DE=53．【点睛】本题考查了旋转的性质，全等三角形的性质和判定，勾股定理的应用，首先在特殊图形中找到规律，然后再推广到一般图形中，对学生的分析问题，解决问题的能力要求比较高． 8．（1）证明见解析；（2）α=135°时，AC ⊥OE ；（3）存在，a=120°或150°．【分析】（1）利用旋转的性质得出CO=CE ，∠OCE=60°，即可得出答案；（2）根据∠AOB=90°，∠BOC=α，∠COE=60°，得出∠AOE=210°-α，再利用∠AEO=∠AEC-60°=∠BOC-60°得出α的度数即可；（3）根据当OE ：AO ：AE=132时以及当OA ：EO ：AE=132时，由勾股定理的逆定理及旋转的性质得出α的度数即可．【详解】（1）∵将△BOC绕点C顺时针旋转60°得到△AEC，∴CO=CE，∠OCE=60°，∴△COE是正三角形．（2）当α=135°时，AC⊥OE，理由如下：∵△COE是正三角形，AC⊥OE∴AC垂直平分OE，∴AO=AE，∴∠AOE=∠AEO，∵∠AOB=90°，∠BOC=α，∠COE=60°，∴∠AOE=210°-α，∵将△BOC绕点C顺时针旋转60°得到△AEC，∴∠AEC=∠BOC=α，∴∠AEO=∠AEC-60°=∠BOC-60°=α-60°，∴210°-α=α-60°，解得：α=135°，∴当α=135°时，AC⊥OE．（3）∵△COE是正三角形，将△BOC绕点C顺时针旋转60°得到△AEC，∴AC=BC，EC=CO=EO，BO=AE，∠AEC=∠BOC，①如图，当OC：OA：OB=1：3：2时，OE：OA：AE=1：3：2，∵12+（3）2=22，∴△AOE是直角三角形，∠AOE=90°，∴∠BOC=360°-90°-90°-60°=120°，②当OC：OB：OA=132时，EO：AE：OA=13：2时，∵12+32=22，∴△AOE是直角三角形，∠AEO=90°，∴∠BOC=∠AEC=∠AEO+∠OEC=90°+60°=150°，∴当α=120°或150°时，存在α的值使得点O 到正△ABC 三个顶点的距离之比为1：3：2．【点睛】此题主要考查了旋转的性质、等边三角形的判定与性质以及勾股定理的逆定理等知识，利用分类讨论的思想得出不同情况是此题的易错点．9．10【分析】将DAF ∆绕点A 顺时针旋转90度到BAF ∆'位置，根据旋转的性质得出45EAF ∠'=︒，进而得出FAE EAF ∆≅∆'，即可得出EF EF BE BF BE DF '==+'=+，从而可得ECF △的周长=CD CB +．【详解】解：将DAF ∆绕点A 顺时针旋转90度到BAF ∆'位置，由题意可得出：DAF BAF ∆≅∆'，DF BF ∴='，DAF BAF ∠=∠'，45EAF ∴∠'=︒，在FAE ∆和EAF ∆'中，AF AF FAE EAF AE AE ='⎧⎪∠=∠'⎨⎪=⎩，()FAE EAF SAS ∴∆≅∆'，EF EF ∴='，∴EF EF BE BF BE DF '==+'=+∴ECF △的周长=EF EC FC DF FC BE EC CD BC ++=+++=+，∵正方形ABCD 的边长为5，即==5CD BC ，∴ECF △的周长25=10⨯．故答案为：10．【点睛】此题主要考查了旋转的性质以及全等三角形的判定与性质等知识，得出FAE EAF∆≅∆'是解题关键．10．（1）答案见试题解析；（2）①答案见试题解析；②不成立，2CM-BE=AE．【详解】试题分析：（1）由全等三角形的判定方法，判断出△CAD≌△CBE，即可判断出AD=BE．（2）①由△ACB和△DCE均为等腰直角三角形，得到CA=CB，CD=CE，∠ACB=∠DCE=90°，从而有∠ACD=∠BCE，得到△ACD≌△BCE，有AD=BE，由CD=CE，CM⊥DE，得到DM=ME．由∠DCE=90°，得到DM=ME=CM，故DE=2CM，从而得到结论；②不成立．2CM-BE=AE．试题解析：（1）证明：∵∠ACB=∠DCE=90°，∴∠ACD =∠BCE，∵△ACB和△DCE均为等腰直角三角形，∴AC=BC，CD=CE，在△CAD和△CBE中，∵AC=BC，∠ACD =∠BCE ，CD=CE，∴△CAD≌△CBE，∴AD=BE．（2）①证明：∵△ACB和△DCE均为等腰直角三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=90°，∴∠ACD=∠BCE，在△ACD和△BCE中，∵CA=CB，∠ACD=∠BCE，CD=CE，∴△ACD≌△BCE，∴AD=BE，∵CD=CE，CM⊥DE，∴DM=ME．∵∠DCE=90°，∴DM=ME=CM，∴DE=2CM，∵点A，D，E在同一直线上，∴DE+AD=AE，∴2CM+BE=AE；②不成立．2CM-BE=AE．考点：1．全等三角形的判定与性质；2．等腰直角三角形．。

专题01与旋转有关的计算(30题)(原卷版)

专题第01讲与旋转有关的计算1．（2023春•秦都区期末）如图，△ABC是等边三角形，点E在AC边上，连接BE，将BE绕点B逆时针旋转60°得到BD，连接DE、AD．（1）求证：AD＝CE；（2）若BC＝8cm，BE＝7cm，求△ADE的周长．2．（2023春•北林区期末）如图，在正方形ABCD中，E，F是对角线BD上两点，且∠EAF＝45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ．（1）求证：EF＝EQ；（2）求证：EF2＝BE2+DF2．3．（2022秋•同心县期末）如图，△ABC是等边三角形，点D在AC边上，将△BCD绕点C旋转得到△ACE．（1）求证：△CDE是等边三角形；（2）若AB＝8，BD＝7，求△ADE的周长．4．（2023春•清远期末）如图，在△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．（1）求证：BC＝EF；（2）若∠ABC＝64°，∠ACB＝25°，求∠AGE的度数．5．（2023春•白银期中）如图，在四边形ABCD中，∠BCD＝120°，BC＝CD，AC⊥BD，点E在对角线BD上，将线段CE绕点C顺时针旋转120°，得到线段CF，连接DF．（1）求证：BE＝DF；（2）若EB＝EC，求证：AC⊥CF．6．（2023春•南城县期中）如图，点O是等边三角形ABC内一点，将CO绕点C顺时针旋转60°得到CD，连接OD，AO，BO，AD．（1）求证：BO＝AD；（2）若OA＝10，OB＝8，OC＝6，求∠BOC的度数．7．（2023春•罗源县校级期中）如图，先将△ABC绕点C顺时针旋转90°得到△DEC，再将线段DE绕点D顺时针旋转90°得到DG，连接BE、BG、AD，且AC＝4．（1）若∠ABC＝135°．B、E、D三点在同一条直线上，求BG的长；（2）若∠ABC＝90°，AC＝2CE，点P在边AB上，求线段PD的最小值．8．（2023春•成武县期中）已知△ABC≌△DEC，AB＝AC，AB＞BC．（1）如图（1），CB平分∠ACD，求证：四边形ABDC是菱形；（2）如图（2），将（1）中的△CDE绕点C逆时针旋转（旋转角小于∠BAC），BC，DE的延长线相交于点F，用等式表示∠ACE与∠EFC之间的数量关系，并证明．9．（2023春•九江期末）如图，在Rt△ABC中，∠BCA＝90°，将△ABC绕点A逆时针旋转至△ADE处，分别延长BC与ED交于点F，连接AF、CE．（1）求证：F A平分∠CFE；（2）若S四边形ABFD＝12，AC＝4，求CE的长．10．（2023春•盱眙县期末）如图，将矩形ABCD绕点C旋转得到矩形FECG，点E在AD上，延长ED交FG于点H．连接BE、CH．（1）四边形BEHC是怎样的特殊四边形？证明你的结论；（2）若BC长为2，则AB的长为时，四边形BEHC为菱形．11．（2023春•平山县期末）如图，PQ∥MN，A、B分别为直线MN、PQ上两点，且∠BAN＝45°，若射线AM绕点A顺时针旋转至AN后立即回转，射线BQ绕点B逆时针旋转至BP后立即回转，两射线分别绕点A、点B不停地旋转，若射线AM转动的速度是a°/秒，射线BQ转动的速度是b°/秒，且a、b满足|a﹣5|+（b﹣1）2＝0．（友情提醒：钟表指针走动的方向为顺时针方向）（1）a＝，b＝；（2）若射线AM、射线BQ同时旋转，问至少旋转多少秒时，射线AM、射线BQ互相垂直．（3）若射线AM绕点A顺时针先转动18秒，射线BQ才开始绕点B逆时针旋转，在射线BQ到达BA之前，问射线AM再转动多少秒时，射线AM、射线BQ互相平行？12．（2023春•振兴区校级期中）如图（1），在△ABC中，AB＝AC＝2，∠ABC＝30°，射线BM⊥BC于点C，动点D从点B出发沿射线BM方向运动；以每秒1个单位长度的速度运动，运动时间为t秒；（1）以点A为旋转中心，将AD逆时针旋转120°，得到线段AE，连接BE，BE是否存在最小值，不存在，则说明理由，存在则求出BE最小时的t值及BE的最小值；（2）若射线BN为∠ABM的平分线，当点D从B点出发时，点F从点A向B点与点D同时同速运动（0≤t≤2），连接FD交BN于点G，当△BGF为等腰三角形时，直接写出所有可能的t值．13．（2023春•迁安市期中）老师在黑板上出示题目：如图1，在△ABC中，∠A＝32°，∠C＝55°，线段CB′与CB边重合，CB′从现在的位置绕着点C按逆时针方向旋转一周回到原来的位置是否有一位置使CB′∥AB？如果有这样的位置，请画出示意图，并求出∠BCB′的度数，如果没有说明理由（1）（如图2）嘉嘉认为：有这样一个位置，使得CB′∥AB，如图．请你按照嘉嘉的做法，求出∠BCB′的度数．（2）（如图3）琪琪认为：嘉嘉的想法不全面，还存在另外一种情况使得CB′∥AB你是否同意琪琪的说法？如果同意，请画出图形，并求出此时∠BCB′的度数；如果不同意，请说明理由．14．（2022秋•青山湖区期末）阅读下面材料，并解决问题：（1）如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段P A、PB、PC转化到一个三角形中，从而求出∠APB＝；（2）基本运用请你利用第（1）题的解答思想方法，解答下面问题已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF2＝BE2+FC2；（3）能力提升如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．15．（2023春•清江浦区期末）如图1，MN∥PQ，点A在直线MN上，点B在直线PQ上，射线AC绕点A 顺时针从射线AM旋转至射线AN后便立即回转；射线BD绕点B顺时针从射线BP旋转至射线BQ后便立即回转：射线AC、射线BD不停地来回旋转．若射线AC转动的速度是a度/秒，射线BD转动的速度是b度/秒，且a、b是方程a+3b＝6的正整数解．（1）a＝，b＝；（2）如图2，若∠BAN＝45°，两条射线同时转动，在射线AC到达AN之前，若两条射线交于点E，过E作EF⊥AC交PQ于F，若∠BEF＝20°，求∠BAC的度数；（3）若射线BD先转动30秒，射线AC才开始转动，在射线BD到达BQ之前，射线AC转动几秒，射线AC与射线BD互相平行？16．（2023春•蒸湘区期末）如图，有一副直角三角板如图1放置（其中∠D＝45°，∠C＝30°），P A，PB 与直线MN重合，且三角板P AC，三角板PBD均可以绕点P逆时针旋转．（1）在图1中，∠DPC＝；（2）①如图2，若三角板PBD保持不动，三角板P AC绕点P逆时针旋转，转速为10°/秒，转动一周三角板P AC就停止转动，在旋转的过程中，当旋转时间为多少时，有PC∥DB成立；②如图3，在图1基础上，若三角板P AC的边P A从PN处开始绕点P逆时针旋转，转速为3°/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为2°/秒，当PC转到与PM位置重合时，两三角板都停止转动，在旋转过程中，当∠CPD＝∠BPM时，求旋转的时间是多少？17．（2023春•雄县期中）教材中有这样一道题：如图1，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG于点E，BF∥DE，且交AG于点F．求证：AF﹣BF＝EF．小明通过证明△AED≌△BF A解决了问题，在此基础上他进一步提出了以下以下回题，请你解答．（1）若图1中的点G为CB延长线上一点，其余条件不变，如图2所示，猜想此时AF，BF，EF之间的数量关系，并证明你的结论．（2）将图1中的△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为点F'，如图3所示，若正方形的边长为3，求EF'的长度．18．（2023春•长垣市期末）综合与实践数学社团的同学以“两条平行线AB，CD和一块含45°角的直角三角尺EFG（∠EFG＝90°）”为主题开展数学活动，已知点E，F不可能同时落在直线AB和CD之间．探究：（1）如图1，把三角尺的45°角的顶点E，G分别放在AB，CD上，若∠BEG＝150°，求∠FGC 的度数；类比：（2）如图2，把三角尺的锐角顶点G放在CD上，且保持不动，若点E恰好落在AB和CD之间，且AB与EF所夹锐角为25°，求∠FGC的度数；迁移：（3）把三角尺的锐角顶点G放在CD上，且保持不动，旋转三角尺，若存在∠FGC＝5∠DGE（∠DGE＜45°），直接写出射线GF与AB所夹锐角的度数．19．（2023春•阳城县期末）如图1，将一副直角三角板放在同一条直线AB上，其中∠ONM＝30°，∠OCD＝45°．（1）观察猜想：将图1中的三角尺OCD沿AB的方向平移至图2的位置，使得点O与点N重合，CD 与MN相交于点E，则∠CEN＝；（2）操作探究：将图1中的三角尺OCD绕点O按顺时针方向旋转，使一边OD在∠MON的内部，如图3，且OD恰好平分∠MON，CD与NM相交于点E，求∠CEN的度数；（3）深化拓展：将图1中的三角尺OCD绕点O按沿顺时针方向旋转一周，在旋转的过程中，当边OC 旋转多少度时，边CD恰好与边MN平行？20．（2023春•岱岳区期末）知识探究：如图1，点E是正方形ABCD对角线AC上任意一点，以点E为直角顶点的直角△EFG两边EF，EG分别角与AD，AB相交于M点，N点．当EF⊥AD时，请探究EM与EN的数量关系，并说明理由；拓展探究：当△EFG绕点E顺时针旋转到点M与点D重合时，如图2，请探究EM与EN的数量关系，并说明理由；迁移运用：在图2的基础上，过点E作EH⊥AB于点H，如图3，证明H是线段BN的中点．21．（2023春•顺平县期末）如图，正方形ABCD的对角线相交于点O，点O又是正方形EFGO的一个顶点，且这两个正方形边长相等．OE与BC相交于点M，OG与CD相交于点N．（1）求证：△OBM≌△OCN；（2）嘉琪说：当正方形EFGO绕点O转动，且OE与BC垂直时，四边形OMCN的面积最小．你同意嘉琪的说法吗？请说明理由；（3）若正方形ABCD的边长为a，用含a的代数式表示两个正方形重叠部分的面积为．22．（2023春•沈丘县期末）如图，点O在直线AB上，OC⊥AB，△ODE中，∠ODE＝90°，∠EOD＝60°，先将△ODE一边OE与OC重合，然后绕点O顺时针方向旋转，当OE与OB重合时停止旋转．（1）当OD在OA与OC之间，且∠COD＝20°时，则∠AOE＝；（2）试探索：在△ODE旋转过程中，∠AOD与∠COE大小的差是否发生变化？若不变，请求出这个差值；若变化，请说明理由；（3）在△ODE的旋转过程中，若∠AOE＝7∠COD，试求∠AOE的大小．23．（2023春•东昌府区期末）在等边三角形ABC的内部有一点D，连接BD，CD，以点B为中心，把BD 逆时针旋转630°得到HD′，连接AD′，DD′．以点C为中心，把CD顺时针旋转60°得到CD″，连接AD″，DD″．（1）判断∠D′BA和∠DBC的大小关系，并说明理由；（2）求证：D′A＝DC；（3）求证：四边形AD'DD″是平行四边形．24．（2022秋•河口区期末）感知：如图①，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点B在线段AD上，点C在线段AE上，我们很容易得到BD＝CE，不需证明．探究：如图②，将△ADE绕点A逆时针旋转α（0＜α＜90°），连结BD和CE，此时BD＝CE是否依然成立？若成立，写出证明过程；若不成立，说明理由．应用：如图③，当△ADE绕点A逆时针旋转，使得点D落在BC的延长线上，连结CE．求：①∠ACE的度数；②若AB＝AC＝2，CD＝2，则线段DE的长是多少？25．（2023春•内乡县期末）将一副直角三角板如图1，摆放在直线MN上（直角三角板ABC和直角三角板EDC，∠EDC＝90°，∠DEC＝60°，∠ABC＝90°，∠BAC＝45°），保持三角板EDC不动，将三角板ABC绕点C以每秒5°的速度顺时针旋转，旋转时间为t秒，当AC与射线CN重合时停止旋转．（1）如图2，当AC为∠DCE的角平分线时，求此时t的值；（2）当AC旋转至∠DCE的内部时，求∠DCA与∠ECB的数量关系；（3）在旋转过程中，当三角板ABC的其中一边平行于三角板EDC的某一边时，求此时t等于（直接写出答案即可）．26．（2023春•衡山县期末）一副三角板如图1摆放，∠C＝∠DFE＝90°，∠B＝30°，∠E＝45°，点F 在BC上，点A在DF上，且AF平分∠CAB，现将三角板DFE绕点F以每秒5°的速度顺时针旋转（当点D落在射线FB上时停止旋转），设旋转时间为t秒．（1）当t＝秒时，DE∥AB；当t＝秒时，DE⊥AB；（2）在旋转过程中，DF与AB的交点记为P，如图2，若△AFP有两个内角相等，求t的值；（3）当边DE与边AB、BC分别交于点M、N时，如图3，连接AE，设∠BAE＝x°，∠AED＝y°，∠DFB＝z°，试问x+y+z是否为定值？若是，请求出定值；若不是，请说明理由．27．（2023春•太原期中）如图，已知△ABC中，AB＝AC，∠BAC＝100°，点D是平面内一点，将线段AD 绕点A按逆时针方向旋转100°得到线段AE．（1）当点D在△ABC内部时，连接BD，CE．请判断线段BD与CE的数量关系，并说明理由；（2）请从A，B两题中任选一题作答．A．当点D在△ABC内部时，若直线DE恰好经过点B，直接写出∠BEC的度数．B．当点D在△ABC外部时，若直线DE恰好经过点C，直接写出∠BDC的度数．28．（2023春•遂平县期末）如图1，将一副三角板的直角重合放置，其中∠A＝30°，∠CDE＝45°．（1）如图1，求∠EFB的度数；（2）若三角板ACB的位置保持不动，将三角板CDE绕其直角顶点C顺时针方向旋转．①当旋转至如图2所示位置时，恰好CD∥AB，则∠ECB的度数为°；②若将三角板CDE继续绕点C旋转，直至回到图1位置．在这一过程中，是否还会存在△CDE其中一边与AB平行？如果存在，请你画出示意图，并直接写出相应的∠ECB的大小；如果不存在，请说明理由．29．（2023•碑林区校级模拟）似曾相识（1）如图①，正方形ABCD的边长等于4，中心为O，正方形OA′B′C′的边长也等于4，在正方形OA′B′C′绕着点O旋转的过程中，若将这两个正方形重叠部分的面积记为S，那么S是否为定值？若S为定值，请直接写出该定值；若S变化，请直接写出它的变化范围．类比探索（2）如图②，等边△ABC的边长等于4，中心为O，等边△OA′B′的边长也等于4，在等边△OA′B′绕着点O旋转的过程中，若将这两个等边三角形重叠部分的面积记为S，那么S是否为定值？若S为定值，请直接写出该定值；若S变化，请求出它的变化范围．30．（2023•青山湖区模拟）●问题发现如图1，△ABC和△DEF都是等边三角形，边BC和EF在同一直线上，O是边BC的中点，BE＝CF，连接AD，则下列结论正确的是．（填序号即可）①OE＝OF；②AD＝BE；③AD⊥BE；④整个图形是轴对称图形．●数学思考将图1中的△DEF绕着点O旋转，△ABC不动，连接AD和BE，如图2，则AD和BE具有怎样的数量和位置关系？请给出证明过程；●拓展应用已知AB＝8cm，DE＝4cm，在图1中的△DEF绕着点O旋转的过程中，当BE⊥DF时，求线段AD的长度．#ZZA0。

初二数学全等三角形角6090旋转知识点及练习题含答案

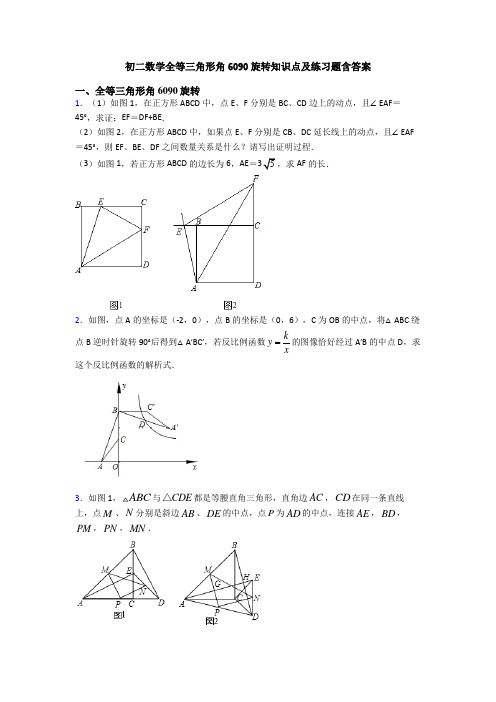
初二数学全等三角形角6090旋转知识点及练习题含答案一、全等三角形角6090旋转1．（1）如图1，在正方形ABCD中，点E、F分别是BC、CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．（2）如图2，在正方形ABCD中，如果点E、F分别是CB、DC延长线上的动点，且∠EAF ＝45°，则EF、BE、DF之间数量关系是什么？请写出证明过程．（3）如图1，若正方形ABCD的边长为6，AE＝35，求AF的长．2．如图，点A的坐标是（-2，0），点B的坐标是（0，6），C为OB的中点，将△ABC绕点B逆时针旋转90°后得到△A′BC′，若反比例函数kyx的图像恰好经过A′B的中点D，求这个反比例函数的解析式．3．如图1，ABC与CDE△都是等腰直角三角形，直角边AC，CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE，BD，PM，PN，MN．（1）观察猜想：图1中，PM 与PN 的数量关系是______，位置关系是______．（2）探究证明：将图1中的CDE △绕着点C 顺时针旋转()090αα︒<<︒，得到图2，AE 与MP 、BD 分别交于点G 、H ，判断PMN 的形状，并说明理由；（3）拓展延伸：把CDE △绕点C 任意旋转，若4AC =，2CD =，请直接写出PMN 面积的最大值． 4．已知，四边形ABCD 中，,,,120,60AB AD BC CD BA BC ABC MBN ︒︒⊥⊥=∠=∠=，MBN ∠绕B 点旋转，它的两边分别交,AD DC （或它们的延长线）于E ，F ．当MBN ∠绕B 点旋转到AE CF =时，如图（1），易证：AE CF EF +=．当MBN ∠绕B 点旋转到AE CF ≠时，在图（2）和图（3）中这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段,,AE CF EF 又有怎样的数量关系？请写出你的猜想，不需证明．5．已知：等边三角形ABC ，直线l 过点C 且与AB 平行，点D 是直线l 上不与点C 重合的一点，作射线DB ，并将射线DB 绕点D 顺时针转动60︒，与直线AC 交于点E （即60BDE ∠=︒）．（1）如图1，点E 在AC 的延长线上时，过点D 作AC 的平行线与CB 的延长线交于点F ，求证：DE DB =；（2）如图2，2AB =，4CD =，依题意补全图2，试求出DE 的长；（3）当点D 在点C 右侧时，直接写出线段CE 、BC 和CD 之间的数量关系．6．（探索发现）如图①，已知在△ABC 中，∠BAC= 45°，AD ⊥BC ，垂足为D ，BE ⊥AC ，垂足为E ，AD 与BE 相交于F ．（1）线段AF 与BC 的数量关系是：AF BC ，（用>，<，=填空）；（2）若∠ABC=67.5°，试猜想线段AF 与BD 有何数量关系，并说明理由．（拓展应用）（3）如图②，在△ABC 中，AD ⊥BC ，垂足为D ，已知∠BAC=45°，∠C=22.5°，AD=22 ，求△ABC 的面积．7．如图1，已知△ABC 是边长为8的等边三角形，∠EBD ＝30°，BE ＝DE ，连接AD ，点F 为AD 的中点，连接EF ．将△BDE 绕点B 顺时针旋转．（1）如图2，当点E 位于BC 边上时，延长DE 交AB 于点G ．①求证：BG ＝DE ；②若EF ＝3，求BE 的长；（2）如图3，连接CF ，在旋转过程中试探究线段CF 与EF 之间满足的数量关系，并说明理由．8．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 是BC 上一动点、连接AD ，过点A 作AE AD ⊥，并且始终保持AE AD =，连接CE ，（1）求证：ABD ACE ≅；（2）若AF 平分DAE ∠交BC 于F ，①探究线段BD ，DF ，FC 之间的数量关系，并证明；②若3BD =，4CF =，求AD 的长，9．如图，点O是正△ABC内一点，∠AOB=90°，∠BOC=α，将△BOC绕点C顺时针旋转60°得到△AEC，连结OE．（1）求证，△COE是正三角形；（2）当α为何值时，AC⊥OE，并说明理由；（3）探究是否存在α的值使得点O到正△ABC三个顶点的距离之比为1:3:2，若存在请直接写出α的值，若不存在请说明理由．10．（1）如图，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．求证：AD=BE．（2）如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE边DE上的高，连接BE．①求证：2CM+BE=AE；②若将图2中的△DCE绕点C旋转至图3所示位置，①中的结论还成立吗？若不成立，写出它们之间的数量关系．【参考答案】***试卷处理标记，请不要删除一、全等三角形角6090旋转1．（1）见解析；（2）EF＝DF﹣BE，见解析；（3）210【分析】（1）把△ABE绕点A顺时针旋转90°至△ADG，由“SAS”可证△EAF≌△GAF，可得出EF＝FG，则结论得证；（2）将△ABE绕点A顺时针旋转90°至△ADM，根据SAS可证明△EAF≌△MAF，可得EF ＝FM，则结论得证；（3）由全等三角形的性质可得AE＝AG＝35，EF＝FG，BE＝DG，由勾股定理可求DG的长，FD的长，AF的长．【详解】（1）把△ABE绕点A顺时针旋转90°至△ADG，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），∴EF＝FM＝DF﹣DM＝DF﹣BE；（3）如图，由（1）可得AE＝AG＝35EF＝FG，BE＝DG，∵DG2245363AG AD-=-=，∴BE＝DG＝3，∴EC＝BC﹣BE＝3，∵EF2＝EC2+CF2，∴（DF+3）2＝9+（6﹣DF）2，∴DF＝2，∴AF22AD DF+436+10．【点睛】本题考查了全等三角形的判定和性质，勾股定理，旋转等知识，此题为半角模型，∠EAF 是∠BAD的一半，故命名半角模型，半角模型必旋转，再证全等即可．2．15yx =．【分析】作A′H⊥y轴于H．证明△AOB≌△BHA′（AAS），推出OA=BH，OB=A′H，求出点A′坐标，再利用中点坐标公式求出点D 坐标即可解决问题．【详解】作A ′H ⊥y 轴于H .∵∠AOB =∠A ′HB =∠ABA ′=90°，∴∠ABO +∠A ′BH =90°，∠ABO +∠BAO =90°，∴∠BAO =∠A ′BH ，∵BA =BA ′，∴△AOB ≌△BHA ′(AAS )，∴OA =BH ，OB =A ′H ，∵点A 的坐标是(−2,0)，点B 的坐标是(0,6)，∴OA =2，OB =6，∴BH =OA =2，A ′H =OB =6，∴OH =4，∴A ′(6,4)，∵BD =A ′D ，∴D (3,5)，∵反比例函数的图象经过点D ，∴这个反比例函数的解析式15y x =【点睛】本题考查反比例函数图形上的点的坐标特征，坐标与图形的变化-旋转等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．3．（1）PM PN =，PM PN ⊥；（2）PMN 的形状为等腰直角三角形，理由见解析；（3）PMN 的面积的最大值为92．【分析】（1）延长AE 交BD 于点H ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（2）设AE 交BC 于⊙O ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（3）易证ΔPMN 是等腰直角三角形，PM=12BD ，当B 、C 、D 共线时，BD 的值最大，进而求解．【详解】解：（1）如图1，延长AE 交BD 于点H ，∵ΔACB 和ΔECD 是等腰直角三角形，∴AC=BC ，EC=CD ，∠ACB=∠ECD=90°，∴∠ACB+∠BCE=∠ECD+∠BCE ，∴∠ACE=∠BCD ，∴ΔACE ≌ΔBCD （SAS ），∴AE=BD ，∠CAE=∠CBD ，又∵∠AEC=∠BEH ，∴∠BHA=∠ACE=90°，∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴PM=12BD ，PM//BD ，PN=12AE ，PN//AE ， ∴PM=PN ，∴PM ⊥AH ，∴PM ⊥PN ．（2）如图中，设AE 交BC 于O ．∵ACB △和ECD 是等腰直角三角形，∴AC BC =，EC CD =，90ACB ECD ∠=∠=︒∴ACB BCE ECD BCE ∠+∠=∠+∠∴ACE BCD ∠=∠.∴ACE BCD ≅∴AE BD =，CAE CBD ∠=∠又∵AOC BOE ∠=∠，CAE CBD ∠=∠，∴90BHO ACO ∠=∠=︒∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴12PM BD =，//PM BD ； PN AE =，//PN AE .∴PM PN =∴180MGE BHA ∠+∠=︒∴90MGE ∠=︒∴90MPN ∠=︒∴PM PN ⊥（3）PMN 的面积的最大值为92．由（2）可知PMN 是等腰直角三角形，12PM BD =， ∴当BD 的值最大时，PM 的值最大，PMN 的面积最大，∴当B 、C 、D 共线时，BD 的最大值6BC CD =+=，∴3PM PN ==，∴PMN 的面积的最大值193322=⨯⨯=．【点睛】本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质和判定定理，掌握旋转全等三角形模型，是解题的关键．4．图（2）成立，图（3）不成立；图（2）中有AE CF EF +=，理由见解析；在图（3）中，有结论EF AE CF =-，理由见解析【分析】根据已知可以利用SAS 证明△ABE ≌△CBF ，从而得出对应角相等，对应边相等，从而得出∠ABE ＝∠CBF ＝30°，△BEF 为等边三角形，利用等边三角形的性质及边与边之间的关系，即可推出AE +CF ＝EF ．同理图2可证明是成立的，图3不成立．【详解】解：∵AB ⊥AD ，BC ⊥CD ，AB ＝BC ，AE ＝CF ，在△ABE 和△CBF 中，90AB BC A C AE CF =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABE ≌△CBF （SAS ）；∴∠ABE ＝∠CBF ，BE ＝BF ；∵∠ABC ＝120°，∠MBN ＝60°，∴∠ABE ＝∠CBF ＝30°，∴AE ＝12BE ，CF ＝12BF ； ∵∠MBN ＝60°，BE ＝BF ，∴△BEF 为等边三角形；∴AE +CF ＝12BE +12BF ＝BE ＝EF ；图2成立，图3不成立．证明图2．延长DC 至点K ，使CK ＝AE ，连接BK ，在△BAE 和△BCK 中，90AB CB A BCK AE CK =⎧⎪∠=∠=︒⎨⎪=⎩则△BAE ≌△BCK ，∴BE ＝BK ，∠ABE ＝∠KBC ，∵∠FBE ＝60°，∠ABC ＝120°，∴∠FBC +∠ABE ＝60°，∴∠FBC +∠KBC ＝60°，∴∠KBF ＝∠FBE ＝60°，在△KBF 和△EBF 中，BK BE KBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩∴△KBF ≌△EBF ，∴KF ＝EF ，∴KC +CF ＝EF ，即AE +CF ＝EF ．图3不成立，AE 、CF 、EF 的关系是AE ﹣CF ＝EF ．理由如下：延长DC 至G ，使CG ＝AE ，同理可知，△BAE≌△BCG（SAS），∴BE＝BG，∠ABE＝∠GBC，∠GBF＝∠GBC﹣∠FBC＝∠ABE﹣∠FBC＝120°+∠FBC﹣60°﹣∠FBC＝60°，∴∠GBF＝∠EBF，∵BG＝BE，∠GBF＝∠EBF，BF＝BF，∴△GBF≌△EBF，∴EF＝GF，∴AE﹣CF＝CG﹣CF＝GF＝EF．【点睛】本题几何变换综合题，考查的是全等三角形的判定和性质，正确作出辅助性、掌握全等三角形的判定定理和性质定理是解题的关键．5．（1）见解析；（2）DE的长为23或27；（3）CD= BC+CE或BC=CD+CE．【分析】（1）过点D作AC的平行线与CB的延长线交于点F．根据平行线的性质结合等边三角形的判定和性质可得出∠DFB=∠ACB=60°，∠ECD=60°，∠EDC=∠FDB，CD=DF．由此即可证出△CDE≌△BDF，从而得出DE=DB；（2）分两种情况：①当D在点C右侧时，过点D作AC的平行线与CB的延长线交于点F；②当D在点C左侧时，过点D作BC的平行线与CA于点F，作BH⊥CD于H．画出图形利用等边三角形的判定和性质、全等三角形的判定和性质分别求解即可；（3）分两种情况考虑：①当点E在AC的延长线上时，过点D作AC的平行线与CB的延长线交于点F；②当点E在线段AC上时，过点D作AC的平行线与CB交于点F．画出图形利用等边三角形的判定和性质、全等三角形的判定和性质分别求解即可．【详解】解：（1）如图1，过点D作AC的平行线与CB的延长线交于点F．∵△ABC 为等边三角形，∴∠ACB=∠ABC=60°，∵DF ∥AC ，CD ∥AB ，∴∠DFB=∠ACB=60°，∠DCF=∠ABC=60°，∴△CDF 是等边三角形，∠ECD=60°，∴∠CDF=60°，CD=DF ，∵∠BDE=60°，∴∠EDC+∠CDB=60°，∠FDB+∠CDB=60°，∴∠EDC=∠FDB ．在△CDE 和△BDF 中，有60ECD BFD CD DFEDC BDF ⎧∠=∠=⎪=⎨⎪∠=∠⎩， ∴△CDE ≌△BDF （ASA ），∴DE=DB ．（2）分两种情况：①当D 在点C 右侧时，过点D 作AC 的平行线与CB 的延长线交于点F ．如图2所示．由（1）可知，CF=CD=4，CB=AB=2，∴BF=2，∴BD 是等边三角形△CDF 的高，∴BD=32CD=23 ∴DE=BD=3②当D 在点C 左侧时，过点D 作BC 的平行线与CA 于点F ，作BH ⊥CD 于H ．如图3所示．∵△ABC 为等边三角形，∴∠ACB=∠CAB=60°，∵DF ∥BC ，CD ∥AB ，∴∠DFC=∠ACB=60°，∠DCF=∠CAB=60°，∴△CDF 是等边三角形，∠DCB=120°，∠DFE=120°，∴∠CDF=60°，CD=DF ，∵∠BDE=60°，∴∠EDF+∠FDB=60°，∠FDB+∠CDB=60°，∴∠EDF=∠CDB ．在△CDB 和△EDF 中，有120BCD EFD CD DFBDC EDF ⎧∠=∠=⎪=⎨⎪∠=∠⎩， ∴△CDB ≌△EDF （ASA ），∴DE=DB ．在R t △BCH 中，∠BCH=60°，∠CBH=30°，CB=AB=2，∴CH=1，3在R t △BDH 中，DH=DC+CH=5，3 ∴22225(3)27DB DH BH =+=+=∴DE=7，综上，DE 的长为327（3）分两种情况：①当点E 在AC 的延长线上时，过点D 作AC 的平行线与CB 的延长线交于点F ．如图1所示．由（2）可知，CD=CF ，CE=BF ，∴CD=BC+BF=BC+CE ，②当点E 在线段AC 上时，过点D 作AC 的平行线与CB 交于点F ．如图4所示．∵△ABC 为等边三角形，∴∠ACB=∠ABC=60°，∵DF ∥AC ，CD ∥AB ，∴∠DFC=∠ACB=60°，∠DCF=∠ABC=60°，∴△CDF 是等边三角形，∠CFD=60°，∴∠CDF=60°，CD=DF=CF ，∠BFD=120°，∠DCE=120°，∵∠BDE=60°，∴∠EDC+∠EDF=60°，∠FDB+∠EDF=60°，∴∠EDC=∠FDB ．在△CDE 和△BDF 中，有120ECD BFD CD DFEDC BDF ⎧∠=∠=⎪=⎨⎪∠=∠⎩， ∴△CDE ≌△BDF （ASA ），∴CE=BF ．∴BC=CF+BF=CD+CE ．综上所述，当点D 在点C 右侧时，线段CE 、BC 和CD 之间的数量关系是CD= BC+CE 或BC=CD+CE ．【点睛】本题是三角形综合题，考查了等边三角形的判定及性质，全等三角形的判定与性质，作辅助线构造等边三角形和全等三角形是解题的关键．6．（1）=；（2）AF=2BD ，见解析；（3）8【分析】（1）证出△ABE 是等腰直角三角形，得出BE=AE ，证明△CBE ≌△FAE （ASA ），即可得出结论；（2）结论：AF=2BD ．只要证明△ABC 是等腰三角形，利用等腰三角形的三线合一的性质以及（1）得到的结论即可解决问题；（3）如图中，作CH ⊥AB 交AB 的延长线于H ，延长CH 交AD 的延长线于G ．只要证明BC=2AD ，利用三角形面积公式12BC AD ⨯，即可解决问题．【详解】（1）∵∠BAC=45°，BE ⊥AC ，∴△ABE 是等腰直角三角形，∴BE=AE ，∵AD ⊥BC ，∴∠C+∠CBE=∠C+∠FAE=90°，∴∠CBE =∠FAE ，在△CBE 和△FAE 中， 90 CEB FEA BE AE CBE FAE ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴△CBE ≌△FAE （ASA ），∴AF=BC ；（2）结论AF=2BD ．理由：∵∠BAC=45°，∠ABC=67.5°，∴∠C=180︒-∠BAC-∠ABC=67.5°，∴∠C=∠ABC ，∴△ABC 是等腰三角形，且AB=AC ，∵AD ⊥BC ，∴BD=CD=12BC ，由（1）得：AF=BC=2BD ；（3）如图，作CH ⊥AB 交AB 的延长线于H ，延长CH 交AD 的延长线于G ．∵∠AHC=90°，∠HAC=∠HCA=45°，∴AH=HC ，∵AD ⊥CD ，∴∠ADB=∠BHC=90°，∵∠ABD=∠CBH ，∴∠GAH=∠BCH ，∵∠AHG=∠CHB=90°，∴△AHG ≌△CHB ，∴BC=AG ，∵∠ACB=22.5°，∠HCA=45°，∴∠ACD=∠GCD=22.5°，又∵CD ⊥AG ，∴△AGC 是等腰三角形，且GC=AC ，∴2，∴2，∴△ABC 的面积为：114222822BC AD ⨯=⨯=．【点睛】本题考查了全等三角形的判定和性质、等腰三角形的判定、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．7．（1）①见解析；②2；（2）EC 3EF ，EC ⊥EF ，见解析【分析】（1）①想办法证明△BEG 是等边三角形即可解决问题；②利用三角形的中位线定理求出AG ，再求出BG 即可解决问题．（2）结论：EC 3，EC ⊥EF ．延长DF 交CA 的延长线于M ，延长FE 到K ，使得EK ＝EF ，连接AK ，CK ，CF ，在FM 上截取FN ＝DF ，连接BN ．证明图中，红色三角形全等，推出△CFK 是等边三角形即可解决问题．【详解】（1）①证明：如图2中，∵△ABC是等边三角形，∴∠ABC＝60°，∵EB＝ED，∴∠EBD＝∠EDB＝30°，∴∠GBD＝∠ABC+∠EBD＝90°，∴∠BGD＝60°，∴△BEG是等边三角形，∴BG＝BE，∴BG＝ED．②解：由①可知，BG＝GE＝BE＝DE，又∵AF＝DF，∴AG＝2EF＝6，∵AB＝8，∴BG＝AB﹣AG＝8﹣6＝2，∴BE＝BG＝2．（2）结论：EC3，EC⊥EF．理由：如图2中，延长DF交CA的延长线于M，延长FE到K，使得EK＝EF，连接AK，CK，CF，在FM上截取FN＝DF，连接BN．∵FB＝FD＝FN，∴∠DBN＝90°，∵∠DBF＝30°，∴∠FBN＝60°，∴△FBN是等边三角形，∴BN＝BF，∵∠ABC＝∠NBF＝60°，∴∠ABN＝∠CBF，∵AB＝BC，∴△ABN≌△CBF（SAS），∴AN＝CF，∵FN＝DF，AE＝ED，∴EF∥AN，AN＝2EF，∵2EF＝FK，∴AN＝FK，AN∥FK，∴四边形ANFK是平行四边形，∴AK∥DM，AK＝FN＝BN，∴∠CAK＝∠M，∵∠AOM＝∠BON，∠OAM＝∠BNO＝120°，∴∠M＝∠OBN，∴∠ABN＝∠CAK，∵AB＝AC，∴△ABN≌△CAK（SAS），∴AN ＝CK ，∴CF ＝CK ＝FK ，∴△CFK 是等边三角形，∠CFE ＝60°∵2EF ＝FK ，∴CE ⊥FK ，∵∠EFC ＝60°，∴tan ∠CFE ＝EC EF ＝3， ∴EC ＝3EF ，EC ⊥EF ．【点睛】本题主要考查了三角形的综合应用，准确应用等边三角形的性质进行分析是关键． 8．（1）见详解（2）①结论：222BD FC DF +=，证明见详解②35【分析】（1）根据SAS ，只要证明BAD CAE ∠=∠即可解决问题；（2）①结论：222BD FC DF +=．连接EF ，进一步证明90ECF ∠=︒，DF EF =，再利用勾股定理即可得证；②过点A 作AG BC ⊥于点G ，在Rt ADG 中求出AG 、DG 即可求解．【详解】解：（1）∵AE AD ⊥∴90DAC CAE ∠+∠=︒∵90BAC ∠=︒∴90DAC BAD ∠+∠=︒∴BAD CAE ∠=∠∴在ABD △和ACE △中 AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴ABD △≌ACE △()SAS（2）①结论：222BD FC DF +=证明：连接EF ，如图：∵ABD △≌ACE △∴B ACE ∠=∠，BD CE =∴90ECF BCA ACE BCA B ∠=∠+∠=∠+∠=︒∴222FC CE EF +=∴222FC BD EF +=∵AF 平分DAE ∠∴DAF EAF ∠=∠∴在DAF △和EAF △中AD AE DAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴DAF △≌EAF △()SAS∴DF EF =∴222FC BD DF +=即222BD FC DF +=②过点A 作AG BC ⊥于点G ，如图：∵由①可知222223425DF BD FC =+=+= ∴5DF =∴35412BC BD DF FC =++=++=∵AB AC =，AG BC ⊥ ∴1112622BG AG BC ===⨯= ∴633DG BG BD =-=-= ∴在Rt ADG 中，22223635AD DG AG =+=+=故答案是：（1）见详解（2）①结论：222BD FC DF +=，证明见详解②35【点睛】本题考查了全等三角形的判定和性质、直角三角形的判定和性质以及角平分线的性质．综合性较强，属中档题，学会灵活应用相关知识点进行推理证明．9．（1）证明见解析；（2）α=135°时，AC ⊥OE ；（3）存在，a=120°或150°．【分析】（1）利用旋转的性质得出CO=CE，∠OCE=60°，即可得出答案；（2）根据∠AOB=90°，∠BOC=α，∠COE=60°，得出∠AOE=210°-α，再利用∠AEO=∠AEC-60°=∠BOC-60°得出α的度数即可；（3）根据当OE：AO：AE=1：3：2时以及当OA：EO：AE=1：3：2时，由勾股定理的逆定理及旋转的性质得出α的度数即可．【详解】（1）∵将△BOC绕点C顺时针旋转60°得到△AEC，∴CO=CE，∠OCE=60°，∴△COE是正三角形．（2）当α=135°时，AC⊥OE，理由如下：∵△COE是正三角形，AC⊥OE∴AC垂直平分OE，∴AO=AE，∴∠AOE=∠AEO，∵∠AOB=90°，∠BOC=α，∠COE=60°，∴∠AOE=210°-α，∵将△BOC绕点C顺时针旋转60°得到△AEC，∴∠AEC=∠BOC=α，∴∠AEO=∠AEC-60°=∠BOC-60°=α-60°，∴210°-α=α-60°，解得：α=135°，∴当α=135°时，AC⊥OE．（3）∵△COE是正三角形，将△BOC绕点C顺时针旋转60°得到△AEC，∴AC=BC，EC=CO=EO，BO=AE，∠AEC=∠BOC，①如图，当OC：OA：OB=1：3：2时，OE：OA：AE=1：3：2，∵12+（3）2=22，∴△AOE是直角三角形，∠AOE=90°，∴∠BOC=360°-90°-90°-60°=120°，②当OC：OB：OA=132时，EO：AE：OA=13：2时，∵12+32=22，∴△AOE是直角三角形，∠AEO=90°，∴∠BOC=∠AEC=∠AEO+∠OEC=90°+60°=150°，∴当α=120°或150°时，存在α的值使得点O到正△ABC三个顶点的距离之比为13 2．【点睛】此题主要考查了旋转的性质、等边三角形的判定与性质以及勾股定理的逆定理等知识，利用分类讨论的思想得出不同情况是此题的易错点．10．（1）答案见试题解析；（2）①答案见试题解析；②不成立，2CM-BE=AE．【详解】试题分析：（1）由全等三角形的判定方法，判断出△CAD≌△CBE，即可判断出AD=BE．（2）①由△ACB和△DCE均为等腰直角三角形，得到CA=CB，CD=CE，∠ACB=∠DCE=90°，从而有∠ACD=∠BCE，得到△ACD≌△BCE，有AD=BE，由CD=CE，CM⊥DE，得到DM=ME．由∠DCE=90°，得到DM=ME=CM，故DE=2CM，从而得到结论；②不成立．2CM-BE=AE．试题解析：（1）证明：∵∠ACB=∠DCE=90°，∴∠ACD =∠BCE，∵△ACB和△DCE均为等腰直角三角形，∴AC=BC，CD=CE，在△CAD和△CBE中，∵AC=BC，∠ACD =∠BCE ，CD=CE，∴△CAD≌△CBE，∴AD=BE．（2）①证明：∵△ACB和△DCE均为等腰直角三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=90°，∴∠ACD=∠BCE，在△ACD和△BCE中，∵CA=CB，∠ACD=∠BCE，CD=CE，∴△ACD≌△BCE，∴AD=BE，∵CD=CE，CM⊥DE，∴DM=ME．∵∠DCE=90°，∴DM=ME=CM，∴DE=2CM，∵点A，D，E在同一直线上，∴DE+AD=AE，∴2CM+BE=AE；②不成立．2CM-BE=AE．考点：1．全等三角形的判定与性质；2．等腰直角三角形．。

初二数学全等三角形旋转模型复习题及答案(1)

初二数学全等三角形旋转模型复习题及答案(1)一、全等三角形旋转模型1．ABC △和ADE 都是等腰直角三角形，CE 与BD 相交于点,M BD 交AC 于点,N CE 交AD 于点H .试确定线段BD CE 、的关系.并说明理由.解析：BD CE ⊥且BD CE =【分析】由已知条件可证明BAD CAE ≅△△，再根据全等三角形的性质，得到BD CE ∴= ADB AEC ∠=∠，在AEH △中90AEC AHE ∠+∠=︒，又AHE MHD ∠=∠，可得：90HMD ∠=︒，即可证明BD CE ⊥且BD CE =.【详解】解： ABC 和ADE 是直角三角形BAC DAE ∴∠=∠AB AC =AD AE =则BAC CAD DAE CAD ∠+∠=∠+∠即BAD CAE ∠=∠在BAD 与CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩S )AS BAD CAE ∴≅（△△BD CE ∴= ADB AEC ∠=∠在AEH △中90AEC AHE ∠+∠=︒又AHE MHD ∠=∠90ADB MHD ∴∠+∠=︒则MHD 中90HMD ∠=︒，即，BD CE ⊥，综上所述，BD CE ⊥且BD CE =.【点睛】本题主要考查三角形全等的判定方法和性质定理和等腰直角三角形的性质，从复杂的图形中找到全等三角形和“8”字形三角形是解题的关键.2．一位同学拿了两块45︒三角尺MNK ∆，ACB ∆做了一个探究活动：将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处，设4AC BC ==.（1）如图1所示，两三角尺的重叠部分为ACM ∆，则重叠部分的面积为______，周长为______.（2）将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒，得到如图2所示，此时重叠部分的面积为______，周长为______.（3）如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形，如图3所示，请你猜想此时重叠部分的面积为______.（4）在如图3所示情况下，若1AD =，求出重叠部分图形的周长.答案：A解析：（1）4，442+；（2）4，8；（3）4；（4）425+【分析】()1根据4AC BC ==，90ACB ∠=，得出AB 的值，再根据M 是AB 的中点，得出AM MC =，求出重叠部分的面积，再根据AM ，MC ，AC 的值即可求出周长；()2易得重叠部分是正方形，边长为12AC ，面积为214AC ，周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ，垂足为H 、.E 求得Rt MHD ≌Rt MEG ，则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ，MH AC ⊥于点H ，根据DMH EMH ∠∠=，MH ME =，得出Rt DHM ≌Rt EMG ，从而得出HD GE =，CE AD =，最后根据AD 和DF 的值，算出5DM =.【详解】解：()14AC BC ==，90ACB ∠=，22224442AB AC BC ∴=++= M 是AB 的中点，22AM ∴=45ACM ∠=，AM MC ∴=，∴22224⨯=，∴周长为：22224442AM MC AC ++=++=+；故答案为4，442+；()2重叠部分是正方形，∴边长为1422⨯=，面积为14444⨯⨯=，周长为248⨯=．故答案为4，8．()3过点M 分别作AC 、BC 的垂线MH 、ME ，垂足为H 、E ，M 是ABC 斜边AB 的中点，4AC BC ==，12MH BC ∴=， 12ME AC =， MH ME ∴=，又90NMK HME ∠∠==，90NMH HMK ∠∠∴+=，90EMG HMK ∠∠+=，HMD EMG ∠∠∴=，在MHD 和MEG 中，HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩， MHD ∴≌()MEG ASA ，∴阴影部分的面积等于正方形CEMH 的面积，正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=； ∴阴影部分的面积是4；故答案为4．()4如图所示，过点M 作ME BC ⊥于点E ，MH AC ⊥于点H ，∴四边形MECH 是矩形，MH CE ∴=，45A ∠=，45AMH ∠∴=，AH MH ∴=，AH CE ∴=，在Rt DHM 和Rt GEM 中，DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩， Rt DHM ∴≌.Rt GEMGE DH ∴=，AH DH CE GE ∴-=-，CG AD ∴=，1AD =，1.DH ∴=DM ∴==．∴四边形DMGC 的周长为：CE CD DM ME +++2AD CD DM =++4=+【点睛】此题考查了等腰直角三角形，利用等腰直角三角形的性质，等腰直角三角形的面积公式，正方形的面积公式，全等三角形的判定和性质求解．3．△CDE 和△AOB 是两个等腰直角三角形，∠CDE ＝∠AOB ＝90°，DC ＝DE ＝1，OA ＝OB ＝a （a ＞1）．（1）将△CDE 的顶点D 与点O 重合，连接AE ，BC ，取线段BC 的中点M ，连接OM ． ①如图1，若CD ，DE 分别与OA ，OB 边重合，则线段OM 与AE 有怎样的数量关系？请直接写出你的结果；②如图2，若CD 在△AOB 内部，请你在图2中画出完整图形，判断OM 与AE 之间的数量关系是否有变化？写出你的猜想，并加以证明；③将△CDE 绕点O 任意转动，写出OM 的取值范围（用含a 式子表示）；（2）是否存在边长最大的△AOB ，使△CDE 的三个顶点分别在△AOB 的三条边上（都不与顶点重合）？如果存在，请你画出此时的图形，并求出边长a 的值；如果不存在，请说明理由．答案：A解析：（1）①OM ＝12AE ；②OM ＝12AE ，证明详见解析；③12a -≤OM ≤12a +；（2）5【分析】（1）①利用△CDE ≌△AOB 得出BC ＝AE ，再由直角三角形斜边的中线等于斜边的一半求解．②作辅助线，利用△COF ≌△EOA 及三角形中位线得出OM ＝12AE ． ③分两种情况，当OC 与OB 重合时OM 最大，当OC 在BO 的延长线上时OM 最小，据此求出OM 的取值范围．（2）分两种情况：当顶点D 在斜边AB 上时，设点C ，点E 分别在OB ，OA 上．由DM +OM ≥OF 求出直角边a 的最大值；当顶点D 在直角边AO 上时，点C ，点E 分别在OB ，AB 上时，利用△EHD ≌△DOC ，得出OD ＝EH ，在Rt △DHE 中，运用勾股定理ED 2＝DH 2+EH 2，得出方程，由△判定出a 的最大值．【详解】解：（1）①∵△CDE 和△AOB 是两个等腰直角三角形，∴CD ＝ED ，AO ＝B 0，∠CDE ＝∠AOB ，在△CDE 和△AOB 中，CD ED CDE AOB AO BO =⎧⎪∠=∠⎨⎪=⎩∴△CDE ≌△AOB （SAS ），∴BC ＝AE∵M 为BC 中点，∴OM ＝12BC ， ∴OM ＝12AE ．②猜想：OM ＝12AE ．证明：如图2，延长BO 到F ，使OF ＝OB ，连接CF ，∵M 为BC 中点，∴OM ＝12CF ， ∵△CDE 和△AOB 是两个等腰直角三角形，∴CD ＝ED ，AO ＝BO ＝OF ，∠CDE ＝∠AOB ，∵∠AOC +∠COB ＝∠BOE +∠COB ＝90°，∴∠AOC ＝∠BOE ，∠FOC ＝∠AOE ，在△COF 和△EOA 中，CD ED FOC AOE OF AO =⎧⎪∠=∠⎨⎪=⎩∴△COF ≌△EOA ，∴CF ＝AE ，∴OM ＝12AE ． ③Ⅰ、如图3，当OC 与OB 重合时，OM 最大，OM＝11122 a a-++=Ⅱ、如图4，当OC在BO的延长线上时，OM最小，OM＝12a+﹣1＝12a-，所以12a-≤OM≤12a+，（2）解：根据△CDE的对称性，只需分两种情况：①如图5，当顶点D在斜边AB上时，设点C，点E分别在OB，OA上．作OF⊥AB于点F，取CE的中点M，连接OD，MD，OM．∵△AOB和△CDE是等腰直角三角形，∠AOB＝∠CDE＝90°，OA＝OB＝a（a＞1），DC＝DE＝1，∴AB ＝2a ，OF ＝12AB ＝22a ， ∴CE ＝2，DM ＝12CE ＝22，在RT △COE 中，OM ＝12CE ＝22，在RT △DOM 中，DM +OM ≥OD ，又∵OD ≥OF ， ∵DM +OM ≥OF ，即22+22≥22a ， ∴a ≤2，∴直角边a 的最大值为2．②如图6，当顶点D 在直角边AO 上时，点C ，点E 分别在OB ，AB 上，作EH ⊥AO 于点H ． ∵∠AOB ＝∠CDE ＝∠DHE ＝90°，∵∠HED +∠EDH ＝∠CDO +∠EDH ＝90°，∴∠HED ＝∠CDO ，∵DC ＝DE ，在△EHD 和△DOC 中，EHD COD HED CDO DE DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EHD ≌△DOC （AAS ）设OD ＝x ，∴OD ＝EH ＝AH ＝x ，DH ＝a ﹣2x ，在Rt △DHE 中，ED 2＝DH 2+EH 2，∴1＝x 2+（a ﹣2x ）2，整理得，5x 2﹣4ax +a 2﹣1＝0，∵x 是实数，∴△＝（4a ）2﹣4×5×（a 2﹣1）＝20﹣4a 2≥0，∴a 2≤5，∴a 2的最大值为5，∴a的最大值为5．综上所述，a的最大值为5．【点睛】本题主要考查了几何变换综合题及三角形全等的判定和性质，解题的关键是在取最大值时，对三角形的位置进行讨论分别求值．4．已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点(点D不与B、C重合)．以AD为边作正方形ADEF，连接CF．（1）如图1，当点D在线段BC上时，请直接写出线段BD与CF的数量关系：；（2）如图2，当点D在线段BC的延长线上时，其它条件不变，若AC=2，CD=1，则CF= ；（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系：；②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．答案：B解析：（1）BD=CF；（2）221；（3）①CD=CF+BC，②等腰三角形，见解析【分析】（1）△ABC是等腰直角三角形，利用SAS即可证明△BAD≌△CAF；（2）同（1）相同，利用SAS即可证得△BAD≌△CAF，从而证得BD=CF，即可得到CF=CD+BC，然后求出答案；（3）中的①与（1）相同，可证明BD=CF，又点D、B、C共线，故：CD=BC+CF；②由（1）猜想并证明BD⊥CF，从而可知△FCD为直角三角形，再由正方形的对角线的性质判定△AOC三边的特点，再进一步判定其形状．【详解】解：（1）证明：∵∠BAC=90°，AB=AC，∴∠ABC=∠ACB=45°，∵四边形ADEF是正方形，∴AD=AF，∠DAF=90°，∵∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°，∴∠BAD=∠CAF，在△BAD和△CAF中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAF （SAS ），∴BD=CF ，（2）与（1）同理，证△BAD ≌△CAF ；∴BD=CF ，∴CF=BC+CD ，∵AC=AB=2，CD=1，∴BC ==∴CF=1；（3）①BC 、CD 与CF 的关系：CD=BC+CF理由：与（1）同法可证△BAD ≌△CAF ，从而可得：BD=CF ，即：CD=BC+CF②△AOC 是等腰三角形理由：与（1）同法可证△BAD ≌△CAF ，可得：∠DBA=∠FCA ，又∵∠BAC=90°，AB=AC ，∴∠ABC=∠ACB=45°，则∠ABD=180°-45°=135°，∴∠ABD=∠FCA=135°∴∠DCF=135°-45°=90°∴△FCD 为直角三角形．又∵四边形ADEF 是正方形，对角线AE 与DF 相交于点O ，∴OC=12DF ， ∴OC=OA ∴△AOC 是等腰三角形．【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点，一般情况下，要证明两条线段相等，就得证明这两条线段所在的两个三角形全等，关键是掌握图形特点挖掘题目所隐含的条件．5．如图1，在等腰Rt △ABC 中，∠ABC ＝90°，AB ＝BC ＝6，过点B 作BD ⊥AC 交AC 于点D ，点E 、F 分别是线段AB 、BC 上两点，且BE ＝BF ，连接AF 交BD 于点Q ，过点E 作EH ⊥AF 交AF 于点P ，交AC 于点H ．（1）若BF ＝4，求△ADQ 的面积；（2）求证：CH ＝2BQ ；（3）如图2，BE ＝3，连接EF ，将△EBF 绕点B 在平面内任意旋转，取EF 的中点M ，连接AM ，CM ，将线段AM 绕点A 逆时针旋转90°得线段AN ，连接MN 、CN ，过点N 作NR ⊥AC 交AC 于点R ．当线段NR 的长最小时，直接写出△CMN 的周长．答案：A解析：（1）1.8；（2）证明见解析；（3）3263351022+．【分析】（1）利用等腰直角三角形的性质求出1322BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ，最后利用三角形面积公式即可求解；（2）如图，先作辅助线构造()AEH CFG ASA ∆∆≌，得到AH CG =，再通过转化得到2AH DQ =，最后利用AC ，得到一个相等关系，即()2AH HC BQ QD +=+，利用等式性质即可得到所求；（3）如图，通过做辅助线构造全等三角形确定出当HN ⊥AC ，且N 点位于H 、R 之间时，此时NR 的长最小，接着利用勾股定理和等腰直角三角形的性质，分别求出CM 、MN 、CN 的长，相加即可．【详解】解：6AB BC ==，°90ABC =∠，262AC ==∴又∵AC BD ⊥∴BD 平分AC ，且BD 是∠ABC 的角平分线 ∴1322BD AD CD AC ====Q 点到BA 和BC 边的距离相等； ∵4BF =， ∴6342ABQBFQ S S ∆∆==，∴32AQ FQ =，∵AF ===∴355AQ AF ==，∴5QD ===，∴1 1.825ADQ S ∆=⨯⨯=， ∴△ADQ 的面积为1.8．（2）如图，作CG ⊥AC ，垂足为C ，交AF 的延长线于点G ，∴°90ACG =∠∵°45ACB CAB ==∠∠，∴°45GCB CAB ==∠∠，∵EH ⊥AF ，∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠，∴AEP CFG =∠∠∵BE BF =，BA BC =∴AE CF =，在AEH ∆和CFG ∆中，AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =；∵BD ⊥AC ，CG ⊥AC ，∴BD ∥CG ，∵D 点是AC 的中点，且BD ∥CG ，∴DQ 是ACG ∆的中位线，∴12DQ CG =， ∴2DQ CG AH ==； ∵AC =2BD ，∴()2AH HC BQ QD +=+，∵2AH DQ =，∴CH ＝2BQ ．（3）如图①，作AH ⊥AB ,且AH =AB ，∴∠NAH +∠HAM =∠HAM +∠BAM =90°，∴∠BAM =∠NAH ，∵AB =AH ，AM =AN ，∴()ABM AHN SAS ∆∆≌，∴HN =BM ，∵BE =BF =3，∠EBF =90°， ∴232EF BE ==∴由M 点是EF 的中点，可得1322BM EF == ∴32NH =， ∴N 点在以H 点为圆心，322为半径的圆上，如图②，当HN ⊥AC ，且N 点位于H 、R 之间时，此时NR 的长最小，为32NR HR HN HR =-=-∵∠BAC =45°，∴∠HAC =45°，∴∠AHN =45°，HR =AR ，∵222HR AR AH +=， ∴322HR AR ===， ∴323222NR HR =-=， ∵262AC AB ==∴32CR AC AR =-=， ∴()22333221022CN AN ⎛⎫==+= ⎪⎝⎭， ∵∠MAN =90°，AM =AN ，∴235MN AN ==，∴∠ABM =45°，∴∠EBM =45°，∴F 点在BA 上，E 点在CB 延长线上，如图，作MP ⊥EC ，垂足为P ，∴1322BP MP EB ===， ∴315622PC PB BC =+=+=， ∴223262MC MP PC =+=， ∴3263351022MC MN CN ++=++， ∴△CMN 的周长为3263351022++．【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识，要求学生熟练掌握相关概念并能灵活应用它们，本题的综合性较强，难点在于作辅助线构造全等三角形以及线段之间的关系转化等，考查了学生综合分析和推理论证以及计算的能力，本题属于压轴题，蕴含了数形结合和转化的思想方法等．6．在ABC 中，,AB AC BAC α=∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接,DB DC ．（1）如图1，当60α=︒时，请直接写出线段PA 与线段CD 的数量关系是__________，DCP ∠为______度；（2）如图2，当120α=︒时，写出线段PA 和线段DC 的数量关系，并说明理由；（3）如图2，在（2）的条件下，当23AB =13BP PC +的最小值．答案：A解析：（1）PA ＝DC ，60；（2）CD 3PA ．理由见详解；（232【分析】（1）先证明△ABC ，△PBD 是等边三角形，再证明△PBA ≌△DBC ，进而线段PA 与线段CD 的数量关系，利用全等三角形的性质以及三角形内角和等于180°，解决问题即可；（2）证明△CBD ∽△ABP ，可得3CD BC PA AB== （3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ，过点B 作BG ⊥BA 于点G ，当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小，由BGP CNP ∽，得13GP NP BP CP ==，结合勾股定理求出GP ，从而得CP ，进而即可求解．【详解】（1）①证明： ∵将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，∴PB ＝PD ，∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝60°，∴△ABC ，△PBD 是等边三角形，∴∠ABC ＝∠PBD ＝60°，∴∠PBA ＝∠DBC ，∵BP ＝BD ，BA ＝BC ，∴△PBA ≌△DBC （SAS ），∴PA ＝DC ．设BD 交PC 于点O ，如图1，∵△PBA ≌△DBC ，∴∠BPA ＝∠BDC ，∵∠BOP ＝∠COD ，∴∠OBP ＝∠OCD ＝60°，即∠DCP ＝60°．故答案是：PA ＝DC ，60；（2）解：结论：CD 3．理由如下：∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝120°，∴BC ＝2•AB •cos30°3，BD ═2BP •cos30°3， ∴BC BD BA BP=3 ∵∠ABC ＝∠PBD ＝30°，∴∠ABP ＝∠CBD ，∴△CBD ∽△ABP ， ∴3CD BC PA AB== ∴CD 3；（3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ，过点B 作BG CA ⊥于点G ，则BG =AB ×sin ∠BAG 3=3，AG = AB ×cos ∠BAG 3 当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小， ∵∠BGP =∠CNP =90°，∠BPG =∠CPN ， ∴BGP CNP ∽， ∴13GP NP BP CP ==，设GP =x ，则AP 3-x ，BP =3x ，∴()22233x x +=，解得：x 324∴BP =924，AP =3-324， ∴CP =AC +AP =23+3-324=33-324， ∴13BP PC +最小值=924+13×(33-324)=3+22．【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等知识，第（1）（2）题解题的关键是正确寻找全等三角形或相似三角形解决问题，第（3）题的关键是过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ．7．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB ∠＝ °，线段BD 、CE 之间的数量关系是；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．答案：C解析：（1）60BD CE ，＝；（2）45CEB BD ∠︒＝，，理由见解析；（3）CE 的长为或【分析】（1）证明ACE ABD ≌，得出CE ＝BD ，AEC ADB ∠=∠，即可得出结论；（2）证明ACE ABD ∽，得出AEC ADB ∠=∠，BD =，即可得出结论；（3）先判断出BD =，再求出AB =：①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出AP ＝DP ＝AE ＝2，再根据勾股定理求出，BP ＝6，得出BD ＝4；②当点E 在点D 下方时，同①的方法得，AP ＝DP ＝AE ＝1，BP ＝6，进而得出BD ＝BP +DP ＝8，即可得出结论．【详解】解：（1）ABC 为等腰三角形，60AC BC ACB ∠︒＝，＝，∴ABC 是等边三角形，同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAE AD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒＝≌（）故答案为：60CEB BD CE ∠=︒=；．（2）45CEB BD ∠︒＝，，理由如下：在等腰三角形ABC 中，AC ＝BC ，90ACB ∠︒＝，45AB CAB ∴∠︒，＝，同理，45AD ADE DAE ∠∠︒，＝＝， ∴AE AC AD AB =，DAE CAB ∠∠＝， EAC DAB ∴∠∠＝，ACE ABD ∴∽ ，∴BD AD CE AE==∴2AEC ADB BD CE ∠∠＝，＝，点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒＝＝135AEC ∴∠︒＝45CEB AEC AED ∴∠∠-∠︒＝＝；（3）由（2）知，ACE ABD ∽，2BD CE ∴＝，在Rt ABC 中，25AC ＝，2210AB AC ∴＝＝，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ，DE BD ⊥，PDE AED APD ∴∠∠∠＝＝，∴四边形APDE 是矩形，AE DE ＝，∴矩形APDE 是正方形，2AP DP AE ∴＝＝＝，在Rt APB △中，根据勾股定理得，226BP AB AP -＝＝，4BD BP AP ∴-＝＝，1222CE BD ∴＝＝； ②当点E 在点D 下方时，如图④同①的方法得，AP ＝DP ＝AE ＝2，BP ＝6，∴BD ＝BP +DP ＝8，122CE BD ∴＝＝4，综上CE 的长为22或42．【点睛】本题是几何变换的综合题，主要考查了旋转的性质，全等三角形的判定和定理，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出三角形ACE和三角形ABD相似是关键．8．如图1所示，矩形ABCD中，点E，F分别为边AB，AD的中点，将△AEF绕点A逆时针旋转α（0°＜α≤360°），直线BE、DF相交于点P．（1）若AB＝AD，将△AEF绕点A逆时针旋转至如图2所示的位置，则线段BE与DF的数量关系是．（2）若AD＝nAB（n≠1），将△AEF绕点A逆时针旋转，则（1）中的结论是否仍然成立？若成立，请就图3所示的情况加以证明，若不成立，请写出正确结论，并说明理由．（3）若AB＝8，BC＝12，将△AEF旋转至AE⊥BE，请算出DP的长．答案：B解析：（1）BE＝DF；（2）不成立，结论：DF＝nBE；理由见解析（3）634或634【分析】（1）如图2中，结论：BE＝DF，BE⊥DF．证明△ABE≌△ADF（SAS），利用全等三角形的性质可得结论；（2）结论：DF＝nBE，BE⊥DF，证明△ABE∽△ADF（SAS），利用相似三角形的性质可得结论；（3）分两种情形画出图形，利用相似三角形的性质以及勾股定理求解即可．【详解】解：（1）结论：BE=DF，BE⊥DF，理由：∵四边形ABCD是矩形，AB=AD，∴四边形ABCD是正方形，AE=12AB，AF=12AD，∴AE=AF，∵∠DAB=∠EAF=90°，∴∠BAE=∠DAF，∴△ABE≌△ADF（SAS），∴BE=DF，故答案为：BE=DF；（2）结论不成立，结论：DF=nBE，∵AE=12AB，AF=12AD，AD=nAB，∴AF=nAE，∴AF∶AE=AD∶AB，∴AF∶AE=AD∶AB，∵∠DAB=∠EAF=90°，∴∠BAE=∠DAF，∴△BAE∽△DAF，∴DF∶BE=AF∶AE=n，∠ABE=∠ADF，∴DF=nBE；（3）如图4-1中，当点P在BE的延长线上时，在Rt△AEB中，∵∠AEB=90°，AB=8，AE=12AB=4，∴22AB AE-=3∵△ABE∽△ADF，∴ABAD =BE DF，∴81243∴DF=63∵四边形AEPF是矩形，∴AE=PF=4，∴PD=DF-PF=634-；如图4-2中，当点P在线段BE上时，同法可得DF=63，PF=AE=4， ∴PD=DF ＋PF=634+，综上所述，满足条件的PD 的值为634-或634+．【点睛】此题考查了矩形的性质，全等三角形的判定及性质，旋转的性质，相似三角形的判定及性质，勾股定理，注意应用分类思想解决问题，是一道较难的几何综合题． 9．已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”．请利用上面信息解决以下问题：已知Rt ABC 中，AC BC =，90C ∠=︒，D 为AB 边的中点，90EDF ∠=︒，EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．（1）当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图①），求证：12DEF CEF ABC S S S +=△△△；（2）当EDF ∠绕D 点旋转到DE 和AC 不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABCS 又有怎样的数量关系？请写出你的猜想，不需要证明．答案：D解析：（1）见解析；（2）图2成立，图3不成立：12DEF CEF ABC S S S -=△△△ 【分析】（1）根据等腰直角三角形和正方形的性质得到AED 、DFB △、EDF 、ECF △为全等的等腰直角三角形，据此即可证明；（2）对于图2：过点D 作DM AC ⊥，DN BC ⊥，根据中位线的性质和等量代换证得MD ND =和MDE NDF ∠=∠，结合90DME DNF ∠=∠=︒，证得DME DNF ∆≅∆，根据全等三角形的性质即可求证；对于图3：根据ASA 证明DME DNF ∆≅∆，根据全等三角形的性质即可求证．【详解】（1）证明：连接CD∵D 为AB 边的中点，AC BC = ∴AD=CD=BD∴45DAC DCA DCB DBC ∠=∠=∠=∠=︒ 又∵DE AC ⊥，90EDF ∠=︒，90C ∠=︒， ∴四边形ECFD 为矩形 ∴∠CFD=90° 又∵∠DCF=45° ∴CF=DF∴四边形ECFD 是正方形 ∴DE=DF∴DEF CEF DEC DFC S S S S +=+△△△△又∵12DCF DBF ABC S S S +=△△△，且DCF DBF S S =△△ ∴12DEF CEF ABC S S S +=△△△ （2）图2成立，图3不成立对于图2：过点D 作DM AC ⊥，DN BC ⊥，如图2，则90DME DNF MDN ∠=∠=∠=︒又∵90C ∠=︒ ∴DMBC ，DN AC∵D 为AB 边的中点∴根据中位线定理得到：12DN AC =，12MD BC = ∵AC=BC ∴MD=ND ∵90EDF ∠=︒∴90MDE EDN ∠+∠=︒，90NDF EDN ∠+∠=︒ ∴MDE NDF ∠=∠ 在DME ∆与DNF ∆中DME DNFMD NDMDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DME DNF ∆≅∆ ∴DME DNF S S ∆∆=∴DEF CEF DMCN DECF S S S S ∆∆==+四边形四边形∴12DMCN ABC S S =△ ∴12DEF CEF ABC S S S +=△△△对于图3：连接DC ，在DEC ∆与DBF ∆中135DCE DBF DC DBCDE BDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴DEC DBF ∆≅∆∴12DEF CFE DBC CFE ABC DBFEC S S S S S S ∆∆∆∆∆==+=+五边形 ∴12DEF CEF ABC S S S ∆∆∆-=．【点睛】本题考查了全等三角形的判定和性质，中位线的性质，等腰直角三角形的性质，题目较为综合，利用作出的辅助线将不规则的三角形转化为直角三角形进行解决． 10．如图，在四边形ABCD 中，AB AC =，AD 是对角线，60BAC ∠=︒，4B C ADB BAC ∠+∠+∠=∠，（1）求ADC ∠的度数；（2）若AD BD CD =+，求证：AD 平分BDC ∠；（3）在（2）的条件下，E 、F 分别在AC 、AB 上，连接BE 、CF ，交于点P ，使得BPC BDC ∠=∠，若7BD EF ==，15AD =，求EFP ∆的面积答案：A解析：（1）=60∠︒ADC ；（2）证明见详解；（3）4003129．【分析】（1）先由四边形内角和得到++300B C BDC ∠∠∠=︒，再由4B C ADB BAC ∠+∠+∠=∠可得答案；（2）把ABD △绕点A 逆时针旋转60︒得到ACE △，由（1）及题意易得D 、C 、E 三点共线，从而得到ADE 是等边三角形，由等边三角形的性质及旋转的性质易得60ADB E ∠=∠=︒，故得证；（3）过点B 、点F 分别作BG ⊥CD ，FH ⊥AC ，分别交CD 的延长线于点G 、AC 于点H ，连接BC ，由（2）及题意易得DC=8，由BPC BDC ∠=∠易得EBC FCA ∠=∠，进而得到AFC CEB △≌△，设AF=CE=x ，根据勾股定理得到AF 、CE 、BC 的长，最后根据BFE BPC 、的面积比等于FP 与PC 的比，进而求解即可．【详解】（1）解：=60BAC ∠︒，∴++36060300B C BDC ∠∠∠=︒-︒=︒，又BDC ADB ADC ∠=∠+∠，4B C ADB BAC ∠+∠+∠=∠，∴30024060ADC ∠=︒-︒=︒；（2）证明：把ABD △绕点A 逆时针旋转60︒得到ACE △，由（1）得：∴AD=AE ，BD=CE ，=ADC=60DAE ∠∠︒AD BD CD =+，DE=DC+CE ，∴D 、C 、E 三点共线，∴ADE 是等边三角形，∴60ADB E ∠=∠=︒， ∴60ADB ADC ∠=∠=︒，∴AD 平分BDC ∠；（3）解：过点B 、点F 分别作BG ⊥CD ，FH ⊥AC ，分别交CD 的延长线于点G 、AC 于点H ，连接BC ，由题意及（2）可得：ABC 是等边三角形，120BDC ∠=︒,∴AB=AC=BC ，60BDG ∠=︒，7BD EF ==，15AD =，∴72DG =，32BG =，DC=AD-BD=8， ∴723822GC GD DC =+=+=，在Rt BGC △中，222273231322BC BG GC ⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，又=120BPC BDC ∠=∠︒，∴18012060PBC PCB ∠+∠=︒-︒=︒，60ECP PCB ∠+∠=︒，∴=ECP EBC ∠∠，=60,FAC BCA AC BC ∠∠=︒=，∴AFC CEB △≌△，∴CE=AF ，设133,1313222CE AF x AE x AH x FH x EH x ==∴=-==∴=-，，，， ∴在Rt FHE 中，222FH EH EF +=即2223313722x x ⎛⎫⎛⎫+-= ⎪ ⎪ ⎪⎝⎭⎝⎭，解得125,8x x ==，①当CE=AF=5时，则AE=8，∴11536531322BECAFCSSAC FH ==⋅=⨯=16936532634ABEABCBECSSS =-== ∴263103163BFE ABEAFESSS=-==设BFPEFPBPCEPCSa Sb Sc Sd ====，，，，则有：a cb d FP PC ==∶∶∶，,BFE BFPFEP BEC BPCEPC SSSSSS=+=+，∴BFEBECSSFP PC =∶∶，∴6465BFE BECSS FP PC =∶∶，又11522FECSCE FH =⋅=⨯=∴64641291294129EFP FECSS ==⨯=； ②当CE=AF=8时，AE=5，则有：∴111322BEAAFCSSAC FH ==⋅=⨯=，1694CBEABCBECSSS =-==∴654BFEABEAFESSS=-=-=由①可得：25104BFEBECSS FP PC =∶∶，又11822FECSCE FH =⋅=⨯⨯=∴2525129129EFPFECSS ==⨯=综上所述：EFPS =【点睛】本题主要考查三角形与四边形的综合问题，主要是利用全等三角形、等边三角形、三角形面积比的转换及勾股定理，熟练掌握各个知识点是解题的关键，尤其是第三问的面积转换问题是本题的难点．11．（1）问题感知如图1，在△ABC 中，∠C ＝90°，且AC ＝BC ，点P 是边AC 的中点，连接BP ，将线段PB 绕点P 顺时针旋转90°到线段PD ．连接AD ．过点P 作PE ∥AB 交BC 于点E ，则图中与△BEP 全等的三角形是，∠BAD ＝ °；（2）问题拓展如图2，在△ABC 中，AC ＝BC ＝43AB ，点P 是CA 延长线上一点，连接BP ，将线段PB 绕点P 顺时针旋转到线段PD ，使得∠BPD ＝∠C ，连接AD ，则线段CP 与AD 之间存在的数量关系为CP ＝43AD ，请给予证明；（3）问题解决如图3，在△ABC 中，AC ＝BC ＝AB ＝2，点P 在直线AC 上，且∠APB ＝30°，将线段PB 绕点P 顺时针旋转60°到线段PD ，连接AD ，请直接写出△ADP 的周长．答案：A解析：（1）△PAD ，90；（2）证明见解析；（3）623+．【分析】（1）由“SAS”可证△PAD ≌△BEP ，可得∠PAD=∠BEP=135°，依据∠ABC=45°，可得∠BAD=90°；（2）过点P 作PH ∥AB ，交CB 的延长线于点H ，由“SAS”可证△APD ≌△HBP ，可得PH=AD ，通过证明△CAB ∽△CPH ，可得HAC AB CPP =，即可得结论；（3）分两种情况讨论，由直角三角形的性质和相似三角形的性质可求解．【详解】证明：（1）∵点P 是边AC 的中点，PE ∥AB ， ∴点E 是BC 的中点， ∴CE ＝BE ， ∵AC ＝BC ， ∴BE ＝AP ，∵将线段PB 绕点P 顺时针旋转90°到线段PD ． ∴PB ＝PD ，∵∠APD+∠BPC ＝90°，∠EBP +∠BPC ＝90°， ∴∠EBP ＝∠APD ，又∵PB ＝PD ，∴△PAD ≌△BEP （SAS ）， ∴∠PAD ＝∠BEP ， ∵∠C ＝90°，AC ＝BC ， ∴∠BAC ＝∠ABC ＝45°， ∵PE ∥AB ，∴∠ABC ＝∠PEC ＝45°， ∴∠BEP ＝135°，∴∠BAD ＝∠PAD ﹣∠BAC ＝135°﹣45°＝90°，故答案为：△PAD ，90；（2）如图，过点P 作PH ∥AB ，交CB 的延长线于点H ，∴∠CBA ＝∠CHP ，∠CAB ＝∠CPH ， ∵CB ＝CA ， ∴∠CBA ＝∠CAB ， ∴∠CHP ＝∠CPH ， ∴CH ＝CP ， ∴BH ＝AP ，∵将线段PB 绕点P 顺时针旋转90°到线段PD ． ∴PB ＝PD ， ∵∠BPD ＝∠C ，∴∠BPD+∠BPC ＝∠C+∠BPC ， ∴∠PBH ＝∠APD ， ∴△APD ≌△HBP （SAS ）， ∴PH ＝AD ， ∵PH ∥AB ， ∴△CAB ∽△CPH ，∴H AC PC ABP = ∴HAC AB CPP = ∵AC ＝BC ＝43AB ，∴43CP PH =， ∴CP ＝43PH ＝43AD ；（3）当点P 在CA 的延长线上时， ∵AC ＝BC ＝AB ＝2， ∴△ABC 是等边三角形， ∴∠ACB ＝60°，∵将线段PB 绕点P 顺时针旋转60°到线段PD ， ∴BP ＝PD ，∠BPD ＝60°＝∠ACB ，过点P 作PE ∥AB ，交CB 的延长线于点E ，∵∠ACB ＝∠APB+∠ABP ，∴∠ABP ＝∠APB ＝30°，∴AB ＝AP ＝2，∴CP ＝4，∵AB ∥PE ， ∴P AB PE CA C = ∴CP ＝PE ＝4，由（2）得，PE ＝AD ＝4，∵∠APD ＝∠APB+BPD ＝90°，∴DP ＝2216423AD DP -=-=，∴△ADP 的周长＝AD+AP+DP ＝23+6，当点P 在AC 延长线上时，如图，同理可求△ADP 的周长＝6+23综上所述：△ADP 的周长为6+23【点睛】本题几何变换综合题，主要考查了相似三角形的判定与性质，全等三角形的判定与性质以及含30°角的直角三角形的性质的运用，解决问题的关键是作辅助线构造全等三角形或相似三角形，利用全等三角形的对应边相等，相似三角形的对应边成比例进行推算． 12．如图，△ABC 和△CEF 中，∠BAC ＝∠CEF ＝90°，AB ＝AC ，EC ＝EF ，点E 在AC 边上．（1）如图1，连接BE ，若AE ＝3，BE 58FC 的长度；（2）如图2，将△CEF 绕点C 逆时针旋转，旋转角为α（0°＜α＜180°），旋转过程中，直线EF 分别与直线AC ，BC 交于点M ，N ，当△CMN 是等腰三角形时，求旋转角α的度数；（3）如图3，将△CEF 绕点C 顺时针旋转，使得点B ，E ，F 在同一条直线上，点P 为BF 的中点，连接AE ，猜想AE ，CF 和BP 之间的数量关系并说明理由．答案：C解析：（1）42；（2）22.5°或45°或112.5°；（3）CF ＋AE ＝2BP ，见解析【分析】（1）利用勾股定理求出AB ＝AC ＝7，求出EC ＝EF ＝4即可解决问题；（2）分三种情形分别画出图形，利用等腰三角形的性质求解即可；（3）结论：CF ＋AE ＝2BP ．如图3中，过点A 作AD ⊥AE ，利用全等三角形的性质以及等腰直角三角形的性质求解即可．【详解】解：（1）如图1中，在Rt △ABE 中，AB ＝()2222583497-=-==BF AE ，∴AC ＝AB ＝7，∴EF ＝EC ＝AC ﹣AE ＝7﹣3＝4，∵∠CEF ＝90°，EC ＝EF ＝3， ∴CF ＝22224442+=+=EF CE ；（2）①如图2﹣1中，当CM ＝CN 时，α＝∠MCE ＝∠ECN ＝12∠ACB ＝22.5°．如图2﹣2中，当NM ＝NC 时，α＝∠MCN ＝45°．如图2﹣3中，当CN＝CM时，∠BCM＝67.5°，α＝∠ACE＝45°＋67.5°＝112.5°．∠NCE＝12综上所述，满足条件的α的值为22.5°或45°或112.5°．（3）结论：CF＋AE＝2BP．理由：如图3中，过点A作AD⊥AE，∴∠DAE＝∠BAC＝90°，∴∠BAD＝∠CAE，∵∠BAC＝∠BEC＝90°，∴∠ABP＝∠ACE，∵AB＝AC，∴△ABD≌△ACE（ASA），∴BD＝EC＝EF，AD＝AE，∴△ADE是等腰直角三角形，∴DE2AE，∵P是BF的中点，∴BP＝1BF，2∵BP ＝12BF ＝12（2EF ＋DE ），CF ＝2EF ，DE ＝2AE ， ∴BP ＝12（2CF ＋2AE ）， ∴CF ＋AE ＝2BP ．【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题． 13．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是，位置关系是；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．解析：（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492．【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =，点P ，M 是CD ，DE 的中点，//PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =，利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠，90BAC ∠=︒，90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=在Rt ABC ∆中，10AB AC ==，52AN =22522MN ∴=最大，222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大．方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==， PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．14．探究问题：(1)方法感悟：如图①，在正方形ABCD 中，点E ，F 分别为DC ，BC 边上的点，且满足∠BAF ＝45°，连接EF ，求证DE ＋BF ＝EF ．感悟解题方法，并完成下列填空：将△ADE 绕点A 顺时针旋转90°得到△ABG ，此时AB 与AD 重合，由旋转可得：AB ＝AD ，BG ＝DE ，∠1＝∠2，∠ABG ＝∠D ＝90°，∴ ∠ABG ＋∠ABF ＝90°＋90°＝180°，因此，点G ，B ，F 在同一条直线上．∵∠EAF＝45°∴∠2＋∠3＝∠BAD－∠EAF＝90°－45°＝45°．∵∠1＝∠2，∠1＋∠3＝45°．即∠GAF＝∠________．又AG＝AE，AF＝AE∴△GAF≌△________．∴ _________＝EF，故DE＋BF＝EF．(2)方法迁移：如图②，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF ＝∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．答案：E解析：(1)EAF、△EAF、GF；(2)DE＋BF＝EF.【解析】【分析】（1）利用角之间的等量代换得出∠GAF=∠FAE，再利用SAS得出△GAF≌△EAF，得出答案；（2）将△ADE顺时针旋转90°得到△ABG，再证明△AGF≌△AEF，即可得出答案；【详解】解：（1）如图①所示；根据等量代换得出∠GAF=∠FAE，利用SAS得出△GAF≌△EAF，∴GF=EF，故答案为：FAE；△EAF；GF；(2)DE＋BF＝EF，理由如下：假设∠BAD 的度数为m ，将△ADE 绕点A 顺时针旋转，m °得到△ABG ，如图，此时AB 与AD 重合，由旋转可得：AB ＝AD ，BG ＝DE ，∠1＝∠2，∠ABG ＝∠D ＝90°，∴ ∠ABG ＋∠ABF ＝90°＋90°＝180°，因此，点G ，B ，F 在同一条直线上．∵， ∴．∵ ∠1＝∠2，∴ ∠1＋∠3＝．即∠GAF ＝∠EAF ．∵在△AGF 和△AEF 中，，∴ △GAF ≌△EAF （SAS ）．∴ GF ＝EF ．又∵ GF ＝BG ＋BF ＝DE ＋BF ，∴ DE ＋BF ＝EF ．【点睛】此题主要考查了全等三角形的判定和性质、以及折叠的性质和旋转变换性质等知识，证得△GAF ≌△EAF 是解题的关键．15．问题背景：如图1，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，120ABC ∠=︒，60MBN ∠=︒，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．探究图中线段AE ，CF ，EF 之间的数量关系．小李同学探究此问题的方法是：延长FC 到G ，使CG AE =，连接BG ，先证明BCG BAE △≌△，再证明BFC BFE △≌△，可得出结论，他的结论就是_______________；探究延伸1：如图2，在四边形ABCD 中，90BAD ∠=︒，90BCD ∠=︒，BA BC =，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？请直接写出结论（直接写出“成立”或者“不成立”），不要说明理由．探究延伸2：如图3，在四边形ABCD 中，BA BC =，180BAD BCD ∠+∠=︒，2ABC MBN ∠=∠，MBN ∠绕B 点旋转，它的两边分别交AD 、DC 于E 、F ．上述结论是否仍然成立？并说明理由．。

初二数学全等三角形双等腰旋转练习题含答案

初二数学全等三角形双等腰旋转练习题含答案一、全等三角形双等腰旋转1．如图1是实验室中的一种摆动装置，BC 在地面上，支架ABC 是底边为BC 的等腰直角三角形，摆动臂AD 可绕点A 旋转，摆动臂DM 可绕点D 旋转，15AD =，6DM =．（1）在旋转过程中，①当A ，D ，M 三点在同一直线上时，求AM 的长；②当A ，D ，M 三点为同一直角三角形的顶点时，求AM 的长；（2）若摆动臂AD 顺时针旋转90︒，点D 的位置由ABC 外的点1D 转到其内的点2D 处，即1290D AD ︒∠=，连结12D D ，如图2，此时2135AD C ︒∠=，2202CD =2BD 的长．答案：（1）①21或9；②或；（2）【分析】（1）①分两种情形分别求解即可．②显然不能为直角．当为直角时，根据，计算即可，当时，根据，计算即可．（2）连接．首先利用勾股定理求出，再利用全等三角形的解析：（1）①21或9；②3213292）252【分析】（1）①分两种情形分别求解即可．②显然MAD ∠不能为直角．当AMD ∠为直角时，根据222AM AD DM =-，计算即可，当90ADM ∠=︒时，根据222AM AD DM =+，计算即可．（2）连接1CD ．首先利用勾股定理求出1CD ，再利用全等三角形的性质证明21BD CD =即可．【详解】解：（1）①由题意可得：21AM AD DM =+=，或9AM AD DM =-=．②显然MAD ∠不能为直角．当AMD ∠为直角时，22222156189AM AD DM =-=-=，321AM ∴=321-当90ADM ∠=︒时，22222156261AM AD DM =+=+=， 293AM ∴=或932-（舍弃）．综上所述，满足条件的AM 的值为321或329．（2）如图2中，连接1CD ．由题意：1290D AD ∠=︒，1215AD AD ==，2145AD D ∴∠=︒，12152D D =2135AD C ∠=︒，2190CD D ∴∠=︒，()()22221212202152252CD CD D D ∴=+=+=1290BAC D AD ∠=∠=︒，2212BAC CAD D AD CAD ∴∠-∠=∠-∠，21BAD CAD ∴∠=∠，AB AC =，21AD AD =，21()BAD CAD SAS ∴∆≅∆，21252BD CD ∴==．【点睛】本题属于四边形综合题，考查了等腰直角三角形的性质，勾股定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．2．如图1，已知ABC 和EFC 都是等边三角形，且点E 在线段AB 上．（1）过点E 作//EG BC 交AC 于点G ，试判断AEG △的形状并说明理由；（2）求证：//BF AC ；（3）如图2，若点D 在射线CA 上，且ED EC =，求证：AB AD BF =+．答案：（1）是等边三角形，理由见解析；（2）证明见解析；（3）证明见解析．【分析】（1）如图（见解析），先根据等边三角形的性质可得，再根据平行线的性质可得，然后根据等边三角形的判定即可得；（2）先根解析：（1）AEG △是等边三角形，理由见解析；（2）证明见解析；（3）证明见解析．【分析】（1）如图（见解析），先根据等边三角形的性质可得60BAC ABC ACB ==︒=∠∠∠，再根据平行线的性质可得60AEG ABC ∠=∠=︒，然后根据等边三角形的判定即可得；（2）先根据等边三角形的性质可得,,60AC BC CE CF ACB ECF ==∠=∠=︒，从而可得ACE BCF ∠=∠，再根据三角形全等的判定定理与性质可得60CBF CAE ∠=∠=︒，从而可得CBF ACB ∠=∠，然后根据平行线的判定即可得证；（3）先根据平行线的性质、三角形全等的性质可得,DAE EB AE F BF ∠=∠=，再根据等腰三角形的性质可得D ACE ∠=∠，从而可得D BCF ∠=∠，然后根据三角形的内角和定理可得BEF BCF D ∠=∠=∠，最后根据三角形全等的判定定理与性质可得AD BE =，据此根据线段的和差、等量代换即可得证．【详解】（1）AEG △是等边三角形，理由如下：如图，过点E 作//EG BC 交AC 于点G ， ABC 是等边三角形，60BAC ABC ACB ∴∠=∠=∠=︒，60AEG ABC ∴∠=∠=︒， ∴AEG 是等边三角形；（2）ABC 和EFC 是等边三角形，,,60AC BC CE CF ACB ECF ==∠=∠=∴︒，ACB BCE ECF BCE ∴∠-∠=∠-∠，即ACE BCF ∠=∠，在ACE △和BCF △中，AC BC ACE BCF CE CF =⎧⎪∠=∠⎨⎪=⎩，()ACE BCF SAS ∴≅，60CBF CAE ∴∠=∠=︒，CBF ACB ∴∠=∠，//BF AC ∴；（3）由（2）知，//BF AC ，ACE BCF ≅，DAE EBF ∴∠=∠，AE BF =，ED EC =，D ACE ∴∠=∠，由（2）已证：ACE BCF ∠=∠，D BCF ∴∠=∠， ABC 和EFC 是等边三角形，60ABC EFC ∠∴∠==︒，在BEF 中，180120BEF EBC CBF BFE CBF BFE ∠=︒-∠-∠-∠=︒-∠-∠，在BCF △中，180120BCF EFC CBF BFE CBF BFE ∠=︒-∠-∠-∠=︒-∠-∠， BEF BCF D ∴∠=∠=∠，在ADE 和BEF 中，DAE EBF D BEF AE BF ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ADE BEF AAS ∴≅，AD BE ∴=，AB BE AE AD BF ∴=+=+．【点睛】本题考查了三角形全等的判定定理与性质、等边三角形的性质、平行线的判定与性质、等腰三角形的性质等知识点，较难的是题（3），正确找出两个三角形全等的条件是解题关键．3．如图，ABC 是等腰直角三角形，90,ACB ∠=︒分别以,AB AC 为直角边向外作等腰直角ABD △和等腰直角,ACE G 为BD 的中点，连接,,CG BE ,CD BE 与CD 交于点F ．（1）证明：四边形ACGD 是平行四边形；（2）线段BE 和线段CD 有什么数量关系，请说明理由；（3）已知2,BC =求EF 的长度(结果用含根号的式子表示)．答案：（1）见解析；（2）BE=CD ，理由见解析；（3）EF= ．【分析】（1）利用等腰直角三角形的性质易得BD=2BC ，因为G 为BD 的中点，可得BG=BC ，由∠CGB=45°，∠ADB=45得AD ∥解析：（1）见解析；（2）BE =CD ，理由见解析；（3）EF 3105【分析】（1）利用等腰直角三角形的性质易得BD=2BC ，因为G 为BD 的中点，可得BG=BC ，由∠CGB=45°，∠ADB=45得AD ∥CG ，由∠CBD+∠ACB=180°，得AC ∥BD ，得出四边形ACGD 为平行四边形；（2）利用全等三角形的判定证得△DAC ≌△BAE ，由全等三角形的性质得BE=CD ；首先证得四边形ABCE 为平行四边形，再利用全等三角形的判定定理得△BCE ≌△CAD ，易得∠CBE=∠ACD ，由∠ACB=90°，易得∠CFB=90°，得出结论．（3）先证明△DBF 是直角三角形，再利用勾股定理进行计算，即可求出答案．【详解】解：（1）∵△ABC 和△ABD 都是等腰直角三角形∴∠CAB =∠ABD = 45°，BD 2AB 22BC =2BC =2AC∴AC ∥BD又∵G 为BD 的中点，∴BD =2DG ，∴AC =DG ，AC ∥DG∴四边形ACGD 为平行四边形；（2）BE =CD ，理由如下∵△AEC 和△ABD 都是等腰直角三角形AE =AC ，AB =AD∠EAB =∠EAC +∠CAB =90°+45°=135°，∠CAD =∠DAB +∠BAC =90°+45°=135°，∴∠EAB =∠CAD ，在△DAC 与△BAE 中，AD AB CAD EAB AC AE =⎧⎪∠=∠⎨⎪=⎩，∴△DAC ≌△BAE ，∴BE =CD ；（3） ∵△DAC ≌△BAE∴∠AEB=∠ACD又∵∠EAC=90°∴∠EFC=∠DFB=90°∴ △DBF 是直角三角形∵BC，∴BD根据勾股定理得CD， ∴11••22CD BF BC BD = ∴12=12•∴BF∴EF =BE -BF =CD -BF【点睛】本题主要考查了等腰直角三角形的性质，平行四边形和全等三角形的判定及性质定理，综合运用各种定理是解答此题的关键．4．已知，ABC 中，AB AC =，2BAC α∠=︒，点D 为BC 边中点，连接AD ，点E 为AD 的中点，线段CE 绕点E 顺时针旋转2α︒得到线段EF ，连接FC ，FD ．（1）如图1，当60BAC ∠=︒时，请直接写出DF DC的值；（2）如图2，当90BAC ∠=︒时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请写出正确的结论，并说明理由；（3）如图3，当2BAC α∠=︒时，请直接写出DF DC的值(用含α的三角函数表示)．答案：（1）；（2）不成立，，理由见解析；（3）．【分析】（1）如图1（见解析），先根据中位线定理得出，再根据旋转的性质、等边三角形的性质得出，，，然后根据三角形全等的判定定理与性质可得，由此即可得出解析：（1）12；（2）不成立，22DF DC =3）sin DF DC α=︒．【分析】（1）如图1（见解析），先根据中位线定理得出12EG DC =，再根据旋转的性质、等边三角形的性质得出EC FC =，CD CG =，DCF GCE ∠=∠，然后根据三角形全等的判定定理与性质可得DF EG =，由此即可得出答案；（2）如图2（见解析），先根据中位线定理、等腰三角形的三线合一得出90AEM ∠=︒，再根据等腰直角三角形的性质得出ACE BCF ∠=∠，22AC CE BC CF ==，然后根据相似三角形的判定与性质可得CBF CAE ∠=∠，2AE BF =AE AM BF BD =，最后根据相似三角形的判定与性质可得90BFD AEM ∠=∠=︒，据此利用正弦三角函数值即可得；（3）如图3（见解析），参照题（2）的思路，先根据相似三角形的判定与性质得出,90CBF CAE BFD AEN α∠=∠=︒∠=∠=︒，再在Rt BFD 中，利用正弦三角函数值即可得．【详解】（1）如图1，取AC 的中点G ，连接EG ，则12CG AC = 点E 为AD 的中点 EG ∴是ACD 的中位线12EG DC ∴=，即12EG DC =由旋转的性质可知，EC EF =，60FEC ∠=︒CEF ∴是等边三角形60ECF ∴∠=︒，EC FC =AB AC =，60BAC ∠=︒ABC ∴是等边三角形60,ACB AC BC ∴∠=︒=点D 为BC 边中点1122CD BC AC CG ∴=== 60ECF ECD DCF ∠=∠+∠=︒，60ACB ECD GCE ∠=∠+∠=︒DCF GCE ∴∠=∠在DCF 和GCE 中，CD CG DCF GCE FC EC =⎧⎪∠=∠⎨⎪=⎩()DCF GCE SAS ∴≅DF EG ∴=12DF EG DC DC ∴==；（2）不成立，2DF DC =，理由如下：如图2，连接BF ，取AC 的中点M ，连接EM∵E 是AD 的中点∴//EM BC∴AEM ADC ∠=∠∵AB AC =ABC ∴是等腰三角形∵D 是BC 中点, 2BAC α∠=︒∴AD BC ⊥，12CAD BAC α∠=∠=︒，BD DC = ∴90ADC ∠=︒∴90AEM ∠=︒当90BAC ∠=︒时，则90CEF ∠=︒ABC ∴和CEF △为等腰直角三角形∴45ACB ECF ∠=∠=︒，即45ECD ACE ECD BCF ∠+∠=∠+∠=︒∴ACE BCF ∠=∠，cos 45AC CE BC CF ==︒= ∴ACE BCF ~∴90452CBF CAE α︒∠=∠=︒==︒，2AE AC BF BC ==∵12122AC AM BD BC == ∴AE AM BF BD = ∴BDF AME ~ ∴90BFD AEM ∠=∠=︒在Rt BFD 中，sin DF DF CBF BD DC ∠==，即sin 45DF DC ︒=则2DF DC =；（3）sin DF DCα=︒，求解过程如下：如图3，连接BF ，取AC 的中点N ，连接EN 参照（2），同理可得：12CAD BAC α∠=∠=︒，BD DC =，90AEN ADC ∠=∠=︒ 当2BAC α∠=︒时，则2CEF α∠=︒AB AC =，EC EF =（旋转的性质）ABC ∴和EFC 为等腰三角形 ∴1(180)902ACB ABC BAC α∠=∠=︒-∠=︒-︒ 1(180)902ECF EFC CEF α∠=∠=︒-∠=︒-︒ 90ACB ECF α∴∠=∠=︒-︒ABC EFC ∴~AC CE BC CF∴= 又,ACB ECD ACE ECF ECD BCF ∠=∠+∠∠=∠+∠∴ACE BCF ∠=∠∴ACE BCF ~∴CBF CAE α∠=∠=︒，AE AC BF BC = ∵1212AC AN AC BD BCBC ==∴AE AN BF BD = ∴BDF ANE ~ ∴90BFD AEN ∠=∠=︒在Rt BFD 中，sin DF DF CBF BD DC ∠== 即sin DF DC α=︒．【点睛】本题考查了等腰三角形的性质、旋转的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点，通过作辅助线，构造全等三角形和相似三角形是解题关键． 5．如图1，在等腰直角三角形ABC 中，动点D 在直线AB （点A 与点B 重合除外）上时，以CD 为一腰在CD 上方作等腰直角三角形ECD ，且90ECD ∠=︒，连接AE ．（1）判断AE 与BD 的数量关系和位置关系；并说明理由．（2）如图2，若4BD =，P ，Q 两点在直线AB 上且5EP EQ ==，试求PQ 的长．（3）在第（2）小题的条件下，当点D 在线段AB 的延长线（或反向延长线）上时，判断PQ 的长是否为定值．分别画出图形，若是请直接写出PQ 的长；若不是请简单说明理由．答案：（1）AE=BD 且AE ⊥BD ；（2）6；（3）PQ 为定值6，图形见解析【分析】（1）由“SAS”可证△ACE ≌△BCD ，可得AE=BD ，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰解析：（1）AE=BD且AE⊥BD；（2）6；（3）PQ为定值6，图形见解析【分析】（1）由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长；（3）分两种情况讨论，由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC，可得AE⊥BD，由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长．【详解】解：（1）AE=BD，AE⊥BD，理由如下：∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠EAC=∠DBC=45°，∴∠EAC+∠CAB=90°，∴AE⊥BD；（2）∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴，∴PQ=2AQ=6；（3）如图3，若点D在AB的延长线上，∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠CBD=∠CAE=135°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴，∴PQ=2AQ=6；如图4，若点D在BA的延长线上，∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠CBD=∠CAE=45°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴AQ=22=2516=3--，EQ AE∴PQ=2AQ=6.【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理等知识，证明AE⊥BD是本题的关键．6．如图，将两块含45°角的大小不同的直角三角板△COD和△AOB如图①摆放，连结AC，BD．（1）如图①，猜想线段AC与BD存在怎样的数量关系和位置关系，请写出结论并证明；（2）将图①中的△COD绕点O顺时针旋转一定的角度（如图②），连结AC，BD，其他条件不变，线段AC与BD还存在（1）中的关系吗？请写出结论并说明理由．（3）将图①中的△COD绕点O逆时针旋转一定的角度（如图③），连结AC，BD，其他条件不变，线段AC与BD存在怎样的关系？请直接写出结论．答案：（1）AC=BD，AC⊥BD，证明见解析；（2）存在，AC=BD，AC⊥BD，证明见解析；（3）AC=BD，AC⊥BD【分析】（1）延长BD交AC于点E．易证△AOC≌△BOD（SAS），可得A解析：（1）AC=BD，AC⊥BD，证明见解析；（2）存在，AC=BD，AC⊥BD，证明见解析；（3）AC=BD，AC⊥BD【分析】（1）延长BD交AC于点E．易证△AOC≌△BOD（SAS），可得AC=BD，∠OAC=∠OBD，由∠ADE=∠BDO，可证∠AED=∠BOD=90º即可；（2）延长BD交AC于点F，交AO于点G．易证△AOC≌△BOD（SAS），可得AC=BD，∠OAC=∠OBD，由∠AGF=∠BGO，可得∠AFG=∠BOG=90º即可；（3）BD交AC于点H，AO于M，可证△AOC≌△BOD（SAS），可得AC=BD，∠OAC=∠OBD，由∠AMH=∠BMO，可得∠AHM=∠BOH=90º即可．【详解】（1）AC=BD，AC⊥BD，证明：延长BD交AC于点E．∵△COD和△AOB均为等腰直角三角形，∴OC=OD，OA=OB，∠COA=∠BOD=90º，∴△AOC≌△BOD（SAS），∴AC=BD，∴∠OAC=∠OBD，∵∠ADE=∠BDO，∴∠AED=∠BOD=90º，∴AC⊥BD；（2）存在，证明：延长BD交AC于点F，交AO于点G．∵△COD和△AOB均为等腰直角三角形，∴OC=OD，OA=OB，∠DOC=BOA=90º，∵∠AOC=∠DOC－∠DOA，∠BOD=∠BOA－∠DOA，∴∠AOC=∠BOD，∴△AOC≌△BOD（SAS），∴AC=BD，∠OAC=∠OBD，∵∠AGF=∠BGO ，∴∠AFG=∠BOG=90º，∴AC ⊥BD ；（3）AC=BD ，AC ⊥BD ．证明：BD 交AC 于点H ，AO 于M ，∵△COD 和△AOB 均为等腰直角三角形，∴OC=OD ，OA=OB ，∠DOC=BOA=90º，∵∠AOC=∠DOC+∠DOA ，∠BOD=∠BOA+∠DOA ，∴∠AOC=∠BOD ，∴△AOC ≌△BOD （SAS ），∴AC=BD ，∠OAC=∠OBD ，∵∠AMH=∠BMO ，∴∠AHM=∠BOH=90º，∴AC ⊥BD ．【点睛】本题考查三角形旋转变换中对应相等的位置与数量关系，掌握三角形全等的证明方法，及其角度计算是解题关键．7．在ABC 中，AB AC =，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作ADE ，使AD AE =，DAE BAC ∠=∠，连接CE ．（1）如图，当点D 在线段BC 上，如果90BAC ∠=︒，则BCE ∠=______度．（2）设BAC α∠=，BCE β∠=．①如图，当点D 在线段BC 上移动时，α、β之间有怎样的数量关系？请直接写出你的结论．②如图，当点D 在线段BC 的反向延长线上移动时，α、β之间有怎样的数量关系？请说明理由．答案：（1）90；（2）①，理由见解析；②，理由见解析【分析】（1）由等腰直角三角形的性质可得∠ABC=∠ACB=45°，由“SAS”可证△BAD ≌△CAE ，可得∠ABC=∠ACE=45°，可求∠BC解析：（1）90；（2）①180αβ+=︒，理由见解析；②αβ=，理由见解析【分析】（1）由等腰直角三角形的性质可得∠ABC=∠ACB=45°，由“SAS”可证△BAD ≌△CAE ，可得∠ABC=∠ACE=45°，可求∠BCE 的度数；（2）①由“SAS”可证△ABD ≌△ACE 得出∠ABD=∠ACE ，再用三角形的内角和即可得出结论；②由“SAS”可证△ADB ≌△AEC 得出∠ABD=∠ACE ，再用三角形外角的性质即可得出结论．【详解】（1）∵AB=AC ，∠BAC=90°，∴∠ABC=∠ACB=45°，∵∠DAE=∠BAC ，∴∠BAD=∠CAE ，在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAE （SAS ）∴∠ABC=∠ACE=45°，∴∠BCE=∠ACB+∠ACE=90°，故答案为：90；（2）①180αβ+=︒．理由：∵∠BAC=∠DAE ，∴∠BAC-∠DAC=∠DAE-∠DAC ．即∠BAD=∠CAE ．在△ABD 与△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ），∴∠B=∠ACE ．∴∠B+∠ACB=∠ACE+∠ACB ．∵∠ACE+∠ACB=β，∴∠B+∠ACB=β，∵α+∠B+∠ACB=180°，∴α+β=180°；② 当点D 在射线BC 的反向延长线上时，αβ=．理由如下：∵DAE BAC ∠=∠，∴DAB EAC ∠=∠，在△ABD 与△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△≌△ADB AEC(SAS)， ∴ABD ACE ∠=∠，∵ABD BAC ACB ∠=∠+∠，ACE BCE ACB ∠=∠+∠，∴BAC ABD ACB ∠=∠-∠，BCE ACE ACB ∠=∠-∠，∴BAC BCE ∠=∠，即αβ=．此题考查了全等三角形的判定和性质，等腰直角三角形的性质，三角形的内角和定理，以及三角形外交的性质，证明△ABD ≌△ACE 是解本题的关键．8．如图，锐角ABC 中，分别以AB 、AC 为边向外作等腰直角ABE △和等腰直角ACD △，使AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，可以通过全等三角形的知识证得BD 与CE 相等．（1）如图，锐角ABC 中分别以AB 、AC 为边向外作等腰ABE △和等腰ACD △，AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，试猜想BD 与CE 的数量关系，并说明理由．（2）如图，在中ABC ，45ACB ∠=︒，以AB 为直角边，A 为直角顶点向外作等腰直角ABD △，连接CD ，若2,3AC BC ==，求CD 的长．（3）如图，在四边形中ABCD ，60,15,8,ADC BC AB AD CD ∠=︒===，求BD 的最大值．答案：（1），证明见解析；（2）；（3）23．（1）由等腰三角形的性质解得，继而可证及，再由全等三角形对应边相等解题；（2）过A 作交于点，连接，先证明是等腰直角三角形，得到，，再证明，由全解析：（1）BD CE =，证明见解析；（2）13；（3）23．【分析】（1）由等腰三角形的性质解得,,AE AB AD AC BAE CAD ==∠=∠，继而可证EAC BAD ∠=∠及(SAS)EAC BAD ≌，再由全等三角形对应边相等解题；（2）过A 作AE AC ⊥交BC 于点E ，连接DE ，先证明EAC 是等腰直角三角形，得到 AE AC =，DAE BAC ∠=∠，再证明(SAS)DAE BAC ≌，由全等三角形的性质得到3,45DE BC DEA BCA ==∠=∠=︒，接着在等腰直角三角形EAC 中，由勾股定理解得22222EC AC AE AC =+=，最后在Rt DEC △中，由勾股定理即可解得CD 的长；（3）先证明ACD △为等边三角形，再由等边三角形的性质可得，,60AC CD ACD =∠=︒将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转的性质得815DE AB BC EC ====，，继而证明BCE 是等边三角形，由等边三角形的性质得到75BE BC ==，最后根据三角形三边关系解题即可．【详解】解：（1）∵ABE △和ACD △是等腰三角形，,,AE AB AD AC BAE CAD ∴==∠=∠，BAE BAC CAD BAC ∴∠+∠=∠+∠，即：EAC BAD ∠=∠，在EAC 中BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩，(SAS)EAC BAD ∴≌，CE BD ∴=；（2）如图（1）所示，过A 作AE AC ⊥交BC 于点E ，连接DE ，45,ACB AE AC ∠=︒⊥，90EAC ∴∠=︒，EAC ∴△是等腰直角三角形，AE AC ∴=，又ABD 是等腰直角三角形，,90AB AD BAD ∴=∠=︒，90BAD EAC ∴∠=∠=︒，BAD BAE EAC BAE ∴∠+∠=∠+∠，即：DAE BAC ∠=∠，在DAE △和BAC 中,AD AB DAE BAC AE AC =⎧⎪∠=∠⎨⎪=⎩(SAS)DAE BAC ∴≌，3,45DE BC DEA BCA ∴==∠=∠=︒，在等腰直角三角形EAC 中，45AEC ∠=︒，90DEC DEA AEC ∴∠=∠+∠=︒，由勾股定理得：22222EC AC AE AC =+=.在Rt DEC △中，由勾股定理得： 229413CD DE EC =+=+=；（3）,60AD CD ADC =∠=︒，∴ACD △为等边三角形，,60AC CD ACD ∴=∠=︒，如图（2）所示，将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转性质可得∶815DE AB BC EC ====，60BCE ∠=︒，∴BCE 是等边三角形，∴75BE BC ==，又∴BE DE BD +≥，即158BD BE DE ≤+=+，即23BD ≤，∴BD的最大值为23．【点睛】本题考查全等三角形的判定与性质、旋转、勾股定理、等边三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．9．已知Rt△OAB和Rt△OCD的直角顶点O重合，∠AOB=∠COD=90°，且OA=OB，OC=OD．（1）如图1，当C、D分别在OA、OB上时，AC与BD的数量关系是AC BD（填“>”，“<”或“=”）AC与BD的位置关系是AC BD（填“∥”或“⊥”）；（2）将Rt△OCD绕点O顺时针旋转，使点D在OA上，如图2，连接AC，BD，求证：AC=BD；（3）现将Rt△OCD绕点O顺时针继续旋转，如图3，连接AC，BD，猜想AC与BD的数量关系和位置关系，并给出证明．答案：（1）=；⊥（2）见解析（3）AC=BD且AC⊥BD；证明见解析【分析】（1）根据等式的性质可得AC与BD的数量关系，根据∠AOB=∠COD=90°，可证AC与BD的位置关系；（2）证解析：（1）=；⊥（2）见解析（3）AC=BD且AC⊥BD；证明见解析【分析】（1）根据等式的性质可得AC与BD的数量关系，根据∠AOB=∠COD=90°，可证AC与BD 的位置关系；（2）证明△OCA≌△ODB，即可得到AC=BD；（3）证明△OCA≌△ODB，可得AC=BD，∠BDO=∠ACO，进而可证∠DEF=90°．【详解】解：（1）∵OA=OB，OC=OD∴OA-OC=OB-OD，∴AC=BD．∵∠AOB=∠COD=90°，∴AO⊥BO，∵C、D分别在OA、OB上，∴AC ⊥BD ；（2）在△OCA 和△ODB 中，90OC OD COA BOD AO BO =⎧⎪∠==⎨⎪=⎩，∴△OCA ≌△ODB ，∴AC=BD ；（3）AC=BD ，AC ⊥BD ．理由：∵∠AOB=∠COD=90°，∴∠AOB+∠AOD=∠COD+∠AOD ，∴∠AOC=∠BOD ，在△OCA 和△ODB 中，OC OD COA BOD AO BO =⎧⎪∠=⎨⎪=⎩，∴△OCA ≌△ODB ，∴AC=BD ，∠BDO=∠ACO ，∵∠ACO+∠CFO=90°，∠CFO=∠DFE ，∴∠BDO+∠DFE=90°，∴∠DEF=180°-90°=90°，∴AC ⊥BD ．【点睛】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定与性质等知识，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．10．在直线上次取A ，B ，C 三点，分别以AB ，BC 为边长在直线的同侧作正三角形，作得两个正三角形的另一顶点分别为D ，E ．（1）如图①，连结CD ，AE ，求证：CD AE =；（2）如图②，若1AB =，2BC =，求DE 的长；（3）如图③，将图②中的正三角形BEC 绕B 点作适当的旋转，连结AE ，若有222DE BE AE +=，试求∠DEB 的度数．答案：（1）见解析；（2）；（3）∠DEB ＝30°.【分析】（1）欲证明CD ＝AE ，只要证明△ABE ≌△DBC 即可；（2）如图②，取BE 中点F ，连接DF ，首先证明△DBF 是等边三角形，然后证明△BD解析：（1）见解析；（2）3DE =3）∠DEB ＝30°.【分析】（1）欲证明CD ＝AE ，只要证明△ABE ≌△DBC 即可；（2）如图②，取BE 中点F ，连接DF ，首先证明△DBF 是等边三角形，然后证明△BDE 是直角三角形，再利用勾股定理计算即可；（3）如图③，连接DC ，先证明△ABE ≌△DBC ，再利用勾股定理的逆定理证明△DEC 是直角三角形，得到∠DEC ＝90°即可解决问题．【详解】解：（1）∵△ABD 和△ECB 都是等边三角形，∴AD ＝AB ＝BD ，BC ＝BE ＝EC ，∠ABD ＝∠EBC ＝60°，∴∠ABE ＝∠DBC ，在△ABE 和△DBC 中，AB BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△DBC （SAS ），∴CD ＝AE ；（2）如图②，取BE 中点F ，连接DF ，∵BD ＝AB ＝1，BE ＝BC ＝2，∠ABD ＝∠EBC ＝60°，∴BF ＝EF ＝1＝BD ，∠DBF ＝60°，∴△DBF 是等边三角形，∴DF ＝BF ＝EF ，∠DFB ＝60°，∵∠BFD ＝∠FED ＋∠FDE ，∴∠FDE ＝∠FED ＝30°∴∠EDB ＝180°−∠DBE−∠DEB ＝90°，∴DE ＝2222213BE BD ；（3）如图③，连接DC ，∵△ABD 和△ECB 都是等边三角形，∴AD ＝AB ＝BD ，BC ＝BE ＝EC ，∠ABD ＝∠EBC ＝60°，∴∠ABE ＝∠DBC ，在△ABE 和△DBC 中，AB BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△DBC （SAS ），∴AE ＝DC ，∵DE 2＋BE 2＝AE 2，BE ＝CE ，∴DE 2＋CE 2＝CD 2，∴∠DEC ＝90°，∵∠BEC ＝60°，∴∠DEB ＝∠DEC−∠BEC ＝30°．【点睛】本题考查了全等三角形的判定和性质、勾股定理以及勾股定理逆定理、等边三角形的性质等知识，寻找全等三角形是解决问题的关键，要学会添加辅助线的方法，属于中考常考题型．二、全等三角形手拉手模型11．（1）如图1，ABC 和DCE 都是等边三角形，且B ，C ，D 三点在一条直线上，连接AD ，BE 相交于点P ，求证：BE AD =．（2）如图2，在BCD 中，若120BCD ∠<︒，分别以BC ，CD 和BD 为边在BCD 外部作等边ABC ，等边CDE △，等边BDF ，连接AD 、BE 、CF 恰交于点P ． ①求证：AD BE CF ==；②如图2，在（2）的条件下，试猜想PB ，PC ，PD 与BE 存在怎样的数量关系，并说明理由．解析：（1）详见解析；（2）①详见解析；②PB PC PD BE ++=，理由详见解析【分析】（1）根据等边三角形的性质得出BC=AC ，CE=CD ，∠ACB=∠DCE=60°，进而得出∠BCE=∠ACD ，判断出BCE ACD ≌（SAS ），即可得出结论；（2）①同（1）的方法判断出≌ACD BCE （SAS ），ABD CBF ≌（SAS ），即可得出结论； ②先判断出∠APB=60°，∠APC=60°，在PE 上取一点M ，使PM=PC ，证明CPM △是等边三角形，进而判断出PCD MCE ≌（SAS ），即可得出结论．【详解】（1）证明：∵ABC 和DCE 都是等边三角形，∴BC=AC ，CE=CD ，∠ACB=∠DCE=60°，∴∠ABC+∠ACE=∠DCE+∠ACE ，即∠BCE=∠ACD ，∴BCE ACD ≌（SAS ），∴BE=AD ；（2）①证明：∵ABC 和DCE 是等边三角形，∴AC=BC ，CD=CE ，∠ACB=∠DCE=60°，∴∠ACB+∠BCD=∠DCE+∠BCD ，即∠ACD=∠BCE ，∴≌ACD BCE （SAS ），∴AD=BE ，同理：ABD CBF ≌（SAS ），∴AD=CF ，即AD=BE=CF ；②解：结论：PB+PC+PD=BE ，理由：如图2，AD 与BC 的交点记作点Q ，则∠AQC=∠BQP ，由①知，≌ACD BCE ，∴∠CAD=∠CBE ，在ACQ 中，∠CAD+∠AQC=180°-∠ACB=120°，∴∠CBE+∠BQP=120°，在BPQ 中，∠APB=180°-（∠CBE+∠BQP ）=60°，∴∠DPE=60°，同理：∠APC=60°，60,CPE ∴∠=︒ ∠CPD=120°，在PE 上取一点M ，使PM=PC ，∴CPM △是等边三角形，∴CP CM PM ==，∠PCM=∠CMP=60°，∴∠CME=120°=∠CPD ，∵CDE △是等边三角形，∴CD=CE ，∠DCE=60°=∠PCM ，∴∠PCD=∠MCE ，∴PCD MCE ≌（SAS ），∴PD=ME ，∴BE=PB+PM+ME=PB+PC+PD ．【点睛】此题是三角形综合题，主要考查了三角形的内角和定理，等边三角形的性质和判定，全等三角形的判定和性质，构造出全等三角形是解本题的关键．12．在平面直角坐标系中，已知A （3，0），以OA 为一边在第一象限内画正方形OABC ，D （m ，0）为x 轴上的一个动点，以BD 为一边画正方形BDEF （点F 在直线AB 右侧）．（1）当m ＞3时（如图1），试判断线段AF 与CD 的数量关系，并说明理由．（2）当AF=5时，求点E 的坐标；（3）当D 点从A 点向右移动4个单位，求这一过程中F 点移动的路程是多少？解析：（1）AF CD =，理由见解析；（2）点E 的坐标为(7,1)E 或(1,7)E --；（3）这一过程中F 点移动的路程是向上移动4个单位．【分析】（1）先根据正方形的性质得出,,90AB CB BF BD ABC BDF ==∠=∠=︒，再根据角的和差求出CBD ABF ∠=∠，然后根据三角形全等的判定定理与性质即可得；（2）分点D 在点A 的右侧和点D 在点A 的左侧，分别画出图形．①如图1，先利用（1）的结论可得5CD =，再利用勾股定理求出4OD =，从而可得1AD =，然后过点E 作EG x ⊥轴于点G ，根据三角形全等的判定定理与性质可得1,3GE GD ==，从而可得7OG =，由此即可得；②如图2，同①的方法，利用三角形全等的判定定理与性质得出7,3HE HD ==，从而可得1OH =，由此即可得；（3）参照（2）①的方法，求出点F 的坐标，从中可发现点F 的坐标与m 的关系，由此即可得出答案．【详解】（1）AF CD =，理由如下：四边形OABC 和四边形BDEF 都是正方形,,90AB CB BF BD ABC BDF ∴==∠=∠=︒ABC ABD BDF ABD ∴∠+∠=∠+∠，即CBD ABF ∠=∠在BAF △和BCD 中，AB CB ABF CBD BF BD =⎧⎪∠=∠⎨⎪=⎩()BAF BCD SAS ∴≅AF CD ∴=；（2）由题意，分以下两种情况：①如图1，点D 在点A 的右侧四边形OABC 和四边形BDEF 都是正方形，(30)A ，3OC AB OA ∴===，BD DE =，90OAB BDE ∠=∠=︒90ABD ADB GDE ADB ∴∠+∠=∠+∠=︒，即ABD GDE ∠=∠由（1）可知，5AF CD ==在Rt COD中，4OD ===431AD OD OA ∴=-=-=过点E 作EG x ⊥轴于点G在ABD △和GDE △中，90BAD DGE ABD GDE BD DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()ABD GDE AAS ∴≅1,3AD GE AB GD ∴====437OG OD GD ∴=+=+=此时点E 的坐标为(7,1)E②如图2，点D 在点A 的左侧由（1）可知，5AF CD ==在Rt COD 中，2222534OD CD OC =-=-=437AD OD OA ∴=+=+=过点E 作EH x ⊥轴于点H同理可证：ABD HDE ≅7,3AD HE AB HD ∴====431OH OD HD ∴=-=-=此时点E 的坐标为(1,7)E --综上，点E 的坐标为(7,1)E 或(1,7)E --；（3）由题意，只需求出点D 在点A 的右侧，即3m >时，点F 的坐标即可解决问题如图1，过点F 作FM x ⊥轴于点M由（1）已证：BAF BCD ≅AF CD ∴=，BAF BCD ∠=∠90BAD BCO ∠=∠=︒BAD BAF BCO BCD ∴∠-∠=∠-∠FAM DCO ∴∠=∠在AFM △和CDO 中，90AMF COD FAM DCO AF CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()AFM CDO AAS ∴≅3,MA OC MF OD m ∴====336OM OA MA ∴=+=+=此时点F 的坐标为(6,)F m由此可知，当D 点从A 点向右移动4个单位时，点F 向上移动4个单位即这一过程中F 点移动的路程是向上移动4个单位．【点睛】本题考查了正方形的性质、三角形全等的判定定理与性质、点的坐标变换规律等知识点，较难的是题（2），依据题意，分两种情况讨论，然后分别通过作辅助线，构造全等三角形是解题关键．13．问题发现：如图1，在Rt ABC ∆中，AB AC =，D 为BC 边所在直线上的动点(不与点B 、C 重合)，连结AD ，以AD 为边作Rt ADE ∆，且AD AE =，根据BAC CAD CAD DAE ∠+∠=∠+∠，得到BAD CAE ∠=∠，结合AB AC =，AD AE =得出BAD CAE ∆≅∆，发现线段BD 与CE 的数量关系为BD CE =，位置关系为BD CE ⊥；（1）探究证明：如图2，在Rt ABC ∆和Rt ADE ∆中，AB AC =，AD AE =，且点D 在BC 边上滑动(点D 不与点B 、C 重合)，连接EC ．①则线段BC ，DC ，EC 之间满足的等量关系式为_____；②求证: 2222BD CD AD +=；（2）拓展延伸：如图3，在四边形ABCD 中，45ABC ACB ADC ∠=∠=∠=︒．若13BD cm =，5CD cm =，求AD 的长．解析：（1）①BC =CE+CD ；②见解析；（2）AD ＝2．【分析】（1）①根据题中示例方法，证明△BAD ≌△CAE ，得到BD ＝CE ，从而得出BC=CE+CD ； ②根据△BAD ≌△CAE ，得出∠ACE ＝45°，从而得到∠BCE ＝90°，则有DE 2＝CE 2+CD 2，再根据222DE AD =可得结论；（2）过点A 作AG ⊥AD ，使AG=AD ，连接CG 、DG ，可证明△BAD ≌△CAG ，得到CG ＝BD ，在直角△CDG 中，根据CD 的长求出DG 的长，再由DG 和AD 的关系求出AD.【详解】解：（1）①如图2，在Rt △ABC 中，AB ＝AC ，∴∠B ＝∠ACB ＝45°，∵∠BAC ＝∠DAE ＝90°，∴∠BAC ﹣∠DAC ＝∠DAE ﹣∠DAC ，即∠BAD ＝∠CAE ，在△BAD 和△CAE 中，AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩，∴△BAD ≌△CAE （SAS ），∴BD ＝CE ，∴ BC=BD+CD=CE+CD ，故答案为：BC=BD+CD=CE+CD．②∵△BAD≌△CAE，∴∠B＝∠ACE＝45°，∵∠ACB＝45°，∴∠BCE＝45°+45°＝90°，∴DE2＝CE2+CD2，∵AD＝AE，∠DAE＝90°，∴22=，DE AD2∴2AD2＝BD2+CD2；（3）如图3，过点A作AG⊥AD，使AG=AD，连接CG、DG，则△DAG是等腰直角三角形，∴∠ADG＝45°，∵∠ADC＝45°，∴∠GDC＝90°，同理得：△BAD≌△CAG，∴CG＝BD＝13，在Rt△CGD中，∠GDC＝90°，2222=-=-=，DG CG CD13512∵△DAG是等腰直角三角形，∴22DG AD=，2∴AD2．2【点睛】本题是四边形的综合题，考查的是全等三角形的判定和性质、勾股定理，掌握全等三角形的判定定理和性质定理是解题的关键．14．在菱形ABCD中，∠ABC＝60°，P是射线BD上一动点，以AP为边向右侧作等边△APE，连接CE．（1）如图1，当点P在菱形ABCD内部时，则BP与CE的数量关系是，CE与AD的位置关系是．（2）如图2，当点P在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；（3）如图2，连接BE，若AB＝23，BE＝219，求AP的长．解析：（1）BP=CE，CE⊥AD；（2）结论仍然成立，理由见解析；（3）7【解析】【分析】（1）由菱形ABCD和∠ABC=60°可证△ABC与△ACD是等边三角形，由等边△APE可得AP=AE，∠PAE=∠BAC=60°，减去公共角∠PAC得∠BAP=∠CAE，根据SAS可证得△BAP≌△CAE，故有BP=CE，∠ABP=∠ACE．由菱形对角线平分一组对角可证∠ABP=30°，故∠ACE=30°即CE平分∠ACD，由AC=CD等腰三角形三线合一可得CE⊥AD．（2）结论不变．证明过程同（1）．（3）在Rt△AOP中，求出OA，OP即可解决问题．【详解】（1）BP=CE，CE⊥AD．理由：∵菱形ABCD中，∠ABC=60°∴AB=BC=CD=AD，∠ADC=∠ABC=60°∴△ABC、△ACD是等边三角形∴AB=AC，AC=CD，∠BAC=∠ACD=60°∵△APE是等边三角形∴AP=AE，∠PAE=60°∴∠BAC-∠PAC=∠PAE-∠PAC即∠BAP=∠CAE，∴△BAP≌△CAE（SAS）∴BP=CE，∠ABP=∠ACE∵BD平分∠ABC∠ABC=30°∴∠ACE=∠ABP=12∴CE平分∠ACD∴CE⊥AD．故答案为BP=CE，CE⊥AD．（2）结论仍然成立．理由如下：如图，设CE交AD于H，连接AC．∵四边形ABCD是菱形，∠ABC=60°，∴△ABC，△ACD都是等边三角形，∠ABD=∠CBD=30°．∵△APE是等边三角形，∴AB=AC，AP=AE，∠BAC=∠PAE=60°．∴△BAP≌△CAE．∴BP=CE，∠ABP=∠ACE=30°．∵∠CAH=60°，∴∠CAH+∠ACH=90°．∴∠AHC=90°，即CE⊥AD．（3）如图，连接BE，由（2）可知CE⊥AD，BP= CE．在菱形ABCD中，AD∥BC，∴CE⊥BC．∵3，BE=219在Rt△BCE中，22(219)(23)-=8．∴BP=CE=8．∵AC与BD是菱形的对角线，∴∠ABD=12∠ABC=30°，AC⊥BD．∴OA=12322AB AO-，∴OP=BP－BO=5，在Rt△AOP中，22PO AO+1，【点睛】本题考查了菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理．第（2）题的证明过程可由（1）适当转化而得，第（3）题则可直接运用（2）的结论解决问题．15．如图①，在菱形ABCD 中，AC 与BD 交于点O ，13AB =，24BD =，点F 是BD 上一动点（不与点B 重合），将线段AF 绕点A 顺时针旋转60︒得到线段AM .（1）求OA 的长.（2）若点M ，F ，C 在同一条直线上，求证：3AC AM =. （3）如图②，以AB 为边作等边ABE ∆，40AEM S ∆=，求AF 的长.解析：（1）5（2）3AC AM =（3）41【分析】（1）在Rt OAB ∆中，利用勾股定理22OA AB OB =-,求解即可. （2）由四边形ABCD 是菱形，求出△AFM 为等边三角形，∠M=∠AFM=60°，再求出∠MAC=90°，可得∠ACM=30°.（3）求出△MEM ≌△ABF ，利用△AEAM 的面积为40求出BF ，在利用勾股定理22225441AF AO FO =+=+=..【详解】（1）四边形ABCD 是菱形，AC BD ∴⊥，12OB OD BD ==. 24BD =，12OB ∴=在Rt OAB ∆中，13AB =，222213125OA AB OB ∴=-=-=.（2）如图2四边形ABCD 是菱形，BD ∴垂直平分AC ，FA FC ∴=，FAC FCA ∴∠=∠.由已知AF AM =，60MAF ∠=︒.AFM ∆为等边三角形，60M AFM ∴∠=∠=︒.。

人教版初二数学全等三角形双等腰旋转达标提优专项训练(1)

人教版初二数学全等三角形双等腰旋转达标提优专项训练(1)一、全等三角形双等腰旋转1．如图，△ABC 和△CEF 中，∠BAC ＝∠CEF ＝90°，AB ＝AC ，EC ＝EF ，点E 在AC 边上．（1）如图1，连接BE ，若AE ＝3，BE ＝58，求FC 的长度；（2）如图2，将△CEF 绕点C 逆时针旋转，旋转角为α（0°＜α＜180°），旋转过程中，直线EF 分别与直线AC ，BC 交于点M ，N ，当△CMN 是等腰三角形时，求旋转角α的度数；（3）如图3，将△CEF 绕点C 顺时针旋转，使得点B ，E ，F 在同一条直线上，点P 为BF 的中点，连接AE ，猜想AE ，CF 和BP 之间的数量关系并说明理由．答案：（1）；（2）22.5°或45°或112.5°；（3）CF ＋AE ＝BP ，见解析【分析】（1）利用勾股定理求出AB ＝AC ＝7，求出EC ＝EF ＝4即可解决问题；（2）分三种情形分别画出图形，利用等解析：（1）42；（2）22.5°或45°或112.5°；（3）CF ＋AE ＝2BP ，见解析【分析】（1）利用勾股定理求出AB ＝AC ＝7，求出EC ＝EF ＝4即可解决问题；（2）分三种情形分别画出图形，利用等腰三角形的性质求解即可；（3）结论：CF ＋AE ＝2BP ．如图3中，过点A 作AD ⊥AE ，利用全等三角形的性质以及等腰直角三角形的性质求解即可．【详解】解：（1）如图1中，在Rt △ABE 中，AB ()2222583497-=-==BF AE ，∴AC ＝AB ＝7，∴EF ＝EC ＝AC ﹣AE ＝7﹣3＝4，∵∠CEF ＝90°，EC ＝EF ＝3， ∴CF 22224442+=+=EF CE（2）①如图2﹣1中，当CM＝CN时，α＝∠MCE＝∠ECN＝12∠ACB＝22.5°．如图2﹣2中，当NM＝NC时，α＝∠MCN＝45°．如图2﹣3中，当CN＝CM时，∠NCE＝12∠BCM＝67.5°，α＝∠ACE＝45°＋67.5°＝112.5°．综上所述，满足条件的α的值为22.5°或45°或112.5°．（3）结论：CF＋AE＝2BP．理由：如图3中，过点A作AD⊥AE，∴∠DAE＝∠BAC＝90°，∴∠BAD＝∠CAE，∵∠BAC＝∠BEC＝90°，∴∠ABP＝∠ACE，∵AB＝AC，∴△ABD≌△ACE（ASA），∴BD＝EC＝EF，AD＝AE，∴△ADE是等腰直角三角形，∴DE＝2AE，∵P是BF的中点，∴BP＝12BF，∵BP＝12BF＝12（2EF＋DE），CF＝2EF，DE＝2AE，∴BP＝12（2CF＋2AE），∴CF＋AE＝2BP．【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．2．在等腰Rt△ABC中，AB＝AC，∠BAC＝90°（1）如图1，D，E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45°，将△ABE绕点A逆时针旋转90后，得到△AFC，连接DF①求证：△AED≌△AFD；②当BE＝3，CE＝7时，求DE的长；（2）如图2，点D是等腰Rt△ABC斜边BC所在直线上的一动点，连接AD，以点A为直角顶点作等腰Rt△ADE，当BD＝3，BC＝9时，求DE的长．答案：（1）①见解析；②DE＝；（2）DE的值为3或3【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2解析：（1）①见解析；②DE＝297；（2）DE的值为517【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2＝CD2+CF2，CF＝BE＝3，可得x2＝（7﹣x）2+32，解方程即可；（2）分两种情形：①当点E在线段BC上时，如图2中，连接BE．由△EAD≌△ADC，推出∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，推出∠EBD＝90°，推出DE2＝BE2+BD2＝62+32＝45，即可解决问题；②当点D在CB的延长线上时，如图3中，同法可得DE2＝153．【详解】（1）①如图1中，∵将△ABE绕点A逆时针旋转90°后，得到△AFC，∴△BAE≌△CAF，∴AE＝AF，∠BAE＝∠CAF，∵∠BAC＝90°，∠EAD＝45°，∴∠CAD+∠BAE＝∠CAD+∠CAF＝45°，∴∠DAE＝∠DAF，∵DA＝DA，AE＝AF，∴△AED≌△AFD（SAS）；②如图1中，设DE＝x，则CD＝7﹣x．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵∠ABE＝∠ACF＝45°，∴∠DCF＝90°，∵△AED≌△AFD（SAS），∴DE＝DF＝x，∵在Rt△DCF中， DF2＝CD2+CF2，CF＝BE＝3，∴x2＝（7﹣x）2+32，∴x＝29，7∴DE＝29；7（2）∵BD＝3，BC＝9，∴分两种情况如下：①当点E在线段BC上时，如图2中，连接BE．∵∠BAC＝∠EAD＝90°，∴∠EAB＝∠DAC，∵AE＝AD，AB＝AC，∴△EAB≌△DAC（SAS），∴∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝9-3=6，∴∠EBD＝90°，∴DE2＝BE2+BD2＝62+32＝45，∴DE ＝35； ②当点D 在CB 的延长线上时，如图3中，连接BE ．同理可证△DBE 是直角三角形，EB ＝CD ＝3+9=12，DB ＝3，∴DE 2＝EB 2+BD 2＝144+9＝153，∴DE ＝317，综上所述，DE 的值为35或317．【点睛】本题主要考查旋转变换的性质，三角形全等的判定和性质以及勾股定理，添加辅助线，构造旋转全等模型，是解题的关键．3．如图，在ABC ∆中，ABC ∠为锐角，点D 为直线BC 上一动点，以AD 为直角边且在AD 的右侧作等腰直角三角形ADE ，90DAE ∠=︒，AD AE =.（1）如果AB AC =，90BAC ∠=︒.①当点D 在线段BC 上时，如图1，线段CE 、BD 的位置关系为___________，数量关系为_____________②当点D 在线段BC 的延长线上时，如图2，①中的结论是否仍然成立，请说明理由. （2）如图3，如果AB AC ≠，90BAC ∠≠︒，点D 在线段BC 上运动。

初二数学全等三角形双等腰旋转测试试题含答案

初二数学全等三角形双等腰旋转测试试题含答案一、全等三角形双等腰旋转1．在正方形ABCD 中，对角线AC 、BD 交于点O ，以BC 为斜边作直角三角形BCP ，连接OP ．（1）如图所示，易证：2CP BP OP =+；（2）当点P 的位置变换到如第二幅图和第三幅图所示的位置时，线段CP 、BP 、OP 之间又有怎样的数量关系？请写出你的猜想，并对第二幅图加以证明．答案：（1）见解析；（2）第二幅图：，第三幅图：【分析】（1）在CP 上截取CE=BP ，连接OE ，记OB 与CP 交于点F ，根据正方形的性质证明，得到是等腰直角三角形，所以有，从而证得；（2）第二幅图的证解析：（1）见解析；（2）第二幅图：2BP CP OP =+，第三幅图：2BP CP OP +=【分析】（1）在CP 上截取CE=BP ，连接OE ，记OB 与CP 交于点F ，根据正方形的性质证明()OCE OBP SAS ≅，得到EOP △是等腰直角三角形，所以有2PE OP =，从而证得2CP CE PE BP OP =+=；（2）第二幅图的证明过程类似（1）中的证明过程，在BP 上截取BE=CP ，连接OE ，记OC 与BP 交于点F ，证明()OBE OCP SAS ≅，得到OEP 是等腰直角三角形，可以证得2BP CP OP =+；第三幅图的结论是2BP CP OP +=，证明方法一样是构造三角形全等，由()OBE OCP SAS ≅可以证出结论．【详解】解：（1）如图，在CP 上截取CE=BP ，连接OE ，记OB 与CP 交于点F ，∵四边形ABCD 是正方形，∴OB=OC ，90BOC ∠=°，∵BP CP ⊥，∴90BOC BPC ∠=∠=︒，∵OFC PFB ∠=∠，∴OCE OBP ∠=∠，在OCE △和OBP 中，OC OB OCE OBP CE BP =⎧⎪∠=∠⎨⎪=⎩，∴()OCE OBP SAS ≅，∴OE OP =，COE BOP ∠=∠，∵BOC BOE COE ∠=∠+∠，EOP BOE BOP ∠=∠+∠，∴90EOP BOC ∠=∠=︒，∴EOP △是等腰直角三角形， ∴2PE OP =， ∴2CP CE PE BP OP =+=；（2）第二幅图：2BP CP OP =+，第三幅图：2BP CP OP +=，证明第二幅图的结论：如图，在BP 上截取BE=CP ，连接OE ，记OC 与BP 交于点F ，同（1）中证明()OCE OBP SAS ≅的过程证明()OBE OCP SAS ≅，同理OEP 是等腰直角三角形， ∴2EP OP =， ∴2BP BE EP CP OP =+=；第三幅图的证明过程是：如图，延长PB 至点E ，使BE=CP ，证明()OBE OCP SAS ≅，得到OEP 是等腰直角三角形， ∴2EP OP =， ∵EP EB BP CP BP =+=+， ∴2OP CP BP =+．【点睛】本题考查全等三角形的性质和判定，等腰直角三角形的性质和进行的性质，解题的关键是掌握这些性质定理进行证明求解，并且学会构成全等三角形的方法．2．如图，△AOB 和△COD 均为等腰直角三角形，∠AOB ＝∠COD ＝90°，点C 、D 分别在边OA 、OB 上的点．连接AD ，BC ，点H 为BC 中点，连接OH ．（1）如图1，求证：OH ＝12AD ，OH ⊥AD ；（2）将△COD 绕点O 旋转到图2所示位置时，⑴中结论是否仍成立？若成立，证明你的结论；若不成立，请说明理由．答案：（1）见解析；（2）成立，证明见解析【分析】（1）只要证明△AOD ≌△BOC （SAS ），即可解决问题；（2）如图2中，结论：OH=AD ，OH ⊥AD ．延长OH 到E ，使得HE=OH ，连接BE ，证明解析：（1）见解析；（2）成立，证明见解析【分析】（1）只要证明△AOD ≌△BOC （SAS ），即可解决问题；（2）如图2中，结论：OH=12AD ，OH ⊥AD ．延长OH 到E ，使得HE=OH ，连接BE ，证明△BEH ≌△CHO （SAS ），可得OE=2OH ，∠EBC=∠BCO ，证明△BEO ≌△ODA （SAS ）即可解决问题；【详解】（1）∵△OAB 与△OCD 为等腰直角三角形，∠AOB ＝∠COD ＝90°．∴OC ＝OD ，OA ＝OB在△AOD 与△BOC 中OA OB AOD BOC OD OC =⎧⎪∠=∠⎨⎪=⎩∴△AOD ≌△BOC （SAS ）∴∠ADO ＝∠BCO ，∠OAD ＝∠OBC ，BC ＝AD∵点H 是BC 的中点，∠AOB ＝90°∴OH ＝HB ＝12BC ∴∠OBH ＝∠HOB ＝∠OAD ，OH ＝12AD ∵∠OAD ＋∠ADO ＝90°∴∠ADO ＋∠BOH ＝90°∴OH ⊥AD（2）（1）中结论成立；如图，延长OH 到E ，使得HE ＝OH ，连接BE ，CE∵CH ＝BH∴四边形BOCE 是平行四边形∴BE ＝OC ，EB ∥OC ，OH ＝12OE ∴∠EBO ＋∠COB ＝180°∵∠COB ＋∠BOD ＝90°，∠BOD ＋∠1＝90°∴∠1＝∠COB∵∠AOD ＋∠1＝180°∴∠AOD ＝∠EBO∴△BEO ≌△ODA∴∠EOB ＝∠DAO ，OE ＝AD∴OH ＝12AD ∴∠DAO ＋∠AOH ＝∠EOB ＋∠AOH ＝90°∴OH ⊥AD【点晴】本题属于几何变换综合题，考查了旋转变换，等腰直角三角形的性质，全等三角形的判定和性质，三角形三边关系等知识，构造全等三角形解决问题是解题的关键.3．如图1，在等腰直角三角形ABC 中，动点D 在直线AB （点A 与点B 重合除外）上时，以CD 为一腰在CD 上方作等腰直角三角形ECD ，且90ECD ∠=︒，连接AE ．（1）判断AE 与BD 的数量关系和位置关系；并说明理由．（2）如图2，若4BD =，P ，Q 两点在直线AB 上且5EP EQ ==，试求PQ 的长．（3）在第（2）小题的条件下，当点D 在线段AB 的延长线（或反向延长线）上时，判断PQ的长是否为定值．分别画出图形，若是请直接写出PQ的长；若不是请简单说明理由．答案：（1）AE=BD且AE⊥BD；（2）6；（3）PQ为定值6，图形见解析【分析】（1）由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰解析：（1）AE=BD且AE⊥BD；（2）6；（3）PQ为定值6，图形见解析【分析】（1）由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长；（3）分两种情况讨论，由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC，可得AE⊥BD，由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长．【详解】解：（1）AE=BD，AE⊥BD，理由如下：∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠EAC=∠DBC=45°，∴∠EAC+∠CAB=90°，∴AE⊥BD；（2）∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴，∴PQ=2AQ=6；（3）如图3，若点D在AB的延长线上，∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠CBD=∠CAE=135°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴，∴PQ=2AQ=6；如图4，若点D在BA的延长线上，∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠CBD=∠CAE=45°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴AQ=22=2516=3--，EQ AE∴PQ=2AQ=6.【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理等知识，证明AE⊥BD是本题的关键．4．在等腰Rt△ABC中，AB＝AC，∠BAC＝90°（1）如图1，D，E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45°，将△ABE绕点A逆时针旋转90后，得到△AFC，连接DF①求证：△AED≌△AFD；②当BE＝3，CE＝7时，求DE的长；（2）如图2，点D是等腰Rt△ABC斜边BC所在直线上的一动点，连接AD，以点A为直角顶点作等腰Rt△ADE，当BD＝3，BC＝9时，求DE的长．答案：（1）①见解析；②DE＝；（2）DE的值为3或3【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2解析：（1）①见解析；②DE＝297；（2）DE的值为517【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2＝CD2+CF2，CF＝BE＝3，可得x2＝（7﹣x）2+32，解方程即可；（2）分两种情形：①当点E在线段BC上时，如图2中，连接BE．由△EAD≌△ADC，推出∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，推出∠EBD＝90°，推出DE2＝BE2+BD2＝62+32＝45，即可解决问题；②当点D在CB的延长线上时，如图3中，同法可得DE2＝153．【详解】（1）①如图1中，∵将△ABE绕点A逆时针旋转90°后，得到△AFC，∴△BAE≌△CAF，∴AE＝AF，∠BAE＝∠CAF，∵∠BAC＝90°，∠EAD＝45°，∴∠CAD+∠BAE＝∠CAD+∠CAF＝45°，∴∠DAE＝∠DAF，∵DA＝DA，AE＝AF，∴△AED≌△AFD（SAS）；②如图1中，设DE＝x，则CD＝7﹣x．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵∠ABE＝∠ACF＝45°，∴∠DCF ＝90°，∵△AED ≌△AFD （SAS ），∴DE ＝DF ＝x ，∵在Rt △DCF 中， DF 2＝CD 2+CF 2，CF ＝BE ＝3，∴x 2＝（7﹣x ）2+32，∴x ＝297， ∴DE ＝297；（2）∵BD ＝3，BC ＝9，∴分两种情况如下：①当点E 在线段BC 上时，如图2中，连接BE ．∵∠BAC ＝∠EAD ＝90°，∴∠EAB ＝∠DAC ，∵AE ＝AD ，AB ＝AC ，∴△EAB ≌△DAC （SAS ），∴∠ABE ＝∠C ＝∠ABC ＝45°，EB ＝CD ＝9-3=6，∴∠EBD ＝90°，∴DE 2＝BE 2+BD 2＝62+32＝45，∴DE ＝35；②当点D 在CB 的延长线上时，如图3中，连接BE ．同理可证△DBE 是直角三角形，EB ＝CD ＝3+9=12，DB ＝3，∴DE 2＝EB 2+BD 2＝144+9＝153，∴DE ＝317，综上所述，DE 的值为35或317．【点睛】本题主要考查旋转变换的性质，三角形全等的判定和性质以及勾股定理，添加辅助线，构造旋转全等模型，是解题的关键．5．感知：如图①，已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上，连结AE 、CG ，易证AED CGD ≌△△．（不需要证明）探究：将图①中正方形DEFG 绕点D 按顺时针方向旋转，使点E 落在BC 边上，如图②．连结AE 、CG ，证明：AE=CG ．应用：如图③，正方形ABCD 中，AD =3，点E 在CB 的延长线上，BE =1，DE=DF ，∠EDF =90°．直接写出点F 与点C 的距离．答案：探究：证明见解析；应用：点F 与点C 的距离为．【分析】探究：结合旋转模型，利用“边角边”证明即可得出结论；应用：连接FC ，根据前序问题中的方法证明△AED ≌△CFD ，从而得到CF=AE ，即在Rt解析：探究：证明见解析；应用：点F 与点C 10．【分析】探究：结合旋转模型，利用“边角边”证明AED CGD ≌△△即可得出结论；应用：连接FC ，根据前序问题中的方法证明△AED ≌△CFD ，从而得到CF =AE ，即在Rt △AED 中求解AE 即可．【详解】探究：证明：在正方形ABCD 和正方形DEFG 中，AD =CD ，DE =DG ，90ADC EDG ∠=∠=︒，∴ADE CDG ∠=∠，∴AED CGD ≌△△，∴AE CG =；应用：连接FC ，∵∠EDF =∠ADC =90°，∴∠ADE =∠CDF ，又∵AD =CD ，DE=DF ，∴△AED ≌△CFD ，∴CF =AE ，在Rt △AED 中，2210AE AB BE =+=∴点F 与点C 10．【点睛】本题考查全等三角形的判定与性质，掌握基本的旋转模型，根据全等三角形的性质求解问题是解题关键．6．已知：如图1，AOB和COD都是等边三角形．（1）求证：①AC＝BD；②∠APB＝60°；（2）如图2，在AOB和COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，则AC与BD 间的等量关系为，∠APB的大小为答案：（1）①见解析，②见解析；（2）AC＝BD，α【分析】（1）①根据△AOB和△COD都是等边三角形，求出∠AOC=∠BOD，根据SAS 推出△AOC≌△BOD，根据全等三角形的性质得出AC=BD；解析：（1）①见解析，②见解析；（2）AC＝BD，α【分析】（1）①根据△AOB和△COD都是等边三角形，求出∠AOC=∠BOD，根据SAS推出△AOC≌△BOD，根据全等三角形的性质得出AC=BD；②由△AOC≌△BOD，可得∠CAO=∠DBO，根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，推出∠APB=∠AOB即可；（2）根据∠AOB=∠COD=α，求出∠AOC=∠BOD，根据SAS推出△AOC≌△BOD，根据全等三角形的性质得出AC=BD，∠CAO=∠DBO，根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，推出∠APB=∠AOB即可．【详解】证明：（1）①∵△AOB和△COD都是等边三角形，∴OA=OB ，OC=OD，∠AOB＝∠COD＝60°，∴∠AOC＝∠BOD，在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD （SAS ），∴AC ＝BD ，∠CAO ＝∠DBO ，②设AC 与BO 交于E ，∵△AOC ≌△BOD ，∴∠CAO ＝∠DBO ，∵∠AEO=∠BEP ，∴∠CAO+∠AOB ＝∠DBO+∠APB ，∴∠APB ＝∠AOB ＝60°．（2）AC=BD ，∠APB=α，理由如下：∵∠AOB=∠COD=α，∴∠AOC=∠BOD ，在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD ，∴AC=BD ，∠CAO=∠DBO ，设AC 与BO 交于E ，∵∠AEO=∠BEP ，∴∠CAO+∠AOB=∠DBO+∠APB ，∴∠APB=∠AOB=α，故答案为AC=BD ，α．【点睛】本题考查三角形旋转，三角形全等判定与性质，三角形内角和，掌握三角形旋转，三角形全等判定与性质，三角形内角和是解题关键．7．如图，将两块含45°角的大小不同的直角三角板△COD和△AOB如图①摆放，连结AC，BD．（1）如图①，猜想线段AC与BD存在怎样的数量关系和位置关系，请写出结论并证明；（2）将图①中的△COD绕点O顺时针旋转一定的角度（如图②），连结AC，BD，其他条件不变，线段AC与BD还存在（1）中的关系吗？请写出结论并说明理由．（3）将图①中的△COD绕点O逆时针旋转一定的角度（如图③），连结AC，BD，其他条件不变，线段AC与BD存在怎样的关系？请直接写出结论．答案：（1）AC=BD，AC⊥BD，证明见解析；（2）存在，AC=BD，AC⊥BD，证明见解析；（3）AC=BD，AC⊥BD【分析】（1）延长BD交AC于点E．易证△AOC≌△BOD（SAS），可得A解析：（1）AC=BD，AC⊥BD，证明见解析；（2）存在，AC=BD，AC⊥BD，证明见解析；（3）AC=BD，AC⊥BD【分析】（1）延长BD交AC于点E．易证△AOC≌△BOD（SAS），可得AC=BD，∠OAC=∠OBD，由∠ADE=∠BDO，可证∠AED=∠BOD=90º即可；（2）延长BD交AC于点F，交AO于点G．易证△AOC≌△BOD（SAS），可得AC=BD，∠OAC=∠OBD，由∠AGF=∠BGO，可得∠AFG=∠BOG=90º即可；（3）BD交AC于点H，AO于M，可证△AOC≌△BOD（SAS），可得AC=BD，∠OAC=∠OBD，由∠AMH=∠BMO，可得∠AHM=∠BOH=90º即可．【详解】（1）AC=BD，AC⊥BD，证明：延长BD交AC于点E．∵△COD和△AOB均为等腰直角三角形，∴OC=OD，OA=OB，∠COA=∠BOD=90º，∴△AOC≌△BOD（SAS），∴AC=BD，∴∠OAC=∠OBD，∵∠ADE=∠BDO，∴∠AED=∠BOD=90º，∴AC⊥BD；（2）存在，证明：延长BD交AC于点F，交AO于点G．∵△COD和△AOB均为等腰直角三角形，∴OC=OD，OA=OB，∠DOC=BOA=90º，∵∠AOC=∠DOC－∠DOA，∠BOD=∠BOA－∠DOA，∴∠AOC=∠BOD，∴△AOC≌△BOD（SAS），∴AC=BD，∠OAC=∠OBD，∵∠AGF=∠BGO，∴∠AFG=∠BOG=90º，∴AC⊥BD；（3）AC=BD，AC⊥BD．证明：BD交AC于点H，AO于M，∵△COD和△AOB均为等腰直角三角形，∴OC=OD，OA=OB，∠DOC=BOA=90º，∵∠AOC=∠DOC+∠DOA，∠BOD=∠BOA+∠DOA，∴∠AOC=∠BOD，∴△AOC≌△BOD（SAS），∴AC=BD，∠OAC=∠OBD，∵∠AMH=∠BMO，∴∠AHM=∠BOH=90º，∴AC⊥BD．【点睛】本题考查三角形旋转变换中对应相等的位置与数量关系，掌握三角形全等的证明方法，及其角度计算是解题关键．△和等腰直角8．如图，锐角ABC中，分别以AB、AC为边向外作等腰直角ABEACD △，使AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，可以通过全等三角形的知识证得BD 与CE 相等．（1）如图，锐角ABC 中分别以AB 、AC 为边向外作等腰ABE △和等腰ACD △，AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，试猜想BD 与CE 的数量关系，并说明理由．（2）如图，在中ABC ，45ACB ∠=︒，以AB 为直角边，A 为直角顶点向外作等腰直角ABD △，连接CD ，若2,3AC BC ==，求CD 的长．（3）如图，在四边形中ABCD ，60,15,8,ADC BC AB AD CD ∠=︒===，求BD 的最大值．答案：（1），证明见解析；（2）；（3）23．【分析】（1）由等腰三角形的性质解得，继而可证及，再由全等三角形对应边相等解题；（2）过A 作交于点，连接，先证明是等腰直角三角形，得到，，再证明，由全解析：（1）BD CE =，证明见解析；（2）13；（3）23．【分析】（1）由等腰三角形的性质解得,,AE AB AD AC BAE CAD ==∠=∠，继而可证EAC BAD ∠=∠及(SAS)EAC BAD ≌，再由全等三角形对应边相等解题；（2）过A 作AE AC ⊥交BC 于点E ，连接DE ，先证明EAC 是等腰直角三角形，得到 AE AC =，DAE BAC ∠=∠，再证明(SAS)DAE BAC ≌，由全等三角形的性质得到3,45DE BC DEA BCA ==∠=∠=︒，接着在等腰直角三角形EAC 中，由勾股定理解得22222EC AC AE AC =+=，最后在Rt DEC △中，由勾股定理即可解得CD 的长；（3）先证明ACD △为等边三角形，再由等边三角形的性质可得，,60AC CD ACD =∠=︒将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转的性质得815DE AB BC EC ====，，继而证明BCE 是等边三角形，由等边三角形的性质得到75BE BC ==，最后根据三角形三边关系解题即可．【详解】解：（1）∵ABE △和ACD △是等腰三角形，,,AE AB AD AC BAE CAD ∴==∠=∠，BAE BAC CAD BAC ∴∠+∠=∠+∠，即：EAC BAD ∠=∠，在EAC 中BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩，(SAS)EAC BAD ∴≌，CE BD ∴=；（2）如图（1）所示，过A 作AE AC ⊥交BC 于点E ，连接DE ，45,ACB AE AC ∠=︒⊥，90EAC ∴∠=︒，EAC ∴△是等腰直角三角形，AE AC ∴=，又ABD 是等腰直角三角形，,90AB AD BAD ∴=∠=︒， 90BAD EAC ∴∠=∠=︒，BAD BAE EAC BAE ∴∠+∠=∠+∠，即：DAE BAC ∠=∠，在DAE △和BAC 中,AD AB DAE BAC AE AC =⎧⎪∠=∠⎨⎪=⎩(SAS)DAE BAC ∴≌，3,45DE BC DEA BCA ∴==∠=∠=︒，在等腰直角三角形EAC 中，45AEC ∠=︒，90DEC DEA AEC ∴∠=∠+∠=︒，由勾股定理得：22222EC AC AE AC =+=.在Rt DEC △中，由勾股定理得： 229413CD DE EC =+=+=；（3）,60AD CD ADC =∠=︒，∴ACD △为等边三角形，,60AC CD ACD ∴=∠=︒，如图（2）所示，将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转性质可得∶815DE AB BC EC ====，60BCE ∠=︒，∴BCE 是等边三角形，∴75BE BC ==，又∴BE DE BD +≥，即158BD BE DE ≤+=+，即23BD ≤，∴BD 的最大值为 23．【点睛】本题考查全等三角形的判定与性质、旋转、勾股定理、等边三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．9．（1）问题发现：如图①，ABC 与ADE 是等边三角形，且点B ，D ，E 在同一直线上，连接CE ，求BEC ∠的度数，并确定线段BD 与CE 的数量关系．（2）拓展探究：如图②，ABC 与ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，且点B ，D ，E 在同一直线上，AF BE ⊥于点F ，连接CE ，求BEC ∠的度数，并确定线段AF ，BF ，CE 之间的数量关系．答案：（1）的度数为，线段与之间的数量关系是；（2）．【分析】（1）首先根据和均为等边三角形，可得，，，，据此判断出．然后根据全等三角形的判定方法，判断出≌，即可判断出，．进而判断出∠BEC 的度数为6 解析：（1）BEC ∠的度数为60︒，线段BD 与CD 之间的数量关系是BD CE =；（2）BF CE AF =+．【分析】（1）首先根据ABC 和ADE 均为等边三角形，可得AB AC =，AD AE =，60BAC DAE ∠=∠=︒，60ADE AED ∠=∠=︒，据此判断出BAD CAE ∠=∠．然后根据全等三角形的判定方法，判断出ABD △≌ACE △，即可判断出BD CE =，DBA CEA ∠=∠．进而判断出∠BEC 的度数为60°即可；（2）首先根据ABC 和ADE 均为等腰直角三角形，可得AB AC =，AD AE =，90BAC DAE ∠=∠=︒，45ADE AED ∠=∠=︒，据此判断出BAD CAE ∠=∠．然后根据全等三角形的判定方法，判断出ABD △≌ACE △，即可判断出,BD CE =ADB AEC ∠=∠．进而判断出∠BEC 的度数为90°即可；最后根据90DAE ∠=︒，AD AE =，AF DE ⊥，得到AF DF EF ==于是得到结论．【详解】解：（1）因为ABC 和ADE 均为等边三角形，所以AB AC =，AD AE =，60BAC DAE ∠=∠=︒，60ADE AED ∠=∠=︒，所以BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠．在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，所以ABD △≌ACE △，所以BD CE =，DBA CEA ∠=∠．因为点B ，D ，E 在同一直线上，所以18060120ADB ∠=︒-︒=︒，所以120AEC ∠=︒，所以1206060BEC AEC AED ∠=∠-∠=︒-︒=︒．综上可得，BEC ∠的度数为60︒，线段BD 与CD 之间的数量关系是BD CE =．（2）因为ABC 和ADE 均为等腰直角三角形，所以AB AC =，AD AE =，90BAC DAE ∠=∠=︒，45ADE AED ∠=∠=︒，所以BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠．在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，所以ABD △≌ACE △，所以BD CE =，ADB AEC ∠=∠．因为点B ，D ，E 在同一直线上，所以18045135ADB ∠=︒-︒=︒，所以135AEC ∠=︒，所以1354590BEC AEC AED ∠=∠-∠=︒-︒=︒．因为90DAE ∠=︒，AD AE =，AF DE ⊥，易证AF DF EF ==，所以BF BD DF CE AF =+=+．10．探究：(1)如图①，在等腰直角三角形ABC 中，∠ACB=90，作CM 平分∠ACB 交AB 于点M ，点D 为射线CM 上一点，以点C 为旋转中心将线段CD 逆时针旋转90°得到线段CE ，连接DE 交射线CB 于点F ，连接BD 、BE填空：①线段BD 、BE 的数量关系为______．②线段BC 、DE 的位置关系为______．推广：(2)如图②，在等腰三角形ABC 中，顶角∠ACB=a ，作CM 平分∠ACB 交AB 于点M ，点D 为△ABC 外部射线CM 上一点，以点C 为旋转中心将线段CD 逆时针旋转α度得到线段CE ，连接DE 、BD 、BE 请判断(1)中的结论是否成立，并说明理由．应用：(3)如图③，在等边三角形ABC中，AB=4．作BM平分∠ABC交AC于点M，点D为射线BM上一点，以点B为旋转中心将线段BD逆时针旋转60°得到线段BE，连接DE交射线BA 于点F，连接AD、AE．当以A、D、M为顶点的三角形与△AEF全等时，请直接写出DE的值．答案：(1)①BD=CE；②BD⊥CE；(2)结论：(1)中的结论仍然成立，理由见解析；(3)满足条件的DE的值为或4．【解析】【分析】①由CA=CB，∠ACB=90°，CM平分∠ACB，得出∠EC解析：(1)①BD=CE；②BD⊥CE；(2)结论：(1)中的结论仍然成立，理由见解析；(3)满足条件的DE的值为433或43．【解析】【分析】①由CA=CB，∠ACB=90°，CM平分∠ACB，得出∠ECF=∠DCF=45°，易证△CBD≌△CBE，即可得出BD=BE；②由CD=CE即可得出BC⊥DE.（2）由CA=CB，∠ACB=α，CM平分∠ACB，得出∠ECF=∠DCF=12α，易证△CBD≌△CBF，即可得出BD=BE，再由等腰三角形的性质得出BC⊥DE.（3）分两种情况，根据三角形全等的性质及三角函数即可得出.【详解】(1)如图①中，∵CA=CB，∠ACB=90°，CM平分∠ACB，∴∠ACM=∠BCM=45°，∵∠ECD=90°，∴∠ECF=∠DCF=45°，∵CD=CE，CB=CB，∴△CBD≌△CBE(SAS)，∴BD=BE，∵CD=CE，∴BC垂直平分线段DE，∴BC⊥DE．故答案为BD=CE，BD⊥CE．(2)结论：(1)中的结论仍然成立．理由：如图②中，∵CA=CB，∠ACB=α，CM平分∠ACB，∴∠ACM=∠BCM=1α，2∵∠ECD=α，∴∠ECF=∠DCF=1α，2∵CD=CE，CB=CB，∴△CBD≌△CBF(SAS)，∴BD=BE，∵CD=CE，∴BC垂直平分线段DE，∴BC⊥DE．(3)如图③中，当△AFE≌△AMD时，AF=AM，∵∠AFD=∠AMD=90°，∵AD=AD，∴Rt△ADF≌Rt△ADM(HL)，∴∠DAF=∠DAM=30°，∴∠DBA=∠DAB=30°，∴DA=DB，∵DF⊥AB，∴∠BDF=60°，BF=AF=2，∵BD=BE，∴△BDE是等边三角形，∴DF=EF=BF•tan30°=233，∴DE=2EF=433．如图③-1中，当点D在AM的延长线时，易证AF=AM=2，DE=2DF=43．综上所述，满足条件的DE 43或3.【点睛】本题考查了等腰三角形，全等三角形的判定与性质，解直角三角形，解题的关键是熟练掌握性质定理.二、全等三角形手拉手模型11．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB ∠＝ °，线段BD 、CE 之间的数量关系是；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．解析：（1）60BD CE ，＝；（2）452CEB BD CE ∠︒＝，＝，理由见解析；（3）CE 的长为2或2【分析】（1）证明ACE ABD ≌，得出CE ＝BD ，AEC ADB ∠=∠，即可得出结论；（2）证明ACE ABD ∽，得出AEC ADB ∠=∠，2BD CE =，即可得出结论；（3）先判断出2BD CE =，再求出210AB =：①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出AP ＝DP ＝AE ＝2，再根据勾股定理求出，BP ＝6，得出BD ＝4；②当点E 在点D 下方时，同①的方法得，AP ＝DP ＝AE ＝1，BP ＝6，进而得出BD ＝BP +DP ＝8，即可得出结论．【详解】解：（1）ABC 为等腰三角形，60AC BC ACB ∠︒＝，＝，∴ABC 是等边三角形，同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAEAD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒＝≌（）故答案为：60CEB BD CE ∠=︒=；．（2）45CEB BD ∠︒＝，，理由如下：在等腰三角形ABC 中，AC ＝BC ，90ACB ∠︒＝，45AB CAB ∴∠︒，＝，同理，45AD ADE DAE ∠∠︒，＝＝， ∴AE AC AD AB =，DAE CAB ∠∠＝， EAC DAB ∴∠∠＝，ACE ABD ∴∽ ，∴BD AD CE AE==∴AEC ADB BD ∠∠＝，，点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒＝＝135AEC ∴∠︒＝45CEB AEC AED ∴∠∠-∠︒＝＝；（3）由（2）知，ACE ABD ∽，BD ∴，在Rt ABC中，AC ＝AB ∴＝，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ，DE BD ⊥，PDE AED APD ∴∠∠∠＝＝，∴四边形APDE 是矩形，AE DE ＝，∴矩形APDE 是正方形，2AP DP AE ∴＝＝＝，在Rt APB △中，根据勾股定理得，226BP AB AP -＝＝，4BD BP AP ∴-＝＝，1222CE BD ∴＝＝； ②当点E 在点D 下方时，如图④同①的方法得，AP ＝DP ＝AE ＝2，BP ＝6，∴BD ＝BP +DP ＝8，122CE BD ∴＝＝4，综上CE 的长为22或42．【点睛】本题是几何变换的综合题，主要考查了旋转的性质，全等三角形的判定和定理，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出三角形ACE 和三角形ABD 相似是关键．12．在Rt ABC 中，90BAC ∠=︒，AB AC =．（1）如图1，点D 为BC 边上一点，连接AD ，以AD 为边作Rt ADE △，90DAE ∠=︒，AD AE =，连接EC ．直接写出线段BD 与CE 的数量关系为，位置关系为．（2）如图2，点D 为BC 延长线上一点，连接AD ，以AD 为边作Rt ADE △，90DAE ∠=︒，AD AE =，连接EC ．①用等式表示线段BC ，DC ，EC 之间的数量关系为．②求证：2222BD CD AD +=．（3）如图3，点D 为ABC 外一点，且45ADC ∠=︒，若13BD =，5CD =，求AD 的长．解析：（1）BD CE =，BD CE ⊥；（2）①BC DC EC +=，②见解析；（3）62【分析】（1）由等腰直角三角形的性质得到45B ACB ∠=∠=︒，根据题意可知BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠，再利用SAS 证明BAD ≌CAE ，可得到BD CE =，45ABC ACE ∠=∠=︒，从而算出BCE ∠的度数，进而得到线段BD 与CE 的位置关系；（2）①根据角度的运算得到BAD CAE ∠=∠，再利用SAS 证得BAD ≌CAE ，得到BD CE =，再根据BD BC CD =+，等量代换即可求出答案；②由①中BAD ≌CAE ，得到BD CE =，ABC ACE ∠=∠，在根据等腰直角三角形的性质即可得出ACE ∠的度数，进而证得90BCE DCE ∠=∠=︒，根据勾股定理得到222AE AD DE +=，222CE CD DE +=，等量代换后得到2222AE AD CE CD +=+，又因为AE AD =，BD CE =，代入即可得出答案；（3）过点A 作AE AD ⊥，并且AE AD =，连接DE ，CE ，得到ADE 是等腰直角三角形，由（2）得BAD ≌CAE ，得到BD CE =，在Rt CDE △中，通过勾股定理求出DE 的长度，在Rt ADE △中又由勾股定理得：222AE AD DE +=，再根据AE AD =，代入数据即可求出AD 的长度．【详解】（1）在Rt ABC 中，90BAC ∠=︒，AB AC =，∴45B ACB ∠=∠=︒，90DAE ∠=︒，∴BAC DAC DAE DAC ∠-∠=∠-∠，即BAD CAE ∠=∠，在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴BAD ≌CAE ()SAS ，∴BD CE =，45ABC ACE ∠=∠=︒，∴90BCE ACB ACE ∠=∠+∠=︒，∴BD CE ⊥．故答案为：BD CE =，BD CE ⊥．（2）①90BAC ∠=︒，90DAE ∠=︒，∴BAC CAD DAE CAD ∠+∠=∠+∠，即BAD CAE ∠=∠，在BAD 和CAE 中 AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴BAD ≌CAE ()SAS ，∴BD CE =，BD BC CD =+，∴BC DC EC +=．故答案为：BC DC EC +=．②证明：由①得：BAD ≌CAE ，∴BD CE =，ABC ACE ∠=∠，ABC 和ADE 都是等腰直角三角形，∴45ACE ABC ACB ∠=∠=∠=︒，∴90BCE DCE ∠=∠=︒，在Rt ADE △和Rt ECD △中，由勾股定理得：222AE AD DE +=，222CE CD DE +=，∴2222AE AD CE CD +=+，AE AD =，BD CE =，∴2222AD BD CD =+，即2222BD CD AD +=．（3）过点A 作AE AD ⊥，并且AE AD =，连接DE ，CE ，如图，∴ADE 是等腰直角三角形，∴45ADE ∠=︒，45ADC ∠=︒，∴90CDE ∠=︒，由（2）中②可知，BAD ≌CAE ，∴BD CE =，13BD =，5CD =，∴13CE =，在Rt CDE △中，由勾股定理得：222DE CD CE +=， ∴2212DE CE CD =-，在Rt ADE △中，由勾股定理得：222AE AD DE +=，∴22144AD =， ∴62AD =【点睛】本题考查了全等三角形的判定和性质，勾股定理，等腰三角形的性质，解题的关键是合理添加辅助线找出两个三角形全等．13．（1）如图1，ABC 和DCE 都是等边三角形，且B ，C ，D 三点在一条直线上，连接AD ，BE 相交于点P ，求证：BE AD =．（2）如图2，在BCD 中，若120BCD ∠<︒，分别以BC ，CD 和BD 为边在BCD 外部作等边ABC ，等边CDE △，等边BDF ，连接AD 、BE 、CF 恰交于点P ． ①求证：AD BE CF ==；②如图2，在（2）的条件下，试猜想PB ，PC ，PD 与BE 存在怎样的数量关系，并说明理由．解析：（1）详见解析；（2）①详见解析；②PB PC PD BE ++=，理由详见解析【分析】（1）根据等边三角形的性质得出BC=AC ，CE=CD ，∠ACB=∠DCE=60°，进而得出∠BCE=∠ACD ，判断出BCE ACD ≌（SAS ），即可得出结论；（2）①同（1）的方法判断出≌ACD BCE （SAS ），ABD CBF ≌（SAS ），即可得出结论； ②先判断出∠APB=60°，∠APC=60°，在PE 上取一点M ，使PM=PC ，证明CPM △是等边三角形，进而判断出PCD MCE ≌（SAS ），即可得出结论．【详解】（1）证明：∵ABC 和DCE 都是等边三角形，∴BC=AC ，CE=CD ，∠ACB=∠DCE=60°，∴∠ABC+∠ACE=∠DCE+∠ACE ，即∠BCE=∠ACD ，∴BCE ACD ≌（SAS ），∴BE=AD ；（2）①证明：∵ABC 和DCE 是等边三角形，∴AC=BC ，CD=CE ，∠ACB=∠DCE=60°，∴∠ACB+∠BCD=∠DCE+∠BCD ，即∠ACD=∠BCE ，∴≌ACD BCE （SAS ），∴AD=BE ，同理：ABD CBF ≌（SAS ），∴AD=CF ，即AD=BE=CF ；②解：结论：PB+PC+PD=BE ，理由：如图2，AD 与BC 的交点记作点Q ，则∠AQC=∠BQP ，由①知，≌ACD BCE ，∴∠CAD=∠CBE ，在ACQ 中，∠CAD+∠AQC=180°-∠ACB=120°，∴∠CBE+∠BQP=120°，在BPQ 中，∠APB=180°-（∠CBE+∠BQP ）=60°，∴∠DPE=60°，同理：∠APC=60°，60,CPE ∴∠=︒ ∠CPD=120°，在PE 上取一点M ，使PM=PC ，∴CPM △是等边三角形，∴CP CM PM ==，∠PCM=∠CMP=60°，∴∠CME=120°=∠CPD ，∵CDE △是等边三角形，∴CD=CE ，∠DCE=60°=∠PCM ，∴∠PCD=∠MCE ，∴PCD MCE ≌（SAS ），∴PD=ME ，∴BE=PB+PM+ME=PB+PC+PD ．【点睛】此题是三角形综合题，主要考查了三角形的内角和定理，等边三角形的性质和判定，全等三角形的判定和性质，构造出全等三角形是解本题的关键．14．如图1，在Rt ABC 中，,A 90AB AC ∠==，点,D E 分别在边,AB AC 上，AD AE =，连接DC ，点,,M P N 分别为,,DE DC BC 的中点．（1）图1中线段PM 与PN 的数量关系是，位置关系是；（2）把ADE 绕点A 逆时针旋转到图2的位置，连接,,MN BD CE .请判断ABD ∠与ACE ∠是否相等，请说明理由；（3）试判断PMN 的形状，并说明理由．解析：（1）PM PN =，PM PN ⊥；（2）ABD ACE ∠=∠，理由见解析；（3）PMN ∆是等腰直角三角形，理由见解析．【分析】（1）利用三角形的中位线得出11,22PM CE PN BD ==，进而判断出BD=CE ，即可得出结论，再利用三角形的中位线得出PM ∥CE 得出∠DPM=∠DCA ，最后用互余即可得出结论；（2）先判断出△ABD ≌△ACE 可得结论．（3）先判断出△ABD ≌△ACE ，得出BD=CE ，同（1）的方法得出11,22PM CE PN BD ==，即可得出PM=PN ，同（1）的方法即可得出结论；【详解】解：（1）如图1中，∵点P ，N 是BC ，CD 的中点，1//,2PN BD PN BD ∴= ∵点P ，M 是CD ，DE 的中点，1//,2PM CE PM CE ∴= ∵AB=AC ，AD=AE ，∴BD=CE ，∴PM=PN ，∵PN ∥BD ，∴∠DPN=∠ADC ，∵PM ∥CE ，∴∠DPM=∠DCA ，∵∠BAC=90°，∴∠ADC+∠ACD=90°，∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM ⊥PN ，故答案为：PM=PN ，PM ⊥PN ．（2）ABD ACE ∠=∠理由如下AB AC =，AD AE =由旋转得BAD CAE ∠=∠∴()ABD ACE SAS ∆≅∆∴ABD ACE ∠=∠（3）PMN ∆是等腰直角三角形ABD ACE ∆≅∆∴BD CE =点M P N 、、分别为DE DC BC 、、的中点∴12PM EC =，12PN BD = ∴PN PM =点M P N 、、分别为DE DC BC 、、的中点∴//PM CE ，//PN BD∴DPM DCE ∠=∠，PNC DBC ∠=∠∴MPN DPM DPN ∠=∠+∠DCE DCB DBC =∠+∠+∠DCA ACE DCB DBC =∠+∠+∠+∠DCA ABD DCB DBC =∠+∠+∠+∠ACB ABC =∠+∠90BAC ∠=∴90ACB ABC ∠+∠=∴90MPN ∠=∴PMN ∆是等腰直角三角形．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；15．如图，已知△ABC ，分别以AB,AC 为直角边，向外作等腰直角三角形ABE 和等腰直角三角形ACD ，∠EAB=∠DAC=90°，连结BD,CE 交于点F ，设AB=m ，BC=n.（1）求证：∠BDA=∠ECA ．（2）若m=2，n=3，∠ABC=75°，求BD 的长.（3）当∠ABC=____时，BD 最大，最大值为____（用含m ，n 的代数式表示）（4）试探究线段BF,AE,EF 三者之间的数量关系．解析：（1）证明见解析；（2193）135︒2m n +；（4）2222EF BF AE +=．【分析】（1）由已知条件证ABD AEC ≅，再根据三角形全等的性质即可得证；（2）过点E 作EG ⊥CB 交CB 的延长线于点G ，由已知条件易得60,2EBG BE ∠=︒=，这样在Rt BEG △中可得1,3BG EG ==CG 4=，再利用勾股定理可得19CE =，结合ABD AEC ≅，利用三角形全等的性质即可得；（3）由（2）可知，22,BE AB m BC n ===，再根据三角形的三边关系定理、两点之间线段最短可得当E 、B 、C 三点共线时，CE 取得最大值，由此即可得；（4）由ABD AEC ≅可得AEC ABD ∠=∠，结合△ABE 是等腰直角三角形可得△EFB 是直角三角形、222BE AE =，然后利用勾股定理、等量代换即可得．【详解】（1）∵△ABE 和△ACD 都是等腰直角三角形，且90EAB DAC ∠=∠=︒，∴AE=AB ，AC=AD ，∠EAB+∠BAC=∠BAC+∠DAC ，即∠EAC=∠BAD ，∴ABD AEC ≅，∴BDA ECA ∠=∠；（2）如图，过点E 作EG ⊥CB 交CB 的延长线于点G ，∴90EGB ∠=︒，∵在等腰直角△ABE ，90,2BAE AB m ∠=︒==， ∴45,22ABE BE AB ∠=︒==， ∵75ABC ∠=︒，∴180754560EBG ∠=︒-︒-︒=︒，∴1,3BG EG ==，∴4GC BG BC =+=，∴2219CE GC EG =+=，由（1）已证：ABD AEC ≅，则19BD CE ==；（3）由（2）可知，22,BE m BC n ===，由三角形的三边关系定理、两点之间线段最短得：当E 、B 、C 三点共线时，CE 取得最大值，最大值为2CE BE BC m n =+=+，∵BD CE =，∴BD 2m n +，此时180********ABC ABE ∠=︒-∠=︒-︒=︒，即当135ABC ∠=︒时，BD 2m n +；。

初中三角形旋转经典例题

初中三角形旋转经典例题示例文章篇一：哎呀呀，说起初中三角形旋转的经典例题，那可真是让我又爱又恨呢！记得有一次上数学课，老师在黑板上画了一个三角形，然后神秘兮兮地说：“同学们，今天咱们来研究一下这个三角形旋转的问题。

” 我当时心里就嘀咕：“这能有多难？”老师给出的例题是这样的：有一个等腰直角三角形ABC，直角顶点是C，把这个三角形绕着点C 顺时针旋转90 度，得到三角形A'B'C，让咱们求旋转后的三角形和原来三角形重合部分的面积。

我看着那个图，眼睛都快花了，心里直犯愁：“这可咋整啊？” 同桌小明倒是挺自信，他拿着笔在纸上比划着，嘴里还念念有词：“这还不简单，先找出旋转后的对应边和对应角呗。

” 我白了他一眼，说：“你倒是会说，那你快做出来给我看看呀！”这时，前桌的小红转过头来，说：“别着急，咱们一起想想。

” 我们三个人就凑在一起，开始研究起来。

我就想啊，这三角形旋转就好像是一个人在跳舞，转了一圈又一圈，但是它的形状和大小可没变。

这不就跟咱们玩的万花筒似的，看起来图案变来变去，其实那些碎片还是那些碎片嘛。

我们先把能找到的条件都标出来，发现重合部分也是个三角形。

小明突然一拍脑袋，说：“我知道啦，咱们可以通过三角形的相似来求面积。

” 我赶紧问：“咋相似啊？” 他说：“你看，这两个三角形的对应角相等，对应边成比例，不就是相似嘛。

” 小红也点点头，说：“对呀对呀，那咱们就能算出边长的比例，进而求出面积啦。

”经过一番计算，我们终于算出了答案。

老师看到我们做出来了，笑着说：“不错不错，继续努力！” 那一刻，我心里别提多高兴了，就像吃了蜜一样甜。

你说，这三角形旋转的问题是不是很有趣？它就像是一个藏着宝藏的迷宫，只要我们认真思考，就能找到通往答案的路。

我觉得啊，数学虽然有时候让人头疼，但当我们解开难题的时候，那种成就感真是无与伦比！所以，可别害怕难题，只要咱们勇敢去探索，就一定能战胜它们！示例文章篇二：哎呀，一提到初中三角形旋转的经典例题，我这脑袋瓜就开始嗡嗡响啦！你们能想象得到吗？那一个个三角形就像调皮的小精灵，不停地转呀转。

人教版初二数学全等三角形角6090旋转专项训练学能测试

人教版初二数学全等三角形角6090旋转专项训练学能测试一、全等三角形角6090旋转1．如图，在四边形ABCD 中，∠ABC ＝30°，将△DCB 绕点C 顺时针旋转60°后，点D 的对应点恰好与点A 重合，得到△ACE ，若AB ＝3，BC ＝4，求BD 的长？2．在△ABC 中90AOB ∠=︒，AO=BO ，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D(1) 当直线MN 绕点O 旋转到图①的位置时，求证：CD=AC+BD ；(2) 当直线MN 绕点O 旋转到图②的位置时，求证：CD=AC-BD ；(3) 当直线MN 绕点O 旋转到图③的位置时，试问：CD 、AC 、BD 有怎样的等量关系？请写出这个等量关系，并加以证明．3．（1）如图1，在正方形ABCD 中，点E 、F 分别是BC 、CD 边上的动点，且∠EAF ＝45°，求证：EF ＝DF+BE ．（2）如图2，在正方形ABCD 中，如果点E 、F 分别是CB 、DC 延长线上的动点，且∠EAF ＝45°，则EF 、BE 、DF 之间数量关系是什么？请写出证明过程．（3）如图1，若正方形ABCD 的边长为6，AE ＝35，求AF 的长．4．如图，点M ，N 分别在正方形ABCD 的边BC ，CD 上，且45MAN ∠=︒，把ADN △绕点A 顺时针旋转90︒得到ABE △．（1）求证：AEM △≌ANM ．（2）若3BM =，2DN =，求正方形ABCD 的边长．5．如图，点A 的坐标是（-2，0），点B 的坐标是（0，6），C 为OB 的中点，将△ABC 绕点B 逆时针旋转90°后得到△A′BC′，若反比例函数k y x=的图像恰好经过A′B 的中点D ，求这个反比例函数的解析式．6．如图1，ABC 与CDE △都是等腰直角三角形，直角边AC ，CD 在同一条直线上，点M 、N 分别是斜边AB 、DE 的中点，点P 为AD 的中点，连接AE ，BD ，PM ，PN ，MN ．（1）观察猜想：图1中，PM 与PN 的数量关系是______，位置关系是______．（2）探究证明：将图1中的CDE △绕着点C 顺时针旋转()090αα︒<<︒，得到图2，AE 与MP 、BD 分别交于点G 、H ，判断PMN 的形状，并说明理由；（3）拓展延伸：把CDE △绕点C 任意旋转，若4AC =，2CD =，请直接写出PMN 面积的最大值． 7．在ABC 中，AB AC =，点P 在平面内，连接AP ，并将线段AP 绕A 顺时针方向旋转与BAC ∠相等的角度，得到线段AQ ，连接BQ ．（1）如图，如果点P 是BC 边上任意一点．则线段BQ 和线段PC 的数量关系是__________．（2）如图，如果点P 为平面内任意一点．前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．请仅以图所示的位置关系加以证明（或说明）；（3）如图，在DEF 中，8DE =，60EDF ∠=︒，75DEF ∠=︒，P 是线段EF 上的任意一点，连接DP ，将线段DP 绕点D 顺时针方向旋转60°，得到线段DQ ，连接EQ ．请直接写出线段EQ 长度的最小值．8．（1）如图，在四边形ABCD 中，AB AD =，180B D ∠+∠=︒，E 、F 分别是边BC 、CD 上的点，且12EAF BAD ∠=∠．求证：EF BE FD =+；（2）如图，在四边形ABCD 中，AB AD =，180B ADC ∠+∠=︒，E 、F 分别是边BC 、CD 延长线上的点，且12EAF BAD ∠=∠．（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．9．如图1，在平面直角坐标系中，直线y =−2x +6交坐标轴于A ，B 两点，过点C （-6，0）作CD 交AB 于D ，交y 轴于点E ，且△COE ≌△BOA ．（1）求点B 的坐标，线段OA 的长；（2）确定直线CD 的解析式，求点D 的坐标；（3）如图2，点M 是线段CE 上一动点(不与点C ，E 重合)，ON ⊥OM 交AB 于点N ，连接MN ，当△OMN 的面积最小时，请求点M 的坐标和△OMN 的面积．（4）如图3，点M 是直线CD 上一动点，过点M 作x 轴的垂线，交轴于点Q ，连接EQ ，若∠EQM=∠ACD ，求点M 的坐标．10．在等腰ABC ∆中，AB AC =,AE 为BC 边上的高，点D 在ABC ∆的外部且60CAD ∠=，AD AC =,连接BD 交直线AE 于点F ，连接FC ．=；(1)如图①，当120BAC∠<时，求证：BF CF∠的度数；(2)如图②，当40∠=时，求AFDBAC=+．(3)如图③，当120BAC∠>时,求证：CF AF DF【参考答案】***试卷处理标记，请不要删除一、全等三角形角6090旋转1．5【分析】连接BE，如图，根据旋转的性质得∠BCE=60°，CB=CE，BD=AE，再判断△BCE为等边三角形得到BE=BC=4，∠CBE=60°，从而有∠ABE=90°，然后利用勾股定理计算出AE即可．【详解】解：连接BE，如图，∵△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，∠BCE=60°，CB=CE，BD=AE，∴△BCE为等边三角形，∴BE=BC=4，∠CBE=60°，∵∠ABC=30°，∴∠ABE=90°，在Rt△ABE中，223+4=5，∴BD=5．故答案为：5．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．2．（1）证明见解析；（2）证明见解析；（3）CD=BD-AC ，证明见解析.【分析】（1）通过证明△ACO ≌△ODB 得到OC=BD ，AC=OD ，则CD=AC+BD ；（2）通过证明△ACO ≌△ODB 得到OC=BD ，AC=OD ，则CD=AC-BD ；（3）通过证明△ACO ≌△ODB 得到OC=BD ，AC=OD ，则CD=BD-AC ．【详解】解：（1）如图1，∵△AOB 中，∠AOB=90°，∴∠AOC+∠BOD=90°，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D ，∴∠ACO=∠BDO=90°∴∠AOC+∠OAC=90°，∴∠OAC=∠BOD ，在△ACO 和△ODB 中，90ACO ODB OAC BOD AO OB ⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△ACO ≌△ODB （AAS ），∴OC=BD ，AC=OD ，∴CD=AC+BD ；（2）如图2，∵△AOB 中，∠AOB=90°，∴∠AOC+∠BOD=90°，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D ，∴∠ACO=∠BDO=90°∴∠AOC+∠OAC=90°，∴∠OAC=∠BOD ，在△ACO 和△ODB 中，90ACO ODB OAC BOD AO OB ⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△ACO ≌△ODB （AAS ），∴OC=BD ，AC=OD ，∴CD=OD ﹣OC=AC ﹣BD ，即CD=AC ﹣BD ．（3）如图3，∵△AOB 中，∠AOB=90°，∴∠AOC+∠BOD=90°，直线MN 经过点O ，且AC ⊥MN 于C ，BD ⊥MN 于D ，∴∠ACO=∠BDO=90°∴∠AOC+∠OAC=90°，∴∠OAC=∠BOD ，在△ACO 和△ODB 中，90ACO ODB OAC BOD AO OB ⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△ACO ≌△ODB （AAS ），∴OC=BD ，AC=OD ，∴CD=OC ﹣OD=BD ﹣AC ，即CD=BD ﹣AC ．【点睛】此题是一道几何变换综合题，需要掌握全等三角形的判定和性质，直角三角形的性质，是一个探究题目，对于学生的能力要求比较高.3．（1）见解析；（2）EF ＝DF ﹣BE ，见解析；（3）10【分析】（1）把△ABE 绕点A 顺时针旋转90°至△ADG ，由“SAS”可证△EAF ≌△GAF ，可得出EF ＝FG，则结论得证；（2）将△ABE绕点A顺时针旋转90°至△ADM，根据SAS可证明△EAF≌△MAF，可得EF ＝FM，则结论得证；（3）由全等三角形的性质可得AE＝AG＝35，EF＝FG，BE＝DG，由勾股定理可求DG的长，FD的长，AF的长．【详解】（1）把△ABE绕点A顺时针旋转90°至△ADG，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），∴EF ＝FM ＝DF ﹣DM ＝DF ﹣BE ；（3）如图，由（1）可得AE ＝AG ＝35EF ＝FG ，BE ＝DG ，∵DG 2245363AG AD -=-=，∴BE ＝DG ＝3，∴EC ＝BC ﹣BE ＝3，∵EF 2＝EC 2+CF 2，∴（DF+3）2＝9+（6﹣DF ）2，∴DF ＝2，∴AF 22AD DF +436+10．【点睛】本题考查了全等三角形的判定和性质，勾股定理，旋转等知识，此题为半角模型，∠EAF 是∠BAD 的一半，故命名半角模型，半角模型必旋转，再证全等即可．4．（1）证明见解析；（2）正方形ABCD 的边长为6．【分析】（1）先根据旋转的性质可得,AE AN BAE DAN =∠=∠，再根据正方形的性质、角的和差可得45∠=︒MAE ，然后根据三角形全等的判定定理即可得证；（2）设正方形ABCD 的边长为x ，从而可得3,2CM x CN x =-=-，再根据旋转的性质可得2BE DN ==，从而可得5ME =，然后根据三角形全等的性质可得5MN ME ==，最后在Rt CMN 中，利用勾股定理即可得．【详解】（1）由旋转的性质得：,AE AN BAE DAN =∠=∠四边形ABCD 是正方形90BAD ∴∠=︒，即90BAN DAN ∠+∠=︒90BAN BAE ∴∠+∠=︒，即90EAN ∠=︒45MAN ∠=︒904545MAE EAN MAN ∴∠=∠-∠=︒-︒=︒在AEM △和ANM 中，45AE AN MAE MAN AM AM =⎧⎪∠=∠=︒⎨⎪=⎩()ANM A S S EM A ≅∴；（2）设正方形ABCD 的边长为x ，则BC CD x ==3,2BM DN ==3,2CM BC BM x CN CD DN x ∴=-=-=-=-由旋转的性质得：2BE DN ==235ME BE BM ∴=+=+=由（1）已证：AEM ANM ≅5MN ME ∴== 又四边形ABCD 是正方形90C ∴∠=︒ 则在Rt CMN 中，222CM CN MN +=，即222(3)(2)5x x -+-=解得6x =或1x =-（不符题意，舍去）故正方形ABCD 的边长为6．【点睛】本题考查了正方形的性质、旋转的性质、三角形全等的判定定理与性质、勾股定理等知识点，较难的是题（2），熟练掌握旋转的性质与正方形的性质是解题关键．5．15y x=．【分析】作A′H ⊥y 轴于H ．证明△AOB ≌△BHA′（AAS ），推出OA=BH ，OB=A′H ，求出点A′坐标，再利用中点坐标公式求出点D 坐标即可解决问题．【详解】作A ′H ⊥y 轴于H .∵∠AOB =∠A ′HB =∠ABA ′=90°，∴∠ABO +∠A ′BH =90°，∠ABO +∠BAO =90°，∴∠BAO =∠A ′BH ，∵BA =BA ′，∴△AOB ≌△BHA ′(AAS )，∴OA =BH ，OB =A ′H ，∵点A 的坐标是(−2,0)，点B 的坐标是(0,6)，∴BH =OA =2，A ′H =OB =6，∴OH =4，∴A ′(6,4)，∵BD =A ′D ，∴D (3,5)，∵反比例函数的图象经过点D ，∴这个反比例函数的解析式15y x = 【点睛】本题考查反比例函数图形上的点的坐标特征，坐标与图形的变化-旋转等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．6．（1）PM PN =，PM PN ⊥；（2）PMN 的形状为等腰直角三角形，理由见解析；（3）PMN 的面积的最大值为92．【分析】（1）延长AE 交BD 于点H ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（2）设AE 交BC 于⊙O ，易证ΔACE ≌ΔBCD ，得AE=BD ，∠CAE=∠CBD ，进而得∠BHA=90°，结合中位线的性质，得PM=12BD ，PM//BD ，PN=12AE ， PN//AE ，进而得PM=PN ，PM ⊥PN ；（3）易证ΔPMN 是等腰直角三角形，PM=12BD ，当B 、C 、D 共线时，BD 的值最大，进而求解．【详解】解：（1）如图1，延长AE 交BD 于点H ，∵ΔACB 和ΔECD 是等腰直角三角形，∴AC=BC ，EC=CD ，∠ACB=∠ECD=90°，∴∠ACB+∠BCE=∠ECD+∠BCE ，∴ΔACE ≌ΔBCD （SAS ），∴AE=BD ，∠CAE=∠CBD ，又∵∠AEC=∠BEH ，∴∠BHA=∠ACE=90°，∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴PM=12BD ，PM//BD ，PN=12AE ，PN//AE ， ∴PM=PN ， ∴PM ⊥AH ，∴PM ⊥PN ．（2）如图中，设AE 交BC 于O ．∵ACB △和ECD 是等腰直角三角形，∴AC BC =，EC CD =，90ACB ECD ∠=∠=︒∴ACB BCE ECD BCE ∠+∠=∠+∠∴ACE BCD ∠=∠.∴ACE BCD ≅∴AE BD =，CAE CBD ∠=∠又∵AOC BOE ∠=∠，CAE CBD ∠=∠，∴90BHO ACO ∠=∠=︒∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴12PM BD =，//PM BD ； PN AE =，//PN AE .∴PM PN =∴180MGE BHA ∠+∠=︒∴90MGE ∠=︒∴90MPN ∠=︒∴PM PN ⊥（3）PMN 的面积的最大值为92．由（2）可知PMN 是等腰直角三角形，12PM BD =， ∴当BD 的值最大时，PM 的值最大，PMN 的面积最大，∴当B 、C 、D 共线时，BD 的最大值6BC CD =+=，∴3PM PN ==，∴PMN 的面积的最大值193322=⨯⨯=．【点睛】本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质和判定定理，掌握旋转全等三角形模型，是解题的关键．7．（1）相等；（2）成立，证明见解析；（3）2622-【分析】（1）先判断出∠BAQ=∠CAP ，进而用SAS 判断出△BAQ ≌△CAP ，即可得出结论；（2）结论BQ=PC 仍然成立，理由同（1）的方法；（3）先构造出△DEQ ≌△DHP ，得出EQ=HP ，进而判断出要使EQ 最小，当HP ⊥EF （点P 和点M 重合）时，EQ 最小，最后用解直角三角形即可得出结论．【详解】解：（1）由旋转知：AQ=AP ，∵PAQ BAC ∠=∠，∴PAQ BAP BAC BAP ∠-∠=∠-∠，∴BAQ CAP ∠=∠，∵AB AC =，∴()BAQ CAP SAS ∆≅∆，∴BQ CP =故答案为：相等．（2）BQ PC =仍成立，理由如下：证明：由旋转知：AQ=AP ，∵PAQ BAC ∠=∠，∴PAQ BAP BAC BAP ∠-∠=∠-∠，∴BAQ CAP ∠=∠，∵AB AC =，∴()BAQ CAP SAS ∆≅∆，∴BQ C =Ｐ（3）如图：在DF 上取一点H ，使8DH DE ==，连接ＰＨ，过点Ｈ作HM EF ⊥于Ｍ，由旋转知，DQ DP =，60PDQ ∠=︒，∵60EDF ∠=︒，∴PDQ EDF ∠=∠，∴EDQ HDP ∠=∠，∴()DEQ DHP SAS ∆≅∆，∴EQ HP =，要使EQ 最小，则有HP 最小，而点H 是定点，点P 是EF 上的动点，∴当HM EF ⊥（点P 和点M 重合）时，HP 最小，即：点P 与点M 重合，EQ 最小，最小值为HM ，过点E 作EG DF ⊥于G ，在Rt DEG ∆中，8DE =，60EDF ∠=︒，∴30DEG ∠=︒， ∴142DG DE ==， ∴EG ==在Rt EGF ∆中，753045FEG DEF DEG ∠=∠-∠=︒-︒=︒，∴9045F FEG FEG ∠=︒-∠=︒=∠，FG EG == ∴4DF DG FG =+=+∴484FH DF DH =-=+=，在Rt HMF ∆中，45F ∠=︒，∴)422HM FH ===即：EQ 的最小值为．【点睛】本题考查旋转的性质、最值问题，属于几何变换综合题，掌握全等三角形的证明方法，点到直线的距离等知识为解题关键．8．（1）见证明；（2）结论EF ＝BE +FD 不成立，应当是EF ＝BE ﹣FD ，证明见详解．【分析】（1）延长CB 至M ，使BM ＝DF ，连接AM ．先证明△ABM ≌△ADF ，得到AF ＝AM ，∠2＝∠3，再证明△AME ≌△AFE ，得到EF ＝ME ，进行线段代换，问题得证；（2）在BE 上截取BG ，使BG ＝DF ，连接AG ．先证明△ABG ≌△ADF ，得到AG ＝AF ，再证明△AEG ≌△AEF ，得到EG ＝EF ，进行线段代换即可证明EF ＝BE ﹣FD ．【详解】解：（1）证明：如图，延长CB 至M ，使BM ＝DF ，连接AM ．∵∠ABC +∠D ＝180°，∠1+∠ABC ＝180°，∴∠1＝∠D ，在△ABM 与△ADF 中，1D BM DF ⎪∠=∠⎨⎪=⎩，∴△ABM ≌△ADF （SAS ）．∴AF ＝AM ，∠2＝∠3．∵∠EAF 12=∠BAD ， ∴∠2+∠412=∠BAD ＝∠EAF ． ∴∠3+∠4＝∠EAF ，即∠MAE ＝∠EAF ．在△AME 与△AFE 中，AM AF MAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△AME ≌△AFE （SAS ）．∴EF ＝ME ，即EF ＝BE +BM ，∴EF ＝BE +DF ；（2）结论EF ＝BE +FD 不成立，应当是EF ＝BE ﹣FD ．证明：如图，在BE 上截取BG ，使BG ＝DF ，连接AG ．∵∠B +∠ADC ＝180°，∠ADF +∠ADC ＝180°，∴∠B ＝∠ADF ．∵在△ABG 与△ADF 中，AB AD ABG ADF BG DF =⎧⎪∠=∠⎨⎪=⎩，∴△ABG ≌△ADF （SAS ），∴∠BAG ＝∠DAF ，AG ＝AF ，∴∠BAG +∠EAD ＝∠DAF +∠EAD ＝∠EAF 12=∠BAD ， ∴∠GAE ＝∠EAF ．在△AGE 与△AFE 中，GAE EAF AE AE ⎪∠=∠⎨⎪=⎩，∴△AEG ≌△AEF ，∴EG ＝EF ，∵EG ＝BE ﹣BG ，∴EF ＝BE ﹣FD ．【点睛】本题属于三角形综合题，考查了三角形全等的判定和性质等知识，解题的关键是学会利用旋转变换的思想添加辅助线，构造全等三角形解决问题，解题时注意一些题目虽然图形发生变化，但是证明思路和方法是类似的，属于中考压轴题．9．（1）（0，6），3；（2）（61855，）；（3）（65-，125），185；（4）（32-，94），（32，154）．【分析】（1）利用x 轴与y 轴的特征求直线y=-2x+6与两轴的交点即可；（2）利用△COE ≌△BOA ．求出E （0，3）设CD 的解析式为y=kx+b ，将C 、E 代入求出CD 解析式，由CD 交AB 于D ，联立解方程组13226y x y x ⎧=+⎪⎨⎪=-+⎩即可；（3）由△COE ≌△BOA ．推出CO=BO ，∠OCE=∠OBA ，利用同角的余角相等推出∠COM =∠EON ，进而可证△COM ≌△BON(ASA)，得△MON 为等腰直角三角形，要使△OMN 的面积最小，需OM 最小，此时OM ⊥CE 由△COE 面积桥OC OE 65OM==CE 5即可求出面积最小值，利用△MFO ∽△COE ，得MF FO 2==635可求MF ，FO 即可；（4）可证△EQO ∽△CEO 由性质QO OE =OE OC求出OQ ，当点Q 在x 轴的负半轴上时，Q（32-，0）由点M在CD上，当32x=-时求函数值得M1（32-，94）；当点Q在x轴的正半轴上时，Q（32，0）由点M在CD上，当32x=时求函数值M2（32，154），综合得M的坐标为（32-，94），（32，154）．【详解】（1）当x=0时，y=6，则B（0，6），当y=0时，-2x+6=0，x=3，A(3，0)，OA=3；（2）∵△COE ≌△BOA，∴OE=OA=3，OC=OB=6，∴E（0，3），C(-6,0)，设CD的解析式为y=kx+b，过C（-6，0）和E（0，3），则360 bk b=⎧⎨-+=⎩，解得312 bk=⎧⎪⎨=⎪⎩，CD的解析式为：132y x=+，∵CD交AB于D，∴13226 y xy x⎧=+⎪⎨⎪=-+⎩，解得65185xy⎧=⎪⎪⎨⎪=⎪⎩，点D坐标为D（61855，）；（3）∵△COE ≌△BOA，∴CO=BO，∠OCE=∠OBA，∵ON⊥OM，∠COB=90º，∴∠COM+∠MOE=90º,∠MOE+∠EON=90º，∴∠COM =∠EON，∴△COM≌△BON(ASA)，∴OM=ON，∴△MON为等腰直角三角形，S △MON =211OM ON=OM 22，要使△OMN 的面积最小，需OM 最小，此时OM ⊥CE ， CE=22OC +OE =35，由△COE 面积得，11CE OM=OC OE 22， OC OE 6365OM===CE 535⨯， S △MON 最小=22116518OM =?=2255⎛⎫ ⎪ ⎪⎝⎭，过M 作MF ⊥OC 于F ，∴∠FMO+∠FOM=90º，∠MCO+∠MOC=90º，∴∠FMO=∠MCO ，∵∠MFO=∠COE=90º，∴△MFO ∽△COE ，∴MF FO OM ==OC OE CE 即65MF FO 25===63535， ∴212MF=6=55⨯，6FO=5， ∵点M 在第二象限，∴M （65-，125）；（4）∵MQ ⊥x 轴，∴MQ ∥OE ，∴∠MQE=∠QEO ，∵∠EQM=∠ACD ，∴∠QEO=∠OCE ，∵∠QOE=∠EOC ，∴△EQO ∽△CEO ， ∴QO OE =OE OC ， ∴OQ=2OE 93==OC 62，当点Q 在x 轴的负半轴上时，Q （32-，0），由点M 在CD 上，CD 的解析式为：132y x =+，当32x =-时1393224y ⎛⎫=⨯-+= ⎪⎝⎭， M 1（32-，94），当点Q 在x 轴的正半轴上时，Q （32，0），由点M 在CD 上，CD 的解析式为：132y x =+，当32x =时13153224y ⎛⎫=⨯+= ⎪⎝⎭， M 2（32，154），综合得M 的坐标为（32-，94），（32，154）．．【点睛】本题考查直线与两轴的交点，直线解析式，两直线的交点，最小面积，三角形全等的性质，勾股定理，三角形相似，掌握直线与两轴的交点求法，会用待定系数法求直线解析式，会利用解方程组求两直线的交点，会利用点到直线的距离最小求最小面积，利用三角形全等的性质进行线段、角的转化，利用勾股定理求边长，会利用三角形相似的性质解决问题是关键．10．（1）见解析；（2）60AFD ∠=；（3）见解析【分析】（1）根据等腰三角形三线合一的性质，可得AE 垂直平分BC ，F 为垂直平分线AE 上点，即可得出结论；（2）根据（1）的结论可得AE 平分∠BAC ，∠BAF=20°，由AB=AC=AD ，推出40ABD ADB ∠=∠=，根据外角性质可得AFD BAF ABF ∠=∠+∠计算即可；（3）在CF 上截取CM=DF ，连接AM ，证明△ACM ≌△ADF （SAS ），进而证得△AFM 为等边三角形即可．【详解】（1）证明：∵AE 为等腰△ABC 底边BC 上的高线，AB=AC ，AE BC ∴⊥，∠AEB=∠AEC=90°，BE=CE ，∴AE 垂直平分BE ，F 在AE 上，BF CF ∴=；(2) ,AB AC AD AC ==，AB AD ∴=，100BAD BAC CAD ∠=∠+∠=，40ABD ADB ∴∠=∠=，由（1）知，AE 平分∠BAC ，20BAF CAF ∴∠=∠=，60AFD BAF ABF ∴∠=∠+∠=，故答案为：60°；(3) 在CF 上截取CM=DF ，连接AM ，由（1）可知，∠ABC=∠ACB ，∠FBC=∠FCB ，ABF ACF ∴∠=∠，AB AC AD ==，ABF D ∴∠=∠，ACF D ∴∠=∠，在△ACM 和△ADF 中，AC AD ACM ADF CM DF =⎧⎪∠=∠⎨⎪=⎩∴△ACM ≌△ADF （SAS ），,AF AM FAD MAC ∴=∠=∠，60FAM DAC ∴∠=∠=，∴△AFM 为等边三角形，FM AF ∴=，CF FM MC AF DF ∴=+=+．【点睛】本题考查了等腰三角形的性质，垂直平分线的性质，三角形全等的判定和性质，等边三角形的判定和性质，掌握三角形全等的判定和性质是解题的关键．。

初二数学全等三角形双等腰旋转测试基础卷(1)

初二数学全等三角形双等腰旋转测试基础卷(1)一、全等三角形双等腰旋转1．如图1是实验室中的一种摆动装置，BC 在地面上，支架ABC 是底边为BC 的等腰直角三角形，摆动臂AD 可绕点A 旋转，摆动臂DM 可绕点D 旋转，15AD =，6DM =．（1）在旋转过程中，①当A ，D ，M 三点在同一直线上时，求AM 的长；②当A ，D ，M 三点为同一直角三角形的顶点时，求AM 的长；（2）若摆动臂AD 顺时针旋转90︒，点D 的位置由ABC 外的点1D 转到其内的点2D 处，即1290D AD ︒∠=，连结12D D ，如图2，此时2135AD C ︒∠=，2202CD =2BD 的长．答案：（1）①21或9；②或；（2）【分析】（1）①分两种情形分别求解即可．②显然不能为直角．当为直角时，根据，计算即可，当时，根据，计算即可．（2）连接．首先利用勾股定理求出，再利用全等三角形的解析：（1）①21或9；②3213292）252【分析】（1）①分两种情形分别求解即可．②显然MAD ∠不能为直角．当AMD ∠为直角时，根据222AM AD DM =-，计算即可，当90ADM ∠=︒时，根据222AM AD DM =+，计算即可．（2）连接1CD ．首先利用勾股定理求出1CD ，再利用全等三角形的性质证明21BD CD =即可．【详解】解：（1）①由题意可得：21AM AD DM =+=，或9AM AD DM =-=．②显然MAD ∠不能为直角．当AMD ∠为直角时，22222156189AM AD DM =-=-=，321AM ∴=321-当90ADM ∠=︒时，22222156261AM AD DM =+=+=， 293AM ∴=或932-（舍弃）．综上所述，满足条件的AM 的值为321或329．（2）如图2中，连接1CD ．由题意：1290D AD ∠=︒，1215AD AD ==，2145AD D ∴∠=︒，12152D D =2135AD C ∠=︒，2190CD D ∴∠=︒，()()22221212202152252CD CD D D ∴=+=+=1290BAC D AD ∠=∠=︒，2212BAC CAD D AD CAD ∴∠-∠=∠-∠，21BAD CAD ∴∠=∠，AB AC =，21AD AD =，21()BAD CAD SAS ∴∆≅∆，21252BD CD ∴==．【点睛】本题属于四边形综合题，考查了等腰直角三角形的性质，勾股定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．2．已知，ABC 中，AB AC =，2BAC α∠=︒，点D 为BC 边中点，连接AD ，点E 为AD 的中点，线段CE 绕点E 顺时针旋转2α︒得到线段EF ，连接FC ，FD ．（1）如图1，当60BAC ∠=︒时，请直接写出DF DC的值；（2）如图2，当90BAC ∠=︒时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请写出正确的结论，并说明理由；（3）如图3，当2BAC α∠=︒时，请直接写出DF DC的值(用含α的三角函数表示)．答案：（1）；（2）不成立，，理由见解析；（3）．【分析】（1）如图1（见解析），先根据中位线定理得出，再根据旋转的性质、等边三角形的性质得出，，，然后根据三角形全等的判定定理与性质可得，由此即可得出解析：（1）12；（2）不成立，22DF DC =3）sin DF DC α=︒．【分析】（1）如图1（见解析），先根据中位线定理得出12EG DC =，再根据旋转的性质、等边三角形的性质得出EC FC =，CD CG =，DCF GCE ∠=∠，然后根据三角形全等的判定定理与性质可得DF EG =，由此即可得出答案；（2）如图2（见解析），先根据中位线定理、等腰三角形的三线合一得出90AEM ∠=︒，再根据等腰直角三角形的性质得出ACE BCF ∠=∠，22AC CE BC CF ==，然后根据相似三角形的判定与性质可得CBF CAE ∠=∠，2AE BF =AE AM BF BD =，最后根据相似三角形的判定与性质可得90BFD AEM ∠=∠=︒，据此利用正弦三角函数值即可得；（3）如图3（见解析），参照题（2）的思路，先根据相似三角形的判定与性质得出,90CBF CAE BFD AEN α∠=∠=︒∠=∠=︒，再在Rt BFD 中，利用正弦三角函数值即可得．【详解】（1）如图1，取AC 的中点G ，连接EG ，则12CG AC = 点E 为AD 的中点 EG ∴是ACD 的中位线12EG DC ∴=，即12EG DC =由旋转的性质可知，EC EF =，60FEC ∠=︒CEF ∴是等边三角形60ECF ∴∠=︒，EC FC =AB AC =，60BAC ∠=︒ABC ∴是等边三角形60,ACB AC BC ∴∠=︒=点D 为BC 边中点1122CD BC AC CG ∴=== 60ECF ECD DCF ∠=∠+∠=︒，60ACB ECD GCE ∠=∠+∠=︒DCF GCE ∴∠=∠在DCF 和GCE 中，CD CG DCF GCE FC EC =⎧⎪∠=∠⎨⎪=⎩()DCF GCE SAS ∴≅DF EG ∴=12DF EG DC DC ∴==；（2）不成立，2DF DC =，理由如下：如图2，连接BF ，取AC 的中点M ，连接EM∵E 是AD 的中点∴//EM BC∴AEM ADC ∠=∠∵AB AC =ABC ∴是等腰三角形∵D 是BC 中点, 2BAC α∠=︒∴AD BC ⊥，12CAD BAC α∠=∠=︒，BD DC = ∴90ADC ∠=︒∴90AEM ∠=︒当90BAC ∠=︒时，则90CEF ∠=︒ABC ∴和CEF △为等腰直角三角形∴45ACB ECF ∠=∠=︒，即45ECD ACE ECD BCF ∠+∠=∠+∠=︒∴ACE BCF ∠=∠，cos 45AC CE BC CF ==︒= ∴ACE BCF ~∴90452CBF CAE α︒∠=∠=︒==︒，2AE AC BF BC ==∵12122AC AM BD BC == ∴AE AM BF BD = ∴BDF AME ~ ∴90BFD AEM ∠=∠=︒在Rt BFD 中，sin DF DF CBF BD DC ∠==，即sin 45DF DC ︒=则2DF DC =；（3）sin DF DCα=︒，求解过程如下：如图3，连接BF ，取AC 的中点N ，连接EN 参照（2），同理可得：12CAD BAC α∠=∠=︒，BD DC =，90AEN ADC ∠=∠=︒ 当2BAC α∠=︒时，则2CEF α∠=︒AB AC =，EC EF =（旋转的性质）ABC ∴和EFC 为等腰三角形 ∴1(180)902ACB ABC BAC α∠=∠=︒-∠=︒-︒ 1(180)902ECF EFC CEF α∠=∠=︒-∠=︒-︒ 90ACB ECF α∴∠=∠=︒-︒ABC EFC ∴~AC CE BC CF∴= 又,ACB ECD ACE ECF ECD BCF ∠=∠+∠∠=∠+∠∴ACE BCF ∠=∠∴ACE BCF ~∴CBF CAE α∠=∠=︒，AE AC BF BC = ∵1212AC AN AC BD BCBC ==∴AE AN BF BD = ∴BDF ANE ~ ∴90BFD AEN ∠=∠=︒在Rt BFD 中，sin DF DF CBF BD DC ∠== 即sin DF DC α=︒．【点睛】本题考查了等腰三角形的性质、旋转的性质、三角形全等的判定定理与性质、相似三角形的判定与性质等知识点，通过作辅助线，构造全等三角形和相似三角形是解题关键． 3．如图1，在等腰直角三角形ABC 中，动点D 在直线AB （点A 与点B 重合除外）上时，以CD 为一腰在CD 上方作等腰直角三角形ECD ，且90ECD ∠=︒，连接AE ．（1）判断AE 与BD 的数量关系和位置关系；并说明理由．（2）如图2，若4BD =，P ，Q 两点在直线AB 上且5EP EQ ==，试求PQ 的长．（3）在第（2）小题的条件下，当点D 在线段AB 的延长线（或反向延长线）上时，判断PQ 的长是否为定值．分别画出图形，若是请直接写出PQ 的长；若不是请简单说明理由．答案：（1）AE=BD 且AE ⊥BD ；（2）6；（3）PQ 为定值6，图形见解析【分析】（1）由“SAS”可证△ACE ≌△BCD ，可得AE=BD ，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰解析：（1）AE=BD且AE⊥BD；（2）6；（3）PQ为定值6，图形见解析【分析】（1）由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC=45°，可得AE⊥BD；（2）由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长；（3）分两种情况讨论，由“SAS”可证△ACE≌△BCD，可得AE=BD，∠EAC=∠DBC，可得AE⊥BD，由等腰三角形的性质可得PA=AQ，由勾股定理可求PA的长，即可求PQ的长．【详解】解：（1）AE=BD，AE⊥BD，理由如下：∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠EAC=∠DBC=45°，∴∠EAC+∠CAB=90°，∴AE⊥BD；（2）∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴，∴PQ=2AQ=6；（3）如图3，若点D在AB的延长线上，∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠CBD=∠CAE=135°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴，∴PQ=2AQ=6；如图4，若点D在BA的延长线上，∵△ABC，△ECD都是等腰直角三角形，∴AC=BC，CE=CD，∠ACB=∠ECD=90°，∠ABC=∠CAB=45°，∴∠ACE=∠DCB，且AC=BC，CE=CD，∴△ACE≌△BCD（SAS）∴AE=BD，∠CBD=∠CAE=45°，且∠CAB=45°，∴∠EAB=90°，∵PE=EQ，AE⊥BD，∴PA=AQ，∵EP=EQ=5，AE=BD=4，∴AQ=22=2516=3--，EQ AE∴PQ=2AQ=6.【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理等知识，证明AE⊥BD是本题的关键．4．在等腰Rt△ABC中，AB＝AC，∠BAC＝90°（1）如图1，D，E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45°，将△ABE绕点A逆时针旋转90后，得到△AFC，连接DF①求证：△AED≌△AFD；②当BE＝3，CE＝7时，求DE的长；（2）如图2，点D是等腰Rt△ABC斜边BC所在直线上的一动点，连接AD，以点A为直角顶点作等腰Rt△ADE，当BD＝3，BC＝9时，求DE的长．答案：（1）①见解析；②DE＝；（2）DE的值为3或3【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2解析：（1）①见解析；②DE＝297；（2）DE的值为517【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2＝CD2+CF2，CF＝BE＝3，可得x2＝（7﹣x）2+32，解方程即可；（2）分两种情形：①当点E在线段BC上时，如图2中，连接BE．由△EAD≌△ADC，推出∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，推出∠EBD＝90°，推出DE2＝BE2+BD2＝62+32＝45，即可解决问题；②当点D在CB的延长线上时，如图3中，同法可得DE2＝153．【详解】（1）①如图1中，∵将△ABE绕点A逆时针旋转90°后，得到△AFC，∴△BAE≌△CAF，∴AE＝AF，∠BAE＝∠CAF，∵∠BAC＝90°，∠EAD＝45°，∴∠CAD+∠BAE＝∠CAD+∠CAF＝45°，∴∠DAE＝∠DAF，∵DA＝DA，AE＝AF，∴△AED≌△AFD（SAS）；②如图1中，设DE＝x，则CD＝7﹣x．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵∠ABE＝∠ACF＝45°，∴∠DCF ＝90°，∵△AED ≌△AFD （SAS ），∴DE ＝DF ＝x ，∵在Rt △DCF 中， DF 2＝CD 2+CF 2，CF ＝BE ＝3，∴x 2＝（7﹣x ）2+32，∴x ＝297， ∴DE ＝297；（2）∵BD ＝3，BC ＝9，∴分两种情况如下：①当点E 在线段BC 上时，如图2中，连接BE ．∵∠BAC ＝∠EAD ＝90°，∴∠EAB ＝∠DAC ，∵AE ＝AD ，AB ＝AC ，∴△EAB ≌△DAC （SAS ），∴∠ABE ＝∠C ＝∠ABC ＝45°，EB ＝CD ＝9-3=6，∴∠EBD ＝90°，∴DE 2＝BE 2+BD 2＝62+32＝45，∴DE ＝35；②当点D 在CB 的延长线上时，如图3中，连接BE ．同理可证△DBE 是直角三角形，EB ＝CD ＝3+9=12，DB ＝3，∴DE 2＝EB 2+BD 2＝144+9＝153，∴DE ＝317，综上所述，DE 的值为35或317．【点睛】本题主要考查旋转变换的性质，三角形全等的判定和性质以及勾股定理，添加辅助线，构造旋转全等模型，是解题的关键．5．在ABC 中，AB AC =，点D 是直线BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作ADE ，使AD AE =，DAE BAC ∠=∠，连接CE ．（1）如图，当点D 在线段BC 上，如果90BAC ∠=︒，则BCE ∠=______度．（2）设BAC α∠=，BCE β∠=．①如图，当点D 在线段BC 上移动时，α、β之间有怎样的数量关系？请直接写出你的结论．②如图，当点D 在线段BC 的反向延长线上移动时，α、β之间有怎样的数量关系？请说明理由．答案：（1）90；（2）①，理由见解析；②，理由见解析【分析】（1）由等腰直角三角形的性质可得∠ABC=∠ACB=45°，由“SAS”可证△BAD ≌△CAE ，可得∠ABC=∠ACE=45°，可求∠BC解析：（1）90；（2）①180αβ+=︒，理由见解析；②αβ=，理由见解析【分析】（1）由等腰直角三角形的性质可得∠ABC=∠ACB=45°，由“SAS”可证△BAD ≌△CAE ，可得∠ABC=∠ACE=45°，可求∠BCE 的度数；（2）①由“SAS”可证△ABD ≌△ACE 得出∠ABD=∠ACE ，再用三角形的内角和即可得出结论；②由“SAS”可证△ADB ≌△AEC 得出∠ABD=∠ACE ，再用三角形外角的性质即可得出结论．【详解】（1）∵AB=AC ，∠BAC=90°，∴∠ABC=∠ACB=45°，∵∠DAE=∠BAC ，∴∠BAD=∠CAE ，在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△CAE （SAS ）∴∠ABC=∠ACE=45°，∴∠BCE=∠ACB+∠ACE=90°，故答案为：90；（2）①180αβ+=︒．理由：∵∠BAC=∠DAE ，∴∠BAC-∠DAC=∠DAE-∠DAC ．即∠BAD=∠CAE ．在△ABD 与△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ），∴∠B=∠ACE ．∴∠B+∠ACB=∠ACE+∠ACB ．∵∠ACE+∠ACB=β，∴∠B+∠ACB=β，∵α+∠B+∠ACB=180°，∴α+β=180°；② 当点D 在射线BC 的反向延长线上时，αβ=．理由如下：∵DAE BAC ∠=∠，∴DAB EAC ∠=∠，在△ABD 与△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△≌△ADB AEC(SAS)， ∴ABD ACE ∠=∠，∵ABD BAC ACB ∠=∠+∠，ACE BCE ACB ∠=∠+∠，∴BAC ABD ACB ∠=∠-∠，BCE ACE ACB ∠=∠-∠，∴BAC BCE ∠=∠，即αβ=．【点睛】此题考查了全等三角形的判定和性质，等腰直角三角形的性质，三角形的内角和定理，以及三角形外交的性质，证明△ABD ≌△ACE 是解本题的关键．6．如图，锐角ABC 中，分别以AB 、AC 为边向外作等腰直角ABE △和等腰直角ACD △，使AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，可以通过全等三角形的知识证得BD 与CE 相等．（1）如图，锐角ABC 中分别以AB 、AC 为边向外作等腰ABE △和等腰ACD △，AE AB =，AD AC =，90BAE CAD ∠=∠=︒，连接BD 、CE ，试猜想BD 与CE 的数量关系，并说明理由．（2）如图，在中ABC ，45ACB ∠=︒，以AB 为直角边，A 为直角顶点向外作等腰直角ABD △，连接CD ，若2,3AC BC ==，求CD 的长．（3）如图，在四边形中ABCD ，60,15,8,ADC BC AB AD CD ∠=︒===，求BD 的最大值．答案：（1），证明见解析；（2）；（3）23．【分析】（1）由等腰三角形的性质解得，继而可证及，再由全等三角形对应边相等解题；（2）过A 作交于点，连接，先证明是等腰直角三角形，得到，，再证明，由全解析：（1）BD CE =，证明见解析；（23）23．【分析】（1）由等腰三角形的性质解得,,AE AB AD AC BAE CAD ==∠=∠，继而可证EAC BAD ∠=∠及(SAS)EAC BAD ≌，再由全等三角形对应边相等解题；（2）过A 作AE AC ⊥交BC 于点E ，连接DE ，先证明EAC 是等腰直角三角形，得到 AE AC =，DAE BAC ∠=∠，再证明(SAS)DAE BAC ≌，由全等三角形的性质得到3,45DE BC DEA BCA ==∠=∠=︒，接着在等腰直角三角形EAC 中，由勾股定理解得22222EC AC AE AC =+=，最后在Rt DEC △中，由勾股定理即可解得CD 的长；（3）先证明ACD △为等边三角形，再由等边三角形的性质可得，,60AC CD ACD =∠=︒将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转的性质得815DE AB BC EC ====，，继而证明BCE 是等边三角形，由等边三角形的性质得到75BE BC ==，最后根据三角形三边关系解题即可．【详解】解：（1）∵ABE △和ACD △是等腰三角形，,,AE AB AD AC BAE CAD ∴==∠=∠，BAE BAC CAD BAC ∴∠+∠=∠+∠，即：EAC BAD ∠=∠，在EAC 中BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩，(SAS)EAC BAD ∴≌，CE BD ∴=；（2）如图（1）所示，过A 作AE AC ⊥交BC 于点E ，连接DE ，45,ACB AE AC ∠=︒⊥，90EAC ∴∠=︒，EAC ∴△是等腰直角三角形，AE AC ∴=，又ABD 是等腰直角三角形，,90AB AD BAD ∴=∠=︒，90BAD EAC ∴∠=∠=︒，BAD BAE EAC BAE ∴∠+∠=∠+∠，即：DAE BAC ∠=∠，在DAE △和BAC 中,AD AB DAE BAC AE AC =⎧⎪∠=∠⎨⎪=⎩(SAS)DAE BAC ∴≌，3,45DE BC DEA BCA ∴==∠=∠=︒，在等腰直角三角形EAC 中，45AEC ∠=︒，90DEC DEA AEC ∴∠=∠+∠=︒，由勾股定理得：22222EC AC AE AC =+=.在Rt DEC △中，由勾股定理得：229413CD DE EC =+=+=；（3）,60AD CD ADC =∠=︒，∴ACD △为等边三角形，,60AC CD ACD ∴=∠=︒，如图（2）所示，将BCA 绕点C 顺时针旋转60°得到ECD ，连接BE ，由旋转性质可得∶815DE AB BC EC ====，60BCE ∠=︒，∴BCE 是等边三角形，∴75BE BC ==，又∴BE DE BD +≥，即158BD BE DE ≤+=+，即23BD ≤，∴BD 的最大值为 23．【点睛】本题考查全等三角形的判定与性质、旋转、勾股定理、等边三角形的判定与性质、三角形三边关系等知识，是重要考点，难度一般，掌握相关知识是解题关键．7．△ABC 中，∠BAC ＝90°，AB ＝AC ，点D 为直线BC 上一动点（点D 不与B ，C 重合），以AD 为边在AD 右侧作正方形ADEF ，连接CF ．（1）观察猜想：如图1，当点D 在线段BC 上时，AC ，CD ，CF 之间的数量关系为____________；（将结论直接写在横线上）（2）如图2，当点D 在线段CB 的延长线上时，（1）中的结论是否仍然成立？若成立，不需证明；若不成立，请你写出正确结论，并说明理由．答案：（1）CD+CF=AC ；（2）不成立，CD-CF=AC ；理由见解析．【分析】（1）根据正方形的性质可得∠DAF=90°，AD=AF ，利用同角的余角相等可得∠BAD=∠CAF ，利用SAS 可证明△B解析：（1）2AC ；（2）不成立，2AC ；理由见解析．【分析】（1）根据正方形的性质可得∠DAF=90°，AD=AF ，利用同角的余角相等可得∠BAD=∠CAF ，利用SAS可证明△BAD≌△CAF，可得CF=BD，即可得出BC=CD+CF，根据等腰直角三角形的性质可得AC，进而可得答案；（2）同（1）可证明△BAD≌△CAF，可得BD=CF，即可得出CD=BC+CF，根据等腰直角三角形的性质可得AC，可得AC，即可得答案．【详解】（1）∵四边形ADEF是正方形，∴∠DAF=90°，AD=AF，∴∠CAF+∠DAC=90°，∵∠BAC＝90°，∴∠BAD+∠DAC=90°，∴∠BAD=∠CAF，在△BAD和△CAF中，AB ACBAD CAF AD AF=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAF，∴CF=BD，∴CD+CF=CD+BD=BC，∵∠BAC=90°，AB=AC，∴AC，∴AC．故答案为：AC（2）不成立，AC．理由如下：同（1）可证△BAD≌△CAF，∴CF=BD，∴CD=BC+BD=BC+CF，∵AC，∴AC．【点睛】本题考查正方形的性质、全等三角形的判定与性质及等腰直角三角形的性质，熟练掌握相关性质及判定定理是解题关键．8．已知Rt△OAB和Rt△OCD的直角顶点O重合，∠AOB=∠COD=90°，且OA=OB，OC=OD．（1）如图1，当C、D分别在OA、OB上时，AC与BD的数量关系是AC BD（填“>”，“<”或“=”）AC与BD的位置关系是AC BD（填“∥”或“⊥”）；（2）将Rt△OCD绕点O顺时针旋转，使点D在OA上，如图2，连接AC，BD，求证：AC=BD；（3）现将Rt△OCD绕点O顺时针继续旋转，如图3，连接AC，BD，猜想AC与BD的数量关系和位置关系，并给出证明．答案：（1）=；⊥ （2）见解析（3）AC=BD 且AC ⊥BD ；证明见解析【分析】（1）根据等式的性质可得AC 与BD 的数量关系，根据∠AOB=∠COD=90°，可证AC 与BD 的位置关系；（2）证解析：（1）=；⊥ （2）见解析（3）AC=BD 且AC ⊥BD ；证明见解析【分析】（1）根据等式的性质可得AC 与BD 的数量关系，根据∠AOB=∠COD=90°，可证AC 与BD 的位置关系；（2）证明△OCA ≌△ODB ，即可得到AC=BD ；（3）证明△OCA ≌△ODB ，可得AC=BD ，∠BDO=∠ACO ，进而可证∠DEF=90°．【详解】解：（1）∵OA=OB ，OC=OD∴OA-OC=OB-OD ，∴AC=BD ．∵∠AOB=∠COD=90°，∴AO ⊥BO ，∵C 、D 分别在OA 、OB 上，∴AC ⊥BD ；（2）在△OCA 和△ODB 中，90OC OD COA BOD AO BO =⎧⎪∠==⎨⎪=⎩，∴△OCA ≌△ODB ，∴AC=BD ；（3）AC=BD ，AC ⊥BD ．理由：∵∠AOB=∠COD=90°，∴∠AOB+∠AOD=∠COD+∠AOD ，∴∠AOC=∠BOD ，在△OCA 和△ODB 中，OC OD COA BOD AO BO =⎧⎪∠=⎨⎪=⎩，∴△OCA ≌△ODB ，∴AC=BD ，∠BDO=∠ACO ，∵∠ACO+∠CFO=90°，∠CFO=∠DFE ，∴∠BDO+∠DFE=90°，∴∠DEF=180°-90°=90°，∴AC ⊥BD ．【点睛】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定与性质等知识，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．9．在Rt △ABC 中,AB=AC,D 为BC 边上一点(不与点B,C 重合),将线段AD 绕点A 逆时针旋转90°得到AE.(1)连接EC ，如图①，试探索线段BC ，CD ，CE 之间满足的等量关系，并证明你的结论；(2)连接DE ，如图②，求证：BD 2+CD 2=2AD 2(3)如图③,在四边形ABCD 中，∠ABC=∠ACB=∠ADC=45°，若BD=13，CD=1，则AD 的长为 ▲ .(直接写出答案）答案：（1）BC=DC+EC ，理由见解析；（2）见解析；（3）【分析】（1）根据本题中的条件证出△BAD ≌△CAE （SAS ）, 得到BD=CE,再根据条件即可证出结果.（2）由（1）中的条件可得∠解析：（1）BC=DC+EC ，理由见解析；（2）见解析；（3）6【分析】（1）根据本题中的条件证出△BAD ≌△CAE （SAS ）, 得到BD=CE,再根据条件即可证出结果. （2）由（1）中的条件可得∠DCE=∠ACE+∠ACB=90°, 所以CE 2+CD 2=ED 2,可推出BD 2+CD 2=2ED ,再根据勾股定理可得出结果.（3）作AE ⊥AD,使AE=AD ，连接CE,DE,可推出△BAD ≌△CAE （SAS ）,所以BD=CE=13,再根据勾股定理求得DE.【详解】解：（1）结论：BC=DC+EC理由：如图①中,∵∠BAC=∠DAE=90°,∴∠BAC-∠DAC=∠DAE-∠DAC ，即∠BAD=∠CAE,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAE （SAS ）;∴BD=CE,∴BC=BD+CD=EC+CD,即：BC=DC+EC.（2）BD 2+CD 2=2AD 2,理由如下：连接CE,由（1）得，△BAD ≌△CAE,∴BD=CE ，∠ACE=∠B,∴∠DCE=∠ACE+∠ACB=90°,∴CE 2+CD 2=ED 2,即：BD 2+CD 2=ED 2;在Rt △ADE 中,AD 2+AE 2=ED 2,又AD=AE,∴ED 2=2AD 2;∴BD 2+CD 2=2AD 2;（3）AD 的长为6(学生直接写出答案）.作AE ⊥AD,使AE=AD,连接CE,DE,∵∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△BAD 与△CAE 中,AB=AC ，∠BAD=∠CAE ，AD=AE.∴△BAD ≌△CAE （SAS ）,∴13∵∠ADC=45°,∠EDA=45°,∴∠EDC=90°,∴DE 2=CE 2-CD 2=132-12=12,∴3∵∠DAE=90°,AD 2+AE 2=DE 2,∴6.【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质，旋转变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．10．ABD ∆和BEP ∆都是等腰直角三角形，90BAD BEP ∠=∠=︒，O 为BD 中点（1）若P 、E 分别在AB 、BD 上，如图所示，求证：2AP OE =；（2）将如图所示中BEP ∆绕B 点顺时针旋转45︒，如图所示，问（1）中的结论是否仍然成立？请说明理由；（3）将如图所示中BEP ∆绕B 点顺时针旋转到如图所示，问（1）中的结论是否仍然成立？请说明理由.答案：（1）见解析；（2）仍然成立，理由见解析.【解析】【分析】（1）根据等腰三角形的两直角边相等，和勾股定理求得BP、OB的值．则易证AP与OE的数量关系；（2）将图1中的△BPE绕B点顺时针旋解析：（1）见解析；（2）仍然成立，理由见解析.【解析】【分析】（1）根据等腰三角形的两直角边相等，和勾股定理求得BP、OB的值．则易证AP与OE的数量关系；（2）将图1中的△BPE绕B点顺时针旋转45゜，问（1）中的结论成立，通过证明△BOA∽△BEP，即可得到问题答案．【详解】（1）证明：∵△ABD为等腰直角三角形，∠BAD=∠BEP=90゜，∴设AB=AD=a，则2．又∵点O为BD的中点，∴OB=12BD=22a．同理，设EP=BE=b，则2b．∴2b，OE=OB-BE=22a-b，则2222AP bOEa b==-，∴2；（2）∵△BEP是等腰直角三角形，∴∠B=∠BPE=45°，∵△ABD是等腰直角三角形，O是BD的中点，∴AO⊥BD，∴∠BOA=∠BEP=90°，∠BAO=180°-∠BOA-∠B=45°，∴△BOA ∽△BEP ， ∵2BP BA BE BO ==， ∴2BP BA BE BO==， ∴AP=2OE ．方法二（1）连结AO ，过P 作PC AO ⊥，垂足为CABD ∆是等腰直角三角形，90BAD ∠=︒，O 为BD 中点ABO ∴∆是等腰直角三角形 PC AO ⊥APC ∴∆是等腰直角三角形四边形PCOE 为矩形OE PC ∴= 2AP CP = 2AP OE ∴=（2）在AB 上取点F ，使AF BE =，连结FO ，FE ，AO由条件知四边形AFEP 为平行四边形 AP FE ∴=AO BO = OAF OBE ∠=∠ FAO EBO ∴∆≅∆FO EO ∴=，AOF BOE ∠=∠ 90FOE ∴∠=︒ 2FE OE ∴= 2AP OE = （3）作MO EO ⊥，且使MO EO =，连结AM ，ME ，AOMOE ∴∆为等腰直角三角形，又AOB ∆为等腰直角三角形AMO BEO ∴∆≅∆ AM BE ∴= 易证AM BE ⊥，AM PE ∥又BE PE =，AM PE ∴= ∴四边形AMEP 为平行四边形AP ME ∴= 在等腰直角三角形MOE 中，2ME OE =2AP OE ∴=【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等腰直角三角形的判定与性质以及相似三角形的判定和性质，题目的综合性很强难度不小．二、全等三角形手拉手模型11．如图，已知ABC 和ADE 均为等腰三角形，AC ＝BC ，DE ＝AE ，将这两个三角形放置在一起．（1）问题发现：如图①，当60ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，则CEB∠＝ °，线段BD 、CE 之间的数量关系是；（2）拓展探究：如图②，当90ACB AED ∠∠︒＝＝时，点B 、D 、E 在同一直线上，连接CE ，请判断CEB ∠的度数及线段BD 、CE 之间的数量关系，并说明理由；（3）解决问题：如图③，90ACB AED ∠∠︒＝＝，25AC ＝，AE ＝2，连接CE 、BD ，在AED 绕点A 旋转的过程中，当DE BD ⊥时，请直接写出EC 的长．解析：（1）60BD CE ，＝；（2）452CEB BD CE ∠︒＝，＝，理由见解析；（3）CE 的长为2或2【分析】（1）证明ACE ABD ≌，得出CE ＝BD ，AEC ADB ∠=∠，即可得出结论；（2）证明ACE ABD ∽，得出AEC ADB ∠=∠，2BD CE =，即可得出结论；（3）先判断出2BD CE =，再求出210AB =：①当点E 在点D 上方时，先判断出四边形APDE 是矩形，求出AP ＝DP ＝AE ＝2，再根据勾股定理求出，BP ＝6，得出BD ＝4；②当点E 在点D 下方时，同①的方法得，AP ＝DP ＝AE ＝1，BP ＝6，进而得出BD ＝BP +DP ＝8，即可得出结论．【详解】解：（1）ABC 为等腰三角形，60AC BC ACB ∠︒＝，＝，∴ABC 是等边三角形，同理可得ADE 是等边三角形6018012060BAD DAC DAC CAE BAD CAE AD AE AB ACEAC DAB ACE ABD SAS BD CEAEC ADB ADE AEC AED CEBCEB ∠+∠=∠+∠=︒∴∠=∠=⎧⎪=⎨⎪∠∠⎩∴∴=∠=∠=︒-∠=︒∠=∠+∠∴∠=︒＝≌（）故答案为：60CEB BD CE ∠=︒=；．（2）45CEB BD ∠︒＝，，理由如下：在等腰三角形ABC 中，AC ＝BC ，90ACB ∠︒＝，45AB CAB ∴∠︒，＝，同理，45AD ADE DAE ∠∠︒，＝＝， ∴AE AC AD AB =，DAE CAB ∠∠＝， EAC DAB ∴∠∠＝，ACE ABD ∴∽ ，∴BD AD CE AE== ∴AEC ADB BD ∠∠＝，，点B 、D 、E 在同一条直线上:180135ADB ADE ∴∠︒-∠︒＝＝135AEC ∴∠︒＝45CEB AEC AED ∴∠∠-∠︒＝＝；（3）由（2）知，ACE ABD ∽，BD ∴，在Rt ABC 中，AC ＝AB ∴＝，①当点E 在点D 上方时，如图③，过点A 作AP BD ⊥交BD 的延长线于P ，DE BD ⊥，PDE AED APD ∴∠∠∠＝＝，∴四边形APDE 是矩形，AE DE ＝，∴矩形APDE 是正方形，2AP DP AE ∴＝＝＝，在Rt APB △中，根据勾股定理得，6BP ，4BD BP AP ∴-＝＝，CE BD ∴＝ ②当点E 在点D 下方时，如图④同①的方法得，AP ＝DP ＝AE ＝2，BP ＝6，∴BD ＝BP +DP ＝8，CE ∴＝综上CE 的长为22或42．【点睛】本题是几何变换的综合题，主要考查了旋转的性质，全等三角形的判定和定理，相似三角形的判定和性质，勾股定理，等边三角形的性质，判断出三角形ACE 和三角形ABD 相似是关键．12．如图，在ABC 和ADE 中，∠BAC=∠DAE=90°，点P 为射线BD ，CE 的交点．（1）问题提出：如图1，若AD=AE ，AB=AC ．①BD 与CE 的数量关系为；②∠BPC 的度数为．（2）猜想论证：如图2，若∠ADE=∠ABC=30°，则（1）中的结论是否成立？请说明理由．如果不正确请写出正确结论．（3）拓展延伸：在（1）的条件中，若AB=3，AD=1，若把ADE 绕点A 旋转，当∠EAC=90°时，直接写出PB 的长．解析：（1）①相等，②90°；（2）结论①不成立，3BD CE=，结论②成立；（3）310或105 【分析】（1）①依据等腰三角形的性质得到AB AC =，AD AE =，依据同角的余角相等得到DAB CAE ∠=∠，然后依据“SAS ”可证明ADB AEC ≅，最后，依据全等三角形的性质可得到BD CE =；②由三角形内角和定理可求BPC ∠的度数；（2）先判断出ADB AEC △∽△，即可得出结论；（3）分为点E 在AB 上和点E 在AB 的延长线上两种情况画出图形，然后再证明△∽△PEB AEC ，最后依据相似三角形的性质进行证明即可．【详解】解：（1）①ABC 和ADE 是等腰直角三角形，90BAC DAE ∠=∠=︒， AB AC ∴=，AD AE =，DAB CAE ∠=∠．45ABC ACB ∠=∠=︒()ADB AEC SAS ∴≅△△BD CE ∴=，故答案为：相等；②18018045()BPC ABD ABC BCP BCP ACE ∠=︒-∠-∠-∠=︒-︒-∠+∠90BPC ∴∠=︒故答案为： 90︒（2）（1）中结论①不成立，3BD CE =；结论②成立，理由：在Rt ABC ∆中，30ABC ∠=︒，3AB AC ∴=，在Rt ADE 中，30ADE ∠=︒，3AD AE ∴=， ∴AD AE AB EC=， 90BAC DAE ∠=∠=︒，BAD CAE ∴∠=∠，ADB AEC ∴∽．ABD ACE ∴∠=∠；=3BD AD CE AE=； 18018030()BPC ABD ABC BCP BCP ACE ∠=︒-∠-∠-∠=︒-︒-∠+∠90BPC ∴∠=︒（3）解：①如图，当点E 在AB 上时，2BE AB AE =-=．90EAC ∠=︒，22221310CE AE AC ∴=++同（1）可证ADB AEC ≅．DBA ECA ∴∠=∠．又PEB AEC ∠=∠，PEB AEC ∴△∽△．∴PB BE AC CE = ∴2310PB = 3105PB ∴=②如图，当点E 在BA 延长线上时，4BE AB AE =+=．90EAC ∠=︒，10CE ∴=同（1）可证ADB AEC ≅．DBA ECA ∴∠=∠．BEP CEA ∠=∠，PEB AEC ∴△∽△．∴PB BE AC CE= ∴310PB =610PB ∴综上所述，PB 310或105．【点睛】本题是三角形综合题，主要考查的是旋转的性质、等腰三角形的性质、全等三角形的性质和判定、相似三角形的性质和判定，证明得PEB AEC ∽是解题的关键．13．如图，AOB 和COD △都是以O 为直角顶点的等腰直角三角形，连接AC ，BD ．（1）如图1，试判断AC 与BD 的数量关系和位置关系，并说明理由．（2）如图2，若点D 哈好在AC 上，且D 为AC 的中点，5AB =，求BOD 的面积．（3）如图3，设AC 与BD 的交点为E ，若AE CE =，60AOD ∠=︒，4AB =，求CD 的长．解析：（1）AC BD =，AC BD ⊥，见解析；（2）12BOD S =△；（3）252CD =．【分析】(1) 结论: AC=BD ，AC ⊥BD .如图1中，设AC 交BD 于K ，OA 交BD 于 E .证明△AOC ≌△BOD (SAS )即可解决问题.(2)如图2中，作OH ⊥CD 于H .首先证明OH=DH=CH ，设OH=DH=CH=m ，构建方程求出m 即可解决问题.(3)如图3中，连接BC ，作BH ⊥CO 交CO 的延长线于H .依次求出OB ，OH ，BH ，CH ，再求出 OC 即可解决问题.【详解】（1）如图，设AC 交BD 于点K ，OA 交BD 于点E ，图1所以90DOC AOB ∠=∠=︒， ∴AOC BOD ∠=∠， ∴OA OB =，OC OD =， ∴AOC △≌BOD （SAS ）， ∴AC BD =，OAC OBD ∠=∠， ∴90OBD BEO ∠+∠=°，BEO AEK ∠=∠， ∴90OAC AEK ∠+∠=°， ∴90AKB ∠=︒，∴AC BD ⊥．（2）如图，作OH CD ⊥于点H ，图2∵OD OC =，90COD ∠=︒，OH CD ⊥， ∴OH DH CH ==，设OH DH CH m ===，则2CD AD m ==， ∵5AB =OA OB =，90AOB ∠=︒， ∴102OA =，在Rt AOH 中，∵222OA OH AH =+，∴()2221032m m ⎛⎫+= ⎪ ⎪⎝⎭，解得12m =或12m =-（舍）， ∴12OH =，2AC =， ∵AOC △≌BOD ，111122222BOD AOC S S AC OH ==⋅⋅=⨯⨯=△△．（3）如图，连接BC ，图3作BH OC ⊥交CO 的延长线于点H ，∵OA OB =，90AOB ∠=︒，4AB =， ∴22OA OB ==，∵AC BD ⊥，AE EC =，∴4AB BC ==，∵60AOD ∠=︒，90AOB COD ∠=∠=︒，∴120COB ∠=︒，∴18060BOH BOC ∠=-∠=°°，∴122OH OB ==，6BH =，在Rt BCH 中，()22224610CH BC BH =-=-=∴102OC CH OH =-=∵2=CD OC ，∴252CD =．【点睛】本题属于三角形综合题，考查了全等三角形的判定和性质，勾股定理，30°角的直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题.14．如图，ABC ∆和BDE ∆都是等边三角形，点,E F 分别在,AB BC 边上,60DAF ︒∠=，（1）求证：.ABD ACF ∆≅∆（2）判断四边形DFCE 的形状．解析：（1）见解析；（2）平行四边形【分析】（1）由ABC ∆和BDE ∆都是等边三角形得到,60AB AC ABD ACB BAC ︒=∠=∠=∠=，根据60DAF ︒∠=推出DAB CAF ∠=∠，即可证得结论；（2）根据△ABD ≌△ACF 得到BD=CF ，再根据等边三角形的性质得到,3560BD DE ︒=∠=∠=，推出,//DE FC DE FC =即可得到结论.【详解】证明：（1）ABC ∆和BDE ∆是等边三角形，,60AB AC ABD ACB BAC ︒∴=∠=∠=∠=，∵60DAF ︒∠=，∴DAB CAF ∠=∠，∴△ABD ≌△ACF （ASA ）；（2）四边形DFCE 是平行四边形．理由如下：∵△ABD ≌△ACF ，∴.BD CF =又BDE ABC ∆∆,是等边三角形，,3560BD DE ︒∴=∠=∠=．,//.DE FC DE FC ∴=∴四边形DFCE 是平行四边形.【点睛】此题考查等边三角形的性质，三角形全等的判定及性质，内错角相等两直线平行的判定定理，证明四边形是平行四边形.15．如图1，在Rt ABC 中，,A 90AB AC ∠==，点,D E 分别在边,AB AC 上，AD AE =，连接DC ，点,,M P N 分别为,,DE DC BC 的中点．（1）图1中线段PM 与PN 的数量关系是，位置关系是；（2）把ADE 绕点A 逆时针旋转到图2的位置，连接,,MN BD CE .请判断ABD ∠与ACE ∠是否相等，请说明理由；（3）试判断PMN 的形状，并说明理由．解析：（1）PM PN =，PM PN ⊥；（2）ABD ACE ∠=∠，理由见解析；（3）PMN ∆是等腰直角三角形，理由见解析．【分析】（1）利用三角形的中位线得出11,22PM CE PN BD ==，进而判断出BD=CE ，即可得出结论，再利用三角形的中位线得出PM ∥CE 得出∠DPM=∠DCA ，最后用互余即可得出结论；（2）先判断出△ABD ≌△ACE 可得结论．（3）先判断出△ABD ≌△ACE ，得出BD=CE ，同（1）的方法得出11,22PM CE PN BD ==，即可得出PM=PN ，同（1）的方法即可得出结论；【详解】解：（1）如图1中，∵点P ，N 是BC ，CD 的中点，1//,2PN BD PN BD ∴= ∵点P ，M 是CD ，DE 的中点，1//,2PM CE PM CE ∴= ∵AB=AC ，AD=AE ，∴BD=CE ，∴PM=PN ，∵PN ∥BD ，∴∠DPN=∠ADC ，∵PM ∥CE ，∴∠DPM=∠DCA ，∵∠BAC=90°，∴∠ADC+∠ACD=90°，∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM ⊥PN ，故答案为：PM=PN ，PM ⊥PN ．（2）ABD ACE ∠=∠理由如下AB AC =，AD AE =由旋转得BAD CAE ∠=∠∴()ABD ACE SAS ∆≅∆∴ABD ACE ∠=∠（3）PMN ∆是等腰直角三角形ABD ACE ∆≅∆∴BD CE =点M P N 、、分别为DE DC BC 、、的中点 ∴12PM EC =，12PN BD = ∴PN PM =点M P N 、、分别为DE DC BC 、、的中点∴//PM CE ，//PN BD∴DPM DCE ∠=∠，PNC DBC ∠=∠∴MPN DPM DPN ∠=∠+∠DCE DCB DBC =∠+∠+∠DCA ACE DCB DBC =∠+∠+∠+∠DCA ABD DCB DBC =∠+∠+∠+∠ACB ABC =∠+∠90BAC∠=∴90ACB ABC∠+∠=∴90MPN∠=∴PMN∆是等腰直角三角形．【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；16．如图1，已知△ACB和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，以CE、BC 为边作平行四边形CEFB，连CD、CF．（1）如图2，△ADE绕点A旋转一定角度，求证：CD＝22CF；（2）如图3，AE＝2，AB＝26，将△ADE绕A点旋转一周，当四边形CEFB为菱形时，求CF的长．解析：（1）见解析（2）6或4【分析】（1）连接FD，证明△ADC≌△EDF（SAS），推出△DFC为等腰直角三角形即可解决问题；（2）分两种情形分别画出图形，利用（1）中结论求出CD即可解决问题．【详解】（1）解：连接FD，设DE与AC交于点G∵四边形CEFB是平行四边形∴BC∥EF∵AC⊥BC。

初二数学全等三角形角6090旋转练习题附解析

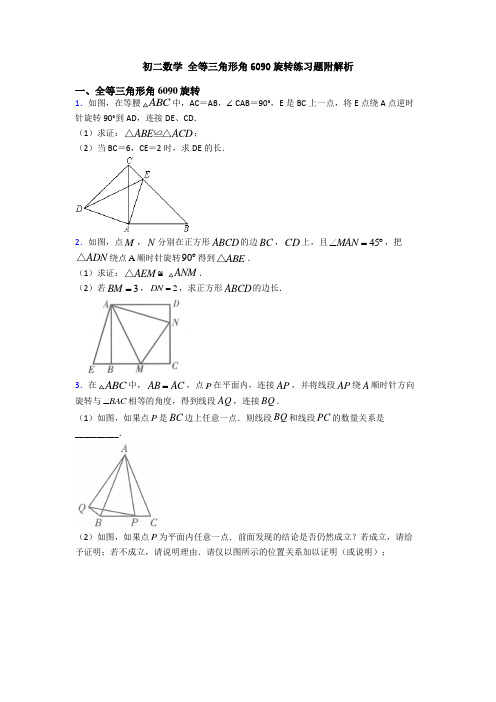
初二数学全等三角形角6090旋转练习题附解析一、全等三角形角6090旋转1．如图，在等腰ABC 中，AC ＝AB ，∠CAB ＝90°，E 是BC 上一点，将E 点绕A 点逆时针旋转90°到AD ，连接DE 、CD ．（1）求证：ABE ACD △≌△；（2）当BC ＝6，CE ＝2时，求DE 的长．2．如图，点M ，N 分别在正方形ABCD 的边BC ，CD 上，且45MAN ∠=︒，把ADN △绕点A 顺时针旋转90︒得到ABE △．（1）求证：AEM △≌ANM ．（2）若3BM =，2DN =，求正方形ABCD 的边长．3．在ABC 中，AB AC =，点P 在平面内，连接AP ，并将线段AP 绕A 顺时针方向旋转与BAC ∠相等的角度，得到线段AQ ，连接BQ ．（1）如图，如果点P 是BC 边上任意一点．则线段BQ 和线段PC 的数量关系是__________．（2）如图，如果点P 为平面内任意一点．前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．请仅以图所示的位置关系加以证明（或说明）；（3）如图，在DEF 中，8DE =，60EDF ∠=︒，75DEF ∠=︒，P 是线段EF 上的任意一点，连接DP ，将线段DP 绕点D 顺时针方向旋转60°，得到线段DQ ，连接EQ ．请直接写出线段EQ 长度的最小值．4．（1）如图，在四边形ABCD 中，AB AD =，180B D ∠+∠=︒，E 、F 分别是边BC 、CD 上的点，且12EAF BAD ∠=∠．求证：EF BE FD =+；（2）如图，在四边形ABCD 中，AB AD =，180B ADC ∠+∠=︒，E 、F 分别是边BC 、CD 延长线上的点，且12EAF BAD ∠=∠．（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．5．如图1，在平面直角坐标系中，直线y =−2x +6交坐标轴于A ，B 两点，过点C （-6，0）作CD 交AB 于D ，交y 轴于点E ，且△COE ≌△BOA ．（1）求点B 的坐标，线段OA 的长；（2）确定直线CD 的解析式，求点D 的坐标；（3）如图2，点M 是线段CE 上一动点(不与点C ，E 重合)，ON ⊥OM 交AB 于点N ，连接MN ，当△OMN 的面积最小时，请求点M 的坐标和△OMN 的面积．（4）如图3，点M 是直线CD 上一动点，过点M 作x 轴的垂线，交轴于点Q ，连接EQ ，若∠EQM=∠ACD ，求点M 的坐标．6．（探索发现）如图①，已知在△ABC 中，∠BAC= 45°，AD ⊥BC ，垂足为D ，BE ⊥AC ，垂足为E ，AD 与BE 相交于F ．（1）线段AF 与BC 的数量关系是：AF BC ，（用>，<，=填空）；（2）若∠ABC=67.5°，试猜想线段AF 与BD 有何数量关系，并说明理由．（拓展应用）（3）如图②，在△ABC 中，AD ⊥BC ，垂足为D ，已知∠BAC=45°，∠C=22.5°，AD=22，求△ABC 的面积．7．已知在Rt ABC ∆中，90ACB ∠=︒，AC BC =，CD AB ⊥于D ．（1）如图1，将线段CD 绕点C 顺时针旋转90︒得到CF ，连接AF 交CD 于点G ．求证：AG GF =；（2）如图2，点E 是线段CB 上一点（12CE CB <），连接ED ，将线段ED 绕点E 顺时针旋转90︒得到EF ，连接AF 交CD 于点G ．①求证：AG GF =；②若7AC BC ==，2CE =，求DG 的长．8．如图1，已知△ABC 是边长为8的等边三角形，∠EBD ＝30°，BE ＝DE ，连接AD ，点F 为AD 的中点，连接EF ．将△BDE 绕点B 顺时针旋转．（1）如图2，当点E 位于BC 边上时，延长DE 交AB 于点G ．①求证：BG ＝DE ；②若EF ＝3，求BE 的长；（2）如图3，连接CF ，在旋转过程中试探究线段CF 与EF 之间满足的数量关系，并说明理由．9．观察推理：如图1，△ABC 中，∠ACB =90°，AC =BC ，直线l 过点C ，点A 、B 在直线l 同侧，BD ⊥l ，AE ⊥l ，垂足分别为D 、E ．（1）求证：△AEC ≌△CDB ；（2）类比探究：如图2，Rt △ABC 中，∠ACB =90°，AC=6，将斜边AB 绕点A 逆时针旋转90°至AB ′，连接B′C ，求△AB′C 的面积；（3）拓展提升：如图3，∠E =60°，EC=EB=4cm ，点O 在BC 上，且OC =3cm ，动点P 从点E 沿射线EC 以2cm /s 速度运动，连结OP ，将线段OP 绕点O 逆时针旋转120°得到线段OF ．要使点F 恰好落在射线EB 上，求点P 运动的时间．10．已知90ACD ∠=︒，MN 是过点A 的直线，AC DC =，DB MN ⊥于点B ，如图（1）所示.易证BD AB 2CB +=，过程如下：过点C 作CE CB ⊥于点C ，与MN 交于点E90ACB BCD ∠+∠=︒，90ACB ACE ∠+∠=︒，BCD ACE ∴∠=∠.四边形ACDB 内角和为360︒，180BDC CAB ∴∠+∠=︒.180EAC CAB ∠+∠=︒，EAC BDC ∴∠=∠.又AC DC =，ACE DCB ∴∆≅∆，AE DB ∴=，CE CB =，ECB ∴∆为等腰直角三角形BE 2CB ∴=.又BE AE AB =+，BE BD AB ∴=+，BD AB 2CB ∴+=.（1）当MN 绕A 旋转到如图（2）所示和如图（3）所示两个位置时，BD 、AB 、CB 满足什么样关系式，请写出你的猜想，并对如图所示给予证明.（2）MN 在绕点A 旋转过程中，当30BCD ∠=︒，2BD =时，则CD =______，CB =______.【参考答案】***试卷处理标记，请不要删除一、全等三角形角6090旋转1．（1）见解析；（2）【分析】（1）根据E 点绕A 点逆时针旋转90°到AD ，可得AD ＝AE ，∠DAE ＝90°，进而可以证明△ABE ≌△ACD ；（2）结合（1）△ABE ≌△ACD ，和等腰三角形的性质，可得∠DCE ＝90°，再根据勾股定理即可求出DE 的长．【详解】（1）证明：∵E 点绕A 点逆时针旋转90°到AD ，∴AD ＝AE ，∠DAE ＝90°，∵∠CAB ＝90°，∴∠DAC ＝∠EAB ，∵AC ＝AB ，∴△ABE ≌△ACD （SAS ）；（2）∵等腰△ABC 中，AC ＝AB ，∠CAB ＝90°，∴∠ACB ＝∠ABC ＝45°，∵△ABE ≌△ACD ，∴BE ＝CD ，∠DCA ＝∠ABE ＝45°，∴∠DCE ＝90°，∵BC ＝6，CE ＝2，∴BE ＝4＝CD ，∴DE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、等腰直角三角形的性质，解决本题的关键是综合运用以上知识．2．（1）证明见解析；（2）正方形ABCD 的边长为6．【分析】（1）先根据旋转的性质可得,AE AN BAE DAN =∠=∠，再根据正方形的性质、角的和差可得45∠=︒MAE ，然后根据三角形全等的判定定理即可得证；（2）设正方形ABCD 的边长为x ，从而可得3,2CM x CN x =-=-，再根据旋转的性质可得2BE DN ==，从而可得5ME =，然后根据三角形全等的性质可得5MN ME ==，最后在Rt CMN 中，利用勾股定理即可得．【详解】（1）由旋转的性质得：,AE AN BAE DAN =∠=∠四边形ABCD 是正方形90BAD ∴∠=︒，即90BAN DAN ∠+∠=︒90BAN BAE ∴∠+∠=︒，即90EAN ∠=︒45MAN ∠=︒904545MAE EAN MAN ∴∠=∠-∠=︒-︒=︒在AEM △和ANM 中，45AE AN MAE MAN AM AM =⎧⎪∠=∠=︒⎨⎪=⎩()ANM A S S EM A ≅∴；（2）设正方形ABCD 的边长为x ，则BC CD x ==3,2BM DN ==3,2CM BC BM x CN CD DN x ∴=-=-=-=-由旋转的性质得：2BE DN ==235ME BE BM ∴=+=+=由（1）已证：AEM ANM ≅5MN ME ∴== 又四边形ABCD 是正方形90C ∴∠=︒则在Rt CMN 中，222CM CN MN +=，即222(3)(2)5x x -+-=解得6x =或1x =-（不符题意，舍去）故正方形ABCD 的边长为6．【点睛】本题考查了正方形的性质、旋转的性质、三角形全等的判定定理与性质、勾股定理等知识点，较难的是题（2），熟练掌握旋转的性质与正方形的性质是解题关键．3．（1）相等；（2）成立，证明见解析；（3）【分析】（1）先判断出∠BAQ=∠CAP ，进而用SAS 判断出△BAQ ≌△CAP ，即可得出结论；（2）结论BQ=PC 仍然成立，理由同（1）的方法；（3）先构造出△DEQ ≌△DHP ，得出EQ=HP ，进而判断出要使EQ 最小，当HP ⊥EF （点P 和点M 重合）时，EQ 最小，最后用解直角三角形即可得出结论．【详解】解：（1）由旋转知：AQ=AP ，∵PAQ BAC ∠=∠，∴PAQ BAP BAC BAP ∠-∠=∠-∠，∴BAQ CAP ∠=∠，∵AB AC =，∴()BAQ CAP SAS ∆≅∆，∴BQ CP =故答案为：相等．（2）BQ PC =仍成立，理由如下：证明：由旋转知：AQ=AP ，∵PAQ BAC ∠=∠，∴PAQ BAP BAC BAP ∠-∠=∠-∠，∴BAQ CAP ∠=∠，∵AB AC =，∴()BAQ CAP SAS ∆≅∆，∴BQ C =Ｐ（3）如图：在DF 上取一点H ，使8DH DE ==，连接ＰＨ，过点Ｈ作HM EF ⊥于Ｍ，由旋转知，DQ DP =，60PDQ ∠=︒，∵60EDF ∠=︒，∴PDQ EDF ∠=∠，∴EDQ HDP ∠=∠，∴()DEQ DHP SAS ∆≅∆，∴EQ HP =，要使EQ 最小，则有HP 最小，而点H 是定点，点P 是EF 上的动点，∴当HM EF ⊥（点P 和点M 重合）时，HP 最小，即：点P 与点M 重合，EQ 最小，最小值为HM ，过点E 作EG DF ⊥于G ，在Rt DEG ∆中，8DE =，60EDF ∠=︒，∴30DEG ∠=︒， ∴142DG DE ==， ∴343EG DG ==在Rt EGF ∆中，753045FEG DEF DEG ∠=∠-∠=︒-︒=︒，∴9045F FEG FEG ∠=︒-∠=︒=∠，43FG EG == ∴443DF DG FG =+=+ ∴4438434FH DF DH =-=+=，在Rt HMF ∆中，45F ∠=︒，∴)422HM FH === 即：EQ的最小值为．【点睛】本题考查旋转的性质、最值问题，属于几何变换综合题，掌握全等三角形的证明方法，点到直线的距离等知识为解题关键．4．（1）见证明；（2）结论EF ＝BE +FD 不成立，应当是EF ＝BE ﹣FD ，证明见详解．【分析】（1）延长CB 至M ，使BM ＝DF ，连接AM ．先证明△ABM ≌△ADF ，得到AF ＝AM ，∠2＝∠3，再证明△AME ≌△AFE ，得到EF ＝ME ，进行线段代换，问题得证；（2）在BE 上截取BG ，使BG ＝DF ，连接AG ．先证明△ABG ≌△ADF ，得到AG ＝AF ，再证明△AEG ≌△AEF ，得到EG ＝EF ，进行线段代换即可证明EF ＝BE ﹣FD ．【详解】解：（1）证明：如图，延长CB 至M ，使BM ＝DF ，连接AM ．∵∠ABC +∠D ＝180°，∠1+∠ABC ＝180°，∴∠1＝∠D ，在△ABM 与△ADF 中，1AB AD D BM DF =⎧⎪∠=∠⎨⎪=⎩，∴△ABM ≌△ADF （SAS ）．∴AF ＝AM ，∠2＝∠3．∵∠EAF 12=∠BAD ， ∴∠2+∠412=∠BAD ＝∠EAF ． ∴∠3+∠4＝∠EAF ，即∠MAE ＝∠EAF ．在△AME 与△AFE 中，AM AF MAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△AME ≌△AFE （SAS ）．∴EF ＝ME ，即EF ＝BE +BM ，∴EF ＝BE +DF ；（2）结论EF ＝BE +FD 不成立，应当是EF ＝BE ﹣FD ．证明：如图，在BE 上截取BG ，使BG ＝DF ，连接AG ．∵∠B +∠ADC ＝180°，∠ADF +∠ADC ＝180°，∴∠B ＝∠ADF ．∵在△ABG 与△ADF 中，AB AD ABG ADF BG DF =⎧⎪∠=∠⎨⎪=⎩，∴△ABG ≌△ADF （SAS ），∴∠BAG ＝∠DAF ，AG ＝AF ，∴∠BAG +∠EAD ＝∠DAF +∠EAD ＝∠EAF 12=∠BAD ， ∴∠GAE ＝∠EAF ．在△AGE 与△AFE 中， AG AF GAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△AEG ≌△AEF ，∴EG ＝EF ，∵EG ＝BE ﹣BG ，∴EF ＝BE ﹣FD ．【点睛】本题属于三角形综合题，考查了三角形全等的判定和性质等知识，解题的关键是学会利用旋转变换的思想添加辅助线，构造全等三角形解决问题，解题时注意一些题目虽然图形发生变化，但是证明思路和方法是类似的，属于中考压轴题．5．（1）（0，6），3；（2）（61855，）；（3）（65-，125），185；（4）（32-，9 4），（32，154）．【分析】（1）利用x轴与y轴的特征求直线y=-2x+6与两轴的交点即可；（2）利用△COE ≌△BOA．求出E（0，3）设CD的解析式为y=kx+b，将C、E代入求出CD解析式，由CD交AB于D，联立解方程组13226y xy x⎧=+⎪⎨⎪=-+⎩即可；（3）由△COE ≌△BOA．推出CO=BO，∠OCE=∠OBA，利用同角的余角相等推出∠COM =∠EON，进而可证△COM≌△BON(ASA)，得△MON为等腰直角三角形，要使△OMN的面积最小，需OM最小，此时OM⊥CE 由△COE 面积桥OC OE65OM==CE5即可求出面积最小值，利用△MFO∽△COE，得MF FO2==635可求MF，FO即可；（4）可证△EQO∽△CEO由性质QO OE=OE OC求出OQ，当点Q在x轴的负半轴上时，Q（32-，0）由点M在CD上，当32x=-时求函数值得M1（32-，94）；当点Q在x轴的正半轴上时，Q（32，0）由点M在CD上，当32x=时求函数值M2（32，154），综合得M的坐标为（32-，94），（32，154）．【详解】（1）当x=0时，y=6，则B（0，6），当y=0时，-2x+6=0，x=3，A(3，0)，OA=3；（2）∵△COE ≌△BOA，∴OE=OA=3，OC=OB=6，∴E（0，3），C(-6,0)，设CD的解析式为y=kx+b，过C（-6，0）和E（0，3），则360 bk b=⎧⎨-+=⎩，解得312 bk=⎧⎪⎨=⎪⎩，CD的解析式为：132y x=+，∵CD 交AB 于D ， ∴13226y x y x ⎧=+⎪⎨⎪=-+⎩，解得65185x y ⎧=⎪⎪⎨⎪=⎪⎩，点D 坐标为D （61855，）；（3）∵△COE ≌△BOA ，∴CO=BO ，∠OCE=∠OBA ，∵ON ⊥OM ，∠COB=90º，∴∠COM+∠MOE=90º,∠MOE+∠EON=90º，∴∠COM =∠EON ，∴△COM ≌△BON(ASA)，∴OM=ON ，∴△MON 为等腰直角三角形， S △MON =211OM ON=OM 22，要使△OMN 的面积最小，需OM 最小，此时OM ⊥CE ，由△COE 面积得，11CE OM=OC OE 22，OC OE 63OM==CE 35⨯， S △MON 最小=221118OM =?=2255⎛⎫ ⎪ ⎪⎝⎭，过M 作MF ⊥OC 于F ，∴∠FMO+∠FOM=90º，∠MCO+∠MOC=90º，∴∠FMO=∠MCO ，∵∠MFO=∠COE=90º，∴△MFO ∽△COE ， ∴MFFO OM ==OC OE CE即MF FO 2=635，∴212MF=6=55⨯，6FO=5， ∵点M 在第二象限，∴M （65-，125）；（4）∵MQ ⊥x 轴，∴MQ ∥OE ，∴∠MQE=∠QEO ，∵∠EQM=∠ACD ，∴∠QEO=∠OCE ，∵∠QOE=∠EOC ，∴△EQO ∽△CEO ， ∴QO OE =OE OC， ∴OQ=2OE 93==OC 62，当点Q 在x 轴的负半轴上时，Q （32-，0），由点M 在CD 上，CD 的解析式为：132y x =+，当32x =-时1393224y ⎛⎫=⨯-+= ⎪⎝⎭， M 1（32-，94），当点Q 在x 轴的正半轴上时，Q （32，0），由点M 在CD 上，CD 的解析式为：132y x =+，当32x =时13153224y ⎛⎫=⨯+= ⎪⎝⎭，M 2（32，154），综合得M 的坐标为（32-，94），（32，154）．．【点睛】本题考查直线与两轴的交点，直线解析式，两直线的交点，最小面积，三角形全等的性质，勾股定理，三角形相似，掌握直线与两轴的交点求法，会用待定系数法求直线解析式，会利用解方程组求两直线的交点，会利用点到直线的距离最小求最小面积，利用三角形全等的性质进行线段、角的转化，利用勾股定理求边长，会利用三角形相似的性质解决问题是关键．6．（1）=；（2）AF=2BD ，见解析；（3）8【分析】（1）证出△ABE 是等腰直角三角形，得出BE=AE ，证明△CBE ≌△FAE （ASA ），即可得出结论；（2）结论：AF=2BD ．只要证明△ABC 是等腰三角形，利用等腰三角形的三线合一的性质以及（1）得到的结论即可解决问题；（3）如图中，作CH ⊥AB 交AB 的延长线于H ，延长CH 交AD 的延长线于G ．只要证明BC=2AD ，利用三角形面积公式12BC AD ⨯，即可解决问题．【详解】（1）∵∠BAC=45°，BE ⊥AC ，∴△ABE 是等腰直角三角形，∴BE=AE ，∵AD ⊥BC ，∴∠C+∠CBE=∠C+∠FAE=90°，∴∠CBE =∠FAE ，在△CBE 和△FAE 中， 90 CEB FEA BE AE CBE FAE ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴△CBE ≌△FAE （ASA ），∴AF=BC ；（2）结论AF=2BD ．理由：∵∠BAC=45°，∠ABC=67.5°，∴∠C=180︒-∠BAC-∠ABC=67.5°，∴∠C=∠ABC ，∴△ABC 是等腰三角形，且AB=AC ，∵AD ⊥BC ，∴BD=CD=12BC ，由（1）得：AF=BC=2BD ；（3）如图，作CH ⊥AB 交AB 的延长线于H ，延长CH 交AD 的延长线于G ．∵∠AHC=90°，∠HAC=∠HCA=45°，∴AH=HC ，∵AD ⊥CD ，∴∠ADB=∠BHC=90°，∵∠ABD=∠CBH ，∴∠GAH=∠BCH ，∵∠AHG=∠CHB=90°，∴△AHG ≌△CHB ，∴BC=AG ，∵∠ACB=22.5°，∠HCA=45°，∴∠ACD=∠GCD=22.5°，又∵CD ⊥AG ，∴△AGC 是等腰三角形，且GC=AC ， ∴2，∴2，∴△ABC 的面积为：114222822BC AD ⨯=⨯=．【点睛】本题考查了全等三角形的判定和性质、等腰三角形的判定、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．7．（1）证明见详解；（2）①证明见详解，②324．【分析】（1）由旋转的性质得出90FCD ∠=︒，CF CD =，证得CF AD =，可证明()ADG FCG AAS ∆≅∆，则可得结论；（2）①过点E 作EM CB ⊥交CD 于点M ，连接MF ，证明()CED MEF SAS ∆≅∆，由全等三角形的性质得出CD MF =，45MEF ECD ∠=∠=︒，证明()ADG FMG AAS ∆≅∆，则可得结论；②由勾股定理求出AB ，CD ，CM ，则可求出答案．【详解】（1）证明：将线段CD 绕点C 顺时针旋转90︒得到CF ，90FCD ∴∠=︒，CF CD =，90ACB ∠=︒，AC BC =，CD AB ⊥于D ，AD BD ∴=，CF//AD ，CD AD BD ∴==，CF AD ∴=，又AGD CGF ∠=∠，()ADG FCG AAS ∴∆≅∆，AG GF ∴=；（2）①证明：过点E 作EM CB ⊥交CD 于点M ，连接MF ，由（1）知D 为AB 的中点，45DCB ∴∠=︒，CD AD =，CEM ∴∆为等腰直角三角形，CE ME ∴=，又90CEM DEF ∠=∠=︒，DE EF =，CED MEF ∴∠=∠，()CED MEF SAS ∴∆≅∆，CD MF ∴=，45MEF ECD ∠=∠=︒，AD MF ∴=，90CMF ∠=︒，又90ADG ∠=︒，ADG FMG ∴∠=∠，MGF AGD ∠=∠，()ADG FMG AAS ∴∆≅∆，AG GF ∴=；②解：90ACB ∠=︒，7AC BC ==， 2272AB AC BC ∴=+=，17222CD AB ∴==， 2CE =，CE ME =，22222222CM CE ME ∴=+=+=，72322222DM CD CM ∴=-=-=，又ADG FMG ∆≅∆，13224DG MG DM ∴===．【点睛】本题是几何变换综合题，考查了旋转的性质，等腰直角三角形的判定与性质，全等三角形的判定和性质，勾股定理等知识，熟练掌握旋转的性质及全等三角形的判定和性质是解题的关键．8．（1）①见解析；②2；（2）EC ＝3EF ，EC ⊥EF ，见解析【分析】（1）①想办法证明△BEG 是等边三角形即可解决问题；②利用三角形的中位线定理求出AG ，再求出BG 即可解决问题．（2）结论：EC ＝3EF ，EC ⊥EF ．延长DF 交CA 的延长线于M ，延长FE 到K ，使得EK ＝EF ，连接AK ，CK ，CF ，在FM 上截取FN ＝DF ，连接BN ．证明图中，红色三角形全等，推出△CFK 是等边三角形即可解决问题．【详解】（1）①证明：如图2中，∵△ABC 是等边三角形，∴∠ABC ＝60°，∵EB＝ED，∴∠EBD＝∠EDB＝30°，∴∠GBD＝∠ABC+∠EBD＝90°，∴∠BGD＝60°，∴△BEG是等边三角形，∴BG＝BE，∴BG＝ED．②解：由①可知，BG＝GE＝BE＝DE，又∵AF＝DF，∴AG＝2EF＝6，∵AB＝8，∴BG＝AB﹣AG＝8﹣6＝2，∴BE＝BG＝2．（2）结论：EC＝3EF，EC⊥EF．理由：如图2中，延长DF交CA的延长线于M，延长FE到K，使得EK＝EF，连接AK，CK，CF，在FM上截取FN＝DF，连接BN．∵FB＝FD＝FN，∴∠DBN＝90°，∵∠DBF＝30°，∴∠FBN＝60°，∴△FBN是等边三角形，∴BN＝BF，∵∠ABC＝∠NBF＝60°，∴∠ABN ＝∠CBF ，∵AB ＝BC ，∴△ABN ≌△CBF （SAS ），∴AN ＝CF ，∵FN ＝DF ，AE ＝ED ，∴EF ∥AN ，AN ＝2EF ，∵2EF ＝FK ，∴AN ＝FK ，AN ∥FK ，∴四边形ANFK 是平行四边形，∴AK ∥DM ，AK ＝FN ＝BN ，∴∠CAK ＝∠M ，∵∠AOM ＝∠BON ，∠OAM ＝∠BNO ＝120°，∴∠M ＝∠OBN ，∴∠ABN ＝∠CAK ，∵AB ＝AC ，∴△ABN ≌△CAK （SAS ），∴AN ＝CK ，∴CF ＝CK ＝FK ，∴△CFK 是等边三角形，∠CFE ＝60°∵2EF ＝FK ，∴CE ⊥FK ，∵∠EFC ＝60°，∴tan ∠CFE＝EC EF ∴EC，EC ⊥EF ．【点睛】本题主要考查了三角形的综合应用，准确应用等边三角形的性质进行分析是关键． 9．（1）证明见详解；（2）18；（3）2.5【分析】(1）根据题干可知本题考查全等三角形证明，先利用等角的余角相等得到∠EAC=∠BCD ，则可根据“AAS”证明△AEC ≌△CD ．(2)根据图2和条件，作B'D ⊥AC 于D ，先证明△B'AD ≌△A B'D 得到B'D=AC=6，则可根据三角形面积公式计算；(3)根据图3，利用旋转的性质得∠FOP=120°，OP=OF ，再证明△BOF ≌△CPO 得到PC=OB=1，则EP=CE ＋CP=5，然后计算点P 运动的时间t ．【详解】(1)∵∠ACB=90°，∴∠ACE+∠DCB=90°，∵BD⊥l，AE⊥l，∴∠AEC=∠BDC=90°，∴∠EAC＋∠ACE=90°，∴∠EAC=∠DCB，又∵AC=BC，∴△AEC≌△CDB(AAS)；(2)如图2，作B'D⊥AC于D，∵斜边AB绕点A逆时针旋转90°至AB'，∴AB’=AB，∠B’AB=90°，即∠B′AC＋∠BAC=90°，而∠B＋∠CAB=90°，∴∠B=∠B'AC，∴△B’AD≌△A BD(AAS)，∴B′D=AC=6，∴△A B′C的面积=6×6÷2=18；(3)如图3，由旋转知，OP=OF，∵△BCE是等边三角形，∴∠CBE=∠BCE=60°∴∠OCP=∠FBO=120°，∠CPO＋∠COP=60°，∵∠POF=120°，∴∠COP＋∠BOF=60°，∴∠CPO=∠BOF，在△BOF和△PCO中∠OBF=∠PCO=120°,∠BOF=∠CPO，OF=OP∴△BOF ≌△PCO ，∴CP=OB ，∵EC=BC=4cm ，OC=3cm ，∴OB=BC-OC=1，∴CP=1，∴EP=CE ＋CP=5，∴点P 运动的时间t=5÷2=2.5秒．【点睛】本题难道角度特别是需要作辅助线，要明确本题考点几何的综合变换，结合全等三角形及辅助线技巧，大胆猜想，小心求证．10．（1）详见解析；（2）2CD =，31CB =+或31-【解析】【分析】 ()1过点C 作CE CB ⊥于点C ，与MN 交于点E ，证明ACE ≌DCB ，则ECB 为等腰直角三角形，据此即可得到2BE CB =，根据BE AB AE =-即可证得；()2过点B 作BH CD ⊥于点H ，证明BDH 是等腰直角三角形，求得DH 的长，在直角BCH 中，利用直角三角形中30的锐角所对的直角边等于斜边的一半，即可求得．【详解】解：()1如图()2：2AB BD CB -=．证明：过点C 作CE CB ⊥于点C ，与MN 交于点E ，90ACD ∠=，90ACE DCE ∠∠∴=-，90BCD ECD ∠∠=-，BCD ACE ∠∠∴=．DB MN ⊥，90CAE AFC ∠∠∴=-，90D BFD ∠∠=-，AFC BFD ∠∠=，CAE D ∠∠∴=，又AC DC =，ACE ∴≌DCB ，AE DB ∴=，CE CB =，ECB ∴为等腰直角三角形， 2BE CB ∴=．又BE AB AE =-，BE AB BD ∴=-， 2AB BD CB ∴-=．如图()3：2BD AB CB -=．证明：过点C 作CE CB ⊥于点C ，与MN 交于点E ，90ACD ∠=，90ACE ACB ∠∠∴=+，90BCD ACB ∠∠=+，BCD ACE ∠∠∴=．DB MN ⊥，90CAE AFB ∠∠∴=-，90D CFD ∠∠=-，AFB CFD ∠∠=，CAE D ∠∠∴=，又AC DC =，ACE ∴≌DCB ，AE DB ∴=，CE CB =，ECB ∴为等腰直角三角形， 2BE CB ∴=．又BE AE AB =-，BE BD AB ∴=-， 2BD AB CB ∴-=．()2MN 在绕点A 旋转过程中，有两种情况：i .如图（1）：易证ACE ≌DCB ，CE CB =，ECB ∴为等腰直角三角形，45AEC CBD ∠∠∴==，过D 作.DH CB ⊥则DHB 为等腰直角三角形．BD =，1BH DH ∴==．直角CDH 中，30DCH ∠=，22CD DH ∴==，CH =1CB CH HB ∴=+=ii .如图（2）：过D 作DH CB ⊥交CB 延长线于H ．同理可得，2CD =，1CB CH HB =-=．【点睛】本题考查了全等三角形的性质和判定的应用，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，全等三角形的性质是全等三角形的对应边相等，对应角相等．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初二数学专题练习三角形旋转
1.D为等腰Rt△ABC斜边AB的中点，DM⊥DN，DM，DN分别交BC，CA于点E，F．
（1）当∠MDN绕点D转动时，求证：DE=DF．
（2）若AB=2，求四边形DECF的面积．
2.如图，在等腰Rt△ABC中，∠CAB=90°，P是△ABC内一点，且PA=1，PB=3，PC=．请利用旋转的方法
求：∠CPA的大小．
3.已知△ABC中，∠ACB=135°，将△ABC绕点A顺时针旋转90°，得到△AED，连接CD，CE．
（1）求证：△ACD为等腰直角三角形；
（2）若BC=1，AC=2，求四边形ACED的面积．
4.如图所示，△ABC为等边三角形，以AB为边向外作△ABD，使∠ADB=120°，然后把△BCD绕着点C按顺时针方向旋转60°得到△ACE，如图所示，已知
BD=5，AD=3．
（1）由旋转可知线段BC，CD，BD的对应线段分别是什么？
（2）求∠DAE的度数；
（3）求∠BDC的度数；
（4）求CE的长．
5.如下图是两个等边△ABC、等边△CDE的纸片叠放在一起的图形．
（1）固定△ABC，将△CDE绕点C按顺时针方向旋转30°，连AD，BE，线段BE、AD之间的大小关系如何？证明你的结论；
（2）若将△CDE绕点C按顺时针方向任意旋转一个角度，连AD、BE，线段BE、AD之间大小关系如何？证明你的结论．
6.将两块斜边长相等的等腰直角三角形按如图A摆放，斜边AB分别交CD、CE 于M、N点，
（1）如果把图A中的△BCN绕点C逆时针旋转90°得到△ACF，连接FM，如图B，求证：△CMF≌△CMN：
（2）将△CED绕点C旋转：
①当点M、N在AB上（不与A、B重合）时，线段AM、MN、NB之间有一个不变的关系式，请你写出这个关系式，并说明理由；
②当点M在AB上，点N在AB的延长线上（如图C）时，①中的关系式是否仍然成立？请说明理由．
7.在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
（1）当直线MN绕点C旋转到图1的位置时，①求证：△ADC≌△CEB；②若AD=3，BE=2，求DE长．
（2）当直线MN绕点C旋转到图2的位置时，AD=3，BE=1.5，求DE长；（3）当直线MN绕点C旋转到图3的位置时，AD=1.5，BE=3，求DE长．
8.小阳遇到这样一个问题：如图（1），O为等边△ABC内部一点，且OA：OB：OC=2，求∠AOB的度数．
小阳是这样思考的：图（1）中有一个等边三角形，若将图形中一部分绕着等边三角形的某个顶点旋转60°，会得到新的等边三角形，且能达到转移线段的目的．他的作法是：如图（2），把△ACO绕点A逆时针旋转60°，使点C与点B 重合，得到△ABO′，连接OO′．则△AOO′是等边三角形，故OO′=OA，至此，通过旋转将线段OA、OB、OC转移到同一个三角形OO′B中．
（1）请你回答：∠AOB=______°．
（2）参考小阳思考问题的方法，解决下列问题：
已知：如图（3），四边形ABCD中，AB=AD，∠DAB=60°，∠DCB=30°，AC=5，CD=4．求四边形ABCD的面积．。

初二数学专题练习 三角形旋转

八年级数学旋转经典练习题

初二数学专题练习三角形旋转

初中数学《旋转》专题100题含答案

八年级数学旋转练习题

初二数学 全等三角形角6090旋转知识点-+典型题含答案

专题01与旋转有关的计算(30题)(原卷版)

初二数学全等三角形角6090旋转知识点及练习题含答案

初二数学 全等三角形旋转模型复习题及答案(1)

初二数学 全等三角形双等腰旋转练习题含答案

人教版初二数学全等三角形双等腰旋转达标提优专项训练(1)

初二数学全等三角形双等腰旋转测试试题含答案

初中三角形旋转经典例题

人教版初二数学全等三角形角6090旋转专项训练学能测试

初二数学全等三角形双等腰旋转测试基础卷(1)

初二数学 全等三角形角6090旋转练习题附解析

初二数学专题练习三角形旋转

初二数学全等三角形角6090旋转知识点-+典型题含答案

初二数学全等三角形旋转模型复习题及答案(1)

初二数学全等三角形双等腰旋转练习题含答案

初二数学全等三角形角6090旋转练习题附解析