5逻辑函数化简题.docx
2.5逻辑函数的化简(2011)

消去B
11 10
结论: 1、 2 n 个最小项合并,消去n 个变量。 2、消去K圈中变量取值发生过 变化的量。保留取值没有变 化的量。
ABC D + ABC D + ABC D + ABC D
消去A、C
A BCD + ABCD + ABCD + A BCD + ABC D + ABC D + ABC D + ABC D = ACD + ACD + AC D + AC D = CD + C D = C
消去A、B、D
4、 用卡诺图化简逻辑函数 (1)求最简与或式 化简的步骤: • 作出逻辑函数的卡诺图; • 圈卡诺圈; • 将每个卡诺圈中的最小项合并成相应的与项。 圈卡诺圈的原则: 在卡诺图上,以最少的卡诺圈数和尽可能大的卡诺圈覆盖所有填1的 方格。(即:最小覆盖原则) 注释: • 将 2 n个相邻的填1方格圈起来,圈子尽可能大; • 所有填1格都必须被圈过,在此前提下K圈的个数尽可能少; • 任何一个填1格可以被不同的K圈多次圈过,但如果在一个K圈中, 所有的1格均已被别的K圈圈过,则该圈为多余的。
F = A BC + ABC + D + AD
AB CD
01
11
10
00 01
11 10
1 0 0 1
1 0 1 0
1 0 1 0
0 1 0 1 1 1 1 1 1 1 1 1 1 1
原则:分别寻找各与项中变量相交的小方格填1. (0——反变量,1——原变量)
(3)由或与式填卡诺图(填0) 举例:
F = ∏ M (0, 2, 6) = ( A + B + C )( A + B + C )( A + B + C )
3.化简逻辑表达式习题及答案

化简逻辑表达式习题及答案1.用逻辑代数的基本公式和定律将下列逻辑函数化简为最简与—或表达式。
(1)C B BC BC A ABC A Y ++++= (2)AB B A AB B A Y ++⊕=)( (3)C AB C B BC A AC Y +++= 解:(1)C B BC BC A ABC A Y ++++=)()1(B B C BC BC A ++++= CA +=(2)AB B A AB B A Y ++⊕=)(AB B A B A +⊕⊕=))((AB B A +⊕=AB B A B A ++=)( )(B B A B A ++=A B A +=B A +=(3)C AB C B BC A AC Y +++=C AB B B A A C +++=)( C AB B B A C +++=)(C AB C += C =2.证明下列恒等式(证明方法不限 )。
(1)C B A C B A A +=++)((2)C B A C B A C B A C B A ABC ⊕⊕=+++解:(1)证明:左边C B A C B A A C B A A +=+++=++=)(=右边(2)证明:C B A C B A C B A ABC +++=左边=⊕⊕=⊕+⊕=C B A C B A C B A )()(右边3.用卡诺图化简下列逻辑函数为最简与一或表达式。
(1)C B AC C B B A Y +++= (2)D BC A D BC BD B A Y +++= (3)D C B B A D B BCD D C A Y ++++= 解:(1)C B AC C B B A Y +++=AC B Y +=(2)D C B A D BC BC B A Y +++=BC BD B A Y ++=(3)D C B B A D B BCD D C A Y ++++=B AC AD Y ++=4.用卡诺图化简下列逻辑函数为最简与—或表达式。
逻辑函数的卡诺图法化简

精品课件
26
输入变量ABC取值为001、010、100时,
逻辑函数Y有确定的值,根据题意,有任一命令(正 转、反转和停止)时为1,否则为0。
反变 函换 数为
CD BD
CD
AB
00 01 11 10
Y AB AC BD CD AB
00 1
0
1
1
01 1
0
0
1
11 0
0
0
0
10 0
0
1
1
AC
精品课件
13
4、卡诺图的性质
(1)任何两个(21个)标1的相邻最小项,可以合并为一项, 并消去一个变量(消去互为反变量的因子,保留公因子)。
AB C
但是,若 F= ABCD+ABC+BC+ABC ,显然,该函数式
难于找到相邻项。
精品课件
1
2.4.2 逻辑函数的标准式——最小项表达 式
问题的提出:逻辑函数 F= ABC+ABC ,之所以易于看出它们 的乘积项是逻辑相邻项,是因为它们的每一个乘积项中都包 含了所有的变量。而F= ABCD+ABC+BC+ABC,每个乘积项没有 包含所有的变量,所以逻辑相邻关系不直观。于是引入了最 小项的概念。
15
AB CD
00 01 11 10
00 0
1
1
0
01 1 0 0 1
11 1
0
0
1 AD
10 0 1 1 0
BD
AB CD
00 01 11 10
00 1
0
0
1
01 0
1
1
0
11 0
数字逻辑化简题(已整理)

公式化简习题:1、用公式化简法将C B BC BC A ABC A ++++=F 化为最简与或式。
(要求化简过程)解:F=A +ABC +ABC̅̅̅̅+BC +B ̅C =A (1+BC )+ABC̅̅̅̅+BC +B ̅C =A+A BC̅̅̅̅+BC +B ̅C =A(1+BC̅̅̅̅)+BC+B ̅C =A+C(B+B̅) =A+C2、用公式化简法将AB B A B A C B A Y ++=),,(化为最简与或式(要求写出过程)。
解:Y (A,B,C )=AB̅+A ̅B +AB =A (B +B̅)+A ̅B =A +A̅B =A +B3、用公式化简法将)(),,(C A B B A C B A Y +++=化为最简与或式(要求写出过程)。
解:Y (A,B,C )=AB ̅+B +(A +C̅)̅̅̅̅̅̅̅̅̅̅ =AB̅+B +A ̅C =A +B +C4、用公式化简法将BD A CD B A D C B A Y ++=),,,(化为最简与或式(要求写出过程)。
解:Y (A,B,C,D )=A +B̅CD +A ̅BD =A +BD +B̅CD =A +D (B +B̅C ) =A +D (B +C )=A +BD +CD5、用公式化简法将D C A ABD CD B A D C B A Y ++=),,,(化为最简与或式(要求写出过程)。
解:Y (A,B,C,D )=AB̅CD +ABD +AC ̅D =AD(B̅C +B +C ̅) =AD(B +C +C̅) =AD (B +1)=AD卡诺图化简习题:1. 用卡诺图法化简函数Y(A 、B 、C 、D)= ∑m(1,2,5,6,9)+ ∑d(10,11,12,13,14,15)。
式中d 表示无关项,求其最简与或表达式。
(要求圈出过程)卡诺图如下:2. 用卡诺图法化简函数Y(A 、B 、C 、D)=,求其最简与或表达式(要求圈出过程)。
数字电子技术基础—精彩试题—解答-电子技术化简与或式

三、逻辑函数化简(每题5分,共10分)1、用代数法化简为最简与或式Y= A +1、Y=A+B2、用卡诺图法化简为最简或与式 Y= + C +A D,约束条件:A C + A CD+AB=02、用卡诺图圈0的方法可得:Y=( +D)(A+ )( + )四、分析下列电路。
(每题6分,共12分)1、写出如图4所示电路的真值表及最简逻辑表达式。
图 41、该电路为三变量判一致电路,当三个变量都相同时输出为1,否则输出为0。
2、写出如图5所示电路的最简逻辑表达式。
2、B =1,Y = A ,B =0 Y 呈高阻态。
五、判断如图 6所示电路的逻辑功能。
若已知 u B =-20V,设二极管为理想二极管,试根据 u A 输入波形,画出 u 0 的输出波形(8分)t图 6五、 u 0 = u A · u B ,输出波形 u 0 如图 10所示:图 10六、用如图 7所示的8选1数据选择器CT74LS151实现下列函数。
(8分)Y(A,B,C,D)=Σm(1,5,6,7,9,11,12,13,14)图 7 答:七、用 4位二进制计数集成芯片CT74LS161采用两种方法实现模值为10的计数器,要求画出接线图和全状态转换图。
(CT74LS161如图8所示,其LD端为同步置数端,CR为异步复位端)。
(10分)图 8七、接线如图 12所示:图 12全状态转换图如图 13 所示:( a )( b )图 13八、电路如图 9所示,试写出电路的激励方程,状态转移方程,求出Z 1 、Z 2 、Z 3 的输出逻辑表达式,并画出在CP脉冲作用下,Q 0 、Q 1 、Z 1 、Z 2 、Z 3 的输出波形。
(设 Q 0 、Q 1 的初态为0。
)(12分)八、,,波形如图 14所示:三、将下列函数化简为最简与或表达式(本题 10分)1. (代数法)2、F 2 ( A,B,C,D)=∑m (0,1,2,4,5,9)+∑d (7,8,10,11,12,13)(卡诺图法)三、1. 2.四、分析如图 16所示电路,写出其真值表和最简表达式。
组合逻辑电路的分析和设计—逻辑函数的化简
式,并且使矩阵的横方向和纵方向的逻辑变量的取值按 照格雷码的顺序排列,这样构成的图形就是卡诺图。
2.卡诺图的特点
卡诺图的特点是任意两个相邻的最小项在图中也是 相邻的。(相邻项是指两个最小项只有一个因子互为反 变量,其余因子均相同,又称为逻辑相邻项) 。
约束项:函数可以随意取值(可以为0,也可以为1)或不会出现 的变量取值所对应的最小项称为也叫做约束项。
例如:判断一位十进制数是否为偶数。
ABCD Y
ABCD Y
说明
0000 1 1000 1
0001 0 1001 0
0 0 1 0 1 1 0 1 0 × 不会出现
0 0 1 1 0 1 0 1 1 × 不会出现
0
1
1
0
1
1
0
1
1
1
1 CD
0
0
0
0
BD
冗余项
的将
乘代
3
积表
项每
相个
加圈
最简与或表达式 Y (A, B,C, D) BD CD AC D
两点说明
① 在有些情况下,最小项的圈法不只一种,得到的 各个乘积项组成的与或表达式各不相同,哪个是最简的, 要经过比较、检查才能确定。
AB
CD
00 01 11 10
Y A B C ABC ABC ABC (A B C ABC) (ABC ABC) (ABC ABC) AC AB BC
4
1.4逻辑函数的图形法化简
(1)最小项
①最小项的定义
如果一个函数的某个乘积项包含了函数的全部变量,其中 每个变量都以原变量或反变量的形式出现,且仅出现一次,则 这个乘积项称为该函数的一个标准积项,通常称为最小项。
5逻辑函数化简题.docx

解:
Y = ABCD + ABC + ABD + BCD+BCD =为加(1,4,5,6,9,11,12,14)
Y = BD + ABC + AC D + ABD
2、Y = ABC1AB+ADf+AB1CD+AB1C
解:
Y = AB + AC+AD
一、利用逻辑代数的基本公式和常用公式化简下列齐式:
(2)AB+AC+BC = (^AB+X+K=(QA0C+(A4-^a =^X+MC+K+ABC =
(^AC+ABC+BC+ABC =GO) AC+ABC+ACD+CD =
二、证明等式:AB + AB = A B + AB
证明:
^ii=A^BAB =(A + B)(A + B)= AA + AB + AB + BB = AB + AB = /Eii
3、乙=a'bC+a + b + c +(AbG
解:乙=1
4、Y}=ABf^AC^BfC
解:r, = A B + AC
5、Y}=A(BCy-}-ABC,
解:Y}=AB ^-ACf
6、Y = A BC + ABC'+ABC!+BC
解:Y = AB + BC
7、F =(AB + BC)+(BC + AB)
2第二章逻辑函数及其简化.docx

笫二章逻辑函数及其简化一、选择题1.以下表达式屮符合逻辑运算法则的是—0A・C・Og B. 1+1=10 C. 0<1 D. A+l=l2.逻辑变量的取值1和0町以表示:_________ 。
A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无3.当逻辑函数有n个变量时,共有 ______ 个变量取值组合?A. nB. 2n C・ r? D. 2n4.逻辑函数的表示方法屮具有唯一性的是 _______ 。
A •真值表 B.表达式 C.逻辑图D.卡诺图5.F二A B +BD+CDE+ A D= _______ 。
A. AB + DB. (A + B)DC. (A + D)(B + D)D. (4 + D)(B +万)6.逻辑函数1:二A㊉(A㊉8) = ___ oA.BB. AC. A㊉BD.勿㊉B7.求一个逻辑函数F的对偶式,可将F中的 _______ oA •“ •” 换成“ + ”,“ + ”换成“ •”B.原变量换成反变量,反变量换成原变量C.变量不变D.常数中“0”换成“1”,“1”换成“0”E.常数不变& A+BC 二____ oA . A+B B. A+C C. (A+B) (A+C) D. B+C9.在何种输入情况下,“与非”运算的结果是逻辑0。
—A.全部输入是0B.任一输入是0C.仅一输入是0D.全部输入是110.在何种输入情况下,“或非”运算的结果是逻辑0。
—A.全部输入是0B.全部输入是1C.任一输入为0,其他输入为1D.任一输入为1二、判断题(正确打J,错误的打X)1.逻辑变量的取值,1比0大。
()。
2.异或函数与同或函数在逻辑上互为反函数。
()。
3.若两个函数具有相同的真值表,则两个逻辑函数必然相等。
()o4.因为逻辑表达式A+B+AB二A+B成立,所以AB=O成立。
()5.若两个函数具有不同的真值表,则两个逻辑函数必然不相等。
()6.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。
逻辑函数的公式化简法

几个变量(一个以上)的公共非号保持不变。
第一章 数字电路基础
3. 对偶法则
对任意一个逻辑函数表达式,若将0→1,1→0,+→∙,∙→+,并保持原来的运算 顺序,则新的逻辑式与原来的逻辑式互为对偶式。
A(B+C)=AB+AC A+BC=(A+B)(A+C)
A+AB=A
BC AB
AC BC
第一章 数字电路基础
小结
公式化简法的优点是不受变量数目的限制。缺点 是:没有固定的步骤可循;需要熟练运用各种公式和 定理;需要一定的技巧和经验;有时很难判定化简结 果是否最简。
公式法化简的一般规律(经验总结): 1. 提公因式; 2. 使用最频繁的是反演律、互补律、吸收律和冗 余律。
A C D(B B) CB BD
A C D CB BD (利用A A 1)
第一章 数字电路基础
例4:化简逻辑函数,配项法(两解) 。
L AB BC BC AB
解法1: L AB BC BC AB AC (增加冗余项 AC)
例5:化简逻辑函数。
F AB C ABD AD AD( AB C B 1)
AD
F A ACD ABC
A A CD BC
A CD BC
F ABC ABC ABC
F AC AB B C
( ABC ABC ) ( ABC ABC ) AC AB BC
学习内容
• 逻辑函数的公式化简法。
学习目标
能运用公式法对逻辑函数进行化简。
逻辑代数和逻辑函数化简.共70页

31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 9、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
电子技术基础-6.6 逻辑代数的公式法化简

二、逻辑函数化简的意义与标准
F1 ABC ABC ABC ABC
A B C A B C A B C A B C
&
&
≥1
F1
&
&
二、逻辑函数化简的意义与标准
F2 AB AC BC
A B A C B C
F3 AB AC
A B
&
&
≥1
&
&
≥1
F3
F2
A
C
&
二、逻辑函数化简的意义与标准
三、逻辑函数的公式法化简方法
2、吸收法 (1)利用公式A+AB=A,消去多余的项。 余这 一 的另 个 Y1 AB ABCD (E F) AB 如 。 外 乘 运用摩根定律 一积果 个项乘 Y2 A B C D ADB A BC D AD B 乘的积 ( A AD) (B BC D ) AB 积因项 项子是 是,另 多则外
F AB AC 与——或表达式 ( A C)(A B) 或——与表达式
AB AC
与非——与非表达式
A C A B 或非——或非表达式
AB AC
与——或——非表达式
其中,与—或表达式是逻辑函数的最基本表达形式。
一、逻辑函数不同表达形式之间的转换
1. 与非-与非表达式
Y AB AC
一、逻辑函数不同表达形式之间的转换
3、或与表达式
Y AB AC
Y ( A B)(A C)
将与或非式用摩根定律展开,即得或与表达式。
一、逻辑函数不同表达形式之间的转换 4、或非-或非表达式
逻辑函数的化简逻辑函数的最简形式逻辑函数的公式化简法

AB BC
上页
11
下页
返回
2019/1/10
第五节 逻辑函数的化简
根据公式
A A 1
( A A) ,
可在逻辑函数式中的某一项乘
然后拆成两项分别与其他项合并。 [例2.5.13]: Y
BC AC AB
( A A)BC AC AB
ABC ABC AC AB
Y A( BC ) ABC [例2.5.3]: A(( BC ) BC ) A
上页
5
下页
返回
2019/1/10
第五节 逻辑函数的化简
[例2.5.4]:用并项法将
Y BCD BCD BCD BCD
化简为最简与-或表达式。 解: Y BCD BCD BCD BCD
AB AC
上页
12
下页
返回
2019/1/10
第五节 逻辑函数的化简
综合法
[例2.5.14]:
Y AC BC BD CD A( B C ) ABCD ABDE
AC BC BD CD A( BC ) ABCD ABDE AC ( BC A( BC )) BD (CD ABCD) ABDE
上页
10
下页
返回
2019/1/10
第五节 逻辑函数的化简
5.配项法 根据公式
A A A
可在逻辑函数式中重复写入某一项。 [例2.5.12]: Y
ABC ABC ABC
ABC ABC ABC ABC
AB(C C ) ( A A)BC
返回
逻辑函数的公式化简法
分配律 吸收律 分配律 吸收律 并项 吸收律
逻辑函数的公式化简法
化简逻辑函数表达式的方法 ◇公式化简法
◆没有固定的步骤可以遵循 ◆依赖于对逻辑代数公式的熟练掌握 ◆需要一些化简技巧 ◆难以确定被化简过的逻辑函数是否最简 ◇卡诺图化简法 √简便、直观
= B (A+AC)+ AC + BCD = B (A+C)+ AC + BCD = AB + AC + BC (1 + D) = AB + AC + BC = AB + AC
化简逻辑函数表达式的方法 公式化简法 卡诺图化简法
逻辑函数的公式化简法
(1) 并项、配项 A + A = 1 ; 1 = A + A
逻辑函数的公式化简法
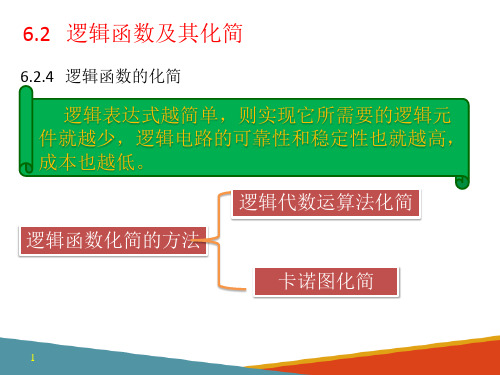
逻辑函数式越简单,逻辑电路越简单,所使用的元器件越少, 成本越低,工作越可靠
AB + AC + BC = AB + AC
A
&
B
1 &
C
&
1
Y
逻辑函数的公式化简法
☆最简与—或表达式 也最少
Y = AB + AC + BCD + ABC
分配律 吸收律
逻辑函数的公式化简法
Y = ABCD + ABD + BCD + ABC + BD + BC = ABC(D + 1)+ BD(A + 1)+ BCD + BC = ABC+ BD + BCD + BC = B(AC + C)+ B(D + CD) = B(A + C)+ B(D + C) = AB + BD + B(C + C) =B
逻辑函数化简

0 0 1 1
0 1 1 1
0 0 0 0
0 1 1 0
0 0 0 0
0 0 0 0
(1-7)
0 1 1
AD
11 10
0 1
2. 先找面积尽量大的组合进行化简,可以减少每项 先找面积尽量大的组合进行化简, 的因子数。 的因子数。 3. 各最小项可以重复使用。 各最小项可以重复使用。 4. 注意利用无所谓状态,可以使结果大大简化。 注意利用无所谓状态,可以使结果大大简化。 5. 所有的1都被圈过后,化简结束。 所有的 都被圈过后,化简结束。 都被圈过后 6. 化简后的逻辑式是各化简项的逻辑和。 化简后的逻辑式是各化简项的逻辑和。
0 φ
0 1
0 1
A
认为是1 认为是 F=A
(1-12)
结束
(1-13)
C 0 1 0 1 0 0 1
F 0 0 0 0 1 1 1
101状态未给出,即是无所谓状态。 状态未给出,即是无所谓状态。 状态未给出
(1-11)
化简时可以将无所谓状态当作1或 , 化简时可以将无所谓状态当作 或 0,目的 是得到最简结果。 是得到最简结果。 BC 00 A 0 1
01
11
10
0 1
(1-2)
例1: F :
= AB + AB ⋅ BC + BC
( = AB + AB + (BC + BC) )
反演
= AB + A B ( C + C ) + BC ( A + A ) + B C
配项
= AB + A BC + ABC
被吸收
被吸收
《数字电路逻辑设计》--逻辑函数及其化简练习题

《数字电路逻辑设计》练习题------ 逻辑函数及其化简一.用公式证明下列各等式。
1. AB AC (B C)D AB AC D 原式左边二AB AC BD CD=AB AC+BC+BCD=AB AC+D=右边2. A C A B A C D+BC A BC 原式左边A C(1+D)+A B+BC=A C + A B+BC=(C+B+BC =AB C+BC=A+BC=右边3. BCD BCD ACD+ABC D+A BCD +BC D+BCD BC BC+BD原式左边=BCD+A BCD BCD+BCD+ABC D+BC D+ACD=BCD+A BCD+BD+BC D+ACD=BCD+ACD+B CD+BD+B^ D=BCD+ACD+BD+DC+B^ D=BCD+BD+DC+B C D=C(D+B)+ B( D+C)=BC+BD+BC=右边2. F=AB+AB+BC=m (2,3,4,5,7)F m(0,1,6)F*= m(1,6,7)3. F=AB+C BD+A D B C=m(1,5,6,7,8,9,13,14,15 )F m(0,2,3,4,10,1,2 )F*= m(3 ,4,5,11,12,3,5)三.用公式法化简下列各式1. F=ABC+A CD+AC=A(BC+C)+A CD=AC AB A CD =C(A AD) A B=A C+C D+AET2. F=A C D+BC+BD+A B+AC+^ C =AC D+BC+BD+A B+AC+BC+^ C =ACD+BC+AC+B=AD+C+B3. F=(A+B)(A+B+C)(A+C)(B+C+D)Q F*= AB+ABC+AC+BCD=AB+AC+BCD=AB+ACF=(F*)*=(A+B)(A+C)=AC+AB —4. AB B+D CD+BC+A BD+A+CD=1原式左边=AB B+D C D BC+A BD A+C+D =(AB+ B+D+C D)(B+C)+C+D=(B+D)(B+C)+C+D =BC+BD+CD+C+D=1=右边二.写出下列各逻辑函数的最小项表达式及其对偶式、反演式的最小项表达式1. F=ABCD+ACD+BD= m( 4,6,11,12,14,15 )F m(0,1,2,3,5,7,8,9,10,13)F*= m(2,5,6,7,8,10,12,13,14,15) 4. F=AB+A B?BC+B CF AB+A B BC+B CAB+A B BC+B C ACAB BC B C AC AB B C5. F=AC+BC B(AC AC)F (A C)(B C) ABC ABCAB A C BC C ABC ABCAB C (A B)C AC BC四.用图解法化简下列各函数。
10.3.5 逻辑函数的卡诺图化简_电工电子技术_[共3页]
![10.3.5 逻辑函数的卡诺图化简_电工电子技术_[共3页]](https://img.taocdn.com/s3/m/f5866876b0717fd5370cdc55.png)
10.3逻辑函数的表示及化简169 例2:Y AD AD AB AC BD ABEF BEF A AB AC BD ABEF BEF A BD BEF=++++++=+++++=++ 例3: ()()()()()()()()()(1)(1)()Y AC ABC BC ABC AC ABC BC ABCA C ABC B C ABCA ABC B C C A B C B C ABCA B C B C C A B B ABCA BC BC C C ABC AC C ABC =+++=+=+++++=++++++++=+++++++=++++=++=+=i i在数字电路中大量使用与非门,所以如何把一个化简了的与或表达式转换为与非-与非式,并用与非门去实现它是十分重要的。
一般,用两次求反法可以将一个化简了的与或式转换成与非-与非式。
例 Y AB BC CD AB BC CD AB BC CD =++=++=⋅⋅ 10.3.5 逻辑函数的卡诺图化简1.最小项(1)最小项的定义对于N 个变量,如果P 是一个含有N 个因子的乘积项,而在P 中每一个变量都以原变量或反变量的形式出现一次,且仅出现一次,那么就称P 是N 个变量的一个最小项。
因为每个变量都以原变量和反变量两种可能的形式出现,所以N 个变量有2N 个最小项。
(2)最小项的性质表10-11列出了三个变量的全部最小项真值表。
由表可以看出最小项具有下列性质。
表10-11三变量最小项真值表性质1:每个最小项仅有一组变量的取值会使它的值为“1”,而其他变量取值都使它的值为“0”。
性质2:任意两个不同的最小项的乘积恒为“0”。
性质3:全部最小项之和恒为“1”。
由函数的真值表可以很容易地写出函数的标准与或式,此外,利用逻辑代数的定律、公式,可以将任何逻辑函数式展开或变换成标准与或式。
例1:将逻辑函数式变换成标准与或式。
数字电子技术-逻辑函数的化简(公式化简)

冗余项
AB AC BC
[例]
Y AB AC B C AB A C BC
AB AC B C 或 AB AC B C AB A C BC
AB A C BC
A (BC B C) A (BC BC) A B C A(B C) A
二、吸收法: A AB A
[例]
Y AB AD BE
A B AD BE A B
[例] Y AB ACD BCD AB ( A B) CD AB AB CD AB A B
[例] Y A A BC ( A B C D) BC ( A BC) ( A BC) ( A B C D)
A BC
三、消去法: A AB A B
[例]
Y AB AC BD
A B AC BD A B C D
[例] Y AB AC BC AB ( A B)C AB AB C AB C
2.3 逻辑函数的化简
思考: 为什么要对逻辑函数进行化简?
Y F ( A ,B ,C ) ABC ABC ABC AB B BC
பைடு நூலகம்
逻辑函数的标准与或式和最简与或式
最简式
[例]
Y F ( A ,B ,C ) AB AC
AB(C C ) AC( B B)
ABC ABC ABC ABC
[例] Y AB AB ABC ABC
A (B B C) A (B BC) A (BC) A (BC) AB AB AC AC AB AB C
四、配项消项法: AB AC BC AB AC
[例]
Y BC AC AC BC AB
BC AC AB 或 BC AC AC BC AB
标准与 或式
最小项
标准与或式就是最小项之和的形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、y(AB, C, D)二工加(1,5,6,7,11,12,13,15)
5、K(A,B,C, D)=工加(1,7,910,11,12,13,15)
6、Y( A, B,C)二工加(0,1,2,3,6,7)
解:Y = Af+B
形式二
1、利用卡诺图化简法将所给函数Y化为最简的与或表达形式。
用卡诺图法化简
形式_
1、利用卡诺图化简法Biblioteka 所给函数Y化为最简的与或表达形式。
y(AB,C,£>)=工加(0,1,2,3,4,5,&10,11,12)
解:
r=A5+CO+AC+BC
2、y(A,B,C, D)=工加(0,1,2,3,4,6,&9,10,11,14)
解:Y = Bf+AD +CD
3、Y(A,3,CQ)=为加(0,1,2,5,8,910,12,14)
6、y = (AB + A C +B D)(AB C'D + A CD + BCD + B C)
解:Y = CD + ABC^ABD
7、F = A-^-ABCDABC + BC + BC
解:
8、F(A,B,C,D) = ABC + AB + AD + C + BD
解:F(A,B,C,D) = A + C^BD
三、用代数法化简Y = ABC+ABC+ABC+ABC,写出最简与非表达式。 解:/ =AM
公式法化简
二变量
1、Y\=EP + E F + EF' +EF
解:乙=1三变量
1、Y}=A + CB + C^^A + B" +C)(A+B + C)解:Y}=A+B C
2、Y = JK‘+JQ;+ K'Q
解:Y = JQ^KQ
9、F(A,B,C,D) = AD + AC^CD^-AD
解:F(AB,C,D) = A + CD
10、F = ABC + AB + AD + C + BD
解:F = C ++ D
五变量
1、Y=ABD+ AB1CD!+ACDE+ A
解:
2、
Y(A,B,C,£>,E) = APCD + ABCD+BCD,+ BC D + BCD+ BfCD + BfCfDE解、Y(A,B,C,D,E) = C'D + B」D + BD‘
3、Y = ABCD + ABD + BCD,+ ABC + BD + BC‘
解:Y = B
4、F( A, B, C, D) = (AE +亦•C +ABC)•(AZ)+BC)
解:F( A, B, C, D,) =ABC + ACD
5、Y = AB D-v ASB CD + B CD + (ABf+ C )'(B +D)解:Y = B D + BC/
解:F = BC
8、Y = (A㊉C)B + ABC' + A BC
解:
9、Y = [{AB1+ABC)'+A(B+A)]z
解:Y = 0
四变量
1、Y = AC + ABC + ACD + CD
解:Y = A + CD
2、Y = AB C1+A-^-A D + C + BD
解:K = Az+C + B£>
3、乙=a'bC+a + b + c +(AbG
解:乙=1
4、Y}=ABf^AC^BfC
解:r, = A B + AC
5、Y}=A(BCy-}-ABC,
解:Y}=AB ^-ACf
6、Y = A BC + ABC'+ABC!+BC
解:Y = AB + BC
7、F =(AB + BC)+(BC + AB)
Y=ABCD+ABC+ABD+BCD+BCD
解:
Y = ABCD + ABC + ABD + BCD+BCD =为加(1,4,5,6,9,11,12,14)
Y = BD + ABC + AC D + ABD
2、Y = ABC1AB+ADf+AB1CD+AB1C
解:
Y = AB + AC+AD
一、利用逻辑代数的基本公式和常用公式化简下列齐式:
(2)AB+AC+BC = (^AB+X+K=(QA0C+(A4-^a =^X+MC+K+ABC =
(^AC+ABC+BC+ABC =GO) AC+ABC+ACD+CD =
二、证明等式:AB + AB = A B + AB
证明:
^ii=A^BAB =(A + B)(A + B)= AA + AB + AB + BB = AB + AB = /Eii
3、y(AB,C,D,£) = AC+B C + BD!+ C” ++ C,) + ABCD + AB DE
解、Y(A,B,C,D,E) = A + B C + BD‘
4、
y(AB,C,D, £) =A B C D+AB C!D+BCD1+ BC1D + BC D+ B CD+B’C’DE解、Y(A,B,C,D,E) = C‘D + B‘D + BD‘
