固体物理导论
固体中学物理学导论

固体物理学导论第一章晶体结构1.1 原子的周期性阵列一个晶体的所有各面的方向指数都是精确的整数。
衍射实验决定性的证明了晶体是由原子或原子团的周期性阵列组成的。
在理想情况下,晶体是由全同的原子团在空间无限重复排列而构成的,这样的原子团被称为基元。
在数学上这些基元可以抽象为几何点,而这些点的集合被称为晶格。
原胞是体积最小的晶胞,初基基元是包含原子数目最少的基元。
1.2 晶格的基本类型晶格可以通过晶格平移或其它各种对称操作与其自身重合。
典型的对称操作是围绕一个通过格点的晶轴进行转动。
,,,与这些角度相对应的转动轴分别被称为一重、二重、三重、四重和六重轴,通常用符号1、2、3、4和6分别表示这些转动轴。
晶格平移矢量具有任意性,由此给出的一般性晶格通常被称为斜方晶格。
二维晶格的分类:有五种,即一种斜方晶格和四种特殊晶格。
布拉维晶格(Bravais lattice)是对某种具体晶格类型的统称,于是有五种二维布拉维晶格。
三维晶格的分类:有14种,即三斜晶格和13种特殊晶格。
为方便起见,通常按照七种惯用晶胞将这14种晶格划分为7种晶系,即三斜(1)、单斜(2)、正交(4)、四角(2)、立方(3)、三角(1)和六角晶系(1)。
立方晶系包括简单立方(sc),体心立方(bcc)和面心立方(fcc)三种晶格。
1.3 晶面指数系统一个晶面的取向可以由这个晶面上的任意三个不共线的点确定。
晶体中某一方向的指数是指这样一组最小整数,这组最小整数间的比率等于该方向的一个矢量在轴上的诸分量的比率。
1.4 简单晶体结构氯化钠型结构:面心立方。
基元由一个钠离子和一个氯离子组成,每个原子有六个异类原子作为最近邻。
每一个单位立方体中有4个氯化钠基元。
氯化铯型结构:简单立方,基元由一个铯离子和一个氯离子组成,每个原子有八个异类原子作为最近邻。
每个原胞有1个分子。
六角密堆积型结构(hcp):与面心立方结构的总体积被球占据的体积比率一样,都为0.74。
固体物理pdf

固体物理pdf
《固体物理导论》
摘要:本文介绍了固体物理的基本概念、原理和应用。
通过对固
体物理学的探讨,读者可以了解到固体的结构、性质以及固体在电学、热学和光学等领域的应用。
第一部分:固体的基本结构与性质
1. 固体的分类与特点
2. 晶体结构与晶格
3. 晶体缺陷与固体缺陷的性质和影响
4. 固体中的电子行为:导体、绝缘体和半导体的基本概念
5. 固体中的振动:声子和声子的产生、传播与吸收
第二部分:固体物理的应用
1. 固体的热学性质及其应用:热导率、热膨胀等
2. 固体的电学性质及其应用:导体、绝缘体和半导体的应用
3. 固体的光学性质及其应用:折射、吸收和反射等基本原理
第三部分:现代固体物理的发展与前沿
1. 低维固体物理:纳米材料和薄膜的研究进展
2. 新型材料的发现与应用:石墨烯、拓扑绝缘体等
3. 固体物理与纳米电子学、光电子学的交叉研究
结论:固体物理作为一门重要的物理学科,不仅有助于我们理解
固体的性质和行为,还为现代技术的发展提供了重要的理论支持。
希
望通过本文的介绍,读者能够对固体物理有一个全面的了解,为深入
研究和应用固体物理奠定基础。
关键词:固体物理、晶体结构、电学性质、热学性质、光学性质、纳米材料、新型材料、纳米电子学、光电子学。
固体物理导论读书随笔

《固体物理导论》读书随笔1. 固体物理导论概述在开始阅读这本《固体物理导论》时,我被其深厚的理论底蕴和丰富的实践应用所吸引。
这本书作为固体物理学的入门教材,为初学者提供了一个全面、系统的学习框架,让我对固体物理学有了更加清晰的认识。
固体物理学是研究固体物质的物理性质和行为的一门科学,它不仅探究固体的微观结构,还研究固体中的电子行为、力学性质、热学性质等。
在现代科技领域,固体物理学的重要性日益凸显,因为固体材料的应用几乎无处不在,涉及到能源、电子、光学、磁学等多个领域。
这本书的导论部分详细介绍了固体的基本性质,包括晶格结构、晶体缺陷、相变等。
接着介绍了固体的电子理论,包括能带理论、费米能级等概念。
还介绍了固体的力学性质、热学性质以及电磁性质等。
这些内容构成了固体物理学的核心知识体系。
固体物理的研究方法涉及到实验和理论两个方面,实验方面主要包括各种物理性质的测量和表征,如X射线衍射、电子显微镜等。
理论方面则涉及到量子力学的应用,如波函数、量子力学方程等。
计算机模拟也成为现代固体物理研究的重要工具。
通过阅读《固体物理导论》的导论部分,我对固体物理学有了更深入的了解。
这本书为我揭示了固体物理学的奥秘,激发了我对这门学科的浓厚兴趣。
在接下来的学习中,我将继续深入探索固体的微观世界,理解固体的各种物理性质和行为。
通过不断学习和实践,我将能够更好地掌握固体物理学的基本原理和应用。
1.1 固体物理的定义与意义在量子力学和现代物理学的宏大舞台上,固体物理以其独特的魅力占据了重要的一席之地。
它不仅仅是对微观粒子在固态条件下的行为进行研究,更是探讨物质的基本组成、结构、性质以及演变规律的学科。
当我们谈论固体物理时,我们实际上是在探索物质世界的本质,以及在这些性质中体现出来的宏观现象。
固体的定义多种多样,但最基本的特征是具有固定的晶格结构和电子排布。
晶格结构为固体提供了稳定的几何外形,而电子排布则决定了物质的内在特性,如导电性、磁性等。
基泰尔. 固体物理导论. 参考文献

基泰尔. 固体物理导论. 参考文献一、概述1. 介绍固体物理学的重要性和研究对象2. 引出本文主要内容二、基泰尔固体物理导论概述1. 基泰尔的学术背景和成就2. 《固体物理导论》的出版历史和影响三、固体物理导论的主要内容1. 原子结构和晶体学1) 原子的结构和性质2) 晶体的分类和性质2. 晶格振动和声学性质1) 晶格振动的基本理论2) 固体中的声波传播3. 电子结构和导电性1) 原子的电子结构2) 固体中的电子行为与导电性4. 磁性与磁介质1) 磁性材料的分类与特性2) 磁介质的应用与研究5. 绝缘体和半导体1) 绝缘体与半导体的性质对比2) 半导体材料与器件的发展四、《固体物理导论》的学术贡献1. 对固体物理学的理论框架和实验研究的影响2. 在教学和科研领域的地位和价值五、结论1. 总结基泰尔的《固体物理导论》对固体物理学研究的重要性和影响2. 展望固体物理学领域的未来发展方向参考文献基泰尔. 固体物理导论. Springer-Verlag出版社. 1986.六、基泰尔固体物理导论概述基泰尔(Charles Kittel)是一位美国著名的物理学家,生于1916年。
他曾在伯克利加州大学任教并从事磁性物理学、凝聚态物理学等领域的研究工作。
基泰尔教授是固体物理学领域的权威专家,他在磁性、声子、电子结构等方面的研究成果丰硕,对固体物理学的发展做出了杰出贡献。
《固体物理导论》是基泰尔教授于1953年首次出版的著作,其后多次修订,成为固体物理学领域最为权威和经典的教材之一。
这部著作系统全面地介绍了固体物理学的基本理论和方法,对研究者和学习者有着重要的指导意义。
《固体物理导论》对于推动固体物理学的研究和教学有着深远的影响,被誉为固体物理学领域的“圣经”。
七、固体物理导论的主要内容1.原子结构和晶体学《固体物理导论》首先介绍了固体物理学的基本概念和原子结构的特点。
基泰尔教授深入浅出地阐述了原子结构的基本理论,包括原子核和电子的构成,以及原子的能级和轨道结构。
1.1 固体物理导论--半导体物理
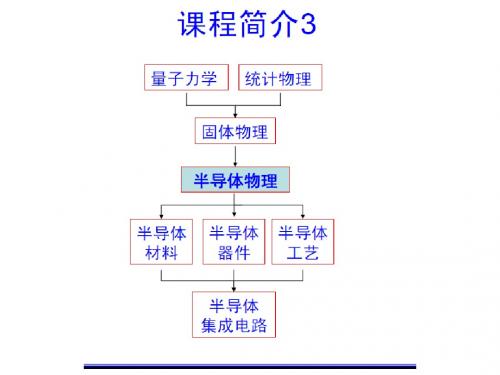
—— 金刚石结构的半导体晶体
Ge、Si等
6. 几种化合物晶体的晶格
1) NaCl晶体的结构 氯化钠由Na+和Cl-结合而成 —— 一种典型的离子晶体 Na+构成面心立方格子;Cl-也构成面心立方格子
的整数倍
的倒数是晶面族中最靠近原点的晶面的截距
密勒指数 —— 标记这个晶面系 —— 以单胞的基矢为参考, 所得出的晶列指数和晶面的
密勒指数,有着重要的意义
立方晶格的几种主要晶面标记
面等效的晶面数分别为:3个 表示为
面等效的晶面数分别为:6个 表示为
面等效的晶面数分别为:4个 表示为
—— 符号相反的晶面指数只是在区别晶体的外表面时才有 意义, 在晶体内部这些面都是等效的
CsCl的复式晶格 —— CsCl结构是由两个简立方的子晶格彼此沿立方体空间 对角线位移1/2 的长度套构而成
ZnS的复式晶格 立方系的ZnS —— S和Zn分别组成面心立方结构的子晶格沿 空间对角线位移 1/4 的长度套构而成
复式晶格:任一原子A的位矢
原胞中各种等价原子之间的相对位移 —— 金刚石晶格
蚀刻:使用化学物质溶解掉暴露出来的晶圆部分,而剩 下的光刻胶保护着不应该蚀刻的部分 清除光刻胶:蚀刻完成后,光刻胶的使命宣告完成,全 部清除后就可以看到设计好的电路图案。
光刻胶:再次浇上光刻胶(蓝色部分),然后光刻,并洗掉曝光 的部分,剩下的光刻胶还是用来保护不会离子注入的那部分材 料。 离子注入(Ion Implantation):在真空系统中,用经过加速的、 要掺杂的原子的离子照射(注入)固体材料,从而在被注入的 区域形成特殊的注入层,并改变这些区域的硅的导电性。经 过电场加速后,注入的离子流的速度可以超过30万千米每小 时 清除光刻胶:离子注入完成后,光刻胶也被清除,而注入区 域(绿色部分)也已掺杂,注入了不同的原子。注意这时候的 绿色和之前已经有所不同。
物理学专业优质课固体物理学导论

物理学专业优质课固体物理学导论物理学专业优质课 | 固体物理学导论导言物理学是自然科学中探讨物质、能量及其相互作用的学科,而固体物理学则是物理学中一个广泛且重要的分支。
固体物理学研究固体物质的性质、结构与行为,对于了解材料科学、电子学、光学、能源领域等具有重要的应用价值。
本文将介绍物理学专业中一门优质课程——固体物理学导论。
第一章 | 课程简介固体物理学导论是物理学专业本科阶段的一门核心课程。
该课程旨在培养学生对固体物理学基本概念、现象和理论的初步了解,以及运用物理学方法解决实际问题的能力。
通过学习固体物理学导论,学生将对材料的结构、热学性质、电学和磁学性质等有一个全面的认识。
第二章 | 课程内容1. 固体物质的结构与晶体学在固体物理学导论中,学生将学习固体内部的结构和晶体学原理。
了解晶体的结构对于理解固体物理学的基本概念和性质具有重要意义。
通过讲授晶体的点阵、晶胞和晶面,学生能够了解晶体的周期性结构以及晶体学中的基本术语和概念。
2. 热学性质固体物理学导论也涵盖了固体的热学性质,包括热膨胀、热导率和热容等。
学生将学习热学性质与固体内部结构的关系,以及如何应用热学性质来解决实际问题。
3. 电学性质电学性质是固体物理学的另一个重要方面。
在固体物理学导论中,学生将了解固体材料中电子的行为以及带电粒子在晶格中的运动。
电导率、介电常数等概念将被介绍,并与固体材料的特性相关联。
4. 磁学性质通过固体物理学导论,学生将初步了解固体材料的磁性。
课程将包括磁场的概念、磁畴理论、铁磁性等相关内容。
通过学习磁学性质,学生将了解磁场对固体物质的影响以及如何利用磁学性质来设计和开发磁性材料。
第三章 | 学习方法与实践1. 理论学习固体物理学导论侧重于理论知识的学习。
学生将通过教材阅读、课堂讲解和小组讨论等学习方式,掌握固体物理学导论的基本概念和理论框架。
2. 实验研究为了加深对固体物理学的理解,课程还包含实验研究的环节。
现代固体物理学导论

现代固体物理学导论
1.固体结构和晶格理论:介绍晶体结构的基本概念和晶格理论,包括晶体对称性、布拉伐格子、倒格子和布里渊区等。
2. 基本电子理论:介绍电子在晶体中的行为和能带理论,包括原子轨道、价带、导带、费米面和能级密度等。
3. 载流子输运理论:介绍电子、空穴、声子在晶体中的输运行为和输运方程,包括欧姆定律、霍尔效应、电学迁移率、热导率和热电效应等。
4. 磁性和自旋电子学:介绍自旋和磁矩在固体中的运动和相互作用,包括磁矩和磁性的基本概念、磁性材料和磁性现象、自旋电子学和磁隧道效应等。
5. 光学和声学性质:介绍光和声在固体中的传播和相互作用,包括光的吸收、折射、反射、透射和散射,以及声波的传播、吸收、衍射和散射等。
本课程旨在让学生了解固体物理学的基本原理和现代研究进展,能够理解和分析固体材料的物理性质和行为,为后续的学习和研究打下坚实的基础。
- 1 -。
固体物理导论基泰尔

固体物理导论基泰尔
固体物理(基泰尔)导论是一门研究固体物质的基本性质和行为
的学科。
它涵盖了固体物质的结构、晶体学、物理性质以及与固体中
的电子和声子相关的现象。
该学科的目标是深入理解固体物理学的原则,并应用它们来解释和预测固体材料的行为。
固体物理导论基于基本定律和量子力学原理,探讨了原子和分子
如何在固体中组合成结晶结构,以及固体结构如何与其物理性质相互
关联。
在这门学科中,我们学习了晶体学的基本概念和方法,包括点
阵结构、晶胞和布拉伐格点。
我们还研究了晶体中的缺陷和扩散问题,以及固体中的晶格振动和声子特性。
固体物理导论还包括对固体中的电子行为的研究。
我们研究了固
体中的能带结构、导电性和磁性等现象,并探讨了电子在固体中的输
运性质。
我们还研究了金属、绝缘体和半导体等不同类型的固体以及
它们的性质。
固体物理导论基泰尔的一个重要应用领域是材料科学和工程。
通
过深入了解固体物理的原理,我们可以设计和合成具有特定性质的新
材料,并优化现有材料的性能。
例如,在电子器件和能源存储领域,
我们可以利用对固体中电子行为的理解来设计更高性能的材料。
总之,固体物理导论基泰尔是一门重要的学科,它研究了固体物
质的基本性质和行为,并为我们理解和应用材料科学提供了基础。
通
过学习固体物理导论,我们能够探索和理解固体世界中的奇妙现象,
并为解决现实世界中的问题做出贡献。
固体物理导论总结第二部分资料

电子枪发射稀疏到,任何时刻空间至多一个电子,但时间足够长后,量子力学的适用范围:量子力学的适用范围:判定常数:h =6.626×10-34J.S ---普朗克常数判定常数:h =6.626×10-34J.S ---普朗克常数hp x x ≥Δ⋅Δhp y y ≥Δ⋅Δhp z z ≥Δ⋅Δ体系的作用量= [长度] ×[动量]体系的作用量= [长度] ×[动量]= [时间] ×[能量]hE t ≥Δ⋅Δ= [角度] ×[角动量]体系的作用量与h 相比拟时,经典力学不再适用。
体系的作用量与h 相比拟时,经典力学不再适用。
¾一个原子内部不可能同时有两个或两个以上的电子具有完全相同的量子数。
泡利不相容原理¾两个自旋相同的电子不可能同时占据同一个状态。
即:同一个状态上只能容纳两个自旋相反的电子lnlm ψlnlm ψ研究的历史发展:1900年,Drude和Lorrentz—金属的经典电子气理论——麦克斯韦—玻尔兹曼统计1928年,Sommerfeld—索末菲自由电子理论—费米—狄拉克统计量子自由电子理论三十年代初期,Bloch和Brilliouin—能带理论量子自由电子理论可作为一种零级近似纳入能带理论!特鲁德模型:①价电子→自由电子(组成电子气),离子实保持原子在自由状态时的构型;③电子气遵从麦克斯韦—玻尔兹曼统计(M -B )②自由电子之间的相互作用忽略不记;二、模型的成功可定性解释金属的电导、霍尔(Hall )效应和热传导等问题!例如:证明了金属热导率除以电导率与绝对温度的积是一个与温度无关的普适常数(Lorentz 常数)κT σ1、模型2、边界条件3、薛定谔方程的解4、K 空间和能态密度5、费米—狄拉克(Fermi-Driac )分布6、电子热容量量子力学建立后,索末菲将薛定谔方程应用于自由电子气体模型,建立了量子自由电子理论。
基泰尔固体物理导论pdf

基泰尔固体物理导论pdf全文共四篇示例,供读者参考第一篇示例:《基泰尔固体物理导论》是一本深入浅出、详实全面的固体物理教材,涵盖了固体物理学的基础知识和重要理论。
本书以清晰易懂的语言阐述了固体的基本特性、晶体结构、物理性质以及固体物理学的各种理论模型和实验方法,为学习者提供了理论知识和实践技能的完整指南。
在《基泰尔固体物理导论》中,读者将了解到固体是由原子或离子组成的,在空间中有规则的周期性排列形成了晶体结构,而这种结构决定了固体的物理性质。
作者从最基本的晶体结构开始讲起,介绍了几何晶体学的概念和原理,例如晶体的对称性、点阵、晶胞等。
接着讲解了固体的晶格缺陷、热学性质、电学性质、磁学性质等内容,全面掌握固体物理学的基本理论。
本书的独特之处在于将理论知识与实际应用相结合,通过各种案例分析和实验技术的介绍,帮助读者更深入地理解固体物理学的概念和原理。
书中还包含大量的习题和实例,有助于读者巩固所学知识,提高解题能力。
无论是作为固体物理学的教材还是作为自学的工具,都非常实用和可靠。
通过学习《基泰尔固体物理导论》,读者将对固体物理学有一个全面深入的了解,能够从微观角度理解固体的性质和行为,为进一步学习和研究提供了坚实的基础。
这本书不仅适合物理专业的学生和研究人员,也适合对固体物理学感兴趣的读者阅读,是一部不可多得的精彩之作。
第二篇示例:《基泰尔固体物理导论》是一本经典的固体物理学教材,由基泰尔(Kittel)教授撰写。
该书系统地介绍了固体物理学的基本概念和理论,为学生和研究者提供了深入理解固体物理学的良好基础。
固体物理学是物理学的一个重要分支,研究固体物质的结构、性质和行为。
固体物理学的发展对理解材料的性能和应用至关重要,广泛应用于半导体器件、材料科学、凝聚态物理等领域。
在《基泰尔固体物理导论》中,基泰尔教授首先介绍了晶体结构和对称性的基本概念。
晶体是固体物质中最常见的形态,其结构具有高度有序性和周期性。
基泰尔固体物理导论第二版答案

基泰尔固体物理导论第二版答案1、17.影视剧中,为了防止演员受伤,砸向演员的道具石头一般是用泡沫塑料制成的。
将小石块和道具石头分别放在调节好的天平左右盘,横梁静止后的情景如图所示。
下列说法正确的是()[单选题] *A.道具石头的质量比小石块的质量大B.道具石头的密度比小石块的密度大C.质量相同时,道具石头的体积比小石块的体积小D.体积相同时,道具石头的质量比小石块的质量小(正确答案)2、53.下列实例中不能用光的直线传播解释的是()[单选题] *A.水中倒影(正确答案)B.手影的形成C.日食和月食D.小孔成像3、曾侯乙编钟是我国古代的一种打击乐器,如图所示。
青铜编钟按钟体大小依次悬挂,可以演奏出美妙的乐曲。
下列关于编钟的说法,正确的是()[单选题]A.编钟正在发声,但不一定在振动B.编钟钟体越小,发出声音的音调越高(正确答案)C.编钟钟体越大,发出声音的响度越大D.编钟可以奏出美妙的音乐,但不会产生噪声4、下列说法正确的是()*A.一定质量的理想气体,放热的同时外界对其做功,其内能可能减少(正确答案)B.单晶体有固定的熔点,多晶体和非晶体没有固定的熔点C.热量能够自发地从高温物体传递到低温物体,但不能自发地从低温物体传递到高温物体(正确答案)D.当分子间的距离增大时,分子之间的引力和斥力均同时减小,而分子势能一定增大5、B.对于一定质量的理想气体,当分子热运动变剧烈时,压强可以不变(正确答案)C.熵增加原理说明一切自然过程总是向着分子热运动的无序性增大的方向进行(正确答案)D.由于液体表而分子间距离大于液体内部分子间的距离,所以液体表面具有收缩的趋势(正确答案)答案解析:分子距离为平衡距离时分子势能最小【判断题】骑自行车下坡时,若遇到紧急情况要刹车,为安全起见,不能只刹住前轮。
[判断题] *6、当绝缘棒接触验电器的金属球时箔片张开,说明绝缘棒带正电[判断题] *对错(正确答案)答案解析:金属箔片张开是由于箔片带同种电荷,无法确定具体带正电还是负电7、35.已知甲液体的密度ρ甲=5g/cm3,乙液体的密度ρ乙=2g/cm3,现在取一定量的甲乙液体混合,混合液体的密度为3g/cm3,液体混合前后总体积保持不变,则所取甲乙体积比V甲:V乙=()[单选题] *A.5:2B.2:5C.1:2(正确答案)D.2:18、95.小明家的厨房里有一个恰好能装下1kg水的玻璃瓶子,现有汽油、酒精和硫酸三种液体,它能够装下1kg的哪种液体()(已知ρ汽油<ρ酒精<ρ水<ρ硫酸)[单选题] *A.汽油B.酒精C.硫酸(正确答案)D.都能装下9、人潜水的深度不能太大,这是因为大气压随着水的深度的增加而增大[判断题] *对错(正确答案)答案解析:液体压强随着水的深度的增加而增大10、司机驾车时必须系安全带,这是为了防止向前加速时惯性带来的危害[判断题] *对错(正确答案)答案解析:防止刹车时惯性带来的危害11、错磁悬浮列车是利用同名磁极相互排斥,增大列车与地面的摩擦[判断题] *对错(正确答案)答案解析:磁悬浮列车是利用同名磁极相互排斥或者异名磁极相互吸引,让车和轨道分离,减小摩擦12、65.卢瑟福用α粒子(带正电)轰击金箔实验为现代原子理论打下了基础,如图线条中,可能是α粒子在该实验中的运动轨迹,能说明原子核带正电且质量较大的是()[单选题] *A. aB. bC. cD.d(正确答案)13、下列物体中,质量约为2×105mg的是()[单选题] *A. 一颗图钉B. 一本初二物理课本(正确答案)C. 一张课桌D. 一支黑水笔14、下列选项中符合安全用电要求的是()[单选题]A.用湿手拨动空气开关B.电线的绝缘皮破损时应及时更换(正确答案)C.在未断开电源开关的情况下更换灯泡D.把用电器的三脚插头改为两脚插头接在两孔插座上使用15、73.铝的密度是木头的5倍,质量相同的铝块和木块,它们的体积之比为1:4,则下列说法正确的是()[单选题] *A.铝块和木块一定都是空心的B.铝块和木块一定都是实心的C.木块一定是空心的D.铝块一定是空心的(正确答案)16、47.夏天刚从冰箱中取出冰棒后,发现以下四种现象:①冰棒上粘着“白粉”;②剥去纸后冰棒会冒出“白雾”;③冰棒放进茶杯后,一会儿杯的外壁就会“出汗”;④冰棒放进嘴里变成“糖水”。
固体物理导论教学课件

a2 0 a1
3. 原胞 ➢ 空间点阵原胞 • 空间点阵最小的重复单元 • 每个空间点阵原胞中只含有一个格点 • 对于同一空间点阵,原胞有多种不同的取法,但
原胞的体积均相等
原胞体积: va a1 a 2 a 3
➢ 晶格原胞=空间点阵原胞+基元
➢ Wigner-Seitz原胞(对称原胞)
体心立方的基矢和Wigner-Seitz原胞
面心立方基矢、原胞和Wigner-Seitz原胞
4. 晶格的分类
➢ 简单晶格:每个晶格原胞中只含有一个原子, 晶格中所有原子在化学、物理和几何环境 上都是完全等同的。
例:Na、Cu、Al等晶格均为简单晶格
倒格子原胞体积:
vab 8 3
b b1 b2 b3
Rl G n 2 h h为整数
研究到易点阵的意义
利用倒易点阵的概念可以很方便地导出晶体几何学中 各种重要关系
可以方便而形象地表示晶体衍射几何学 倒易矢量可以理解为波失
由倒易点阵基失所张的空间成为倒易空间, 可理解为状态空间(k空间)
bcc:
a1
a2
b
0
a
a3
a 1 b c a j k
12
2
a 1 c a a k i
22
2
a 1 a b a i j
32
2
a 1 a b c a i j k
12
2
a 1 a b c a i j k
22
2
a 1 a b c a i j k
§1.3 晶体的宏观对称性
一、点对称操作 ➢ 对称操作:若一个空间图形经过一空间操作 (线性变换),其性质复原,则称此 空间操作为对称操作——正交变换
固体物理导论1.7

1、反映面(对称面,m) 反映面(对称面,m)
反映: 反映:在镜面的作用下使 晶体自身重合的动作。 晶体自身重合的动作。 立方体有3 立方体有3类反映面
2、旋转轴(n) 旋转轴(n)
旋转: 旋转:在某一个固定轴作用下使 晶体自身重合的对称操作。 晶体自身重合的对称操作。 只能取1,2,3,4,6 1,2,3,4,6。 n只能取1,2,3,4,6。 立方体有3个四次轴, 立方体有3个四次轴, 4个三次轴,6个二次轴。 个三次轴,6个二次轴。 ,6个二次轴
第七节 晶体的宏观对称性
对称性:经过某种对称操作后物体能自身重合的性质。 对称性:经过某种对称操作后物体能自身重合的性质。 对称操作:能使物体复原的动作。 对称操作:能使物体复原的动作。 对称元素:对称操作凭借的几何元素。 对称元素:对称操作凭借的几何元素。
四种对称操作反映、旋转、反演、 四种对称操作:反映、旋转、反演、象转 四种对称元素:反映面、旋转轴、反演中心、 四种对称元素:反映面、旋转轴、反演中心、象转轴
(4)6次象转轴等价于3次轴和反映面。 (4)6次象转轴等价于3次轴和反映面。 次象转轴等价于
(5)4次象转轴是一个独立的对称元素。 (5)4次象转轴是一个独立的对称元素。 次象转轴是一个独立的对称元素
5、晶体的宏观对称操作中只有8种独立的基本对称元素: 晶体的宏观对称操作中只有8种独立的基本对称元素: 1,2,3,4,6, ,i ,m 6、点群 描述晶体宏观对称性的全部操作构成群。 描述晶体宏观对称性的全部操作构成群。 晶体的基本对称元素的组合称为点群。 晶体的基本对称元素的组合称为点群。 32种晶体点群 32种晶体点群
3、反演中心(i) 反演中心(i) (i 反演:在某一固定点作用下使晶体自身重合的对称操作。 反演:在某一固定点作用下使晶体自身重合的对称操作。 立方体只有一个反演中心,即体心。 立方体只有一个反演中心,即体心。 象转轴( 4、象转轴( ) 象转:经过旋转后再作反演的对称操作。 象转:经过旋转后再作反演的对称操作。 象转轴并不都是独立的基本对称元素。 n次(度)象转轴并不都是独立的基本对称元素。 (1)1次象转轴就是反演中心 次象转轴就是反演中心。 (1)1次象转轴就是反演中心。 (2)2次象转轴等价于反映面 次象转轴等价于反映面。 (2)2次象转轴等价于反映面。 (3)3次象转轴等价于 次轴和反演中心。 次象转轴等价于3 (3)3次象转轴等价于3次轴和反演中心。
固体物理导论部分考前复习精彩试题

第一章1.以堆积模型计算由同种原子构成的同体积的体心和面心立方晶体中原子数之比.解:设原子的半径为R, 体心立方(bcc)晶胞的体对角线为4R, 晶胞的边长为, 晶胞的体积为, 一个晶胞包含两个原子, 一个原子占的体积为,单位体积晶体中的原子数为; 面心立方(fcc)晶胞的边长为, 晶胞的体积为, 一个晶胞包含四个原子, 一个原子占的体积为, 单位体积晶体中的原子数为. 因此, 同体积的体心和面心立方晶体中的原子数之比为=0.918.2.解理面是指低指数的晶面还是高指数的晶面?为什么?解:晶体容易沿解理面劈裂,说明平行于解理面的原子层之间的结合力弱,即平行解理面的原子层的间距大. 因为面间距大的晶面族的指数低, 所以解理面是面指数低的晶面.3.基矢为a1=ai a2=aj a3=a(i+j+k)/2的晶体为何种结构?解:有已知条件, 可计算出晶体的原胞的体积由原胞的体积推断, 晶体结构为体心立方. 按照本章习题14, 我们可以构造新的矢量,,.对应体心立方结构. 根据14题可以验证, 满足选作基矢的充分条件.可见基矢为, , 的晶体为体心立方结构.若 +,则晶体的原胞的体积,该晶体仍为体心立方结构.4. 面心立方元素晶体中最小晶列周期多大?该晶列在哪些晶面?解:周期最小的晶列一定在原子面密度最大的晶面. 若以密堆积模型, 则原子面密度最大的晶面就是密排面. [l1,l2,l3]晶列上格点周期为∣R l∣=∣l1a+l2a+l3a∣密勒指数(111)是一个密排面晶面族, 最小的晶列周期为∣R l∣=. 根据同族晶面族的性质, 周期最小的晶列处于{111}面.5.在晶体衍射中,为什么不能用可见光?解:晶体中原子间距的数量级为米,要使原子晶格成为光波的衍射光栅,光波的波长应小于米. 但可见光的波长为7.6 4.0米, 是晶体中原子间距的1000倍. 因此, 在晶体衍射中,不能用可见光.6.高指数的晶面族与低指数的晶面族相比,对于同级衍射,哪一晶面族衍射光弱?为什么?解:对于同级衍射, 高指数的晶面族衍射光弱, 低指数的晶面族衍射光强. 低指数的晶面族面间距大, 晶面上的原子密度大, 这样的晶面对射线的反射(衍射)作用强. 相反, 高指数的晶面族面间距小, 晶面上的原子密度小, 这样的晶面对射线的反射(衍射)作用弱. 另外, 由布拉格反射公式可知, 面间距大的晶面, 对应一个小的光的掠射角. 面间距小的晶面, 对应一个大的光的掠射角. 越大, 光的透射能力就越强, 反射能力就越弱.7.确定fcc结构中粒子密度最大的晶面.解:8.温度升高时,衍射角如何变化?X光波长变化是,衍射角如何变化?解:温度升高时, 由于热膨胀, 面间距逐渐变大. 由布拉格反射公式可知, 对应同一级衍射, 当X光波长不变时, 面间距逐渐变大, 衍射角逐渐变小.所以温度升高, 衍射角变小.当温度不变, X光波长变大时, 对于同一晶面族, 衍射角随之变大.第二章1.离子键,金属键,共价键,德瓦尔斯键和氢键中,哪些键可能形成绝缘体和半导体?哪些键具有饱和性和方向性?为什么?解:2.试证由两种离子组成的,间距为R的一维晶格的马德隆常数M=2Ln2.3.只考虑最近邻和次近邻,试计算Nacl和Cscl结构的马德隆常数.第三章1.长光学格波与长声学格波本质上有何区别?解:长光学支格波的特征是每个原胞的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.2.晶体中声子数目是否守恒?声子与光子有何区别?解:频率为的格波的(平均) 声子数为即每一个格波的声子数都与温度有关, 因此, 晶体中声子数目不守恒, 它是温度的变量.按照德拜模型, 晶体中的声子数目N’为.作变量代换,其中是德拜温度. 高温时,,即高温时, 晶体中的声子数目与温度成正比.低温时, ,, 即低温时, 晶体中的声子数目与T 3成正比.3.温度一定,光学波的声子数目多还是声学波的声子数目多?解:频率为的格波的(平均) 声子数为.因为光学波的频率比声学波的频率高, ()大于(), 所以在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.{7. 对同一个振动模式, 温度高时的声子数目多呢, 还是温度低时的声子数目多?解:设温度T H>T L, 由于()小于(), 所以温度高时的声子数目多于温度低时的声子数目.8. 高温时, 频率为的格波的声子数目与温度有何关系?解:温度很高时, , 频率为的格波的(平均) 声子数为.可见高温时, 格波的声子数目与温度近似成正比. }4,长声学格波能否导致离子晶体的宏观极化?解:长光学格波所以能导致离子晶体的宏观极化, 其根源是长光学格波使得原胞不同的原子(正负离子)产生了相对位移. 长声学格波的特点是, 原胞所有的原子没有相对位移. 因此, 长声学格波不能导致离子晶体的宏观极化.5.爱因斯坦模型所得固体热容量在低温下与试验存在偏差,为什么?解:按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.{18.在甚低温下, 德拜模型为什么与实验相符?解:在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.19.在绝对零度时还有格波存在吗? 若存在, 格波间还有能量交换吗?解:频率为的格波的振动能为,其中是由个声子携带的热振动能, ()是零点振动能, 声子数.绝对零度时, =0. 频率为的格波的振动能只剩下零点振动能.格波间交换能量是靠声子的碰撞实现的. 绝对零度时, 声子消失, 格波间不再交换能量.}第四章1.晶体中缺陷分为哪几种?各有什么特点?2.何为弗仑克缺陷和肖脱基缺陷?3.根据刃型位错模型解释金属性变形。
固体物理导论总结第二部分

电子枪发射稀疏到,任何时刻空间至多一个电子,但时间足够长后,量子力学的适用范围:量子力学的适用范围:判定常数:h =6.626×10-34J.S ---普朗克常数判定常数:h =6.626×10-34J.S ---普朗克常数hp x x ≥Δ⋅Δhp y y ≥Δ⋅Δhp z z ≥Δ⋅Δ体系的作用量= [长度] ×[动量]体系的作用量= [长度] ×[动量]= [时间] ×[能量]hE t ≥Δ⋅Δ= [角度] ×[角动量]体系的作用量与h 相比拟时,经典力学不再适用。
体系的作用量与h 相比拟时,经典力学不再适用。
¾一个原子内部不可能同时有两个或两个以上的电子具有完全相同的量子数。
泡利不相容原理¾两个自旋相同的电子不可能同时占据同一个状态。
即:同一个状态上只能容纳两个自旋相反的电子lnlm ψlnlm ψ研究的历史发展:1900年,Drude和Lorrentz—金属的经典电子气理论——麦克斯韦—玻尔兹曼统计1928年,Sommerfeld—索末菲自由电子理论—费米—狄拉克统计量子自由电子理论三十年代初期,Bloch和Brilliouin—能带理论量子自由电子理论可作为一种零级近似纳入能带理论!特鲁德模型:①价电子→自由电子(组成电子气),离子实保持原子在自由状态时的构型;③电子气遵从麦克斯韦—玻尔兹曼统计(M -B )②自由电子之间的相互作用忽略不记;二、模型的成功可定性解释金属的电导、霍尔(Hall )效应和热传导等问题!例如:证明了金属热导率除以电导率与绝对温度的积是一个与温度无关的普适常数(Lorentz 常数)κT σ1、模型2、边界条件3、薛定谔方程的解4、K 空间和能态密度5、费米—狄拉克(Fermi-Driac )分布6、电子热容量量子力学建立后,索末菲将薛定谔方程应用于自由电子气体模型,建立了量子自由电子理论。
基泰尔固体物理导论pdf

基泰尔固体物理导论pdf基泰尔固体物理导论是一本非常重要的教材,它以简洁明了的方式介绍了固体物理学的基础知识和理论。
本书系统地阐述了固体的结构、电子结构、磁性、光学性质等方面。
通过对基础理论的深入讨论和实例的详细说明,读者可以全面了解和掌握固体物理学的核心概念和研究方法。
首先,基泰尔固体物理导论详尽地介绍了固体的结构。
它从晶体结构的基本概念出发,引导读者了解不同晶体结构的特征和分类方法。
通过图文并茂的解释,读者可以直观地了解到晶格常数、晶体面、晶体点阵等概念。
此外,本书还详细介绍了非晶体、多晶体等其他结构类型,使读者对不同结构类型的固体有更加全面的认识。
其次,基泰尔固体物理导论还深入剖析了固体的电子结构。
它从带隙理论出发,讲解了固体的导电性和绝缘性。
通过理论模型和实例分析,读者可以了解到电子能带理论、费米能级、能带隙等重要概念。
同时,本书还介绍了波函数、布洛赫定理等量子力学原理在固体物理中的应用。
这些内容的讲解,有助于读者全面掌握固体电子结构的基本原理。
此外,基泰尔固体物理导论还详细讨论了固体的磁性和光学性质。
本书首先介绍了自发磁化、顺磁性、反磁性等磁性现象的理论解释。
接着,它详细讨论了固体的磁性相变和磁性材料的应用。
在光学性质方面,本书从电磁波理论出发,解释了固体对光的吸收、散射、折射等现象。
通过大量的实例和图表,读者可以更好地理解固体的磁性和光学性质的原理和应用。
最后,基泰尔固体物理导论还提供了丰富的习题和解答,帮助读者巩固所学知识。
这些习题既包括理论推导题,又包括实例分析题,涵盖了固体物理的不同方面。
通过解答这些习题,读者可以检验自己对固体物理学的掌握程度,同时也可以加深对理论原理的理解。
总的来说,基泰尔固体物理导论是一本生动、全面、有指导意义的教材。
它通过详细的理论讲解、实例分析和习题练习,帮助读者全面掌握固体物理学的基础知识和研究方法。
无论是从事固体物理学研究的学者,还是对固体物理学感兴趣的普通读者,都可以从这本教材中受益匪浅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Bonding in solids: Ionic solids
Properties of ionic solid crystals: • relatively stable and hard • poor electrical/heat conductors • high melting/boiling temperatures • transparent to visible light • strong IR absorption • soluble in polar solvents (e.g., water)
(Ohm’s law)
! E =0
! ! vd = v (t ) = 0 ! ! ! vd = v (t ) = − µE
v rms =
L = v rms τ (mean free path)
! 3kBT v (t )2 = m
eτ 2 s = vd τ = E m
2 τ ne −1 σ=ρ = y t i m ity tiv v c i u t nd sis co re ne 2L ne 2L = = mv rms 3kBTm
experimentally ρ~T and not T1/2 !!!
Heat conduction: Wiedemann-Franz law
Heat current density:
dQ dT = −K JT ≡ Adt dx
thermal conductivity
1 1 2 = K = C v L k nv v rms " rms τ B " 3 3 2 v τ
Physics 215 Winter 2002
Introduction to Modern Physics
Prof. Ioan Kosztin Lecture #23
Solid State Physics
• Bonding in solids (metals, isolators, semiconductors) • Classical free electron theory of metals • Quantum theory of metals • Band theory of solids • Semiconductors • Lasers
Amorphous solids
• Ideal solid crystals exhibits structural long range order (LRO) • Real crystals contain imperfections, i.e., defects and impurities , which spoil the LRO • Amorphous solids lack any LRO [though may exhibit short range order (SRO)]
Classical free electron theory of metals
• Free electron model of metals: metal = an ideal gas of conduction electrons moving through the fixed lattice of positive ion cores • Features of the free electron model: • explains the high electrical (σ) and σ ~ 106 (Ωm) −1 − ~ 10 100 W/mK K thermal (K) conductivity of metals ! ! J = σE • explains the functional form of Ohm’s law • explains the relationship between σ and K [K / σT = const ] (Wiedemann-Franz law) • fails to predict accurately the experimental values of σ and K
Electrical conduction: Ohm’s Law
! ! J = envd , ! ! vd = v (t )
drift velocity
! ! vd = − µE ,
current density
electron density
eτ µ= m
! ! J = σE
mobility
mean free time
K mkB 2 3kB2 v = 2T = 2 rms 2e σ 2e ⇓ K 3kB2 −8 2 1.1 10 W Ω /K = const = = × ⋅ 2e 2 $ σT #$$$$$$ %$$$$$$$ &
= Lorentz nums different from the experimental value !!!
Classification of solids
• Phases of matter: • solid (well defined shape and volume) • liquid (only well defined volume) • gas (no defined shape or volume) • plasma (an overall neutral collection of charged and neutral particles) • Solids • crystalline (atoms form a regular periodic structure) • amorphous (atoms have irregular spatial distribution) • Solids • metals (good electrical/heat conductors) • semiconductors • insulators (poor electrical/heat conductors)
Bonding in solids: Ionic solids
Ionic solid crystals (e.g. NaCl) are held together by the Coulomb attractive interaction between ions with opposite sign (ionic bonding)
Crystal
Glass (amorphous)
Gas
Degree of (dis)ordering in a solid
can be quantified by the two particle correlation (radial distribution) function g2(r) = probability of finding a 2nd atom at a distance r from a given atom; g2(r) can be measured experimentally and calculated theoretically/numerically.
Bonding in solids: Metallic solids
Atoms in a metallic crystal are held together by the effective attractive electrostatic interaction mediated by the conduction (valence) electron gas (metallic bonding) Properties of metallic crystals: • smaller cohesive energies (~1 eV) than in covalent/ionic crystals • sufficiently hard and stable • good electrical/heat conductors • strong interaction with light • form solid solutions
Bonding in solids: Covalent solids
Atoms in the crystal are held together by covalent bonding C atoms in diamond form a tetragonal crystal structure Properties of covalent crystals: • very hard and stable • high melting point • good insulators • do not absorb light • larger cohesive energies (~10 eV) than in ionic crystals
Metal ion
Conduction electron gas
Bonding in solids: Molecular crystals
Molecules in the crystal are held together by: • weak Van der Waals bonds exp: solid methane (Ec=0.10 eV/molecule) solid argon (Ec=0.076 eV/molecule) • relatively strong hydrogen bonds exp: solid ice (Ec=0.53 eV/molecule)
e2 b U = −αk + m r r
(α = 1.7476 for Na +Cl − )
(m ~ 10)
k = 1 / 4πε 0
Madelung constant
Ionic cohesive energy:
