连续时间信号卷积运算的MATLAB实现
信号与系统 连续时间信号卷积运算
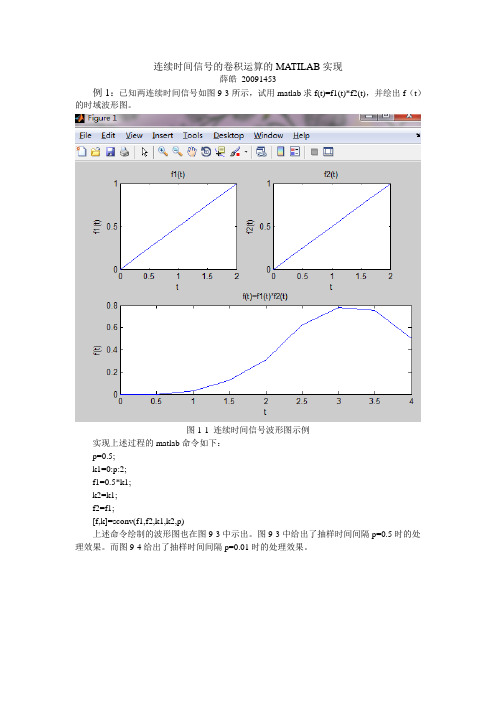
连续时间信号的卷积运算的MATILAB实现薛皓20091453例1:已知两连续时间信号如图9-3所示,试用matlab求f(t)=f1(t)*f2(t),并绘出f(t)的时域波形图。
图1-1 连续时间信号波形图示例实现上述过程的matlab命令如下:p=0.5;k1=0:p:2;f1=0.5*k1;k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)上述命令绘制的波形图也在图9-3中示出。
图9-3中给出了抽样时间间隔p=0.5时的处理效果。
而图9-4给出了抽样时间间隔p=0.01时的处理效果。
图1-2 例1的连续时间信号波形图习题1:已知f1(t)=1(2t 1≤≤),f2(t)=1(3t 2≤≤),用matlab 实现其卷积并绘制出卷积曲线。
解:程序代码如下:>> p=0.01;k1=1:p:2;f1=ones(size(k1)).*(k1>1);k2=2:p:3;f2=ones(size(k2)).*(k2>2);f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=k1(length(k1))+k2(length(k2));subplot(2,2,1)plot(k1,f1)title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);h=get(gca,'position');h(3)=2.5*h(3); 0set(gca,'position',h)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')绘制图形如图2-1所示。
实验一 连续时间信号的Matlab表示与计算

实验一连续时间信号的Matlab表示与计算一、实验目的1、初步学习MATLAB语言,熟悉MATLAB软件的基本使用。
2、掌握用MA TLAB描述连续时间信号方法,能够编写MATLAB程序,实现各种信号的时域变换和运算,并且以图形的方式再现各种信号的波形。
二、实验原理连续信号是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干个不连续点之外,信号都有确定的值与之对应。
严格来说,MATLAB并不能处理连续信号,而是用等时间间隔点的样值来近似表示连续信号。
当取样时间间隔足够小时,这些离散的样值就能较好地近似连续信号。
在MATLAB可视化绘图中,对于以t为自变量的连续信号,在绘图时统一用plot函数;而对n为自变量的离散序列,在绘图时统一用stem函数。
对于连续时间信号f(t),可用f、t两个行向量来表示。
例:t=-10:1.5:10;f=sin(t)./ t ;可以产生t= -10~10,间隔1.5的序列以及t tf)sin(=的值。
用命令:plot(t,f)可得如下图形,显然显示效果较差,这是因为t的间隔过大,只要改变为:t=-10:0.5:10;可得图1.2。
图1.1 图1.21. 信号的时域表示方法MATLAB提供了大量用以生成基本信号的函数,比如最常用的指数信号、正弦信号等就是MATLAB的内部函数,即不需要安装任何工具箱就可以调用的函数。
1.1单位阶跃信号u(t)function y=heaviside(t) %阶跃信号y = (t>=0); % y = 1 for t > 0, else y = 01.2单位冲激信号δ(t)function chongji(t1,t2,t0) %冲激信号δ(t- t 0),t 1和t 2分为起始时间和终止时间dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(t0-t1)/dt+1)=1/dt;stairs(t,x); %以阶梯方式绘画axis([t1,t2,0,1.1/dt]) 或function y = delta(t)dt = 0.01;y = (u(t)-u(t-dt))/dt;1.3指数信号指数信号atAe 在MATLAB 中可以用exp 函数表示,其调用形式为:y=A*exp(a*t)例如图1-3所示指数衰减信号的MATLAB 源程序如下(取A=1,a=-0.4):%program7_1 Decaying expponential signalA=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;1.4正弦信号正弦信号)cos(ϕω+t A o 和)sin(ϕω+t A o 分别用MATLAB 的内部函数cos 和sin 表示,其调用形式为:)*cos(*phi t A o +ω)*sin(*phi t A o +ω 例如图1-4所示MATLAB 源程序如下(取A=1,πω20=,6/πϕ=):%program7_2 Sinusoidal signalA=1;w0=2*pi;phi=pi/6;t=0:0.01:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on;图1-3 单边指数衰减信号 图1-4 正弦信号 除了内部函数外,在信号处理工具箱(Signal Processing Toolbox )中还提供了诸如抽样 函数、矩形波、三角波、周期性矩形波和周期性三角波等在信号处理中常用的信号。
信号卷积在 MATLAB 中的实现

信号卷积在 MATLAB 中的实现宋德周【摘要】The core digital signal processing algorithm is the Discrete Fourier Transform (DFT), is the DFT to the signal in the digital domain and frequency domain are realized discrete,general-purpose computer which can handle discrete signal. Discrete Fourier transform, in communications, voice processing, image processing, radar, medical imaging and other fields is widely used, but this is by convolution and correlation operations on continuous signals and sequences based on spectral analysis. Volume integral for the circular convolution, linear convolution. This paper analyzes under what circumstances can use cyclic convolution operation instead of linear convolution and the corresponding program codes in MATLAB to achieve this on two sequences of arbitrary input cyclic convolution, the keyboard sequence can input the final results and waveform display.%核心的数字信号处理算法是离散傅立叶变换(DFT),是在数字域和频率域对信号的DFT 实现离散,通用计算机可以处理离散信号。
毕业设计(论文)-信号与系统中的典型问题的matlab分析[管理资料]
![毕业设计(论文)-信号与系统中的典型问题的matlab分析[管理资料]](https://img.taocdn.com/s3/m/02bc8d067c1cfad6185fa741.png)
2011届学士学位论文信号与系统中典型问题的MATLAB分析系别: 电子信息系专业: 电子信息科学与技术学号:姓名:指导教师:指导教师职称: 教授2011年4月30日信号与系统中典型问题的MATLAB分析摘要从信号与系统课程的特点出发,结合MATLAB软件优势,针对实例进行分析。
主要从连续信号、离散信号两方面应用MATLAB软件进行仿真和分析。
分别对连续信号和离散信号中线性时不变(LTI)系统信号分析,应用MATLAB软件进行仿真和分析。
对连续时间信号和离散时间信号的线性时间不变(LTI)系统的变换域,卷积和采样定理进行了模拟。
实例中运用了连续模块库、离散模块库等。
通过实例表明了MATLAB软件的便捷性,可以提高工作效率。
实践证明,采用MATLAB软件进行辅助分析可以我们对知识点的理解更深入更透彻。
关键词MATLAB仿真;时域分析;频域分析;卷积;序列卷和;冲激响应;阶跃响应;The Applied Research of Signal ProcessingBased on MATLABAbstract we give an overview of the examples from the characteristics of signal and system course, combining with MATLAB software advantages. The main idea is that MATLAB simulation and analysis software were applied in the continuous-time signals and discrete-time signals. In continuous-time signals and discrete-time signals the response signal of linear time invariant(LTI) system and its analysis of the transform domain and convolution and Sampling theorem were simulated. The examples used the continuous and discrete blocks library and communication toolbox, etc. Some examples show that processing signals can bring us great convenience and high efficiency. Practice has proved, using MATLAB software were aided analysis on knowledge points we can understand deeper and more thoroughly.Key-words MATLAB; the Time-domain Analysis;Frequency domain analysis;convolution ;Sequence convolution ;Impulse response ;Order step-response目录1引言 (1)2 MATLAB软件介绍 (2)3 MATLAB对连续时间信号的分析 (3)MATLAB仿真线性时不变(LTI)系统响应的信号表示 (3)MATLAB对连续信号变换域的分析 (4)连续时间信号的卷积计算及MATLAB的实现 (5)连续时间系统抽样定理的验证 (6)84 MATLAB对离散时间信号的分析 (10)离散系统的单位样值响应 (11)离散系统的变换域分析 (12)离散时间信号的卷积计算 (13)结论 (15)参考文献 (16)致谢 (17)附录一 (18)附录二 (19)附录三 (21)1 引言随着软件的发展,为仿真实验提供了另一思路,MATLAB软件具有强大的数值计算和矩阵处理功能。
实验一 连续时间信号的Matlab表示与计算

实验一连续时间信号的Matlab表示与计算一、实验目的1、初步学习MATLAB语言,熟悉MATLAB软件的基本使用。
2、掌握用MA TLAB描述连续时间信号方法,能够编写MATLAB程序,实现各种信号的时域变换和运算,并且以图形的方式再现各种信号的波形。
二、实验原理连续信号是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干个不连续点之外,信号都有确定的值与之对应。
严格来说,MATLAB并不能处理连续信号,而是用等时间间隔点的样值来近似表示连续信号。
当取样时间间隔足够小时,这些离散的样值就能较好地近似连续信号。
在MATLAB可视化绘图中,对于以t为自变量的连续信号,在绘图时统一用plot函数;而对n为自变量的离散序列,在绘图时统一用stem函数。
对于连续时间信号f(t),可用f、t两个行向量来表示。
例:t=-10:1.5:10;f=sin(t)./ t ;可以产生t= -10~10,间隔1.5的序列以及t tf)sin(=的值。
用命令:plot(t,f)可得如下图形,显然显示效果较差,这是因为t的间隔过大,只要改变为:t=-10:0.5:10;可得图1.2。
图1.1 图1.21. 信号的时域表示方法MATLAB提供了大量用以生成基本信号的函数,比如最常用的指数信号、正弦信号等就是MATLAB的内部函数,即不需要安装任何工具箱就可以调用的函数。
1.1单位阶跃信号u(t)function y=heaviside(t) %阶跃信号y = (t>=0); % y = 1 for t > 0, else y = 01.2单位冲激信号δ(t)function chongji(t1,t2,t0) %冲激信号δ(t- t 0),t 1和t 2分为起始时间和终止时间dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(t0-t1)/dt+1)=1/dt;stairs(t,x); %以阶梯方式绘画axis([t1,t2,0,1.1/dt]) 或function y = delta(t)dt = 0.01;y = (u(t)-u(t-dt))/dt;1.3指数信号指数信号atAe 在MATLAB 中可以用exp 函数表示,其调用形式为:y=A*exp(a*t)例如图1-3所示指数衰减信号的MATLAB 源程序如下(取A=1,a=-0.4):%program7_1 Decaying expponential signalA=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;1.4正弦信号正弦信号)cos(ϕω+t A o 和)sin(ϕω+t A o 分别用MATLAB 的内部函数cos 和sin 表示,其调用形式为:)*cos(*phi t A o +ω)*sin(*phi t A o +ω 例如图1-4所示MATLAB 源程序如下(取A=1,πω20=,6/πϕ=):%program7_2 Sinusoidal signalA=1;w0=2*pi;phi=pi/6;t=0:0.01:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on;图1-3 单边指数衰减信号 图1-4 正弦信号 除了内部函数外,在信号处理工具箱(Signal Processing Toolbox )中还提供了诸如抽样 函数、矩形波、三角波、周期性矩形波和周期性三角波等在信号处理中常用的信号。
信号的时域表示以及卷积运算(MATLAB)

信号的时域表示【实验目的】利用MATLAB 实现信号的时域表示利用MATLAB 实现图形表示【实验内容(步骤)】软件仿真实验在此部分只需写出代码及相应的注释。
例题实验:clear;%清除工作空间的变量clf;%清除图形clc;%清除命令窗口中的命令t0=-1;%给t0赋值1,作为横轴的最小值tf=5;%给tf赋值5,作为横轴的最大值dt=0.05;%作为冒号表达式的步长t1=0;t=t0:dt:tf; %建立向量Len_t = length(t);%把向量t的长度赋值给Len_tn1 = floor((t1-t0)/dt);%选出t=0在向量t中对应的元素序号x1 = zeros(1,Len_t);%建立一个与t等长的一维零矩阵x1(n1) = 1/dt;%选出t=0在向量t中对应的元素subplot(2,2,1),stairs(t,x1),grid on%把图形窗口分割成2*2的四个部分,第一个部分用stairs函数画出单位冲击函数axis([-1,5,0,22])%控制坐标轴,横轴在-1到5之间,纵轴在0到22之间title('1.冲击信号');%给第一个图形命名% x2 = [zeros(1,n1-1),ones(1,Len_t-n1+1)];% x2 = (t>0);% x2 = 1/2*(sign(t-0)+1);%利用符号函数实现单位阶跃函数x2 = stepfun(t,t1);%建立一个向量x2,当t<t1时,元素都为0,当t>=t1时,元素都为1subplot(2,2,3),stairs(t,x2),grid on%在图形窗口的第三个部分画出单位阶跃函数axis([-1,5,0,1.1]) %设置显示的坐标轴的最大最小值title('2.单位阶跃信号'); %给第二个图形命名alpha = -0.5;%为x3中的alpha赋值omega = 10;%为x3中的omega赋值x3 = exp((alpha+j*omega)*t);%产生了一个复指数信号subplot(2,2,2),plot(t,real(x3)),grid on%在图形窗口的第二部分画出复指数信号的实部title('3.复指数跃信号(实部)'); %命名subplot(2,2,4),plot(t,imag(x3)),grid on%在图形窗口中的第四部分画出复指数信号的虚部title('4.复指数跃信号(虚部)'); %命名【实验结果及分析】图像截图:10HZ和16HZ的周期方波实验:实验步骤:t = linspace(-10,10,100); 产生一百个元素y = (square(t) + 1)./2; y的函数subplot(211); 分割成两块,进入第一块界面plot(t./(2*pi*10),y,'r-');grid on 产生10HZ 的方波axis([0,0.3,-1.2,1.2]);xlabel('t'),ylabel('y1'),title('10Hz');subplot(212); 进入第二块界面plot(t./(2*pi*16),y,'c-');grid on 产生16HZ 的方波axis([0,0.3,-1.2,1.2]);xlabel('t'),ylabel('y2'),title('16Hz');图像截图:连续信号的卷积实验实验步骤:clear %清除Workspace中的变量clc %清除Command Window中的命令uls=ones(1,10); %建立一个1*10的矩阵Length_u = length(uls); %把向量uls的长度赋给Length_uhls = exp(-0.1*(1:15)); %建立一个长度为15的向量hlsLength_h = length(hls); %把向量hls的长度赋给Length_hlmax = max(Length_u,Length_h); %把向量u的长度与向量h的长度中的最大值赋给lmax%if end 语句确定了nh与nu的值,用于下面的向量u与向量h中,保证两者长度相等if Length_u>Length_hnu=0; nh = Length_u - Length_h;elseif Length_u<Length_hnh=0; nu = Length_h - Length_u;elsenu=0; nh=0;end%nh=0 nu=5dt = 0.5;lt = lmax;%把向量u的长度与向量h的长度中的最大值赋给ltu = [zeros(1,lt),uls,zeros(1,nu),zeros(1,lt)];% 建立一个长度为45的向量,uls的值在中间,易于卷积t1 = (-lt+1:2*lt)*dt;%建立了一个长度为45,步长为0.5的向量,从-7到15h = [zeros(1,2*lt),hls,zeros(1,nh)];% 建立一个长度为45的向量,hls的值在末尾一段hf = fliplr(h);%将h进行反褶运算y = zeros(1,3*lt);%建立一个1*45的零矩阵for k = 0:2*lt%设置循环31次p = [zeros(1,k),hf(1:end-k)];%p是长度为45的向量,由向量hf平移k个单位而来y1 = u.*p*dt;%卷积中的相乘yk = sum(y1);%卷积中的积分(求和)y(k+lt+1) = yk;%给y中的元素赋值subplot(4,1,1);stairs(t1,u)%分割图形窗口为4*1,在第一部分画出要进行卷积的函数uaxis([-lt*dt,2*lt*dt,min(u),max(u)]),hold on%设置坐标轴的最值,并让图形等待ylabel('u(t)')%给y轴命名subplot(4,1,2);stairs(t1,p)%在图形窗口的第二部分画出要进行卷积的函数h(k-t)axis([-lt*dt,2*lt*dt,min(p),max(p)])%控制坐标轴的最值ylabel('h(k-t)')%给y轴命名subplot(4,1,3);stairs(t1,y1)%在图形窗口的第三部分画出u(t)*h(k-t)的阶梯状图形axis([-lt*dt,2*lt*dt,min(y1),max(y1)+eps])%控制坐标轴的最值ylabel('s=u*h(k-t)')%给y轴命名subplot(4,1,4);stem(k*dt,yk)%在图形窗口的第四部分画出卷积结果的点状图 axis([-lt*dt,2*lt*dt,floor(min(y)+eps),ceil(max(y+eps))])%控制坐标轴的最值hold on,ylabel('y(k)=sum(s)*dt')%给y轴命名pause(1),%每次循环暂停一秒,方便看清各个图形的变化End图像截图:矩形脉冲信号与锯齿波信号的卷积实验步骤:>> cleardt=0.001; 时间间隔t=0:dt;1; 变化范围f1=(t>0&t<1); 矩形脉冲subplot(311); 分割版面plot(t,f1);grid onxlabel('t'),ylabel('f1'),title('矩形脉冲');axis([-0.3,1.7,0,1.2]);f2=(t>0&t<1).*t; 锯齿波subplot(312);plot(t,f2);grid onxlabel('t'),ylabel('f2'),title('锯齿波');axis([-0.3,1.7,0,1.2]);f3=conv(f1,f2);f3=f3*dt; 实现卷积功能n=length(f1)+length(f2)-2;x=0:dt:n*dt;subplot(313);plot(x,f3);grid onxlabel('x'),ylabel('f3'),title('卷积');axis([-0.3,1.7,0,1.2]);图像截图:。
运用MATLAB进行连续时间信号卷积运算

实验项目名称:运用MATLAB进行连续时间信号卷积运算(所属课程:信号与系统)院系:电子信息与电气工程专业班级:电气工程及其自动化姓名:安永军学号:201002040062实验日期:2012年4月12 号实验地点:A-07-408合作者:张德扬指导老师:李静本实验项目成绩: 教师签字: 日期:一:实验目的1,掌握连续时间信号的基本运算的实现方法。
2,熟悉连续LTI 系统在典型激励信号下的响应及其特征。
3、掌握连续LTI 系统单位冲激响应的求解方法。
4、重点掌握用卷积法计算连续时间系统的零状态响应。
5、熟悉MATLAB 相关函数的调用格式及作用。
6、会用MATLAB 对系统进行时域分析。
二、实验原理1、信号的运算包括:信号的基本运算,包括加、减、乘、除等;信号的时域变换,包括信号的平移、翻转、尺度变换等;两个信号的卷积运算等。
2、连续时间线性时不变系统(LTI )可以用如下的线性常系数差分方程来描述:()(1)()(1)110110()()()()()()()()n n m m n m n n r t r t r t r t e t e t e t e t a a a a b b b b ----++++=++++''其中,n m ≥,系统的初始条件为(0)r -,(0)r -',(0)r -'', (1)(0)n r--。
系统的响应一般包括两个部分,即由当前输入所产生的响应(零状态响应)和由历史输入(初始状态)所产生的响应(零输入响应)。
对于低阶系统,一般可以通过解析的方法得到响应。
但对于高阶系统,手工计算就比较困难,这时MATLAB 强大的计算功能就能比较容易地确定系统的各种响应,如冲激响应、阶跃响应、零输入响应、零状态响应、全响应等。
1)直接求解法在MATLAB 中,要求以系数相量的形式输入系统的微分方程。
因此,在使用前必须对系统的微分方程进行变换,得到其传递函数。
连续时间信号的卷积及信号的频域分析实验报告(1)

连续时间信号的卷积及信号的频域分析实验报告(1)连续时间信号的卷积及信号的频域分析实验报告一、实验目的本实验的主要目的是通过对于两个时间域信号的卷积运算,掌握信号卷积运算的基本原理及操作方法;同时,利用MATLAB软件完成信号的傅里叶变换,了解信号在频域的频谱特征。
二、实验内容1、连续时间信号的卷积运算利用MATLAB软件中conv函数进行两个信号的卷积运算,并观察结果。
2、信号在频域的频谱特征- 利用MATLAB软件中fft函数对信号进行傅里叶变换,并获取其频域表示;- 利用MATLAB软件中ifft函数对信号进行逆傅里叶变换,恢复其原始时间域信号;- 观察不同频率成分对于信号的影响,并分析其原因。
三、实验步骤1、连续时间信号的卷积运算首先在MATLAB软件中定义两个连续时间信号,如下所示:t1 = 0:0.1:10;x1 = sin(2*pi*5*t1); % 正弦波信号t2 = 0:0.1:10;x2 = exp(-(t2-5).^2); % 高斯脉冲信号然后,使用conv函数进行卷积运算,并绘制出卷积后的信号图像。
x3 = conv(x1,x2,'same'); % 卷积运算figure; % 绘制卷积后的信号图像subplot(3,1,1);plot(t1,x1);xlabel('时间/s');ylabel('幅值');title('正弦波信号');subplot(3,1,2);plot(t2,x2);xlabel('时间/s');ylabel('幅值');title('高斯脉冲信号');subplot(3,1,3);plot(t1,x3);xlabel('时间/s');ylabel('幅值');title('卷积信号');2、信号在频域的频谱特征首先,通过fft函数对于时间域信号进行傅里叶变换,获取其频域表示。
如何通过Matlab进行卷积与卷积运算

如何通过Matlab进行卷积与卷积运算使用Matlab 进行卷积与卷积运算引言:卷积与卷积运算在信号处理、图像处理、机器学习等领域中起着至关重要的作用。
Matlab作为一款强大的数学工具,提供了丰富的函数和工具箱,能够便捷地进行卷积与卷积运算。
本文将介绍如何使用Matlab进行卷积与卷积运算,并通过实例说明其应用。
一、卷积的基本概念卷积是一种数学运算,常用于信号处理中。
它将两个函数进行混合,输出一个新的函数。
在离散卷积中,输入的两个函数通常是序列或矩阵。
卷积的定义如下:[f * g](n) = ∑[f(k) * g(n-k)] (k=-∞ to ∞)其中,f * g 表示卷积运算,f 表示输入函数,g 表示卷积核函数,n 表示输出函数的索引。
二、Matlab中的卷积函数在Matlab中,可以使用conv函数来进行一维离散卷积的计算。
conv函数的语法如下:y = conv(x,h)其中,x 表示输入函数,h 表示卷积核函数,y 表示输出函数。
在使用conv函数时,需要注意输入函数和卷积核函数的维度匹配,以及输入函数和卷积核函数的长度关系。
在长度不一致的情况下,可以使用padarray函数进行填充。
三、卷积运算的应用举例为了更好地理解卷积与卷积运算的应用,下面将通过几个实例进行详细讲解。
实例一:图像模糊图像模糊是一种常见的图像处理技术,可以用于去除图像中的噪声和细节。
在Matlab中,可以通过卷积运算实现图像模糊。
首先,需要构建一个卷积核函数,例如:h = ones(5, 5) / 25;此处构建了一个5x5的全1卷积核函数,并将其除以25,以实现平均模糊。
然后,使用conv函数对输入图像进行卷积运算:blurred_image = conv(input_image, h);实例二:音频信号滤波在音频处理中,常常需要对音频信号进行滤波以去除噪声或者强调特定频率。
卷积运算可以实现各种滤波器的设计和应用。
MATLAB信号卷积

利用MATLAB实现信号的时域卷积一.引言MATLAB具有强大的图形处理功能及符号运算功能,为实现信号的可视化以及时域分析提供了强有力的工具,所以我们要利用MATLAB编程辅助分析与计算。
现在我们利用MATLAB 编程辅助计算连续时间信号、离散时间信号的卷积。
我们利用MATLAB编制一个M函数dconv(),该函数可以计算离散序列x1n 和x2n的卷积xn=x1n*x2n,此程序要计算xn,返回xn的非零点对应向量,还将绘制出序列x1n, x2n和xn 的时域波形图;我们要验证并调用这个dconv()函数计算“hn=xn=un-u(n-4)”这两个序列的卷积和运算,并绘制图像。
现在我们再利用MATLAB编制一个计算连续时间信号卷积积分的M函数ddconv(),此函数要计算出两个连续信号f1(t)和f2(t)的卷积积分f (t)的近似值,并绘制f1(t)、f2(t)和f (t)的时域波形图。
编完之后,我们利用ddconv()函数求“et=ut+12-ut-1,ht=12t[ut-ut-2]”这两个连续时间信号的卷积积分运算,并绘制图形。
二.基本原理对于信号的时域卷积有:(1)离散时间信号的卷积和:它的定义为,离散时间信号x1n和x2n的卷积和为:xn=x1n*x2n=m=-∞∞x1(m)x2n-m设序列x1n在区间n1~ n2非零,序列x2n在m1~ m2非零,那么就有xn=x1n*x2n的非零区间就为n1+m1~(n2+m2)并且区间长度为n1+m1-n2+m2+1,则只需计算序列xn的非零区间就可以表示整个序列.那么由上可知,在利用MATLAB的conv()函数的时候就要注意其卷积后的区间长度已经发生变化,在绘制卷积后的图像的时候就要有意识的先减去扩大的区间长度,不然绘制的卷积后的时域图像就是错误的,和横坐标不是正确的对应关系,并且我们在使用conv()函数的时候要先构造x1n和x2n,让它们有限,才能返回序列xn的非零样值时间序列。
MATLAB信号卷积

利用MATLAB实现信号的时域卷积一.引言具有强大的图形处理功能及符号运算功能,为实现信号的可视化以及时域分析提供了强有力的工具,所以我们要利用编程辅助分析与计算。
现在我们利用编程辅助计算连续时间信号、离散时间信号的卷积。
我们利用编制一个M 函数,该函数可以计算离散序列和的卷积,此程序要计算,返回的非零点对应向量,还将绘制出序列,和的时域波形图;我们要验证并调用这个函数计算“”这两个序列的卷积和运算,并绘制图像。
现在我们再利用MATLAB编制一个计算连续时间信号卷积积分的M 函数,此函数要计算出两个连续信号和的卷积积分的近似值,并绘制、和的时域波形图。
编完之后,我们利用函数求“”这两个连续时间信号的卷积积分运算,并绘制图形。
二.基本原理对于信号的时域卷积有:(1)离散时间信号的卷积和:它的定义为,离散时间信号和的卷积和为:页脚内容1设序列在区间非零,序列在非零,那么就有的非零区间就为并且区间长度为,则只需计算序列的非零区间就可以表示整个序列.那么由上可知,在利用的函数的时候就要注意其卷积后的区间长度已经发生变化,在绘制卷积后的图像的时候就要有意识的先减去扩大的区间长度,不然绘制的卷积后的时域图像就是错误的,和横坐标不是正确的对应关系,并且我们在使用函数的时候要先构造和,让它们有限,才能返回序列的非零样值时间序列。
对于连续的时间信号和的卷积积分其定义为:那么可以用分段求和来实现,即:令则有当足够小的时候,的结果就是连续时间信号的较好的近似值。
所以当用MATLAB 实现和的卷积积分的时候要先对和以的间隔进行采样,得到它们的离散序列和,构造它们相应的时间向量;调用系统的函数计算卷积,计算的近似页脚内容2值;最后构造的时间向量,并用命令将波形图画出来。
三.实现方法(1)先编制一个M函数dconv(),能是实现两个序列的卷积和,并绘制这两个序列的时域波形图和卷积之后的波形图。
编程思路如框图1:对应好卷积后的时间向量,用框图1程序如下所示:function xn=dconv(x1,x2) %任意两序列卷积x11=-5:length(x1)-6; %设定x1(n)的时间向量页脚内容3x22=-5:length(x2)-6; %设定x2(n)的时间向量subplot(131),stem(x11,x1,’fill’),grid on; %画x1(n)的图像title('x1(n)=u(n)-u(n-4)');xlabel('n');ylabel('x(n)');set(gca,'xtick',-20:20);axis([(min(x11)-1),(max(x11)+1),(min(x1)-1),(max(x1)+1)]) subplot(132),stem(x22,x2,’fill’),grid on; %画x2(n)的图像title('x2(n)=u(n)-u(n-4)');xlabel('n');ylabel('x(n)');set(gca,'xtick',-20:20);axis([(min(x22)-1),(max(x22)+1),(min(x2)-1),(max(x2)+1)]) xmin1=min(x11);xmax1=max(x11);xmin2=min(x22);xmax2=max(x22);t=(xmax2+xmax1)-(xmin2+xmin1)+1;页脚内容4页脚内容5xx=-10:(t-6-5); %设定x(n)的时间向量 xn=conv(x1,x2) %求x(n)=x1(n)*x2(n)subplot(133),stem(xx,xn,’fill ’),grid on; %画x(n)的图像title('x(n)=x1(n)*x2(n)') xlabel('n'); ylabel('x(n)');set(gca,'xtick',-100:100);axis([(min(xx)+5),(max(xx)-7),(min(xn)-0.5),(max(xn)+0.5)]) end(2)再编制一个M 函数ddconv(n),求两个连续时间信号的卷积,能是实现两个连续信号的卷积和,并绘制这两个信号的时域波形图和卷积之后的波形图。
实验四-使用matlab实现卷积的运算

实验四-使用m a t l a b实现卷积的运算(总5页)-本页仅作为预览文档封面,使用时请删除本页-实验四 使用matlab 实现卷积的运算一 实验目的1、学习MATLAB 语言的编程方法及熟悉MATLAB 指令; 2、深刻理解卷积运算,利用离散卷积实现连续卷积运算; 二 实验内容1、 完成)(1t f 与)(2t f 两函数的卷积运算其中:)4()()(),()(221--==-t u t u t f t u e t f t 在一个图形窗口中,画出)(1t f 、)(2t f 以及卷积结果。
要求每个坐标系有标题、坐标轴名称。
p = ; %定义时间间隔t= 0:p:10;%定义时间向量f1=exp(-2*t).*u(t); %将f (t )表示出来f2=u(t)-u(t-4);f=conv(f1,f2);subplot(1,2,1);plot(t,f1,t,f2); title('f1=e^-2t*u(t)'' / ''f2=u(t)-u(t-4)');xlabel('t(sec)'); % 这行代码是给出x 坐标的标签ylabel('f(t)');grid on ;subplot(1,2,2);plot(f); title('f=f1*f2');xlabel('t(sec)'); % 这行代码是给出x 坐标的标签ylabel('f')grid on2、 若系统模型为:)(3)()(4)(4)(''''t f t f t y t y t y +=++ 其中 )()(t u e t f t -=求零状态响应,画出波形(函数本身画出一幅图,自己再画出一幅输入波形图)。
零状态响应:a= [1 4 4]; %将y (t )各阶导数的系数放在向量a 中b= [1 3]; %将f (t )各阶导数的系数放在向量b 中sys = tf(b, a); %求系统函数systd = ; %定义时间间隔t = 0 : td : 10; %定义时间向量f = exp(-t).*u(t); %将f (t )表示出来y = lsim(sys, f, t); %求系统的零状态响应yplot(t, y); %绘出零状态响应的波形xlabel('t(sec)'); % 这行代码是给出x 坐标的标签ylabel('y(t)'); % 这行代码是给出y 坐标的标签grid on输入波形图:a= [1 4 4]; %将y(t)各阶导数的系数放在向量a中b= [1 3]; %将f(t)各阶导数的系数放在向量b中sys = tf(b, a); %求系统函数systd = ; %定义时间间隔t = 0 : td : 10; %定义时间向量f = exp(-t).*u(t);plot(t,f);xlabel('t(sec)'); % 这行代码是给出x坐标的标签ylabel('f(t)');grid on三 实验原理:1、 离散卷积和:调用函数:conv ()∑∞-∞=-==i i k f i f f f conv S )()(1)2,1(为离散卷积和, 其中,f1(k), f2 (k) 为离散序列,K=…-2, -1, 0 , 1, 2, …。
实验三 信号卷积的MATLAB实现

实验三信号卷积的MATLAB实现一、实验名称:信号卷积的MATLAB实现二、实验目的:1.增加学生对卷积的认识2.了解MATLAB这个软件的一些基础知识3.利用MATLAB计算信号卷积4.验证卷积的一些性质三、实验原理:用MATLAB实现卷积我们先必须从信号下手,先把信号用MATLAB语句描述出来,然后再将这些信号带入到我们写好的求卷积的函数当中来计算卷积。
在本章中我们将信号分为连续信号和离散序列两种来实现卷积并验证卷积的一些性质。
MATLAB强大的图形处理功能及符号运算功能,为我们实现信号的可视化提供了强有力的工具。
在MATLAB中通常有两种方法来表示信号,一种是用向量来表示信号,另一种则是用符号运算的方法来表示信号。
用适当的MATLAB 语句表示出信号后,我们就可以利用MATLAB的绘图命令绘制出直观的信号波形。
连续时间信号,是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干不连续点以外,信号都有确定的值与之对应的信号。
从严格意义上来讲,MATLAB并不能处理连续信号,在MATLAB中,是用连续信号在等时间间隔点的样值来近似地表示连续信号的,当取样时间间隔足够小时,这些离散的样值就能较好地近似出连续信号。
在MATLAB中连续信号可用向量或符号运算功能来表示。
1.向量表示法对于连续时间信号f(t),我们可以用两个行向量f和t来表示,其中向量t是行如t=t1:p:t2的MATLAB命令定义的时间范围向量,t1为信号起始时间,t2为中止时间,p为时间间隔。
向量f为连续信号f(t)在向量t所定义的时间点上的样值。
例如对于连续信号f(t)=sin(t),我们可以用如下两个向量来表示:t=-10:1.5:10;f=sin(t)用上述向量对连续信号表示后,就可以用plot命令来绘出该信号的时域波形。
Plot命令可将点与点间用直线连接,当点与点间的距离很小时,绘出的图形就成了光滑的曲线。
命令如下:plot(t,f)title(‘f(t)=sint’)xlabel(‘t’)axis([-10,10,-1.1,1.1])绘制的信号波形如图3.1所示,当把时间间隔p取得更小(如0.01)时,就可得到sint较好的近似波形,如图3.2所示。
用MATLAB实现信号的时域卷积

用MATLAB 实现信号的时域卷积摘要:利用抽样方法绘制连续信号和离散信号.编制函数计算连续时间信号,离散时间信号的卷积.关键字:MATLAB ;离散卷积;连续卷积实验原理:卷积运算在信号与系统分析中具有非常重要的意义,是信号与系统分析的基本方法之一.线性是不变系统的零状态响应就可以通过求解驶入激励信号与系统单位冲击响应的卷积运算获得.在连续时间系统中,卷积运算成为卷积积分,表示为在离散时间系统中,卷积运算称为卷积和,表示为:实验任务与实现方法:⑴ 编制计算离散时间序列卷积核的M 函数()dconv ,该函数课计算两离散序列()n x 1和()n x 2的卷积和()()()n x n x n x 21*=.程序计算出卷积和()n x 的同时,还绘制出序列()n x 1、()n x 2和()n x 的时域波形图,并返回()n x 的非零样值点的对应向量.任务〔1〕程序:function dconv<x1,x2,y1,y2>%任意两序列卷积x1=input<'请输入x1='>;x2=input<'请输入x2='>;y1=input<'请输入y1='>;y2=input<'请输入y2='>;subplot<131>,stem<x1,y1>,gridon ,title<'y1'>,axis<[<min<x1>-1>,<max<x1>+1>,<min<y1>-1>,<max<y1>+1>]>subplot<132>,stem<x2,y2>,gridon ,title<'y2'>,axis<[<min<x2>-1>,<max<x2>+1>,<min<y2>-1>,<max<y2>+1>]>%_____________________________________________xmin1=min<x1>;xmax1=max<x1>;xmin2=min<x2>;xmax2=max<x2>;t=<xmax2+xmax1>-<xmin2+xmin1>+1;xx=0:<t-1>;ft=conv<y1,y2>subplot<133>,stem<xx,ft>,grid on ,title<'*'>axis<[<min<xx>+0.5>,<max<xx>+0.5>,<min<ft>-0.5>,<max<ft>+0.5>]>⑵ 调用()dconv 来完成下面两离散序列的卷积和运算,并绘制图形:任务〔2〕程序:function f=ddconv<m1,m2>%-----------------------------%离散序列1t1=m1-5;t2=m1+5;t=t1:t2; %横坐标n=length<t>;tt=t1:m1; %起始到跳变n1=length<tt>;f1=[zeros<1,n1-1>,ones<1,n-n1+1>];%subplot<141>,stem<t,f1>,grid on,title<'阶跃函数序列 u<n-m1> '>,axis<[t1 t2 -0.2 1.5]>%-------------------------------%离散序列2p1=m1-5;p2=m1+5;p=p1:p2; %横坐标z=length<p>;pp=p1:m2; %起始到跳变z1=length<pp>;f2=[zeros<1,z1-1>,ones<1,z-z1+1>];%subplot<142>,stem<p,f2>,grid on,title<'离散阶跃序列 u<n-m2> '>,axis<[p1 p2 -0.2 1.5]>%------------------------------------%两离散序列相减k=min<min<t>,min<p>>:max<max<t>,max<p>>; %共同横坐标s1=zeros<1,length<k>>;s2=s1;s1<find<<k>=min<t>>&<k<=max<t>>==1>>=f1;s2<find<<k>=min<p>>&<k<=max<p>>==1>>=f2;f=s1-s2;subplot<131>,stem<k,f>,grid on,title<'x<n>=u<n>-u<n-4>'>axis<[<min<min<t>,min<p>>-1>,<max<max<t>,max<p>>+1>,<min<f>-0.5>,<max <f>+0.5>]>subplot<132>,stem<k,f>,grid on,title<'h<n>=u<n>-u<n-4>'>axis<[<min<min<t>,min<p>>-1>,<max<max<t>,max<p>>+1>,<min<f>-0.5>,<max <f>+0.5>]>%----------------------------xmin1=min<k>;xmax1=max<k>;xmin2=min<k>;xmax2=max<k>;t=<xmax2+xmax1>-<xmin2+xmin1>+1;xx=0:<t-1>;ft=conv<f,f>subplot<133>,stem<xx,ft>,grid on,title<'h<n>*x<n>'>axis<[<min<xx>+0.5>,<max<xx>+0.5>,<min<ft>-0.5>,<max<ft>+0.5>]>⑶编制计算连续时间信号卷积积分的M函数()sconv,该函数在计算出两信号()t f1和()t f 2的卷积积分()t f的数值近似的同时,还绘制出()t f1、()tf2和()t f的时域波形图. 实现方法:与第〔4〕任务用同一个程序.⑷调用函数()sconv来完成下面两连续时间信号的卷积积分运算,并绘制图形:()()121--⎪⎭⎫⎝⎛+=tutut e,()()()[]221--=tututth任务〔3、4〕程序:function sconv<>%u<t>m1=0;t1=m1-10;t2=m1+10;t=t1:0.01:t2;n=length<t>;tt=t1:0.01:m1;n1=length<tt>;f1=[zeros<1,n1-1>,ones<1,n-n1+1>];%subplot<131>,plot<t,f1>,grid on,title<'ÀëÉ¢½×Ô¾ÐòÁÐ u<t> '>,axis<[t1 t2 -0.2 1.5]>%u<t+1/2>tx1=t-1/2;fx1=f1;%subplot<241>,stairs<tx1,fx1>,grid on,title<' u<t+1/2> '>,axis<[t1 t2 -0.2 1.5]>%u<t-1>tx2=t+1;fx2=f1;%subplot<242>,stairs<tx2,fx2>,grid on,title<' u<t-1> '>,axis<[t1 t2 -0.2 1.5]>k=min<min<tx1>,min<tx2>>:0.01:max<max<tx1>,max<tx2>>;s1=zeros<1,length<k>>;s2=s1;s1<find<<k>=min<tx1>>&<k<=max<tx1>>==1>>=fx1;s2<find<<k>=min<tx2>>&<k<=max<tx2>>==1>>=fx2;e=s1-s2;subplot<131>,stairs<k,e>,grid on,title<'e<t>=u<t+1/2>-u<t-1>'>axis<[<min<min<tx1>,min<tx2>>+5>,<max<max<tx1>,max<tx2>>-5>,<min<e>-0 .5>,<max<e>+0.5>]>tx3=t;fx3=f1;%subplot<243>,stairs<tx3,fx3>,grid on,title<' u<t> '>,axis<[t1 t2 -0.2 1.5]>tx4=t+2;fx4=f1;%subplot<244>,stairs<tx4,fx4>,grid on,title<' u<t-2> '>,axis<[t1 t2 -0.2 1.5]>k1=min<min<tx3>,min<tx4>>:0.01:max<max<tx3>,max<tx4>>;s3=zeros<1,length<k1>>;s4=s1;s3<find<<k1>=min<tx3>>&<k1<=max<tx3>>==1>>=fx3;s4<find<<k1>=min<tx4>>&<k1<=max<tx4>>==1>>=fx4;h=s3-s4;%subplot<236>,stairs<k1,h>,grid on,title<' u<t>-u<t-2>'>%axis<[<min<min<tx3>,min<tx4>>+5>,<max<max<tx3>,max<tx4>>-5>,<min<h>-0.5>,<max<h>+0.5>]>h<t>=1/2*t*[u<t>-u<t-2>]kk1=length<k1>;ont=0:0.01:kk1;ks=min<min<k1>,min<ont>>:0.01:max<max<k1>,max<ont>>;s5=zeros<1,length<ks>>;s6=s5;s5<find<<ks>=min<ont>>&<ks<=max<ont>>==1>>=ont;s6<find<<ks>=min<k1>>&<ks<=max<k1>>==1>>=h;ffu=1/2*<s5.*s6>;subplot<132>,stairs<ks,ffu>,grid on,title<'1/2*t*[u<t>-u<t-2>]'>axis<[-5,5,<min<ffu>-0.5>,<max<ffu>+0.5>]>xmin1=min<k>;xmax1=max<k>;xmin2=min<ks>;xmax2=max<ks>;ttx=<xmax2+xmax1>-<xmin2+xmin1>+0.01;xx=0:0.01:<ttx-0.01>;ft=conv<e,ffu>;subplot<133>,stairs<xx,ft>,grid on,title<'h<n>*x<n>'>axis<[15,55,<min<ft>-0.5>,<max<ft>+0.5>]>实验总结:通过本次实验学会了用MATLAB实现线性系统的时域分析.能自己完成的东西一定要自己独立完成,这样收获的东西才是自己的.。
连续时间信号在MATLAB中的运算

课程名称:MATLAB 实验实 验 目 的:学会运用MATLAB 进行连续信号的时移、反折和尺度变换;学会运用MATLAB 进行连续信号的相加、相乘运算;学会运用MATLAB 数值计算方法求连续信号的卷积。
实 验 环 境:硬件:PC 机,Inter (R )Core (TM )i5-4210U CPU @1.7GHz ,内存4G ;软件:Matlab 版本2013b实 验 内 容 及 过 程:1、试用MATLAB 命令绘制信号/2()sin(10)sin(9)t t f t e t e t ππ--=+的波形图。
2、已知信号()()(1)(1)[(1)()]f t u t u t t u t u t =--+-+-,画出()f t 、(2)f t +、()f t -、(21)f t -+的波形。
3、求信号1()()(2)f t u t u t =--与2()()(1)(2)(3)f t u t u t u t u t =+-----的卷积结果12()()*()f t f t f t =,并画出12(),()f t f t 和()f t 的波形。
4、求信号1()(0.5)(0.5)f t u t u t =+--与自身的卷积结果11()()*()f t f t f t =,并画出1()f t 和()f t 的波形。
实验结果及分析:卷积就是进行反转,平移,但信号又是连续的,通过时间间隔取足够小的离散时间信号的数值计算方法来实现,间隔越小,卷积的结果图像越接近真实的图像。
实验心得:根据例子,之后在自己写,去了解一些函数,比如subplot(3,2,4),三行两列,第四个位置(第二行第一个)subplot(3,2,[4,6])第四,五,六个位置合成整体(第二行合成一行)。
多去网上找一些例子来实践,尽量是编成函数文件,并且可移植性强,加上注释之类的。
方便下次的使用。
MATLAB实验一连续时间信号在Matlab中的运算

实验一连续时间信号在Matlab中的运算一、实验目的1、学会运用Matlab进行连续时间信号的时移、反褶和尺度变换;2、学会运用Matlab进行连续时间信号微分、积分运算;3、学会运用Matlab进行连续时间信号相加、相乘运算;4、学会运用Matlab进行连续时间信号卷积运算..二、实验原理及实例分析1、信号的时移、反褶和尺度变换信号的平移、反转和尺度变换是针对自变量时间而言的;其数学表达式和波形变换中存在着一定的变化规律..从数学表达式上来看;信号的上述所有计算都是自变量的替换过程..所以在使用Matlab进行连续时间信号的运算时;只需要进行相应的变量代换即可完成相关工作..2、连续时间信号的微分和积分符号运算工具箱有强大的积分运算和求导功能..连续时间信号的微分运算;可使用diff命令函数来完成;其语句格式为:difffunction; ‘variable’;n其中;function表示需要进行求导运算的函数;或者被赋值的符号表达式;variable为求导运算的独立变量;n为求导阶数;默认值为一阶导数..连续时间信号积分运算可以使用int命令函数来完成;其语句格式为:intfunction; ‘variable’; a; b其中;function表示被积函数;或者被赋值的符号表达式;variable为积分变量;a为积分下限;b为积分上限;a和b默认时则求不定积分..3、信号的相加和相乘运算信号的相加和相乘是信号在同一时刻取值的相加和相乘..因此Matlab对于时间信号的相加和相乘都是基于向量的点运算..4、连续信号的卷积运算卷积积分是信号与系统时域分析的重要方法之一..定义为:⎰+∞∞-=*=-2121d )t (f )(f )t (f )t (f )t (f τττMatlab 进行卷积计算可通过符号运算方法和数值计算方法实现.. 1Matlab 符号运算法求连续信号卷积从卷积定义出发;可以利用Matlab 符号运算法求卷积积分;但要注意积分变量和积分限的选取..例:试用Matlab 符号运算法求卷积yt=ut-ut-1*ut-ut-1..2Matlab 数值计算法求连续信号的卷积例:试用Matlab 数值计算法求信号)2t (u )t (u )t (f 1--=和)t (u e )t (f 3t2-=的卷积..三、实验内容1、已知信号的波形课本P11例题;画出()()()()2332----tftftftf,,,的波形图..2、使用微分命令求xsinxlnxy=关于变量x的一阶导数;使用积分命令计算不定积分dxxaxx⎰⎪⎪⎭⎫⎝⎛+-225;定积分()dxxxe x⎰+121..Hz f 12=Ω=π3、已知()()()t t f t t f Ω=Ω=8sin ,sin 21;使用命令画出两信号和及两信号乘积的波形图..其中;4、。
实验2 连续时间信号在MATLAB中的运算

信息工程学院实验报告学会运用MA TLAB 进行连续信号的时移、反折和尺度变换;学会运用MATLAB 进行连续信号的相加、相乘运算;学会运用MATLAB 数值计算方法求连续信号的卷积。
实 验 环 境:Windows 7 MATLAB7.1实 验 内 容 及 过 程:4.1 试用MATLAB 命令绘制信号/2()sin(10)sin(9)tt f t e t et ππ--=+的波形图。
4.2 已知信号()()(1)(1)[(1)()]f t u t u t t u t u t =--+-+-,画出()f t 、(2)f t +、()f t -、(21)f t -+的波形。
4.3 求信号1()()(2)f t u t u t =--与2()()(1)(2)(3)f t u t u t u t u t =+-----的卷积结果12()()*()f t f t f t =,并画出12(),()f t f t 和()f t 的波形。
4.4 求信号1()(0.5)(0.5)f t u t u t =+--与自身的卷积结果11()()*()f t f t f t =,并画出1()f t 和()f t 的波形。
4.1、MATLAB 源程序为:clear; clc;t=-2:0.001:3;ft=exp(-t).*sin(10*pi*t)+exp((-t)/2).*sin(9*pi*t); plot(t,ft);grid on axis([-2 3 -2 2]); title('f(t)波形图');波形图如图T2-1所示:图T2-1 4.2、MATLAB源程序为:clear;clc;t=-3:0.01:4;ft1=funct1(t);ft2=funct1(t+2);ft3=funct1(-t);ft4=funct1(-2*t+1);subplot(221)plot(t,ft1);grid ontitle('f(t)');axis([-2 3 -2.5 1.5]);subplot(222)plot(t,ft2);grid ontitle('f(t+2)');axis([-4 3 -2.5 1.5]);subplot(223)plot(t,ft3);grid ontitle('f(-t)');axis([-3 4 -2.5 1.5]);subplot(224)plot(t,ft4);grid ontitle('f(-2*t+1)');axis([-2 3 -2.5 1.5]); 波形图如图T2-2所示:图T2-24.3、MATLAB源程序为:clear;clc;dt = 0.01; t = -1:dt:3.5;f1 = uCT(t)- uCT(t-2);f2 = uCT(t)+uCT(t-1)-uCT(t-2)-uCT(t-3);f = conv(f1,f2)*dt;n =length(f);tt = (0:n-1)*dt-2;subplot(221), plot(t,f1),grid on;axis([-1, 3.5, -0.2,1.2]);title('f1(t)'); xlabel('t');subplot(222), plot(t,f2),grid on;axis([-1, 3.5, -0.2,2.2]);title('f2(t)'); xlabel('t');subplot(212), plot(tt,f),grid on;title('f(t)=f1(t)*f2(t)'); xlabel('t');波形图如图T2-3所示:图T2-34.4、MATLAB源程序为:clear;clc;dt = 0.01; t = -2:dt:2.5;f1 = uCT(t+0.5)- uCT(t-0.5);f = conv(f1,f1)*dt;n =length(f);tt = (0:n-1)*dt-2;subplot(211), plot(t,f1),grid on;axis([-2, 2.5, -0.2,1.2]);title('f1(t)'); xlabel('t');subplot(212), plot(tt,f),grid on;title('f(t)=f1(t)*f1(t)'); xlabel('t'); 波形图如图T2-4所示:图T2-4阅读与思考:MATLAB运算符中.*和* 的区别?可结合例子说明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续时间信号卷积运算的MATLAB 实现
一、实验目的
(1) 理解掌握卷积的概念及物理意义。
(2) 理解单位冲击响应的概念及物理意义。
二、实验原理
根据前述知识,连续信号卷积运算定义为
1212()()()()()f t f t f t f f t d τττ∞
-∞
=*=-⎰
卷积计算可以通过信号分段求和来实现,即
1212120
()()()()()lim
()()k f t f t f t f f t d f k f t k τττ∞
∞
-∞
∆→=-∞
=*=-=ƥ-ƥƷ
⎰
如果只求当t n =∆(n 为整数)时()f t 的值()f n ∆,则由上式可得
1212()()()()[()]k k f n f k f n k f k f n k ∞
∞
=-∞
=-∞
∆=∆•
∆•∆-∆=∆•
ƥ-Ʒ
∑
上式中的
12()[()]k f k f n k ∞
=-∞
ƥ-Ʒ
实际上就是连续信号1()f t 和2()f t 经等时间间隔∆均
匀抽样的离散序列1()f k ∆和2()f k ∆的卷积和。
当∆足够小时,()f n ∆就是卷积积分的结果——连续时间信号()f t 的较好的数值近似。
例题:1()t t-1f t εε=()-(),21
()()t t-22
f t R t εε=
*【()-()】
,利用matlab 绘出其卷积波形; 理论分析如下:
当0t <时,12()()()0f t f t f t =*=
当01t <<时,2
120()()()1()24
t
t
t f t f t f t dt τ-=*=•-
=⎰ 当12t <<时,1
120
1
()()()1()2
24
t
t f t f t f t dt τ-=*=
•-
=
-⎰
当23t <<时,21
12t-23()()()1()2424
t
t t f t f t f t dt τ-=*=•-
=-++⎰ 当3t >时,12()()()0f t f t f t =*= 手工绘图如下:
三、仿真
1、源程序
调用函数sconv编辑如下:
调用函数heaviside编辑如下:
主函数编辑如下:
2、图形
运行matlab后,图形如下:
四、结论
通过本次实验理解掌握了卷积的概念及物理意义。
运用基本的matlab语言即可编写成功。
整体思路是这样的:首先是要对函数进行离散化处理,编写sconv()函数与heaviside (),然后再在主函数中调用sconv()函数与heaviside()。
在编写程序其间,掌握了matlab
的一些基本语言,学会了试用matlab对卷积进行仿真,收获很大。
例题9-2 设信号
()(1)(2)(2)2
t
f t t t εε=++-【-】,试用
MATLAB 求解
(2)()(2)()f t f t f t f t +-、、、-,画出相应的波形。
所用MATLAB 命令如下:
首先利用下列语句创建函数文件heaviside.m
然后再建立下列主程序hsys.m 并运行,结果如下图所示。
例9-4 已知两个连续时间信号图形如下:试用MATLAB 求12()()()f t f t f t =*,并绘出()f t 的时域波形图。
编辑主函数如下:
得到题目所给的图形,当p 足够小的时候函数sconv ()的计算结果就是连续时间卷积
12()()()f t f t f t =*的较好的数值近似,因而取p=0.01。
得到图形如下:
可见,当抽样时间p 足够小时,函数sconv ()的计算结果就是连续卷积12()()()f t f t f t =*的较好的数值近似。
