历届国际物理奥林匹克竞赛试题及解答
第1届国际物理奥林匹克竞赛试题与解答

第1届国际物理奥林匹克竞赛试题与解答(1967年于波兰的华沙)【题1】质量M=0.2kg 的小球静置于垂直柱上,柱高h=5m 。
一粒质量m=0.01kg 、以速度 0=500m/s 飞行的子弹水平地穿过球心。
球落在距离柱s =20m 的地面上。
问子弹落在地面何处?子弹动能中有多少转换为热能?解:在所有碰撞情况下,系统的总动量均保持不变:MV mv mv +=0其中v 和V 分别是碰撞后子弹的速度和小球的速度. 两者的飞行时间都是01.12==gh t s 球在这段时间沿水平方向走过20m 的距离,故它在水平方向的速度为:8.1901.120==V (m/s ) 由方程0.01×500=0.01v +0.2×19.8可求出子弹在碰撞后的速度为:v =104m/s子弹也在1.01s 后落地,故它落在与柱的水平距离为S =vt =104×1.01=105m 的地面上。
碰撞前子弹的初始动能为=2021mv 1250 J 球在刚碰撞后的动能为=221MV 39.2 J 子弹在刚碰撞后的动能为=221mv 54 J 与初始动能相比,两者之差为1250 J -93.2 J =1156.8 J这表明原来动能的92.5%被系统吸收而变为热能。
这种碰撞不是完全非弹性碰撞。
在完全弹性碰撞的情形下,动能是守恒的。
而如果是完全非弹性碰撞,子弹将留在球内。
【题2】右图(甲)为无限的电阻网络,其中每个电阻均为r ,求A、B两点间的总电阻。
解:如图(乙)所示 A、B两点间的总电阻应等于C、D两点间的总电阻与电阻r的并联,再与r串联 图(甲) 后的等效电阻。
如果网络是无限的,则A、B两点间的总电阻应等于C、D 两点间的总电阻,设为Rx 。
根据它们的串并联关系有:rR rR r R x x x ++= 图(乙)A B r r r r r r r r A B r rr r r r r r CD解上式可得: r R x 251+= 【题3】给定两个同样的球,其一放在水平面上,另一个以细线悬挂。
第1届国际物理奥林匹克竞赛试题与解答

第1届国际物理奥林匹克竞赛试题与解答(1967年于波兰的华沙)【题1】质量M=0.2kg 的小球静置于垂直柱上,柱高h=5m 。
一粒质量m=0.01kg 、以速度 0=500m/s 飞行的子弹水平地穿过球心。
球落在距离柱s =20m 的地面上。
问子弹落在地面何处?子弹动能中有多少转换为热能?解:在所有碰撞情况下,系统的总动量均保持不变:MV mv mv +=0其中v 和V 分别是碰撞后子弹的速度和小球的速度. 两者的飞行时间都是01.12==gh t s 球在这段时间沿水平方向走过20m 的距离,故它在水平方向的速度为:8.1901.120==V (m/s ) 由方程0.01×500=0.01v +0.2×19.8可求出子弹在碰撞后的速度为:v =104m/s子弹也在1.01s 后落地,故它落在与柱的水平距离为S =vt =104×1.01=105m的地面上。
碰撞前子弹的初始动能为=2021mv 1250 J 球在刚碰撞后的动能为=221MV 39.2 J 子弹在刚碰撞后的动能为=221mv 54 J 与初始动能相比,两者之差为1250 J -93.2 J =1156.8 J这表明原来动能的92.5%被系统吸收而变为热能。
这种碰撞不是完全非弹性碰撞。
在完全弹性碰撞的情形下,动能是守恒的。
而如果是完全非弹性碰撞,子弹将留在球内。
【题2】右图(甲)为无限的电阻网络,其中每个电阻均为r ,求A、B两点间的总电阻。
解:如图(乙)所示 A、B两点间的总电阻应等于C、D两点间的总电阻与电阻r的并联,再与r串联 图(甲) 后的等效电阻。
如果网络是无限的,则A、B两点间的总电阻应等于C、D 两点间的总电阻,设为Rx 。
根据它们的串并联关系有:rR rR r R x x x ++= 图(乙)A B r r r r r r r r A B r rr r r r r r CD解上式可得: r R x 251+= 【题3】给定两个同样的球,其一放在水平面上,另一个以细线悬挂。
物理奥林匹克竞赛题

物理奥林匹克竞赛题一、选择题(每题5分,共20分)1. 关于力的作用,下列说法正确的是:A. 力只能改变物体的形状,不能改变物体的运动状态B. 力只能改变物体的运动状态,不能改变物体的形状C. 力既能改变物体的形状,也能改变物体的运动状态D. 力既不能改变物体的形状,也不能改变物体的运动状态答案:C2. 在光滑的水平地面上,有一个质量为m的小球以速度v做匀速直线运动。
现给小球施加一个恒力F,使其在时间t内速度变为2v。
则该恒力F 的大小为:A. m(3v)/tB. m(2v)/tC. m(4v)/tD. m(5v)/t答案:C3. 关于电磁感应现象,下列说法正确的是:A. 只要闭合电路中的部分导体在磁场中运动,就一定会产生感应电流B. 只有当闭合电路中的部分导体在磁场中切割磁感线运动时,才会产生感应电流C. 只要穿过闭合电路的磁通量发生变化,就一定会产生感应电流D. 只有当闭合电路中的部分导体在磁场中做变速运动时,才会产生感应电流答案:C4. 关于光的折射现象,下列说法正确的是:A. 光从一种介质进入另一种介质时,传播方向一定会发生改变B. 光从空气进入水中时,传播速度会变大C. 光从水中射入空气时,折射角小于入射角D. 光在不同介质中传播时,其速度不变答案:A二、填空题(每题5分,共20分)5. 在自由落体运动中,若忽略空气阻力,物体下落的高度h与时间t的关系式为:h = _________。
答案:gt^2 / 26. 质量为m的物体以速度v在半径为R的圆周上做匀速圆周运动,则其所受向心力的大小为:F = _________。
答案:mv^2 / R7. 在一个闭合电路中,电源的电动势为ε,内阻为r,外电阻为R。
当外电阻R增大时,电路中的电流I将_________(填“增大”或“减小”)。
答案:减小8. 一束单色光从空气斜射到水面上,入射角为θ,折射角为γ。
若逐渐增大入射角θ,则折射角γ将_________(填“增大”或“减小”)。
奥林匹克物理竞赛试题及答案

奥林匹克物理竞赛试题及答案国际奥林匹克物理竞赛是国际中学生的物理大赛,高中同学可以用来提升物理解题能力。
下面店铺给大家带来奥林匹克物理竞赛试题,希望对你有帮助。
奥林匹克物理竞赛试题国际物理奥林匹克竞赛简介竞赛设立由参赛成员国组成的国际物理奥林匹克委员会。
竞赛章程规定:目的是为增进中学物理教学的国际交流,通过竞赛促进开展物理学科的课外活动,以加强不同国家青年之间的友好关系和人民间的相互了解合作。
同时帮助参赛者发展物理方面的创造力,把从学校学到的知识用于解决实际问题的能力。
国际物理奥林匹克竞赛每年举办一次。
由各会员国轮流主办,并由各代表团团长和一名主办国指定的主席组成国际委员会。
国际委员会的任务是公平合理地评卷,监督章程规定的执行情况,决定竞赛结果。
每一会员国可选派5名高中学生或技术学校学生参加竞赛。
参加者的年龄到竞赛开始的那一天不能超过20岁。
参赛代表队要有2名团长,2名团长是国际委员会的成员,条件是能胜任解答赛题,能参加竞赛试卷的讨论和评分工作,并能通晓一种国际物理奥林匹克的工作语言。
国际物理奥林匹克的工作语言是英文、法文、德文和俄文。
代表团到达主办国时,团长要将参加学生及团长的情况告诉主办国家组织人员。
竞赛于每年6月底举行。
竞赛分两天进行。
第一天进行3道理论计算题竞赛,另一天的竞赛内容是1—2道实验题。
中间有一天的休息。
参赛者可使用计算尺、不带程序编制的计算器和对数表、物理常数表和制图工具,但不能使用数学和物理公式一览表。
竞赛题由参加国提供题目,主办国命题。
在竞赛前,赛题要保密。
竞赛题内容包括中学物理的4个部分(力学、热力学和分子物理学、光学及原子和核物理学、电磁学) ,解题要求用标准的中等数学而不要用高等数学。
主办国提出评卷标准并指定评卷人。
每题满分为10分。
各代表团团长同时对自己团员竞赛卷的复制品进行评定,最后协商决定成绩。
评奖标准是以参赛者前三名的平均分数计为100%,参赛者达90% 以上者为一等奖,78—90%者为二等奖,65—78%者为三等奖,同时发给证书。
07历届国际物理奥林匹克竞赛试题与解答汇总

历届国际物理奥林匹克竞赛试题与解答第7届(1974年于波兰的华沙)【题1】一个处于基态的氢原子与另一个静止基态的氢原子碰撞。
问可能发生非弹性碰撞的最小速度为多少?如果速度较大而产生光发射,且在原速度方向可以观察到光。
问这种光的频率与简正频率相差多少?氢原子质量是1.67×10-27kg ,电离能E =13.6 eV =2.18×10-18 J 。
解:处于基态的氢原子能量为2111⋅-=E E ,第一激发态能量为2221⋅-=E E 。
被氢原子吸收的最小能量为18221210163.143)2111(-⨯==-=-=∆E E E E E J 我们必须求出在碰撞中能量损失为以上数据代最小速度。
如果碰撞是完全非弹性的,则碰撞中能量损失最大,碰撞后的速度将是v /2,初动能与末动能之差为:42)2(22222mv v m mv =- 这个值应等于最小的能量子42m v E =∆因此41026.64⨯=∆=mEv m/s 非弹性碰撞后,两个原子的速度为41013.32⨯=vm/s 本题第二问的解答与多普勒效应有联系。
对于比光速小很多的速度,相对速度之比给出频率相对变化的极好近似:6.26×104∶3×108=2.09×10-4=2.09×10-2 % 两束光的频率按此比率稍小于或稍大于简正频率。
【题2】给定一厚度为d 的平行平板,其折射率按下式变化rx n x n -=1)(0一束光在O 点由空气垂直射入平板,并在A 点以角度α射出,如图7.1所示。
求A 点的折射率n A ,并确定A 点的位置及平板的厚度。
(设n 0=1.2,r =13cm ,α=300) 解:首先考虑光的路线,如解图7.1所示。
对于经过一系列不同折射率的平行平板的透射光,可以应用斯奈尔 图7.1 定律:1221s i n s i n n n =ββ, 2332s i n s i n n n =ββ 更简单的形式是:===332211sin sin sin βββn n n …这个公式对任意薄层都是成立的。
2024国际物理奥林匹克竞赛试题

选择题一个质子和一个中子结合形成一个氘核时,会释放能量。
这一过程中,以下哪个物理量守恒?A. 质量B. 电荷量C. 质量与电荷量均守恒(正确答案)D. 仅有能量守恒在双缝干涉实验中,当光屏上某点到两缝的光程差为半个波长时,该点将出现:A. 明条纹B. 暗条纹(正确答案)C. 无法确定条纹明暗D. 既非明条纹也非暗条纹关于黑洞的视界,以下描述正确的是:A. 视界是黑洞内部与外部的分界线,物质和光可以穿越B. 视界是黑洞的“表面”,但实际上并不存在物理意义上的表面C. 视界内部的事件对外部观察者而言是不可见的(正确答案)D. 视界的大小与黑洞的质量无关在量子力学中,波函数的平方代表什么?A. 粒子的动量B. 粒子的位置C. 粒子在某处出现的概率密度(正确答案)D. 粒子的能量以下哪个现象不能用经典力学解释?A. 行星绕太阳的运动B. 电磁波的传播(正确答案)C. 炮弹的弹道D. 地球的自转在相对论中,当物体的速度接近光速时,以下哪个物理量将显著增加?A. 物体的质量(正确答案)B. 物体的体积C. 物体的密度D. 物体的电荷关于原子核的裂变,以下说法正确的是:A. 裂变过程中,原子核的总质量增加B. 裂变过程中,会释放大量的能量(正确答案)C. 裂变只能发生在重元素中,如铅D. 裂变是原子核自发分裂的过程,无需外部粒子轰击在电磁感应现象中,当导体在磁场中运动时,感应电流的方向由什么定律决定?A. 欧姆定律B. 库仑定律C. 楞次定律(正确答案)D. 法拉第电磁感应定律关于量子纠缠,以下哪个描述是正确的?A. 量子纠缠是经典物理中的常见现象B. 量子纠缠意味着两个粒子在任何时刻的状态都是完全相同的C. 量子纠缠的两个粒子之间,对其中一个粒子的测量会瞬间影响到另一个粒子的状态,无论它们相距多远(正确答案)D. 量子纠缠可以通过经典通信来复制和传递。
国际物理奥赛试题及答案

国际物理奥赛试题及答案一、选择题(每题3分,共30分)1. 光在真空中的速度是多少?A. 299,792,458 m/sB. 299,792,458 km/sC. 299,792,458 cm/sD. 299,792,458 mm/s答案:A2. 根据量子力学,一个粒子的波函数代表什么?A. 粒子的位置B. 粒子的速度C. 粒子的概率密度D. 粒子的能量答案:C3. 以下哪项不是电磁波的特性?A. 波长B. 频率C. 质量D. 能量答案:C4. 根据牛顿第三定律,作用力和反作用力的关系是什么?A. 相等且相反B. 相等且相同C. 不相等且相反D. 不相等且相同答案:A5. 热力学第一定律表述了什么?A. 能量守恒定律B. 熵增定律C. 热力学第二定律D. 热力学第三定律答案:A6. 一个物体在自由落体运动中,其加速度是多少?A. 9.8 m/s²B. 10 m/s²C. 11 m/s²D. 12 m/s²答案:A7. 以下哪种力不属于基本力?A. 重力B. 电磁力C. 强核力D. 弱核力答案:A8. 一个完全弹性碰撞中,动量守恒和能量守恒是否都成立?A. 是B. 否答案:A9. 光的双缝干涉实验中,干涉条纹的间距与什么有关?A. 光的波长B. 双缝间的距离C. 观察屏的距离D. 所有以上因素答案:D10. 根据相对论,时间膨胀和长度收缩的效应是否只发生在高速运动的物体上?A. 是B. 否答案:A二、填空题(每题2分,共20分)1. 光年是______单位,表示光在一年内通过的距离。
答案:长度2. 绝对零度是温度的下限,其数值为______开尔文。
答案:03. 一个物体的动能与其速度的平方成正比,其比例系数是______。
答案:1/24. 根据库仑定律,两个点电荷之间的力与它们电荷量的乘积成正比,与它们距离的平方成______。
答案:反比5. 根据麦克斯韦方程组,变化的磁场可以产生______。
物理奥林匹克竞赛试题

物理奥林匹克竞赛试题一. 选择题1. 下列哪个物理定律描述的是静电场中电势的变化情况?A. 波尔定律B. 焦耳定律C. 库伦定律D. 爱因斯坦关系式2. 在弹性碰撞中,除了动量守恒外,还满足下列哪个条件?A. 能量守恒B. 力守恒C. 加速度守恒D. 角动量守恒3. 下列哪个物理量描述的是物体转动的惯性?A. 质量B. 动量C. 力D. 速度4. 一颗质量为2kg的物体,以1m/s的速度和一颗质量为1kg的物体发生碰撞,碰撞后两物体的速度分别是2m/s和?A. 2m/sB. 3m/sC. 4m/sD. 5m/s5. 是谁提出了相对论?A. 爱因斯坦B. 牛顿C. 麦克斯韦D. 高斯二. 填空题1. 牛顿第一定律也被称为___________。
2. 牛顿第二定律的数学表达式是___________。
3. 下列哪个公式描述的是功的定义?功 = ___________4. 波长与频率的关系由___________定律描述。
5. 物体的密度等于物体的___________除以物体的体积。
三. 解答题1. 描述一下牛顿第三定律,并给出一个实际的例子。
2. 一台电视机的重量是500N,如果放在木板上,木板支持住了电视机的质量,木板对电视机的支持力是多大?3. 一辆汽车在匀加速的情况下行驶,初始速度为20m/s,加速度为2m/s²,求汽车在3秒后的速度和位移。
4. 一个质量为2kg的物体以4m/s的速度沿着光滑水平面运动,撞上了一面质量为5kg的墙壁并弹回,求墙壁对物体的冲量。
四. 应用题1. 一个物体从高度5m自由落下,假设匀加速度为10m/s²,求物体落地所需的时间以及落地时的速度。
2. 一个长为3m、宽为2m、高为1m的箱子,质量为100kg,求箱子的密度。
3. 有一根长为2m、质量为1kg的细杆,细杆的一个端点连接一个质量为1kg的小球,细杆另一端固定在墙上。
小球和杆组成一个单摆,求该单摆的周期。
第4届国际物理奥林匹克竞赛试题及解答.doc

第4届国际物理奥林匹克竞赛试题与解答(1970年于苏联的莫斯科)【题1】如图4.1(a )、(b ),在质量M =1kg 的木板上有质量m =0.1kg 的小雪橇。
雪橇上的马达牵引着一根绳子,使雪橇以速度v 0=0.1m/s 运动。
忽略桌面与木板之间的摩擦。
木板与雪橇之间的摩擦系数μ=0.02。
把住木板,起动马达。
当雪橇达到速度v 0时,放开木板。
在此瞬间,雪橇与木板端面的距离L =0.5m 。
绳子拴在(a )远处的桩子,(b )木板的端面上。
试描述两种情形下木板与雪橇的运动。
雪橇何时到达木板端面?图4.1(a ) 图4.1(b )解:(a )在第一种情形中(如图4.1(a )),雪橇处于匀速运动状态。
雪橇与木板以不同的速度运动。
这样引起的最大摩擦力为μ mg ,它作用在木板上,产生的加速度Mmga μ=,直至木板达到雪橇的速度v 0为止。
加速时间为mgMv a v t μ000===5.1s 在这段时间内,雪橇的位移为mgM v a v S μ2220200===0.255m 因此,雪橇离木板右端点的距离为 0.5m -0.255m =0.245m雪橇不能达到木板的一端,因为这段时间以后,木板与雪橇以相同的速度v 0一起运动。
在木板加速期间,马达必须用力μ mg 牵引绳子,但以后马达不能施加力的作用,它只是卷绳子。
(b )在第二种情形中(如图4.1(b )),木板与桌面之间无摩擦。
木板与雪橇形成一个孤立系统,可以用动量守恒定律。
当我们放开木板时,雪橇的动量为mv 0,释放后的木板具有速度v 2,它由下式决定: mv 0=M v 2+m (v 0+v 2)此式表明v 2=0,所以木板保持不动,雪橇以同一速度继续前进。
雪橇达到木板右端的时间为 1.05.00==v L t =5 s【题2】NaCl 的晶体点阵由边长为5.6×10-8cm 的立方晶胞组成,它是面心立方点阵。
钠原子量约为23,氯原子量为35.5,NaCl 密度为2.22g/cm 3。
第8届国际物理奥林匹克竞赛试题与解答

第 1 页 共 3 页第8届国际物理奥林匹克竞赛试题与解答(1975年于德意志民主共和国的居斯特罗)【题1】一根杆以恒定的角速度ω绕竖直轴旋转,杆与轴的夹角为(900-α)。
质量为m 的质点可以沿杆滑动,摩擦系数为μ 。
求转动过程中,质点保持在同一高度的条件(如图8.1)。
解:我们发现,采用所谓“滑动摩擦角”概念是有用的。
如果滑动摩擦系数等于某一角度的正切值,就称这个角ε为“滑动摩擦角”(如解图8.1所示),即tan ε=μ我们必须求出把物体压向平台的合力。
如果合力与平面法线之间的夹角在滑动摩擦角之内,则摩擦力大到足以阻止运动。
极限情形是合力与摩擦角的一臂重合。
对于本题,当我们寻找质点在旋转杆上向上滑动的极限情况时,合力应位于(α+ε)角的双臂内(如解图8.2所示)。
图8.1ε解图8.1 解图8.2把质点压在杆上的力是重力mg 与m ω2r =m ω2L cos α的合力。
故质点在向上滑动的极限情形下,角(α+ε)的正切为gL mg L m αωαωεαcos cos )tan(22==+ 同理,质点向下滑动的极限情形可用角(α+ε)的正切得到。
于是,如果)tan(cos )tan(2εααωεα+≤≤gL -则质点在旋转杆上处于平衡。
从边界条件可以看出,存在着一个较高位置(L f )和一个较低位置(L a ),质点在这两位置之间的任何地方将处于随遇解图8.3平衡状态。
在这两边界之外,质点无法平衡,质点将向上或向下滑动。
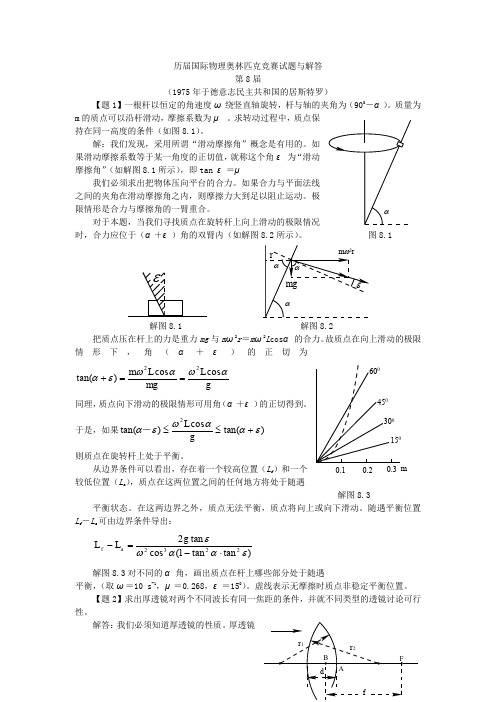
随遇平衡位置L f -L a 可由边界条件导出:)tan tan 1(cos tan 22232εααωε⋅-=-g L L a f 解图8.3对不同的α角,画出质点在杆上哪些部分处于随遇平衡,(取ω=10 s -1,μ=0.268,ε=150)。
虚线表示无摩擦时质点非稳定平衡位置。
【题2】求出厚透镜对两个不同波长有同一焦距的条件,并就不同类型的透镜讨论可行性。
0.10.20.3m 450600150300第 2 页 共 3 页解答:我们必须知道厚透镜的性质。
第3届国际物理奥林匹克竞赛试题与解答

第3届国际物理奥林匹克竞赛试题与解答【题1】右图的力学系统由三辆车组成,质量分别为m A =0.3kg ,m B =0.2kg ,m C =1.5kg 。
(a )沿水平方向作用于C 车的力F 很大。
使A 、B 两车相对C 车保持静止。
求力F 及绳子的张力。
(b )C 车静止,求A 、B 两车的加速度及绳子的张力。
(忽略阻力和摩擦力,忽略滑轮和车轮的转动惯量) 解:(a )A 、B 两车相对C 车保持静止,A 车在竖直方向没有加速度,因此它对绳的拉力为m A g 。
这个力使B 车得到加速度g m m a BAB =。
又三车系统以相同的加速度运动,则: g m m m m m F BAC B A )(++= 由给定的数值得:a B =a C =a A =1.5g =14.7m/s 2 绳中的张力为:T =m A g =2.94N 水平推力为:F =29.4N(b )如果C 车静止,则力m A g 使质量m A +m B 加速,加速度为:BA A AB m m gm a +==0.6g =5.88N绳中的张力为: T /=m A g -m A ×0.6g =1.176N【题2】在质量为m 1的铜量热器中装有质量为m 2的水,共同的温度为t 12;一块质量为m 3、温度为t 3的冰投入量热器中(如右图所示)。
试求出在各种可能情m 3c 3t 3形下的最终温度。
计算中t 3取负值。
铜的比热c 1=0.1kcal/kg·0C ,水的比热c 2=1kcal/kg·0C ,冰的比热c 3=0.5kcal/kg·0C ,冰的熔解热L =80kcal/kg 。
解:可能存在三种不同的终态:(a )只有冰;(b )冰水共存; (c )只有水。
(a )冰温度升高,但没有熔化,达到某一(负)温度t a ; 放出的热量和吸收的热量相等:c 3 m 3(t a -t 3)=(c 1 m 1+c 2 m 2)(t 12-t a )+m 2L 得出最终的温度为3332112333122211)(c m c m c m Lm t c m t c m c m t a +++++=(1)情况(a )的条件是t a <0(注:指00C ),如果上式的分子为负值,我们得到下列条件: (c 1 m 1+c 2 m 2)t 12<―c 3 m 3t 3―m 2L (2)(c )现在让我们讨论冰块全部熔化的情况。
历届国际物理奥林匹克竞赛试题与解答
历届国际物理奥林匹克竞赛试题与解答第8届(1975年于德意志民主共和国的居斯特罗)【题1】一根杆以恒定的角速度ω绕竖直轴旋转,杆与轴的夹角为(900-α)。
质量为m 的质点可以沿杆滑动,摩擦系数为μ 。
求转动过程中,质点保持在同一高度的条件(如图8.1)。
解:我们发现,采用所谓“滑动摩擦角”概念是有用的。
如果滑动摩擦系数等于某一角度的正切值,就称这个角ε为“滑动摩擦角”(如解图8.1所示),即tan ε=μ我们必须求出把物体压向平台的合力。
如果合力与平面法线之间的夹角在滑动摩擦角之内,则摩擦力大到足以阻止运动。
极限情形是合力与摩擦角的一臂重合。
对于本题,当我们寻找质点在旋转杆上向上滑动的极限情况时,合力应位于(α+ε)角的双臂内(如解图8.2所示)。
图8.1ε解图8.1 解图8.2把质点压在杆上的力是重力mg 与m ω2r =m ω2L cos α的合力。
故质点在向上滑动的极限情形下,角(α+ε)的正切为gL mg L m αωαωεαcos cos )tan(22==+ 同理,质点向下滑动的极限情形可用角(α+ε)的正切得到。
于是,如果)tan(cos )tan(2εααωεα+≤≤g L -则质点在旋转杆上处于平衡。
从边界条件可以看出,存在着一个较高位置(L f )和一个较低位置(L a ),质点在这两位置之间的任何地方将处于随遇解图8.3平衡状态。
在这两边界之外,质点无法平衡,质点将向上或向下滑动。
随遇平衡位置L f -L a 可由边界条件导出:)tan tan 1(cos tan 22232εααωε⋅-=-g L L a f 解图8.3对不同的α角,画出质点在杆上哪些部分处于随遇平衡,(取ω=10 s -1,μ=0.268,ε=150)。
虚线表示无摩擦时质点非稳定平衡位置。
【题2】求出厚透镜对两个不同波长有同一焦距的条件,并就不同类型的透镜讨论可行性。
解答:我们必须知道厚透镜的性质。
物理奥林匹克竞赛试题

1.在一个密闭容器中,有一定量的理想气体。
当容器体积减小时,气体的压强会如何变化?A.减小B.不变C.增大(答案)D.无法确定2.一个物体在地球表面受到的重力加速度是9.8米/秒²。
如果将该物体移到月球表面,它受到的重力加速度会:A.保持不变B.增大C.减小(答案)D.变为零3.光的色散现象是由于:A.光的波长不同(答案)B.光的速度不同C.光的强度不同D.光的方向不同4.一个物体做简谐振动,当它的位移达到最大时,它的:A.速度最大B.加速度最大(答案)C.动能最大D.势能最小5.在电路中,电阻、电感和电容对电流的作用分别是:A.阻碍、储存电能、产生磁场B.阻碍、产生磁场、储存电能(答案)C.储存电能、阻碍、产生磁场D.产生磁场、储存电能、阻碍6.一个物体在真空中自由下落,它下落的高度h与时间t的关系是:A.h = gt²(答案)(其中g为重力加速度)B.h = gtC.h = g/t²D.h = g/t7.光的干涉现象是:A.两束光相遇时互相抵消的现象B.两束光相遇时加强的现象C.两束相干光波叠加产生明暗相间的条纹的现象(答案)D.光在介质中传播速度改变的现象8.在量子力学中,描述微观粒子运动状态的函数是:A.波动函数(答案)B.概率函数C.密度函数D.分布函数9.一个物体在水平面上做匀速圆周运动,它的线速度与角速度的关系是:A.v = rω(答案)(其中v为线速度,r为半径,ω为角速度)B.v = r/ωC.v = ω/rD.v = r +ω。
ipho试题

ipho试题IPhO(国际物理奥林匹克竞赛)是一个为青年学生举办的国际性物理竞赛,旨在鼓励和促进对物理学的兴趣和研究。
每年,来自不同国家和地区的学生会参加这个竞赛,以展示他们的物理知识和解决问题的能力。
在本文中,我们将探讨一些IPhO试题,并解答它们。
第一道题:一名学生拿着一个装满水的容器站在电梯上。
当电梯上升或下降时,水面的高度会发生变化。
现在,假设该容器的底部水平面积为A,水柱高度变化为∆h。
试计算由于电梯上升而引起的水面受力的变化。
解答:根据万有引力定律,水面受到的重力为F = ρVg,其中ρ是水的密度,V是水的体积,g是重力加速度。
当电梯上升时,水面发生变化,导致水的位能增加。
根据能量守恒定律,水受力的变化应等于电梯升高所做的功。
首先,计算水的位能变化ΔE = mgh,其中m是水的质量,h是水的高度变化。
由于密度等于质量除以体积,我们可以得到m = ρV,将其带入上式得到ΔE = ρVgh。
因此,水受力的变化ΔF = ΔE/∆h = ρVg。
根据题意,我们可以将V = A∆h代入上式,得到ΔF = ρAg。
第二道题:一辆小汽车沿一条直线行驶,速度随时间的变化与时间的关系如图所示。
请计算:a) 小汽车的加速度在t = 4s时的数值。
b) 小汽车在t = 2s到t = 6s时间段内行驶的距离。
解答:a) 加速度可以通过速度与时间的变化率来计算。
在t = 4s时,速度的变化率可以通过速度-时间图上的斜率来确定。
在这种情况下,斜率为2 m/s²。
因此,小汽车在t = 4s时的加速度为2 m/s²。
b) 行驶的距离可以通过速度乘以时间的积分来计算。
在t = 2s到t = 6s时间段内,小汽车的速度保持不变,为4 m/s。
因此,小汽车行驶的距离为4 m/s乘以时间间隔6s减去2s,即24m。
第三道题:一束光通过一个狭缝后被分成两束光,然后再次聚合,产生干涉图案。
干涉图案中的亮条纹和暗条纹的产生原因是什么?当光通过狭缝时,存在哪些因素会影响干涉条纹的间距?解答:亮条纹和暗条纹的产生是由光的干涉引起的。
04历届国际物理奥林匹克竞赛试题与解答

历届国际物理奥林匹克竞赛试题与解答第4届(1970年于苏联的莫斯科)【题1】如图4.1(a )、(b ),在质量M =1kg 的木板上有质量m =0.1kg 的小雪橇。
雪橇上的马达牵引着一根绳子,使雪橇以速度v 0=0.1m/s 运动。
忽略桌面与木板之间的摩擦。
木板与雪橇之间的摩擦系数μ=0.02。
把住木板,起动马达。
当雪橇达到速度v 0时,放开木板。
在此瞬间,雪橇与木板端面的距离L =0.5m 。
绳子拴在(a )远处的桩子,(b )木板的端面上。
试描述两种情形下木板与雪橇的运动。
雪橇何时到达木板端面?图4.1(a ) 图4.1(b )解:(a )在第一种情形中(如图4.1(a )),雪橇处于匀速运动状态。
雪橇与木板以不同的速度运动。
这样引起的最大摩擦力为 m g ,它作用在木板上,产生的加速度M mga μ=,直至木板达到雪橇的速度v 0为止。
加速时间为mgM v a v t μ000===5.1s 在这段时间内,雪橇的位移为mgM v a v S μ2220200===0.255m 因此,雪橇离木板右端点的距离为0.5m -0.255m =0.245m雪橇不能达到木板的一端,因为这段时间以后,木板与雪橇以相同的速度v 0一起运动。
在木板加速期间,马达必须用力 m g 牵引绳子,但以后马达不能施加力的作用,它只是卷绳子。
(b )在第二种情形中(如图 4.1(b )),木板与桌面之间无摩擦。
木板与雪橇形成一个孤立系统,可以用动量守恒定律。
当我们放开木板时,雪橇的动量为mv 0,释放后的木板具有速度v 2,它由下式决定:mv 0=M v 2+m (v 0+v 2)此式表明v 2=0,所以木板保持不动,雪橇以同一速度继续前进。
雪橇达到木板右端的时间为1.05.00==v L t =5 s【题2】NaCl 的晶体点阵由边长为5.6×10-8cm 的立方晶胞组成,它是面心立方点阵。
钠原子量约为23,氯原子量为35.5,NaCl密度为2.22g/cm 3。
历届物理竞赛试题及答案

历届物理竞赛试题及答案一、选择题(每题5分,共20分)1. 一个物体在水平面上受到一个恒定的力F作用,其运动状态将会如何变化?A. 速度保持不变B. 速度逐渐增大C. 速度逐渐减小D. 物体静止不动答案:B2. 光在真空中传播的速度是多少?A. 299,792,458 m/sB. 299,792,458 km/sC. 299,792,458 km/hD. 299,792,458 m/h答案:A3. 根据牛顿第三定律,作用力和反作用力的关系是什么?A. 作用力和反作用力大小相等,方向相反B. 作用力和反作用力大小不相等,方向相反C. 作用力和反作用力大小相等,方向相同D. 作用力和反作用力大小不相等,方向相同答案:A4. 一个物体从静止开始做自由落体运动,其下落时间t秒时的速度v 是多少?A. v = gtB. v = g * t^2C. v = 2gtD. v = gt^2答案:A二、填空题(每题5分,共20分)1. 根据能量守恒定律,一个物体的动能和势能之和在没有外力作用下______。
答案:保持不变2. 在国际单位制中,电流的单位是______。
答案:安培3. 一个电路中的电阻R、电流I和电压V之间的关系由______定律描述。
答案:欧姆4. 按照量子力学的观点,电子在原子中的运动状态可以用______来描述。
答案:波函数三、计算题(每题10分,共30分)1. 一辆质量为1000kg的汽车以20m/s的速度行驶,求其动能。
答案:E_k = 1/2 * m * v^2 = 1/2 * 1000kg * (20m/s)^2 =200,000 J2. 一个电流为2A的电路,通过一个电阻为10Ω的电阻器,求电路中的电压。
答案:V = I * R = 2A * 10Ω = 20V3. 一个物体从高度为10m的平台上自由下落,忽略空气阻力,求物体下落到地面所需的时间。
答案:t = √(2h/g) = √(2 * 10m / 9.8m/s^2) ≈ 1.41s四、简答题(每题15分,共30分)1. 简述牛顿第一定律的内容及其物理意义。
国际物理奥林匹克竞赛试题与解答(第2届)

1968年第二届国际奥林匹克物理竞赛试题(理论部分)题1在30°的斜面上,质量m2=4千克的木块经轻绳与质量m1=8千克、半径r=5百米的实圆柱体相连(图2-1)。
求放开物体后的加速度。
木块与斜面之间的摩擦系数μ=0.2。
忽略轴承中的摩擦和滚动摩擦。
题2一个杯里装有300厘米3、温度为0℃的甲苯,另一个标里装有110厘米3、温度为100℃ 的甲苯。
两体积之和为410厘米3。
求两杯中甲苯混合以后的最终体积。
甲苯的体膨胀系数为β=0.001(℃)-1,忽略热量损失。
题3光线在垂直于玻璃半圆柱体轴的平面内,以45o角射在半圆柱体的平表面上(图2-4)。
玻璃折射率为2。
问光线在何处离开圆柱表面?(实验部分)题4每人领取三个封闭的盒子,每个盒子上有两个插孔。
要在不打开盒子的情况下,确定盒内有什么元件,并测量其特性。
可供使用的器件有;内阻和精度已知的交流和直流仪器,以频率50周的交流电源和直流电源。
参考答案题1:〔解〕如果绳子拉紧的,则圆柱体与木块以同一加速度a运动。
设绳中的张力为F,圆柱体与斜面之间的摩擦力为S(图2-2)。
圆柱体的角加速度等于。
木块的运动方程为:m2a=m2gsinα-μm2gcosα+F。
圆柱体的运动方程为m1a=m1gsinα-S-F圆柱体转动的运动方程为:Sr=θ其中θ是圆柱体的转动惯量,Sr是摩擦力矩。
联立上述三个方程,解得a=g (1) S=*g* (2) F=m2g (3)均匀圆柱体的转动惯量为θ=利用题中所给的数值,得到a=S==13.01牛顿F=m2g=0.196牛顿讨论(见图2-3)系统开始运动的条件是a>0。
把a>0代入(1)式,得出倾角的极限α1为:tgα1=μ=0.0667α1=3o49′单从圆柱体来看,α1=0;单从木块来看,则α1=tg-1μ=11o如果绳子没有拉紧,则两物体分开运动。
将F=0代入(3)式,得出极限角为tgα2=μ(1+)=0.6α2=30o58′当α1<α<α2时,绳子能够拉紧,木块与圆柱体一同向下运动。
历届国际物理奥林匹克竞赛试题与解答

历届国际物理奥林匹克竞赛试题与解答第3届(1969年于捷克斯洛伐克的布尔诺)【题1】右图的力学系统由三辆车组成,质量分别为m A =0.3kg ,m B =0.2kg ,m C =1.5kg 。
(a )沿水平方向作用于C 车的力F 很大。
使A 、B 两车相对C 车保持静止。
求力F 及绳子的张力。
(b )C 车静止,求A 、B 两车的加速度及绳子的张力。
(忽略阻力和摩擦力,忽略滑轮和车轮的转动惯量)解:(a )A 、B 两车相对C 车保持静止,A 车在竖直方向没有加速度,因此它对绳的拉力为m A g 。
这个力使B 车得到加速度g m m a BAB =。
又三车系统以相同的加速度运动,则: g m m m m m F BAC B A )(++= 由给定的数值得:a B =a C =a A =1.5g =14.7m/s 2绳中的张力为:T =m A g =2.94N 水平推力为:F =29.4N(b )如果C 车静止,则力m A g 使质量m A +m B 加速,加速度为:BA A AB m m gm a +==0.6g =5.88N绳中的张力为:T /=m A g -m A ×0.6g =1.176N【题2】在质量为m 1的铜量热器中装有质量为m 2的水,共同的温度为t 12;一块质量为m 3、温度为t 3的冰投入量热器中(如右图所示)。
试求出在各种可能情形下的最终温度。
计算中t 3取负值。
铜的比热c 1=0.1kcal/kg·0C ,水的比热c 2=1kcal/kg·0C ,冰的比热c 3=0.5kcal/kg·0C ,冰的熔解热L =80kcal/kg 。
解:可能存在三种不同的终态:(a )只有冰;(b )冰水共存;(c )只有水。
(a )冰温度升高,但没有熔化,达到某一(负)温度t a ; 放出的热量和吸收的热量相等:c 3 m 3(t a -t 3)=(c 1 m 1+c 2 m 2)(t 12-t a )+m 2L得出最终的温度为3332112333122211)(c m c m c m Lm t c m t c m c m t a +++++=(1)情况(a )的条件是t a <0(注:指00C ),如果上式的分子为负值,我们得到下列条件: (c 1 m 1+c 2 m 2)t 12<―c 3 m 3t 3―m 2L (2)(c )现在让我们讨论冰块全部熔化的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
历届国际物理奥林匹克竞赛试题与解答第1届(1967年于波兰的华沙)【题1】质量M=0.2kg 的小球静置于垂直柱上,柱高h=5m 。
一粒质量m=0.01kg 、以速度0=500m/s 飞行的子弹水平地穿过球心。
球落在距离柱s =20m 的地面上。
问子弹落在地面何处?子弹动能中有多少转换为热能?解:在所有碰撞情况下,系统的总动量均保持不变:MV mv mv +=0其中v 和V 分别是碰撞后子弹的速度和小球的速 度. 两者的飞行时间都是01.12==ght s 球在这段时间沿水平方向走过20m 的距离,故它在水平方向的速度为:8.1901.120==V (m/s ) 由方程0.01×500=0.01v +0.2×19.8可求出子弹在碰撞后的速度为:v =104m/s子弹也在1.01s 后落地,故它落在与柱的水平距离为S =vt =104×1.01=105m 的地面上。
碰撞前子弹的初始动能为=2021mv 1250 J 球在刚碰撞后的动能为=221MV 39.2 J 子弹在刚碰撞后的动能为=221mv 54 J与初始动能相比,两者之差为1250 J -93.2 J =1156.8 J 这表明原来动能的92.5%被系统吸收而变为热能。
这种碰撞不是完全非弹性碰撞。
在完全弹性碰撞的情形下,动能是守恒的。
而如果是完全非弹性碰撞,子弹将留在球内。
【题2】右图(甲)为无限的电阻网络,其中每个电阻均为r ,求A、B两点间的总电阻。
解:如图(乙)所示A、B两点间的总电阻应等于C、D两点间的总电阻与电阻r的并联,再与r串联 图(甲) 后的等效电阻。
如果网络是无限的,则A、B两点间的总电阻应等于C、D 两点间的总电阻,设为Rx 。
根据它们的串并联关系有:m M h SsυABr r r r r r r rA B r r r r r r r r CDrR rR r R x xx ++= 图(乙) 解上式可得: r R x 251+=【题3】给定两个同样的球,其一放在水平面上,另一个以细线悬挂。
供给两球相同的热量,问两球温度是否趋于相同?说明你的理由(忽略各种热量损失)解答:如右图所示,球体受热,体积增大。
放在水平面上的球重心升高,克服重力做功要耗费一部分热量,于是剩下提高球体温度的热量减少了些。
以细线悬挂的球与之相反。
结果放在水平面上球的温度将稍小于以细线悬挂球的温度。
(这一差别是很小的,对于半径为10cm 的铜球来说,相对差值约为10-7 K )【实验题】测定石油的比热。
可供使用的物品有:天平、量热器、温度计、电源、开关、导线、停表、电热器、容器、水和石油。
解答:把已知温度t 1和质量m 1的水,与已知温度t 2和质量m 2的石油在量热器里混合,测出混合物的温度t 3。
从包含一方放热和另一方吸热的方程中可算出石油的比热。
这是通常测定石油比热的方法。
也可以先用电热器加热水,再加热等量的石油,并且及时观察温度的改变。
两条温度曲线起始点的切线斜率与比热成反比关系,据此可以测定石油的比热。
【替换题】(为在校没有上过电学的学生而设。
)密闭容器中装有一个大气压、温度为 0℃的干燥空气10升,加入3克水后将系统加热到100℃,求容器的压强。
解:在100℃时,全部水都处于汽相。
3克水是61摩尔(18÷3=6),它们在100℃和1atm 下的体积是:11.5273373614.22=⨯⨯(升)㎏ 由状态方程求出61摩尔水蒸气的压强: 373102734.2261⨯=⨯水气p 解得:水气p =0.507 atm 由空气的状态方程:3732731空气p = 解得:空气p =1.366 atm 把两部分压强相加得到总压强为:水气空气p p p +==1.366 atm +0.507 atm =1.873 atm历届国际物理奥林匹克竞赛试题与解答第2届(1968年于匈牙利的布达佩斯)【题1】 在倾角为300的斜面上,质量为m 2=4 kg 的木块经细绳与质量为m 1=8 kg 、半径为r =5 cm 的实心圆柱体相连。
求放开物体后的加速度。
木块与斜面之间的动摩擦系数μ=0.2,忽略轴承的摩擦和滚动摩擦。
解:如果绳子是拉紧,则圆柱体与木块一同加速运动, 设加速度为a ,绳子中的张力为F ,圆柱体与斜面之间 的摩擦力为S ,则圆柱体的角加速度为a /r 。
对木块有:m 2a =m 2g sin α-μm 2g cos α+F对圆柱体有:m 1a =m 1g sin α-S -FS r =Ia /r其中I 是圆柱体的转动惯量,S r 是摩擦力矩。
解以上方程组可得 221221cos sin )(rIm m m m m ga ++-+=αμα (1)2212212cos sin )(rI m m m m m g rI S ++-+=αμα (2) 2212212sin cos )(rIm m r I r I m gm F ++-+=ααμ (3)均匀圆柱体的转动惯量为221r m I =代入数据可得a =0.3317g =3.25m/s 2 S =13.01 N F =0.196 N讨论:系统开始运动的条件是a >0。
把a >0代入(1)式,得出倾角的极限α1为:==+=3tan 2121μμαm m m 0.0667α1=3049/单从圆柱体来看,α1=0;单从木块来看,α1=tg -1μ=11019/如果绳子没有拉紧,则两物体分开运动,将F =0代入(3)式,得出极限角为:==+=μμα3)1(tan 212Ir m 0.6 α2=30058/m 1m 2a圆柱体开始打滑的条件是S 值(由(2)式取同样的动摩擦系数算出)达到μ m 1g cos α,由此得出的α3值与已得出的α2值相同。
圆柱体与木块两者的中心加速度相同,都为g (sin α-μ g cos α)圆柱体底部的摩擦力为μ m 1g cos α,边缘各点的切向加速度为a =μ(Ir m 21)g cos α,【题2】 一个杯里装有体积为300 cm 3、温度为00C 的甲苯,另一个杯里装有体积为110 cm 3、温度为1000C 的甲苯,两体积之和为410 cm 3。
求两杯甲苯混合以后的最终体积。
甲苯的体膨胀系数为β=0.001(0C )-1,忽略混合过程中的热量损失。
解:若液体温度为t 1时的体积为V 1,则在00C 时的体积为 11101t V V β+=同理,若液体温度为t 2时的体积为V 2,则在00C 时的体积为 22201t V V β+=如果液体在00C 时的密度为d ,则质量分别为 m 1=V 10d m 2=V 20d混合后,液体的温度为 212211m m t m t m t ++=在该温度下的体积分别为V 10(1+βt )和V 20(1+βt )。
所以混合后的体积之和为V 10(1+βt )+V 20(1+βt )=V 10+V 20+β(V 10+V 20)t = V 10+V 20+β21221121m m t m t m d m m ++⋅+ = V 10+V 20+β(dt m d t m 2211+) =V 10+βV 10t 1+V 20+βV 20t 2=V 10(1+βt 1)+V 20(1+βt 2)=V 1+V 2体积之和不变,在本题仍为410 cm 3。
当把多杯甲苯不断地加入进行混合,对任何数量的甲苯这个结果都成立。
【题3】光线在垂直玻璃半圆柱体轴的平面内,以450角射在半圆柱体的平面上(如右图),玻璃的折射率为2。
试 问光线在何处离开圆柱体表面?解:用角度Ψ描述光线在玻璃半圆柱体内 的位置如解图2.3所示。
按照折射定律:2sin 45sin 0=β得:sin =,=300所有折射光线与垂直线的夹角均为 300,有必要研究一下,当Ψ角从00增至1800的过程中发生了什么现象。
不难看出,Ψ角不可能小于600。
光线从玻璃射向空气全反射的临界角 由解图3.2221sin ==n t β 求出:t =450,则:Ψt =1800―600―450=750如果Ψ角大于750,光线将离开圆柱体。
随着Ψ角的增加,光线将再次发生全反射,此时Ψt =900+300+450=1650 故当:750<Ψ<1650时光线离开圆柱体。
出射光线的圆弧所对应的圆心角为1650―750=900。
【实验题】参加者每人领取三个封闭的盒子,每个盒上有两个插孔。
不许打开盒子,试确定盒中元件的种类,并测定其特性。
可供使用的是,内阻和精度已知交流和直流仪器,以及交流电源(频率50 HZ )和直流电源。
解:在任何一对插孔中都测不到电压,因此,盒子都不含有电源 先用交流,再用直流测电阻,有一盒给出相同的结果。
结论是:该盒包含一个简单电阻,其阻值由测量确定。
另一盒有极大的直流电阻,但对交流来说是导体。
结论是:该盒包含一个电容,其电容值由RC ω1=算得。
第三个盒子对交流和直流都是导体,而交流电阻较大。
结论是:该盒包含一个电阻和电感,两者串联。
电阻和电感值可从测量中算得。
历届国际物理奥林匹克竞赛试题与解答第3届ϕαβAOB(1969年于捷克斯洛伐克的布尔诺)【题1】右图的力学系统由三辆车组成,质量分别为m A =0.3kg ,m B =0.2kg ,m C =1.5kg 。
(a )沿水平方向作用于C 车的力F 很大。
使A 、B 两车相对C 车保持静止。
求力F 及绳子的张力。
(b )C 车静止,求A 、B 两车的加速度及绳子的张力。
(忽略阻力和摩擦力,忽略滑轮和车轮的转动惯量)解:(a )A 、B 两车相对C 车保持静止,A 车在竖直方向没有加速度,因此它对绳的拉力为m A g 。
这个力使B 车得到加速度g m m a BAB =。
又三车系统以相同的加速度运动,则: g m m m m m F BAC B A )(++= 由给定的数值得:a B =a C =a A =1.5g =14.7m/s 2 绳中的张力为:T =m A g =2.94N 水平推力为:F =29.4N(b )如果C 车静止,则力m A g 使质量m A +m B 加速,加速度为:BA A AB m m gm a +==0.6g =5.88N绳中的张力为:T /=m A g -m A ×0.6g =1.176N【题2】在质量为m 1的铜量热器中装有质量为m 2的水,共同的温度为t 12;一块质量为m 3、温度为t 3的冰投入量热器中(如右图所示)。
试求出在各种可能情形下的最终温度。
计算中t 3取负值。
铜的比热c 1=0.1kca l/kg·0C ,水的比热c 2=1kcal/kg·0C ,冰的比热c 3=0.5kcal/kg·0C ,冰的熔解热L =80kcal/kg 。
