多边形知识点及经典习题
专题23多边形-重难点题型(学生版)
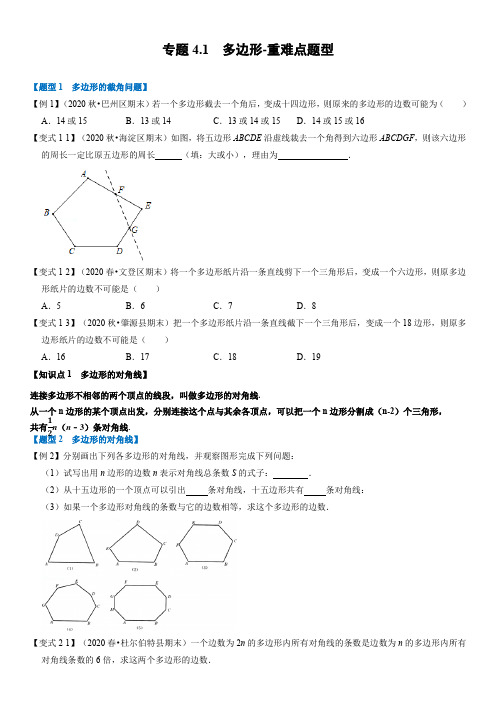
专题4.1 多边形-重难点题型【题型1 多边形的截角问题】【例1】(2020秋•巴州区期末)若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )A .14或15B .13或14C .13或14或15D .14或15或16【变式1-1】(2020秋•海淀区期末)如图,将五边形ABCDE 沿虚线裁去一个角得到六边形ABCDGF ,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .【变式1-2】(2020春•文登区期末)将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是( )A .5B .6C .7D .8【变式1-3】(2020秋•肇源县期末)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )A .16B .17C .18D .19【知识点1 多边形的对角线】连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.从一个n 边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个n 边形分割成(n -2)个三角形, 共有12n (n ﹣3)条对角线. 【题型2 多边形的对角线】【例2】分别画出下列各多边形的对角线,并观察图形完成下列问题:(1)试写出用n 边形的边数n 表示对角线总条数S 的式子: .(2)从十五边形的一个顶点可以引出 条对角线,十五边形共有 条对角线:(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数.【变式2-2】(2020春•福清市校级期末)阅读下列内容,并答题:我们知道计算n 边形的对角线条数公式为n(n−3)2,如果有一个n 边形的对角线一共有20条,则可以得到方程n(n−3)2=20,去分母得n (n ﹣3)=40;∵n 为大于等于3的整数,且n 比n ﹣3的值大3,∴满足积为40且相差3的因数只有8和5,符合方程n (n ﹣3)=40的整数n =8,即多边形是八边形.根据以上内容,问:(1)若有一个多边形的对角线一共有14条,求这个多边形的边数;(2)A 同学说:“我求得一个多边形的对角线一共有30条.”你认为A 同学说地正确吗?为什么?【变式2-3】(2020秋•东湖区校级月考)如图,先研究下面三角形、四边形、五边形、六边形…多边形的边数n 及其对角线条数t 的关系,再完成下面问题:(1)若一个多边形是七边形,它的对角线条数为 ,n 边形的对角线条数为t = (用n 表示).(2)求正好65条对角线的多边形是几边形.【知识点2 多边形的内角和】n 边形的内角和为(n -2)·180°(n ≥3).【题型3 多边形的内角和】【例3】(2021春•江阴市校级月考)下列哪个度数不可能是一个多边形的内角和( )A .360°B .450°C .900°D .1800°【变式3-1】(2020秋•路南区期中)小红:我计算出一个多边形的内角和为2020°;老师:不对呀,你可能少加了一个角!则小红少加的这个角的度数是( )A .110°B .120°C .130°D .140°【变式3-2】(2021春•玄武区校级月考)一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )A .10或11B .11或12或13C .11或12D .10或11或12【变式3-3】(2020春•新化县月考)如果一个正五边形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .【知识点3 多边形的外角和】在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n 边形的外角和恒等于360°,它与边数的多少无关.【题型4 多边形的外角和】【例4】(2021春•金牛区校级期中)若正多边形的一个外角是45°,则该正多边形的内角和为( )A .720°B .540°C .1080°D .900°【变式4-1】(2020春•永州期末)富有灿烂文化的永州,现今保留着许多具有历史和文化价值的建筑,古朴的建筑代表,无规则多边形的形状,蕴含了丰富而和谐的数学美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的多边形,根据绘制的图形,则∠1+∠2+∠3+∠4+∠5的度数为()A.72°B.108°C.360°D.540°【变式4-2】(2020秋•越秀区校级月考)五边形ABCDE中,∠A、∠B、∠C、∠D对应的邻补角和等于215°,则∠E的度数为()A.30°B.35°C.40°D.45°【变式4-3】(2020春•郓城县期末)如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,∠AED的度数是()A.120°B.115°C.105°D.100°【题型5 多边形的内角和与外角和的实际应用】【例5】(2020秋•汤阴县期中)八年级一班的同学体育课上玩游戏,让小聪同学从A出发前进10米后左转30°,再前进10米后左转30°,按照这样方法一直走下去,当他回到A时,共走了()A.60米B.100米C.120米D.150米【变式5-1】(2020秋•兰山区期末)科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为()A.12米B.16米C.18米D.20米【变式5-2】(2020春•永年区期末)小磊利用最近学习的数学知识,给同伴出了这样一道题:假如从点A出发,沿直线走5米后向左转θ,接着沿直线前进5米后,再向左转θ……如此下去,当他第一次回到A点时,发现自己走了60米,θ的度数为()【变式5-3】(2021•昆明模拟)将若干个大小相等的正五边形排成环状,如图所示是前3个五边形,要完成这一圆环还需_______个正五边形()A.6B.7C.8D.9【题型6 多边形的内角和与外角和的综合应用】【例6】(2020春•遂宁期末)如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是()A.50°B.55°C.40°D.45°【变式6-1】(2020秋•朝阳区校级月考)如图,l1∥l2,正五边形ABCDE的顶点A、B分别落在l1、l2上,若∠1=25°,则∠2的大小为()A.60°B.61°C.62°D.65°【变式6-2】(2021春•宜兴市期中)如图,四边形ABCD中,∠A=110°,∠C=70°,点M、N分别在AB、BC 上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,则∠B的度数为°.【变式6-3】(2020秋•路北区期中)如图,在六边形ABCDEF中,若∠A+∠B+∠C+∠D=500°,∠DEF与∠AFE 的平分线交于点G,则∠G等于()。
多边形的内角和与外角和知识点-例题-习题

第二十四讲 多边形的内角和与外角和【要点梳理】知识点一、多边形的概念1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形. 2.相关概念:边:组成多边形的各条线段叫做多边形的边. 顶点:每相邻两条边的公共端点叫做多边形的顶点.内角:多边形相邻两边组成的角叫多边形的内角,一个n 边形有n 个内角. 外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角. 对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:要点诠释:(1)正多边形必须同时满足“各边相等”,“各角相等”两个条件,二者缺一不可; (2)过n 边形的一个顶点可以引(n-3)条对角线,n 边形对角线的条数为(3)2n n -;(3)过n 边形的一个顶点的对角线可以把n 边形分成(n-2)个三角形. 知识点二、多边形内角和n 边形的内角和为(n-2)·180°(n≥3). 要点诠释:(1)内角和公式的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数;(2)正多边形的每个内角都相等,都等于(2)180n n-°;知识点三、多边形的外角和 多边形的外角和为360°. 要点诠释:(1)在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n 边形的外角和恒等于360°,它与边数的多少无关;(2)正n 边形的每个内角都相等,所以它的每个外角都相等,都等于360n°;(3)多边形的外角和为360°的作用是:①已知各相等外角度数求多边形边数;②已知多边形边数求各相等外角的度数.凸多边形 凹多边形【典型例题】类型一、多边形的概念例1.如图,在六边形ABCDEF中,从顶点A出发,可以画几条对角线?它们将六边形ABCDEF分成哪几个三角形?【答案与解析】解:如图,P从顶点A出发,可以画三条对角线,它们将六边形ABCDEF分成的三角形分别是:△ABC、△ACD、△ADE、△AEF.【总结升华】从一个多边形一个顶点出发,可以连的对角线的条数(n-3)条,分成的三角形数是个数(n-2)个.举一反三:【变式】过正十二边形的一个顶点有条对角线,一个正十二边形共有条对角线【答案】9,54。
(完整版)《多边形》练习题

《多边形》学习指导一、知识梳理【知识点一】相关概念:在同一平面内,由不在同一条直线上的假设干条(不少于3条)线段首尾顺次相接形成的图形叫做多边形。
【知识点二】相关性质: 四边形的内角和等于360°;四边形的外角和等于360°;任何一个多边形的外角和等于360°。
【知识点三】相关公式:n边形的内角和为(n-2)×180°;n边形从一个顶点引出的对角线有〔n–3〕条,将n边形分成〔n–2〕个三角形;n边形的对角线共有()n n 32条。
二、实战演练:1. 五边形的内角和为,外角和为,假设它的每一个内角的度数都相等,那么每个内角等于________,每个外角等于________;2.四边形有2条对角线,五边形有5条对角线,那么六边形有条对角线,十边形有条对角线;3.过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是;4.从九边形的一个顶点出发,可以画出m条对角线,它们将九边形分成n个三角形.那么m、n的值分别为,;5. 如果一个多边形的内角和是900°,那么这个多边形是_____边形;6.假设一个n 边形的每一个内角都等于150°,那么n=___________;7.假设一个多边形的每一个外角都等于40°,那么这个多边形的边数是__________;8. 四边形ABCD中,∠A,∠B,∠C,∠D的度数比为2:3:4:3,那么∠D等于;9.一个多边形的内角和是外角和的2倍,这个多边形的边数为;10.一个多边形的外角和是内角和的,这个多边形的边数为;11.一个多边形的内角和比它的外角和的2倍还大180°, 这个多边形的边数;12.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,那么∠P的度数是;13.一个多边形除一个内角外其余内角的和为810°,那么这个多边形是边形;14.如图,在四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=32,AD=2, 那么四边形ABCD的面积是;AD15.机器人在一平面上从点A 处出发开始运动,规定“向前走1米再向左转60° 〞为1次运动,那么运动2021次后机器人距离出发点A 的距离为 米。
第9章《多边形》常考题集(12):9.2-多边形的内角和与外角和

第9章《多边形》常考题集〔12〕:9.2多边形的内角和与外角和第9章《多边形》常考题集〔12〕:9.2 多边形的内角和与外角和选择题31.若一个多边形的边数增加2倍,它的外角和〔〕A.扩大2倍B.缩小2倍C.保持不变D.无法确定32.〔2001•##〕如果正多边形的一个内角是144°,则这个多边形是〔〕A.正十边形B.正九边形C.正八边形D.正七边形33.下面说法正确的是〔〕A.一个三角形中,至多只能有一个锐角B.一个四边形中,至少有一个锐角C.一个四边形中,四个内角可能全是锐角D.一个四边形中,不能全是钝角34.一个多边形的每一个内角都是135°,则这个多边形是〔〕A.七边形B.八边形C.九边形D.十边形35.多边形的每一个内角都等于150°,则此多边形从一个顶点出发的对角线共有〔〕条.A.7B.8C.9D.1036.一个多边形除了一个内角外,其余内角之和为257°,则这一内角等于〔〕A.90°B.105°C.103°D.120°37.若一个n边形n个内角与某一个外角的总和为1350°,则n等于〔〕A.6B.7C.8D.938.一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是〔〕A.17 B.16 C.15 D.16或15或17填空题39.〔2003•##〕如图,∠1+∠2+∠3+∠4=_________度.40.〔2008•##〕如图所示,①中多边形〔边数为12〕是由正三角形"扩展〞而来的,②中多边形是由正方形"扩展〞而来的,…,依此类推,则由正n边形"扩展〞而来的多边形的边数为_________.41.从七边形的某个顶点出发,分别连接这个顶点与其余各顶点,可以把七边形分成_________个三角形.43.〔2010•##〕如果一个多边形的内角和等于外角和的2倍,那么这个多边形的边数n=_________.44.〔2009•##〕一个n边形的内角和等于720°,那么这个多边形的边数n=_________.45.〔2009•##〕八边形的内角和等于_________度.46.〔2008•永春县〕四边形的内角和等于_________度.47.〔2008•宿迁〕若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是_________.48.〔2008•##〕一个凸多边形的内角和与外角和相等,它是_________边形.49.〔2008•##〕六边形的内角和等于_________度.50.〔2007•##〕若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于_________度.51.〔2007•##〕如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了_________m.52.〔2006•##〕若一个多边形的每一个外角都等于40°,则这个多边形的边数是_________.53.〔2006•临安市〕用一条宽相等的足够长的纸条,打一个结,如图〔1〕所示,然后轻轻拉紧、压平就可以得到如图〔2〕所示的正五边形ABCDE,其中∠BAC= _________ 度. 54.〔2006•##〕把一副三角板按如图方式放置,则两条斜边所形成的钝角α= _________ 度. 55.〔2006•##〕如图,小亮从A 点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A 点时,一共走了 _________ 米. 56.〔2006•##〕正五边形的一个内角的度数是 _________ 度. 57.〔2005•##〕有一个多边形的内角和是它外角和的5倍,则这个多边形是 _________ 边形. 58.〔2005•##〕一个多边形的内角和为1080°,则这个多边形的边数是 _________ . 59.〔2004•##〕正n 边形的内角和等于1080°,那么这个正n 边形的边数n= _________ . 60.一个多边形的每个内角都等于150°,则这个多边形是 _________ 边形.第9章《多边形》常考题集〔12〕:9.2 多边形的内角和与外角和参考答案与试题解析选择题31.若一个多边形的边数增加2倍,它的外角和〔 〕 A . 扩大2倍 B .缩小2倍 C . 保持不变 D .无法确定考点:多边形内角与外角. 分析:所有凸多边形的外角和是360度,这个数值与边数的大小无关. 解答: 解:若一个多边形的边数增加2倍,它的外角和是360°,保持不变. 故选C .点评: 本题主要考查了多边形的外角和定理,对这个定理的正确理解是关键. 32.〔2001•##〕如果正多边形的一个内角是144°,则这个多边形是〔 〕 A . 正十边形 B .正九边形 C . 正八边形 D .正七边形考点:多边形内角与外角. 分析: 正多边形的每个角都相等,同样每个外角也相等,一个内角是144°,则外角是180﹣144=36°.又已知多边形的外角和是360度,由此即可求出答案.解答: 解:360÷〔180﹣144〕=10,则这个多边形是正十边形. 故选A .点评:本题主要利用了多边形的外角和是360°这一定理. 33.下面说法正确的是〔 〕A . 一个三角形中,至多只能有一个锐角B . 一个四边形中,至少有一个锐角C . 一个四边形中,四个内角可能全是锐角D . 一个四边形中,不能全是钝角考点: 多边形内角与外角;三角形内角和定理.专题: 计算题.分析: 根据多边形的内角和定理分别可以判定那个正确. 解答: 解:A 、不对,例如:90,45,45;B 、不对,例如:90,90,90,90;C 、不对,四个角都是锐角那么不能满足内角和360°;D 、正确. 故本题选D .点评: 此题考查了三角形,四边形内角与外角的性质.34.一个多边形的每一个内角都是135°,则这个多边形是〔 〕 A . 七边形 B .八边形 C . 九边形 D .十边形考点:多边形内角与外角. 分析: 已知每一个内角都等于135°,就可以知道每个外角是45度,根据多边形的外角和是360度就可以求出多边形的边数.解答: 解:多边形的边数是:n=360°÷〔180°﹣135°〕=8. 故选B .点评:通过本题要理解已知内角或外角求边数的方法. 35.多边形的每一个内角都等于150°,则此多边形从一个顶点出发的对角线共有〔 〕条. A . 7 B . 8 C . 9 D . 10 考点:多边形内角与外角;多边形的对角线. 专题:计算题. 分析: 多边形的每一个内角都等于150°,多边形的内角与外角互为邻补角,则每个外角是30度,而任何多边形的外角是360°,则求得多边形的边数;再根据不相邻的两个顶点之间的连线就是对角线,则此多边形从一个顶点出发的对角线共有n ﹣3条,即可求得对角线的条数. 解答: 解:∵多边形的每一个内角都等于150°, ∴每个外角是30°,∴多边形边数是360°÷30°=12,则此多边形从一个顶点出发的对角线共有12﹣3=9条. 故选C .点评: 本题主要考查了多边形的外角和定理,已知外角求边数的这种方法是需要熟记的内容.多边形从一个顶点出发的对角线共有n ﹣3条.36.一个多边形除了一个内角外,其余内角之和为257°,则这一内角等于〔 〕A . 90°B . 105°C . 103°D .120° 考点:多边形内角与外角. 分析: 设这个多边形是n 边形,则内角和是〔n ﹣2〕•180°,这个度数与257°的差一定小于180°并且大于0,则可以解方程:〔n ﹣2〕•180°=257°,多边形的边数n 一定是大于x 的最小的整数,这样就可以求出多边形的边数,从而求出内角和,得到这一内角的度数. 解答: 解:根据题意,得 〔n ﹣2〕•180°=257,得n=,则多边形的边数是4,因为四边形的内角和是360度,所以这一内角等于360°﹣257°=103°.故选C .点评:本题解决的关键是正确求出多边形的边数. 37.若一个n 边形n 个内角与某一个外角的总和为1350°,则n 等于〔 〕 A . 6 B . 7 C . 8 D . 9 考点: 多边形内角与外角. 分析:根据n 边形的内角和定理可知:n 边形内角和为〔n ﹣2〕×180.设这个外角度数为x 度,利用方程即可求出答案. 解答:解:设这个外角度数为x °,根据题意,得 〔n ﹣2〕×180+x=1350, 180n ﹣360+x=1350,x=1350+360﹣180n,即x=1710﹣180n, 由于0<x <180,即0<1710﹣180n <180,可变为:解得8.5<n <9.5, 所以n=9. 故选D . 点评:主要考查了多边形的内角和定理. n 边形的内角和为:180°•〔n ﹣2〕.38.一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是〔 〕 A . 17 B . 16 C . 15 D . 16或15或17考点:多边形内角与外角. 分析: 因为一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,根据多边形的内角和即可解决问题.解答: 解:多边形的内角和可以表示成〔n ﹣2〕•180°〔n ≥3且n 是整数〕,一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,根据〔n ﹣2〕•180°=2520°解得:n=16, 则多边形的边数是15,16,17. 故选D .点评: 本题主要考查多边形的内角和定理的计算方法. 填空题 39.〔2003•##〕如图,∠1+∠2+∠3+∠4= 280 度. 考点: 三角形内角和定理;多边形内角与外角. 分析: 运用了三角形的内角和定理计算.解答: 解:∵∠1+∠2=180°﹣40°=140°,∠3+∠4=180°﹣40°=140°,∴∠1+∠2+∠3+∠4=280°. 故答案为:280°.点评: 此题主要是运用了三角形的内角和定理. 40.〔2008•##〕如图所示,①中多边形〔边数为12〕是由正三角形"扩展〞而来的,②中多边形是由正方形"扩展〞而来的,…,依此类推,则由正n 边形"扩展〞而来的多边形的边数为 n 〔n+1〕 . 考点: 多边形.专题:规律型.分析:①边数是12=3×4,②边数是20=4×5,依此类推,则由正n边形"扩展〞而来的多边形的边数为n〔n+1〕.解答:解:∵①正三边形"扩展〞而来的多边形的边数是12=3×4,②正四边形"扩展〞而来的多边形的边数是20=4×5,③正五边形"扩展〞而来的多边形的边数为30=5×6,④正六边形"扩展〞而来的多边形的边数为42=6×7,∴正n边形"扩展〞而来的多边形的边数为n〔n+1〕.点评:首先要正确数出这几个图形的边数,从中找到规律,进一步推广.正n边形"扩展〞而来的多边形的边数为n 〔n+1〕.41.从七边形的某个顶点出发,分别连接这个顶点与其余各顶点,可以把七边形分成5个三角形.考点:多边形的对角线.分析:根据七边形的概念和特性即可解.从简单图形说起:从四边形的一个顶点出发,连接这个点与其余各顶点,可以把一个四边形分割成〔4﹣2〕=2个三角形.解答:解:根据以上规律,从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成〔7﹣2〕=5个三角形.故答案为5.点评:本题考查的知识点为:过n边形一个顶点作对角线,最多可把n边形分成〔n﹣2〕个三角形.43.〔2010•##〕如果一个多边形的内角和等于外角和的2倍,那么这个多边形的边数n=6.考点:多边形内角与外角.分析:任何多边形的外角和是360度,内角和等于外角和的2倍则内角和是720度.n边形的内角和是〔n﹣2〕•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:根据题意,得〔n﹣2〕•180=720,解得:n=6.点评:已知多边形的内角和求边数,可以转化为方程的问题来解决.44.〔2009•##〕一个n边形的内角和等于720°,那么这个多边形的边数n=6.考点:多边形内角与外角.专题:计算题.分析:n边形的内角和可以表示成〔n﹣2〕•180°,设这个多边形的边数是n,就得到方程,从而求出边数.解答:解:由题意可得:〔n﹣2〕•180°=720°,解得:n=6.所以,多边形的边数为6.点评:此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程求解.45.〔2009•##〕八边形的内角和等于1080度.考点:多边形内角与外角.分析:n边形的内角和可以表示成〔n﹣2〕•180°,代入公式就可以求出内角和.解答:解:〔8﹣2〕•180°=1080°.点评:本题主要考查了多边形的内角和公式,是需要熟记的内容.46.〔2008•永春县〕四边形的内角和等于360度.考点:多边形内角与外角.分析:n边形的内角和是〔n﹣2〕•180°,代入公式就可以求出内角和.解答:解:〔4﹣2〕•180°=360°.点评:本题主要考查了多边形的内角和公式,是需要识记的内容.47.〔2008•宿迁〕若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是8.考点:多边形内角与外角.分析:任何多边形的外角和是360°,即这个多边形的内角和是3×360°.n边形的内角和是〔n﹣2〕•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:设多边形的边数为n,根据题意,得〔n﹣2〕•180=3×360,解得n=8.则这个多边形的边数是8.点评:已知多边形的内角和求边数,可以转化为方程的问题来解决.48.〔2008•##〕一个凸多边形的内角和与外角和相等,它是四边形.考点:多边形内角与外角.分析:任何多边形的外角和是360度,因而这个多边形的内角和是360度.n边形的内角和是〔n﹣2〕•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:根据题意,得〔n﹣2〕•180=360,解得n=4,则它是四边形.点评:已知多边形的内角和求边数,可以转化为方程的问题来解决.49.〔2008•##〕六边形的内角和等于720度.考点:多边形内角与外角.分析:n边形的内角和是〔n﹣2〕•180°,把多边形的边数代入公式,就得到多边形的内角和.解答:解:〔6﹣2〕•180=720度,则六边形的内角和等于720度.点评:解决本题的关键是正确运用多边形的内角和公式,是需要熟记的内容.50.〔2007•##〕若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于1800度.考点:多边形内角与外角.专题:计算题.分析:根据任何多边形的外角和都是360°,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.n边形的内角和是〔n﹣2〕•180°,把多边形的边数代入公式,就得到多边形的内角和.解答:解:多边形的边数:360°÷30°=12,正多边形的内角和:〔12﹣2〕•180°=1800°.点评:根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.51.〔2007•##〕如图,小亮从A点出发前10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了240m.考点:多边形内角与外角.专题:应用题.分析:根据多边形的外角和定理即可求出答案.解答:解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,∴根据外角和定理可知正多边形的边数为360÷15=24,则一共走了24×10=240米.故答案为:240.点评:本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°,用外角和求正多边形的边数可直接让360度除以一个外角度数即可.52.〔2006•##〕若一个多边形的每一个外角都等于40°,则这个多边形的边数是9.考点:多边形内角与外角.分析:根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.解答:解:360÷40=9,即这个多边形的边数是9.点评:根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.53.〔2006•临安市〕用一条宽相等的足够长的纸条,打一个结,如图〔1〕所示,然后轻轻拉紧、压平就可以得到如图〔2〕所示的正五边形ABCDE,其中∠BAC=36度.考点:多边形内角与外角.分析:利用多边形的内角和定理和等腰三角形的性质即可解决问题.解答:解:∵∠ABC==108°,△ABC是等腰三角形,∴∠BAC=∠BCA=36度.点评:本题主要考查了多边形的内角和定理和等腰三角形的性质.n边形的内角和为:180°〔n﹣2〕.54.〔2006•##〕把一副三角板按如图方式放置,则两条斜边所形成的钝角α=165度.考点:多边形内角与外角;三角形内角和定理;三角形的外角性质.分析:根据三角形的一个外角等于与它不相邻的两个内角的和或者根据四边形的内角和等于360°得出.解答:解:本题有多种解法.解法一:∠α为下边小三角形外角,∠α=30°+135°=165°;解法二:利用四边形内角和,∠α等于它的对顶角,故∠α=360°﹣90°﹣60°﹣45°=165°.点评:本题通过三角板拼装来求角的度数,考查学生灵活运用知识能力.55.〔2006•##〕如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了120米.考点:多边形内角与外角.专题:应用题.分析:根据多边形的外角和即可求出答案.解答:解:∵360÷30=12,∴他需要走12次才会回到原来的起点,即一共走了12×10=120米.点评:本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°.56.〔2006•##〕正五边形的一个内角的度数是108度.考点:多边形内角与外角.分析:因为n边形的内角和是〔n﹣2〕•180°,因而代入公式就可以求出内角和,再用内角和除以内角的个数就是一个内角的度数.解答:解:〔5﹣2〕•180=540°,540÷5=108°,所以正五边形的一个内角的度数是108度.点评:本题考查正多边形的基本性质,解题时应先算出正n边形的内角和再除以n即可得到答案.57.〔2005•##〕有一个多边形的内角和是它外角和的5倍,则这个多边形是12边形.考点:多边形内角与外角.分析:一个多边形的内角和等于它的外角和的5倍,任何多边形的外角和是360度,因而这个正多边形的内角和为5×360度.n边形的内角和是〔n﹣2〕•180°,代入就得到一个关于n的方程,就可以解得边数n.解答:解:根据题意,得〔n﹣2〕•180=5×360,解得:n=12.所以此多边形的边数为12.点评:已知多边形的内角和求边数,可以转化为解方程的问题解决.58.〔2005•##〕一个多边形的内角和为1080°,则这个多边形的边数是8.考点:多边形内角与外角.分析:n边形的内角和是〔n﹣2〕•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:根据题意,得〔n﹣2〕•180=1080,解得n=8.所以这个多边形的边数是8.点评:已知多边形的内角和求边数,可以转化为方程的问题来解决.59.〔2004•##〕正n边形的内角和等于1080°,那么这个正n边形的边数n=8.考点:多边形内角与外角.分析:n边形的内角和是〔n﹣2〕•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:设这个多边形是n边形,由题意知,〔n﹣2〕×180°=1080°,∴n=8.故该多边形的边数为8.点评:已知多边形的内角和求边数,可以转化为方程的问题来解决.60.一个多边形的每个内角都等于150°,则这个多边形是12边形.考点:多边形内角与外角.专题:计算题.分析:根据多边形的内角和定理:180°•〔n﹣2〕求解即可.解答:解:由题意可得:180°•〔n﹣2〕=150°•n,解得n=12.故多边形是12边形.点评:主要考查了多边形的内角和定理.n边形的内角和为:180°•〔n﹣2〕.此类题型直接根据内角和公式计算可得.参与本试卷答题和审题的老师有:hnaylzhyk;zhjh;feng;lanchong;开心;心若在;zzz;蓝月梦;HJJ;kuaile;HLing;CJX〔排名不分先后〕菁优网20##6月1日。
多边形及其内角和经典例题透析

知识要点梳理定义:由三条或三条以上的线段首位顺次连接所组成的封闭图形叫做多边形。
凸多边形分类1:凹多边形正多边形:各边相等,各角也相等的多边形叫做正多边形。
分类2:多边形非正多边形:1、n边形的内角和等于180°(n-2)。
多边形的定理2、任意凸形多边形的外角和等于360°。
3、n边形的对角线条数等于1/2·n(n-3)只用一种正多边形:3、4、6/。
镶嵌拼成360度的角只用一种非正多边形(全等):3、4。
知识点一:多边形及有关概念1、多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.(1)多边形的一些要素:边:组成多边形的各条线段叫做多边形的边.顶点:每相邻两条边的公共端点叫做多边形的顶点.内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角。
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
(2)在定义中应注意:①一些线段(多边形的边数是大于等于3的正整数);②首尾顺次相连,二者缺一不可;③理解时要特别注意“在同一平面内”这个条件,其目的是为了排除几个点不共面的情况,即空间多边形.2、多边形的分类:(1)多边形可分为凸多边形和凹多边形,画出多边形的任何一条边所在的直线,如果整个多边形都在这条直线的同一侧,则此多边形为凸多边形,反之为凹多边形(见图1).本章所讲的多边形都是指凸多边形.凸多边形凹多边形图1(2)多边形通常还以边数命名,多边形有n条边就叫做n边形.三角形、四边形都属于多边形,其中三角形是边数最少的多边形.知识点二:正多边形各个角都相等、各个边都相等的多边形叫做正多边形。
如正三角形、正方形、正五边形等。
正三角形正方形正五边形正六边形正十二边形要点诠释:各角相等、各边也相等是正多边形的必备条件,二者缺一不可. 如四条边都相等的四边形不一定是正方形,四个角都相等的四边形也不一定是正方形,只有满足四边都相等且四个角也都相等的四边形才是正方形知识点三:多边形的对角线多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 如图2,BD为四边形ABCD的一条对角线。
多边形(8种题型)-2023年新八年级数学核心知识点与常见题型(人教版)(解析版)

多边形(8种题型)【知识梳理】1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.2.相关概念:边:组成多边形的各条线段叫做多边形的边.顶点:每相邻两条边的公共端点叫做多边形的顶点.内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.3. 多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:凹多边形凸多边形【考点剖析】题型一:多边形及其概念例1.(2023春·全国·八年级专题练习)如图所示的图形中,属于多边形的有()A.3个B.4个C.5个D.6个【答案】A【分析】根据多边形定义,逐个验证即可得到答案.【详解】解:所示的图形中,第一个是三角形、第二个是四边形、第三个是圆、第四个是正六边形、第五个是正方体,属于多边形的有第一个、第二个、第四个,共有3个,故选:A.【点睛】本题考查多边形定义,熟记多边形定义是解决问题的关键.【变式】.下列图形不是凸多边形的是( )解析:根据凸多边形的概念,如果多边形的边都在任意一条边所在的直线的同旁,该多边形即是凸多边形,否则即是凹多边形.由此可得选项D的图形不是凸多边形.故选D.方法总结:多边形可分为凸多边形和凹多边形,辨别凸多边形可有两种方法:(1)画多边形任何一边所在的直线,整个多边形都在此直线的同一侧;(2)每个内角的度数均小于180°.通常所说的多边形指凸多边形.题型二:确定多边形的边数例2.(2023春·全国·八年级专题练习)若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是()A.5或6B.6或7C.5或6或7D.6或7或8【答案】C【分析】实际画图,动手操作一下,可知六边形可以是五边形、六边形、七边形截去一个角后得到.【详解】解:如图,原来多边形的边数可能是5,6,7.故选C【点睛】本题考查的是截去一个多边形的一个角,解此类问题的关键是要从多方面考虑,注意不能漏掉其中的任何一种情况.【变式1】(2022·全国·八年级专题练习)若一个多边形截去一个角后,变成六边形,则原来多边形的边数可能是_____.【答案】5,6,7.【分析】直接画图,动作操作即可知答案.【详解】如图可知,原多边形的边数可能为5,6,7故填5,6,7..【变式2】若一个多边形截去一个角后,变成十五边形,则原来的多边形的边数可能为( )A.14或15或16 B.15或16C.14或16 D.15或16或17解析:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,则多边形的边数是14,15或16.故选A.方法总结:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,解决此类问题可以亲自动手画一下.【变式3】(2022·全国·八年级专题练习)把一张长方形纸片剪去一个角后,还剩_____个角.【答案】3或4或5.【分析】剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者边数不变.【详解】解:如图所示,把一张长方形纸片剪去一个角后,可得三角形或四边形或五边形,故还剩3或4或5个角,故答案为:3或4或5.【点睛】本题考查了剪长方形的问题,掌握剪长方形的性质是解题的关键.题型三:确定多边形的对角线的条数例3.从四边形的一个顶点出发可画________条对角线,从五边形的一个顶点出发可画________条对角线,从六边形的一个顶点出发可画________条对角线,请猜想从七边形的一个顶点出发有________条对角线,从n 边形的一个顶点出发有________条对角线,从而推导出n 边形共有________条对角线.解析:根据n 边形从一个顶点出发可引出(n -3)条对角线.从n 个顶点出发引出n(n -3)条对角线,而每条重复一次,可得答案.解:从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,从七边形的一个顶点出发有4条对角线,从n 边形的一个顶点出发有(n -3)条对角线,从而推导出n 边形共有n (n -3)2条对角线. 方法总结:(1)多边形有n 条边,则经过多边形的一个顶点的对角线有(n -3)条;(2)多边形有n 条边,对角线的条数为n (n -3)2. 【变式1】(2022春·八年级课时练习)一个十边形有多少条对角线? 【答案】35【分析】根据多边形对角线计算公式进行求解即可.【详解】解:由题意得,一个十边形有()10103352⨯−=条对角线,答:一个十边形有35条对角线.【点睛】本题主要考查了多边形对角线条数问题,熟知从n 边形一个顶点出发可以引()3n −条对角线是解题的关键.【变式2】(2023秋·辽宁阜新·八年级统考期末)我们知道,三角形有0条对角线,四边形有2条对角线,五边形有5条对角线,那么n 边形有______条对角线. 【答案】(3)2n n −【分析】由于n 边形从一个顶点出发可画(3)n −条对角线,所以n 边形共有(3)2n n −条对角线,根据以上关系直接计算即可.【详解】解:三角形有0条对角线,四边形有2条对角线,五边形有5条对角线, n ∴边形有(3)2n n −条对角线. 故答案为:(3)2n n −.【点睛】本题考查了多边形对角线的定义及计算公式,熟记多边形的边数与对角线的关系式是解决此类问题的关键.【变式3】(2023春·浙江·八年级专题练习)我们学习多边形后,发现凸多边形的对角线有一定的规律,①中的四边形共有2条对角线,②中的五边形共有5条对角线,③中的六边形共有9条对角线,…,请你计算凸十边形对角线的总条数( )A .54B .44C .35D .27【答案】C【分析】根据一个n 边形的对角线条数为()32n n −进行求解即可.【详解】解:一个四边形共有2条对角线,一个五边形共有5条对角线,一个六边形共有9条对角线……一个十边形共有()10103352⨯−=条对角线,故C 正确.故选:C .【点睛】本题主要考查了对角线条数问题,解题的关键是熟练掌握一个n 边形的对角线条数为()32n n −.题型四:根据对角线条数确定多边形的边数例4.从一个多边形的任意一个顶点出发都只有5条对角线,则它的边数是( )A .6B .7C .8D .9解析:设这个多边形是n 边形.依题意,得n -3=5,解得n =8.故这个多边形的边数是8.故选C. 【变式】.(2023春·全国·八年级专题练习)若从一个多边形的一个顶点出发,最多可画2014条对角线,则它是( )边形. A .2017 B .2016C .2015D .2014【答案】A【分析】n边形一个顶点可以画()3n−条对角线,代入数据计算即可.【详解】解:设这个多边形是n边形.依题意,得32014n−=,∴2017n=.故这个多边形是2017边形,故选:A.【点睛】本题考查了多边形的对角线条数,熟记公式是解题关键.题型五:根据分成三角形的个数,确定多边形的边数例5.连接多边形的一个顶点与其他顶点的线段把这个多边形分成了6个三角形,则原多边形是( ) A.五边形 B.六边形 C.七边形 D.八边形解析:设原多边形是n边形,则n-2=6,解得n=8.故选D.方法总结:从n边形的一个顶点出发可引出(n-3)条对角线,这(n-3)条对角线把n边形分成(n-2)个三角形.【变式1】(2023春·浙江·八年级专题练习)过多边形一个顶点的所有对角线,将这个多边形分为5个三角形,则这个多边形是()A.五边形B.六边形C.七边形D.八边形【答案】C【分析】根据n边形从一个顶点出发可引出()3n−条对角线,可组成()2n−个三角形,依此可求出n的值,得到答案.【详解】解:设这个多边形是n边形,由题意得:25n−=,解得:7n=,即这个多边形是七边形,故选C.【点睛】本题考查了多边形的对角线,求对角线条数时,直接代入边数n的值计算,而计算边数时,需利用方程思想,解方程求n.【变式2】.(2023秋·八年级课时练习)连接多边形的一个顶点与其他顶点的线段把这个多边形分成了6个三角形,求多边形的边数.【答案】8【分析】根据过n 边形的一个顶点可以引(3)n −条对角线,将n 边形分成(2)n −个三角形即可得出结果. 【详解】解:设多边形的边数为n ,依题意得26n −=,解得8n =. ∴多边形的边数为8.【点睛】本题考查了多边形对角线的相关知识,掌握过n 边形的一个顶点可以引(3)n −条对角线,将n 边形分成(2)n −个三角形是本题的关键.题型六:正多边形的有关概念例6.下列图形中,是正多边形的是( )A .等腰三角形B .长方形C .正方形D .五边都相等的五边形解析:根据正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形进行解答.正方形四个角相等,四条边都相等,故选C.方法总结:解答此类问题的关键是要搞清楚正多边形的定义,各个角相等、各条边相等的多边形是正多边形,这两个条件缺一不可.【答案】A【分析】A. 由正多边形的性质可得 B. 举反例判断即可 C. 举反例判断即可 D. 举反例判断即可【详解】A. 由正多边形的性质:各边相等,各角相等,正确 B. 菱形不是正方形,错误 C. 矩形不是正方形,错误D. 正方形与边长相等的等边三角形拼成的五边形不是正多边形,错误 故选:A .【点睛】本题考查了正多边形的定义:平面内各边相等,各角相等的多边形是正多边形,准确理解定义及性质是解题关键.题型七:多边形面积例7.(2022秋·福建宁德·八年级校考阶段练习)如图小方格都是边长为1的正方形,则四边形ABCD的面积是()A.25B.12.5C.9D.8.5【答案】B【详解】试题分析:根据求差法,让大正方形面积减去周围四个直角三角形的面积即可解答.试题解析:如图:小方格都是边长为1的正方形,∴四边形EFGH是正方形,S□EFGH=EF•FG=5×5=25S△AED=12DE•AE=12×1×2=1,S△DCH=12•CH•DH=12×2×4=4,S△BCG=12BG•GC=12×2×3=3,S△AFB=12FB•AF=12×3×3=4.5.S四边形ABCD=S□EFGH-S△AED-S△DCH-S△BCG-S△AFB=25-1-4-3-4.5=12.5.故选B.【变式】(2022·全国·八年级专题练习)如图,小个方格都是边长为1的正方形,图中四边形ABCD的面积为________.【答案】1122【分析】利用大正方形的面积减去四边形周围的小三角形面积即可. 【详解】解:四边形ABCD 的面积为: 111155411142342222⨯−⨯⨯−⨯⨯−⨯⨯−⨯⨯=1122,故答案为:1122.【点睛】此题主要考查了四边形面积求法,掌握割补法是解题的关键. 题型八:确定三角形个数例8.(2023·全国·八年级假期作业)从十六边形的一个顶点出发的所有对角线,把这个十六边形分成__________个三角形. 【答案】14/十四【分析】从n 边形的一个顶点出发有()3n −条对角线,共分成了()2n −个三角形.【详解】解:当16n =时,16214−=, 即可以把这个十六边形分成了14个三角形, 故答案为:14.【点睛】本题考查了多边形的对角线,熟记相关公式是解题的关键,如果记不住公式,可以从四边形、五边形开始,画图探索规律.【变式】(2023春·上海长宁·八年级上海市延安初级中学校考阶段练习)从n 边形的一个顶点出发画对角线,可以将这个n 边形分割成__________个三角形. 【答案】()2n −/()2n −+【分析】从n 边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成()2n −个三角形,据此即可解答.【详解】解:从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成()2n−个三角形.故答案为:()2n−.【点睛】本题主要考查多边形的对角线,掌握从n边形的一个顶点出发,分别连接这个点与其余各顶点,形成的三角形个数为2n−是解答本题的关键.【过关检测】一、单选题1.(2023·全国·八年级假期作业)从多边形的一个顶点出发,可以画出4条对角线,则该多边形的边数为()A.5B.6C.7D.8【答案】C【分析】根据从n边形的一个顶点可以作对角线的条数公式()3n−求出边数即可得解.【详解】解:设多边形的边数为n,由题意,得:34n−=,∴7n=,∴该多边形的边数为7;故选C.【点睛】本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.掌握n边形从一个顶点出发可引出()3n−条对角线是解题的关键.2.(2023春·全国·八年级专题练习)若一个多边形截去一个角后,变成四边形,则原来的多边形的边数可能为()A.4或5B.3或4C.3或4或5D.4或5或6【答案】C【分析】根据多边形截去一个角的位置可得:比原多边形可能少1条边,可能边的条数不变,也可能增加1条边;据此求解即可.【详解】解:当多边形是五边形时,截去一个角时,可能变成四边形;当多边形是四边形时,截去一个角时,可能变成四边形;当多边形是三角形时,截去一个角时,可能变成四边形;所以原来的多边形的边数可能为:3或4或5.故选:C .【点睛】本题主要考查了多边形,解题的关键是理解多边形截去一个角的位置可得:比原多边形可能少1条边,可能边的条数不变,也可能增加1条边. 3.(2023春·浙江·八年级专题练习)如图,在探究过多边形的一个顶点引出的对角线把多边形分成三角形的个数时,画出的图形如下:根据图形可知,过n 边形的一个顶点引出的对角线,把n 边形分成的三角形的个数是( )A .()3n −个B .()2n −个C .()1n −个D .()1n +个【答案】B【分析】观察图形,找出规律,列出代数式即可.【详解】解:观察图形可得:第1个图,过四边形的一个顶点引出1条对角线,把四边形分成了2个三角形;第2个图,过五边形的一个顶点引出2条对角线,把四边形分成了3个三角形;第3个图,过六边形的一个顶点引出3条对角线,把四边形分成了4个三角形;……第()3n −个图,过n 边形的一个顶点引出()3n −条对角线,把n 边形分成()2n −个三角形;故选:B .【点睛】本题考查了找规律-图形变化类,仔细观察图形,找到变化规律是解题的关键.4.(2023春·浙江绍兴·八年级校联考期中)一个n 边形从一个顶点可引3条对角线,则n 为()A .6B .5C .4D .3【答案】A【分析】可根据n 边形从一个顶点引出的对角线与边的关系:3n −,列方程求解.【详解】解:设多边形有n 条边,则33n −=,解得,6n =.故选:A .【点睛】本题考查了多边形的对角线.解题的关键是明确多边形有n 条边,则经过多边形的一个顶点所有的对角线有(3)n −条,经过多边形的一个顶点的所有对角线把多边形分成(2)n −个三角形. 5.(2023·全国·八年级假期作业)下列说法错误的是( )A .五边形有5条边,5个内角,5个顶点;B .四边形有2条对角线;C .连接对角线,可以把多边形分成三角形;D .六边形的六个角都相等;【答案】D【分析】运用多边形的定义及其内角、对角线等知识分别判断后即可确定正确的选项.【详解】解:A 、五边形有5条边,5个内角,5个顶点,原选项正确,故不符合题意;B 、四边形有2条对角线,原选项正确,故不符合题意;;C 、连接对角线,可以把多边形分成三角形,原选项正确,故不符合题意;D 、六边形的六个角不一定相等,只有正六边形的六个内角相等,原选项错误,故符合题意;故选:D .【点睛】本题考查了多边形的定义及其内角、对角线等知识点,解决本题的关键是熟练掌握多边形的定义.【答案】C【分析】根据n 边形从一个顶点出发,可引出()3n −条对角线,即可求解.【详解】解:设这个多边形的边数为n ,则32n −=,解得5n =,故选:C .【点睛】本题考查了多边形的对角线,连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,掌握n 边形从一个顶点出发,可引出()3n −条对角线是解题的关键.7.(2022秋·河南洛阳·八年级校考期末)将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是( )A .5B .6C .7D .8【答案】D【分析】根据一个n边形剪去一个角后,剩下的形状可能是n边形或()1n+边形或()1n−边形即可得出答案.【详解】如图可知,原来多边形的边数可能是5,6,7.不可能是8.故选:D.【点睛】本题考查了多边形,剪去一个角的方法可能有三种:经过两个相邻顶点,则少了一条边;经过一个顶点和一边,边数不变;经过两条领边,边数增加.8.(2023春·全国·八年级专题练习)一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为()A.15或16或17B.15或17C.16或17D.16或17或18【答案】A【分析】分三种情况讨论,当截线不经过多边形的顶点时,当截线经过多边形的一个顶点时,当截线经过多边形的两个顶点时,再利用数形结合的方法可得答案.所以当被截后的多边形为16边形,则原多边形为15边形,如图,当截线经过多边形的一个顶点时,被截后的多边形与原多边形边数相同,所以当被截后的多边形为16边形,则原多边形为16边形,如图,当截线经过多边形的两个顶点时,被截后的多边形比原多边形少一条边,所以当被截后的多边形为16边形,则原多边形为17边形,故选:.A【点睛】本题考查的是用直线截多边形的一个角后,被截后的多边形的边数与原多边形的边数之间的关系,解题的关键是清晰的分类讨论.二、填空题 9.(2023秋·八年级单元测试)如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2023个三角形,那么这个多边形的边数为___________.【答案】2025【分析】从n 边形的一个顶点出发作它的对角线,将n 边形分成(2)n −个三角形,由此即可解决问题.【详解】解:从n 边形的一个顶点出发作它的对角线,将n 边形分成(2)n −个三角形,22023n ∴−=,2025n ∴=,故答案为:2025.【点睛】本题考查多边形的有关知识,解题的关键是掌握,从n 边形的一个顶点出发作它的对角线,将n 边形分成(2)n −个三角形. 10.(2023春·八年级单元测试)若从一个n 边形的一个顶点出发,最多可以引10条对角线,则n =_____.【答案】13【分析】根据对角线构成,不是一条边上的两个端点连线构成对角线,一个顶点所在两条边上与其相邻的两个顶点除外,n 边形的一个顶点引出(3)n −条对角线直接求解即可得到答案.【详解】解:从一个n 边形的一个顶点出发,最多可以引10条对角线, ∴根据题意得310n −=,解得13n =,故答案为:13.n−条对角线是解决问题的关键.【点睛】本题考查多边形对角的规律,掌握n边形的一个顶点引出(3)11.(2023·全国·八年级假期作业)若一个多边形无对角线,则这个多边形是_______________【答案】三角形【分析】由多边形的对角线的定义可得答案.【详解】解:一个多边形无对角线,则这个多边形是三角形,故答案为:三角形【点睛】本题考查的是多边形的对角线的含义,熟记图形特点与对角线的定义是解本题的关键.12.(2022·全国·八年级专题练习)一张七边形卡片剪去一个角后得到的多边形卡片可能的边数为______.【答案】6或7或8【分析】存在三种情况,根据图示进行分析.【详解】解:七边形卡片剪去一个角,存在以下三种,如图1、图2、图3:∴一个七边形卡片剪去一个角后可以变成的多边形卡片可能的边数为6或7或8,故答案为:6或7或8.【点睛】本题主要考查多边形,解题的关键是进行分类讨论进行求解.13.(2023·全国·八年级假期作业)若一个多边形截去一个角后,得到的新多边形为十五边形,则原来的多边形边数为______.【答案】14或15或16【分析】分三种情况进行讨论,得出答案即可.【详解】解:如图,一个多边形减去一个角后,比原来多边形少了一条边,+=;∴此时原多边形的边数为15116如图,一个多边形减去一个角后,与原来多边形的边数相同,∴此时原多边形的边数为15;−=;∴此时原多边形的边数为15114综上分析可知,原来的多边形边数为14或15或16.故答案为:14或15或16.【点睛】本题主要考查了多边形的边数问题,解题的关键是数形结合,注意进行分类讨论.14.(2023春·广西贵港·八年级统考期中)若一个多边形经过一个顶点的对角线将该多边形分成8个三角形,则该多边形为___________边形.【答案】十【分析】根据过多边形的一个顶点的所有对角线,将这个多边形分成()2n −个三角形,计算可求解.【详解】解:设这是个n 边形,由题意得:28n −= 10n ∴=,故答案为:十.【点睛】本题考查了多边形的对角线,掌握多边形对角线的性质是解题的关键. 15.(2023·全国·八年级假期作业)一个多边形从同一个顶点引出的对角线,将这个多边形分成5个三角形.则这个多边形有______条边.【答案】7【分析】根据过多边形的一个顶点的所有对角线,将这个多边形分成()2n −个三角形,即可求解得到答案. 【详解】解:设多边形有n 条边,则25n −=,解得:7n =.所以这个多边形有7条边,故答案为:7.16.(2022秋·湖北黄石·八年级校考期末)过m 边形的一个顶点有7条对角线,n 边形没有对角线,k 边形有2条对角线,则()n m k −=______.【答案】216【分析】根据m 边形从一个顶点发出的对角线有()3m −条,从而可求得m 的值;又根据n 边形没有对角线,只有三角形没有对角线,从而可求得n 的值;再根据k 边形共有对角线()32k k −条,从而可求得k 的值,代入即可求出代数式的值.【详解】解:∵m 边形从一个顶点发出的对角线有()3m −条,∴7310m =+=,又∵n 边形没有对角线,∴3n =,又∵k 边形有2条对角线,∴()322k k −=,∴4k =,1k =−(舍去)∴()()3104216n m k −=−=.故答案为:216.【点睛】本题考查了多边形的对角线,解决本题的关键是熟记n 边形从一个顶点发出的对角线有()3n −条,共有对角线()32n n −条. 17.(2021秋·内蒙古呼和浩特·八年级呼和浩特市实验中学校考期中)把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,则原多边形纸片的边数可能是 ___.【答案】十七边形,或十八边形,或十九边形【分析】结合题意,根据多边形截角后边数的性质,分三种截下的方式分析,即可得到答案.【详解】把一个多边形纸片沿一条直线截下一个三角形后,变成一个十八边形,有三种截下的方式: 下图为多边形局部图,如按下图所示沿虚线截下三角形:∴原多边形纸片的边数是:十七边形 如按下图所示沿虚线截下三角形:∴原多边形纸片的边数是:十八边形如按下图所示沿虚线截下三角形:∴原多边形纸片的边数是:十九边形∴原多边形纸片的边数可能是:十七边形,或十八边形,或十九边形故答案为:十七边形,或十八边形,或十九边形.【点睛】本题考查了多边形的知识;解题的关键是熟练掌握多边形的性质,从而完成求解.18.(2023春·全国·八年级专题练习)一个四边形截去一个角后,所形成的一个新多边形的边数是____.【答案】3或4或5【分析】一个四边形剪去一个角后,分三种情况求解即可,①边数可能减少1,②边数可能增加1,③边数可能不变.【详解】解:一个四边形截去一个角后得到的多边形可能是三角形,可能是四边形,也可能是五边形.故答案为:3或4或5.【点睛】本题考查的知识点是多边形的定义,解题关键是列举出所有可能的情况.三、解答题(1)如图①从多边形的一个顶点出发画对角线,把多边形分割成三角形;(2)如图②从多边形的一条边上的一点出发画对角线,把多边形分割成三角形;(3)如图③从多边形的内部一点出发画对角线,把多边形分割成三角形.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)连接两个不相邻的顶点即可;(2)在一边上找一点,分别跟与这条边不相邻的两个顶点相连即可;(3),在四边形内取一点,分别与四个顶点相连即可;【详解】(1)解:如图①所示,连接一组不相邻的顶点即可;(2)解:如图②所示,在一边上找一点,分别跟与这条边不相邻的两个顶点相连即可;(3)解:如图③所示,在四边形内取一点,分别与四个顶点相连即可;【点睛】本题考查多边形的对角线问题,能够熟练画出多边形的对角线是解决本题的关键.【答案】九边形【分析】根据n边形从一个顶点出发可引出()3n−条对角线,可组成()2n−个三角形,依此可得n的值.【详解】设这个多边形是n边形,由题意得,n-2=7,解得:n=9,故这个多边形是九边形.【点睛】本题考查了多边形的对角线分成三角形的问题,理解n边形从一个顶点出发可引出()3n−条对角线,可组成()2n−个三角形是解题的关键.21.(2022秋·湖北恩施·八年级校考阶段练习)在日常生活中,观察各种建筑物的地板,你就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌),这显然与正多边形的内角大小有关,当围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.。
多边形内角和(7种题型)-2023年新八年级数学核心知识点与常见题型(人教版)(解析版)

多边形内角和(7种题型)【知识梳理】一、多边形内角和n 边形的内角和为(n-2)·180°(n ≥3).要点诠释:(1)内角和公式的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数;(2)正多边形;二、多边形的外角和多边形的外角和为360°.要点诠释:(1)在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n 边形的外角和恒等于360°,它与边数的多少无关;(3)多边形的外角和为360°的作用是:①已知各相等外角度数求多边形边数;②已知多边形边数求各相等外角的度数.三.平面镶嵌(密铺)(1)平面图形镶嵌的定义:用形状,大小完全相同的一种或几种平面图形进行拼接.彼此之间不留空隙,不重叠地铺成一片,这就是平面图形的镶嵌.(2)正多边形镶嵌有三个条件限制:①边长相等;②顶点公共;③在一个顶点处各正多边形的内角之和为360°.判断一种或几种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不能.(3)单一正多边形的镶嵌:正三角形,正四边形,正六边形.(4)两种正多边形的镶嵌:3个正三角形和2个正方形、四个正三角形和1个正六边形、2个正三角形和2个正六边形、1个正三角形和2个正十二边形、1个正方形和2个正八边形等.(5)用任意的同一种三角形或四边形能镶嵌成一个平面图案.180°【考点剖析】题型一:利用内角和求边数例1.一个多边形的内角和为540°,则它是( )A.四边形 B.五边形 C.六边形 D.七边形解析:熟记多边形的内角和公式(n-2)·180°.设它是n边形,根据题意得(n-2)·180=540,解得n=5.故选B.方法总结:熟记多边形的内角和公式是解题的关键.【变式1】(2021·河北承德市·八年级期末)一个多边形的内角和是900°,这个多边形的边数是()A.3 B.4 C.5 D.7【答案】D【分析】根据多边形的内角和公式:(n-2)•180°去求.【详解】解:设该多边形的边数为n则:(n-2)•180°=900°,解得:n=7.故选:D.【点睛】本题考查了多边形的内角和,关键是要记住公式并会解方程【变式2】(2021·浙江省余姚市实验学校八年级期中)若一个多边形的内角和是720°,则这个多边形的边数为()A.4 B.5 C.6 D.7【答案】C【分析】根据正多边形的内角和定义(n−2)×180°,先求出边数,再用内角和除以边数即可求出这个正多边形的每一个内角.【详解】解:(n−2)×180°=720°,∴n−2=4,∴n=6.∴这个多边形的边数为6.故选:C.【点睛】考查了多边形内角与外角.解题的关键是掌握好多边形内角和公式:(n−2)×180°.题型二:求多边形的内角和例2.一个多边形的内角和为1800°,截去一个角后,得到的多边形的内角和为( )A.1620° B.1800°C.1980° D.以上答案都有可能解析:1800÷180=10,∴原多边形边数为10+2=12.∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,∴新多边形的边数可能是11,12,13,∴新多边形的内角和可能是1620°,1800°,1980°.故选D.方法总结:一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1.根据多边形的内角和公式求出原多边形的边数是解题的关键.【变式1】(2021·云南临沧·八年级期末)一个八边形的内角和度数为()A.360°B.720°C.900°D.1080°【答案】D【分析】应用多边形的内角和公式计算即可.【详解】(n﹣2)•180=(8﹣2)×180°=1080°.故选:D.【点睛】此题主要考查了多边形内角和定理,关键是熟练掌握计算公式:(n−2)•180 (n≥3)且n为整数).【变式2】(2021·广西来宾市·八年级期中)已知一个多边形的每一个内角都比它相邻的外角的4倍多30°,求这个多边形是几边形?并求出这个多边形的内角和.【答案】十二边形,1800°【分析】首先设外角为x°,则内角为(4x+30)°,根据内角与相邻的外角是互补关系可得x+4x+30=180,解方程可得x的值,再利用外角和360°÷外角的度数可得边数,进而求出内角和.【详解】解:设外角为x°,由题意得:x+4x+30=180,解得:x=30,360°÷30°=12,∴(12−2)×180=1800°,∴这个多边形的内角和是1800°,是十二边形.【点睛】本题主要考查多边形内角与外角的知识点,此题要结合多边形的内角和公式以及外角和,构建方程求解即可.【变式3】(2020·南京市宁海中学八年级开学考试)问题1:如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,∠AOC与∠A、∠C、∠P的数量关系为∠AOC=∠A+∠C+∠P.问题2:如图(2),已知AP平分∠BAD,CP平分∠BCD,∠B=28°,∠D=48°,求∠P的大小;小明认为可以利用“镖形”图的结论解决上述问题:由问题1结论得:∠AOC=∠PAO+∠PCO+∠APC,所以2∠AOC=2∠PAO+2∠PCO+2∠APC,即2∠AOC=∠BAO+∠DCO+2∠APC;由“”得:∠AOC=∠BAO+∠B,∠AOC=∠DCO+∠D.所以2∠AOC=∠BAO+∠DCO+∠B+∠D.所以2∠APC= .所以∠APC= .请帮助小明完善上述说理过程,并尝试解决下列问题(问题1、问题2中得到的结论可以直接使用,不需说明理由);解决问题1:如图(3)已知直线平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系为解决问题2:如图(4),已知直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,则∠P与∠B、∠D的关系为【答案】问题1、问题2答案见解析;解决问题1:∠P=180°-12(∠B+∠D);解决问题2:∠P=90°+12(∠B+∠D)【分析】问题1:根据三角形的外角的性质即可得到结论;问题2:根据三角形外角的性质和问题1的结论求解即可;解决问题1:根据四边形的内角和等于360°可得(180°-∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°-∠3)+∠D=360°,然后整理即可得解;解决问题2:根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.【详解】解:问题1:连接PO并延长.则∠1=∠A+∠2,∠3=∠C+∠4,∵∠2+∠4=∠P,∠1+∠3=∠AOC,∴∠AOC=∠A+∠C+∠P;故答案为:∠AOC=∠A+∠C+∠P;问题2:如图2,由问题1结论得:∠AOC=∠PAO+∠PCO+∠APC,所以2∠AOC=2∠PAO+2∠PCO+2∠APC,即2∠AOC=∠BAO+∠DCO+2∠APC;由“三角形外角的性质”得:∠AOC=∠BAO+∠B,∠AOC=∠DCO+∠D.所以2∠AOC=∠BAO+∠DCO+∠B+∠D.所以2∠APC=∠B+∠D.所以∠APC= 12(∠B+∠D)=38°.解决问题1:如图3,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴(180°-2∠1)+∠B=(180°-2∠4)+∠D,在四边形APCB中,(180°-∠1)+∠P+∠4+∠B=360°,在四边形APCD中,∠2+∠P+(180°-∠3)+∠D=360°,∴2∠P+∠B+∠D=360°,∴∠P=180°-12(∠B+∠D);解决问题2:如图4,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°-2∠3)+∠D,∠2+∠P=(180°-∠3)+∠D,∴2∠P=180°+∠D+∠B,∴∠P=90°+12(∠B+∠D).故答案为:∠P=90°+12(∠B+∠D).【点睛】本题主要考查了三角形外角的性质,角平分线的性质,四边形的内角和,解题的关键在于能够熟练掌握相关知识进行求解.题型三:复杂图形中的角度计算例3.如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )A.450° B.540° C.630° D.720°解析:如图,∵∠3+∠4=∠8+∠9,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠8+∠9+∠5+∠6+∠7=五边形的内角和=540°,故选B.方法总结:根据图形特点,将问题转化为熟知的问题,体现了转化思想的优越性.【变式1】(2021·全国八年级单元测试)如图,在五边形ABCDE中,∠D=120°,与∠EAB相邻的外角是80°,与∠DEA,∠ABC相邻的外角都是60°,则∠C为________度.【答案】80【分析】利用邻补角的定义分别求出∠DEA,∠ABC,∠EAB的度数;再利用五边形的内角和为540毒,可求出∠C的度数.【详解】解:∵与∠EAB相邻的外角是80°,与∠DEA,∠ABC相邻的外角都是60°,∴∠DEA=180°-60°=120°,∠ABC=180°-60°=120°,∠EAB=180°-80°=100°;五边形的内角和为(5-2)×180°=540°;∴∠C=540°-120°-120°-120°-100°=80°.故答案为:80.【点睛】此题考查了多边形内角和的性质,涉及了邻补角的定义,熟练掌握相关基本性质是解题的关键.【变式2】(2020·南京市宁海中学八年级开学考试)如图,五边形ABCDE的两个内角平分线相交于点O,∠1,∠2,∠3是五边形的3个外角,若∠1+∠2+∠3=220°,则∠AOB=___________.【答案】70°【分析】先求出与∠EAB和∠CBA相邻的外角的度数和,然后根据多边形外角和定理即可求解.【详解】如图,∵∠1+∠2+∠3=220°,∴∠4+∠5=360°-220°=140°,∴∠EAB+∠CBA=220°,∵AO,BO分别平分∠EAB,∠ABC,∴∠OAB+∠OBA=110°,∴∠AOB=180°-(∠OAB+∠OBA)=70°.故答案是:70°.【点睛】本题主要考查了多边形外角和定理,三角形的内角和定理,熟练掌握多边形的外角和等于360°是解题的关键.【变式3】(2022春•武冈市期中)如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.【分析】利用三角形内角和定理将不规则图形转化成规则图形:五边形.【解答】解:如图,由三角形内角和定理得:∠1+∠5=∠8+∠9,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠5+∠2+∠3+∠4+∠6+∠7=∠8+∠9+∠2+∠3+∠4+∠6+∠7=180°×(5﹣2)=540°.【点评】本题主要考查多边形内角和,解题关键是利用三角形内角和定理将不规则图形转化成规则图形.【变式4】(2022春•宿城区校级月考)利用“模型”解决几何综合问题往往会取得事半功倍的效果.几何模型:如图(1),我们称它为“A”型图案,易证明:∠EDF=∠A+∠B+∠C.运用以上模型结论解决问题:(1)如图(2),“五角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5=?分析:图中A1A3DA4是“A”型图,于是∠A2DA5=∠A1+∠A3+∠A4,所以∠A1+∠A2+∠A3+∠A4+∠A5=;(2)如图(3),“七角星”形,求∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7的度数.【分析】(1)根据三角形外角的性质把5个角转化到一个三角形中可得答案;(2)根据三角形外角的性质把7个角转化到一个三角形中可得答案.【解答】解:(1)如图,由三角形外角的性质可得,∠1=∠A1+∠A4,∵∠A2DA5=∠1+∠A3,∴∠A2DA5=∠A1+∠A4+∠A3,∵∠A2DA5+∠A2+∠A5=180°,∴∠A1+∠A2+∠A3+∠A4+∠A5=180°,故答案为:180°;(2)如图,由(1)得,∠1=∠A1+∠A4+∠A5,∠2=∠A2+∠A3+∠A6,∵∠1+∠2+∠A7=180°,∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7=180°.【点评】本题考查多边形的内角和与三角形外角的性质,能够根据三角形外角的性质进行转化是解题关键.题型四:利用方程和不等式确定多边形的边数例4.一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?解析:本题首先由题意找出不等关系列出不等式,进而求出这一内角的取值范围;然后可确定这一内角的度数,进一步得出这个多边形的边数.解:设此多边形的内角和为x ,则有1125°<x <1125°+180°,即180°×6+45°<x <180°×7+45°,因为x 为多边形的内角和,所以它是180°的倍数,所以x =180°×7=1260°.所以7+2=9,1260°-1125°=135°.因此,漏加的这个内角是135°,这个多边形是九边形.方法总结:解题的关键是由题意列出不等式求出这个多边形的边数. 【变式1】.(2023春·全国·八年级专题练习)看图回答问题:(1)内角和为2014°,小明为什么说不可能?(2)小华求的是几边形的内角和?【答案】(1)理由见详解(2)13【分析】(1(2)根据题意设多边形的边数为x ,根据多边形的内角和定理即可求解.【详解】(1)解:∵设多边形的边数为n ,则n 边形的内角和是180(2)n ︒⨯−,∴内角和一定是180︒度的倍数,∵20141801134÷=,∴内角和为2014︒不可能.(2)解:设多边形的边数为x ,∴180(2)2014x ︒⨯−<︒,解得,171390x <, ∴多边形的边数是13,∴小华求的是十三边形的内角和.【点睛】本题主要考查多边形的内角和定理,掌握多边形的内角和定理是解题的关键.【变式2】(2023春·全国·八年级专题练习)解决多边形问题:(1)一个多边形的内角和是外角和的3倍,它是几边形?(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是1170︒,这个多边形是几边形?【答案】(1)八边形(2)八边形【分析】(1)根据多边形的内角和公式、多边形的外角和等于360︒建立方程,解方程即可得;(2)设这个多边形是n 边形,重复加的一个角的度数为x ,则0180x ︒<<︒,再根据多边形的内角和公式建立等式,结合0180x ︒<<︒建立不等式组,解不等式组即可得.【详解】(1)解:设这个多边形是n 边形,由题意得:()18023360n ︒−=⨯︒,解得8n =,答:这个多边形是八边形.(2)解:设这个多边形是n 边形,重复加的一个角的度数为x ,则0180x ︒<<︒,由题意得:()18021170n x ︒−+=︒,解得1530180x n =︒−︒,则01530180180n ︒<︒−︒<︒,即153018001530180180n n ︒−︒>︒⎧⎨︒−︒<︒⎩,解得151722n <<, n Q 为正整数,8n ∴=,答:这个多边形是八边形.【点睛】本题考查了多边形的内角和与外角和、一元一次不等式组的应用,正确建立方程和不等式组是解题关键.题型五:已知各相等外角的度数,求多边形的边数例5.正多边形的一个外角等于36°,则该多边形是正( )A .八边形B .九边形C .十边形D .十一边形解析:正多边形的边数为360°÷36°=10,则这个多边形是正十边形.故选C.方法总结:如果已知正多边形的一个外角,求边数可直接利用外角和除以这个角即可.【变式1】.(2022春·八年级单元测试)已知一个多边形的每个外角都是30︒,那么这个多边形的边数是__________.【答案】12【分析】利用任何多边形的外角和是360︒除以外角度数即可求出答案.÷=,【详解】解:多边形的外角的个数是3603012所以多边形的边数是12,故答案为:12.【点睛】本题主要考查了多边形的外角和定理,已知外角求边数的这种方法是需要熟记的内容.【变式2】(2021·广西八年级期中)己知一个n边形的每一个外角都等于30°.(1)求n的值.(2)求这个n边形的内角和.【答案】(1)12;(2)1800°【分析】(1)用360°除以外角度数可得答案.(2)先求出每个内角的度数,再利用内角度数×内角的个数即可.【详解】解:(1)∵n边形的每一个外角都等于30°∴n=360°÷30°=12;(2)∵每个内角=180°-30°=150∴内角和=12×150°=1800°.【点睛】此题主要考查了多边形的内角和、外角和,关键是掌握多边形的外交和等于360°.题型六:多边形内角和与外角和的综合运用例6.一个多边形的内角和与外角和的和为540°,则它是( )A.五边形 B.四边形 C.三角形 D.不能确定解析:设这个多边形的边数为n,则依题意可得(n-2)×180°+360°=540°,解得n=3,∴这个多边形是三角形.故选C.方法总结:熟练掌握多边形的内角和定理及外角和定理,解题的关键是由已知等量关系列出方程从而解决问题.【变式1】(2021·陕西)一个多边形的内角和与外角和的度数之和为1260︒,求这个多边形的边数.【答案】多边形的边数为7【分析】设这个多边形的边数为n,根据这个多边形的内角和+外角和360°=1800°,列出方程求解即可.【详解】解:设多边形的边数是n,由题意得,()21803601260n−⨯︒+︒=︒,n=.解得:7答:多边形的边数为7.【点睛】本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是360°,与边数无关,熟练多边形的内角和定理是解题的关键.【变式2】(2021·广西来宾市·八年级期中)已知一个多边形的每一个内角都比它相邻的外角的4倍多30°,求这个多边形是几边形?并求出这个多边形的内角和.【答案】十二边形,1800°【分析】首先设外角为x°,则内角为(4x+30)°,根据内角与相邻的外角是互补关系可得x+4x+30=180,解方程可得x的值,再利用外角和360°÷外角的度数可得边数,进而求出内角和.【详解】解:设外角为x°,由题意得:x+4x+30=180,解得:x=30,360°÷30°=12,∴(12−2)×180=1800°,∴这个多边形的内角和是1800°,是十二边形.【点睛】本题主要考查多边形内角与外角的知识点,此题要结合多边形的内角和公式以及外角和,构建方程求解即可.【变式3】(2021秋•泰州期末)【相关概念】将多边形的内角一边反向延长,与另一条边相夹形成的那个角叫做多边形的外角.如图,将△ABC中∠ACB的边CB反向延长,与另一边AC形成的∠ACD即为△ACB的一个外角.三角形外角和与三角形内角和对应,为与三个内角分别相邻的三个外角的和.【求解方法】借助一组内角与外角的数量关系,可以求出三角形的外角和.如图,△ABC的外角和=(180°﹣∠ACB)+(180°﹣∠CAB)+(180°﹣∠ABC)=540°﹣(∠ACB+∠ABC+∠CAB)=540°﹣180°=360°.【自主探究】根据以上提示,完成下列问题:(1)将下列表格补充完整.(2)如果一个八边形的每一个内角都相等,请用两种不同的方法求出这个八边形一个内角的度数.【分析】(1)根据n 边形的内角和为(n ﹣2)×180°,n 边形的外角和为360°即可得出答案;(2)根据多边形的内角和公式和多边形的外角和360°即可得出答案.【解答】解:(1)内角和分别为:四边形内角和是:(4﹣2)×180°=360°,,五边形内角和是:(5﹣2)×180°=540°,n 边形内角和是:180°(n ﹣2);外角和分别为:360°、360°、360°;故答案为:360°、540°、180°(n﹣2),360°、360°、360°;(2)这个八边形一个内角的度数是:方法一:(8﹣2)×180°÷8=135°,方法二:180°﹣360°÷8=135°.【点评】本题考查了多边形内角与外角:n边形的内角和为(n﹣2)×180°;n边形的外角和为360°.题型七:平面镶嵌例7.(2022春·八年级单元测试)用同一种下列形状的图形地砖不能进行平面镶嵌的是()A.正三角形B.长方形C.正八边形D.正六边形【答案】C【分析】分别求出各个正多边形的每个内角的度数,结合镶嵌的条件即可求出答案.【详解】解:A.正三角形的每个内角是60︒,能整除360︒,能密铺,故A不符合题意;B.长方形的每个内角是90︒,能整除360︒,能密铺,故B不符合题意;C.正八边形的每个内角为:1803608135︒−︒÷=︒,不能整除360︒,不能密铺,故C符合题意;D.正六边形的每个内角为120︒度,能整除360︒,能密铺,故D不符合题意.故选:C.【点睛】本题主要考查了平面镶嵌,解题的关键是熟练掌握一种正多边形的镶嵌应符合一个内角度数能整除360︒.【变式】(2022春·八年级单元测试)用正多边形来镶嵌平面的原理是共顶点的各个角之和必须等于360︒.现在有七种不同的正多边形:①正三角形、②正方形、③正六边形、④正八边形、⑤正十边形、⑥正十二边形、⑦正十五边形.请你用其中的不同的三种正多边形来镶嵌平面,这三种正多边形可以是:________.(请用序号表示,只需写出两种即可)【答案】①②③或①②⑥或②③⑥【分析】先分别求出正三角形、正方形、正五边形、正六边形、正七边形、正八边形的每个内角,然后根据平面镶嵌的条件解答即可.【详解】解:用公式()1802nn︒⨯−分别计算出正三角形的内角为60︒,正方形的内角为90︒,正六边形的内角为120︒,正八边形内角为135︒,正十边形的内角为144︒,正十二边形的内角为150︒,正十五边形的内角为156︒,∵609090120360︒+︒+︒+︒=︒,∴正三角形、正方形、正六边形可以进行平面镶嵌;∵606090150360︒+︒+︒+︒=︒,∴正三角形、正方形、正十二边形可以进行平面镶嵌;∵90120150360︒+︒+︒=︒,∴正方形、正六边形、正十二边形可以进行平面镶嵌;故答案为:①②③或①②⑥或②③⑥.【点睛】本题主要考查了镶嵌的条件,镶嵌的条件是看位于同一顶点处的几个角之和能否为360︒.【过关检测】一、单选题A.180︒B.360【答案】B【分析】根据多边形的外角和等于360︒解答即可.【详解】解:由多边形的外角和等于360︒可知,123456360∠+∠+∠+∠+∠+∠=︒,故选:B.【点睛】本题考查的是多边形的外角和,掌握多边形的外角和等于360︒是解题的关键.2.(2023春·山东泰安·八年级校考期末)正多边形的内角和为720︒,则这个多边形的一个内角为()A.90︒B.60︒C.120︒D.135︒【答案】C【分析】由正多边形的内角和为720︒,可得()2180720n−︒=︒,再求解n可得答案.【详解】解:∵正多边形的内角和为720︒,∴()2180720 n−︒=︒,解得:6n=,∴这个多边形的一个内角为720=1206︒︒;故选C【点睛】本题考查的是正多边形的内角和问题,熟记多边形的内角和公式与正多边形的定义是解本题的关键.3.(2023春·浙江·八年级专题练习)一个多边形的内角和是其外角和的2倍,则这个多边形是()A.六边形B.七边形C.八边形D.九边形【答案】A【分析】设这个多边形的边数为n,根据多边形的内角和公式和多边形的外角和都是360︒,列出方程即可求出结论.【详解】解:设多边形的边数是n,根据题意得,()21802360n−⨯︒=⨯︒,解得:6n=,∴这个多边形为六边形.故选:A.【点睛】本题主要考查了多边形的内角和公式与外角和定理,根据题意列出方程是解题的关键.4.(2023春·浙江·八年级专题练习)一个多边形的每个内角都相等,这个多边形的外角不可能是()A.30︒B.40︒C.50︒D.60︒【答案】C【分析】根据多边形的每个内角都相等,则这个多边形的每一个外角均相等,根据外角和等于360︒即可求解.【详解】解:由题意得,多边形的每个内角都相等,∴这个多边形的每一个外角均相等.∴每一个外角的度数整除360︒,∵30︒、40︒、60︒均能整除360︒,50︒不能整除360︒,∴选项C 符合题意.故选:C .【点睛】本题考查了多边形的外角和,熟记知识点是解题关键. 5.(2023春·全国·八年级专题练习)如图,A B C D E F ∠+∠+∠+∠+∠+∠等于( )A .240︒B .300︒C .360︒D .540︒【答案】C 【分析】连接BD ,根据四边形内角和可得360A ABO OBD BDO CDO C ∠+∠++∠+∠+∠=︒,再由“8”字三角形可得OBD ODB E F ∠+∠=∠+∠,进而可得答案.【详解】解:连接BD ,如图,∵360A ABO OBD BDO CDO C ∠+∠+∠+∠+∠+∠=︒,OBD ODB E F ∠+∠=∠+∠,∴360A ABO E F CDO C ∠+∠+∠+∠+∠+∠=︒,故选C .【点睛】本题考查了多边形的内角和,以及“8”字三角形的特点,正确作出辅助线是解答本题的关键.6.(2022春·八年级单元测试)将一个多边形切去一个角后所得的多边形内角和为2520,则原多边形的边数为( )A .15或16B .16或17C .15或16或17D .16或17或18【答案】C【分析】因为一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,根据多边形的内角和即可解决问题.【详解】解:多边形的内角和可以表示成()2180n −⋅︒(3n ≥且n 是正整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,根据题意得()21802520n −⋅︒=︒,解得:16n =,则多边形的边数是15或16或17,故C 正确.故选:C .【点睛】本题主要考查了多边形的内角和定理,本题容易出现的错误是:认为截取一个角后角的个数减少1. 7.(2023秋·广西钦州·八年级统考期末)小红:我计算出一个多边形的内角和为2020︒;老师:不对呀,你可能少加了一个角!则小红少加的这个角的度数是( )A .110︒B .120︒C .130︒D .140︒【答案】D【分析】设这个多边形的边数为n ,少加的角的度数为x ,由多边形内角和定理可得等式:180(2)2020n x −=+,由n 为整数即可确定x 的值.【详解】设这个多边形的边数为n ,少加的角的度数为x ,由题意得:180(2)2020n x −=+,4013180xn +∴=+,由于n 为整数,x 为正数且小于180,40180x ∴+=,则140x =,故选:D .【点睛】本题考查了多边形内角和定理,关键是设多边形的边数及少加的角的度数,由多边形内角和定理得到等式,根据边数为整数确定少加的角.8.(2023·全国·八年级假期作业)已知一个多边形内角和为1080︒,则这个多边形可连对角线的条数是( )A .10B .16C .20D .40【答案】C【分析】先根据多边形内角和计算公式求出这个多边形是八边形,再根据多边形对角线计算公式求解即可.【详解】解:设这个多边形为n边形,由题意得,()180210802n⨯−=,∴8n=,∴这个多边形为八边形,∴这个多边形可连对角线的条数是()883202⨯−=,故选C.【点睛】本题主要考查了多边形内角和定理,多边形对角线计算公式,熟知n边形的对角线条数是()32 n n−是解题的关键.9.(2023秋·八年级课时练习)一个多边形截去一角后,变成一个八边形,则这个多边形原来的边数是()A.8或9B.7或8C.7或8或9D.8或9或10【答案】C【分析】画出所有可能的情况,即可作答.【详解】如图所示∴这个多边形原来是7边形或8边形或9边形故选C.【点睛】本题考查的知识点是多边形内角与外角,解题关键是注意分情况作答.二、填空题10.(2023春·安徽淮北·八年级淮北一中校联考阶段练习)若n边形的每个内角都是108,则边数n为___.【答案】5【分析】根据多边形的内角和公式()2180n︒−⋅列方程求解即可.【详解】解:由题意得, ()2180108n n ︒︒−⋅=⋅解得:5n =.故答案为:5.【点睛】本题考查了多边形的内角和,熟记内角和公式并列出方程是解题的关键. 11.(2022春·八年级单元测试)如图是由射线AB 、BC 、CD 、DA 组成的平面图形,则1234∠+∠+∠+∠=______°.【答案】360【分析】根据多边形的外角和为360︒求解即可.【详解】解:由图可知,1∠、2∠、3∠、4∠为组成的四边形的外角,∴1234360∠+∠+∠+∠=︒,故答案为:360.【点睛】本题考查多边形的外角性质,熟知多边形的外角和为360︒是解题的关键.12.(2023春·浙江宁波·八年级校联考期中)一个正n 多边形的一个内角是它的外角的4倍,则n =___________.【答案】10【分析】由多边形的每一个内角与相邻的这个外角互补先求解每一个外角,从而可得答案.【详解】解:∵一个正n 多边形的一个内角是它的外角的4倍,∴正多边形的每一个外角为:180365︒=︒,∴3601036n ︒==︒,故答案为:10.【点睛】本题考查的是正多边形的内角和与外角和的综合,熟记多边形的每一个内角与相邻的这个外角互补是解本题的关键.13.(2023春·全国·八年级专题练习)若一个多边形的每个外角均为36︒,则这个多边形的内角和为_______度.【答案】1440【分析】依据多边形外角和为360︒求得边数,再依据多边形内角和公式代入求解即可.【详解】解:因为多边形的每个外角均为36︒,且外角和为360︒,所以这个多边形边数:3603610︒÷︒=,则这个多边形的内角和为:()1021801440−⨯︒=︒,故答案为:1440.【点睛】本题考查了多边形内角和公式、外角和为360︒;通过外角和求得边数是解题的关键.【答案】12【分析】设这个多边形的边数为n,根据题意得多边形的内角和是外角和的5倍,列出方程求解即可.【详解】解:设这个多边形的边数为n,根据题意得多边形的内角和是外角和的5倍,∴() 36052180n⨯=−⨯,解得:12n=,所以这个多边形的边数为12.故答案为:12.【点睛】题目主要考查一元一次方程的应用及多边形的内角和与外角和等,理解题意,列出方程是解题关键.15.(2023春·陕西西安·八年级西安行知中学校考阶段练习)一个多边形的内角和是外角和的3倍,则它是____________边形.【答案】八【分析】多边形的外角和是360度,多边形的内角和是外角和的3倍,则多边形的内角和是()3603︒⨯度,根据多边形的内角和可以表示成()2180n−⋅︒,依此列方程可求解.【详解】解:设多边形边数为n.则() 36032180n⨯=−⋅,解得8n=.∴这个多边形是八边形.故答案为:八.【点睛】本题主要考查了多边形内角和公式及外角的特征.求多边形的边数,可以转化为方程的问题来解决.16.(2023·全国·八年级假期作业)一个n边形的所有内角和等于540︒,则n的值等于__.【答案】5【分析】已知n边形的内角和为540︒,根据多边形内角和的公式易求解.【详解】解:依题意有()2180540n−⋅︒=︒,解得5n=.故答案为:5.【点睛】主要考查的是多边形的内角和公式,本题的难度简单.掌握多边形的内角和为()2180n−⋅︒是解题的关键.【答案】1080°【分析】连KF,GI,根据n边形的内角和定理得到7边形ABCDEFK的内角和=(7-2)×180°=900°,则∠A +∠B+∠C+∠D+∠E+∠F+∠K+(∠1+∠2)=900°,由三角形内角和定理可得到∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,则∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠3+∠4)+∠5+∠6+∠H=900°+180°,即可得到∠A +∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数.【详解】解:连KF,GI,如图,。
中考数学复习----《正多边形》知识点总结与专项练习题(含答案解析)

中考数学复习----《正多边形》知识点总结与专项练习题(含答案解析)知识点总结1.正多边形的概念:每一条边都相等且每个角都相等的多边形叫做正多边形。
2.正多边形的内角度数:正多边形的每个内角度数为:()nn︒⨯−1802。
(n表示多边形的边数)3.正多边形的外角度数:正多边形的每个外角度数为:n ︒360。
(n表示多边形的边数)4.正多边形内外角的关系:正多边形的每一个内角与它每一个外角互补。
即()︒=︒+︒⨯−1803601802nnn练习题1、(2022•江西)正五边形的外角和为度.【分析】根据多边形外角和等于360°即可解决问题.【解答】解:正五边形的外角和为360度,故答案为:360.2、(2022•湘西州)一个正六边形的内角和的度数为()A.1080°B.720°C.540°D.360°【分析】利用多边形的内角和定理解答即可.【解答】解:一个正六边形的内角和的度数为:(6﹣2)×180°=720°,故选:B.3、(2022•通辽)正多边形的每个内角为108°,则它的边数是()A.4 B.6 C.7 D.5【分析】方法一:根据相邻的内角与外角互为邻补角求出每一个外角的度数为72°,再用外角和360°除以72°,计算即可得解;方法二:设多边形的边数为n,然后根据多边形的内角和公式(n﹣2)•180°列方程求解即可.【解答】解:方法一:∵正多边形的每个内角等于108°,∴每一个外角的度数为180°﹣108°=72°,∴边数=360°÷72°=5,方法二:设多边形的边数为n,由题意得,(n﹣2)•180°=108°•n,解得n=5,所以,这个多边形的边数为5.故选:D.4、(2022•烟台)一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是()A.正方形B.正六边形C.正八边形D.正十边形【分析】设这个外角是x°,则内角是3x°,根据内角与它相邻的外角互补列出方程求出外角的度数,根据多边形的外角和是360°即可求解.【解答】解:∵一个正多边形每个内角与它相邻外角的度数比为3:1,∴设这个外角是x°,则内角是3x°,根据题意得:x+3x=180,解得:x=45,360°÷45°=8(边),故选:C.5、(2022•南充)如图,在正五边形ABCDE中,以AB为边向内作正△ABF,则下列结论错误的是()A.AE=AF B.∠EAF=∠CBF C.∠F=∠EAF D.∠C=∠E【分析】根据正多边形定义可知,每一个内角相等,每一条边相等,再根据内角和公式求出每一个内角,根据以AB为边向内作正△ABF,得出∠FAB=∠ABF=∠F=60°,AF=AB=FB,从而选择正确选项.【解答】解:在正五边形ABCDE中内角和:180°×3=540°,∴∠C=∠D=∠E=∠EAB=∠ABC=540°÷5=108°,∴D不符合题意;∵以AB为边向内作正△ABF,∴∠FAB=∠ABF=∠F=60°,AF=AB=FB,∵AE=AB,∴AE=AF,∠EAF=∠FBC=48°,∴A、B不符合题意;∴∠F≠∠EAF,∴C符合题意;故选:C.6、(2022•徐州)正十二边形的一个内角的度数为.【分析】首先求得每个外角的度数,然后根据外角与相邻的内角互为邻补角即可求解.【解答】解:正十二边形的每个外角的度数是:=30°,则每一个内角的度数是:180°﹣30°=150°.故答案为:150°.7、(2022•菏泽)如果正n边形的一个内角与一个外角的比是3:2,则n=.【分析】设外角为2x,则其内角为3x,根据其内外角互补可以列出方程求得外角的度数,然后利用外角和定理求得边数即可.【解答】解:设外角为2x,则其内角为3x,则2x+3x=180°,解得:x=36°,∴外角为2x=72°,∵正n边形外角和为360°,∴n=360°÷72°=5,故答案为:5.8、(2022•泰州)正六边形的一个外角的度数为°.【分析】根据正多边形的每一个外角都相等和多边形的外角和等于360度解答即可.【解答】解:∵正六边形的外角和是360°,∴正六边形的一个外角的度数为:360°÷6=60°,故答案为:60.9、(2022•株洲)如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO=度.【分析】根据正五边形的性质求出∠EAB,根据三角形的外角性质计算,得到答案.【解答】解:∵五边形ABCDE是正五边形,∴∠EAB==108°,∵∠EAB是△AEO的外角,∴∠AEO=∠EAB﹣∠MON=108°﹣60°=48°,故答案为:48.10、(2022•遂宁)如图,正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6,则正六边形ABCDEF的边长为.【分析】根据正多边形的性质和直角三角形中,30°角所对的边是斜边的一半可以求得AF的长.【解答】解:设AF=x,则AB=x,AH=6﹣x,∵六边形ABCDEF是正六边形,∴∠BAF=120°,∴∠HAF=60°,∵∠AHF=90°,∴∠AFH=30°,∴AF=2AH,∴x=2(6﹣x),解得x=4,∴AB=4,即正六边形ABCDEF的边长为4,故答案为:4.11、(2022•舟山)正八边形一个内角的度数为.【分析】首先根据多边形内角和定理:(n﹣2)•180°(n≥3,且n为正整数)求出内角和,然后再计算一个内角的度数.【解答】解:正八边形的内角和为:(8﹣2)×180°=1080°,每一个内角的度数为×1080°=135°.故答案为:135°.12、(2022•西宁)若正n边形的一个外角是36°,则n=.【分析】利用多边形的外角和即可解决问题.【解答】解:n=360°÷36°=10.故答案为:10.13、(2022•资阳)小张同学家要装修,准备购买两种边长相同的正多边形瓷砖用于铺满地面.现已选定正三角形瓷砖,则选的另一种正多边形瓷砖的边数可以是.(填一种即可)【分析】分别求出各个多边形的每个内角的度数,结合镶嵌的条件即可求出答案.【解答】解:正三角形的每个内角是60°,正四边形的每个内角是90°,∵3×60°+2×90°=360°,∴正四边形可以,正六边形的每个内角是120°,∵2×60°+2×120°=360°,∴正六边形可以,正十二边形的每个内角是150°,∵1×60°+2×150°=360°,∴正十二边形可以,故答案为:4答案不唯一.14、(2022•甘肃)大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为()A.2mm B.22mm C.23mm D.4mm【分析】根据正六边形的性质和题目中的数据,可以求得正六边形ABCDEF的边长.【解答】解:连接BE,CF,BE、CF交于点O,如右图所示,∵六边形ABCDEF是正六边形,AD的长约为8mm,∴∠AOF=60°,OA=OD=OF,OA和OD约为4mm,∴AF约为4mm,故选:D.。
八年级上册数学多边形知识点和典型习题分类汇总附答案

第 1 页第17讲 多边形❖ 基本知识(公式要会推导,能画图的要画图理解) 1、多边形:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形。
2、三角形是多边形吗? 【当然,是!】3、连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
4、三角形有对角线吗? 【当然,没有!】5、凸多边形:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。
6、凹多边形:如果多边形存在至少一条边,画出多边形的这条边所在直线,如果整个多边形不全在这条直线的同一侧,那么这个多边形就是凹多边形。
【初中范围内,如不专门说明,多边形就是指凸多边形。
】7、各个角都相等,各条边都相等的多边形叫做正多边形。
8、每一个内角都相等的多边形是正多边形吗? 【不一定】9、每一条边都相等的多边形是正多边形吗?【不一定】 10、多边形的内角和公式:n 边形的内角和为(n -2)×180°。
11、多边形的外角和等于360°。
12、n 边形的相关数据【借助图形和推导记住,勿死记!】 (1)边数:n ; (2)内角数:n ;(3)外角数:n ; (4)从一个顶画出的对角线数:(n -3); 2)3(-n n (5)对角线总数: (6)从一个顶点画出的对角线,把n 边形分成的三角形数:(n -2);(7)内角和:(n -2)×180°;(8)外角和:360°;(9)正n n n 180)2(⨯-边形的内角大小:;(10)正n n360边形的外角大小:。
❖ 习题精练【多边形的对角线】1、若多一个多边形的一个顶点出发,最多可以引10条对角线,则它是_________边形.2、从n 边形的一个顶点出发作对角线,可以把这个n 边形分成9个三角形,则n 等于___________.3、一个7边形共有几条对角线?4、5人互相握手,共需握几次?5、6人互赠贺卡,共需几张贺卡?6、平面上任意三者不共线的8个点,两两相连,能得几条直线?几条射线?7、如图,在∠ABC 的内部再画6条射线,可得多少个角?参考答案1、132、113、144、105、306、28条直线,56条射线7、28【多边形的内角】1、一个多边形的内角和是900度,这个多边形的边数是________.2、一个多边形的每个内角都是120度,这个多边形的边数是________.【两种方法:内角和或外角和】3、已知两个多边形的内角和为1800度,且两多边形的边数之比为2:5,求这两个多边形的边数.4、如图在四边形ABCD 中,∠A=∠D 、∠B=∠C ,试判断AD 与BC 的位置关系,并说明理由.5、如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4x ,则=______.第 2 页6、【难】如图,六边形ABCDEF 的内角都相等,∠DAB=60°,AB 与DE 有什么关系?BC 与EF 有这种关系吗?这些结论是怎样得出的?7、将一个长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和是_______________.8、一个多边形截取一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是_________.9、若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为________.10、若一个多边形的每一个内角均为135°,则从此多边形的一个顶点出发,可以画______条对角线.11、如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.参考答案1、72、63、4和104、AD//BC5、36°6、AB//DE ,BC//EF7、360°,540°或720°8、10、11或129、130° 10、5 9、540°【多边形的外角和】1、已知一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.2、一个多边形中,每个内角都相等,并且每个外角都等于41其相邻内角的,求这个多边形的边数及内角和.3、如图所示,分别以n 边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为______个平方单位.4、一个多边形的内角和与某一个外角的度数之和为1350°,求这个多边形的边数.5、多边形的内角和加上它的一个外角是750°,这个多边形的边数是多_______,这个外角是________.6、【难】(1)如图∠∠,试研究其中∠1、∠2与∠3、∠4之间的数量关系;(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;(3)用你发现的结论解决下列问题:如图∠,AE 、DE 分别是四边形ABCD 的外角∠NAD 、∠MDA 的平分线,∠B+∠C=240°,求∠E 的度数.参考答案1、72、边数为10,内角和为1440° 3 、 4、9 5、6 6、(1)∠1+∠2=∠3+∠4;(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和;(3)∠E=60°。
专题18 多边形-中考数学一轮复习精讲+热考题型(解析版)

专题18 多边形【知识要点】多边形的相关知识:➢在平面中,由一些线段首尾顺次相接组成的图形叫做多边形,多边形中相邻两边组成的角叫做它的内角。
多边形的边与它邻边的延长线组成的角叫做外角。
➢连接多边形不相邻的两个顶点的线段叫做多边形的对角线。
➢一个n边形从一个顶点出发的对角线的条数为(n-3)条,其所有的对角线条数为2)3(nn凸多边形:画出多边形的任何一条边所在的直线,如果多边形的其它边都在这条直线的同侧,那么这个多边形就是凸多边形。
正多边形:各角相等,各边相等的多边形叫做正多边形。
(两个条件缺一不可,除了三角形以外,因为若三角形的三内角相等,则必有三边相等,反过来也成立)⏹多边形的内角和➢n边形的内角和定理:n边形的内角和为(n−2)∙180°➢n边形的外角和定理:多边形的外角和等于360°,与多边形的形状和边数无关。
【考查题型】考查题型一多边形截角后的边数问题【解题思路】多边形减去一个角的方法可能有三种:经过两个相邻点:则少了一条边:经过一个顶点和一边:边数不变:经过两条邻边:边数增加一条.典例1.(云南昭通市模拟)把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是()A.16B.17C.18D.19【答案】A【详解】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n-1)边形.故当剪去一个角后,剩下的部分是一个18边形,则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.故选A.变式1-1.(宁波市一模)把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是()A.六边形B.五边形C.四边形D.三角形【答案】A【解析】当剪去一个角后,剩下的部分是一个四边形,则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.故选A.考查题型二计算多边形的周长【解题思路】考查多边形的周长,解题在于掌握计算公式典例2.(隆化县模拟)下列图形中,周长不是32 m的图形是( )A.B.C.D.【答案】B【提示】根据所给图形,分别计算出它们的周长,然后判断各选项即可.【详解】A. L=(6+10)×2=32,其周长为32.B. 该平行四边形的一边长为10,另一边长大于6,故其周长大于32.C. L=(6+10)×2=32,其周长为32.D. L=(6+10)×2=32,其周长为32.采用排除法即可选出B故选B.变式2-1.(海南中考模拟)如图:□ABCD纸片,:A=120°:AB=4:BC=5,剪掉两个角后,得到六边形AEFCGH ,它的每个内角都是120°,且EF=1:HG=2:则这个六边形的周长为( )A.12B.15C.16D.18【答案】B【解析】如图,分别作直线AB:BC:HG的延长线和反向延长线使它们交于点B:Q:P.∵六边形ABCDEF的六个角都是120°:∴六边形ABCDEF的每一个外角的度数都是60°.∴△APH:△BEF:△DHG:△CQG都是等边三角形.∴EF=BE=BF=1:DG=HG=HD=2.∴FC=5-1=4:AH=5-2= 3:CG=CD-DG=4−2=2.∴六边形的周长为1+3+3+2+2+4=15.故选B.考查题型三计算网格中的多边形面积【解题思路】利用分割法即可解决问题典例3.(辽宁葫芦岛市模拟)如图是边长为1的正方形网格,A、B、C、D均为格点,则四边形的面积为()A .7B .10C .152D .8【答案】A【提示】利用分割法即可解决问题. 【详解】解:S 四边形ABCD =3×4﹣12×2×1×2﹣12×1×3×2=12﹣5=7,故选:A . 变式3-1.(山东烟台市模拟)如图,在边长为1的小正方形网格中,△ABC 的三个顶点均在格点上,若向正方形网格中投针,落在△ABC 内部的概率是( )A .12B .14C .38D .516【答案】D【提示】用正方形的面积减去四个易求得三角形的面积,即可确定△ABC 面积,用△ABC 面积除以正方形的面积即可.【详解】解:正方形的面积=4×4=16,三角形ABC 的面积=11116434221222-⨯⨯-⨯⨯-⨯⨯ =5, 所以落在△ABC 内部的概率是516,故选D .变式3-2.(江西九年级零模)如图,在边长为1的小正方形网格中,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形图中①,②,③,④四个格点多边形的面积分别记为1234,,,,S S S S 下列说法正确的是( )A .12S SB .23S S =C .124S S S +=D .134S S S +=【答案】B【提示】根据题意判断格点多边形的面积,依次将1234S S S S 、、、计算出来,再找到等量关系. 【详解】观察图形可得12342.5,3,3,6,S S S S ==== ∴23234,6S S S S S =+==, 故选:B .考查题型四 计算多边形对角线条数【解题思路】熟记n 边形从一个顶点出发可引出(n-3)条对角线是解答此题的关键.典例4.(山东济南市·中考真题)一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( ) A .12 B .13C .14D .15【答案】C【解析】解:根据题意,得::n:2:•180=360°×2+180°,解得:n=7: 则这个多边形的边数是7,七边形的对角线条数为7(73)2⨯-=14:故选C: 变式4-1.(山东济南市·中考模拟)若凸n 边形的每个外角都是36°,则从一个顶点出发引的对角线条数是( )A .6B .7C .8D .9 【答案】B【解析】360°÷36°=10,10−3=7.故从一个顶点出发引的对角线条数是7. 故选:B.变式4-2.(莆田市二模)从n 边形的一个顶点出发可以连接8条对角线,则n =( ) A .8 B .9 C .10 D .11【答案】D【提示】根据n 边形从一个顶点出发可引出(n-3)条对角线,可得n-3=8,求出n 的值即可. 【详解】解:由题意得:n-3=8,解得n=11,故选:D .变式4-3.(湖南长沙市模拟)已知一个正n 边形的每个内角为120°,则这个多边形的对角线有( ) A .5条 B .6条 C .8条 D .9条【答案】D【提示】多边形的每一个内角都等于120°,则每个外角是60°,而任何多边形的外角是360°,则求得多边形的边数;再根据多边形一个顶点出发的对角线=n﹣3,即可求得对角线的条数.【详解】解:∵多边形的每一个内角都等于120°,∴每个外角是60度,则多边形的边数为360°÷60°=6,则该多边形有6个顶点,则此多边形从一个顶点出发的对角线共有6﹣3=3条.∴这个多边形的对角线有12(6×3)=9条,故选:D.变式4-4.(广东茂名市·中考模拟)若一个多边形从同一个顶点出发可以作5条对角线,则这个多边形的边数为()A.6B.7C.8D.9【答案】C【提示】可根据n边形从一个顶点引出的对角线有n-3条,即可求解.【详解】解:设这个多边形的边数为n,则n-3=5,解得n=8,故这个多边形的边数为8,故选:C.变式4-5.(河北模拟)过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是()A.六边形B.七边形C.八边形D.九边形【答案】D【提示】根据n边形从一个顶点出发可引出(n-3)条对角线,可组成n-2个三角形,依此可得n的值.【详解】解:设这个多边形是n边形,由题意得,n-2=7,解得:n=9,即这个多边形是九边形,故选:D:考查题型五多边形内角和问题【解题思路】考查多边形的内角和公式,解题关键是牢记多边形的内角和公式.典例5.(山东济宁市·中考真题)如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC、∠BCD,则∠P的度数是( )A .60°B .65°C .55°D .50°【答案】A【解析】根据五边形的内角和等于540°,由:A+:B+:E=300°,可求:BCD+:CDE 的度数,再根据角平分线的定义可得:PDC 与:PCD 的角度和,进一步求得:P 的度数. 解::五边形的内角和等于540°,:A+:B+:E=300°, ::BCD+:CDE=540°﹣300°=240°,::BCD 、:CDE 的平分线在五边形内相交于点O , ::PDC+:PCD=(:BCD+:CDE )=120°, ::P=180°﹣120°=60°. 故选A .变式5-1.(甘肃庆阳市·中考真题)如图,足球图片正中的黑色正五边形的内角和是( ).A .180°B .360°C .540°D .720°【答案】C【提示】根据多边形内角和公式2180()n -⨯︒即可求出结果.【详解】解:黑色正五边形的内角和为:5218540(0)-⨯︒=︒,故选C .变式5-2.(湖南湘西土家族苗族自治州·中考真题)已知一个多边形的内角和是1080°,则这个多边形是( ) A .五边形 B .六边形 C .七边形 D .八边形【答案】D【提示】根据多边形的内角和=(n ﹣2)•180°,列方程可求解. 【详解】设所求多边形边数为n ,∴(n ﹣2)•180°=1080°,解得n=8.故选D.考查题型六正多边形内角和问题【解题思路】掌握并能运用多边形内角和公式是解题的关键典例6.(湖南怀化市·中考真题)若一个多边形的内角和为1080°,则这个多边形的边数为()A.6B.7C.8D.9【答案】C【提示】设这个多边形的边数为n,由n边形的内角和等于180°(n﹣2),即可得方程180(n﹣2)=1080,解此方程即可求得答案:n=8.故选C.变式6-1.(湖北宜昌市·中考真题)游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行.成功的招数不止一招,可助我们成功的一招是().A.每走完一段直路后沿向右偏72°方向行走B.每段直路要短C.每走完一段直路后沿向右偏108°方向行走D.每段直路要长【答案】A【提示】根据题意可知封闭的图形是正五边形,求出正五边形内角的度数即可解决问题.【详解】根据题意可知,从起点走五段相等直路之后回到起点的封闭图形是正五边形,∵正五边形的每个内角的度数为:(52)1801085-⨯︒=︒∴它的邻补角的度数为:180°-108°=72°,因此,每走完一段直路后沿向右偏72°方向行走,故选:A.变式6-2.(河北中考真题)正六边形的一个内角是正n边形一个外角的4倍,则n=_________.【答案】12【提示】先根据外角和定理求出正六边形的外角为60°,进而得到其内角为120°,再求出正n边形的外角为30°,再根据外角和定理即可求解.【详解】解:由多边形的外角和定理可知,正六边形的外角为:360°÷6=60°,故正六边形的内角为180°-60°=120°,又正六边形的一个内角是正n 边形一个外角的4倍, :正n 边形的外角为30°,:正n 边形的边数为:360°÷30°=12. 故答案为:12.变式6-3.(福建中考真题)如图所示的六边形花环是用六个全等的直角三角形拼成的,则ABC ∠等于_______度.【答案】30【提示】先证出内部的图形是正六边形,求出内部小正六边形的内角,即可得到∠ACB 的度数,根据直角三角形的两个锐角互余即可求解.【详解】解:由题意六边形花环是用六个全等的直角三角形拼成, 可得BD=AC ,BC=AF , ∴CD=CF ,同理可证小六边形其他的边也相等,即里面的小六边形也是正六边形,∴∠1=()1621801206-⨯︒=︒, ∴∠2=180°-120°=60°, ∴∠ABC=30°, 故答案为:30.考查题型七 截角后的内角和问题【解题思路】剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个是解决本题的关键.典例7.(五莲县一模)一个正方形被截掉一个角后,得到一个多边形,这个多边形的内角和是( ) A .360° B .540°C .180°或360°D .540°或360°或180°【答案】D【提示】剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个,根据多边形的内角和定理即可求解. 【详解】n 边形的内角和是(n ﹣2)•180°,边数增加1,则新的多边形的内角和是(4+1﹣2)×180°=540°,所得新的多边形的角不变,则新的多边形的内角和是(4﹣2)×180°=360°, 所得新的多边形的边数减少1,则新的多边形的内角和是(4﹣1﹣2)×180°=180°, 因而所成的新多边形的内角和是540°或360°或180°, 故选D .变式7-1.(河北九年级其他模拟)一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是( ) A .17 B .16 C .15 D .16或15或17【答案】D【详解】多边形的内角和可以表示成()2180n -⋅︒ (3n ≥且n 是整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条, 根据()21802520,n -⋅︒=解得:n=16, 则多边形的边数是15,16,17. 故选D .变式7-2.(贵州铜仁市·九年级零模)一个多边形切去一个角后得到的另一个多边形的内角和为900︒,那么原多边形的边数为( ) A .6或7或8 B .6或7 C .7或8 D .7【答案】A【提示】首先求得内角和为900°的多边形的边数,即可确定原多边形的边数. 【详解】解:设内角和为900°的多边形的边数是n ,则(n-2)•180°=900°,解得:n=7,如图,有如下几种切法,则原多边形的边数为6或7或8.故选:A.考查题型八正多边形的外角问题【解题思路】解决问题的关键是掌握多边形的外角和等于360度.典例8.(江苏无锡市·中考真题)正十边形的每一个外角的度数为()A.36︒B.30C.144︒D.150︒【答案】A【提示】利用多边形的外角性质计算即可求出值.【详解】解:360°÷10=36°,故选:A.变式8-1.(江苏扬州市·中考真题)如图,小明从点A出发沿直线前进10米到达点B,向左转45︒后又沿直线前进10米到达点C,再向左转45︒后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为()A.100米B.80米C.60米D.40米【答案】B【提示】根据题意,小明走过的路程是正多边形,先用360°除以45°求出边数,然后再乘以10米即可.【详解】解:∵小明每次都是沿直线前进10米后再向左转45︒,∴他走过的图形是正多边形,边数n=360°÷45°=8,∴小明第一次回到出发点A时所走的路程=8×10=80米.故选:B.变式8-2.(湖南娄底市·中考真题)正多边形的一个外角为60°,则这个多边形的边数为()A.5B.6C.7D.8【答案】B【提示】根据正多边形的外角和以及一个外角的度数,求得边数.【详解】解:正多边形的一个外角等于60°,且外角和为360°,则这个正多边形的边数是:360°÷60°=6,故选:B.考查题型九多边形外角和的实际应用【解题思路】典例9.(湖北黄冈市·中考真题)如果一个多边形的每一个外角都是36°,那么这个多边形的边数是()A.7B.8C.9D.10【答案】D【提示】根据多边形的外角的性质,边数等于360°除以每一个外角的度数.【详解】∵一个多边形的每个外角都是36°,∴n=360°÷36°=10.故选D.变式9-1.(山东德州市·中考真题)如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°……照这样走下去,他第一次回到出发点A时,共走路程为()A.80米B.96米C.64米D.48米【答案】C【提示】根据多边形的外角和即可求出答案.【详解】解:根据题意可知,他需要转360÷45=8次才会回到原点,所以一共走了8×8=64米.故选:C考查题型十多边形内角和与外角和的综合应用【解题思路】熟悉多边形的内角和公式:n边形的内角和是(n-2)×180°;多边形的外角和是360度.典例10.(西藏中考真题)一个多边形的内角和是外角和的4倍,则这个多边形的边数是()A.8B.9C.10D.11【答案】C【提示】利用多边形的内角和公式及外角和定理列方程即可解决问题.【详解】设这个多边形的边数是n,则有(n-2)×180°=360°×4,所有n=10.故选C.变式10-1.(陆丰市模拟)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于(:A.108°B.90°C.72°D.60°【答案】C【提示】首先设此多边形为n边形,根据题意得:180(n-2)=540,即可求得n=5,再由多边形的外角和等于360°,即可求得答案.【详解】解:设此多边形为n边形,根据题意得:180(n-2)=540,解得:n=5,∴这个正多边形的每一个外角等于:3605=72°.故选C.变式10-2.(中江县模拟)已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是()A.8B.9C.10D.12【答案】A【解析】试题提示:设这个多边形的外角为x°,则内角为3x°,根据多边形的相邻的内角与外角互补可的方程x+3x=180,解可得外角的度数,再用外角和除以外角度数即可得到边数.解:设这个多边形的外角为x°,则内角为3x°,由题意得:x+3x=180,解得x=45,这个多边形的边数:360°÷45°=8,故选A.变式10-3.(西宁市模拟)一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是()A.5B.6C.7D.8【答案】C【解析】解:设这个多边形的边数是n:根据题意得::n-2:•180°=2×360°+180°: n=7:故选C:考查题型十一平面镶嵌【解题思路】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角:典例11.下列多边形中,不能够单独铺满地面的是()A.正三角形B.正方形C.正五边形D.正六边形【答案】C【提示】由镶嵌的条件知:在一个顶点处各个内角和为360°:【详解】∵正三角形的内角=180°÷3=60°:360°÷60°=6:即6个正三角形可以铺满地面一个点:∴正三角形可以铺满地面:∵正方形的内角=360°÷4=90°:360°÷90°=4:即4个正方形可以铺满地面一个点:∴正方形可以铺满地面:∵正五边形的内角=180°:360°÷5=108°:360°÷108°≈3.3:∴正五边形不能铺满地面:∵正六边形的内角=180°:360°÷6=120°:360°÷120°=3:即3个正六边形可以铺满地面一个点:∴正六边形可以铺满地面:故选C:变式11-1 小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可能...是()A.正三角形B.正方形C.正五边形D.正六边形【答案】C【提示】平面图形镶嵌的条件:判断一种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角,若能构成360,则说明能够进行平面镶嵌;反之则不能.【详解】解:因为用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,所以小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可以是正五边形.故选:C变式11-2.能够铺满地面的正多边形组合是()A.正六边形和正方形B.正五边形和正八边形C.正方形和正八边形D.正三角形和正十边形【答案】C【解析】A、正六边形的每个内角是120°,正方形的每个内角是90°,120m+90n=360°,显然n取任何正整数时,m不能得正整数,故不能铺满;B、正五边形每个内角是180°-360°÷5=108°,正八边形每个内角为135度,135m+108n=360°,显然n取任何正整数时,m不能得正整数,故不能铺满;C、正方形的每个内角为90°,正八边形的每个内角为135°,两个正八边形和一个正方形刚好能铺满地面;D、正三角形每个内角为60度,正十边形每个内角为144度,60m+144n=360°,显然n取任何正整数时,m不能得正整数,故不能铺满.故选C.变式11-3 下列边长相等的正多边形能完成镶嵌的是()A.2个正八边形和1个正三角形B.3个正方形和2个正三角形C.1个正五边形和1个正十边形D.2个正六边形和2个正三角形【答案】D【提示】只需要明确几个几何图形在一点进行平铺就是几个图形与这一点相邻的所有内角之和等于360°即可。
五上多边形面积知识点归纳总结及习题

五年级数学上册第五单元多边形面积知识点归纳总结一、基本图形(一)长方形1、长方形面积=长×宽字母公式:s=ab长方形周长=(长+宽)×2字母公式:c=(a+b)×2(长=周长÷2-宽;宽=周长÷2-长)2、★长方形中面积、周长与长和宽之间的变化关系:(1)长方形的长加宽等于长方形周长的一半。
即 a + b = c ÷ 2(2)当长方形的周长不变时,长与宽的差越大,这个长方形的面积就越小;反之,长与宽的差越小,这个长方形的面积就越大。
(3)当长方形的面积不变时,长与宽的差越大,这个长方形的周长就越长;长与宽的差越小,这个长方形的周长就越短。
(4)长方形框架拉成平行四边形,周长不变,面积变小。
(二)正方形1、正方形面积=边长×边长字母公式:s= a²或者s=a×a2、正方形周长=边长×4字母公式:c=4a 或者c= a×4(三)平行四边形1、平行四边形面积=底×高字母公式:s=ah2、★平行四边形面积公式的推导过程:剪拼、平移沿着平行四边形的任意一条高剪开,将其一部分平移与另一部分正好拼成一个长方形,这个长方形的长就是平行四边形的底,这个长方形的宽就是平行四边形的高。
因为长方形的面积=长×宽,所以平行四边形的面积=底×高,用字母表示S=a×h。
3、★等底等高的平行四边形面积相等。
(四)三角形1、三角形面积=底× 高÷2字母公式:s=ah÷2(底=面积×2÷高;高=面积×2÷底)2、★三角形面积公式的推导过程:旋转、平移将两个完全一样的三角形拼成一个平行四边形,拼成的平行四边形的底就是三角形的底,拼成的平行四边形的高就是三角形的高,拼成的平行四边形的面积是三角形面积的2倍。
一个三角形的面积是这个平行四边形的面积一半。
多边形及其内角和练习题(答案)

第9章 多边形总复习一、知识点1.三角形:由三条不在同一直线上的线段首尾顺次连结组成的平面图形叫做三角形。
2.三角形的内角:在三角形中,每两条边所组成的角叫做三角形的内角。
3.三角形的外角:三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角。
4.三角形的分类:⑴按角分类:三角形 ⎝⎛钝角三角形直角三角形锐角三角形⑵按边分类:三角形 ⎝⎛ ⎝⎛)()(正三角形等边三角形三角形底边和腰不相等的等腰等腰三角形三条边互不相等不等边三角形 5.三角形的三条重要线段⑴中线:连结三角形的一个顶点与对边中点的线段叫做三角形的中线。
⑵高:从三角形的一个顶点向对边作垂线,顶点与垂足间的线段叫做三角形的高。
钝角三角形有两条边上的高在三角形外。
⑶三角形的角平分线:三角形一个内角的平分线与对边相交于一点,顶点与交点之间的线段叫做三角形的角平分线。
⑷重要规律:①三角形的三条中线相交于一点,该点叫做三角形的重心。
②三角形的三条高(或其所在直线)相交于一点。
三角形的三条高(或其所在直线)相交于一点,该点叫做三角形的垂心。
③三角形的三条角平分线相交于一点,这一点叫做三角形的内心,它到三角形的三边的距离相等。
6.三角形的内角和等于180°。
7.三角形的外角和等于360°。
8.三角形的外角性质:⑴三角形的一个外角等于和它不相邻的两个内角的和; ⑵三角形的一个外角大于任何一个与它不相邻的内角。
9.三角形的三边关系:⑴三角形任意两边之和大于第三边; ⑵三角形的任意两边之差小于第三边。
10.多边形的定义:由n 条不在同一直线上线段首尾顺次连结组成的平面图形叫做n 边形。
11.正多边形的定义:各边相等且各内角也相等的多边形叫做正多边形。
12.多边形的对角线:连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
经过)3(≥n n 多边形的一个顶点....有)3(-n 条对角线;)3(≥n n 边形共有..2)3(-n n 条对角线。
第六讲 多边形(含解析)(人教版)

第六讲多边形【学习目标】1.掌握多边形的定义及有关概念,能区分凹凸多边形.2.掌握正多边形的概念.3.会求多边形的对角线的条数.【新课讲解】知识点1:多边形的定义及相关概念1.在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.2.了解多边形、内角、外角、对角线等数学概念以及凸多边形的形状的辨别多边形相邻的两边组成的角叫做它的内角,如图,∠A,∠B,∠C,∠D,∠E是五边形ABCDE的5个内角,多边形的边与它的邻边延长线组成的角叫做多边形的外角.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线,线段AC、 AD是五边形ABCDE的对角线.3.凸多边形和凹多边形请分别画出下列两个图形各边所在的直线,:你能得到什么结论?图(2)此类多边形被一条边所在的直线分成了两部分,不在这条直线同侧是凹多边形.如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形.只讨论凸多边形.【例题1】凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.【答案】见解析。
【解析】∵六边形截去一个角的边数有增加1、减少1、不变三种情况,∴新多边形的边数为7、5、6三种情况,如图所示.注意:一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.知识点2:多边形的对角线1.定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.线段AC是五边形ABCDE的一条对角线,线段AD是五边形ABCDE的一条对角线,多边形的对角线通常用虚线表示.规律总结:从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.n(n≥3)边形共有对角线条.【例题2】过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为27,求这个多边形的边数.【答案】11【解析】设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,∴n-3+n-2=27,解得n=11.答:该多边形的边数有11条.知识点3:正多边形1. 正多边形的定义像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.2.判断是否为正多边形的方法判断一个多边形是不是正多边形,各边都相等,各角都相等,两个条件必须同时具备.【例题3】如图是菱形和矩形。
初中数学 四边形模块6-1 多边形讲义(含答案解析) - 副本

第一部分多边形题型练题型一多边形及相关定义1.多边形定义在平面内,由若干不在同一条直线上的线段首尾顺次连接所组成的封闭图形叫做多边形组成多边形的线段叫做多边形的边,相邻两边的公共端点叫做多边形的顶点;多边形一般按边数命名,用它各个顶点字母顺次排列来表示,多边形具有不稳定性2.正多边形定义平面内各边相等,各角也相等的多边形叫做正多边形例1.有下列说法:①由许多条线段连结而成的图形叫做多边形;②多边形的边数是不小于4的自然数;③从一个多边形(边数为n)的同一个顶点出发,分别连结这个顶点和其余与之不相邻的各顶点,可以把这个多边形分割成(n-2)个三角形;④在平面内,由5条线段首尾顺次相接组成的封闭图形叫做五边形.其中正确的说法有()A.1个B.2个C.3个D.4个【解析】(1)因为“多边形的定义是:由3条及3条以上的线段首尾顺次连接形成的封闭图形叫多边形”,所以①中说法错误;(2)因为“多边形中边数最少的是三角形,只有3条边”,所以②中说法错误;(3)因为“从n边形的一个顶点出发引出的所有对角线刚好把多边形分成(n-2)个三角形”,所以③中说法正确;(4)因为“五边形的定义是:在平面内,由五条线段首尾顺次连接形成的封闭图形叫做五边形”,所以④中说法正确综上所述,上述四种说法中正确的有2个变式1.下列说法不正确的是()A.各边相等的多边形是正多边形B.等边三角形是正多边形C.正多边形的各个内角都相等D.正多边形的各条边都相等【答案】A【解析】【分析】根据正多边形的定义:各个边相等,各个角相等的多边形是正多边形,除正三边形以外,各边相等,各角相等,两个条件必须同时成立.【详解】A.各个边相等,各个角相等的多边形是正多边形,故选项A错误;B.等边三角形三条边相等,三个角相等,是正多边形,故选项B正确;C.正多边形的各个内角都相等,故选项C正确;D.正多边形的各条边都相等,故选项D正确.故选A.【点睛】本题考查了正多边形的定义,注意各边相等,各角相等,两个条件必须同时成立.题型二多边形内角及n边形内角和1.多边形中相邻两边组成的角叫做多边形的内角,简称多边形的角2.n边形内角和公式(n-2)×180°(n为不小于3的整数)例2.若一个多边形的内角和是900°,则这个多边形是_____边形.【解析】设这个多边形是n边形,根据题意得,()2180900⋅︒,n-︒=n=.解得7变式2.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是_____度.【答案】540【解析】【详解】【分析】利根据题意得到2条对角线将多边形分割为3个三角形,然后根据三角形内角和可计算出该多边形的内角和.【详解】从某个多边形的一个顶点出发的对角线共有2条,则将多边形分割为3个三角形.所以该多边形的内角和是3×180°=540°,故答案为540.【点睛】本题考查了多边形的内角和与对角线,熟知n边形从一个顶点出发的对角线将n边形分成(n-2)个三角形是关键.这里体现了转化的数学思想.题型三多边形外角和1.在多边形顶点处,一边与另一边延长线所组成的角叫做多边形的外角2.多边形外角和为360°例3:一个多边形的每个外角都等于60︒,则这个多边形的边数是__________.【解析】︒÷︒=360606故个多边形是六边形变式3.正六边形的一个内角是正n边形一个外角的4倍,则n=_________.【答案】12【解析】【分析】先根据外角和定理求出正六边形的外角为60°,进而得到其内角为120°,再求出正n边形的外角为30°,再根据外角和定理即可求解.【详解】解:由多边形的外角和定理可知,正六边形的外角为:360°÷6=60°,故正六边形的内角为180°-60°=120°,又正六边形的一个内角是正n边形一个外角的4倍,∴正n边形的外角为30°,∴正n边形的边数为:360°÷30°=12.故答案为:12.【点睛】本题考查了正多边形的外角与内角的知识,熟练掌握正多边形的内角和和外角和定理是解决此类题目的关键.题型四多边形截角后内角和变化在多边形中,截去一角后内角和变化分三种情况讨论;第一种情况,被截去三角形含原多边形1个顶点,内角和为(n+1-2)×180°;第二种情况,被截去三角形含原多边形2个顶点,内角和为(n-2)×180°;第三种情况,被截去三角形含原多边形3个顶点,内角和为(n-1-2)×180°例4:一个五边形切去一个角后,形成的另一个多边形的内角和为().A .360°B .540°C .720°D .360°或540°或720°【解析】一个五边形切去一个角后,第一种情况,被截去三角形含原五边形1个顶点,新多边形内角和为(n +1-2)×180°=720°;第二种情况,被截去三角形含原五边形2个顶点,新多边形内角和为(n -2)×180°=540°;第三种情况,被截去三角形含原多边形3个顶点,新多边形内角和为(n -1-2)×180°=360°综上,形成的另一个多边形的内角和为360°或540°或720°.变式4.一个多边形截去一个角后,形成另一个多边形的内角和为2520°,则原多边形的边数是()A.17B.16C.15D.16或15或17【答案】D【解析】【详解】多边形的内角和可以表示成()2180n -⋅︒(3n ≥且n 是整数),一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条,根据()21802520,n -⋅︒= 解得:n =16,则多边形的边数是15,16,17.故选D .题型五多边形对角线条数问题在多边形中,从一个顶点发出的对角线条数为(n 为大于3的整数),多边形对角线总条数为n ×(n-3)÷2例5:一个多边形的内角和与外角和相等,则这个多边形的对角线条数是___________.【解析】设多边形的边数为n,根据题意(n-2)•180°=360°,解得n=4.则四边形的对角线为(3)412 22n n-⨯==.变式5.一个多边形对角线的条数与它的边数相等,这个多边形的边数是_____.【答案】5【解析】【分析】可根据多边形的对角线与边的关系列方程求解.【详解】设多边形有n条边,则()32n n-=n,n(n−3)−2n=0n(n−5)=0解得n1=5,n2=0(舍去),故多边形的边数为5.故答案为5.【点睛】此题考查多边形的对角线,解题关键在于掌握运算公式.实战练6.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是()A.16B.17C.18D.19【答案】A【解析】【详解】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n-1)边形.故当剪去一个角后,剩下的部分是一个18边形,则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.【点睛】此题主要考查了多边形,减去一个角的方法可能有三种:经过两个相邻点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条. 7.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是()A.三角形B.四边形C.五边形D.六边形【答案】D【解析】【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n-1)边形,由此即可解答.【详解】当剪去一个角后,剩下的部分是一个四边形,则这张纸片原来的形状可能是四边形或三角形或五边形,不可能是六边形.故选D.【点睛】剪去一个角的方法可能有三种:经过两个相邻顶点,则少了一条边;经过一个顶点和一边,边数不变;经过两条邻边,边数增加一条.8.如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是()A.100米B.110米C.120米D.200米【答案】A【解析】【分析】根据多边形的外角和即可求出答案.【详解】解:∵360÷36=10,∴他需要走10次才会回到原来的起点,即一共走了10×10=100米.【点睛】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360º.9.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于()A.108°B.90°C.72°D.60°【答案】C【解析】【分析】首先设此多边形为n边形,根据题意得:180(n-2)=540,即可求得n=5,再由多边形的外角和等于360°,即可求得答案.【详解】解:设此多边形为n边形,根据题意得:180(n-2)=540,解得:n=5,∴这个正多边形的每一个外角等于:3605=72°.故选C.【点睛】此题考查了多边形的内角和与外角和的知识.注意掌握多边形内角和定理:(n-2)•180°,外角和等于360°.10.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是_____度.【答案】540【解析】【详解】【分析】利根据题意得到2条对角线将多边形分割为3个三角形,然后根据三角形内角和可计算出该多边形的内角和.【详解】从某个多边形的一个顶点出发的对角线共有2条,则将多边形分割为3个三角形.所以该多边形的内角和是3×180°=540°,故答案为540.【点睛】本题考查了多边形的内角和与对角线,熟知n边形从一个顶点出发的对角线将n边形分成(n-2)个三角形是关键.这里体现了转化的数学思想.11.如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是_____.【答案】40°【解析】【详解】【分析】根据外角的概念求出∠ADC的度数,再根据垂直的定义、四边形的内角和等于360°进行求解即可得.【详解】∵∠ADE=60°,∴∠ADC=120°,∵AD⊥AB,∴∠DAB=90°,∴∠B=360°﹣∠C﹣∠ADC﹣∠A=40°,故答案为40°.【点睛】本题考查了多边形的内角和外角,掌握四边形的内角和等于360°、外角的概念是解题的关键.12.如图,AC是正五边形ABCDE的一条对角线,则∠ACB=_____.【答案】36°【解析】【分析】由正五边形的性质得出∠B=108°,AB=CB,由等腰三角形的性质和三角形内角和定理即可得出结果.【详解】∵五边形ABCDE是正五边形,∴∠B=108°,AB=CB,∴∠ACB=(180°﹣108°)÷2=36°;故答案为36°.13.如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是__________.【答案】180°或360°或540°【解析】【详解】分析:剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个,根据多边形的内角和定理即可求解.详解:n边形的内角和是(n-2)•180°,边数增加1,则新的多边形的内角和是(4+1-2)×180°=540°,所得新的多边形的角不变,则新的多边形的内角和是(4-2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4-1-2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°.故答案为540°或360°或180°.点睛:本题主要考查了多边形的内角和的计算公式,理解:剪掉一个多边形的一个角,则所得新的多边形的角可能增加一个,也可能不变,也可能减少一个,是解决本题的关键.14.如果一个多边形的内角和为1260°,那么这个多边形的一个顶点有____条对角线.【答案】6【解析】【分析】首先根据多边形内角和公式可得多边形的边数,再计算出对角线的条数.【详解】解:设此多边形的边数为x,由题意得:(x-2)×180=1260,解得;x=9,从这个多边形的一个顶点出发所画的对角线条数:9-3=6,故答案为:6.【点睛】此题主要考查了多边形的内角和计算公式求多边形的边数,关键是掌握多边形的内角和公式180(n-2).15.已知一个多边形的内角和与一个外角的差为1560°,求这个多边形的边数和这个外角的度数.【答案】11,60°.【解析】【分析】根据n 边形的内角和定理可知:n 边形内角和为(n-2)×180°.设这个内角度数为x 度,利用方程即可求出答案.【详解】解:设这个内角度数为x ,根据题意,得(n-2)×180°-(180-x )=1560°,解得:x=1560°-180°n+540°=2100°-180°n ,由于0180<<x ,即0<2100°-180°n<180°,解得:22101133n <<,所以n=11.将n=11代入x=2100°-180°n 中得:x=120°,所以这个外角为180°-120°=60°.故多该多边形的边数是11,这个外角的度数为60°.【点睛】本题主要考查了多边形的内角和定理.掌握n 边形的内角和为180°(n-2)是解答本题的关键.培优练16.(1)填表:n (凸多边形的边数)345…m (凸多边形中角度等于135°的内角个数的最大值)…(2)猜想给定一个正整数n ,凸n 边形最多有m 个内角等于135°,则m 与n 之间有怎样的关系?(3)取n =7验证你的猜想是否成立?如果不成立,请给出凸n 边形中最多有多少个内角等于135°?并说明理由.【答案】(1)1,2,3;(2)m =n ﹣2;(3)不成立,当3≤n ≤5时,凸n 边形最多有n ﹣2个内角等于135°;当6≤n ≤7时,凸n 边形最多有n ﹣1个内角等于135°;当n=8时,凸n边形最多有8个内角等于135°;当n>8时,凸n边形最多有7个内角等于135°,理由见解析【解析】【分析】(1)根据三角形、四边形、五边形的内角和,可求得答案;(2)根据(1)可猜想凸n边形中角度等于135°的内角个数的最大值为:n﹣2;(3)设凸n边形最多有m个内角等于135°,则每个135°内角的外角都等于45°,由凸n边形的n个外角和为360°,分类讨论,可确定凸n边形中最多有多少个内角等于135°.【详解】解:(1)∵三角形中只有一个钝角,∴三边形中角度等于135°的内角个数的最大值为1;∵四边形的内角和为360°,∴四边形中角度等于135°的内角个数的最大值为2;∵五边形的内角和为540°,∴五边形中角度等于135°的内角个数的最大值为3;答案:1,2,3;(2)由(1)得:凸n边形中角度等于135°的内角个数的最大值为:n﹣2.即m=n﹣2;(3)取n=7时,m=6,验证猜想不成立;设凸n边形最多有m个内角等于135°,则每个135°内角的外角都等于45°,∵凸n边形的n个外角和为360°,∴k≤36045=8,只有当n=8时,m才有最大值8,讨论n≠8时的情况:(1)当时n>8,m的值是7;(2)当n=3,4,5时,m的值分别为1,2,3;(3)当n=6,7时,m的值分别为5,6;综上所述,当3≤n≤5时,凸n边形最多有n﹣2个内角等于135°;当6≤n≤7时,凸n 边形最多有n﹣1个内角等于135°;当n=8时,凸n边形最多有8个内角等于135°;当n>8时,凸n边形最多有7个内角等于135°.【点睛】此题考查了多边形的内角和与外角和的知识.此题难度较大,注意掌握分类讨论思想的应用是解此题的关键.。
多边形和内角和知识点及练习

多边形和内角和知识点及练习知识点一、多边形及其相关概念(1)多边形的概念:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.(2)多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.(3)正多边形的概念:各个角都相等,各条边都相等的多边形叫做正多边形.(4)多边形的内角:多边形相邻两边组成的角叫做它的内角.(5)多边形的外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角. (6)正多边形的定义:边、角都相等的多边形才是正多边形知识点二、多边形的分类多边形可分为凸多边形和凹多边形,辨别凸多边形可用两种方法:①画多边形任何一边所在的直线整个多边形都在此直线的同一侧;②每个内角的度数均小于180°,通常所说的多边形指凸多边形.知识点三、多边形相关公式巩固练习1.下面图形是多边形的是()A B C D2.下列是正多边形的是()A.三条边都相等的三角形 B.四个角都是直角的四边形C.四条边都相等的四边形 D.六条边都相等的六边形3. 在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形()A.5 个 B.6 个 C.7 个 D.8 个4. 从十二边形的一个顶点画出所有的对角线,对角线的条数为()A.12 B.11 C.10 D.95. 从多边形的一个顶点出发,可以引出 2003 条对角线,则这个多边形的边数为()A.2001 B.2005 C.2004 D.20066.把一个多边形纸片沿一条直线截下一个三角形后,变成一个 7 边形,则原多边形纸片的边数不可能是()A.6 B.7 C.8 D.97.若一个多边形截去一个角后,变成十五边形,则原来的多边形的边数可能为()A.14 或 15 或 16 B.15 或 16C.14 或 16 D.15 或 16 或 178. 下列说法:①正多边形的各边都相等;②各边都相等的多边形是正方形;③各角都相等的多边形一定是正多边形;④正多边形的各个外角都相等.其中结论正确的个数有()A.1个B.2个C.3个D.4个9.已知一个多边形的内角和是 1080°,则这个多边形是()A.六边形 B.七边形 C.八边形 D.九边形10.下列关于多边形的说法不正确的是()A.内角和与外角和相等的多边形是四边形B.七边形的内角和为 900°C.多边形的内角中最多有四个直角D.十边形共有 40 条对角线11. 正多边形的一个内角是144°,则该正多边形的边数为()A.7B.8C.9D.1012. 一个正n边形的每个外角为72°,则这个正n边形的所有对角线的条数为()A.3B.4C.5D.613. 一个正多边形的内角和是720°,则这个多边形的每个外角等于()A.60°B. 72°C.90°D.108°14.一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为 1800°,则原多边形的边数为()A.11 B.12 C.13 D.11 或 1215.如图,五边形 ABCDE 中,AB∥CD,∠1.∠2.∠3 分别是∠BAE.∠AED.∠EDC 的外角,若∠1=32°,∠3=60°,则∠2 等于()A.92° B.88° C.98° D.无法确定二、填空题16.若凸 n 边形的每个外角都是 30°,则从一个顶点出发引的对角线条数是_________17. 若凸 n 边形的每个外角都是 60°,则n边形对角线条数是_________18. 如果多边形的每个内角都比它相邻的外角的 4 倍多30°,则这个多边形的内角和____19. 一个多边形的对角线的条数等于它的边数的4倍,则这个多边形的边数是_________20. 八边形的对角线条数为____________,内角和为__________21. 正十四边形的内角和为___________,外角和为___________三、解决问题22.分别求出图(1),(2),(3)中x的值23.一个多边形的内角和与外角和相加是 1620°,求这个多边形的边数.24.一个多边形,除一个内角外,其余各内角之和等于 2020°,求这个内角的度数及多边形的边数.25.已知两个多边形内角和相加的结果为1440°,这两个多边形的比为 1:3(1)求两个多边形的边数分别是多少;(2)求两个多边形的对角线的和是多少拓展拔高题1.如图所示,从 O 点出发,沿直线前进 10 米后左转 36°,再沿直线前进 10 米,又向左转 36°,…,照这样走下去,他第一次回到出发地 A 点时,一共走的路程是()A.100 米 B.120 米C.130 米 D.140 米2.求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的值.3.解答下列问题(1)如图①,求证:∠A+∠B=∠C+∠D.(2)如图②,求证:∠A+∠B+∠C=∠BDC.(3)如图③,则:∠A+∠B+∠C+∠D+∠E=_________ (4)如图④,则:∠A+∠B+∠C+∠D+∠E+∠F= _________ (5)如图⑤,则:∠A+∠B+∠C+∠D+∠E= _________ (6)如图⑥,则:∠A+∠B+∠C+∠D+∠E+∠F= _________。
多边形的认识知识点

多边形的认识知识点
以下是 7 条关于多边形的认识知识点:
1. 多边形是由好多条线段首尾相连组成的图形呢!比如说三角形,它可是多边形家族里最简单的啦!就像我们用积木搭成的小房子的屋顶,那就是三角形的形状呀!
2. 嘿,多边形的边数可不一样哦!四边形就有四条边,像我们平时玩的飞盘不就是四边形嘛!它比三角形可就复杂一些了呢,多了一条边呢,是不是很神奇!
3. 多边形还有角呢!每个角都有它的特点。
你看长方形的四个角都是直角,这就像桌子的四个角一样直直的,多规整呀!
4. 很多多边形组合在一起能变成更漂亮更有趣的形状哦!就像拼图一样,把三角形和四边形拼在一起,哇,能出来一个全新的图形,多有意思呀!
5. 多边形的周长你知道是什么吗?就是绕着它一圈的长度呀!比如正方形,你量量它四条边加起来就是周长啦,就像给多边形围了一圈绳子一样呢!
6. 面积也是多边形的重要方面哦!三角形的面积和四边形的面积计算方法都不一样呢,这就好像不同口味的糖果有不同的甜美度,是不是很有趣呐!
7. 多边形里面还有正多边形呢,它们的边和角都相等,很整齐的哦!像正六边形,不就像蜂巢的一格一格嘛!多奇妙呀!
我的观点结论就是:多边形的世界丰富多彩,等着我们去深入探索和发现它们的奇妙之处呢!。
多边形知识点及经典习题

多边形一. 考点:三角形的角度,边长关系,内角和与外角和,用正多边形铺设地板 二. 热点:内角和与外角和 三. 知识讲解★★★主要知识点:1、三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、三角形的分类.⎪⎩⎪⎨⎧钝角三角形直角三角形锐角三角形⎪⎪⎩⎪⎪⎨⎧)(等边三角形等腰三角形不等边三角形 3、一般三角形的性质(1)三角形的内角和定理及性质 定理:三角形的内角和等于180°. 推论1:直角三角形的两个锐角互补。
推论2:三角形的一个外角等于不相邻的两个内角的和。
推论3:三角形的一个外角大于与它不相邻的任何一个内角。
(2)三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边.(3)边与角的大小对应关系:在一个三角形中,等边对等角;等角对等边。
(4) 三角形具有稳定性(5)三角形的主要线段的性质(见下表):(1)三角形共有三条中位线,并且它们又重新构成一个新的三角形。
(2)要会区别三角形中线与中位线。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的作用: 位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
常用结论:任一个三角形都有三条中位线,由此有:名称基本性质角平分线①三角形三条内角平分线相交于一点(内心);内心到三角形三边距离相等;②角平分线上任一点到角的两边距离相等。
中线 三角形的三条中线相交于一点。
(重心);性质:到顶点的距离等于到对边中点的距离的2倍。
高 三角形的三条高相交于一点。
(垂心)边的垂直平分线 三角形的三边的垂直平分线相交于一点(外心);外心到三角形三个顶点的距离相等。
中位线连接三角形两边中点的线段是三角形的中位线;性质:中位线平行第三边并且等于第三边的一半三角形 (按角分) 三角形 (按边分)C结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
正多边形模型总结及经典练习题

正多边形模型总结及经典练习题
正多边形是一个具有相等边长和相等内角的多边形。
在几何学中,正多边形是非常重要的概念,它有许多有趣的性质和应用。
在本文档中,我们将总结正多边形的特点,并提供一些经典的练题来加深研究。
正多边形的特点
正多边形具有以下特点:
1. 边长相等:正多边形的每条边都具有相同的长度。
2. 内角相等:正多边形的每个内角都具有相同的大小。
3. 外角相等:正多边形的每个外角都具有相同的大小。
4. 中心对称:正多边形以中心为对称轴,对称的各个部分完全相同。
经典练题
以下是一些经典的正多边形练题,供大家练和巩固所学知识:
1. 一个正三角形的内角和是多少?
2. 一个正五边形的外角和是多少?
3. 如果一个正七边形的边长是5厘米,它的周长是多少?
4. 一个正十边形的内角和是多少?
5. 如果一个正十二边形的外角是30度,它的内角是多少度?
希望通过对以上练题的思考和求解,能够加深对正多边形的理解和掌握。
以上就是对正多边形模型的总结及经典练习题的介绍。
希望本文档能够帮助大家更好地理解和运用正多边形的概念。
如果有任何疑问或需要进一步的解释,请随时向我提问。
谢谢!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多边形一. 考点:三角形的角度,边长关系,内角和与外角和,用正多边形铺设地板 二. 热点:内角和与外角和 三. 知识讲解★★★主要知识点:1、三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2、三角形的分类.⎪⎩⎪⎨⎧钝角三角形直角三角形锐角三角形⎪⎪⎩⎪⎪⎨⎧)(等边三角形等腰三角形不等边三角形 3、一般三角形的性质(1)三角形的内角和定理及性质 定理:三角形的内角和等于180°. 推论1:直角三角形的两个锐角互补。
推论2:三角形的一个外角等于不相邻的两个内角的和。
推论3:三角形的一个外角大于与它不相邻的任何一个内角。
(2)三角形的三边关系:三角形任意两边之和大于第三边,任意两边之差小于第三边.(3) (4) 三角形具有稳定性(5)(见下表):(1)三角形共有三条中位线,并且它们又重新构成一个新的三角形。
(2)要会区别三角形中线与中位线。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
三角形中位线定理的作用: 位置关系:可以证明两条直线平行。
数量关系:可以证明线段的倍分关系。
三角形 (按角分) 三角形 (按边分)常用结论:任一个三角形都有三条中位线,由此有:结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形。
结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论5:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等。
3. 几种特殊三角形的特殊性质 1、等腰三角形的性质(1)等腰三角形的性质定理及推论:定理:等腰三角形的两个底角相等(简称:等边对等角)推论1:等腰三角形顶角平分线平分底边并且垂直于底边。
即等腰三角形的顶角平分线、 底边上的中线、底边上的高重合。
(三线合一)这条线段所在的直线是等腰三角 形的对称轴。
推论260°。
(1)直角三角形的特殊性质:A/直角三角形的两个锐角互为余角;B/在直角三角形中如果 有一个角等于30°,那么这个角的对边等于斜边的一半;如果有一条边等于另一条边的一半,那么这条边所对的角等于30°。
C/直角三角形斜边上的中线等于斜边的一半D/直角三角形两直角边a ,b 的平方和等于斜边c 的平方,即222c b a =+4. 三角形的面积一般三角形:S △ = 21a h ( h 是a 边上的高 )4、多边形、1、任意多边形的外角和恒为360°2、多边形及多边形的对角线①正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.②凸凹多边形:画出多边形的任何一条边所在的直线,若整个图形都在这条直线的同一侧,这样的多边形称为凸多边形;,若整个多边形不都在这条直线的同一侧, 称这样的多边形为凹多边形。
③多边形的对角线的条数:A.从n 边形的一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
B.n 边形共有2)3(-n n 条对角线。
9、边形的内角和公式及外角和①多边形的内角和等于(n-2)×180°(n ≥3)。
②多边形的外角和等于360°。
10、平面镶嵌及平面镶嵌的条件。
①平面镶嵌:用形状相同或不同的图形封闭平面,把平面的一部分既无缝隙,又不重叠地全部覆盖。
②平面镶嵌的条件:有公共顶点、公共边;在一个顶点处各多边形的内角和为360°。
A CB 第 8 题DC DB A 第 14 题例1: (基础题)①在△ABC 中,已知∠B = 40°,∠C = 80°,则∠A = (度)②如图,△ABC 中,∠A = 60°,∠C = 50°,则外角∠CBD = 。
③已知,在△ABC 中, ∠A + ∠B = ∠C ,那么△ABC 的形状为( ) A 、直角三角形 B 、钝角三角形 C 、锐角三角形 D 、以上都不对④下列长度的三条线段能组成三角形的是( ) A.3cm ,4cm ,8cm B.5cm ,6cm ,11cm C.5cm ,6cm ,10cm D.3cm ,8cm ,12cm⑤如果一个三角形的三边长分别为x ,2,3,那么x 的取值范围是 。
⑥小华要从长度分别为5cm 、6cm 、11cm 、16cm 的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒的长度分别是_ .⑦已知等腰三角形的一边长为6,另一边长为10,则它的周长为⑧在△ABC 中,AB = AC ,BC=10cm,∠A = 80°,则∠B = ,∠C = 。
BD=______,CD=________⑨如图,AB = AC ,BC ⊥ AD ,若BC = 6,则BD = 。
例3: (提高)①△ABC 中,∠C=90°,∠B-2∠A=30°,则∠A= ,∠B=③在等腰三角形中,一个角是另一个角的2倍,求三个角?_______________________ ④:在等腰三角形中,,周长为40cm,一个边另一个边2倍,求三个边?_________________例6.ABC 为等边三角形,D 是AC 中点,E 是BC 延长线上一点,且CE = 21BC求证: BD = DE一、选择题:等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为( ) A.150° B.80° C.50°或80° D.70°2. 在△ABC 中, ∠A =50°, ∠B ,∠C 的角平分线相交于点O ,则∠BOC 的度数是( ) A . 65° B . 115° C . 130° D . 100°3.如图,如果∠1=∠2=∠3,则AM 为△AN 为△ 的角平分线。
三、解答题:14、如图4,∠1+∠2+∠3+∠4= 度;15、如图;ABCD 是一个四边形木框,为了使它保持稳定的形状,需在AC 或BD 上钉上一根木条,现量得AB=80㎝,BC=60㎝,CD=40㎝,AD=50㎝,试问所需的木条长度至少要多长?16、图1-4-27,已知在△ABC 中,AB=AC ,∠A=40°, ∠ABC 的平分线BD 交AC 于D. 求:∠ADB 和∠CDB 的度数. .18。
已知等腰三角形的周长是25,一腰上的中线把三角形分成两个,两个三角形的周长的差是4。
求等腰三角形各边的长。
23.、如图,BE 、CD 相交于点A ,CF 为∠BCD 的平分线,EF 为∠BED 的平分线。
试探求∠F 与∠B 、∠D 之间的关系,并说明理由。
例1、填空:(6)正二十边形的每个内角都等于 。
(7)一个多边形的内角和为1800°,则它的边数为 。
(8)n 多边形的每一个外角是36°,则n 是 。
(9)多边形的每一个内角都等于150°,则从此多边形一个顶点出发引出的对角线有 条。
(10)如果把一个多边形截去一个三角形,剩下的多边形的内角和是2160°,那么原来的多边形的边数是 。
(11)一多边形除一内角外,其余各内角之和为2570°,则这个内角等于 。
AE FD C BA与三角形有关的线段一、 三角形的基本概念:⑴三角形的定义:由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形.三角形具有稳定性.⑵三角形的内角:三角形的每两条边所组成的角叫做三角形的内角.在同一个三角形内,大边对大角.⑶三角形的外角:三角形的任意一边与另一边的反向延长线所组成的角叫做三角形的外角. ⑷三角形的分类:()()():⎧⎪⎧⎨⎨⎪⎩⎩⎧⎪⎧⎨⎨⎪⎩⎩直角三角形:三角形中有一个角是直角三角形按角分锐角三角形:三角形中三个角都是锐角斜三角形钝角三角形:三角形中有一个角是钝角不等边三角形:三边都不相等的三角形三角形按边分底边和腰不相等的等腰三角形:有两条边相等的三角形等腰三角形等边三角形正三角形有三边相等的三角形注意:每个三角形至少有两个锐角,而至多有一个钝角.三角形的三个内角中,最大的一个内角是锐角(直角或钝角)时,该三角形即为锐角三角形(直角三角形或钝角三角形).二、 与三角形相关的边⑴三角形中的三种重要线段①三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.注:每个三角形都有三条角平分线且相交于一点,这个点叫做三角形的内心,而且它一定在三角形内部.②三角形的中线:在三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线. 注:每个三角形都有三条中线,且相交于一点,这个点叫做三角形的中心,而且它一定在三角形内部.③三角形的高:从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线. 注:每个三角形都有三条高且三条高所在的直线相交于一点,这个点叫做三角形的垂心. 锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部;钝角三角形的高线中有两个垂足落在边的延长线上,这两条高落在三角形的外部,直角三角形有两条高分别与两条直角边重合.反之也成立.画三角形的高时,只需要向对边或对边的延长线作垂线,连接顶点与垂足的线段就是该边的高. ⑵三角形三条边的关系①三角形三边关系:三角形任何两边的和大于第三边.②三角形三边关系定理的推论:三角形任何两边之差小于第三边.即a 、b 、c 三条线段可组成三角形⇔b c a b c -<<+⇔两条较小的线段之和大于最大的线段.注意:在应用三边关系定理及推论时,可以简化为:当三条线段中最长的线段小于另两条线段之和时,或当三条线段中最短的线段大于另两条线段之差时,即可组成三角形.一.三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )A.2个B.3个C.4个D.5个二、为解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路.现已知这四个村庄及电厂之间的距离如图所示(距离单位:公里),则能把电力输送到这四个村庄的输电线路的最短总长度应该是( )A.19.5B.20.5C.21.5D.25.5三、下列长度的三条线段,不能组成三角形的是( )A.3,8,4B.4,9,6C.15,20,8D.9,15,8为估计池塘两岸A 、B 间的距离,杨阳在池塘一侧选取了一点P ,测得16PA =m ,12PB =m ,那么AB 间的距离不可能是( )A.5mB.15mC.20mD.28m四、如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依次类推,则第6个图中共有三角形 _________ 个.11 6.55.59678854电厂DCAB五、已知三角形的两边为8、10,求第三边的范围,求周长的范围.六、下列长度的三条线段能组成三角形的是( )A.1cm,2cm,5cm B.4cm,5cm,9cmC.5cm,8cm,15cm D.6cm,8cm,9cm11、已知三角形的三边长分别为4、5、x,则x不可能是( )A.3B.5C.7D.14、已知三角形中两边长为2和7,(1)若第三边长为奇数,则这个三角形的周长为_________.(2)若这个三角形的周长为奇数,则第三边长为_________.15、有三条线段,其中两条线段的长为3和5,第三条线段的长为x,若这三条线段不能构成三角形,则x的取值范围是.16、已知ABC<,则其周长l一定满足( ).∆有两边长为a、b,其中a bA.22()b l a b<<+B.22<<+a l a b<<C.a l a b<<+D.2a l b--+--+--,若此三角形周长为11,求上面17、a、b、c为三角形的三边长,化简a b c b c a c a b式子的值.18、下列长度的线段能否组成三角形:23a+(0a+、24a+、27a≠);21、周长为整数的三角形三边长分别为3、4、x ,且x 满足不等式12327x x ->⎧⎨<⎩,这样的三角形有 个.22、如图,在ABC ∆中取一点P ,使CP CB =,求证:AB AP >.已知,如图,P Q ,为三角形ABC 内两点,B P Q C ,,,构成凸四边形,求证:AB AC BP PQ QC +>++.多边形的内角和与外角和1.n 边形的内角和=________度,外角和=_______度。
